Robustness in Escherichia coli Glutamate and Glutamine Synthesis Studied by a Kinetic Model

Abstract

Metabolic control of glutamine and glutamate synthesis from ammonia and oxoglutarate in Escherichia coli is tight and complex. In this work, the role of glutamine synthetase (GS) and glutamate dehydrogenase (GDH) regulation in this control was studied. Both enzymes form a linear pathway, which can also have a cyclic topology if glutamate–oxoglutarate amino transferase (GOGAT) activity is included. We modelled the metabolic pathways in the linear or cyclic topologies using a coupled nonlinear differential equations system. To simulate GS regulation by covalent modification, we introduced a relationship that took into account the levels of oxoglutarate and glutamine as signal inputs, as well as the ultrasensitive response of enzyme adenylylation. Thus, by including this relationship or not, we were able to model the system with or without GS regulation. In addition, GS and GDH activities were changed manually. The response of the model in different stationary states, or under the influence of N-input exhaustion or oscillation, was analyzed in both pathway topologies. Our results indicate a metabolic control coefficient for GDH ranging from 0.94 in the linear pathway with GS regulation to 0.24 in the cyclic pathway without regulation, employing a default GDH concentration of 8 μM. Thus, in these conditions, GDH seemed to have a high degree of control in the linear pathway while having limited influence in the cyclic one. When GS was regulated, system responses to N-input perturbations were more sensitive, especially in the cyclic pathway. Furthermore, we found that effects of regulation against perturbations depended on the relative values of the glutamine and glutamate output first-order kinetic constants, which we named k₆ and k₇, respectively. Effects of regulation grew exponentially with a factor around 2, with linear increases of (k₇ − k₆). These trends were sustained but with lower differences at higher GS concentration. Hence, GS regulation seemed important for metabolic stability in a changing environment, depending on the cell’s metabolic status.

Introduction

The biosynthesis of glutamate (E) and glutamine (Q) from NH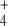 as N-source and 2-oxoglutarate (OG) as C-skeleton source in prokaryotes holds a key position among meta-/break bolic processes. It links N incorporation to all cellular components with tricarboxylic acids cycle, a main pathway for aerobic energy production and C-skeleton synthesis for diverse biological compounds. Therefore, regulation of this N-assimilatory pathway must be very accurate in order to preserve the necessary balance among the cell’s C, N and energy demands.

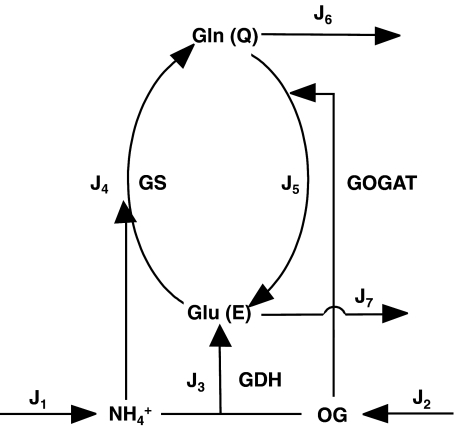
In Escherichia coli, three enzymes catalyze the reactions of this pathway (Fig. 1). Glutamate dehydrogenase (GDH, EC 1.4.1.4) catalyzes the reductive amination of OG with NH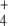 to give E in a single step using nicotinamide adenosine dinucleotide phosphate (NADPH) as electron donor. This enzyme has relatively high K_M values for both substrates. Furthermore, glutamine synthetase (GS, EC 6.3.1.2) uses E and a second NH 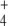molecule to produce Q, consuming 1 mol of adenosine triphosphate (ATP) per mole of Q produced. On the other hand, GS integrates a cycle with glutamine–oxoglutarate amino transferase (GOGAT, EC 1.4.1.13, also known as glutamate synthase), which also produces E, this time using Q and OG as substrates. Hence, E biosynthesis can be achieved in two ways: GDH reaction or GS/GOGAT cycle, while Q may be synthesized in a linear GDH-GS pathway, or it can also be obtained from the GS/GOGAT cycle. Therefore, for both amino acids, two alternative routes may coexist: a linear pathway with the participation of GDH, or a cyclic pathway with the additional participation of GOGAT. Since E biosynthesis through the cyclic pathway always involves the ATP-consuming GS reaction, this pathway is, in general, more expensive in terms of ATP consumption and, as a whole, possesses lower K_M values for the substrates OG and NH 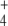(for a review, see [1]).

Fig. 1.

Schematic representation of the E and Q production pathways. In the linear topology, the reaction catalyzed by GOGAT (J₅) was removed

All three enzymes were purified and fully characterized four decades ago, and the control of expression of genes encoding them is also well known. Of particular interest is the complex regulation of GS since, in contrast to the other enzymes in the pathway, it is subjected to allosteric regulation and covalent modification, in addition to gene expression regulation [2]. As in many other examples in metabolism, such a tight regulation of enzyme activity occurs at the energy-consuming step, and thus, this reaction could be a main control point for the whole flux in this pathway.

GS is a dodecamer of 12 identical subunits. Each subunit may be covalently modified by adenylylation at a specific tyrosine residue in response to the intracellular OG/Q (C/N) ratio, the modified subunits becoming inactive. The adenylylation state of each subunit seems not to condition the state of the others, and in this sense, each subunit is modified independently. While low C/N ratios indicate N abundance and promote adenylylayion (inactivation) of GS, high C/N ratios promote GS deadenylylation (activation). Thus, GS-AMP₁₂ can be considered as completely inactive. In addition, adenylylation of each GS subunit renders GS more sensitive to allosteric inhibition by several metabolites, including products of Q metabolism [3, 4]. A recent in silico study of GS regulation indicated that covalent modification accounts for 60% of total regulation and, therefore, can be considered as the main response of the system against changes in C/N ratio [5].

Sensing of C/N ratio for GS adenylylation is carried out by a bicyclic cascade where the protein PII plays a central role [6]. PII is a trimeric protein that may exist in two forms: uridylylated (PII~UMP) or deuridylylated (PII). Uridylylation takes place at each subunit as catalyzed by a urydylyl-transferase/uridylyl-removing enzyme (UT/UR) [7] according to the Q concentration inside the cell: high Q concentrations promote UR, while low Q concentrations promote UT. On the other hand, OG can directly bind to PII depending on the protein uridylylation state. Unmodified PII binds OG to each subunit with negative cooperativity, while PII uridylylation reduces this negative cooperativity, and thus, less OG concentration is required to saturate PII~UMP binding sites [6]. PII is able to interact with another modifying/demodifying enzyme, giving rise to the second step of the cascade. This enzyme has adenylyl-transferase/adenylyl-removing activities (AT/AR), which are exerted on GS. When PII is unmodified and with OG bound to only one subunit, it induces AT activity, thus inactivating GS in response to a low C/N intracellular ratio. Conversely, PII~UMP, with its three subunits saturated with OG, induces AR activity and, therefore, activates GS in response to a high intracellular C/N ratio.

This bicyclic cascade has been proven as robust since variation in the concentration of its components did not alter the response [8, 9]. Although ambiguous modifying enzymes like AT/AR and UT/UR were regarded as lacking ultrasensitivity in their response [8], allosteric regulation in PII and GS seems to provide robustness and ultrasensitivity with a Hill coefficient of around 2 [9].

Regulation of GS has been thought of as a means to ensure Q provision under N scarcity given its low K_M for NH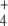 and its increasing activation rate with increases in C/N ratio. However, regulation of this enzyme seems exceedingly complex for that adaptation alone, for which gene regulation would suffice, as is the case with other enzymes catalyzing biosynthesis of elementary biological molecules. Instead, this complex and ultrasensitive regulation might serve to coordinate C and N metabolic demands in a changing environment where supplies of one or both of these nutrients may vary over short time periods.

In addition, the role of superimposed cyclic GS/GOGAT and linear GDH pathways is still unclear. Studies with mutant strains suggested that GDH would be used under nutrient-abundance and energy-limiting conditions since it is able to provide E at a lower ATP expense than the GS-GOGAT pathway [10, 11]. However, both GDH and GOGAT seem to be present at the same time, and therefore, both enzymes compete for OG. Since GOGAT has a K_M ~100 times lower for this metabolite, OG concentration should be, in principle, quite high for significant GDH activity (Fig. 1). GDH is also placed at the beginning of both pathways. In other metabolic pathways, the total activity of the first enzyme in the pathway may exert a significant control on pathway flux. However, no studies were carried out to assess the possible control ability of GDH.

Here, we tried to better understand the role of GS regulation and GDH activity in the metabolic control of this pathway under changing C and N availabilities, as well as how the simultaneous presence of GDH and GOGAT might affect E and Q production. To this end, we developed a kinetic model where regulated and unregulated GS enzymes were compared, GDH amounts were varied, and different pathway topologies exchanging mass with the exterior were used (Fig. 1). We focused our study of GS regulation on covalent modification ultrasensitivity by applying a relation that estimates the mean fraction of adenylylated GS subunits per dodecamer [9]. This relation considers intracellular concentrations of OG and Q as input variables. Therefore, we could not apply the above-mentioned in silico model to evaluate the effects of GS covalent modification under nonstationary state conditions because, in that model, OG and NH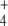 concentrations were held fixed [5]. Therefore, we developed a simpler and more restricted model that considered only GS covalent modification for GS regulation, and all metabolite concentrations were allowed to vary.

Materials and Methods

Pathway Topology and Stoichiometry

The system outlined in Fig. 1 was employed with two different topologies, namely, the cyclic topology – as in Fig. 1 – or the linear topology—where the reaction catalyzed by GOGAT was removed. Therefore, the pathway can be described in terms of the following stoichiometry equations:

For the cyclic topology (full pathway):

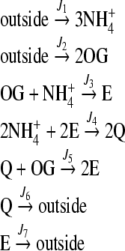For the linear topology (without GOGAT):

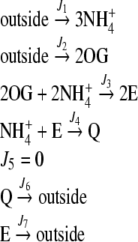The pairs [adenosine diphosphate (ADP) + Pi/ATP] and [NADP⁺ + H⁺/NADPH] were considered as internal to the system, with constant concentrations [9], as follows (in mM): ATP, 5.0; ADP, 1.0; phosphate (Pi), 10.0; NADPH, 0.15; and NADP, 0.05 [5].

Calculation of Fluxes and Metabolite Concentrations

The magnitudes J₃, J₄, and J₅ represent the internal J_i fluxes in the system, whose sum gives:

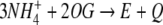which are compensated by the J_e external fluxes J₁, J₂, J₆, and J₇. All J_i values were calculated by applying previously described kinetic equations [5, 12], considering the reactions catalyzed by GDH and GS as reversible, and GOGAT-catalyzed reaction as almost irreversible [13]. Hence, each J_i value was calculated as:

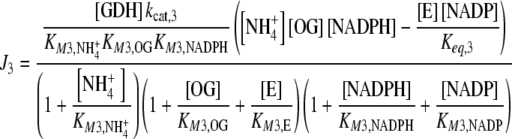1

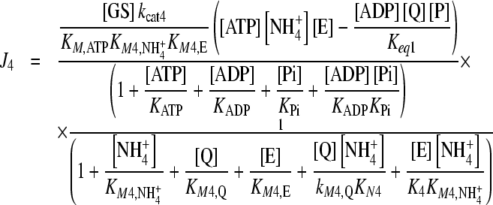2

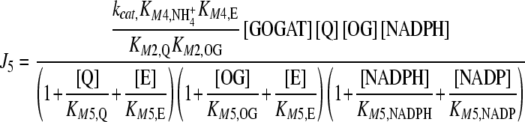3

The input fluxes are defined in Section 3. The output fluxes are defined for both topologies as: 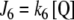, , 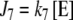where k₆ and k₇ are first-order kinetic constants whose values are defined for each simulation in Section 3.

With these fluxes and stoichiometry relationships, matrices were constructed to obtain a system of coupled differential equations expressing J values as time functions for all metabolite concentrations.

The set of differential equations used to represent the instantaneous concentrations of each metabolite, as well as the internal fluxes, depended on the particular topology. For the cyclic topology, the instantaneous concentrations were calculated by the following differential equations [14–16]:

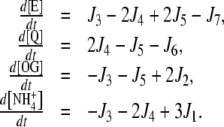In turn, for the linear topology, the instantaneous concentrations were calculated as:

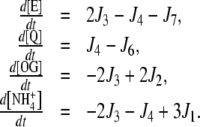Coefficient values used in these equations were obtained from the literature and are listed in Table 1.

Table 1.

Parameters used in this study

Enzyme	Parameter	Value	Reference
GS	Concentration	240 nM	[23]
	kcat	1.6 106 min − 1	[23]
	KM,E	4.1 mM	[5]
	K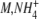	0.1 mM	[5]
	KM,ATP	0.35 mM	[5]
	KM,Q	5.65 mM	[5]
	KM,ADP	0.0585 mM	[5]
	KM,Pi	3.7 mM	[5]
	Keq	460	[5]
GOGAT	Concentration	130 nM	[13]
	kcat	2.1 104 min − 1	[13]
	KM,Q	0.175 mM	[5]
	KM,OG	0.007 mM	[5]
	KM,NADPH	0.0015 mM	[5]
	KM,E	11.0 mM	[5]
	KM,NADP	0.0037 mM	[5]
GDH	Concentration	8,000 nM	[24]
	kcat	5.3 104 min − 1	[24]
	K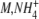	1.1 mM	[5]
	KM,OG	0.32 mM	[5]
	KM,NADPH	0.04 mM	[5]
	KM,E	10.0 mM	[5]
	KM,NADP	0.042 mM	[5]
	Keq	1,290 mM − 1	[5]

Enzyme Regulation

To assess the influence of gene expression on total GDH or GS activity, total enzyme concentrations were changed manually. In addition, total GS activity was associated with the fraction f of adenylylated subunits per dodecamer. For simplicity, we considered each unmodified subunit as fully active, and each adenylylated one as totally inactive.

Values of f were obtained according to Mutalik et al. [9] from the concentrations of OG and Q as:

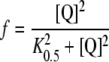4

where K_0.5 represents the half-saturation constant, whose value depends on the OG concentration according to the relationship:

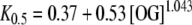5

which was fitted from Fig. 2 in [9].

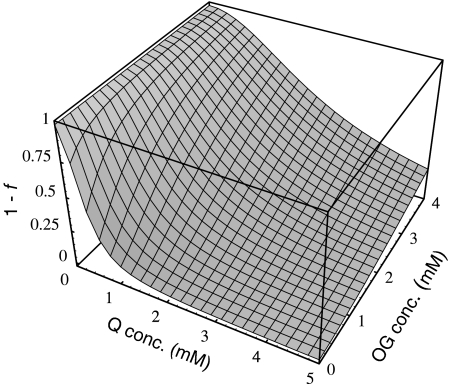
Fig. 2.

Three-dimensional representation of the GS activation state (1− f ) as a function of Q and OG concentrations

Results and Discussion

Regulation of Glutamine Synthetase

Figure 2 displays the 1 − f values (i.e., the fraction of GS activity) obtained for different OG and Q concentrations. To avoid restrictions on K_0.5 values, we developed our differential equation coupled model in a way that OG (as well as NH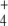) concentration is variable. In addition, the present model did not include subnetworks, given that reactions catalyzed by UT/UR and AT/AR are contained in effective form in Eq. 4, which relates the OG and Q concentrations. This allowed a more direct and simple calculation of regulation effects.

In the following, we will compare the behavior of the systems with regulated or unregulated GS by multiplying or not [GS] by 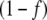. For brevity, we will refer to these cases as regulated and unregulated systems, respectively.

Steady State Fluxes Trough the Regulated and Unregulated Systems

As first approximation, we assessed whether, by maintaining the external fluxes J₁ and J₂ unrestricted and equal to 1 mM min^− 1, and first order output kinetic constants k₆ and k₇ equal to 1 min^− 1, a steady state for the other fluxes and metabolite concentrations was obtained. Under this situation, the magnitude of all internal fluxes J₃, J₄, and J₅, as well as J₆ and J₇ external fluxes, did not change with time, as expected for the steady state regime. We also observed that, for the cyclic topology, internal fluxes J₄ and J₅ were higher in the unregulated system – i.e. when f was set as 0, irrespective of the OG and Q concentrations – than in the regulated system—where the fractional activity of GS was obtained by multiplying J₄ by 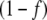. However, J₃ was lower in the unregulated system, in agreement with previous results [5], while external fluxes J₆ and J₇ were almost unchanged between the regulated and unregulated systems. To confirm that these differences were due to GS regulation, we obtained the 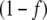value at steady state, which in the present conditions was approximately 0.13. We then multiplied J₄ in the unregulated system by this value and obtained exactly the same curves as in the regulated system. In contrast to the cyclic topology, no flux changes between regulated or unregulated systems were observed for the linear topology.

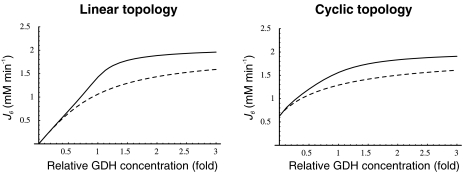
When GDH amounts were varied between 0.1 and 3 times the default concentration, J₆ and J₇ also did not change. Instead, these flux values were very sensitive to changes in the input J₁ and J₂ values. In this sense, almost all flux control is at the substrate inputs. Therefore, this constancy in boundary flux injection [15] could be too stringent for the system to allow some study of the flux control exerted by the enzymes internal to the pathway. To relax this stringency in order to transfer some flux control to J_i, we leave only the limitation that absolute values of J₁ = J₂ = J₇. With this new setting, we again varied the concentration of GDH and studied its effects on J₆ and J₇ in the regulated and unregulated systems, with both pathway topologies. Since both fluxes had exactly the same values, in the following, we show only the results obtained with J₆, because this represents the releasing step in the synthesis of the final product in the linear topology (Fig. 1). Interestingly, as observed in Fig. 3, J₆ was always higher in the regulated system where GS, the enzyme responsible for its synthesis, was 53% inactivated by adenylylation. A higher E concentration is not surprising since it is a substrate of GS, and therefore lowering the enzyme activation state would lead to substrate accumulation. However, the higher Q production is not as predictable, since this amino acid is a product of GS. The higher Q production was due to the combination of higher NH and E concentrations, which more than compensated for the GS partial inactivation, and indeed, it was this inactivation that led to those levels of NH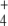 and E concentration rising in the first place. Since this rise was also obtained with different system settings (different GDH concentrations, external kinetic constants, or initial metabolite concentrations), this behavior is a system property and not an outcome obtained by chance with a particular setting. At least part of this system behavior could be attributed to the ultrasensitivity of GS regulation. In this regard, GS regulation potentiates E and Q production even when NH 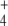influx is not limiting, and the OG/Q relationship is low.

Fig. 3.

J₆ as a function of GDH concentrations, expressed as fold-concentration relative to the default GDH concentration (8 μM) for both pathway topologies. Continuous line, regulated system; dashed line, unregulated system

The flux control coefficient [17] of GDH on J₆ was more than twofold higher in the linear than in the cyclic topology (Table 2), pointing out that (1) the cyclic topology was more robust in maintaining E and Q production levels against small changes in the amount of GDH in the vicinity of its default concentration and (2) pathway control is transferred to GDH when GOGAT activity is omitted. In addition, pathway control by GDH was almost complete in the linear topology at GDH concentrations up to 4 μM, in agreement with a recent study where GOGAT null mutants were spontaneously reverted by GDH expression mutants that accumulated 2–5 times more GDH than the parental strain [18]. Since the GDH default concentration employed by us is quite high (Table 1), such reversion might be explained if the wild-type GDH concentration was around 1–4 μM, considering that regulation operated normally (Fig. 3).

Table 2.

Flux control coefficients of 8 μM GDH on J₆

	GS reg.	GS unreg.
Linear topology	0.94	0.57
Cyclic topology	0.34	0.24

Values for J₇ were exactly the same

As observed in Fig. 3, J₆ values tended to a plateau as GDH concentrations increased. Therefore, we also tested further increases in GDH up to 200 times the default concentration, and confirmed that even at these high GDH values there were no changes in J₆ once the plateau was reached. This behavior indicates that, beyond a GDH concentration threshold, large fluctuations in enzyme amounts can be tolerated by the metabolic network without compromising the balance among metabolic fluxes, especially in the cyclic topology. Bacterial cell cultures are not completely homogeneous even when cells are clonal and culture conditions are held constant [19] . In a study on individual bacterial swimming, it was estimated that protein levels among individual cells may fluctuate 10% around the mean value for the culture [20]. Our results suggest that this observation could be extended to central metabolism as well.

Calculated steady-state NH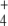, OG, E, and Q concentrations are shown in Table 3. They agree with those previously reported, and interestingly, NH 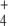and OG concentrations spontaneously tended to similar values as experimental estimates from previous studies of this pathway in wild-type cells under N-limitation [5, 21]. Nevertheless, it has to be kept in mind that this model only deals with the pathway schematized in Fig. 1 and ignores other pathways such as the tricarboxylic acid cycle or the protein degradation and amino acid recycling, both of which also determine the cellular concentrations of OG, E, and Q, or the use of E to balance intracellular K⁺.

Table 3.

Steady state metabolite concentrations (mM) k₆ = 3, k₇ = 1

Metabolite	Linear topology		Cyclic topology
	GS regulated	GS unregulated	GS regulated	GS unregulated
E	1.42	1.06	1.56	1.29
Q	0.47	0.35	0.52	0.43
OG	0.30	0.47	0.23	0.36
NH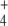	0.02	0.01	0.03	0.01

Initial concentrations E= 1, Q= 1, OG= 1, N= 1

System Responses to Depletion of NH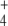 External Concentration

Fluctuations in environmental N source are often experienced by bacteria. Among these fluctuations, source depletion occurs when bacteria grow without a continuous provision of the nutrient. To assess the effects of source depletion caused by bacterial growth, we proposed J₁ as a time function e^− αt where α is the duplication constant, which, for a 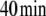duplication time, was 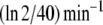. We choose this law for the initial value J_1,0 = 1 mM min^− 1.

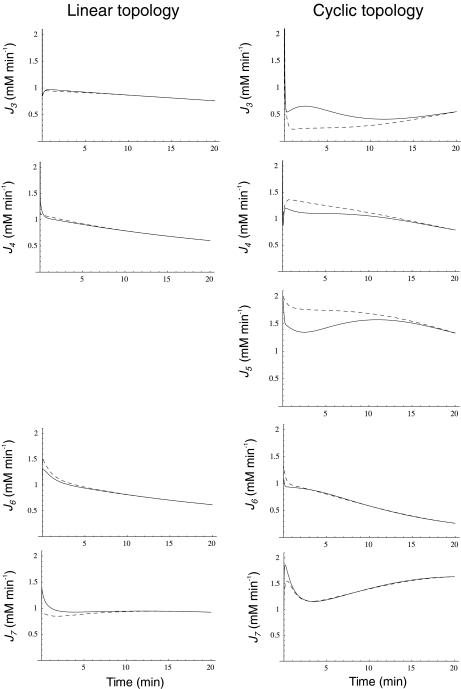
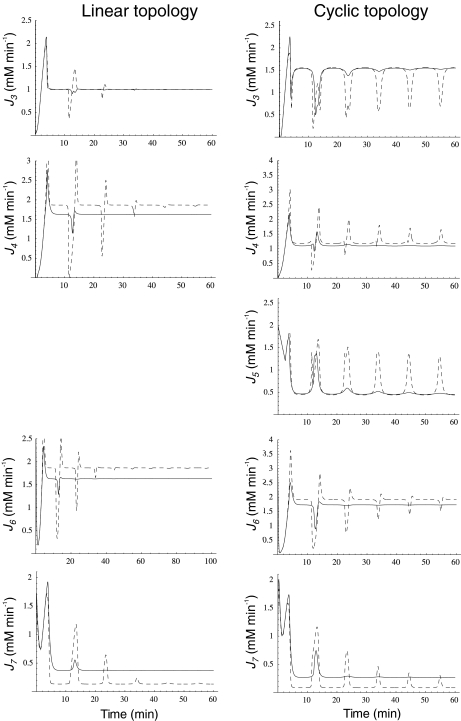
We analyzed the system responses in 20-min simulations, thus encompassing half cell generation at the set duplication time. When the external N-source was decaying and the C-source was maintained unlimited by giving J₂ a constant value of 1 mM min^− 1, differences in internal and external fluxes between regulated and unregulated systems were surprisingly small (not shown). Nevertheless, such differences could be highlighted by diminishing k₆ from 3.0 to 1.0. In the linear topology, J₃ and J₄ diminished, following NH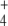 depletion, again with small differences between regulated and unregulated systems (Fig. 4). In contrast, in the cyclic topology, J₃ was higher in the regulated system during the first 20 , while the contrary trend was observed for J₄ and J₅, which were higher in the unregulated system. This result indicates that the regulated system provides a better energy usage for these biosynthetic processes, as suggested by previous physiological experiments [10, 11]. Metabolite export also showed different behaviors. In the unregulated system, J₆ was always a little lower than in the regulated one, while J₇ was higher in the regulated system, for both topologies, both J_e being very similar between linear and cyclic topologies despite the above-mentioned differences in J_i. Differences in J_e between regulated and unregulated systems were smaller in the cyclic topology.

Fig. 4.

J_i and J_e as a function of time when the N-source was diminishing at a rate defined by 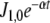for both pathway topologies. Continuous line, regulated system; dashed line, unregulated system

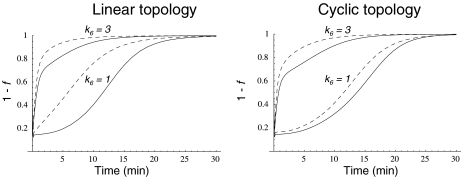
Since these different behaviors between the regulated and unregulated systems depended on the k₆ and k₇ values, we investigated the relationship between these values, the regulation, and the differences in J_i. Regulation kinetics depended on k₆ and k₇ values. For instance, when k₇ was 1, (1 − f ) approached the maximum value of 1 earlier, as k₆ values were higher (Fig. 5). A similar behavior was observed with different k₇ values (not shown). This means that, as long as k₆ is comparatively higher than k₇, Q leaves the system faster, and therefore, its accumulation is lowered, thus increasing the OG/Q relationship earlier. 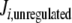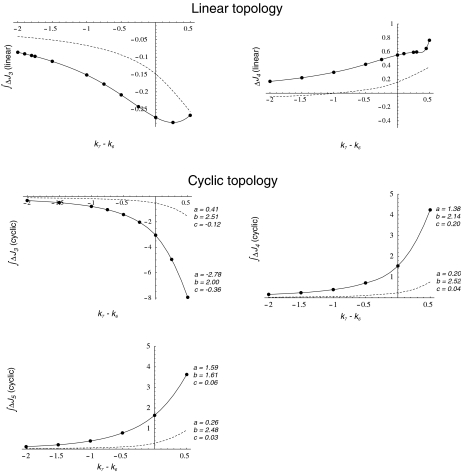To better study this effect on internal J_i fluxes, we integrated the differences between the − 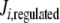(integrated ΔJ_i) for different (k₇ − k₆) values. This study was restricted to a 10-min simulation for the linear and cyclic topologies, since it is during this period that significant regulation takes place (Fig. 5). In Fig. 6, it is shown that differences in J_i between the unregulated and regulated systems were always higher for the cyclic topology, as observed by comparing the scale differences in 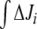axes. Furthermore, the linear topology did not show a defined trend as the cyclic topology did. In the cyclic topology J₃ values were higher for the regulated system, while J₄ and J₅ were always higher for the unregulated one, with these differences approaching minimal but positive values when k₆ exceeded k₇ but exponentially increasing as k₆ approached k₇. By fitting data in Fig. 6, we found that, for the cyclic topology, the relationship between flux differences and (k₇ − k₆) may be represented as:

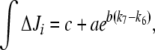6

with b values around 2. This indicated that, for any infinitesimal increment in the difference (k₇ − k₆), the corresponding 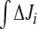was duplicated. Since k₆ and k₇ represent the cellular metabolic demands of Q and E, respectively, this observation indicates that regulation effects depend also on the general metabolic context. In particular, in vivo E concentration was regarded as more than enough to fulfill cell N demands, having an additional role in counterbalancing intracellular K⁺ concentration [22]. If we consider this role of E as an additional output, this might configure a situation where, most frequently, k₇ ≥ k₆, i.e., in the positive range of the (k₇ − k₆) axis.

Fig. 5.

GS fractional activity (1 − f ) due to adenylylation of a fraction f of GS subunits as a function of time when the N-source was diminishing at a rate defined by 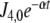for both pathway topologies, with k₇ = 1 and different k₆ values. Continuous line, GS 240 nM; dashed line, GS 2,400 nM

Fig. 6.

Integrated ΔJ_i (in nonregulated minus regulated systems) as function of the difference k₇ − k₆ calculated for the first 10-min simulation, when the N-source was diminishing at a rate defined by 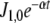. Dots, calculated values from the simulations. Lines, interpolations for the linear topology (upper panel) or resolution of 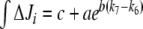for the cyclic topology (lower panel) with values for a, b, and c as indicated. Continuous line, GS 240 nM; dashed line, GS 2,400 nM

Another known effect of N-source depletion in E. coli is stimulation of glnA gene expression [1] whereby GS total concentration rises. To see whether such an enzyme concentration change may affect GS adenylylation effects, we repeated the above studies with 10 times higher total GS concentration (dashed lines in Figs. 5 and 6). After raising GS concentration, we saw that regulation followed the same trend but similar levels of total activation were achieved earlier, both in the linear and cyclic pathways. As a consequence, the response to regulation with different k₆ and k₇ values also followed the same trend as with default GS concentration, but the magnitudes of differences in J_i between unregulated and regulated systems were lowered. Interestingly, in the cyclic topology, the same law fitted the relationship between 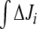and (k₇ − k₆) with b values in the same order as with default GS concentration (Fig. 6).

System Responses to Oscillations in NH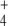 External Concentration

In addition to depletion, the external N source could be perturbed in different ways, for instance, oscillating as a consequence of cycles of nutrient input pulses and/or washes. To introduce oscillations, we multiplied J₁ by 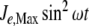, where ω = 0.3, with 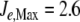, leaving J₂ at a constant value of 1 mM min^− 1.

When external NH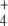 was subjected to oscillation between 0 and 2.6 mM with a period of 10 min, internal and external fluxes varied following N-source oscillations in the unregulated system, while the same fluxes rapidly stabilized after a few oscillations in the regulated system. This trend was more pronounced in the cyclic than in the linear topology (Fig. 7). In the cyclic topology, J₄ and J₅ showed bursts of activity in the unregulated system that coincided with deep valleys in J₃. Thus, regulation avoided these peaks of energy consumption for E synthesis. Furthermore, J₇ tended to almost zero in the unregulated system with both topologies while significant E provision was sustained in the regulated system, with this trend being more remarkable when the difference between k₆ and k₇ decreased, as observed previously for N-depletion (not shown). This behavior of J₇ may be explained by the decreased amount of NH 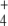consumption by regulated GS, which “keeps” some NH 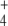from the previous peak in the system, thus controlling the NH 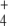availability better during the next valley. Therefore, an important role of GS regulation under conditions of external N-source uncontrolled variation (as should be the most frequent case in natural bacterial environments) might be to control the internal cell availability of NH 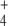as a raw material for amino acid biosynthesis in order to decouple this process from external source fluctuations.

Fig. 7.

J_i and J_e as a function of time when the N-source was oscillating as defined by 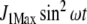where ω = 0.3 for both pathway topologies. Continuous line, regulated system; dashed line, unregulated system

Concluding Remarks

A prominent feature suggested by simulations carried out in this article is that GS regulation provided higher robustness to internal fluxes and outcome external fluxes against changes in enzyme concentrations or N-source perturbations. This was especially important for J₇ when N oscillated (Fig. 7), the unregulated system being very weak in sustaining E production under these conditions. The quality of this regulation seems to reside in the partial inhibition of a highly efficient enzyme (specificity constant for NH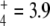 10⁵) through an ultrasensitive mechanism. Both characteristics (enzyme efficiency and ultrasensitivity of the regulation cascade) allow rapid responses to the stimulus.

As a general trend, the responses to N-source perturbations were more important in the cyclic than in the linear topology. In this regard, the GS-GOGAT cycle might add sensitivity to the GS regulation response [17].