A Hierarchical Approach to Cooperativity in Macromolecular and Self-Assembling Binding Systems

Abstract

The study of complex macromolecular binding systems reveals that a high number of states and processes are involved in their mechanism of action, as has become more apparent with the sophistication of the experimental techniques used. The resulting information is often difficult to interpret because of the complexity of the scheme (large size and profuse interactions, including cooperative and self-assembling interactions) and the lack of transparency that this complexity introduces into the interpretation of the indexes traditionally used to describe the binding properties. In particular, cooperative behaviour can be attributed to very different causes, such as direct chemical modification of the binding sites, conformational changes in the whole structure of the macromolecule, aggregation processes between different subunits, etc. In this paper, we propose a novel approach for the analysis of the binding properties of complex macromolecular and self-assembling systems. To quantify the binding behaviour, we use the global association quotient defined as K_c = [occupied sites]/([free sites] L), L being the free ligand concentration. K_c can be easily related to other measures of cooperativity (such as the Hill number or the Scatchard plot) and to the free energies involved in the binding processes at each ligand concentration. In a previous work, it was shown that K_c could be decomposed as an average of equilibrium constants in two ways: intrinsic constants for Adair binding systems and elementary constants for the general case. In this study, we show that these two decompositions are particular cases of a more general expression, where the average is over partial association quotients, associated with subsystems from which the system is composed. We also show that if the system is split into different subsystems according to a binding hierarchy that starts from the lower, microscopic level and ends at the higher, aggregation level, the global association quotient can be decomposed following the hierarchical levels of macromolecular organisation. In this process, the partial association quotients of one level are expressed, in a recursive way, as a function of the partial quotients of the level that is immediately below, until the microscopic level is reached. As a result, the binding properties of very complex macromolecular systems can be analysed in detail, making the mechanistic explanation of their behaviour transparent. In addition, our approach provides a model-independent interpretation of the intrinsic equilibrium constants in terms of the elementary ones.

Introduction

Living organisms exhibit a large variety of macromolecular receptors capable of recognising molecular signals. These ligand-receptor systems are central protagonists of supra-cellular, cellular and subcellular control systems. Macromolecular receptors frequently show complicated binding phenomena. For instance, they can manifest cooperative behaviour with respect to some of their ligands or can present ligand-controlled self-assembling processes. Classical examples of this kind of receptors are respiratory proteins like the hemoglobins, the hemocyanins and the erythrocruorins, allosteric enzymes like aspartate-transcarbamilase, glucosamine-6P-deaminase and gene expression control proteins like the lac repressor protein, the cro protein and nuclear receptor ligand binding domains [1–4]. Complex macromolecules, able to connect the binding of neurotransmitters with ion channel opening, display rich cooperative processes and can be modelled using an allosteric network mechanism derived from the classical two-state Monod–Wyman–Changeux allosteric model [5]. Furthermore, recent advances in the field of supra-molecular chemistry have recently renewed the interest in concepts such as allosterism, cooperativity or self-assembly, all of them taken from the field of biochemistry. In effect, supra- molecular chemistry studies the spontaneous but controlled generation of complex organic and/or inorganic architectures, and in this sense, such systems mimic many features of macromolecular binding systems found in biological structures [6, 7]. Such investigations have resulted in new proposals for the assessment of cooperative behaviours in sophisticated self-assembling structures [8]. Also in this context, novel thermodynamic approaches have recently been developed [7].

A complex macromolecular binding system can be composed of several molecular mechanisms, each one with its own binding properties and thus its own contribution to the cooperative behaviour of the whole system. For instance, macromolecular species, either of equal or different structure, can link to form self-assembled aggregates. In many cases, these aggregates will be in equilibrium not only with the ligand but also with those subunits from which they are composed, as described in the pioneering nested models proposed by Wyman to interpret structural and functional aspects of haemocyanin binding systems [9]. In addition, each state of aggregation can exhibit different conformations, and each conformation may in turn present subunits of different primary protein structure. Finally, there is a microscopic level where the site-specific properties are described. This type of complex scheme is regulated by the ligand concentration, which can change the proportions of the various structures in which the macromolecule is present [1, 10, 11]. A model that reproduces the properties of this type of binding system usually involves a large number of microscopic parameters, resulting in a saturation function that is difficult to analyse and interpret.

The starting point in the study of such an intricate system of equilibrium is a suitable choice of a macroscopic magnitude, which would describe and assess, as clearly as possible, the cooperative behaviour. Among them, several quantities have been proposed, such as the Hill number, the binding capacity [1] and the Scatchard plot [12]. The underlying physicochemical processes taking place are further related to these magnitudes by using thermodynamical and statistical mechanics techniques [10, 11, 13–15].

The present article is centred in the investigation of the properties of an experimental parameter that allows a highly sensitive measure of the cooperative behaviour of macromolecular binding systems [11, 16–18]. This parameter, which we have called “global association quotient”, is directly related to the Hill number and has a cardinal property: It presents a simple inner structure related to the binding properties of the subsystems that are responsible for the observed cooperative behaviour, making its interpretation transparent [17].

The global association quotient (also called average equilibrium function [18], affinity function [10], global equilibrium quotient [17] or apparent equilibrium constant [11]) is defined by:

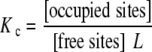1

where L is the ligand concentration. Expression (1) defines an equilibrium relationship for the association process that involves two formal species, the occupied sites and the free sites. These are defined by the sum of the concentrations of all the types of occupied sites and free sites of the system, respectively. The global association quotient represents the global affinity of the macromolecule for the ligand and is, in general, a function of the ligand concentration. It has a transparent physical interpretation. Acerenza and Mizraji showed that for a system amenable to the Adair equation, the global association quotient is an average of the intrinsic constants (stoichiometric decomposition). In the same contribution, it was also shown that a similar decomposition could be applied for arbitrary equilibrium binding systems, provided that there is a one-to-one relationship between free and occupied sites. In this case, the average is taken over the elementary equilibrium constants of the sites (microscopic decomposition) [17].

In the present paper, it is shown that these two types of decompositions (stoichiometric and microscopic) are particular cases of a more general pseudo-linear decomposition of the global affinity. From this relationship, two important results related to the analysis of the behaviour of binding systems are obtained. On one hand, this more general formulation connects, at each level of the hierarchy of macromolecular structures, the population fractions with the phenomenological affinities of the binding process. As a result, a succession of different linear expressions is obtained when we climb, one by one, the ladder of hierarchical levels of macromolecular organisation, providing a useful tool to investigate the properties of very complex binding systems. On the other hand, such an approach reveals a simple link between the stoichiometric and microscopic decompositions, leading to a model-free interpretation of the experimentally determined intrinsic equilibrium constants in terms of the elementary constants of the individual sites.

Interpretation of the Global Association Quotient for Adair Binding Systems

Background: The Adair Equation and the Intrinsic Equilibrium Constants

The binding behaviour of a wide group of macromolecular systems in equilibrium can be expressed as a set of s reactions,

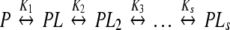2

where s is the number of sites of the macromolecule, P, and the association constants K_j, stoichiometric or stepwise equilibrium constants [10, 11, 14], are given by

3

PL_j represents the macromolecule bound to j ligand molecules, regardless of the specific sites to which they are bound. This is why the PL_j cannot be considered as a real chemical species and why they are usually known as stoichiometric or stepwise species. In fact, the stoichiometric species PL_j are defined by their concentrations, which are calculated as the sum of the concentrations of all the real chemical species with j occupied sites [14]. A sequential binding scheme given by (2) will be called here an Adair binding system.

The mean occupation number ν(L) (i.e. the number of sites of the macromolecule bound to the ligand) of a system like the one appearing in (2) is given by the Adair equation [14, 19]

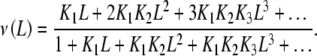4

When the system is not cooperative, K_j is given by

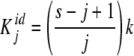5

which corresponds to a number s of identical and independent binding sites [14]. k repre- sents the equilibrium constant for a particular site (and is called the elementary equilibrium constant) and the statistical factor (s − j + 1)/j reflects that the actual value of K_j decreases with j due to the loss of free sites in the oligomeric protein as the fractional saturation increases. As usual, for Adair binding systems, we will consider such a system as ‘ideal’ and cooperativity as a deviation from this ideal behaviour [10, 11].

On the other hand, when (positive or negative) cooperativity is present, (5) will take the more general form

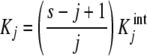6

where the 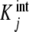are called intrinsic equilibrium constants [1, 11, 14] and are obtained by eliminating the statistical factor (s − j + 1)/j from the stoichiometric constants. Intuitively, one can consider that the represent the average binding properties of a site when j – 1 sites have already been occupied. In Section 6, we will express quantitatively this idea as a natural consequence of the formalism developed in the present contribution.

Decomposition of the Global Association Quotient for Adair Binding Systems

We will focus on the global association quotient, K_c, which, as defined in (1), defines a formal equilibrium relationship between the concentration of ligand, free and occupied sites. Notice that K_c is, in general, a function of the ligand concentration and thus cannot, a priori, be regarded as an equilibrium constant, as defined in the standard chemical thermodynamics. However, it was stated in a previous contribution [17] that when a system can be represented by an Adair equation (4), the global association quotient (1) can be decomposed in terms of 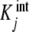as

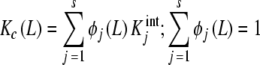7a

where ϕ_j(L) are the proportions of free sites that belong to the stoichiometric species PL_j − 1, i.e. the proportions of free sites that bind with an intrinsic equilibrium constant ,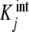

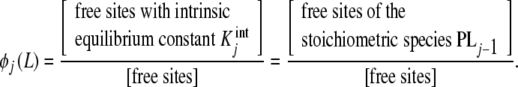7b

The interest of result (7a, 7b) lies in the fact that it provides a very simple physical interpretation for the global association quotient. This is the average of the 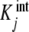weighted by the corresponding proportions of free sites with that intrinsic equilibrium constant, and it is the mathematical confirmation of the intuitive idea that K_c(L) is a measure of the average affinity of the system for the ligand. Thus, K_c(L) actually maps the average intrinsic free energies involved in the binding of a site of the system. Or, alternatively, K_c(L) represents the affinity of an “average free site”. For the ideal, non-cooperative, system, 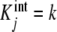for all j values, and according to (7a, 7b), K_c(L) takes the constant value k.

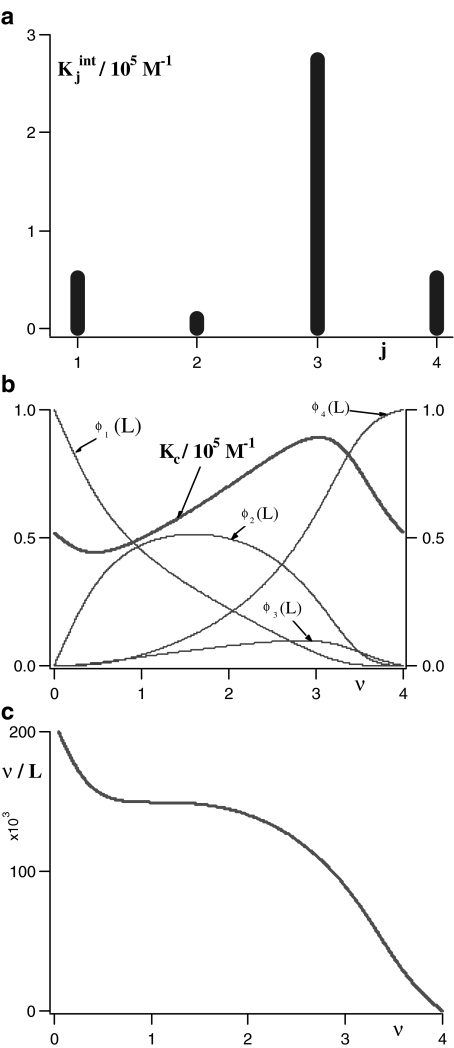
In Fig. 1a, we have plotted the constants 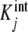, obtained from the literature for the binding of the enzyme pyruvate-carboxylase to acetyl-coenzyme-A (s = 4) [14] and, in Fig. 1b, the curve K_c(L) versus ν(L) for the same system. Comparing these plots, we see that the shape of K_c(L) clearly maps the values of 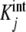. At the limits L→0 (i.e. ν →0) and L → ∞ (i.e. ν→s), K_c(L) takes the limiting values 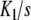and sK_s, respectively [1, 10, 11]. For intermediate values of ν, K_c(L) changes according to the tendency determined by the set of equilibrium constants 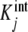. The contribution of each 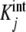to the total value of the global association quotient is determined by ϕ_j(L) (Fig. 1b).

Fig. 1.

Binding curve of acetylcoenzyme-A to the enzyme pyruvate-carboxylase (s = 4 sites): a intrinsic constants 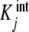versus j : 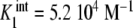, , 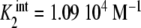, 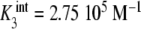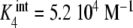; b global association quotient, K_c, and fractions of free sites, ϕ_j, versus mean occupation number, ν; c Scatchard plot, ν/L versus ν

These properties of the plot K_c versus ν can be of great practical importance. Let us assume that we are interested in the binding properties of an experimental binding system. We have determined the mean occupation number ν as a function of the ligand concentration L. We have also tested that this relationship is independent of the total protein concentration, and therefore, our system can be described by an Adair equation. Then, the plot K_c versus ν provides the sign of the cooperativity exhibited by the system in the different levels of saturation. In the portions where K_c increases with ν, we have positive cooperativity and, in the portions where K_c decreases with ν, negative cooperativity. If K_c is constant, the system is non-cooperative. Notice that cooperativity is a ‘local property’, since, as in the example depicted in Fig. 1b, it can be positive for certain ligand concentrations and negative for others.

The global association quotient can be related to other measures of cooperativity proposed previously in the literature. The Hill number can be easily obtained from the global association quotient by [10, 17] as:

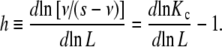8

An interesting feature of the global association quotient is that it provides a simple and general explanation of the usefulness of the Scatchard plot (perhaps the most popular way of fitting experimental binding curves) in detecting cooperative behaviours. The Scatchard plot [12] consists in plotting the quantity [occupied sites]/L or ν/L versus ν. That quantity can be expressed in terms of K_c as

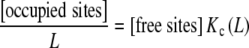9

and using the decompositions (7a, 7b), we obtain

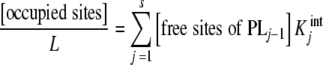10

i.e., what we are plotting is the sum of the intrinsic equilibrium constants of the free sites multiplied by the concentration of free sites with that equilibrium constant. Equation (10) explains in a very simple way the convexity of the Scatchard plot when positive cooperativity is present. On one hand, 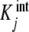increases with j, and according to (10), [occupied sites]/L tends to increase. But on the other hand, the number of free sites of the different species is decreasing when ν increases. The result is a non-decreasing function and, for a highly cooperative system, an increasing function, as is the case in the oxygen–hemoglobin cooperative binding system, at low occupation numbers and a decreasing function for large ones, with a maximum at intermediate ν values. This behaviour is shown in Fig. 1c for the binding of acetyl-coenzyme-A to the enzyme pyruvate-carboxylase.

Relationship Between Global Association Quotient and Binding Free Energy

In the last subsection, we have paid attention to the relationship between the global association quotient and the intrinsic equilibrium constants. However, we know that a fundamental property of any equilibrium constant K is its relationship with the standard Gibbs free energy of the process, ΔG^o = − RTln K. Let us show that, at least for Adair binding systems, this property is retained by the global association quotient.

Following Wyman, the work (or the Gibbs free energy) needed to occupy an average number of sites ν, starting from the naked macromolecule, is given by [1]

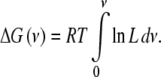11

Using the definition of the global association quotient 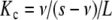, (11) adopts the form

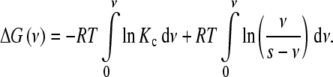12

This equation indicates that the Gibbs free energy can be decomposed in two contributions: a term depending on K_c plus a logarithmic term. In order to clarify the physical meaning of the latter, let us calculate ΔG(ν) for a non-cooperative (ideal) system, i.e., for which K_c is independent of the ligand concentration K_c = k. The result is

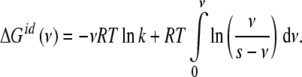13

We can see that the first term in the right-hand side of (13) corresponds to the free energy involved in the binding of the macromolecular sites, while the second accounts for the entropy due to the existence of different microstates compatible with a given ν value. Since we are only interested in the free energy corresponding to the occupation of the macromolecular sites, we can define the intrinsic free energy of the sites ΔG^int as

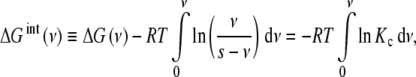14

and taking derivatives over ν (14) reduces to

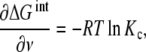15

which is the sought counterpart in macromolecular binding to the relationship between the equilibrium constants and the Gibbs free energy, ΔG^o = − RTln K, in single equilibrium. Notice that (15) expresses that − RTln K_c is the average change in the free energy that occurs when a macromolecular site is occupied for a given ν value. Again, one finds that cooperativity is a property that depends on the concentration.

General Decomposition of the Global Association Quotient

In the previous section, we described how the global association quotient, K_c, of an Adair binding system can be expressed as the weighted average of the intrinsic equilibrium constants, 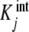(7a, 7b). The Adair description is a stoichiometric approach that puts together all the macromolecular species with the same number of bound ligands into a single species. This is a minimal description because it includes the minimum number of constants required to reproduce the binding behaviour of the system. However, it is useful to analyse experimental data because it can be used even if the details of the underlying mechanism are not available. In the Adair description, the number of intrinsic constants is equal to the maximum number of molecules of ligand that the macromolecule can bind. However, the number of sites with different binding properties is generally greater than this number, and therefore, the Adair approach does not allow a full description of the binding process. Furthermore, the decomposition of the global association quotient derived for sequential binding systems (7a, 7b) cannot be applied to systems that show macromolecular aggregation.

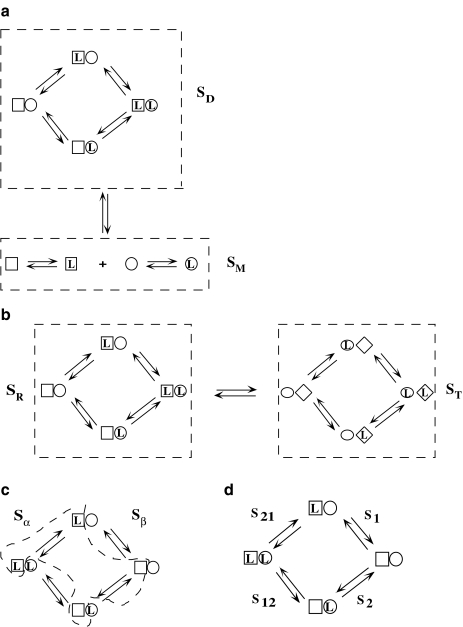
Let us face the problem following a different strategy. For a given ligand concentration, one can classify the set of free sites in a number of groups or subsystems, according to some criteria. For instance, in Fig. 2a, we have the whole system consisting of two proteins that can form a dimer. One can thus classify the free sites as those belonging to the monomer (subsystem S_M) and the ones belonging to the dimer (subsystem S_D). In the example depicted in the Fig. 2b, we represent a protein with two binding sites, which can be present in two different conformations, R and T. One could also classify the free sites of the system in two categories: the ones belonging to the protein in the R conformation (subsystem S_R), and those belonging to the protein in the T conformation (subsystem S_T). A different criterion, which we call ‘site-specific’ or ‘structural’, classifies the sites according to the primary structure of the protein. In Fig. 2c, we have plotted a protein with two sites, which are, in general, non-independent. We split the system into two subsystems, 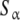and 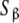, which contain the sites of the subunits 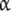and 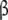, respectively. Finally (Fig. 2d), we could also decide to group the free sites into four categories (subsystems S₁, S₂, S₂₁, S₁₂), chemically distinct, and therefore, we take into account that the binding properties of a site depend on the occupation state of the others. This would be the most detailed description of the whole system and here will be called the ‘microscopic’ decomposition.

Fig. 2.

Schematic model for a monomer–dimer protein including different kinds of subsytems: a aggregation level—the global system is decomposed into two subsystems, monomer (S_M) and dimer (S_D); b conformational level: the dimer subsystem (S_D) is decomposed into two conformational subsystems, S_R and S_T; c structural level—one conformation of the dimer is decomposed into two structural subsystems, 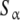and 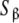; d microscopic level—the structural subsystems are decomposed resulting in four microscopic subsystems

Let us consider a general binding system S at equilibrium that can be decomposed in n subsystems, S₁, S₂,..., S_i,..., S_n. For each of these subsystems, we can define a partial association quotient, K_c,i(L),

16

which has the same form as the definition of the global association quotient K_c(L) (1).

Since the subsystems are disjoint, we know that the occupied sites can be split according to

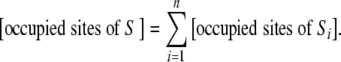17

Replacing (17) in (1) we obtain:

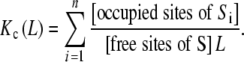18

Multiplying and dividing by the concentration of free sites of S_i, [free sites of S_i], (18) becomes:

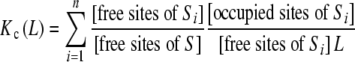19

and, using (16), the global association quotient K_c(L) for the system S can be decomposed in terms of the n partial association quotients, K_c,i(L):

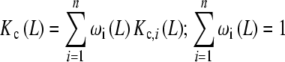20a

where ω_i(L) is the fraction of free sites belonging to the subsystem S_i:

20b

We highlight the similarity between (20a, 20b) and (7a, 7b). In these equations, ω_i(L) and ϕ_j(L) play the same role: they are the fraction of free sites (referred to the total concentration of free sites) under consideration. In addition, K_c,i(L) has a similar meaning to 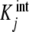, as they are both measures of the affinity of the free sites of the corresponding subsystem. The main difference between (20a) and (7a, 7b) is that K_c,i(L) may be a function of the ligand concentration L, while 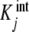is not.

Equations (20a, 20b) contain a central result. They show that for every partition of the system in subsystems, there is a decomposition of its global association behaviour, quantitatively described by K_c(L), in terms of the association behaviour of its components, described by K_c,i(L). Moreover, as we shall see, this decomposition can be applied to the successive levels of organisation of a macromolecular binding system, resulting in a hierarchical decomposition of the quantitative binding properties.

The decomposition (20a) has some useful properties. When the system is divided according to a suitable criterion, the partial association quotient of a given subsystem will only depend on equilibrium constants of the corresponding subsystem, provided that all the macromolecular species from which it is composed are not shared with any other subsystem. This is the case, for instance, when the system is divided according to an aggregation criterion into two subsystems, e.g. monomer and dimer. Otherwise, the partial association quotient of the subsystem will depend, in general, on the equilibrium constants of other subsystems. This may happen, for example, when we make a structural decomposition of the system (i.e. according to the primary protein structure of the subunits) and the different subunits in the macromolecule interact. These properties are useful for the interpretation of the results obtained with the formalism here proposed and will be illustrated in the examples analysed in the next section.

The dependence of the global association quotient on the ligand concentration is a qualitative indication of the existence of cooperative behaviour in the binding process. To quantify the extent of the change in K_c let us use the derivative of K_c with respect to L, defined as κ [17]. The combination of the decompositions (20a, 20b) with the definition of κ results in the following relationship:

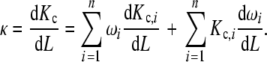21

This equation shows that the resulting cooperative behaviour depends on two types of contributions. The first one [first term on the right hand side of (21)] corresponds to the non-ideality of the subsystems implicit in the dependence of K_c,i(L) on L. The second type of contribution [second term on the right hand side of (21)] is related to the shift in the fractions of the different types of free sites. If the subsystems are ideal, the first contribution vanishes.

Microscopic Decomposition of the Global Association Quotient and the Scatchard Plot

An important consequence of the application of (20a, 20b) is that it allows relating the global association quotient to the equilibrium constants of the elementary events taking place. Let us classify the sites of the system in n types of sites with different elementary equilibrium constants k_i. This would correspond to the microscopic description introduced in the previous section (see Fig. 2d). Then, the partial association quotients corresponding to each subsystem, so defined, will be independent of the ligand concentration and equal to the elementary equilibrium constants K_c,i(L) = k_i. Equations (20a, 20b) adopts the form

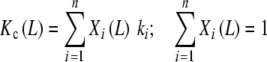22

where the weights (X_i) are the fractions of free sites with the corresponding elementary association constants. This ‘microscopic’ decomposition of the global association quotient was previously obtained in a slightly different manner [17]. It provides an alternative physical interpretation of K_c as an average of the elementary equilibrium constants weighted by the fraction of free sites with those equilibrium constants.

As an example, let us consider a system with two types of free sites in the absence of ligand (see Fig. 2d). In the binding process, there intervene four different types of free sites and, as a consequence, four different association constants.

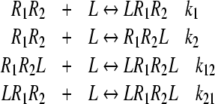23

For this particular system, the global association quotient is written as:

24

which, according to (22), can be decomposed as

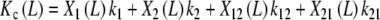25a

where X₁(L), X₂(L), X₁₂(L) and X₂₁(L) are the fraction of free sites with elementary equilibrium constants k₁, k₂, k₁₂ and k₂₁, respectively, given by:

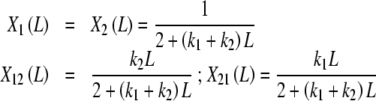25b

where the condition of detailed balance, k₁k₂₁ = k₂k₁₂, has been used.

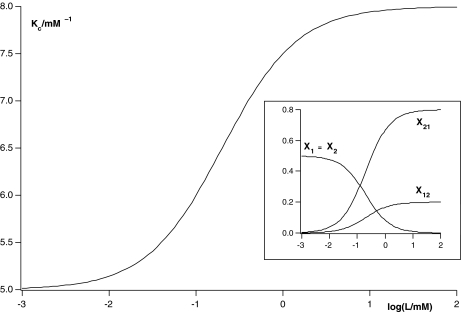
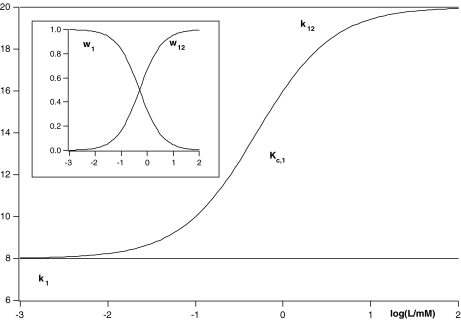
In Fig. 3, it is shown how the global association quotient changes with the ligand concentration, together with the fraction of free sites. Clearly, the global association quotient maps the elementary binding processes taking place.

Fig. 3.

Global association quotient, K_c, as a function of the logarithm of the ligand concentration log(L/mM) for the scheme depicted in Fig. 2d and (23) and its decomposition into the four elementary equilibrium constants. In the inset, we show the fractions of free sites, X_i(L), related to each subsystem associated with every elementary equilibrium constant. The parameter values used are k₁ = 8 mM^− 1, k₂ = 2 mM^− 1, k₂₁ = 5 mM^− 1 and k₁₂ = 20 mM^− 1

The Scatchard plot can also be interpreted, with the help of K_c, and similar arguments to those used in Section 2, in terms of elementary equilibrium constants. Now, the result is

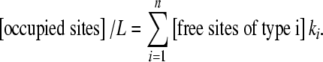26

Finally, there is an important property of the microscopic decomposition introduced above. Notice that we have not used at any moment the fact that the system can be described by a set of sequential equilibria. This means that (22) is valid even in the case that the Adair equation does not apply. This is an important property, since, in the field of self-assembly, it has been claimed that the classical measures of cooperativity used in Adair equilibrium, such as the Scatchard plot, cannot be applied in general [8]. Equations (20a, 20b) and (22) show that both the global association quotient and the Scatchard plot can be very useful in the analysis of self-assembled binding systems if they are properly used and interpreted.

The Global Association Quotient and the Hierarchical Analysis of Complex Cooperative Systems

A very interesting feature of the decompositions (20a, 20b) is that they can be applied in a recursive way. We can take a certain subsystem S_j, to which corresponds the partial association quotient K_c,j(L) and split it into smaller subsystems. To those ‘sub-subsystems’ into which the subsystem j is divided, we can assign a partial association quotient K_c,ji(L). Then, (20a, 20b) will apply again

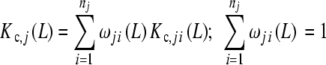27a

where

27b

Moreover, every sub-subsystem could be decomposed into sub-sub-subsystems and so on, so that the binding properties of the free sites of a subsystem can be interpreted as an average of those of the lower level of description.

Let us apply these ideas to the example schematised in (23) (see also Fig. 2d). Instead of classifying the set of free sites directly in four categories (S₁, S₂, S₁₂ and S₂₁, each one corresponding to an elementary equilibrium constant), we can decompose the sites into only two subsystems: 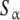(composed by S₁ and S₁₂) and 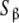(composed by S₂ and S₂₁). In other words, we classify the sites at the ‘structural’ or ‘sites-specific’ level of description presented in Section 3. This kind of description seems quite natural if experimental techniques as those developed in the recent years [10] are sensitive, for instance, to the occupation of specific sites of the macromolecule. Accepting a partition of the free sites of this kind and using (20a, 20b), K_c(L) can be decomposed into two terms:

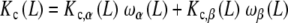28

where K_c,α (L) and K_c,β(L) are the partial association quotients corresponding to the sites R_α and R_β, respectively, which are given by:

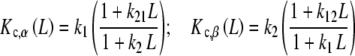29a

and, using (25b)

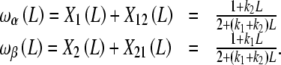29b

The obtained partial association quotients represent the average affinities that, for a given value of L, the sites 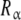and 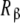have for the ligand. In Fig. 4, we have depicted K_c,α(L) and K_c,β(L) and their corresponding weights, ω_α(L) and ω_β(L) = 1 − ω_α(L). For instance, at low ligand concentrations, it is expected that the sites 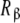are empty, and hence the affinity of the sites 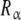tend to k₁. Conversely, at high ligand concentrations, the sites 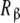are saturated, and the affinity of 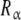tends to the value k₁₂. The affinity of the site in the 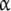-subunit is seen, from this point of view, as an average of the affinity of the site when the other site is occupied or the same site when the other one is empty.

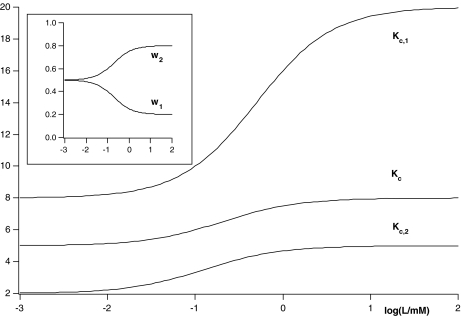
Fig. 4.

Global association quotient, K_c, as a function of the logarithm of the ligand concentration log(L/mM) for the scheme depicted in Fig. 2d and (23) and its structural decomposition into the two partial association quotients, K_c,i(L). In the inset, we show the fractions of free sites, ω_i(L), related with each subsystem associated to each partial association quotient. The parameter values used are the same as Fig. 3

The functions K_c,α(L) and K_c,β(L) are also called in the literature site-specific affinity functions [10], and the decomposition of K_c(L) (28) provides the connection between the global association quotient, obtained using the usual experimental techniques, and the site-specific affinity functions, for which more sophisticated techniques must be used.

As explained in the beginning of this section, we can now decompose the subsystems R_α and 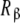in sub-subsystems whose behaviour will inform the microscopic level of description. For instance, applying the general decompositions (20a, 20b), K_c,α(L), given by (29a), can be expressed as:

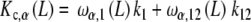30a

where ω₁(L), ω₁₂(L) are the fraction of free sites in the 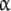-unit with elementary equilibrium constant k₁, k₁₂, respectively:

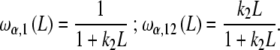30b

We have thus expressed, in a hierarchical way, the binding properties of the sites at the site-specific level in terms of the binding properties of the microscopic level. This idea is depicted in Fig. 5, where we have plotted K_c,α(L) versus L together with the weights ω₁(L) and ω₁₂(L). The limiting values at L→0 (k₁) and L→ ∞ (k₁₂) are also indicated in the graph. As discussed above, the affinity of the site in the α-subunit can be interpreted as the average affinity of the site when the other site is occupied or the same site when the other one is empty.

Fig. 5.

Partial association quotient, K_c,1, as a function of the logarithm of the ligand concentration log(L/mM) for the scheme depicted in Fig. 2d and (23) and its microscopic decomposition into the two elementary equilibrium constants. In the inset, we show the fractions of free sites, ω_i(L), related to each subsystem associated with every elementary equilibrium constant. The parameter values used are the same as Fig. 3

As explained in the Section 1, cooperative behaviour at equilibrium may result from several different types of molecular mechanisms. Conformational transitions in oligomeric proteins, pre-existing or induced by changes in ligand concentration, and self-assembling processes are widespread in biological systems and artificial supra-molecular structures. This type of complex scheme, regulated by the ligand concentration, can exhibit cooperative behaviours at different levels of organisation: microscopic, structural, conformational, or self-assembling levels. For instance, in the MWC model [20], cooperativity does not arise from the microscopic binding properties of the sites but from the conformational equilibrium itself. In general, a realistic model that includes the main features of a binding system usually involves a large number of microscopic parameters, resulting in a saturation function that is difficult to analyse and interpret. In this sense, the general decompositions (20a, 20b) can help to analyse the different possible sources of cooperativity of complex macro- and supra-molecular binding systems.

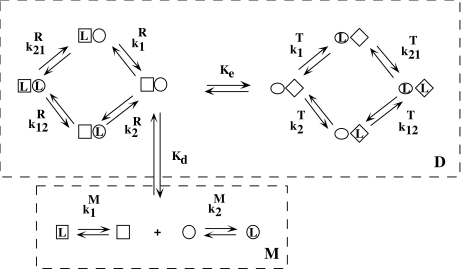
As an example, let us consider the system depicted in Fig. 6. The system analysed above (Fig. 2) is a part of this more general scheme, which includes the formation of a dimer, which, in turn, can adopt two possible conformations. The length and complexity of the saturation function suggests that the complete analysis of the cooperative properties of this system is a very difficult task. However, using the ideas discussed above, we can now divide the system into different contributions, coming from different levels of complexity. The whole system is composed of two subsystems characterised by their aggregation state, the first of them including the free sites of the monomer (M) and the second one those of the dimer (D). Again, the corresponding partial association quotients 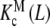and are related to K_c(L) through the general decompositions (20a, 20b)

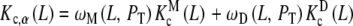31

where P_T is the total monomer concentration. It is clear that, for this type of system, the Adair equation does not apply, since it cannot be reduced to the sequential binding scheme indicated in (2). On the other hand, notice that the dependence on the monomer concentration appears only through the weights ω_M(L, P_T) and ω_D(L, P_T). This is not surprising since 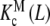and 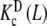are intrinsic binding properties of the subsystem whose affinity they quantify, and P_T only determines the proportions of sites in the dimer and monomer forms, via the equilibrium constant K_d. Indeed, once the overall system is reduced to the binding properties of the two subsystems, the binding properties of the latter are in fact autonomous. In other words, 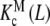and 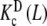would be the ‘pieces’ from which the whole system is composed, each with its own binding properties, while the weights ω_M (L, P_T) and ω_D (L, P_T) are the way in which both pieces interplay to compose the global behaviour of the system.

Fig. 6.

Schematic model including monomer–dimer aggregation, different conformations and primary structure subunits

Following the scheme depicted in Fig. 7, a next step is to decompose the dimeric system into two conformational subsystems, R and T. The decomposition of 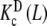, which follows the general decompositions (20a, 20b), is given by:

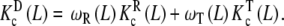32

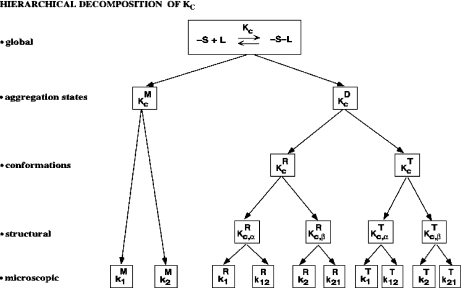
Fig. 7.

Hierarchical decomposition of the global association quotient, K_c, into partial association quotients, K_c,i, corresponding with the different hierarchical levels of binding, of the model system described in Fig. 6 and associated to the different subsystems: a aggregation level—the global system (S) is decomposed into two subsystems, monomer (M) and dimer (D); b conformational level—the dimer subsystem (D) is decomposed into two conformational subsystems, R and T; c structural level—the monomer (M) is divided into two structural subsystems corresponding to different primary structures of the subunits (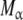 and 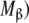, and each conformation of the dimer is decomposed into two structural subsystems (R for conformation T); d microscopic level—the structural subsystems are decomposed into ten microscopic subsystems

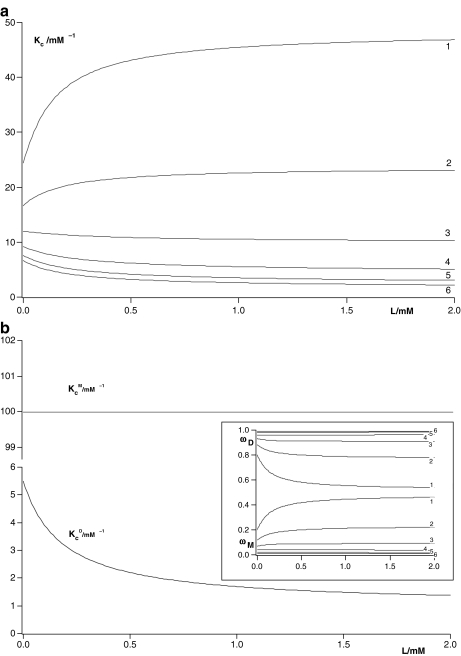
In Fig. 8a, we have plotted K_c(L) corresponding to the system represented in Fig. 6 for different total monomer concentrations (P_T). For the particular set of parameters chosen, a change in P_T produces very different cooperative behaviours. At low P_T values, K_c(L) increases with L and thus positive cooperativity is observed. On the contrary, at high P_T values, the detected cooperativity is negative (decreasing K_c(L) values). How can one unravel the origin of this behaviour by using the procedures proposed in this work? Firstly, we have plotted in Fig. 8b 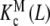and 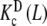, which represent the intrinsic binding properties of the monomeric and dimeric systems, respectively, together with the corresponding weights ω_M(L, P_T) and ω_D(L, P_T). One can observe that cooperativity is absent for binding to the monomer, while it is negative for the dimer. Notice that two subsystems that do not show positive cooperativity result in a system which does present this behavior for certain monomer concentrations. This means that the cooperativity observed arises at the aggregation level of organisation. In effect, at low P_T values, both monomeric and dimeric subsystems coexist (ω_M(L, P_T) ≈ 0.2–0.4 and ω_D(L, P_T) ≈ 0.6–0.8, see Fig. 8b). However, for all the range of L values, the monomer has a higher affinity for the ligand that the dimer. This means that, in adding more ligand to the system, the equilibrium is shifted to the monomer, and as a consequence, the global affinity of the system (which is, according to (31), an average of the affinities of the dimer and the monomer) increases. This analysis explains why, at low monomer concentrations, the system exhibits positive cooperativity. On the contrary, in increasing the monomer concentration, the aggregation equilibrium is fully shifted to the dimer (ω_D(L, P_T) ≈ 1 for all L values). Since the dimer presents negative cooperativity, the whole system presents negative cooperativity for high monomer concentrations. Notice that 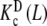is in turn an average of the partial association quotients for the conformations R and T, 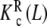(which decreases with L) and 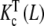(which increases with L). They are depicted in Fig. 8c. However, although the conformation T presents positive cooperativity, this trend is not reflected in the global binding properties of the dimer.

Fig. 8.

a Global association quotient, K_c, as a function of the ligand concentration, L, for different total monomer (mM) concentrations, P_t = 1 (1); 10^0.5 (2); 10 (3); 10^1.5 (4); 10² (5); 10^2.5 (6). The parameter values used are 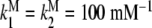; K_d = 10 mM; 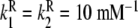; ; 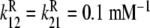; 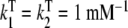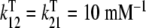and K_e = 1. Partial association quotients, K_c,i and fractions of free sites, ω_i, as functions of the ligand and total monomer concentrations, for the different levels of the hierarchical decomposition of K_c: b 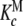and 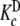(aggregation level); c 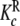and (conformational level)

In the same way, we could continue separating, by means of new association quotients, the different contributions to cooperativity arising from the other levels of complexity introduced above (structural and microscopic). The resulting analysis can be represented by the scheme depicted in Fig. 7.

As a result of the procedure proposed here, a succession of equilibrium quotients and their corresponding decompositions are obtained when we climb, rung by rung, the ladder of hierarchical levels of molecular organisation, allowing us to investigate the properties of very complex binding systems.

A Model-Free Relationship Between Intrinsic and Elementary Equilibrium Constants: Stoichiometric Versus Microscopic Approaches

Another consequence of the general equation (20a, 20b) is that it provides a simple physical interpretation of the intrinsic equilibrium constants, corresponding to the Adair description, in terms of the elementary constants.

In Section 2.1, we discussed that the concentrations of the stoichiometric species PL_j are defined as the sum of the concentrations of the chemical species with j ligands bound or s–j free sites. Let us show that the partial association quotient (16) related to the equilibrium:

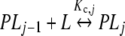33

is no other than the intrinsic equilibrium constant 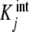. By definition, the partial association quotient is

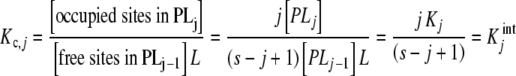34

where (3) and (6) have been used. Note that when calculating the [occupied sites], we only consider PL_j and not PL_j − 1. Similarly, we do not consider PL_j when calculating the [free sites]. This is because the occupied sites in PL_j − 1 and the free sites in PL_j do not participate in the binding processes represented in (33).

Since 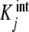is a partial association quotient, we can express it in terms of the elementary association constants k_i according to the decomposition property (22) obtaining:

35

where the weights X_i, fractions of free sites with elementary constants k_i, are independent of the ligand concentrations. Therefore, the intuitive idea that the intrinsic constants 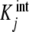are a sort of average of the elementary constants k_i, corresponding to the microscopic binding subsystems grouped in one stoichiometric species, has its algebraic counterpart in decomposition (35).

For instance, for the case of the dimeric protein schematised by (23) (Fig. 2d), the expressions for the intrinsic association constants can be written in the following form:

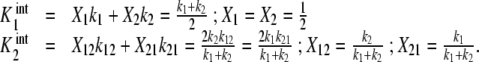36

We highlight that the decompositions (20a, 20b) for the global association quotient act as a sort of invariant relationship underlying the strongly non-linear behaviour of macromolecular binding systems at all the different levels of description. Equation (35) is clearly another expression of the generality of the formalism proposed here.

Final Comments

Realistic models of macromolecular binding systems may include a substantial number of states and equilibrium constants. Their cooperative properties can arise from different origins (microscopic, conformational, and self-assembly). This usually results in complicated expressions for the saturation functions, making their behaviour difficult to analyse and interpret. In these cases, the expression for the global association quotient of the system K_c(L), defined in (1) also appears to challenge any useful analysis. However, we have shown that there is a general way to study the binding behaviour of complex macromolecular models that can, in principle, be applied to schemes of any structure and size. This consists in decomposing the system in subsystems following, step by step, the levels of macromolecular organisation. The affinity of the system (represented by K_c(L)) can be expressed in terms of the affinities of the subsystems (represented by K_c,i(L)) that are in the level immediately below, according to the pseudo-linear decomposition given in (20a, 20b). This process is repeated, descending the ladder of hierarchical levels of organisation until the fundamental microscopic level is reached. The power of this approach was illustrated in Section 5, where we precisely diagnose the mechanistic origin of the cooperative behaviour exhibited by a rather complex binding model, which includes several cooperativity-generating minimal molecular mechanisms. In addition, we have shown (Section 6) that the formalism here presented provides a general model-free interpretation of the experimental intrinsic equilibrium constants of an Adair equation in terms of the elementary equilibrium constants of the microscopic level of description.

The hierarchical approach was applied starting from the whole system and successively decomposing it until the most elementary level was reached, i.e. in a top–down way. Alternatively, one could have followed the inverse bottom–up direction, starting from the elementary pieces and grouping them in modules that are structurally or functionally related. Whatever the direction we follow, the outcome of our approach is a smooth transition between the highly complex behaviour of a macroscopic binding system and the microscopic states from whose interplay the macroscopic behaviour emerges. This is a rare and very desirable property for an approach that aims to explain, in a complex system, the emergent properties of one level from the properties of the component elements and their interactions.