Individual-based Modelling: An Essential Tool for Microbiology

Abstract

Micro-organisms play a central role in every ecosystem and in the global biomass cycle. They are strongly involved in many fields of human interest, from medicine to the food industry and waste control. Nevertheless, most micro-organisms remain almost unknown, and nearly 99% of them have not yet been successfully cultured in vitro. Therefore, new approaches and new tools must be developed in order to understand the collective behaviour of microbial communities in any natural or artificial setting. In particular, theoretical and practical methodologies to deal with such systems at a mesoscopic level of description (covering the range from 100 to 10⁸ cells) are required. Individual-based modelling (IBM) has become a widely used tool for describing complex systems made up of autonomous entities, such as ecosystems and social networks. Individual-based models (IBMs) provide some advantages over the traditional whole-population models: (a) they are bottom-up approaches, so they describe the behaviour of a system as a whole by establishing procedural rules for the individuals and for their interactions, and thus allow more realistic assumptions for the model of the individuals than population models do; (b) they permit the introduction of randomness and individual variability, so they can reproduce the diversity found in real systems; and (c) they can account for individual adaptive behaviour to their environmental conditions, so the evolution of the whole system arises from the dynamics that govern individuals in their pursuit of optimal fitness. However, they also present some drawbacks: they lack the clarity of continuous models and may easily become rambling, which makes them difficult to analyse and communicate. All in all, IBMs supply a holistic description of microbial systems and their emerging properties. They are specifically appropriate to deal with microbial communities in non-steady states, and spatially explicit IBMs are particularly appropriate to study laboratory and natural microbiological systems with spatial heterogeneity. In this paper, we review IBM methodology applied to microbiology. We also present some results obtained from the application of Individual Discrete Simulations, an IBM of ours, to the study of bacterial communities, yeast cultures and Plasmodium falciparum-infected erythrocytes in vitro cultures of Plasmodium falciparum-infected erythrocytes.

Introduction

Microbiology is an excellent field to apply the tools of physics, both experimental and theoretical. Physics supplies an innovative way to study unresolved problems and provides a better understanding of the physical principles underlying biological processes. Furthermore, microbial systems offer a framework to deal with complex systems and a fruitful field to develop a more holistic understanding of complex systems.

Transport phenomena through microbial ecosystems are extremely relevant, and they are coupled with the behaviour of autonomous micro-organisms that interact with each other and with the surrounding environment. Spatially explicit models based on molecular dynamics (MD) simulation methodologies under the scope of an ecological approach, such as individual-based modelling (IBM), are useful tools to deal with microbial systems.

Integrative Microbiology

Despite their small size, micro-organisms are an essential part of the biosphere. Bacteria alone are estimated to contain up to 60–100% of the carbon found in plants, accounting for 50% of the total biomass of carbon, and they are, by far, the largest pool of organic bound nitrogen and phosphorus [1]. Microbes represent a great share of the planet’s total biological abundance, and they are also a huge reserve of biological diversity [2]. Unicellular organisms play a central role in every ecosystem and in the global biomass cycle, and have a major impact on many human activities and disciplines such as medicine, agriculture, food industry and waste processing, among others [3]. The microbial rate of evolution is very rapid due to the brevity of their individual lifetimes, so the impact mentioned above is in a continual state of changeover. For this reason, microbiology demands a continual stream of new approaches evolving along with microbes themselves.

Great advances have been achieved in accounting for microbes at both the individual and macroscopic levels of description. However, microbiology is split into highly specialised subdisciplines. An integrative approach to microbial systems is arising, in order to obtain more comprehensive knowledge and shed light on many unsolved problems of each of the subdisciplines [3]. Such an approach requires the description of the system-level population dynamics of microbial communities and an understanding of their emergence from the underlying individual traits and interactions.

A difficulty often stressed when dealing with microbial communities is that they are complex systems only poorly explained by reduction. In addition, observed microbial populations contain up to 10¹⁰ cells, which makes them quite difficult to cover item-by-item. Moreover, laboratory and field experiments with micro-organisms are costly and often difficult to carry out or even unfeasible. Nearly 99% of the known microbial species have not yet been successfully cultured in vitro [4]. New tools and approaches are required to tackle the challenge of building an integrative microbiology.

Theoretical Approach to Microbiological Systems at Different Levels of Description

A theoretical approach to observed phenomena consists in building coherent models with descriptive and predictive capacity. Models are theoretical accounts, and they are always simplifications of the systems they represent. Modelling is an attempt to capture the essence of a system well enough to address specific questions about the system [5]. Models in microbiology tackle the systems under study through approaches at different levels of description. We roughly distinguish three different levels of description (molecular, cellular and population levels), according to their specific spatial and temporal scales. We also propose a “mesoscopic” approach to microbial communities that builds bridges between the descriptions at the cellular and population levels of description.

Molecular, Cellular and Population Levels of Description

The contribution of models based on molecular dynamics to the description and understanding of the building blocks and specific mechanisms of biological systems is broad [6–8]. The study of the structure and behaviour of biomolecules requires the use of a wide and assorted set of models from physics and demands using techniques typical from non-equilibrium thermodynamics, theoretical mechanics and network theory, among other disciplines [9]. The studied phenomena at this level of description typically deal with up to 10⁹ atoms and cover temporal scales that range from 10^− 15 to 10^− 4 s. Models at a molecular level of description constitute the object of study of bioinformatics and computational biology [10]. Indeed, these subdisciplines also cover the models stated at a cellular level of description, so research on the two levels overlaps.

An average cell contains 10¹³ atoms. Many metabolic processes inside the cell, such as enzymatic limiting reactions or diffusion of substances across the cell, have a duration on the order of 10^− 3 s [11], and many relevant processes such as DNA replication may last hours. Models at a cellular level of description are focussed on the interactions among biochemical kinetics, cellular structure and whole cell regulatory mechanisms. The study of phenomena at this level of description requires a hierarchical and rigorous pruning and simplification of the involved molecular models and implies reducing a great amount of information in order to obtain a functional description [12]. This is achieved by assuming some phenomenological laws and through the compilation and treatment of experimental data obtained from thoroughgoing analysis (-omics) [13]. Cellular models are developed to explain cell physiology and are the specific targets of novel interdisciplinary subfields of biomedical informatics, such as computational biology [14] and systems biology [15]. Approaches at a cellular level of description are tackled through continuous models which describe the kinetics within the cell using differential equations [16, 17] and through stochastic discrete models, which account for the molecules individually [18, 19].

Experimental microbial cultures typically deal with populations of up to 10¹⁰ cells and last several hours or days. Models at a population level of description account for microbial communities as a whole and are designed to study their structure and evolution. They offer a dynamic description of the total population by means of differential equations controlling variables defined for the population as a whole (i.e. total biomass, average growth rate, among others), and they are also often referred to as continuous models. Continuous models have been fruitfully applied to predictive microbiology in foods [20], microbial exploitation by the pharmaceutical industry [21], waste control and water treatment [22] and the study of microbial ecology and evolution of population diversity in wild or artificial ecosystems [2], among many other fields of human interest.

Population Models and the Mesoscopic Level of Description

Models at a population level of description deal with macroscopic variables and fix a set of governing laws which are based on, or at least consistent with, an assemblage of assumptions about the individual behaviour of microbes. Therefore, they face questions regarding microbial physiology and, at least implicitly, they also propose models at a cellular level [23].

However, the strictly macroscopic or top-down approach faces two limitations: (a) it deals with system-level variables which are not always easily related to individual characterisation of the micro-organisms, so they can easily fail to provide a validation of the assumptions at the cellular level; and (b) it assumes a “mean-field-like” approximation and uses averaged values to characterise the individuals, so the information concerning local phenomena or individual peculiarities and variability is not taken into account. This approach will not be appropriate to study a system whenever the individual singularities are relevant to the collective behaviour.

This drawback can be avoided through an approach to microbial systems at a mesoscopic level of description. This often implies the study of small populations, but the crucial point of such formulation is that the approach is centred first and foremost on the individual characteristics and interactions, and that the laws at the system level are built through a bottom-up strategy. A bottom-up critical review of the laws set at a macroscopic level of description can provide novel hints to tackle a difficult problem, or to delimit an elusive problem [24, 25].

A very explicit kind of bottom-up approach is required to overcome the latter limitation. Models that account for individual singularities are called individual-based models (IBMs) or agent-based models (ABMs). They are a widespread tool in many fields (from sociology to information science) and find assorted applications (from the design of telecommunication networks to traffic analysis and the optimisation of industrial processes). Their role in microbiology is seen in overview in the following section.

Individual-based Models in Microbiology

Grimm [26] defines individual-based models as “simulation models that treat individuals as unique and discrete entities which have at least one property in addition to age that changes during the life cycle.” Continuous models work with differential equations applied on the variables that represent the state of the system at a certain moment. In fact, they operate with finite differences between states set at discrete time steps, but these differences can be considered infinitesimal to a desired degree of approximation. In contrast, IBMs are discrete models that consider rules (equations) governing variables that characterise each individual at each time step, and the state of the whole system is statistically inferred. The output collective behaviour of systems containing a statistical number of individuals is studied and compared to experimental observations, or to theoretical results obtained from population models.

IBM was coined to name these discrete bottom-up approaches to biological communities in ecology during the 1970s. The term “spatially explicit IBM” refers to a model that includes a representation of the spatial configuration of the system to be represented [27]. An alternative to IBM is the cellular automata (CA) approach [28, 29]. CA models are also discrete in space and time, but differ from IBM in that they operate on the spatial cells instead of considering the individuals settled in them. CA approaches focus on global geometric patterns arising from the local interactions, while IBMs focus on individual diversity and how this affects collective behaviour. Recently, many publications have critically reviewed the contribution of IBMs to theoretical biology and to ecology, their status and the challenges they must face [5, 30–36].

During the last decade, IBM has also become a commonly used tool in microbiology [37–41]. A brief analysis of the goals and challenges of this approach is outlined below.

Although IBM is also used in microbiology for its predictive scope, the advantage of this approach is the increase in understanding it offers. As a bottom-up approach, an IBM is an appropriate tool to determine the interrelationships between individual traits of the micro-organisms, their local interactions and the population structure and dynamics of the whole system. IBM allows a staggered study of the system’s complexity; the mechanisms operating at a cellular level can be gradually introduced into the individual model and their global effects can be studied separately, so IBMs are specifically useful for assessing the impact of different elements of a model and the appearance of emergent collective behaviours, which were not explicitly introduced in the individual model [26, 30]. The possibility of introducing complexity at an individual level at will allows the building of models with the desired degree of generalisation or specificity. This special feature makes IBM useful also for the study of cellular processes within multicellular organisms [42] such as tumour growth [43, 44], tissue formation and culturing [45, 46] and blood circulation [47], among others.

Models based on individuals are required when dealing with systems composed of distinguishable entities that behave according to different rules, and which depend on the state of the individual and on its local environment. They are particularly useful to check the validity of any proposed mechanism operating at an individual level whose outcome is assessed by the macroscopic observation of a community as a whole: IBMs allow the gradual introduction of complexity at an individual level and the staggered study of its global effects. Phenomena which are not evident or self-contained in the input rules of the model are frequently observed. They are called emergent behaviours [26].

Experiments are the acid test of science. They are essential for testing proposed theories, and they are also a creative motor because they allow for the detection of unexpected situations, and they generate questions. Nevertheless, some experimental studies in microbiology are difficult to perform and analyse, and often they are simply not feasible [4]. In these cases, IBM simulations can contribute to experimental research by means of virtual experiments [48, 49]. For instance, IBM simulations may help in experiment design by testing possible configurations, or they can be used for exploring ranges experimental conditions that cannot be assessed in the laboratory [50]. Field observations of microbial ecosystems are often difficult to interpret. IBM permits tackling microbial ecosystems through a multiscale approach [51, 52] and studying the mechanisms that govern microbial evolution [53]. IBMs can isolate the mechanisms that may be responsible for the individual microbial dynamics and thus assist in the interpretation of experimental results.

Despite the advantages they offer, IBMs are far from being as readily accepted and widespread as continuous models. Indeed, not only their novelty, but also their key assets (the possibility of dealing with complexity, and the chance of including uncertainty in the described processes and variability among the modelled population) entail the limitations that hinder their acceptance.

Firstly, they are not easily built; it is difficult to determine the appropriate degree of development of a model, i.e. the amount of complexity to be introduced, or the sensitivity of the model to slight modifications and how it will respond to uncertainty and errors in the input data. Sometimes it is just not possible to discriminate among two proposed IBMs that offer the same macroscopic response through different rules operating at a cellular level.

Secondly, they are difficult to handle and analyse, which also makes them difficult to disseminate and less readily accepted. A great amount of data are usually required to set the rules of an IBM, and it is often very difficult to assess the relevance of the input information a priori. In addition, most of the models are too big to be described in a single typical paper, and a conventional language to put the models across is still being generalised [34]. The lack of standards and accepted building blocks for IBM, due to the relative novelty of the discipline, is another obstacle to be recognised in this sense.

There are two main tools to overcome these obstacles. First, there is parsimony when the design is implemented. Prior to designing an IBM, it is essential that modellers have a clear formulation of the question they are addressing with the ongoing model, and highly advisable that they have an idea of the expected results. Then, even when models are designed to account for a very specific mechanism, they should be built through a strict bottom-up approach, meaning that the effect of each introduced process, relation or independent variable is assessed by comparison with a simpler model that does not contain this mechanism. The model to be taken into account should be the simplest one that reproduces the expected pattern of the real system. The second tool is the consistency of the proposed model. When a model is chosen as a good representation of a real system, it is important to study whether secondary outcomes and patterns produced by the model are in agreement with experimental observations. The consistency of the model with real patterns at different levels of observation may increase confidence that the proposed model accounts for an underlying mechanism governing the real system. The abovementioned discussion is of general application for any bottom-up approach to complex systems. Challenges to be faced by the ABM and IBM approaches have been analysed in detail before [5, 54].

Lastly, it is important to point out that applying IBM to microbiology represents an ongoing opportunity to study complexity in many aspects [30] and implies developing new methodologies that may be useful for solving problems in many other fields as well [55].

To sum up, IBM is a complementary tool to check the relations between theoretical assumptions and experimental observations, so it enhances their development. Microbial systems offer a particular and unique opportunity: the spatially explicit aspects of the model that account for the transport phenomena (diffusion and random motion), chemical reactions and physical interactions between individuals have been studied through many approaches at a molecular and at a cellular level of description. In the following section, INDISIM, an IBM methodology developed by our group to deal with microbial systems, is presented.

INDISIM: An Individual-based Model Applied to Microbial Systems

INDISIM stands for individual discrete simulations. It is a methodology used for modelling and simulating microbial communities under different environmental conditions. It arose from the merging of a discrete approach to ecosystems through individual-based modelling [56] with the formalism employed to model molecular dynamics in fluids (MD) [57]. INDISIM settles and controls a group of microbial cells in a discrete space: a regular lattice that consists of a group of spatial cells, and which is subject to the appropriate boundary conditions. Then it models the global evolution of the group by governing the individual behaviour of each bacterium and spatial cell in discrete events, called time steps. INDISIM uses stochastic rules and allows variability among the microbial population, and follows the philosophy of other individual-based models, such as BacSim [58].

Prokaryotic Cells

INDISIM was developed as the standardisation of a methodology used to deal with generic microbial ecosystems [37, 59, 60] and was specifically designed for simulating the behaviour and growth of bacterial communities [40]. INDISIM modelling rules require the input of only a few parameters. Each bacterium is defined by a set of variables: total individual mass, minimum mass to start the reproduction cycle, duration of the reproduction cycle [61], instantaneous state of the reproduction cycle, position in the spatial grid and time in culture, among others. Individual variables are set around a mean value and according to a previously fixed variance in order to allow individual variability.

The medium surrounding the cells is locally characterised by concentrations of solutes and temperature. The total simulated space is always a small fraction of a macroscopic system. INDISIM accounts for physical transport phenomena through the culture medium (heat conduction and diffusion of suspended particles), and models some biological processes of each individual cell: uptake, metabolism and reproduction. At each time step, it checks the viability of every bacterium, driving its modelled behaviour according to its state and local environmental conditions and allowing for stochasticity. Lastly, it updates the global state of the system once all the bacteria have acted.

It must be stated that the cellular model presented is very schematic. It might seem an extreme over-simplification of micro-organisms, but even with such a simple model for each individual, many system-level behaviours have been reproduced. We will show some of them later in this section. A detailed description of how the model works is provided in Appendix 1.

Collective Properties of Bacterial Cultures Arising from Physical Constraints on Individual Cells: Effects of a Stochastic Treatment of the Processes

INDISIM proposes mechanistic models for the microscopic processes to be covered and introduces randomness in the application of the modelled rules. Some collective phenomena emerge from these basic statements:

1. Observed evolution of the colony total biomass (m) and individual uptake rate.

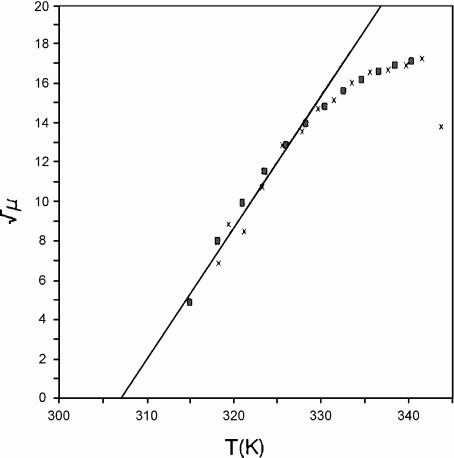
   Experimental observations state that the bacterial colony growth rate, 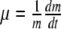, is affected mainly by two environmental conditions: concentration of nutrient particles in the medium (C) and temperature (T), which is directly related with the mean velocities of nutrient particles. In particular, Ratkowsky et al. [62, 63] account for a quadratic relation between μ and T. This behaviour is usually explained by means of the enzymatic kinetics that govern the uptake of metabolites through the cellular membrane at an individual level and described by means of a Monod-like function or by more complicated models [64]. However, the same collective behaviour can be obtained with a simpler model for the individual cellular uptake (Blackman kinetics), provided that it introduces variability among the population (Fig. 1). The main underpinnings of our model are: (a) prior to the uptake, suspended nutrients must reach the cellular surface; (b) there is a maximum rate of nutrient particles which a cell may take up; if more particles impact on the cellular membrane, it would not be able to take them up; and (c) bacteria have similar uptake saturation rates, but there is variability among the population. The behaviour of real systems is reproduced by a simple model that only accounts for the number of nutrient particles that interact with the cell membrane. With no intention of discrediting the widespread Monod model, which has been checked through many other observations, the principle of parsimony supports the use of this simpler model that explains the observed phenomena without assuming a specific mechanism for nutrient transport through the cell membrane. A detailed discussion of the presented results can be found at [37, 40].

2. Biomass distribution function and maximum diversity.

   A thermodynamic treatment of biological communities may consider the biotic ensemble as a black box, an open dissipative system interacting with its local environment. It is then possible to propose variational principles to account for the system-level variables observed at the stationary states of the system.

Fig. 1.

Square root of the rate of growth of B. stearothermophilus versus temperature. Black cross marks indicate experimental data, red rectangles indicate simulation results and the solid line represents the linear term of the Ratkowsky model. Reprinted from [40] with permission from Elsevier

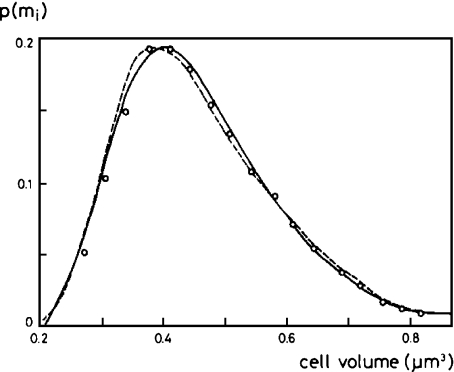
Observations show that biotic communities exhibit stable statistical structures at a population level of description; for example, empirical data for the biomass distribution function among a bacterial colony at a fixed temperature, both during the exponential and stationary growth phases, fit well with a log-normal distribution function [65, 66]. On another front, such observed shape can be theoretically obtained from the maximisation of biological diversity among the bacterial population, once the physical constraints on the whole system have been taken into account [67]. Specifically, histograms showing the biomass distribution among bacteria take on the log-normal shape when diversity among the population is maximised assuming the following conditions: normalisation of the biomass distribution, observed mean mass of the culture and variability in the distribution of the cellular reproduction mass [68] (Fig. 2). The quantification of the population diversity is carried out using the Shannon diversity index, with the different classes of organisms as the bins in the histogram [69].

Fig. 2.

Comparison of the observed biomass distribution function for a bacterial culture (dashed line; after Koch and Higgins [77]), the theoretical prediction from the maximisation of entropy (solid line) and the simulation results obtained with Barcelonagrama, a preliminary version of INDISIM (dots). Reprinted from [68] with permission from Elsevier

INDISIM proposes a set of rules governing the bacterial nutrient uptake and the cellular division process that allows individual variability and reproduces both the observed and theoretically expected behaviour of bacterial communities [37, 70] (Fig. 2). This result does not mean that the mechanisms stated by the model are the cause of the presented behaviour. It neither implies that INDISIM completely explains the experimental observations nor does it validate the theory quoted above, which is in any case already accepted. INDISIM just builds bridges between these two approaches.

The main point is that this behaviour is one of the secondary predictions of the model. It arises solely from the individual model and from the statistical treatment of a large and diverse population. Indeed, this is a good acid test for an IBM because it concerns very general and essential physical laws.

Spatial Complexity of Microbial Cultures

Bacterial colonies exhibit a variety of morphological patterns in response to environmental conditions, such as nutrient concentration, agar moisture and temperature [71, 72]. These patterns are indicative of sophisticated modes of collective behaviour and self-organisation [73] and have been explained by means of diffusion-limited aggregation models [74], and, more thoroughly, by reaction-diffusion models [75]. INDISIM allows us to go a step further in specifying the underlying mechanisms that give rise to the emergent observed patterns, and proposes mechanisms for the individual cells that reproduce the collective behaviour [70] (Fig. 3). Individual-based approaches to bacterial motility have produced useful results in explaining other bacterial behaviour such as migration due to chemotaxis [76].

Fig. 3.

Morphological changes of simulated bacterial colonies, growing from a single inoculum placed at the centre of the lattice, changing initial concentrations of nutrient particles C (S_x,y(0)), and/or different values for the microscopic diffusion parameter D. The input parameters are as follows: C1 = 100; C2 = 200; C3 = 300; C4 = 500 and D1 = 0.005; D2 = 0.010; D3 = 0.020; D4 = 0.040; D5 = 0.060 and D6 = 0.100 (simulation units). Reprinted from [70] with permission from Elsevier

Temporal Evolution of Bacterial Populations

In the natural environment, bacteria overcome long periods of nutrient shortage and seldom encounter conditions that allow fast growth. Microbial colonies under controlled conditions exhibit complex temporal patterns such as synchronisation and cyclic behaviours [78, 79]. In axenic cultures, bacterial growth is roughly split into four stages: a lag phase characterised by a slow or even no growth, an exponential growth phase, a stationary phase with no change in the total cell concentration and a decay or death phase. Commonly, the growth of a colony is fast enough to be manageable by means of experimental observations [80].

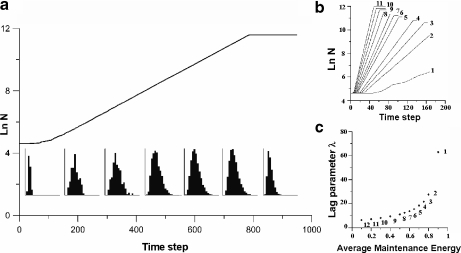
Predictive microbiology is the theoretical approach to population dynamics of bacterial colonies [81]. It aims to uncover the mechanisms that rule bacterial growth. Predictive models are mainly addressed to the study of the lag and stationary phases [20, 82]. IBM has proved to be a valid tool to tackle the dynamics of bacterial cultures [83, 84]. INDISIM, for instance, accounts for the relationship between individual characteristics, such as shape, size and metabolic rate, and population growth in the exponential phase [85]. It also describes the relation among the individual cellular reproduction, population biomass distribution function and population dynamics [86] (Fig. 4). INDISIM is especially appropriate for the study of individual lag times and the tackling of low-population cultures.

Fig. 4.

a Total population (solid line) and biomass distribution function (histograms) of a simulated culture through time. b Results of the series of simulations performed with different maintenance energy constants: growth curves (ln N) of the different simulations. c Lag time duration versus maintenance energy constant for the simulations shown in (b). Reprinted from [86] with permission from Elsevier

Structural Complexity of Microbial Communities

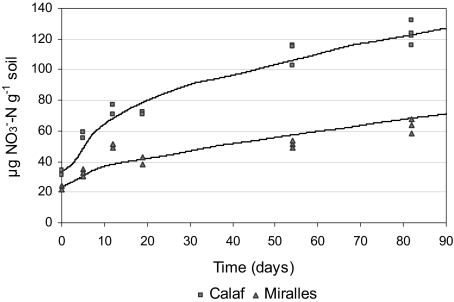
A systems approach to microbial communities is essential to understand their behaviour and function in natural environments. Systems approaches require an accurate yet exhaustive analysis of the local properties of the environment at a cellular level of description [87]. INDISIM has been used to study the dynamics and evolution of organic matter in soils, by means of a multispecies model which also accounts for spatial heterogeneity (Fig. 5) [88]. This approach not only provides a direct route from the microscopic details of the individual cells to the macroscopic properties, but it also deals with an important increase in its complexity with respect to the models presented above. The model for individual cells is more exhaustive; there are many species interacting and the spatial structure of the system must be studied in different scales. Thus, some methodological innovations such as the use of superindividuals [89] have been introduced into this model.

Fig. 5.

Simulation results for the effects of nitrifier populations on different soils. Simulated accumulation in the soil of the produced nitrate in two different soils (solid lines), compared to experimental data corresponding to each soil (marks). Reprinted from [88] with permission from Elsevier

Eukaryotic Cells

Eukaryotic cells are much bigger than prokaryotes, and they also have a more complex structure. Therefore, slight changes must be made to the model of individual cells in order to deal with eukaryotes in the framework of IBM at a mesoscopic stage. Higher structural complexity and different parameters for the interactions with the environment must be considered. We present two applications of INDISIM in the modelling of communities formed by eukaryotic cells. They are specifically focussed on local interactions among cells and how geometric and physical constraints at a system level affect them.

Plasmodium falciparum Infection Dynamics in Red Blood Cell In Vitro Cultures

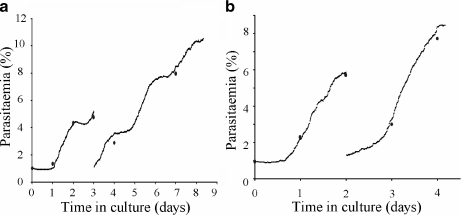
Malaria is still one of the most fatal diseases in the world. Development of an effective treatment or vaccine requires the cultivation of the parasite that causes it: P. falciparum. Current methods for in vitro cultivation of P. falciparum-infected erythrocytes are based on the candle-jar-method [90]. The lack of a suitable model for global culture behaviour makes the assay of new culturing methodologies a costly and difficult task. INDISIM has been used to qualitatively reproduce the whole system dynamics of a culture. The study is focussed on the geometric constraints and physical design of experiments and protocols. Several published experimental cultures have been reproduced, showing that the observed experimental behaviour can be explained by means of individual interactions and statistical laws [91] (Fig. 6).

Fig. 6.

Simulated data compared to experimental results obtained from two different commercial culture media, performed according to the MR4 protocol after one week of culture. Blue dots represent experimental results. Black small dots represent simulation results. a Simulated and experimental results from a synchronous culture. b Simulated and experimental results from an asynchronous culture. Reprinted from [91] with permission from Elsevier

Flocculation in Brewing Yeasts

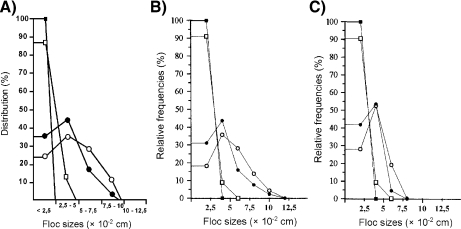
Yeast flocculation is a phenomenon of reversible cell aggregation to form macroscopic structures (flocs). IBM has already been used to study cellular aggregation in biofilms and sludge flocs [92]. INDISIM has been used to examine the predictions of two different models of yeast flocculation [93]. The first, proposed by Calleja [94], is known as the ‘addition’ model. The second, proposed by Stratford [95], is known as the ‘cascade’ model. The simulations show that the latter model exhibits a better agreement with available experimental data [96] (Fig. 7).

Fig. 7.

Size distribution of the flocs, as a function of their magnitude, of the brewing yeast S. cerevisiae at different agitation rates: (open circles) 250 rpm; (filled circles) 500 rpm; (open squares) 750 rpm; (filled squares) 1,000 rpm. a Experimental results after [96]. b Simulation results for the cascade model. c Simulation results for the addition model. Reprinted from [88] with permission from Elsevier

Conclusions and Outlook

Microbes are essential for processes that impinge on nearly every aspect of the biosphere. Microbiology covers a wide range of scales, from the molecular description of cellular mechanisms to the broad perspective of microbial ecosystems in the natural environment. Up to now, most of the knowledge has been provided by these two ends of the spectrum. Yet the study of microbial systems requires a multiscalar description in order to merge the insight obtained at the different levels and obtain a holistic view of the phenomena at hand.

Computational and systems biology reach the cellular level of description through a molecular approach. IBM builds bridges between the cellular and population levels of description. The state of the ongoing development for both methodologies suggests that the connection between the molecular and population levels still needs much more clarification.

In addition to its role in providing this connection, the use of IBM has proved its utility in many areas of microbiology. IBM is useful to check the relations between experimental data and theoretical assumptions, allowing testing of the consistency of different cellular models, and supplying holistic knowledge of the systems under study. Although many challenges hinder the acceptance and productive use of the IBM approaches, models based on individuals have proved that they work well in theoretical and practical applications and are capable of supporting both general and specific treatments of the systems under study.

Starting from the IBM bottom-up approach and taking advantage of the methodologies used in CA models to account for geometrical interactions and MD models to model the microscopic transport phenomena in fluids, our group developed INDISIM, an IBM used to deal with microbial communities at a mesoscopic level of description. Such an approach has proved to be a useful tool to improve understanding of theoretical frameworks and to tackle specific practical applications.

The key point of INDISIM is that it reproduces many observed patterns and relations simultaneously (dependence of bacterial growth rate on the environmental temperature and solute concentration, geometric pattern formation and population dynamics, among others). All the observed phenomena are reproduced with a very simple and general model for the individual cells, and through accurate treatment of the transport phenomena occurring at a mesoscopic scale. For eukaryotic cells, more specific rules have been introduced to account for particular interactions. This generality and the simplicity of the physical assumptions accepted ad hoc make INDISIM a versatile and reliable tool, not to prove any theoretical statement on its own, nor to replace experimentation, but rather to complement and provide support to both approaches.

Appendix 1

Overview of INDISIM according to the ODD protocol [34]

Purpose: INDISIM is designed to simulate the collective behaviour of microbial cultures. In its basic and simplest version, it simulates bacterial growth in a certain culture medium and the growth takes place in a two-dimensional space, but it can be easily extended to three dimensions and modified to deal with other micro-organisms. It is discrete in space and time. The environment is divided into a regular grid of spatial cells. Each spatial cell contains a discrete number of micro-organisms and a fraction of the culturing environment. Events take place at discrete time steps: during a time step, all actions take place, and at the end of each time step, the information about the effects of the set of actions is updated to provide the state of the next time step.

State variables and scales: The main entities of the model are: i) the individual micro-organism, each one characterized by a vector containing its variables B; and ii) the spatial cell locally describing the environmental conditions, each one being characterized by the vector E. Thus, the population composed of N individuals and the whole modeled environment containing M spatial cells are respectively described by the matrices: 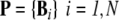and 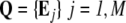. The scales covered by INDISIM range from 1–10 minutes for the time step, and several hours or days for the time horizon, and comprise cell sizes from several microns to a millimeter, while the model extent may reach the centimeter scale.

Process overview and scheduling: The set of rules governing the individual behaviour constitutes the “model of the individual”. This model varies from version to version, depending on the applications encountered by INDISIM. It usually comprises individual processes such as motion, uptake of nutrients, metabolism, excretion, reproduction and death. The set of rules governing the environment at a local scale is called the “spatial model”. It may comprise processes such as diffusion, heat transport, convection, and externally imposed flows, among others.

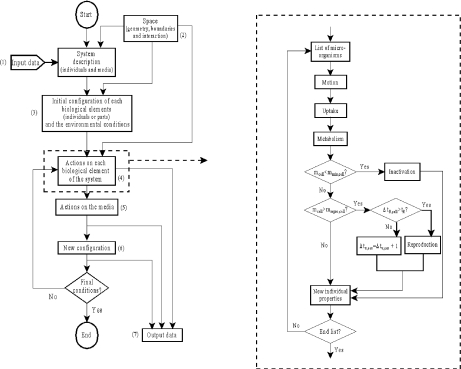
At each time step, individuals act sequentially, but randomness is introduced when setting the order of actions, to minimize the effects of sequential action through consecutive time steps. Once the micro-organisms have performed their set of actions, then the processes regarding the local configuration of the environment are taken into account through actions on each spatial cell. Spatial cells also act sequentially and in random order. Interactions between spatial cells usually comprise solely interactions between first-neighbouring spatial cells. Actions on the system as a whole, such as external inputs, are carried out after individual and local actions have been taken into account. The updating of the state of the system and the outcome of data provided by the model are the last actions performed at each time step. Figure 8 shows flowcharts depicting the global scheduling of the model and the individual set of actions.

Fig. 8.

Flowchart of the computer code (INDISIM). Note that there are three main parts: Initialisation, where the input parameters are read (1), the spatial structure is defined according to the cellular method and periodic boundary conditions [57] (2), and the environment and initial population are configured (3); the main loop, repeated for each time step, which comprises the actions carried out by the micro-organisms (described in more detail in the right box) (4), the actions over the medium (nutrient diffusion or redistribution, enzyme action over polymers, extracellular enzyme diffusion, etc.) (5), and updating of the state of the system (6); and outcome, where the necessary calculations are made to obtain the results (7)

Design concepts: INDISIM is not specifically focused on ecological modeling, so many of the typical aspects that are targets for IBMs in an ecological context are not very relevant for the INDISIM approach. The individual adaptive behaviour, optimization of fitness and the individual’s sensitivity which can modulate such optimization are only addressed under certain conditions of the model. Collectivities such as social groups are not taken into account. The design concepts most carefully studied are the effects on the global behaviour of stochasticity in the individual and local processes, and the variability among the population. Interactions between individuals are also carefully described. Understanding of the emerging phenomena arising from these complexities at a local level is the main goal of this kind of model.

Initialization and input variables: Initialization and input parameters are obtained from experimental measurements or from accepted values found in the literature. This means that most of the values that are used to characterize the system at a cellular level of description are inferred from information obtained at a system level. Initialization parameters give the geometry and spatial structure of the culture system, and the initial population distribution, among others. Input parameters account for the external manipulation of the culture system, for instance the renewal of the culture medium, and imposed flows and agitation of the system, among others.

Submodels: Submodels are specified for each INDISIM application. See references for more detail.