Use of Game-Theoretical Methods in Biochemistry and Biophysics

Abstract

Evolutionary game theory can be considered as an extension of the theory of evolutionary optimisation in that two or more organisms (or more generally, units of replication) tend to optimise their properties in an interdependent way. Thus, the outcome of the strategy adopted by one species (e.g., as a result of mutation and selection) depends on the strategy adopted by the other species. In this review, the use of evolutionary game theory for analysing biochemical and biophysical systems is discussed. The presentation is illustrated by a number of instructive examples such as the competition between microorganisms using different metabolic pathways for adenosine triphosphate production, the secretion of extracellular enzymes, the growth of trees and photosynthesis. These examples show that, due to conflicts of interest, the global optimum (in the sense of being the best solution for the whole system) is not always obtained. For example, some yeast species use metabolic pathways that waste nutrients, and in a dense tree canopy, trees grow taller than would be optimal for biomass productivity. From the viewpoint of game theory, the examples considered can be described by the Prisoner’s Dilemma, snowdrift game, Tragedy of the Commons and rock–scissors–paper game.

Introduction

The mathematical modelling of processes and reaction systems in living cells has recently attracted increasing interest and is an essential part of Systems Biology. This type of modelling is often based on the assumption that biological systems have been optimised during evolution (cf. [1–4]). This is in line with Darwin’s theory of survival of the fittest. In biochemistry, for example, optimality criteria such as maximisation of the adenosine triphosphate (ATP) synthesis flux through a metabolic pathway [1, 2, 5], thermodynamic efficiency [6], biomass production [4], and minimisation of intermediate concentrations [7] have been proposed and analysed.

Traditional optimisation is, however, often insufficient for understanding biological evolution. It needs to be acknowledged that evolution is nearly always co-evolution (cf. [8]); that is, there is a mutual relationship between the properties optimised by evolution and properties of the environment. By evolving towards optimal properties, organisms change their environment, which involves, for example, competing organisms. This, in turn, affects the optimum. Organisms competing against each other can be considered as players in the sense of game theory. Accordingly, evolutionary game theory provides an appropriate framework for analysing evolution in dynamic fitness landscapes [9–12]. Prior to those studies, Eigen and Winkler [13] considered many biological processes, including prebiotic evolution, to have properties of games. Recently, it has become more and more evident that game theory is relevant for biophysics [14–16] and biochemistry [17–21].

In this review, we present several examples showing that evolutionary game theory is indeed useful for biochemistry (Section 3) and biophysics (Section 4). The examples mainly concern the evolution of biochemical pathways and of plant growth. In Section 4, we also briefly discuss to what extent game theory could be relevant in (non-biological) physics and chemistry. Section 2 gives some theoretical background on game theory. It can be skipped by readers familiar with that theory.

Theoretical Background

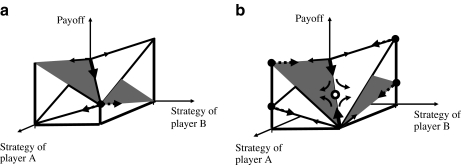
Due to its somewhat counter-intuitive properties, the Prisoner’s Dilemma (PD) has become a very famous game (cf. [10, 11]). The term comes from a hypothesised situation where two suspects of a crime have two possible strategies: to confess or not to confess. However, this game has a wide range of applicability in biology, economics, politics etc. If both players cooperate, their payoff R (reward for mutual cooperation) is higher than their payoff P (punishment for mutual defection) when both defect. A defector playing against a cooperator receives payoff T (temptation to defect), which is higher than R, while a player cooperating with a defector receives payoff S (sucker’s payoff), which is the least payoff. The rank order of payoffs (Table 1) thus is T > R > P > S. Because of this inequality, it is best for a player to choose defection irrespective of the choice of the other player. However, since both players are tempted this way, they end up in the situation where they both get P. This is the only Nash equilibrium of that game. A Nash equilibrium is a situation where none of the players would benefit from changing strategy unilaterally (cf. [11]). As shown in Fig. 1, this paradoxically implies that the players’ tendency to maximise their payoff actually results in a decrease of their payoff (e.g. fitness). In Fig. 1, strategies are considered as continuous variables changing between two extreme states. This can be considered as a generalisation of a game with only two discrete strategies. In fact, continuous strategies are relevant in many situations in biology, e.g. in the variable superposition of two biochemical pathways.

Table 1.

Payoff matrix for the Prisoner’s Dilemma and snowdrift games^a

	Cooperate	Defect
Cooperate	R	S
Defect	T	P

^aThe matrix shows the payoff for the player using the strategies indicated in the row when playing against a player employing the strategies indicated in the column. The payoff for the other player is obtained by interchanging rows and columns. “Defect” stands for the non-cooperative behaviour

Fig. 1.

Plot of the payoffs vs. the strategies of the two players in the Prisoner’s Dilemma (a) and snowdrift game (b). Strategies are here continuously varying between two extreme values, with the origin of coordinates corresponding to the strategy pair “cooperate, cooperate”. Grey (white) planes Payoffs of player A (B). Solid thin black arrows Temptation of leaving a point by player A or B. Solid thick black arrows Resultant effects. Dashed arrows Only possibilities to leave the Nash equilibria when switching alone. These are not chosen because they decrease the payoff. Filled circles Nash equilibria. In b, the point indicated by an empty circle is (in the two-player game) unstable with respect to small fluctuations

A game that is also important in biology is the so-called snowdrift game (cf. [22]). The term comes from an illustration in terms of two car drivers caught in a blizzard. This game is also known as the hawk–dove game or the game of chicken (cf. [11]). In the payoff matrix of this game, the order relation T > R > S > P holds (Fig. 1b). The game has two Nash equilibria: “cooperate/defect” and “defect/cooperate”. In the example of two cars stuck in a snowdrift, this means that one (and only one) driver gets out of the car and clears the road, which is better for this driver than not clearing the snowdrift at all.

In biology, often more than two individuals or more than two species interact. Maynard-Smith [9] put forward a generalisation in that he considered the interaction between many players. This generalisation can be achieved by considering consecutive encounters of two players (such as male deer competing for females in a forest) or the quasi-simultaneous interaction of each player with all other players, often called “playing the field” [9]. Maynard-Smith generalised the concept of Nash equilibrium to that of evolutionarily stable strategies (ESS). Strictly speaking, the latter term is somewhat more restrictive. Each ESS is a Nash equilibrium, but not vice versa. A strategy played by a population is evolutionarily stable if it cannot be invaded by a rare mutant playing another strategy. Note that these strategies can be mixed; that is, a certain percentage of the population plays the first strategy (e.g. “cooperate”) and the remaining percentage plays the other strategy. In fact, the (only) ESS of the snowdrift game is mixed. By contrast, the only ESS of the PD is the pure strategy of “defecting” (cf. [11]). In the PD, defection is always the “better” strategy, even at a high frequency (percentage) of defectors where they mostly play against other defectors, gaining payoff P. In contrast, in the snowdrift game, the fitness of defectors playing with other defectors is lower than the fitness of cooperators playing with defectors. This makes the snowdrift game more appropriate for many biological examples than the more stringent Prisoner’s Dilemma.

The generalisation of the PD to more than two players has been termed “Tragedy of the Commons” [23] (see also [24]). Commons are public goods such as the pasture of a village or the fish stock in the ocean. Each of n users of the commons is tempted to exploit the commons as much as possible. However, when all users act in this way, the commons are emptied. In situations of a Tragedy of the Commons, the ideas on ESS can be applied [9]. Thus, defecting is again the only stable strategy.

Game Theory and Biochemistry

Choosing the “Best” Metabolic Pathway

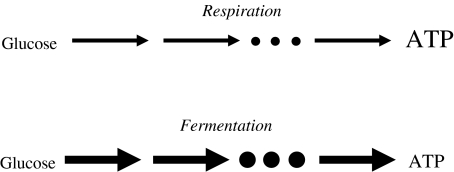
Many organisms have had multiple possibilities of choosing a biochemical pathway for a given biochemical transformation during evolution or can change pathway usage even during the life span of one individual by regulation. For example, many bacteria such as Escherichia coli show the phenomenon of catabolite repression; that is, utilisation of some sugar (e.g. lactose) is repressed as long as glucose is available, and when glucose is depleted, they change pathway usage. Another example is provided by Saccharomyces cerevisiae (baker’s yeast), which, for degrading glucose to produce ATP, uses respiration (oxidative phosphorylation) and respiro-fermentation at low and high glucose levels, respectively (Fig. 2). The former pathway has a ATP-over-glucose yield of about 32 and a relatively low rate, while fermentation only allows for a yield of two, but its rate of ATP production is usually higher than that of oxidative phosphorylation. For example, in muscle cells, where both pathways exist as well, it is up to 100 times faster (cf. [25]). Respiro-fermentation means that respiration is used at maximum rate, and fermentation is used in addition.

Fig. 2.

Schematic picture showing the two different pathways of ATP formation from glucose. The thickness of arrows (schematically) represents ATP production rate, while the size of the symbol ATP (schematically) represents the amount of ATP produced per mole of glucose

When two species or strains compete for the same substrate, a typical game-theoretical situation arises. The fitness of either organism depends not only on its own strategy (pathway usage in this case) but also on that of the other because both strategies affect the common substrate pool. In order to use external glucose as economically as possible, it would be best if all organisms in a given habitat opted for respiration. However, baker’s yeast uses respiro-fermentation even under aerobic conditions, provided that sufficient glucose is available. The evolutionary reason for this profligate utilisation of glucose is that it thus out-competes organisms using pathways with lower ATP production rate even if their yield is higher. However, as we will discuss later in this section, many wild yeasts tend to respire glucose under aerobic conditions (cf. [26]).

The dynamics of two competing populations (labelled by indices 1 and 2) able to choose between two different pathways can be described by the following differential equations [17]:

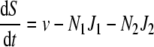1

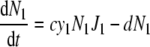2

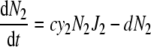3

with the following symbols: S, substrate concentration, v, input rate of substrate, y, ATP-over-substrate yield, N, population density, J, rate of substrate consumption, and d, death rate. J₁ and J₁ are functions of S, for example, Michaelis–Menten functions. c denotes the proportionality constant connecting growth rate with ATP formation rate. It is assumed to be equal for both populations in order that the only difference between the populations is their usage of different pathways for ATP production. The above equation system describes a simple growth situation where the nutrient comes in at a constant rate and is consumed only by the two populations. The populations grow as a function of the nutrient level and die with a constant rate constant. Note that growth in a chemostat requires somewhat modified equations, in which the outflow of nutrient and cells needs to be included.

Two-player games are often formalised by using payoff matrices (see [9, 11, 27]). The question arises as to what the relevant payoff is in the above-mentioned rate vs. yield “game”. A careful choice of payoff is clearly crucial. In game theory, usually, per capita reproduction rate is taken as payoff. For growth in biofilms [19], a more suitable choice is reproduction rate per area covered by the biofilm, which depends less on the specific growth rate but more on the efficiency with which the diffusional substrate flux into the biofilm is converted into biomass – the yield. It would be useful to have a time-invariant payoff. Therefore, for systems that do not reach a steady state, reproduction rate, which usually changes in time, should be integrated over the entire life span of the individual. This is equivalent to direct fitness, that is, the component of fitness gained through the reproduction of the individual itself, but does not consider indirect fitness through helping the reproduction of relatives [28]. In our example, as can be seen from the above equation system, we have a system with constant substrate input and mortality, so the substrate level and both population densities attain a steady state (in which population density might be zero). At steady state, reproduction rate equals death rate, which is a constant parameter for either species. Thus, it does not depend on the strategies chosen. As an alternative to taking reproduction rate as the payoff, it has been suggested that, in situations where a steady state is reached, the steady-state population densities could be taken as payoffs [29]. For the case that the two populations use the same strategy, the steady-state population densities should then be divided by two, since each species has a 50% chance of survival, due to the principle of mutual exclusion (cf. [30]). Taking the steady-state densities as payoffs is supported by a suggestion by Rieck [31] concerning the description of autocatalytic polymerisation reactions by game theory (cf. Section 4). He proposed to take the final relative amount of the macromolecules as payoffs. However, for the respiration vs. fermentation game, this choice has the drawback that the Nash equilibrium calculated in this way does not always coincide with the stable steady state resulting from the population dynamics Eqs. 1, 2 and 3. Further work is needed for defining an appropriate payoff function for the “rate vs. yield game”, especially because the payoffs depend on the extent of mixing in the population (population viscosity) and the spatial scale of competition. This work may benefit from game theory as applied to economics, where dilemmas exist in the competition between companies using efficient and wasteful strategies.

With parameter values from Pfeiffer et al. [17], a payoff matrix as shown in Table 1 with the order relation T > R > P > S can be established for well-mixed populations with global competition [28]. Thus, the conditions for a Prisoner’s Dilemma are fulfilled (see Section 1). Although it would be best for both players to opt for respiration (which can be considered as a cooperative strategy), they are tempted to switch to respiro-fermentation (which can be considered as a selfish strategy). As this applies to both, they end up in the situation that they both use the selfish strategy, as is typical for the PD. In game-theoretical terms, this is the Nash equilibrium of the game and the evolutionarily stable strategy (cf. [11]). It is the stable solution because it cannot be left without a mutual agreement of the two players, which cannot be expected from microorganisms. This is visualised in Fig. 1. It is worth noting that the Nash equilibrium of the PD is even more relevant in microbiology than in the original cover story or other sociological applications because the psychological factors (which may lead to cooperation) are absent in microorganisms. Alternatively, the rate vs. yield game can be regarded as a Tragedy of the Commons [17].

From the above game-theoretical arguments, it follows that microorganisms should have evolved in a way that ATP synthesis flux rather than yield was maximised. In fact, several yeasts, for instance, S. cerevisiae, Saccharomyces bayanus, Schizosaccharomyces pombe, Kluyveromyces thermotolerans, and Dekkera bruxelensis, use the competitive strategy of fermenting sugars even under aerobic conditions. In contrast, other yeast species, such as Yarrowia lipolytica and Pichia membranifaciens, rely on respiration and are non-fermentative. Still some other yeasts, for example Kluyveromyces marxianus and Pichia fermentans, are able to use fermentation but do so practically only under anaerobic conditions (a nice overview of these three groups is given in [26]). It may be hypothesised that S. cerevisiae regressed to respiro-fermentation during domestication because it was selected for this pathway, which produces the ethanol desired in brewing [32]. However, as some wild yeasts are also respiro-fermentative, the above game-theoretical explanation appears to be relevant not only for domesticated species. Another hypothesis, which is supported by genome analyses, says that a genome duplication in an ancestor of S. cerevisiae has led to an increased gene dosage of glycolytic enzymes and thus to an increased flux of fermentation [33]. That genome duplication appears to have occurred in the same era as the emergence of angiosperms and hence of glucose-rich fruits, so that fermentation allowed a high ATP production flux. The question remains why some yeast species have opted for cooperative strategies although these are unstable with respect to invasion by selfish mutants.

Two possible explanations for cooperative pathway usage have been given by MacLean and Gudelj [34]. In very instructive experiments, a respiro-fermenter (cheater) strain of S. cerevisiae competed against an otherwise identical respirator strain, TM6*. In the chemostat, the cheater had a higher fitness than the cooperator, and competition resulted in exclusion of the cooperator strain, in line with the above-mentioned Nash equilibrium (sometimes, the terms cheater and defector are used with a somewhat different meaning, in that a defector is only called a cheater if it gains an advantage from this behaviour. Here, we will use both terms synonymously). A second set of experiments was carried out in batch cultures in such a way that a fixed amount of glucose was supplied at the beginning, which then becomes increasingly depleted, and the survivor cells were transferred into a new medium with the same amount of initial glucose, and so on. In this case, stable coexistence of the two strains was observed. MacLean and Gudelj [34] could explain the permanent survival of the cooperators by mathematical modelling: the combination of a seasonal environment provided by batch cultures, where metabolic intermediates can accumulate, with the toxic effects of the intermediates preferentially produced by the cheater strains, such as ethanol, is crucial. These toxic effects increase the costs of cheating with increasing frequency of cheaters producing the toxic intermediates so that the fitness of cheaters drops below the fitness of cooperators at sufficiently high frequency of cheaters. This frequency dependence suggests that the payoffs in this seasonal system correspond to the snowdrift game. It had been shown earlier that coexistence is favoured in an oscillating environment and that periodicity increases the number of niches in the sense of the principle of competitive exclusion [35].

MacLean and Gudelj [34] also studied local competition in isolated patches, where the cooperators persisted in the metapopulation consisting of all local populations in the patches, provided that the frequency of the cheaters and the density of the population were low enough so that sufficiently many patches were dominated by cooperators. Analogous to this study of respiratory vs. respiro-fermentative yeasts, T4 phages also differ in their efficiency of exploiting their resource, E. coli cells, where the faster reproducing phages produce fewer offspring from their commons [36]. As predicted by models of competition of fast and inefficient vs. slow and efficient strategies in different environments with spatial structure [17, 37, 38], local dispersal of the competitors allows the cooperative strategy of efficient resource use to evolve.

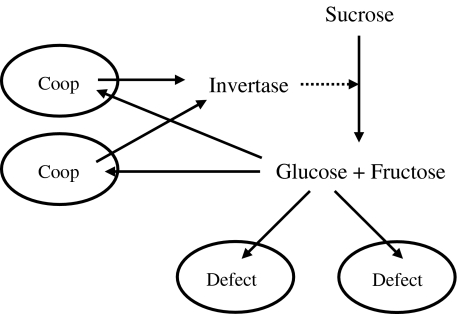
S. cerevisiae is involved in yet another interesting game, which concerns the secretion of invertase [18] (Fig. 3). Invertase is secreted as a “public good” when the medium involves sucrose (and no glucose), which is digested by this enzyme. The resulting glucose is then taken up by the yeast cells. Since production and secretion of invertase are costly, a cheating strategy is to take up glucose without making a contribution to the common pool of invertase. Greig and Travisano [18] observed experimentally that defectors had a higher growth rate when the density of secreting cells was high but were less fit when cell density was low (the experiment started with a mixed population consisting of equal amounts of defecting and cooperating cells spread out on an agar plate). The former observation can be explained by the lower costs of cheater cells not investing into invertase production and secretion, and the latter by the finite diffusion coefficient of invertase and glucose, implying that extracellular glucose levels in this non-mixed environment are lower around defector cells. Thus, the spatial separation of invertase-producing cells from defector cells guarantees a coexistence of cooperator and defector cells. A simple scenario would be that yeast cells secrete invertase only if there is lack of glucose and switch off invertase secretion if the glucose level is high enough. That should regulate production to an optimal level. Greig and Travisano [18] classify the type of game to be a Prisoner’s Dilemma, although their data are not sufficient to support that conclusion [37]. Indeed, since the payoff for the case where all cells defect is the minimum payoff (cells die due to lacking glucose), it is more likely to be a snowdrift game. This can best be seen by assuming that there are only two cells. Then, if they are near to each other and one of them secretes invertase, the other can easily benefit from that (resulting in payoff T), while the invertase producer has a higher fitness (payoff S) than if both would defect (payoff P). The exact type of the game might, however, depend on the availability of alternative nutrients.

Fig. 3.

To digest sucrose, baker’s yeast secretes the enzyme invertase, which splits sucrose into glucose and fructose outside of the cytoplasm. Cheater cells (marked Defect) do not produce invertase and benefit from the glucose resulting from the enzyme secreted by other cells (Coop). As the synthesis of invertase implies metabolic costs, cheater cells can grow faster. However, at low cell densities, the glucose concentration around cheater cells becomes so low that they grow more slowly than cooperating cells (cf. [18])

Invertases in yeast are encoded by the members of the SUC multigene family, which is remarkably polymorphic in that the number and functionality of these genes vary considerably between different yeast strains [39]. Greig and Travisano [18] “played” the game by measuring the fitness of defector cells with a deleted SUC2 gene relative to an otherwise isogenic cooperator with a functional SUC2 gene. SUC genes show the interesting phenomenon of “silencing”. They are repressed at random, and normal expression is resumed only after several generations. Thus, changing strategies is easily feasible. Silencing might allow defectors to keep an unused backup copy of a SUC gene. Random restoration of this gene could be selected for when cell density is low.

Another example is provided by the metabolism of E. coli. Populations of ‘wild-type’ E. coli K12 arrest growth before the nutrient has been completely depleted. This occurs in response to several extracellular and intracellular signals. This programmed transition to a non-dividing state of reduced metabolic activity allows E. coli to survive longer because it can be sustained on the remaining resources for a longer time. However, there are the so-called growth advantage in stationary phase (GASP) mutants, which do not respond to the signals and therefore continue growing at the expense of the scarce resources still available [40]. This results in an increasing frequency of the GASP mutants during stationary phase in mixed cultures. GASP mutants show a higher relative fitness than the cooperating wild type at all relative frequencies in mixed cultures, but the advantage decreases with increasing frequency of GASP. In contrast, pure cultures of GASP mutants have higher death rates in the stationary phase. The competition between the wild-type and GASP mutants is equivalent to a Prisoner’s Dilemma (cf. [37]).

Transition to Cooperation

During evolution towards multicellular organisms, a transition to cooperative behaviour between the cells belonging to the same organism has taken place [41]. The cooperative, efficient use of resources could have been an immediate fitness advantage of multicellular organisms because it does not require the consecutive evolution of specialisation, that is, the division of labour between different types of cells of the multicellular organism [17, 38]. In fact, most cell types in multicellular organisms rely on respiration. There are some exceptions, though. Mature mammalian erythrocytes do not harbour mitochondria (or any other organelles) and, consequently, synthesise their ATP exclusively by glycolysis. The reason is likely to be that almost their entire volume is needed for haemoglobin used for oxygen transport. The volume, in turn, is restricted because erythrocytes need to pass thin capillaries. In a sense, erythrocytes can be considered as “slaves” of mammals including humans because they transport oxygen but are not allowed to use it. Interestingly, erythrocytes of nearly all other vertebrates do contain mitochondria.

Another exception is provided by striated muscle cells in higher animals. While these cells use respiration when mechanical demand is low, they include pure glycolysis above a critical threshold of demand, for example, during heavy exercise. This is due to diffusion limitation of oxygen. Although the lactate produced in muscle and erythrocyte glycolysis is recycled to give glucose in the liver, this cycle is costly in terms of ATP. Interestingly, skeletal muscles consist of two types of fibres: slow- and fast-twitch fibres (cf. [25]). Fast-twitch fibres are predominant in muscles capable of short bursts of fast movement and do not contain any, or only a few, mitochondria. These fibres obtain nearly all ATP by glycolysis. Examples are provided by flight muscles of chicken and turkey and the tail muscle of crocodiles (cf. [42]), which are only used for short bursts. Slow-twitch fibres, in contrast, predominate in muscles contracting slowly and steadily. They involve many mitochondria, which perform oxidative phosphorylation. Examples are provided by flight muscles of migratory birds, which are therefore characterised by dark breast meat (the dark colour arising from the haem group in the cytochromes of mitochondria). Migratory birds need to get by with a restricted amount of energy over long flying distances and, thus, have to use the resource very economically. For other birds, it is important to escape a dangerous situation very quickly, and moreover, it is favourable for them to reduce the number of mitochondria in order to save space for more contractile fibres per volume.

The meat of domesticated animals such as the domestic pig is usually brighter than that of their wild counterparts, indicating that they contain less mitochondria. This is probably due to a lighter use of their muscles and, hence, of a reduction in oxidative phosphorylation. Thus, there is an interesting analogy to the “domesticated” yeast, S. cerevisiae.

Another interesting example is provided by astrocytes in mammals. These are brain cells working together with neurons in many respects. One way of cooperation is that astrocytes secrete lactate originating from degrading glucose by glycolysis, while neurons feed on both glucose and lactate and degrade these to carbon dioxide and water by respiration [43]. This division of labour is reminiscent of cross-feeding in microorganisms, and although it may have evolutionary reasons different from those put forward for the case of microorganisms [44, 45], it shows that the analysis of intracellular networks should be extended to intercellular networks. This is indeed a current trend [21, 44, 45]. Game theory is then helpful as well.

As for most other cells types, the question arises as to how the evolution towards economic resource utilisation by respiration has been possible, although cooperative strategies are unstable unless other factors intervene, as mentioned above. This can clearly be seen by malignant tumours. As had been observed by Otto Warburg, tumour cells essentially rely on fermentation as long as they are not yet vascularised, using glucose and glutamine as their main substrates [46]. Tumour cells have smaller numbers of mitochondria and overproduce several glycolytic enzymes [42]. Recently, it has been shown experimentally that stimulation of respiration by frataxin in colon cancer cells reduced growth rate [47]. Thus, cancer can be regarded as a regression to selfish behaviour of cells. Healthy higher organisms possess regulation mechanisms to suppress cancer. However, in early evolution of multicellularity, these mechanisms probably did not yet exist. Analysis of cancerigenesis by game-theoretical methods appears to be a promising approach [48]. Interestingly, the differential equations for the glucose level and the populations of healthy cells and various tumour genotypes proposed in that paper are similar to Eqs. 1, 2 and 3.

One potential mechanism supporting the emergence of cooperation is the phenomenon of stochastic extinction. Species with low population numbers will eventually die out due to fluctuations because they cannot recover from a fluctuation leading to a population number below a critical threshold [49]. Importantly, species opting for fermentation or respiro-fermentation attain, after the respirators have been out-competed completely, lower population densities than respirators would alone because the former use the substrate less economically. Thus, they are more susceptible to stochastic extinction. It remains to be checked, though, how relevant this is for microorganisms as compared to higher organisms because the former are usually present in higher numbers. Furthermore, stochastic extinction will only occur in a certain patch, which might subsequently be re-colonised from neighbouring patches.

Another important aspect is organisation in space, as seen above for the spatial heterogeneity of invertase and glucose surrounding yeast cells. In the respiration vs. fermentation game, coupled aggregates of respirators can support each other. As respirators can live on lower substrate levels, such aggregates can hinder selfish cells from invading. In fact, two types of invasion need to be distinguished: immigration from outside of the aggregate and mutation of cooperator cells into selfish cells (as in cancer). The former scenario may be impeded by physical hindrance [50] and the latter by stochastic extinction [51]. Numerical simulations on a two-dimensional grid show that, at low substrate input and slow cell diffusion, respirators can win due to stochastic and spatial effects [17]. It is understandable that cell diffusion must be slow because, otherwise, cell aggregates are destroyed by diffusion. In the mathematical description, care should be taken when spatial structure changes the payoff matrix.

Game Theory and Biophysics

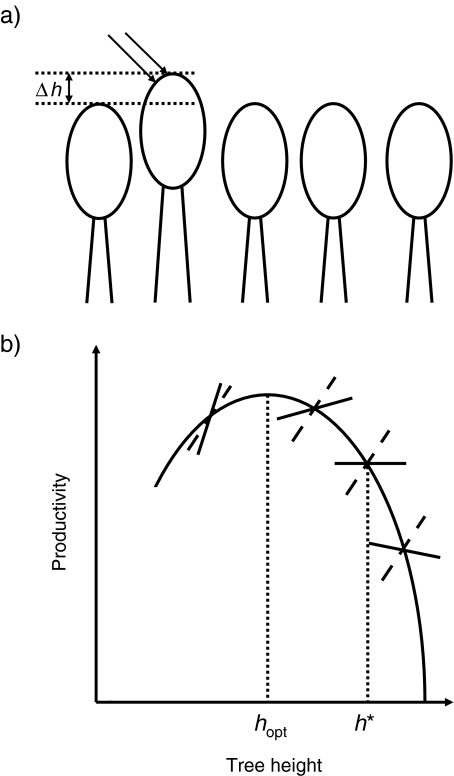
An important field where game-theoretical methods are applied in biophysics is photosynthesis and the growth of trees. The competition for light among plants in dense canopies leads to a “Tragedy of the Commons” [14–16]. This can easily be explained by the example of tree height (Fig. 4). Plotting the rate of biomass production vs. tree height gives a parabola-like curve showing a maximum ([52], see Fig. 4b). Among other things, this is due to the fact that, as height increases, plants have to invest disproportionate amounts of biomass into support structures such as stems. It would be best for all trees in a forest to reach exactly the height optimal for biomass production. However, this is not an evolutionarily stable strategy. It can be invaded by trees that are taller. Although they have a lower production rate, they reduce the light available to neighbouring trees so that those have an even lower production rate in the end. Different approaches have been proposed to compute the evolutionarily stable tree height (for review, see [15]). A phenomenological approach proposed by King [52] is illustrated in Fig. 4b. The evolutionarily stable height is somewhat larger than the optimum height. This Tragedy of the Commons can be decomposed into PD’s between pairs of neighbouring trees. Let us, for simplicity’s sake, discretise the height into two values, the optimal and a somewhat higher value. The cooperator strategy is to grow until reaching the optimal height, while the defector strategy is to grow taller because this would increase productivity at the expense of the productivity of the other tree because the former takes away some sunlight from the other. However, since both trees are “tempted” that way, they both grow taller, resulting in a lower productivity for both of them.

Fig. 4.

Illustration of the game of tree growth. a Schematic representation of a tree canopy in which all but one tree have reached an optimal height. The selfish outlier tree is taller and invests a higher percentage of biomass into supporting structure (stem). Although it can thus invest less into other parts, it has a competitive advantage because it absorbs sunlight (shown as two arrows) that would otherwise reach the neighbouring trees. Therefore, the other trees are forced to grow taller as well or are out-competed (cf. [16]). Δh Height difference. b Determining the evolutionarily stable tree height. The parabola-like curve shows the empirically determined dependence of productivity, p (biomass production per time) on tree height, h. Assuming that one tree is taller than all neighbouring trees by Δh, this gives it an advantage in productivity of Δp, which is approximately independent of h itself. The dashed straight lines have the slope Δp/Δh, that is, they depict the gain in productivity by growing taller. The solid straight lines represent the net effect. The evolutionarily stable height, h*, is reached when this net effect is zero due to investing more into supporting structures, that is, when the straight line is horizontal. Clearly, h* is larger than the optimal height, h_opt

The carbon gain from photosynthesis is influenced also by the vertical distribution of leaf area, nitrogen, and light. For maximal carbon gain by a canopy, nitrogen should be distributed according to the light gradient such that the content per unit leaf area is high at the top of the vegetation and low at the bottom. However, plants following this strategy are out-competed by invading plants that increase their specific leaf area (SLA, leaf area per leaf mass; cf. [14]). As a consequence, the light interception and the photosynthetic nitrogen-use efficiency (PNUE, the rate of photosynthesis per unit organic nitrogen) is greater for the invaders and so is the carbon gain. The invading strategy succeeds. However, since the nitrogen is diluted over a larger leaf area, the rate of photosynthesis based on leaf area decreases [14].

Round per round of the game, the SLA increases to a maximum value limited by a minimum nitrogen content per unit leaf area required for photosynthesis besides preventing the leaves from becoming frail. As this evolutionary stable strategy is reached, the total leaf area per unit ground area has reached a higher value. On the other hand, the canopy photosynthesis and carbon gain of each individual are lower than in the optimum stand. In fact, the maximisation of PNUE in upper parts of the canopy during the game does not outweigh the losses of light in lower parts of the canopy associated with a lower PNUE [14]. Moreover, plants that grow in the proximity of neighbours appear to over-invest in roots to acquire soil resources that would otherwise be acquired by neighbours [16].

While game theory has been applied in many fields such as economy, psychology and biology (including behavioural sciences, microbiology and biochemistry), applications in (non-biological) physics and chemistry are rare. Preliminary ideas on how to use game theory in chemistry have been put forward by Bartel [53] and Goodman [54]. The latter author compared the synthesis of organic compounds in a lab with a chess game because each “move” can have dramatic consequences at later stages. Adopting ideas of Eigen and Winkler [13], Rieck [31] suggested describing autocatalytic polymerisation reactions by game theory. When two macromolecules, A and B, compete for the same set of monomers, the final state corresponds to a Nash equilibrium.

As explained above, game theory can be considered as an extension of the theory of optimisation in that not only one objective function is maximised (or minimised) but two or more, corresponding to the payoffs for the two or more players. Maximisation and minimisation problems also occur in physics. For example, the Lagrangian and Hamiltonian formalisms in classical mechanics are based on extremality principles. The Second Law of thermodynamics says that the entropy in closed systems becomes maximised. In isothermic systems, free energy is minimised. If the effect of entropy can be neglected, this is practically equivalent to a minimisation of energy.

Can situations occur that can be described by physics and involve two or more extremality principles such that methods from game theory can be helpful? One might think of systems that consist of two subsystems, each of which tends to maximise its entropy or minimise its energy. However, these state variables are additive. Thus, one can find a total entropy or energy of the entire system, which tends to an extremum value. This differs from the typical game-theoretical situations where a global payoff does not govern the evolution of the system even if it can be defined mathematically. When there is an interaction energy between the two subsystems, this must also be added. In such cases, partitioning the energy into the two subsystems is difficult. Nevertheless, some ideas in that direction have been put forward (most of them for biophysical applications, though). For example, Kovács et al. [55] suggested that the binding of two proteins to give a protein complex can be regarded as a “game” in which both proteins have two possible strategies. Elaborating on their ideas, one could imagine that each of the proteins can be either flexible or rigid. If both are rigid and their shapes do not coincidentally match, binding is impossible. If one of them is rigid and the other flexible, they are able to bind. If both are flexible, they can bind, but with no fixed resulting shape of the complex, which may be biologically useless. Therefore, speaking in anthropomorphic terms, it is best if one of them is rigid and dictates the shape while the other surrenders. This is the classical hawk–dove game (snowdrift game, see Section 2). Although complex formation is accompanied by a binding energy, energy is here not the only relevant parameter. Rigidity is the parameter describing the strategy. The payoff may be identified with the molecule numbers of the two proteins, which need not be the same.

Another relationship between game theory and physics arises by utilising methods from physics to solve game-theoretical problems. For example, cooperation in the PD can emerge when the game is played in a spatially structured population. Then, methods from percolation theory on square lattices and small world networks can be employed (cf. [56]). When studying the emergence of cooperation in the PD in a spatial setup, the effect of noise added to the payoffs leads to the phenomenon of coherence resonance [57]. Another example is the use of irreversible thermodynamics in analysing the switch between competition and cooperation in metabolism [58].

Recently, an interesting extension of game theory by concepts from quantum mechanics has been proposed [59, 60] (cf. [61]). In contrast to “classical games”, where only pure states can occur, in quantum game theory, mixed states are also allowed, such as an equal mixture of heads and tails in each state when tossing a coin [59]. Moreover, an entanglement of the players such as the entanglement of elementary particles in quantum mechanics can lead to a Nash equilibrium “cooperate, cooperate” in the PD [60].

Discussion

In this review, we have discussed several examples of relevant and insightful applications of game theory to biochemistry and biophysics. Of course, it is difficult to draw a clear-cut boundary between biochemical and biophysical problems, and some of the examples concern neighbouring fields such as plant physiology.

The term “game theory” may suggest that it is only applicable when a game is played rather than to “serious” things. However, as the subtitle of the monograph by 2007 Nobel prize winner R.B. Myerson, “Analysis of Conflict” [27], suggests, it describes situations of conflict, warfare and other extremely serious situations. A situation of chemical warfare in biology is the production of anti-bacterial toxins (bacteriocins) by bacteria. This can be regarded as a “rock–scissors–paper game” because toxin producers out-compete sensitive strains, sensitive strains grow faster than resistant strains, and resistant strains grow faster than toxin producers [36, 62, 63]. The rock–scissors–paper game has attracted ample interest in game theory [11]. Note that the order relation of fitness is then not transitive, so that there is no fittest organism.

A difficult issue in the study of optimality properties of biological organisms is to find the relevant optimisation principle. As for metabolic pathways, several authors started from the assumption that pathway flux (i.e. product formation per time unit) should be maximised [2, 3, 5] while others argued that molar yield (i.e. product formation per mole of substrate) should be maximised [64–66]. Both assumptions sound plausible. Importantly, in many situations, they are not, however, equivalent. This can be understood by the analogy to a car. At low driving velocities, increasing the velocity implies reducing the gas consumption per mile. Above an optimal speed, however, increasing the velocity implies increasing the gas consumption per mile. In that range, both criteria are contradictory. Game-theoretical approaches can help one to decide what the relevant optimisation principle is. For a more detailed comparison of the optimality principles of maximising rate and maximising yield, both with respect to the experimental literature and theoretical arguments, see [17, 67, 68].

Studying the trade-off between rate and yield of ATP production on the basis of evolutionary game theory reveals that competition for shared energy resources should lead to the evolution of fast but inefficient ATP production when competition is global, although slow but efficient ATP production would be more beneficial for all users of the resource. This paradoxically implies that the users’ tendency to maximise their fitness actually results in a decrease of their fitness. Thus, the whole can be worse than the sum of its parts (as in any arms race). From a game-theoretical point of view, this can be regarded as a Prisoner’s Dilemma or a Tragedy of the Commons.

Applying game theory does not imply that the players must be rational beings (cf. [9]). The change in strategy can occur, for example, by mutation epigenetic modifications and selection. Thus, interactions between microorganisms can certainly be described by that theory. Nevertheless, this is accompanied by some epistemological issues. Because microorganisms have neither reason nor motivation, they are entirely “rational” players in the sense of being selected so as to increase their fitness, in contrast to human behaviour that is influenced by moral and sociological factors and often shows non-rational behav/-break iour such as acts of defiance. Nevertheless, in most game theoretical studies, human behaviour is assumed to be rational. The rationality of microorganisms does not stem from reason but from a “choice” of strategies by mutation, epigenetic modifications and selection, which can, in large part, be treated by the same mathematical methods as a deliberate choice by rational beings. An objection against using game theory in biology is that it involves a number of anthropomorphic concepts, such as strategy, cooperation, altruism, competition and selfishness. However, it should be realised that the mathematical results obtained by game theory are not influenced by the terminology of the payoffs but only by their values. In addition, the same results can be obtained by population dynamics without using anthropomorphic concepts. An advantage of game theory is that the kinetic parameters for simulating the time behaviour of reaching the final state (e.g. the Nash equilibria of game theory) are not needed. This is analogous to the advantage of structural (stoichiometric) modelling in comparison to dynamic modelling of metabolic networks [2]. Another advantage of game theory is that the results can be interpreted more readily because the above-mentioned anthropomorphic concepts are easily understandable by humans. Thus, these concepts are auxiliaries for understanding co-evolution more easily. The same applies to optimisation approaches because optimality is an anthropomorphic concept as well. However, when using terms such as “optimal”, “advantage” or “benefit”, one should take care to specify for whom a strategy, behaviour or property is optimal or advantageous, for the individual or the community.

The considerations on cancer in Section 3 exemplify some aspects of the emerging field of evolutionary medicine [69]. The disease of cancer can be regarded as a regression (by mutation) to selfish behaviour of cells. In a sense, it shows that selfish behaviour is advantageous in the short run, although in the long run, it may kill the organisms and thus the tumour. Studying the evolution of control mechanisms that normally prevent the occurrence of cancer is an interesting question.

In Section 4, we reviewed some work on evolutionary stable strategies in photosynthesis and plant growth. It can be concluded that the structure and productivity of plant stands apparently exhibit the result of a Tragedy of the Commons because maximisation of individual fitness is often in conflict with maximisation of stand productivity. Plants in dense canopies over-invest in height growth and leaf area production. This over-investment reduces the net photosynthetic rate and the associated growth of the vegetation stand.

An interesting question is whether also interactions between proteins, genes and/or other structures on the molecular level can be described by game theory. As genes are units of replication, they are subject to mutation and selection. In that context, the concept of the “selfish gene” proposed by Richard Dawkins (cf. [70]) is also worth mentioning. If genes really act rather independently and selfishly, they can certainly be considered as players in the sense of game theory and so can the corresponding gene products, for example, proteins or regulatory RNAs. For example, a protein that is very flexible at the outset can, by mutation, become more rigid in the next generation of the organism harbouring that protein. It is worth noting that the so-called Shapley value, which is a concept from game theory, has been applied to computational neuroscience, with different brain areas considered as “players” [71]. The Shapley value is used for calculating the contribution of players in a coalition to the overall performance (cf. [27]). We also discussed some ideas on how to apply game theory to physics. It is, however, not yet completely clear whether separate and non-additive payoff functions for two or more subsystems can be found in physical systems.