Muscles do more positive than negative work in human locomotion

Summary

Muscle work during level walking and ascent and descent ramp and stairway walking was assessed in order to explore the proposition that muscles perform more positive than negative work during these locomotion tasks. Thirty four healthy human adults were tested while maintaining a constant average walking velocity in the five gait conditions. Ground reaction force and sagittal plane kinematic data were obtained during the stance phases of these gaits and used in inverse dynamic analyses to calculate joint torques and powers at the hip, knee and ankle. Muscle work was derived as the area under the joint power vs time curves and was partitioned into positive, negative and net components. Dependent t-tests were used to compare positive and negative work in level walking and net joint work between ascent and descent gaits on the ramp and stairs (P<0.010). Total negative and positive work in level walking was −34 J and 50 J, respectively, with the difference in magnitude being statistically significant (P<0.001). Level walking was therefore performed with 16 J of net positive muscle work per step. The magnitude of the net work in ramp ascent was 25% greater than the magnitude of net work in ramp descent (89 vs −71 J m⁻¹, P<0.010). Similarly, the magnitude of the net work in stair ascent was 43% greater than the magnitude of net work in stair descent (107 vs −75 J step⁻¹, P<0.000). We identified three potential causes for the reduced negative vs positive work in these locomotion tasks: (1) the larger magnitude of the accelerations induced by the larger ground reaction forces in descending compared to ascending gaits elicited greater energy dissipation in non-muscular tissues, (2) the ground reaction force vector was directed closer to the joint centers in ramp and stair descent compared to ascent, which reduced the load on the muscular tissues and their energy dissipating response, and (3) despite the need to produce negative muscle work in descending gaits, both ramp and stair descent also had positive muscle work to propel the lower extremity upward and forward into the swing phase movement trajectory. We used these data to formulate two novel hypotheses about human locomotion. First, level walking requires muscles to generate a net positive amount of work per gait cycle to overcome energy losses by other tissues. Second, skeletal muscles generate more mechanical energy in gait tasks that raise the center of mass compared to the mechanical energy they dissipate in gait tasks that lower the center of mass, despite equivalent changes in total mechanical energy.

Introduction

Animal locomotion is a complex process that includes the generation and dissipation of mechanical energy (i.e. positive and negative work) throughout the stride cycle. Locomotion at constant average velocity and on level terrain utilizes equivalent and counterbalancing phases of positive and negative work to maintain a singular average energy level. Non-level gaits such as walking on stairs or a slope are biased towards positive or negative work for ascent or descent, respectively. When performed at a constant average velocity this work reflects the change in gravitational potential energy of the body mass (Daley and Biewener, 2003; Gabaldon et al., 2004; Laursen et al., 2000; McIntosh et al., 2006; Riener et al., 2002; Saibene and Minetti, 2003). Positive and negative work in both level and non-level gaits have been directly attributed to the work generated or dissipated by skeletal muscles through either shortening (concentric) or lengthening (eccentric) contractions. Positive muscle work occurs in shortening contractions in which the force and displacement vectors are in the same direction, which increases mechanical energy. Negative muscle work occurs in lengthening contractions in which the force and displacement vectors are in opposite directions, which decreases mechanical energy. These fundamental muscle roles have been determined mostly through combinations of empirical measurements and biomechanical modeling (Cavagna and Kaneko, 1977; Elftman, 1940; Lay et al., 2007; McFadyen and Winter, 1988; McIntosh et al., 2006; Neptune et al., 2004; Riener et al., 2002; Winter, 1983c), and more recently through direct measurement techniques (Daley and Biewener, 2003; Gabaldon et al., 2004; McGowan et al., 2005; Roberts et al., 1997).

Positive and negative muscle work assessed through inverse dynamics and subsequent calculations of joint powers have been performed on level surfaces and non-level, ascending and descending gaits on ramps and stairs (DeVita and Hortobagyi, 2000; Duncan et al., 1997; Eng and Winter, 1995; Lay et al., 2007; McFadyen and Winter, 1988; McIntosh et al., 2006; Nadeau et al., 2003; Riener et al., 2002; Swanson and Caldwell, 2000). Nearly all these studies reported joint power values or muscle work during selected phases of the stride or at selected joints. To our knowledge, however, few studies have reported total muscle work throughout the entire stride by integrating the joint power vs time curves in these gait tasks. Eng and Winter reported total negative work and total positive work from joint powers at each lower extremity joint in level walking (Eng and Winter, 1995). They did not sum these values, however, nor discuss the observed discrepancy between the summed negative (−0.77 J kg⁻¹) and positive work (1.17 J kg⁻¹) per stride. Duncan et al. reported muscle work from joint powers at each lower extremity joint in stair ascent and descent (Duncan et al., 1997). These authors also did not calculate total positive and negative muscle work nor discuss the apparent discrepancy between the magnitudes of work in ascent and descent. Their data, however, showed that positive muscle work was two- to threefold greater in stair ascent compared to negative muscle work in descent (Duncan et al., 1997). Upon closer examination of other literature, it is clear that ascending vs descending gaits have longer stance durations and higher average joint powers (Lay et al., 2007; McFadyen and Winter, 1988; McIntosh et al., 2006; Riener et al., 2002) and this combination of factors dictates that muscle work derived from joint powers would in fact be greater in ascent than in descent. Since it is widely assumed that net muscle work would be zero in level gaits and equivalent in ascending and descending gaits of equal vertical displacements (e.g. Laursen et al., 2000), it was surprising that neither Eng and Winter (Eng and Winter, 1995) nor Duncan et al. (Duncan et al., 1997) supported these suppositions. This possible inequity in negative and positive muscle work in both level and non-level gaits has not been addressed in the literature. We think the integration of these results suggests two interesting biomechanical phenomena: (1) despite the maintenance of a constant average level of total mechanical energy, positive muscle work is greater than negative muscle work in level gait, and (2) despite equivalent changes in total mechanical energy in ascending and descending gaits of identical vertical displacements, positive muscle work is greater than negative muscle work in ascending compared to descending gaits. The purposes of the present study were to compare positive and negative muscle work in level walking and net positive and negative muscle work in ascending and descending walking on a ramp and on a stairway. We suggest that the assessment of positive, negative and net muscle work in level and non-level gaits would increase our understanding of the functional roles of muscles in cyclic human movement and the potential bias towards energy generation vs dissipation in muscle function.

Materials and methods

Participants

Thirty four adults, 16 males and 18 females, volunteered for the study. Their mean (± s.d.) age, mass, height and body mass index were 22.2±2.0 years, 69.0±13.5 kg, 1.73±0.11 m, and 22.4±2.9 kg m⁻². All participants were ostensibly healthy, recreational athletes without history of lower extremity injury. All participants gave written informed consent before participating in the study, according to East Carolina University policy.

Experimental set-up

Three experimental arrangements were used in this study. A 15 m level walkway, a 5 m ramp inclined 10° and a four-step stairway were fitted with one of two force platforms (AMTI, models OR6-6-2000 and LG6-4-2000, Newton, MA, USA) in the middle of the walkway and ramp and on the second stairway step. The stairway had a standard commercial design that included a 0.19 m rise and a 0.28 m run (Irvine et al., 1990). Three-dimensional ground reaction forces (GRFs) and the free moments were measured with the force platforms at 960 Hz and stored on computer. The vertical force channels were calibrated with known weights ranging from 0 to 2100 N. The voltage outputs were highly linear throughout the tested range and the coefficient of determination between force and voltage were R²=0.999 for both instruments. Sagittal plane kinematics was recorded at 120 Hz for each gait task using an infrared digital camera system (Qualisys MacReflex 240, Gothenburg, Sweden). The analysis was limited to the sagittal plane, which included all anteroposterior and vertical kinematics, because these represent the fundamental motions and energetic characteristics in level and inclined gaits.

An infrared timing system (Model 63520, Lafayette, Lafayette, IN, USA) was used to constrain walking velocity to a nominal value of 1.50 m s⁻¹ in level and ramp tests. The observed average (± s.d.) velocities over the timed intervals were 1.52±0.06, 1.49±0.04 and 1.50±0.06 m s⁻¹ in level, ramp ascent and ramp descent conditions, respectively. A metronome set to 1.33 Hz was used to constrain stairway speed by matching foot-strike on each step to this frequency. This technique produced an average (± s.d.) nominal walking velocity of 0.45±0.04 m s⁻¹ on the stairs. It was necessary to constrain walking speed so that kinetic energies did not change over the stance phases and were equivalent during ascent and descent on the ramp and stairway. Thus any differences in positive and negative muscle work in level walking and net muscle work between ascending and descending gaits could not be attributed to increasing or decreasing kinetic energy in any gait. We verified that kinetic energy was relatively stable in ramp and stair gaits by noting the average resultant linear velocity of the shoulder joint and the change in this velocity over the stance phases. The observed average (± s.d.) shoulder velocities over the analyzed stance phases in ramp ascent and descent were 1.50±0.05 and 1.52±0.07 m s⁻¹, respectively. The observed average velocities over the analyzed stance phases in stair ascent and descent were 0.44±0.04 and 0.45±0.05 m s⁻¹, respectively. These velocities changed less than 2% from initial and final moments in the stance phases in these movements. For level walking, we compared negative and positive impulses from the anteroposterior GRF and found they were also less than 2% different.

Testing protocol

Participants wore black spandex bicycle shorts, a tight fitting T-shirt, and athletic shoes. Standing height and mass were measured along with circumferences of the proximal right thigh, knee, ankle and metatarsal heads. Reflective markers were placed on the participants' right side on the lateral border of their fifth metatarsal head, the lateral heel of the shoe, lateral malleolus, lateral femoral condyle, greater trochanter and the shoulder. Participants walked on the walkway, ramp and stairway for several minutes until they were relaxed and comfortable. A starting point was selected so that the right foot would contact the force platform in a normal stride. Trials were discarded if the subject's velocity was more than 5% different than the target speed, if the foot was not completely on the force platform or if the subject made visually obvious stride alterations to contact the force platform. Five successful trials were collected as a minimum for each subject and gait condition. The order of testing level, ramp and stair conditions was counterbalanced among the participants. No participants reported fatigue or required rest during the test session. The level walking data were obtained as a reference for interpreting the ramp and stair results.

We chose to evaluate three locomotion tasks to reduce the possibility of particular task-specific characteristics of a single gait causing the outcome in this study. Level, ramp and stairway gait have distinct biomechanical characteristics. Conceptual agreement among the results from all three gaits would eliminate the task-specific characteristics of one gait and support conclusions generalized to human locomotion. Level, ramp and stair gaits cover a continuum of characteristics that broadly include constant vs changing energy levels (level vs non-level gaits), low vs high kinematic constraints (level and ramp vs stair gaits), and work primarily concentrated at a single joint vs multiple joints (ramp descent vs ramp ascent). Additionally, these gaits are the most common locomotion tasks used by humans. Thus, testing these three different tasks enables us to interpret the results in a broad and fundamental way.

In addition to the gait tests, two planar movements were analyzed to verify that positive and negative joint work are equivalent in some cyclic movements. We measured frontal plane motion of the upper extremity during 90° of shoulder abduction followed by shoulder adduction to the starting position in one subject standing erect. We also measured sagittal plane lower extremity motion during a cyclic squat movement performed on a force platform. The movement started and ended in the standing position and included flexion and extension rotations at the hips and knees and dorsiflexion and plantarflexion rotations at the ankle. Both shoulder and squat movements were performed slowly and lasted ∼2.2 s and ∼1.7 s, respectively. Reflective markers were placed on the wrist, elbow and shoulder for the adduction–abduction task and as described above for the squat task. These motions were analyzed identically to the gait tasks, with the exception that total joint work for the shoulder movement was summed from elbow and shoulder joint work.

Data reduction

The digitized Cartesian coordinates of the reflective markers describing the stance phase on the force platform were processed through a second order low-pass digital filter, which automatically selected the cut-off frequency based on Winter's method (Winter, 1990). The mean cut-off frequency was ∼5.0 Hz. Linear velocity and acceleration were calculated for each point during the stance phase. Joint angular position and velocity were calculated at the hip, knee and ankle.

Inverse dynamics using linear and angular Newton–Euler equations of motion were used to calculate the joint reaction forces and torques at each lower extremity joint throughout the stance phase. The process was also applied to the elbow and shoulder joints and the lower extremity joints during the shoulder and squat movement tasks. Magnitude of the segmental masses, their moments of inertia, and the locations of the mass centers were estimated from the position data using a mathematical model (Hanavan, 1964), segmental masses reported by Dempster (Dempster, 1959), and the individual subject's anthropometric data. Center of pressure during the gait and squat trials was calculated from the ground reaction forces and the mediolateral moment on the force platform and used to identify the point location of the ground reaction forces. Joint powers were calculated as the product of the joint torques and joint angular velocities. Summed torque and power curves were then calculated as the sum of the ankle, knee and hip joint torques and powers and used to provide a visual description of the simultaneous torque and power output of the three joints. Positive, negative and net work throughout the stance phases were calculated from the hip, knee and ankle powers as the areas under the joint power curves. Because step length during ramp descent walking was 10% shorter than in ascent walking (0.66 m vs 0.74 m), all ramp work values were normalized to step length and expressed in J m⁻¹. Work values in level and stair gait were expressed as J step⁻¹. Positive and negative work indicated that the muscles crossing the particular joints generated or dissipated mechanical energy. The fundamental assumption in this study was that joint work calculated from joint powers represents the work done by muscles. This interpretation of joint power and work is well established and has a long history in biomechanics, beginning in 1939 (Elftman, 1939) and continuing (e.g. Winter, 1983b), through our previous work (e.g. DeVita and Hortobagyi, 2000) and newer work in animals (e.g. Dutto et al., 2006) to our present study. The basic premise in these and other studies is that joint torques are produced principally by muscle forces and therefore work from joint torques (i.e. area under the joint power vs time curves) is a reasonable and accurate estimate of muscle work.

Statistical analysis

We limited the statistical comparisons to the pertinent work values in each gait. Level, ramp and stairway gait were analyzed independently because the work values depended primarily on the slope of each environment and the gait speed used with each condition. Dependent t-tests were used to compare positive and negative work at each joint and the net positive and negative work in level walking and net joint work in ascent and descent gaits on the ramp and stairs. A conservative P<0.010 was used to indicate statistical significance in all tests because of the multiple comparisons.

Results

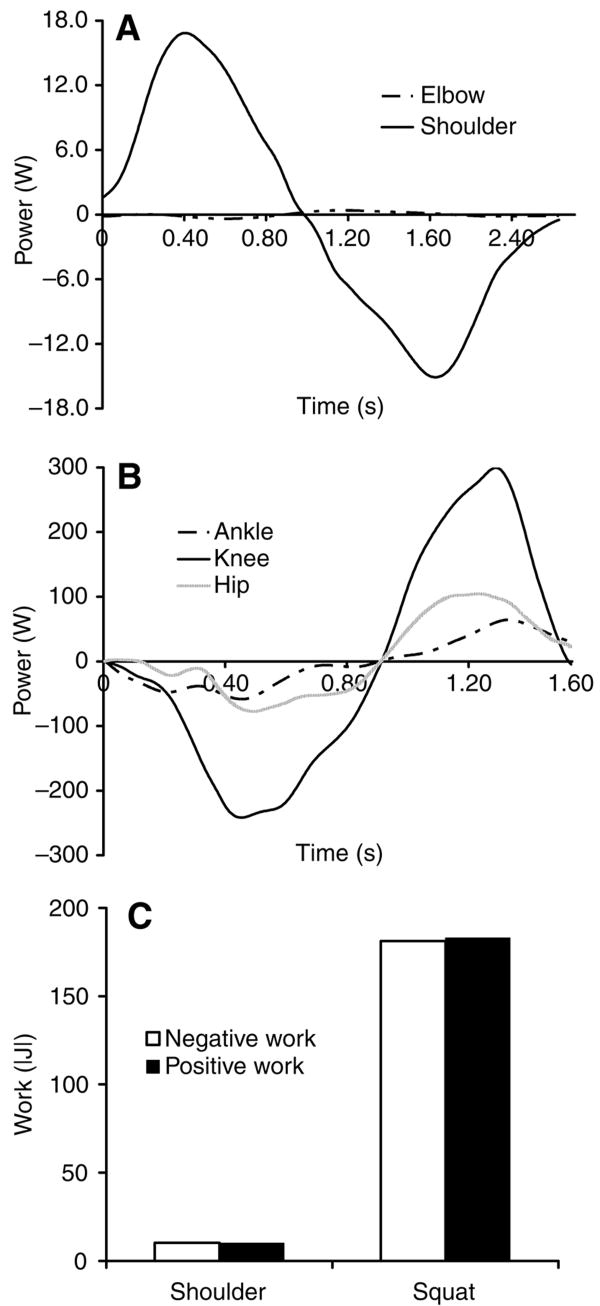
The shoulder movement was produced nearly entirely by work at the shoulder joint (elbow work was negligible; Fig. 1). The magnitudes of the total positive and negative joint work were less than 1% different (10.1 J vs −10.2 J). The results for the more complex, multi-joint squat movement were nearly identical to the shoulder results. Magnitudes of total positive and negative joint work were virtually identical in the squat task (183 J vs −181 J). These data strongly suggested that positive and negative joint work can be equivalent in cyclic, uni- and multi-joint movements.

Fig. 1.

Joint powers in shoulder (A) and squat (B) movements. Both cyclic activities had positive and negative joint powers that were associated with lowering and raising either one upper extremity or all body mass above the ankles. (C) Total positive and negative joint work were virtually identical in the negative and positive phases of the shoulder and squat tasks (i.e. differences were less than 1%). These data strongly suggest that positive and negative joint and muscle work can be equivalent in certain uni- and multi-joint, cyclic movements.

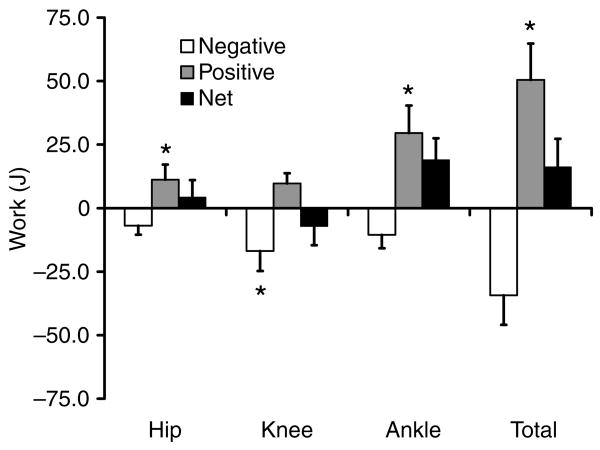
Level walking was performed with a summed extensor torque throughout most of the stance phase that was produced by a proximal to distal sequencing of extensor torques at the hip, knee and ankle joints (Fig. 2A,B). These torques produced negative and positive work phases during the stance phase at each joint and alternating positive and negative summed joint power (Fig. 2C,D). Negative work was 74% larger than positive work at the knee (P<0.001, Fig. 3). Positive work was 62% and 180% larger than negative work at the hip and ankle, respectively (both P<0.001). The negative and positive work at each joint totaled −34.3 J and 50.5 J, respectively, and the difference between the absolute values of these variables was also statistically significant (P<0.001). Thus on average, joint work during the stance phase of level walking was biased towards 16.2 J of positive work. To verify this result we examined individual participant's data. Of the 34 participants, 33 had net positive work produced during the stance phase.

Fig. 2.

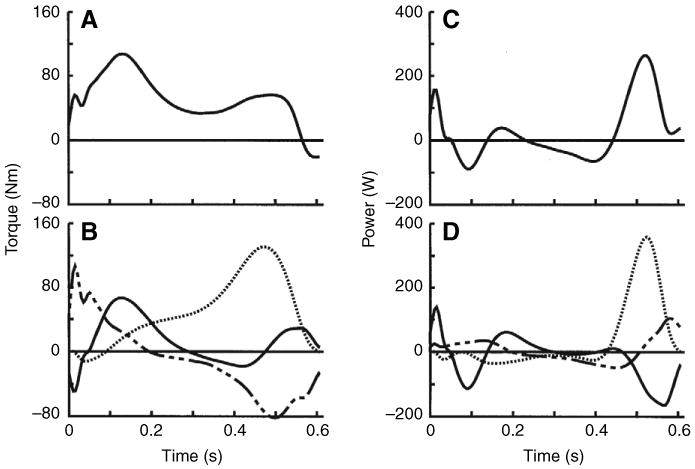
(A,C) Summed joint torque (A) and joint power (C) and (B,D) individual hip (broken line), knee (solid line) and ankle (dotted line) joint torques (B) and joint powers (D) during the stance phase of level walking averaged across all subjects. Positive torques are extensors and positive powers are energy generation. Summed torque showed extensor bias throughout most of stance that was produced primarily by hip and knee extensor torques in early stance and ankle plantarflexor torque in late stance. Individual joint powers showed that each joint torque generated and dissipated energy during the stance phase. Summed joint power showed alternating positive and negative work phases, with the largest power magnitude being the positive power in late stance.

Fig. 3.

Mean hip, knee, ankle and total joint work in level walking across all subjects. Values are means ± s.d. Muscles at each joint produced both negative and positive work during the stance phase of level walking. Net work was negative at the knee but positive at the hip and ankle. Total net work was positive at 16.2 J. The magnitudes of negative and positive work were significantly different at each joint; the asterisk indicates the larger value (P<0.010).

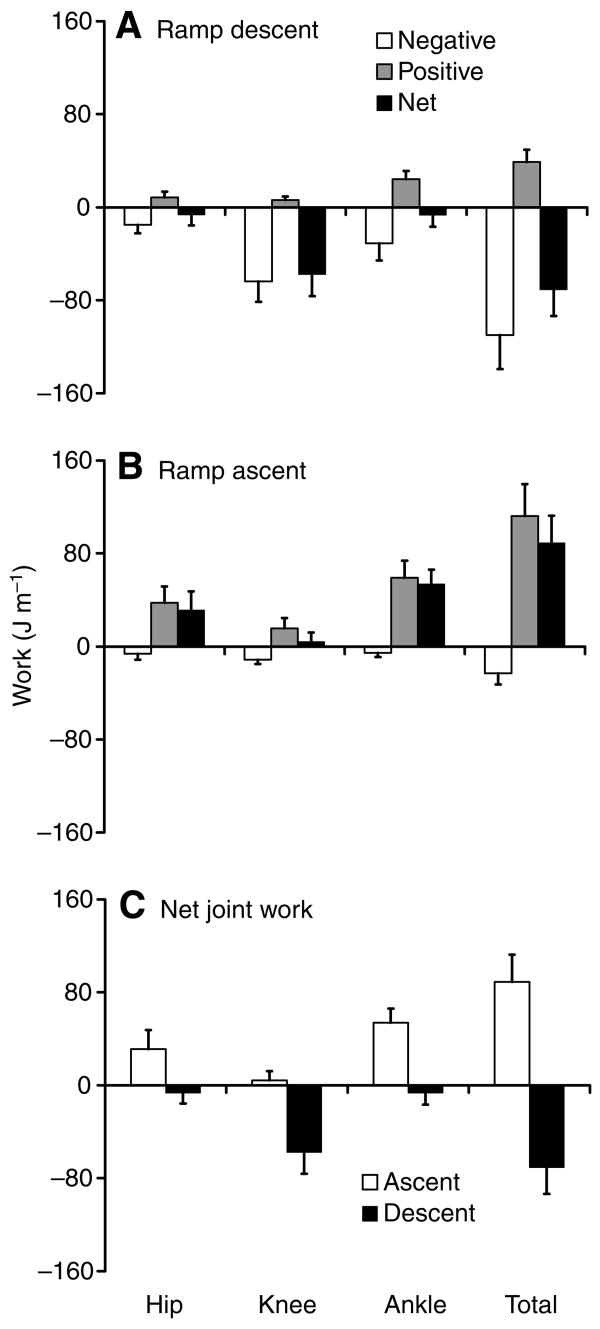
Ramp descent and ascent walking were performed with similar summed extensor torques throughout most of their stance phases (Fig. 4). These summed torques were produced by extensor torques at each joint. Knee extensor torque was larger in descent, however, whereas hip and ankle extensor torques were larger in ascent. In contrast to the similarity in summed torques, the summed powers in ramp descent and ascent were nearly entirely negative and positive, respectively. The individual joint powers, however, showed that muscles crossing each joint contributed both negative and positive power and work to both movements (Fig. 5). Knee muscles were the primary dissipaters of mechanical energy in ramp descent, performing 58% and 81% of the negative and net muscular work. Ankle and hip muscles were the primary energy generators in ramp ascent combining to perform 86% and 95% of the positive and net work. Of the 34 subjects, 30 had greater net work in ramp ascent compared to descent. Joint work was larger in ramp ascent vs descent because both average power across all joints (92 W vs 78 W, respectively) and the time duration of stance (0.70 s vs 0.62 s, respectively) were larger in the ascending gait (see total ascent and descent work in Fig. 5C and Fig. 8, below).

Fig. 4.

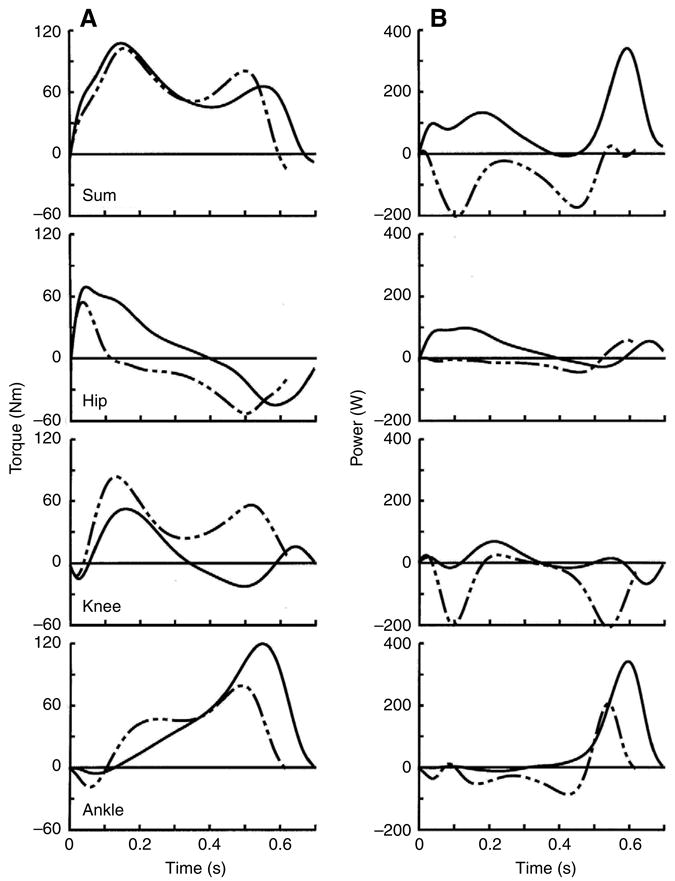
Individual and summed joint torque (A) and power (B) curves during the stance phases of ramp descent (broken lines) and ascent (solid lines) walking, averaged across all subjects. Positive torques are extensors and positive powers are energy generation. Summed torques were similar in shape and magnitude and showed that both gaits were produced by net extensor torques across all joints. Hip and ankle extensor torques were larger in ascent vs descent, whereas knee extensor torque was larger in descent. Summed powers in ramp descent and ascent were nearly entirely negative and positive, respectively. The individual joint powers, however, showed that muscles crossing each joint contributed both negative and positive power and work to both movements. Negative power occurred primarily at the knee and then ankle joints in descent whereas positive power occurred primarily at the ankle and hip joints in ascent. Ramp descent had a 15% shorter stance phase, partially leading to reduced area under the joint power curves and reduced muscle work compared to ramp ascent.

Fig. 5.

Mean joint work in ramp gait across all subjects. Values are means ± s.d. Knee muscles were the primary energy dissipaters in ramp descent, performing 58% and 81% of the negative and net muscular work, respectively. Ankle and hip muscles were the primary energy generators in ramp ascent combining to perform 86% and 95% of the positive and net work, respectively. Negative work in ramp ascent was relatively evenly distributed among the muscle groups, whereas positive work in descent was produced primarily (i.e. 62%) by the ankle muscles.

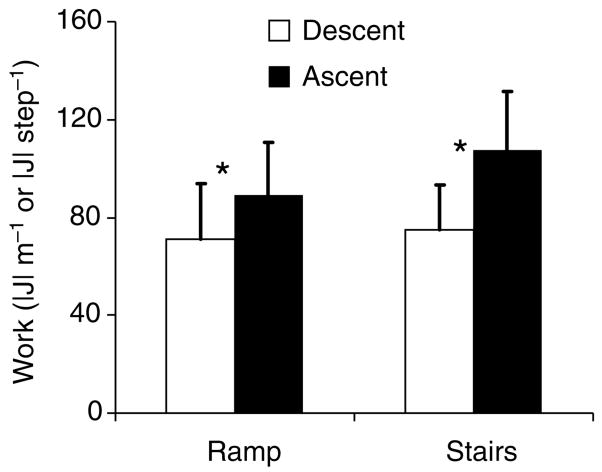
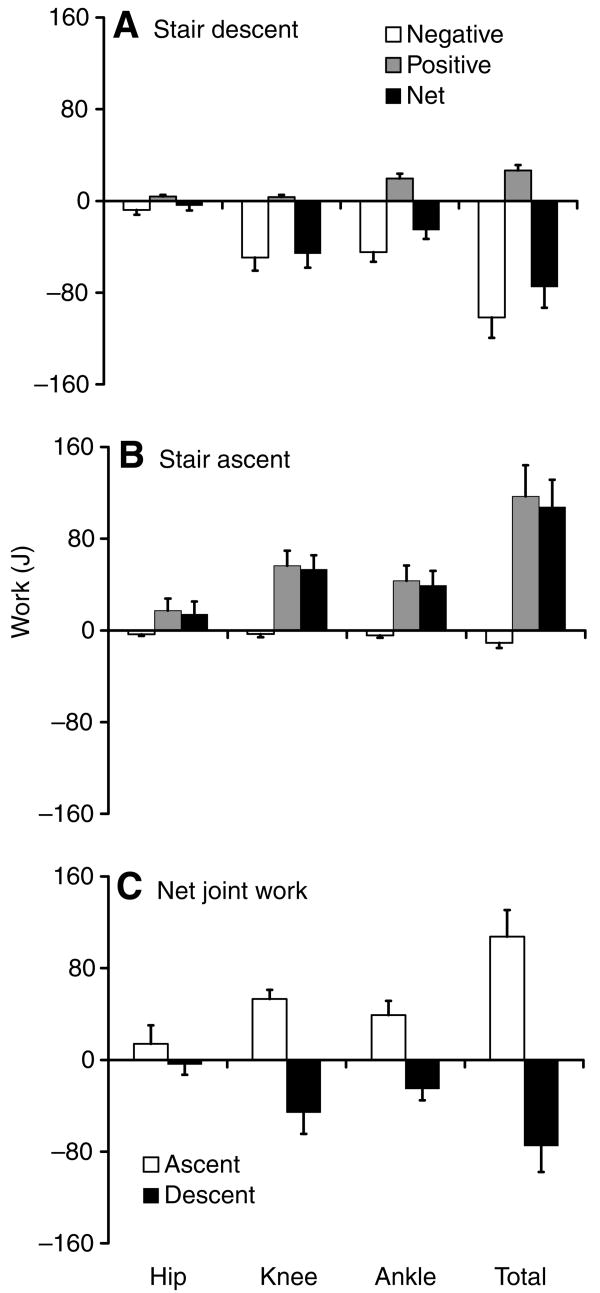
Fig. 8.

Mean total joint work in both ascending and descending gaits (in |J| m⁻¹ for ramp, and |J| step⁻¹ for stairs) across all subjects. Values are means ± s.d. Ascent work was 25% (*P<0.010) and 43% (*P<0.000) greater than descent work in ramp and stair gait, respectively.

As in ramp gait, stair descent and ascent were performed with similar summed extensor torques throughout most of their stance phases (Fig. 6). The first and second maximum values in the summed torques were lower and higher, respectively, in stair descent compared to ascent. These summed torques were produced by extensor torques at each joint in descent and ascent. Hip and ankle torques were similar in descent and ascent. The knee torque, however, had two smaller extensor torque peaks in descent and one larger extensor torque peak in ascent. Also similar to ramp gait, the summed powers in stair descent and ascent were nearly entirely negative and positive, respectively. Unlike ramp gait, however, the individual joint powers showed that muscles crossing the knee and ankle joints were the primary contributors to negative and positive power and work in both stairway gaits. Hip power and work were low particularly in stair descent but also in ascent. Both knee and ankle muscles produced significant negative power and work, sharing the dissipation of mechanical energy in stair descent (Fig. 7). These muscles produced 49% and 44% of the negative work and 61% and 34% of net muscular work in this movement, respectively. Knee and ankle muscles were the primary energy generators in stair ascent, performing 38% and 37% of the positive work and 49% and 36% of net muscular work in this movement, respectively. All 34 subjects had greater net work in stair ascent compared to descent. As in ramp walking, average joint power (91 W vs −61 W) and stance phase duration (0.80 s vs 0.75 s) were both larger in stair ascent vs descent. Thus, joint work was larger in stair ascent because both the rate of energy change and the time duration of this change were larger in ascent vs descent (see total ascent and descent work in Fig. 7C and Fig. 8 below).

Fig. 6.

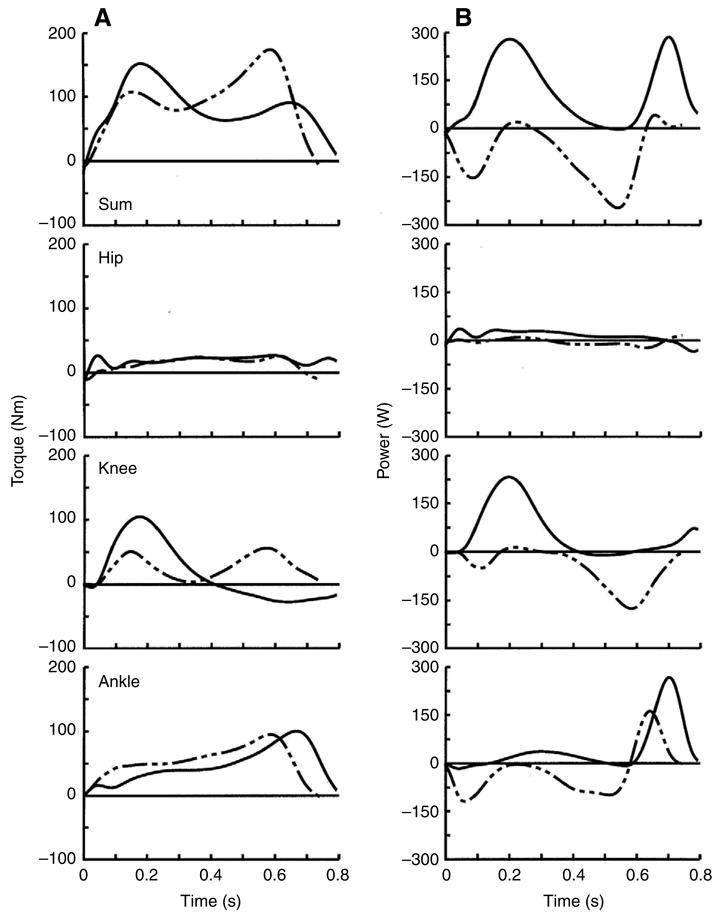
Individual and summed joint torque (A) and power (B) curves during the stance phases of stair descent (broken lines) and ascent (solid lines) walking averaged across all subjects. Positive torques are extensors and positive powers are energy generation. Summed torques were similar in shape and showed that both gaits were produced by net extensor torques across all joints. Hip and ankle torques were similar in the stair gaits, whereas knee torque had one larger extensor phase in ascent and two smaller extensor phases in descent. As in ramp gait, summed powers in stair descent and ascent were nearly entirely negative and positive, respectively. In contrast to ramp gait, there was minimal power and work at the hip on the stairs. Energy dissipation in stair descent was done at the ankle joint in early stance and at the knee joint in later stance. Stair ascent was produced by positive power and work at the knee joint in early stance and at the ankle joint in later stance. Stair descent had an 8% shorter stance phase, partially leading to reduced area under the joint power curves and reduced muscle work compared to stair ascent.

Fig. 7.

Mean joint work in stair gait across all subjects. Values are means ± s.d. Knee and ankle muscles were the primary energy dissipators and generators in stair descent and ascent. They performed 92% and 95% of the negative and net muscular work in descent, respectively and 85% and 87% of the positive and net muscular work in ascent, respectively. As in ramp walking, negative work in ramp ascent was relatively evenly distributed among the muscle groups, whereas positive work in descent was produced primarily (i.e. 73%) by the ankle muscles.

Total joint work in both ascending and descending gaits is shown in Fig. 8. Ascent work was 25% (P<0.010) and 43% (P<0.000) greater than descent work in ramp and stair gait, respectively. Despite ascending and descending the same inclined ramp and standard stairway, work by the lower extremity muscles was significantly larger when mechanical energy was increased in ascending gaits than when it was decreased in descending gaits.

Discussion

Formulation of two novel hypotheses

The data from the present experiments support the idea that muscle function in human walking is biased towards the generation of mechanical energy over that of dissipation of mechanical energy, i.e. energy production by muscles during the concentric phases of stance exceeded energy dissipation by muscles during the eccentric phases of stance in walking. This novel observation was derived from two distinct locomotion paradigms. First, level walking at a constant average speed is by definition the maintenance of a constant average level of mechanical energy. However, positive muscle work was larger in magnitude than negative muscle work by 47% or ∼16 J step⁻¹. To further interpret this value, without dissipating this additional energy the participants would have more than doubled their walking speed from 1.50 to 3.02 m s⁻¹ in only 16 steps. Second, gait tasks that raise or lower an individual's center of mass while maintaining constant average velocity change the person's total energy by either increasing or decreasing gravitational potential energy. These increases and decreases would be identical if the changes in vertical positions were identical [e.g. see fig. 3, external work in gradient walking, in Minetti et al. (Minetti et al., 1993)]. We observed, however, that in both ramp and stair gait muscle work was larger in ascent than in descent, despite equivalent changes in vertical position and total body energy. Thus, muscles contributed more to lifting the center of mass than they contributed to lowering the center of mass in two different modes of walking. A similar result was also observed in two individual muscles through direct measurement techniques. Muscle work in the gastrocnemius and peroneus longus of wild turkeys (Meleagris gallopavo) was assessed through length measuring sonomicrometry and force measuring strain gages during incline and decline running on a 12° slope (Gabaldon et al., 2004). Gabaldon et al. showed that muscle work shifted from generating 7.0 and 8.1 J kg⁻¹ in gastrocnemius and peroneus longus in ascent to dissipating only 4.6 and 2.4 J kg⁻¹, respectively, in descent. In total, these muscles performed ∼2.4-fold greater work in ascent compared to descent running. Admittedly, other muscles may have compensated for this reduced negative work by increasing their negative work during descent running as suggested by these authors. For example, as seen in the present study, knee muscles are principle energy dissipators in at least two descending gaits. We are also cautious when comparing the present results with those of Gabaldon et al. because the ankle joint muscles and the general anatomy of the ankle region may not be as well adapted to dissipating compared to generating energy. We do, however, think the similarity between these sets of results is interesting and it at least suggests that work from other individual muscles be directly compared between ascending and descending gaits for the purpose of determining whether the net positive bias in muscle work as presently observed can be supported by such a bias in individual muscles.

On average for the two non-level gait tasks presently measured, the magnitude of the observed positive muscle work in ascent was 25 J greater than the magnitude of the negative muscle work in descent on a per step basis. This value may simply be one estimate of the differences between negative and positive muscle work that would be observed in various gait situations. Gait mode (i.e. walking, running, skipping), slope of the inclined surface or stairs, gait velocity, population characteristics, and other factors may alter this basic result and have yet to be investigated. By integrating the results for level and non-level gaits, we can provide an initial partitioning of the difference between positive and negative muscle work in non-level gaits into the amount of additional positive work required to maintain a constant average energy level and the amount of additional positive work required to raise one's center of mass. Since level walking required a bias of 16 J of positive work, it appears that ∼60% of the difference in energy generation vs energy dissipation in non-level gaits (i.e. 16 J of the 25 J difference in ascent and descent) may be associated with the attempt to maintain a constant level of mechanical energy, and the remaining ∼40% may be due to the mechanics of raising one's mechanical energy.

The present study is the first to purposefully investigate and report empirical data demonstrating the differences in the amount of muscle work in ascending and descending gaits. The outcome of this investigation was that, despite equivalent changes in total body mechanical energy while ascending and descending a ramp or a stairway, muscles produce more work in ascent than in descent. This study was not, however, the first to show that muscles produce more positive than negative work during constant speed level gait. Elftman calculated muscle work through joint powers as we did and he reported that in a complete cycle of level running, lower extremity muscles performed nearly twice as much positive (205 J) work than negative work (−112 J) (Elftman, 1940). The difference was attributed to air resistance, missing upper extremity work, and slippage of the foot with subsequent loss of energy during ground contact. These factors, however, probably do not account for the present differences in level walking nor in the non-level gaits. Loss of energy due to air resistance should be negligible since walking is a relatively slow activity and our data were collected indoors in the absence of wind. To our knowledge there was no perceptible foot slippage and appreciable energy loss due to friction even in ramp descent. Upper extremity work as discussed below should also not account for the present discrepancy. We also derived total positive and negative work during a complete stride in level walking from Eng and Winter (Eng and Winter, 1995) by summing their individual work values from each lower extremity joint. The ratio of their summed positive (1.17 J kg⁻¹) and negative (0.77 J kg⁻¹) values is 1.52, which is similar to the 1.47 ratio from our data. Interestingly, a similar result was also observed in the limbs of horses trotting on a level surface. Dutto et al. (Dutto et al., 2006) measured joint work in the forelimb and hindlimb of horses trotting at a constant speed. They expected to observe counterbalancing negative forelimb and positive hindlimb work over the stride cycle. While the hindlimb did produce net positive work (i.e. 0.34 J kg⁻¹), forelimb work was essentially zero. The net joint work was therefore positive despite the maintenance of a constant level of total mechanical energy. Dutto et al. conjectured the net zero work in the forelimb was due to their inability to ‘account, experimentally, for the negative work done by the extrinsic muscles connecting the scapula and the thorax’. While this may be the case, our data suggest that this additional negative work may not have completely balanced the positive hindlimb work. In short, the data from Dutto et al. showing a bias towards positive muscle work may in fact be entirely and accurately descriptive of muscle work in trotting horses on level surfaces.

The present results suggest two novel hypotheses regarding muscle energetics in human locomotion. First, we hypothesize that level walking requires muscles to generate a net positive amount of work per gait cycle to overcome energy losses by other tissues. Thus level walking does not balance muscle work through concentric and eccentric contractions but emphasizes the ‘over-production’ of energy through shortening contractions to maintain a constant level of total mechanical energy. The hypothesis suggests that some of the positive work produced by muscle is not used to maintain gait velocity (i.e. kinetic energy) and upright posture (i.e. potential energy) but is wasted through various energy sinks. Second, we hypothesize the biomechanical principle that skeletal muscles generate more mechanical energy in gait tasks that raise the center of mass compared to the mechanical energy they dissipate in gait tasks that lower the center of mass despite equivalent changes in total mechanical energy. Level and non-level gaits require mechanical energy generation and dissipation throughout the gait cycle. The single source of mechanical energy generation in locomotion is the conversion of chemical energy stored in adenosine triphosphate (ATP) into mechanical energy through the rotation of myosin heads after cross bridge formation within sarcomeres (i.e. the ‘power stroke’) (Huxley, 1969). Conversely, energy dissipation is most likely performed within all body tissues to varying extents. For example, in both level and non-level gaits, the ‘wobbling mass’ (Nigg and Liu, 1999) of muscle bellies along with adipose tissues lose mechanical energy, as do the compression and subsequent vibrations of joint cartilage, knee meniscii, intervertebral discs and boney structures, including the vertebral bodies. The idea that tissues other than muscle perform negative work in gait was expressed by Williams and Cavanagh, who conceptually partitioned negative work in running to that performed by muscles and that performed by ‘non-muscular tissues’ (Williams and Cavanagh, 1983).

The two new hypotheses can be investigated through a variety of models and approaches that would enable us to understand how various factors influence the magnitude of the positive bias in muscle work in locomotion. We observed the positive bias within a discrete combination of methodological factors. This bias may be affected by numerous physiological and biomechanical characteristics, along with ecological and environmental factors. For example, population characteristics such as obesity may be directly related to differences in positive and negative work in non-level gaits. Obese individuals may dissipate more energy in their soft tissues than lean and thus have a greater discrepancy between positive and negative muscle work in level or non-level gaits. We showed previously that old adults ascended a stairway by performing the same amount of joint work as young adults (1.50 J kg⁻¹) but they descended by performing less joint work than the ascent amount (−1.15 J kg⁻¹) and also less work than the young adults (−1.25 J kg⁻¹) performed in descent (DeVita et al., 2001). Thus, it appears some populations may alter their neuromuscular control strategy to selectively reduce muscle work in descending gaits. Ecological characteristics such as type of gait, gait velocity and load carrying may also influence the disparity in positive and negative muscle work. Finally, environmental characteristics such as ramp slope, stair height and surface and footwear stiffnesses may also interact with the relative amounts of positive and negative muscle work in level and non-level gaits.

Three potential causes of the reduced muscle work in descending gaits

We first compared negative and positive work in cyclic activity by investigating two simpler movements, the shoulder and squat tasks. These applications showed that positive and negative muscle work can be equivalent in cyclic tasks. Why then was the negative joint work in descending gaits lower than the positive work in ascending gaits? We propose that the principle biomechanical cause of this outcome was the relatively high magnitude of the accelerations occurring in the descending gaits, and in particular the accelerations in the initial portion of the stance phase. These accelerations are directly related to the applied ground reaction forces (GRFs), which are shown in Fig. 9. Both the rate of force application in early stance phase and the first maximum force were ∼27% larger in the descending vs ascending tasks. The first maximum forces in ramp descent and ascent walking produced accelerations of 13.2 and 10.7 m s⁻², respectively, on the subjects' centers of mass. The corresponding values for stairway gait were 13.8 and 10.5 m s⁻². In excellent agreement with our results, Loy and Voloshin reported 130% higher shock waves in stair descent vs ascent (Loy and Voloshin, 1991). A similar result was also observed in stiff (less joint flexion) and soft (more joint flexion) landings from a vertical drop (DeVita and Skelly, 1992). Stiff compared to soft landings had 23% larger GRFs and 18% less total joint work derived from joint powers. In contrast, the maximum accelerations in both shoulder and squat tasks were ∼2.5 m s⁻² in both lifting and lowering phases. The high accelerations in descent walking most likely placed relatively large loads on various non-muscular tissues initiating an energy-dissipation response (e.g. Pain and Challis, 2001; Weijers et al., 2005). This dissipation response has been well described in various running gaits as an attenuation of the shock wave that travels from the foot to the head during each step (Derrick et al., 1998; Mercer et al., 2003). This explanation also agrees with the idea that collisions with the support surface are a major factor for energy losses and subsequent energy generation by muscle during locomotion (Kuo et al., 2005; Ruina et al., 2005). We now add to this concept by suggesting that relatively larger collisions (i.e. more forceful collisions) exact more of their energetic cost on non-muscular tissues.

Fig. 9.

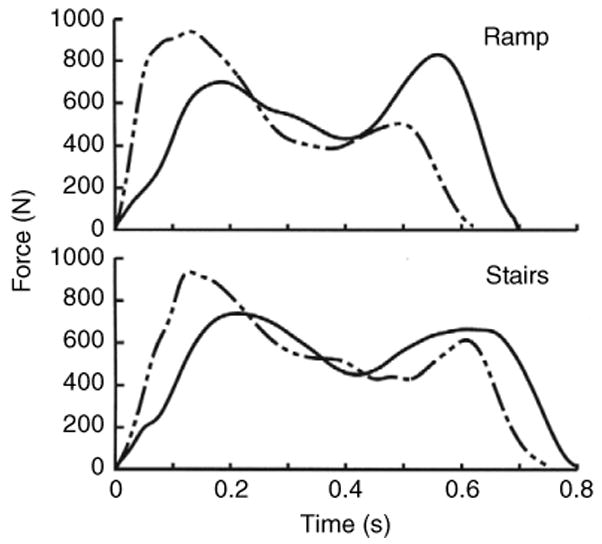
Mean normal GRFs (N) for ramp and stairway walking averaged across all subjects. Descending gaits had larger first maximum forces and greater rates of force application during the initial portion of the stance phase. These forces produced higher accelerations of the body mass compared to those in the ascending gaits.

A second factor leading to the reduced muscle work in descent vs ascent may be a difference in the direction of the floor reaction force vector relative to the lower extremity joints. We observed that despite the larger initial GRF peaks in both descending gaits, the initial peaks in the summed joint torque curves were not larger in the descending than ascending gaits. In fact, while the initial GRF peak was larger in stair descent compared to ascent, the initial peak in the summed torque curves was larger in stair ascent compared to descent. We interpret these disparities between GRFs and joint torque responses as indicating that the larger GRF vector was directed closer to the joint centers in the descending compared to ascending gaits. This orientation would increase the muscle mechanical advantage by creating shorter lever arms for the external ground force and lead to smaller joint torque and power responses per unit GRF. Surface slope has been shown to alter muscle mechanical advantage such as theorized here in inclined vs level running (Roberts and Belliveau, 2005). While the larger GRFs in descending gaits may have had a reduced effect on the musculature through this mechanism, they are still applied to the other body tissues, including the skeleton, most directly through foot contact with the floor and to the remaining tissues through their attachments to the skeleton. Vibrations in these non-muscular tissues induced by impact forces would initiate an energy dissipating response and reduce the work required by muscles. Pain and Challis (Pain and Challis, 2002) quantified the energy dissipating capabilities of soft tissues in the upper extremity during impacts to the hand. They reported that these tissues could dissipate up to 70% of the energy within the extremity through their subsequent vibrations.

A third factor leading towards reduced negative work in descending gaits may be the need for musculature to perform positive work to propel the lower extremity upward and forward into the swing phase movement trajectory. Even though the individuals reduced their vertical positions and potential energy in descent, they needed to lift their limbs upward off the surfaces to initiate the swing phase. Muscles at all joints performed positive work in both ramp and stair descent (Figs 4, 6). The ankle muscles were, however, the primary generators of this work in both gaits, doing 62% of the total positive work in ramp descent (24.2 J m⁻¹) and 73% in stair descent (19.4 J step⁻¹). Plantarflexor torque by the ankle muscles and its resultant positive work in late stance is considered to be an important source of power for propelling the limb into the swing phase (Meinders et al., 1998; Neptune et al., 2001). Positive work at all joints, and in particular the ankle joint, led to a larger total positive work during both descending gaits than the total negative work in ascending gaits. Positive work in ramp descent was in fact 1.7-fold larger than negative work in ramp ascent and the corresponding ratio for the stairs was 2.5. These results indicated that ascending gaits are performed with a more singular muscle role of generating mechanical energy whereas descending gaits are performed with a more dichotomized muscle role of dissipating but also generating mechanical energy. Upon closer examination, it is evident that total negative work in each descending gait was similar to the total positive work in each ascending gait (−110 vs 112 J m⁻¹ in ramp descent and ascent, respectively; −102 vs 117 J step⁻¹ in stair descent and ascent, respectively). However, the biomechanical necessity to generate positive work in the amount of ∼30% of the negative work in descending gaits is an important element in the difference in net energy generation and dissipation by muscles in non-level gaits.

Muscle function in non-level gaits

The present power curves are similar in shape and agree well with those reported by others for ramp (Lay et al., 2007; McIntosh et al., 2006), stairway (Duncan et al., 1997; McFadyen and Winter, 1988; Riener et al., 2002), and level walking (DeVita and Hortobagyi, 2000; Winter, 1983a). There were some differences between the present work and maximum power values and some of those in the literature. These differences, however, were due to simple procedural differences among the studies. For example, our maximum hip power in ramp ascent was ∼65% lower than those reported by Lay et al. (Lay et al., 2007). This difference is most likely due to the difference in surface slope. Our ramp was inclined 10° whereas Lay et al.'s ramp was twice as steep at ∼21°. Lay et al.'s previous work showed that hip torques are directly and strongly related to surface inclination angle (Lay et al., 2006). The larger hip torque on the steeper slope used by Lay et al. (Lay et al., 2007) would directly cause higher joint power and work. Positive hip work in stair ascent also appears to be highly variable across many studies. For example, we have relatively low positive hip work in stair ascent whereas Kowalk et al. reported that hip muscles produced the greatest amount of work compared to knee and ankle muscles (Kowalk et al., 1997). Others showed the hip work to be intermediate between ankle and knee work (McFadyen and Winter, 1988; Nadeau et al., 2003; Riener et al., 2002). Most likely other procedural differences such as walking speed and step height on the stairway at least partially accounted for these differences in maximum joint powers and muscle work.

Present power and work results show both the complexity of muscle function in non-level gaits and the differences in muscle function across gaits. Within each of the four non-level gait tasks, each muscle group produced both negative and positive work during the stance phase (Figs 4 and 6, top two panels). The net work output for each muscle group, however, was always negative in descending and always positive in ascending gaits. This agrees with other studies on ramp (Lay et al., 2007; McIntosh et al., 2006) and stair walking (Duncan et al., 1997; McFadyen and Winter, 1988; Riener et al., 2002) except for the hip work in ramp descent (McIntosh et al., 2006) and stair descent (Riener et al., 2002). Both these studies reported a net positive bias in hip work even while descending these surfaces. The positive work was produced by hip flexor torques in late stance, indicating the subjects were actively flexing their hips to contribute to lifting the limb into the swing phase (i.e. add to the ankle muscle function described above). Most likely they were not generating positive work at the hip to accelerate the trunk forward and downward since trunk angular positions in descending gaits are relatively stable near the vertical. Our data and those in the other studies listed showed hip power and work to be almost negligible compared to knee and ankle power and work in the descending gaits. Thus, it appears that hip muscle work is least important in descending gaits and that humans have some flexibility in how they use their hip muscles for energy generation or dissipation in these gaits.

The kinematic characteristics of ascending gaits seemed to influence how each joint torque contributed to the task more so than those in descending gaits. The large knee extensor torques were the primary energy dissipators in both ramp (58% of the negative work) and stair descent (49% of the negative work) and the ankle plantarflexor torques provided secondary dissipating roles (28% and 44% in ramp and stair gaits, respectively). Relative muscle function in ramp ascent, however, differed from that in stair ascent. The ankle plantarflexor torque was the primary energy generator in ramp ascent (53% of the positive work) and hip extensor torque provided the secondary contribution (33% of the positive work). Stair ascent was produced principally from energy generation by the knee extensor torque (48% of the positive work) and a secondary contribution from ankle plantarflexor torque (37% of the positive work). The stance phase in ramp ascent was initiated with only 28° of knee flexion and the knee flexed only 7° more in early stance, whereas the stance phase in stair ascent began with 75° of knee flexion. Ramp ascent had only 30° of knee extension whereas stair ascent had 65° of knee extension during the stance phases. The smaller range of motion towards extension limited positive work production at the knee joint while ascending the ramp and the larger range of motion on the stairs enabled the knee extensor torque to perform more work. Also, the general movement trajectory was more vertically oriented on the stairs (35° to the horizontal) than on the ramp (10°). It appears, therefore, that as the general inclination in human gaits rotates towards a more vertical orientation, positive work production shifts from hip extensor torque to knee extensor torque. This interpretation is supported by the level walking data in which positive work was larger at the hip than at the knee and that net work was also positive at the hip but negative at the knee.

Ankle plantarflexors (i.e. the muscle–tendon unit) store and release energy during the stance phase and perform more like energy-saving elastic springs than other lower extremity muscles (Alexander, 1991; Biewener and Roberts, 2000; Dutto et al., 2006). Present data suggest this functional role in descent walking on ramps and stairs. Ankle plantarflexors were the only muscle group to perform relatively large negative work followed by relatively large positive work in either descending gait. Ramp descent in particular was done with positive ankle work in late stance, reaching 80% of the amount of the preceding negative work (∼−31 vs ∼24 J, respectively), while stair descent had positive ankle work in the amount of 44% of the preceding negative work in late stance (∼−45 vs 19 J, respectively). These values compare well with the intermediate value of ∼60% returned energy in the gastrocnemius muscle–tendon measured in turkeys performing inclined running (Roberts et al., 1997). The potential spring-like action of the ankle plantarflexors also showed that despite the loss of total mechanical energy in these gaits, descending locomotor tasks may employ the stretch–shortening cycle to enhance necessary concentric, energy generating contractions. No muscle group in either ascending gait had significant energy dissipation, particularly in stair ascent. Muscle function seemed to be strongly biased towards concentric, energy generating, shortening contractions in ascending gaits but less biased towards eccentric, energy dissipating, lengthening contractions in descending gaits. We can provide approximations of the potential energy savings through elastic mechanisms by calculating ratios of the negative and positive work in the four gaits. It appears that ascending gaits may store and return only ∼10% of the total energy whereas descending gaits may return ∼30% of the total energy.

Limitations in the present methodology

The purpose of these experiments was to determine if muscles generate more energy than they dissipate during level and non-level gaits. To our knowledge this study is the first attempt to investigate this biomechanical phenomenon objectively. Our methods were based on well-accepted biomechanical analyses, including inverse dynamics and subsequent joint power calculations. However, there are several limitations to our methods that must be acknowledged. First, the present analyses were limited to the stance phase of walking and did not include swing phase biomechanics. Thus, the differences between positive and negative work in all gaits may be accounted for by work done within the swinging limb. We expect this proposition to be incorrect, however, because numerous studies have shown swing phase mechanics, including power and work, to be relatively low compared to stance phase mechanics (Gottschall and Kram, 2005; Lay et al., 2007; McFadyen and Winter, 1988; Neptune et al., 2004; Riener et al., 2002). Also, swing phase typically includes two phases of positive work at the hip and two phases of negative work at the knee, all of which are similar in magnitude and should, for the most part, counterbalance each other (DeVita and Hortobagyi, 2000; Winter, 1983a). The analyses were also limited to the sagittal plane of the lower extremity. While there are few reports of work done in non-sagittal planes in level and non-level gaits, it appears that work in these planes may be ∼15%, 10% and 6%, respectively, of the sagittal plane work in level walking (Eng and Winter, 1995) and stair descent and ascent walking (Duncan et al., 1997). Non-sagittal plane work, however, was also distributed between positive and negative phases that would largely counterbalance each other and not substantially reduce the differences between positive and negative work as presently observed. One other study showed relatively high power and positive work in the frontal plane during stair ascent and this result would strengthen our position that positive muscle work in ascending gaits is larger than negative muscle work in descending gaits (Nadeau et al., 2003). Work done by upper extremity muscles was also not included in the present analysis and is also infrequently reported. Mechanical energy fluctuations in the arm and forearm during level walking have been reported (Cavagna and Kaneko, 1977; Willems et al., 1995). These fluctuations were small relative to those in the lower extremity and Cavagna and Kaneko estimated them to be ∼10% of the total work. Data in both studies also showed similar positive and negative work fluctuations indicating similar positive and negative work by the upper extremities. Admittedly, upper extremity work may be larger in non-level vs level gaits and thus may account for some of the observed differences between ascent and descent. We conjecture, however, that upper extremity work may be larger in ascending vs descending gaits and thus might increase the differences between positive and negative work in these gaits. In any case, upper extremity work patterns most likely would not account for the differences in positive and negative work observed in the present gaits. Lastly, the results were limited to only one lower extremity and recent evidence suggests that some asymmetry in muscle function may exist between left and right limbs during level walking (Sadeghi et al., 2001). Thus the positive bias in muscle function during level walking observed in the present subjects may be offset by a negative bias in their other limb. This effect may be relatively small, however, since the difference in the limb speeds was only 1.5% in Sadeghi et al.'s analysis whereas positive work was 47% larger than negative work in the present level walking data. We attempted to determine whether muscles perform more positive than negative work during level walking and ramp and stair ascending and descending gaits. While our methods were not able to assess all muscle work throughout the body we propose that they were sufficiently valid for an initial empirical investigation into this interesting concept. Further, while more precise methods may yield more accurate numeric results, we propose that the qualitative interpretation would not be altered from the present understanding.

Conclusions

The present data were obtained to empirically explore the concept that muscle work is biased towards energy generation over energy dissipation in level and non-level gaits. The magnitude of the total positive muscle work was significantly larger than the magnitude of the total negative muscle work in level walking by 47%. The magnitudes of the positive net muscle work in ramp and stair ascent were significantly larger than the magnitudes of the negative net muscle work in ramp and stair descent by 25% and 43%, respectively. These data did in fact confirm the proposition and they formed the basis of two novel hypotheses about muscle work during locomotion on level and non-level surfaces. We also used two non-locomotion movements to demonstrate that positive and negative muscle work can be equivalent in other cyclic movements. Thus we do not propose that muscle work is always biased towards the positive but that it may certainly be in human gait. Further investigations are necessary to test the hypotheses more precisely and to determine how environment, population, and form of locomotion interact with the basic finding.