Genome-wide nucleotide-level mammalian ancestor reconstruction

Abstract

Recently attention has been turned to the problem of reconstructing complete ancestral sequences from large multiple alignments. Successful generation of these genome-wide reconstructions will facilitate a greater knowledge of the events that have driven evolution. We present a new evolutionary alignment modeler, called “Ortheus,” for inferring the evolutionary history of a multiple alignment, in terms of both substitutions and, importantly, insertions and deletions. Based on a multiple sequence probabilistic transducer model of the type proposed by Holmes, Ortheus uses efficient stochastic graph-based dynamic programming methods. Unlike other methods, Ortheus does not rely on a single fixed alignment from which to work. Ortheus is also more scaleable than previous methods while being fast, stable, and open source. Large-scale simulations show that Ortheus performs close to optimally on a deep mammalian phylogeny. Simulations also indicate that significant proportions of errors due to insertions and deletions can be avoided by not assuming a fixed alignment. We additionally use a challenging hold-out cross-validation procedure to test the method; using the reconstructions to predict extant sequence bases, we demonstrate significant improvements over using closest extant neighbor sequences. Accompanying this paper, a new, public, and genome-wide set of Ortheus ancestor alignments provide an intriguing new resource for evolutionary studies in mammals. As a first piece of analysis, we attempt to recover “fossilized” ancestral pseudogenes. We confidently find 31 cases in which the ancestral sequence had a more complete sequence than any of the extant sequences.

Multiple sequence alignments produced by many programs, such as ClustalW (Thompson et al. 1994), MLAGAN (Brudno et al. 2003a), MAVID (Bray and Pachter 2004), MUSCLE (Edgar 2004), and Probcons (Do et al. 2005), attempt to group together homologous bases in columns, placing “gaps” within columns to account for insertions and deletions. Such sequence alignments have proven useful for numerous purposes and provide a bedrock for many current phylogenetic methods (Felsenstein 2004).

However, traditional multiple sequence alignments confound insertions and deletions together as gaps. It is therefore not possible to look at an alignment and determine without further reasoning whether a gap corresponds to an insertion, a deletion, or some more complex arrangement of these two processes. Additionally, the most frequently used objective functions to generate multiple alignments, such as the sum-of-pairs (Durbin et al. 1998) and consensus functions (Gusfield 1997), while apparently producing reasonable alignments, are not phylogenetically realistic, so that they do not properly model the evolution of indels and substitutions along the branches of a tree.

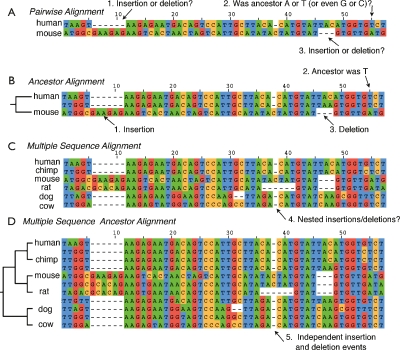
One alternative to producing an alignment only of the input sequences is, for a given tree, to produce a so-called ancestor (also referred to as phylogenetic or tree) alignment (Sankoff and Cedergren 1983; Gusfield 1997) additionally containing inferred ancestral sequences, which thereby explicitly anchor substitutions, insertions, and deletions to specific branches of a tree, and so avoid confounding indels as simply gaps. Figure 1 visually explains the difference between these two types of alignment. When the residues for positions in the ancestral sequences are not explicitly labeled (i.e., they are labeled as “Felsenstein wildcards”), then this form of alignment has also been called an “indel” alignment (Kim and Sinha 2006; Snir and Pachter 2006).

Figure 1.

Ancestor alignments. Examples of different forms of sequence alignment. (A) A pairwise alignment of two sequences. (B) The same pairwise alignment as in A, but with the addition of an ancestor sequence that resolves the ambiguous questions posed in A. (C) A multiple sequence alignment containing the sequences in A and B. By eye, it is possible to resolve the questions in A with some confidence, although the multiple sequence alignment provides no explicit answers and contains nested indel events. (D) A multiple sequence ancestor alignment, which contains explicit ancestor sequences for every node in the phylogeny. The inference of such alignments is the task of Ortheus.

Methods for computing ancestor alignments have advanced in several directions in recent years. In terms of models, Thorne et al. (1991) originally described a continuous time model of nucleotide evolution that was capable of integrating over both substitution and indel events under the assumption that individual insertion and deletion events were all a single base pair long. This was then revised, with some constraints, to model grouped gaps later (Thorne et al. 1992); subsequently, even more general models have been proposed (Knudsen and Miyamoto 2003; Miklós et al. 2004; Rivas 2005). Practical implementations of these models exist for multiple short DNA and amino acid sequences, using either multidimensional programming (Hein 2001) or a combination of progressive alignment and Gibbs sampling (Holmes and Bruno 2001).

For larger genomic sequences, methods for computing indel alignments from fixed multiple sequence alignments initially took parsimony-based approaches, trying to explain the indel history in terms of the smallest number of individual events (Blanchette et al. 2004a; Snir and Pachter 2006). Parsimony methods have been implemented using greedy algorithms (Blanchette et al. 2004a) and brute-force search (Snir and Pachter 2006). Drawing on some principles of phylogenetic alignment models, the Indelign program (Kim and Sinha 2006) takes a limited probabilistic evolutionary model and searches for an indel history based on a dynamic programming method. Notably, it does not allow for nested indels within a column. It is also capable of iteratively improving the resulting indel history by a method of subsequent random search that permutes the input multiple sequence alignment of the leaf sequences. Recently a new “treeHMM” method capable of computing the posterior probabilities of individual insertion and deletion events has been published (Chindelevitch et al. 2006; Diallo et al. 2007). Unfortunately, all the fully enumerative methods mentioned have exponential scaling properties. The Kim and Sinha method scales, theoretically at least, approximately exponentially with the length of the sequences involved, while the Chindelevitch et al. method is exponential in the terms of the number of sequences, although they impose principled heuristics to reduce this somewhat in practice. This scaling behavior therefore limits the sequence depth of current methods for large-scale reconstruction. More troubling perhaps for current data sets is that they rely on the initial construction of the indel alignment on a fixed alignment. All the published methods for creating large-scale multiple sequence nucleotide alignments, such as MLAGAN (Brudno et al. 2003a), MAVID (Bray and Pachter 2004), TBA (Blanchette et al. 2004b), and MAUVE (Darling et al. 2004), implement phylogenetically unrealistic objective functions. Recent work (Löytynoja and Goldman 2008) has shown how such objective functions introduce structural bias.

Here we describe a new method, Ortheus, which overcomes some of these challenges. In common with the discussed large-scale indel-alignment methods, it takes as input a phylogenetic tree and a multiple sequence alignment. However, it scales linearly with sequence length and is practical for the alignment of greater numbers of sequences than previous large-scale methods. It is also, crucially, able to explore a user-definable envelope of leaf alignments around the input alignment during construction, making it much less dependent on this input. Finally, it is based on a complete probabilistic transducer model (Holmes and Bruno 2001; Holmes 2003; Bradley and Holmes 2007) able to describe the full range of possible nested insertion, deletion, and substitution events.

Ortheus is a progressive alignment method (Feng and Doolittle 1987) that breaks down the alignment computation into a series of pairwise stages. However, unlike traditional progressive alignment methods, it models uncertainty in the ancestor sequences by generating sequence graphs at each stage, which allow for multiple paths through the putative ancestor sequence. This is particularly useful for indel reconstruction because choices as to whether a gap was an insertion or deletion event can be deferred until more sequence information is available further up the tree.

Sequence graph-based progressive alignment was originally proposed for the investigation of ties between Viterbi alignment paths (Hein 1989) and has subsequently been adapted to explore suboptimal detours from Viterbi paths (Schwikowski and Vingron 1997). Unlike previous methods, we have implemented the Forward algorithm (Durbin et al. 1998) to allow samples to be taken from the alignments created at each progressive step. This has the attraction over previous methods that we can strictly limit the maximum sizes of the produced graphs by limiting the number of samples. In contrast, methods that explore all suboptimal detours of the Viterbi paths up to a prescribed limit can behave unpredictably when a large number of alignments have a similar probability, for example, within regions containing low-complexity repeats.

Unlike previous graph-based methods suitable for handling short amino acid or nucleotide sequences, we implement a system to impose sequence constraints on the alignment process (Chao et al. 1993; Myers et al. 1996), which allows us to scale the alignment process linearly with the lengths of the input sequences. We will show how the method produces very consistent, parsimonious results for large alignments while being reasonably fast and robust.

Indel and ancestor alignments are likely to prove useful for several purposes. For example, phylogenetic, substitution-based methods for detecting changes in genomic selection patterns (Cooper et al. 2005; Siepel et al. 2005) are being joined by methods based solely on indels (Lunter et al. 2006), or integrating indel information (Siepel et al. 2006). Ancestral alignments are also likely to prove useful for studying lineage-specific selection (Siepel et al. 2006), the turnover of functional elements (Moses et al. 2006), and acting as a basis for consistent, combined evolutionary-aware annotations of multiple extant genomes. Using a new whole-genome alignment pipeline, whose implementation is described in related work in this issue (Paten et al. 2008), we investigate whether we can discover genes present in the ancestor that were not present in extant genomes. This contrasts with recent work (Wang et al. 2006; Zhu et al. 2007), which instead relies on a process of careful mapping back from extant sequences to infer gene loss. The obvious benefit of searching within accurately inferred ancestor sequence is that features no longer clearly visible in any single extant genome can be located.

Results

Evolutionary model introduction

Given a rooted phylogenetic tree 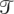and a set ℒ of leaf sequences numbered 1 . . . n, Ortheus attempts to find a sequence for each internal node of the tree so that for each branch b^x (where 1 ≤ x ≤ 2n − 1, including the root branch) the score 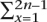σ(b^x,a,b^x,d,χ(b^x)) is maximized, where σ assigns a score to transforming an ancestor sequence b^x,a into a descendant sequence b^x,d given the evolutionary distance χ(b^x), by means of substitution, insertion, and deletion operations. The decomposition of this function into a sum of scores for each branch is a natural consequence of the conditional independence of the different lineages. It is therefore sufficient to describe a general class of evolutionary model accounting for a single branch that can then be adapted to each individual branch in turn.

To define the σ function, we use the intuitive theory of evolutionary transducers, a subclass of hidden Markov model (HMM) recently introduced within biological sequence analysis (Holmes 2003). We start by briefly and informally describing a probabilistic branch transducer, which models the transforming events between two sequences and is hence the simplest class of evolutionary transducer. Unlike a standard pair-HMM that computes the joint probability P (x,y|θ) of two sequences, given a generative model θ, a transducer computes the conditional probability P (x,y|θ) of one sequence given the other. A branch transducer can therefore compute P (d|a,χ,ψ), the probability of a descendant sequence given its ancestor, an evolutionary distance χ, and a branch model ψ.

There are several ways of representing transducers: as Moore machines (which absorb and emit symbols from their states) or as Mealy machines (which absorb and emit on transitions between states). Here, we represent transducers as Moore machines, which is consistent with the way HMMs are usually represented in bioinformatics.

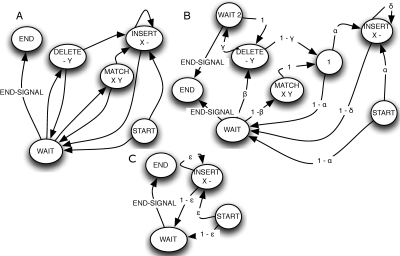
Figure 2A shows a simple complete evolutionary branch transducer. The states can be decomposed into four types, the start state, wait states (e.g., the WAIT state in Fig. 2A), receive states (DELETE, MATCH, and END in Fig. 2A), and insert states (INSERT in Fig. 2A). The model begins in the start state and then enters either the wait or insert state. In the wait state, the model is forced to pause for an ancestral input symbol. Upon receiving an ancestral symbol, the model leaves the wait state and enters a receiving state, which, in this case, allows it to match the symbol (and hence emit a possibly modified symbol in the descendant sequence), delete the symbol (and hence emit nothing to the descendant sequence), or enter the end state, emitting the received terminating symbol. After acting on the received symbol (or coming from the start state), the model may then enter an insert state before returning to the wait state. This state is allowed to emit symbols to the descendant sequence independently of the ancestor.

Figure 2.

Branch transducers and sequence graphs. State diagrams showing transducers. (A) A simple branch transducer. The START, END, WAIT, and unlabeled states are silent states. Emissions are labeled beneath the state name. Output emissions to the descendant sequence are labeled X, and input symbols from the ancestor are labeled Y; gaps are labeled “–”. (B) An affine branch transducer with labeled transition parameters. (C) Root branch transducer with labeled transition parameters.

We place three important general conditions on the branch transducers considered:

1. Ancestral symbols can only be absorbed in transitions from wait states to receiving states (in this case, DELETE, MATCH, and END).

2. Correspondingly, only transitions from wait states can enter receiving states.

3. Transitions into receiving states are conditionally normalized on the absorbed ancestral symbol; for example, upon receiving a terminating symbol, the model is forced into the end state.

Overall, for each branch model, the input ancestor sequence is conditionally dependent on the emissions of its ancestral lineage. Similarly the output descendant sequence of a model is received and transduced by descendant branches. For a given tree, it is therefore possible to combine the set of branch models into a single model by connecting and ordering the component inputs and outputs to generate a combined state space in a unified model.

In developing Ortheus, we have initially chosen to use a simple branch transducer for non-root node branches. The model in Figure 2A allows for affine log-probability insertion functions of the form i + j × k, where i is the initial fixed cost of an insertion, j is the log-probability of extending the insertion, and k is the insertion length. However, it is restricted to linear deletion log-probability functions of the form j × k. We therefore used the branch model shown in Figure 2B, which adds an extra wait state to the model. For clarity, we have added silent states to group together common transition parameters.

To informally restate the optimization problem given in the Introduction, we need to combine the probability of the events on the different branches and create a root branch transducer to model the probability of the root sequence. The transducer shown in Figure 2C is equivalent to such a model; it simply enters an insert state, whose duration and output are independent of any input sequence. Let 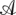represent an alignment (see Methods for a definition) of the set of extant and internal sequences for a given 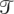. Furthermore, let

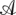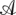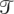denote the branch alignment dictated by of sequences b^x,a and b^x,d. Combining the transducer models introduced, we can state the probability of given as:

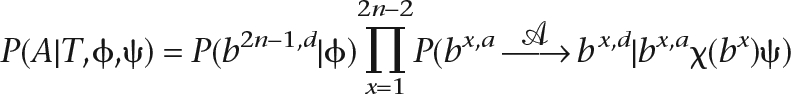where ϕ is the model for the root sequence; and we reserve the index 2n − 1 for the root branch of 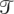. We wish to optimize this function in terms of 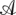to find the alignment with the highest probability. A more precise definition of the probability is laid out in the Methods.

Implementation

Several algorithmic possibilities exist for the optimization of Equation 1. Considering our aim of aligning entire mammalian genomes using Ortheus, we decided that rather than creating a Markov chain Monte Carlo (MCMC) method, we would implement a constrained, graph-based dynamic programming solution that we reasoned would be computationally much faster for reasonable numbers of sequences. The type of graph our implementation is based on is called a “sequence graph” (Hein 1989). Standard dynamic programming algorithms (Durbin et al. 1998) for sequences are naturally extendable to sequence graphs (Schwikowski and Vingron 1997), which allow us to handle uncertainty in the composition of ancestor sequences.

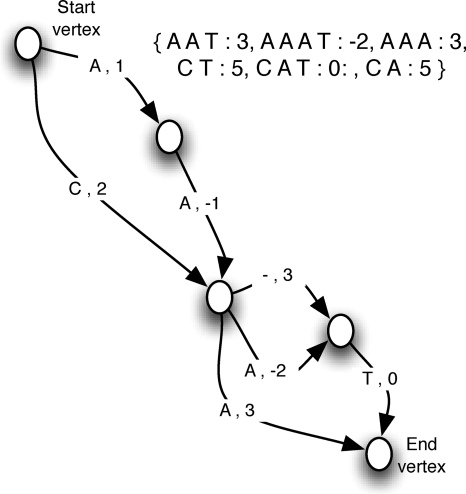
A sequence graph is a directed acyclic graph (DAG) whose edges represent sequence residues. An example is shown in Figure 3. In the example, various paths are possible, each producing a sequence. For the type of graph we consider, all maximal sequences encoded in the graph must start from a unique start vertex and end in a unique end vertex. Such graphs can be used to represent uncertainty in the composition of a sequence. By attaching weights to each edge in the graph, different costs can be calculated for each sequence encoded in the graph. For ancestor reconstruction, residues labeled as gaps represent insertions in descendant lineages not present in the ancestor. By weighting these “silent” transitions in the ancestor, it is possible to keep track of the cost of operations in descendant lineages.

Figure 3.

Sequence graph. A weighted sequence graph labeled with symbols from the set containing the alphabet {ACGT−}. (Inset) The set of possible sequences encoded by this graph (minus “–” gaps).

In common with previous multiple sequence alignment algorithms using sequence graphs (Hein 1989), we construct the ancestral alignment progressively. That is, for a given tree, the multiple alignment of an associated set of sequences is broken down into a series of ordered steps, one for each internal node of the tree. At each step, an alignment of the subtree from the left descendant branch, represented as a sequence graph, is aligned with an alignment of the subtree from the right descendant branch, also represented as a sequence graph, to produce an ancestral sequence graph, working backward in time up to and including the root of the tree. To infer sequence graphs at each step, we implement the Forward algorithm and then sample alignments from it. Upon finishing the final progressive step, the produced graph contains sequences representing multiple potential root ancestors. The highest-scoring Viterbi path through this graph is found, representing a single chosen ancestor sequence. By maintaining links between ancestor and descendant sequence graphs constructed during the progressive alignment process, we are able to trace the alignment of the descendant sequences linked to this root ancestor, and thus construct a full ancestral history.

Each progressive step involves three branches in the tree; we therefore construct a three-branch model (see Supplemental Fig. S1). This model is derived by combining two instances of the affine branch transducer shown in Figure 2B for the descendant branches, and incorporating the root sequence model shown in Figure 2C for the ancestor branch. For progressive alignments of internal nodes not at the root of the tree, we simply remove the probabilities associated with the root transducer after each alignment step to avoid double counting.

Without further modification, the method would scale approximately quadratically in the worst case with the length of the two largest input sequences. However, through the imposition of pairwise sequence constraints on the alignment process, we limit the computation time to linear in the length of the sequences. This method is a generalization of a constrained pairwise sequence alignment algorithm, the difference being that instead of constraining the alignment of two sequences, we constrain the alignment of two sequence graphs. The constraints used are taken from an alignment of the leaf sequences. An association between the edges in the graph and the residues in the leaf sequences allows us to place these constraints on the sequence graph. For each aligned pair of residues, x_i,y_j, in the leaf alignment, four constraints are created: x_i◃y_j+k, x_i−k◃y_j, y_j◃x_i+k, y_j−k◃x_i, where we use the notation ◃ to mean that the left residue must occur before the right residue in the alignment and where k is a variable allowing the relaxation of the constraint envelope. Depending on the size of k, this definition allows optimization around smaller gaps and fixes the positioning of larger gaps. We call k the diagonal constraint relaxation.

Simulation study

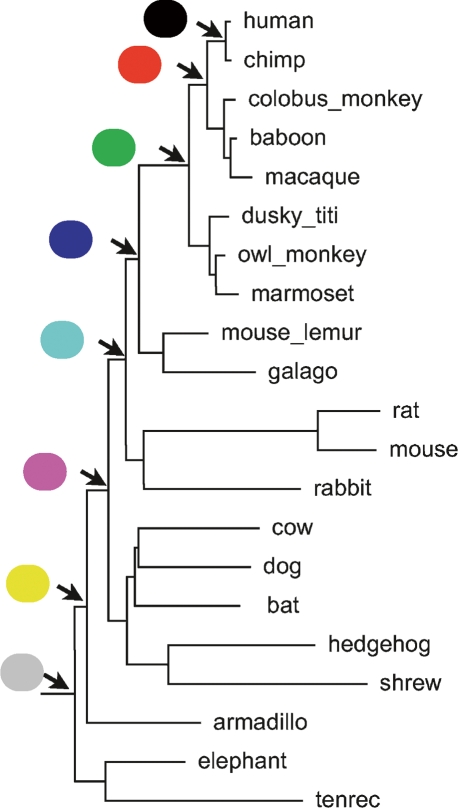
Previously, simulations have been used to assess the performance of ancestor reconstruction methods (Blanchette et al. 2004a; Kim and Sinha 2006). Unfortunately, these simulations are either not public or not sufficiently large to use for evaluation. We have generated a new set of simulations based on the same phylogeny as that used by the ENCODE consortium (The ENCODE Project Consortium 2007; Margulies et al. 2007). We used the complete set of 21 placental mammals in the phylogeny, the putative phylogeny of which is shown in Figure 4. We used a new transducer-based simulator, called “GSimulator” (A. Varadarajan, R. Bradley, and I. Holmes, unpubl.), capable of training from biological data models containing mixtures of affine gap states as well as contextually dependent nucleotides. We tested four simulation sets each comprising a megabase of root-ancestor sequence, with either one or a mixture of two affine gap states and with or without a single contextually dependent nucleotide. Details of these simulations can be found in the Methods.

Figure 4.

Color key for ancestral nodes. The phylogeny of the considered reconstruction with a key used in Figures 5 and 6 coloring the different ancestors on the path to human from the common Eutherian ancestor.

Prior to testing upon the simulations, we parameterized the transducer used by Ortheus using a stochastic EM (expectation-maximization) method (Diebolt and Ip 1995), detailed in the Methods, trained on the ENCODE data set sequences and phylogeny for the well-studied cystic fibrosis trans-membrane conductance region (CFTR) locus. This region covers ∼1.87 Mb of the human genome sequence. Apart from the parameters of the transducer model used, two parameters of Ortheus are likely to be critical to its performance: the number of alignments sampled at each progressive step (sample rate) and the degree of constraint relaxation. The sample rate affects how likely it is that a good alignment will be found given the input constraints and transducer model. The constraint relaxation determines how far away the method is able to explore from the constraining input alignment.

To compare the predicted and true simulated ancestor sequences, we used Pecan (Paten et al. 2008) to align them and then calculated three disagreement metrics from the resulting pairwise alignment. These metrics are similar to those used by Blanchette et al. (2004a).

1. Insertion errors: The number of bases present in the predicted sequence but absent in the simulated sequence, divided by the length of the alignment.

2. Deletion errors: The number of bases present in the simulated sequence but absent in the predicted sequence, divided by the length of the alignment.

3. Substitution errors: The number of alignment columns containing mismatched residues divided by the length of the alignment.

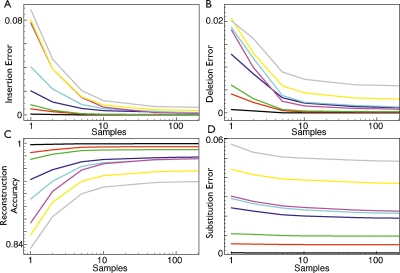
Subtracting the values of these metrics from 1, we get the proportion of bases identical between the simulated and predicted sequences and call this value the “reconstruction accuracy.” It is important to note that because of the extra alignment step needed to compare the two sequences, these numbers do not perfectly reflect the number of miscalled mutations. However, given the closeness of the two ancestor sequences, we do not expect alignment artifacts to be significant for most comparisons. Figures 5 and 6 show how the sample rate and constraint relaxation, respectively, affect the ability to reconstruct simulated ancestral sequences. For clarity, only ancestors on the path to the human lineage are represented. Ancestors can be identified using the coloring shown in Figure 4.

Figure 5.

The effects of sample rate and the accuracy of simulation reconstruction. The effects of changing the sample rate on the accuracy of reconstructing simulations. (A) Samples versus insertion errors. (B) Samples versus deletion errors. (C) Samples versus reconstruction accuracy. (D) Samples versus substitution errors.

Figure 6.

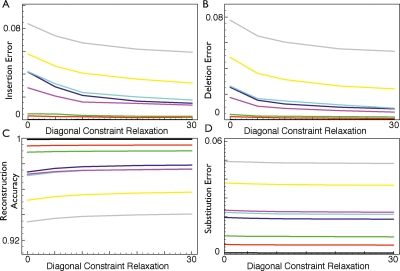
The effects of diagonal constraint relaxation on the accuracy of simulation reconstruction. The effects of changing the diagonal constraint relaxation on the accuracy of reconstructing simulations. (A) Samples versus insertion errors. (B) Samples versus deletion errors. (C) Samples versus reconstruction accuracy. (D) Samples versus substitution errors.

As expected, increasing the sample rate improves the alignments, with the rate of improvement appearing to converge to 0 at close to the default sampling rate of 100. As the rate increases, insertion errors, deletion errors, and substitution errors all decrease, although at different rates and in different relative amounts. When the sampling rate is 1, Ortheus is essentially analogous to a naive algorithm that randomly chooses to assign an insertion or deletion label to each gap. The difference between this setting and the default setting shows the utility of the Ortheus method. At the default rate (100), the total observed error is ∼6% in the Eutherian ancestor, decreasing to <1% for the common ancestor of the apes and monkeys; overall, the average error is 3.2% for all ancestors. A previous study (Blanchette et al. 2004a) gave a figure of ∼99% accuracy for the reconstruction of nonrepetitive regions of the boroeutherian ancestor (the common ancestor in this phylogeny of shrews and humans). We calculate a statistic of 97.5% accuracy for this ancestral node. Were we able to exclude substitution error, then the accuracy would be 99.8%. The discrepancy between our result and theirs is therefore likely explained by the difference in phylogeny of the tree they simulated. Their tree, which involves an idealized selection of mammals arranged in a crown phylogeny, with the boroeutherian at the root, gave them very high confidence in making residue predictions. However, given this caveat, our independent simulation resulted in a reasonably close agreement with their findings.

At a sample rate of 1, most of the errors come from insertion and deletion errors (56% average). At a sample rate of 100, the proportion of total error coming from insertion and deletion errors is only ∼21% on average. The converse of this is that although the substitution error also falls as the sample rate increases, its decline is much more shallow, such that most of the residual error is left in substitution errors. To a large extent, this must reflect information loss in the columns of aligned residues, where the maximum-likelihood (ML) character call is incorrect, even though the prediction of the existence of an ancestral base for a column of aligned leaf sequence positions is fundamentally correct.

The effect of increasing the constraint relaxation is a positive increase in the number of correctly predicted bases in all ancestor sequences, equal to 0.26% on average between no relaxation and the highest setting. Although this absolute improvement is small, the proportion of insertion and deletion errors falls by a more significant amount: 16.5% and 22.9% on average, respectively, while the number of substitution errors does not change as significantly (5.5% average). While relaxing the alignment constraints is able to significantly reduce the number of incorrect indel events (and thus improve the input alignment), it naturally cannot assist in improving the prediction of ancestral substitution events other than by increasing the number of correctly aligned residues.

Empirical performance

Having established the performance of Ortheus using simulations, we reconstructed the CFTR locus using real biological data from the ENCODE data set (The ENCODE Project Consortium 2007; Margulies et al. 2007). This data set covers 1.87 Mb of the human genome sequence. To undo large-scale rearrange ments within the sequences of this set, we used a previously published rearrangement map computed using Shuffle-LAGAN (Brudno et al. 2003b). We then carried out an empirical analysis of the Ortheus output. We looked at the predicted number of micro insertion and deletion events, of up to 10 bases each, and the number of predicted substitutions (from ML estimates of the sequences, with Jukes-Cantor correction) (Jukes and Cantor 1969) on each branch of the tree, as well as the overall log-probability and run time of the program (including the generation of the constraining alignment). The stability of predicted ancestor sequences generated between runs of the program was also tested using a similar methodology to that described in Blanchette et al. (2004a). This analysis is in the Supplemental material.

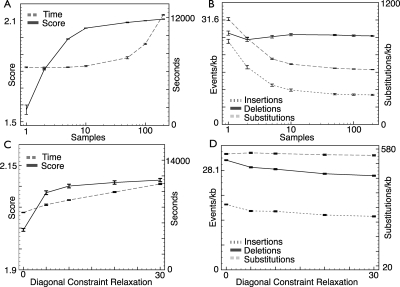
Figure 7A,B shows the effects of different sample rates on the reconstructions. Figure 7A shows that the overall log-probability of the alignment increases by ∼31%, moving from 1 (the lowest) to 200 (the highest) samples/per node. The curve also resembles an asymptote, such that the average log-probability produced at a sample rate of 100 is nearly indistinguishable from the highest sample rate. Figure 7B shows the predicted rates of insertions and deletions of up to 10 bases as well as the rates of substitutions. For Figures 7B,D, the rates are all in events per kilobase, and for consistency, the event counts are all not corrected for the effects of multiple hits. The predicted numbers of insertions and substitutions fall by similar proportions as the sample rate increases, appearing to reach asymptotic limits of ∼60% and 52%, respectively, of their initial value. The fall in substitutions is larger than was seen in the simulations; this appears to correspond to decreases in the proportions of total bases aligned in regions that Ortheus concludes are more likely to be the result of independent indel events. Interestingly, the total number of deletions does not change significantly as the sample rate increases; although for computational convenience the parameters of the current method tie the rates of insertions and deletions in equilibrium, it is clear that the data show otherwise. We also note that there is very little variance in these predictions, between higher sampling rates (100–200 samples) and experiment repetitions.

Figure 7.

The effects of sample rate and constraint relaxation on time, likelihood, and mutation rates. The effects of changing the sample rate and diagonal constraint relaxation on (A,C) the log-likelihood (arbitrary scale), computation time and (B,D) rates of insertions (of up to 10 bases), deletions (of up to 10 bases), and substitutions for the ancestor reconstruction of the CFTR region. Results are the average of five runs; error bars represent the maximum variation (plus or minus) observed. Runs were performed on Xeon (Pentium 4) processors with 2.4-GHz clock speeds and 4 GB of memory. The sample rates examined were 1, 2, 5, 10, 50, 100 (default), and 200 samples. Log scales are shown for the sample rate x-axis. Diagonal constraint relaxations of 0, 5, 10 (default), 15, 20, and 30 were used. All other parameters were set at their default values.

The overall run time of the method (Fig. 7A) appears to increase approximately linearly (although it appears curved when plotted on a log scale) with the sample rate. This is perhaps surprising and probably reflects the diminishing number of new pathways added to the graphs with each added sample. Overall, at a sample rate of 100, it took ∼22 h to produce a complete reconstruction of the CFTR region. Subtracting out the time the initial alignment program takes to run, Ortheus is able to compute a reconstruction for the entire region at a 100× sampling rate in a little over 3 h and 10 min on a 2.4-GHz Pentium-4 class CPU.

The effect of constraint relaxation on log-probability, time, and observed rates is shown in Figure 7C,D. An increase in log-probability of ∼4.5% is observed between the 0 and 30 constraint relaxation point, with the curve appearing to start leveling out toward 30. The run time is affected approximately linearly with increasing constraint relaxation, which we would perhaps expect given that this relaxation causes a linear increase in the width of the alignment envelope.

Figure 7D shows that relaxing the constraints changes the overall rates of deletions, insertions, and substitutions. The number of insertions and deletions predicted is reduced by ∼24% and 16.5%, respectively, when comparing no relaxation with the highest setting; these curves appearing to reach an asymptotic limit quite quickly. Although both curves show similar absolute reductions in the predicted number of events, the ratio of insertions to deletions does change significantly. With no relaxation, the ratio of deletions to insertions is ∼1.57; at the highest relaxation, it is ∼1.74. The number of substitutions does not change significantly as the constraints are relaxed. These changes must reflect differences between the choices made by the program producing the constraining input alignment (Pecan; Paten et al. 2008) and Ortheus. As both Ortheus and Pecan were trained using sequences from the CFTR region, we speculate that the differences probably to some degree reflect fundamental differences between objective functions and alignment optimization procedures used by the two programs. This illustrates how on real data the assumption of a fixed alignment may bias the resulting alignment.

Cross-validation

Simulations are clearly useful, but must be interpreted with an understanding of the assumptions that they make. For example, we did not attempt to simulate the effects of transposons and modeled only limited contextual nucleotide patterns (i.e., we could model CpG dinucleotidides, but not longer low-complexity repeats). In addition to simulations, we have taken a different, more ambitious biological approach: to attempt to cross-validate our reconstruction by holding out and then predicting extant species.

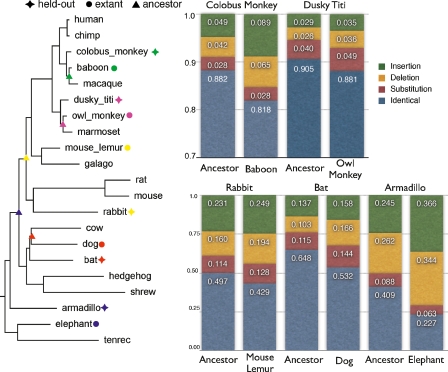
To do this, we selected five extant species from the given phylogeny—two primates: colobus monkey and dusky titi, and three other placental mammals: rabbit, bat and armadillo. For each held-out species in turn, we created a reconstruction missing the given sequence. We then attempted to predict the held-out sequence using the ML prediction of the sequence taken from the reconstruction. For comparison, we then contrasted the results of this prediction with the results of using the closest extant species in the phylogeny to predict the held-out sequence. For each of the five species chosen, the ML prediction corresponds to an internal node in the tree. The left side of Figure 8 shows projected on the putative phylogeny the choices of held-out species and the corresponding extant and ML predicted nodes.

Figure 8.

Hold-one-out cross-validation experiments. (Left) Tree showing species held out, their closest extant relative, and the internal nodes from which the ML ancestor predictions were derived. (Right) Histograms showing the proportions of bases in the held-out species substituted, deleted, inserted, or correctly predicted by the extant and ancestor sequences.

To compare the predictive sequences with the true sequences, we aligned them using Pecan and then, as detailed previously, calculated insertion, deletion, and substitution error statistics in reference to the held-out sequence. The right side of Figure 8 shows histograms of these statistics.

For all the hold-out experiments we observe a significant improvement in the total number of correctly predicted bases between the extant and ML sequences. The most extreme absolute difference is the armadillo (+18.2%), while the smallest is the dusky titi sequence (+2.4%), with the others in between. The increases come largely as a fall in the numbers of insertions and deletions, with the total number of substitutions observed staying largely the same. Table 1 compares the observed substitution distances, with the expected distances derived from the input phylogeny. The observed distances were calculated with Jukes-Cantor (Jukes and Cantor 1969) correction from the pairwise alignments between the held-out sequence and the predicted ancestor or nearest extant species. The expected distances were calculated as the sum of path lengths between the held-out species and the predicted ancestor or nearest-extant in the input phylogeny.

Table 1.

A comparison of the observed and expected substitution distances for the hold-one-out cross-validation experiments

Expected distances are calculated from path lengths between the held-out species and the ancestor or nearest-extant in the input phylogeny. Observed distances are calculated from pairwise alignments of the held-out species and the extant or predicted ancestor sequence using the Jukes-Cantor (Jukes and Cantor 1969) correction.

For the two primates, the difference between the observed and expected distances is quite close. For the rabbit and bat predictions, the ancestor prediction diverges from expectation more significantly. Only the armadillo comparison is widely far off the expectation, probably as a result of the ancestor sequence’s position in the tree and the long branch lengths involved. The loss of information due to deletions and varying assembly coverage makes it inevitable that the ML sequences fall shorter than might be predicted by the distances in the estimated phylogeny, because they will frequently have less than a complete set of leaf sequences to create an ancestral prediction from.

Predicted rates

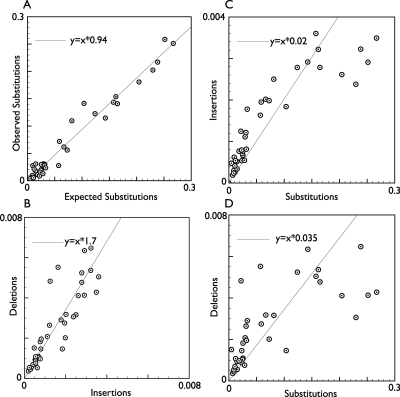
Figure 9 shows scatterplots of the predicted rates of micro-insertions, micro-deletions (both up to 10 bp), and substitutions (both observed and expected) for each lineage. In the Supplemental material, Supplemental Figure S3 contains trees showing the predicted rates of insertions and deletions for each lineage.

Figure 9.

Observed insertion, deletion, and substitution rates. Scatterplots showing expected versus observed substitutions (A), insertions versus deletions (B), insertions versus expected substitutions (C), and deletions versus expected substitutions for all the branches in the phylogeny, excluding the three branches emanating from the root sequence, where measurements are likely to be very imprecise (D). Linear regression lines are shown estimating the overall ratios.

The curves show overall an approximately linear relationship between the substitution, insertion, and deletion rates, although one with considerable variance. We note that the observed rate of substitutions was slightly lower than the expected (neutral) rate; however, this was expected, given that we had not tried to assess the neutral rate but instead had taken the overall rate. The overall ratio of micro insertions to deletions is estimated to be ∼1.7. This estimate is on the low side of previous studies that have measured the ratio higher at 1.8 (Cooper et al. 2004), 2 (Gibbs et al. 2004), and 2–3 (Blanchette et al. 2004a).

Figure 9C,D plots of the insertion and deletion rates against the expected substitution rate are somewhat skewed right as the substitution rate increases, and slightly skewed left at lower substitution rates. It is important to realize that our predictions are to some extent affected by the transducer parameterization and on the accuracy of the branch lengths of the input phylogeny. We note that the branches displaying the greatest rate deviation from the average are internal and have a very short predicted branch length, and where we might not therefore expect a particularly accurate estimate, for example, the ancestor to cow–dog. Overall, we find the rate of substitutions to deletions to be ∼20×, which broadly agrees with the ranges observed by Blanchette et al. (2004a) for the CFTR and the genome-wide estimates from analysis of human, mouse, and rat genomes (Cooper et al. 2004; Gibbs et al. 2004).

Detecting fossilized pseudogenes in the ancestors

The new whole-genome multiple alignment pipeline in Paten et al. (2008) allows us to compute a near complete “segmentation” of a group of input genomes into a set of collinear segments that includes duplications, and each of which is unbroken by any large-scale rearrangement event. From such sets of alignments, we have generated segment trees and a complete set of ancestor alignments that include ancestor sequences. In a first piece of analysis involving this pipeline, we have used alignment segments involving the human, mouse, rat, dog, and cow genomes. This analysis attempts the detection of ancestral pseudogenes no longer clearly visible in the extant genomes. These are most likely to be pseudogenes (either retrotransposed or duplication pseudogenes) in the ancestor, and more rarely would be genes under selection in the ancestor that have become niche-loss pseudogenes in all extant species. Although in theory we could investigate differential pseudogenic loss in specific lineages, the presence of some regions of poor gene prediction, owing to assembly and sequence error in the draft genomes, present an additional disambiguation problem. It is also impossible to assign absolutely whether an ancestral sequence was an active gene or not. We therefore call these regions “ancestral genic regions” (AGRs) to encompass both possibilities.

To find AGRs, we used the exonerate program (Slater and Birney 2005) to match the current human protein set to the primate/rodent ancestor, which is the deepest ancestor with high information for its reconstruction, being the central node to human, mouse/rat, and dog/cow lineages.

By tracking the genomic segment of the human gene prediction to the ancestral sequence, we designated the match from the extant human gene to the ancestral sequence as the “orthologous match.” This match therefore deliminated a series of exons in the ancestor. To screen out paralogous matches from other extant proteins in other parts of the genome, if a matching protein overlapped with any of these homologous exons, this match was excluded from further analysis. We also aggressively screened out transposon family matches (some of which are present in extant human genes), matches due to low-complexity regions in extant proteins and hypothetical coding sequences, which often correspond to open reading frames called in long 3′ UTRs that have terminated before a main gene. We then looked for cases in which (1) the matched protein originated from a different chromosome to the chromosome in the ancestor and (2) in which the matching score to the ancestor was higher than to all the extant sequences, using a tolerant alignment model allowing disabling mutations (Birney et al. 2004). These stringent criteria reduced an initial set of around 20,000 AGRs to a set of 31 high-confidence cases, listed in Table 2, and expanded in more detail in the Supplemental material. This set is an intriguing set of likely pseudogene fossils present in the ancestral sequences. Figure 10 shows one example, a fossil from the ferratin heavy chain (FTH1 gene). The FTH1 gene is a 3-intron gene on chromosome 11. On the chromosome X in all extant sequences, there is a weak pseudogene match, each with disabling mutations relative to the extant source gene. The ancestor sequence from X, generated with no knowledge of the extant sequence on chromosome 11, is both a better match than the pseudogene to the extant gene and has no disabling mutations. It is hard to definitively assess whether this sequence was a recent duplication pseudogene that had not accumulated mutations or an active gene in the ancestor, but its presence on X and lack of introns in the ancestor suggest a retrotransposed copy.

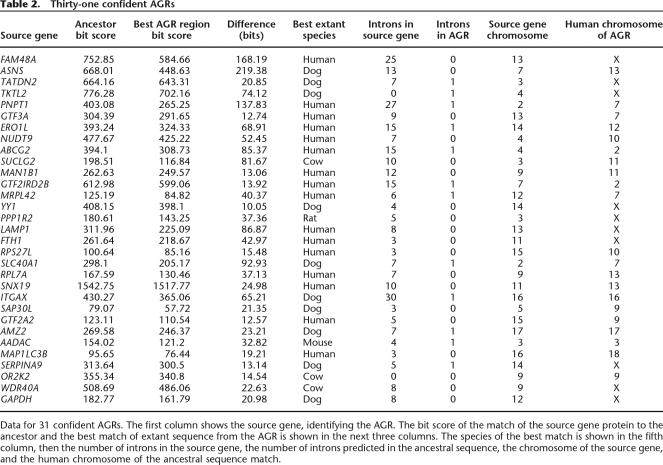
Table 2.

Thirty-one confident AGRs

Data for 31 confident AGRs. The first column shows the source gene, identifying the AGR. The bit score of the match of the source gene protein to the ancestor and the best match of extant sequence from the AGR is shown in the next three columns. The species of the best match is shown in the fifth column, then the number of introns in the source gene, the number of introns predicted in the ancestral sequence, the chromosome of the source gene, and the human chromosome of the ancestral sequence match.

Figure 10.

An alignment of the FTH1 gene from chromosome 11. An alignment of the FTH1 gene from chromosome 11, the ancestral sequence predicted from the X chromosome, and the best alignments to the current extant sequences of the X chromosome. (Dark gray) Disabling mutations (either stops or frameshifts).

The set of ancestor genic regions shows a strong bias toward the chromosome X (10 out of 31, 32% of AGRs compared to its 5% of the genome). This is consistent with the long-held observation that the X chromosome accumulates more retrotransposed pseudogenes than other chromosomes and reinforces the idea that most of these AGRs are likely to be pseudogenes inserted into the ancestor sequences. It was more common for dog or human (26 out of the 31 cases) to provide the AGR region with the best match, consistent with their branch lengths to the ancestor being shorter than the rodents or cow. There was no particularly obvious functional bias of the source gene.

The criterion for determining AGRs in this analysis was particularly stringent. Relaxing this stringency dramatically increases the number of AGRs, but results in many of the matches coming from low-complexity sequences, in particular, triplet repeat matches that occur even when the protein database has been purged of obvious low-complexity sequences (e.g., via the program Seg; Wootton and Federhen 1996). Many of the matches are also close to the source gene, in particular, in tandem duplications and pericentromeric regions. As these are regions with challenging gene prediction and potentially multiple duplication and pseudogenization events, distinguishing the different possibilities of erroneous gene prediction from pseudogenization and from a real ancestral gene is complex and likely to require even more sophistication in the alignment and reconstruction methodologies.

Discussion

We have described a probabilistic method for phylogenetic alignment that creates highly accurate and stable output while being practical for large numbers of long sequences. We have also shown by simulation and empirical biological data analysis that by relaxing constraints from the initial input alignment, we are able to create better reconstructions. In real data relaxing, the fixed alignment increased the likelihood of the alignment and reduced the total numbers of indel and substitution events. In simulations, relaxing the alignment reduced significantly the amount of errors attributable to misplaced indels. We observed this effect despite using an initial probabilistic alignment method trained with the same input data. Ancestor reconstruction methods that assume a fixed alignment and rely on alignment programs that have phylogenetically unrealistic objective functions are likely therefore to produce systematically biased results.

The sampling rate and constraint relaxation parameters of our method are quite flexible and can be altered to achieve different objectives. For small examples, the method can be used to completely enumerate all possibilities and thus find an optimal reconstruction. For larger alignments, constraints can be incorporated to achieve good results while still being practical in terms of memory and run time.

Apart from being the first large-scale indel reconstruction method capable in a single pass of simultaneously exploring the alignment and indel reconstruction, Ortheus is also able to infer simultaneous descendant deletion operations events not possible in previous deferred-choice progressive alignment methods, of the type pioneered by Hein (1989). Additionally, the use of a general and fully probabilistic transducer model coupled with a sampling-based approach allows several future options. For example, the method could be simply adapted to incorporate more complex branch transducers; we note that it would be particularly valuable to model more realistic gap duration functions.

Using similar methods to those implemented by Holmes (Holmes and Bruno 2001), a Gibbs sampling strategy could also be fairly easily incorporated to allow sampling from the posterior distribution of reconstructions given an initially computed indel history. This would allow us to potentially assess the confidence of different operations.

One problem with estimating rates from our model is that they rely on a fixed input phylogeny with fixed branch lengths and a single parametrization of the transducer model (although this model’s parameters are trained). In principle, it is possible to sum over branch lengths and transducer parameters using an MCMC strategy to make measurements averaged over a representative sample of alignments, although this would likely prove to be computationally expensive.

Ortheus currently treats DNA homogenously; perhaps most obviously, it does not specifically address transposons and other repetitive elements. Insertions via transposition cause significant spiked deviations from geometric or even logarithmic gap duration functions (Kent et al. 2003), while low-complexity repeats make many regions of intergenic DNA hard if not impossible to accurately align. During the generation of the initial alignment that is passed to Ortheus, our aligner does use soft-masked annotations generated using RepeatMasker (http://www. repeatmasker.org). This allows it to organize the initial sparse alignment map around repetitive structures that might otherwise produce aberrant homology assignment. We note that Blanchette et al. (2004a) found particular utility in masking out repeats known to be lineage-specific, for example, Alus in the primate lineage, during reconstruction. The most desirable extension to Ortheus would incorporate a generalized-transducer formulation of the sort developed for generalized pair-HMMs (Alexandersson et al. 2003). In such a scenario, it would be possible to specifically recognize transposon-mediated insertions and better model gap duration functions, as well as potentially incorporating nucleotide substitution dependencies. Given the constraint framework that Ortheus uses, such an extension might be computationally feasible.

The use of a cross-validation procedure to validate our method highlights some of the benefits and difficulties in creating genome-scale reconstructions. We suspect that there is much room for improvement, certainly by our alignment and reconstruction methods, but perhaps more significantly in the production of accurate global synteny maps and underlying sequence assemblies. We believe that these tasks must be better addressed if we are truly to accurately reconstruct complete ancestral mammalian genomes.

In this study, we have mentioned the benefits of full ancestral reconstructions over traditional multiple alignments. We believe tools such as phylogrammers (Siepel and Haussler 2004a; Klosterman et al. 2006), which use standard multiple alignments and rely on the patterns of substitutions, are likely to be joined by potentially richer methods using transducers (Holmes 2003) and other indel-aware evolutionary models (Diallo et al. 2007). However, these methods are computationally demanding, and just as fixed alignments are normally assumed by substitution-based methods, it seems likely that fixed indel histories or complete ancestral reconstructions will be assumed by these techniques. We therefore view Ortheus as providing a valuable stepping stone toward these methods.

The set of ancestral sequences provides an intriguing new resource for evolutionary studies in mammals. To our knowledge, this is the first public genome-wide set of such sequences for mammals. In this study, we have presented an initial analysis on recovering “fossilized” pseudogenes. For the fossilized pseudogenes, we confidently discovered 31 cases in which the ancestral sequence had a more complete sequence than any of the extant sequences. These cases all looked consistent with retrotransposed pseudogenization, being single exon genes from a multigene copy, and with a predominance of copies on the X chromosome. Future analyses of genome-wide conservation, turnover, and evolution will be greatly enhanced by the availability of genome-wide alignments and ancestral reconstructions, and all this information is freely available for all researchers to use.

Methods

Ortheus

We first precisely describe the objective function optimized by Ortheus. We then describe the parameterization of the branch models used. We then give overviews of the system of sequence constraints, the method of training, and an important memory-saving technique used by Ortheus. We finally give an informal runtime analysis of Ortheus and describe the program source code and availability. An extended technical manuscript describing the Ortheus program is in preparation.

Ortheus objective function

In this section, we formally define a multiple alignment with ancestral reconstructions as a two-dimensional symbol matrix. We then specify various procedures for extracting or calculating the pairwise alignments, the state paths, the column probabilities, and the state path probabilities. Finally, we use these accumulated definitions to precisely specify the objective function maximized by Ortheus.

Let $ denote the transducer termination symbol. Let π represent the basic nonterminal symbol alphabet (i.e., {A, C, T, G} for DNA). Denote ‘–’ as the gap symbol. Let π′ = π∪{−}. A sequence represents a member of 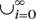πⁱ, where πⁱ represents the set of all strings of length i comprised of π characters. The inputs to Ortheus are a fixed, rooted binary phylogenetic tree 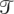with positive real-valued branch lengths and a list of leaf sequences ℒ₁ . . . ℒ_n, one member of which can be assigned to each leaf of 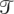. Let b denote a branch of 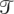. Let χ represent an evolutionary distance. Let χ(b) denote the evolutionary distance of b (the words “distance” and “length” are synonymous in this context). We number the leaf branches b¹ . . . bⁿ, and the internal branches excluding the root bⁿ⁺¹ . . . b²ⁿ⁻², we number the root branch b²ⁿ⁻¹. A reconstruction by Ortheus assigns an ancestral sequence to every internal node in 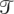. After reconstruction every b^x in 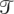therefore has an associated descendant b^x,d and ancestor b^x,a sequence. It is always the case that b^2n−1,a = [], where [] denotes a sequence of zero length. We use the convention of denoting residue i in sequence y using the subscript y_i. Putting it all together in an example, b_i^x,a represents the ith residue of the ancestor sequence of branch x.

We define an alignment as a two-dimensional matrix whose cells all contain a symbol from π′. Each row represents the symbols of a sequence interleaved with gaps. Each column represents an aligned group of π′, the gaps representing symbols missing because of insertion or deletion. For an alignment 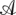, we denote a residue in the xth row of the ith column 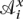. The output of Ortheus is an ancestor alignment 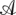′ representing a reconstruction. An 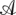′ of a given and ℒ has rows numbered 1 . . . 2n − 1 such that the sequence in row x generated by concatenation after removal of “–” symbols represents sequence b^x,d (note that this definition differs from the ancestor alignment shown in Fig. 1).

Let ϒ(x) denote the index of the direct ancestor branch of b^x. 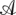′^x and 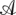′^ϒ(x) define a subalignment of b^x. Let Φ(a,d) denote a function that takes an ancestor a and descendant symbol d from π′ and returns a symbol from {M, I, D, S}. Φ(a,d) returns M if both a and d are symbols in π, Φ(a,d) returns D if a is in π, and d is “–”, Φ(a,d) returns I if d is in π and a is “–”, and Φ(a,d) returns S if both a and d are “–”. Let ∏(A′^x,A′^ϒ(x)) denote the ordered list of {M, I, D} symbols created by applying Φ to each symbol pair 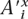and 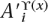for each i in 1 . . . N and then removing all S symbols.

A branch transducer converts one sequence into another. Let θ_i denote the i-th state of a transducer θ. Let Φ′(θ_i) denote a function that takes a transducer state and outputs a symbol from {M, I, D, S, E} according to the following rules:

• If θ_i receives an input symbol from π and then outputs a symbol from π, then Φ′(θ_i) outputs M.

• If θ_i receives an input symbol from π but does not output any symbol, then Φ′(θ_i) outputs D.

• If θ_i receives a $ symbol, it must then output a $ symbol, in this case Φ′(θ_i) outputs E.

• If θ_i does not receive an input symbol but outputs a symbol from π′, then Φ′(θ_i) outputs I.

• If θ_i does not receive or output a symbol, then Φ′(θ_i) outputs S.

Let θ_i → θ_j represent a transition from state θ_i to state θ_j. Let Ψ(θ) denote an ordered list (1. . . m) of states in θ that starts in the transducer start state and ends in the transducer end state such that

Let ∏′(Ψ(θ)) denote the list of {M, I, D} symbols created by applying in order Φ′ to each member of Ψ(θ) and then removing the E and S symbols from the resulting list. Let Ψ(θ, 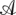′^x, 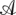′^ϒ(x)) be equivalent to Ψ(θ) but under the condition that

Let ϕ denote the root transducer model and ψ denote the branch transducer model. ϕ is time-invariant; however, ψ is parameterized by evolutionary distance. We denote such a parameterized model ψ(x). With our inputs, we search for an 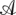′ and

Rather than explicitly defining the π symbols in b^d,n+1 . . . b²ⁿ⁻¹, we marginalize over the probability of every distinct labeling of π symbols in b^d,n . . . b²ⁿ⁻¹. Let 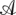″ represent a transformed 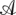′, where every “–” is replaced with a * symbol, a wildcard symbol representing a member of π without specifying which one. Let σ denote a substitution model for π and τ denote the stationary frequencies of π. We can now reprise Equation 1 to exactly state the probability that Ortheus assigns to a reconstruction. In theory, we can compute 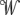optimally given 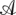′. In practice, however, owing to the stochastic nature of the sampling technique used, our method does not guarantee this optimality, so we describe the probability function optimized by Ortheus in terms of both 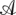′ and .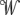

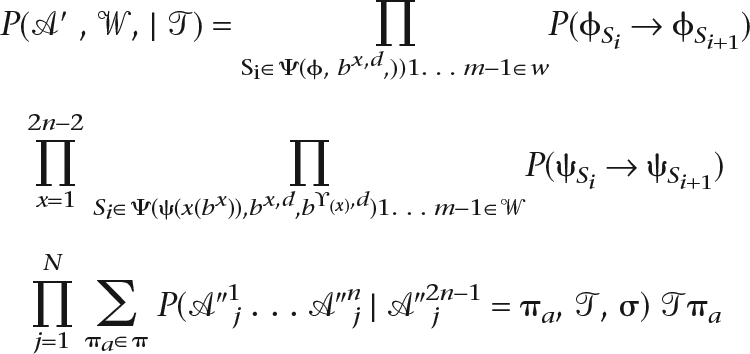This probability is therefore an independent product of probabilities from transitions of the root and branch transducers and the probabilities of the columns of observed residues in 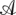″. The flip side of this is that deletions are treated as missing data for the purposes of substitution, and therefore have no effect on the substitution probabilities, something discussed in Siepel and Haussler (2004b). The ability to factorize the problem like this is the result of the clean separation of the process of substitutions and residue substitutions, a feature of many (but not all) transducer-based methods.

Ortheus model parameters

The model in Figure 2B is the branch transducer model (ψ) used by Ortheus. The model in Figure 2C is the root transducer model (ϕ) used by Ortheus. Making the probability of entering the insert state from the start state the same as the probability of entering from the silent state labeled 1, then the branch model has five generative transition parameters: insert-open α, delete-open β, delete-continue γ, insert-continue δ, and the root transducer probability ∈. The default transition probabilities set α = β and γ = δ. α and β are by default linearly time-dependent, while γ and δ are time-invariant. For evolutionary distances considered across the mammalian clade, with which Ortheus was trained, a relatively good fit between these linear and static approximations was observed. For simplicity, all input symbols from the ancestor sequence do not alter the outlined transition parameters, with the exception that the transition probability of entering the end state will be zero for all nonterminating input symbols, and one for the terminating symbol. As defined, the transitions of the current model are time-reversible, which is a convenient but not strictly necessary condition of the method.

Ortheus implements standard continuous time DNA nucleotide models to handle substitutions (σ). By default, Ortheus uses the HKY model, with the ratio of transitions to tranversions set to 2, and a stationary GC frequency set to 40% (this can optionally be empirically estimated from the input data).

Sequence constraints

Sequence constraints are generated from an existing input alignment; by default, the Pecan (Paten et al. 2008) program is used. The input alignment essentially represents a set of aligned pairs from which, after a process of constraint relaxation described above, a set of constraints are inferred. To build the set of nonredundant constraints from the input alignment, we use the algorithm of Myers et al. (1996). Each edge in a sequence graph is associated with zero or one position from each leaf sequence. During each progressive alignment step, we check that the alignment of each pair of edges in the two sequence graphs is compatible with the set of leaf constraints. The leaf constraints therefore act like “banding” constraints that prevent the exploration of much of the alignment space, and therefore make the alignment process efficient.

As the alignment progresses up the tree, it is possible for new transitive sequence constraints to be generated by the interplay between the set of constraints and paths within the newly generated sequence graphs. This can result in mutual incompatibilities being generated between different alignment paths such that, in the worst case, no single alignment is possible for two input graphs. To avoid this scenario, after each progressive alignment we take the single most probable (Viterbi) path through the resulting sequence graph and add any new constraints implied by this alignment to the set of sequence constraints. It is easy to see that this procedure guarantees at least one consistent path through the alignment at each progressive step. Although this strategy can potentially make certain paths illegal that needn’t be, in practice, this procedure seems to have few side effects.

Reducing memory consumption

The memory consumption of the algorithm, in practice, scales linearly with the sequence length, and approximately between linearly and quadratically with the number of sequences, owing to the cost of storing the sequence constraints. To allow the alignment of sequences of arbitrary size, we use a method to break up the sequences into several fragments, compute alignments for the individual fragment sets, and then rejoin the fragments into one large phylogenetic alignment. To do this effectively, we allow an overlap between the fragments and implement a method to stitch the fragments across a common set of sequence positions and transducer states. In practice, for even very small fragment overlaps (200 columns by default) and large numbers of fragments (every 5000 columns), we achieve alignments nearly indistinguishable from those computed as a single fragment (see the Supplemental material). This is because regions in the dynamic programming matrix separated by a sufficient gap prove to be essentially conditionally independent of one another.

Iterative training

To train our transducer models, we have implemented a stochastic EM algorithm (Diebolt and Ip 1995). Briefly, using the output graph computed in the final progressive alignment step, we calculate the posterior probability of each transition given the graph. Using these values in an EM-like step, we then re-estimate the parameters given these approximate expectations and our branch transducer model. Parameters are deemed either linearly time-dependent or fixed. For fixed parameters, we take the average across the branches of the phylogeny; for linearly time-dependent parameters, we use linear regression on the set of estimates to calculate a time-dependent value. Iteration can be run either until the likelihood of the resulting graph approximately converges, or for a maximum number of generations. This method clearly makes many assumptions about the nature of the final graph and the methodology upon which it was built, but we observe reasonable behavior for the limited number of alignments we have tested. During training, a random small value for each trained parameter was chosen. Training was then performed for 20 generations using the entire CFTR sequence set and repeated five times; each time convergence to approximately the same set of parameters was observed.

Runtime analysis

We examine the average case cost of alignment for each pairwise progressive alignment step to create an ancestral graph. We assume a fixed sample rate and fixed constraint relaxation and that all indels are assumed to be deletions, and hence there are no silent edges. Finally we assume that for each pair x_{0. . .n}, y_{0. . .m} in the leaf sequence set, the constraining input alignment contains aligned pairs at regular intervals. By a “regular interval,” we mean that the maximum size of a subsequence in either x or y between aligned pairs and/or the start/end of the sequences is bounded by some reasonable constant. This ensures that the maximum area between constraints, analogous to a square in a standard edit graph, is bounded along both axes. Thus, using arguments analogous to that for standard banded alignment algorithms (Brudno et al. 2003a), the total volume of dynamic programming performed will stay, on average, proportional to, n′ + m′, where n′ is equal to the number of edges and vertices in the sequence graph containing x, and similarly m′ for the graph containing y. The method will therefore scale linearly in terms of the length of the sequences. The total number of progressive alignment steps is equal to 1 minus the number of input sequences. However, the cost of computing and checking for compatibility with the set of sequence constraints introduces a factor cubic in terms of the number of sequences. However, this cubic factor is dominated by the cost of each dynamic programming step. When insertions are allowed, and hence there are runs of silent edges, then the cost of the method appears more difficult to analyze. In practice, we observe linear scaling with sequence length and for moderate numbers of sequences, as the transducer calculations within the dynamic programming steps dominate, linear scaling with sequence number.

Program and data availability

The core of Ortheus was coded initially in Python and then transcribed into C. The genome-wide alignments are available from Ensembl (http://www.ensembl.org/). There is a complete ftp dump in the EMF (Ensembl Multiple Format), a format that allows us to present extant sequences, ancestor sequences, and conservation metrics in a single file.

Data analyses

We now describe the methodological details of the simulations and AGR discovery.

Transducer simulations

To generate simulated alignments of DNA, we used the forthcoming GSimulator program (A. Varadarajan, R. Bradley, and I. Holmes, unpubl.), for generating synthetic DNA alignments. This program simulates local sequence-dependent fluctuations in substitution and indel rates, modeling effects such as CpG aversion or microsatellite expansion and contraction. Specifically, the tool generates a root sequence using a Markov model, then evolves the sequence along each branch of a phylogenetic tree using a finite-state transducer. Both the Markov model at the root and the transducers on the branches are context-dependent; that is, the emission and transition probabilities of the state machine depend on the last few absorbed and emitted nucleotides. (Note that the transducers used for simulation are, therefore, more parameter-rich than the transducers used for reconstruction.) GSimulator can be “trained” directly on pairwise alignment data; for the simulations described here, the program was trained on a random subset of human chromosome 1 to chimpanzee BLASTZ (Schwartz et al. 2003) alignments (downloaded from Ensembl [Flicek et al. 2007] version 49 and totaling just over 20 Mb). The trained models and phylogeny can be found in the Supplemental material.

AGR discovery

The whole-genome ancestor alignments were created using the Enredo/Pecan/Ortheus pipeline as fully described in Paten et al. (2008). We used the human protein set from Ensembl 45 as the source of protein information. These were then compared against the predicted primate/rodent ancestral sequence from each Enredo segment using the protein2 genome model in exonerate (Slater and Birney 2005). By using the correspondence of the human sequence in the Enredo block to the human gene match, we could identify the orthologous exons in the ancestral sequences. These matches were labeled, and all other matches overlapping these matches (mainly from paralogous genes) were discarded. This left 2,456,789 exonic matches. Examination of these matches showed that a large number came from exapted or erroneous incorporation of transposon sequences into the human genes or from low-complexity regions; frequent matching proteins (more than 50 matches after this screen) were then removed, and matches that overlapped regions that were flagged as “low-complexity” by Seg (Wootton and Federhen 1996) were removed. Further examination led to the identification of complex tandem duplication cases, where it is unclear whether one is dealing with misassemblies, duplications followed by pseudogenization or erroneous gene prediction. To concentrate on clear-cut cases, we therefore applied a final filter: we took only those cases in which the chromosome of the source gene was different from that containing the AGR region. This provided 1658 candidate AGR regions of which only 312 cases had representation from all five extant species. These 312 cases were then aligned using a tolerant GeneWise model (-subs 0.05, -indel 0.05, allowing for higher levels of frameshifting), and cases chosen where the alignment to the source-ancestor alignment had >10 bits more information than the GeneWise alignment of the source and best-scoring extant sequence. This led to 31 cases enumerated in the Supplemental material. The other candidate regions are available upon request.