Enredo and Pecan: Genome-wide mammalian consistency-based multiple alignment with paralogs

Abstract

Pairwise whole-genome alignment involves the creation of a homology map, capable of performing a near complete transformation of one genome into another. For multiple genomes this problem is generalized to finding a set of consistent homology maps for converting each genome in the set of aligned genomes into any of the others. The problem can be divided into two principal stages. First, the partitioning of the input genomes into a set of colinear segments, a process which essentially deals with the complex processes of rearrangement. Second, the generation of a base pair level alignment map for each colinear segment. We have developed a new genome-wide segmentation program, Enredo, which produces colinear segments from extant genomes handling rearrangements, including duplications. We have then applied the new alignment program Pecan, which makes the consistency alignment methodology practical at a large scale, to create a new set of genome-wide mammalian alignments. We test both Enredo and Pecan using novel and existing assessment analyses that incorporate both real biological data and simulations, and show that both independently and in combination they outperform existing programs. Alignments from our pipeline are publicly available within the Ensembl genome browser.

The changes affecting genomes, commonly called mutations, as they undergo evolution are complex and varied. Although it is not possible to observe these past changes, for reasonably close genomes, it is possible to search for relatively unambiguous mappings of the results of this process. This problem, of producing a base-level homology map between a set of input genomes, is the subject of this paper.

For computational convenience it is possible to classify the mutations operating upon genomes into two types: those which maintain colinearity of the DNA sequence in the genomes, and those which do not. In the latter, nonlinear case we also include duplication events that result in copies of parts of the genome. An important distinction within the class of duplication events is the relatively common and small scale processes of transposition (giving rise to the majority of dispersed repeats in a genome) and the larger, less frequent process of segmental duplication. As transposition events involve relatively small and often repetitive subsequences, mapping the results of the transposition process is perceived to be harder and, for many analyses, less interesting than unraveling the results of the segmental duplication process. We have therefore attempted to provide a homology map that excludes the transposition events, in line with the common practice of masking out these elements in a single genome’s sequence.

When genome sequences are only affected by linear mutations their homology can be represented in a colinear alignment, where the sequences and their alignment are arranged linearly. While in the general case of multiple sequences the problem of finding an optimal alignment under common objective functions is NP-hard (Elias 2006), efficient and principled heuristic methods are available and discussed below. In this paper we introduce a new method, Pecan, which we will show outperforms available previous methods for colinear alignment. When genomes are additionally affected by the nonlinear categories of mutations then more complex data structures (Kent et al. 2003; Blanchette et al. 2004; Raphael et al. 2004) are needed to represent the evolutionary relationships between the genomes. This more general alignment problem presents many challenges. When the homology map is known, for pairs of sequences the minimum number of inversions (Hannenhalli et al. 1995), or general two breakpoint operations (an operation that cuts the genome at two places and then sticks the resulting free ends back together in any order; Yancopoulos et al. 2005), necessary to transform one genome into the other can be efficiently computed. However, the same problems involving three or more sequences, or using models incorporating duplications, are intractable (Caprara 1999). Perhaps as a result of this knowledge, very little work has been done on optimization algorithms that attempt the inference of the homology map while explicitly accounting for the costs related to the number of rearrangement operations, with a few innovative exceptions (Brudno et al. 2003b; Pevzner et al. 2004).

In this paper we make the simplifying assumption that we can broadly separate large-scale evolutionary events, which involve both rearrangements and duplications, from small-scale evolution, which is assumed to involve only linear mutations. The problem can therefore be broken down into two principle parts. First, the creation of a large-scale homology map, for which we utilize our new tool Enredo. Secondly, the generation of detailed base-pair alignments, for which we use our new colinear alignment tool Pecan. The resulting data structure therefore contains a series of “segment-groups,” each of which contains a set of sequences (which we will often refer to as segments) whose homology is colinear over their entire length, and whose evolutionary intrarelationships can be modeled with a linear alignment. Between segment-groups are so called breakpoints, representing places in an ancestral genome where larger evolutionary operations have occurred, potentially breaking synteny, adding duplicated sequences or reorganizing the ordering of segments within chromosomes.

The Enredo method naturally uses data structures with similarities to graphs used in related biological problems. The Enredo graph somewhat resembles a breakpoint graph (Bafna and Pevzner 1993), used for computing rearrangement distances between pairs of sequences, except that here the graph involves multiple genomes and represents duplication. It also has analogies with a de Bruijn graph (Pevzner et al. 2001), a graph used most frequently for sequence assembly tasks (Medvedev et al. 2007; Zerbino and Birney 2008). In terms of related methods, Enredo has similarities with the orthology map constructor Mercator (Dewey 2007). Mercator builds a graph in which the edges represent homology relationships between orthologous exons. Cliques of exons containing a sequence from every species are found and neighboring cliques are joined together to form runs. The central practical difference between Mercator and Enredo is that Mercator does not consider duplications, but instead attempts to group sequences into species compatible orthology groups. Additionally, while Mercator uses exons as vertices, Enredo considers all genomic regions.

Having computed an initial segmentation, the challenge is to align the colinear set of sequences in each segment-group. Generating colinear multiple alignments is a long standing problem in bioinformatics (Sankoff and Cedergren 1983; Carrillo and Lipman 1988; Lipman et al. 1989; Thompson et al. 1994; for reviews, see Gusfield 1997; Durbin et al. 1998). The computational challenges present in this problem can generally be related to the number and length of the sequences being compared. The former increases the dimensionality of the problem, the latter increases the basic search space needed to be considered. The combination of both means that naive implementations of many common objective functions (such as sum-of-pairs scoring) are simply unfeasible. Traditionally, the problem of multiple sequences has been solved by progressive methods, based on the original work of Feng and Doolittle (1987) and others (Hogeweg and Hesper 1984; Waterman and Perlwitz 1984), where the alignment is broken down into a series of generally pairwise stages that are recursively combined, guided, typically, by a phylogenetic tree. The second problem has been handled by different types of constraint heuristics, mostly relying on finding confident regions of high similarity that can be detected using more aggressive methods (Bray et al. 2003; Kurtz et al. 2004).

All the available programs capable of very large-scale multisequence alignment use a progressive method based upon a guide tree and varying types of constraint heuristics. Surveying the constraint strategies used by these methods, Mlagan (Brudno et al. 2003a) uses a k-mer (each k-mer is an ungapped local alignment of length k) chaining procedure to find initial local alignments around which a global alignment is constructed. Mavid (Bray and Pachter 2004) recursively defines a global alignment using maximally nonrepetitive ungapped subsequences before applying standard pairwise alignment methods to join these segments. Finally TBA/MULTIZ (Blanchette et al. 2004) uses a BLAST (Altschul et al. 1990) like algorithm (Schwartz et al. 2003) to find gapped local alignments, which it arranges together in a partially ordered block-set representing a “global” set of local alignments. For our new program, Pecan, we use the framework of constrained multiple sequence alignment, developed by Myers et al. (1996), to construct an initial set of constraints.

Because of the complexity of the heuristics involved with large-scale colinear alignment, many of the previously developed methods have focused on improving technical aspects of the computation rather than introducing particularly novel objective functions. In developing Pecan we have chosen to use a consistency-based objective function, not previously implemented for large-scale alignment. Consistency-based methods in multiple alignment were developed to mitigate a commonly observed problem in progressive alignments. Progressive alignment is inherently “greedy,” fixing on sub-solutions in sub-trees before aligning to more distant sequences. However, quite frequently clearly erroneous results in this process can be resolved with out-group information. This often occurs when there are many near equivalent possibilities for a particular gap placement, a phenomenon described as edgewander (Holmes and Durbin 1998). Consistency methods mitigate this problem by incorporating information from out-group sequences in the alignment of sub-trees. Consistency methods therefore have a flavor of global optimization while still inherently working in a pairwise fashion.

The first widely used consistency algorithm, T-Coffee (Notredame et al. 2000), computes a collection of global and local pairwise alignments for every pair of sequences being aligned. A “consistency transform” is then applied that incorporates scores created transitively by triangular projection of scores between the different constituent pairwise alignments. Later Probcons (Do et al. 2005) introduced a probabilistic consistency transform, based upon posterior match probabilities computed using the Forward and Backward algorithms. The objective function used by Pecan is the same basic objective function used by Probcons, and it is reviewed below. Lunter et al. (2008) recently introduced a pairwise genome alignment method based upon posterior decoding. However, Pecan is the first program to make posterior decoding and the consistency methodology practical for very large multiple alignments, both by accelerating the alignment process with principled constraint heuristics and limiting the memory consumption to a practical amount.

Results and Discussion

First, we describe the Enredo program and detail assessments of its performance, before giving an overview of the Pecan program and assessments of it, and, finally, we describe combined assessments of the entire pipeline.

The Enredo graph for segment homology assignment

Enredo takes two inputs. The first input to Enredo is a set of complete (or near complete) genomes. Each input genome is comprised of a set of chromosomes. Each chromosome is a non-zero length linear or circular string of double-stranded DNA. If data are missing the chromosomes may be more fragmented than in biological reality.

A segment defines a single contiguous, unoriented range of positions in an input genome, each position representing a single pair of complementary nucleotides (i.e., A−T, T−A, C−G, G−C). There are two technical details of our definition of a segment worth expanding upon. First, we allow zero length segments, which define a range lying between two genomic positions. Second, because segments are not oriented, we do not distinguish between forward- and reverse-complement segments representing the same range. However, segments can be oriented with respect to one another; we call such a segment set “directed.”

Let a segment-group be defined as a set of directed segments. A segment-group is globally homologous if the global (end-to-end) alignment of the set of directed segments (oriented with respect to one another) is significant. Segment-groups overlap if their segments share any common positions. The aim of the Enredo method is to partition the input genomes into a set of nonoverlapping globally homologous segment-groups, which we call a “segmentation.”

Let the term genome point anchor (GPA) be synonymous for a short segment-group containing two or more homologous segments, each of which is between 50 and a few hundred positions in length. The second input to Enredo is a set of nonoverlapping GPAs. We generally prefer GPAs to be short because this makes it easier to avoid overlap between the ends of GPAs, though GPAs must necessarily be long enough for us to be confident of the homology relationships they contain. Such a set can be computed using a local-alignment program; in the supplement we describe the current methodology for building this set. Importantly, our methods do not constrain GPAs to contain only a single segment from each input genome, rather we allow the processes of insertion, deletion, and duplication to create GPAs whose genome copy number composition is variable.

Given a nonoverlapping GPA set we construct the initial Enredo graph. Each GPA has two ends, comprising the two ends of the set of directed segments. The vertices of the graph represent the GPA ends for the set of nonoverlapping GPAs. The graph has two sets of edges: link-edges (inside the GPA) and adjacency-edges (between the GPAs). Let ∗A and A∗ represent the two ends of a GPA A. For each A in the set of nonoverlapping GPAs a linkedge connects the vertices representing ∗A and A∗. For each segment x in a GPA A, let e(x,∗A) denote the position in x closest in the order of the segment to the GPA end ∗A. Let e′(∗A) = ∪_xe(x,∗A). We define the criteria to create an adjacency-edge as follows: An adjacency-edge exists between the vertices representing two GPA ends a and b if and only if there exists a segment that (1) defines a contiguous, maximal range between a member of e′(a) and e′(b); (2) does not contain any position that is a member of a GPA in the nonoverlapping GPA set; (3) is <200 kb in length (it is unlikely that segments will be globally homologous if there is no intervening GPA within this range). We allow only a single adjacency-edge between the vertices representing two GPA ends. We label each adjacency-edge with a segment-group containing the set of segments that meet the criteria to define the adjacency-edge and call this the adjacency-edge segment-group (AESG). Each adjacency-edge therefore has one or more segments, each of which is bounded by two GPAs, one on each side.

We use this basic graph, and modifications to it, to derive a segmentation more complete than the initial set of nonoverlapping GPAs and adjacency-edges. This derivation is nontrivial. To get traction on the problem we make the simplifying assumption that segments in an AESG are globally homologous. This assumption will be valid providing the density of GPAs is sufficient that no rearrangements have occurred between segments in an AESG. Prior to generating the final segmentation we apply a series of modifications to the Enredo graph. These modifications have two key stages. The modifications in the first stage (termed joining and annealing) are primarily designed to increase the sensitivity of the segmentation, by further pushing together homologous segments and joining contiguous edges. In the second stage of graph modifications we attempt to remove remnant, aberrant homologies between segments within segment-groups, which can be recognized in the context of the graph.

Joining and annealing adjacency-edges

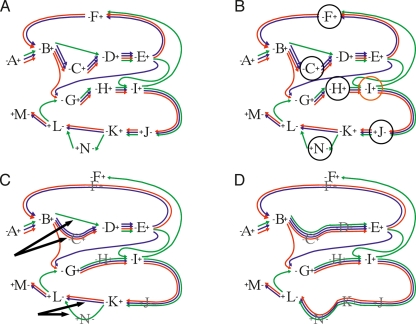
We first describe the conditions under which edges can be joined, we then describe a strategy to anneal (merge) adjacency-edges, whose AESGs we deem likely to be globally homologous. This two-step process is shown visually in Figure 1, starting with the initial graph in Figure 1A. We use the notation a−b to denote an adjacency-edge between two vertices representing two GPA ends a and b. Let A∗−∗X and X∗−∗B be two edges connecting four distinct vertices, including the two vertices representing GPA X. For a segment p in the AESG of A∗−∗X, we say X∗−∗B is continuous with respect to p if there is a segment q in X and segment r in the AESG of X∗−∗B such that the concatenation of pqr defines a single contiguous segment in an input genome. We say X is redundant with respect to A∗−∗X and X∗−∗B if and only if X∗−∗B is continuous with respect to all the segments in the AESG of A∗−∗X, and vice versa for A∗−∗X and the segments in the AESG of X∗−∗B. Joining proceeds as follows. For each pair of adjacency-edges of the form A∗−∗X, X∗−∗B in which X is redundant, we remove A∗−∗X and X∗−∗B from the graph and replace them with a single joined adjacency-edge. We denote the replaced edge A∗−(X)−∗B, to keep track of the GPA(s) from which it was split. This process results in the removal of the segments in X that overlap those in the adjacency segment-group of A∗−(X)−∗B; we call this the splitting of X. This joining and splitting process is shown in Figure 1B. Computing the closure of this process results in merged adjacency-edges split from multiple redundant GPAs, for example, a chain of edges A∗−∗X, X∗−∗Y, Y∗−∗Z, Z∗−∗B in which X, Y, and Z are redundant results in a merged adjacency-edge A∗−(X,Y,Z)−∗B.

Figure 1.

Schematic diagrams showing the joining and annealing modifications within the Enredo graph. (A) The initial graph. The GPAs are shown as numbers, with pluses and minuses denoting their end vertices. In this schematic construction we do not show the link edges. The adjacency-edges are represented by a series of different color lines between the GPAs, representing the multiple species within their AESGs. (B, black circle) The GPAs which are trivially redundant in the graph, being connected to only two other GPAs; these can be removed without effect. GPA I (orange circle) is not redundant because H∗–∗I is not contiguous with respect to all the segments in the AESG of I∗–∗J. (C) The result of such removal. The black arrows show subgraph edges that are redundant at an edit distance of 1; these edges are then merged leaving the graph shown in D.

After joining adjacency-edges, multiple adjacency-edges may link the same pair of GPA-end vertices, i.e., the graph has become a multigraph (Fig. 1C). It is natural therefore to employ a second process, which we term annealing, that merges adjacency-edges. The assumption is that a small number of GPAs will be missing segments present in some extant genomes due to sequencing coverage, and/or some segments may appear in GPAs due to spurious segment homology. Our process of adjacency-edge annealing attempts to account for these issues, while not merging edges are unlikely to be globally homologous. For the edge A∗−(X,Y,Z)−∗B let us call X, Y, Z the redundant-GPA string. An adjacency-edge C∗−∗D that has not been joined can be denoted C∗−()−∗D, and thus has a zero length redundant-GPA string. We define the edit distance between two possible adjacency-edges as the number of changes needed to transform the redundant-GPA string of the first edge into the redundant-GPA string of the second, or vice versa, this function being symmetric. For instance, the edit distance between the redundant-GPA strings X, Y, Z and X, Z is 1. Annealing two adjacency-edges results in their removal from the graph and replacement with a single adjacency-edge that contains the union of their AESGs. In the second stage of modification all adjacency-edges linking two vertices are annealed if the edit distance between them is ≤4 (this number being a parameter of the method, derived after some experimentation). After joining and annealing adjacency-edges, the resulting graph may contain new adjacency-edges that are candidates for joining. We compute the partial closure of both these modifications by iterating the processes a set number of times (Fig. 1D).

Removing aberrant homologies from the graph

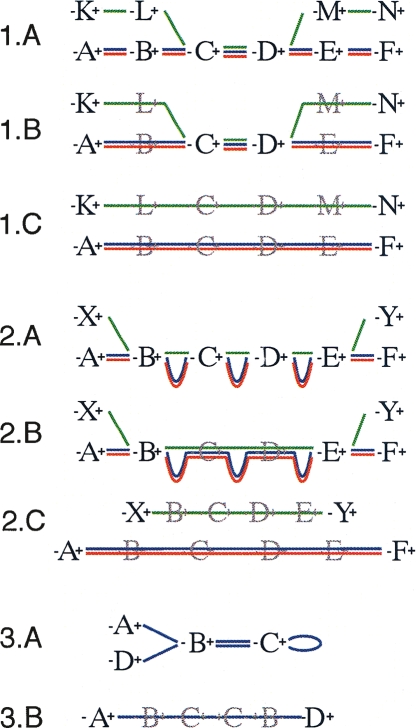
Each graph modification in this second stage recognizes a different type of characteristic aberrant graph structure, generally caused by distinct underlying biological phenomena. Each distinct modification is illustrated in Figure 2.

Figure 2.

Schematic diagrams representing the three secondary modifications within the Enredo graph. The graph representation mirrors that in Figure 1. (1) Splitting small edges. (1.A) An initial set of GPAs on three genomes in which the green sequence contains a small region apparently homologous to the others. (1.B) The graph after removing redundant GPAs. GPAs C and D represent breakpoints in the graph only because of the green sequence. (1.C) The effect of splitting the green sequence from the others and removing new redundant edges. (2) The removal of retrotransposed pseudogenes paired with a homologous gene. (2.A) Typically GPAs match exons rather than introns, therefore a retrotransposed pseudogene can show a high similarity at the level of GPAs with the homologous gene, although adjacent-edges will be much smaller (green sequence). (2.B) The graph after removing redundant GPAs. The AESG of B∗−(C,D)−∗E contains two segments much longer than the third one. (2.C) The effect of separating the putative retrotransposed pseudogene from the other segments. Usually this results in the creation of a longer AESG after removing new redundant edges. (3) The removal of small circular paths. Here a palindromic circle, typically caused by short tandem repeats or transposition, is broken by the creation of the joined adjacency-edge A∗−(B,C)−∗D.

The first modification (Fig. 2, part 1) of the second stage attempts to split out segments from AESGs that then allow us to join triplets of neighboring adjacency-edges. For example, for the chain of adjacency-edges A∗−∗B, B∗−∗C, C∗−∗D, we test if the removal of one or a few segments from B∗−∗C will allow us to join the chain into one edge A∗−(B,C)−∗D, using the adjacency-edge joining rules previously outlined. The intuition behind this modification being that one or a few small “visiting” extant segments, created most often by small transposition events and assembly errors, may disrupt the joining of much longer edges.

The second modification (Fig. 2, part 2) of this stage attempts to alleviate the effect retrotransposed pseudogenes have on the graph. Given our stated aim of not aligning homologies created by transposition and our desire to create longer segment-groups, we attempt to recognize and remove these homologies from the graph. We give an example to outline this process. Let E₁, I₁, E₂, I₂, E₃, I₃, E₄ denote a chain of exons and intron sequences that form an ancestral gene structure, where E_i and I_j denote the ith exon and jth intron respectively. Assume that this complete gene structure is present in multiple homologous copies in the input genomes, and call each of these copies a gene segment. Secondly, assuming that the gene’s exons have also been retrotransposed and perhaps subsequently copied once or a few times, let us call these instances retrotransposed pseudogene segments. Due to the higher relative conservation of exons vs. introns, each copy of each exon sequence will be contained within a corresponding GPA, in order: A, B, C, D for exons E₁. . . E₄. In the graph, vertices representing the ends of these GPAs will be linked by the adjacency-edges A∗−∗B, B∗−∗C, C∗−∗D, the segments in the segment-groups of these adjacency-edges can be partitioned into two length classes. Those segments contained within gene segments will have a length approximately proportional to the length of the common ancestral intron, for example, in A∗−∗B they will have a length proportional to I₁. However, those segments derived from retrotransposed pseudogene segments will be dramatically compressed, the introns having been excised during copying. For many different gene structures this pattern is prevalent and repeated within the Enredo graph. We recognize adjacency-edge chains of length 3 or greater in which we can partition the set of segments running through the chain into putative gene segments and putative retrotransposed pseudogene segments. The criterion for the partitioning is that the average length of the segments in the AESGs of the gene segments be three times the length of their retrotransposed pseudogene segment counterparts. To complete the modification, we remove from the graph the putative retrotransposed pseudogene segments of adjacency-edge chains fitting the pattern, if their removal allows the joining (using the modification described in the previous section) of the remaining adjacency-edges in the chain. Clearly this modification will not only split out pseudogenes, but in some cases will also result in the breaking of other homologies. However, manual investigation of many of these cases leads us to believe this is a useful heuristic.

The third and final modification (Fig. 2, part 3) of the second stage aims to recognize small-scale assembly errors and duplications that result in circular chains of edges. A chain of adjacency-edges is circular if it can be made to start and end at the same vertex, e.g., the chain of adjacency-edges A∗−∗B, ∗B−∗A is circular. Such a definition allows single adjacency-edges to be circular, for example H∗−∗I and A∗−A∗ are both circular. Similar to the whirl removal step outlined in Pevzner et al. (2004), we search the graph exhaustively for small circular (and often palindromic) chains of adjacency-edges and test by brute-force search the effects of removing adjacency-edges to break these cycles. We then remove from the graph those adjacency-edges whose AESGs contain segments of length <10 kb and which allow us to join a chain of remaining adjacency-edges into a single larger adjacency-edge.

Deriving the final segmentation from the Enredo graph

At the end of these modifications the Enredo graph is far more compact, with fewer but longer adjacency-edges. In this initial version of the program, for recovering segment-groups from the human, mouse, rat, dog, and cow genomes, we have by choice not attempted to recover segment-groups <10 kb. This is primarily because we have found segment-groups derived from the Enredo graph below this length are much more likely to contain aberrant homology relationships, caused mostly by the activity of transposons or short tandem duplications that are very hard to reliably align. To derive the final segmentation we first partition all the adjacency-edges into two classes: primary and secondary. Primary adjacency-edges are those whose AESGs contain segments >10 kb and are supported by at least three GPAs (i.e., they have a nonempty redundant-GPA string). The final segmentation consists of the set of primary AESGs (and their flanking GPAs), and a set of “bridge” adjacency-edges. In a triplet chain of adjacency-edges A∗−∗B, B∗−∗C and C∗−∗D, B∗−∗C are a bridge adjacency-edge if the chain could be joined, using the previously defined rules, to form A∗−(B,C)−∗C, except for the fact that the AESGs of A∗−∗B and C∗−∗D have one or more additional segments. This typically happens when these additional segments represent the two parts of a breakpoint in one of the genomes. We include bridge adjacency-edges in the final segmentation, because the homology relationships they represent are supported at both ends by other flanking, often much larger, primary adjacency-edges.

Assessment of the stages of Enredo graph manipulation

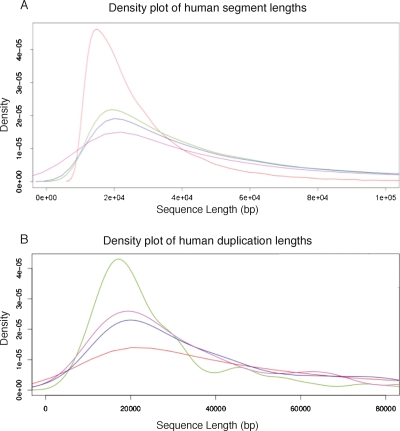
Figure 3 shows the distribution of lengths of human segments from the segmentation at different stages of the Enredo process. It shows that Enredo successfully joins previously separate segments at each stage to create longer ones. In the initial graph, the weighted median length (N50) is 31,515 bases. This number more than doubles after four iterations of adjacency-edge joining and annealing (N50 = 73,301). The largest increase happens in the last step, when dealing with retrotransposed pseudogenes and small circles, where the N50 rises from 98,558 to 237,998 bases.

Figure 3.

Density plots of the length of segments in the Enredo graph. (A) Red line, the distribution of segment lengths in the original graph; green line, the graph after applying joining and annealing up to edit distances of 4; blue line, the graph after removing splitting small edges; magenta line, the final graph, after resolving circular segment paths, removing the retrotransposed pseudogenes and validating the bridging edges. The peak of ∼10 kb interanchor distance is rapidly converted to a broader distribution of segment lengths, with the mode slightly longer (∼20 kb). The weighted median (N50) is considerably longer (∼230 kb). (B) The distribution of human segment lengths in the final Enredo graph where the segment has one, two, three, or four or more copies in human. The plot, therefore, contrasts human single-copy regions vs. regions possessing duplications of different degree.

As well as assessing the changes in coverage and N50 length of our segments after the multiple stages of graph manipulation, we sought evidence that we were not introducing significant error into the segmentation by these processes. To do so we devised an exon-based segmentation metric independent of either base-level alignment or tree inference. The exons of a multi-exon gene are generally under strong negative selection to stay in linear ordering. Although over the evolutionary distances studied we expect a very few genuine cases where this constraint has been overcome (most probably by gene death), a segmentation that mainly maintains these constraints between species is likely to be more correct than one that significantly does not. Importantly the Enredo segmentation was not built with explicit knowledge of gene structures; this test is therefore a relatively independent check of its abilities.

Taking the chains of exons implied by the single longest transcript of a protein-coding gene in a source species, we project through the segmentation to find the corresponding chain of homologous segments in a target species. We then ask if this chain of segments is complete (i.e., for every exon there is a covering target segment), maintains synteny, the same strand orientation, and the same linear order in the target species. These checks are independent of the base-level alignments, and are performed only at the resolution of the segmentation. We also avoid the problem of tree inference at this stage; thus, to deal with paralogs we require that only one chain of segments (out of potentially several in some cases) in the target genome pass the above checks.

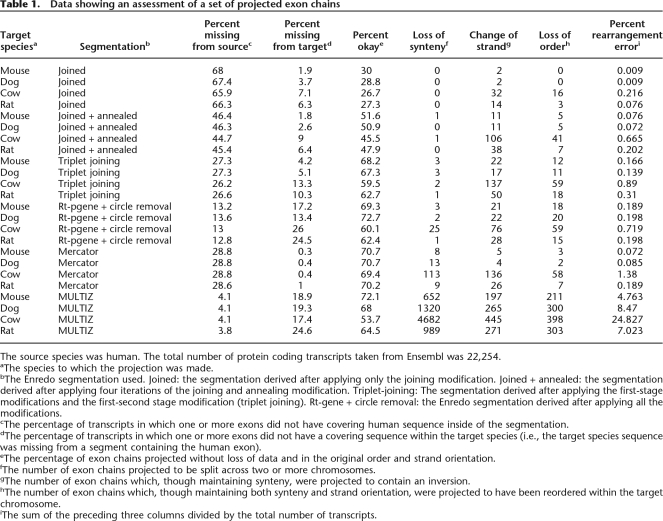
Using human as the source species and the other genomes in the input set as the targets (mouse, rat, dog, cow), Table 1 shows the results of this assessment for each stage of the Enredo graph manipulation. Taking the human–mouse comparison as an example, and complementing our assessment of coverage, we find a large increase (19.2%) in the number of fully mapped genes between the original (30%) and fully manipulated graph (69.3%). Importantly, we find very few cases (again using the human–mouse example) where synteny (three cases), strand (21 cases), or order (18 cases) assumptions (total 0.189% of genes) are violated by the projection through the segmentation. Some of these errors may in fact be related to misassemblies in the aligned genomes, for example, through the creation of phantom inversions. For instance, we find a much higher rate of inversion in the cow genome (76 cases), relative to the dog (22 cases) and mouse (21 cases) when projecting from human (this result is also observed in the other segmentations assessed; see final rows of Table 1). This might be a biological phenomenon but is more likely a result of a less refined assembly.

Table 1.

Data showing an assessment of a set of projected exon chains

The source species was human. The total number of protein coding transcripts taken from Ensembl was 22,254.

^aThe species to which the projection was made.

^bThe Enredo segmentation used. Joined: the segmentation derived after applying only the joining modification. Joined + annealed: the segmentation derived after applying four iterations of the joining and annealing modification. Triplet-joining: The segmentation derived after applying the first-stage modifications and the first-second stage modification (triplet joining). Rt-gene + circle removal: the Enredo segmentation derived after applying all the modifications.

^cThe percentage of transcripts in which one or more exons did not have covering human sequence inside of the segmentation.

^dThe percentage of transcripts in which one or more exons did not have a covering sequence within the target species (i.e., the target species sequence was missing from a segment containing the human exon).

^eThe percentage of exon chains projected without loss of data and in the original order and strand orientation.

^fThe number of exon chains projected to be split across two or more chromosomes.

^gThe number of exon chains which, though maintaining synteny, were projected to contain an inversion.

^hThe number of exon chains which, though maintaining both synteny and strand orientation, were projected to have been reordered within the target chromosome.

ⁱThe sum of the preceding three columns divided by the total number of transcripts.

Comparison of the final Enredo segmentation to existing methods

To assess the Enredo segmentation we compare it with two commonly used alternative segmentations: those generated by Mercator (Dewey 2007) and those implied by the UCSC MULTIZ alignments (Blanchette et al. 2004). We looked at three metrics designed to assess coverage and accuracy within and outside of coding regions.

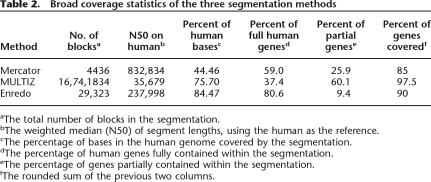
Firstly, we simply assessed the coverage of the human genome by each segmentation program (Table 2). We looked at overall coverage, and the coverage of genes (including introns). These results show that Enredo covers the highest proportion of the human genome with alignment (84.47%), vs. MULTIZ (75.70%) and Mercator (44.46%). Enredo also covers higher proportions of genes fully (all bases mapped, including introns) than the other programs. However, MULTIZ, which contains many small segments, matches partially or fully the highest proportion of human genes overall.

Table 2.

Broad coverage statistics of the three segmentation methods

^aThe total number of blocks in the segmentation.

^bThe weighted median (N50) of segment lengths, using the human as the reference.

^cThe percentage of bases in the human genome covered by the segmentation.

^dThe percentage of human genes fully contained within the segmentation.

^eThe percentage of genes partially contained within the segmentation.

^fThe rounded sum of the previous two columns.

Secondly, we applied the previously introduced exon chain metrics to the MULTIZ and Mercator programs. These results are shown in the final rows of Table 1. We would expect Mercator to perform well in these metrics as its segmentation is generated using cliques of orthologous exons (analogous to our GPAs) only, and cannot therefore be influenced by intergenic homology relationships. Indeed Mercator consistently maps fully ∼70% of all human exon chains to the other species in the set. Enredo and MULTIZ map between 60% and 70% of exon chains to each of the other species, except in the case of cow, where MULTIZ maps substantially fewer chains without probable error (54.7%). Mercator and Enredo contain very few cases where a projected exon chain is disrupted by loss of synteny, inversion, or loss of exon ordering. Contrasting this, MULTIZ, which maps the overall highest proportion of exon chains to all species, contains a much higher level of putative rearrangement error (see final column of Table 1).

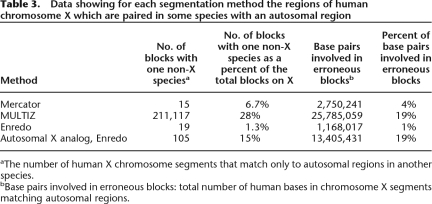
As a final comparison of the different methods we used the behavior of the mammalian X chromosome segmentation. As all male eutherian mammals are hemizygous for the majority of X, we expect deletions or translocations of portions of X to be extremely rare in mammalian evolution. However, none of the programs are parameterized to consider the X chromosome differently from autosomes. Table 3 lists the frequencies of Enredo, Mercator, and MULTIZ blocks that show an incompatible synteny relationship between a human chromosome X region and an autosomal segment in another species. As expected, the Enredo segmentation contains a very low percentage of blocks (1.3%) with an inconsistent relationship. Some of these inconsistencies are probably related to genome assembly issues. In particular, they may be related to the issue of placing large contigs onto chromosomal scaffolds in the draft genome sequences. Using this same metric for the autosomal chromosomes shows them to be almost entirely scrambled with regard to one another. For the sake of comparison we also show in Table 3 the most common five-way other chromosomal pairing (being 17 human, 11 mouse, 10 rat, 9 dog, and 19 cow), as if this was analogous to the X chromosome case. This shows a dramatically higher (15%) rate of mispaired blocks in autosomes. When comparing Enredo’s human X mispairing (1.3%) with the other segmentation programs, we observe that Mercator has a higher rate (6%) and MULTIZ an even higher rate (24%). Manual inspection of a random subset of these MULTIZ blocks shows that many of these are short matches. We did not observe any particular evidence that these were due to retrotransposons, which was one plausible explanation. Rather, they looked like spurious matches, perhaps from very divergent dispersed repeats. We believe that the tuning of MULTIZ to allow short genic matches also allows the placement of these spurious matches.

Table 3.

Data showing for each segmentation method the regions of human chromosome X which are paired in some species with an autosomal region

^aThe number of human X chromosome segments that match only to autosomal regions in another species.

^bBase pairs involved in erroneous blocks: total number of human bases in chromosome X segments matching autosomal regions.

The conclusions of this assessment are that Enredo provides higher coverage and a better segmentation than Mercator within intergenic regions, as judged by the X chromosome assessment. MULTIZ has a higher coverage, as judged by the partial overlap on coding sequences, but this comes at a considerable expense in specificity, as judged by the number of rearranged exon chains and the number of non-X species blocks matched to the human X chromosome.

Pecan: Large-scale probabilistic consistency alignment

Having described and analyzed the construction of the segmentation we turn now to the problem of aligning the colinear segments derived from each segment-group using our new tool Pecan. Up to now we have used the term segment to define a specific range of positions in an input genome. Pecan disregards this genomic location information and treats the segments simply as sequences. We will therefore use the term sequence (as defined below), in addition to the term segment when describing Pecan and the remainder of the methods.

Pecan implements the same basic objective function as the amino acid aligner Probcons (Do et al. 2005) does. We briefly review this function. Let π represent the basic symbol alphabet (i.e. {A, C, T, G} for DNA). A sequence represents a member of ∪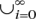πⁱ, where πⁱ represents the set of all strings of length i comprised of characters from π. Denote “–” as the gap symbol and letπ′ = π∪{− }.We use the convention that x_i denotes position i in sequence x. Let x_i◊y_j denote that position x_i and position y_j are aligned. Thus let P(x_i◊y_j|θ) represent the posterior match probability that position x_i and position y_j are aligned given the pairwise alignment model θ. For Pecan, θ represents a pair-hidden Markov model (pair-HMM) (Durbin et al. 1998). Let ℒ_{1. . .n} represent the list of sequences being aligned. Let P′(x_i◊y_j|θ) define the transformed probability that x_i and y_j are aligned given by the following operation:

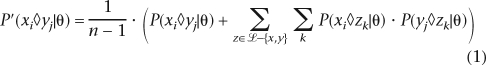We define an alignment A as a two-dimensional matrix whose cells all contain a symbol from π′. Each row represents the symbols of a sequence interleaved with gaps. Each column represents an aligned group of π′, the gaps representing characters missing due to insertion or deletion. Positions from two sequences are therefore aligned if they occur in the same alignment column. The score of an alignment S(A|θ) of a set of leaf sequences is therefore:

where I_A is an indicator function such that

For a set of leaf sequences the optimization challenge faced by Pecan is to find an alignment whose score maximizes the above. Any algorithm that addresses this problem therefore naturally has three stages.

1. The computation of a set of posterior match probabilities for every unordered pair of distinct leaf sequences.

2. The modification of the probabilities computed in the first stage using the transform given in Equation 1.

3. The search for an alignment to maximize Equation 2 given the modified probabilities produced in the second stage.

The first stage is computed using the Forward and Backward algorithms for pair-HMMs, fully described in Durbin et al. (1998). The second stage is straightforward, though it introduces a cubic term into the scaling of the algorithm with the number of sequences (see the supplement for a runtime analysis). In theory the third stage could be solved optimally by multidimensional dynamic programming; however, such a method would then scale exponentially in terms of the number of sequences. In practice, in common with Probcons, we use the same basic method of progressive, sparse dynamic programming with a guide tree, to compose the final alignment in n − 1 stages. Three major challenges exist in adapting this alignment methodology for large-scale alignment on current computer hardware. We describe the solutions to these challenges in overview, though more details are given in Methods.

1. For each pair of sequences, using the Forward-Backward algorithm for pair-HMMs, the computation of a set of posterior match probabilities grows quadratically with their average sequence length. This is fine for small sequences but impractical for sequences of more than a few hundred kilobases.

2. The number of unordered sequence pairs is (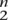), which, because the cost of computing the Forward-Backward algorithms dominates, makes it expensive to align even moderate numbers of sequences (>20).

3. The total number of posterior match probabilities grows linearly with the average length of the sequences involved and quadratically with the number of sequences. In practice, this can introduce a heavy memory burden if not dealt with.

To solve the first challenge we use a system of sequence constraints, precomputed using the local alignment program Exonerate (Slater and Birney 2005), to reduce the alignment search space. To describe this we make particular use of the explicit concept of constrained alignment. Briefly, pairwise constrained alignment algorithms that allow the definition of constraints between sequence indices of the form x_i ≤ y_j (i.e., that position x_i must precede or be aligned to position y_j in the final alignment), and similarly x_i < y_j (i.e., that position x_i must precede position y_j) can be thought of as specialized types of banded alignment algorithm (Chao et al. 1993; Delcher et al. 1999; Batzoglou et al. 2000). This is because they limit the possible paths of the alignment to a restricted region, henceforth called an alignment “band” of the edit graph (Supplemental Fig. S1A gives an example). Around a set of ungapped local alignments (which we call “anchors”), an expanded band is constructed (shown as black lines in Supplemental Fig. S1A). Expanding the band in this way allows the incorporation of the probability of detour alignments around the constraining set of local alignments. If the width of this band along the diagonal axis of the edit graph never exceeds a prespecified constant, then the area of computation is limited to linear in the average lengths of the sequences.

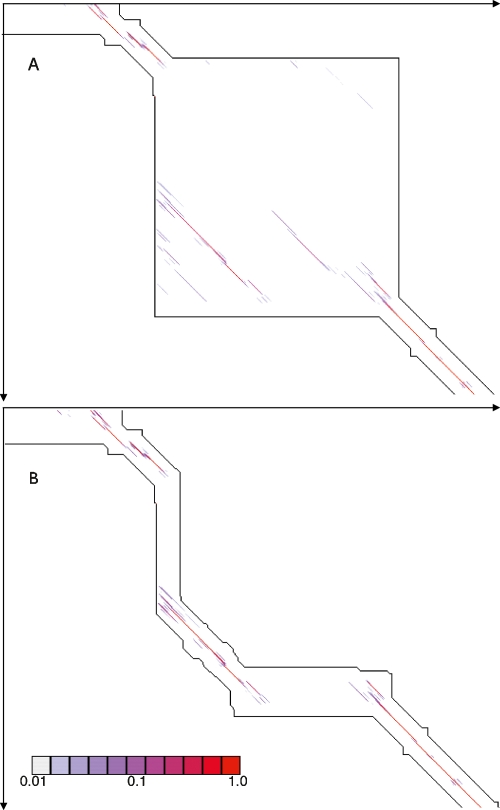
To reduce the severity of the second problem we implement a strategy we term “transitive anchoring,” which utilizes a triangulation property between related alignments to further constrain, and hence reduce the total area of pairwise dynamic programming performed. As an example, consider the alignment of three sequences, e.g., human, chimp, and rhesus monkey. Once two pairwise alignments have been generated (e.g., human to chimp and human to rhesus monkey), an effective approximation to the third alignment (in this case, chimp to rhesus monkey) can be made. These “transitive anchors” are then used as additional constraints in this third comparison, dramatically reducing the costs of computation. Figure 4A,B shows the before and after results of using transitive anchoring on a small region of alignment. In general, for every unique triangle of sequences in the input set of sequences we utilize this method to find highly probable regions in unseen alignments. We assessed the effects transitive anchoring has on the runtime needed to reconstruct the simulated alignments described below. For these alignments we had the true simulated alignment with which to compare the reconstructed alignment. We found that transitive anchoring had negligible effects on the quality of the alignments (in terms of the sensitivity and specificity of predicting aligned bases) and allowed a significant reduction in runtime of between 12% and 43%, dependant on if the initial constraint map was allowed to constrain the alignment of sequences labeled as repeats (Supplemental Table S1).

Figure 4.

(A) An edit-graph showing an alignment band generated without transitive anchors. Alignment pairs whose posterior probability is between 0.01 and 1.0 are plotted, colored according to their probability. (B) An edit-graph showing the alignment band for the same region as in A, but with transitive anchors. Certain edges are now excluded from the alignment, but the majority of the probability is well enveloped.

The third challenge, of efficiently storing the set of pair probabilities, proved to be the most difficult. We solved the challenge by using a methodology that we call “Sequence Progressive alignment,” In brief, this involves computing all three main stages of the algorithm in near parallel by iterating in stages over the alignment from left to right. Due to its complexity we will describe this methodology in full separately (B. Paten, J. Herrero, K. Beal, and E. Birney, in prep.).

In addition to making the consistency objective function described above practical for very large colinear sequences, we have trained the pair-HMM model used over very large pairwise sequence alignments, and tested pair-HMMs with single and mixtures of affine gap states (see Supplemental material).

Simulation comparison of Pecan to existing methods

Using a set of independently produced evolutionary simulations (Blanchette et al. 2004), it is possible to compare the default Pecan program with a previously published comparison of other alignment programs. The simulations attempt to model the neutral region evolution of nine extant mammalian species: human, chimp, baboon, mouse, rat, dog, cat, cow, and pig. The simulations comprise 50 50 k alignments. The mutational operators considered included point substitutions, C_pG effects, insertions, including the action of repetitive elements, and, finally, deletions. Parameters for the simulations were carefully chosen using empirically estimated frequencies. Previously, the authors of the simulation had shown their program (TBA) to function the best in these metrics. We benchmarked Pecan on these simulations without using any prior training to the data.

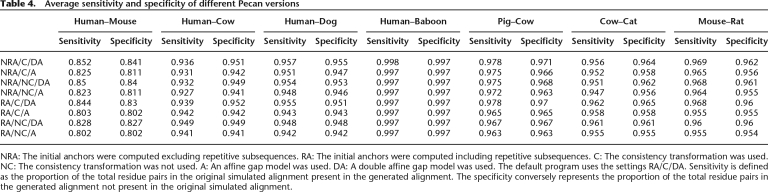
Table 4 shows how three different configuration choices affect performance: first, the initial placement of constraints within subsequences labeled as repeats; second, the use of the consistency transformation outlined in Equation 1; third, the use of a double affine gap model (a model with two sets of affine gap states) instead of a single affine gap model. Short of reproducing data for all the constituent pairwise comparisons (36 total), we have reproduced data for the same subset of pairwise comparisons chosen by the original authors of the simulation, which is reasonably representative.

Table 4.

Average sensitivity and specificity of different Pecan versions

NRA: The initial anchors were computed excluding repetitive subsequences. RA: The initial anchors were computed including repetitive subsequences. C: The consistency transformation was used. NC: The consistency transformation was not used. A: An affine gap model was used. DA: A double affine gap model was used. The default program uses the settings RA/C/DA. Sensitivity is defined as the proportion of the total residue pairs in the original simulated alignment present in the generated alignment. The specificity conversely represents the proportion of the total residue pairs in the generated alignment not present in the original simulated alignment.

The data indicate that the use of the double affine gap model makes the biggest positive difference to performance in these metrics (2.6%–4.1% sensitivity, 2.5%–3.0% specificity at human–mouse distance). This is perhaps unsurprising given that the authors used biologically derived estimates of indel lengths, which are known to significantly diverge from a simple affine model. The second most important factor was whether the program constrained the alignment using repeats. When constraints on repeats were allowed, performance generally declined, with an average of 0.8%–2.2% in sensitivity and 0.9%–1.3% in specificity at the human–mouse distance. This indicates that allowing less constrained posterior match probability calculation in areas containing repeats improves performance. The difference caused by the consistency transformation was smallest, but still positive (0.1%–1.4% sensitivity, 0.0%–0.3% specificity). This contrasts strongly with that observed for protein alignment benchmarks, such as BAliBASE, where the Probcons and T-Coffee programs have been able to show very much greater improvements for a variety of mostly sensitivity-dependent metrics (Bahr et al. 2001). It is quite possible that this observation is particular to the features of this simulated benchmark and phylogeny of the sequences, and hence we wish to avoid overgeneralizing; however, we leave as further work a more detailed exploration of this issue and the numerous possible modifications to the consistency procedure.

The runtime of Pecan is significantly affected by the different configurations chosen (varying between 230 and 130 sec on average for the alignment of a single group of sequences from the simulation set on a Pentium 4 machine). Unsurprisingly, Pecan is slower than Mlagan (66 sec average) in all settings, which given the use of the double-pass Forward-Backward algorithms is not surprising. However, Pecan is still fast enough to be used in place of programs like Mlagan in most circumstances. As defaults for Pecan we have chosen to use the double-affine model, the consistency transform, and to constrain upon repeats (average runtime 160 sec). Placing constraints on repeat subsequences does degrade performance somewhat, but makes the program faster and computationally more robust to highly repetitive input sequences.

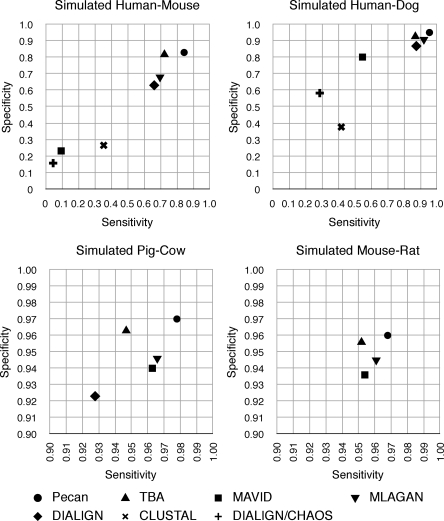
Figure 5 updates the alignment program comparison made by the original authors. Where a substantially newer version of a program is available we have produced updated statistics, choosing the default parameters for each program (see legend for details). Pecan is significantly more sensitive than the other programs in all the pairwise comparisons. The absolute differences are greatest for the most diverged sequence pairs, where comparisons of the default Pecan version to the next most sensitive program show Pecan to be ∼12.2% higher for human–mouse and 8.6% higher for the human–dog comparison. Pecan also has higher specificity for all the comparisons than any other program, being ∼1.1% and 2.3% higher with respect to the next best programs for the human–mouse and human–dog comparisons, respectively.

Figure 5.

A comparison of different alignment algorithms on 50 50k simulated nine-way alignments (Blanchette et al. 2004). Graphs show representative alignment pair comparisons. Data for MAVID (Blanchette et al. 2004), TBA (Blanchette et al. 2004), and Mlagan (Brudno et al. 2003a) computed using the latest publicly available release. Data for Dialign (Morgenstern et al. 1998; Morgenstern 1999), ClustalW (Thompson et al. 1994), and Dialign-Chaos (Brudno et al. 2004) reproduced from Blanchette et al. (2004).

Comparisons of the more closely related sequences, such as mouse–rat, pig–cow, also suggest that Pecan is able to resolve correctly many remaining errors, where an increase in sensitivity and specificity of 3.1% and 0.7%, respectively, for the pig–cow comparison implies a near halving in the number of true-negatives and quarter reduction in false-positives, with respect to the next best program. Supplemental Table S2 shows these results in full.

Assessment of the complete Enredo-Pecan pipeline

We assess the entire pipeline, comparing it to the Mercator segmentation program followed by either Mlagan or Pecan (Mercator-Mlagan, and Mercator-Pecan), and to the MULTIZ alignments from UCSC. For the assessment we use a metric based upon ancestral repeats, similar to that introduced in Margulies et al. (2007). Briefly, this scheme relies on the presence of ancestral repeats due to a burst of transposon activity in the common ancestral lineage of the sequences (human, mouse, rat, dog, cow) in the alignment. The repeat copies can be aligned by two independent methods: firstly, via the extant homologous sequences, without reference to the repeat consensus, and secondly, via the set of pairwise alignments of each copy of the repeat to the consensus. Although there is ambiguity in the alignment of the extant copy to the transposon consensus, this latter method has two key advantages. First, the alignment to the consensus problem is simpler than the homologous sequence alignment problem. Naively the divergence distance from the consensus to an extant copy is roughly half of the distance of that between any two extant copies, due to the star-like phylogeny in the early mammalian radiation. Second, any ambiguity in the alignment to the consensus is unlikely to favor any particular homologous aligner. Fixing the alignment to the consensus as the gold standard therefore provides a fairly objective measure of alignment accuracy that does not explicitly favor any alignment scheme.

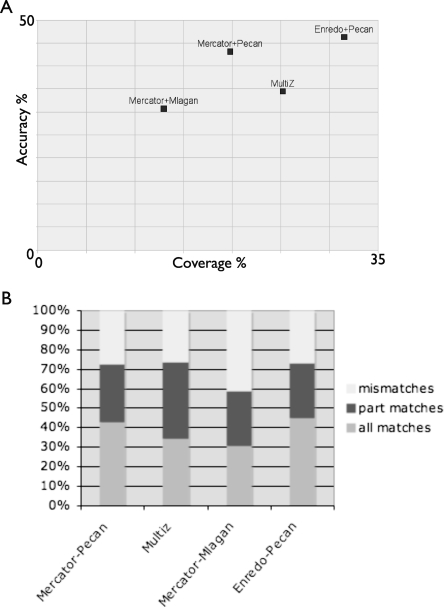
We classified alignment columns containing ancestral repeats into three classes: (1) full matches, being all species consistent with the consensus alignment, (2) partial matches, being that at least two species are consistent and the other species have other, nonrepeat matches, and (3) mismatches, being that the homologous alignment places two ancestral positions from different consensus positions in the same column. Figure 6A shows the coverage (proportion of ancient repeat bases aligned, analogous to sensitivity) vs. accuracy (proportion of ancient repeat bases covered by a full match, analogous to specificity) for Mercator-Mlagan, Mercator-Pecan, Enredo-Pecan, and MULTIZ. Figure 6B shows a more complete breakdown of the specificity of the different methods. There is no significant difference by ancient repeat type (see Supplemental Data). It is clear here that Enredo-Pecan produces both higher coverage alignments and more accurate alignments than any other combination of programs. Closer examination of the results indicate the main problem with the Mercator-based pipelines is the lack of a significant number of ancestral repeats in any alignment, due to the inability of its model to handle inversion or duplication events. Turning to the alignment programs, Pecan provides a consistently higher sensitivity and specificity of alignments than Mlagan, agreeing with the simulation results. MULTIZ, where we cannot separate out the segmentation process from the base-pair alignment, performs better than the Mercator-Mlagan combination, but not as well, either in coverage or accuracy, as Enredo-Pecan.

Figure 6.

(A) Plots showing the coverage and accuracy of different alignments to inferred ancient repeat sequences. Coverage is measured as the proportion of all ancient repeat bases aligned. Accuracy is measured as the proportion of all columns categorized as full matches. (B) A bar chart showing the distribution of different types of agreement (full, partial, and mismatch) to the repeat consensus alignment for different combinations of segmentation and alignment methods.

Overall Enredo-Pecan alignments can align (cover) around one third of the bases of ancient repeats at ∼45% complete accuracy (full matches), and align ∼75% of ancient repeat bases to at least two species with a consistent alignment (partial matches). The alignment of ancient repeats, which are mainly neutrally evolving and have accumulated many lineage specific deletions, is one of the more challenging criteria to assess alignments. Firstly, some of these repeats were inserted significantly earlier than the mammalian radiation, and thus have accumulated specific mutations in each instance, increasing alignment ambiguity. Taking the most accurately aligned repeat, MER82, 60% of the ancient repeat positions in the Enredo-Pecan alignments have a full match, and 78% have a full or partial match. Secondly, many of these repeats present in human will not have any orthologous counterpart in the other species due to deletions in early lineages of the mammalian tree. Thus, our coverage estimates are likely to be a significant underestimate of the coverage of alignments in regions undergoing selection.

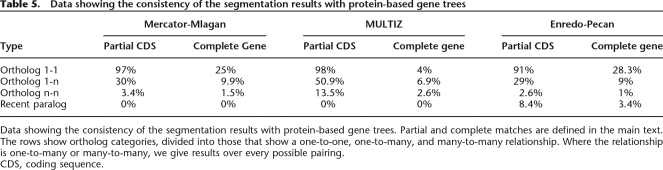
As a final assessment we reprise the previously described assessment of projected exon chains to compare the final Enredo-Pecan alignments with the Mercator-Mlagan and MULTIZ alignments. In this more detailed comparison we used the independent phylogenetic trees, based on protein coding sequences (A.J. Vilella, J. Severin, A. Ureta-Vidal, R. Durbin, L. Heng, and E. Birney, in prep.) to check for each human gene if it was aligned to its predicted orthologous sequence in each of the other species. Table 5 shows the number of gene tree relationships that are consistent with the different segmentation programs using two criteria. The first, a more liberal method, records a match as soon as there is a one base-pair overlap in the coding sequence between the segmentation results and the gene tree results (labeled “partial CDS” in Table 5). The second, more stringent criterion, the gene extent measure, requires the segmentation result to encompass all the gene structure on both species (labeled “complete gene” in Table 5). As well as handling orthologs, the criterion was also extended to look at recent (Ape or later) duplications in human (timed via the presence of outgroups in the tree from other primates). By definition, as Mercator and MULTIZ do not generate lineage-specific duplications, these programs have 0% recovery. Manual investigation of a number of the cases where MULTIZ captured an ortholog which Enredo did not showed a tendency toward regions of poor assembly, suggesting that MULTIZ’s more local, aggressive matching approach is more tolerant to assembly errors. This suggests that improvements in mammalian assemblies will automatically improve the Enredo segmentation.

Table 5.

Data showing the consistency of the segmentation results with protein-based gene trees

Data showing the consistency of the segmentation results with protein-based gene trees. Partial and complete matches are defined in the main text. The rows show ortholog categories, divided into those that show a one-to-one, one-to-many, and many-to-many relationship. Where the relationship is one-to-many or many-to-many, we give results over every possible pairing.

CDS, coding sequence.

Conclusions

We have developed and benchmarked a multistep pipeline for providing a segmentation of extant genomes into homologous colinear regions that can handle deletions, duplications, and rearrangements. We have also developed a new large-scale multiple alignment program that makes practical the method of consistency alignment at a genome scale. These two methodologies perform in isolation at least as well as existing methods and, in many metrics, have clear benefits. In particular the ability to accurately handle duplicated regions has long been unfeasible in other analyses. These multiple alignments can also be used for more sophisticated inference, such as the inference of ancestral sequences described in Paten et al. (2008, this issue).

This pipeline runs robustly and is now a standard part of the Ensembl (Flicek et al. 2007) project pipeline for mammalian sequences. As part of this integration we have developed a number of display and access methods for the data within the Ensembl genome browser. The alignments can be shown in the main contigview of all the aligned species, and, when zoomed in, as a base-pair alignment. We have also developed a specialized view, the AlignSliceView, that provides a browsable representation of the multiple alignment containing annotations projected from the underlying species to the multiple alignment. As well as these web browsable resources, we provide a number of programmatic and direct download views of the genome. There is a complete ftp dump of the multiple alignments for each segmentation block, in Ensembl Multiple Format (EMF), a format which allows us to present both extant sequences, ancestor sequences, and conservation metrics (such as GERP; Cooper et al. 2005) in a single file. The Ensembl Compara API also provides flexible methods to access these alignments.

The construction of the Enredo graph has some similarities to the use of de Bruijn-like graphs in sequence analysis (Chaisson et al. 2004; Price et al. 2005; Zerbino and Birney 2008), where consistent sequences between two nodes in extant species are collapsed on to the same edge. Clearly the Enredo graph and the de Bruijn graph are radically different in terms of elements. The nodes in the Enredo graph are sets of genomic anchor points, and the edges are the large intervening sequences, whereas the nodes in a de Bruijn are strings of length k (k-mers) and the edges represent the adjacencies between these k-mers in an observed sequence. However, the key property used in both schemes is that any subsequence considered to be “identical” or homologous by some metric is represented only once in the graph.

Enredo does not attempt to reverse-engineer the ancestral history of large-scale rearrangements. However, our pipeline provides a near ideal starting point for grappling with such a challenge. Essentially what is required as input to such a method is a set of colinear segment-groups, each of which is unbroken by any large scale rearrangement, and a set of segment-group trees, giving the evolutionary relationships between the extant sequences in the segment-group. Given these data, which is exactly analogous to our set of alignments and trees, a method for reversing evolution, such as Ma et al. (2006, 2008), can apply algorithms to infer a history.

One issue currently with Enredo is the number of free parameters. Given the nature of the graph it is difficult to devise training strategies to learn these parameters from the data. The tuning of the current implementation of the program has therefore relied on careful manual analyses of the results. Another feature of the current alignments, though this is not a requirement of Enredo, is the human-specific way the GPA set was constructed. In the future we will improve on both these limitations, firstly, by extending and developing further the set of Enredo graph modifications, and secondly, by investigating new ways to build the set of GPAs.

The Pecan program attacks the multiple sequence alignment problem, which even at the genome scale has quite a long pedigree. However, fundamentally, we have shown that taking a methodology developed primarily for protein alignments and engineering it to be practical at a genome scale gives rewards, by providing the comparative genomics community with a valuable new tool and good or better alternative alignment sets. It is unfortunately very difficult to make absolute, quantitative judgments about the biological performance of different alignment strategies, and this is best done by independent groups to the alignment program developers. Recent assessment metrics (Margulies et al. 2007) indicate that Pecan performs well compared to preexisting programs. Backing these findings up, our larger-scale comparisons of ancient repeat data give us further direct biological evidence of Pecan’s abilities.

While metrics based upon real data are preferable to simulations for making useful, biologically realistic conclusions, they often address only certain subclasses of sequence, i.e., exons or particular types of repeats. They are also of often unknown accuracy. We therefore believe that simulations are also useful in this field, but that they are limited and should be judged only in the context of what they attempt to model. The set of simulations that we tested Pecan upon indicate that Pecan outperforms all other available programs for large-scale nucleotide alignment, in terms of both sensitivity and specificity, at a wide range of approximate divergence distances.

In general we believe that it is important and possible to improve alignment assessment metrics for genomic sequences, both for the problem of colinear alignment, and fully incorporating nonlinear rearrangement operations. For simulations it would be useful for further high-quality data sets to be created, both using different simulation methodologies and different sources of biological data to generate the parameters. In this way bias in simulations might be more easily identified and discounted. We note that the unsupervised training method employed to train the pair-HMM model used by Pecan produced parameters which appear to fit the tested alignment simulations well.

The near-term future goals of our pipeline are twofold. First we will incorporate other mammalian sequences, many of them currently sequenced at 2×, into our alignments. This will give rise to a potential greater than 20-way species alignment. We will pragmatically extend the alignment to the 2× genomes, by using the pairwise alignment to human as a guide to which sequences are present in which Enredo segment. However, this will necessarily overcollapse recently duplicated sequences in each of the 2× genomes. Given the presence of next generation sequencing technologies we hope that improvements to these 2× genomes will be rapidly achieved to remove this problem. Secondly we will apply the pipeline to the teleost (bony fish) lineages. In teleosts, the presence of an additional whole genome duplication followed by a process of differential retention and loss means that modeling duplications and deletions will be critical for effective whole genome alignments.

Methods

Assessment methodologies

The following describes extra details of the assessment methodologies used. Detailed further descriptions of the methods for Enredo and Pecan can be found in the Supplemental material.

Projection of exon chains using the Enredo segmentation

To assess the conservation of order and orientation of exon chains we used the Ensembl Human (version 49) gene set, taking only the single longest transcript for each gene.

Enredo coverage of complete genes

We used the human gene set from Ensembl version 47, available at http://oct2007.archive.ensembl.org/. Full matches correspond to genes that are fully covered by the segmentation method, including UTRs and introns. For genes with alternative splicing, we consider a gene fully covered if a matching genomic region includes the first nucleotide of the first transcript and goes to the last nucleotide of the last transcript. It is worth noting that a gene can be covered by different contiguous segments and still be counted as a full match. If there is at least one uncovered nucleotide we count the match as a partial match.

Pairing of human chromosome X

In order to assess the quality of the segmentation programs we looked at whether human X regions pair with autosomal regions. The test is very conservative. Regions paired with either chromosome Y or an unmapped contig are not considered as mismatches. Additionally, cases where a segment of the human chromosome X is paired to both a region of chromosome X or Y and an autosomal region are still regarded as valid matches. Only when a multiple alignment has a region of human chromosome X matching only regions definitively within non-X chromosomes is it considered incompatible.

Ancestral repeats assessment

We used the following Type II transposons for this analysis: MER82, Charlie4, MER119, Charlie1, MER20, MER5A, Cheshire, MER45B, and MER58B. All these repeats are present in all the genomes considered. The repeat instances were detected using RepeatMasker (http://www.repeatmasker.org). Each repeat instance found was aligned to the consensus of the ancestral repeat using Exonerate (Slater and Birney 2005). We then tested whether the nucleotides aligned in the multiple alignments corresponded to the same position in the consensus sequence.

On several occasions, we found a human repeat instance aligned to a related repeat in another species. For instance, Charlie4a can be considered a subrepeat of Charlie4 in which the central region has been deleted. To improve the coverage of our test, we aligned the consensus sequence of these related repeats to the consensus sequence of the repeat found in the human genome. This, for example, allowed us to transform Charlie4a coordinates into the Charlie4 ones. More details on the list of repeats and their relatives can be found in the Supplemental Material.

Homology assessment using gene trees

We used data from Ensembl version 47 to assess the Mercator-Mlagan and Enredo-Pecan alignments. The MULTIZ data were compared with data from Ensembl version 46, as the MULTIZ alignments included an older version of the mouse assembly.

Segmentation data sets

The Mercator-Pecan and Mercator-Mlagan alignments are available upon request. The MULTIZ alignments were downloaded from http://hgdownload.cse.ucsc.edu/goldenPath/hg18/multiz17way/. The latest Enredo-Pecan-(Ortheus) alignments are available from ftp://ftp.ensembl.org/pub/release-50/emf/ensembl-compara/. The original five-way Enredo-Pecan data set used in this analysis is available on request.