Interaural Level Difference Discrimination Thresholds for Single Neurons in the Lateral Superior Olive

Abstract

The lateral superior olive (LSO) is one of the earliest sites in the auditory pathway that is involved in processing acoustical cues to sound location. Here, we tested the hypothesis that LSO neurons can signal small changes in interaural level differences (ILDs), a cue to horizontal sound location, of pure tones based on discharge rate consistent with psychophysical performance in the discrimination of ILDs. Neural thresholds for ILD discrimination were determined from the discharge rates and associated response variability of single units in response to 300 ms tones in the LSO of barbiturate-anesthetized cats using detection theory. Neural response variability was well described by a power function of the mean rate, both in individual neurons and collectively; LSO neurons were less variable than expected from a Poisson process. Compared with psychophysical data, the best-threshold ILDs of single LSO neurons were comparable with or better than behavior over the full range of frequencies (0.3–35 kHz) and pedestal ILDs (±25 dB) explored in this study. With a pedestal ILD of 0 dB, ILD increments of 1 dB could be discriminated by some neurons, with a median of 4.35 dB across neurons. For pedestal ILDs away from 0 dB, the best-threshold ILDs were as low as 0.5 dB, with a median of 2.3 dB. These findings support the hypothesis that the LSO plays a role in the extraction of ILD, and that the representation of ILD by LSO neurons may set a lower bound on the behavioral sensitivity to ILDs.

Introduction

Unlike the retinotopic representation of light sources by photoreceptors, sound location is not encoded explicitly by the peripheral receptors. Instead, location must be computed centrally based on neural representations of minute differences in direction-dependent spectral and temporal characteristics of the sounds arriving at the two ears. The difference in the sound pressure levels (SPLs) of stimuli at the two ears is a primary acoustical cue for horizontal sound location by humans (Rayleigh, 1907; Stevens and Newman, 1936; Mills, 1958), nonhuman primates (Houben and Gourevitch, 1979), cats (Casseday and Neff, 1973; May and Huang, 1996), and other mammals, particularly for sounds with high-frequency content. These interaural level differences (ILDs) arise from the spatial- and frequency-dependent acoustic shadow that is cast by the head and varies systematically with source azimuth (Martin and Webster, 1989; Wightman and Kistler, 1989; Spezio et al., 2000).

The neural mechanisms by which ILDs contribute to the perceptual discrimination of location are not known, but evidence suggests that the lateral superior olive (LSO) performs the initial extraction of ILDs (Yin, 2002; Tollin, 2008). First, LSO neurons are some of the most peripheral where afferents from both ears systematically converge; they receive excitatory input from the glutamatergic spherical bushy cells of the ipsilateral anteroventral cochlear nucleus (AVCN) and inhibitory inputs indirectly from the contralateral AVCN globular bushy cells via the glycinergic neurons of the ipsilateral medial nucleus of the trapezoid body (MNTB). Second, discrimination of horizontal locations is impaired in animals in which the input pathways to or the LSO neurons themselves are lesioned (Masterton et al., 1967; Kavanagh and Kelly, 1992). Third, mammals that use predominantly high-frequency ILD cues for localization have large well developed LSOs (Glendenning and Masterton, 1998). Fourth, LSO neurons are sensitive to predominantly high-frequency sounds corresponding to the frequency range over which ILDs are physically available acoustically (Tsuchitani and Boudreau, 1966). Finally, the discharge rates of LSO neurons are systematically modulated by ILDs (Boudreau and Tsuchitani, 1968).

Humans, primates, and cats can discriminate differences in ILDs of sounds presented over headphones as small as 1–4 dB (Mills, 1960; Houben and Gourevitch, 1979; Scott et al., 2007; Wakeford and Robinson, 1974). The behavioral resolution of sound source location will be ultimately limited by the variability in the neural representation of the localization cues such as ILDs. Empirical evidence cited previously supports the hypothesis that ILDs are first processed in a functionally meaningful way in LSO. But can the responses of LSO neurons account for ILD-based human, primate, or cat perceptual abilities, or is further processing by higher centers required? Here, we use the common framework of signal detection theory to test the hypothesis that the neural responses of the LSO can account for psychophysical ILD discrimination thresholds by comparing neuronal thresholds to psychophysical thresholds measured previously in cat, primate, and human. Our experiments follow from Siebert (1965, 1970) and Yue and Johnson (1997), who first used the statistical details of auditory nerve responses or used modeled LSO neuron responses to sounds, respectively, to predict psychophysical performance.

Materials and Methods

The results presented in this study are based on experiments performed at the University of Wisconsin (UW) and at the University of Colorado Health Sciences Center (UCHSC). Unless otherwise noted, techniques and equipment for both series of experiments were very similar and examination of their results revealed no substantial differences so that both sets of data were pooled. All surgical and experimental procedures complied with the guidelines of the University of Wisconsin and University of Colorado Health Science Center Animal Care and Use Committees and the National Institutes of Health.

Animals, apparatus, and experimental procedures.

Adult cats with clean external ears were initially anesthetized with ketamine hydrochloride (20 mg/kg) along with acepromazine (0.1 mg/kg). Atropine sulfate (0.05 mg/kg) was also given to reduce mucous secretions, and a tracheal cannula was inserted. Supplemental doses of sodium pentobarbital (3–5 mg/kg) were administered intravenously into the femoral vein as needed to maintain areflexia. Heart rate was monitored continuously, as was core body temperature (with a rectal probe), the latter maintained with a heating pad at 37°C (model TC 100; CWE, Ardmore, PA). Additionally, in the UCHSC experiments, blood-oxygen levels, respiratory rate, and end-tidal CO₂ were measured continuously via a capnograph (V90040; Surgivet, Waukesha, WI) and mean arterial blood pressure (femoral artery) was monitored with a pressure transducer (research blood pressure transducer; Harvard Apparatus, Holliston, MA). In all experiments, both pinnae were cut transversely, removed, and tight-fitting custom-built hollow earpieces were fitted snugly into the external auditory meatuses. Polyethylene tubing (Intramedic, PE-90, 30 cm, 0.9 mm inner diameter) was glued into a small hole made in each bulla to maintain normal middle ear pressure.

The LSO was approached ventrally by drilling small holes into the basioccipital bone. Parylene-coated tungsten microelectrodes (1–2 MΩ; Microprobe, Clarksburg, MD) were advanced ventromedially to dorsolaterally at an angle of 26–30° into the brainstem by a microdrive (model 662; Kopf, Tujunga, CA) affixed to a micromanipulator that could be remotely advanced outside the double-walled sound-attenuating chamber (Industrial Acoustics, Bronx, NY). Electrical activity was amplified (ISO-80, World Precision Instruments, Sarasota, FL; SRS 560, Stanford Research Systems, Sunnyvale, CA) and filtered (300–3000 Hz). Unit responses were discriminated with a BAK Electronics (Mount Airy, MD) amplitude–time window discriminator (model DDIS-1) and spike times were stored at a precision of 1 μs via custom hardware (UW) or a Tucker-Davis Technologies (Alachua, FL) RV8 (UCHSC).

Stimuli: general.

All stimuli were generated digitally at 16-bit (UW) or 24-bit (UCHSC) resolution and converted to analog at a nominal rate of 100 kHz by custom-built hardware (UW) or a Tucker-Davis Technologies RX-6 (UCHSC). The overall stimulus level to each ear was independently controlled in 1 dB steps using custom-built programmable attenuators (UW) or a pair of Tucker-Davis Technologies PA-5s (UCHSC). The conditioned output of the digital-to-analog converter was sent to an acoustic assembly (one for each ear) comprising an electrodynamic speaker (40-1377; Realistic, Fort Worth, TX) (UW) or a Tucker-Davis Technologies EC1 electrostatic speaker (UCHSC), a calibrated probe-tube microphone (type 4182; Bruel and Kjaer, Norcross, GA), and a hollow earpiece that was fit snugly into the cut end of the auditory meatus and sealed with petroleum jelly. The hollow earpiece accommodated the small probe-tube microphone by which the sound delivery system to each ear was calibrated for tones between 50 Hz and 40 kHz in 50–100 Hz steps. The calibration data were used to compute digital filters that equalized the responses of the acoustical system and typically yielded flat frequency responses within ±2 dB for frequencies <30 kHz.

Tone bursts of varying frequency were used as search stimuli with the SPL of the tone to the ipsilateral ear being 5–10 dB higher than the tone to the contralateral ear so that the binaural cells of the LSO would not be missed. Once a single unit was isolated, the characteristic frequency (CF), spontaneous activity, and threshold were measured using an automated threshold tracking routine or by measuring a frequency-intensity response area. Initial rate level functions were measured by presenting 200 repetitions of a 50 ms tone pip at CF (4 or 5 ms rise/fall times) every 100 ms from which the resulting peristimulus time histograms (PSTHs) were examined on-line. A tonic response with chopping, or multiple modes in the PSTHs unrelated to the frequency of the stimulus, is characteristic of most LSO cells (Tsuchitani, 1982) and the incidence of chopping was measured by computing the coefficient of variation (CV) of the interspike interval (the ratio of the SD of the interspike interval to the mean interspike interval) over the first 25 ms of the response (Young et al., 1988).

After the initial characterizations of the neurons as described above, for each neuron an ipsilateral-ear-only rate-level function was measured with 300 ms duration CF tones. Sensitivity to ILDs was measured with 300 ms duration tones at the CF of the neuron presented every 500 ms with a linear rise/fall time of 5 ms. ILD was manipulated by holding constant the stimulus to the ipsilateral ear at 4–25 dB above the ipsilateral-ear-only threshold level while the level of the same stimulus presented to the contralateral ear was varied in 5 dB steps over a range to cover ILDs of at least ±25 dB; this procedure reveals whether ipsilaterally evoked neural responses can be inhibited by contralateral stimulation, another hallmark of LSO cells. The ipsilateral-ear level was generally held fixed at an SPL that produced a response that was about half of the maximum response produced by ipsilateral-ear stimulation alone. In a small number of neurons, ILDs were varied in steps of 1 dB. There were at least 20 (and up to 100, on occasion) repetitions of the stimulus at each ILD.

Histology.

In many experiments, electrolytic DC lesions (5 μA × 10 s) were made to differentiate electrode tracks, mark locations of interest, and assist in estimating tissue shrinkage after histological processing. At the conclusion of each experiment, the brain was fixed in formaline (UW) or 4% buffered paraformaldehyde (UCHSC) by immersion or perfusion through the heart. The fixed tissue was cut into 50 μm frozen sections and stained with cresyl violet so that electrode tracks and lesions made during the recordings could be seen.

Data analysis: computation of neural discrimination thresholds.

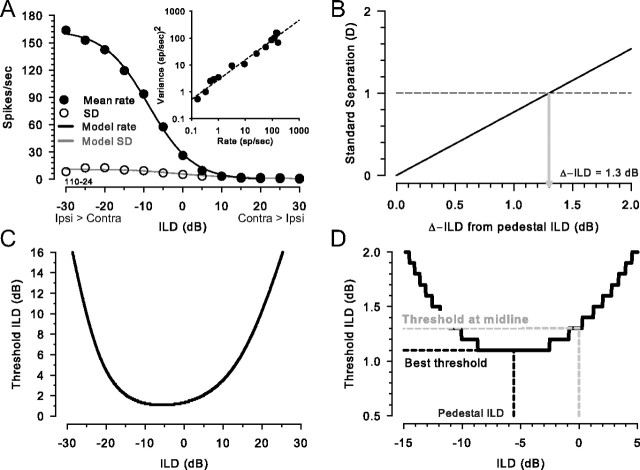
Figure 1A shows the mean discharge rate and associated response variability (SD) over repeated (20) presentations of the stimuli at the same ILDs of one LSO neuron as a function of ILD. In this study, the stimulus duration and the window over which the discharge rate was computed was fixed at 300 ms. The primary goal of this study was to examine the ability of LSO neurons, like the one in Figure 1A, to signal small differences in ILD via changes in discharge rate and associated response variability using methods adapted from ideal observer theory (Green and Swets, 1966). Ideally, discrimination thresholds would be computed directly from the comparison of the distributions of discharge rates (or counts) constructed from many presentations of the stimuli at finely spaced ILD values using receiver operating characteristic (ROC) analysis. ROC analysis is desirable because it makes no assumptions about the underlying distributions of responses (i.e., they need not be Gaussian). However, because of limitations in our ability to maintain extracellular recordings of LSO neurons for prolonged time periods, and our desire to study a large range of stimulus parameters, it was not always possible to sample finely enough along the ILD axis to compute thresholds in this way. We therefore adopted an alternative approach after verifying in a subset of the data its concordance with ROC analysis.

Figure 1.

Determination of ILD discrimination threshold of an LSO neuron (unit 110–24). A, Mean discharge rate (•) and SD (○) of an LSO neuron to variations in the ILD of a 300 ms duration CF (16 kHz) tone. The black line shows the best-fitting sigmoid to the rate and the gray line shows the SD computed from the fitted power function of the rate (inset). The inset shows the variance of the rate as a function of the rate on double-log coordinates along with the best-fitting power function (dashed line). B, Example of computing threshold ILD via standard separation metric, D (see definition in Materials and Methods), as a function of increment ILD from the pedestal. The threshold for discrimination was defined as the smallest increment ILD that results in D of 1. C, ILD thresholds as a function of pedestal ILD for the neuron in A. D, A magnified view of C, which delineates three points of interest: the best threshold, corresponding to the minimum of the function, the pedestal ILD at the best threshold, and the threshold at midline, corresponding to pedestal ILD of 0 dB.

Instead of using ROC methods, an adaptation of the well known detectability index, d′, was used to compute neural discrimination thresholds (Green and Swets, 1966). One issue with d′ is that the technique assumes that the neural responses to the two different stimuli being compared are Gaussian distributed and have equal variance. We did not systematically evaluate these criteria for our data. Instead, we used the nonparametric standard separation metric, D (Sakitt, 1973). This has been used by other investigators in analyzing neuronal thresholds in the inferior colliculus (IC) (Jiang et al., 1997; Shackleton et al., 2003; Coffey et al., 2006). Note, however, that use of d′ instead of D in the analysis of the data in this study produced virtually identical results in all neurons.

To facilitate the analysis of the data and to explore a larger stimulus space using the standard separation metric, we used a mathematical description of the responses of each LSO neuron to ILDs. This required a description of not only the discharge rate as a function of ILD, but also an accurate description of the variability of the rate (e.g., SD) over repeated presentations of the stimuli at each ILD. To this end, descriptive functions (Geisler and Albrecht, 1997) were fitted for each neuron to both the discharge rate as a function of ILD (see Fig. 1A) and the variance of the rate as a function of the rate itself (see Fig. 1A, inset). A trust-region method was used to calculate a robust nonlinear least-squares fit to a sigmoid function, whereas a robust linear least-squares fit was obtained to a power function (Matlab 7.2.0.232; Mathworks, Natick MA). The descriptive functions have no functional biological significance; rather, they simply allow for the computation of a discharge rate and associated variance for each neuron at any arbitrary ILD value throughout the range of ILDs tested. The function used for discharge rate-ILD data was a four-parameter sigmoid function of the following form:

where x is the ILD, y is the discharge rate, and a, b, c, and d are free parameters. (Note that the sigmoid function is a special case of the more general logistical function, and the logistical function is the inverse of the logit function.) The function relating the variance to the mean discharge rate was a two-parameter power function:

where x is the discharge rate and a and b are free parameters. Because a power function reduces to a linear function when plotted on double-log coordinates, to facilitate the fitting, the rates and variances were first log-transformed and then fit with a linear function of the form log(y) = log(f) + g × log(x); parameters for the two-parameter power function were then computed as b = g and a = e^f. The SD of the rate as a function of ILD was computed by inputting the fitted sigmoid function of the rate (Eq. 1) into the power function (Eq. 2) to get the variance of the rate and then taking the square root. Both functions provided accurate descriptions of the data (see Results). The parameters of the fitted functions for each neuron can be found in the supplemental material (available at www.jneurosci.org).

Next, to predict performance using the mathematical descriptions of the rate and SDs, the standard separation metric D (Sakitt, 1973) was computed for each neuron:

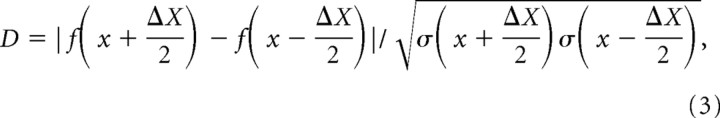where f is the discharge rate, x and Δx are the pedestal and increment ILDs, respectively, and ς is the SD of the discharge rate; the discharge rate and SD were computed from the fitted functions as described above. Note that in Equation 3, the total ILD increment from the pedestal ILD was implemented by symmetrically incrementing and decrementing the ILD by one-half of the intended ILD. In this study, it is the total ILD increment that is reported. Under conditions where the distribution of the discharge rates is Gaussian with equal variance, D equals d′ and, thus, D equals 1 corresponds to ∼75% correct in a two-alternative forced-choice (2AFC) psychophysical experiment (Green and Swets, 1966). Here, we define the smallest increment in ILD that corresponds to a D of 1 as the ILD threshold at a particular pedestal ILD. Threshold ILDs were computed for a range of pedestal ILDs between +25 and −25 dB in 0.05–0.1 dB increments (see Fig. 1C,D, magnified view). Finally, from these threshold ILD versus pedestal ILD functions, we could find the threshold at the 0 dB pedestal ILD (i.e., the midline), and the best threshold as well as the pedestal where it occurred (see Fig. 1D). Figure 1B shows for one neuron how D changed as ILD was varied from a pedestal of 0 dB. A D of 1 was first reached for an increment of 1.3 dB, which was taken as the threshold at that pedestal ILD. The pedestal ILD was then changed and the process repeated. Figure 1C shows for the same neuron the ILD thresholds as a function of pedestal ILD.

In some cases, rate-ILD data were collected at 1 dB increments for a range of ±10 dB around the pedestal ILD near the steepest slope of the rate-ILD function (typically, but not always, around the 0 dB pedestal ILD) and repeated 60–100 times. These data allowed the calculation of the percentage correct in discriminating two stimuli with different ILDs in a two-interval 2AFC task (i.e., a neurometric function) using standard ROC analysis (Shackleton et al., 2003). Briefly, at each pedestal ILD, the distribution of rates was compared with the distribution of rates obtained for successive 1 dB ILD increments. From these two distributions, the probabilities of both correctly discriminating the ILD increment, the “hit rate,” and of making errors in discriminating the ILD, the “false-alarm rate” (e.g., false-positive error), based on discharge rate could be determined; this was done by sweeping a criterion along the ILD axis and at each point computing the hit and false-alarm rates. The ROC is a plot of hit rate as a function of the false-alarm rate for a given ILD increment. The area under the ROC represents the probability, or percentage correct, that the ILD increment can be correctly discriminated from the pedestal ILD based only on the distributions of discharge rates, analogous to the two-interval, 2AFC task commonly used in human psychophysics (Green and Swets, 1966). This process was repeated for the discharge-rate distributions for larger ILD increments away from the pedestal ILD. Then, for each pedestal ILD, a neurometric function was obtained by plotting the percentage correct discrimination computed from the ROCs as a function of the ILD increment. When the rate distributions overlap completely, the percentage correct is 50% and when the distributions do not overlap at all, the percentage correct is 100%. For each pedestal ILD, the ILDs were also decremented in 1 dB steps. For these cases, the proportion correct tended to go from 50% when the distributions overlapped to 0% when there was no overlap. At each pedestal ILD, the threshold ILD was computed as the smallest ILD increment or decrement from the pedestal ILD necessary to produce 75 or 25% correct performance, respectively. In some neurons at some pedestal ILDs, a 1 dB increment or decrement produced performance >75% or <25% correct, respectively. In these cases, linear interpolation was used to determine approximately the threshold ILD necessary to produce 75 or 25% on the neural discrimination function. This latter technique of linear interpolation was also used to compute ILD thresholds using the empirically measured discharge rates and associated variances and Equation 3 directly (see Results).

Results

Results are based on recordings from 42 single LSO units in 14 cats. Of the 42 units, 36 (86%) had CFs between 3 and 35 kHz and responses characteristic of LSO neurons: low spontaneous rates, chopping PSTHs to short tone pips (mean CV, 0.45 ± 0.12), and all neurons exhibited “IE” binaural interaction in that they were excited (E) by ipsilateral and inhibited (I) by contralateral acoustical stimulation. Electrode tracks were able to be reconstructed from the histology for eight cats, allowing us to verify that the 25 of the 36 high-CF units from those cats were indeed located in the LSO. The localization of all units as a function of CF was in general agreement with the tonotopic organization of LSO (Tsuchitani and Boudreau, 1966; Guinan et al., 1972); high-CF neurons located medioventral and lower-CF neurons located more dorsolateral in the nucleus. Although histology was not available for the remaining 11 high-CF units, they are included here because both the neural response characteristics and the electrode depth at which these units were encountered relative to other common types of neurons (medial nucleus of the trapezoid body and medial superior olive) typically found in successful, and histologically verified, penetrations were consistent with LSO neurons. Six (14%) low-CF (<3 kHz) LSO neurons were included from a previous study (Tollin and Yin, 2005). Because it is commonly believed that the LSO is responsible primarily only for high-frequency ILD encoding (Tollin, 2008), where appropriate, the low- and high-CF data will be treated seperately to highlight differences or similarities.

For the data in this study, the ipsilateral-ear sound level about which the rate-ILD curves were measured was not chosen completely arbitrarily; rather, it was set to the level that yielded approximately the half-maximal discharge rate in the ipsilateral-ear-only rate-level curve. It is well known that some aspects of the rate-ILD curves for LSO neurons are not invariant to changes in the ipsilateral-ear sound level (Tollin and Yin, 2002; Park et al., 2004); with increases in ipsilateral-ear level, the rate-ILD curves have larger maximum discharge rates and the curves shift position along the ILD axis, typically toward ILDs favoring the ipsilateral ear (Fig. 1A, negative ILDs). Such changes in the rate-ILD functions with ipsilateral-ear sound level will likely have some effect on the neural threshold ILDs as computed in this study. However, the procedure used here provided consistency in the data in that the rate-ILD functions were measured in the same way, relative to the ipsilateral-ear rate-level function, for each neuron.

We examined some of the consequences of our method of choosing the ipsilateral-ear sound level for rate-ILD curve measurement. For all 42 neurons, the monaural ipsilateral-ear excitatory rate-level curves were sigmoidally shaped and monotonic with SPL (data not shown), with mean thresholds of 23.5 ± 14.43 dB (median, 21.5 dB). Rate-ILD functions (Fig. 1A) were measured by holding the sound level at the ipsilateral ear constant at 4–25 dB (mean, 16.5 ± 6.43 dB; median, 15 dB; n = 42) above the ipsilateral-ear threshold of each neuron and varying the sound level to the contralateral ear. Across neurons, this ipsilateral-ear sound level chosen for the rate-ILD measurements yielded a responses that was 67% (±16%; n = 42) of the maximum response of the neuron. Neither the ipsilateral-ear threshold (r = 0.16; p = 0.33), nor the sound level above ipsilateral-ear threshold (r = 0.22; p = 0.17) or the percentage of ipsilateral-ear-alone maximum response (r = 0.19; p = 0.24) used for the rate-ILD curve measurement was correlated with the best-threshold ILDs obtained across neurons. Thus, the specific choice of the ipsilateral-ear-only sound level around which the binaural rate-ILD curves were measured had little impact on the ultimate ILD acuity measured from neuron to neuron.

Finally, although the rate-ILD functions, and the neural threshold ILDs based on those functions, were measured here by fixing the sound level at one ear and varying the sound level at the other ear, Stellmack et al. (2004) has shown that human threshold ILDs measured in this way (their “monaural with contra” task) were not significantly different from those measured in the more traditional way by symmetrically incrementing and decrementing the sound levels at the two ears (their “interaural” task).

The rate-ILD functions of LSO neurons are characterized by a sigmoid function

One of the hallmarks of ILD processing by LSO neurons is illustrated in Figure 1. When discharge rate to a 300 ms duration CF tone is plotted as a function of ILD, the resulting function is sigmoid shaped, with high discharge rates for ILDs favoring the ipsilateral excitatory ear (negative ILDs in our convention) and low rates for ILDs favoring the contralateral inhibitory ear (positive ILDs). None of the 42 neurons exhibited nonmonotonic rate-ILD functions. The responses of each LSO neuron to ILDs were characterized by the four-parameter sigmoid function (Eq. 1). Figure 1A shows an example of the fit for one neuron (r² = 0.999). Across the population of neurons, the sigmoid provided an excellent fit to the rate-ILD curves for both high- and low-CF neurons (high CF: mean adjusted r² = 0.98 ± 0.022; range, 0.90–1.0; n = 36; low CF: mean adjusted r² = 0.98 ± 0.015; range, 0.95–0.99; n = 6).

The response variances of LSO neurons are characterized by a power function of their mean discharge rates

For each neuron, a two-parameter power function (Eq. 2) was fitted to the variance versus mean discharge rate (Fig. 1A, inset) (r² = 0.97). Mean and variance were computed over the stimulus duration, which was fixed at 300 ms for all neurons. Across the population, the power function provided a reasonable description of the variance in terms of the mean rate for both high-CF [mean adjusted r² = 0.89 ± 0.14; range, 0.36–1.0; n = 34; the data from two additional neurons (SOC06008_12_3_2 and SOC06004_5_11) (see the supplemental material, available at www.jneurosci.org) were not well described by a power function] and low-CF neurons (mean adjusted r² = 0.8 ± 0.16; range, 0.53–0.98; n = 6). Note that because the power function reduces to a linear function if the exponent equals one, the power-function description can accommodate models of noise whose variance is proportional to the mean (Tolhurst et al., 1983). The parameters of the fitted functions [sigmoid (Eq. 1) and power law (Eq. 2)] for each neuron are provided in the supplemental material (available at www.jneurosci.org).

Some investigations of neural discrimination using populations of neurons have used the discharge statistics (particularly the description of the variance) computed from of an ensemble of neurons rather than the statistics from individual neurons [e.g., auditory (May and Huang, 1997; Hancock and Delgutte, 2004) and vision (Lehky and Sejnowski, 1990; Geisler and Albrecht, 1997)]. We examined here whether this was a viable option for our data. Figure 2A is a scatter plot of the variance and mean firing rates for the entire population of 36 high-CF LSO neurons in all experiments where 300 ms duration tonal stimuli at the CF of each neuron was used (i.e., ipsilateral-ear rate-level curves and ILD curves); the low-CF data were not included in this analysis or in Figure 2A–C (Tollin and Yin, 2005). For the high-CF neurons, a power function (Eq. 2) provided a good fit to this collective set of data (r² = 0.9), whereas a linear function (y = mx+b) did not (r² = 0.5). For the population data, the parameters extracted from the double log plot lead to the formula y = 2.85x^0.88.

Figure 2.

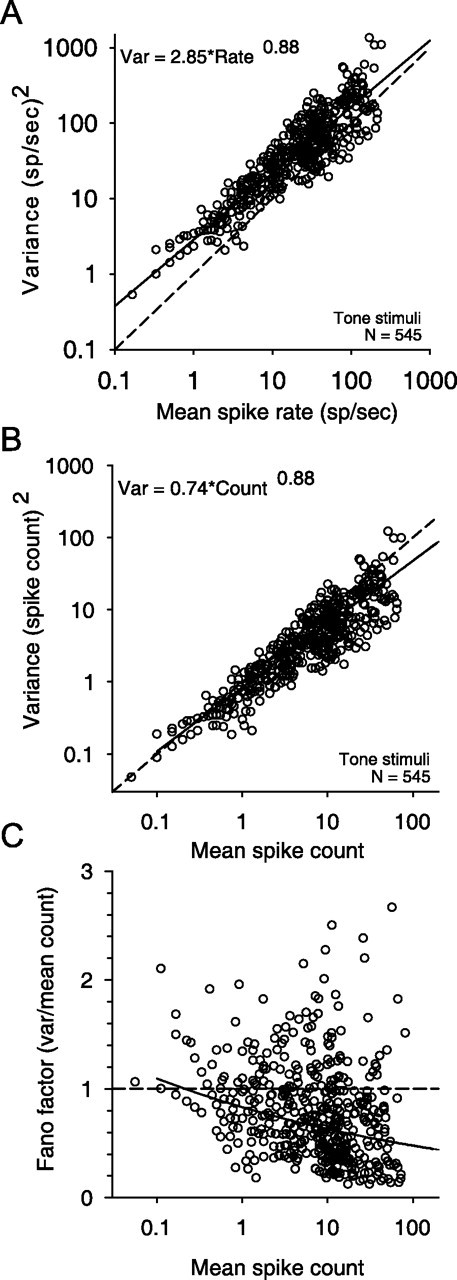
The variance of the responses of LSO neurons to repeated presentations of CF tones is well described by a power function of mean response when plotted on double-log coordinates. A, Variance of discharge rate as a function of the mean discharge rate (○). The line (solid) shows the best-fitting power function (for details of the goodness of the fit, see Results). n is the number of variance-rate pairs from 36 neurons. For all neurons, the stimuli were 300 ms duration tones at the CF. B, Variance of spike count over the 300 ms duration of the stimuli as a function of the mean spike count (○). The line (solid) shows the best-fitting power function. C, The Fano factor (ratio of the variance to the mean spike count) decreases as a function of mean spike count. The solid line shows the Fano factor computed from the power function in B. In both B and C, the results expected for a Poisson process (variance equal to the mean, and FF equals 1) is also shown (dashed line).

We hypothesized that if the population of high-CF LSO neurons where homogenous such that the response variability for all neurons was only dependent on the discharge rate, then a power function (Eq. 2) fit to the population data (Fig. 2A) should be a reasonable approximation for individual neurons. To test this hypothesis, we separately fitted a power function (Eq. 2) to the variance versus mean discharge rate for each neuron and experiment. From this fit, we computed the 95% confidence limits, which were then compared with predictions of the variance produced by the population model (Fig. 2A) using the discharge rates of the individual neuron as input. In 30 of 36 high-CF (83%) and four of six (67%) low-CF neurons, the power-law fit to the population data produced predictions of the variance that fell within the 95% confidence region of the individual neuron power-law functions, suggesting that a relationship between variability and discharge rate may be reasonably summarized by a generic power function; that is, the variances predicted using the population power function (Fig. 2A) with the discharge rates from a particular neuron as inputs were not significantly different from the actual response variance produced by that neuron at the same discharge rates. For the remaining four high-CF (two neurons mentioned earlier are excluded) and two low-CF units, the adjusted coefficient of determination (r²) of the individual power-law fits had means of 0.97 ± 0.06 and 0.95 ± 0.05, respectively, indicating that the reason for the failure of the population model to account for the individual neuron data was not a poor fit of the power function to these data. Although significant, the differences for these six neurons were not large. In the rest of the study, we used each neuron's own parametric power-law fit to minimize descriptive errors in the variance. However, we will also show that results are qualitatively unchanged if the population parameters were used instead.

One of the goals of this study was to provide a simple description of the trial-to-trial variability of the responses of LSO neurons to ILDs. The above analysis considered the relationship between the discharge rates and associated variability. However, the variability of neural responses is also often expressed formally in terms of the Fano factor (FF), which is computed as the ratio of the variance to the mean spike count (Teich and Khanna, 1985). The FF for a given counting time (300 ms for the stimuli in this study) is the ratio of the variance to the mean number of spike counts over that time. Figure 2B plots the relation between the variance to the mean spike count. A power function also provided a good fit to these data (Fig. 2B, solid line) [variance (var) = 0.74x^0.88, where x is the mean spike count in 300 ms; r² = 0.9]. [The power functions based on spike rates (Fig. 2A) and spike counts (B) are simply related by a scale factor of the time window, T, over which the rate is computed. Spike-rate variance is given by var_rate = (1/T²) × var_count. If var_count = ac^b, where c is the spike count, and spike rate is given by r = c/T (and thus c = rT), then substituting for c we obtain var_rate = (1/T²)a(rT)^b, which reduces to aT^{(b − 2)}r^b. Substituting the parameters a and b, 0.74 and 0.88, respectively, and T = 0.3 s, yields the expected var_rate = 2.85r^0.88.] Figure 2C plots the FF of the spike count as a function of the count for all data from all 36 high-CF neurons. For these LSO neurons with 300 ms stimuli, the FF decreases with increasing spike count. The variability of LSO neurons in terms of spike counts was less than that expected from a Poisson process (i.e., variance equal to the mean count) for counts >1 (Fig. 2B,C, dashed lines); plotting in terms of discharge rate (Fig. 2A) obscures this fact. For the remainder of the study, all analyses are based on spike rate, not spike count. Because the duration of the stimuli was fixed at 300 ms, the results presented in this study are the same whether rate or count is used.

ILD thresholds computed using ROC analysis are comparable with those using the standard separation metric

In five neurons, sufficient data were collected to calculate threshold using standard ROC analysis (see Materials and Methods). Spike-rate mean and variance for 60–100 stimulus presentations measured at 1 dB intervals were used to calculate threshold ILDs for a range of pedestal ILDs spanning ±10 dB around the point of the maximum slope of the rate-ILD function using three different methods: ROC analysis, standard separation metric (D) directly (Eq. 1) using the empirical mean and SD of the spike rates, and standard separation using the fitted rate-ILD and variance-rate functions. To avoid edge effects in the calculation of thresholds, data from a smaller range of ±5–6 dB pedestal ILDs were used. By edge effects we mean calculations of threshold ILD that would require extrapolation of the data sets beyond pedestal ILDs that were empirically measured. For the example neuron shown in Figure 3A, B shows threshold ILDs as a function of pedestal ILD obtained by ROC analysis, standard separation via the direct method by using the mean and SDs computed from the distribution of discharge rates of the empirical data (“empirical”), and standard separation after fitting analytic functions to the means and variances before computing D (“function-based”). On average, across the five neurons and pedestal ILDs used for each neuron (for a total of 65 data points), mean threshold ILDs were 1.68 ± 0.83 dB, 2.3 ± 1.2 dB, and 2.68 ± 0.95 dB for ROC, empirical, and function-based methods, respectively (medians, 1.7, 2.5, and 2.85 dB, respectively).

Figure 3.

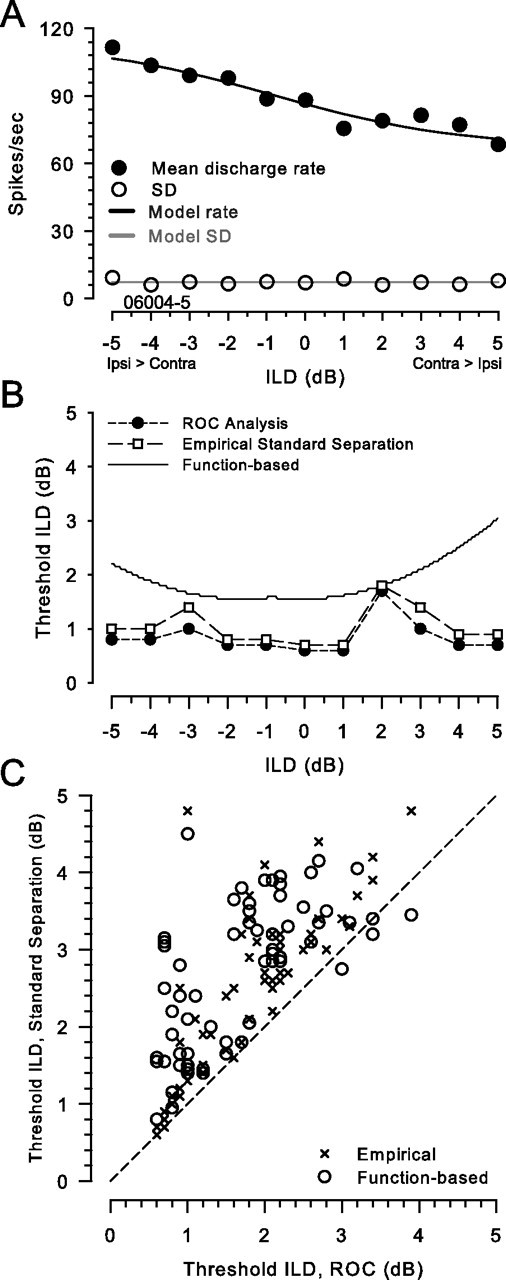
ROC analysis and standard separation metric yield similar estimates of neuronal threshold ILDs. A, Mean rate (•), SD of rate (○), and model function fits (lines) as functions of ILD for one neuron (CF, 31.1 kHz). Mean and SD of rate are based on 100 presentations of the 300 ms stimulus at each ILD. Symbols and lines are as in Figure 1A. B, ILD thresholds computed by three different methods are shown for the neuron in A. Results from ROC analysis (•) using the response distributions, the standard separation metric (□) using the computed mean and SDs of the response distributions measured at 1 dB intervals of pedestal ILD, and the standard separation metric using mean and variance obtained from the best-fitting functions (line) are shown. Threshold was defined as either the ILD increment or decrement that results in an area under the ROC curve of 0.75 or 0.25, respectively, or a standard separation of 1. C, Thresholds of five neurons at pedestal ILDs from ±5 to 6 dB in 1 dB intervals are shown as a scatter plot (n = 65). Thresholds calculated by the standard separation metric, directly using the empirical distributions (×) or via the function-based approach (○), are plotted against thresholds from ROC analysis. The dashed line is the line of equality.

Standard separation analysis using the empirical distribution statistics significantly (see below, ANOVA) overestimates the threshold ILDs compared with the ROC analysis (Fig. 3C), although the magnitude of the difference was quite small (mean difference, 0.62 ± 0.63 dB; median, 0.4 dB; n = 65). In addition, fitting analytic functions to the raw data also introduced additional discrepancy from the ROC analysis in the calculation of thresholds (Fig. 3B,C). By calculating D from the fitted functions, threshold ILD estimates were generally greater than those by ROC analysis, but again the magnitude of the deviation was quite small (mean difference, 1.0 ± 0.76 dB; median, 0.85 dB; n = 65). Overall, the ANOVA revealed a significant difference between the thresholds calculated via these different methods (F_(2,192) = 17.36; p < 0.001). The Scheffe post hoc comparison revealed significant differences between the ROC-based thresholds and both standard separation methods, the empirical (p < 0.001) and the function-based method (p = 0.002). However, there were no significant differences between the thresholds computed using the standard separation metrics, the empirical and the function-based (p = 0.088).

On close examination of the data, we determined that larger deviations of the function-based thresholds from those computed via ROC analysis occurred where the residual errors in fitting the sigmoid functions to the empirical data (Fig. 3A) were great. These observations suggest that these threshold deviations were caused by stochastic fluctuations in the data from one pedestal ILD to the next that are not accounted for by the fitting functions. For example, for the neuron in Figure 3A, there was always enough rate fluctuation (i.e., rate slope) within 1–2 dB (or less) of any pedestal ILD to exceed the threshold criteria (with either ROC or D). The function fitting procedure effectively eliminates these local rate fluctuations, which has the effect of reducing the local rate slope, with the ultimate consequence of increasing the threshold ILDs relative to the other two methods. The differences between the ROC-based and empirical standard separation thresholds may be attributable to a slight deviation of our datasets from normality and equal variance such that ROC analysis gives lower thresholds than expected based only on the statistics of the underlying rate distributions. Our interpretation of these results is not that the threshold ILDs computed via the function-based method are misleadingly high, but rather that the threshold ILDs computed using ROC analysis and the empirical standard separation are, in a sense, misleadingly low because of the local rate fluctuations (Fig. 3A). Although the magnitude of the difference is not large, the data in Figure 3, A and B, shows an extreme case of the disagreement between the thresholds computed using the “empirical” metrics and those based on a fitted function.

We have demonstrated that the computationally efficient standard separation analysis provides very similar estimates of threshold to those computed using ROC analysis in our data sets, with a difference in computed thresholds less than ∼1 dB. Thus, our approach closely approximates the standard ROC analysis, but allows the additional advantage of determination of thresholds over a much greater range of stimulus space (e.g., ILDs, overall sound level, frequency, etc.) of interest and at a better ILD resolution than could be reasonably done by ROC analysis (Shackleton et al., 2003). Throughout the rest of the study, thresholds are computed using the function-based method.

ILD thresholds across LSO neurons are independent of CF

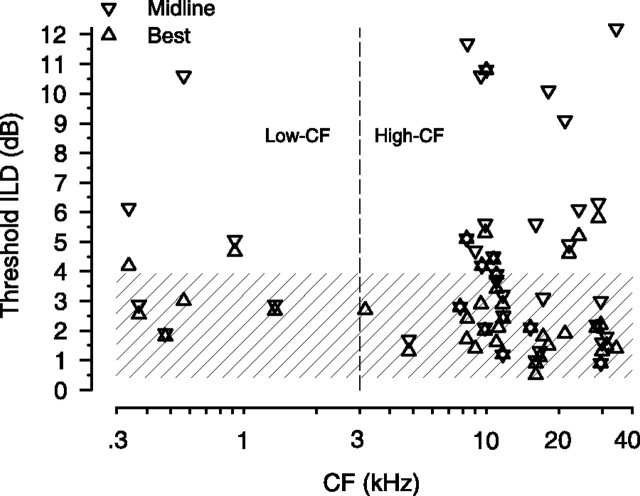
Figure 4 shows the ILD thresholds as a function of the CF of each neuron. The shaded area marks the typical human ILD discrimination threshold of tones (for which there is often considerable intersubject variability), which is approximately constant between 0.5 and 4 dB across the bulk of audible frequency range 200 Hz to 10 kHz (Mills, 1960; Grantham, 1984; Yost and Dye, 1988; Wright and Fitzgerald, 2001; Stellmack et al., 2004). The best ILD thresholds in nonhuman primates also range from 1 to 4 dB for frequencies from 0.5 to 10 kHz (Houben and Gourevitch, 1979; Scott et al., 2007). And cats can discriminate ILDs of 1 dB with stimuli in the range of 0.5–3 kHz (Wakeford and Robinson, 1974), suggesting comparable performance between humans, cats, and nonhuman primates. Psychophysical ILD thresholds in the cat are not available for frequencies >3 kHz.

Figure 4.

Threshold ILDs of individual LSO neurons are comparable with psychophysical thresholds. Best threshold (▵) and threshold at midline (0 dB pedestal ILD) (▿) as a function of the CF of the neuron (n = 42). For comparison, the shaded region depicts the range of ILD discrimination thresholds (∼0.5–4 dB) in human, monkey, and cat psychophysical data (see Results). Three data points with values >12 dB are not shown for the sake of clarity. Data from low-CF (<3 kHz) and high-CF (>3 kHz) neurons are separated by the dashed line.

In the current study, across the stimulus frequencies over which the ILD cue is effective for localizing free-field sounds (high CF, >3 kHz in cats) (Casseday and Neff, 1973), for the high-CF neurons, 78% (28 of 36) of best-threshold ILDs and 47% (17 of 36) of the threshold ILDs at the midline are within the expected range of behavioral thresholds for ILD discrimination (Fig. 4, shaded region). Similar results occurred for low-CF neurons, where 66% (four of six) of the best-threshold ILDs and 50% (three of six) of the thresholds at midline are within the range of behavioral thresholds. Threshold ILDs for low-CF and high-CF neurons were not significantly different when computed at the midline (t₍₄₀₎ = −0.65; p = 0.52) or the best thresholds (t₍₄₀₎ = 0.47; p = 0.64). Moreover, for all neurons the magnitude of the threshold ILDs at the midline (r = −0.12; p = 0.27; n = 42) or the best thresholds (r = −0.034; p = 0.28; n = 42) were independent of the CF. Remarkably, at this most peripheral stage of ILD processing, we find single neurons in the LSO with CFs from 300 Hz to 35 kHz that can signal changes in ILD with a resolution comparable with, or better than, the behaviorally obtained thresholds in humans, nonhuman primates, or cats.

ILD thresholds as function of pedestal ILD

The best-threshold ILDs of the neurons are plotted against the pedestal ILD where they occur for high- and low-CF neurons (Fig. 5A). The distributions of the pedestal ILDs at the best-threshold ILD for the population of neurons is shown in Figure 5B. The “lower envelope” of the threshold versus pedestal ILD functions of the 42 neurons studied is also shown (Fig. 5A, solid line). This lower envelope was computed by plotting the threshold ILD versus pedestal ILD curves (Fig. 1C) for all neurons on a single plot and then simply finding the minimum threshold ILD at each pedestal ILD; 11 of 42 neurons, with CFs ranging from 4.8 to 29.6 kHz, contributed to the lower envelope. None of the six low-CF neurons contributed to the lower envelope. Over the bulk of the pedestal ILDs used in this study, ±20 dB, the lower envelope of the ILD thresholds lies between 0.5 and 2 dB, with the threshold at the midline of 0.9 dB. Thus, across the population of LSO neurons in Figure 3A, the threshold ILDs of those neurons contributing to the lower envelope show little dependence on pedestal ILD over a wide range of pedestal ILDs. This provides only an estimate of the rate of change of threshold ILD with pedestal ILD in response to pure tones because the lower envelope was obtained by finding the lowest threshold of neurons that could be tuned to different CFs. Note, however, as shown in Figure 4, that many LSO neurons yielded small threshold ILDs of 1–2 dB, regardless of their CF.

Figure 5.

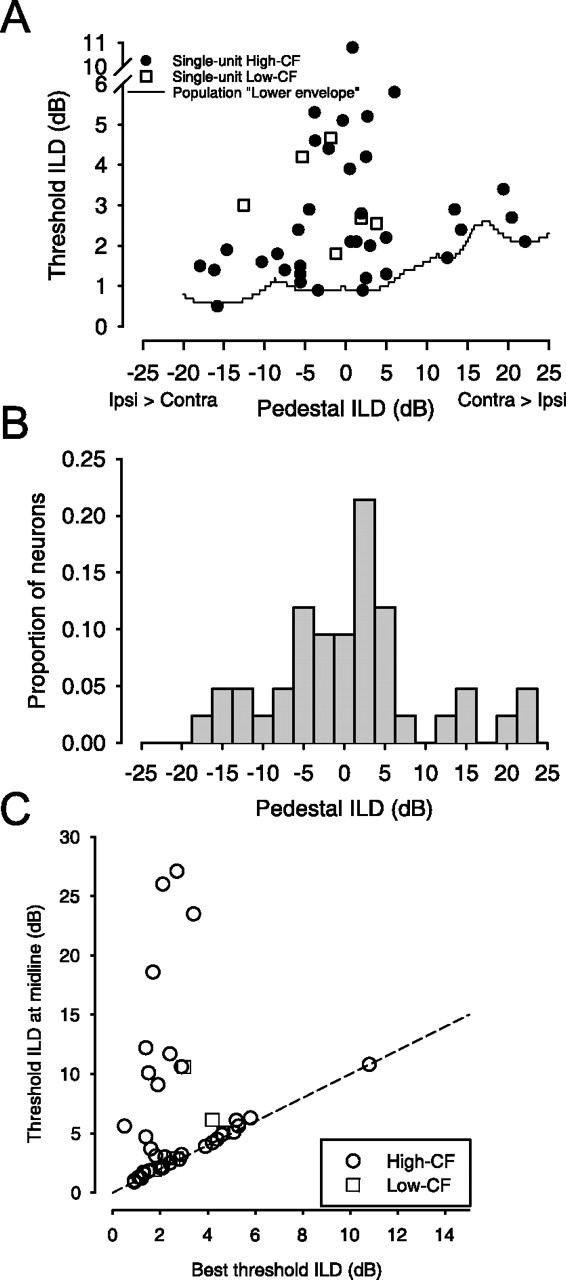
A, Best-threshold ILDs (•, high CF; □, low CF) of individual neurons as a function of the pedestal ILD at which they occurred. The minimum of the threshold-ILD functions of the population (line), the lower envelope, is relatively invariant with pedestal ILD. The invariance of threshold as a function of pedestal ILD increases from the midline is consistent with human psychophysical data (see Results). B, Distribution of pedestal ILDs corresponding to best-threshold ILDs. Across the population of neurons, the best thresholds tended to occur near the midline. C, Threshold ILDs at midline as a function of the best-threshold ILDs (○, high CF; □, low CF). Best thresholds of LSO neurons are not always found at midline (pedestal ILD of 0 dB). The dashed line is the line of equality.

Yost and Dye (1988) measured human ILD discrimination thresholds of tones with frequencies between 0.2 and 5 kHz and a pedestal ILD of 0–15 dB. Their data show threshold ILDs were also relatively invariant to pedestal ILD, increasing at a rate of 0.04–0.07 dB/dB. Hafter et al. (1977), using short-duration bandpass stimuli, reported human ILD thresholds that increased with pedestal ILD by ∼0.03 dB/dB over a 24 dB range of pedestal ILDs. The data from Yost and Dye (1988) and Hafter et al. (1977) are comparable with the neural data in that the range of best-threshold ILDs, as reflected by the lower envelope (Fig. 3A), show only a small dependence on the pedestal ILD. Yost and Dye (1988) also report thresholds at midline (ILD, 0 dB) ranged from 0.6 to 1.2 dB (depending on frequency), which is comparable with the 0.9 dB (value of the lower envelope at 0 dB ILD) threshold ILD found here. Hafter et al. (1977) found thresholds of ∼1.5 dB at midline. Recall that low neural threshold ILDs were found across a broad range of neural CFs and, thus, stimulus frequencies (Fig. 4). As pointed out previously, human threshold ILDs measured at midline may include sizable (∼1–4 dB) intersubject variability (Grantham, 1984). We are aware of no experiment in cats that studied the behavioral threshold as a function of pedestal. Nevertheless, our data show that the lower envelope of LSO thresholds can represent changes in ILD similar to human performance over a range of ILDs comparable with that used in human psychophysical studies.

Best neural ILD thresholds do not occur at the midline

Across the population of high-CF neurons studied, the best ILD thresholds (mean, 2.75 ± 1.96 dB; median, 2.1 dB; range, 0.5–10.8 dB; n = 36) were significantly different from the threshold at 0 dB pedestal ILD (6.8 ± 6.9 dB, 4.35 dB, and 0.9–27.1 dB; two-tailed paired t₍₃₅₎ = 3.48; p < 0.001). For the low-CF neurons, the best ILD thresholds (mean, 3.15 ± 1.08 dB; median, 2.84 dB; range, 1.8–4.66 dB; n = 6) were not significantly different from the threshold at 0 dB pedestal ILD (4.91 ± 3.2 dB, 3.97 dB, and 1.9–10.6 dB; two-tailed paired t₍₅₎ = −1.47; p = 0.2). Figure 5C plots the threshold ILD at the midline (0 dB pedestal ILD) against the best threshold. Although most neurons do have their best ILD thresholds near a pedestal ILD of 0 dB (mean, −0.29 ± 9.4 dB; n = 42) (Fig. 5B), a sizable fraction of the neurons have the best threshold at a pedestal ILD well away from midline. Neurons producing the best-threshold ILDs at pedestals away from the midline do so because their rate-ILD functions are correspondingly shifted along the ILD axis. For example, shifting the rate-ILD curve in Figure 1A to the left by 10 dB would also shift the pedestal ILD of the best-threshold ILD to the left by 10 dB. The pedestal ILD corresponding to best ILD threshold spans a wide range (from −18 to +22 dB) without a bias toward either the ipsilateral (21 of 42 neurons) or contralateral (21 of 42 neurons) ear. Although the bulk of measurements of ILD thresholds in human psychophysical studies were done at a pedestal ILD of 0 dB (corresponding to the ILD of a free-field sound directly in front of the observer) and, behaviorally, sound location acuity is often thought to be best at this point (Mills, 1958), only 52% (22 of 42) of the LSO neurons have their best sensitivity within ±5 dB ILD of the midline. The scatter of best sensitivity at different pedestal ILDs in different LSO neurons may be important for absolute sound localization and discrimination of sound sources that are located away from the midline.

Best threshold ILDs across LSO neurons are predominantly determined by changes in discharge rate rather than the variability in rate

In classical signal-detection theory, neural discrimination thresholds for changes in some stimulus parameter, like ILD, are determined by a change in discharge rate relative to the associated variability in discharge rate. Therefore, small discrimination thresholds can be obtained by either large changes in the rate and/or low variability in the rate. To determine which of these factors (or both) influenced the threshold ILDs from neuron to neuron, the best threshold for each neuron was plotted against the SD of discharge rate (Fig. 6A) and against the reciprocal of slope of the rate-ILD function at the pedestal ILD where the best threshold occurred (Fig. 6B). There was a significant, but weak, negative correlation between threshold ILD and the SD of discharge rate at the pedestal ILD of the threshold (r = −0.42; p = 0.007; n = 40; note that the two obvious outliers were not included in the fitting in Fig. 6A; omitting these data points did not change the sign of the correlation.) The weakness in the correlation occurs because there was a wide range of threshold ILDs regardless of the magnitude of the SD.

Figure 6.

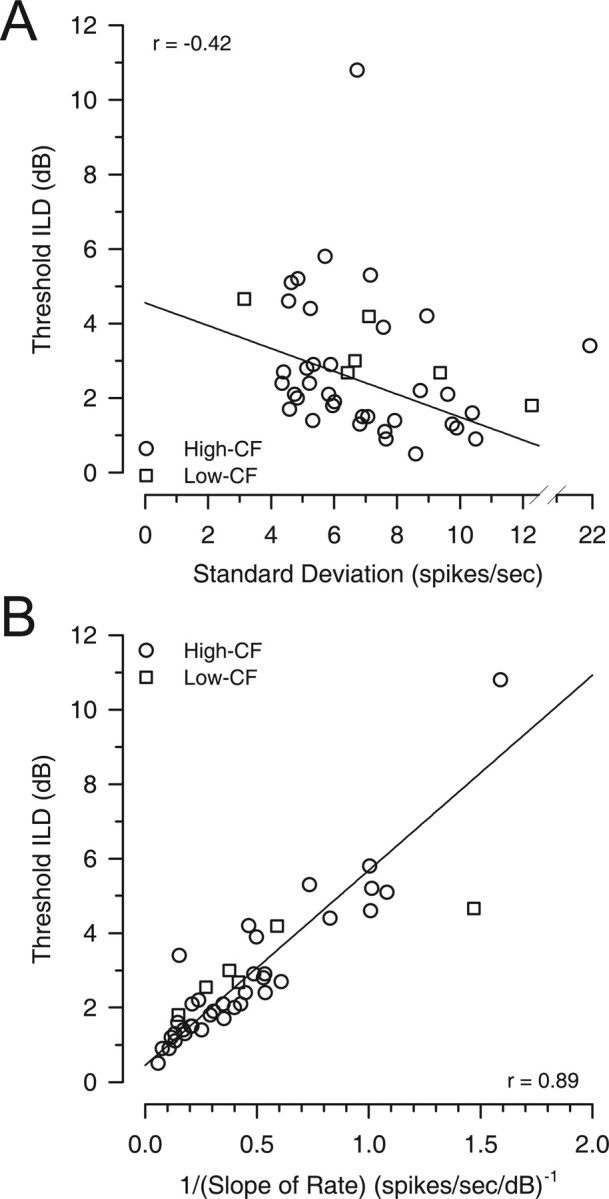
The neural determinants of the best ILD thresholds. A, The contribution of response variability to threshold ILD was examined by comparing best-threshold ILD as a function of the SD of the discharge rate at the pedestal ILD of best threshold (○, high CF; □, low CF). If response variability was a major determinant of the threshold ILD, then a positive correlation would be expected. Rather, a significant negative correlation was observed (the two obvious outliers were not included in the regression). B, Contribution of the rate of change of the discharge rate with changes in ILD (slope) was examined by comparing best-threshold ILD as a function of the reciprocal of the slope at the pedestal ILD of best threshold (○, high CF; □, low CF). If the slope of the rate was a major determinant of the threshold ILD, then a positive correlation would be expected because a larger change in mean discharge rate (i.e., smaller reciprocal of the slope) results in better discrimination (smaller threshold). A significant positive correlation was observed.

Because the threshold ILD was only weakly correlated with the SD, the change in discharge rate with changes in ILD, the rate-ILD slope, might then be the main determinant of the small threshold ILDs across LSO neurons. Here, the slope of the rate-ILD function at the pedestal ILD of best threshold may be obtained directly from the fitted sigmoid function. We hypothesize that an increase in the slope of the rate-ILD function will result in lower thresholds; therefore, a plot of threshold against the reciprocal of the slope (1/slope) would show a positive correlation. Confirming our hypothesis, Figure 6B shows a significant trend of increasing threshold with decreasing slope (i.e., increasing 1/slope) (r = 0.89; p < 0.0001; n = 42), suggesting that rate changes might be a primary determinant of neuronal threshold ILDs across LSO. However, there was also a significant positive correlation between SD and rate slope (r = 0.51; p = 0.0006; n = 42) (data not shown), which might explain the negative relation between thresholds and SD.

Because of the significant correlation between SD and slope, partial correlations (Hays, 1988) were computed to examine which of these two factors explains most of the variance in the threshold ILDs. This analysis was based on 40 of 42 neurons, with the two neurons giving the obvious outliers in Figure 6A being omitted. Based on these 40 neurons, there was a significant negative correlation between SD and 1/slope (r = −0.66; p < 0.0001) and the correlation between threshold ILD and 1/slope remained the same as above (r = 0.89). When the contribution of the reciprocal of the slope (1/slope) was held constant, a significant positive partial correlation between the threshold ILD and SD emerged (r = 0.49; p = 0.0012; n = 40). Thus, when the correlation with the slope was factored out, the expected relationship between threshold ILD and SD was revealed (i.e., lower threshold ILDs result from lower SDs). The negative correlation in Figure 6A, then, results directly from the correlation between SD and slope. However, SD by itself explains only 24% of the variability (r² = 0.24) in the threshold ILDs across neurons. When the contribution of the SD was factored out, there was also a significant positive partial correlation between the reciprocal of the slope (1/slope) and threshold ILD (r = 0.9; p < 0.0001). In contrast to the SD, the slope explains 81% of the variance (r² = 0.81) in threshold ILD across neurons.

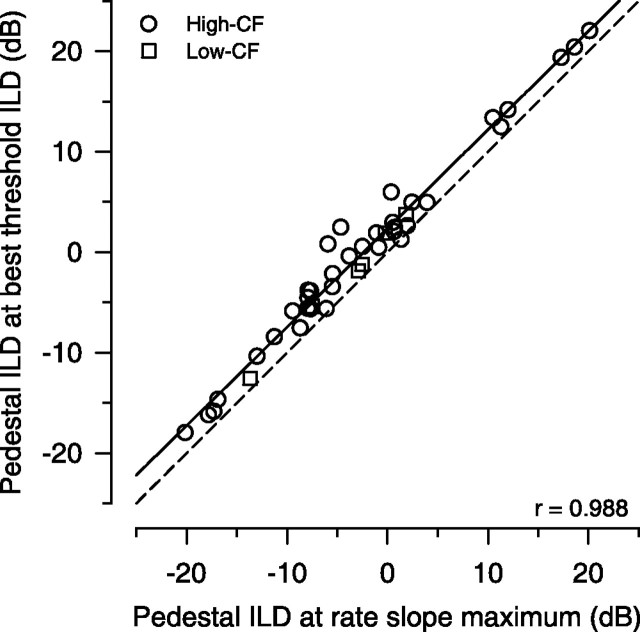
In the preceding analysis, we do not mean to imply that the slope is more important than the SD in determining the threshold ILDs. For example, a simple reduction in the SD for a given slope would lower all thresholds. Rather, the slope simply varies more from neuron to neuron than the SD, and thus appears to be more influential in determining the ultimate value of the best-threshold ILD. As such, slope explains more of the variance in threshold ILD than SD. But clearly both slope and SD are necessary. Case in point, if the slope of the rate-ILD function were indeed the sole determinant of best threshold regardless of the SD of the rate, then one would expect the best thresholds to be found exactly at the inflection point of the rate-ILD function, the midpoint, where the slope of the rate of the sigmoidally shaped function is maximal. Figure 7 plots the empirical pedestal ILD where the best threshold occurs against the pedestal ILD of the maximal slope of the rate-ILD function (high CF: mean pedestal ILD of maximum slope, −2.44 ± 10 dB; median, −4.24; range, −20.14–20.11; n = 36; low CF: mean, −4.17 ± 5.61 dB; median, −2.73; range, −13.68–1.84; n = 6). The best thresholds were found to be consistently, and significantly, just contralateral to the point of maximal slope (paired t₍₄₁₎ = 10.46; p < 0.0001; r = 0.988). The average shift in pedestal ILD for best threshold relative to the ILD of maximum slope was 2.4 ± 1.48 dB (n = 42).

Figure 7.

The best ILD thresholds do not occur where the rate-ILD curve is the steepest. The function relating the pedestal ILD at the best-threshold ILD as a function of the pedestal ILD corresponding to the maximum slope of the rate-ILD function exhibits a consistent offset (○, high CF; □, low CF). The pedestal ILD at best threshold for all neurons was always larger than the pedestal ILD of maximal slope of the rate-ILD function, suggesting that the best threshold does not depend exclusively on the maximum rate of change in response. The dashed line is the line of equality.

The explanation for this consistent shift is shown graphically in Figure 8. Figure 8A shows the mean rate, SD, and function fits as a function of ILD for one neuron. Figure 8B shows how both the local slope of the rate-ILD function, the SD of the rate, and the ratio of the slope to the SD change with pedestal ILD. The threshold ILD as a function of pedestal ILD is also shown for this neuron. For illustration purposes, the ILD axis for this neuron has been adjusted so that the maximum of the slope occurs at 0 dB ILD. As expected, the slope is maximal at the inflection point of the rate-ILD function (i.e., the midpoint of the sigmoid function at 0 dB ILD in this example). However, the ratio of the slope to the SD, which is the quantity that directly determines both the threshold ILD and the pedestal ILD where it occurs, has its maximum at a pedestal ILD slightly contralateral to 0 dB. This contralateral shift occurs because of the way the SD varies with changes in the rate and associated slope. Recall that we demonstrated a power function relationship between the variance and rate of LSO neurons (Figs. 1A, inset, 2A). The SD of the response at any rate, then, is simply the square root of the variance and this value increases monotonically with rate. The slope is also increasing with the rate, up to the maximum slope. Because of the sigmoidally shaped rate-ILD function, the slope begins to change rapidly as the rate increases. Note that for low rates (Fig. 8A, A–B), the rate of change of the SD with ILD is much more rapid than that for the slope (Fig. 8B). However, as rates begin to rise (Fig. 8A, B–C), the slope changes much more rapidly than the SD (8B). As a consequence, the maximum ratio of slope/SD (e.g., the discrimination index D, Eq. 3) occurs not when the slope is maximal (e.g., 0 dB ILD in this example), but when the slope is large relative to the SD. For sigmoidally shaped receptive fields, such as for the LSO neurons, this point lies contralateral to the pedestal ILD evoking the largest slope.

Figure 8.

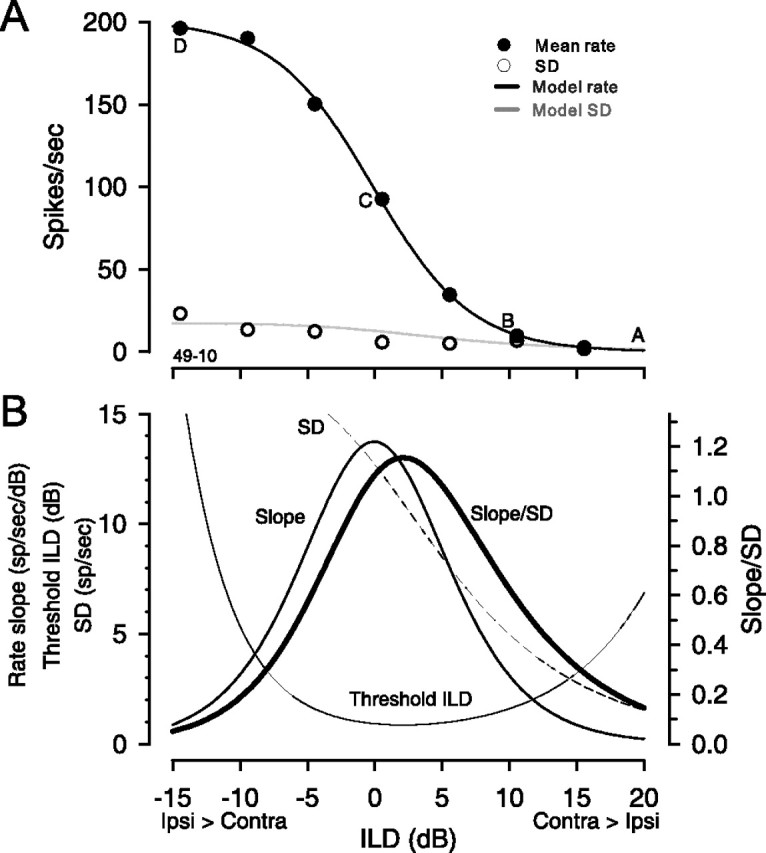
Relationship between the mean and SD of the neuronal discharge rate reveals why best threshold does not occur at the steepest slope. A, Mean rates, SDs, and model fits as functions of ILD for one neuron (CF, 16 kHz). Symbols and lines are as in Figure 1A. B, The slope of the rate, the SD, the ratio of the slope and SD, and the threshold ILD as functions of pedestal ILD for the neuron in A. Note that the ILD axis for this neuron has been slightly adjusted so that the rate slope maximum occurs at 0 dB ILD. The maximum ratio of slope and SD and thus, the best-threshold ILD, does not occur where the slope is maximal (point C in A), but at a point slightly contralateral (positive ILDs between B and C in A).

ILD thresholds using population variance–mean relationship

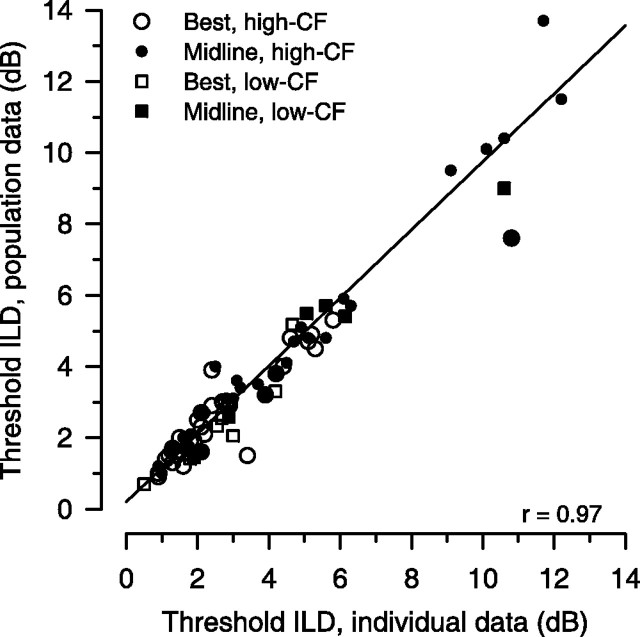
Figure 9 compares the thresholds computed using the population variance–mean relationship based on discharge rate, i.e., [var = 2.85rate^0.88], with those using individual neurons' own variance–mean relationship. ILD thresholds, both best and at 0 dB pedestal ILD, computed in these two ways were not significantly different (paired t test, t₍₄₁₎ = 1.11, p = 0.27 and t₍₄₁₎ = 0.69, p = 0.5, respectively). The linear regression of the data indicates a strong correlation (r = 0.97; p < 0.0001). A bootstrap analysis of the regression data revealed that neither the slope nor the intercept was significantly different from 1.0 (95% confidence interval for slope, 0.76–1.06) and 0.0 (95% confidence interval for intercept, −0.27 to +0.79), respectively. Thus the calculation of ILD thresholds for LSO neurons may be simplified in modeling studies by using the relationship between variance and mean discharge rate from our population of LSO neurons. The result also suggests that LSO neurons in response to tonal stimuli at CF are fairly homogenous in their relationship between discharge rate and response variability.

Figure 9.

Neuronal thresholds obtained by using the generalized description of response variance computed from the population of LSO neurons (e.g., Fig. 2A) are plotted against those obtained by using each neuron's own variance–mean relationship: the best threshold (○, high CF; □, low CF) and threshold at midline (•, high CF; ■, low CF; n = 42). For clarity, four data points with values >14 dB were not plotted (these data were included in the regression analysis). Regression of the data revealed a significant positive correlation (r = 0.97; p < 0.0001; n = 84).

Discussion

The approach of this study follows that of Siebert (1965, 1970), who first used the statistical details of auditory nerve responses to sounds to predict psychophysical performance. Although our results are the first to use actual LSO responses to characterize performance, there have been efforts to relate modeled LSO responses to psychophysical data (Yue and Johnson, 1997).

We found here that individual LSO neurons can signal ILD changes via their discharge rate and associated response variability with a resolution comparable with behavior. Human ILD discrimination thresholds for tones are relatively invariant to stimulus frequency, being approximately constant between 0.5 and 4 dB across a range from 200 Hz to 10 kHz (Mills, 1960; Grantham, 1984; Yost and Dye, 1988; Wright and Fitzgerald, 2001; Stellmack et al., 2004). The most sensitive single neurons in the LSO could also signal changes in ILD with a resolution comparable with, or better than, the behaviorally obtained thresholds in humans, nonhuman primates, or cats over a wide range of CFs from 300 Hz to 35 kHz. Moreover, the best-threshold ILDs of most neurons occurred near the midline, for pedestal ILDs between +5 and −5 of 0 dB. The low-threshold ILDs <1 dB near pedestals of 0 dB are consistent with psychophysical findings of best acuity for ILD (Hafter et al., 1977; Yost and Dye, 1988) and azimuth (Mills, 1958).

Determinants of neuronal ILD thresholds and implications for ILD coding

Thresholds for some neurons were equal to or smaller than behavioral thresholds, suggesting that perception does not simply reflect the activity of the most sensitive neurons [e.g., the lower envelope hypothesis (Parker and Newsome, 1998)]. Instead, several alternatives exist: (1) the system lacks access to the most sensitive neurons; (2) signals from sensitive peripheral neurons are degraded in the process of reaching more central locations (Shadlen et al., 1996); (3) suboptimal pooling of responses occurs in which precise and imprecise neural information is combined. Evidence for the latter has been shown in the IC (Fitzpatrick et al., 1997; Bala et al., 2003; Hancock and Delgutte, 2004).

Behavioral thresholds are often better than neuronal sensitivity (Tolhurst et al., 1983; Purushothaman and Bradley, 2005; Lemon and Smith, 2006). In the IC, sensitivity of neurons to another cue to sound location, interaural time differences (ITDs), falls slightly short of human thresholds (Shackleton et al., 2003; Griffin et al., 2005). Moreover, in LSO neurons, the rate-ILD functions are not invariant to changes in overall sound level at the ears in that a given ILD does not correspond to a fixed discharge rate when measured at different overall levels (Tollin and Yin, 2002; Park et al., 2004). Therefore, for single neurons, threshold ILDs may improve or deteriorate at different sound levels depending on how the rate-ILD functions change (Tsai and Tollin, 2007). Human ILD thresholds, however, are largely invariant to changes in overall sound level (Grantham, 1984; Hartmann and Constan, 2002; Bernstein, 2004). Results such as these suggest some form of response pooling across neurons may be necessary. Because LSO neurons were found to produce low-threshold ILDs over a broad range of frequencies and sound levels comparable with human, cat, and monkey psychophysical abilities, the role of pooling need not be to lower thresholds. Either way, the IC is a potential candidate to pool LSO responses; IC neurons receive excitatory inputs from the contralateral LSO (Glendenning and Masterton, 1983) and the rate-ILD functions of many IC neurons have been shown to be more invariant to overall level changes than LSO neurons (Park et al., 2004). Together, these studies imply that a mismatch between neuronal and behavioral thresholds, regardless of which is better, indicates the presence of response pooling at some point in the system. Proper treatment of pooling schemes for ILD discrimination by LSO neurons is beyond the scope of this study.

The range of ILD cues available to cats are ±20–30 dB (Martin and Webster, 1989). The pedestal ILD, where the highest sensitivity occurred over the population of LSO neurons, spanned a range from −20 to 20 dB without bias for either hemifield. Therefore, the population LSO neurons on one side of the brainstem could potentially encode ILDs that arise from sound sources in both hemifields. This physiological range may be created by differing thresholds of excitatory and inhibitory afferent inputs in different LSO neurons (Reed and Blum, 1990). The range may also be the result of the method by which the ipsilateral-ear SPL was chosen for the measurement of the rate-ILD functions. For the data in this study, the ipsilateral-ear SPL about which the rate-ILD curves were measured was set to the level that yielded approximately the half-maximal discharge rate in the ipsilateral-ear-only rate-level curve. Some aspects of the rate-ILD curves for LSO neurons are not invariant to changes in the ipsilateral-ear sound level (Tollin and Yin, 2002; Park et al., 2004); with increases in ipsilateral-ear level, the rate-ILD curves have larger maximum discharge rates and the curves shift position along the ILD axis typically toward ILDs favoring the ipsilateral ear (Fig. 1A, negative ILDs). Such changes in the rate-ILD functions will likely have some effect on the neural threshold ILDs. However, we found that the specific choice of the ipsilateral-ear-only sound level had little impact on the ultimate threshold ILDs measured from neuron to neuron; threshold ILDs were not correlated with the ipsilateral-ear threshold nor the sound level above ipsilateral-ear threshold or the percentage of ipsilateral-ear-alone maximum response used for the rate-ILD curve measurement. The properties of the monaural ipsilateral-ear-only rate-level functions from neuron to neuron had little bearing on the ultimate binaural ILD acuity, at least over the limited range of these properties examined in this study.

The ability of neurons to convey information is often considered to be limited by their response variability. We found that the diversity of best-threshold ILDs across different neurons was more correlated with rate slope than with rate variance. Shackleton et al. (2005) reported a similar finding for interaural correlation discrimination in IC neurons. Neurons are often thought to be most sensitive to stimulus changes, such as ILD or azimuthal location of sounds, when the change produces responses at the steepest portion of the rate curve. Here, best thresholds were found contralateral to the point of maximal slope. A similar offset in ITD pedestal for ITD discrimination has been reported in the IC (Shackleton et al., 2003). We showed that this result arises from the form of the tuning curve (sigmoidal), the associated rate slope, and the power-law relationship between rate and variance. The best neural acuity does not occur where the rate slope is steepest, but rather where the slope is largest relative to the rate variance, and this point occurs where the rate itself is relatively small. These findings are in agreement with results obtained in different sensory systems with differently shaped tuning curves (Seung and Sompolinsky, 1993; Butts and Goldman, 2006).

Finally, small mammals that hear and localize high-frequency sounds (presumably based on ILDs), like bats, rats, and cats, have well developed LSOs and MNTBs (Irving and Harrison, 1967; Masterton and Diamond, 1973). Conversely, larger mammals that use lower-frequency sounds for localization and communication, like nonhuman primates and humans, tend to have smaller, less-developed LSOs and MNTBs (Harrison and Feldman, 1970; Moore, 2000). The human LSO, although small, has similar neuron morphology and arrangement as has been reported in animals with a well developed LSO (Kulesza, 2007); however, MNTB neurons are either few in number (Richter et al., 1983; Glendenning and Masterton, 1998) (R. J. Kulesza, personal communication) or nonexistent (Moore, 2000; Bazwinsky et al., 2003). So, despite the extraordinary sensitivity to ILDs, human ILD discrimination might be based on a neural circuit that is different from the classical MNTB–LSO circuit. The inhibition to the LSO may come directly from the CN, or the ILD may be computed elsewhere, such as the IC.

Implications for modeling

Our results have implications for modeling. First, for computing neural discrimination thresholds, indices such as d′ or standard separation D, which require only response mean and variance, can be used instead of ROC analysis provided the response distributions are approximately normal. Second, the rate-ILD relationship of LSO neurons may be modeled from a limited set of measurements by fitting a sigmoid-shaped function. Third, response variance was well described by a power function of the mean rate for individual LSO neurons. Fourth, the variance–mean relationship can be simplified by adopting parameters that are generally applicable to a population of LSO neurons. From these assumptions, it is possible to construct a population of model LSO neurons based on physiologically derived ILD tuning functions.

In addition to the anatomic and physiological evidence (see Introduction), we have now found comparable performance between the LSO and psychophysical performance in ILD discrimination, adding additional support to the hypothesis that the LSO is critical to the representation of the ILD cue to sound location. In effect, we believe that the extraction and representation of ILD by LSO neurons sets a lower bound on the perceptual discrimination of ILDs and their use for sound localization.