Urea denaturation by stronger dispersion interactions with proteins than water implies a 2-stage unfolding

Abstract

The mechanism of denaturation of proteins by urea is explored by using all-atom microseconds molecular dynamics simulations of hen lysozyme generated on BlueGene/L. Accumulation of urea around lysozyme shows that water molecules are expelled from the first hydration shell of the protein. We observe a 2-stage penetration of the protein, with urea penetrating the hydrophobic core before water, forming a “dry globule.” The direct dispersion interaction between urea and the protein backbone and side chains is stronger than for water, which gives rise to the intrusion of urea into the protein interior and to urea's preferential binding to all regions of the protein. This is augmented by preferential hydrogen bond formation between the urea carbonyl and the backbone amides that contributes to the breaking of intrabackbone hydrogen bonds. Our study supports the “direct interaction mechanism” whereby urea has a stronger dispersion interaction with protein than water.

Urea, a small hydrophilic molecule, present in all taxa, is a widely used protein denaturant in in vitro unfolding/refolding experiments (1). Despite extensive studies (2–6), it has been difficult to dissect the molecular origin of the denaturation mechanism of urea because the free energy of transfer of globular proteins from water to aqueous urea solution is small. Consequently, there are uncertainties in estimating the contributions that the various groups make to the denaturant-induced destabilization of proteins from experiments alone. Insights into the action of urea come largely from experiments that measure transfer free energies of amino acid side chains and peptide backbone (3, 7). Based on these experiments, 2 different mechanisms have been proposed: an “indirect mechanism” in which urea is presumed to disrupt the structure of water, thus making hydrophobic groups more readily solvated (8–13); and a “direct mechanism” in which urea interacts either directly with the protein backbone, via hydrogen bonds and other electrostatic interactions, or directly with the amino acids through more favorable van der Waals attractions as compared with water (14, 15), or both, thus causing the protein to swell, and then denature. Even within the direct mechanism there is controversy over which of the forces is dominant, electrostatic or van der Waals (7, 16–18).

The “direct electrostatic mechanism” suggests that urea interacts directly with the protein backbone, via hydrogen bonds, and other electrostatic interactions with charged and polar side chains predominantly. This was first proposed by Robinson and Jencks (14) to explain their data on the effects of urea on the solubility of acetyltetraglycine ethyl ester. They postulated that the direct binding of urea to the backbone of this model compound, which has no hydrophobic side chains, best explained the solubility data and that tetramethylated urea acted by an entirely different mechanism. One consequence is that denaturation begins from the outside. However, the “direct van der Waals mechanism” suggests that urea denatures proteins predominantly through its stronger dispersion interactions with the protein than water (18).

Most molecular dynamics (MD) simulations have focused on simple model systems and small peptides for which exhaustive sampling of the conformations can be performed (7, 15–17, 19–23). In the small peptides, almost all of the backbone and the side chains are solvent exposed. As a consequence, the interplay of the interactions between urea and the buried side chains and backbone and the propensity of urea to engage in hydrogen bond formation with solvent-exposed groups cannot be discerned. Therefore, to obtain a structural basis of the denaturation mechanism of urea, it is necessary to perform reliable MD simulations on proteins with well-defined cores.

Very few MD studies have been performed on large proteins in aqueous urea solutions and these have led to qualitatively different conclusions (24, 25). For barnase, only partial unfolding, even at elevated temperatures, was observed, which suggests that more sampling is needed to obtain a clearer picture of the unfolding process. Tirado-Rives et al. (24) found that almost all of the urea molecules in the first shell of the protein were hydrogen bonded to barnase, whereas a subsequent work found that half of the urea molecules were hydrogen bonded with barnase (25). It was asserted that interactions of urea with both hydrophobic and polar groups contributed to the denaturation process. Unfortunately both simulations were of such short duration (0.9–2 ns) that the protein barnase did not unfold even at the elevated temperature of 360 K.

In this article, we use the extensive (μs) MD trajectory of hen egg-white lysozyme in 8 M urea, generated on the massively parallel IBM BlueGene/L computer (26), to analyze the denaturation by urea, which has been observed experimentally (27) and in simulations (26). We find that denaturation occurs predominantly by the direct interactions of urea with the protein via dispersion or van der Waals interactions. The more favorable van der Waals interactions of urea relative to water with both protein backbone and side chains attract urea to the protein surface, which makes urea a “surfactant” that further solubilizes the side chains in water. We also find that urea does not disrupt the water structure or its hydrogen-bonded network [see supporting information (SI) Fig. S2 and related SI Text] because of its interaction with water, and it also does not change much the orientational dynamics of water (see Fig. S3, Table S1, and related SI Text). A kinetic consequence of the direct-interaction model is that urea may intrude into the protein interior before water does at the early stage of denaturation. The “outside-in” action of urea molecules predicts that, in the early stages of protein denaturation, a “dry globule” may be populated transiently before global unfolding.

Results

Lysozyme Unfolds Globally in 8 M Urea.

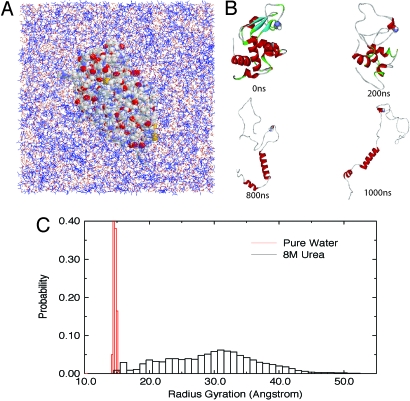
Fig. 1 shows the simulation system (Fig. 1A) and a few snapshots during one representative 1-μs MD simulation (Fig. 1B) in 8 M urea for the W62G single-mutant lysozyme. Here, we use the mutant lysozyme for illustration, because it unfolds more globally in 8 M urea than the wild type (WT). (See Fig. S1 and related SI Text for some comparison between the WT and the mutant. The WT eventually unfolds in 8 M urea too, but with more residual structures (26).) As shown in Fig. 1B, the mutant unfolds and samples highly extended conformations during the 1-μs simulation. A total of 5 independent simulations starting from different initial configurations were performed, with each up to 1-μs duration. Fig. 1C compares the distributions P (R_g) of the radius of gyration (R_g) in water and 8 M urea. The distribution in 8 M urea was obtained over the entire 5-μs simulation, whereas P (R_g) in water was obtained only from the 100-ns simulation, since the protein was fairly stable in the absence of urea [the backbone-rmsd plateaued at 2–3 Å after a 10- to 20-ns simulation, and we had to raise the temperature considerably to 450–500 K to observe complete unfolding in a reasonable time (28)].* Obviously, R_g of the W62G mutant samples a much wider range of values in 8 M urea (as large as 55 Å) than in water (the mutant remains folded with a narrower range of R_g in water). The reasonably fast unfolding kinetics of the lysozyme mutant in 8 M urea is amenable to the microsecond timescales of modern computer simulations and presents us with an opportunity to analyze the denaturation mechanism during the entire unfolding trajectory. In the following, we focus our analysis on the urea–protein interactions by using the W62G lysozyme mutant in 8 M urea.

Fig. 1.

Unfolding of lysozyme in 8 M urea. (A) The solvated system of W62G mutant lysozyme in 8 M urea (the protein is represented by VDW balls, and solvent by wires with urea colored blue). (B) A few snapshots of the mutant lysozyme during 1-μs unfolding simulation (at 0 ns, 200 ns, 800 ns, and 1,000 ns). (C) Comparison of the radius gyration of protein lysozyme in pure water and 8 M urea. (The 8 M urea data are from an aggregate of 5-μs simulations, and the pure water data are from 100-ns simulation only because the protein is fairly stable in pure water at room temperature. See text for more details.)

Urea Displaces Water in the First Solvation Shell (FSS) of the Protein.

The ratio, ρ_W/U, of the number of water to urea molecules in the first solvation shell (FSS, which is defined as any water or urea molecules within 5Å of any protein atoms) decreases from ≈4 to ≈1.8 in the first 25 ns, and fluctuates ≈1.8 at longer times. For comparison, ρ_W/U is ≈4.2 in the bulk. Therefore, the concentration of urea in the FSS of lysozyme increases significantly, by a factor of 2.3, an observation that is consistent with previous studies (16, 29).

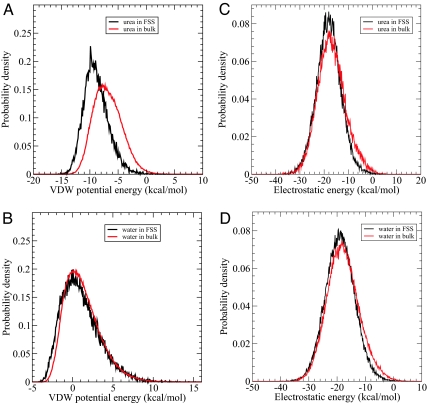
The growth in the fraction of urea molecules in the FSS relative to bulk can be explained from an energetic and structural perspective. First, we computed the van der Waals (VDW) interaction energy between each urea/water molecule in the FSS of the protein and in bulk (defined as 6 Å away from any protein atoms) with the rest of the system. A spherical cutoff of 13.0 Å of the VDW potential was applied in this calculation. Urea in the FSS of mutant lysozyme has a distribution of VDW energy with a sharper peak at lower energy (peaked at ≈−9.6 kcal/mol) than that for urea in the bulk (peaked at ≈−7.6 kcal/mol) (Fig. 2A). In contrast, there is relatively little change in the VDW energy distribution of water in the FSS and bulk in both the peak magnitude and position (Fig. 2B). The difference in the averaged VDW energy for urea in the FSS and in the bulk is −2.04 kcal/mol, whereas for water it is only −0.24 kcal/mol. Thus, accumulation of urea in the FSS might be partially due to the more favorable VDW interaction between urea and protein. We also calculated the electrostatic energy distribution for the urea/water molecule in the FSS and bulk (with no cutoff for the long-range electrostatic interactions). Fig. 2 C and D shows these distributions for both urea and water. Clearly, there is no significant change in the electrostatic interaction energy when a urea molecule moves from the bulk to the FSS, even though the absolute value of average electrostatic interactions is indeed larger than the VDW interactions in both the FSS and bulk regions. The same is true for the water molecules. Therefore, it is the more favorable VDW interactions between urea and protein that drive the urea molecules to the protein surface. This can further be seen from a detailed decomposition of interaction energies of a urea/water molecule in the FSS with the protein only (Table 1). Again, we observe that the electrostatic interaction energy of water with protein is comparable to that of urea with protein in the FSS. However, there is a significant stabilization from the van der Waals interactions with protein when going from water to urea. For example, in the first 10 ns, E_up (urea-protein VDW energy) is lower than E_wp (water-protein VDW energy) by 1.98 kcal/mol [i.e., −2.19 – (−0.21)], with the backbone contributing 0.76 kcal/mol, the hydrophobic side chain 0.22 kcal/mol, and the hydrophilic side chain 0.94 kcal/mol (see Table 1). Therefore, on average, hydrophilic residues have stronger dispersion interactions with urea (−0.92 kcal/mol) than hydrophobic ones (−0.31 kcal/mol). These decomposition results are consistent with the energy distribution analysis shown in Fig. 2. It should be noted that even though each urea displaces 2–3 water molecules in the FSS; on average, each urea is still gaining >1.5 kcal/mol.

Fig. 2.

Interaction energy distribution. (A and B) The probability distribution function of Van der Waals energy of urea (A) and water (B) in the first solvation shell of mutant lysozyme and in the bulk region, respectively, with the rest of system. (C and D) The probability distribution function of electrostatic energy of urea (C) and water (D) in the first solvation shell of mutant lysozyme and in the bulk region, respectively, with the rest of system. The first solvation shell (FSS) is defined as within 5.0 Å of protein and the bulk region is defined as not within 6.0 Å of protein.

Table 1.

The nonbonded energy [van der Waals (VDW) and electrostatic] between protein and each urea/water within 5 Å of protein, which is represented asE_up for urea and E_wp for water

	VDW energy		Electrostatic energy
	First 10 ns	Last 10 ns	First 10 ns	Last 10 ns
Eup	−2.1898	−2.1585	−3.4397	−2.7699
Eub	−0.8931	−0.8194	0.4275	−0.5826
Eunps	−0.3114	−0.5440	−0.0394	−0.0605
Eups	−0.9230	−0.7349	−2.2290	−1.5158
Ewp	−0.2099	−0.2241	−4.0880	−2.7906
Ewb	−0.1278	−0.0996	0.1814	−0.8033
Ewnp	−0.0888	−0.1035	−0.0282	−0.0345
Ewps	0.0210	−0.0081	−3.0143	−1.7998

The decompositions of nonbonded energy between each solvent and backbone, nonpolar side chains and polar side chains, are represented as E_?b, E_?nps and E_?ps, respectively, where ? is u for urea and w for water.

Swelling of Lysozyme Is Linked to an Increase in the Extent of Urea–Backbone Interactions.

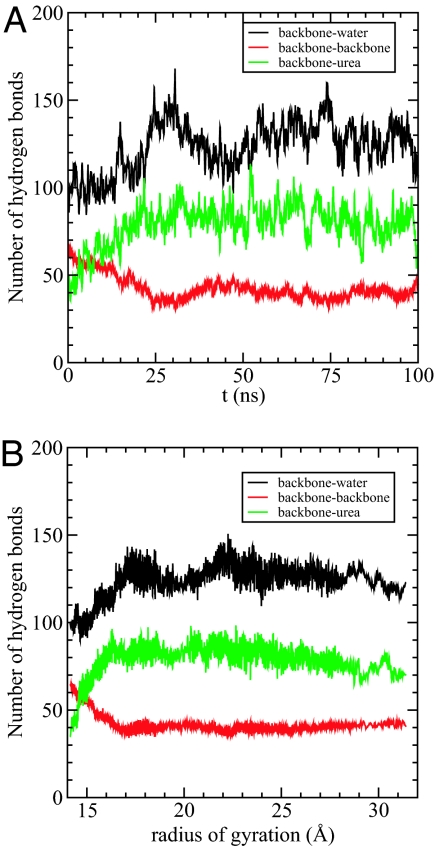
The changes in the numbers of hydrogen bonds formed between the protein backbone (B) with water (N_BW) and urea (N_BU) with time (t) (Fig. 3A) and the radius of gyration, R_g, of the protein (Fig. 3B) illustrate the events in the urea-induced swelling of the protein. The number of intraprotein hydrogen bonds, N_BB, decreases most rapidly in ≈35 ns, which results in an increase in R_g (Fig. 3). On the timescale during which R_g increases from its the native value to 17 Å, N_BU increases from ≈40 to ≈85. In the earliest stages (t ≈ 10 ns) when there is a large increase in N_BU (Fig. 3A) N_BW is approximately constant (Fig. 3A). Only after urea penetrates the lysozyme protein, thus disrupting the structure sufficiently, does water penetrate the interior (see the increase in N_BW after 10 ns in Fig. 3A). These results suggest a 2-stage kinetic mechanism for the action of urea. In the first stage, an increase in the urea–backbone interaction results in the swelling of the protein. Subsequently, water also invades the protein interior although its density around the protein is diminished relative to the bulk value.

Fig. 3.

Hydrogen bonds with backbone. (A) The number of hydrogen bonds formed between backbone and water (black), between backbone and backbone (red), and between backbone and urea (green), respectively, as a function of time. (B) The number of hydrogen bonds as a function of the radius of gyration of the mutant lysozyme. Black is for backbone–water hydrogen bonds, red is for backbone–backbone hydrogen bonds, and green is for backbone–urea hydrogen bonds.

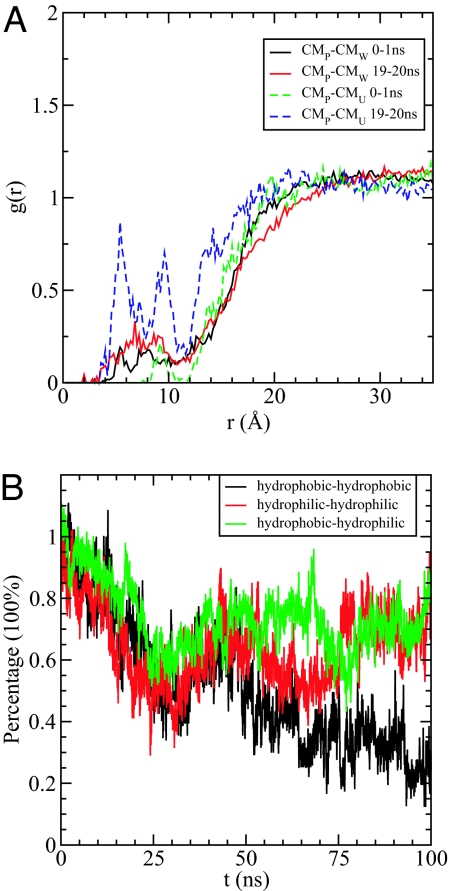
The competition between urea and water for lysozyme can also be illustrated through the time dependence of the number of contacts between hydrophobic side chains and urea/water [a contact is defined when any atom of solvent, urea or water, is within a given cutoff (6.0 Å) of any atom of a hydrophobic side chain]. During the first 20 ns, the number of contacts between urea and the hydrophobic side chains increases by a factor of 2.3, whereas no significant change is observed in the number of such contacts for water even though the exposed nonpolar surface-accessible area increased from ≈1,200Ų to ≈2,000 Ų (see Fig. S1). Therefore, urea makes favorable contacts with hydrophobic residues and seems to enter the protein before water on the exposure of hydrophobic side chains. In addition, the calculated radial distribution functions, between the center of mass (COM) of the protein and the COM of urea and water, show that the concentration of urea increases much faster than water within the core of the protein (≈20 Å from COM), indicating that urea intrudes into the protein ahead of water, as shown in Fig. 4A. Urea molecules can subsequently act as “surfactant” to further solubilize the side chains in water. The surfactant urea molecules can hydrogen bond to water and thereby stabilize the further disaggregation of the hydrophobic groups.

Fig. 4.

Dry globule formation. (A) The radial distribution functions g(r) between the center of mass (COM) of the protein and the COM of urea and water in the first 1 ns and 19th ns (19–20 ns). It clearly shows that the concentration of urea increases much faster than water within the core of the protein (≈20 Å), indicating that urea might intrude into the protein ahead of water. (B) The time dependence of the percentage of the initial backbone–backbone hydrogen bonds formed by the residue pairs of hydrophobic–hydrophobic (black), hydrophilic–hydrophilic (red), and hydrophobic–hydrophilic (green), respectively.

It is also interesting to do a detailed analysis of intrabackbone hydrogen bonds by decomposing them into 3 categories in terms of the hydrophobicity of the residue side chains: hydrophobic–hydrophobic, hydrophobic–hydrophilic, and hydrophilic–hydrophilic side chains. As shown in Fig. 4B, all 3 types of backbone–backbone hydrogen bonds decrease at the same rate in the first 30 ns. Subsequently, only the hydrophobic–hydrophobic backbone hydrogen bonds persistently decrease from ≈60% to ≈20%, whereas hydrophobic–hydrophilic, and hydrophilic–hydrophilic backbone hydrogen bonds, fluctuate around their average values. The depletion of hydrophobic–hydrophobic backbone hydrogen bonds provides further insight into unfolding. After the mutant lysozyme is structurally loosened, its hydrophobic core is solvent-exposed resulting in the disruption of the backbone–backbone hydrogen bonds involving the hydrophobic residues. Eventually, further disruption spreads to other types of backbone–backbone hydrogen bonds.

Direct Interaction Between Urea and Protein Disrupts the Folded Structure of Lysozyme.

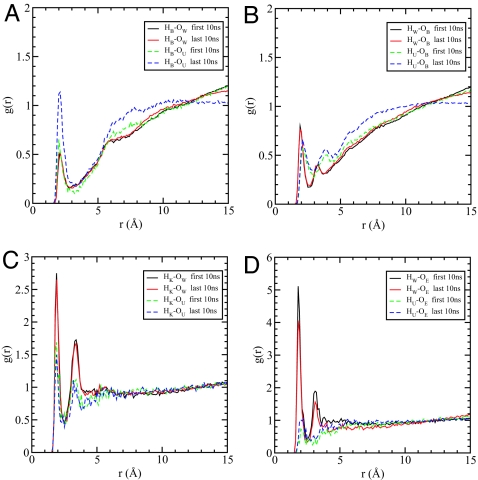
To probe the structural changes due to the electrostatic interactions between urea and protein, we calculated a number of atomic radial distribution functions [g(r)] of urea atoms with both the peptide groups and the charged side chains. The time-dependent changes in the g_OUHB(r) between the carbonyl oxygen (O_U) of urea and the backbone amide hydrogen (H_B) provides a kinetic scenario for urea-induced destabilization of lysozyme (Fig. 5A). The magnitude of the first peak of g_OUHB(r) fluctuates in the range of 0.65–1.55 at different times that is suggestive of conformational changes due to urea. Fig. 5 (a) shows g_OUHB(r) and g_OWHB(r) in the first 10 ns and in the last 10 ns.

Fig. 5.

Radial distribution functions. (A) The pair radial distribution function g(r) between backbone amide hydrogen H_B and water oxygen O_W (solid), as well as urea oxygen O_U (dash). (B) The pair radial distribution function g(r) between backbone carbonyl oxygen O_B and water hydrogen H_W (solid), as well as urea hydrogen H_U (dash). (C) The pair radial distribution function g(r) between positively charged lysine side-chain hydrogen H_K and water oxygen O_W (solid), as well as urea oxygen O_U (dash). (D) The pair radial distribution function g(r) between negatively charged glutamic acid side-chain oxygen O_E and water hydrogen H_W (solid), as well as urea hydrogen H_U (dash). All of the g(r) functions are averaged over the first 10 ns (black, green) and the last 10 ns (red, blue) of total 100 ns, respectively.

There are many more ordered urea oxygen atoms near H_B in the last 10 ns than in the first 10 ns, but almost no change is found for water oxygen around H_B. The results show that urea forms hydrogen bonds more tightly with the protein backbone than water. The preferential binding of O_U to the amide proton of the peptide backbone is the primary mechanism by which urea disrupts the native backbone–backbone hydrogen bonds, and hence, the folded structure. To further examine the extent of hydrogen bonding between urea and the protein, we also calculated g_HUOB(r) and g_HWOB(r), where H_U and O_B are, respectively, the amide hydrogen of urea and the carbonyl oxygen of the peptide group. The results for the first and the last 10 ns, given in Fig. 5B, shows that water solvates O_B slightly better than urea, but the concentration of urea around O_B increases with time, whereas the concentration of water is almost unchanged during the last 10 ns. We also find that H_U does not form as strong a hydrogen bond as H_W does with O_B, largely because the NH in urea forms weaker hydrogen bonds in general (see SI Text) (30, 31). The paucity of water molecules near the peptide rules out any significant role in its ability to destabilize the backbone hydrogen bonds.

To investigate whether the solvation of the charged side chains by urea plays an important role in the denaturation of the mutant, we also analyzed the solvation of both lysine (K) and glutamic acid (E) side chains. As shown in Fig. 5C, the positively charged side-chain hydrogens (H_K) of K are well solvated by both urea and water, but the extent of solvation by water is greater than that by urea. The solvation of the negatively charged side-chain oxygens (O_E) of glutamic acid by urea is greatly decreased compared with that of H_K. In contrast, water interacts strongly with the side chain of E (Fig. 5D), which is in accord with a previous study that showed that negatively charged methane is preferentially solvated by water (17). Thus, water can solvate the charged residues better than urea, indicating that urea's effect in the unfolding of the mutant is not mainly due to the solvation of the charged side chains.

Enhanced Solubility of Nonpolar Residues in Urea Also Promotes Denaturation.

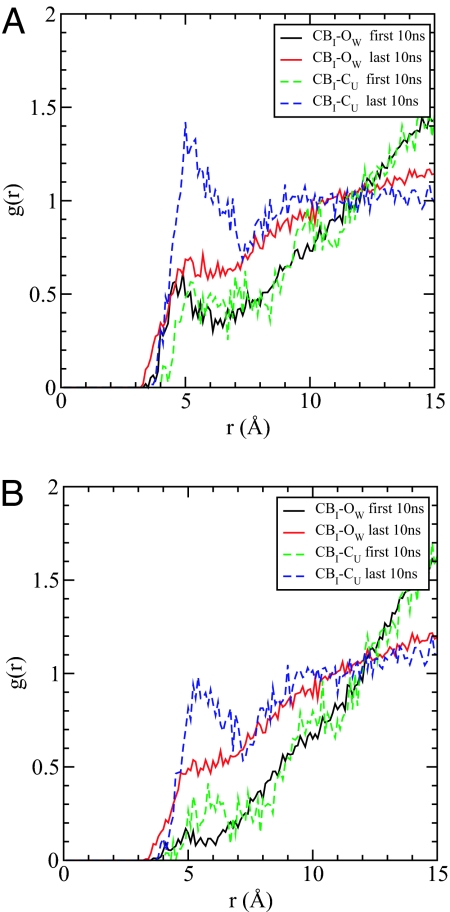
The denaturation of lysozyme by urea involves the disruption of hydrophobic interaction as shown by the increase of the solvent-accessible surface area (SASA) of nonpolar groups (data shown in SI Text). It is known that the solubility of isolated hydrophobic side chains is increased in aqueous urea solution (3), and hence, we expect that the interactions with hydrophobic side chains must also contribute to some extent to the unfolding of proteins. We probed the interaction between urea and hydrophobic side chains by using radial distribution functions between the β-carbon of ILE and the O_W of water and C_U of urea. The concentration of urea around ILE side chains increases in the last 10 ns relative to that in the first 10 ns and relative to the bulk value. In contrast, the water distributions near ILE side chains were found to be more or less the same in the first 10 ns and the last 10 ns, with the hydration in the last 10 ns slightly better than that in the first 10 ns, because the protein is more stretched or expanded (Fig. 6A). We have shown that urea preferentially forms hydrogen bonds with the peptide backbone; thus, it is expected that some of these urea molecules would be in close proximity to the hydrophobic side chains. We recalculated the radial distribution functions by excluding urea molecules that form hydrogen bonds with the backbone (Fig. 6B). Similar results were obtained except that the heights of the first peaks were diminished. That urea has more favorable interactions with the hydrophobic side chains seems to explain the increase in solubility of the hydrophobic side chains in 8 M urea. These results are in agreement with previous transfer experimental studies (8, 32, 33). Although the interactions between the hydrophobic side chains and urea are relatively weak, they are important enough that urea can disrupt aggregates of hydrophobic particles even in the absence of any favorable electrostatic interactions.

Fig. 6.

Enhanced solubility of nonpolar residues. (A) The pair radial distribution function g(r) between the β-carbon of isoleucine CB_I and center of mass of solvent, represented by oxygen atom of water O_W and carbon atom of urea C_U. (B) The same as A, except that urea or water that forms hydrogen bonds with backbone is excluded in the calculation of g(r). All of the g(r) functions are averaged over the first 10 ns (black, green) and the last 10 ns (red, blue) of total 100 ns, respectively.

Discussion and Conclusion

In a previous report we showed, by using a large-scale MD simulations (28), that both the WT and the less stable single-mutant (W62G) hen egg-white lysozyme unfold in 8 M urea within 1 μs simulation. Here, we have used data from these large-scale MD simulations to provide a structural and a kinetic picture of the denaturation mechanism of proteins by using the mutant as a case study. Urea-induced protein denaturation proceeds through a 2-pronged attack in which urea preferentially binds to the protein with which it has stronger van der Waals dispersion interactions than does water (dominant force), thus allowing urea to act as a surfactant; its carbonyl oxygen can form an intimate hydrogen bond with the amide proton of the backbone. The ability of urea to form hydrogen bonds with proteins can be rationalized by noting that urea can be a surrogate for the peptide backbone. As argued by Kuharsky and Rossky (20), there may be a favorable free energy of exchange of several geometrically restrained hydration shell water molecules for one larger urea molecule near a hydrophobic surface. Our results, which provide a molecular basis for the denaturating action of urea, have previously been inferred primarily based on studies of model compounds and peptides. With this study, the validity of the direct-interaction model, which has its genesis in the early study of Robinson and Jencks by using peptides lacking hydrophobic side chains, has been firmly established.

The present study also gives a kinetic view of how denaturation occurs. Our work suggests a 2-stage process by which urea denatures proteins. In the first step, urea displaces the water molecules within the first solvation shell of the protein that allows it to bind tighter with protein surface through more favorable dispersion interactions and form strong hydrogen bonds with the peptide backbone. Urea, in principle, can form 6 hydrogen bonds (involving both its carbonyl oxygen and the 4 amide hydrogens), but only the carbonyl oxygen engages in strong electrostatic interaction with the amide protons of the peptide backbone (see SI Text). In the second kinetic stage, urea and water solvate the exposed hydrophobic, polar, and charged residues. Because during the unfolding process the increase in accessible surface area is the largest for the hydrophobic residues, these hydrophobic residues exhibit the most drastic changes (Fig. 6).

The “outside-in” action (15, 34), in which interactions with the peptide backbone are followed by solvation of the side chains in aqueous urea, leads to a prediction concerning the nature of plausible intermediates along the unfolding pathway. In the first stage we propose that an ensemble of native-like intermediates should form. In such structures, in which the protein core is largely undisrupted, urea preferentially interacts with the peptide backbones and the exposed side chains. Because of the limited lifetimes of the ensemble of such structures, they may be hard to determine experimentally. The ensemble of the intermediate structures can be termed “dry globules” in which there is a paucity of water molecules near the protein but with the enhanced presence of urea in the FSS. The formation of dry globule is largely a consequence of the direct-interaction model and cannot be predicted by using the “indirect hydrophobic” mechanism. The dry globule globally unfolds in the second stage driven by both favorable interactions of urea with the peptide backbone and the side chains. Interestingly, this dry globule was also found in a recent simulation of γ-D crystalline in 8 M urea solution (data not shown).

Although we find that the preferential interaction of urea is the predominant force driving urea-induced unfolding, it should be emphasized that the solubility of hydrophobic residues is also enhanced in aqueous urea. It follows that urea can unfold collapsed globules of homopolymer chains made of purely hydrophobic monomers (methyl methacrylate, for example). In accord with this expectation, it has been shown that, at high urea concentrations, a hydrocarbon chain would unfold and nanoscale graphene plates would dissociate (R. Zangi, R.Z., and B.J.B., unpublished data). These examples illustrate that the cooperative nature of urea-induced unfolding is most evident because there are only small changes, at pairwise level, that is, in interaction between 2 methane molecules (17).

Methods

Choice of Proteins.

Most of the simulations were performed by using the mutant, W62G, of hen lysozyme, which consists of 2 domains. The α-domain runs from residues 1–35 and 85–129, whereas the β-domain comprises residues 36–84. Lysozyme has 4 α-helices [helix A (5–14), helix B (25–36), helix C (90–100), and helix D (110–115)], 2 β-strands [strand 1 (43–46) and strand 2 (51–54)], a loop (60–78) region, and a 3₁₀-helix (81–85) (Fig. 1). The mutant W62G unfolds to a greater extent in urea than the WT; hence, we focused on it to elucidate the nature of urea–protein interactions. The starting structure for the WT was taken from the Protein Data Bank (PDB ID code 193L), and the initial coordinates for W62G were obtained by replacing Trp by Gly.

Urea-Induced Unfolding.

We followed a variant of a previously used method (25) to initiate the simulations. Thirty urea molecules were randomly placed (without clashes) in an equilibrated 18.6 Å × 18.6 Å × 18.6 Å box containing 216 water molecules. If any urea molecule overlaps with other urea molecules, it will be replaced by another randomly distributed one. We removed water molecules if the distance between the water oxygen, O_W, atom and urea heavy atoms was <2.7 Å. Our procedure generated a box of 30 urea and 128 water molecules, which was equilibrated for a 100-ps NVT simulation at 310 K. The resulting small water–urea box was periodically replicated to generate a box of 74.4 Å × 74.4 Å × 74.4 Å that contained 1,920 urea and 8,192 water molecules. We further equilibrated the urea–water sample for 10 ns by using the NPT ensemble at 310 K and 1 atm. The final box was 73.1 Å × 73.1 Å × 73.1 Å, corresponding to an approximate urea concentration of 8 M urea, and a density of 1.12 g/cm³.

On inserting the protein in the equilibrated 8 M urea box, we removed those water and urea molecules if the distance between O_W and any heavy protein atom was <2.7 Å, or if the distance between any heavy atom of urea and protein was <2.4 Å. The final molecular system consisted of 1 lysozyme centered in the box with 7,793 water and 1,809 urea molecules at neutral pH. Eight Cl⁻ counter ions were added to neutralize the solvated system, giving a total system size of ≈40,000 atoms. Protein in 8 M urea was further equilibrated for an additional 10 ns.

For the WT and W62G systems, we generated 5 trajectories, each up to 1-μs duration, at 310 K and 1 atm. Simulations were performed by using the NAMD2 molecular dynamics program (36) with the CHARMM force field (37) for lysozyme and the solvent urea. A slightly modified TIP3P water model (35, 38) was used for water.