Genome annotation in the presence of insertional RNA editing

Abstract

Motivation: Insertional RNA editing renders gene prediction very difficult compared to organisms without such RNA editing. A case in point is the mitochondrial genome of Physarum polycephalum in which only about one-third of the number of genes that are to be expected given its length are annotated. Thus, gene prediction methods that explicitly take into account insertional editing are needed for successful annotation of such genomes.

Results: We annotate the mitochondrial genome of P.polycephalum using several different approaches for gene prediction in organisms with insertional RNA editing. We computationally validate our annotations by comparing the results from different methods against each other and as proof of concept experimentally validate two of the newly predicted genes. We more than double the number of annotated putative genes in this organism and find several intriguing candidate genes that are not expected in a mitochondrial genome.

Availability: The C source code of the programs described here are available upon request from the corresponding author.

Contact: bundschuh@mps.ohio-state.edu

1 INTRODUCTION

RNA editing is a process in which RNA molecules are modified through replacement, insertion or deletion of individual bases. RNA editing occurs in many different organisms from humans to plants and viruses. The mechanisms of RNA editing are diverse and in many cases not very well understood (Horton and Landweber, 2002; Keegan et al., 2001; Smith et al., 1997).

In organisms with insertional or deletional RNA editing, DNA sequence annotation is complicated. In the absence of insertional and deletional RNA editing, protein-coding genes can be identified as long stretches without a stop codon in one of the three frames with statistical properties reflecting the codon usage of the organism. However, in organisms with insertional or deletional RNA editing only the (unknown) edited messenger RNA has these properties. When only the genomic sequence is known, each insertional (or deletional) editing event appears as a frame shift. Thus, it is considerably less obvious where protein-coding genes are located within a genome and in which frame a portion of a gene should be read, i.e. what the amino acid sequence of a gene product actually is. Thus, traditional approaches to genome annotation fail in these organisms.

One organism with extensive insertional RNA editing is the slime mold P.polycephalum. In this organism, all known mitochondrial genes are edited including the structural RNAs. By far, the most frequent editing event is the insertion of single Cs. It occurs on average every 25 nt in mRNAs and on average every 40 nt in the structural RNAs (Gott, 2001; Horton and Landweber, 2002; Smith et al., 1997). It has been shown in vivo that editing is extremely reliable (Visomirski and Gott, 1995), i.e. that nearly every transcript is completely edited at exactly the correct positions. There is very little known about the mechanism by which editing sites are recognized and utilized.

The difficulty of annotating genomes in the presence of insertional RNA editing can be appreciated by noting that in the mitochondrial genome of P.polycephalum the editing sites of only 11 (Gott et al., 2005) genes are experimentally known and the approximate locations of another eight genes have been annotated (Takano et al., 2001). This should be compared to 42 known protein-coding genes in the mitochondrial genome of Dictyostelium discoideum, which is of similar length (Ogawa et al., 2000). The difference between these two numbers leads to one of two conclusions: (i) large parts of the mitochondrial genome of P.polycephalum are void of genes (a quite unlikely scenario given that mitochondrial genomes usually have their genes closely packed) or (ii) the apparently void regions contain genes that are obscured to common genome annotation methods by the need for RNA editing.

Here, we show how the number of predicted, annotated genes in the mitochondrial genome of P.polycephalum can be approximately doubled by using genome annotation methods that are specifically designed to take insertional RNA editing into account. In addition to finding known mitochondrial genes with comparative gene-finding approaches, we corroborate these findings and detect some unexpected putative genes with a broader comparative and a de novo gene finding method. As a proof of concept, we experimentally verify two of the newly predicted mitochondrial genes.

2 METHODS

In order to find novel putative genes in the mitochondrial genome of P.polycephalum we apply three different computational approaches. These approaches differ in their tradeoff between sensitivity and ability to discover unexpected genes. Here, we describe the three approaches as well as the experimental methods used to verify the computational predictions. The computational results are discussed and compared in the next section.

2.1 Comparative gene finding by model building

The most sensitive, but also the most laborious and computationally intensive method we use is our previously developed PIE (predictor of insertional editing) algorithm (Bundschuh, 2004). Due to its requirements of computational and manual effort, we can apply PIE only to a select group of genes that are expected to be found in a mitochondrial genome. Thus, PIE is not able to find completely new types of genes.

PIE has been presented in detail elsewhere (Bundschuh, 2004, 2007; Gott et al., 2005). Nevertheless, we include here a short overview over PIE for the sake of completeness. We start by choosing a mitochondrial gene that we want to identify in the genome. We then choose a protein sequence for this gene from another organism and use PSI-BLAST (Altschul et al., 1997) to build a multiple alignment and a corresponding position-specific scoring matrix (PSSM) characterizing this gene.

This PSSM together with the default BLAST (Altschul et al., 1997) protein gap initiation and extension costs of 11 and 1 are used to construct a standard hidden Markov model (HMM; Hughey and Krogh, 1996) for the protein family of interest. This protein HMM is converted into an HMM that scores DNA instead of protein sequences by replacing every amino acid emitting state in the protein HMM by a whole sequence of states that emit DNA bases according to the codons corresponding to the amino acids. Lastly, insertional editing is included by adding a silent ‘editing’ node in parallel to every node that emits a C. The transition probabilities for such editing nodes are reduced by an insertion penalty that reflects the overall frequency of editing. Taking into account observed preferences for the sequence pattern immediately upstream of editing sites, this insertion penalty is less severe if the inserted C follows a purine–pyrimidine combination. Specifically we use a penalty of α=6 for the purine–pyrimidine combinations and β=12 for the other cases if expressed in the same units as the amino acid gap costs. These parameters have been determined to perform optimally on genes with known editing sites (Bundschuh, 2004). The final model is matched against genomic sequences from the mitochondrial genome of P.polycephalum via the Viterbi algorithm for HMMs.

In practice, we divide the mitochondrial genome of P.polycephalum into overlapping pieces of 1260 bases each. We apply the Viterbi algorithm to the forward and to the reverse sequence of each of the pieces of the genome and collect all the scores. If one of these scores is much higher than the others, we denote the gene as putatively identified. In this case, the beginning and the end of the local alignment between the edited version of the high scoring segment of the mitochondrial genome and the PSSM is reported as the location of the gene. We apply this procedure to every gene on the list of standardized names for mitochondrial genes (http://megasum.bch.umontreal.ca/gobase/gene_and_prod.html) with the exception of the genes that have been identified experimentally or are already annotated in the GenBank entry of the mitochondrial genome (Takano et al., 2001).

2.2 Comparative gene finding by database searches

The first approach described above can only be applied to a small set of known mitochondrial genes. This approach is very sensitive. However, it is by design not able to find any new genes. In the second approach, we look for new genes by systematically comparing the mitochondrial genome of P.polycephalum to every protein in the non-redundant protein database.

To this end, we use the Smith–Waterman algorithm (Smith and Waterman, 1981) modified to include C insertions during alignment. Such an algorithm was first introduced to detect mitochondrial genes with U insertional RNA editing (von Haeseler et al., 1992). We adapt this algorithm to suit the C insertions in the mitochondrial genome of Physarum. The main idea of the algorithm is that it matches parts of the genomic DNA sequence against the amino acids in a protein sequence. In the absence of editing, this match is between three consecutive bases in the DNA sequence and one amino acid in the protein sequence. The score of a match is determined by translating the three bases into an amino acid using the genetic code and then comparing this amino acid to the amino acid in the protein sequence using one of the standard amino acid scoring matrices. In addition, matches between two consecutive bases and an amino acid are possible in the presence of C insertional editing. In such matches a putatively inserted C is added at the beginning, in between or after the two bases and all three possible codons are translated and scored against the amino acid in the protein sequence.

Formally, the algorithm compares an amino acid sequence a₁…a_M and a genomic DNA sequence b₁…b_N with each other. It uses as an intermediate quantity the score S_i,j of the optimal comparison between a₁…a_i and b₁…b_j. In the easier case of a linear gap cost, this score fulfils the following recursion equation:

(1)

Here, δ is the linear amino acid gap cost, is the match score for comparing amino acid a with the amino acid resulting from translating the codon 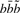via the genetic code and 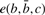is the editing cost for a C insertion in codon position c following the bases . In practice, we use the BLOSUM62 scoring matrix (Henikoff and Henikoff, 1992) for the amino acid comparisons and an affine gap cost with gap initiation and extension penalty 11 and 1, respectively. For the editing cost 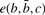we use two terms. As in PIE we use an editing penalty α if 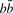is a purine pyrimidine and β if not. To capture an additional feature of C insertions, we add to this a score that takes into account the known preference of C insertions for the third codon position (Mahendran et al., 1991). Specifically, the additional score is γ × (0.3/1.1/−0.65) for C insertions at the 1st/2nd/3rd codon position, respectively, where the numbers are determined as log(f_i/(1/3)) from the observed frequencies f_i of unambiguous C insertions at codon position i in the genes with known editing sites. The parameter γ controls the weight of the codon position score.

The values of the three parameters are determined through optimizing the performance of this algorithm. The performance is judged by the percentage of the correctly predicted amino acids and editing positions for the 11 mitochondrial genes of Physarum with experimentally known editing sites (atp8, atpA, cox1, cox2, cox3, cytb, pL, nad2, nad4L, nad6 and nad7). During optimization, we sweep through the parameter space, but avoid false positive errors from overpredicting the frequency of C insertions by accepting only parameter choices in which about one in every 25 bases is edited on average. Besides, we disallow combinations of the parameters that drive the alignment with random sequences into the linear regime (Waterman et al., 1987), where the maximal alignment score does not follow the Gumbel distribution in order to be able to later assess the statistical significance of our hits. As a result, the parameter values α=8, β=14 and γ=2 give the most accurate prediction of amino acids and editing sites.

We then apply this algorithm to every protein sequence in the non-redundant protein database. The score Σ=max_i,j{S_i,j} is a measure of the similarity of a putative edited gene in the mitochondrial genome and the database protein. For proteins with appropriately large scores Σ, we report the position of the corresponding local alignment as a putative gene together with the accession number of the protein sequence that resulted in the hit. If more than one protein sequence with the same annotation in the non-redundant protein database results in a hit at the same position in the mitochondrial genome, only the most significant one is reported.

2.3 Significance assessment

Both comparative approaches classify matches between the mitochondrial genome and a PSSM or a single protein sequence, respectively, by a score and report high scoring matches as putative genes. In order to select the correct score threshold for reporting a putative gene, an analysis of the statistical significance of the observed high score is necessary.

Since both comparative approaches are essentially local alignment tools, the distribution of scores Σ on random data is expected to be a Gumbel or extreme value distribution (Gumbel, 1958)

(2)

where M and N are the lengths of the PSSM or protein and the genomic sequence, respectively, and K and λ are parameters that depend on all the scoring parameters and the statistical properties of the sequences under investigation.

For the first approach, we generated 1000 random DNA sequences of length N=600 each. Since, it is well known that genomic sequences show a high degree of correlations, we generated these random sequences with the help of a third-order Markov model. The transition probabilities of this Markov model were directly determined from the actual frequencies of all possible base quartets in the mitochondrial genome of P.polycephalum. The order of the Markov model was chosen to be three, since this is on the one hand a minimum number needed to represent the correlations imposed by the genetic code (note that typically a very large fraction of mitochondrial genomes is protein-coding) and on the other hand the frequencies of a higher order model could not be reliably estimated any more due to the limited size of the mitochondrial genome. For each gene in question, we calculated the PIE-score for the given PSSM and each of the 1000 random sequences and their reverse complements, verified that these PIE-scores were indeed distributed according to an extreme value distribution, and estimated the parameters λ and K. These parameters were then used to assign a P-value to the observed score.

For the second approach, the genomic sequence is fixed and the protein sequence is variable. Thus, we randomly generate 250000 protein sequences of length 2000 according to the Robinson–Robinson amino acid frequencies (Robinson and Robinson, 1991) for the alignment with the mitochondrial DNA sequence of Physarum in which the genomic regions of the 11 known genes were deleted. By fitting the resulting distribution of scores with the Gumbel distribution we estimate the parameters λ and K. In order to obtain the P-value, we set M=48 359 as the length of the mitochondrial DNA (excluding the known genes) and N as the total sequence length in the non-redundant protein database with its about 3.7 million sequences, which is about 1.3 billion bp.

For proteins deemed statistically significantly similar to a putative gene in the Physarum mitochondrial genome, this apparent statistical significance can be caused by the low GC content of the mitochondrial genome of Physarum that leads to high scores for comparisons to other proteins encoded by AT rich genomes simply on the basis of the amino acid composition. To filter this GC effect, we in addition randomly shuffle the protein sequences with a significant initial score 1000 times and obtain a p_GC-value based on the distribution of the scores of the shuffled sequences again by fitting to Equation (2). Only matches with a sufficiently small p_GC-value are reported as putative genes.

2.4 De novo gene finding

Our comparative gene-finding approaches can only find genes related to known genes. In order to eliminate this restriction and in order to cross-check the predictions of the comparative gene-finding approaches, we also apply a de novo gene-finding method.

In the absence of RNA editing, very sophisticated gene-finding tools have been developed based on HMMs (Burge and Karlin, 1997; Hughey and Krogh, 1996; Lukashin and Borodovski, 1998; Snyder and Stormo, 1995). Here, we use the same basic approach and adapt it to the case of insertional RNA editing.

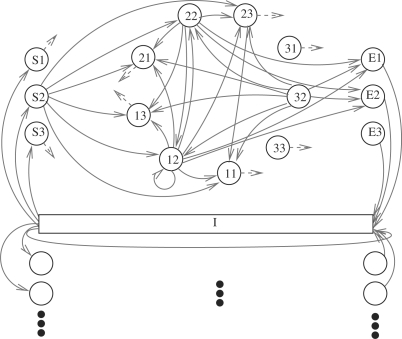
Our HMM that is inspired by the HMM used by GENSCAN (Burge and Karlin, 1997) is shown in Figure 1. Due to the relative simplicity of the known mitochondrial genes of Physarum we do not explicitly model UTRs and introns, and focus on intergenic and protein-coding regions. Intergenic regions are modeled by a single state (I in the Fig. 1) that emits individual bases. The state for intergenic regions can either transition to itself and emit another intergenic base, to the beginning of a gene in the forward strand, or to the end of a gene in the reverse strand. Since genes in the forward and reverse strand are modeled identically, we will discuss in the following only genes in the forward strand. All states describing genes are modeled with an explicit length distribution and emission probabilities. Each state describes the complete coding sequence of the gene from one editing site to the next. Because the emission probabilities of bases within a protein-coding region strongly depend on the codon position, our HMM has to explicitly keep track of the codon positions of the editing sites. Thus, there are three possible states to start a gene with (S1–S3 in Fig. 1), one for each codon position of the final base of the sequence stretch represented by the state. Similarly, there are three states to end a gene with (E1–E3 in Fig. 1), namely one for each codon position of the first base after the last editing site of the gene. In addition, nine intermediate states represent the stretches of a gene from one editing site to the next, one for each combination of codon positions of the first and of the last base of the stretch. In this architecture, the editing sites themselves correspond to the transitions from one state to another. For example, a transition from a state (beginning or intermediate) that ends on the second codon position into a state (intermediate or ending) that begins on the first codon position corresponds to a single nucleotide insertion with the inserted nucleotide at the third codon position. In the same way, a transition from a state ending on the second codon position into a state beginning on the second codon position, corresponds to a dinucleotide insertion. Transitions from a state ending in the second codon position to a state beginning in the third codon position (and the other two analogous transitions) are not allowed.

Fig. 1.

HMM for de novo gene-finding in the presence of insertional RNA editing. The model contains an intergenic state I and various protein-coding states that denote pieces of the gene beginning and ending at well-defined codon positions. States S1, S2 and S3 represent protein-coding genes beginning from the start codon and ending at a nucleotide at the first, second and third codon position, respectively. Similarly, the states E1, E2, E3 represent protein-coding states that begin with a nucleotide at the first, second and third codon position, respectively, and end with a stop codon. The remaining states are indexed by the codon positions of their first and last nucleotide. A transition between protein-coding states corresponds to an editing insertion event. In order to keep the figure more legible, the states for genes in the reverse strand are only vaguely indicated at the bottom. In addition, only transitions from protein-coding states ending in the second codon position are shown. All states with a dashed arrow have the corresponding transitions, which have been suppressed.

In order to model the emissions of all protein-coding states, we again use a third-order Markov model. Since the two nucleotides just before an editing site are known to have specific patterns, we explicitly model the joint probabilities of the three bases at the end of each state. Then, the emission probability for the fourth base from the end is determined from the three bases following it via a Markov model the transition matrix of which depends on the codon position of this fourth base. Then, the fifth base from the end is emitted depending on the second to fourth base to the end and so on. The first three bases of a beginning state are required to be a start codon and the last three bases of a final state are required to be the TAA stop codon, since all known mitochondrial genes in the Physarum mitochondrial genome end with this stop codon.

The transition and emission probabilities of the HMM are trained on the 11 genes in the Physarum mitochondrial genome with experimentally known editing sites. Due to the scarceness of training data, all transition probabilities that represent dinucleotide insertions are chosen equal independently of the codon position. The transition probabilities that correspond to single nucleotide insertions are chosen to depend only on the codon position and not on the specific pair of states the transition takes place between. The average number of editing sites per gene in each codon position globally determines the ratio of the transition probabilities for transitions out of an intermediate state into a final state relative to those into another intermediate state. Taking into account the very few instances where neighboring genes have been experimentally verified, we set the transition probabilities for transitions from the intergenic state such that the average length of an intergenic region is 10 bases.

The length distributions for starting, intermediate and final regions were determined separately, but independently of the respective codon positions. Because the data were too sparse to estimate a full distribution, we determined the histogram of the lengths of all regions between two consecutive editing sites and smoothed this histogram by taking a running average with a window size of 10 bases. In addition, we used the observation that editing sites never occur any closer than nine bases from each other and set the probability for intermediate stretches of length less than nine to zero.

The emission probabilities of the intergenic state were chosen according to the observed nucleotide frequencies of the whole mitochondrial genome. For the emission probabilities of the starting, intermediate and final protein-coding states, we measured the base triplet distributions of the last three bases preceding an editing site independently for each codon position. In addition, we estimated one third-order Markov model transition matrix for each codon position that describes the dependence of a base in a protein-coding region on the three bases following it using the bases in every non-edited codon in the 11 reference genes.

After training all the parameters, we applied the resulting model via the Viterbi algorithm to the complete mitochondrial genome of P.polycephalum. This yielded a set of predictions for genes and their editing sites. In order to identify these genes, we searched the predicted messenger RNA sequences against the non-redundant protein database with BLASTX (Gish and States, 1993).

2.5 Experimental validation

In order to experimentally validate the computational predictions, two of the putative genes (atp6 and nad9) were chosen and their editing sites predicted with the PIE algorithm as described previously (Bundschuh, 2007; Gott et al., 2005). Based on these predictions the following oligonucleotide primers were designed:

• 1atp6: AGAATTCAATATAACTCGTATTACAGC;

• 2atp6: AGAATTCTTTATGGTTATTACCTTTATTAA;

• 3atp6: TTTGCAAATAAACGAAGACC;

• 4atp6: GTATTAAACAAATAATTAATAAGC;

• 1nad9: AAAGCCGTAGATCTAGACA;

• 2nad9: TCGACCTTTATTTTTGTACG.

Mitochondrial DNA and RNA were isolated and PCR and RT-PCR were carried out as described previously (Gott et al., 1993) using those primers. Automated DNA sequencing was carried out by Biotic Solutions, Inc. (NY, USA) on a fee for service basis. The sequences are available from GenBank under the accession nos FJ154098 (atp6) and FJ154099 (nad9).

3 RESULTS

3.1 Previously annotated putative genes

The mitochondrial genome of Physarum has upon its publication been annotated using traditional (not editing aware) genome annotation methods (Takano et al., 2001). This annotation comprises—in addition to 7 of the 11 genes for which the editing sites are experimentally known today — eight putative protein-coding genes with a specific annotated function. Since these eight genes are considered already known, we did not look for them with our model building approach. Table 1 summarizes the results of the database and the de novo approach for these eight genes. It can be seen that three of the previously annotated putative genes are found by both methods and another three of them are found only by the comparative approach. Their predicted positions agree with each other and with the annotations in the genome within reason [note that the presence of RNA editing introduces uncertainty in the prediction of both ends of a gene, since any start (stop) codon in any of the three frames is a candidate for the beginning (end) of the gene]. The only putative gene with severe discrepancies in predicted position between our traditional methods is the RNA polymerase (rpo) in positions 12100–16702. In our prediction it stretches much further than the original annotation at positions 14822–16813. In fact, our prediction is that this one gene covers four previously predicted hypothetical proteins. The two putative genes mlp1 and secY are not found by either of our two methods at statistically significant levels. The database search approach does find both of them with significant p_db, but after the shuffling test p_GC is not significant in either of the two cases. This suggests that these two putative genes are artifacts due to the low GC content of the Physarum genome.

Table 1.

Putative mitochondrial genes of P.polycephalum previously annotated by traditional approaches

Gene	Database				De novo		Traditional
	gi	Position	pdb	pGC	Position	E-value	position
mlp1							2354–4573
secY							11731–12861
rpo	10119856	12100–16702	1.3 × 10−15	1.5 × 10−4			14822–16813
nad5	11466469	17275–19132	1.7 × 10−80	6.2 × 10−29	17400–19150	1 × 10−84	16807–19132
rpS12	91222399	21770–22095	9.0 × 10−11	4.1 × 10−20	21750–22150	4 × 10−21	21865–22095
nad4	11466666	38131–36981	9.1 × 10−71	3.1 × 10−47	38400–36900	3 × 10−38	38265–37228
nad3	11466536	38814–38477	3.2 × 10−14	1.6 × 10−16			38811–38473
nad1	10444170	58907–59818	3.9 × 10−50	4.6 × 10−40			58936–59751

Genes in which the range of genomic positions is backwards are located on the reverse strand. The first block of columns refers to comparative gene-finding through database searches. The p_db- and p_GC-values quantify the statistical significance of the prediction as described in the main text. The gi number specifies the protein sequence in the alignment. The second block of columns refers to de novo gene-finding. The E-value is the BLASTX E-value from the comparison of the predicted putative mRNA sequence to the non-redundant database. The last block shows the annotated position of the putative gene in the GenBank entry of the full mitochondrial genome (Takano et al., 2001).

3.2 Novel putative genes

Table 2 lists all other statistically significant putative genes reported by the three methods. We will first discuss the putative genes located at genomic positions higher than 17 000 and come back to the other ones later. The putative genes beyond position 17 000 are all typical mitochondrial genes. None of these putative genes overlap with each other or with any of the other experimentally verified or putative genes in the mitochondrial genome of Physarum. In addition, many of these putative genes are relatively close to each other or to known genes. These features render these predictions quite plausible. With the exception of atp6 and nad9, all these putative genes are identified by the model-based comparative gene-finding approach. This approach has previously been shown by experimental verification of its predictions to be able to correctly identify the locations of new genes (Gott et al., 2005). In addition to identifying the locations of new genes, the PIE algorithm also predicts the actual location of editing sites. On the six protein-coding genes of which the editing sites were known before the algorithm was developed, it predicts 70% of the C insertions correctly and another 10% to within 3 nt (Bundschuh, 2004). On the four genes the location of which PIE identified for the first time the precision of PIE is reduced to 33% correctly predicted C insertions and another 22% C insertions predicted to within 3 nt. This is likely due to their higher degree of divergence from the sequences available for model building. Yet, even this level of prediction accuracy has been experimentally shown to be sufficient to successfully design primers, since the algorithm can estimate which regions of the gene lead to reliable predictions and which do not (Gott et al., 2005). Thus, at least those predictions with P-values below 10⁻⁵ from the model-based approach are to be considered very reliable predictions. [Since we tested about 100 different genes using the model-based approach, a P-value should according to the Bonferroni correction (Bonferroni, 1936) be considered significant only if it is well below 0.01]. Most of these reliably identified putative genes are corroborated by the de novo approach at least if we allow a somewhat higher E-value cutoff than the usual 0.005 for these mitochondrial genes. (while BLASTX E-values larger than 0.005 are not considered statistically significant by themselves, they would be highly significant had we restricted our search of the non-redundant protein database to mitochondrial proteins only, and thus are still likely to be correct assignments. The positions of the de novo predictions of these putative genes are shown in italic to indicate the increased threshold.)

Table 2.

Novel putative mitochondrial genes of P.polycephalum

Gene	Model-based			Database				De novo		Organism
Gene	gi	Position	pm	gi	Position	pdb	pGC	Position	E-value
dpo III α				47458220	2064–4459	9.7 × 10-8	4.5 × 10−5			Rickettsia
rpo σ				42410833	2445–3380	2.3 × 10-4	5.8 × 10−5			Reclinomonas
rpL9	33301538	2564–2726	1.7 × 10−3							Rickettsia
spoU								3800–4500	2 × 10−4
rpL20	31563135	8353–8121	3.0 × 10−4							Reclinomonas
comP								12650–13300	3 × 10−5
php21								14150–13350	4 × 10−3
rpS2	40795007	20315–20923	6.3 × 10−7					20300–20950	2 × 10−1	Dictyostelium
rpS7	50346830	22429–22719	1.0 × 10−5					22250–22700	1 × 10−3	Dictyostelium
rpL2	1785717	23044–23573	1.3 × 10−12	11466652	23132–23689	1.5 × 10−8	3.3 × 10−15	23000–23650	5 × 10−20	Dictyostelium
rpS19	38638297	23832–24011	6.4 × 10−9					23800–24150	9 × 10−3	Dictyostelium
rpL29	34395761	24060–24146	1.3 × 10−3							Rickettsia
rpL19	39931893	35221–35350	1.1 × 10−3							Reclinomonas
atp6				8954375	36072–36771	9.1 × 10−24	5.4 × 10−17	36150–36800	3 × 10−40	Dictyostelium
rpL14	7524998	38993–39321	8.3 × 10−19					39000–39350	6 × 10−9	Dictyostelium
rpS14	49147157	39839–40084	2.2 × 10−8							Dictyostelium
rpS8	50261297	40110–40422	2.6 × 10−4							Dictyostelium
rpS13	49147226	41178–41319	8.8 × 10−4					40950–41300	7 × 10−1	Dictyostelium
nad9				10802934	41550–41954	3.9 × 10−8	4.8 × 10−11	41500–42000	3 × 10−16	Dictyostelium
atp4	7521805	53555–53816	2.3 × 10−4							Reclinomonas
rpL16	50261293	57181–56962	7.9 × 10−10							Dictyostelium
rpS3	27734542	57818–57443	3.6 × 10−6					57600–57300	1 × 10−1	Reclinomonas

Genes in which the range of genomic positions is backwards are located on the reverse strand. The first block of columns refers to the comparative gene-finding approach through model building. It reports the accession number of the protein used to build the protein family model, the position at which the gene was found, and the P-value that quantifies the statistical significance of the prediction as described in the main text. The second and third block of columns refer to the comparative gene-finding approach through database search and the de novo gene-finding approach, respectively. They are organized identically to their respective blocks in Table 1. The last column indicates in which other organism a gene can be found. Dictyostelium indicates that the gene is in the mitochondrial genome of D.discoideum, Reclinomonas indicates that the gene is not in D.discoideum, but it is in the mitochondrial genome of Reclinomonas americana, while Rickettsia indicates that the gene is in neither of the two mitochondrial genomes, but in the genome of Rickettsia rickettsii.

Atp6 and nad9 are not initially identified by the model-based comparative gene-finding approach. However, they are identified by the two other approaches. We use the proteins identified as homologs by the database approach as starting proteins to build models for the model-based approach. This leads to an identification by the model-based approach with highly significant P-values of 4.2 × 10⁻⁴⁰ and 1.6 × 10⁻²⁰, respectively. Thus these two putative genes should also be considered highly reliable predictions.

Putative genes with intermediate P-values from the model-based approach are rpL29, rpL19, rpS8, rpS13 and atp4. Among those, only rpS13 is corroborated by one of the other methods. While most of the highly reliably predicted genes can also be found in the mitochondrial genome of Dictyostelium discoideum, the closest relative of P.polycephalum for which a full mitochondrial genome is available, out of the six less reliably predicted putative genes again only rpS13 can be found in the mitochondrial genome of D.discoideum. All but rpL29 can still be found in the extremely gene rich mitochondrial genome of Reclinomonas americana (Lang et al., 1997); rpL29 cannot even be found in that genome, but is present in the genome of Rickettsia rickettsii, which is considered an ancient relative of today's mitochondria (Andersson et al., 1998). This indicates that some of these putative genes might actually be false positives.

We now come back to the region before genomic position 17 000. All putative genes in this region are predicted by only one method. In addition, several of these putative genes overlap each other or the putative RNA polymerase or secY from Table 1. Thus, it is likely that several of these putative genes are false positives. Nevertheless, each one is interesting in its own right.

The two genes predicted by the model-based approach are the two mitochondrial genes rpL9 and rpL20. Both are predicted with only moderately significant P-values and none of them can be found in the mitochondrial genome of D.discoideum.

The two putative genes exclusively predicted by the database search are a DNA polymerase III α subunit and an RNA polymerase σ factor that are both located in the same region of the mitochondrial genome. They are relatively weak; however, they are interesting since insertional editing in Physarum is experimentally known to be co-transcriptional (Visomirski and Gott, 1997) and thus whatever the enzyme performing the editing is has to be very closely associated with the RNA polymerase. As for atp6 and nad9 above, we built a protein model-based on the homologs identified by the database search and used this model to see if the model-based approach can identify the gene. However, this did not result in significant P-values (0.44 and 0.80, respectively). We would like to stress, however, that this in and of itself does not mean that these putative genes must be false positives. For example, if we use the homolog of nad1 listed in Table 1 to build a model, the model-based approach also only gives a non-significant P-value of 0.16 although nad1 has been experimentally verified (Mahendran et al., 1991), albeit without publishing the actual edited sequence in either print or electronic form.

Finally, there are three putative genes only identified by the de novo approach, namely matches to a tRNA/rRNA methyltransferase SpoU family protein from D.discoideum (gi111226655), a Sensor protein comP from Bacillus cereus (gi30019036) and a hypothetical mitochondrial protein (which we name php21) from Leishmania tarentolae (gi11467606) and from Trypanosoma brucei (gi84040). The last gene does not have a very convincing E-value and could be just a coincidental similarity due to the low GC content of all three mitochondrial genomes involved, but is very intriguing given that L.tarentolae and T.brucei are known to have extensive RNA editing in their mitochondria (Simpson et al., 2003; Stuart et al., 2001).

3.3 Experimental validation

In order to judge the reliability of the computationally predicted putative genes, we chose two for experimental validation. As it has already been established in (Gott et al., 2005) that genes identified by PIE can be experimentally validated, we specifically chose the two mitochondrial genes not identified by PIE, namely atp6 and nad9, for this purpose.

We experimentally determined the mRNA sequences derived from these two genes as described in Section 2.5. These mRNA sequences verify the existence of an atp6 gene at genomic positions 36067–36774 and a nad9 gene at genomic positions 41520–41994, thereby validating the computational predictions. These atp6 and nad9 genes harbor 33 and 23 editing sites, respectively, all of which are C insertions. Of these 56 total editing sites, 23 (41%) were correctly predicted by the computational methods, and for another 18 (32%) the computational predictions did not deviate from the correct positions by more than 3 nt. Remarkably, the nad9 gene is the first experimentally verified mitochondrial protein-coding gene in P.polycephalum that is terminated by the UGA stop codon. However, it is also possible that this UGA encodes an amino acid, e.g. Tryptophan as in several other mitochondrial codes (Knight et al., 2001), and the immediately following UAA is the true stop codon.

4 CONCLUSION

We have found (depending on the stringency of the P-value cutoff) between 10 and 22 newly annotated putative genes in the mitochondrial genome of the slime mold P.polycephalum using three independent methods (see Fig. 2). Together with the previously annotated 19 genes, this yields a total of up to 41 annotated putative genes, close to the 42 known genes in the mitochondrial genome of D.discoideum of similar length. The mitochondrial genome of P.polycephalum is at the same time interesting and difficult to annotate due to the presence of insertional RNA editing. Our doubling of the number of putatively annotated genes is based on computational approaches that explicitly take into account the existence of insertional RNA editing. Our newly annotated putative genes include many typical mitochondrial genes predicted with high confidence and independently by the different approaches. We experimentally verified two of these mitochondrial genes harboring a total of 56 new editing sites. This leaves the other putative genes as good candidates for experimental verification and extension of the arsenal of known editing sites as well with the goal of identifying common features of these sites that guide the editing machinery. A few additional putative genes are not typical mitochondrial genes. Verifying if they are indeed expressed and determining their function in the mitochondrion will be of interest in their own right.

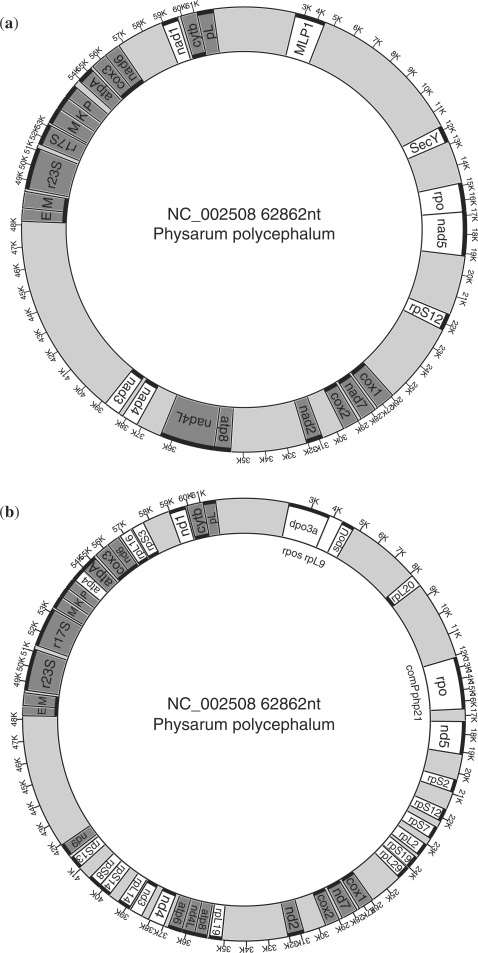
Fig. 2.

Mitochondrial genome of P.polycephalum without (a) and with (b) the putative genes identified by the three approaches presented here. The genes shown in dark color are experimentally verified, while putative genes are shown in white. Genes labeled by a single (amino acid) letter denote tRNAs for the corresponding amino acid. The genomic position is indicated by the tick marks around the outer circumference and increases clockwise.

Funding

National Science Foundation (grant numbers DMR-0404615 and DMR-0706002 to R.B., PHY-0242665 to REU program in which C.B. performed parts of this work and SBE-0245054 (Lynn Singer, PI), a sub-project (to J.G.) of which supported M.C.). National Institutes of Health (grant number GM-54663 to J.G. and NIAID/NIH contract N01-AI-50020 to H.Y.L). An Ohio State University Postdoctoral Fellowship to H.Y.L.

Conflict of Interest: none declared.