Stimulus-Induced Rotary Saturation (SIRS): a potential method for the detection of neuronal currents with MRI

Abstract

Neuronal currents produce local transient and oscillatory magnetic fields that can be readily detected by MEG. Previous work attempting to detect these magnetic fields with MR focused on detecting local phase shifts and dephasing in T2 or T2* weighted images. For temporally biphasic and multi-phasic local currents the sensitivity of these methods can be reduced through the cancellation of the accrued phase induced by positive and negative episodes of the neuronal current. The magnitude of the phase shift is also dependent on the distribution of the current within the voxel. Since spins on one side of a current source develop an opposite phase shift relative to those on the other side, there is likely to be significant cancellation within the voxel.

We introduce a potential method for detecting neuronal currents though their resonant T1ρ saturation during a spin-lock preparation period. The method is insensitive to the temporal and spatial cancellation effects since it utilizes the multi-phasic nature of the neuronal currents and thus is not sensitive to the sign of the local field. To produce a T1ρ reduction, the Larmor frequency in the rotating frame, which is set by γB_1lock (typically 20 Hz – 5 kHz), must match the major frequency components of the stimulus- induced neuronal currents. We validate the method in MRI phantom studies. The rotary saturation spectra showed a sharp resonance when a current dipole within the phantom was driven at the Larmor frequency in the rotating frame. A 7 minute block design experiment was found to be sensitive to a current dipole strength of 56 nAm, an approximate magnetic field of 1 nT at 1.5 mm from the dipole. This dipole moment is similar to that seen using the phase shift method in a similar experimental setup by Konn et.al. (2003), but is potentially less encumbered by temporal and spatial cancellation effects.

Introduction

Magnetoencephalography measures magnetic fields near the scalp and infers a distribution of dipole current sources within the cortex. The rationale is that postsynaptic currents occurring synchronously in a population of tens of thousands of cortical pyramidal cells can be modeled as a single current dipole. Because the cells are aligned almost perfectly parallel to each other, the dipolar fields of all the neurons add constructively. Unfortunately it is difficult to learn the microscopic distribution or even amplitude of the currents based on the detected MEG field pattern since MEG measures fields at the scalp (far from the dipole) where the structure of the dipole is not easily discernable. For example, it can be difficult to distinguish between a single larger dipole or a group of parallel small dipoles (Hämäläinen et al., 1993). Also, there could be cancellation among local dipoles in the folded cortex (Hämäläinen et al., 1993). Nevertheless, an estimate of the equivalent dipole current strengths can be made within the assumption of the MEG reconstruction and typical numbers range from 5 to 120 nAm with many robust stimulus paradigms giving dipole sources in the tens of nAm range (Hari, 1991). The temporal characteristics of the MEG-detected dipoles show a range of responses, most typically temporally asymmetric bipolar and multi-phasic responses with significant spectral power at frequencies below 100 Hz (Niedermeyer and Lopes da Silva, 1999). In addition to the transient evoked response, oscillatory fields can be evoked, for example using auditory click- trains (Lin et al., 2004). Thus in this case, a narrow-band peak at the stimulus repetition frequency is clearly visible in the MEG-detected fields. Similar narrow-band fields have been detected by MEG during visual paradigms with alternating checkerboard stimuli (Tallon-Baudry et al., 2001).

The direct detection of neuronal activity using MR imaging techniques has been pursued for over a decade (Bandettini et al., 2005; Bodurka and Bandettini, 2002; Bodurka et al., 1999; Konn et al., 2003; Konn et al., 2004; Parkes et al., 2007; Petridou et al., 2006; Singh, 1994; Xiong et al., 2003) and the progress has recently been reviewed (Bandettini et al., 2005). Most of the proposed techniques are based on the detection of phase shifts or dephasing caused by the extremely small changes in the local B₀ field induced by local neuronal currents. The phase shift or dephasing of the detected MR magnetization accumulates during the TE period of either a gradient echo or spin echo sequence. The phase shift experienced by a given spin within the voxel, γ⊗B_neuralTE, can be either positive or negative depending on the sign of the z-component of the field produced by the local current. The total dephasing measured in the image is proportional to the integral of this phase shift over the voxel volume and its temporal integral over the sensitive period of the sequence. The phantom findings are generally encouraging, with detectable local magnetic fields as small as 0.2 nT (Bodurka and Bandettini, 2002) and current dipoles as small as 6.3 nAm (Konn et al., 2003), but the in vivo literature contains some positive findings (Chow et al., 2006; Xiong et al., 2003), but mostly negative findings (Chu et al., 2004), including a failure to reproduce the the paradigm of Xiong et al (Parkes et al., 2007).

Understanding the microscopic spatial distribution and time course of the neuronal currents is critical to assessing the potential ability of these MR-based methods to detect neuronal activation. The phase sensitive portion of the MR sequence must be properly timed relative to the transient or oscillating neuronal current to insure that cancellation of the induced phase during a biphasic or multi-phasic current is minimized. For example, the phase sensitive portion of the sequence (the TE period of a gradient recalled echo sequence) might be limited to a single lobe of a biphasic response. Or, for a spin echo sequence, the timing of the 180° pulse can be chosen to occur at the transition between the two phases of the response allowing the biphasic signal to be detected without cancellation (Singh, 1994). Finally, the conventional methods using T2 and T2* are only sensitive to the component of the local field along the applied external B₀ field.

The spatial distribution of the current within the voxel can also lead to cancellation of the phase shift induced in the MR signal. Even a DC current in a small, straight wire running through the center of the voxel will not induce a net phase shift in the MR signal in that voxel; the current must be offset from the voxel center to produce a net phase accrual (Bandettini et al., 2005). This arises since the phase is sensitive to the sign of the magnetic field and thus the integral of the phase shift over the voxel is zero for this symmetric case. In other cases, the magnetic field is expected to cancel for points within the voxel. For example, for a uniform distribution of discrete parallel wires there are some areas where the magnetic field itself cancels, but the integral of the phase shift over the region cancels everywhere but at the edge of the distribution (Park and Lee, 2007). In this case the signal will experience magnitude dephasing but not a net phase shift. In a recent simulation study, Park et.al. (2007) numerically calculated the effects of neuronal magnetic fields on voxel magnitude and phase, simulating both dendritic as well as axonal currents. They estimate average neuronal fields of 0.3 nT for simultaneous dendritic currents.

Recently, the use of ultra-low-field MRI has been proposed to detect neuronal currents (Kraus, 2006) (Kraus et al., 2008). An extremely low B₀ measurement field allows resonant interactions between the neuronal currents and spin magnetization if γB₀ is brought into the frequency range of the neuronal currents. Although their first measurements were at significantly higher fields, Kraus and colleagues proposed static measurement fields weaker than 0.025 Gauss using a SQUID magnetometer to detect the MR signals at a Larmor frequency of less than 100 Hz (Matlachov et al., 2004; Volegov et al., 2004). In this scenario, the transient neuronal fields can possibly act as resonant excitation pulse providing the initial excitation of the proton magnetization. Thus, the neuronal current supplies the local B₁ field for excitation and no transverse magnetization should be detected in locations without neuronal currents. Contrary to the high-field MRI-based phase shift approaches mentioned above, multi- phasic or oscillatory currents are beneficial for increasing the tip angle and thus the detected response— provided they have significant spectral power at the Larmor frequency. However, like the high-field phase shift methods, the technique is still susceptible to cancellation effects from the spatial symmetry of the currents within a voxel. Also, the method is sensitive only to the component of the neuronal field perpendicular to the z axis and the effect is still dependent on the sign of the neuronal current. Thus, a small, straight wire running through the center of the voxel along the static magnetizing field direction produces an excitation giving transverse magnetization along opposite directions in the x-y plane on opposite sides of the wire. Thus, no net signal from the voxel is expected for this situation. The low-field method is also adversely affected by the small Boltzmann population and other technical confounds of the low-frequency MRI apparatus.

In this work, we introduce a new approach to effectively lower the Larmor frequency below 100 Hz in high-field MR systems based on the spin-locking mechanism (Abragam, 1961). During a spin-lock, the magnetization is locked in the rotating frame by an RF field, the so-called spin-lock field B_1lock. The effective resonance frequency in the rotating frame during the spin-lock condition is very close to ω_1lock = γB_1lock, deviating only by a potential Bloch-Siegert shift (Bloch and Siegert, 1940). This latter small shift in resonance frequency results from the counter- rotating field component of a linearly polarized time varying field. The Larmor frequency in the rotating frame can be chosen by setting the RF power of the spin-lock pulse. In this work, we acquire phantom data with γB_1lock ranging from 20 Hz to 200 Hz. T_1ρ relaxation occurs in the spin-lock state from external magnetic field fluctuations with a z component at the resonant frequency γB_1lock and harmonics.

Redfield described the saturation of the spin-locked magnetization with an external coil and audio frequency source as “rotary saturation”. (Redfield, 1955) Redfield analyzed rotary saturation in solids using B_1lock fields large compared to the local fields. They derived a steady state magnetization change in the detected spin locked magnetization M_ρ compared to its initial value M₀ for the solid state which is given by:

$$(M_0-M_{\rho })/M_0={\gamma }^2{B}_{\mathit{rotarysat}}^2\pi T_{1\rho }f({\omega }_{1\mathit{lock}})$$ Eq. 1

Where, B_rotarysat is the applied rotary saturation field (a function hopefully carried out by the oscillating neuronal fields), T_1ρ is the spin-lattice relaxation in the spin-locked state and f(ω_1lock) is the Lorentzian shape function which has a value of 1s on resonance, when γB_1lock = γB_rotarysat (Abragam, 1961).

Since Eq. 1 was derived for solids and describes a steady state effect, it cannot be used to accurately model the SIRS mechanism. In order to model the effect in liquids and for transitory applications of a rotary saturation field, we model the Rotary saturation effect as a coherent rotation away from the B_1lock direction by the rotary saturation field (neuronal field). The equations of motion for the magnetization in the spin-lock state are formulated in the doubly rotating frame as:

$$\begin{array}{rl}\frac{dM}{dt}=& \gamma M\times [H_{\text{eff}}(1-\frac{{\omega }_{\text{rotarysat}}}{\gamma \left|H_{\text{eff}}\right|})+B_{\text{rotarysat}}]-R(M-M_{\rho }),\text{with}\\ R=& \left(\begin{array}{ccc}\frac{1}{T_2^{*}}& 0& 0\\ 0& \frac{1}{T_2^{*}}& 0\\ 0& 0& \frac{1}{T_{1\rho }}\end{array}\right),\end{array}$$ Eq. 2

where H_eff is the effective field formed from the applied B_1lock and the off-resonance pseudo-field ⊗ω/γ, Mρ denotes the equilibrium magnetization in the rotating frame, which is very small since B_1lock is small. Here H_eff is the relevant axis toward which the magnetization is at equilibrium, is not the static magnetic field direction. If both the spin-lock RF and the Rotary Saturation field B_rotarysat is on resonance, then H_eff is B_1lock. B_rotarysat is the audio-frequency field applied orthogonal to the spin-lock axis (here B_1lock is taken to be along the x-axis in the singly rotating frame). To preserve the analogy to the singly rotating from, the axes of the doubly rotating frame are renamed so that the z-axis is the equilibrium direction. Thus in the doubly rotating frame, the z axis is the direction B_1lock. Then B_rotarysat must be applied orthogonal to B_1lock to produce a rotation. The magnetization relaxes along H_eff with the time constant T1ρ, and in the other two directions with the time constant T₂*. We propose to utilize spin-locking to sensitize the spins to neuronal magnetic fields oscillating at the Larmor frequency in the rotating frame, where γB_1lock ranges between 20 and 500Hz, as set by the applied B_1lock. Oscillating neuronal currents with spectral power at γB_1lock are then capable of producing rotary saturation of the spin-locked magnetization. Thus, the neuronal currents produce a resonant saturation effect on the MR signal in the rotating frame during the spin-lock state, and the spin-lock state can be tuned to be sensitive to a frequency of interest by adjusting γB_1lock. In practice, we anticipate choosing γB_1lock to the expected frequency of the neuronal oscillations to sensitize the sequence to these frequencies. Thus the neuronal currents induced by the stimulus create the rotary saturation effect. In analogy with the classic rotary saturation experiment of Redfield (1955), we refer to this potential method as Stimulus-Induced Rotary Saturation (SIRS).

To validate the potential of SIRS to detect local current dipoles associated with neuronal activation, we performed two different experiments. The first is the measurement of rotary saturation spectra to characterize the rotary saturation effect from a current dipole. Secondly, we performed a block-design experiment in order to establish detection limits of the method compared to conventional phase-sensitive methods.

Methods

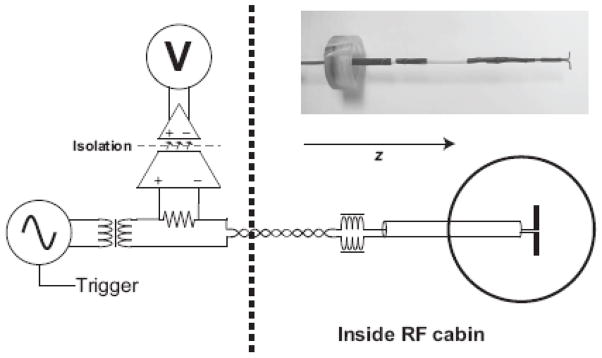
The measurements were performed in a 17-cm diameter spherical phantom filled with a solution of saline (0.9% NaCl) and 0.25 ml of Gadopentetate dimeglumine (Magnevist, Berlex Laboratories) yielding a T₁ measured by inversion recovery of 1100 ms. The current dipole had a length of 1 cm was formed from 0.89 mm diameter insulated copper wire exposed only at the tips. The current dipole (nAm) produced by this phantom is therefore the product of the current and the dipole length. A photograph of the dipole and a schematic of the driving circuit is shown in Fig. 1. The return path for the current was therefore an ionic current distributed within the saline. The dipole was placed 3.9 cm from the edge (4.6 cm from center) of the phantom and the phantom was aligned so that the current dipole was perpendicular to the B₀ field. The dipole was on the end of an insulated rigid copper coaxial cable that extended approximately 2 cm out of the phantom. Thus, with the exception of the two 0.5 cm portions of the dipole, the current was confined to a semi-rigid coaxial cable. Outside of the phantom, the coax was wound into a four-turn solenoid and tuned with a parallel capacitor to form a trap circuit resonant at the Larmor frequency (123 MHz) to reject RF common-mode currents that might be induced by the RF onto the dipole supply leads.

Figure 1.

Circuit diagram of the apparatus for applying oscillating currents to the dipole phantom during the spin locking. The function generator is gated by a logic pulse generated by the pulse sequence so that its output is non-zero only during TSL. The output of the function generator then goes through an isolation transformer to eliminate DC and common-mode currents and drives the dipole phantom through a series resistor (10 k∧) and series RF chokes to block RF pickup on the lines. The current in the phantom is measured by monitoring the voltage drop across the 10 k∧ series resistor using an optically isolated operational amplifier with a gain of 10 and 500 k∧ input impedance. The RMS amplitude of the output of the operational amplifier is measured with a digital oscilloscope.

The magnetic field strengths generated by the current dipole were calculated from the current dipole moment using the equations published by (Heller et al., 2004). The exact dipole location in the sphere was determined based on a high-resolution, 3D turbo spin echo image of the phantom. The calculation was performed for a 2 cm × 2 cm region of interest centered at the current dipole. Since the equations of Heller et.al (2004) assume an infinitely small dipole, we modeled our extended dipole by superposition of 1000 dipoles distributed with 10-μm spacing along the extent of our dipole.

The dipole is connected to a digital frequency synthesizer (Global Specialties model 2003) via an audio transformer to eliminate DC offsets and a twisted pair cable with 1 μH series RF chokes to prevent the conduction of signals at RF frequencies. The frequency synthesizer uses a gating pulse controlled by the MR pulse sequence in order to supply current only during the spin-lock portion of the sequence. The current through the phantom was determined by measuring the voltage across a 10-kOhm series resistor using an optically isolated differential probe with approximately 500kOhm input impedance.

A 3 T whole-body MR scanner (Siemens Medical Solutions, Erlangen, Germany) was used with a transmit and receive birdcage head coil. The spin-lock prepared EPI pulse sequence (Borthakur et al., 2006) used is shown in Fig. 2. It consists of a 90° hard pulse in y- direction, immediately followed by a rectangular spin-lock pulse in x direction, which remains on for the duration TSL. The spin-lock period is followed by a hard 90° pulse in −y direction which returns the spin-locked magnetization to the longitudinal axis for detection by the standard gradient echo EPI sequence. All remaining transverse magnetization is spoiled by immediately following spoiler gradients. The entire spin-lock preparation is non-selective. Following the preparation a single slice EPI sequence is used to acquire the T_1ρ–weighted image (64 × 64 matrix, 20-cm FOV, 3.1 × 3.1 mm, 4-mm thickness with a TE of 19 ms, TR of 1 s, and a BW of 2298 Hz). For the studies addressing the sensitivity of the technique to dipolar fields, the spin- lock duration, TSL, was 100 ms. In order to determine the T_1ρ of the phantom, TSL was set to 0, 15, 30, 50, and 70 ms, and the resulting image intensity was fit to the relation I = M₀exp(− T_SL/T_1ρ).

Figure 2.

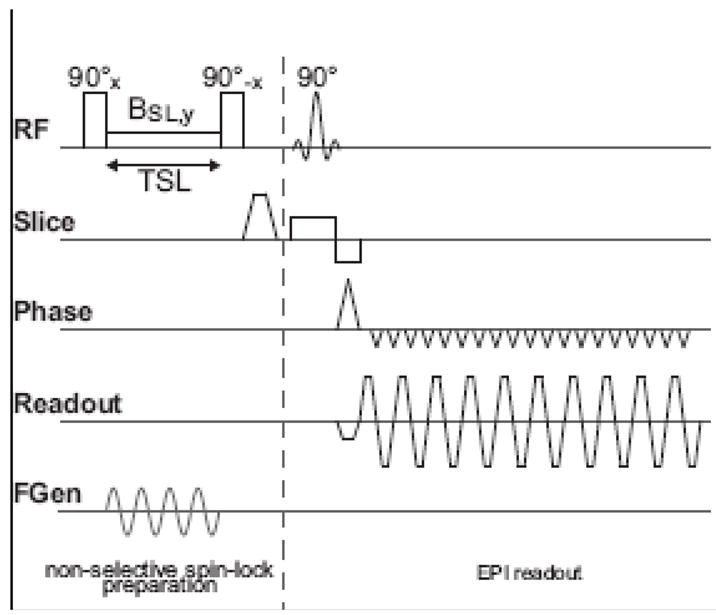
Pulse sequence diagram for the spin-lock prepared EPI sequence. After the initial 90° excitation, the magnetization is spin-locked along the y axis by a continuous wave RF pulse applied for a time TSL. Immediately following the spin-lock period, TSL, the magnetization is rotated back to the z axis by the 90 ° _-x pulse. Then a traditional EPI sequence images the magnetization which experienced the spin lock state. T1ρ relaxation processes during TSL are therefore expected to diminish the signal intensity in the EPI image. The sinusoidal current input to the phantom is applied during the spin-lock period and is shown schematically in the bottom trace.

Bloch Equation simulation

The simulation starts with the magnetization aligned along the spin-lock field. During the spin-lock phase the audio-frequency saturation field acts to rotate the magnetization away from the spin-lock field. The Bloch simulator tracks all three components of the magnetization in Eq. 2, however only the component along the spin-lock field is of interest since this component will be returned to the z axis for subsequent imaging. The other components of the magnetization are dephased by the spoiler gradients following the 90 degree pulse. We simulated the Bloch equations in the doubly rotating frame using an MATLAB code solver with parameters matching the phantom (T₁ = 1.1s, T₂ = 0.95s, T_1ρ = 0.98s, T₂* = 50ms) and human brain gray matter at 1.5T (T₁ = 0.9s, T₂ = 80ms, T_1ρ = 147ms, T₂* = 50ms). Here T_1ρ was taken from the R₂ = 1/T₂ and R₁ = 1/T₁ values using the equation: T_1ρ = 2/(R₂ + R₁). (Abragam, 1961) The rotary saturation spectra simulate the case where a B_rotarysat field of 1nT and 5nT is swept in frequency past the γB_1lock resonance value. Spectra were obtained for B_1lock = 10, 20 and 40Hz for both the phantom and human relaxation parameters with a spin-lock duration of 100ms.

Rotary saturation spectra

In order to measure the rotary saturation spectra, the frequency of the synthesizer was swept from below resonance to above the expected rotary saturation resonance, in 1 Hz steps. Each frequency was repeated for 20 images. In order to exclude potential systematic errors, the frequencies were alternately swept up from 20 Hz to 60 Hz or down from 60 Hz to 20 Hz. The spectra taken with ω_1lock set to 10Hz and 20Hz were swept from 2Hz to 60Hz. The entire rotary saturation spectrum measurement was repeated for each B_1lock amplitude in order to experimentally confirm the resonance frequency in the rotating frame. Due to capacitive effects in the phantom, the impedance of the phantom, and therefore the current amplitude depends on the frequency of the applied current. The currents reported for the rotary saturation spectra refer to the current measured when the synthesizer was set to the resonance frequency γB_1lock. Since the other measurements were performed at a fixed frequency this effect was a limited disruption. For a 50-Hz driving source, the impedance of the phantom was measured to be 950∧.

Block design experiment

In the block detection experiment the gating of the function generator was activated to produce the oscillating current for “on” blocks and deactivated for “off” blocks. Thus, a driving current was present only during the spin-locking period of the “on” blocks. The function generator was set to the resonance frequency previously determined with a rotary saturation spectrum measurement. Although γB_1lock was set to be 40 Hz based on the scanners transmit adjustment procedure, the minimum was detected at 37 Hz. All block-design measurements were thus performed with the function generator set to 37 Hz.

The on-resonance and off-resonance blocks lasted for 20 TR periods of 1s each and were repeated 10 times during each run. Total run time was 6 min, 40s for the blocks plus 20 dummy scans to insure that the magnetization was in steady state. For high current levels two runs were collected, for the low current levels six runs were collected and analyzed together. Statistical significance was established using a two-sided t-test between the “on” and “off” blocks for each voxel in the image.

Block detection experiments were performed at function generator voltage settings of 4V, 0.4V and 0.2V, yielding a measured current (from the voltage drop across the series 10 k∧ resistor) of 118 μA, 11.5 μA, and 5.6 μA, respectively, corresponding to current dipoles of 1180 nAm, 115 nAm, and 56 nAm respectively.

Results

Spinlock Images

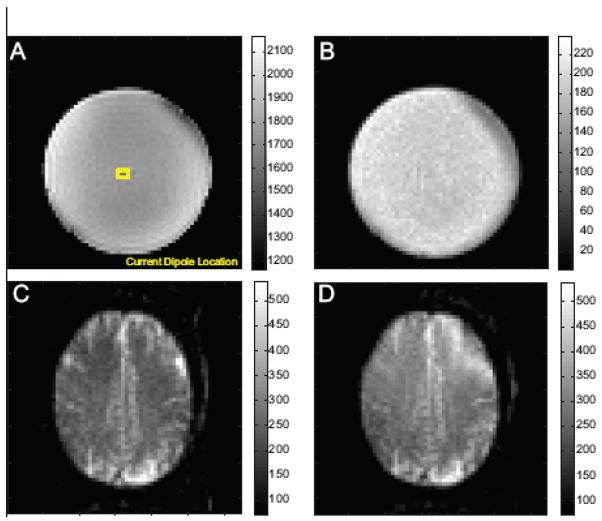
Figure 3 shows representative spinlock images for both the phantom with ω_1lock = 40Hz as well as a human image obtained with ω_1lock = 40 Hz and 10Hz.

Figure 3.

Representative spin-locked prepped images from the sequence of Fig. 2. A) phantom image spin-locked with γB_1lock = 40 Hz shown with the location of the current dipole overlaid in yellow. B) Time series standard deviation from a time series of 420 of the spinlock prepped images. C) Brain image obtained with the spinlock prep sequence with γB_1lock = 40 Hz and D) γB_1lock = 10 Hz.

Magnetic field calculation

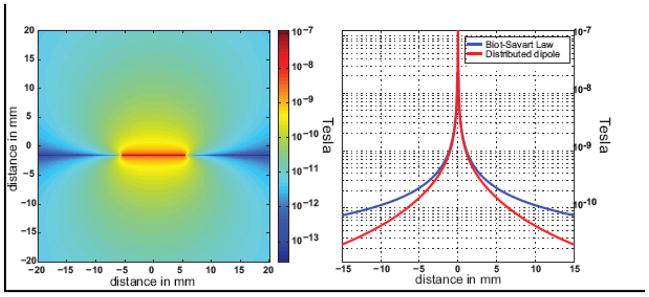
Figure 4 shows the magnitude of the z-component of the magnetic field associated with a 56 nAm current dipole shown in an axial plane centered on the dipole. Figure 3 also shows a plot of magnetic field of the dipole along with a reference plot derived from the Biot-Savart law for a thin, long straight wire. The field is calculated to be 1 nT at a distance of 1.5 mm from the dipole. At this distance the 1cm extended dipole looks approximately like an infinite wire.

Figure 4.

Magnitude of the z-component of the magnetic field associated with the current dipole phantom. Left, axial image of the z-component of the field for a 5.6 μA current in the dipole (56 nAm dipole) based on the distributed dipole model. A field of 1 nT is estimated for a distance of 1.5 mm from the wire. Right, plot along the y-axis showing both the field values derived from the distributed dipole model and the Biot-Savart law for a long thin wire.

Bloch simulation

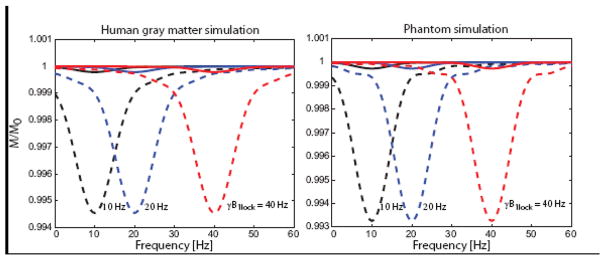
Figure 5 shows the simulation results for the phantom and the human gray matter relaxation parameters. Rotary saturation spectra are shown for γB_1lock of 10, 20 and 40 Hz and applied audio-field strengths of 1 nT and 5 nT. In each case, as the frequency of the simulated B_1rotarysat field is swept past the resonance condition at γB_1lock, a reduction of signal is observed which peaks when B_1rotarysat = γB_1lock. The line width and degree of saturation in the Bloch simulations was found to be independent of γB_1lock. The effect is roughly linear with B_rotarysat for small B_rotarysat. For neuronal oscillations at 10, 20 and 40 Hz, a B_rotarysat field of 6.8 nT reduced the magnetization by 0.1% for the 100ms spin-lock duration experiment using gray matter relaxation parameters at 1.5T. The neuronal field causing a 0.1% magnetization change decreased to 4.0 nT and 2.2 nT for spin-lock durations of 200 ms and 500 ms respectively.

Figure 5.

Simulation of the rotary saturation effect based on the Bloch equations in the rotating frame. The simulations show the fraction of the spin-locked magnetization as a function of the frequency of the applied B_rotarysat field. When the frequency of B_rotarysat reaches the resonance condition in the rotating frame (equal to γB_1lock) the spin-locked magnetization is rotated away from the spin-lock field B_1lock. In the spin-lock prep experiment, only the spin-lock magnetization is returned to the z-axis for subsequent imaging

Simulations were performed for human gray matter at 1.5 T (T₁ = 900 ms, T₂ = 80 ms, T₂* = 50 ms) and for the phantom used in this study (T₁ = 1100 ms, T₂ = 950 ms, T₂* = 100 ms). The effect is shown for rotary saturation at ω_rotarysat of 10 Hz, 20 Hz and 40 Hz (black, blue and red curves respectively) using B_rotarysat of 1 nT (solid line) and 5 nT (dashed line).

Rotary saturation spectra

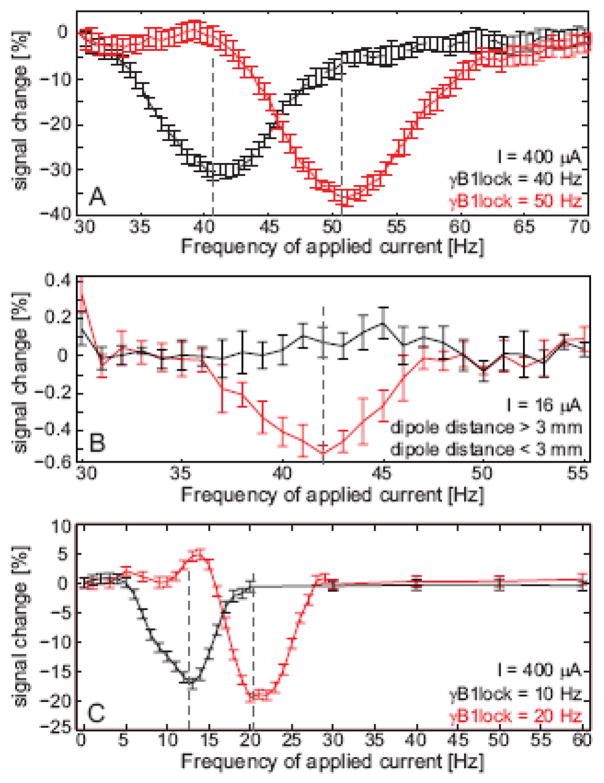
The phantom data (Fig. 6) show a decrease in image amplitude when the applied current in the phantom oscillates at close to the Larmor frequency in the rotating frame, γB_1lock. The observed line width of the saturation spectra is about 6 Hz FWHM. The peak often appeared at a slightly (2 Hz) higher frequency than expected from the B_1lock level determined from the instruments standard transmit calibration, possibly due to the Bloch-Siegert shift (Bloch and Siegert, 1940) or a mis-calibrated B₁ level. For high dipole current strengths (400 μA), the rotary saturation effect achieved a 30% amplitude decrease. For a small dipole current (16 μA), the shape of the rotary saturation spectrum can still be observed in voxels immediately neighboring the dipole (Fig. 4). The amplitude minimum still occurs close to the selected Larmor frequency in the rotating frame as expected. The observed line width of the rotary saturation spectra is also about 6 Hz.

Figure 6.

Image intensity as a percentage of the mean near the current dipole as a function of the frequency of the applied current to the dipole. a) Intensity changes in a single voxel adjacent to the dipole using a 400 μA applied current (4 μAm dipole strength), 10 averages. The black curve shows the rotary saturation effect with the spin-lock field set to γB_1lock = 40 Hz and the red trace shows a similar measurement with γB_1lock = 50 Hz. b) Intensity changes in a 5 voxel ROI immediately below the dipole using a16 μA applied current (160 nAm dipole strength), 160 averages. The red curve shows the rotary saturation effect with the spin-lock field set to γB_1lock = 40 Hz and the black trace shows a 5 pixel ROI distant from the dipole.

Block detection experiment

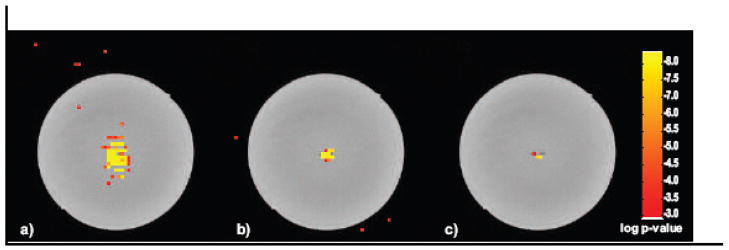
The t-test maps from the block design runs at each of the three current levels are shown in Fig. 6. The t-test results are overlaid on a high-resolution Turbo-spinecho image, but an example of an individual spinlock-prepped echoplanar image is shown in Fig. 3a. The two runs performed with 4 V function generator setting (118 μA current through the dipole) resulted in a large number of significant (p < 0.001) voxels above and below the dipole, in approximate agreement with the expected distribution of the z-component of the dipolar field. The six runs performed with 0.4 V function generator setting (11.5 μA in the dipole) showed significant voxels only within 5 mm above and below the dipole. The lowest current experiment performed with a 0.2 V function generator setting (5.6 μA in the dipole) yielded three significant voxels, all immediately below the dipole. The percentage signal change observed was 0.15% for the 5.6 μA current in the dipole.

Discussion

The validation of this methodology is based on the equivalent current dipole model which is commonly utilized in MEG data analysis. The rationale is that postsynaptic currents occurring synchronously in a population of tens of thousands of cortical pyramidal cells can be modeled as a single current dipole because the cells themselves are almost perfectly parallel to each other and thus the dipolar fields of all the neurons add constructively. From the far field it is impossible to distinguish between a single larger dipole or a group of parallel small dipoles. Thus, this phantom study is an appropriate benchmark for the MEG experiment. Here our phantom tries to match the magnetic fields observed in MEG using a single artificial dipole. For the MR experiment, however, the dipolar fields are detected locally by their effect on the MR signal, in our case due to their rotary saturation effect on neighboring water. In this case, the relevant magnetic fields are not the far-fields of the dipole, as in MEG, but the local fields among the neurons. Nonetheless, a single current dipole provides an easy-to-construct approximation which at least matches the neural situation very closely in the far field but likely only to an order of magnitude in the local fields of activated cortex.

While we show that the rotary saturation method appears to have adequate sensitivity to local magnetic fields using a current dipole phantom, T₂*-based phase and amplitude methods are also adequate by these measures. For example, Konn et al are able to see a minimum dipole moment of 6.3 nAm (current of 1.3 μA and dipole size of 5 mm) using the phase shift in EPI in a phantom similar to ours using 62 minutes of averaging (Konn et al., 2003). Normalizing for averaging time, this corresponds to a dipole moment of 77 nAm (10 μA current) in a minute of scan time. Pell et al used the magnitude changes and observed a minimum current of 1.7 μA in a 1.8 min run; a normalized sensitivity of 2.3 μA in a minute of scan time. The block design results shown in Fig. 7 show a non-Bonferroni corrected p-value of 10⁻⁷ for a 56 nAm dipole (5.6 μA current) in 40 minutes of imaging time. However, unlike the phase and magnitude EPI experiments, the signal change in the SIRS experiment does not scale linearly with current. The method detects the reduction in magnetization as the spin-locked magnetization is rotated away from the spin-lock axis, thus scales as 1 − cos(ϕ) ≈ ϕ²/2 where ϕ is the small tip angle induced by the rotary saturation field in the doubly rotating frame. Since ϕ is proportional to B_rotarysat, and thus the current, the effect is expected to scale with the square of the current. Thus, for the SIRS experiment a 1 minute experiment would be expected to detect a 2.5 fold smaller current than the 40 min experiment. This suggests the ability to detect a 22.4 nAm dipole or 2.2 μA current in the normalized 1 minute of imaging time. While larger than that of the other two studies, or result occurred with a Bonferroni corrected p value of approximately 2 × 10⁻⁵ compared to the threshold for statistical significance of p = 10⁻³ used in the Pell result.

Figure 7.

Two-sided t-test results (not Bonferroni corrected) from the block design paradigm shown with a lower threshold of p < 10⁻³ and a color scale saturation level of p < 10⁻⁸. All block designs were 20 s per period, and γB_1lock = 40 Hz. T-test results are overlaid on a high resolution Turbo Spin Echo (TSE) image which allows visualization of the current dipole’s wires. a) 118 μA applied current, b) 11.5 μA applied current, c) 5.6 μA applied current. The statistical parametric map is overlaid over a high-resolution fast spin-echo image of the phantom to visualize the location of the dipole wire.

The failure of the T₂*-weighted imaging to detect actual neuronal currents in human experiments suggest that the single current dipole phantom does not adequately mimic the local phenomena near the neurons. Our best insight into whether or not the SIRS method (or other MR methods) is sufficiently sensitive to allow detection of neuronal fields comes from microSQUID measurements of evoked fields near the cortex. Okada and colleagues has measured the magnetic fields 1.2 mm above the cortex of juvenile swine. (Okada et al., 1999) They measure fields in excess of 1 pT in response to snout stimulation.

While the current dipole model used provides a diffuse current return path similar to that expected in vivo, practical implementation of the phantom causes problems which make it difficult to use for DC current measurements. When a DC current is used, electrolysis at the electrode tips occurs causing gas bubbles and alteration of the current. Eventually the tips must be sanded. Although platinum exhibits reduced electrolysis, unlike copper it is severely diamagnetically different from water and altered the EPI images. Thus, we did not perform a direct comparison to the DC current measurements in the literature using T2* weighted EPI phase and amplitude measures and rely on the extensive literature for the sensitivity of these methods.

A major difference between the macroscopic phantom’s local fields and that within the microscopic distribution of neurons is likely caused by the spatial cancellation effects in both field and MR phase arising from the multiple parallel neuronal currents in neighborhood of activated cortex. We break this down into two effects. First is the cancellation of the neuronal magnetic fields at some spatial locations within the distribution of synchronous neurons. For water at spatial locations where this cancellation occurs, it is unlikely that any MR method will be able to detect a signal change. For example, a region with uniformly spaced, current- carrying discrete wires with aligned currents, the magnetic field cancels at spatial locations half way between the wires and is reduced near these locations. The second concern is based on how the surviving fields affect the MR signal. The signal changes are determined by integrating the local effects over both time and space. Spatially, the magnitude and phase changes in a T₂*-weighed experiment are determined by integrating over the voxel. In this case, the effect can be reduced by the symmetry of the voxel with respect to the current distribution. For example, a single current-carrying wire centered on the voxel will not produce a net phase shift, and will exhibit a reduced magnitude reduction. Park and colleagues estimate the signal and magnitude changes for a region of activated cortex larger than a voxel. In this case, the voxels near the edge of the activated region have the strongest effect.

Considering time-domain effects is important for neuronal currents which reverse polarity during the measurement period. In the case of a symmetric multi-phasic current time course, there can be complete elimination of the accrued phase shift in the MR signal. MEG experiments suggest that at least partial cancellation will occur for many stimuli. This effect can be reduced by carefully timing the MR pulse sequence relative to the evoked response so that the phase sensitive part of the MR experiment only occurs during one phase of the response, or exactly straddles the refocusing pulse of a spin echo experiment (Singh, 1994).

An additional source of cancelation of the neuronal magnetic fields can derive from a lack of phase coherence among the neuronal currents. This leads to incomplete superposition among the individual neurons fields. This is a problem common to all neuronal magnetic field measurements including MEG since the distal nature of the MEG detectors is unlikely to help a lack of phase superposition. Although phase cancellation among the local fields undoubtedly occurs, a 1 nT estimate for the strength of local neuronal fields within millimeters of the activation is supported MicroSQUID measurements close to the cortex indicate the presence of neuronal magnetic fields above 1 nT 1 mm above active cortex (Okada et al., 1999) (Ikeda et al., 2005).

The rotary saturation approach presented here cannot offer improved detection in areas where the fields from the local neuronal currents cancel, but likely has advantageous spatial and temporal averaging properties relative to MR phase measurements and T2*-weighted imaging. The saturation method does not suffer from intra-voxel cancellation due to the phase of the saturation field; local water molecules will be saturated by the neuronal fields regardless of the phase of these fields, and the averaged effect over the voxel or time-period of the spin locking will always further reduce the signal intensity.

A further limitation that is common to both our approach and the T₂*-based methods is that the neuronal magnetic field needs to be parallel to B₀ in order to have an effect. When investigating the cerebral cortex and assuming large pyramidal neurons to be the main generator of the neuronal magnetic field, only certain regions of the cortex satisfy this condition for a given head position, thus, in an in vivo experiment the target area needs to be carefully selected and the subjects head appropriately positioned. A similar “orientation blindness” occurs in MEG which is insensitive to radial dipoles. For the Rotary Saturation experiment, the neuronal fields must be oriented orthogonal to the spinlock field. If needed the experiment could be repeated with the spinlock along the other axis to eliminate the orientation blind spot.

Furthermore, there are additional limitations to an in vivo rotary saturation experiment. The spin-locking period is limited in time by both SAR restrictions and the T_1ρ time. The method, as implemented, was limited to single slice measurements, although multislice spin-locking sequences have been developed for other purposes (Wheaton et al., 2004). In a motional narrowed regime, such as the bulk water that is usually imaged in MRI, the T_1ρ time is almost identical to T₂ when the spin-lock is performed on resonance (Moran and Hamilton, 1995). Practically this limits the spin-lock duration to about 100 ms. Furthermore, the selected Larmor frequency in the rotating frame has an upper limit due to the SAR restrictions and a lower limit imposed by the ability to create a spin-lock. However, our initial tests with in vivo imaging have found that Larmor frequencies in the rotating frame as low as 10 Hz are feasible (see Fig. 3). Additionally, the method is currently sensitive to only a single frequency of neuronal currents but could, in principle, be extended to at least several frequencies.

We designed our phantom experiment to demonstrate the SIRS effect in the frequency range of evoked responses commonly observed in MEG/EEG measurements of the human brain. Virtually all magnetic fields originating from postsynaptic currents have frequencies of less than 120 Hz, with the bulk of fields being below 20 Hz. Examples for experiments that evoke narrow-band oscillations are auditory click-trains (Lin et al., 2004), somatosensory stimulation with rapid electrical or mechanical pulse trains (Prevec and Ribaric-Jankes, 1996) and visual stimulation with periodic rapidly changing intensity (Muller et al., 1997). It is also possible to evoke or induce so called gamma oscillations (30 Hz-60 Hz) with specific stimuli, which will give rise to narrow-band magnetic fields occurring often from the sensory cortex associated with the modality.

Contamination by the BOLD effect is a problem common to all MR neuronal current methods and several studies have attempted to address this.(Bandettini et al., 2005) For example, eliminating BOLD contamination might be achieved by timing to make the experiment sensitive only to the early response and not the later BOLD signal. This requires a long Inter- Stimulus Interval (ISI) and renders the experiment inefficient. A second approach is to saturate the BOLD effect by attempting to have similar BOLD responses for all conditions. For the SIRS method this might involve altering the stimulus frequency by approximately 10 Hz so that the Rotary saturation effect is on-resonance for one condition and off resonance for the other. This gives full SIRS contrast but little BOLD changes if the two stimuli have similar BOLD response. A third method is to attempt to reduce the BOLD effect by performing the study at low B₀ fields. Unlike BOLD, most neuronal current methods (including SIRS) are expected to have little dependence on B₀. The contrast itself is not altered for SIRS except through secondary effects such as relaxation times changes. Since T₂ and thus T_1ρ are expected to lengthen at lower B₀, SIRS contrast should slightly improve with experiments at lower B₀ field. Similarly the reduced Specific Absorption Rate (SAR) constraints will allow longer TSL and more sensitive detection. The time series SNR is expected to have only modest decreases as the B₀ is lowered due to the dominance of physiological noise at high field for conventional voxel volumes (Triantafyllou et al., 2005). Finally, there is some hope that pharmacologic preparation might help for neuronal current studies in animal models. Here agents are being sought which act only on astrocytes and effect the flow response but not electrophysiology (Baslow et al., 2005).

The sensitivity of the method is limited by T_1ρ and the spinlock duration TSL. T_1ρ is influenced by many parameters including the B₀ field, the spinlock field amplitude (B_1lock) the temperature, and the tissue type. Borthakur et al found T_1ρ for gray and white matter to be 99ms and 85ms respectively at ω_1lock = 500 Hz at 1.5 T. The corresponding T₂ values were 75ms and 66ms. Thus, the T_1ρ in the brain is similar in magnitude to T₂, but not identical.

Conclusion

We introduce a new method by which neuronal currents might be construed to affect MR signals. We demonstrate that the method has the sensitivity to detect the magnetic fields of dipole current sources of similar magnitude and frequencies to that observed in MEG experiments. The method is an analog to the excitation of MR signal by neuronal fields proposed by Kraus (2006) for ultra-low field MRI, but has the advantage of being applicable to standard high-field MR instrumentation. While we have not yet demonstrated its ability to detect neuronal fields in vivo, the method has many favorable spatial and temporal averaging properties which may be holding back conventional MR phase and T2* magnitude-based studies.