Do synergies improve accuracy?

Abstract

We explored possible effects of negative co-variation among finger forces in multi-finger accurate force production tasks on the classical Fitts’ speed-accuracy trade-off. Healthy subjects performed cyclic force changes between pairs of targets “as quickly and accurately as possible”. Tasks with two force amplitudes and six ratios of force amplitude to target size were performed by each of the four fingers of the right hand and four finger combinations. There was a close to linear relation between movement time and the log-transformed ratio of target amplitude to target size across all finger combinations. There was a close to linear relation between standard deviation of force amplitude and movement time. There were no differences between the performance of either of the two “radial” fingers (index and middle) and the multi-finger tasks. The “ulnar” fingers (little and ring) showed higher indices of variability and longer movement times as compared to both “radial” fingers and multi-finger combinations. We conclude that potential effects of the negative co-variation and also of the task sharing across a set of fingers are counter-balanced by an increase in individual finger force variability in multi-finger tasks as compared to single-finger tasks. The results speak in favor of a feed-forward model of multi-finger synergies. They corroborate a hypothesis that multi-finger synergies are created not to improve overall accuracy but to allow the system larger flexibility, for example to deal with unexpected perturbations and concomitant tasks.

Introduction

Several recent studies have reported force-stabilizing synergies in finger force production tasks (Latash, Scholz, Danion, and Schöner 2001, 2002; Scholz, Danion, Latash, and Schöner 2002; Shim, Olafsdottir, Zatsiorsky, and Latash 2005; reviewed in Latash, Scholz, and Schöner 2002, 2007). In those studies, synergies have been defined as neural organizations that allow for co-variation of elemental variables (those produced by elements of a system) that stabilize important performance variables (Gelfand and Latash 1998; Latash 2002b). In multi-finger force production studies, elemental variables were associated with individual finger forces or commands to fingers (i.e., finger modes, Danion et al. 2003), while performance variables were associated with the total force produced or total moment of force produced. In particular, during slow accurate force production tasks, individual finger forces (and finger modes) have been shown to co-vary negatively across trials, leading to a drop in the total force variability as compared to what could be expected in the absence of co-variation.

However, do synergies actually improve accuracy? Surprisingly, there is no clear answer to this question. One reason is that variability of individual finger forces may increase in multi-finger tasks as compared to single-finger tasks such that, even in the presence of negative co-variation among finger forces, the total force may show higher, lower, or unchanged variability. Another complicating factor is that indices of force variability scale with force magnitude (Newell and Carlton 1988; Carlton, Kim, Liu, and Newell, 1993), and finger groups are known to be stronger as compared to single fingers in isometric force production tasks (Li, Latash, and Zatsiorsky, 1998). This means that tasks should be set differently to allow comparisons between single-finger and multi-finger tasks.

Previously, one study examined how finger force variability changed as the number of fingers in a cyclic force production task changed (Latash et al 2001). In that study, using two fingers decreased the coefficient of variation of the total force as compared to one-finger tasks. However, adding a third finger did not change the coefficient of variation. In all cases, the tasks were set as equal percentages of the maximal force producing ability of the explicitly involved finger groups (cf. Christou, Grossman, and Carlton, 2002).

In this study, we address the issue of variability in force production between single- and multi-finger tasks using two types of speed-accuracy trade-off. The first is the famous Fitts’ law (Fitts 1954; Fitts and Peterson 1964; reviewed in Plamondon and Alimi 1997), which states that, when humans are required to perform movements to a target “as fast and as accurately as possible”, movement time (MT, the time between the initiation and the end of an action) is a logarithmic function of the ratio between movement amplitude (A) and target width (W): MT = a + b* log₂(2A/W). This relation is frequently expressed using the notion of index of difficulty (ID), ID = log₂(2A/W). Fitts’ law has been confirmed over a variety of populations, conditions and tasks, including isometric force production tasks (Kantowicz and Elvers 1988; Billon, Bootsma, and Mottet, 2000). Although the location of mechanisms that produce Fitts’ law is still under debate (Meyer, Smith, and Wright, 1982; Plamondon and Alimi 1997), it is likely to reflect processes at the level of motor planning (Gutman and Latash 1993; Duarte and Latash 2007).

Hence, our first hypothesis is that the central neural controller will take advantage of the negative force co-variation in multi-finger tasks and show faster force production (smaller MT) for comparable IDs as compared to single-finger tasks. We expected the decrease in MT (as compared to what could be expected in the absence of multi-finger force stabilizing synergies) to be higher for tasks with higher ID, which require slower force rates, since such tasks are associated with stronger negative force co-variation (Latash et al. 2002a). We expected the decrease in MT to be absent during very fast movements (low ID and low MT) since negative co-variation is commonly absent in such tasks (Latash et al. 2002a; Olafsdottir, Yoshida, Zatsiorsky, and Latash, 2005).

Another well-established paradigm of the speed-accuracy trade-off links variability in final position (expressed as the effective target width, W_E) and actual movement amplitude to movement time: W_E = a + b*(A/MT), where a and b are constants (Schmidt, Zelaznik, Hawkins, Frank, and Quinn, 1979). To test whether negative co-variation among finger forces helps improve finger force variability in multi-finger tasks, we explored the relation between MT and W_E. Our second hypothesis is that multi-finger tasks will be associated with smaller W_E expressed in percentage of maximal voluntary force for similar MT values.

Methods

Participants

Four male and four female students served as subjects in this study. Average data for the subjects were (mean ± SD): 27 ± 3 years of age, 1.71 ± 0.11 m in height, 70.9 ± 12.8 kg in mass, 18.8 ± 1.8 cm for right hand length, 8.5 ± 1.0 cm for right hand width, 18.9 ± 1.9 cm for left hand length, and 8.3 ± 1.0 cm for left hand width. Hand length was measured as the distance from the tip of the distal phalanx of digit three to the distal crease of the wrist with the hand in a neutral flexion/extension pose. Hand width was measured between the lateral aspects of the index and little finger metacarpophalangeal (MCP) joints. All subjects were strongly right-handed according to their preferential use of the hand during daily activities such as writing, drawing, and eating. The subjects had no previous history of neuropathies or traumas to the upper limbs. None of the subjects had a history of long-term involvement in hand or finger activities such as typing and playing musical instruments. All subjects gave informed consent according to the procedures approved by the Office of Regulatory Compliance of the Pennsylvania State University.

Experimental Setup

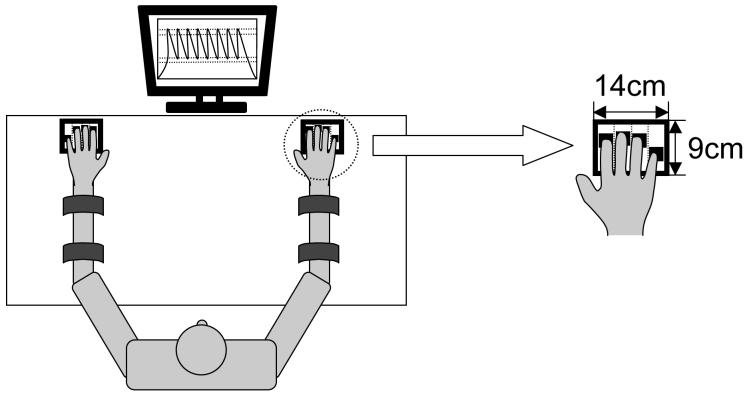
Eight unidirectional piezoelectric force sensors (model 208AO3; PCB Piezotronic Inc., Depew, NY, USA), were used to measure forces produced by the tips of individual fingers of both hands. Each sensor was covered with a cotton pad to increase friction and prevent the influence of finger skin temperature on the force measurements. Two groups of four force sensors were placed within aluminum frames (14cm × 9cm each) in a groove on a wooden board. The two frames were spaced 40 cm apart. The sensors were medio-laterally spaced 3 cm apart from each other within the aluminum frames. The position of the sensors in the anterior-posterior direction could be adjusted within 6 cm in order to fit individual subject hand anatomy, see Figure 1. Subjects were instructed to rest their fingers on the sensor, but to apply no force prior to each trial. At the beginning of each trial, the signal from each of the sensors was set to zero with the subject’s fingers resting on the sensors.

Figure 1.

An illustration of the sensor setup and visual feedback display for this experiment.

During the experiment, the subject sat in a chair facing the testing table with his/her upper arms at approximately 45° of abduction in the frontal plane and 45° of flexion in the sagittal plane, and the elbow at approximately 45° of flexion (Figure 1). The forearms were secured to the wooden board via two sets of Velcro straps. The midline of the board was aligned with the midline of the participant’s body, and the positions of the hands were symmetrical with respect to the midline of the body. A custom-fitted support object was placed underneath each of the participant’s palms to help maintain a constant configuration of the hand and fingers. The MCP joints were approximately 20° in flexion and all interphalangeal joints were slightly flexed such that each hand formed a dome. Subjects were permitted to select comfortable positions of the thumbs during the experiment. A computer monitor was located 0.65 m away from the subject. The monitor displayed the task (described in the next section). Force data were sampled at 200 Hz with a National Instruments A/D board (NI PCI-6023E, National Instruments, Austin, TX, USA) and LabView-based program (LabView 6.1, National Instruments, Austin, TX, USA).

Procedure

The experiment consisted of a few control trials and a main set of tasks. In the control trials, the subjects were required to produce maximal voluntary contraction (MVC) force by finger sets used in the main task. The nine finger sets were: I_R, M_R, R_R, L_R, M_L, IM_R, IMR_R, IMRL_R, and I_RM_L; where I = index, M = middle, R = ring, L = little, and the subscripts denote the hand to which the fingers belong (R = right, L = left). These particular fingers and finger combinations were selected to explore possible differences across the four fingers, across finger combinations with different numbers of fingers, and across one-hand and two-hand finger combinations. The subjects were required to press with the instructed set of fingers “as hard as possible”. Each MVC trial started with the subject sitting quietly with the hands resting on the sensors. A sound signal was given and then a cursor showing the total force produced by the instructed fingers started to move over the screen. The subject was given a time interval of 3 s to reach maximal force by pressing down with the instructed set of fingers. There were intervals of at least 30 s between successive MVC trials. Two MVC trials per finger combination were collected and the trial with the highest total peak force produced by the instructed fingers (MVC_IF) was selected for setting subsequent tasks.

In the set of main tasks, subjects were instructed to press with the specified set of fingers such that the total force produced by the fingers oscillated between two target windows as quickly as possible. Subjects were instructed to complete a minimum of twelve accurate oscillations (out of fifteen consecutive oscillations) between the two target windows in each trial. After the oscillations, subjects were instructed to stop producing finger forces in order to reduce the effects of fatigue. The distance (A) between the centers of the two targets was set at 10% and 20% of MVC_IF. The lowest of the two targets was centered at 10% MVC_IF to avoid the floor effect on the target window. For the A = 10% MVC_IF condition, the targets were centered at 10% and 20% MVC_IF; for the A = 20% MVC_IF, the targets were centered at 10% and 30% MVC_IF, respectively. The width of the target windows (W) displayed for the subjects was selected to correspond to six indices of difficulty (ID), ID = log₂(2A/W), such that IDs = 1.5, 2.0, 2.5, 3.0, 3.5, and 4.0 were used. For the 10% MVC distance between targets, these IDs correspond to target widths of 7.07, 5.00, 3.54, 2.50, 1.77, and 1.25% MVC. For the 20% MVC distance between targets, these IDs correspond to target widths of 14.14, 10.00, 7.07, 5.00, 3.54, and 2.50% MVC. We purposefully explored a broad range of ID values to compare very high rates of force production (that were not expected to show high negative force co-variation - see the Introduction) and relatively slow force production. Thus, each of the nine finger combinations were tested at twelve different target conditions, resulting in 108 trials in the main set of tasks and total minimum of 1296 force cycles. One trial per testing condition (108 testing conditions) was collected for each subject. Trial rejection criterion is presented in the following paragraphs.

Prior to each trial the subject sat relaxed with the digits of each hand resting on the sensors. The computer generated two beeps (a “get ready” signal), and a cursor showing the total force produced by the instructed finger(s) started to move along the screen. The screen also showed the two targets (see Figure 1), and the task was to oscillate between the two targets with the cursor as quickly as possible while keeping the number of errors (landing outside a target) under 20%.

In each condition, subjects performed 1 trial with 60 s intervals between consecutive trials. There were 3-minute rest intervals after every fifteen trials in order to reduce the effects of fatigue. If subjects claimed fatigue between such scheduled rest intervals, an additional rest period of 3-5 minutes was given to the subject immediately. Prior to each trial, subjects were permitted to practice the condition until they were comfortable with the tasks. Typically, subjects did not need a practice trial before most conditions. However, for conditions with high ID values (ID = 3.5 and 4.0), some subjects needed practice trials. On average, subjects performed one practice trial for ID conditions 3.5 and 4.0. Presentation of tasks was randomized across the subjects. Trials in which the subject failed to achieve twelve accurate oscillations out of fifteen consecutive oscillations were rejected and repeated immediately. On average, less than three trials were rejected per subject.

Data Analysis

The data were processed off-line using customized MATLAB software (Mathworks Inc., Natick, MA, USA). The force data from the main task were low-pass filtered at 10 Hz using a 2^nd order, zero-lag Butterworth filter. For the finger force data, the oscillations between targets were considered to consist of two components: increase (UP) and decrease (DN) of total force.

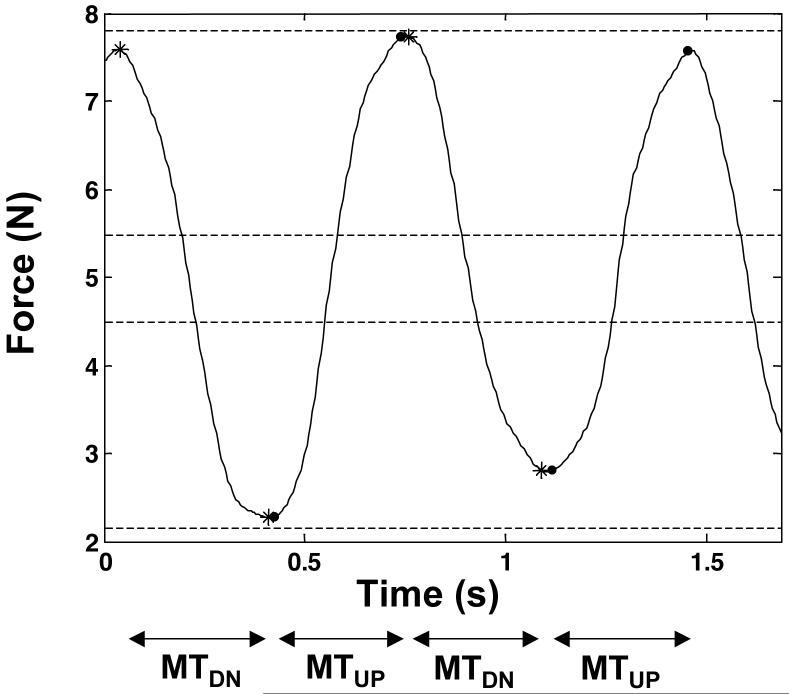
Movement time (MT) was determined as the time between the two consecutive occurrences of 5% of the absolute maximum force rate (|VF_max|) within a half-cycle of an oscillation. The value of VF_max was defined using the first time derivative of the total force produced by the instructed fingers. Thus, MT for the increase component (MT_UP) was determined as the time between the two 5% |VF_max| occurrences of an increase in total force while MT for the decrease component (MT_DN) was determined as the time between the two 5% |v_max| occurrences of a decrease in total force. The first time derivative of the total force was used to determine MT since some subjects exhibited dwell time at the targets during the task, thus the intervals between total force maxima and minima would not accurately reflect actual MT. MT_UP and MT_DN were averaged separately across each trial. An example of MT definitions is shown in Figure 2. Force variability was estimated using the effective target width (W_E), computed as four times the standard deviation (SD) of force amplitude across oscillations within a condition. This interval for W_E corresponds to the range ± 2*SD, which will contain 95.4% of the data of interest (here, final force level) given a normal data distribution (Duarte and Latash, 2007).

Figure 2.

An example of MT definitions for two MT_UP and two MT_DN time intervals for a task (actual data is shown). Force output by instructed fingers is shown as a solid line; targets are denoted by bands between two sets of thin dashed lines. The beginning and end of MT_UP intervals are denoted by filled-in circles; the beginning and end of MT_DN intervals are denoted by asterisks. Both MT_UP and MT_DN intervals are also denoted by arrows for clarity. Note that both MT_UP and MT_DN intervals are defined by 5% of the absolute maximum velocity (|v_max|) within a half-cycle of an oscillation.

Statistics

The data are presented in the text and figures as means and standard errors. Mixed model analyses of variance (ANOVAs) were performed on the MT and W_E data with the factors: Subject (random factor, 8 levels), ID (six levels, 1.5, 2.0, 2.5, 3.0, 3.5, and 4.0), Amplitude (two levels, 10% MVC_IF and 20% MVC_IF), Fingers (nine levels, one for each finger condition, levels were selected depending on particular comparisons), #Fingers (four levels, one for the number of fingers involved in both single and multi-finger tasks), and Force Change (two levels, one for MT_UP and the other for MT_DN). Both the MT and W_E data were log₁₀-transformed in order to comply with normality assumptions during statistical testing. Pair-wise comparisons were performed using Bonferroni statistics to analyze significant effects of ANOVAs. Linear and exponential regressions were also performed in order to determine overall correlations of movement time and effective target width to index of difficulty.

Results

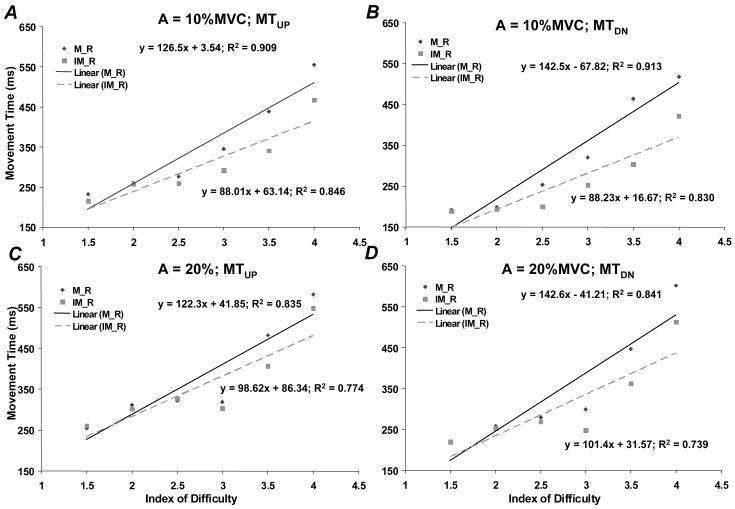
All subjects were able to perform each of the main set of tasks without overt difficulty. Generally, all subjects showed a nearly linear dependence of movement time (MT) on index of difficulty (ID) as elucidated by Fitts Law (see Introduction). Figure 3 shows the performance of a typical subject for several finger combinations across ID levels for both MT_UP and MT_DN. Across all subjects, MT (both MT_UP and MT_DN) could be described by a linear relationship with ID, which was verified with linear regressions. Such models explained, on average, 59.5% of the variance in the data across all finger combinations for MT_UP and 62.0% of the variance in the data across all finger combinations for MT_DN. A summary of the MT data for all subjects in all tested conditions can be found in Table 1.

Figure 3.

An exemplary subject’s movement time performance (MT_UP and MT_DN) across ID levels for both the M_R (solid diamonds) and IM_R (gray squares) finger combinations, as well as their linear regressions with respect to ID. A: MT_UP for force production amplitude = 10% MVC, B: MT_DN for force production amplitude = 10% MVC, C: MT_UP for force production amplitude = 20% MVC, D: MT_DN for force production amplitude = 20% MVC

Table 1. Movement time.

Group averages and standard deviations of movement time data are shown for all force production amplitudes (A) and indices of difficulty (ID). UP refers to force increase half-cylces and DOWN refers to force decrease half-cycles. I = index, M = middle, R = ring, L = little, and the subscripts denote the hand to which the fingers belong (R = right, L = left). Movement time values are presented in ms

A = 10 % MVC

A = 20 % MVC

ID

1.5

2

2.5

3

3.5

4

ID

1.5

2

2.5

3

3.5

4

UP

I

263 ± 22

248 ± 28

311 ± 34

367 ± 40

398 ± 42

464 ± 72

UP

I

235 ± 23

308 ± 35

338 ± 40

316 ± 46

368 ± 45

383 ± 40

M

278 ± 30

257 ± 30

305 ± 39

328 ± 48

344 ± 32

419 ± 57

M

278 ± 38

300 ± 40

264 ± 28

278 ± 31

379 ± 50

429 ± 53

R

263 ± 21

255 ± 19

298 ± 37

336 ± 39

413 ± 525

451 ± 61

R

274 ± 42

286 ± 31

292 ± 34

328 ± 44

405 ± 52

442 ± 63

L

265 ± 16

285 ± 20

294 ± 29

348 ± 48

392 ± 37

484 ± 46

L

240 ± 19

275 ± 32

298 ± 43

353 ± 42

428 ± 49

500 ± 44

M_L

261 ± 25

287 ± 37

293 ± 32

312 ± 45

380 ± 47

492 ± 80

M_L

303 ± 55

289 ± 37

310 ± 31

367 ± 58

394 ± 68

460 ± 66

A = 10 % MVC

A = 20 % MVC

ID

1.5

2

2.5

3

3.5

4

ID

1.5

2

2.5

3

3.5

4

DOWN

I

257 ± 18

237 ± 24

309 ± 29

379 ± 41

403 ± 38

490 ± 90

DOWN

I

245 ± 20

289 ± 26

329 ± 33

323 ± 45

394 ± 35

415 ± 47

M

276 ± 27

260 ± 25

319 ± 33

341 ± 46

405 ±40

439 ± 69

M

267 ± 28

284 ± 29

260 ± 24

285 ± 21

398 ± 38

446 ± 46

R

286 ± 23

264 ± 22

339 ± 36

380 ± 47

454 ± 43

562 ± 77

R

290 ± 37

299 ± 30

311 ± 29

381 ± 42

470 ± 47

516 ± 62

L

279 ± 15

310 ± 20

338 ± 29

394 ± 47

459 ± 48

574 ± 58

L

276 ± 27

309 ± 32

336 ± 48

398 ± 44

466 ± 46

543 ± 50

M_L

275 ± 18

321 ± 34

324 ± 32

324 ± 48

418 ± 51

508 ± 71

M_L

300 ± 46

287 ± 30

297 ± 24

378 ± 50

439 ± 58

505 ± 76

A = 10 % MVC

A = 20 % MVC

ID

1.5

2

2.5

3

3.5

4

ID

1.5

2

2.5

3

3.5

4

UP

M_R

278 ± 30

257 ± 30

305 ± 39

328 ± 48

344 ± 32

419 ± 57

UP

M_R

278 ± 38

300 ± 40

264 ± 28

278 ± 31

379 ± 50

429 ± 53

IM_R

269 ± 35

257 ± 33

260 ± 22

344 ± 55

416 ± 48

425 ± 51

IM_R

293 ± 37

300 ± 35

312 ± 32

320 ± 41

377 ± 51

451 ± 55

IM_RL

251 ± 23

259 ± 35

291 ± 32

329 ± 36

422 ± 58

448 ± 45

IM_RL

266 ± 27

291 ± 37

307 ± 34

317 ± 38

361 ± 46

400 ± 60

IMR_R

237 ± 21

266 ± 28

294 ± 32

339 ± 37

378 ± 38

447 ± 37

IMR_R

251 ± 30

298 ± 38

270 ± 28

325 ± 29

393 ± 54

475 ± 52

IMRL_R

235 ± 24

312 ± 56

310 ± 47

357 ± 60

421 ± 50

493 ± 68

IMRL_R

250 ± 27

257 ± 26

297 ± 36

332 ± 29

411 ± 44

444 ± 50

A = 10 % MVC

A = 20 % MVC

ID

1.5

2

2.5

3

3.5

4

ID

1.5

2

2.5

3

3.5

4

DOWN

M_R

276 ± 27

260 ± 25

319 ± 33

341 ± 46

405 ± 40

439 ± 69

DOWN

M_R

267 ± 28

284 ± 29

260 ± 24

285 ± 21

398 ± 38

446 ± 46

IM_R

251 ± 28

248 ± 30

264 ± 23

353 ± 48

397 ± 54

475 ± 70

IM_R

290 ± 29

302 ± 30

305 ± 28

315 ± 32

387 ± 39

490 ± 67

IM_RL

241 ± 15

263 ± 29

275 ± 26

322 ± 23

421 ± 55

474 ± 38

IM_RL

278 ± 15

286 ± 27

314 ± 27

316 ± 30

364 ± 31

416 ± 58

IMR_R

246 ± 18

260 ± 16

290 ± 23

333 ± 32

364 ± 30

466 ± 41

IMR_R

273 ± 30

306 ± 33

291 ± 22

321 ± 17

420 ± 46

548 ± 67

IMRL_R

230 ± 16

293 ± 44

309 ± 43

349 ± 47

429 ± 40

528 ± 70

IMRL_R

270 ± 23

259 ± 19

295 ± 25

384 ± 53

431 ± 45

474 ± 50

MT dependence on Amplitude, Index of Difficulty, and Force Changes

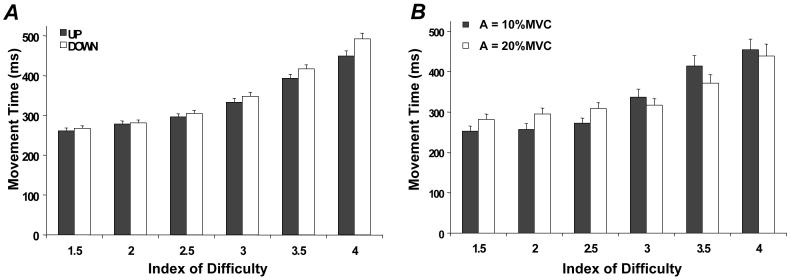
Overall, force production amplitude did not affect MT significantly. However, ID level and force change affected MT across all finger combinations. Namely, MT increased as ID level increased and MT_UP < MT_DN, when MT was analyzed across all finger combinations, as shown in panel A of Figure 4. This was confirmed via a four-way mixed effects ANOVA with factors: Subject, ID, Amplitude, and Force Change. Main effects of Subject [F_7,1697 = 313.41, p < 0.001], ID [F_5,1697= 302.81, p < 0.001], and Force Change [F_1,1697= 29.02, p < 0.001] were found without any significant interactions. Pair-wise Tukey’s comparisons revealed significant differences across all pairs of the ID levels except 1.5 vs. 2.0. The significant effects reflected an increase in MT with ID and smaller MT_UP as compared to MT_DN. This pattern of significant differences among ID levels was consistent across all of the mixed-effect ANOVAs with ID as a factor performed on the MT data.

Figure 4.

Average movement time for different ID levels (across all subjects with standard error bars). A: MT_UP (solid bars) and MT_DN (white bars) both increase as ID level increases, B: The Amplitude × ID interaction for IM_R and I_RM_L tasks is shown. For IDs less than or equal to 2.5, MT (the average of MT_UP and MT_DN) was smaller for the smaller force production amplitude (A₁₀, solid bars). For IDs larger than or equal to 3.0, MT was smaller for the larger force production amplitude (A₂₀, white bars).

An Amplitude × ID interaction was found for MT in only the two two-finger combinations, IM_R and I_RM_L, such that, for IDs less than or equal to 2.5, MT was lower for the smaller force production amplitude (A₁₀) as compared to the larger force production amplitude (A₂₀). For IDs larger than or equal to 3.0, MT was lower for A₂₀ as compared to A₁₀. This was confirmed using a four-way mixed effects ANOVA with the factors: Subject, ID, Amplitude, and Force Change. Main effects of Subject [F_7,353 = 68.06, p < 0.001], ID [F_5,353 = 56.76, p < 0.001], and ID × Amplitude [F_5.353 = 4.3, p < 0.005] were found. This interaction is illustrated in panel B of Figure 4. Pair-wise Tukey’s comparisons revealed significant differences across all pairs of the ID levels except 1.5 vs. 2.0-2.5.

Effects of Finger Combination on Movement Time

To determine possible effects of finger combinations on MT, the following analyses were run. First, we investigated whether or not there were differences for both MT_UP and MT_DN across the single-finger tasks (I_R, M_R, R_R, L_R, and M_L) at each ID level. For MT_UP, there was no difference among the single-finger tasks across ID levels. However, for MT_DN there was a difference among the single-finger tasks such that on average MT_DN for the “radial” fingers (I_R and M_R) was about 50 ms shorter than MT_DN for the “ulnar” fingers (R_R and L_R). It was also found that, on average, MT_DN for the M_R task was 33 ms less than for the M_L task.

This was confirmed with three-way mixed effects ANOVAs, run separately for MT_UP and MT_DN, with the factors: Subject, ID, and Fingers. Main effect of Subject [F_7,443 = 134.33, p < 0.001] and ID [F_5,443 = 81.52, p < 0.001] were found for MT_UP, confirming an increase in MT_UP with ID, with no significant interactions (see Figure 4A). MT_DN showed main effects of Subject [F_7,443 = 79.75, p < 0.001], ID [F_5,443 = 96.92, p < 0.001], and Fingers [F_4,443 = 10.29, p < 0.001] with no significant interactions. Pair-wise Tukey’s comparisons revealed differences between the “radial” and “ulnar” fingers on the right hand (I_R and M_R were significantly different from R_R and L_R) as well as between M_R and M_L. Namely, I_R and M_R showed lower MT_DN as compared to R_R and L_R, while M_R showed lower MT_DN as compared to M_L.

Next, we investigated whether or not there was a difference for both MT_UP and MT_DN between the two two-finger tasks, one task involving the fingers from the right hand and the other task involving fingers from the two hands (IM_R and I_RM_L) at each ID level. For both MT_UP and MT_DN, there was no difference between the two-finger tasks across ID levels. This was confirmed with three-way mixed effects ANOVA with the factors: Subject, ID, and Fingers. Main effects of Subject [F_7,173 = 28.02, p < 0.001; F_7,173 = 43.34, p < 0.001] and ID [F_5,173 = 31.56, p < 0.001; F_5,173 = 25.14, p < 0.001] were found for MT_UP and MT_DN, respectively. However, no effect of Fingers was found as well as no significant interactions.

At the next step, we investigated whether or not there was a difference for both MT_UP and MT_DN across tasks involving different numbers of fingers (single-finger tasks vs. two-finger tasks vs. three-finger tasks vs. four-finger tasks). Since there was no difference among single finger tasks for MT_UP, the M_R task was chosen as the representative single-finger task. Similarly, IM_R was chosen as the representative two-finger combination.

MT_UP showed no dependence on the number of instructed fingers at each of the ID levels. This was confirmed with a three-way mixed effects ANOVA with the factors: Subject, ID, and #Fingers. Main effects of Subject [F_7,353 = 116.6, p < 0.001] and ID [F_5,353 = 76.53, p < 0.001] were found, while there were no effects of #Fingers nor any significant interactions.

Since there were differences in MT_DN between the “radial” and “ulnar” fingers in single-finger tasks, separate analyses were run to study the dependence of MT_DN on the number of instructed fingers. Analysis comparing a “radial” finger (M_R) to multi-finger combinations showed no difference among the tasks at each of the ID levels. This was confirmed with a three-way mixed effects ANOVA with the factors: Subject, ID, and #Fingers. Main effects of Subject [F_7,353 = 68.38, p < 0.001] and ID [F_5,353 = 87.92, p < 0.001] were found, but no effect of #Fingers and no significant interactions.

However when data from an “ulnar” finger (L_R) were used, there were difference in MT_DN among the tasks at each of the ID levels. The multi-finger tasks showed faster force production (lower MT_DN) as compared to the single-finger task (on average, by 44 ms). This was confirmed with a three-way mixed effects ANOVA with the factors: Subject, ID, and #Fingers. Main effects of Subject [F_7,353 = 61.12, p < 0.001], ID [F_5,353 = 95.14, p < 0.001], and #Fingers [F_3,353 = 9.97, p < 0.001] were found with no significant interactions. Pair-wise Tukey’s comparisons revealed significant differences between L_R and each of the multi-finger combinations (IM_R, IMR_R, and IMRL_R), such that MT for L_R was larger as compared to the multi-finger combinations without significant differences across the multi-finger combinations.

Speed-Accuracy Trade-off and Effective Target Width

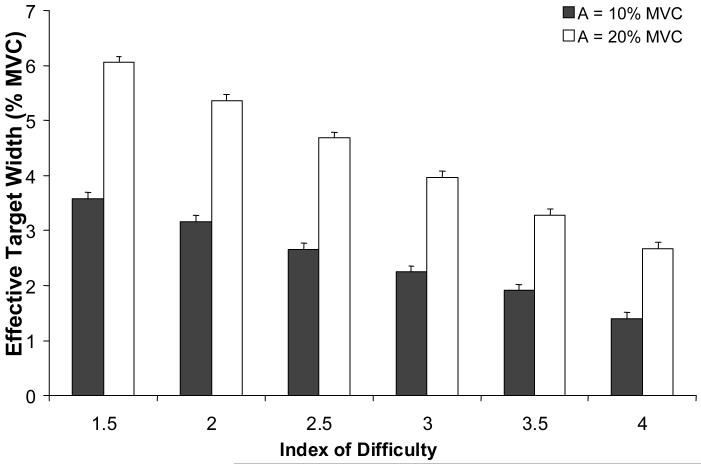
In general, there was a close to linear relationship between presented target width (W) and effective target width (W_E, estimated as 4 times SD of the final position, see Methods) across all finger combinations, force production amplitudes, and force changes, as shown in Figure 5. This was verified with a linear regression between presented target width and effective target width. This model explained 49.6% of the variance in the data across all finger combinations, force production amplitudes, and force changes.

Figure 5.

Average effective target width for different ID levels (across all finger combinations, subjects, and force production directions). Standard error bars are shown. Effective target width with respect to force production amplitude of 10% (solid bars) and 20% (white bars) decreases as ID level increases.

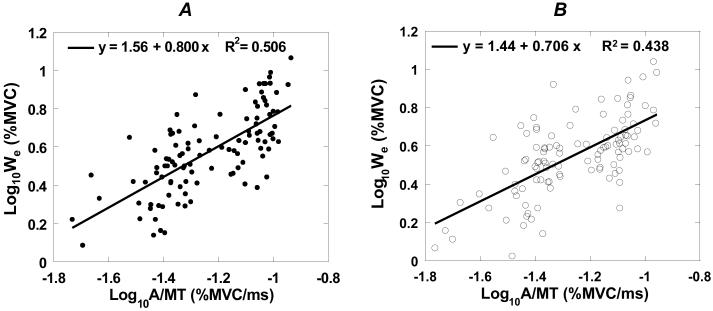
After logarithmic transformation of both variables, W_E and MT showed a linear relationship such that an increase in MT was associated with a drop in W_E. Figure 6 presents a typical subject’s performance across all finger combinations for both force increase and force decrease half-cycles. Across all subjects, log₁₀ (W_E) could be described as a linear function of log₁₀(A/MT), which was verified with linear regressions: log₁₀(W_E) = c + b*log₁₀(A/MT). This model explained 49.9% of the variance in the data across all finger combinations and force changes. A summary of the W_E data for all subjects in all tested conditions can be found in Table 2.

Figure 6.

Dependences of the log-transformed W_E,UP (filled circles, A) and W_E,DN (open circles, B) on the log-transformed ratio Amplitude/MT across all finger combinations with linear regression lines and equations. Data for a typical subject are shown.

Table 2. Effective target width.

Group averages and standard deviations of effective target width data are shown for all force production amplitudes (A) and indices of difficulty (ID). UP refers to force increase half-cycles and DOWN refers to force decrease half-cycles. Abbreviations are the same as in Table 1. Effective target width values are presented in % MVC

A = 10 % MVC

A = 20 % MVC

ID

1.5

2

2.5

3

3.5

4

ID

1.5

2

2.5

3

3.5

4

UP

I

0.033 ± 0.003

0.030 ± 0.002

0.023 ± 0.002

0.018 ± 0.002

0.018 ± 0.002

0.013 ± 0.001

UP

I

0.067 ± 0.007

0.055 ± 0.007

0.050 ± 0.005

0.040 ± 0.003

0.033 ± 0.003

0.026 ± 0.001

M

0.034 ± 0.004

0.030 ± 0.004

0.028 ± 0.002

0.026 ± 0.002

0.019 ± 0.002

0.013 ± 0.001

M

0.062 ± 0.008

0.060 ± 0.008

0.0054 ± 0.008

0.040 ± 0.0003

0.032 ± 0.003

0.035 ± 0.010

R

0.041 ± 0.005

0.035 ± 0.002

0.026 ± 0.002

0.023 ± 0.001

0.030 ± 0.012

0.015 ± 0.001

R

0.073 ± 0.007

0.060 ± 0.003

0.054 ± 0.004

0.041 ± 0.003

0.046 ± 0.008

0.027 ± 0.002

L

0.046 ± 0.003

0.038 ± 0.002

0.032 ± 0.003

0.021 ± 0.001

0.020 ± 0.002

0.015 ± 0.001

L

0.111 ± 0.021

0.066 ± 0.007

0.055 ± 0.006

0.051 ± 0.013

0,039 ± 0.001

0.045 ± 0.020

M_L

0.039 ± 0.005

0.032 ± 0.003

0.029 ± 0.002

0.023 ± 0.002

0.018 ± 0.001

0.014 ± 0.002

M_L

0.064 ± 0.007

0.060 ± 0.006

0.048 ± 0.004

0.045 ± 0.005

0.034 ± 0.004

0.027 ± 0.001

A = 10 % MVC

A = 20 % MVC

ID

1.5

2

2.5

3

3.5

4

ID

1.5

2

2.5

3

3.5

4

DOWN

I

0.032 ± 0.003

0.033 ± 0.003

0.024 ± 0.003

0.023 ± 0.002

0.019 ± 0.001

0.013 ± 0.001

DOWN

I

0.059 ± 0.006

0.045 ± 0.005

0.045 ± 0.009

0.034 ± 0.004

0.029 ± 0.004

0.024 ± 0.001

M

0.032 ± 0.002

0.032 ± 0.002

0.027 ± 0.004

0.026 ± 0.003

0.018 ± 0.001

0.014 ± 0.001

M

0.051 ± 0.007

0.061 ± 0.008

0.044 ± 0.004

0.040 ± 0.004

0.030 ± 0.003

0.026 ± 0.003

R

0.037 ± 0.004

0.044 ± 0.003

0.029 ± 0.002

0.022 ± 0.001

0.017 ± 0.001

0.014 ± 0.001

R

0.056 ± 0.005

0.048 ± 0.004

0.041 ± 0.005

0.041 ± 0.005

0.0031 ± 0.002

0.025 ± 0.002

L

0.041 ± 0.002

0.031 ± 0.004

0.026 ± 0.004

0.022 ± 0.002

0.020 ± 0.002

0.014 ± 0.001

L

0.064 ± 0.006

0.049 ± 0.007

0.049 ± 0.005

0.032 ± 0.003

0.030 ± 0.006

0.023 ± 0.001

M_L

0.040 ± 0.003

0.029 ± 0.002

0.029 ± 0.002

0.025 ± 0.001

0.017 ± 0.002

0.013 ± 0.001

M_L

0.059 ± 0.004

0.062 ± 0.006

0.060 ± 0.006

0.043 ± 0.005

0.036 ± 0.003

0.028 ± 0.001

A = 10 % MVC

A = 20 % MVC

ID

1.5

2

2.5

3

3.5

4

ID

1.5

2

2.5

3

3.5

4

UP

I_R

0.033 ± 0.003

0.030 ± 0.002

0.023 ± 0.002

0.018 ± 0.002

0.018 ± 0.002

0.013 ± 0.001

UP

I_R

0.067 ± 0.007

0.055 ± 0.007

0.050 ± 0.005

0.040 ± 0.003

0.033 ± 0.003

0.026 ± 0.001

IM_R

0.030 ± 0.002

0.033 ± 0.005

0.027 ± 0.002

0.021 ± 0.002

0.017 ± 0.001

0.017 ± 0.004

IM_R

0.056 ± 0.005

0.054 ± 0.005

0.048 ± 0.004

0.037 ± 0.004

0.034 ± 0.003

0.026 ± 0.003

IM_RL

0.034 ± 0.004

0.028 ± 0.003

0.027 ± 0.003

0.017 ± 0.003

0.017 ± 0.002

0.015 ± 0.001

IM_RL

0.058 ± 0.003

0.067 ± 0.008

0.040 ± 0.007

0.039 ± 0.004

0.033 ± 0.004

0.025 ± 0.001

IMR_R

0.039 ± 0.004

0.030 ± 0.002

0.024 ± 0.001

0.024 ± 0.002

0.017 ± 0.002

0.013 ± 0.001

IMR_R

0.066 ± 0.007

0.051 ± 0.005

0.043 ± 0.004

0.040 ± 0.005

0.033 ± 0.002

0.026 ± 0.002

IMRL_R

0.033 ± 0.002

0.027 ± 0.003

0.027 ± 0.002

0.024 ± 0.002

0.021 ± 0.002

0.014 ± 0.001

IMRL_R

0.067 ± 0.010

0.050 ± 0.005

0.047 ± 0.007

0.043 ± 0.003

0.032 ± 0.003

0.023 ± 0.001

A = 10 % MVC

A = 20 % MVC

ID

1.5

2

2.5

3

3.5

4

ID

1.5

2

2.5

3

3.5

4

DOWN

I_R

0.032 ± 0.003

0.033 ± 0.003

0.024 ± 0.003

0.023 ± 0.002

0.019 ± 0.001

0.013 ± 0.001

DOWN

I_R

0.059 ± 0.008

0.045 ± 0.006

0.045 ± 0.009

0.034 ± 0.004

0.029 ± 0.004

0.024 ± 0.001

IM_R

0.034 ± 0.005

0.030 ± 0.003

0.028 ± 0.002

0.023 ± 0.002

0.022 ± 0.003

0.014 ± 0.003

IM_R

0.054 ± 0.007

0.049 ± 0.004

0.047 ± 0.004

0.036 ± 0.004

0.029 ± 0.002

0.025 ± 0.002

IM_RL

0.030 ± 0.003

0.025 ± 0.002

0.023 ± 0.003

0.022 ± 0.001

0.020 ± 0.002

0.012 ± 0.001

IM_RL

0.043 ± 0.004

0.048 ± 0.005

0.043 ± 0.006

0.036 ± 0.004

0.031 ± 0.002

0.028 ± 0.002

IMR_R

0.037 ± 0.003

0.033 ± 0.003

0.025 ± 0.002

0.020 ± 0.002

0.016 ± 0.001

0.016 ± 0.003

IMR_R

0.039 ± 0.003

0.042 ± 0.004

0.037 ± 0.004

0.038 ± 0.002

0.029 ± 0.003

0.021 ± 0.002

IMRL_R

0.033 ± 0.003

0.028 ± 0.0003

0.026 ± 0.003

0.024 ± 0.004

0.019 ± 0.001

0.013 ± 0.001

IMRL_R

0.041 ± 0.003

0.036 ± 0.004

0.037 ± 0.003

0.039 ± 0.003

0.029 ± 0.003

0.023 ± 0.003

Effects of Finger Combination on Effective Target Width

To determine possible effects of finger combinations on W_E, the following analyses were run. First, we investigated whether or not W_E differed among the single-finger tasks (I_R, M_R, R_R, L_R, and M_L). W_E showed a difference between the “radial” single-finger tasks (I_R and M_R) as compared to the “ulnar” single-finger tasks (R_R and L_R) as well as the left middle finger task (M_L) at each of the ID levels and force production amplitudes. On average, W_E,UP for the “radial” fingers was smaller than W_E of the other fingers by 9.6%. This was confirmed with a four-way mixed effects ANOVA with the factors: Subject, ID, Amplitude, and Fingers. Main effects of Subject [F_7,893 = 15.19, p < 0.001], ID [F_5,893 = 235.28, p < 0.001], Amplitude [F_1,893 = 979.38, p < 0.001], and Fingers [F_4,893 = 6.76, p < 0.001] were found with no significant interactions. Pair-wise Tukey’s comparisons revealed significant differences between I_R and R_R, L_R, M_L; M_R and R_R, L_R, M_L; corresponding to smaller W_E in the I_R and M_R tasks as compared to the other three tasks. W_E also showed a difference across force production amplitudes and IDs, such that W_E was higher for the larger force production amplitude and smaller ID values.

There was no difference for W_E between the two two-finger tasks (IM_R and I_RM_L) at each ID level and force production amplitudes. This was confirmed with four-way mixed effects ANOVAs with the factors: Subject, ID, Amplitude, and Fingers. Main effects of Subject [F_7,353 = 7.9, p < 0.001], ID [F_5,353 > 68.29, p < 0.001], and Amplitude [F_1,353 = 376.4, p < 0.001] were found. However, there was no effect of Fingers and no significant interactions. The W_E values were higher for the larger force production amplitude and smaller ID values.

We then investigated whether or not there was a difference in W_E with regard to the number of fingers involved in a task (single-finger tasks vs. two-finger tasks vs. three-finger tasks vs. four-finger tasks). When the “radial” finger (I_R data were used) was evaluated against the multi-finger combinations, W_E did not depend on the number of explicitly involved fingers at each ID level and force production amplitudes. This was confirmed with a four-way mixed effects ANOVA with the factors: Subject, ID, Amplitude, and #Fingers. Main effects of Subject [F_7,713 = 15.57, p < 0.001], ID [F_5,713 = 158.93, p < 0.001], and Amplitude [F_1,713 = 742.44, p < 0.001] were found without any significant interactions or effects of #Fingers. When the “ulnar” finger (L_R data were used) was evaluated against the multi-finger combinations, on average, W_E of the multi-finger combinations was less than W_E of L_R by 17.9%. This was confirmed with a four-way mixed effects ANOVA with the factors: Subject, ID, Amplitude, and #Fingers. Main effects of Subject [F_7,713 = 13.26, p < 0.001], ID [F_5,713 = 159.05, p < 0.001], Amplitude [F_1,713 = 661.84, p < 0.001], and #Fingers [F_3,713 = 11.07, p < 0.001] were found with no significant interactions. Pair-wise Tukey’s comparisons revealed smaller variability in the performance (smaller W_E) by the multi-finger combinations as compared to L_R.

Discussion

Overall, the findings have not been supportive of the hypotheses formulated in the Introduction. There were minimal differences across the fingers and finger combinations in both speed-accuracy relations linking movement time (MT) to task difficulty (ID) and linking motor variability (assessed with W_E) to MT. This is an unexpected finding given the well-documented negative co-variation among finger forces (reviewed in Latash et al. 2002b) and the earlier report on lower coefficients of variation in the total force in two-finger tasks as compared to single-finger tasks (Latash et al. 2001). The remainder of the Discussion is going to be focused on the questions: What do patterns of co-variation among finger force do, if they do not provide for higher accuracy in the total force? Or do they?

Accuracy in multi-element tasks

There are at least two good reasons to expect multi-finger tasks to be more accurate than single-finger tasks. First, the close to linear scaling of force standard deviation with force level (reviewed in Carlton and Newell 1993) allows one to expect lower across-trials variance of force in multi-finger tasks because of the force sharing and the fact that total variance is the sum of standard deviations squared. For example, imagine that a person performs a series of force production trials with one finger to a target at 20 N and shows a standard deviation of force across trials of 2 N (and variance of 4 N²). Now imagine that two fingers share the same task and produce 10 N each. Then, assuming standard deviation scales linearly with the force level, standard deviation of their total force is expected to be 1.4 N and variance is expected to be 2 N². So, simply sharing total force between two fingers is expected to lead to a substantial drop in total force variability because the absolute force produced by each finger is less. If more fingers are involved, the drop is expected to be higher. In the presented example, a three-finger task is expected to show variance of about 1.5 N², and a four-finger task - about 1N² (assuming equal sharing of the total force across the involved fingers).

This example can easily be generalized to forces expressed in percent of MVC, as it was done in the reported experiments. When fingers act in a group, their total MVC is smaller than the sum of MVC values in single-finger tasks. This phenomenon, called force deficit (Ohtsuki 1981; Li et al. 1998) leads to force attenuation by a scaling factor of about 1/N^0.71 (Danion et al. 2003), where N is the number of explicitly involved fingers. However, the scaling factor applies to both force amplitude and standard deviation; hence expressing both in percent of MVC does not lead to a qualitative change in the overall effect.

In addition, a series of earlier studies have shown predominance of negative co-variation among finger forces in multi-finger tasks (reviewed in Latash et al. 2002b, 2007). This negative co-variation is expected to lower variance even more as compared to what could be expected in the absence of the co-variation. So, why did our study show no major difference in W_E across tasks performed with different numbers of fingers? Why did the subjects not speed-up when they used multi-finger combinations as compared to single-finger tasks? What is the purpose of the negative force co-variation if it fails to improve accuracy?

The first point to make is that negative co-variation is expected to improve accuracy as compared to the same data set without negative co-variation, not as compared to a set of single-finger tasks. The total amount of variance in the space of individual finger forces per unit of force production is considerably higher when fingers act in a group as compared to their single-finger tasks (Goodman, Shim, Zatsiorksy, and Latash, 2005). Our results suggest that this increase in each finger’s force variability is so high that it obliterates completely the expected gain from the two mentioned factors. The surprising bottom line is that the expected effects of the two favorable factors are exactly balanced by the increase in single finger force variability in multi-finger tasks. This result speaks in favor of one of the competing hypotheses on motor variability, to be discussed in the next subsection.

The second point is that an increase in variance of individual fingers in combination with negative co-variation that keeps total force variability basically unchanged may be revealing of a particular neural strategy. A recent study has shown that variability of elements (e.g., fingers) along directions in the finger force (or finger mode, see Danion et al. 2003) space that do not affect total force may play an important role in allowing the controller to handle several tasks at the same time while avoiding detrimental interactions among the tasks that share the same elements (Zhang, Scholz, Zatsiorsky, and Latash, in press). Taken together, this idea in combination with the current results suggests the following hypothesis: In multi-element tasks of producing an accurate level of a performance variable, the central nervous system facilitates variability of individual elements and organizes co-variation among the elemental variables that preserves an unchanged (acceptable) level of variability of the performance variable while simultaneously allowing for accurate production of other performance variables by the same set of elements.

Origins of finger force co-variation

There have been several attempts at modeling the experimentally observed phenomena of co-variation among elemental variables that is organized such that it keeps variability of an important performance variable low (reviewed in Latash et al. 2007). Two of the models are based on feedback schemes. In particular, a model by Todorov and Jordan (2002) uses principles of optimal feedback control, while a model by Latash and colleagues (Latash, Shim, Smilga, and Zatsiorsky 2005) is based on action of central back-coupling loops. Two other models assume that the controller is aware of the current Jacobian of the system (a matrix describing the mapping of small changes in the elemental variables on changes in the selected performance variable) but is not using an explicit feedback control scheme. One of these models (Martin, Scholz, and Schöner, 2005) uses a Jacobian augmentation technique developed in robotics (Baillieul 1985) to augment the Jacobian matrix with additional constraints making the matrix invertible. The other model (Goodman and Latash 2006) assumes that the controller uses two separate input signals into the system of elements, one related to changes in a particular performance variables (“relevant”), and the other one that keeps this variable unchanged (“irrelevant”).

Our finding of basically unchanged relations MT(ID) and W_E(MT) seem to be more directly compatible with the two latter models. These results suggest that accuracy of performance is defined by the controller independently of the number of involved effectors corresponding to the “relevant control signal” in the model of Goodman and Latash (2006). This signal is set depending on task constraints as elucidated by the Fitts’ law. In multi-element tasks, elemental variables are allowed to vary more than in single-finger tasks, but only as long as this added variability is not affecting performance compared to a single-finger task. In other words, an “irrelevant control signal” is added in multi-finger tasks that increases variability in the space of elements but does not affect the total force variability, in line with the hypothesis offered at the end of the previous subsection.

The ideas of feed-forward control of multi-digit action has been invoked recently in many studies of grip force adjustments associated with manipulation of hand-held objects (reviewed in Flanagan, Burstedt and Johansson 2006). We would like to emphasize an important distinction between feed-forward grip force adjustments and the feed-forward scheme of multi-finger synergies (as in Goodman and Latash, 2006). The former produces changes in the overall hand action to satisfy constraints imposed by the mechanics of the task including, in particular, friction between the object and the fingertips. The latter generates patterns of co-variation of individual finger actions compatible with the task. For example, when lifting an object, the former mechanism is expected to produce an increase in the grip force prior to the lifting action, while the latter is expected to make sure that individual finger forces co-vary such that the grip force changes show minimal variations from a required time profile.

Origins of the speed-accuracy trade-off

Overall, our subjects scaled MT with ID as expected from the Fitts’ law and scaled effective target width (force variability) with MT in support of earlier reports (reviewed in Schmidt et al. 1979; Keele 1986; Meyer, Smith, Kornblum, Abrams, and Wright, 1990) Why do people slow down when they are asked to move to a small and distant target? We believe that the model linking Fitts’ law to accuracy in specification of two parameters at the level of motor planning (a timing parameter and an amplitude parameter related to the planned movement time and amplitude, respectively; Gutman, Gottlieb, and Corcos, 1992; Gutman and Latash, 1993) offers the most natural and non-controversial explanation for the current findings. In particular, this model is compatible with similar MT(ID) relations for single- and multi-finger tasks. This model has also received support is a recent study (Duarte and Latash 2007) that showed reflections of Fitts’ law in anticipatory postural adjustments that by definition cannot reflect action of feedback signals (reviewed in Massion 1992).

Why do people show higher force variability at higher force levels? Studies by Slifkin and Newell (1999, 2000) attribute this increase in force variability to recruitment of larger motor neurons during tasks that require higher levels of force output, thus reducing the precision of the total force output. Note, however that the relative increase in net force caused by the recruitment of larger motor units has been shown to decrease as a function of muscle force (Fuglevand et al 1993).

Along somewhat different lines, Harris and Wolpert (1998; Jones, Hamilton, and Wolpert, 2002) attribute an increase in force variability to signal dependent noise in the synaptic input to motor neurons leading to variable signals to the muscles. Both these models assume that the source of variability is inherent to the processing of a control signal (that is assumed to be perfectly matching the task) by hierarchically lower structures. In addition, there is also variability in muscle force due to the contractile properties of the muscle fibers. However, given all these factors, when several fingers share a force production task, a substantial drop in the total force variability is expected as illustrated by the example in the opening subsection of the Discussion. The lack of such an improvement in force variability in multi-finger tasks is a sign that force variability is defined at a higher hierarchical level, possibly at a level that defines control signal in each particular trial somewhat differently (as in Goodman and Latash 2006).

Although we did not find consistent, major differences between the performance of single fingers and finger groups, some significant effects were indeed present. These, however, were mostly reflective of differences in the accuracy of individual fingers, not between single- vs. multi-finger tasks. Our results suggest that the two “radial” fingers (index and middle) are significantly more accurate than the two “ulnar” ones (ring and little). This is not a surprising finding. For example, R and L fingers show higher indices of unintended force production in tasks, where they are not supposed to produce force (enslaving, Li et al. 1998; Zatsiorsky, Li, and Latash, 2000). These fingers also tend to show higher indices of variability in prehensile tasks (Zatsiorsky, Gregory, and Latash, 2002; Zatsiorsky, Gao, and Latash, 2003). When fingers from both groups act together, indices of accuracy are closer to those of the I and M fingers and are better than those of the R and L fingers. This finding may be interpreted as corroborating the hypothesis that accuracy in multi-finger tasks is defined at a high hierarchical level, before the signals to neural structures controlling individual fingers are generated.

The conclusions drawn from our study may be task specific. In particular, several recent studies have suggested qualitative differences in the control of discrete and cyclic actions (Schaal, Sternad, Osu and Kawato 2004; Hogan and Sternad 2007). So, we cannot generalize our conclusions to discrete force production tasks. On the other hand, however, a number of recent studies have compared indices of multi-finger synergies during discrete and cyclic force and moment of force production tasks (reviewed in Latash et al. 2002b, 2007). These studies have not revealed qualitative differences between the discrete and cyclic force production. So, while we cannot be confident that our conclusions are valid over a broader range of tasks, this seems likely.