Soft tissue elastometer

Abstract

We have developed a device entitled the ‘Tissue Elastometer’ (TE) for evaluating the Young’s modulus of soft tissues. Soft tissue specimens are compressed between the object plate of an electronic balance and a linearly actuated indenter with a small rounded tip. The hardware of the device was designed such that a deformation model for semi-infinite media is applicable for calculating the Young’s modulus of test specimens from their collected force–displacement data.

Force–elongation measurements were performed on long strips of cured silicone mixtures to produce calibrated, tissue-mimicking test samples for the TE in a Young’s modulus range of 10–400 kPa. When tested with the TE, the Young’s moduli of the silicone samples demonstrated accuracy to within 1–10% of their calibrated values. Testing on excised tissue samples (fresh store-bought poultry breast; bovine liver, kidneys, hind shanks; porcine) was also performed, and a repeatability of elasticity measurements was demonstrated in the range of 8–14%. Results indicate that the TE can be effectively used in laboratory and clinical environments to evaluate the elasticity modulus of tissues.

1. Introduction

For centuries, palpation has been successfully used as a tool for disease diagnosis, for the fact is irrefutable that tissue stiffness is sensitive to structural changes resulting from pathology development. The term ‘elasticity imaging’ represents a range of imaging techniques that non-invasively mimic the use of palpation beneath the skin’s surface to investigate the elastic properties of tissues. Most of the information gleaned from elasticity imaging techniques is qualitative. Published findings usually characterize pathologies by their being some magnitude stiffer than the normal surrounding tissues. To enhance the diagnostic power of elasticity imaging as a more quantitative science, an information database of mechanical properties as they relate to tissue pathology is needed [1].

Mechanical compression tests are often employed to measure the elastic properties of tissues. While there are no commercially available material testing devices specifically intended for the range of elasticity modulus characteristic of soft biological tissues, some studies adapted available instruments to test soft tissues or tissue-mimicking materials [2-4]. Several researchers performed mechanical compression tests on tissues with devices that they had developed specifically for that purpose [5-9]. Most of these devices used the indentation method of elasticity measurements which is highly dependant on the relative dimensions of the indenter tip and geometry of the sample.

The objective of this study is to develop the tissue elastometer (TE) based on the indentation technique and to explore the influence of the indenter parameters, the measurement procedure, and the elasticity calculation algorithms on the accuracy of Young’s modulus evaluation for soft tissue.

2. Methods and materials

2.1. System overview

The TE comprises an electronic balance (1), a linear actuator (2) and a graphical user interface (3) as shown in Fig. 1. The electronic balance (Acculab, USA model VI-350) is used as a base for this device, where it acts as both a platform (object plate) for the placement of tissue samples and as a means for force measurement during operation. The hybrid linear actuator (HSI 35N67-12-405, Haydon Switch & Instrument Corp., CT) vertically drives a rounded cylindrical indenter (4) to compress the test specimen (5) on the object plate of the balance. The indenter has a diameter of 3.0mm and a vertical displacement range of 0–32mm with minimal steps of 0.01mm and a typical linear speed of roughly 0.05–0.1 mm/s. The electronic balance has a resolution of 0.1 mN, and the maximum tissue sample weight can be up to 200 g. The minimum sample thickness and width have to be at least twice and three times the diameter of the indenter, respectively, so that a deformation model for semi-infinite media is applicable for calculating the Young’s modulus of test specimens from the collected force–displacement data. Serial and parallel communication with a computer, in addition to operational software and a graphical user interface, enable complete user control of this device.

Fig. 1.

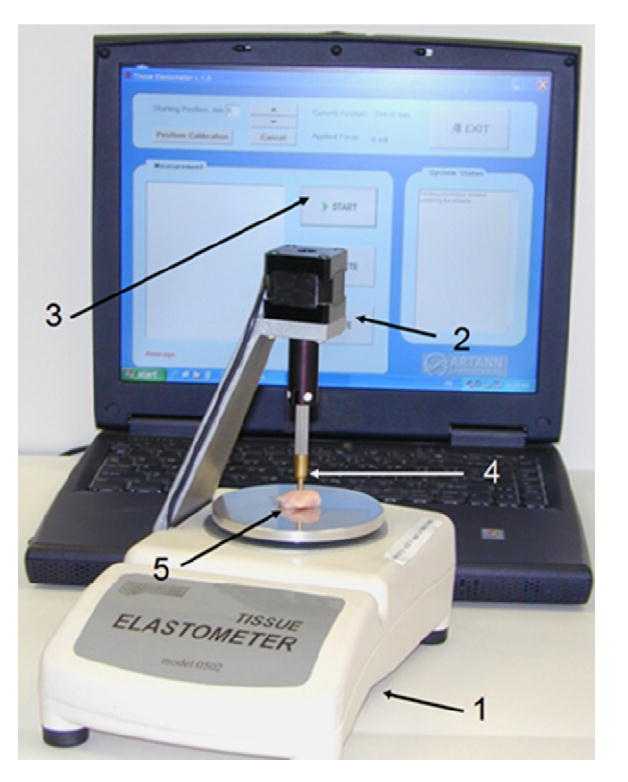
A perspective view of the Tissue Elastometer.

2.2. Experimental procedure

During operation, the TE first records the initial thickness (h₀) of a test specimen; it is the distance between the bottom surface of the indenter tip and the top surface of the balance’s object plate where the indenter first contacts the sample. The specimen is pressed up to a force of 1.7N or 85% of the initial height h₀ (whichever criteria occurs first) in steps of 0.1 mm. Force–height measurements (F_i(h_i), where i denotes step number) are obtained via electronic balance and linear actuator data, respectively. The function F_i(h_i) is the basic characteristic measured by the TE.

The task of performing elasticity measurements on surgically excised samples, which may vary greatly in geometry, is complicated by the fact that the results of force–displacement measurements via the indentation method may highly depend upon boundary conditions. To minimize this dependence and the corresponding error of evaluation for Young’s modulus, we are using a relatively small indenter when compared to sample width and thickness. Obviously, the error in Young’s modulus evaluation resulting from use of the semi-infinite media model, which includes ignoring the effects of various boundary conditions, needs to be quantitatively assessed in the testing and calibration of the TE.

The equation below for semi-infinite media [10] is used:

$$E=\frac{3}{{\pi }^{2}R}\frac{F}{W}$$ (1)

where R is the radius of the indenter tip and F is the applied force. W is indenter displacement defined by W = h₀ – h, where h is the current sample height. The TE estimates Young’s modulus (E) as the slope of the linear approximation of F_i(W_i) between 7.5 and 15% indenter displacement from the initial thickness (h₀) of the sample, where W_i = h₀ – h_i. The lower and upper limits of indenter displacement that define the interval for calculating Young’s modulus were chosen based on a number of factors. The behavior of the loading curve in its initial region depends on specific structural and geometric features of the sample’s surface at the point of contact with the indenter. It is only after a certain level of deformation that the loading curve becomes representative of the mechanical properties of the bulk material of the tested samples. At a higher level of deformation, however, many materials, especially biological tissues, may behave nonlinearly, and it is preferable to stay as close as possible to the initial linear region of the loading curve. The range of displacement used to calculate the slope of the loading curve should be sufficiently wide to provide necessary accuracy when evaluating Young’s modulus. The empirically chosen range of indenter displacement between 7.5 and 15% from the initial thickness of the sample appeared to be optimal for a comparative elasticity evaluation of soft tissues.

The TE estimates Young’s modulus as the slope of the best fit line for a chosen segment of the loading curve F_i(W_i):

$$E=\frac{3}{{\pi }^{2}R}\frac{\left(n{\sum }_{i=1}^n{W}_i{F}_i-{\sum }_{i=1}^n{W}_i{\sum }_{i=1}^n{F}_i\right)}{\left(n{\sum }_{i=1}^n{W}_i^2-{\left({\sum }_{i=1}^n{W}_i\right)}^2\right)}$$ (2)

where n is the number of data points.

The error of E evaluation (from Eq. (2)) is estimated as:

$$\sigma \approx E\sqrt{{\left(\frac{s}{E}\right)}^2+{\left(\frac{s_W}{W_{\mathrm{av}}}\right)}^2+{\left(\frac{s_F}{F_{\mathrm{av}}}\right)}^2}$$ (3)

where the values s_W = 0.03mm and s_F = 0.2mN are the standard errors of W and F measurements as specified by the manufacturers of the linear actuator and electronic balance, respectively. W_av and F_av are the average displacement and applied force values, respectively. Lastly, the standard error of the slope definition s used in Eq. (3) is calculated according to an error analysis described by Taylor [11].

Four parameters are calculated from the data obtained with the Tissue Elastometer: (1) Young’s modulus (Eq. (2)), (2) error in said Young’s modulus (Eq. (3)), (3) a weighted Young’s modulus based on all trial results, and (4) the standard deviation of said weighted Young’s modulus. These parameters enable assessment of device performance by gauging its accuracy, repeatability, and calculation errors.

2.3. Sample materials

To calibrate the device, we needed to test the TE on samples of known Young’s modulus [12]. For this purpose, we fabricated specimens from two-component SEMICOSIL 745, 921, and 934 silicones (Wacker Chemical Corporation, USA). To produce calibrated samples of known Young’s modulus, force-elongation measurements were performed on cylindrical specimens (length = 100 mm, diameter=4mm) from each mixture. Young’s moduli were computed directly from the ratio of tensile stress to tensile strain, so these measurements were used as the gold standard for comparison with TE results. Silicone samples in an applicable Young’s modulus range for soft tissues (between 5 and 500 kPa [1]) were used for TE testing.

All silicone samples were between 7 and 31 mm thick and tested in three widths: (1) ‘large’ = 40mm wide, (2) ‘medium’ = 25mm wide, and (3) ‘small’ = 10mm wide. By varying the size of the silicone samples, we assessed the influence of the sample geometry factor upon the error in Young’s modulus evaluation, in addition to the applicability of the deformation model for semi-infinite media.

Fresh, store-bought poultry breast; bovine liver, kidneys, and hind shanks; and porcine loin were also tested with the TE in a variety of orientations. This series of testing helped to define the repeatability of measurements obtained by the TE in its intended function for use on excised tissues.

3. Results

Fig. 2 illustrates typical loading curves recorded for: (1) a silicone sample with Young’s modulus of 14 kPa, (2) bovine liver and, (3) bovine kidney. The loading curves for all silicone samples within the entire elasticity range tested were nearly linear. This contrasts the tissue samples, which displayed significant nonlinearity even at low levels of strain under 10%.

Fig. 2.

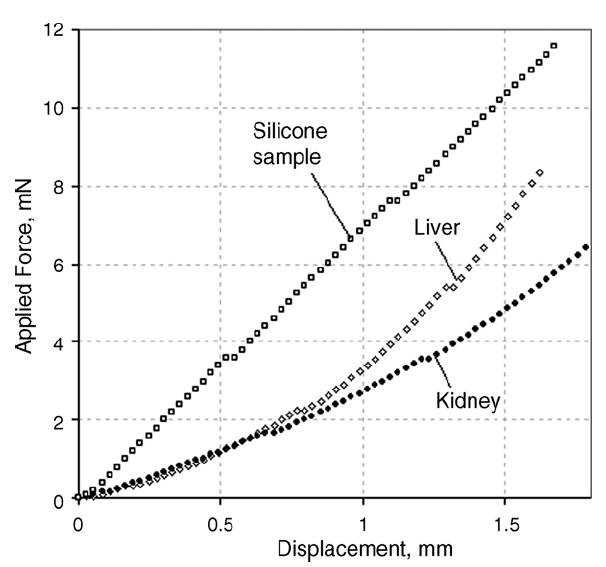
Examples of loading curves for a silicone sample (E = 14 kPa), bovine liver, and bovine kidney.

The experimental data for elasticity measurements as a function of silicone sample width are shown in Table 1 and Fig. 3. Each sample was placed in the center of the electronic balance’s object plate and tested for six trials. The sample heights were in a range of 10–15 mm. Table 1 shows the Young’s modulus values obtained from the force-elongation experiments, as well as the apparent Young’s modulus of each sample evaluated by the TE. The ± values in Table 1 represent the standard deviation of the weighted Young’s moduli.

Table 1.

Young’s moduli for the silicone samples of varying width

	Young’s modulus via force–elongation (kPa)
	14.0	22.0	40.0	100	172	350
Sample width (mm)	Apparent Young’s modulus via TE (kPa)
10	12.0 ± 0.2	20.5 ± 0.4	41.1 ± 0.5	86.7 ± 2.1	164 ± 3	364 ± 10
25	13.0 ± 0.2	22.5 ± 1.1	41.4 ± 1.4	97.5 ± 2.3	177 ± 12	356 ± 21
40	12.7 ± 0.2	23.9 ± 0.7	42.8 ± 0.5	98.4 ± 1.6	176 ± 2	359 ± 13

Fig. 3.

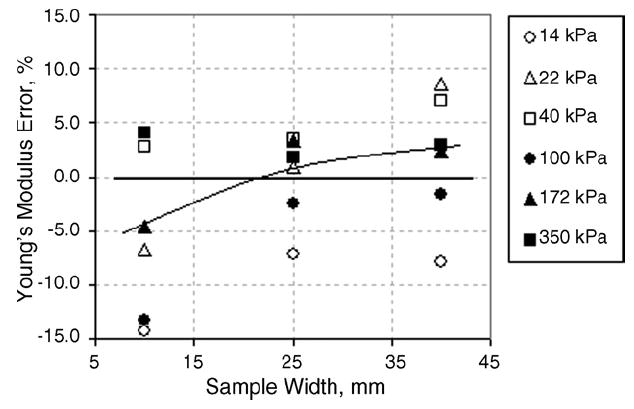
Young’s modulus evaluation error vs. silicone sample width.

The error of Young’s modulus evaluation as a function of sample width for each hardness value is illustrated in Fig. 3. The error was calculated as a percent shift from the “true” modulus of the sample obtained via force–elongation measurements.

To evaluate the influence of sample height, the silicone samples were incrementally layered atop one another and tested with the TE to assess the dependence of the apparent Young’s modulus upon sample height. A single sample was kept as the uppermost surface in contact with the indenter; all subsequent layers (three) were placed underneath. All samples used in this procedure were at least 40mm in width. Fig. 4 illustrates the observed trends for the silicones of different hardness.

Fig. 4.

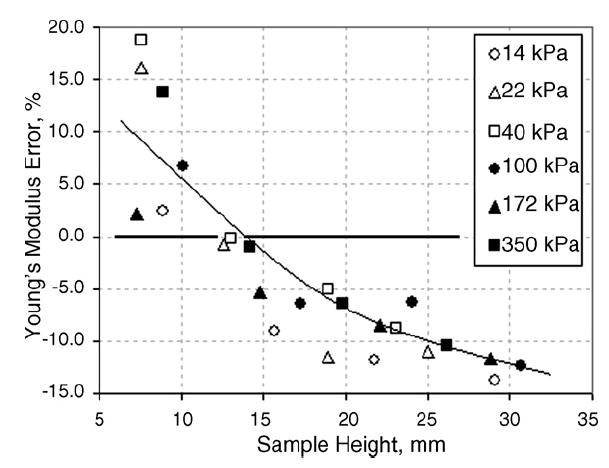
Young’s modulus evaluation error vs. silicone sample height.

As with the silicone samples, animal tissue (bovine muscle) was incrementally layered and tested with the TE to assess the dependence of the apparent Young’s modulus upon sample height. For this purpose, three thin tissue samples of bovine muscle were stacked atop one another. One sample was kept as the upper-most surface while the two subsequent layers were placed underneath. Each layer ‘stack’ was tested two times. Fig. 5 represents three loading curves recorded by the TE for bovine muscle tissue for samples of differing height. Fig. 6 shows the calculated Young’s modulus from these loading curves, accordingly.

Fig. 5.

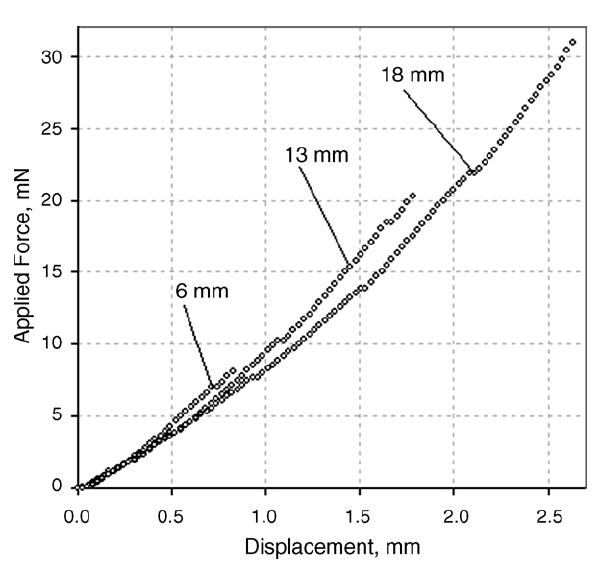
Loading curves for bovine muscle tissue with different sample heights.

Fig. 6.

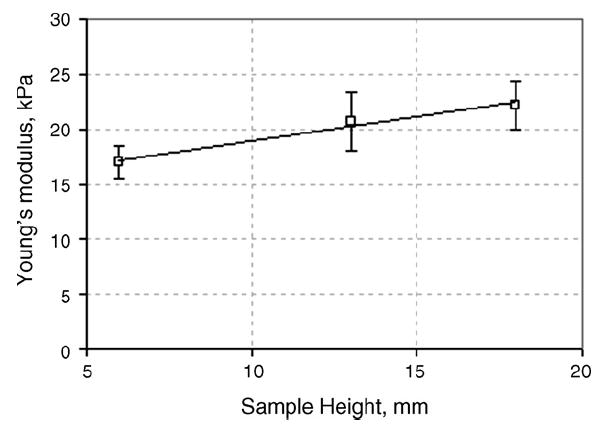
Young’s modulus for bovine muscle vs. sample height.

Similar to the silicone samples, the measured Young’s moduli of tissue samples were greater at lower sample heights. When calculating the elasticity modulus using a deformation model for semi-infinite media, the error is greater for thinner samples because of the increasing influence of the hard platform (object plate) on the stress pattern in the compressed sample.

Animal tissues were systematically tested to evaluate the repeatability of our measurements. The tissues were cut such that five samples of each tissue type were attained. Since preliminary results indicated some degree of anisotropy, each sample was tested in two orientations. Tissues with a noticeable fiber orientation (bovine hind shanks) were tested both perpendicular and parallel to these fibers. Tissues were also tested on both the ‘top’ and ‘bottom’ surfaces (so named for how the meat arrived in the original packaging) because of possible differences in hydration/dehydration conditions. Each sample was tested three times in each orientation. The indicator of error in this procedure was defined via a repeatability range of Young’s modulus measurements. Table 2 shows the results for all animal tissues tested with the TE. The ± values in Table 2 represent the standard deviation of the moduli shown.

Table 2.

TE evaluated Young’s moduli for the animal tissues

Tissue type	Young’s modulus (kPa)	Comments
Poultry
Breast	20.6 ± 2.1	Top
Breast	22.7 ± 2.1	Bottom
Gizzard	35.3 ± 3.8	Half cut
Bovine
Liver	7.4 ± 0.7	Top
Liver	10.0 ± 0.8	Bottom
Kidneys	5.9 ± 0.7	Smooth surface
Kidneys	6.3 ± 0.7	Cut surface
Muscle	16.3 ± 1.4	Perpendicular to fiber
Muscle	13.7 ± 1.4	Parallel to fiber
Porcine
Loin	13.4 ± 1.4	Top
Loin	14.3 ± 1.5	Bottom

Additional experiments were conducted to estimate the mechanical heterogeneity of the soft tissues tested. Tissue specimens were cut into strips and tested lengthwise with 6–7 indenter compressions. Results indicated that Young’s modulus varied between 7 and 40% along the length of each sample due to the structural heterogeneity of the tissues tested. This heterogeneity was more or less obvious by simple visual inspection of the sample.

4. Discussion

The scarcity of reliable experimental data on tissue elasticity is the main limiting factor in fully realizing the potential of elasticity imaging as a means to differentiate normal from diseased tissues. One of the reasons for this lack of quantitative data on the mechanical properties of tissue and their quantitative relation to pathology is the absence of adequate means for measuring said properties on freshly excised surgical samples of soft tissues. The developed TE can fill this gap and serve as a tool needed for creating a database on the Young’s modulus of human tissue.

Strictly speaking, the Young’s modulus is an inadequate parameter for characterizing the mechanical properties of soft tissues, which are anisotropic, nonlinear, and viscoelastic. Multiple parameters need to be introduced for accurate representation of such properties of tissue, such as time dependent strain, nonlinearity, hysteresis in the stress-strain curve, strain hardening, etc. But in most applications, an accurate, comprehensive characterization of tissue mechanical properties is impractical. The intended application of the TE is for exploring the correlation between tissue elasticity and histology and for quantitative differentiation of normal and diseased tissues, which is necessary for quantitative ultrasonic and MR elasticity imaging. Therefore, we are using a linear elastic medium as a simplest first approximation model of the tested tissue, which allows comparison of different tissue specimens in terms of a single parameter such as Young’s modulus.

For the silicone samples, which were roughly eight times wider and three to eight times thicker than the diameter of the indenter tip, the TE exhibited accuracy of its computed Young’s modulus to within 1–8% of force–elongation measurements. The calculation model for semi-infinite media is thus acceptable for samples of these dimensions. For the ‘small’ samples, which were roughly three times wider and two times thicker than the diameter of the indenter tip, the TE showed accuracy to within 3–15%. While this accuracy range is still sufficient for most applications, it implies that for the given indenter tip, the error in Young’s modulus is being significantly influenced by sample geometry/boundary conditions; the deformation model for semi-infinite media becomes less accurate for such samples. Thus, for reasonable accuracy to within 20%, the smallest acceptable indenter-to-sample width ratio is roughly 1:3.

The standard deviation in the moduli shown in Table 1 is obtained by calculating the weighted averages of six trials. The repeatability of these six measurements is assessed as the ratio between the standard deviation (shown as ± values in Table 1) and the weighted moduli. For the tested specimens, all TE results were variable to within 1–10% of their respective weighted modulus. Fig. 3 reveals that there is a positive correlation between Young’s modulus error/deviation with specimen width (correlation coefficient 0.6). Therefore, if necessary, it will be possible to take this correlation into consideration by introducing a correction factor.

Fig. 3 shows that the error in the Young’s modulus measurement may reach about 15% when assessed for a thin sample, which is defined as one layer of sample material (5–7 mm). This finding is concurrent with the results for the ‘small’ samples in Table 1: a ratio of at least 1:3 is needed between the indenter diameter and any sample dimension so that measurement error does not exceed 15–20%. For samples with smaller dimensions, the calculation of Young’s modulus using the deformation model for semi-infinite media becomes inadequate. Figs. 3 and 4 suggest that the best results (closest to E₀) will be obtained for samples 12–20mm in height and 20–40mm in width.

The TE detected an elasticity difference between the ‘top’ and ‘bottom’ surfaces of tissue specimens (bovine liver, porcine loin, poultry breast, see Table 2); the ‘bottom’ value was consistently higher than that of the ‘top’. The ‘bottom’ surface, however, was in contact with the absorbent pad normally placed underneath store-bought animal products. This pad drew moisture from the underside of the meat to avoid leakage, so there is a disparity in water content between the ‘top’ and ‘bottom’ surfaces. This accounts for the higher modulus consistently observed from the ‘bottom’ side during TE testing. This finding illustrates the sensitivity of the TE and its capability to discriminate changes in tissue hardness of less than 10%, whereas a change in Young’s modulus of tissue during the development of a tumor could reach thousands of percent [1].

Different tissue types show varying degrees of nonlinearity as illustrated in Fig. 2, which displays TE data obtained from bovine liver and kidney. For comparison, a loading curve for a silicone phantom is also shown. Both tissue samples are nonlinear, i.e., tissue elasticity changes with increased deformation. This is in contrast to the silicone phantom, which behaves linearly within the range of strain used in TE testing. Nearly exponential nonlinearity was noted in all tested soft tissue samples. This is in agreement with scarce results reported in literature [2,6,13]. We would like to emphasize here again that to standardize Young’s modulus measurements on soft tissue, it is important to define which part of the loading curve is to be used for elasticity evaluation.

The small shifts in the loading curves result from the digitizing of the output signal from the balance having resolution of 0.1 mN. In each tissue measurement the TE collects 35–100 points to calculate the best fit line for a loading curve (see Eq. (2)). We take into account the standard error s_F = 0.2mN of force measurement (F) according to Eq. (3). Therefore, this effect is automatically incorporated into error evaluation.

The slopes of the Young’s modulus error versus sample thickness in silicone (Fig. 4) and tissue (Fig. 6) have different signs. These slopes result from the effect of two factors: (1) the influence of the hard flat surface on which the sample is placed, and (2) the nonlinearity of the sample material. The first factor affects the thinner specimens and its influence disappears at specimen thicknesses over 20mm (see Fig. 4). The second factor plays a greater role with increasing specimen height because absolute specimen vertical deformation is increased proportionally with its height. This is illustrated by the data of Fig. 5, which shows the original loading curves used to calculate the Young’s moduli of tissues shown in Fig. 6. Said two factors affect the slope of the Young’s modulus error versus sample thickness curves in different directions. In the case of the silicone sample, mainly the first factor is effective while in the case of tissue the contribution of the second factor exceeds that of the first.

Since the main motivation for creating a database on tissue elasticity is to be able to differentiate between normal and diseased and benign and malignant tissues, it is important to define what a sufficient accuracy range of Young’s modulus measurements would be. A rough estimate of the required accuracy can be made by using data related to the range of elasticity modulus of tissues in normal and pathological conditions. For example, most normal soft tissues have Young’s modulus on the order of 10 kPa, while the Young’s modulus of some “rock-hard” cancerous tumors can reach 1MPa. Thus, tissue elasticity can vary in a range up to 10,000% of the normal value for soft tissue. Let us then assume that the efficient use of the elasticity modulus as a parameter for tissue characterization and discrimination requires a resolution taken as 1% of the entire variation range of said parameter. This means that even with a Young’s modulus measurement error of 100%, we will be able to satisfy this resolution requirement.

Another criterion for evaluating the required accuracy of Young’s modulus measurements is related to the range of mechanical heterogeneity of normal tissue. Our experimental data showed that the elasticity modulus measured along a strip of a tissue may vary up to 40%. Obviously, the measurement of a parameter with accuracy much higher than the range of normal variability of this parameter will hardly provide additional useful information. It can thus be concluded that the demonstrated accuracy of the TE in evaluating the Young’s modulus of soft tissues to within 20–30% is sufficient for creating a database of tissue elasticity.

5. Conclusions

The Tissue Elastometer has been designed and built as a device to measure the Young’s modulus of small tissue samples. When tested on calibrated silicone samples, the TE demonstrated accuracy to within 1–10% of the reference data for Young’s modulus obtained by direct force-elongation measurements. Testing on excised tissue samples (fresh store-bought poultry breast; bovine liver, kidneys, hind shanks, porcine loin) demonstrated a repeatability of elasticity measurements in the range of 8–14%. Results of preliminary testing demonstrated that the TE can be successfully used to create a database for mechanical properties of tissue needed for quantitative elasticity imaging and other applications such as surgical simulation systems and laparoscopy.