Maximum-likelihood methods in wavefront sensing: stochastic models and likelihood functions

Abstract

Maximum-likelihood (ML) estimation in wavefront sensing requires careful attention to all noise sources and all factors that influence the sensor data. We present detailed probability density functions for the output of the image detector in a wavefront sensor, conditional not only on wavefront parameters but also on various nuisance parameters. Practical ways of dealing with nuisance parameters are described, and final expressions for likelihoods and Fisher information matrices are derived. The theory is illustrated by discussing Shack–Hartmann sensors, and computational requirements are discussed. Simulation results show that ML estimation can significantly increase the dynamic range of a Shack–Hartmann sensor with four detectors and that it can reduce the residual wavefront error when compared with traditional methods.

1. INTRODUCTION

Measurement of optical wavefronts has a long and storied history. Classical interferometry uses a reference beam to learn as much as possible about a wavefront, and phaseretrieval methods attempt to reconstruct a wavefront from one or more measurements of optical irradiance without a reference beam. In recent years, however, a distinctly different requirement has been imposed on systems for wavefront measurement: They have to respond to rapid changes in the wavefront and provide signals that can be used in adaptive systems that correct for wavefront distortions. Such adaptive systems are proving extremely valuable in many applications, including ground-based astronomy, retinal imaging in ophthalmology, and laser machining. In these applications there is no particular interest in the wavefront itself, but instead the goal is to sense a distorted wavefront, correct it, and thereby minimize its influence on the actual task of interest. Wavefront-measurement systems intended for use in adaptive optics (AO) are referred to as real-time wavefront sensors, or simply wavefront sensors for short.

Many different wavefront sensors have been developed for AO; for reviews, see Tyson¹ and Rousset.² The wavefront of interest is usually the pupil function of a telescope or other optical instrument, and the sensors differ in whether they attempt to characterize the wavefront over the entire pupil aperture at once or over selected regions called subapertures. All of the sensors, however, use a set of optical detectors in conjunction with optical elements intended to make the detector outputs sensitive to preselected characteristics of the wavefront. For example, the familiar Shack–Hartmann sensor attempts to measure two components of the wavefront tilt over a subaperture by observing the image of a star or other pointlike source in the back focal plane of a lenslet placed over the subaperture. Because of the lenslet, the image of the source is displaced laterally by an amount proportional to the tilt, and the displacement can be estimated by computing the centroid of the outputs of an array of detectors in the focal plane.

Other wavefront sensors attempt to measure other parameters, such as the local curvature of the wavefront at each subaperture³ or the coefficients in an expansion of the wavefront in orthogonal basis functions over the whole aperture. Many clever techniques have been devised for choosing the configuration of optical elements and the photodetector array and for processing the outputs of the photodetectors to obtain measurements of the parameters of interest.

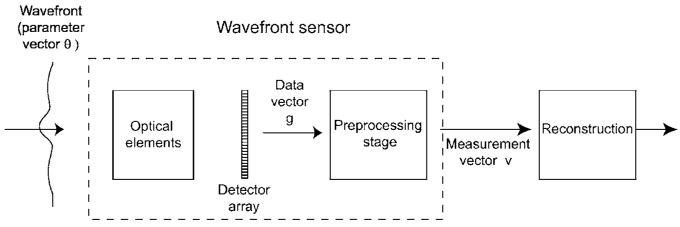
Most current real-time sensors can be described by the general block diagram shown in Fig. 1. The wavefront is assumed to be described by a set of P parameters {θ_p, p =1,…,P}, or equivalently by a P×1 parameter vector θ. Similarly, the raw data are described by a set of M output signals {g_m, m=1,…,M}, or equivalently by an M×1 data vector g. The photodetector signals are then preprocessed, usually by simple, noniterative formulas, to get a set of I derived quantities, {v_i, i=1,…,I} or an I×1 vector v, that can be regarded as measurements of some properties of the wavefront, though not necessarily directly the components of θ. For example, in a Shack–Hartmann sensor for one subaperture, I=2 and the components of v are estimates of the tilts of the wavefront over the subaperture in the x and y directions. The preprocessing step in this case is computation of the centroid. Note that centroid computation, though fast and efficient, is a nonlinear operation on the data (because of the division by the sum of the signals).

Fig. 1.

Block diagram of a generic wavefront sensor and reconstructor.

No matter how the specific boxes in Fig. 1 are realized, it is usually assumed that there is a linear relation between the mean values of v and the actual wavefront parameters; this linear relation is expressed as

$$\stackrel{-}{\mathbf{v}}=\mathbf{H}\theta \text{or}\mathbf{v}=\mathbf{H}\theta +\mathbf{n},$$ (1.1)

where H is an I×P matrix, n is a zero-mean I×1 vector describing the noise in v, and the overbar denotes an average over that measurement noise. Recovery of the unknown θ from the output of the preprocessing stage is then treated as a matrix inversion or pseudoinversion implemented in a separate stage called a reconstructor. The output of the reconstructor can be the final estimates of θ or correction signals to be applied to a control element (deformable mirror or spatial light modulator) in an AO system.

There are several difficulties with this general approach. An immediate concern is the linearity assumed in Eq. (1.1). Even in our example of a Shack–Hartmann sensor and centroid estimation, it is well known that the mean centroid is a nonlinear function of the tilts if the number of photodetectors is small. Moreover, if wavefront parameters other than tilt influence the data, then there is no chance that Shack–Hartmann tilt estimates will be linear functions of the additional parameters.

A more serious issue concerns the dimensionality reduction in going from the M-dimensional raw data g to the I-dimensional vector v;as I is often much less than M, there could be a considerable information loss in this step. In the Shack–Hartmann example, we can expect wavefront curvature and other parameters to influence the data unless the lenslet diameter D_l is significantly smaller than the Fried parameter r₀. The usual choice, however, is to make D_l approximately equal to the mean r₀ at a particular observing site, and it is not clear in that case how much information is lost in centroid estimation.

A related problem is that parameters other than ones associated with the wavefront can influence the data. A simple example is the overall brightness of the guide star or other source, which is one additional scalar parameter. A more complex example is irradiance variations (e.g., scintillation) over the aperture being sensed, which would potentially require a large set of additional parameters. These extraneous parameters, called nuisance parameters, can have important effects on the data statistics.

In contrast to nuisance parameters, null functions are properties of the wavefront that might be of great interest but that do not influence the data. Since the matrix H in Eq. (1.1) has dimensions I×P, with I often very small compared with P, there is a null space representing characteristics of θ that cannot be recovered from knowledge of v, even in the absence of noise.

Another area of difficulty is in describing the statistical properties of both g and v. A centroid or other simple way of computing v from g takes no account of the noise properties of g, and better performance might be obtainable if we used accurate models of the data statistics. Even if we do not use detailed statistical information in the preprocessing stage, it is still possible to compute the variances in the resulting components of v by simple propagation of errors⁴ if we assume that the components of g are uncorrelated, but this assumption is not always justified.

Considerable work has been reported on optimal approaches to the reconstruction step, starting with the pioneering paper by Wallner.⁵ This work starts with the assumption that the available data are noisy measurements of the wavefront tilts averaged over subapertures and that these measurements are unbiased and uncorrelated, both with each other and with the random wavefront itself. From this starting point, Wallner derives an optimal reconstructor that minimizes the mean-square wavefront error, accounting for unmeasured components by using Kolmogorov statistics as prior knowledge. His approach and subsequent related research thus optimize the reconstruction stage in Fig. 1, but they do not consider possible information loss in the preprocessing stage. As we shall demonstrate numerically in Section 6, that information loss can be considerable.

Moreover, the common assumption that the components of v are uncorrelated is almost never correct. Correlations are introduced by the preprocessing stage, and the statistics of v can be complicated, even when g is described by simple uncorrelated Gaussian or Poisson noise. At the least, any discussion of the statistics of the wavefront sensor output should give its mean (or bias), variance, and covariance matrix; a full multivariate probability density function would be desirable for rigorous design of the reconstruction stage.

Finally, there is a need for rigorous methods of evaluating wavefront sensors and comparing competing approaches. Most of the literature on this topic uses the Strehl ratio of the final AO system as the figure of merit, but it is difficult to discern the contribution of the wavefront sensor to this metric or to devise strategies for improving the sensor. Moreover, it is not clear how Strehl ratio itself relates to objective or task-based figures of merit^6-9 for the final system.

Likelihood theory offers a potential way of addressing all of these concerns. A likelihood is a comprehensive statistical description of a data set, showing how the data probability law depends on various parameters and various noise sources. This probability law can then be used to define a maximum-likelihood (ML) estimator, which has many desirable properties to be enumerated in Section 2. The likelihood is also required for Bayesian estimation methods, which augment the likelihood with prior knowledge of the parameters to be estimated.

From the likelihood it is possible to compute a Fisher information matrix (FIM), which describes the information content of a data set for the purpose of estimating the parameters that enter into the likelihood. It is well known that the FIM can be used to compute a fundamental lower bound, the Cramér–Rao bound (CRB), on the variance of the parameter estimates. It is less well known, but the FIM can also be used to find a good approximation to the covariance matrix of the ML estimates, and in this form it can be incorporated into objective theories of image quality.⁸ In addition, likelihood theory provides a systematic way of discussing nuisance parameters.

Application of likelihood methods to wavefront sensing is not new, though their full potential has not yet been exploited. We can trace the beginnings of this line of research to three seminal 1974 papers by Bahaa Saleh,^10-12 in which he studied the statistical limitations in localizing a spot of light and derived ML estimators. Elbaum and Greenebaum¹³ used similar methods for angular tracking, and Winick¹⁴ derived a CRB for spot localization and used it to discuss system design. Various papers by Lane et al.^15-17 have applied ML methods and the CRB to wavefront sensors with the assumption that the positions of individual detected photons were available. Welsh et al.¹⁸ used the CRB to compare the performance of Shack–Hartmann sensors and shearing interferometers. Löfdahl and Duncan¹⁹ gave an ML treatment of the Shack–Hartmann sensor based on an additive Gaussian likelihood model, and they showed how to use the Shack–Hartmann for curvature estimation. Extension of ML methods to Bayesian MAP (maximum a posteriori) estimation is discussed by Sallberg et al.,²⁰ who used a Poisson likelihood and a prior on the correlation of wavefront slopes across subapertures in a Shack–Hartmann sensor.

An important paper by Cannon²¹ considered ML estimation of global wavefront parameters from Shack–Hartmann data without the intermediary step of tilt estimation. His likelihood function took account of the polychromatic nature of the data, but it used an additive Gaussian model and did not consider photon noise.

Several papers^19,22-25 consider simultaneous ML or MAP estimation of a wavefront and an object from phase-diversity data without an explicit wavefront sensor; this problem does not fit into the general schema of Fig. 1, and it is not considered further in this paper.

Perhaps surprisingly, there is also some closely related work in a completely different area, namely gamma-ray detection with scintillation cameras in nuclear medicine. Gray and Macovski²⁶ suggested ML and MAP methods for localizing the spot of light produced by a single gamma ray in this application, and subsequent work at the University of Arizona and elsewhere^27-31 has refined the methodology and applied it to many practical gamma-ray imaging systems.

The objective of this paper is to develop rigorous likelihood models and FIMs for wavefront sensing under various noise assumptions and choices of parameters to estimate. In Section 2 we review some basic concepts in estimation theory, including the effect of null functions and nuisance parameters. In Section 3 we consider various stochastic models for the raw data in a WFS. These models are in the form of conditional probabilities or probability density functions (PDFs) on the photodetector outputs, conditioned on all parameters that influence those probabilities, but they are not yet likelihoods since we have not specified which of the parameters are to be estimated and how to handle those that will not be estimated. These topics are taken up in Section 4, where we consider various parametric descriptions of the wavefront and various choices of parameters to estimate. In Section 5 we combine the results from Sections 3 and 4 into practical likelihood functions and construct the corresponding FIMs. Section 6 applies these ideas specifically to a Shack–Hartmann sensor, and Section 7 discusses ways of finding ML estimates in a time compatible with astronomical adaptive optics.

Appendixes A and B provide some statistical details needed in the main text, and Appendixes C and D examine statistical issues particular to a Shack–Hartmann sensor.

2. BASIC CONCEPTS IN ESTIMATION THEORY

Random data are described by a probability law with one or more free parameters, and the goal of estimation is to obtain numerical values for the parameters from a given data set. Excellent general references on estimation theory include Melsa and Cohn,³² Van Trees,³³ and Scharf.³⁴ An overview using a notation and approach similar to this paper is given by Barrett and Myers,⁶ Chap. 13.

A. Notation and Terminology

Let g be an M×1 vector describing random data. The probability law on g is a PDF denoted pr(g|θ) for the case of continuous-valued data, and it is a probability denoted Pr(g|θ) for the case where the data can take on only discrete values. In both cases it is assumed that the probability law is characterized by a P×1 parameter vector θ. In the remainder of this section we shall consider continuous random variables, but the results are easily translated to discrete data.

The PDF describes the sampling distribution of the data, and we say that an individual sample of g is drawn from pr(g|θ). Once a data vector is measured, however, pr(g|θ) can be regarded as a function of θ called the likelihood of θ for the given g and is denoted by

$$L(\theta \mid \mathbf{g})=\mathrm{pr}(\mathbf{g}\mid \theta ).$$ (2.1)

Note that L(θ|g) is not a PDF on θ.

An estimate of the parameter is denoted θ̂; in most cases the estimate is a deterministic function of the data, so we can also write it as θ̂(g). Since g is random (even for a given θ), so is θ̂(g).

In wavefront sensing, we can choose either the raw photodetector output g or the derived quantities v as the data from which we wish to perform an estimation. In the latter case, the likelihood will be denoted L(θ|v) or pr(v|θ), and an estimate will be denoted θ̂(v).

B. Performance Metrics

There are three distinct approaches to specifying the performance of an estimation procedure (or, indeed, any statistical inference task). There is the classical or frequentist method, which envisions repeated sampling of the data vector from its sampling distribution pr(g|θ) and bases its performance criteria on averages of the resulting estimates. In this view the parameter is unknown but not considered random. A Bayesian approach, on the other hand, considers the parameter being estimated to be random and assigns it a prior probability pr(θ), though this probability may be regarded as a degree of belief rather than something that is necessarily verifiable by repeated experiments. By using pr(θ) and pr(g|θ) in Bayes's rule, it is possible to assign a probability pr(θ|g), called the posterior to the value of θ after the data vector is observed; all performance metrics are derived from the posterior.

The third approach to specification of estimation performance is to consider the use to which the estimate will be put. In an AO system, for example, we are not interested in the parameters of the wavefront but rather in the performance of the overall closed-loop system that uses the estimate. As noted in the introduction, a common way of specifying the overall performance in astronomical AO is in terms of Strehl ratio, but it is also possible to consider specific astronomical tasks such as detection of exoplanets and use a detectability measure as the final performance metric.³⁵ This approach is classical in the sense that it uses long-run averages, but they are averages related to the final task rather than to the estimates themselves.

In this paper we adopt the classical viewpoint. All probabilities and PDFs will be regarded as quantities that in principle can be verified by repeated sampling. Quantities like bias and variance of an estimator will thus have a frequentist (experimental) interpretation, but they will also serve as necessary inputs to a task-based assessment.

1. Bias, Variance, and Covariance of Estimates

In classical estimation theory, the accuracy of an estimate is specified in terms of its sampling distribution pr(θ̂|θ), interpreted as the distribution of θ̂(g) that would be obtained by drawing repeated samples of g from pr(g|θ) and performing the estimation procedure on each. In terms of the sampling distribution, the mean of the P×1 vector of estimates is given by

$$\stackrel{-}{\widehat{\theta }}=\int {\mathrm{d}}^P\widehat{\theta }\mathrm{pr}(\widehat{\theta }\mid \theta )\widehat{\theta }.$$ (2.2)

If the estimation rule and the sampling distribution on g are known, we can also express the mean (expectation) of the estimate as

$$\stackrel{-}{\widehat{\theta }}=\int {\mathrm{d}}^{M}g\mathrm{pr}(\mathbf{g}\mid \theta )\widehat{\theta }\left(\mathbf{g}\right)\equiv \langle \widehat{\theta }\left(\mathbf{g}\right){\rangle }_{\mathbf{g}\mid \theta }.$$ (2.3)

We shall use the overbar and the angle brackets interchangeably to denote means; the latter has the advantage that the subscript can show explicitly which PDF is implied in the averaging process.

The bias in an estimate specifies its average deviation from the true value of the parameter. For a vector parameter, the bias is a vector given by

$$\begin{array}{cc}\hfill \mathbf{b}\left(\theta \right)& \equiv \stackrel{-}{\widehat{\theta }}-\theta \hfill \\ \hfill & \equiv {\int }_{\infty }{\mathrm{d}}^{M}g[\widehat{\theta }\left(\mathbf{g}\right)-\theta ]\mathrm{pr}(\mathbf{g}\mid \theta )\hfill \\ \hfill & ={\int }_{\infty }{\mathrm{d}}^P\theta [\widehat{\theta }-\theta ]\mathrm{pr}(\widehat{\theta }\mid \theta ).\hfill \end{array}$$ (2.4)

A parameter is said to be be estimable or identifiable with respect to some data set if there exists an unbiased estimator of it for all true values of the parameter.

If we denote the mean of the pth element of the random vector θ̂ by 〈θ̂_p〉, the variance of the pth element is given by

$$\begin{array}{cc}\hfill \mathrm{Var}\left({\widehat{\theta }}_p\right)& \equiv {\langle \left[{\widehat{\theta }}_p-\langle {\widehat{\theta }}_p\rangle \right]{\left[{\widehat{\theta }}_p-\langle {\widehat{\theta }}_p\rangle \right]}^{\ast }\rangle }_{\mathbf{g}\mid \theta }\hfill \\ \hfill & ={\int }_{\infty }{\mathrm{d}}^{M}g|{\widehat{\theta }}_p\left(\mathbf{g}\right)-\langle {\widehat{\theta }}_p\left(\mathbf{g}\right)\rangle {|}^2\mathrm{pr}(\mathbf{g}\mid \theta )\hfill \\ \hfill & ={\int }_{\infty }{\mathrm{d}}^P\theta |{\widehat{\theta }}_p-\langle {\widehat{\theta }}_p\rangle {|}^2\mathrm{pr}(\widehat{\theta }\mid \theta ),\hfill \end{array}$$ (2.5)

and the full covariance matrix is given by

$${\left[{\mathbf{K}}_{\widehat{\theta }}\right]}_{{\mathit{pp}}^{\prime }}={\langle \left[{\widehat{\theta }}_p-\langle {\widehat{\theta }}_p\rangle \right]{\left[{\widehat{\theta }}_{p^{\prime }}-\langle {\widehat{\theta }}_{p^{\prime }}\rangle \right]}^{\ast }\rangle }_{\mathbf{g}\mid \theta }$$

or

$${\mathbf{K}}_{\widehat{\theta }}={\langle (\widehat{\theta }-\stackrel{-}{\widehat{\theta }}){(\widehat{\theta }-\stackrel{-}{\widehat{\theta }})}^{†}\rangle }_{\mathbf{g}\mid \theta },$$ (2.6)

where the dagger denotes adjoint (conjugate transpose), or simply transpose for real vectors and matrices.

2. Mean-Square error

The mean-square error (MSE) is a way of specifying the overall error, including bias and variance, in a single scalar quantity; it is defined by

$$\begin{array}{cc}\hfill \mathrm{MSE}=\langle \Vert \widehat{\theta }-\theta {\Vert }^2{\rangle }_{\mathbf{g}\mid \theta }& ={\int }_{\infty }{\mathrm{d}}^{M}g\Vert \widehat{\theta }\left(\mathbf{g}\right)-\theta {\Vert }^2\mathrm{pr}(\mathbf{g}\mid \theta )\hfill \\ \hfill & =\mathrm{tr}\left[{\mathbf{K}}_{\widehat{\theta }}\right]+\mathrm{tr}\left[{\mathbf{bb}}^{†}\right],\hfill \end{array}$$ (2.7)

where tr(·) denotes the trace. Note that the MSE measures the squared deviation from the true value of the parameter, while the variances relate to deviations from the mean of the estimate.

In general, bias, variance, and MSE will all depend on the true value of the parameter. If a realistic sampling distribution of the parameter is known, it can be used to average the MSE, forming a quantity called the ensemble MSE, defined by

$$\mathrm{EMSE}={\langle {\langle \Vert \widehat{\theta }\left(\mathbf{g}\right)-\theta {\Vert }^2\rangle }_{\mathbf{g}\mid \theta }\rangle }_{\theta }.$$ (2.8)

The EMSE can often be estimated by Monte Carlo sampling even when we do not have enough detail about the prior to use it in Bayesian estimation.

3. Cost and Risk

A general approach to estimation is to define a cost function C(θ̂,θ) and to define the risk R as an average cost, R=〈C(θ̂,θ)〉. Depending on the statistical philosophy being adopted, the angle brackets here can have one of three distinct meanings. In a purely frequentist approach, the brackets imply averaging over g for a given θ, so the risk is a function of θ. In a purely Bayesian view, the average is over θ for a given g, so the risk is a function of the particular data set g and no other data set is ever considered. A pragmatic view is to average over both g given θ and then over θ, so that the risk is a pure number. The EMSE in Eq. (2.8) is an example of risk defined this way for a quadratic cost function.

No matter what cost function and definition of risk are used, a nuisance parameter can be defined as one that does not appear in the cost function.

C. Nuisance Parameters and Null Functions

The performance metrics discussed above must be interpreted carefully when the measurement system has null functions or when there are nuisance parameters in the problem.

Null functions do not influence the data and in principle cannot be determined from the data. An example in the context of wavefront sensing is the piston component of the wave over a lenslet in a Shack–Hartmann sensor. We need to know this component to reconstruct the wave-front, but the sensor is not responsive to it. A second example is the so-called waffle effect, which arises when the deformable mirror in an AO system has modes that the wavefront sensor cannot detect; the resulting corrected wavefront then has a corrugated or waffled appearance.

Nuisance parameters do influence the data but are not of interest to the estimation problem, perhaps because they do not influence performance of the real task of interest. An example in astronomical applications is the brightness of the guide star. Like all nuisance parameters, the brightness of the guide star influences the bias and/or variance of the estimates of the parameters of interest, but the value of the brightness itself is irrelevant to further application of the output of the WFS. If there is atmospheric scintillation or if the guide star is laser-induced and hence noisy, however, fluctuations in the brightness can be a serious nuisance.

In a sense it is trivial to deal with null functions. Since they do not affect the data and cannot be estimated from the data, we can just omit them from the likelihood function and the FIM. On the other hand, if we do try to estimate them, for example by trying to solve Eq. (1.1) for the case P>I, then the FIM is singular³⁶ and the CRB is infinite. Stated differently, θ is not estimable. This difficulty often goes unrecognized in the wavefront-sensing literature and in other areas of inverse problems.

In contrast to null functions, it is never correct to omit nuisance parameters from the likelihood, though in fact it is often done. A correct statistical description of the data has the form pr(g|θ), where the vector θ contains all of the parameters that influence the data, not just those we might want to estimate.

Methods of dealing with nuisance parameters are summarized in Barrett and Myers.⁶ If we write

$$\theta =\left(\begin{array}{c}\hfill \alpha \hfill \\ \hfill \beta \hfill \end{array}\right),$$

where α contains the parameters of interest and β contains the nuisance parameters, we can

• (1) Ignore the problem and assume a form for pr(g|α).

• (2) Replace β with some typical value β₀ and assume that pr(g|α,β)≈pr(g|α,β₀).

• (3) Estimate α and β simultaneously from g and discard the estimate of β.

• (4) Estimate β from some auxiliary data set and use it as in option (2).

• (5) Assume (or measure) some prior pr(β) and marginalize over β.

It is shown by Barrett and Myers⁶ (Sec. 13.3.8) that option (5) is optimal in terms of minimizing a particular cost function (the one that leads to MAP estimation), provided that the cost is independent of the nuisance parameter. It is assumed there, however, that pr(β) is a meaningful sampling prior, not something based on belief or chosen for mathematical convenience. For a good discussion of marginalization from a Bayesian perspective, see Berger.³⁷

These five approaches to dealing with nuisance parameters will be discussed further in the context of wavefront sensing in Section 5.

D. Fisher Information and Cramér-Rao Bounds

For a vector parameter with P real components, the FIM, denoted F, is a P×P symmetric matrix with components given by

$$\begin{array}{cc}\hfill F_{\mathit{jk}}& ={\langle \left[\frac{\partial }{\partial {\theta }_j}\ln \mathrm{pr}(\mathbf{g}\mid \theta )\right]\left[\frac{\partial }{\partial {\theta }_k}\ln \mathrm{pr}(\mathbf{g}\mid \theta )\right]\rangle }_{\mathbf{g}\mid \theta }\hfill \\ \hfill & ={\int }_{\infty }{\mathrm{d}}^{M}g\mathrm{pr}(\mathbf{g}\mid \theta )\left[\frac{1}{\mathrm{pr}(\mathbf{g}\mid \theta )}\frac{\partial }{\partial {\theta }_j}\mathrm{pr}(\mathbf{g}\mid \theta )\right]\hfill \\ \hfill & \times \left[\frac{1}{\mathrm{pr}(\mathbf{g}\mid \theta )}\frac{\partial }{\partial {\theta }_k}\mathrm{pr}(\mathbf{g}\mid \theta )\right].\hfill \end{array}$$ (2.9)

Note that the FIM is fully determined by the likelihood function; it is the covariance matrix of the gradient of the logarithm of the likelihood, and the average itself is with respect to the likelihood function. In general the FIM will depend on the true parameter θ.

An important use of the FIM is to determine the lower CRB on the variance of the estimate. It is shown in any standard text^32,33 that the variance of any unbiased estimate must satisfy

$${\left[{\mathbf{K}}_{\widehat{\theta }}\right]}_{\mathit{nn}}=\mathrm{Var}\left\{{\widehat{\theta }}_n\right\}\ge {\left[{\mathbf{F}}^{-1}\right]}_{\mathit{nn}}.$$ (2.10)

Note that inversion of the Fisher information is required to find the lower bound on the variance of a component of the estimate. An unbiased estimator that achieves the bound of inequality (2.10) is called “efficient.”

Inequality (2.10) is a special case of a more general relation, which can be stated with the help of a notational convention known as Loewner ordering (see Barrett and Myers,⁶ Appendix A). If we have two P×P positive-definite matrices A and B, the statement A≥B does not hold on an element-by-element basis. Rather, it means that A−B is positive-semidefinite, or equivalently that x^†Ax≥x^†Bx for all x.

With this convention, it can be shown that the covariance matrix for any unbiased estimator must satisfy

$${\mathbf{K}}_{\widehat{\theta }}\ge {\mathbf{F}}^{-1}.$$ (2.11)

The corresponding relation for a biased estimator is

$${\mathbf{K}}_{\widehat{\theta }}\ge ({\nabla }_{\theta }\mathbf{b}+\mathbf{I}){\mathbf{F}}^{-1}{({\nabla }_{\theta }\mathbf{b}+\mathbf{I})}^t,$$ (2.12)

where I is the P×P unit matrix. Thus the bias of an estimator alters the lower bound on the variance by an amount that depends on the bias gradient. Note that bias can decrease the variance if the bias gradient is negative.

E. Maximum-Likelihood Estimation

So far we have not talked about ways of actually finding an estimate. One general method is ML estimation, defined by

$${\widehat{\theta }}_{\mathrm{ML}}\equiv \underset{\theta }{\mathrm{argmax}}\mathrm{pr}(\mathbf{g}\mid \theta ),$$ (2.13)

where the argmax operator returns the θ argument at which pr(g|θ) is maximized. Since the logarithm is a monotonic function of its argument, Eq. (2.13) can also be written as

$${\widehat{\theta }}_{\mathrm{ML}}\equiv \underset{\theta }{\mathrm{argmax}}\ln \left[\mathrm{pr}(\mathbf{g}\mid \theta )\right].$$ (2.14)

Note that we are not maximizing the probability of θ; we are choosing the value of θ that maximizes the probability of occurrence of the g that we actually observed.

ML estimates have many desirable properties.^6,38 First, they are efficient if an efficient estimate exists for a particular problem. And even when no efficient estimator exists, the ML estimate is asymptotically efficient and asymptotically unbiased in a sense to be explained in the next paragraph. Moreover, the PDF on ML estimates, pr(θ̂|θ), is asymptotically a multivariate normal with the covariance matrix given by taking the equality sign in expression (2.11).

The asymptotic properties listed above are usually stated by assuming that N independent samples of g are drawn from the same pr(g|θ) and then letting N→∞; but in fact they hold also when one gets better data,→for example by collecting more photons if the primary noise is Poisson or by letting the variance go to zero for Gaussian noise. With better data, therefore, the ML estimate approaches an efficient estimate, and its PDF approaches a fully specified multivariate normal law.

Another useful property of ML estimation arises when you want to estimate some function of the θ that appears in the likelihood, rather than θ itself. If we let a(θ) be a prescribed one-to-one vector-valued function, then under mild conditions it can be shown that³⁴

$${\widehat{a}}_{\mathit{ML}}=\mathbf{a}\left({\widehat{\theta }}_{\mathit{ML}}\right).$$ (2.15)

This property is referred to as the invariance of ML estimates.

3. STOCHASTIC DATA MODELS

In this section we present various probability laws for the raw data g (the output of the photodetector array in Fig. 1), and we briefly consider models for the derived measurements v. The probability laws will depend on some set of parameters θ, so we shall give expressions for the conditional probability laws, pr(data|θ), along with the corresponding FIM that would be relevant if we wanted to estimate all components of θ. In practical applications such as wavefront sensing, however, we may not want (or be able) to estimate all components of θ. In Section 4 we shall look more closely at what we can and should estimate, and in Section 5 the probability laws presented in this section will be converted to practical likelihoods and FIMs.

A. Pure Poisson Statistics

If we consider an array of ideal photon-counting detectors and a radiation source that satisfies the conditions for Poisson statistics (see Barrett and Myers⁶ for an extensive discussion), then g_m is the observed number of photocounts (photoelectric interactions) in the mth detector element. Similarly, dark current is frequently modeled as Poisson.

Since Poisson events are inherently independent and the Poisson probability is determined fully by its mean, the multivariate conditional probability on the data (the likelihood for estimation of θ) is given by

$$\mathrm{Pr}(\mathbf{g}\mid \theta )=\prod _{m=1}^M\exp [-{\stackrel{-}{g}}_m\left(\theta \right)]\frac{{\left[{\stackrel{-}{g}}_m\left(\theta \right)\right]}^{\mathit{gm}}}{g_m!},$$ (3.1)

and its logarithm is

$$\ln \mathrm{Pr}(\mathbf{g}\mid \theta )=\underset{m=1}{\overset{M}{\Sigma }}\{-{\stackrel{-}{g}}_m\left(\theta \right)+g_m\ln \left[{\stackrel{-}{g}}_m\left(\theta \right)\right]-\ln (g_m!)\}.$$ (3.2)

If the vector θ includes all parameters that influence the data, and all of these parameters are to be estimated, then Eq. (3.2) can be interpreted as a log-likelihood. The FIM in that case is readily derived from its definition [Eq. (2.9)].

The derivative of the log-likelihood with respect to a component of θ is

$$\frac{\partial }{\partial {\theta }_j}\ln \mathrm{Pr}(\mathbf{g}\mid \theta )=\underset{m=1}{\overset{M}{\Sigma }}\left\{-1+\frac{g_m}{{\stackrel{-}{g}}_m\left(\theta \right)}\right\}\frac{\partial {\stackrel{-}{g}}_m\left(\theta \right)}{\partial {\theta }_j}.$$ (3.3)

Poisson random variables are uncorrelated and have a variance equal to their mean,

$$\langle [g_m-{\stackrel{-}{g}}_m\left(\theta \right)][g_{m^{\prime }}-{\stackrel{-}{g}}_{m^{\prime }}\left(\theta \right)]\rangle ={\stackrel{-}{g}}_m\left(\theta \right){\delta }_{{\mathit{mm}}^{\prime }},$$ (3.4)

so it follows from Eq. (2.9) and a little algebra that

$$F_{\mathit{jk}}=\underset{m=1}{\overset{M}{\Sigma }}\frac{1}{{\stackrel{-}{g}}_m\left(\theta \right)}\frac{\partial {\stackrel{-}{g}}_m\left(\theta \right)}{\partial {\theta }_j}\frac{\partial {\stackrel{-}{g}}_m\left(\theta \right)}{\partial {\theta }_k}.$$ (3.5)

To reiterate, these expressions for likelihood and FIM hold rigorously only if θ includes all parameters that can influence the data (including, for example, the brightness of the guide star).

An example of the pure Poisson model occurs in the work of Winick,¹⁴ who considered Poisson noise arising from a light spot projected onto a CCD detector and also from a dark current in the detector. The parameter vector θ in his case consisted of just the x and y coordinates of the spot.

B. List-Mode Data

One interesting special case of Eq. (3.2) that has been considered in the literature on wavefront sensing^15-17 is the limit of very small detector elements. In that case, no element will detect more than one photon and the array will provide the coordinates of every detected photon. If K photons are detected, the data set, denoted G to distinguish it from the usual binned data, is a set of K+1 quantities, namely each 2D position vector r_k=(x_k,y_k) as well as K itself. This way of expressing information about a collection of photons is known in the nuclear-medicine literature as list mode; the coordinates and other parameters (e.g., time of arrival, photon energy if it can be measured) are stored in a list. List-mode likelihood and image reconstruction from list-mode data have been well studied in the medical literature.^39,40

The likelihood for a photon list can be expressed as

$$\mathrm{pr}(\mathbf{G}\mid \theta )=\mathrm{pr}(\left\{{\mathbf{r}}_k\right\},K\mid \theta )=\mathrm{pr}(\left\{{\mathbf{r}}_k\right\}\mid K,\theta )\mathrm{Pr}(K\mid \theta ),$$ (3.6)

where pr({r_k},K|θ) is a multivariate PDF on the photon positions r_k but a probability on the discrete random variable K. Under the same assumptions that lead to the independent Poisson form in Eq. (3.1), the photons are independent, and we can write

$$\mathrm{pr}(\mathbf{G}\mid \theta )=\mathrm{Pr}(K\mid \theta )\prod _{k=1}^K\mathrm{pr}({\mathbf{r}}_k\mid \theta ),$$ (3.7)

where pr(r_k|θ) is the PDF for the location of the kth photon; since the photons are indistinguishable, this PDF must be the same for all k. In fact, it is known from the theory of Poisson random processes⁶ that

$$\mathrm{pr}({\mathbf{r}}_k\mid \theta )=\frac{b({\mathbf{r}}_k;\theta )}{{\int }_{\mathit{det}}{\mathrm{d}}^{2}rb(\mathbf{r};\theta )},$$ (3.8)

where b(r;θ) is the photon fluence (the mean number of photons per unit area for parameter θ), and the integral is over the area of the detector array.

Since K is a Poisson random variable, the likelihood for the list is given by

$$\begin{array}{cc}\hfill \mathrm{pr}(\mathbf{G}\mid \theta )& =\exp [-\stackrel{-}{K}\left(\theta \right)]\frac{{\left[\stackrel{-}{K}\left(\theta \right)\right]}^K}{K!}\prod _{k=1}^K\frac{b({\mathbf{r}}_k;\theta )}{{\int }_{\mathit{det}}{\mathrm{d}}^{2}rb(\mathbf{r};\theta )}\hfill \\ \hfill & =\frac{\exp [-\stackrel{-}{K}\left(\theta \right)]}{K!}\prod _{k=1}^{K}b(\mathbf{r};\theta ),\hfill \end{array}$$ (3.9)

where the last step follows since ${\int }_{\mathit{det}}{\mathrm{d}}^{2}rb(\mathbf{r};\theta )$ is the total mean number of detected photons, K̄(θ). The log-likelihood is

$$\ln \mathrm{pr}(\mathbf{G}\mid \theta )=-\stackrel{-}{K}\left(\theta \right)-\ln K!+\underset{k=1}{\overset{K}{\Sigma }}\ln b({\mathbf{r}}_k;\theta ).$$ (3.10)

C. Electronic Noise

Electronic noise comes from electrons, and in any practical system a very large number of electrons contribute more or less independently. It therefore follows from the central-limit theorem that electronic noise is accurately described by Gaussian statistics. Moreover, if we consider a discrete array of individual detector elements with no electronic coupling from one element to another, then the noise in different elements is statistically independent. Finally, if we assume that the elements are identical, the noise is modeled as i.i.d. (independent and identically distributed) zero-mean Gaussian. The optical illumination creates a signal that does not have zero mean, but if we assume that all noise sources are independent of the illumination, the effect of the illumination is to shift the noise PDF. Thus the only place that the parameter θ can enter into the PDF on the data is in its mean. The PDF for purely electronic noise (without any photonic contribution) is given by

$$\mathrm{pr}(\mathbf{g}\mid \theta )=\underset{m=1}{\overset{M}{\Sigma }}\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left[-\frac{{[g_m-{\stackrel{-}{g}}_m\left(\theta \right)]}^2}{2{\sigma }^2}\right],$$ (3.11)

and its logarithm is

$$\ln \mathrm{pr}(\mathbf{g}\mid \theta )=-\frac{1}{2}M\ln \left(2\pi {\sigma }^2\right)-\frac{1}{2{\sigma }^2}\underset{m=1}{\overset{M}{\Sigma }}{[g_m-{\stackrel{-}{g}}_m\left(\theta \right)]}^2.$$ (3.12)

Of the various assumptions that enter into Eqs. (3.11) and (3.12), the one that is the most suspect in practice is that the detector elements are identical. The pixels in commercial CCD detectors, for example, have considerable variation in dark current and responsivity. Postacquisition digital processing can correct these effects on average by subtracting a measured dark-current map and dividing the result by a measured gain map, but these corrections do not produce a uniform variance in each element; in fact, they may increase the variance nonuniformity since a pixel with low response will be divided by a small gain factor. A more accurate approach would be to measure the variances after the corrections and express the PDF on the corrected data as

$$\mathrm{pr}(\mathbf{g}\mid \theta )=\prod _{m=1}^M\frac{1}{\sqrt{2\pi {\sigma }_m^2}}\exp \left[-\frac{{[g_m-{\stackrel{-}{g}}_m\left(\theta \right)]}^2}{2{\sigma }_m^2}\right].$$ (3.13)

The FIM corresponding to Eq. (3.13) is readily shown to be

$$F_{\mathit{jk}}=\underset{m=1}{\overset{M}{\Sigma }}\frac{1}{{\sigma }_m^2}\frac{\partial {\stackrel{-}{g}}_m\left(\theta \right)}{\partial {\theta }_j}\frac{\partial {\stackrel{-}{g}}_m\left(\theta \right)}{\partial {\theta }_k}.$$ (3.14)

As with Poisson data, the only dependence of the likelihood or the Fisher information on the parameter is through ḡ_m(θ).

D. Combined Poisson and Gaussian Noise

So far we have discussed Poisson and Gaussian noise as if only one or the other were present, but in practice both will contribute in most cases.

Suppose the mth detector element receives k_m photoelectrons in some exposure time T, responds to each with responsivity R [Volts/photon], and feeds the result into a readout channel with noise variance σ² [Volts²]. The output of the electronics channel is denoted g_m, and its PDF is given by

$$\mathrm{pr}(g_m\mid \theta )=\underset{k_m=1}{\overset{\infty }{\Sigma }}\mathrm{pr}(g_m\mid k_m)\mathit{Pr}(k_m\mid \theta ),$$ (3.15)

where pr(g_m|k_m) is the Gaussian PDF of the electronic signal for a fixed input and Pr(k_m|θ) is the Poisson probability (not PDF) for the photoelectrons. If we assume that all detectors have the same noise variance and responsivity, we obtain⁴¹

$$\begin{array}{cc}\hfill \mathrm{pr}(\mathbf{g}\mid \theta )& =\prod _{m=1}^M\mathrm{pr}(g_m\mid \theta )\hfill \\ \hfill & =\prod _{m=1}^M\frac{1}{\sqrt{2\pi {\sigma }^2}}\underset{k_m=0}{\overset{\infty }{\Sigma }}\exp \left[-\frac{{(g_m-{\mathit{Rk}}_m)}^2}{2{\sigma }^2}\right]\hfill \\ \hfill & \times \exp [-{\stackrel{-}{k}}_m\left(\theta \right)]\frac{{\left[{\stackrel{-}{k}}_m\left(\theta \right)\right]}^{k_m}}{k_m!}.\hfill \end{array}$$ (3.16)

Note that the only dependence on θ in this expression is through the means k̄_m(θ), so pr(g_m|θ) can also be written as pr[g_m|k̄_m(θ)].

The dependence of pr[g_m|k̄_m(θ)] on g_m is illustrated in Figs. 2(a) and 2(b). The distinct peaks in Fig. 2(a) correspond to different integer numbers of detected photons. Figures 2(a) and 2(b) should not be confused with likelihoods; when pr[g|k_m(θ)] is plotted against k̄_m(θ) for fixed g_m as in Figs. 2(c) and 2(d), a smooth unimodal likelihood results even when the variance of the electronic noise is small.

Fig. 2.

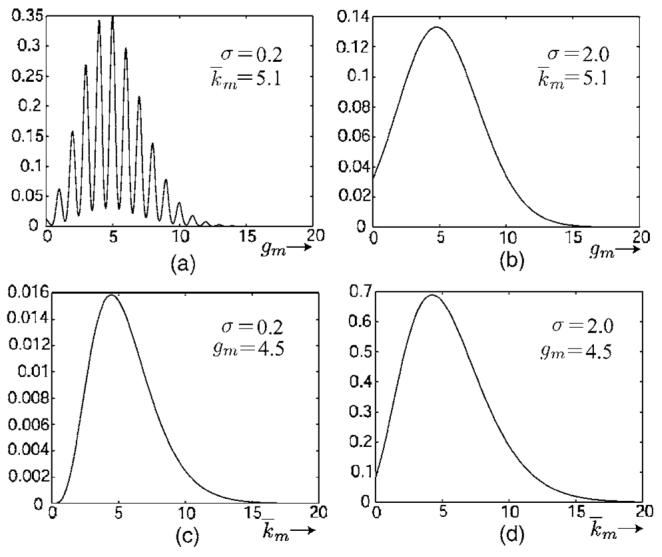
Plots of pr[g_m|k̄_m] for mixed Poisson and Gaussian noise: (a) and (b) show pr[g_m|k̄_m] versus g_m for fixed k̄_m; (c) and (d) show pr[g_m|k̄_m] versus k̄_m for fixed g_m. Plots (a) and (c) are for small electronic noise (σ=0.2 in electron units), and plots (b) and (d) are for larger electronic noise (σ=2.0).

An exact expression for the FIM for combined Poisson and Gaussian noise is derived in Appendix A; a useful approximation is

$$F_{\mathit{jk}}\approx \underset{m=1}{\overset{M}{\Sigma }}\frac{R^2}{{\sigma }^2+R^2{\stackrel{-}{k}}_m\left(\theta \right)}\frac{\partial {\stackrel{-}{k}}_m\left(\theta \right)}{\partial {\theta }_j}\frac{\partial {\stackrel{-}{k}}_m\left(\theta \right)}{\partial {\theta }_k},$$ (3.17)

where k̄_m(θ) is the mean number of photoelectrons. This expression is exact for pure Gaussian noise or pure Poisson noise, and it is a good approximation for all values of k̄_m(θ) so long as σ/R (the standard deviation of the electronic noise in photon units) is at least 0.5.

With combined Gaussian and Poisson noise, all you need to know to compute the FIM is k̄_m(θ) (plus the detector characteristics R and σ², of course).

E. Detectors with Gain

Many detectors, including photomultipliers (PMTs), intensified CCDs, electron-multiplication CCDs, and avalanche photodiodes (APDs), have an internal gain mechanism to increase the level of the signal before subjecting it to electronic noise. Electron-multiplication CCDs are already being used in wavefront sensing, and arrays of APDs and multianode PMTs (essentially many PMTs in a common glass envelope) are also very promising for this application.

Two new features can arise in the stochastic data model for detectors with gain. The obvious one is that the gain process itself is noisy. A less-obvious effect is that in some cases the gain process can introduce correlations in the data values. In intensified CCDs or multianode PMTs, for example, the secondary electrons produced by a single primary photoelectron can spread over several neighboring output pixels.

Gain noise is no issue if the flux is low enough to allow thresholding and photon counting. The distribution of pulse heights is difficult to compute (see, for example, Saleh and Teich⁴²), but it does not matter if the individual photons can be identified and counted.

Even spread of the secondaries to multiple pixels is not necessarily a problem at low photon flux; the electronics can be designed to recognize a cluster of pixels arising from a single primary event and to assign the event to a single pixel by some algorithm.⁴³ If these measures are taken (which they virtually never are), the output statistics remain rigorously uncorrelated Poisson⁶ in spite of the gain noise and charge spread.

At the opposite extreme, if the primary photon flux is high and the detector simply integrates all of the charge at each pixel, then the effect of the gain noise in the absence of charge spread is mainly to increase the variance by a factor studied by Burgess⁴⁴ and Swank.⁴⁵ The case of amplification with spread has been studied by Rabbani and others.^46,47 For a review of this work, see Barrett and Myers,⁶ Chap. 12. The outcome of these studies is easy to summarize if the mean number of primary photons per pixel is high; in that case we can invoke the central-limit theorem to say that the resulting overall PDF is multivariate Gaussian. The covariance matrix can be determined theoretically from the work cited above, or it can be measured for a particular detector. An important simplification in practice is that the correlations arising from charge spread will have short range, if they occur at all, so the covariance matrix will be diagonally dominant.

The intermediate case where the mean number of primary interactions per pixel is not low enough to permit identification of the signals from individual photons, yet not high enough that the central-limit theorem is valid, is just beginning to receive scrutiny.⁴⁸

F. PDF and Likelihood for Correlated Gaussian Noise

As we have seen, there are several possible situations in which the data provided by a WFS can be described as correlated Gaussian. In Subsection 3.E, we discussed correlations arising from charge spread in certain detectors with gain. Without charge spread, the data will be inherently uncorrelated, at least if we define the correlation with respect to the conditional PDF pr(g|θ), where θ includes all parameters that can affect the mean data. When we use some subset of these parameters, however, it often turns out that there are correlations induced by the parameters we choose to leave out (see Subsection 5.A). Finally, as we shall see in Appendix D, computation of centroids or other derived parameters usually results in correlations. In all of these cases, it may turn out that a more realistic data PDF is the correlated multivariate normal Gaussian.

A general multivariate normal PDF has the form:

$$\mathrm{pr}\left(\mathbf{g}\right)={\left[{\left(2\pi \right)}^M\det \left(\mathbf{K}\right)\right]}^{-1∕2}\exp \left[-\frac{1}{2}{(\mathbf{g}-\stackrel{-}{\mathbf{g}})}^t{\mathbf{K}}^{-1}(\mathbf{g}-\stackrel{-}{\mathbf{g}})\right],$$ (3.18)

where ḡ is the mean vector and K is the covariance matrix of g. The most general likelihood function is obtained by letting the mean and covariance both be functions of θ:

$$\begin{array}{cc}\hfill \mathrm{pr}(\mathbf{g}\mid \theta )& ={\left[{\left(2\pi \right)}^M\det \left[\mathbf{K}\left(\theta \right)\right]\right]}^{-1∕2}\hfill \\ \hfill & \times \exp \left\{-\frac{1}{2}{[\mathbf{g}-\stackrel{-}{\mathbf{g}}\left(\theta \right)]}^t{\left[\mathbf{K}\left(\theta \right)\right]}^{-1}[\mathbf{g}-\stackrel{-}{\mathbf{g}}\left(\theta \right)]\right\}.\hfill \end{array}$$ (3.19)

4. PARAMETERIZATION

As in Subsection 2.C, here we shall denote the parameters we want to estimate by the N×1 vector α, but we must recognize that this parameter set is seldom sufficient either to specify the wavefront fully or to completely describe the PDF of the data. In this section we look at some choices for α, what they imply for our representation of the wavefront, and how they have to be augmented to get the full parameter set θ that describes the data.

A. Wavefront Representations

Suppose the wave incident on the WFS has the form exp[ikW(r)], where r=(x,y) and k=2π/λ. Let {γ_n, n=1, … , ∞} denote an infinite set of parameters that can be used to express an arbitrary wavefront exactly as

$$W\left(\mathbf{r}\right)=\underset{n=1}{\overset{\infty }{\Sigma }}{\gamma }_n{u}_n\left(\mathbf{r}\right),$$ (4.1)

where the set {u_n(r)} is some orthonormal basis (e.g., Zernike polynomials). It is safe to say that we are never interested in estimating the full wavefront or the infinite-dimensional vector γ.

Sometimes we are interested in the N lowest-order terms in Eq. (4.1) for their own sake. In ophthalmology, for example, we might want to estimate the first N Zernike coefficients in order to use them for the task of planning laser surgery. In that case a reasonable choice for the parameters of interest would be α_n=γ_n, n=1, … ,N.

In AO, however, the usual objective is to determine the signals to be applied to the actuators of a deformable mirror. The possible phase functions that can be produced by a deformable mirror are assumed to be linear combinations of its influence functions {ψ_n(r), n=1, …N}, where N is the number of actuators. With this consideration in mind, we can write Eq. (4.1) in the form

$$W\left(\mathbf{r}\right)=\underset{n=1}{\overset{N}{\Sigma }}{\alpha }_n{\psi }_n\left(\mathbf{r}\right)+\Delta W\left(\mathbf{r}\right).$$ (4.2)

The N×1 vector α is what is needed for mirror control and hence a reasonable choice of parameters to estimate, and ΔW(r) will be referred to as the residual. If the coefficients {α_n} are chosen by least-squares (LS) fitting, the residual is orthogonal to the sum and Eq. (4.2) is an orthogonal decomposition of the wavefront.

Another way of representing a wavefront is to divide it into regions (subapertures), approximate the wavefront over each region by a small set of known functions that are zero outside the region, and then append a residual as in Eq. (4.2) to make the expansion exact. The coefficients in the regional representation can then be estimated, not for their own intrinsic interest, but so they can be used in a subsequent estimation of the mirror-mode coefficients α.

As an example, consider a representation in terms of local tilts. Suppose the jth region (j=1, … ,J) is centered at r=r_j, or equivalently x=x_j and y=y_j. Let the region itself be defined by a support function S_j(r), which is unity for r inside the region and zero outside. We assume that all regions are identical, so S_j(r)=S(r−r_j), and we assume that different regions do not overlap. Local tilt functions in the x and y directions can now be defined by

$${\chi }_k\left(\mathbf{r}\right)=\{\begin{array}{ccc}S(\mathbf{r}-{\mathbf{r}}_j)(x-x_j)\hfill & j=(k+1)∕2\hfill & \text{if}k\text{odd}\hfill \\ S(\mathbf{r}-{\mathbf{r}}_j)(y-y_j)\hfill & j=k∕2\hfill & \text{if}k\text{even}\hfill \end{array}.\phantom{\}}$$ (4.3)

These functions are orthogonal for square apertures, but they are not normalized.

With the tilt functions, a representation similar to Eq. (4.2) can be given as

$$W\left(\mathbf{r}\right)=\underset{k=1}{\overset{2J}{\Sigma }}{\tau }_k{\chi }_k\left(\mathbf{r}\right)+\delta W\left(\mathbf{r}\right).$$ (4.4)

This representation is particularly useful if the region is small enough (e.g., much smaller than the Fried parameter in the atmospheric case) since then it may be a good approximation to say that the wavefront in the region is described completely by its tilts and pistons. The tilts are accounted for by the sum in Eq. (4.4), and the pistons are contained in δW(r). For a square aperture, the local piston is orthogonal to the tilt function so Eq. (4.4), like Eq. (4.2), is an orthogonal decomposition of the wavefront.

B. Nuisance Parameters

There are two distinct classes of nuisance parameters in wavefront sensing: intrinsic nuisance parameters related to the wavefront expansion itself and extrinsic nuisance parameters that arise from other sources.

Examples of extrinsic nuisance parameters include the brightness of the guide star, length of the sodium column when a laser guide star is used, level and distribution of background light, and scintillation effects. Which of these we need to consider depends on the application and the data-acquisition system; in Section 5 we shall consider brightness of the guide star and background light level as examples.

Intrinsic nuisance parameters are the ones needed to represent the residual in Eq. (4.2) or (4.4). Since the residual is an infinite-dimensional function (technically a vector in the Hilbert space L₂(R²)), it might appear that an infinite set of parameters would be needed, but not all components of the residual influence the data.

One way to parameterize the residual is to recognize that the sum in Eq. (4.2) or (4.4) defines a vector in a subspace of L₂(R²). Following terminology introduced by Paxman,⁴⁹ we can refer to this subspace as interest space and to its orthogonal complement as indifference space. If we are interested in estimating the signals needed to control a deformable mirror as in Eq. (4.2), for example, the mirror influence functions form a (nonorthogonal) basis for interest space, and all functions in indifference space are orthogonal to all influence functions.

We can define an orthonormal basis {Ξ_k(r)} for indifference space by use of projection operators (see Barrett and Myers⁶ for details), and then we can represent the residual as

$$\Delta W\left(\mathbf{r}\right)=\underset{k=1}{\overset{\infty }{\Sigma }}{\beta }_k^{\mathit{int}}{\Xi }_k\left(\mathbf{r}\right).$$ (4.5)

Though this sum is infinite, only a finite subset of the terms, say K of them, will influence the data significantly, and we can use those coefficients to define a K×1 vector β^int that describes the intrinsic nuisance parameters.

C. Summary of Parameters

The vectors that will be needed in Section 5 are summarized in Table 1.

Table 1.

Vectors Relevant to Wavefront Sensing

Vector	Meaning	Dimension
g	Raw data (photodetector outputs)	M×1
α	Parameters of interest (e.g., mirror modes)	N×1
βint	Intrinsic nuisance parameters	K×1
βext	Extrinsic nuisance parameters	L×1
β	All nuisance parameters	(K+L)×1
θ	All parameters that influence data	P×1, (P=N+K+L)
γ	Parameters in exact wavefront representation	∞×1
τ	Coefficients of local tilt functions in J subapertures	2J×1

5. PRACTICAL LIKELIHOOD FUNCTIONS AND FISHER INFORMATION MATRICES

The goal of this section is to show how the general principles discussed above can be used to construct practical likelihood functions and FIMs. Emphasis in this section will be on the problem of directly estimating the mirror modes without the intermediary of the reconstruction stage in Fig. 1, but in Section 6 we consider the more common problem of estimating local tilts from Shack–Hartmann data.

Any of the likelihood functions developed in this section can be used for MAP estimation as well, provided one has a meaningful prior on the parameters to be estimated.

A. General Considerations on Nuisance Parameters

The first decision we have to make in constructing a practical likelihood function is what to do about intrinsic and extrinsic nuisance parameters. The possibilities were enumerated in Subsection 2.C; which option we use depends in large part on the dimensionality of the nuisance parameter.

To be explicit, consider two specific extrinsic nuisance parameters in astronomical wavefront sensing: the brightness of the guide star and the average sky background. These two numbers form the components of a 2×1 extrinsic nuisance parameter vector. Both can affect the mean data strongly, so they should not be ignored [option (1) in Subsection 2.C]. Both vary significantly with site, guide star chosen, and position in the sky, so typical values [option (2)] would not be reliable, and prior PDFs [option (5)] would be broad and relatively uninformative. As we shall see below, however, both parameters can be estimated from the same data as used to estimate the wavefront parameters [option (3)] or from some expanded data set [option (4)], and these would have to be the recommended options.

Often, however, intrinsic and extrinsic nuisance parameters require high-dimensional parameter vectors. The sky background, for example, might be a complicated spatial distribution rather than just a single number, and many different modes can contribute to the intrinsic nuisance parameter β^int. In these cases any attempt to estimate all components will increase the dimension and condition number of the FIM and thereby increase the CRB on the parameters of interest. (For a proof of this statement, see Barrett and Myers,⁶ Sec. 13.3.8.). If the number of nuisance parameters is larger than the number of measurements, the FIM is singular and the CRB is infinite.

With high-dimensional nuisance parameters, therefore, the only remaining options are to ignore them [option (1)] or to marginalize over them [option (5)]. To reiterate a point from Subsection 2.C, marginalization is optimal in terms of risk if a meaningful prior is known.

B. Marginalizing Intrinsic Nuisances

If we are interested in estimating α from a data set g by ML (or MAP) methods, we need the likelihood pr(g|α). What we know from Section 3, however, is pr(g|θ) or pr(g|α, β). If we want to marginalize over all nuisance parameters, we need

$$\mathrm{pr}(\mathbf{g}\mid \alpha )=\int {\mathrm{d}}^{K+L}\beta \mathrm{pr}(\mathbf{g}\mid \alpha ,\beta )\mathrm{pr}(\beta \mid \alpha ),$$ (5.1)

and if we want to marginalize over just the intrinsic nuisance parameters and estimate the extrinsic ones, we need

$$\mathrm{pr}(\mathbf{g}\mid \alpha ,{\beta }^{\mathit{ext}})=\int {\mathrm{d}}^K{\beta }^{\mathit{int}}\mathrm{pr}(\mathbf{g}\mid \alpha ,{\beta }^{\mathit{ext}},{\beta }^{\mathit{int}})\mathrm{pr}({\beta }^{\mathit{int}}\mid \alpha ).$$ (5.2)

Note that we do not write pr(β^int|α, β^ext) in Eq. (5.2) because there is no apparent way that extrinsic parameters like guide-star brightness and sky background can influence the wavefront being sensed.

In both Eqs. (5.1) and (5.2), a conditional prior on β is needed, and in keeping with the spirit of this paper, it has to be a prior with experimental justification.

In astronomy, there is a large body of experimental evidence supporting the Kolmogorov theory of atmospheric turbulence. Central to that theory is the assumption that phase perturbations are zero-mean Gaussian random processes, so the coefficient of any term in any linear representation of a wavefront must be a Gaussian random variable. We may therefore safely take pr(β^int) as a K-dimensional zero-mean multivariate normal density. What we need in Eq. (5.2), however, is pr(β^int|α) rather than pr(β^int), and the dependence on α is a complication since that is the main parameter we want to estimate.

There are two ways we can justify replacing pr(β^int|α) in Eq. (5.2) with a multivariate normal independent of α. The obvious one is simply to assume that β^int is independent of α. A more subtle approach is to recognize that in a closed-loop system where α represents the coefficients of the mirror modes, the effect of the AO system is to drive α close to zero. We can formalize this notion by the closed-loop approximation:

$$\mathrm{pr}({\beta }^{\mathit{int}}\mid \alpha )\approx \mathrm{pr}({\beta }^{\mathit{int}}\mid \alpha =0).$$ (5.3)

It is shown in Appendix B that pr(β^int|α=0) is itself a zero-mean multivariate normal of the form

$$\mathrm{pr}({\beta }^{\mathit{int}}\mid \alpha =0)=𝓝\exp \left[-\frac{1}{2}{\left({\beta }^{\mathit{int}}\right)}^t{\mathbf{C}}^{-1}\left({\beta }^{\mathit{int}}\right)\right],$$ (5.4)

where 𝓝=[(2π)^Kdet(C)]^−1/2 and C is a covariance matrix known as a Schur complement; if β^int and α were uncorrelated, C would be just the covariance matrix of β^int. With Eqs. (5.3) and (5.4), the desired likelihood function [Eq. (5.2)] becomes

$$\begin{array}{cc}\hfill \mathrm{pr}(\mathbf{g}\mid \alpha ,{\beta }^{\mathit{ext}})\approx & 𝓝\int {\mathrm{d}}^K{\beta }^{\mathit{int}}\mathrm{pr}(\mathbf{g}\mid \alpha ,{\beta }^{\mathit{ext}},{\beta }^{\mathit{int}})\hfill \\ \hfill & \times \exp \left[-\frac{1}{2}{\left({\beta }^{\mathit{int}}\right)}^t{\mathbf{C}}^{-1}\left({\beta }^{\mathit{int}}\right)\right].\hfill \end{array}$$ (5.5)

To proceed, we must choose a form for the likelihood conditional on all relevant parameters, pr(g|α, β^ext, β^int). The simplest choice is the i.i.d. normal model presented in Subsection 3.C. Using Eqs. (3.11) and (5.5), we can write

$$\begin{array}{cc}\hfill \mathrm{pr}(\mathbf{g}\mid \alpha ,{\beta }^{\mathit{ext}})\approx & {𝓝}^{\prime }{\int }_{\infty }{\mathrm{d}}^K{\beta }^{\mathit{int}}\hfill \\ \hfill & \times \exp \left[-\underset{m=1}{\overset{M}{\Sigma }}\frac{{[g_m-{\stackrel{-}{g}}_m(\alpha ,{\beta }^{\mathit{ext}},{\beta }^{\mathit{int}})]}^2}{2{\sigma }^2}\right]\hfill \\ \hfill & \times \exp \left[-\frac{1}{2}{\left({\beta }^{\mathit{int}}\right)}^t{\mathbf{C}}^{-1}\left({\beta }^{\mathit{int}}\right)\right],\hfill \end{array}$$ (5.6)

where the integral runs from −∞ to ∞ over all K variables and 𝓝′=𝓝(2πσ²)^−M/2. This integral would be the convolution of two Gaussians, immediately yielding another Gaussian, except that β^int enters into the first factor in the integrand in a complicated way through the mean ḡ_m(α, β^ext, β^int); we can fix this problem by assuming that the effect of β^int is small, performing a Taylor expansion of the mean, and retaining only the first two terms. Details are given in Appendix B, where it is shown that

$$\begin{array}{cc}\hfill \mathrm{pr}(\mathbf{g}\mid \alpha ,{\beta }^{\mathit{ext}})\approx & {𝓝}^{″}\exp \{-\frac{1}{2}{[\mathbf{g}-\stackrel{-}{\mathbf{g}}(\alpha ,{\beta }^{\mathit{ext}},0)]}^t\phantom{\}}\hfill \\ \hfill & \phantom{\{}\times {\mathbf{K}}_{\mathit{tot}}^{-1}{[\mathbf{g}-\stackrel{-}{\mathbf{g}}(\alpha ,{\beta }^{\mathit{ext}},0)]}^t\},\hfill \end{array}$$ (5.7)

where 𝓝″=[(2π)^Mdet(K_tot)]^−1/2 and

$${\mathbf{K}}_{\mathit{tot}}\equiv {\sigma }^2\mathbf{I}+{\mathbf{ACA}}^t,$$ (5.8)

with A being a matrix defined in the appendix. Note that the fact that ḡ_m(α, β^ext, β^int) is evaluated at β^int=0 does not mean that the unwanted modes are being set to zero; rather it comes from the assumption that β^int has zero mean and that excursions about the mean are small enough to allow a first-order Taylor expansion.

To the first order, Eq. (5.7) shows that the likelihood after marginalizing over the intrinsic nuisance parameters is a multivariate normal with mean determined without any consideration of the nuisance parameters. To this order, the only effect of the unwanted modes is to add a new, nondiagonal term to the covariance matrix. This result generalizes easily to include readout noise that varies from detector to detector, gain noise, and even photon noise so long as the Poisson can be approximated by a Gaussian.

In practice, neither C nor A is known, but it is straightforward to simulate realizations of Kolmogorov turbulence, either fully digitally or with a spatial light modulator, and to find a sample covariance matrix that is an experimental approximation to ACA^t. The matrix inversion required in Eq. (5.7) can then be performed by methods described in Chap. 14 of Barrett and Myers,⁶ even if the sample covariance matrix is not full rank.

To summarize this subsection, we have seen that there are several possible approaches to choosing a prior with which to marginalize over the nuisance parameters. In the view of the authors, the final justification for making this choice will have to come from a meaningful, task-based performance assessment of the overall AO system.³⁵

C. Poisson Data with Negligible Intrinsic Nuisances

Sometimes we can get away with the assumption that there are no intrinsic nuisance parameters. In Shack–Hartmann sensors with relatively small subapertures, for example, it is probably valid to neglect aberrations other than piston and tilt; piston does not affect the data, and tilt is what we want to estimate, so there are no intrinsic nuisance parameters.

If there are no significant intrinsic nuisance parameters and we choose to estimate the extrinsic ones, then all of the likelihood functions and FIMs derived in Section 3 are immediately applicable, just by identifying

$$\theta =\left(\begin{array}{c}\hfill \alpha \hfill \\ \hfill {\beta }^{\mathit{ext}}\hfill \end{array}\right).$$

In particular, for pure Poisson data, the log-likelihood is given by Eq. (3.2), which we can rewrite as

$$\ln \mathrm{Pr}(\mathbf{g}\mid \alpha ,{\beta }^{\mathit{ext}})=\underset{m=1}{\overset{M}{\Sigma }}\{-{\stackrel{-}{g}}_m(\alpha ,{\beta }^{\mathit{ext}})+g_m\ln \left[{\stackrel{-}{g}}_m(\alpha ,{\beta }^{\mathit{ext}})\right]\}.$$ (5.9)

The term ln g_m! has been dropped since it is independent of the parameters and hence does not affect the likelihood [Pr(g|θ) regarded as a function of θ for fixed g].

Consider the case where the extrinsic nuisance parameter is only the brightness of the guide star (or other point source), denoted I₀. In that case we can express the mean data as

$${\stackrel{-}{g}}_m(\alpha ,I_0)=I_0{f}_m\left(\alpha \right),$$ (5.10)

where f_m(α) is a characteristic of the individual detector element, defined in such a way that I₀f_m(α) is the mean number of photons detected by the mth element when the wavefront is fully described by the vector α. The log-likelihood is now given by

$$\ln \mathrm{Pr}(\mathbf{g}\mid \alpha ,I_0)=-I_0\underset{m=1}{\overset{M}{\Sigma }}{f}_m\left(\alpha \right)+\underset{m=1}{\overset{M}{\Sigma }}{g}_m\ln \left[f_m\left(\alpha \right)\right]+N_{\mathit{tot}}\ln \left(I_0\right),$$ (5.11)

where $N_{\mathit{tot}}\equiv {\Sigma }_{m=1}^M{g}_m$ is the total number of detected photons.

1. Fisher Information with One Nuisance Parameter

If α is an N×1 vector and the only nuisance parameter is the guide-star brightness, then the FIM is (N+1)×(N+1). The derivatives needed in the FIM are

$$\frac{\partial }{\partial {\alpha }_n}\ln \mathrm{Pr}(\mathbf{g}\mid \alpha ,I_0)=\underset{m=1}{\overset{M}{\Sigma }}\left[\frac{g_m-{\stackrel{-}{g}}_m(\alpha ,I_0)}{f_m\left(\alpha \right)}\right]\frac{\partial f_m\left(\alpha \right)}{\partial {\alpha }_n},$$ (5.12)

$$\frac{\partial }{\partial I_0}\ln \mathrm{Pr}(\mathbf{g}\mid \alpha ,I_0)=\frac{1}{I_0}\underset{m=1}{\overset{M}{\Sigma }}[g_m-{\stackrel{-}{g}}_m(\alpha ,I_0)].$$ (5.13)

The statistical average needed in the FIM is

$$\langle [g_m-{\stackrel{-}{g}}_m(\alpha ,I_0)][g_{m^{\prime }}-{\stackrel{-}{g}}_{m^{\prime }}-(\alpha ,I_0)]{\rangle }_{\mathbf{g}\mid \alpha ,I_0}={\stackrel{-}{g}}_m(\alpha ,I_0){\delta }_{{\mathit{mm}}^{\prime }},$$ (5.14)

and the elements of the FIM are found to be

$$F_{{\mathit{nn}}^{\prime }}=I_0\underset{m=1}{\overset{M}{\Sigma }}\frac{1}{f_m\left(\alpha \right)}\frac{\partial f_m\left(\alpha \right)}{\partial {\alpha }_n}\frac{\partial f_m\left(\alpha \right)}{\partial {\alpha }_{n^{\prime }}}(n,n^{\prime }\le N),$$ (5.15)

$$F_{n,N+1}=F_{N+1,n}=\underset{m=1}{\overset{M}{\Sigma }}\frac{\partial f_m\left(\alpha \right)}{\partial {\alpha }_n}(n\le N),$$ (5.16)

$$F_{N+1,N+1}=\frac{{\stackrel{-}{N}}_{\mathit{tot}}}{I_0^2}=\frac{1}{I_0}\underset{m=1}{\overset{M}{\Sigma }}{f}_m\left(\alpha \right),$$ (5.17)

We see, therefore, that the FIM for this problem is a partitioned matrix with the structure

$$\mathbf{F}=\left[\begin{array}{cc}\hfill {\mathbf{A}}_{N\times N}\hfill & \hfill {\mathbf{B}}_{N\times 1}\hfill \\ \hfill {\mathbf{B}}_{1\times N}^t\hfill & \hfill {\mathbf{C}}_{1\times 1}\hfill \end{array}\right],$$ (5.18)

where the elements of A [given by Eq. (5.15)] scale as I₀, the elements of B [given by Eq. (5.16)] are independent of I₀, and C is proportional to 1/I₀.

2. Inclusion of Sky Background

Now we consider an additional nuisance, the sky background treated as a uniform incoherent source. This additional radiation does not spoil the Poisson assumptions, but instead modifies the mean data with an additional term. If each detector receives the same amount of sky radiation on average, then Eq. (5.10) becomes

$${\stackrel{-}{g}}_m(\alpha ,I_0,b)=I_0{f}_m\left(\alpha \right)+b,$$ (5.19)

where the scalar b, defined as the mean number of detected background photons per pixel, is now one additional nuisance parameter. If dark current is significant, its effect can also be included in b.

With two nuisance parameters, the log-likelihood Eq. (5.11) becomes

$$\begin{array}{cc}\hfill \ln \mathrm{Pr}(\mathbf{g}\mid \alpha ,I_0,b)=& -I_0\underset{m=1}{\overset{M}{\Sigma }}{f}_m\left(\alpha \right)-\mathit{Mb}\hfill \\ \hfill & +\underset{m=1}{\overset{M}{\Sigma }}{g}_m\ln [I_0{f}_m\left(\alpha \right)+b].\hfill \end{array}$$ (5.20)

The FIM is now (N+2)×(N+2), and the derivatives needed for its computation are

$$\frac{\partial }{\partial {\alpha }_n}\ln \mathrm{Pr}(\mathbf{g}\mid \alpha ,I_0,b)=I_0\underset{m=1}{\overset{M}{\Sigma }}\left[\frac{g_m-{\stackrel{-}{g}}_m(\alpha ,I_0,b)}{{\stackrel{-}{g}}_m(\alpha ,I_0,b)}\right]\frac{\partial f_m\left(\alpha \right)}{\partial {\alpha }_n},$$ (5.21)

$$\frac{\partial }{\partial I_0}\ln \mathrm{Pr}(\mathbf{g}\mid \alpha ,I_0,b)=\underset{m=1}{\overset{M}{\Sigma }}[g_m-{\stackrel{-}{g}}_m(\alpha ,I_0,b)]\frac{f_m\left(\alpha \right)}{I_0{f}_m\left(\alpha \right)+b},$$ (5.22)

$$\frac{\partial }{\partial b}\ln \mathrm{Pr}(\mathbf{g}\mid \alpha ,I_0,b)=\underset{m=1}{\overset{M}{\Sigma }}\left[\frac{g_m-{\stackrel{-}{g}}_m(\alpha ,I_0,b)}{{\stackrel{-}{g}}_m(\alpha ,I_0,b)}\right].$$ (5.23)

The elements of F can now be computed with the help of a slight generalization of Eq. (5.14).

D. Maximum-Likelihood Estimation from Gaussian Measurements

Subsection 5.C dealt with purely Poisson noise, but we saw earlier that there are several situations in which the Poisson model is incorrect. Electronic readout noise and gain noise are continuous random variables and hence not Poisson, and we saw in Subsection 5.B that marginalizing over unwanted wavefront modes can yield a multivariate Gaussian likelihood.

It is well known that ML estimation with Gaussian data is basically LS fitting. If the mean data are linear functions of the parameters to be estimated, then ML estimation is the same as linear regression, with the regression function being the negative of the log-likelihood. The ML solution in this case is obtained by matrix inversion or pseudoinversion.⁶ In wavefront sensing and many other applications, however, the mean data depend nonlinearly on the parameters, so no linear method will deliver ML estimates.

1. Independent Gaussian Measurements

A general likelihood for statistically independent Gaussian measurements is given in Eq. (3.13). If we allow the variance to depend on θ for generality, the corresponding log-likelihood boils down to

$$\ln \mathrm{pr}(\mathbf{g}\mid \theta )=-\frac{1}{2}\underset{m=1}{\overset{M}{\Sigma }}\frac{{[g_m-{\stackrel{-}{g}}_m\left(\theta \right)]}^2}{{\sigma }_m^2\left(\theta \right)}+\text{constant}.$$ (5.24)

Because of the leading minus sign, maximizing the log-likelihood is the same thing as minimizing a weighted norm of the difference between the measured data vector g and the predicted mean data ḡ(θ). ML estimation from independent Gaussian data is a nonlinear regression.

2. Correlated Gaussian Measurements

Detectors with gain may deliver inherently correlated Gaussian data, and marginalizing over nuisance parameters may induce correlations even when the detectors themselves do not. The log-likelihood in these cases is given by

$$\begin{array}{cc}\hfill \ln \mathrm{pr}(\mathbf{g}\mid \theta )& =-\frac{1}{2}\underset{m=1}{\overset{M}{\Sigma }}\underset{m^{\prime }=1}{\overset{M}{\Sigma }}[g_m-{\stackrel{-}{g}}_m\left(\theta \right)]{\left[{\mathbf{K}}^{-1}\right]}_{{\mathit{mm}}^{\prime }}[g_{m^{\prime }}-{\stackrel{-}{g}}_{m^{\prime }}\left(\theta \right)]\hfill \\ \hfill & =-\frac{1}{2}{[\mathbf{g}-\stackrel{-}{\mathbf{g}}\left(\theta \right)]}^t{\mathbf{K}}^{-1}[\mathbf{g}-\stackrel{-}{\mathbf{g}}\left(\theta \right)],\hfill \end{array}$$ (5.25)

where K is a covariance matrix which, in the most general case, can depend on θ.

6. APPLICATION TO A SHACK–HARTMANN SENSOR

Though the likelihood models developed above are applicable to any wavefront sensor, the familiar Shack–Hartmann sensor provides an instructive example. In its simplest form, a Shack–Hartmann sensor consists of an array of lenslets in, say, the plane z=0, and an array of photodetectors in a parallel plane, z=z₀ (where z₀ is not necessarily the focal length of the lenslets). The data from the entire detector array can, in principle, be used to estimate the full set of parameters of interest α, but in practice a subset of the data associated with a single lenslet is used to estimate local tilts, which are then used to estimate α in a separate reconstruction step. In this section we first look at the conventional problem of estimation of local tilts and then discuss the application of likelihood principles to estimation of α.

A. Estimation of Local Tilts from Poisson Data

If the geometry in a Shack–Hartmann sensor is chosen so that radiation passing through one lenslet falls only on one subset of the detector pixels, then the local wavefront parameters for each lenslet can be estimated independently of those for other lenslets. Moreover, if the wave over one lenslet is well described as a pure tilt, then there are no intrinsic nuisance parameters, and the likelihood functions given in Subsections 5.C and 5.D are applicable if we simply replace the general parameter α with the 2D tilt vector τ for the lenslet of interest.

In particular, if the noise is Poisson and the unknowns are the guide-star brightness and two components of the local tilt, then the log-likelihood, given by Eq. (5.11), is specified by the set of functions {f_m(τ)}, where the index m now runs over only those detector elements that receive radiation from the particular lenslet. For a normally incident plane wave in a Shack–Hartmann sensor, the lenslet produces an irradiance distribution on the detector plane (a “spot”) denoted by s(r). If z₀ is the focal length of the lenslet, then s(r) is the squared modulus of the (suitably scaled) Fourier transform of the pupil function, but in general it can also be a defocused image of the pupil. In either case, the effect of a pure tilt is to shift the spot, and the mean output of the mth detector element is obtained by multiplying the irradiance by the responsivity function of that element, d_m(r), and integrating

$$f_m\left(\tau \right)={\int }_{\infty }{\mathrm{d}}^{2}r{d}_m\left(\mathbf{r}\right)s(\mathbf{r}-z_0\tau ).$$ (6.1)

The units are again chosen so that I₀f_m(τ) is the mean number of photons from the guide star detected in element m. Thus f_m(τ) is the mean response of the detector element as a function of the shift of the spot.

1. Some Simplifying Assumptions

A common assumption made in analyzing Shack-Hartmann sensors is that there is no light loss as the spot shifts, so that

$$\underset{m=1}{\overset{M_1}{\Sigma }}{f}_m\left(\tau \right)\equiv f_{\mathit{tot}}=\text{constant},$$ (6.2)

where M₁ is the number of detector elements associated with a particular lenslet and τ is the 2D vector of x and y tilts over that lenslet. The assumption in Eq. (6.2) is valid if (a) there are no gaps between detector elements; (b) the responsivity of all detector elements is the same; (c) obliquity and other angular factors are neglected; (d) the spot does not fall off the area of the detector associated with the lenslet; and (e) that detector area does not receive light from adjacent lenslets. With these restrictive physical assumptions and the assumptions of pure Poisson noise, no intrinsic nuisance parameters and no sky background, the log-likelihood from Eq. (5.11) becomes

$$\ln \mathrm{Pr}(\mathbf{g}\mid \tau ,I_0)=-f_{\mathit{tot}}{I}_0+\underset{m=1}{\overset{M_1}{\Sigma }}{g}_m\ln \left[f_m\left(\tau \right)\right]+N_{\mathit{tot}}\ln \left(I_0\right),$$ (6.3)

where τ is now a 2D vector specifying the x and y components of tilt over that lenslet.

Equation (6.3) is the form of the log-likelihood used most commonly in the literature on wavefront sensing, though it is also common to go further and consider a very large number of small detector elements so that d_m(r) can be treated as a delta function.

One advantage of assumption (6.2) is that the FIM becomes block diagonal since

$$\underset{m=1}{\overset{M_1}{\Sigma }}\frac{\partial f_m\left(\tau \right)}{\partial {\tau }_n}=\frac{\partial }{\partial {\tau }_n}\underset{m=1}{\overset{M_1}{\Sigma }}{f}_m\left(\tau \right)=0.$$ (6.4)

Thus, as shown by Eq. (5.16), the off-diagonal blocks B in Eq. (5.18) vanish, and the CRBs on τ and I₀ are readily computed.

A consequence of the block-diagonal FIM is that the CRB on the estimates of the parameters of interest, τ, is obtained just by inverting the A block in Eq. (5.18). Therefore it is the same as if C were not present, and there is no penalty in the performance bound for including I₀ in the parameter list.

Another consequence of model (6.3) and the block-diagonal FIM is that I₀ and τ can be estimated separately. The ML estimate of I₀ is obtained by setting ∂[ln Pr(g|τ,I₀)]/(∂I₀ as given by Eq. (5.13) to zero and by using Eq. (5.10); the result is

$${\widehat{I}}_0=\frac{\underset{m=1}{\overset{M_1}{\Sigma }}{g}_m}{\underset{m=1}{\overset{M_1}{\Sigma }}{f}_m\left(\tau \right)}=\frac{N_{\mathit{tot}}}{\underset{m=1}{\overset{M_1}{\Sigma }}{f}_m\left(\tau \right)}.$$ (6.5)

If Eq. (6.2) holds, the denominator is independent of the τ and the guide-star brightness can be estimated independently of the tilts. The ML tilt estimates τ̂ are then found by setting ∂[ln Pr(g|τ,I₀)]/(∂_τn as given by Eq. (5.12) to zero. The result is

$$\underset{m=1}{\overset{M_1}{\Sigma }}\frac{g_m}{f_m\left(\tau \right)}\frac{\partial f_m\left(\tau \right)}{\partial {\tau }_n}=0\text{when}\tau =\widehat{\tau }.$$ (6.6)

This result does not require knowledge of the guide-star brightness, so we may as well ignore it; we emphasize, however, that this result requires that there be no light loss, no overlapping with adjacent lenslets, no sky background, and pure Poisson noise.

2. Joint Estimation of Tilts and Nuisance Parameters

If Eq. (6.2) does not hold or if there is a sky background, all parameters associated with a single subaperture must be estimated jointly. The derivative formulas are not particularly useful, and the best we can say is that the log-likelihood from Eq. (5.20) must be maximized:

$$\begin{array}{cc}\hfill -I_0\underset{m=1}{\overset{M_1}{\Sigma }}{f}_m\left(\tau \right)-\mathit{Mb}+\underset{m=1}{\overset{M_1}{\Sigma }}{g}_m& \ln [I_0{f}_m\left(\tau \right)+b]=\mathrm{maximum}\hfill \\ \hfill & \text{at}\tau =\widehat{\tau },I_0={\widehat{I}}_0,b=\widehat{b}.\hfill \end{array}$$ (6.7)

In this general case, the FIM is not block diagonal and the CRB is increased by having to estimate I₀ and b.

3. Auxiliary Data

One way to simplify the ML estimation of the parameters of interest and to avoid the increase in variance that results from having to estimate nuisance parameters is to acquire more data. Additional telescopes could be used to measure the guide-star brightness and sky background. Their collection apertures could be much larger than that of a single lenslet in a Shack–Hartmann sensor, and if scintillation effects are not important their integration time could be much longer. The resulting estimates of I₀ and b could have very low variance, so these parameters could be regarded as known.

If additional monitors are not practical, the data from all lenslets could be used to estimate I₀ and b. With J lenslets and the wavefront described by pure tilt, the complete data set is described by 2J+2 parameters (two tilts per lenslets plus two global nuisance parameters), which is an improvement over the 4J we would have if two tilts and two nuisance parameters were to be estimated from the data associated with each lenslet. Even if scintillation does occur, it will not affect the diffuse sky background, so at least b can be treated as a global parameter.

B. Estimation of Global Wavefront Parameters

Above we considered the traditional operation of a Shack-Hartmann sensor in which the goal is assumed to be estimation of local tilts from data associated with individual lenslets. Once that is accomplished, the true goal of estimating global parameters in an expansion like Eq. (4.2) is often considered to be a separate problem.

This dichotomy is tenable in a Shack–Hartmann sensor only if radiation passing through one lenslet does not reach the detector pixels associated with an adjacent lenslet, but this condition is quite restrictive. Even if the detectors lie in the focal plane of the lenslet, the tails of the point-spread function from the lenslet of interest can overlap the pixels associated with an adjacent lenslet. Approaches to dealing with this problem and arriving at final ML estimates of global parameters are discussed below.

1. Likelihood Models with Overlap

Suppose we want to estimate local tilts using only the data from detector elements under a particular lenslet, even though light from other lenslets contributes to the data from those elements. We could simply ignore the problem and find ML estimates of the local tilts from an erroneous likelihood model. A rigorous mathematical treatment of the errors resulting from misspecified likelihood models is given by Halbert White⁵⁰, who showed that there are many circumstances under which such quasi-ML estimators (QMLEs) have very useful properties. As with true ML estimators, the PDFs of QMLEs may asymptotically approach multivariate normals, though not necessarily with the inverse of the FIM as the covariance matrix, and they may be consistent estimators. White also gives several useful tests of the degree of misspecification of the likelihood model. No research has appeared on applying Whites theories to wavefront sensing, so it is not yet clear what can be said about QMLEs of local tilts or when the likelihood specification is adequate.

Rather than ignoring the overlap problem, an alternative would be to treat the tilts in adjacent lenslets as nuisance parameters for the purpose of estimating the tilts over a given lenslet. Then the general theory developed in Subsection 5.B would be applicable and a multivariate normal model, like Eq. (5.7) but with the 2D vector τ in place of α, would result after marginalization.

Finally, we could consider inserting physical dividers between the lenslets to prevent the overlap, ensuring that the local likelihood model was valid. An immediate consequence would be that assumption (6.2) would not hold and hence it would be necessary to estimate the guide-star brightness (or measure it independently) along with the local tilt.

2. Maximum-Likelihood Estimation of Mirror-Mode Coefficients

There are several possible ways of getting ML estimates of the vector of mirror-mode coefficients α, depending on what we use as the initial data.

If we have valid ML estimates of local tilts, we may be able to get ML estimates of α by use of the ML invariance principle (2.15), at least when J (the number of lenslets) and N (the number of mirror actuators) are both large. Details of this approach and conditions for its validity are given in Appendix C, but the conditions are difficult to meet in practice.

Alternatively, if we have any estimates at all of local tilts, even centroid estimates, we can use them as data from which to estimate α so long as we can construct the relevant likelihood model. If we denote the estimates as τ̂, the likelihood we need is pr(τ̂|α). As we show in Appendix D, however, finding the relevant likelihood can be complicated, and without an accurate likelihood, neither ML nor MAP estimation of α can be considered optimal in any sense.

A better approach is to start with the raw data g (the detector outputs {g_m} for all m, not just the ones associated with a single lenslet). The likelihood function in that case is pr(g|α), which is just what we have been discussing throughout this paper. Any of the likelihood models from Section 5 can be used.

C. Simulation Results

To illustrate the theory developed in this paper, we performed several simulation studies of a Shack–Hartmann sensor.

In the first study, designed to test the ability of the ML method to reduce nonlinearity in a Shack–Hartmann sensor, only a single lenslet was considered, and a 2×2 array of photodetectors (often called a quad cell) was placed in its focal plane. The irradiance for a given tilt, s(r−z₀τ) in Eq. (6.1) was assumed to be a 2D Gaussian function, and the mean response functions, f_m(τ), m=1,…,4, were found by performing the integral in Eq. (6.1) numerically; the results are shown in Fig. 3.

Fig. 3.

(Color online) Display of the response functions f_m(τ) used in simulation of a Shack–Hartmann sensor with a single lenslet and a 2×2 array of photodetectors. Each plot represents the mean response of one photodetector as a function of the x and y components of the wavefront tilt.

These response functions were then used to generate pure Poisson data for an 8×8 array of tilts. For each position in the array, 200 realizations of a 4D Poisson random vector (one component for each detector in the quad cell) were generated. These data were used in both a standard centroid estimator (see Appendix D) and a simple ML estimator based on the Poisson statistics. There were no nuisance parameters, and the log-likelihood was given by Eq. (6.3) with I₀ assumed known. The maximization of the likelihood was performed by a Nelder–Mead algorithm implemented in the Matlab function fminsearch. Each of the resulting estimates was plotted as a point in a 2D image, one image for the centroid estimates and one for ML. These images, shown in Fig. 4, are thus approximations to the PDFs of the tilt estimates when the true values are delta functions on an 8×8 array of points.

Fig. 4.

Left, centroid estimates of an 8×8 array of tilts from Poisson data in a quad-cell Shack–Hartmann sensor; right, ML estimates from the same data.

With the centroid estimator, only a 6×6 array of points is seen on the left in Fig. 4; the outermost points overlap with their neighbors, and information about these larger tilts is irretrievably lost. This problem cannot be eliminated by any form of nonlinearity correction; no transformation of the left image in Fig. 4 can remove the complete overlap of the outermost points with their neighbors. With the ML estimator, on the other hand, the nonlinearity is almost completely eliminated (the estimator is nearly unbiased), and the dynamic range of the quad-cell sensor is approximately doubled. Both estimators are nearly unbiased and efficient for a point in the center of the array.

A more extensive comparison of ML and centroid estimations of tilts, taking account of nuisance parameters and null functions and exploring a much wider range of noise characteristics and photodetector arrays, will be published separately.

A second simulation study considered estimation of wavefront parameters directly from photodetector outputs without an intermediate estimation of tilts. A wavefront aberration was simulated using the 12 Zernike polynomials between the 2nd and the 4th radial order with positive coefficients that followed Noll's⁵¹ mean-square residual error distribution for D/r₀=16 (the total wavefront rms was 3.28 rad). A pixellated (CCD) image of the spot pattern of the wavefront aberration in a Shack–Hartmann sensor was simulated on a computer using the discrete Fourier transform (DFT) implementation of the Fresnel diffraction formula. The simulated detector had 128×128 square pixels, and the Shack–Hartmann sensor had 16 square lenslets across the diameter of the full pupil (8×8 pixels on the detector for each lenslet). The focal length of the lenslets was set to approximately 50 times the lateral size of each lenslet.

Fifty realizations of pure Poisson deviates of the CCD image were generated for each of six different light levels: 10^−1/2, 1, 10^−1/2, 10, 10^3/2, and 100 photons/lenslet. The coefficients of the 12 Zernike polynomials included in the wavefront were estimated from the same data by using both ML and traditional centroiding with LS reconstruction. The results of the simulations are shown in Fig. 5. In another study, the aberrated wavefront also included global tip and tilt, for a total of 14 unknown coefficients; the results in that case are shown in Fig. 6.

Fig. 5.

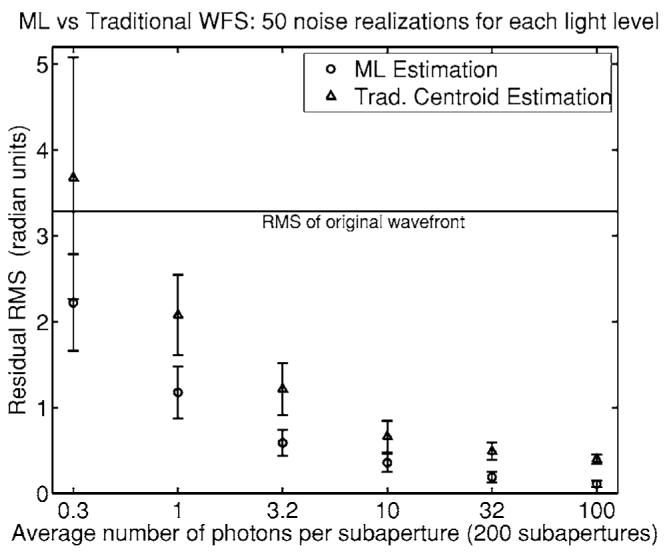
Comparison of traditional LS estimation of wavefront coefficients from centroid data versus direct ML estimation from photodetector outputs. Parameters used in the simulation include: λ=680 nm; pupil diameter=24 μm×128=3072 μm; lenslet size=192 μm; CCD pixel size=24 μm; and focal length=9.9 mm. The wavefront was sampled at 1726 points across the pupil diameter, and 322 rows and columns of zeros were used to pad the wavefront function to a 2048×2048 array before computing the FFT. The markers represent the mean, and the error bars represent the standard deviation of the residual wavefront rms of the 50 estimations for each light level.

Fig. 6.

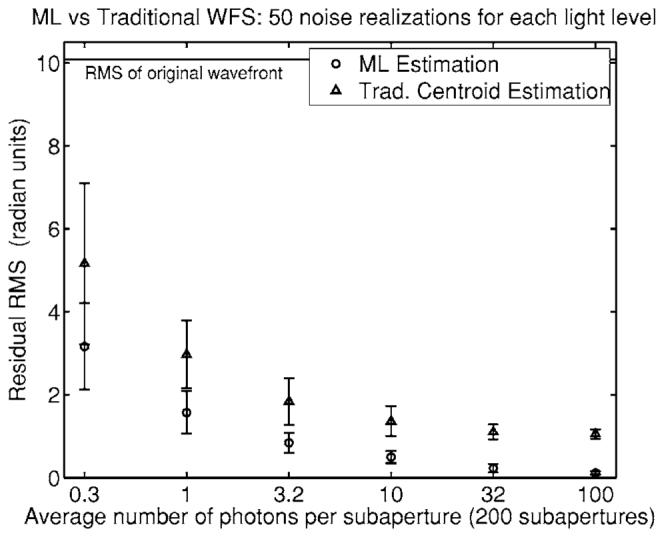
Same as Fig. 5 except that global tip and tilt were not removed from the simulated wavefront and were also included in the coefficients to estimate.

As seen from the figures, direct ML estimation can offer up to a fourfold advantage in residual wavefront error (ninefold if the global tip and tilt terms are not corrected separately), suggesting that there is indeed a significant loss of information in the tilt-estimation step (the preprocessing stage in Fig. 1). Such a loss is not surprising since tilt estimation in this case reduces an 8×8 array of photodetector outputs to just two centroids.

It is also noteworthy that a significant reduction in wavefront error can be achieved with an average of 0.32 photons/subaperture, or 0.005 photons/detector element. Of course this level of performance would not be obtained if sky background or readout noise were considered, but it is possible that ML methods would have even larger advantages over traditional methods in these cases because of more accurate statistical modeling. A detailed study of these issues is in progress.

7. COMPUTATIONAL METHODS

Astronomical WFSs must respond on a time scale of 10–100 ms, depending on wavelength and wind speed, and any computations performed by the sensor must be at least this fast. Since ML estimation usually uses an iterative search for the maximum, it might seem difficult to meet this requirement, but we can draw on methods developed for the closely analogous problem of ML position estimation in scintillation cameras for gamma-ray imaging. In that application, the computation must be carried out in a few microseconds rather than milliseconds, but hardware and software approaches that meet this goal have been demonstrated. In this section we summarize these approaches and then discuss how they can be applied to wavefront sensing.

A. Computational Approaches from Gamma-Ray Imaging

In a scintillation camera, a gamma ray interacts in a scintillation crystal such as sodium iodide and produces a flash of light that illuminates an array of PMTs. The objective is to determine the coordinates of the interaction event and the strength of the light flash, which is proportional to the gamma-ray energy. Since the estimate must be obtained for each gamma-ray photon, and the photons arrive randomly at mean rates that can exceed 10⁵ events/s, it is desirable to carry out the estimation in 1 to 2 μs.

If the scintillation crystal is relatively thin, it suffices to estimate the lateral coordinates (x,y) of the scintillation event, but at high gamma-ray energies a thicker crystal must be used, and the z coordinate (normal to the entrance face of the crystal) also influences the data. Depending on the application, the z coordinate, referred to as the depth of interaction, can be regarded as a nuisance parameter or as another parameter to estimate. If the variables to be estimated are x, y and the brightness of the flash I₀, then the estimation problem in a scintillation camera is equivalent to estimating the two components of tilt and the guide-star brightness in wavefront sensing.

In some problems two gamma rays can be absorbed simultaneously in the scintillation crystal, either because the radioisotope emits two photons in a rapid cascade or because of Compton scatter in the crystal. In these cases the number of parameters to estimate can be as large as eight (three spatial coordinates and energy for each of two photons). Alternatively, the properties of the secondary photon can be treated as additional nuisance parameters.

For the scintillation cameras developed at the Center for Gamma-Ray Imaging of the University of Arizona, the data dimension M is either 4 (a 2×2 array of photomultipliers), 9 (a 3×3 array), or 64 (an 8×8 array). Thus the goal of the processing is to estimate a set of 2–8 parameters from a set of 4–64 measurements in about 2 μs.

The statistical models used with scintillation cameras are remarkably similar to those considered in this paper.⁵² In most cases the log-likelihoods have the structure

$$\ln \mathrm{pr}(\mathbf{g}\mid ϴ)=\underset{m=1}{\overset{M}{\Sigma }}\ln \mathrm{pr}[g_m\mid {\stackrel{-}{g}}_m\left(ϴ\right)],$$ (7.1)

where Θ is the set of parameters to be estimated. In this paper the only log-likelihood not in the form of Eq. (7.1) is Eq. (5.25), where a correlated multivariate normal was obtained by marginalizing over intrinsic nuisance parameters. Similarly, in a scintillation camera, a multivariate normal can be used to describe the likelihood that results from marginalizing over the depth of interaction.

When the log-likelihoods have the form of Eq. (7.1), their dependence on Θ is determined by the set of means {ḡ_m(Θ)}, which we refer to as mean detector response functions or MDRFs.^27,28 The MDRFs can either be measured directly with a collimated source of gamma rays or be simulated by an optical transport code that models the camera. Once they are known, they can be stored as look-up tables, even when the dimension of Θ is as large as 8. For N=2, when the problem is just to estimate the (x,y) coordinates of each scintillation event, then each ḡ_m(Θ) can be stored as a K_x×K_x image, where K_x is the number of discretization steps in x or y (K_x=128 or 256, say). Even with 64 PMTs, therefore, the storage requirements are modest. If we add the depth of interaction z as a parameter to estimate, the necessary storage increases by a factor of K_z, the number of steps in z, but this is typically only 10 or so. Adding the photon energy to the list of parameters requires no additional storage since the MDRF factorizes in the same way as in Eq. (5.10). Estimating the coordinates of two simultaneous events increases N to 8 but does not increase the storage required for the MDRFs, since the total light incident on any PMT from the two events is just the sum of the contributions from the individual event, to a good approximation.

With stored MDRFs, evaluation of the log-likelihood at any Θ can be accomplished rapidly by looking up the value of ḡ_m(Θ) for each m, using a second look-up table to find each ln pr[g_m|ḡ_m(Θ)], and adding the results. The second look-up table has K_m×K_ḡ entries, where K_m is determined by the analog-to-digital (A/D) converter used to digitize the photomultiplier signals and K_ḡ is related to the resolution used for ḡ_m(Θ); the dimension of Θ is irrelevant in this table.

Since it is not so easy to compute and store derivatives of the MDRFs, search algorithms for finding the ML estimates in scintillation cameras have concentrated on methods that require the value of the log-likelihood but not gradients or Hessians. For searching over just the x and y coordinates, it is feasible to choose a reasonable starting point, say the coordinates of the PMT that gets the largest signal, and then do an exhaustive search over a subset of x and y in this vicinity.

Exhaustive search fails when additional parameters are to be estimated, and in those cases useful search algorithms include iterative coordinate descent, variations on the Nelder–Mead simplex, and multigrid algorithms. Iterative coordinate descent performs a sequence of 1D searches on each of the N individual components of Θ in turn, while simplex methods compute the log-likelihoods on a set of N+1 points in the N-dimensional parameter space at each iteration and use some rules for modifying the coordinates of the points in order to go to the next iteration. Multigrid techniques are similar to simplex methods in that the log-likelihood is computed on a set of points at each iteration, but the points are regularly spaced in parameter space; a coarse spacing is used initially and is then reduced as the iteration proceeds. Conjugate gradient searches, as suggested by Cannon²¹ for global wavefront estimation, are very effective when gradients can be calculated analytically. All of these methods work well when the function being searched is smooth and unimodal, as is usually the case with log-likelihoods for scintillation cameras.

Furenlid³¹ and Hesterman⁵³ have recently implemented a multigrid method for scintillation cameras. In initial experiments, a 4×4 grid of points was used in a two-dimensional parameter space, and the grid spacing was halved at each iteration. The algorithm converged in six iterations to exactly the same estimates as those found by an exhaustive search. The calculation requires 16 μs in C on a single Macintosh G5 computer, but Furenlid has shown that it can be converted to a pipeline process in a field-programmable gate array (FPGA). In that case all likelihood calculations are done in parallel, and J iterations of the algorithm require just J clock cycles, where each clock cycle is a few nanoseconds with modern FPGAs. There should be no difficulty in principle in using a similar pipeline architecture with a simplex search.

Finally, we mention that for the special case of estimation from four measurements, as with a 2×2 array of photodetectors, the entire search process can be performed offline and stored in a look-up table for all possible combinations of the four signals. If K_m A/D levels are used for each measurement, then there are 4^K_m locations in the table, and the final ML estimate of up to four parameters can be stored at each location. A useful practical trick is to take the square root of the measurements before coarse discretization in order to make the variance approximately constant, and with this measure it is found that 6-bit quantization (K_m=64) suffices, so the look-up table is easily stored in memory. No real-time search is needed, and the estimate is available in the time required to do a single memory access. This method has been used routinely for two decades with four-PMT scintillation cameras at the University of Arizona.^27,28

B. Methods for Maximum-Likelihood Estimation in Wavefront Sensing

The methods discussed above for scintillation cameras are immediately applicable to estimation of tilts over one subaperture of a Shack–Hartmann sensor, even with one or two nuisance parameters. The multigrid method with an FPGA devoted to each subaperture will give the estimate in less than a microsecond for any realistic number of detectors per subaperture, and data from multiple subapertures can readily be multiplexed through a single FPGA. Even when the multigrid method is implemented on a single processor, it appears that it will allow estimation of all subaperture tilts in less than a millisecond. Moreover, if a Shack–Hartmann sensor with nanosecond response should ever be required, it can be achieved by using 2×2 arrays of fast detectors at each subaperture and look-up tables for the final ML estimates of subaperture tilts.

The computational difficulties in ML estimation increase with the number of parameters being estimated and the number of independent measurements, and it is not so obvious that the speed requirements for astronomical wavefront sensing can be met if we choose to estimate a large number of modal coefficients {α_n, n=1, …N} from the entire set of detector measurements directly. If these coefficients specify the possible configurations of a deformable mirror, then N is the number of actuators, which ranges from 20 to 40 in laboratory systems to hundreds or even thousands in large telescopes.

The dimension of the data vector is also a concern. The number of independent measurements does not exceed the number of pixels in the detector array in the wavefront sensor, but in many cases it can be much less. With a Shack–Hartmann or any other sensor that divides the wavefront into subapertures, the local parameters associated with one subaperture (e.g., local tilts and/or curvatures) can be estimated from the data associated with that subaperture. Moreover, many of the data values will be near zero in practice and can be omitted from the data vector. For example, a diffraction-limited spot in a Shack–Hartmann sensor will illuminate a fraction $\sim {\left(\lambda f_l\right)}^2∕D_l^4$ of the detector pixels, where D_l is the diameter of the lenslet and f_l is its focal length; other pixels can be set to zero by thresholding. Similarly, if the readout noise is low enough that a single photon can be detected, the number of non-zero measurements after thresholding does not exceed the number of detected photons.

The dimension of the data vector used for an estimation problem can be also reduced by computing functions of the raw data called sufficient statistics. By definition, a set of sufficient statistics contains the same information about the estimation problem as the raw data does, but if the dimension of the set is much less than the number of original measurements, a considerable computational saving can be achieved. There is some current activity in finding sufficient statistics for position estimation in scintillation cameras,⁵² and these methods are potentially useful in wavefront sensing as well.

The complexity of the search algorithm depends on the dimensions of both the data and the parameter space. To illustrate the point, consider the Poisson model [Eq. (5.9)], where the only nuisance parameter is a global guide-star brightness I₀; this model is valid if N is large and there is no atmospheric scintillation. Under these same assumptions, the total light reaching the detector plane is independent of the wavefront parameters α, and if the detectors are identical and there are no gaps between them, we can write

$$\underset{m=1}{\overset{M}{\Sigma }}{f}_m\left(\alpha \right)=f_{\mathit{tot}}=\text{constant}.$$ (7.2)

This assumption for modal estimation is more defensible than its counterpart for local tilt estimation, [Eq. (6.2)], since we do not need to worry about light that misses a subset of the detectors or overlap of light from different subapertures; Eq. (7.2) is simply a statement of conservation of energy. With this model, the ML estimate of I₀ is just Î₀=N_tot/f_tot [cf. Eq. (6.5)], and the ML estimate of α must satisfy [cf. Eq. (6.3)]

$$\underset{m=1}{\overset{M}{\Sigma }}{g}_m\ln \left[f_m\left(\alpha \right)\right]=\mathrm{maximum}.$$ (7.3)

The functions {f_m(α)} are the counterparts of the MDRFs for scintillation cameras, but there are more of them and each is a function in a higher-dimensional space. Precomputing and storing them is difficult, and the feasibility of ML estimation of the modal parameters depends on being able to compute the f_m(α) rapidly.

There are several factors that simplify the problem. First, numerical studies (to be published separately) show that the log-likelihood for the modal parameters is smooth and slowly varying, especially at low light level. Thus it suffices to compute f_m(α) on a sparse grid in parameter space and use, say, spline interpolation to find it at intermediate points.

Second, in almost all applications the parameters will change slowly from frame to frame of the wavefront-sensor data, so an estimate found on one frame will be an excellent starting point for the next frame. Moreover, in a closed-loop system with good correction, we need to search only in the vicinity of the origin of parameter space, where all α_n=0.

Third, the problem is amenable to parallel computation in several possible ways. In a simplex or multigrid algorithm, for example, different processors can be assigned to different points in parameter space. In an N-dimensional estimation problem, a simplex requires computing the log-likelihoods at N+1 values of α, which can be performed with N+1 processors. If a full diffraction-theory model is used for the computation, the use of dedicated fast Fourier transform (FFT) chips in each processor might be advantageous.

A less obvious way to parallelize the problem is to divide the data space into subsets, perhaps corresponding to subapertures even if the goal is not to estimate local tilts. The advantage of this division is that the wavefront in the local region is described by a small set of parameters such as the local tilts and curvatures, and these local parameters are easily computed as linear combinations of the components of interest {α_n}. With this simplification we are back to efficient calculations or even look-up tables to find the values ln[f_m(α)] for each m in the data subset, and the overall log-likelihood is found by collecting the results from individual processors and summing as in Eq. (7.3). Again, simplex or multigrid methods can be used for efficient search without computing derivatives.

8. SUMMARY AND CONCLUSIONS

Maximum-likelihood estimation offers several theoretical advantages in general. An ML estimate is efficient if an efficient estimator exists, and it is asymptotically unbiased, efficient, and consistent as more data are acquired in any case. Compared with other computational methods in wavefront sensing, ML can reduce the bias and variance of the estimates of tilts, modal coefficients, or any other wavefront parameters, basically by taking advantage of the knowledge of the data statistics and using a more accurate model of the deterministic properties of the sensor. Unlike MAP or other Bayesian estimates, ML estimates do not incorporate any prior knowledge of the parameters to be estimated, but accurate likelihood models are essential to good MAP estimation also.

It is relatively straightforward to write down conditional PDFs for the data produced by the detectors in a wavefront sensor, but these PDFs are not the likelihoods needed for ML (or MAP) estimation of wavefront parameters for two reasons. First, not all parameters associated with the wavefront influence the data significantly; the ones that do not are called null functions. Second, there may be parameters that do influence the data but that we are not interested in estimating; they are called nuisance parameters. This paper has been concerned largely with the effect of null functions and nuisance parameters in wavefront sensing.

The basic stochastic models considered here included Poisson noise from the photoelectron statistics, Gaussian noise from the electronics, and a mixture of the two. Excess noise from detectors with internal gain was not considered explicitly, but most of the theory is easily adapted to that case. As in all ML problems, the parameters to be estimated were not considered to be random, but nuisance parameters were, and the final likelihoods of interest were obtained by marginalizing with respect to some prior distribution on the nuisance parameters. General expressions for both log-likelihoods and FIMs were derived on this basis. The theory was illustrated by discussing the estimation of local tilts and modal parameters from Shack–Hartmann data.

Computational issues associated with both the Shack–Hartmann subaperture problem and the more general problem of estimating coefficients in a modal expansion of the wavefront were discussed. For the subaperture case it was seen that ML estimation in microseconds or even nanoseconds is feasible, and several approaches that should lead to millisecond computation of modal coefficients were outlined. Work on the latter problem is actively underway and will be reported at a later date.

APPENDIX A: FISHER INFORMATION MATRIX FOR COMBINED POISSON AND GAUSSIAN NOISE

In this appendix we derive the FIM with both Poisson and Gaussian noise. The basic statistical model is the Poisson–Gaussian mixture developed by Snyder et al.⁴¹ The starting point for this appendix is Eq. (3.16), which for a single detector element can be written without the subscripts as

$$\mathrm{pr}(g\mid \theta )=\frac{1}{\sqrt{2\pi {\sigma }^2}}\underset{k=0}{\overset{\infty }{\Sigma }}\exp \left[-\frac{{(g-\mathit{Rk})}^2}{2{\sigma }^2}\right]\frac{{\left[\stackrel{-}{k}\left(\theta \right)\right]}^k}{k!}\exp [-\stackrel{-}{k}\left(\theta \right)].$$ (A1)

The FIM is the covariance matrix of the score vector, defined as the gradient of the log-likelihood with respect to the parameters being estimated. For the PDF of Eq. (A1), the nth component of the score is given by

$$\begin{array}{cc}\hfill \frac{\partial }{\partial {\theta }_n}\ln \mathrm{pr}(g\mid \theta )=\frac{1}{\mathrm{pr}(g\mid \theta )}\frac{\partial }{\partial {\theta }_n}\mathrm{pr}(g\mid \theta )=& \frac{1}{\mathrm{pr}(g\mid \theta )}\frac{1}{\sqrt{2\pi {\sigma }^2}}\underset{k=0}{\overset{\infty }{\Sigma }}\exp \left[-\frac{{(g-\mathit{Rk})}^2}{2{\sigma }^2}\right]\frac{1}{k!}\frac{\partial }{\partial {\theta }_n}\left\{{\left[\stackrel{-}{k}\left(\theta \right)\right]}^k\exp [-\stackrel{-}{k}\left(\theta \right)]\right\}\hfill \\ \hfill =& \frac{1}{\mathrm{pr}(g\mid \theta )}\frac{1}{\sqrt{2\pi {\sigma }^2}}\underset{k=0}{\overset{\infty }{\Sigma }}\exp \left[-\frac{{(g-\mathit{Rk})}^2}{2{\sigma }^2}\right]\frac{\left[\stackrel{-}{k}{\left(\theta \right)}^k\right]}{k!}\exp [-\stackrel{-}{k}\left(\theta \right)]\left(\frac{1}{\stackrel{-}{k}\left(\theta \right)}-1\right)\frac{\partial \stackrel{-}{k}\left(\theta \right)}{\partial {\theta }_n}.\hfill \end{array}$$ (A2)

A change of variables k′=k−1 and some algebra yields

$$\frac{\partial }{\partial {\theta }_n}\ln \mathrm{pr}(g\mid \theta )=\left[\frac{\underset{k^{\prime }=0}{\overset{\infty }{\Sigma }}\exp [-(1∕2{\sigma }^2){(g-R-{\mathit{Rk}}^{\prime })}^2]\exp [-\stackrel{-}{k}\left(\theta \right)]{\left[\stackrel{-}{k}\left(\theta \right)\right]}^{k^{\prime }}∕k^{\prime }!}{\underset{k=0}{\overset{\infty }{\Sigma }}\exp [-(1∕2{\sigma }^2){(g-\mathit{Rk})}^2]\exp [-\stackrel{-}{k}\left(\theta \right)]{\left[\stackrel{-}{k}\left(\theta \right)\right]}^k∕k!}-1\right]\frac{\partial \stackrel{-}{k}\left(\theta \right)}{\partial {\theta }_n}.$$ (A3)

The difference between numerator and denominator is in the shift of the Gaussian factor.

A more explicit notation may clarify the result; if we let pr(g|θ) be denoted by pr_g|θ(g) to indicate a specific function of g, then Eq. (A3) becomes

$$\frac{\partial }{\partial {\theta }_n}\ln {\mathrm{pr}}_{g\mid \theta }\left(g\right)=\left[\frac{{\mathrm{pr}}_{g\mid \theta }(g-R)}{{\mathrm{pr}}_{g\mid \theta }\left(g\right)}-1\right]\frac{\partial \stackrel{-}{k}\left(\theta \right)}{\partial {\theta }_n}$$ (A4)

or

$$\frac{\partial }{\partial {\theta }_n}{\mathrm{pr}}_{g\mid \theta }\left(g\right)=[{\mathrm{pr}}_{g\mid \theta }(g-R)-{\mathrm{pr}}_{g\mid \theta }\left(g\right)]\frac{\partial \stackrel{-}{k}\left(\theta \right)}{\partial {\theta }_n}.$$ (A5)

Since pr_g|θ(g) is, for example, the PDF depicted in Fig. 2(a), and pr_g|θ(g−R) is the same function shifted to the right by an amount R (i.e., shifted over one peak in Fig. 2(a), Eq. (A5) looks like the chain rule of differentiation with one derivative replaced by a finite difference, but in fact the result is exact.

Elements of the FIM (for a single detector) are given by

$$\begin{array}{cc}\hfill F_{{\mathit{nn}}^{\prime }}=& {\langle \left[\frac{\partial }{\partial {\theta }_n}\ln {\mathrm{pr}}_{g\mid \theta }\left(g\right)\right]\left[\frac{\partial }{\partial {\theta }_{n^{\prime }}}\ln {\mathrm{pr}}_{g\mid \theta }\left(g\right)\right]\rangle }_{g\mid \theta }\hfill \\ \hfill =& {\langle {\left[\frac{{\mathrm{pr}}_{g\mid \theta }(g-R)}{{\mathrm{pr}}_{g\mid \theta }\left(g\right)}-1\right]}^2\rangle }_{g\mid \theta }\frac{\partial \stackrel{-}{k}\left(\theta \right)}{\partial {\theta }_n}\frac{\partial \stackrel{-}{k}\left(\theta \right)}{\partial {\theta }_{n^{\prime }}}.\hfill \end{array}$$ (A6)

The expectation can be written in detail as

$$\begin{array}{cc}\hfill {\langle {\left[\frac{{\mathrm{pr}}_{g\mid \theta }(g-R)}{{\mathrm{pr}}_{g\mid \theta }\left(g\right)}-1\right]}^2\rangle }_{g\mid \theta }& \hfill \\ \hfill =& {\int }_{-\infty }^{\infty }\mathrm{d}g{\mathrm{pr}}_{g\mid \theta }\left(g\right){\left[\frac{{\mathrm{pr}}_{g\mid \theta }(g-R)}{{\mathrm{pr}}_{g\mid \theta }\left(g\right)}-1\right]}^2\hfill \\ \hfill =& {\int }_{-\infty }^{\infty }\mathrm{d}g\frac{{\left[{\mathrm{pr}}_{g\mid \theta }(g-R)\right]}^2}{{\mathrm{pr}}_{g\mid \theta }\left(g\right)}-1,\hfill \end{array}$$ (A7)

where the normalization of PDFs has been used to get the second line.

Thus the FIM for one detector element is given by

$$F_{\mathit{jk}}=\left[{\int }_{-\infty }^{\infty }\mathrm{d}g\frac{{\left[{\mathrm{pr}}_{g\mid \theta }(g-R)\right]}^2}{{\mathrm{pr}}_{g\mid \theta }\left(g\right)}-1\right]\frac{\partial \stackrel{-}{k}\left(\theta \right)}{\partial {\theta }_j}\frac{\partial \stackrel{-}{k}\left(\theta \right)}{\partial {\theta }_k}.$$ (A8)

This expression is exact and numerically tractable since the integral is one dimensional.

The reader versed in statistical decision theory will recognize pr_g|θ(g−R)/pr_g|θ(g) as a likelihood ratio Λ. The likelihood ratio is the ideal test statistic for deciding between two hypotheses, in this case the null hypothesis H₀ that g is drawn from the unshifted density pr_g|θ(g) and the alternative hypothesis H₁ that g is drawn from pr_g|θ(g−R). With that interpretation, the integral in Eq. (A8) is the expectation of Λ under H₁, a quantity that is closely related to performance on discrimination tasks,⁶ and Eq. (A8) establishes a relationship between that discrimination task and the estimation task that is the subject of this paper.

The factor in square brackets in Eq. (A8) can be evaluated in several limits. For pure Poisson noise (σ²→0), it is 1/k̄(θ). Pure Gaussian noise corresponds to the limit k̄(θ)→∞ and R→0 in such a way that Rk̄(θ) remains constant, and in that limit the factor tends to R²/σ². Numerical studies show that a useful approximate form in all cases (even when the PDF is highly non-Gaussian) is

$$F_{\mathit{jk}}\approx \frac{R^2}{{\sigma }^2+R^2\stackrel{-}{k}\left(\theta \right)}\frac{\partial \stackrel{-}{k}\left(\theta \right)}{\partial {\theta }_j}\frac{\partial \stackrel{-}{k}\left(\theta \right)}{\partial {\theta }_k}.$$ (A9)

If there are M detectors but the measurements are statistically independent, as we assumed in Subsection 3.D, then the final expression for the FIM [Eq. (3.17)], is obtained by reinstating the subscripts on g_m and k̄_m(θ) and then summing over m.

APPENDIX B: MARGINALIZING OVER NUISANCE PARAMETERS

In this appendix we fill in some details needed in Subsection 5.B regarding marginalizing intrinsic nuisance parameters. Extrinsic nuisance parameters are not considered here, so the P×1 vector of all parameters that influence the data can be written as θ=(α, β)^t, where α is N×1, β is K×1, and N+K=P.

It is assumed that the prior PDF describing β is a multivariate normal of the form

$$\mathrm{pr}\left(\theta \right)=\mathrm{pr}(\alpha ,\beta )={𝓝}_{\theta }\exp \left[-\frac{1}{2}{(\theta -\stackrel{-}{\theta })}^t{\mathbf{K}}_{\theta }^{-1}(\theta -\stackrel{-}{\theta })\right],$$ (B1)

where the covariance matrix can be written in the partitioned form

$${\mathbf{K}}_{\theta }=\left[\begin{array}{cc}\hfill {\mathbf{K}}_{\alpha \alpha }\hfill & \hfill {\mathbf{K}}_{\alpha \beta }\hfill \\ \hfill {\mathbf{K}}_{\alpha \beta }^t\hfill & \hfill {\mathbf{K}}_{\beta \beta }\hfill \end{array}\right],$$ (B2)

and 𝓝_θ=[(2π)^Ndet(K_θ)]^−1/2 is the normalizing constant.

Some well-known results from multivariate statistics⁵⁴,⁵⁵ show that the marginal density needed in Eq. (5.2) has the form

$$\mathrm{pr}(\beta \mid \alpha )={𝓝}_{\beta \mid \alpha }\exp \left[-\frac{1}{2}{(\beta -\tilde{\beta })}^t{\mathbf{K}}_{\beta \mid \alpha }^{-1}(\beta -\tilde{\beta })\right],$$ (B3)

where

$$\tilde{\beta }=\stackrel{-}{\beta }+{\mathbf{K}}_{\beta \alpha }{\mathbf{K}}_{\alpha \alpha }^{-1}(\alpha -\stackrel{-}{\alpha }),$$ (B4)

$${\mathbf{K}}_{\beta \mid \alpha }={\mathbf{K}}_{\beta \beta }-{\mathbf{K}}_{\beta \alpha }{\mathbf{K}}_{\alpha \alpha }^{-1}{\mathbf{K}}_{\alpha \beta }.$$ (B5)

The matrix K_β|α, which arises from taking the inverse of a partitioned matrix, is known as the Schur complement of K_αα. The results in Eqs. (B3)–(B5) are specialized to a wavefront sensor used in a closed-loop AO system discussed in Subsection 5.B.

We also need to evaluate the integral in Eq. (5.6) when the intrinsic nuisance parameters make a small perturbation to the mean data, in which case we can expand the mean data as

$$\begin{array}{cc}\hfill {\stackrel{-}{g}}_m(\alpha ,{\beta }^{\mathit{ext}},{\beta }^{\mathit{int}})\approx & {\stackrel{-}{g}}_m(\alpha ,{\beta }^{\mathit{ext}},0)+\underset{k=1}{\overset{K}{\Sigma }}{A}_{\mathit{mk}}{\beta }_k^{\mathit{int}}\hfill \\ \hfill & \text{where}{\phantom{\mid }{A}_{\mathit{mk}}=\frac{\partial {\stackrel{-}{g}}_m(\alpha ,{\beta }^{\mathit{ext}},{\beta }^{\mathit{int}})}{\partial {\beta }_k^{\mathit{int}}}\mid }_{{\beta }^{\mathit{int}}=0}.\hfill \end{array}$$ (B6)

For notational simplicity we let ḡ(α, β^ext, β^int)=ḡ and ḡ(α, β^ext, 0)=ḡ₀, so Eq. (B11) reads

$$\stackrel{-}{\mathbf{g}}={\stackrel{-}{\mathbf{g}}}_0+\mathbf{A}{\beta }^{\mathit{int}}.$$ (B7)

Then the integral in Eq. (5.6) can be written as

$$\begin{array}{cc}\hfill \mathrm{pr}(\mathbf{g}\mid \alpha ,{\beta }^{\mathit{ext}})\approx & {𝓝}^{\prime }\int {\mathrm{d}}^K{\beta }^{\mathit{int}}\hfill \\ \hfill & \times \exp \left[-\frac{1}{2{\sigma }^2}\Vert \mathbf{g}-{\stackrel{-}{g}}_0-\mathbf{A}{\beta }^{\mathit{int}}{\Vert }^2\right]\hfill \\ \hfill & \times \exp \left[-\frac{1}{2}{\left({\beta }^{\mathit{int}}\right)}^t{\mathbf{C}}^{-1}\left({\beta }^{\mathit{int}}\right)\right],\hfill \end{array}$$ (B8)

We can perform the integral by representing each probability density in terms of its characteristic function. The PDF of an M-dimensional multivariate normal vector x of mean x̄ and covariance matrix K can be written as

$$\begin{array}{cc}\hfill \mathrm{pr}\left(\mathbf{x}\right)=& {\left[{\left(2\pi \right)}^M\det \left(\mathbf{K}\right)\right]}^{-1∕2}\exp \left[-\frac{1}{2}{(\mathbf{x}-\stackrel{-}{\mathbf{x}})}^t{\mathbf{K}}^{-1}(\mathbf{x}-\stackrel{-}{\mathbf{x}})\right]\hfill \\ \hfill =& {\int }_{\infty }{\mathrm{d}}^M\xi \exp \left[2\pi i{\xi }^t(\mathbf{x}-\stackrel{-}{\mathbf{x}})\right]\exp (-2{\pi }^2{\xi }^t\mathbf{K}\xi ).\hfill \end{array}$$ (B9)

Expanding both densities in Eq. (B8) this way yields

$$\begin{array}{cc}\hfill \mathrm{pr}(\mathbf{g}\mid \alpha ,{\beta }^{\mathit{ext}})=& {\int }_{\infty }{\mathrm{d}}^K{\beta }^{\mathit{int}}{\int }_{\infty }{\mathrm{d}}^M\xi {\int }_{\infty }{\mathrm{d}}^K\eta \exp (-2{\pi }^2{\sigma }^2\Vert \xi {\Vert }^2)\hfill \\ \hfill & \times \exp [-2\pi i{\xi }^t({\stackrel{-}{\mathbf{g}}}_0+\mathbf{A}{\beta }^{\mathit{int}})]\exp \left(2\pi i{\xi }^t\mathbf{g}\right)\hfill \\ \hfill & \times \exp (-2{\pi }^2{\eta }^t\mathbf{C}\eta )\exp \left(2\pi i{\eta }^t{\beta }^{\mathit{int}}\right).\hfill \end{array}$$ (B10)

The integral over β^int yields the K-dimensional delta function δ(η−A^tξ), which can then be used to perform the integral over η. The final result is

$$\begin{array}{cc}\hfill \mathrm{pr}(\mathbf{g}\mid \alpha ,{\beta }^{\mathit{ext}})& ={\int }_{\infty }{\mathrm{d}}^M\xi \exp (-2{\pi }^2{\sigma }^2\Vert \xi {\Vert }^2)\hfill \\ \hfill & \times \exp (-2{\pi }^2{\xi }^2{\mathbf{ACA}}^t\xi )\exp \left[2\pi i{\xi }^t(\mathbf{g}-{\stackrel{-}{\mathbf{g}}}_0)\right]\hfill \\ \hfill & ={\left[{\left(2\pi \right)}^M\det \left({\mathbf{K}}_{\mathit{tot}}\right)\right]}^{-1∕2}\hfill \\ \hfill & \times \exp \left\{-\frac{1}{2}{[\mathbf{g}-{\stackrel{-}{\mathbf{g}}}_0]}^t{\mathbf{K}}_{\mathit{tot}}^{-1}{[\mathbf{g}-{\stackrel{-}{\mathbf{g}}}_0]}^t\right\},\hfill \end{array}$$ (B11)

where K_tot≡σ²I+ACA^t.

APPENDIX C: USE OF MAXIMUM-LIKELIHOOD INVARIANCE IN A SHACK–HARTMANN SENSOR

Suppose we have used data from a Shack–Hartmann sensor to obtain ML estimates of tilts. Can we apply the ML invariance principle [Eq. (2.15)] to get ML estimates of the mirror-mode coefficients {α_n}? The answer is yes if we can find a matrix B such that α=Bτ, in which case Eq. (2.15) shows that α̂_ML=Bτ̂_ML.

To seek such a matrix, we first take the scalar product of Eqs. (4.2) and (4.4) with one of the tilt functions defined in Eq. (4.3); the result is

$$({\chi }_k,W)=\underset{n=1}{\overset{N}{\Sigma }}{\alpha }_n({\chi }_k,{\psi }_n)+({\chi }_k,\Delta W)=\frac{1}{\Vert \chi {\Vert }^2}{\tau }_k+({\chi }_k,\delta W),$$ (C1)

where we have used the orthogonality of the tilt functions, and the division by ∥χ∥² is needed since the functions were not normalized. (We assume that all lenslets are identical, so that ∥χ∥²≡(χ_k, χ_k) is the same for all k.)

As we noted in Subsection 4.A, Eq. (4.4) is an orthogonal decomposition if the region defined by the lenslet is small enough; in that case, (χ_k, δW)=0, and we find

$${\tau }_k=\underset{n=1}{\overset{N}{\Sigma }}{M}_{\mathit{kn}}{\alpha }_n+({\chi }_k,\Delta W),$$ (C2)

where M_kn=(χ_k, ψ_n)/∥χ∥².

To proceed, we need to argue that (χ_k, ΔW)=0, but we cannot do so on the basis of orthogonality. The best we can do is assume that N is large so that the sum in Eq. (4.2) represents the wave exactly and the residual ΔW(r) is not needed. In that case we have

$$\tau =\mathbf{M}\alpha .$$ (C3)

where M is a 2J×N matrix.

The N×N matrix M^tM will be nonsingular if 2J≥N, and the functions {ψ_n(r)} are linearly independent, which they always will be in practice. Then we can write

$$\alpha ={\left[{\mathbf{M}}^t\mathbf{M}\right]}^{-1}{\mathbf{M}}^t\tau \equiv \mathbf{B}\tau .$$ (C4)

To summarize, we can write α=Bτ only for a high-order AO system (large N) in which all wavefronts of interest are well represented by a linear superposition of mirror influence functions, and then only if the regions defined by the Shack–Hartmann sensor are small and 2J≥N.

APPENDIX D: STATISTICS OF CENTROID ESTIMATES IN A SHACK–HARTMANN SENSOR

Traditional data processing in a Shack–Hartmann sensor attempts to estimate the centroids of the irradiance distribution I(r) produced by each lenslet on the detector plane. For simplicity we consider a single lenslet centered on the origin of coordinates, and we delete the index j used to distinguish lenslets.

The centroid location is defined in vector form as

$${\mathbf{r}}_c=\frac{{\int }_{\infty }{\mathrm{d}}^{2}r\mathbf{r}I\left(\mathbf{r}\right)}{{\int }_{\infty }{\mathrm{d}}^{2}rI\left(\mathbf{r}\right)},$$ (D1)

where r_c≡(x_c, y_c) is a 2×1 column vector giving the x−y coordinates of the centroid on the detector plane. The traditional centroid estimator is

$${\widehat{\mathbf{r}}}_c\left(\mathbf{g}\right)=\frac{1}{g_{\mathit{tot}}}\underset{m=1}{\overset{M}{\Sigma }}{\mathbf{r}}_m{g}_m,$$ (D2)

where r_m is a 2×1 vector specifying the center location of the mth detector, g_m is the signal from that detector, and g_tot is the total signal, given by

$$g_{\mathit{tot}}=\underset{m=1}{\overset{M}{\Sigma }}{g}_m.$$ (D3)

A useful way of rewriting Eq. (D2) is

$${\widehat{\mathbf{r}}}_c\left(\mathbf{g}\right)=\frac{1}{g_{\mathit{tot}}}\mathbf{Rg},$$ (D4)

where g is the usual M×1 data vector and R is a 2×M matrix with elements R_km=x_m for k=1 and R_km=y_m for k=2. This form shows that r̂_c(g) is almost but not quite a linear function of the data g; the linearity is spoiled by the factor 1/g_tot.

From the estimated centroid, an estimate of the 2D tilt vector associated with a given lenslet is traditionally obtained by

$$\widehat{\tau }\left(\mathbf{g}\right)\equiv {\widehat{\mathbf{r}}}_c∕z_0,$$ (D5)

where z₀ is the distance from the lenslet pupil to the detector plane (usually but not necessarily the focal length). It is hoped (and usually assumed) that τ̂(g) is an unbiased estimator of the true local tilts τ, that the x and y components of the estimate are uncorrelated Gaussian random variables, and that the estimate is optimal in some sense. The likelihood theory developed in this paper gives us the tools to examine these properties in detail.

A complete treatment of the statistical properties of r̂_c requires its conditional PDF pr(r̂_c|θ), where of course θ must include all parameters that influence the data. It is convenient to approach this problem by use of the bivariate characteristic function, defined by

$${\Psi }_{{\widehat{\mathbf{r}}}_c\mid \theta }\left(\xi \right)\equiv \langle \exp \left[2\pi i{\xi }^t{\widehat{\mathbf{r}}}_c\right]{\rangle }_{{\widehat{\mathbf{r}}}_c\mid \theta },$$ (D6)

where ξ is a 2×1 vector and the angle brackets indicate expectation with respect to the PDF pr(r̂_c|θ). Since r̂_c is a known function of g, we can equally well perform this expectation with respect to pr(g|θ). Using Eq. (D4), we can rewrite Eq. (D6) as

$${\Psi }_{{\widehat{\mathbf{r}}}_c\mid \theta }\left(\xi \right)={\langle {\langle \exp \left[2\pi i\frac{1}{g_{\mathit{tot}}}{\xi }^t\mathbf{Rg}\right]\rangle }_{\mathbf{g}\mid \theta ,g_{\mathit{tot}}}\rangle }_{{\mathbf{g}}_{\mathit{tot}}\mid \theta }.$$ (D7)

The inner expectation in Eq. (D7) is related to the conditional characteristic function of the data (conditioned on g_tot as well as θ), defined by

$${\Psi }_{g\mid \theta ,g_{\mathit{tot}}}\left(\rho \right)\equiv \langle \exp \left[2\pi i{\rho }^t\mathbf{g}\right]{\rangle }_{\mathbf{g}\mid \theta ,g_{\mathit{tot}}},$$ (D8)

where ρ is an M×1 vector. Thus,

$${\Psi }_{{\widehat{\mathbf{r}}}_c\mid \theta }\left(\xi \right)\equiv {\langle {\Psi }_{\widehat{\mathbf{g}}\mid \theta ,g_{\mathit{tot}}}\left(\frac{1}{g_{\mathit{tot}}}{\mathbf{R}}^t\xi \right)\rangle }_{{\mathbf{g}}_{\mathit{tot}}\mid {\theta }_t}.$$ (D9)

This result shows that the characteristic function (and hence all statistical properties) of the centroid estimates can be found from the M-dimensional conditional characteristic function of the data by making the substitution indicated in Eq. (D9) and then performing a final one-dimensional average over g_tot. If the PDF pr(r̂_c|θ) is desired, it can be obtained by performing an inverse 2D Fourier transform.

In two important special cases, the conditional characteristic function of the data can be expressed analytically. If g follows Poisson statistics without the condition on g_tot, then the conditional probability law, for g_tot detected photons, is multinomial.⁶

The corresponding conditional characteristic function is⁵⁶

$${\Psi }_{\mathbf{g}\mid \theta ,g_{\mathit{tot}}}\left(\rho \right)={\left[\underset{m=1}{\overset{M}{\Sigma }}{p}_m\left(\theta \right)\exp \left(2\pi i{\rho }_m\right)\right]}^{g_{\mathit{tot}}},$$ (D10)

where p_m(θ) is the probablility that a detected photon will be detected in the mth detector element: p_m(θ)=ḡ_m(θ)/ḡ_tot.

If g follows a multivariate normal law without the condition on g_tot, then the conditional PDF is also normal, and the requisite conditional mean and covariance matrix can be found from Eqs. (B4) and (B5), respectively. The final average over g_tot spoils the normal character of the centroid statistics, however, even with normally distributed data.

No analytic form for the final characteristic function of the centroid estimates has been found for either the Poisson or the normal case, but the average is easily performed numerically since it is one-dimensional.