Exogenously Triggered, Enzymatic Degradation of Photopolymerized Hydrogels With Polycaprolactone Subunits: Experimental Observation and Modeling of Mass Loss Behavior

Abstract

Degradation plays an important role in the evolution of extracellular matrix secreted by chondrocytes encapsulated in PEG-based hydrogels. For this study, macromonomers were synthesized by methacrylating both ends of polycaprolactone-b-poly(ethylene glycol)-b-polycaprolactone (PEG-CAP) tri-block copolymers. These divinyl molecules were photopolymerized to form hydrogels with PEG-CAP crosslinks that were subsequently degraded upon exogenous addition of a lipase enzyme. The rate of degradation and subsequent mass loss depends on both the length of the polycaprolactone units and the concentration of enzyme. Control gels that did not receive lipase did not significantly degrade onthe timescale of these experiments. A model was developed to predict mass loss using enzyme kinetics and a previously described statistical treatment of bulk network degradation. The model was used to predict mass loss profiles at the specific conditions used, and also to demonstrate the importance of potential changes in reaction rate and enzyme stability on temporal mass loss.

INTRODUCTION

Hydrogels are a natural choice as a scaffold for cartilage tissue engineering. The high water content and crosslinked structure of hydrogels mimic the natural environment of articular cartilage with an extracellular matrix consisting of crosslinked collagen and proteoglycans in the aqueous phase. Chondrocytes in native tissue tend to have a rounded morphology and exist in lacunae, small pockets among the extracellular matrix. The same rounded morphology can be easily maintained in hydrogels by choice of appropriate monomer chemistries. For example, hydrogels synthesized from dimethacrylated poly(ethylene glycol) (PEG-DM) macromonomers maintain chondrocyte morphology due to the relatively non-interacting nature of PEG^1,2. Similar macromonomers with poly(lactic acid) (PLA) groups on either side of the PEG core have been used to synthesize gels with hydrolytically degradable crosslinks that also maintain proper cell morphology at early time points³. However, even in hydrogels made from non-interacting materials, degradation begins to play an important role when its rate exceeds that of new extracellular matrix (ECM) development. Encapsulated chondrocytes may begin to lose their rounded morphology and, in turn, their differentiated state, resulting in higher rates of proliferation and production of type I collagen, an undesirable isoform⁴.

Understanding, predicting, and manipulating the degradation profiles of these hydrogels becomes very important when attempting to design an appropriate scaffold material for tissue engineering applications. In the ideal situation, the hydrogel degradation would be tuned to reflect the rate at which encapsulated chondrocytes were producing ECM. If the gel degrades too quickly, major structural defects will be presented that have the potential to affect macroscopic shape and volume of the construct, as well as cell morphology and collagen production⁴. If the gel degrades too slowly, ECM molecules produced by the encapsulated chondrocytes will not have the opportunity to diffuse and remodel new tissue in a timely manner¹. A simple statistical kinetic model has been previously developed to improve understanding and help tune the degradation of gels synthesized from dimethacrylated PLA-b-PEG-b-PLA (PEG-LA-DM) macromonomers⁵. This model gives insight into the parameters that are most important to the degradation of these hydrogels. The kinetic rate of the degradation reaction can be increased simply by adding repeats to the PLA blocks, which increases the number of ester bonds in the crosslink available for hydrolytic cleavage. The onset of a reverse gel point is of particular importance in tissue engineering applications, and is affected only by the initial number of repeat units in the kinetic polymethacrylate chains that form during polymer gelation⁵. In addition, desirable modifications to the degradation profile have been made in the past by addition of small amounts of very slow-degrading PEG-DM to solutions of dimethacrylated PLA-b-PEG-b-PLA tri-block copolymers⁶.

Despite the possibilities that exist for tuning the degradation of hydrolytically degradable gels, limitations still exist. Degradation begins immediately when these crosslinks are placed in an aqueous environment, at a rate predetermined by the macromonomer chemistry. With current knowledge, it is impossible to predict a priori the exact degradation rate required for a specific cell source. In addition to altering the rate, adjustments can be made to the degradation profile by addition of small amounts of macromonomers with longer or shorter PLA repeat units. However, the control that this allows over hydrogel degradation does not necessarily solve any problems associated with different rates of ECM production by different cell sources. One alternative solution is to seek a more robust degradation scheme, such as an exogenously triggerable degradation mechanism for hydrogel crosslinks. By replacing PLA blocks with a block whose degradation depends on the concentration of a particular catalyst, it would be possible to degrade the gel very slowly, very quickly, or not at all. This degradation could be dictated by the delivery of catalyst in a manner that corresponds to the temporal development of ECM by cells encapsulated in the gel.

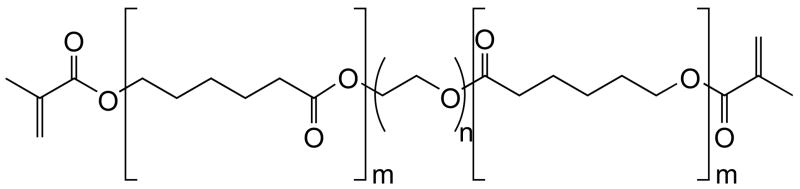
One potential hydrogel with a triggerable degradation pathway is synthesized by polymerization of a dimethacrylated tri-block copolymer, polycaprolactone-b-poly(ethylene glycol)-b-polycaprolactone (PEG-CAP-DM). The structure of this macromonomer is shown in Figure 1. Without the methacrylate groups, these tri-block copolymers have been shown to form micellar structures that can be degraded by a lipase enzyme^7–10. While these studies have shown evidence of biodegradation when lipase was exogenously added to solution, independent studies have shown only minimal erosion of polycaprolactone homopolymer biomaterials over a long time period when implanted subcutaneously¹¹. Therefore, it appears that biomaterials incorporating polycaprolactone subunits may require delivery of lipase in sufficient levels to trigger the degradation process, which provides utility described above for cartilage tissue engineering applications. These biomaterials will have the greatest potential for applications in which engineered tissue is developed in vitro, such as culture in advanced bioreactors, where combinations of online monitoring of tissue evolution with exogenously triggered scaffold degradation may be highly advantageous.

Figure 1.

Structure of macromonomers used to synthesize the hydrogels used in these studies. The average MW of the PEG core was 10,000 Da (n ≈ 227). Macromonomers were synthesized with m = 0, 3, 5.5, and 12.

In this study, hydrogels were synthesized by photopolymerization of PEG-CAP-DM macromonomers, forming crosslinks that are degradable by a lipase enzyme. The mass loss of these gels was monitored with and without the presence of lipase, and compared to model predictions using a Michaelis-Menten-derived kinetic model of reaction rate, coupled with a statistical aspect gleaned from structural information.

MATERIALS AND METHODS

Preparation of Hydrogels

Linear poly(ethylene glycol) (Fluka) with a number average molecular weight of approximately 10,000 Da was used to synthesize poly(ethylene glycol) dimethacrylate (PEG-DM), as well as a tri-block copolymer, poly(e-caprolactone)-b-poly(ethylene glycol)-b-poly(e-caprolactone) dimethacrylate (PEG-CAP-DM) as described previously¹². Macromonomer structures are shown in Figure 1. Both the PEG-DM and PEG-CAP-DM macromonomers form hydrogel crosslinks that do not significantly degrade in aqueous solution at neutral pH on the timescale of the experiments performed in this study (<≤ 8 weeks). ¹H NMR analysis was used to determine m, the average number of caprolactone units per side of each PEG molecule, as well as the extent of methacrylation of all macromonomers. Percent methacrylation was calculated by comparing the integral area under peaks from methacrylate functional groups (δ ≈ 5.6 and 6.1) with the main peak from the PEG backbone (δ ≈ 3.64). The average length of the CAP blocks, m, was calculated by comparing peaks from two of the proton pairs within caprolactone repeats (δ ≈ 2.35 and 4.08) with the main peak from the PEG backbone. Macromonomers with m = 0, 3, 5.5, and 12 were used in these studies, and macromonomer ends were 85–100% substituted with methacrylate groups.

To prepare gels, the individual macromonomers were dissolved in sterile phosphate-buffered saline (PBS) to a final concentration of 10% by weight. The UV photoinitiator, 2-hydroxy-1-[4-(hydroxyethoxy) phenyl]-2-methyl-1-propanone (D2959, Ciba-Geigy), was added to a final concentration of 0.05% by weight. The resulting solution was sterilized by filtration through a 0.2 um syringe filter, and polymerized in 50 ul aliquots under 365 nm UV light for 10 minutes at an intensity of approximately 5 mW/cm². Solutions containing PEG-CAP-DM macromonomers with 12 caprolactone repeats per side were very viscous and therefore were not filtered.

Hydrogel Degradation

Hydrogels were degraded for a period of up to 25 days at 37°C in PBS with 1% Bovine Serum Albumin (Sigma) and 0.0, 0.1, 0.2, 0.4, or 1.0 mg/ml Amano Lipase PS (Sigma). In degradation studies using varying lipase concentrations, PEG-CAP-DM macromonomers with m = 5.5 were used tosynthesize gels. In studies of varying m (CAP repeats per block), gels were degraded in solutions with 0.2 mg lipase/ml. During this degradation period, samples were removed every 1–2 days, freeze-dried for 24 hours, and weighed to determine the mass loss to that point. For calculations of mass loss, the average mass of gels was compared to the average dry mass of gels with the same composition, freeze-dried at the initial time point. The initial time point was taken after all gels were swelled in PBS for 2–3 days following polymerization, to remove the soluble fraction, but before any incubation with lipase. The mass swelling ratio, q, was determined from the ratio of wet weights, as samples were removed from incubation, to the dry weights after freeze-drying for 24 hours.

In addition, the degradation data for studies of varying m values were gathered from experiments in a separate incubator from the degradation studies of varying lipase concentrations. Temperature control was not as rigorous for the experiments with gels with varying m, resulting in frequent temperature fluctuations between 37 and 40 °C. Unfortunately, the values of kinetic constants cannot be directly compared between the two experiments, but only among the conditions investigated in each experiment.

Mechanical Testing

The compressive modulus of elasticity of hydrogels was measured over degradation time. Measurements were made using a Synergic 100 mechanical tester (MTS) in unconfined compression at room temperature. Samples were initially unloaded, and then subjected to compressive strain at a rate of 0.5 mm/min. The compressive modulus was determined by analyzing the linear region of the stress vs. strain curve on samples at low deformation (<15% strain). A sample size of 3–5 was used.

Statistical Analysis

Statistical analysis was performed using single-factor analysis of variance with a confidence interval of 0.05. All values in this text are reported as the average plus or minus one standard deviation, with the exception of mass loss data. Mass loss data contains standard error from each time point, as well as standard error from the initial time point, with standard error propagation through subtraction and quotient calculations.

RESULTS AND DISCUSSION

Hydrogel degradation plays a critical role in the distribution and elaboration of ECM secreted by encapsulated chondrocytes for cartilage regeneration. Degradation of crosslinks increases the mesh size of the gel, allowing for diffusion of larger ECM molecules. While the extent to which this degradation takes place is very important, the timing of the degradation is no less critical, as negative consequences can result when degradation takes place either too quickly or too slowly. In this study, hydrogels were synthesized with externally triggerable, enzymatic degradation sites consisting of short polycaprolactone (CAP) blocks. The dependence of degradation on both CAP content and enzyme concentration were investigated in degradation studies conducted at 37 °C. In addition, a simple model was adapted with typical enzymatic degradation kinetics to improve understanding of the mass loss process and to facilitate the strategic design of enzymatically degradable gels for tissue engineering applications.

Degradation and Erosion in PEG Hydrogels

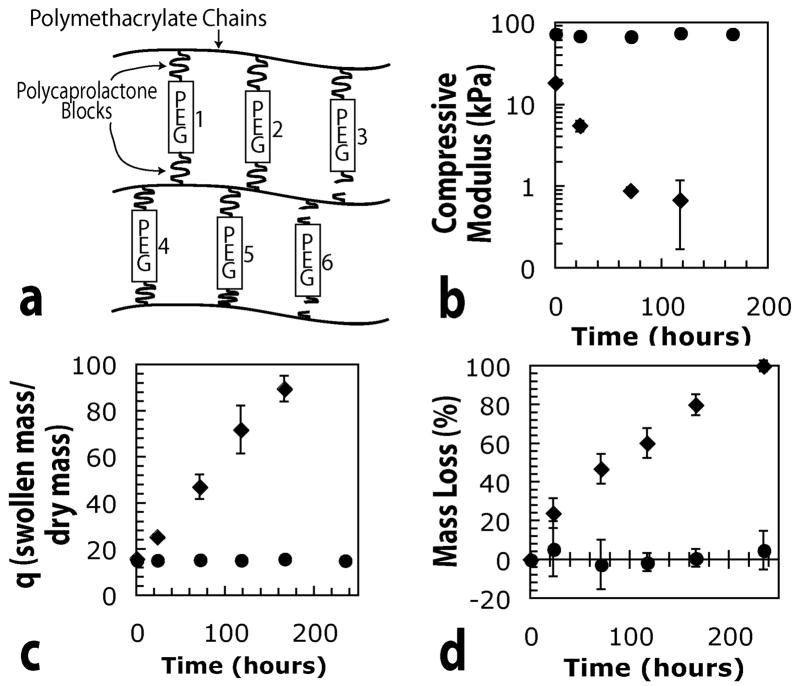
The synthesis and degradation of hydrogels synthesized from PEG-LA-DM macromonomers has been described previously in detail^12,13. Gels formed from the radical polymerization of PEG-CAP-DM macromonomers will degrade and lose mass in a similar manner although an enzyme catalyst is necessary for degradation on a practical time scale. Briefly, these hydrogels undergo bulk degradation with internal crosslinks cleaved homogeneously throughout the gel. Ideally, the divinyl macromonomers should be connected to two separate polymethacrylate kinetic chains as the radical polymerization proceeds. A schematic of the network structure in two dimensions is presented in Figure 2 (a). When a degradable block is cleaved, the crosslink is broken, as illustrated by crosslinks numbered 3 and 6 in Figure 2 (a). When both degradable blocks associated with a particular crosslink are broken, as shown by crosslink number 6, the individual crosslink has been eroded from the gel, and is free to diffuse out of the network and contribute to mass loss. When only a single degradable block is cleaved, as in crosslink number 3, the lost crosslink effects swelling and mechanical properties, but can not contribute to mass loss, since it has not been eroded from the gel network. On a larger scale, broken crosslinks lead to a decrease in crosslinking density and subsequently to a larger mesh size, higher swelling ratio, and lower compressive modulus. Eventually, a point of reverse gelation is reached where the gel structure transitions to an assembly of highly branched, soluble polymer chains.

Figure 2.

Schematic and experimental effects of degradation in gels synthesized from PEG-CAP-DM macromonomers. (a) Two-dimensional schematic of an ideal network, in which crosslinks 3 and 6 have been cleaved, (b) Experimental data indicating the effects of degradation on the compressive modulus, (c) mass swelling ratio, and (d) mass loss of hydrogels synthesized from 10 wt% macromonomer solutions. Experimental data in (b) through (d) corresponds to gels made from macromonomers with m = 0 (circles) and m = 5 (diamonds).

Figure 2, parts (b) through (d) show the results of typical degradation in hydrogels synthesized from divinyl macromonomers with m = 0 (no CAP blocks) or m = 5.5. All gels in this portion of the study were degraded in the presence of 0.2 mg/ml lipase, and as expected, hydrogels without CAP blocks did not appear to undergo any significant amount of degradation, indicated by the lack of change in compressive properties and mass swelling ratio in Figure 2, parts (b) and (c). Since no significant degradation took place, crosslinks were not released, and no significant mass loss is reflected in Figure 2 (d). In contrast, crosslinks containing CAP blocks appear to have been degraded, causing a decrease in crosslinking density that is reflected in the compressive modulus and swelling data. As the crosslinks in these gels were cleaved on both sides and released from the network, mass loss proceeded slowly until the gels finally became completely soluble at their reverse gel point.

Modeling Enzymatic Hydrogel Degradation

To better understand factors that control the mass loss and degradation behavior, gel structure information was incorporated into a model, based on similar approaches reported elsewhere for gels formed from the chain polymerization of divinyl macromolecular monomers⁵. Briefly, the structure is incorporated through a statistical treatment that is based on the probability that a given CAP block has been cleaved. That probability, P, is given by the following equation,

$$P=1-\frac{N_{\mathit{CAP}}}{N_{CA{P}_0}}$$ (1)

in which N_CAP, and N_CAPo represent the number of CAP blocks present in the gel and those initially present in the gel, respectively. This probability is then used to calculate the fraction of crosslinks attached to two kinetic chains ((1−P)²), the fraction that have had a CAP block cleaved on only one side of the crosslink (2*P*(1−P)), and those that have had CAP blocks cleaved on both sides so that they may be released from the gel (P²). These calculations enable the model to predict the release of not only the crosslinks that have been cleaved on both sides of the PEG core, but also of kinetic chains, along with any attached PEGs. These calculations were used to predict all mass loss profiles that are presented in this work.

The previous model was based on a bulk-degrading hydrogel, in which crosslinks were just as likely to break in the middle of the gel as near the surface. Hydrolytic degradation of crosslinks in those gels depended only on the local concentrations of water and individual D,L-Lactide units. A homogeneous distribution was assumed for the degradable units, and since the gels were very swollen, water concentration was similarly high and homogeneous throughout the gel. In the case of an enzymatically cleavable unit, the enzyme must first diffuse into the gel and situate at an active degradation site before crosslinks can be broken. For the purposes of applying only a simplified version of this bulk degradation model with enzyme kinetics, the timescale of diffusion was assumed to be much faster than the timescale of reaction. The ratio of these timescales is very important. As the rate of diffusion decreases or the rate of reaction increases, degradation will occur faster near the surface of these gels, and the assumptions of the bulk degradation model described here will become less valid.

A diffusion coefficient for lipase in these gels can be estimated by first calculating its value in water. Previous study of the structure of this particular lipase enzyme allows the hydrodynamic radius to be conservatively estimated as 25 angstroms¹⁴. This radius was substituted into the Stokes-Einstein equation (eq. (2)), to estimate the diffusivity (D₀) of lipase in water.

$$D_0=\frac{k_{B}T}{6\pi \mu r_S}$$ (2)

In equation (2), k_B is Boltzmann’s constant, T is temperature, μ is the viscosity of water at 37 °C, and r_s is the hydrodynamic radius of the solute, in this case lipase. From equation (2), D₀ was estimated to be on the order of 8 × 10⁻³ mm²/min for lipase in water at 37 °C. The PEG-CAP hydrogels in this study were very swollen, with initial volumetric swelling ratios (Q) of ~ 19 and increasing with degradation. Previous studies of protein release from less swollen gels indicate that the diffusivity of lipase in the PEG-CAP gels used in this study will be on the same order as the diffusivity in water¹⁵. The timescale of diffusion of lipase (MW ~ 30,000 Da) will certainly become critically important for gels with increasing crosslinking density, and may impose practical boundaries on the crosslinking density that can be used with these PEG-CAP gels. Indeed, similar boundaries have been previously explored in the enzymatic degradation of polysaccharides in solution¹⁶.

Physical interactions among macromonomer molecules may also play a role in the network structure of these hydrogels, but were not accounted for in this version of the degradation model. The degradable CAP units in these macromonomers are significantly more hydrophobic than the PEG core, resulting in amphiphilic molecules that affect the network structure through their interactions in solution and during polymerization. This characteristic is another aspect of the network structure that may become a significant factor as the crosslinking density is increased by addition of higher macromonomer concentrations to the polymerization solution.

The kinetics of the degradation of CAP blocks in these gels were modeled from the same starting point as typical Michaelis-Menten (MM) enzyme kinetics¹⁷. These kinetics are based on the following reaction equations that describe the enzyme-catalyzed cleavage of CAP units:

$$\mathit{lipase}+\mathit{CAP}\underset{{\text{k}}_{-1}}{\overset{{\text{k}}_1}{\rightleftharpoons }}E\ast S\stackrel{{\text{k}}_2}{\to }\mathit{lipase}+D$$ (3)

$$\mathit{lipase}\stackrel{{\text{k}}_{\text{d}}}{\to }\mathit{inactive}\mathit{lipase}$$ (4)

In the above reaction equations, lipase is free active lipase, CAP is a degradable CAP block (not individual CAP repeats), E*S is the enzyme-substrate complex, and D is the degradation product. The reaction in equation (3) describes the cleavage of individual CAP blocks, while the reaction in equation (4) describes the deactivation of lipase in solution. In these experiments, 50 ul hydrogels were incubated in individual wells with a relatively very large volume of enzyme or control buffer solution. In the well, the concentration of lipase depends only on the deactivation reaction, and was therefore assumed to follow a first-order decay¹⁸:

$$\frac{[\mathit{lipase}]}{{[\mathit{lipase}]}_0}=e^{-k_{d}t}$$ (5)

In equation (5), the concentrations [lipase] and [lipase]₀ correspond to the current and initial concentrations of lipase, respectively, while k_d is the first-order rate constant for the deactivation of the lipase enzyme. Since it was assumed that the diffusion time scale is much faster than the reaction time scale, the concentration of enzyme on the interior of the hydrogel was assumed to be approximately the same as the enzyme concentration in the well. Therefore, the enzyme concentration in the interior of the hydrogel was also approximated by equation (5). Any time the lipase solution was replaced, the model lipase concentration was returned to the initial value and decreased according to equation (5).

The approximation of the lipase concentration was used to find an expression for the degradation of CAP blocks over time. Going back to the reactions described in equations (3) and (4), the following species balances on lipase and CAP blocks were written directly:

$$\frac{d[\mathit{lipase}]}{dt}=-k_1[\mathit{CAP}][\mathit{lipase}]+k_{-1}[E^{\ast }S]+k_2[E^{\ast }S]-k_d[\mathit{lipase}]$$ (6)

$$\frac{d[\mathit{CAP}]}{dt}=-k_1[\mathit{CAP}][\mathit{lipase}]+k_{-1}[E^{\ast }S]$$ (7)

Each of the concentrations and rate constants in equations (6) and (7) correspond to species and reactions in equations (3) and (4). The time derivative of lipase in equation (6) was set equal to the time derivative of lipase from equation (5), since equation (5) was already assumed to describe the concentration of lipase in the well volume and also inside the hydrogel. This allowed an expression to be written for [E*S], which was then substituted into equation (7), allowing the differential equation to be solved for [CAP]. A simple material balance was written and solved for the number of moles of CAP blocks, leading to the following final equation that was substituted back into equation (1):

$$\frac{N_{\mathit{CAP}}}{N_{CA{P}_0}}=e^{\frac{k^{\ast }{[\mathit{lipase}]}_0}{k_d}\left(e^{-k_{d}t}-1\right)}$$ (8)

In equation (8), the ratio on the left is equal to the fraction of CAP blocks remaining intact, and k* is a combination of kinetic constants from the reactions in equations (3) and (4). To borrow terms common to Michaelis-Menten kinetics, k* is equal to k₂/K_m, where K_m is equal to the ratio of (k₁+k₂)/k₁.

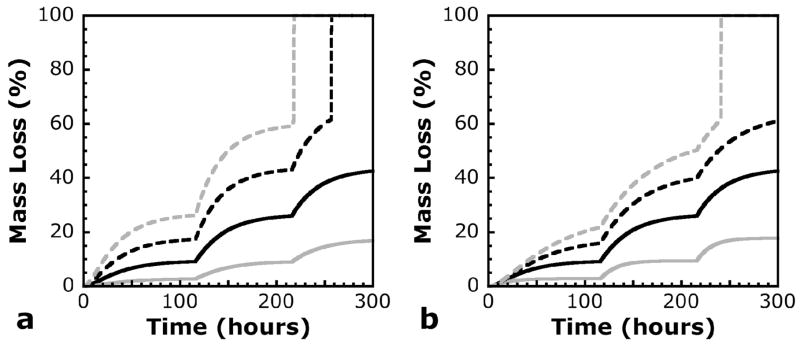
Calculated mass loss profiles are shown in Figure 3 as a function of lipase concentration and half-life. Refreshment of lipase solutions in these model calculations are shown after 116 and 216 hours, to match experimental data that will be discussed later. Figure 3 (a) shows the effects of the kinetic parameter, k*, and the initial lipase concentration on theoretical mass loss profiles. Since these two parameters appear in the same part of the kinetic reaction equation, multiplying by any constant has identical effects on both. The slope of the mass loss curve is sensitive to changes in these parameters, especially at times immediately after the solution has been refreshed. This analysis of the model shows how simple adjustments in the lipase concentration can be used to tune degradation temporally. In addition, since the kinetics used in the model are based on the concentration of CAP blocks as opposed to individual CAP repeats, k* intuitively depends on m, the average number of CAP repeats per CAP block. Both the lipase concentration and the monomer chemistry may therefore be aspects that can be controlled to affect degradation and mass loss in a specific manner.

Figure 3.

Calculated mass loss profiles for varying values of (a) k* or lipase concentration, and (b) the half-life of active lipase in solution. Baseline values are shown in solid black lines, with the following values: k* = 31.4 L*mol⁻¹*min⁻¹, lipase concentration = 0.2 mg/ml, and active lipase half-life = 20.4 hours (corresponding to k_d = 5.66e-04 min⁻¹). Baseline values for each variable were multiplied by 0.5 (solid gray line), 1.5 (dashed black line), and 2.0 (dashed gray line). n₀ = 40 in all calculated profiles.

The effects of the lipase deactivation rate constant, k_d, on theoretical mass loss profiles are shown in Figure 3 (b). Of course, as this rate constant was decreased, the half-life increased, and the mass loss associated with each individual refreshment of enzyme solution also increased, since active lipase was assumed to remain in higher concentrations for a longer period of time. The initial slope of the mass loss curves at times associated with fresh enzyme solution are identical, since each curve was calculated from identical enzyme concentrations at those points. The difference among curves in Figure 3 (b) was seen instead as a slower decrease in the slope of the mass loss curve with longer half-lives of lipase. It is important to understand this effect on the mass loss profile, because a number of factors may affect the stability of active lipase in solution. A very important factor may be stabilization with other proteins. The degradation experiments discussed here were conducted with BSA in the buffer solution along with the lipase. In a complex media with fetal bovine serum, this particular formulation of lipase may be stabilized more or less effectively. Any effects on the half-life of active lipase will consequently affect the mass loss profile, which will be important in future chondrocyte encapsulation experiments using these materials.

Comparison To Experimental Data

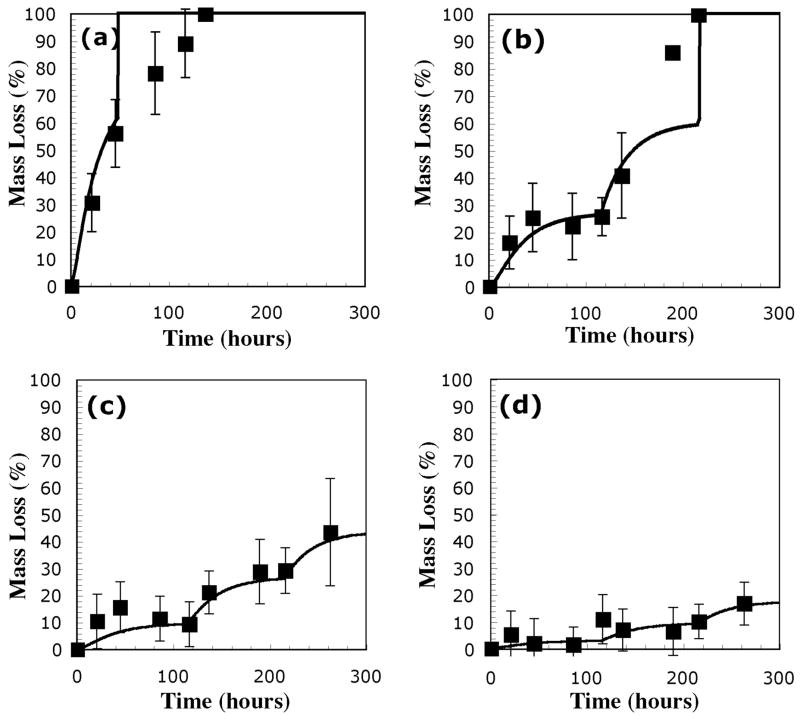
Hydrogel degradation studies were carried out in two stages. In the first stage, the effects of lipase concentration were verified by comparing mass loss profiles of gels synthesized from 10 wt% solutions of PEG-CAP-DM macromonomers with m = 5.5. Gels were incubated with solutions containing 0.0, 0.1, 0.2, 0.4, or 1.0 mg lipase per ml. The results of these mass loss studies are presented in Figure 4. Experimental data for solutions containing 0.0 mg lipase/ml are not shown, because there was no significant mass loss in those gels. It is clear from this data that mass loss was accelerated in solutions with higher concentrations of lipase, and the data in Figure 4 also appear to show a deactivation of the lipase with time. In general, the mass loss profile for the hydrogels at each concentration appears to level off after approximately 40–50 hours. Fresh enzyme was added after 116 and 216 hours, and most data show an accompanying jump in the mass loss profile that seems to indicate that the fresh lipase is more effective than lipase that has been at 37 °C for a number of days. Lines shown in Figure 4 correspond to model calculations for each of the different lipase concentrations.

Figure 4.

Experimental mass loss data and calculated mass loss profiles (solid lines) for hydrogels synthesized from PEG-CAP-DM macromonomers and incubated in solutions with (a) 1.0 mg/ml, (b) 0.4 mg/ml, (c) 0.2 mg/ml, and (d) 0.1 mg/ml Lipase PS. Values of other constants used in calculation of mass loss profiles were k* = 31.4 L*mol⁻¹*min⁻¹, k_d = 5.66e-04, and n₀ = 40.

To most accurately demonstrate the effectiveness of the model, the kinetic constants from equation (7) were estimated from one set of mass loss data, with 0.4 mg lipase/ml. If the rate of decrease of the ratio on the left of equation (8) is defined as a new variable,υ then the expression for the time derivative of N_CAP/N_CAPO can be rearranged to form equation (9),

$$ln\frac{\upsilon }{{[\mathit{lipase}]}_0\left(N_{\mathit{CAP}}/N_{CA{P}_0}\right)}=-k_{d}t+ln{k}^{\ast }$$ (9)

The first three points of experimental mass loss data from Figure 4 (b) were used to estimate the kinetic parameters. From mass loss data, the ratio of remaining CAP blocks to initial CAP blocks was estimated using the statistical portion of the previously developed model. The decrease of this ratio with time, u, was estimated from slopes of lines connecting successive calculated data points. Since each initial enzyme concentration was known, the left side of equation (9) could be calculated and plotted against time. The slope of the line fit to this data was used to estimate k_d, while the intercept was used to estimate k*, according to equation (9). This method was used to approximate a value of k_d equal to 0.034 hr⁻¹, corresponding to a lipase half-life of about 20.4 hours, and a value for k* equal to 31.4 min⁻¹. These values have been used for the kinetic parameters in every model calculation in Figure 4. In addition, the experimental mass loss data in Figure 4 (b) was also used to estimate n₀, the number of repeats in the polymethacrylate kinetic chain. Briefly, n₀ was adjusted to fit the model to approximately match the experimentally observed point of reverse gelation, where remaining hydrogel mass is lost in a final burst. Importantly, the model lines appear to agree with most data points within calculated error, and also capture the most important aspects of the mass loss data, including relatively quick mass loss immediately following addition of fresh lipase solutions, and a tapering of this mass loss as the lipase in solution became less active.

It is impossible to ignore the fact that some data points at high mass loss values in Figure 4 do not appear to be accurately represented. In order to explain these data points, it is important to revisit the previous assumption of bulk degradation due to diffusion of lipase occurring much faster than the degradation of CAP blocks. Using the value for lipase diffusivity estimated earlier, a rate equation for intact CAP blocks can be written in terms of a scaled time variable, τ= (D₀t/L²).

$$\frac{d[\mathit{CAP}]}{d\tau }=\frac{k^{\ast }{L}^2}{D_0}[\mathit{lipase}]e^{\frac{k^{\ast }{[\mathit{lipase}]}_0}{k_d}\left(e^{\frac{-k_d{L}^2\tau }{D_0}}-1\right)}$$ (10)

From equation (10), let A =k*L² [lipase]/D₀. Comparing A to 1 allows estimation of the relative rate of CAP cleavage to lipase diffusion. Estimated values of A for different initial lipase concentrations and length scales are shown in Table 1. It is immediately apparent that the assumption of relatively fast lipase diffusion is poor for gels in environments with high lipase concentration. Therefore, the high mass loss prior to reverse gelation, shown in Figure 4(a), is likely a result of significant surface degradation effects. These effects are expected to be much less significant in gels degraded at lower lipase concentrations, because the reaction time scale is directly related to lipase concentration, and the assumption of relatively fast lipase diffusion is therefore more appropriate. For gels used in this study, a length scale of 2 mm is most appropriate since gels were approximately 4 mm thick when they approached their reverse gel points (data not shown). The other length scales are shown in Table 1 only as examples to show the limitations of the bulk degradation model, especially at high CAP reaction rates caused by high lipase concentrations. Despite these limitations, the length and concentration scales over which the model assumptions apply are certainly reasonable for many in vitro cartilage regeneration studies. It is clear that the size scale, lipase diffusion, and reaction rates of CAP blocks must be controlled carefully in the application of these hydrogel materials.

Table 1.

Approximate values of the timescale for CAP cleavage relative to the diffusion of lipase for various initial lipase concentrations and length scales.

Initial lipase concentration (mg/ml)	Length scale, L (mm)	Relative reaction timescale, A A=k*L2[lipase]/D0
1.0	1	0.1
1.0	2	0.5
1.0	5	3.3
0.1	1	0.01
0.1	2	0.05
0.1	5	0.33

The effects of CAP content were investigated by comparing the mass loss from gels among experimental groups with different values for m, the average number of CAP repeats per side of each PEG molecule. Macromonomers with m of 0, 3, 5.5, and 12 were used in this portion of the study, and all gels were incubated with 0.2 mg lipase/ml. Results of this mass loss study are shown along with model calculations in Figure 5. While the gels synthesized from macromonomers without CAP units did not appear to be significantly affected by the enzyme solution, each of the experimental groups containing CAP repeats eventually showed a significant mass loss over incubation time with the enzyme. Using the half-life value calculated from the experiments shown in Figure 4, the model calculations were adjusted in Figure 5 with different values of k*. These were not calculated in any rigorous manner, but merely estimated to demonstrate the effect of CAP repeat units on k*. The model calculations in Figure 5 have values for k* of 10, 105, and 350 for m = 3, 5.5, and 12, respectively. Since this chemistry is easily modified during synthesis, varying the value of m allows for an extra degree of control over the degradation rate and accompanying mass loss profile for these hydrogels. Changes in k* affect the degradation rate in the same manner as lipase concentration. As a result, increasing k* makes the gel degradation take on more characteristics of surface erosion, indicated by a poor description of the late stages of degradation by the model calculations for gels with m = 5.5 shown in Figure 5. While changing m is clearly a less subtle adjustment than that afforded by varying lipase concentration, the combination of these two levels of control is a very powerful tool for guiding gel degradation.

Figure 5.

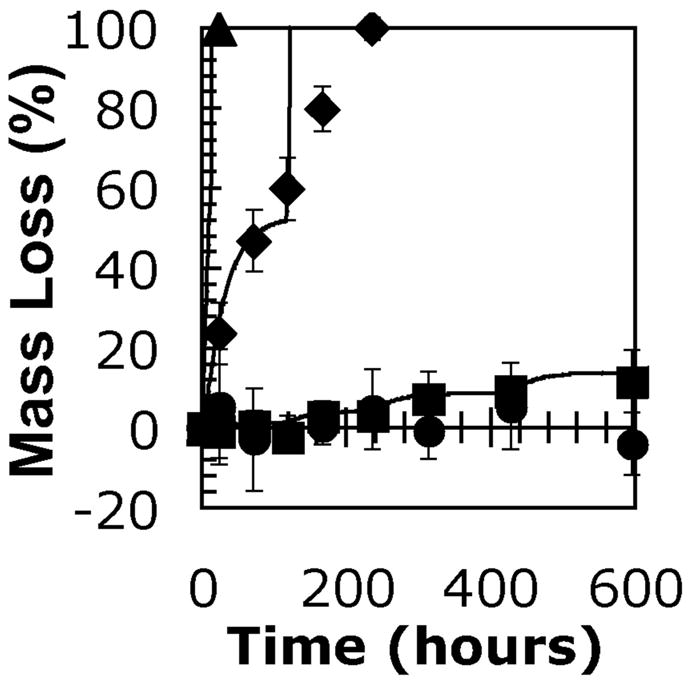
Experimental mass loss data and calculated mass loss profiles (solid lines) for hydrogels synthesized from 10 wt% solutions of macromonomers with varying lengths of CAP repeats. Data points correspond to hydrogels synthesized from macromonomers with m = 0 (circles), 3 (squares), 5.5 (diamonds), and 12 (triangles). Values for k* were estimated as k* = 10 (m = 3), 110 (m = 5.5), and 350 L*mol⁻¹*min⁻¹ (m = 12). Values of other constants used in calculation of mass loss profiles were k_d = 5.66e-04, and n₀ = 40.

While hydrogels with triggerable degradation have been reported in the past^19–21, an important aspect of this triggerable degradation pathway is that no pH or temperature change is required. Either of these aspects have the potential to damage the viability of encapsulated cells, require very rigorous control over these two variables, or both. In addition, enzymatically degradable gels have previously been synthesized from natural proteins and polysaccharides for tissue engineering applications^22–25. The biggest difference between gels that incorporate these natural materials and the synthetic PEG-CAP gels described in this contribution is that the natural materials are meant to be degraded by cells or the in vivo environment. PEG-CAP gels have the utility of not being degraded by the primary cell of interest, chondrocytes, and therefore degradation will only take place when the appropriate lipase enzyme is added exogenously. Addition of lipase to cell culture media in relevant concentrations for timely degradation does not temperature or pH, and it allows for a high degree of control over the extent of degradation, through both the choice of initial concentration and also because of the natural tendency of the lipase to lose activity over time. This external control could potentially be applied to trigger degradation at some important point in new ECM development. Synthetic PEG-CAP hydrogels could maintain a high initial stiffness, as well as shape and volume, and only be degraded when it becomes important for a large ECM molecule to diffuse and remodel, and only when there are sufficient amounts so that these molecules can reorganize quickly. In addition, the controllable degradation of these materials is particularly well suited to potential applications in advanced bioreactors. If the production of important ECM molecules is monitored in a real-time and nondestructive manner, the triggered degradation could serve as a feedback mechanism to allow these molecules to distribute within the gel at the optimal time.

Important limitations exist with hydrogels synthesized from PEG-CAP-DM macromonomers. One important problem associated with the use of this hydrogel system may be the diffusion of lipase in gels with higher crosslinking density. A solution to this problem could be to incorporate another mode of degradation by including a significant amount of hydrolytically degradable crosslinks. These could be incorporated through the use of larger amounts of macromonomer with PLA blocks in place of the CAP blocks. In this way, a gel could be synthesized with a very high initial crosslinking density and consequently, high stiffness and low diffusivity of large ECM molecules. After a period of time that depends on the chemistry of the PEG-PLA crosslinks and the degree to which it was initially incorporated, the mesh size of the gel could be increased enough for lipase to easily diffuse, but not enough to severely weaken the gel or cause changes in shape or volume. With addition of an externally triggerable component to the variety of crosslinks that can be incorporated with this synthetic system, hydrogels can be synthesized with many degradation profiles, allowing them to be fine-tuned to fit numerous specific applications.

CONCLUSIONS

In this study, we synthesized hydrogels from macromonomers with a PEG core and enzymatically degradable CAP blocks. The rate of degradation, characterized by mass loss and mechanical testing, depends on both the number of repeat units in the CAP blocks, and also on the concentration of the active lipase enzyme. Starting from reactions associated with classical enzyme kinetics and a simplified statistical adaptation of degradation in the gel network, a model was developed to describe mass loss in these materials. This model captures important aspects of the experimentally observed mass loss profile, and will provide assistance in experiments that better define the effects of degradation at different stages of development on the outcome of regenerated tissue in PEG hydrogels.