Abstract
Background
Previous studies have shown significant age-related changes in the first-order kernel of multifocal ERG (mfERG) responses. All of these reports were based upon ring averages across the retinal field. This study was carried out to determine age-related changes in the localized response and localized variability in the mfERG parameters: N1P1 amplitude, scalar product and implicit time of P1.
Methods
MfERG recordings from 70 normal phakic subjects (ages 9-80 years) were analyzed with VERIS 4.8. Scalar product values (for each hexagon based on ring average templates) were obtained and analyzed for age-related changes. Statistical measures such as coefficient of variation (CV) and parameters of a linear regression model were applied. Point-by-point comparisons were made across hemifields.
Results
Each localized response showed a significant aging effect either in scalar product or in N1P1 amplitude. The average decline of the response was ∼5% per decade, varying from 3.3% (peripherally) to 7.5% (perifoveally). The decline was significantly higher for the superior than for the inferior retina for amplitude parameters, corresponding to larger increases in P1 implicit time. The relative rate of change with age was similar for the nasal and the temporal retina. The average CV for all subjects at all locations was 29.4% (±4.1%).
Conclusions
The localized approach revealed patterns of age-related change that were not apparent in the ring averages. Information about changes in discrete retinal areas with age should make the mfERG more useful in quantitatively monitoring progression of retinal disease.
Introduction
The multifocal electroretinogram (mfERG), developed by Sutter [53] and Sutter and Tran [54], provides an objective non-invasive method for quick simultaneous functional testing of multiple locations in the retina [25]. As might be expected from full-field ERG analyses, it is now widely accepted that some of the mfERG components demonstrate a relationship with age [17, 19, 27, 37-39, 48]. However, most of these studies were based on limited sample sizes and limited age ranges [17, 27, 37, 38]. In addition, all published studies involved use of ring averages across the retinal field. The use of concentric ring averages is recommended in the guidelines for mfERG recording provided by the International Society for Clinical Electrophysiology of Vision (ISCEV) [35] as a useful way to summarize data. One advantage of this approach is the fact that noise contributions to the signal can be reduced substantially, but that comes at the expense of considerable loss of spatial resolution in detecting local abnormalities, especially in the peripheral rings [34]. With the concentric ring analysis an increasing number of stimulated areas towards the periphery would be averaged (e.g., with a 103-hexagon stimulation as recommended by ISCEV, the first two rings include 1-6 areas, while the outermost ring contains 42 retinal areas; Fig. 1). Therefore, even a pronounced localized abnormality in the outer ring that occupies one stimulated area will contribute just 2.4% of the total averaged response and may remain unnoticed if careful visual inspection of the derived trace array is not performed. More subtle abnormalities at the same location would be hard to detect even with visual inspection of the trace array.
Fig. 1.
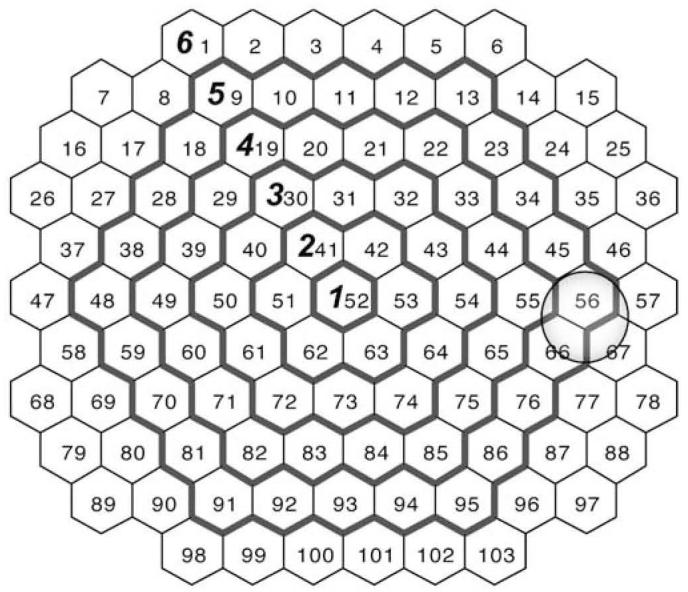
Hexagonal areas and borders of ring average patterns. The numbers inside the hexagonal areas indicate the stimulated areas provided by the VERIS system (field view). The outside borders of the ring average patterns commonly used in clinical practice are denoted by bold contours and designated by bold numerals. The gray circle indicates the approximate location of the optic nerve head
Several retinal disorders can start as focal abnormalities, and, therefore, might be detectable by localized analysis of the mfERG. Such nosologic entities include hereditary central cone dystrophy, early stages of age-related macular degeneration, early stages of diabetic retinopathy or monitoring of retinal function in patients with chloroquine medication or other treatments. The capability of the multifocal ERG to reliably detect and track longitudinal changes in those conditions is still largely unexplored.
Our goal was to examine the localized response for each retinal location stimulated and to quantify age-related changes in retinal response topography. In addition, we determined the localized variability in the mfERG amplitude, timing and scalar product across age.
Methods
Subjects
The mfERG recordings from one, randomly chosen eye of each of 70 normal phakic subjects (ages 9-80 years) were analyzed [19]. The refractive errors of the subjects were in the range +4.0 to −6.0 diopters (Table 1).
Table 1.
Mean and range of refractive errors (in diopters) for each age group
| Age group | Mean refraction | Range | |
|---|---|---|---|
| From | To | ||
| 9-19 years | −0.18 | −5.50 | 4.00 |
| 20-29 years | −1.35 | −5.00 | 0.00 |
| 30-39 years | −1.65 | −4.00 | 0.25 |
| 40-49 years | −0.53 | −2.50 | 1.50 |
| 50-59 years | 0.40 | −2.00 | 2.00 |
| 60-69 years | −0.28 | −2.50 | 1.50 |
| 70-80 years | −0.60 | −5.50 | 2.00 |
Retinal disorders or abnormal ocular media were excluded by evaluating the best-corrected visual acuity, slit-lamp examination, IOP measurement, direct and indirect dilated ophthalmoscopy and stereo fundus photography. Subjects were excluded if their fundus photos revealed more than five small (<63 µm) hard drusen in the central retina, following the guidelines of the international classi-fication system [4] and performed by a retinal specialist. All subjects had normal color vision when tested with the Neitz anoma-loscope, the HRR pseudo-isochromatic plates, and the Farnsworth F-2 plate.
The tenants of the Declaration of Helsinki were followed and written informed consent was obtained after all procedures were explained. This study was approved by the Office of Human Research Protection of the University of California, Davis, School of Medicine.
The mfERG protocol
The protocol used was similar to the ISCEV guidelines for mfERG and was described in detail in this journal [19]. Briefly, the recording was made under room light conditions with a dilated pupil (d >6 mm). Correction of refractive error (between +6 and −6 D) was obtained using the refraction correction unit as part of the VERIS system (EDI, San Mateo, CA). The stimulus consisted of 103 hexagons. The flash intensity was 2.67 cd-sec·m−2 (200 cd·m−2), the intensity of the dark areas was <0.05 cd-sec·m−2 (<4 cd·m−2) and the frame rate was 75 Hz. Burian-Allen contact lens electrodes (Hansen Ophthalmic Development Laboratory, Iowa City, IA) were used as active electrodes. Standard m-sequence stimulation mode (m=14) was used, resulting in a total recording time of 3.38 min.
Data analysis
Data were analyzed with VERIS SCIENCE, version 4.8 (Electro-Diagnostic Imaging, San Mateo, CA). Two iterations of an artifact rejection algorithm were applied to the raw data. The scalar product obtained for each hexagon (0-80 ms) based on ring average templates [54] for the first-order kernel was used, without spatial averaging. In a separate measurement, first-order kernel N1P1 amplitudes (measured on the response density scaled regional traces divided by the stimulated area) and P1 implicit times were obtained. To ensure uniformity of the response distribution, all data from left eyes were converted into right eye responses. Numbering of the hexagonal areas started at the top left end of the stimulation pattern and the numbers increased from left to right (Fig. 1). All data were analyzed in “field view” (corresponding retinal areas flipped upside down).
Theoretically it is possible that a relation could exist between saturation of the signal due to artifacts and age. In such a case, the artifact rejection routine could reduce the response amplitude more in older adults than younger adults, which may bias the data. To evaluate this possibility, scalar product data were analyzed twice, with and without the application of an artifact rejection algorithm. The percent difference between scalar product data values obtained by the two types of analyses failed to reveal a significant relation with age (r=0.064, r2=0.004, P=0.595), indicating that the artifact rejection algorithm did not introduce an age-dependent bias in the data.
Statistical analysis
Coefficient of variation for each hexagonal area was obtained for all subjects. A linear regression model of scalar product with age was applied to the entire sample using Sigma Plot 7.0 (SPSS, Chicago, IL). Parameters for these regressions were used primarily for descriptive rather than inferential purposes. Paired t-tests were used for comparisons between symmetrical areas in the upper and lower or nasal and temporal hemiretinae.
Results
Estimate of overall variation across the stimulated field
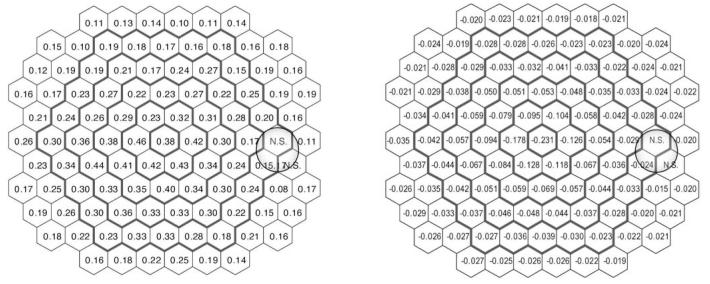
The mean coefficient of variation (CV) of the scalar product values for all subjects and all hexagonal areas was 29.2% (±3.9%). The distribution of CV was fairly homogeneous and consistent across the retina, except for a small region around the optic disc (three hexagonal areas: N-56, 66, 67), where the variability was considerably higher (>+2SD; for all other locations the variation was <2SD) (Fig. 2).
Fig. 2.
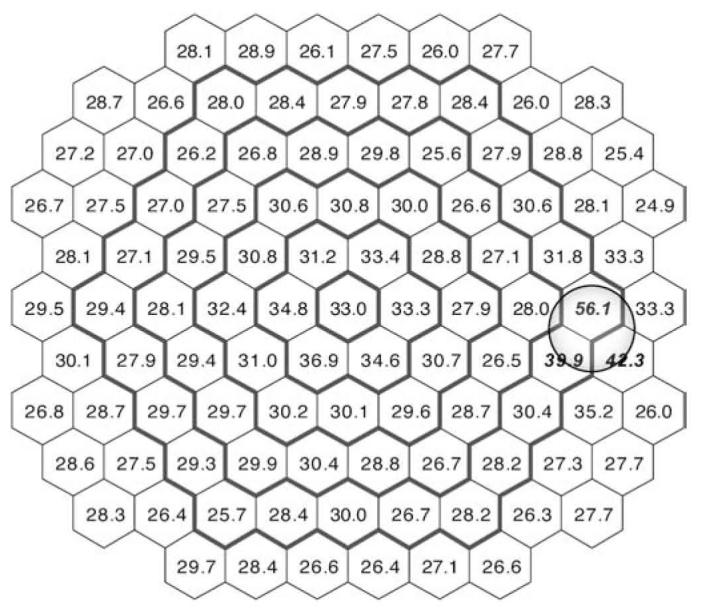
Distribution of the coefficient of variation (in percentage) for individual scalar product values of the first-order kernel. Numbers in italic bold represent locations with greater variability (CV >2 SD above the mean)
The mean CV of the N1P1 amplitude was 27.5% (±2.5%). Two retinal areas around the optic disc (hexagons 56 and 66) and the most central area (hexagon 53) had higher variability (>+2SD).
The mean P1 implicit time across all areas was 28.4 ms (±0.5 ms). The variability of the P1 implicit time was much smaller than the scalar product or N1P1 amplitude. Thus, the mean CV was 6.62% (±0.85%). Local areas of increased variability included only two areas near the optic disc (hexagons 56 and 66).
Age-related change in scalar product
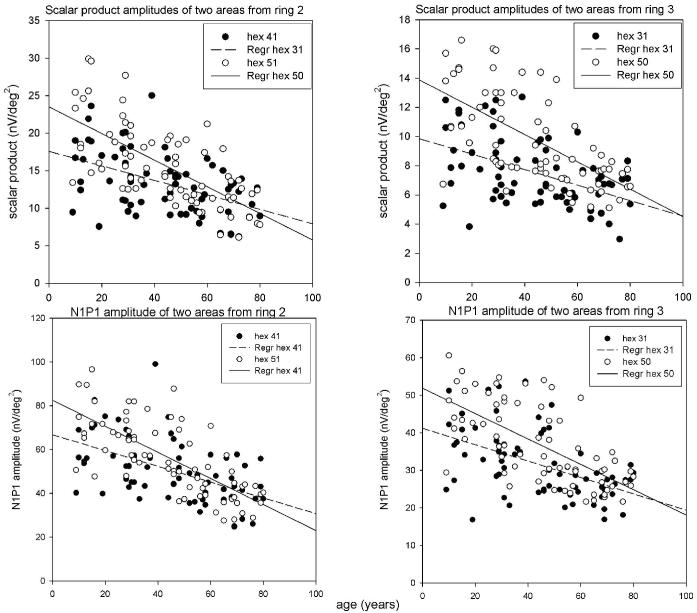
To test the variability in the age-related change of the retinal response around the fovea, a linear regression model was applied to the data from individual hexagonal areas contained within rings 2 and 3 (2-5 deg and 5-10 deg from the foveola, respectively; Fig. 1 and Table 2). As evident from Table 2, the estimate of the goodness of fit of the linear regression model (R2) can vary by as much as ∼200% within the same ring (e.g., areas 41 and 53). In addition, the slope and the intercept of the linear regression can also vary substantially between individual areas (with a range of 54% for the slope and 160% for the intercept). Examples of scalar product values from different areas in rings 2 and 3 are shown in Fig. 3.
Table 2.
Parameters of the linear regression model estimating the relations between first-order kernel scalar product amplitude density values and age in rings 2 and 3. For numbering of the hexagonal areas see Fig. 1. Parameters shown: R2, proportion of variation explained by regression; b, slope (nV/deg2 per year); a, intercept (nV/deg2); CD,change per decade (%; see text). Range was calculated as the ratio (%) of the maximal to the minimal value for each parameter. NB: Probability (P; from the F-test of the analysis of variance for the regression) was less than 0.0001 for all areas
| Areas in ring 2 | N-41 | N-42 | N-51 | N-53 | N-62 | N-63 | Range (%) | |||||||
| Scalar | R2 | 0.226 | 0.321 | 0.441 | 0.439 | 0.419 | 0.429 | 195.2% | ||||||
| product | b | −0.095 | −0.104 | −0.175 | −0.129 | −0.128 | −0.118 | 54.5% | ||||||
| amplitude | a | 17.47 | 16.11 | 23.30 | 17.97 | 16.86 | 16.04 | 145.3% | ||||||
| density | CD | −5.46% | −6.42% | −7.52% | −7.16% | −7.59% | −7.36% | 72.0% | ||||||
| N1P1 | R2 | 0.259 | 0.408 | 0.505 | 0.471 | 0.496 | 0.497 | 195.5% | ||||||
| amplitude | b | −0.355 | −0.427 | −0.587 | −0.474 | −0.483 | −0.438 | 60.5% | ||||||
| a | 66.29 | 64.81 | 81.88 | 67.67 | 65.61 | 61.76 | 132.6% | |||||||
| CD | −5.36% | −6.59% | −7.17% | −7.00% | −7.37% | −7.10% | 72.7% | |||||||
| Areas in ring 3 | N-30 | N-31 | N-32 | N-40 | N-43 | N-50 | N-54 | N-61 | N-64 | N-72 | N-73 | N-74 | Range (%) | |
| Scalar | R2 | 0.206 | 0.228 | 0.269 | 0.287 | 0.323 | 0.366 | 0.319 | 0.413 | 0.346 | 0.349 | 0.403 | 0.348 | 200.5% |
| product | b | −0.049 | −0.052 | −0.047 | −0.077 | −0.059 | −0.091 | −0.055 | −0.083 | −0.066 | −0.059 | −0.069 | −0.057 | 52.1% |
| amplitude | a | 9.71 | 9.84 | 8.62 | 13.27 | 10.21 | 13.76 | 9.8 | 12.48 | 10.66 | 9.51 | 10.62 | 9.33 | 159.6% |
| density | CD | −5.09% | −5.29% | −5.50% | −5.83% | −5.76% | −6.61% | −5.56% | −6.65% | −6.17% | −6.15% | −6.47% | −6.06% | 76.9% |
| N1P1 | R2 | 0.275 | 0.259 | 0.339 | 0.366 | 0.390 | 0.431 | 0.309 | 0.469 | 0.414 | 0.398 | 0.472 | 0.374 | 182.0% |
| amplitude | b | −0.222 | −0.219 | −0.224 | −0.325 | −0.241 | −0.337 | −0.230 | −0.315 | −0.259 | −0.245 | −0.308 | −0.232 | 64.9% |
| a | 40.93 | 41.17 | 38.37 | 53.02 | 41.51 | 51.74 | 40.22 | 48.52 | 42.49 | 37.64 | 42.10 | 36.78 | 138.2% | |
| CD | −5.43% | −5.31% | −5.83% | −6.13% | −5.79% | −6.51% | −5.72% | −6.49% | −6.11% | −6.51% | −7.31% | −6.29% | 81.5% |
Fig. 3.
Scalar product values (upper panels) and N1P1 amplitudes (lower panels) are presented as examples of relations with age for individual areas from ring 2 (left panels) and ring 3 (right panels)
The variation within the rings prompted an extension of the analysis to all hexagonal areas. With the exception of three areas (N-56, 66, 67), all individual locations were well fit with the linear regression model (F statistic P< 0.001). The estimate of the goodness of fit for the linear regression at each area is presented in Fig. 4 (left). Slope values (nV/deg2/year) for each location are presented in Fig. 4 (right).
Fig. 4.
Goodness of fit and slope of the linear regression model for the age-related change in scalar products. Left: Estimate of the goodness of the fit (R2) at each hexagonal area; right: values of the slope (nV/deg2/year) for each area
The slope and the intercept of the linear regression vary with location as illustrated in Table 2. In this respect, a comparison of the age effect in two or more locations based solely on the comparison of the slopes of the scalar product regressions can be misleading. Therefore, we calculated the change with age in each area in relative terms (as percentage decrease). This approach has been used by others for estimating age effects on retinal cell populations [40, 41] and in other parameters [16]. As the percent change per year was less than 1% for all areas, it was considered more convenient to represent the change per decade instead. The relative change varied substantially (up to ∼77%) across the rings (Table 2).
Age-related change in N1P1 amplitude
The N1P1 amplitude exhibited a linear decline with age similar to that of the scalar product values across different retinal areas (Table 1). As with the scalar product, there was substantial variability in the parameters of the linear regression model (up to 200% for R2, up to 65% for the slope, up to 144% for the intercept and up to 73% for change per decade). Again, as with the scalar product amplitude, all individual areas were well fit with the linear regression model (P<0.001), except for the same three areas (56, 66, 67).
The similarity between N1P1 amplitude and scalar product change per decade values prompted a test of the correlation between the two parameters. The Pearson correlation coefficient between N1P1 amplitude and scalar product value for all subjects across all hexagons was 0.965. The distribution of the correlation coefficients for each hexagonal area is shown in Fig. 5 (right). Except for a few responses from the nasal retina, there was a consistently high correlation between the parameters.
Fig. 5.
Percent change per decade for the N1P1 amplitude (nV/deg2) at each location (left) and correlation between N1P1 amplitude and the scalar product values (right). In the left panel, the italicized bold number indicates the location (hexagon N-67) where linear regression was not statistically significant
Despite the overall high degree of correlation in change per decade values, some regional discrepancies between both parameters remained. That prompted a point-by-point comparison of the relative change for both parameters (paired t-test). This comparison showed an overall faster decrease per decade of N1P1 amplitude with age than the scalar product (t=7.67, P<0.001). Scalar products are sensitive to changes in wave shape [54] and can therefore reflect age-related changes in both implicit time and response density.
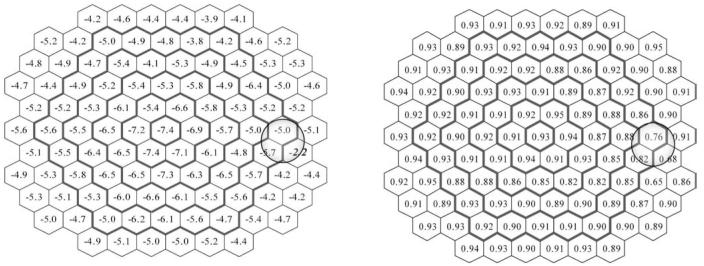
Age-related change in P1 implicit time
Implicit time P1 increased with age for most of the stimulated retinal areas. However, in 13 areas there was no significant linear relation with age. As shown in Fig. 6, the relative change values vary from 0.7% to 2.2%.
Fig. 6.
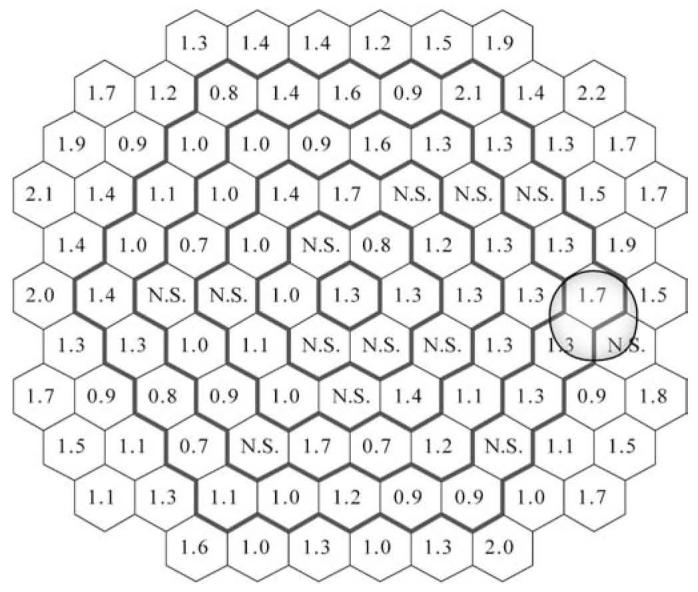
Percent change per decade for P1 implicit time (ms) at each location (N.S. locations where the linear regression model did not reach statistical significance)
Hemifield differences in age-related change of mfERG parameters
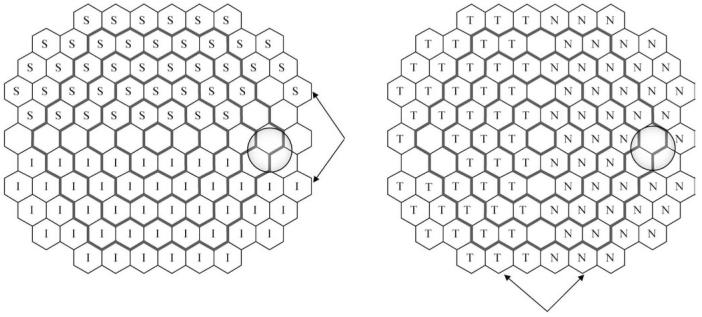
The topographical distribution of the slopes and percent change per decade for all areas (Figs. 3 and 4) suggests asymmetry between upper and lower areas. We tested the significance of these differences by a paired comparison of symmetrical areas along the horizontal meridian. Three hexagonal areas around the optic disc (N-56, 66, 67) were excluded from the analysis due to high variability. Three corresponding regions from the opposite hemifield were also excluded to maintain symmetry of comparison (Fig. 2 and Fig. 7). The same approach but for symmetrical areas along the vertical meridian was applied to test possible differences in age-related changes in areas of the nasal and the temporal hemifield.
Fig. 7.
Schematic representation of the hemifield comparisons between superior (S) and inferior (I) retinal hemifields (left panel) and nasal (N) and temporal (T) retinal hemifields (right panel). The arrows indicate corresponding hemifield areas
The results of the paired comparison between different hemifields are presented in Tables 3 and 4. The lower hemifield was characterized by higher regression coefficients, higher values for the slope, intercept and percent change (decrease) per decade than the upper hemifield. The relations between the temporal and nasal symmetrical areas are more complex. Thus, the slope and intercept were significantly higher in the nasal areas, but this was not reflected in significantly different percentage changes per decade.
Table 3.
Results of the paired comparisons between upper and lower hemifields for scalar product and amplitude (N1P1)
| Scalar product amplitude density | R2 | Slope (nV/deg2/year) | Intercept (nV/deg2) | Change per decade (%) |
| t value | −7.667 | 5.538 | −2.064 | 6.113 |
| P (significance, two-tailed) | <0.001 | <0.001 | 0.045 | <0.001 |
| Degrees of freedom | 42 | 42 | 42 | 42 |
| N1P1 amplitude | R2 | Slope (nV/year) | Intercept (nV) | Change per decade (%) |
| t value | −5.142 | 3.718 | 1.319 | 4.980 |
| P (significance, two-tailed) | <0.001 | <0.001 | N.S. | <0.001 |
| Degrees of freedom | 42 | 42 | 42 | 42 |
| P1 peak time | R2 | Slope (ms/year) | Intercept (ms) | Change per decade (%) |
| t value | 3.373 | 2.360 | −3.425 | 2.473 |
| P (significance, two-tailed) | <0.01 | <0.05 | <0.01 | <0.05 |
| Degrees of freedom | 33 | 33 | 33 | 33 |
Table 4.
Results of the paired comparisons between nasal and temporal hemifields for scalar product and amplitude (N1P1)
| Scalar product amplitude density | R2 | Slope (nV/deg2/year) | Intercept (nV/deg2) | Change per decade (%) |
| t value | 2.229 | 5.141 | 7.561 | −1.990 |
| P (significance, two-tailed) | <0.05 | <0.001 | <0.001 | N.S |
| Degrees of freedom | 44 | 44 | 44 | 44 |
| N1P1 amplitude | R2 | Slope (nV/year) | Intercept (nV) | Change per decade (%) |
| t value | 1.824 | −4.668 | 9.006 | 1.224 |
| P significance, two-tailed | N.S | <0.001 | <0.001 | N.S |
| Degrees of freedom | 44 | 44 | 44 | 44 |
| P1 peak time | R2 | Slope (ms/year) | Intercept (ms) | Change per decade (%) |
| t value | −2.136 | −2.448 | −0.961 | −2.008 |
| P significance, two-tailed | <0.05 | <0.05 | N.S. | N.S |
| Degrees of freedom | 34 | 34 | 34 | 34 |
Discussion
The present study revealed a well-defined linear correlation between age and N1P1 amplitude and the scalar product of the first-order kernel of the mfERG. This is in good agreement with previous studies for the same or similar parameters using ring average analyses [17, 19, 27, 37, 39]. Previous studies have demonstrated that the amplitude decline and latency increase with age could not be explained entirely by changes in optical factors (such as age-related change in pupil size and optical transmission of the lens), and, therefore, neural or metabolic factors should be considered [19, 27, 48]. Numerous works from different areas support the idea of a functional, morphologic and metabolic retinal age-related decline (see [44] for review). Thus, rod photoreceptor loss with age (3.7%-7.3% per decade) [13, 40] and decrease in RPE cell density (∼3% per decade) [41, 56] and central retinal ganglion cell density (3%-5% per decade) [10, 23, 28] are all well documented for the central retina. Small cone photoreceptor losses with age (1.8% per decade) were noted in the central retina in some studies [40], but not in others [13]. Although the mfERG signal generated under the stimulation conditions in the present study is cone-driven [54], there are extensive connections and interactions between rod and cone networks in the retina [5, 50, 51], and, therefore, rod influence cannot be excluded. In addition to the cell density decreases, blood supply to the eye is reduced with age [32]. More specifically, it has been reported that retinal (6-11% per decade) [22, 46] and choroidal [14, 32] blood flow and the number of functioning choroidal arterioles [26] decrease in parallel with age. Increases in the diameter of the capillary-free zone [31] and some atrophy or occlusion of macular capillaries have also been reported [7, 52]. In addition, age-related decreases in global rod and cone photoreceptor high-intensity a-wave ERG responses [3] and peripheral (at 20 deg eccentricity) resolution for stationary and flicker gratings [1] have been described.
In contrast to all previous published work, we focused our analysis on localized age-related changes in mfERG components. Our results demonstrate considerable variation of different retinal regions with respect to variability of the response and characteristics of age-related change. Thus, topographic properties of the retina have to be taken into account when establishing a normative database for clinical and research purposes and when tracking local changes in the response for early and discrete signs of pathology[20].
Variability of the mfERG response
The mean overall variability (expressed as coefficient of variability) of the scalar product for all subjects and all areas was 29%. Mohidin et al. [37] reported the same CV for 90 healthy subjects with a smaller age range (18-52 years), while Penrose et al. [43] found a CV of 21% for 20 subjects ages 19-50 years.
The variability of the mfERG response was highest in a small peripheral area corresponding to the location of the optic disc. The fact that not only one, but three adjacent hexagonal areas (N-56, 66, 67 according to the VERIS numbering system) expressed high variability can be due to several factors. These might include intersubject differences in optic disc size [24, 45, 49], slight differences in the relative position of the optic disc with respect to the fovea [18, 60] and/or interindividual differences in optic disc reflectivity [8] (which changes the contribution of stray light to the mfERG signal). Fixation instability can be an additional source of variation, although eye position was monitored constantly and recordings were interrupted at every detectable deviation. It is difficult to estimate beforehand the size and position of the optic disc relative to the pattern of the stimulus and its reflectivity. Responses from these three areas should, therefore, be interpreted with caution or excluded from a detailed localized analysis.
The variability of the mfERG responses generated from the central retina outside the optic disc area was fairly homogeneous for most of the stimulated areas, but slightly higher around the fovea. This might be due to higher differences in maximal cone density among subjects, which can vary among age cohorts by about a factor of 3 [11, 29].
The variability of P1 implicit time was considerably smaller than that of N1P1 amplitude or scalar product. We are not aware of reports of P1 peak time variability estimates in the literature, but similar findings were reported for the full-field ERG with lower variability for the cone b-wave peak time than the cone b-wave amplitude with age [2, 55, 57].
Global age effect on N1P1 amplitude and scalar product
The present study supports and refines the results from previous studies [17, 19, 27, 48] demonstrating marked age-related change in the N1P1 amplitude and scalar product derived from the first-order kernel of the mfERG. The topography of the change with age for both parameters was similar. However, point-by-point comparison showed that, overall, the relative change per decade was faster for the N1P1 amplitude. As scalar product values reflect retinal activity over a longer time frame (0-80 ms compared to 14-28 ms for N1P1), it is conceivable that processes developing after the first 28 ms are somewhat more resistant to age-correlated change, possibly due to retinal mechanisms of adaptation [21]. Another reason is that the scalar product reflects information about both implicit time and amplitude and, therefore, the contribution of timing changes might diminish the overall age effect on the scalar product.
Global age-related change in P1 implicit time
We found differences in the relations between age and P1 implicit time for different retinal locations within the stimulation pattern. For most of the locations there was a small but statistically significant linear increase of P1 implicit time with age. The average change per decade value was 1.2%, corresponding to an increase of ∼0.3 ms per decade, which is the same as that found by Seiple et al. using slightly different stimulus intensities [48]. Seeliger et al. [47] and Fortune and Johnson [17], using slightly different recording conditions (see discussion by Gerth et al. [19]), reported slightly larger increases of P1 implicit time per decade (0.4 and 0.7 ms). The increase of the S- and LM-cone full-field ERG b-wave implicit times was also slightly larger (0.6 ms and 0.8 ms per decade, respectively) [55]. However, the full-field ERG data are mass responses, and therefore, reflect more general aspects of overall retinal function compared to the localized mfERG responses. In addition, the state of adaptation and the stimulus rate differ substantially between the two tests, which might explain the faster age-related prolongation of retinal activity.
Two main conclusions arise from this analysis of the localized age-related changes in P1 implicit times. First, the calculated increase per decade for the regions where the linear regression model was significant was much smaller compared to the rate of digitization of the signal usually used in VERIS (0.83 ms between samples). That implies that with the currently used rate of digitization, an unequivocal increase in the implicit time can be determined only if the age difference is more than three decades. The second implication is that variation of the implicit time increase within the 103 stimulated areas was greater than expected. For example, in ring 5, the change per decade values can vary by as much as 300% (0.7-2.1) and in one location the increase was not linear (hexagon 34). A cautious and careful approach is needed if detection of subtle localized dysfunction or tracking of localized changes over time are among the goals of a clinical study involving the mfERG.
Hemifield differences associated with age
Superior versus inferior hemifield
The analysis of our data demonstrated clearly that the N1P1 amplitude and the scalar product from the superior retina was strongly correlated with age and decreased faster than the corresponding values from the inferior retina (P<0.001). Nagamoto et al. [39] (using lower mean luminance and fewer stimulating areas) demonstrated larger N1P1 mfERG amplitude in the upper retina, but they did not estimate the effect of age. Similarly, higher amplitudes of the pattern ERG were obtained from stimulation of the upper hemiretina [61]. Regional differences of neuronal cell distribution such as has been shown for rod photoreceptor [29, 59] and ganglion cell [9, 11] density, along with differential rates of age-related change, could have an influence on the mfERG signal. Incomplete digestion of rod outer segments and decreased function of the ABCA4 gene [36, 58] could lead to accumulation of lipofuscin in the RPE. In support of this topographic relation, it was demonstrated that retinal and RPE lipofuscin accumulation with age was slower in the inferior retina than in the superior retina [15]. Furthermore, the faster accumulation of lipofuscin in the superior retina and adjacent RPE could affect adversely the metabolic activity of both tissues and ultimately decrease the mfERG signal to a greater extent.
In addition to the accumulation of lipofuscin, it is possible that there is a relatively accelerated inner retinal loss in the superior retina compared with the inferior retina. It was reported recently that there is a preferential age-related loss of nerve fiber layer thickness in the superior sector of the peripapillary fundus [33]. This difference might be due to a lower mean blood flow in the superior retina and different vascular reactivity of the superior and inferior hemiretinae [6].
Nasal versus temporal hemifield
The slope of the decrease with age for the scalar product, N1P1 amplitude and P1 implicit time in the nasal areas was higher than corresponding areas in the temporal retina. There have been no previous studies to examine such an effect. In general, P1 implicit times from the nasal retina were found to be longer than the ones from the temporal retina [39, 42, 47]. The source of this difference is unclear. One possible explanation might be that cone density is 40-45% higher in nasal than in temporal retina [12], and the nasal retina in the macular region is thicker than the temporal retina [30]. The higher concentration of cellular elements nasally may influence the rate of aging in this part of the retina.
Despite the difference in aging of temporal and nasal implicit times, change per decade values were not different for the two hemifields. This finding underscores the complexities among relations between the three variables and the importance of analyzing them separately.
Summary
The profile of the rate of decrease with age for the scalar product and N1P1 amplitude does not match completely the profile of age change for the same parameters when analyzed by ring averages. Some retinal locations did not show a linear change with age for P1 implicit time. As with the amplitude and scalar product, there was considerable variation in rate of aging change within concentric rings. Symmetrical regions from the upper and lower central retina have different rates of change across age; the response from the upper retina decreases faster with age than the response from the lower retina.
In agreement with the ISCEV recommendations, establishing a normative base for mfERGs is necessary for analyzing clinical data. To detect localized abnormalities it would be beneficial to apply localized response analyses. However, care is needed when analyzing small localized changes or tracking localized changes over time, as there is considerable variability across the stimulated central retina. The mfERG response is highly variable for a small region around the optic disc (three hexagonal areas) and changes in this area should be either ignored or interpreted with caution.
Acknowledgement
We appreciate the technical assistance of Susan Garcia, Lei Ma and Lawrence Morse. This work was funded by the National Institute on Aging (AG04058) and a Jules and Doris Stein Research to Prevent Blindness Professorship.
References
- 1.Anderson RS, McDowell DR. Peripheral resolution using stationary and flickering gratings: the effects of age. Curr Eye Res. 1997;16:1209–1214. doi: 10.1076/ceyr.16.12.1209.5030. [DOI] [PubMed] [Google Scholar]
- 2.Birch DG, Anderson JL. Standardized full-field electroretinography. Normal values and their variation with age. Arch Ophthalmol. 1992;110:1571–1576. doi: 10.1001/archopht.1992.01080230071024. [DOI] [PubMed] [Google Scholar]
- 3.Birch DG, Hood DC, Locke KG, Hoffman DR, Tzekov RT. Quantitative electroretinogram measures of phototransduction in cone and rod photoreceptors: normal aging, progression with disease, and test-retest variability. Arch Ophthalmol. 2002;120:1045–1051. doi: 10.1001/archopht.120.8.1045. [DOI] [PubMed] [Google Scholar]
- 4.Bird AC, Bressler NM, Bressler SB, Chisholm IH, Coscas G, Davis MD, de Jong PT, Klaver CC, Klein BE, Klein R, et al. An international classi-fication and grading system for age-related maculopathy and age-related macular degeneration. The International ARM Epidemiological Study Group. Surv Ophthalmol. 1995;39:367–374. doi: 10.1016/s0039-6257(05)80092-x. [DOI] [PubMed] [Google Scholar]
- 5.Buck SL. In: Rod-cone interactions in human vision. Chalupa LM, Werner JS, editors. The visual neurosciences MIT Press Cambridge; MA: 2004. pp. 863–878. [Google Scholar]
- 6.Chung HS, Harris A, Halter PJ, Kagemann L, Roff EJ, Garzozi HJ, Hosking SL, Martin BJ. Regional differences in retinal vascular reactivity. Invest Ophthalmol Vis Sci. 1999;40:2448–2453. [PubMed] [Google Scholar]
- 7.Cogan DG. Development and senescence of the human retinal vasculature. Trans Ophthalmol Soc UK. 1963;83:465. [PubMed] [Google Scholar]
- 8.Cooper RL, Eikelboom RH, Barry CJ. Correlations between densitometry of red-free photographs and reflectometry with the scanning laser ophthalmoscope in normal subjects and glaucoma patients. Int Ophthalmol. 1992;16:243–246. doi: 10.1007/BF00917969. [DOI] [PubMed] [Google Scholar]
- 9.Curcio CA, Allen KA. Topography of ganglion cells in human retina. J Comp Neurol. 1990;300:5–25. doi: 10.1002/cne.903000103. [DOI] [PubMed] [Google Scholar]
- 10.Curcio CA, Drucker DN. Retinal ganglion cells in Alzheimer's disease and aging. Ann Neurol. 1993;33:248–257. doi: 10.1002/ana.410330305. [DOI] [PubMed] [Google Scholar]
- 11.Curcio CA, Sloan KR, Jr., Packer O, Hendrickson AE, Kalina RE. Distribution of cones in human and monkey retina: individual variability and radial asymmetry. Science. 1987;236:579–582. doi: 10.1126/science.3576186. [DOI] [PubMed] [Google Scholar]
- 12.Curcio CA, Sloan KR, Kalina RE, Hendrickson AE. Human photoreceptor topography. J Comp Neurol. 1990;292:497–523. doi: 10.1002/cne.902920402. [DOI] [PubMed] [Google Scholar]
- 13.Curcio CA, Millican CL, Allen KA, Kalina RE. Aging of the human photoreceptor mosaic: evidence for selective vulnerability of rods in central retina. Invest Ophthalmol Vis Sci. 1993;34:3278–3296. [PubMed] [Google Scholar]
- 14.Dallinger S, Findl O, Strenn K, Eichler HG, Wolzt M, Schmetterer L. Age dependence of choroidal blood flow. J Am Geriatr Soc. 1998;46:484–487. doi: 10.1111/j.1532-5415.1998.tb02471.x. [DOI] [PubMed] [Google Scholar]
- 15.Delori FC, Goger DG, Dorey CK. Age-related accumulation and spatial distribution of lipofuscin in RPE of normal subjects. Invest Ophthalmol Vis Sci. 2001;42:1855–1866. [PubMed] [Google Scholar]
- 16.Fitzgerald ME, Tolley E, Frase S, Zagvazdin Y, Miller RF, Hodos W, Reiner A. Functional and morphological assessment of age-related changes in the choroid and outer retina in pigeons. Vis Neurosci. 2001;18:299–317. doi: 10.1017/s0952523801182143. [DOI] [PubMed] [Google Scholar]
- 17.Fortune B, Johnson CA. Decline of photopic multifocal electroretinogram responses with age is due primarily to preretinal optical factors. J Opt Soc Am A Opt Image Sci Vis. 2002;19:173–184. doi: 10.1364/josaa.19.000173. [DOI] [PubMed] [Google Scholar]
- 18.Garway-Heath DF, Poinoosawmy D, Fitzke FW, Hitchings RA. Map-ping the visual field to the optic disc in normal tension glaucoma eyes. Ophthalmology. 2000;107:1809–1815. doi: 10.1016/s0161-6420(00)00284-0. [DOI] [PubMed] [Google Scholar]
- 19.Gerth C, Garcia SM, Ma L, Keltner JL, Werner JS. Multifocal electroretinogram: age-related changes for different luminance levels. Graefe's Arch Clin Exp Ophthalmol. 2002;240:202–208. doi: 10.1007/s00417-002-0442-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gerth C, Hauser D, Delahunt PB, Morse LS, Werner JS. Assessment of multifocal electroretinogram abnormalities and their relation to morphologic characteristics in patients with large drusen. Arch Ophthalmol. 2003;121:1404–1414. doi: 10.1001/archopht.121.10.1404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gerth C, Sutter EE, Werner JS. MfERG response dynamics of the aging retina. Invest Ophthalmol Vis Sci. 2003;44:4443–4450. doi: 10.1167/iovs.02-1056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Groh MJ, Michelson G, Langhans MJ, Harazny J. Influence of age on retinal and optic nerve head blood circulation. Ophthalmology. 1996;103:529–534. doi: 10.1016/s0161-6420(96)30662-3. [DOI] [PubMed] [Google Scholar]
- 23.Harman A, Abrahams B, Moore S, Hoskins R. Neuronal density in the human retinal ganglion cell layer from 16-77 years. Anat Rec. 2000;260:124–131. doi: 10.1002/1097-0185(20001001)260:2<124::AID-AR20>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- 24.Healey PR, Mitchell P, Smith W, Wang JJ. The influence of age and intraocular pressure on the optic cup in a normal population. J Glaucoma. 1997;6:274–278. [PubMed] [Google Scholar]
- 25.Hood DC. Assessing retinal function with the multifocal technique. Prog Retin Eye Res. 2000;19:607–646. doi: 10.1016/s1350-9462(00)00013-6. [DOI] [PubMed] [Google Scholar]
- 26.Ito YN, Mori K, Young-Duvall J, Yoneya S. Aging changes of the choroidal dye filling pattern in indocyanine green angiography of normal subjects. Retina. 2001;21:237–242. doi: 10.1097/00006982-200106000-00007. [DOI] [PubMed] [Google Scholar]
- 27.Jackson GR, Ortega J, Girkin C, Rosenstiel CE, Owsley C. Aging-related changes in the multifocal electroretinogram. J Opt Soc Am A Opt Image Sci Vis. 2002;19:185–189. doi: 10.1364/josaa.19.000185. [DOI] [PubMed] [Google Scholar]
- 28.Jonas JB, Schmidt AM, Muller-Bergh JA, Schlotzer-Schrehardt UM, Naumann GO. Human optic nerve fiber count and optic disc size. Invest Ophthalmol Vis Sci. 1992;33:2012–2018. [PubMed] [Google Scholar]
- 29.Jonas JB, Schneider U, Naumann GO. Count and density of human retinal photoreceptors. Graefes Arch Clin Exp Ophthalmol. 1992;230:505–510. doi: 10.1007/BF00181769. [DOI] [PubMed] [Google Scholar]
- 30.Kanai K, Abe T, Murayama K, Yoneya S. [Retinal thickness and changes with age] Nippon Ganka Gakkai Zasshi. 2002;106:162–165. [PubMed] [Google Scholar]
- 31.Laatikainen L, Larinkari J. Capillary-free area of the fovea with advancing age. Invest Ophthalmol Vis Sci. 1977;16:1154–1157. [PubMed] [Google Scholar]
- 32.Lam AK, Chan ST, Chan H, Chan B. The effect of age on ocular blood supply determined by pulsatile ocular blood flow and color Doppler ultrasonography. Optom Vis Sci. 2003;80:305–311. doi: 10.1097/00006324-200304000-00008. [DOI] [PubMed] [Google Scholar]
- 33.Lovasik JV, Kergoat MJ, Justino L, Kergoat H. Neuroretinal basis of visual impairment in the very elderly. Graefes Arch Clin Exp Ophthalmol. 2003;241:48–55. doi: 10.1007/s00417-002-0600-x. [DOI] [PubMed] [Google Scholar]
- 34.Marmor MF. Do you, doctor, take the mfERG for better or for worse? Graefes Arch Clin Exp Ophthalmol. 2002;240:241–243. doi: 10.1007/s00417-002-0438-2. [DOI] [PubMed] [Google Scholar]
- 35.Marmor MF, Hood DC, Keating D, Kondo M, Seeliger MW, Miyake Y. Guidelines for basic multifocal electroretinography (mfERG) Doc Ophthalmol. 2003;106:105–115. doi: 10.1023/a:1022591317907. [DOI] [PubMed] [Google Scholar]
- 36.Mata NL, Tzekov RT, Liu X, Weng J, Birch DG, Travis GH. Delayed dark-adaptation and lipofuscin accumulation in abcr+/− mice: implications for involvement of ABCR in age-related macular degeneration. Invest Ophthalmol Vis Sci. 2001;42:1685–1690. [PubMed] [Google Scholar]
- 37.Mohidin N, Yap MK, Jacobs RJ. Influence of age on the multifocal electroretinography. Ophthalmic Physiol Opt. 1999;19:481–488. doi: 10.1046/j.1475-1313.1999.00468.x. [DOI] [PubMed] [Google Scholar]
- 38.Nabeshima T, Tazawa Y, Mita M, Sano M. Effects of aging on the first and second-order kernels of multifocal electroretinogram. Jpn J Ophthalmol. 2002;46:261–269. doi: 10.1016/s0021-5155(02)00475-6. [DOI] [PubMed] [Google Scholar]
- 39.Nagatomo A, Nao-i N, Maruiwa F, Arai M, Sawada A. Multifocal electroretinograms in normal subjects. Jpn J Ophthalmol. 1998;42:129–135. doi: 10.1016/s0021-5155(97)00118-4. [DOI] [PubMed] [Google Scholar]
- 40.Panda-Jonas S, Jonas JB, Jakobczyk-Zmija M. Retinal photoreceptor density decreases with age. Ophthalmology. 1995;102:1853–1859. doi: 10.1016/s0161-6420(95)30784-1. [DOI] [PubMed] [Google Scholar]
- 41.Panda-Jonas S, Jonas JB, Jakobczyk-Zmija M. Retinal pigment epithelial cell count, distribution, and correlations in normal human eyes. Am J Ophthalmol. 1996;121:181–189. doi: 10.1016/s0002-9394(14)70583-5. [DOI] [PubMed] [Google Scholar]
- 42.Parks S, Keating D, Williamson TH, Evans AL, Elliott AT, Jay JL. Functional imaging of the retina using the multifocal electroretinograph: a control study. Br J Ophthalmol. 1996;80:831–834. doi: 10.1136/bjo.80.9.831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Penrose PJ, Tzekov RT, Sutter EE, Fu AD, Allen AW, Jr., Fung WE, Oxford KW. Multifocal electroretinography evaluation for early detection of retinal dysfunction in patients taking hydroxychloroquine. Retina. 2003;23:503–512. doi: 10.1097/00006982-200308000-00010. [DOI] [PubMed] [Google Scholar]
- 44.Pierscionek BK, Weale RA. Risk factors and ocular senescence. Gerontology. 1996;42:257–269. doi: 10.1159/000213800. [DOI] [PubMed] [Google Scholar]
- 45.Quigley HA, Brown AE, Morrison JD, Drance SM. The size and shape of the optic disc in normal human eyes. Arch Ophthalmol. 1990;108:51–57. doi: 10.1001/archopht.1990.01070030057028. [DOI] [PubMed] [Google Scholar]
- 46.Rojanapongpun P, Drance SM. Velocity of ophthalmic arterial flow recorded by Doppler ultrasound in normal subjects. Am J Ophthalmol. 1993;115:174–180. doi: 10.1016/s0002-9394(14)73921-2. [DOI] [PubMed] [Google Scholar]
- 47.Seeliger MW, Kretschmann UH, Apfelstedt-Sylla E, Zrenner E. Implicit time topography of multifocal electroretinograms. Invest Ophthalmol Vis Sci. 1998;39:718–723. [PubMed] [Google Scholar]
- 48.Seiple W, Vajaranant TS, Szlyk JP, Clemens C, Holopigian K, Paliga J, Badawi D, Carr RE. Multifocal electroretinography as a function of age: the importance of normative values for older adults. Invest Ophthalmol Vis Sci. 2003;44:1783–1792. doi: 10.1167/iovs.02-0518. [DOI] [PubMed] [Google Scholar]
- 49.Sing NM, Anderson SF, Townsend JC. The normal optic nerve head. Optom Vis Sci. 2000;77:293–301. doi: 10.1097/00006324-200006000-00009. [DOI] [PubMed] [Google Scholar]
- 50.Sjostrand FS. Sequential pictorial presentation of neural interaction in the retina. 2. The depolarizing and hyperpolarizing bipolar cells at rod terminals. J Submicrosc Cytol Pathol. 2002;34:85–98. [PubMed] [Google Scholar]
- 51.Sjostrand FS. Color vision at low light intensity, dark adaptation, Purkinje shift, critical flicker frequency and the deterioration of vision at low illumination. Neurophysiology at the nanometer range of neural structure. J Submicrosc Cytol Pathol. 2003;35:117–127. [PubMed] [Google Scholar]
- 52.Sugi K. Studies on the pathological changes in the retinal vessels of human eyes, using the trypsin digestion method. Jpn J Ophthalmol. 1966;10:252. [Google Scholar]
- 53.Sutter EE. The fast m-transform: a fast computation of cross-correlations with binary m-sequences. SIAM J Comput. 1991;20:686–694. [Google Scholar]
- 54.Sutter EE, Tran D. The field topography of ERG components in man-I. The photopic luminance response. Vision Res. 1992;32:433–446. doi: 10.1016/0042-6989(92)90235-b. [DOI] [PubMed] [Google Scholar]
- 55.Suzuki S, Horiguchi M, Tanikawa A, Miyake Y, Kondo M. Effect of age on short-wavelength sensitive cone electroretinogram and long- and middle-wavelength sensitive cone electroretinogram. Jpn J Ophthalmol. 1998;42:424–430. doi: 10.1016/s0021-5155(98)00030-6. [DOI] [PubMed] [Google Scholar]
- 56.Watzke RC, Soldevilla JD, Trune DR. Morphometric analysis of human retinal pigment epithelium: correlation with age and location. Curr Eye Res. 1993;12:133–142. doi: 10.3109/02713689308999481. [DOI] [PubMed] [Google Scholar]
- 57.Weleber RG. The effect of age on human cone and rod ganzfeld electroretinograms. Invest Ophthalmol Vis Sci. 1981;20:392–399. [PubMed] [Google Scholar]
- 58.Weng J, Mata NL, Azarian SM, Tzekov RT, Birch DG, Travis GH. In-sights into the function of Rim protein in photoreceptors and etiology of Star-gardt's disease from the phenotype in abcr knockout mice. Cell. 1999;98:13–23. doi: 10.1016/S0092-8674(00)80602-9. [DOI] [PubMed] [Google Scholar]
- 59.Wikler KC, Williams RW, Rakic P. Photoreceptor mosaic: number and distribution of rods and cones in the rhesus monkey retina. J Comp Neurol. 1990;297:499–508. doi: 10.1002/cne.902970404. [DOI] [PubMed] [Google Scholar]
- 60.Williams TD, Wilkinson JM. Position of the fovea centralis with respect to the optic nerve head. Optom Vis Sci. 1992;69:369–377. doi: 10.1097/00006324-199205000-00006. [DOI] [PubMed] [Google Scholar]
- 61.Yoshii M, Paarmann A. Hemiretinal stimuli elicit different amplitudes in the pattern electroretinogram. Doc Ophthalmol. 1989;72:21–30. doi: 10.1007/BF00155210. [DOI] [PubMed] [Google Scholar]