A Decomposition Theory for Phylogenetic Networks and Incompatible Characters

Abstract

Phylogenetic networks are models of evolution that go beyond trees, incorporating non-tree-like biological events such as recombination (or more generally reticulation), which occur either in a single species (meiotic recombination) or between species (reticulation due to lateral gene transfer and hybrid speciation). The central algorithmic problems are to reconstruct a plausible history of mutations and non-tree-like events, or to determine the minimum number of such events needed to derive a given set of binary sequences, allowing one mutation per site. Meiotic recombination, reticulation and recurrent mutation can cause conflict or incompatibility between pairs of sites (or characters) of the input. Previously, we used “conflict graphs” and “incompatibility graphs” to compute lower bounds on the minimum number of recombination nodes needed, and to efficiently solve constrained cases of the minimization problem. Those results exposed the structural and algorithmic importance of the non-trivial connected components of those two graphs.

In this paper, we more fully develop the structural importance of non-trivial connected components of the incompatibility and conflict graphs, proving a general decomposition theorem (first presented in Gusfield and Bansal 2005) for phylogenetic networks. The decomposition theorem depends only on the incompatibilities in the input sequences, and hence applies to phylogenetic networks of all types, and to any phenomena that causes pairwise incompatibilities. More generally, the proof of the decomposition theorem exposes a maximal embedded tree structure that exists in the network when the sequences cannot be derived on a perfect phylogenetic tree. This extends the theory of perfect phylogeny in a natural and important way. The proof is constructive and leads to a polynomial-time algorithm to find the unique underlying maximal tree structure. We next examine and fully solve the major open question from Gusfield and Bansal (2005): Is it true that for every input there must be a fully decomposed phylogenetic network that minimizes the number of recombination nodes used, over all phylogenetic networks for the input. We previously conjectured that the answer is yes. In this paper we show that the answer in is no, both for the case that only single-crossover recombination is allowed, and also for the case that unbounded multiple-crossover recombination is allowed. The latter case also resolves a conjecture recently stated in Huson and Klopper (2007) in the context of general reticulation networks. Although the conjecture from Gusfield and Bansal (2005) is disproved in general, we show that the answer to the conjecture is yes in several natural special cases, and establish necessary combinatorial structure that counterexamples to the conjecture must posses. We also show that counterexamples to the conjecture are rare (for the case of single-crossover recombination) in simulated data.

1 Introduction to Phylogenetic Networks and Problems

With the growth of genomic data, much of which does not fit ideal evolutionary-tree models, and the increasing appreciation of the genomic role of such phenomena as recombination, recurrent and back mutation, horizontal gene transfer, species hybridization, gene conversion, and mobile genetic elements, there is greater need to understand the algorithmics and combinatorics of phylogenetic networks on which extant sequences were derived (Posada and Crandall, 2001; Morrison, 2005). Meiotic recombination between homologous chromosomes is particularly important in deriving chimeric sequences in a population of individuals of the same species, and understanding recombination in populations is a fundamental scientific goal. Moreover, recombination in populations is the key element underlying the logic of “association mapping”, an approach that is widely hoped to be able to efficiently locate genes influencing genetic diseases (Clark, 2003; Zollner and Pritchard, 2005; Minichiello and Durbin, 2006; Wu, 2007). On a much longer time scale, recombination between different species can occur (due to horizontal gene transfer), resulting in a hybrid species. This is called “reticulation” in Huson et al. (2005); Huson and Klopper (2007); Moret et al. (2004). Although meiotic recombination and species reticulation are very different biological events, the evolution of sequences in either biological context can be represented by similar phylogenetic networks and certain mathematical and algorithmic properties of these networks are identical or can be translated from one context to the other. In this paper, we study phylogenetic networks that derive binary sequences. Many of the results apply both to networks representing meiotic recombination and to networks representing species reticulation, while some of the results apply only to the case of meiotic recombination.

The assumption that sequences are binary is justified in the case of meiotic recombination by the infinite sites assumption in population genetics (Hein et al., 2005), which is strongly justified by the current importance of SNP (single nucleotide polymorphism) data. In SNP data, each site can generally take on at most two states (alleles) (Chakravarti, 1998; Hinds et al., 2005) in a population. In the context of reticulation at the species level, the assumption that sequences are binary comes from that fact that complex evolutionary characters are usually considered to be binary (being either present or absent) (Felsenstein, 2004). Moreover, as we will detail later, reticulation problems or often defined by a set of splits (or cuts), each of which must be in some tree in the network, and these splits are represented by binary sequences.

We begin with a formal definition of a phylogenetic network, primarily in the context of meiotic recombination; later when appropriate, we discuss how specific definitions and results can be applied more broadly to general reticulation.

Formal definition of a phylogenetic network

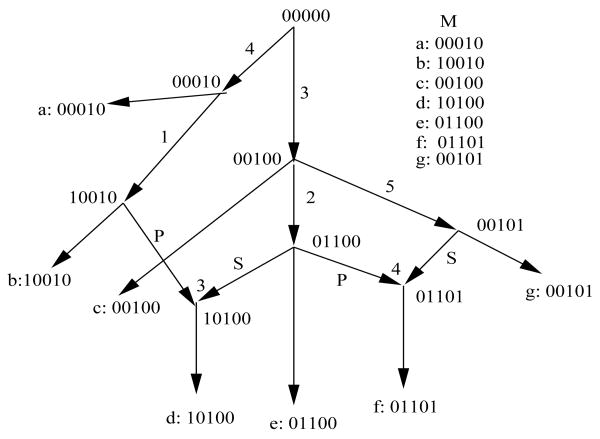
There are four components needed to specify a phylogenetic network that allows recombination (see Figure 1).

Figure 1.

A phylogenetic network that derives the set of sequences M. The two recombinations shown are single-crossover recombinations, and the crossover point is written above the recombination node. In general the recombinant sequence exiting a recombination node may be on a path that reaches another recombination node, rather than going directly to a leaf. Also, in general, not every sequence labeling a node also labels a leaf.

A phylogenetic network is built on a directed acyclic graph containing exactly one node (the root) with no incoming edges, a set of internal nodes that have both incoming and outgoing edges, and exactly n nodes (the leaves) with no outgoing edges. Each node other than the root has either one or two incoming edges. A node x with two incoming edges is called a recombination node.

Each integer (site) from 1 to m is assigned to exactly one edge in , but for simplicity of exposition, none are assigned to any edge entering a recombination node. There may be additional edges that are assigned no integers. We use the terms “column” and “site” interchangeably.

Each node in is labeled by an m-length binary sequence, starting with the root node which is labeled with some sequence R, called the “root” or the “ancestral” sequence. Since is acyclic, the nodes in can be topologically sorted into a list, where every node occurs in the list only after its parent(s). Using that list, we can constructively label the non-root nodes with well-defined sequences in order of their appearance in the list, as follows:

1. For a non-recombination node v, let e be the single edge coming into v. The sequence labeling v is obtained from the sequence labeling v's parent by changing the state (from 0 to 1, or from 1 to 0) of site i, for every integer i assigned to edge e. This corresponds to a mutation at site i occurring on edge e (i.e., during the interval of time represented by edge e).

2. For a recombination node x, let Z and Z′ denote the two m-length sequences labeling the two parent nodes of x. Then the “recombinant sequence” X labeling node x can be any m-length sequence provided that at every site i in X, the state (0 or 1) is equal to the state at site i in (at least) one of the sequences Z or Z′.

The creation of sequence X from Z and Z′ at a recombination node is called a “recombination event”. To fully specify the recombination event, we must specify for every site i in X whether the binary state in X “comes from” Z or Z′. This specification is forced when the states in Z and Z′ at site i are different. When they are the same, a choice must be specified. For a given recombination event, we say that a crossover or breakpoint occurs at site i if the states in X at sites i – 1 and i come from different parents. It is easy to determine the minimum number of crossovers needed to create X by a recombination of specific sequences Z and Z′.

The sequences labeling the leaves of are the extant sequences, i.e., the sequences that can be observed. We say that an phylogenetic network N derives (or explains) a set of n sequences M (each of length m) if and only if each sequence in M labels one of the leaves of . Without loss of generality, we assume that there is no site i where all the sequences have the same state at site i. We also assume throughout that M does not contain any duplicate rows.

With these definitions, the classic “perfect phylogeny” tree (Gusfield, 1991) is a phylogenetic network with no recombination nodes. That is, each site mutates exactly once in the evolutionary history, and there is no recombination between sequences.

Note that in the definition above, there is no bound on the number of crossovers that are allowed at a recombination event (other than the number of sites minus one). Thus, this form of recombination is called “unbounded multiple-crossover” recombination. The main decomposition theorem in this paper applies even when unbounded multiple-crossovers are allowed, and as we will show, multiple crossovers allows us to model a wide variety of biological phenomena. However, in meiotic recombination the number of crossovers is typically small, and the algorithmic/mathematical literature motivated by meiotic recombination has mostly assumed that only one crossover is allowed in a recombination event. This is called “single-crossover recombination”, and when it occurs the recombinant sequence X is formed from a prefix of one of its parent sequences (Z or Z′) followed by a suffix of the other parent sequence. That is the definition of recombination used in our early publications on phylogenetic networks, for example Gusfield et al. (2004a,b). A few papers have studied two-crossover recombination events motivated by “homologous gene-conversion” in Song et al. (2006). For brevity, we will use the phrase “multiple-crossover recombination” to mean “unbounded multiple-crossover recombination”. Some mathematical and algorithmic results depend on whether each recombination event is restricted to a single-crossover, or whether multiple-crossovers are allowed, and we will be very careful about that distinction.

What we have defined here as a phylogenetic network with single-crossover recombination is the digraph part of the stochastic process called an “ancestral recombination graph (ARG)” in the population genetics literature (Griffiths and Marjoram, 1996). (See also Norborg and Tavare 2002 or Hein et al. 2005 for an introduction to ARGs).

Rooted and Root-Unknown problems

Problems of reconstructing phylogenetic networks, given an input set of binary sequences M, can be addressed either in the rooted case, or the root-unknown case. In the rooted phylogenetic network problem, a required root or ancestral sequence R for the network is specified in advance. In the root-unknown phylogenetic network problem, no ancestral sequence is specified in advance, and the algorithm must select an ancestral sequence at the root.

The algorithmic problem of reconstructing a history of recombination events (with mutations), or determining the minimum number of recombination nodes needed in a phylogenetic network (for both rooted and unrooted problems), has been studied in a number of papers (Gusfield et al., 2007; Hein, 1990, 1993; Song and Hein, 2003, 2004; Wang et al., 2001; Myers and Griffiths, 2003; Hudson and Kaplan, 1985; Kececioglu and Gusfield, 1998; Gusfield, 2005a; Gusfield et al., 2004b,a; Nakhleh et al., 2003, 2004; Moret et al., 2004; Bafna and Bansal, 2004, 2006a; Song et al., 2005; Lyngso et al., 2005; Song et al., 2006; Myers, 2003).

2 A Fundamental Decomposition Theory

In this section we define and state the main result of this paper, the decomposition theorem. It will be proved in the next section. We believe the decomposition theorem and insights obtained from its proof are fundamental and extend the theory of perfect phylogeny from trees to general phylogenetic networks. We now begin the needed definitions and facts that lead to the statement of the main result.

2.1 Recombination Cycles and Blobs

In a phylogenetic network , let w be a node that has two paths out of it that meet at a recombination node x. Those two paths together define a “recombination cycle” Q. Node w is called the “coalescent node” of Q, and x is the recombination node of Q. In Figure 1, the nodes labeled 00000 and 00100 are coalescent nodes of two different recombination cycles.

A recombination cycle that is node-disjoint from any other recombination cycle has been defined as a “gall” (Gusfield et al., 2004b; Gusfield, 2005a; Song, 2006b). If a recombination cycle is edge-disjoint from any other recombination cycle in the network, then the network can be modified so that the cycle is node-disjoint from any other cycle. The modification requires adding one new edge and one new node, with the same sequence labeling both ends of the new edge. Repeating this as needed, we can assume that if a recombination cycle does not share an edge with any other recombination cycle, then it also does not share a node with any other recombination cycle. In contrast, consider a recombination cycle that shares at least one edge with some other recombination cycle. We can add another cycle to those two if the new cycle shares an edge with one of the two cycles. Continuing in this way, adding more cycles, we ultimately get a well-defined maximal set of recombination cycles in that form a single connected subgraph of , and each cycle shares at least one edge with some other cycle in the set. We call such a maximal set of recombination cycles a “blob”.

Clearly, because of maximality, the blobs in a phylogenetic network are well-defined, i.e., each blob can be found as above, starting from any recombination cycle in the blob. Moreover, as above, we assume that no blob shares a node with any other blob. Therefore, if we contract each blob in a network to a single point, the resulting network is a directed tree T′. This follows because if the resulting graph had a cycle (in the underlying undirected graph) that cycle would correspond to a recombination cycle in which should have been contracted. We call T′ a “tree of blobs” or a “blobbed tree”. So every phylogenetic network can be viewed as a blobbed tree. The edges in T′ are called “tree edges” of .

2.2 Incompatibility and Perfect Phylogeny

The main tools that we used in Gusfield et al. (2004b, 2007); Gusfield (2005a); Bafna and Bansal (2004); Song (2006b) and other papers were two graphs representing “incompatibilities” and “conflicts” between sites. We introduce these graphs here.

Given a set of binary sequences M, two columns i and j in M are said to be incompatible if and only if there are four rows in M where columns i and j contain all four of the ordered pairs 0,1; 1,0; 1,1; and 0,0. For example, in Figure 1 columns 1 and 3 of M are incompatible because of rows a, b, c, d. The test for the existence of all four pairs is called the “four-gamete test” in the population genetics literature. A site that is not involved in any incompatibility is called a “compatible site”.

Given a sequence S, two columns i and j in M are said to conflict (relative to S) if and only if columns i and j contain all three of the above four pairs that differ from the i, j pair in S. It is easy to see that two columns conflict relative to S if and only if they are incompatible in M + S, the set resulting from adding sequence S to M.

The classic Perfect Phylogeny Theorem (in the terminology of this paper) is: There is a rooted phylogenetic network without recombination cycles that derives a set of binary sequences M, if and only if there is no incompatible pair of columns in M. Network is a directed tree T, with the root labeled by a sequence that need not be in M. Moreover, the undirected tree created by ignoring the directions of the edges of T is invariant over all perfect phylogenies for M. Similarly, there is a unique phylogenetic network that derives M, with ancestral sequence S and without recombination cycles (and hence is a directed tree), if and only if there is no pair of columns that conflict relative to S. For one exposition of these classic results, see Gusfield (1997). For different expositions, see Theorem 3.1.4 in Semple and Steel (2003) or the Pairwise Compatibility Theorem in Felsenstein (2004).

Incompatibility and Conflict Graphs

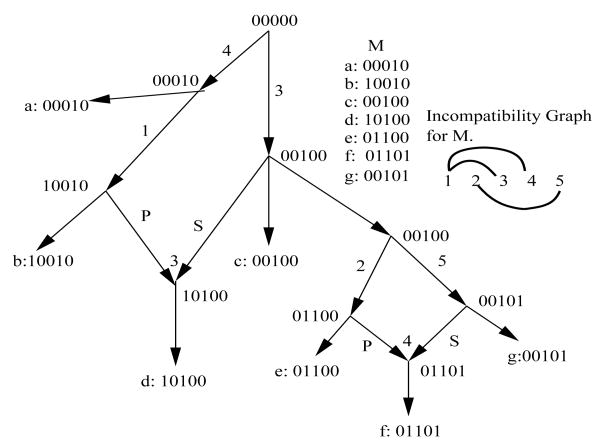
We define the “incompatibility graph” G(M) for M as a graph containing one node for each column (site) in M, and an edge connecting two nodes i and j if and only if columns i and j are incompatible. Similarly, given a sequence S, we define the “conflict graph” G_S(M) for M (relative to S) as a graph containing one node for each column in M, and an edge connecting two nodes i and j if and only if columns i and j conflict relative to S. It is easy to see that G_S(M) = G(M) if S ∈ M, and so G_S(M) = G(M + S). Figure 2 shows the incompatibility graph G(M) for M from Figure 1.

Figure 2.

The incompatibility graph G(M) for the sequences M from Figure 1, and a fully-decomposed phylogenetic network that derives M. This network is also a galled-tree for M.

A “connected component” (or “component” for short), C, of a graph is a maximal subgraph such that for any pair of nodes in C there is at least one path between those nodes in the subgraph. A “trivial” component has only one node, and no edges. The incompatibility graph in Figure 2 has two components. Previously (Gusfield et al., 2004b; Gusfield, 2005a; Gusfield et al., 2007, 2004a; Bafna and Bansal, 2004), the non-trivial connected components of the conflict and incompatibility graphs were shown to be very informative, used both to derive efficient algorithms and to expose combinatorial structure in phylogenetic networks. The structural importance of the non-trivial connected components is further developed in the main result, presented next.

2.3 The Decomposition Theorem

Theorem 1

Let G(M) be the incompatibility graph for M. Then, there is a phylogenetic network that derives M where every blob in contains all and only the sites of a single non-trivial connected component of G(M), and every compatible site is on a tree edge of . The result holds no matter what constraints, if any, are placed on the number of crossovers allowed at a recombination node.

Stated another way, for any input M, there is a blobbed-tree that derives M, where the blobs are in one-one correspondence with the non-trivial connected components of G(M), and if b_C is the blob corresponding to component C, then b_C contains all and only the sites in C. We call a network “fully-decomposed” if it has the structure specified in Theorem 1. Figure 2 shows a fully-decomposed network for the sequences M from Figure 1.

Theorem 1 is an extension of the stronger theorem proved in Gusfield et al. (2004b) about galled-trees. In the case of galled-trees, every reduced galled-tree for M must be fully-decomposed. A galled-tree is “reduced” if every recombination cycle contains some incompatible sites. When there is a galled-tree for M, there is a reduced galled-tree for M, and it can be found in polynomial time (Gusfield et al., 2004b; Gusfield, 2005a). This strong decomposition property of galled-trees was one of the main motivations for investigating decomposition in general phylogenetic networks and the general role of connected components of G(M) in decomposition.

It is easy to prove (Gusfield et al., 2004b) a statement converse to Theorem 1: In any phylogenetic network that derives M, all sites from the same non-trivial connected component of G(M) must appear on the same blob in , and this does not depend on the number of crossovers used at recombination node. That is, it is not possible to split up the sites from a connected component of G(M) into two or more blobs in . Therefore the network that is guaranteed by the Decomposition Theorem is as highly decomposed into distinct blobs as possible, justifying the term “fully-decomposed”.

There is an analogous theorem to Theorem 1 in the case that the ancestral sequence S is known in advance. In that case, there is a phylogenetic network that derives M, with ancestral sequence S, where the blobs in are in one-one correspondence with the non-trivial connected components of G_S(M), and any non-conflicting site is on a tree edge of ; again, no further decomposition is possible. This follows from Theorem 1, and the fact that two sites conflict relative to S if and only if they are incompatible in M + S.

We will prove the Decomposition Theorem in the next section and show that the tree parts of any fully-decomposed phylogenetic network are invariant.

3 Proof of The Decomposition Theorem

In this section we prove Theorem 1.

3.1 The structure of M

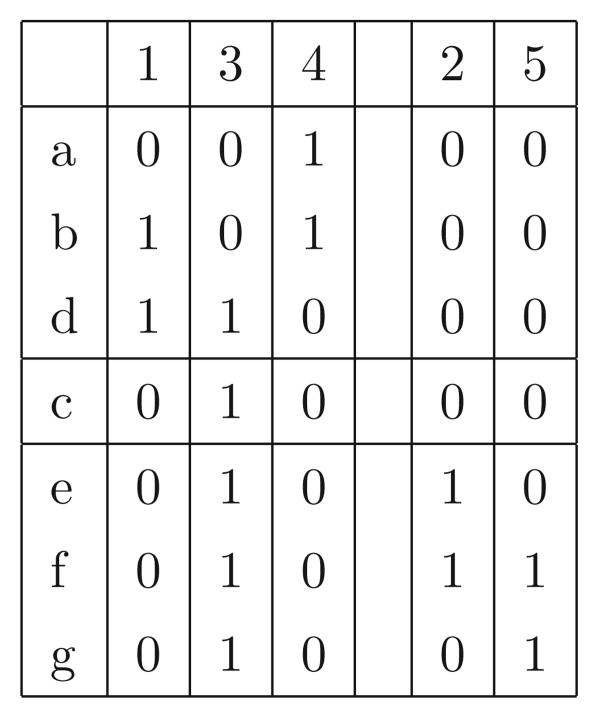
Let C and C′ be two distinct connected components in the incompatibility graph G(M), and assume first that C is non-trivial. C′ might be a trivial connected component, i.e., consist of only a single node. For any pair of sites i ∈ C, i′ ∈ C′ let (X, X̅) and (Y, Y̅) be the respective bipartitions (of the rows of M), associated with sites i and i′. The two bipartitions cannot be identical, for otherwise sites i and i′ would have exactly the same incompatibilities and so be in the same connected component. Each of the four subsets X, X̅, Y, Y̅ is called a “class” of the bipartition it is part of. Sites i and i′ are not incompatible, so one class of the i bipartition must strictly contain one class of the i′ bipartition, and the other class of the i′ bipartition must strictly contain the other class of the i bipartition. Without loss of generality, suppose X ⊃ Y and Y̅ ⊃ X̅. We say that X is the “dominant” class of i, and X̅ is the “dominated” class, with respect to the pair i, i′. Similarly, Y̅ is the dominant class of i′, and Y is the dominated class, with respect to the pair i, i′. For example, in Figure 2, C = {1, 3, 4} and C′ = {2, 5}, and with respect to the pair 1, 2, the set {a, c, e, f, g} is the dominant class, and {b, d} is the dominated class.

Now consider the case that sites i and i′ are the sites of two trivial components C and C′. If i and i′ are not identical, then one class of i, say X, must strictly contain a class, say Y, of i′, and so X and Y̅ are again the well-defined dominant classes of i and i′, with respect to i, i′. If sites i and i′ are identical, and say X = Y, then we arbitrarily choose the pair X, Y̅ or X̅, Y as the two dominant classes of i and i′ respectively.

Lemma 1

Let i, i′, C, C′, X, and Y be as above. Let j′ be any site in C′, and let (Z, Z̅) be the bipartition associated with j′. Then, the dominant class of i with respect to the pair i, j′ is the dominant class of i with respect to the pair i, i′.

Proof

The Lemma is vacuously true if C′ is a trivial connected component, so assume C′ is non-trivial. We need to show that either X ⊃ Z or X ⊃ Z̅. Consider a site k′ ∈ C′ that is incompatible with i′. Such a site k′ must exist since C′ is connected. Let (W, W̅) be the bipartition defined by site k′. If X is not dominant with respect to i, k′, then X̅ is dominant with respect to i, k′, and so either X̅ ⊃ W or X̅ ⊃ W̅. Suppose that X̅ ⊃ W̅, so W ⊃ X. But then W ⊃ Y since X ⊃ Y, and so Y ∩ W̅ = ∅, and i and k′ can't be incompatible, which is a contradiction. Similarly, if X̅ ⊃ W, then W̅ ⊃ X, so W̅ ⊃ Y, and W ∩ Y̅ = ∅, a contradiction. So the dominant class, X, with respect to i, i′ is the dominant class with respect to i, k′, where k′ is any site that is incompatible with i′. The Lemma now follows by transitivity, because C′ is a connected component, so from i′ it is possible to reach any j′ ∈ C′ by a series of incompatibility relations.

Lemma 1 establishes that for any i ∈ C, one class of i is dominant with respect to all sites in C′, and symmetrically, for any i′ ∈ C′ one class of i′ is dominant with respect to all sites in C. So, with respect to the (C, C′) pair of connected components, each site in C ∪ C′ has a well-defined dominant class, and a well-defined dominated class.

Now return focus to the sequences in M and the sites in C and C′. For a site i ∈ C, the bipartition (X, X̅) is encoded with 0's and 1's, where all the rows in X have one character at site i and all the rows in X̅ have the other character at site i. So, with respect to the (C, C′) pair of connected components, and a specific set of sequences M, each site in C has a well-defined dominant character (either 0 or 1). For example, in Figure 3, the dominant character is 0 in all sites except 3, where the dominant character is 1.

Figure 3.

The sites in the two connected components from Figure 2. We denote the component with sites {1, 3, 4} as C, and the component with sites {2, 5} as C′. The dominant sequence for C is 010, and the dominant sequence for C′ is 00. The rows in D[C, C′] are {a, b, d}, and the rows in D[C′, C] are {e, f, g}. The rows and columns have been permuted from their natural order to collect together the sites in the two components, and the rows in D[C, C′] and D[C′, C]. Note that row c is in neither D[C, C′] nor D[C′, C], since row c has the dominant sequence in both its C and C′ sides.

Let D[C, C′] be the union of the rows in the dominated classes of C, with respect to (C, C′). Similarly, let D[C′, C] be union of the rows in the dominated classes of C′, with respect to (C, C′). For example, D[C, C′] is {a, b, d} and D[C′, C] is {e, f, g} in Figure 3.

Let M(C) and M(C′) be the sequences in M, restricted to the sites in C and C′ respectively. Then Lemma 1 implies

Theorem 2

Every row in D[C, C′] has the same sequence in M(C′). In particular, in each row of D[C, C′], every site i′ ∈ C′ has the dominant character with respect to (C, C′). Similarly, every row in D[C′, C] has the same sequence in M(C). In particular, in each row of D[C′, C], every site i ∈ C has the dominant character with respect to (C, C′).

Given Theorem 2, we can define the dominant sequence in M(C) with respect to (C, C′) as the sequence in M(C) where each site has the dominant character with respect to (C, C′). Similarly, we can define the dominant sequence in M(C′) with respect to (C, C′).

Corollary 1

Let C and C′ be two connected components of G(M). There is no row in M which (w.r.t. (C, C′)) contains both a non-dominant sequence in M(C) and a non-dominant sequence in M(C′).

Figure 3 illustrates Lemma 1, Theorem 2 and Corollary 1. Note that a row can have both the dominant sequence in M(C) and the dominant sequence in M(C′). Row c in Figure 3 is an example of this. Corollary 1 is a more refined version, and with a simpler proof, of a result (Theorem 3) first proved in Bafna and Bansal (2004).

We develop here an observation that will be needed in Section 5.2. Consider two sites i ∈ C and i′ ∈ C′, where C and C′ are two distinct non-trivial connected components of G(M). By assumption, every column contains both a 0 and a 1. Also, any two columns in different non-trivial components must not be identical (or exact compliments of each other) or else they would both be incompatible with the same sites in C and C′, and hence would be in the same component. So, there must be at least three distinct pairs of binary characters in columns i, i′. But, since i and i′ are not incompatible, there cannot be four distinct pairs binary characters in those columns, so there must be exactly three distinct pairs of binary characters in columns i, i′. Hence, if we add new sequences to M, creating the set M̅, and i and i′ are not incompatible in M̅, then any pair of binary characters in M̅ in columns i, i′, must already have been a pair of binary characters in columns i, i′ in M. Therefore, with respect to (C, C′), the dominant characters in C and C′ created from M are the same as the dominant characters of C and C′ created from M̅. Extending this observation to all sites in C and C′ we have:

Lemma 2

Suppose C and C′ are non-trivial components of G(M). If we add new sequences to M which do not create any incompatibilities between sites in different components of G(M), then with respect to (C, C′), the dominant sequences of C and C′ remain unchanged.

3.2 The super-characters of M and the new matrix B

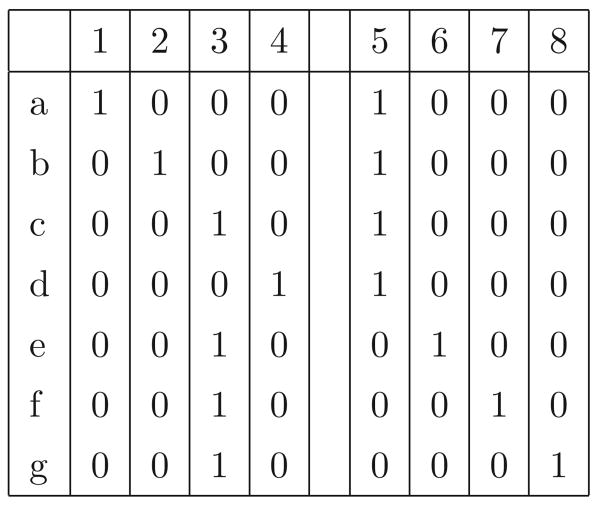
Lemma 1, Theorem 2 and Corollary 1 establish a structure that exists in M, imposed by the partition of the columns of M by the connected components of G(M). We begin now to exploit that structure to prove the Decomposition Theorem. We define a new set of binary sequences B created from M and G(M), and represent the set B as a matrix, as follows. Let C be a connected component of G(M) and let M(C) be the sequences in M restricted to the sites in C. We call each distinct sequence in M(C) a super-character of M (associated with C). For every C, we create one column, s in B for each super-character S of M, where S ∈ M(C). We say that s originates from S and from C. Each such column in B encodes a bipartition of the rows of M where one side of the bipartition contains all the sequences in M that contain subsequence S in M(C), and the other side of the bipartition contains the remaining sequences. More specifically, and without loss of generality, in the new column we assign value 1 to each sequence in M which contains subsequence S in M(C), and assign value 0 to each sequence that does not. The new column defines a binary character derived from M and G(M). Note that if C is a trivial connected-component, so it only contains one site, then B will have two columns derived from that one site, but those columns define the same bipartition. That will cause no problems, and one column can be removed for simplicity. As an example, Figure 4 shows the matrix B that is derived from M and G(M) from Figure 2.

Figure 4.

Matrix B derived from M and G(M) from Figure 2. The super-characters of M associated with C are 001, 101, 010, 110, and the super-characters of M associated with C′ are 00, 10, 11, 01. The columns (characters) of B are ordered to correspond to those ordered lists of super-characters of M.

We will use the characters of B to build a tree in order to prove Theorem 1.

Lemma 3

No pair of characters of B are incompatible.

Proof

Let p and q be distinct characters in B. If p and q originate from the same connected component C in G(M), then by construction, no row can have a 1 in both columns p and q and therefore, characters p and q are not incompatible.

Now suppose p and q originate from two different connected components C and C′ in G(M). If p and q both originate from the non-dominant sequences (w.r.t. (C, C′)) of C and C′, then Corollary 1 guarantees that there is no row with 1, 1 in columns p and q, and so p and q cannot be incompatible. Symmetrically, if p and q both originate from dominant sequences (w.r.t. (C, C′)) of C and C′, then there is no row with 0, 0 in columns p and q. If p originates from the dominant sequence (w.r.t. C, C′) of C and q originates from a non-dominant sequence (w.r.t. C, C′) of C′, then there can be no 0, 1 in columns p and q. The remaining case is symmetric.

Applying the Perfect Phylogeny Theorem, Lemma 3 establishes that there is a perfect phylogeny T̅ where each character of B labels one edge in T̅, and each edge is labeled by one or more characters of B. Since each character of B originates from a super-character of M, it will sometimes also be useful to think of edge labels as being super-characters of M.

3.3 Inflating T̅

The next step is to inflate nodes of T̅ to blobs in order to create a fully-decomposed phylogenetic network for M, proving Theorem 1.

The removal of any edge e in T̅ creates two connected subtrees, and we define a “split of edge e” as the bipartition of the leaves resulting from the removal of edge e from T̅. From the facts that all columns in B are distinct, and that every edge in T̅ is labeled, it follows that all the splits defined by the edges in T̅ are distinct. If e is labeled by character c of B, we define the “1-side” of e as the subtree of T̅ − e that contains the leaves for rows in B that have value 1 for character c. The other side is called the “0-side” of the split. When no root sequence has been specified in advance, the root could be on either side of the split.

Lemma 4

Let C be an arbitrary component of G(M). In T̅, there is a node v_C such that all the edges labeled by characters of B that originate from connected component C, are incident with v_C. That is, these edges form a star around a single central node v_C. Further, v_C is on the 0-side of each split defined by an edge labeled by a character of B that originates from C.

Note however, that Lemma 4 does not assert that v_C is only incident with edges labeled by characters that originate from C.

Proof

First, the Lemma is trivially true if C is a trivial component since only one character originates from C and it labels only one edge. For any non-trivial connected component C, the submatrix M(C) contains at least four distinct sequences since there are must be at least one (incompatible) pair of sites in C where all four binary pairs appear in M(C). Therefore, there are at least four characters in B that originate from C. Let B(C) denote the columns of B restricted to the characters that originate from C.

Consider a non-trivial connected component C and any three of characters of B that originate from C, and let e₁, e₂, e₃ be the three edges in T̅ labeled with those characters. Note that every row in B has value 1 in exactly one column of B(C), so every leaf of T̅ is on the 1-side of exactly one edge labeled by a character from C. Hence, no leaf in T̅ can be on the 1-side of two of the edges e₁, e₂, e₃.

Now, consider the undirected tree created by ignoring the directions of the edges in T̅, but we will still refer to this undirected tree as T̅. If e₁ and e₂ are incident with each other, sharing a node v, then there must be another edge incident with node v, and hence there must be a leaf l_v that is reachable from v without going through e₁ or e₂. If this were not true, then e₁ and e₂ would define the same splits in T̅, which is not possible. If e₁ and e₂ are not incident with each other, then there is a unique shortest path P from an endpoint of e₁ to an endpoint of e₂. Clearly, path P does not contain edge e₁ or e₂. There must be a node v on P and a leaf l_v that is reachable from v via a path that does not go through e₁ or e₂. If this were not true, then again there would be two adjacent edges that define the same splits in T̅.

Now we claim that node l_v must be on the 0-side of both e₁ and e₂. We have already established that it cannot be on the 1-side of both. However, suppose without loss of generality, that l_v is on the 1-side of e₁ and the 0-side of e₂. Then consider the endpoint u of e₂ that is on the 1-side of e₂, and consider a leaf l_u that is reachable from u without going through e₂. Leaf l_u would be on the 1-side of both e₁ and e₂, which is not possible. Hence the 1-sides of both e₁ and e₂ point “away” from each other. It also follows that path P cannot go through edge e₃. If it did, then some leaf on the 1-side of e₃ would also be on the 1-side of e₁ or e₂.

So edges e₁ and e₂ are either incident with each other, or there is an edge e which is incident with e₁ on path P, where e is not labeled by a character of B that originates from C. We will show that such an edge e cannot exist. Every internal edge in T̅ is labeled by some character of B, so suppose e exists and is labeled by a character that originates from a connected component C′. Let v be the common endpoint of e₁ and e. As above, there must be a leaf l_v that is reachable from v without going through either edge e or e₁, for otherwise e and e₁ define the same split, which is not possible. Recall that each character of B and each split in T̅ that originates from C or C′, corresponds to a sequence (super-character) in M(C) or M(C′), and with respect to the pair (C, C′), there is a dominant sequence S in M(C) and a dominant sequence S′ in M(C′). Let e(S) be the edge in T̅ labeled by the character that originates from S, and let e(S′) be the edge in T̅ labeled by the character that originates from S′. Now e₁ is either e(S) or not, and e is either e(S′) or not, so we have four cases to consider.

Case 1

Suppose e₁ is e(S) and e is e(S′). We know that l(v) is on the 0-side of e₁, so it must be on the 1-side of e by Corollary 1. But then, all leaves on the 0-side of e will be on the 0-side of both e and e₁, which contradicts Corollary 1. So e cannot exist in this case.

The three other cases are similar and omitted, and the result is that e cannot exist and hence e₁ and e₂ are incident with each other. Since e₁ and e₂ were arbitrary edges labeled by characters that originated from C, every pair of edges labeled by characters that originate from C must be incident with each other. But in a tree, that is only possible if all those edges share exactly one endpoint, and so form a star around a single center. That endpoint is the claimed node v_C. We also established that if there are two distinct edges labeled with characters that originate from C, then the 1-sides of these edges point away from each other. This holds for any pair of edges labeled with characters that originate from C, so v_C is on the 0-side of every such edge.

3.4 Completion of the proof of the Decomposition Theorem

To finish the proof of the Decomposition Theorem, we first ignore the direction of the edges of T̅ and ignore which node is its root. Instead, we arbitrarily select a node v_r of T̅ to be the root and direct all the edges in T̅ away from that chosen root. Let S be the label written at node v_r (recall that a perfect phylogeny is a phylogenetic network and so each node is labeled). The label S will define the ancestral sequence for the phylogenetic network we will construct. Next, we need to inflate each node v_C in T̅ that is the central node of the star associated with the characters obtained from a non-trivial component C of M(G). Note that v_r might also be a central-star node. We can identify the central-star node v_C by the fact that for the non-trivial connected component C, all of the edges labeled by the characters that originate from C are incident with v_C. Each such edge may also be labeled with characters that originate from another connected component or with a compatible character. Now, each central-star node v_C, other than the root node, has exactly one edge directed into it; the character on it that originates from C must be the super-character S(C), defined as sequence S restricted to the sites in C. We call S(C) the “ancestral sequence” of v_C. Similarly, if the root node is associated with the non-trivial component C, then S(C) is the ancestral sequence of v_r = v_C. Now, any super-character in M that is associated with C can be derived from S(C) using at most one mutation per site, if an unlimited number of recombination nodes are allowed. This is true even if only single-crossovers are allowed, or if multiple-crossovers are permitted¹. So, each central-star node v can be inflated into a blob b_v containing one node labeled by each super-character in M(C), and other nodes if needed. Then for each super-character associated with C, we connect the node in b_v labeled with the character c in B which originates from that super-character, to the edge incident with v_C that is labeled by character c.

After inflating each central-star node in T̅, the end result is a phylogenetic network where each blob contains all and only the sites from one connected component of G(M). Every compatible site labels a tree edge of . The full ancestral sequence for is specified by the ancestral sequences defined above, since each site in M is in the ancestral sequence for exactly one central-star node. This completes the proof of Theorem 1.

Note that the existence and the topology of T̅ depends only on the partition of the nodes of G(M) into connected components, and hence does not depend on the biological causes of the incompatibilities in M. In particular, it does not depend on whether or not multiple-crossovers are allowed at recombination nodes. However, the networks inside each blob of do depend on which biological events (such as single versus multiple-crossover recombination, or recurrent mutation, etc.) occur there.

3.5 Component-wise optimal decomposition

We can now state a fact that follows easily from Theorem 1 and will be needed in Section 5.2. Recall that S(C) is the sequence S restricted to the sites in component C. Let R_S(C)(M(C)) be the minimum number of recombination nodes (events) needed to generate the sequences M(C) in a phylogenetic network with ancestral sequence S(C), when multiple-crossover recombination is allowed. Similarly, let $R_{S(C)}^1(M(C))$ be the minimum number of recombination nodes needed when only single-crossover recombination is allowed. The proof of Theorem 1, when applied to the set of sequences M + S, where S is a required ancestral sequence (which might not be in M), and the root of T̅ is selected to be the node labeled S, establishes the following:

Theorem 3

For any sequence S, there is a fully-decomposed phylogenetic network for M with ancestral sequence S, containing exactly Σ_C∈Gs(M)R_S(C)(M(C)) recombination nodes when multiple-crossover recombination is allowed, and containing exactly $\sum _{C\in G_s(M)}{R}_{S(C)}^1(M(C))$ recombination nodes when only single-crossover recombination is allowed.

3.6 Programs

The proof of the existence of T̅ can be converted into an efficient, constructive method² for finding T̅ from any input M. The program galledtree.pl, available at wwwcsif.cs.ucdavis.edu/∼gusfield/ takes in a set of sequences M and tries to build a galled-tree for M using single-crossover recombination. If it succeeds, then it has produced a complete phylogenetic network for M where each blob is a single cycle, and the cycles are node disjoint. Hence, the program produces a fully-decomposed phylogenetic network for M. If the program determines that there is no galled-tree for M, then it outputs the tree T̅ for M. The running time for the program is O(nm² + m³), but the time used to build T is just O(nm²).

3.7 Uniqueness of T̅

In a network , we say that a node v in blob b is an external node if there is an edge from v to some node outside of b. We say a phylogenetic network is efficient if does not contain two external nodes with the same node labels, and for each external node v (in a blob b), there is exactly one edge from v to a node off of b. Clearly, if is not efficient, it can be easily modified to become efficient without increasing the number of recombinations used. Also, if is fully-decomposed, then the efficient network derived from it is also fully-decomposed. So for any M, there is a efficient fully-decomposed phylogenetic network for M.

Theorem 4

If is any efficient fully-decomposed network for M, and T′ is created by contracting each blob of to a single node, then after the directed edges in T′ are made undirected, the resulting tree is necessarily the tree T̅ defined in the proof of Theorem 1.

Proof

Consider a blob b_C in associated with the component C in G(M); let v be an external node in b_C incident with the edge e = (v, v′), directed from v to a node v′ off of b_C. In the subnetwork reached from v′, all of the sites in C have the same state they have at v′. This is because no site in C mutates outside of b_C, and (by induction on the maximum path length from from v′ to a recombination node x) at any recombination node x in the subtree, the state of any site in C is the same at x as it is in both of the parent sequences of x. Now every super-character in M(C) is a subsequence of some sequence of M, and the super-characters include all the distinct sequences in M(C), therefore (when restricted to the sites in C) each external node on b_C is labeled with a distinct super-character derived from C, and each super-character derived from C labels exactly one external node of b_C. Consider again node v, labeled with super-character S_v(C) from M(C), and consider the edge e = (v, v′). If we remove edge e from , two disconnected subnetworks are created. In one subnetwork, every leaf label contains S_v(C), and in the other subnetwork, no leaf label contains S_v(C). The leaf labels are the sequences of M, and so the removal of e from creates a bi-partition of the sequences in M. Clearly then, edge e defines exactly the same bi-partition of the sequences in M that is defined by the split K in T̅ created by removing from T̅ the edge labeled by the character that derives from super-character S_v(C). Now edge e is also contained in tree T′, and its removal from T′ creates the same bi-partition that it does in , and so the removal of e from T′ creates the split K. Therefore, the splits in T′ are exactly the same as the splits in T̅. By Theorem 3.1.4 (the Splits Equivalence Theorem) in Semple and Steel (2003), the splits of an undirected tree uniquely define the tree, and so the undirected trees, T′ and T̅ are identical.

In other words, T̅ is the invariant underlying structure of any efficient fully-decomposed phylogenetic network for M, and this is true regardless of the biological causes of the incompatibilities in M. We will need this fact in Section 5.1.

3.8 Alternate Proofs of Theorem 1

Theorem 1 was first stated and proved in Gusfield and Bansal (2005). It has been pointed out (Steel, 2005) that Theorem 1 can also be proven by using Buneman graphs (Semple and Steel, 2003), and the details of this approach have been verified (Wu, 2005). However, the proof here is more direct and establishes a polynomial time algorithm to construct T̅. In contrast, it takes exponential time in worst case to build a Buneman graph from M, and so that is not an efficient constructive approach to building T̅ from M. Another direct proof of Theorem 1 that is shorter than the one presented here, but does not establish or emphasize the role of super-characters, appears in a 2006 preprint by Bafna and Bansal (2006b). Subsequent to the development of Theorem 1, a related decomposition theorem was developed (Huson et al., 2005) where the input to the problem is not a set of sequences, but a set of trees that must be subtrees in a constructed phylogenetic network.

4 Broader Applications

4.1 Alternate causes of incompatibility

In the proof of the Decomposition Theorem, there was no mention of recombination until close to the end of the proof, when discussing the inflation of the central-star nodes. Therefore, all the results proven to that point hold for any incompatible characters of M, independent of the biological cause of the incompatibilities. Also, the proof of uniqueness did not depend on recombination. Hence, the existence, structure and uniqueness of T̅ holds for any M and any biological cause of incompatible characters. In this way, we have established that the super-characters of M, defined by the connected components of G(M), generalize standard evolutionary characters (used in phylogenetic trees), and play a role in the theory of phylogenetic networks that tree characters play in the theory of phylogenetic trees. Moreover, if the biological operations that caused the incompatibilities in M allow any set of sequences M(C) to be derived from an arbitrary ancestral sequence, then the Decomposition Theorem holds in that biological context.

Another way to see the generality of the results proven here is to note that multiple crossover recombination can be considered as a mathematical operation on binary sequences rather than a biological event, and can be used to model biological events that don't explicitly involve recombination. For example, an occurrence of back-mutation or recurrent-mutation of a site i in a sequence S can be modeled as a two-crossover recombination between S and some appropriate sequence, in the intervals i − 1, i and i, i + 1. Modeling back and recurrent mutations in this way explicitly creates recombination cycles and blobs, and shows explicitly how Theorem 1 applies when back-mutation and/or recurrent mutation cause incompatibilities. Generally, when back or recurrent mutation is the cause of incompatibility, we seek an evolutionary tree that derives a given set of sequences using as few back or recurrent mutations as possible. Such a tree is called a “maximum parsimony tree” and it is a solution to the maximum parsimony problem (Felsenstein, 2004; Semple and Steel, 2003).

4.2 What is the “most tree-like” phylogenetic network?

When a set of sequences M fails the four-gametes test and hence cannot be generated on a perfect phylogeny, one would still like to derive the sequences on a phylogenetic network that is the “most tree-like”. There is no accepted definition of “treeness”, and under many natural definitions, the problem of finding the most tree-like network would likely be computationally difficult. In this section, we introduce a measure of treeness and relate it to Theorem 1.

Recall that it is assumed that in network no two blobs share a node. We can also assume that has no node with in and out-degrees that are both one. Then if each blob is contracted to a single node, the number of edges in the resulting directed tree measures the “treeness” of . In other words, the “treeness” of is measured by the size of the tree in the underlying tree structure of . For example, if all the sites in M are in a single blob in , then is less tree-like than a network where the sites are distributed between several blobs, connected by several edges in a tree structure.

With the above definition of “treeness”, it is clear that a phylogenetic network is “the most tree-like” if and only if T̅ is the resulting undirected tree, after the blobs of are contracted, and all the edges are made undirected. This follows from Theorem 1 and the fact (Gusfield et al., 2004b) that all the sites in a single non-trivial connected component of G(M) must be together in a single blob in any phylogenetic network.

This definition of “most tree-like” is somewhat crude because it does not consider any details inside of a blob, but it has the advantage of being easy to compute and allowing a clear identification of the most tree-like networks. Further, it seems reasonable that any other natural definition of “most tree-like” would identify a subset of the networks identified by the definition considered here.

5 The Full-Decomposition Optimality Conjectures

Clearly, the task of constructing networks is simplified (both algorithmically and conceptually) if we restrict ourselves to fully-decomposed networks, and we have seen above that there always is a fully-decomposed network for any M. But if our goal is to minimize the number of recombination nodes (events) is it effective to restrict ourselves in this way? The answer is yes when M can be derived on a galled-tree, even if the galled-tree must only use single-crossover recombinations, but any competing phylogenetic network is allowed to use multiple-crossovers Gusfield et al. (2004b); Gusfield (2005a). Now, we address this issue in general.

5.1 Introduction to the conjectures

For a set of sequences M, recall that R(M) is the minimum number of recombination nodes in any phylogenetic network for M when multiple-crossover recombination is allowed; R¹(M) is the minimum number when only single-crossover recombination is allowed. We similarly define R_S(M) and $R_S^1(M)$ as the minimum number of recombination nodes in any phylogenetic network for M with ancestral sequence S when, respectively, multiple-crossovers are allowed and when only single-crossovers are allowed. A network that has the minimum possible number of recombination nodes (and conforms to the chosen crossover model and uses the required ancestral sequence, if any) is called “optimal”.

We say that a set of binary sequences M are “min decomposable” or “min-1 decomposable” respectively, if there is a fully-decomposed phylogenetic network for M, allowing multiple-crossovers or only allowing single-crossovers respectively, using exactly R(M) or R¹(M) recombination nodes respectively.

Similarly, a set of binary sequences M are “S-min decomposable” or “S-min-1 decomposable” respectively, if there is a fully-decomposed phylogenetic network for M with ancestral sequence S, allowing multiple-crossovers or only allowing single-crossovers respectively, using exactly R_S(M) or $R_S^1(M)$ recombination nodes respectively.

In Gusfield and Bansal (2005) we stated the Full-Decomposition Optimality Conjecture, which we now state more precisely as:

Unrooted Full-Decomposition Optimality Conjectures

Every set of binary sequences is min decomposable and min-1 decomposable.

Rooted Full-Decomposition Optimality Conjectures

Every set of binary sequences is S-min decomposable and S-min-1 decomposable for any ancestral sequence S.

A related version of the unrooted conjecture was also recently stated (as Conjecture 1) in (Huson and Klopper, 2007). These (four) conjectures say that there is no loss of optimality in restricting attention to fully-decomposed phylogenetic networks. Note that the rooted conjectures imply the original unrooted conjectures, by letting S be the ancestral sequence that appears in the optimal phylogenetic network using R(M) (respectively R¹(M)) recombination nodes. Hence, we will later restrict attention to the rooted versions of the conjecture when proving positive results, and restrict attention to the unrooted versions of the conjectures when proving negative results. The rooted conjectures are equivalent to the conjectures that R_S(M) = Σ_C∈GS(M)R_S(C)(M(C)) and $R_S^1(M)=\sum _{C\in G_s(M)}{R}_{S(C)}^1(M(C))$. However the unrooted conjectures are not equivalent to the stronger statements that R(M) = Σ_C∈G(M)R(M(C)) and R¹(M) = Σ_C∈G(M)R¹(M(C)). The reason is that the optimal solutions for the separate components may choose different ancestral sequences that cannot be combined into a single network. For example, consider the set of sequences M shown in Figure 5. The incompatible pairs are (1, 3), (1, 4), (2, 3), (2, 4), (5, 7), (5, 8), (6, 7), (6,8), so there are two connected components in G(M): component C₁ containing the first four sites of M, and component C₂ containing the last four sites of M. We can establish, using the program beagle (Lyngso et al., 2005), that R¹(M(C₁)) = R¹(M(C₂)) = 1, but R¹(M) = 3.

Figure 5.

Example showing that R(M) > Σ_C∈G(M)R(M(C)).

In Gusfield and Bansal (2005), we also stated that when the recombination events only model recurrent and back mutations (as detailed in Section 4.1), then every M is min decomposable. We will establish a specialization of this fact with a direct proof below; the general statement follows from results on the maximum parsimony problem using median networks, as established by Bandelt et al. (1995) (see also Semple and Steel 2003). Because of this result, when incompatibilities are caused by recurrent and/or back mutation, one can solve the maximum parsimony problem exactly for each set M(C) separately, and then connect the trees as specified by T̅. Since the maximum parsimony problem is NP-hard and the only known methods to solve it take exponential time in worst-case, decomposing the problem into several smaller problems may allow larger problems to be solved in practice.

In general, whenever M is min decomposable (or S-min, min-1, or S-min-1 decomposable) we can follow a similar approach to finding phylogenetic networks that minimize the number of recombination nodes. This is easiest to explain when M is S-min or S-min-1 decomposable. Then, T̅ is constructed from M + S, S is chosen as the root sequence of T̅, and for each C ∈ G_S(M), S(C) is the ancestral sequence for the blob associated with component C. Hence we can solve a single (rooted) problem for each set M(C) and then connect the trees as specified by T̅. More generally, even if M is not S-min or S-min-1 decomposable, this method will find the minimum number of recombination nodes, denoted F_S(M) and $F_S^1(M)$, used in any fully decomposed network for M with ancestral sequence S, respectively allowing multiple-crossover or allowing only single-crossovers.

The approach is a bit more involved when no ancestral sequence is known in advance. Suppose we choose an interior node v in T̅ to be the root of T̅. That selection determines the ancestral sequence for each blob in the phylogenetic network constructed from T̅, and induces a rooted problem for each connected component, except for the blob b_v and component C_v, associated with node v. However, unlike the situation in the proof of Theorem 1 where the label on v can be used for the ancestral sequence of b_v, we now have to be more careful in selecting the ancestral sequence for b_v. To determine the ancestral sequence for b_v, and hence for the entire phylogenetic network (when v is chosen as root of T̅), we determine the minimum number of recombination nodes needed to derive M(C_v) (obeying the chosen crossover model) allowing any possible ancestral sequence. Then, the best ancestral sequence for the phylogenetic network is found by repeating the above computation for each interior node v in T̅, choosing as the root the node yielding the minimum number of recombinations. The procedure can obviously be sped up by taking advantage of repeated computations.

Even if M is not min-decomposable or min-1 decomposable, the procedure above will correctly compute F(M) or F¹(M), which are defined as the minimum number of recombination nodes used in any fully decomposed network for M, allowing multiple crossover or only single-crossover recombination, respectively. The correctness of the procedure follows from Theorem 4 and the fact that placing the root of T̅ at a leaf or on the interior of an edge will not reduce the number of required recombinations in the resulting network.

When the appropriate conjecture holds for an input M, we can also compute lower bounds on R(M), R¹(M), R_S(M) and $R_S^1(M)$ by computing bounds separately for each M(C), adding these bounds together for a valid overall lower bound. This is correct no matter what lower bound method is used.

5.2 Natural Sufficient Conditions for M to be S-min or S-min-1 decomposable

Recall that when M is S-min (respectively S-min-1) decomposable for all S, then M is min-decomposable (respectively min-1 decomposable), and hence we focus here on the rooted versions of the Full-Decomposition Optimality Conjecture. We will prove several sufficient conditions that guarantee that rooted conjectures hold, and therefore also establish combinatorial properties that counterexamples to the conjectures must possess. In a phylogenetic network for M, L denotes the set of node labels used in . By definition, M ⊆ L. We say that a node is “visible” if it is labeled with a sequence in the input M. So, when L = M (in the unrooted case) or L = M + S (in the rooted case), every node in is visible. The main results we will prove are:

Theorem 5

Let be an optimal phylogenetic network for M with ancestral sequence S, allowing multiple-crossover recombination (respectively allowing only single-crossover recombination), using R_S(M) (respectively $R_S^1(M)$) recombination nodes. Let G_S(L) be the conflict graph for sequences L with respect to S. Then M is S-min (respectively S-min-1) decomposable if G_S(M) and G_S(L) have the same number of connected components.

Theorem 5 says that M will be S-min (respectively S-min-1) decomposable unless every optimal phylogenetic network for M, with ancestral sequence S, allowing multiple-crossovers (respectively only allowing single-crossovers) has nodes whose labels, when added to M, causes significant changes to G_S(M). “Significant” here means a change in the number of connected components.

Corollary 2

Let be an optimal phylogenetic network for M with ancestral sequence S, allowing multiple-crossover recombination (respectively allowing only single-crossover recombination). Then M is S-min (respectively S-min-1) decomposable, if every node in is visible.

Since network in Corollary 2 must be an optimal network, and in practice it may be hard to know that a network is optimal, Corollary 2 may be hard to apply in practice. However, we can prove the following more applicable, but somewhat weaker result:

Theorem 6

Let be a phylogenetic network (which might not be optimal) for M with ancestral sequence S. Then M is S-min or S-min-1 decomposable (depending on the type of crossovers used in ), if every node in is visible, and every edge in is labeled by at most one site.

We now begin to prove Theorem 5, Corollary 2, and Theorem 6. Recall that for any sequence Z and connected component C, Z(C) is Z restricted to the sites in C. Let h be a recombinant sequence created by the recombination of parent sequences h₁ and h₂.

A recombination event (or node) in a network is defined to be a 0-component recombination if for every component C ∈ G_S(M), h(C) = h₁(C) or h(C) = h₂(C). Similarly, a recombination event (or node) is defined to be a 1-component recombination if there is exactly one component C ∈ G_S(M) such that h(C) ≠ h₁(C) and h(C) ≠ h₂(C).

In other words, in a 0-component recombination, the recombinant sequence h, restricted to the sites of any single connected component of G_S(M), is identical to at least one of its parent sequences. Note however that in a 0-component recombination, the full sequence h can differ (and will in an optimal network) from both of its parent sequences. In a 1-component recombination, the above identity property fails for exactly one connected component of G_S(M). Note that the definitions of 0-component and 1-component recombination are independent of any constraints on the number of crossovers allowed. One could define a general notion of k-component recombination, but the above two definitions are sufficient for the following central lemma.

Lemma 5

Let be an arbitrary phylogenetic network for M with ancestral sequence S, and suppose that every recombination in is either a 0 or 1-component recombination. Let R( ) denote the number of recombination nodes in . If multiple-crossover recombinations are allowed in , then

$$R(\mathcal{N})\ge \sum _{C\in G_s(M)}{R}_{S(C)}(M(C)),$$

and if only single-crossover recombinations are allowed, then

$$R(\mathcal{N})\ge \sum _{C\in G_s(M)}{R}_{S(C)}^1(M(C)).$$

Proof

We first define a map f from the 1-component recombination nodes in to the connected components of G_S(M). Let v be any 1-component recombination node in , and let h, h¹, h² be the recombinant and parent sequences respectively at v. Since there is exactly one connected component C* ∈ G_S(M) for which h(C*) ≠ h¹(C*) and h(C*) ≠ h²(C*), we define the map f(v) of node v to component C*. Now, consider any recombination node v′ in that is not mapped to component C*. Restricted to the sites in C*, the recombinant sequence at node v′ must be identical to the sequence of one of its parents, because either v′ is a 0-component recombination or a 1-component recombination node which is mapped to a component other than C*. Therefore, if we remove all such recombination nodes from , and also remove any site that is not in C*, the resulting network is a phylogenetic network _C* that derives the set of sequences M(C*). Network _C* has ancestral sequence S(C*) and every recombination node in _C* is a 1-component recombination that maps to C*. By definition of optimality, the number of recombination nodes in _C*, denoted R( _C*), is at least R_S(C*)(M(C*)). Now, since each recombination node in is mapped to at most one component,

$$R(\mathcal{N})\ge \sum _{\mathcal{C}\in {\mathcal{G}}_{\mathcal{S}}(\mathcal{M})}\mathcal{R}(\mathcal{N}\mathcal{C})\ge \sum _{\mathcal{C}\in {\mathcal{G}}_{\mathcal{S}}(\mathcal{M})}{\mathcal{R}}_{\mathcal{S}(\mathcal{C})}(\mathcal{M}(\mathcal{C})).$$

Theorem 7

Let be a phylogenetic network for M with ancestral sequence S such that every recombination node in is either a 0 or 1-component recombination node, relative to G_S(M). Then there is fully-decomposed phylogenetic network ′ for M, with ancestral sequence S, using at most R( ) recombination nodes, where both and ′ allow the same type of recombinations (single-crossover only or multiple crossover).

Proof

This follows directly from Lemma 5 and Theorem 3.

Corollary 3

When recombinations only model back or recurrent mutations (as detailed in Section 4.1), then M is S-min decomposable for any sequence S, and the maximum parsimony problem for M can be solved by separately solving a maximum parsimony problem for the sites from each connected component of G_S(M).

Proof

Consider the tree T(M) with ancestral sequence S that solves the maximum parsimony problem when S is the required ancestral sequence and back and recurrent mutations are allowed. Let be the phylogenetic network that implements the same derivation from S, using recombinations (as detailed in Section 4.1) to model the back or recurrent mutations. Each recombination event is a two-crossover recombination where the two crossovers occur just before and just after a single site i in a connected component C ∈ G_S(M). Therefore, for every connected component C′ ≠ C, the recombinant sequence is identical to one of its parent sequences at the sites in C′, and so the recombination event is either a 0-component or a 1-component recombination, and Theorem 7 applies.

5.2.1 Spatial disjointness is a sufficient condition

Let {1, 2… m} denote the given ordering of the sites of M, and let S by a given sequence. M is said to be “spatially disjoint” if for every connected component C of G_S(M), the sites in C form a contiguous interval in the ordered set of sites.

Theorem 8

Given S, if M is spatially disjoint, then M is S-min-1 decomposable.

Proof

Let be phylogenetic network for M, with ancestral sequence S, using R¹(M + S) single-crossover recombinations. Since M is spatially disjoint, a single-crossover falls either within the interval of sites for a single connected component of G_S(M), or between two such intervals. In the former case, the recombination must be either a 0 or a 1-component recombination, and in the latter case, the recombination must be a 0-component recombination. The theorem then follows from Theorem 7.

Note that Theorem 8 is proven only for the case of single-crossover recombination.

5.2.2 Component respect is a sufficient condition

Recall that for a phylogenetic network , L is the set of sequences that label the nodes of . If the addition of the sequences L − M to M + S does not create any incompatibilities between sites in different components of G_S(M), then we say that L respects (the component structure of) G_S(M). Since M + S ⊆ L, any incompatible pair in M + S is incompatible in L, so L respects G_S(M) if and only if G_S(L) and G_S(M) have the same number of components, although they need not be identical graphs. Also, if all nodes in are visible, then L = M + S, and so L trivially respects G_S(M).

Theorem 9

Let be a phylogenetic network for M with ancestral sequence S, and suppose that L respects G_S(M). Then there is fully-decomposed phylogenetic network ′ for M, with ancestral sequence S, using at most R( ) recombination nodes, where and ′ allow the same type of recombinations (single-crossover only or multiple crossover).

Proof

Consider a recombination in between sequences h₁ and h₂ resulting in recombinant sequence h. We will show that this recombination is a 0-component or a 1-component recombination with respect to the components of G_S(M). If it is not a 0-component or a 1-component recombination, then there must be two connected components C_a and C_b in G_S(M) such that h(C_a) ≠ h₁(C_a), h(C_a) ≠ h₂(C_a), h(C_b) ≠ h₁(C_b), and h(C_b) ≠ h₂(C_b). We will show that no such pair of connected components exists.

Consider a trivial connected component C in G_S(M). Since C consists of just one site, if h₁(C) ≠ h₂(C) then h(C) = h₁(C) or h(C) = h₂(C), and if h₁(C) = h₂(C) then h(C) = h₁(C). In either case, C can be neither C_a nor C_b. So if C_a and C_b exist, they must both be non-trivial connected components in G_S(M).

Consider two non-trivial connected components C and C′ in G_S(M), and let d_C be the dominant sequence in M(C) with respect to (C, C′), and let d_C′ be the dominant sequence in M(C′) with respect to (C′, C). Now L respects G_S(M), so by Lemma 2, Corollary 1 applies to the sequences L, and hence either h(C) = d_C, or h(C′) = d_C′, or both. We will examine the case that h(C) = d_C (the other case is symmetric and omitted). If either h₁(C) = d_C or h₂(C) = d_C, then C is neither C_a nor C_b. Conversely, if neither h₁(C) nor h₂(C) is d_C, then by Corollary 1, h₁(C′) = h₂(C′) = d_C′, and h(C′) = d_C′ no matter where any crossovers occur in the recombination of h₁ and h₂. In that case, C′ is neither C_a nor C_b. Hence from the assumptions that L respects G_S(M) and that C and C′ are non-trivial components of G_S(M), we have established that the pair C, C′ cannot be the (unordered) pair C_a, C_b. Therefore, the pair C_a, C_b cannot exist, and so the recombination must be a 0-component or a 1-component recombination with respect to G_S(M). The theorem then follows by applying Theorem 7.

Theorem 5 and Corollary 2 follow immediately. Corollary 2 was proven with a more complex proof in Gusfield (2005b). One application of Theorem 5 is to the recently introduced non-degenerate galled-networks (Huson and Klopper, 2007). It is easy to prove that for any non-degenerate galled-network for M, a pair of sites is incompatible in L if and only if it is incompatible in M, and therefore G(L) and G(M) are identical.

5.2.3 The tight haplotype bound is a sufficient condition

Recall that M is assumed to have no identical rows. The following lower bound on R¹(M), called the haplotype bound and denoted H(M), was developed by Myers and Griffiths (2003): H(M) equals the number of rows of M, minus the number of distinct columns of M, minus one. Although originally proved for single-crossover recombination, the same proof establishes that H(M) is also a lower bound on R(M). The haplotype bound is computed on M + S when an ancestral sequence S is specified. Let be an optimal phylogenetic network for M, with ancestral sequence S. From the proof given in Myers and Griffiths (2003) (or see Song et al. 2005) that H(M + S) is a lower bound on R¹(M + S), it follows that H(M + S) = R( ) = ℛ^∞(ℳ + ) (or R(M + S)) only when every node in is labeled by a sequence in M + S. Hence, when the haplotype bound is tight for the appropriate crossover model, every node in must be visible and we can apply Corollary 2 to obtain:

Theorem 10

For a set of sequences M and a specified ancestral sequence S, if H(M + S) = R¹(M + S) then M is S-min-1 decomposable, and if H(M + S) = R(M + S) then M is S-min decomposable.

We can also now provide the

Proof of Theorem 6

First, we can modify , while maintaining the conditions of the theorem, so that does not contain two recombination nodes labeled by the same sequence, and for any non-recombination node v with a directed, labeled (by a site) edge into v, the sequence labeling v does not label any other node. Then, since every node in is visible and each edge is labeled by at most one site, R( ) must be exactly the number of sequences in M + S, minus the number of labeled edges in , minus 1. But, the number of labeled edges in is greater than or equal to the number of distinct sites in M, so R( ) ≤ ℋ(ℳ + ), and R( ) = ℋ(ℳ + ). Therefore, H(M + S) = R¹(M + S) if only uses single-crossover recombination, and H(M + S) = R(M + S) if uses multiple-crossover recombination. Theorem 6 then follows from Theorem 10.

5.3 The Full-Decomposition Optimality Conjectures are False

In this section we show that the Unrooted Full-Decomposition Optimality Conjectures are false, which also implies that the rooted versions are false. This also establishes that Conjecture 1, recently stated in Huson and Klopper (2007), is false. We also show that there is no bound on the deviation between R^l(M) and F^l(M) (the minimum number of single-crossover recombination nodes needed in a fully-decomposed network for M); but in the simulations we conducted, counterexamples are rare, and deviations are small.

5.3.1 The single-crossover case

Consider the 6 by 6 matrix M shown in Figure 6. Its incompatibility graph G(M) consists of two connected components C₁ and C₂, shown on the right hand side of Figure 6. It is easy to see that R¹(M(C₁)) ≥ 2 and R¹(M(C₂)) ≥ 2. For example, the HK lower bound (Hudson and Kaplan, 1985) on R¹(M(C₁)) is 2 as is the HK lower bound on R¹(M(C₂)). (In fact, R¹(M(C₁)) = R¹(M(C₂)) = 2, but this is not needed.) Certainly then, F¹(M) ≥ 4. However, R¹(M) ≤ 3 (as shown in Figure 7), so F¹(M) > R¹(M), showing that the single-crossover case of the Unrooted Full-Decomposition Optimality Conjecture is false.

Figure 6.

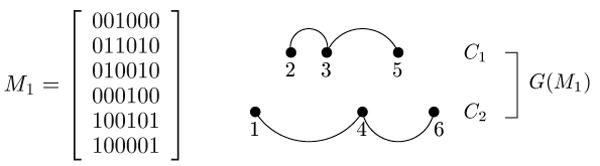
A 6 by 6 binary matrix M and its incompatibility graph G(M), consisting of two connected components C₁ and C₂.

Figure 7.

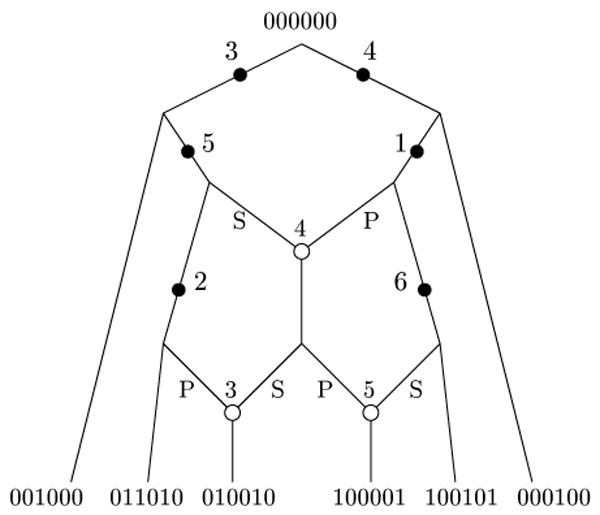
A phylogenetic network for the sequences in Figure 6. Closed and open circles denote mutation and recombination events, respectively.

Note that in the example in Figure 6, every pair of columns already contains the binary pair 0,0, so if we add the ancestral sequence S = 000000 to M, no additional incompatible pairs would be created and so G_S(M) = G(M). Then, since $R_S^1(M(C_k))\ge R^1(M(C_k))$ for k = 1, 2, the example also explicitly shows that the single-crossover case of the rooted version of the Full-Decomposition Optimality Conjecture is false. Note also, that the first recombination creates the sequence 100010; when it is added to M, sites 1 and 5 become incompatible, changing the number of connected components in G_S(M) as required by Theorem 9. This counterexample is also consistent with Theorems 8 and 10, since the sites of the two components are not spatially disjoint, and also the haplotype of one is not tight.

5.3.2 The multiple-crossover case

Figure 8 shows a set of sequences M whose incompatibility graph (not shown) contains two connected components C₁ and C₂. Any phylogenetic network for M(C₁) that uses multiple-crossover recombinations, requires at least two recombination nodes. This was verified by running program multicross.pl, available at http://wwwcsif.cs.ucdavis.edu/gusfield/ and described in Gusfield (2005a). Program multicross.pl determines whether or not a set of sequences can be generated on a galled-tree using multiple-crossover recombination; the program determined that M(C₁) cannot be so generated. Since a network with one recombination node is a galled-tree, the fact that M(C₁) cannot be generated on a galled tree using multiple-crossover recombination (and it can't be generated with zero recombinations) proves that at least two multiple-crossover recombinations are required. Similarly, we used multicross.pl to verify that any network that generates M(C₂) requires at least two multiple-crossover recombinations. It follows that for the sequences M given in Figure 8, F(M) ≥ 4. Figure 9 shows a phylogenetic network that generates M with only three recombination nodes, using multiple-crossover recombination. Hence, the unrooted, multiple-crossover version of the Full-Decomposition Optimality Conjecture is false.

Figure 8.

Counterexample to the unrooted multiple-crossover version of the Full-Decomposition Optimality Conjecture. The incompatibility graph contains two connected components. One component contains sites 1 through 5, and the other contains sites 6 through 10.

Figure 9.

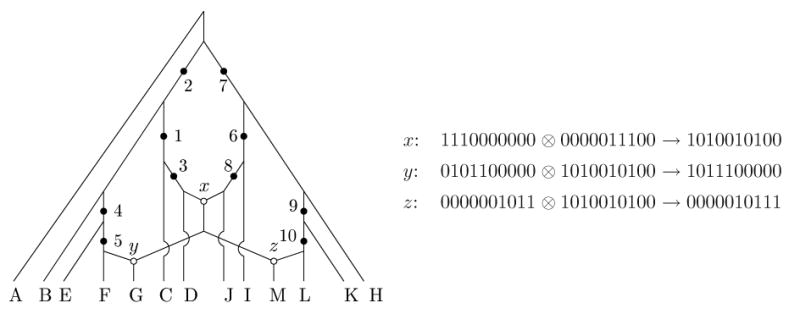
A phylogenetic network, with all-zero ancestral sequence, generating the sequences in Figure 8, allowing multiple-crossover recombination. Filled circles denote mutations and open circles denote the recombination nodes x, y, z. The parental and recombinant sequences at those three nodes are shown in detail. The symbol ⊗ denotes recombination. Note the recombination event at node y uses only a single-crossover, while multiple-crossovers are used at nodes x and z.

5.3.3 Unbounded Deviation

Recall that F¹(M) denotes the minimum number of single-crossover recombination nodes used in any fully decomposed phylogenetic network for M.

Theorem 11

For any positive integer d, there exists a set of sequences M such that F¹(M) − R¹(M) ≥ d.

Proof

Clearly, F¹(M) ≥ Σ_C∈G(M)R¹(M(C)), so it suffices to show that there exists a set of sequences M such that [Σ_C∈G(M) R¹(M(C))] − R¹(M) ≥ d. Let M_d be the 6 by 6d matrix obtained by concatenating d copies of M from Figure 6 as follows:

$$M_d=[MM···M].$$

In other words, M_d contains d repetitions of uxyvxu, where

$$x=\left[\begin{array}{l}0\hfill \\ 1\hfill \\ 1\hfill \\ 0\hfill \\ 0\hfill \\ 0\hfill \end{array}\right],y=\left[\begin{array}{l}1\hfill \\ 1\hfill \\ 0\hfill \\ 0\hfill \\ 0\hfill \\ 0\hfill \end{array}\right],u=\left[\begin{array}{l}0\hfill \\ 0\hfill \\ 0\hfill \\ 0\hfill \\ 1\hfill \\ 1\hfill \end{array}\right],v=\left[\begin{array}{l}0\hfill \\ 0\hfill \\ 0\hfill \\ 1\hfill \\ 1\hfill \\ 0\hfill \end{array}\right].$$

There are two connected components, C₁ and C₂, in G(M_d), the first only containing columns of type x or y, and the second only containing columns of type u or v. It is straightforward to show that

$$R^1(M_d(C_1))=R^1(M_d(C_2))=2d.$$

Therefore, R¹(M_d(C₁)) + R¹(M_d(C₁)) = 4d. We next show that R¹(M_d) ≤ 3d, which will prove the theorem.

A rooted tree T is said to be compatible with a column i in M, if there is some edge in T whose removal creates one subtree with leaves labeled by all the rows with state 0 in column i, and one subtree with leaves labeled by all the rows with state 1 in column i. For example, tree T_y in Figure 10 is compatible with every column of type y in M_d. A rooted tree T is said to be time-ordered if each internal node v in T can be assigned a numerical “time” t_v, so that the times strictly increase along any directed path from the root. In Figure 10, the times of the nodes are represented by the heights of the nodes, with higher nodes representing smaller (earlier) times. Given a time-ordered tree T, a subtree-prune-and-regraft (SPR) operation removes (prunes) one edge e in T, and reconnects (regrafts) the subtree τ below e to some point in T, using a new edge e′ to connect the root of τ to T. In an ordered-SPR operation, the times assigned to all the nodes in τ must remain the same, and the resulting tree must also be time-ordered. It follows that the point where edge e′ connects to T must be earlier in time than the time assigned to the root of τ. See Song (2006a) for a more detailed definition of an ordered-SPR operation.

Figure 10.

Three leaf-labeled time-ordered trees with 6 leaves.

Given two time-ordered trees T and T′ with the same number of leaves, d_oSPR(T, T′) denotes the minimum number of ordered-SPR operations needed to transform T into T′. For example, in Figure 10, tree T_y is transformed to T_v by using one ordered-SPR operation which cuts the subtree consisting of leaves 3 and 6, and then grafts it into the edge leading to leaf 2. Given a length-l sequence P = T₁, T₂…, T_l of time-ordered leaf-labeled trees with n leaves, we define $L(P)={\sum }_{i=1}^{l-1}{d}_{\text{oSPR}}(T_i,T_{i+1})$. The following fact was established in Song and Hein (2005): For any n by m matrix M, if P = T₁, T₂,…, T_m is a sequence of time-ordered leaf-labeled trees in which T_i is compatible with site i in M, for all i = 1,…, m, then R¹(M) ≤ L(P).

We can now show that R(M_d) ≤ 3d. Consider the three time-ordered leaf-labeled trees shown in Figure 10. Note that T_ux is compatible with both columns u and x, T_y with column y, and T_v with column v. Let P_d be the length-6d sequence of trees containing d repetitions of P₁ = T_ux T_ux T_y T_v T_ux T_ux. Then, since d_oSPR(T_ux, T_y) = d_oSPR(T_y, T_v) = d_oSPR(T_v, T_ux) = 1, we obtain L(P_d) = 3d ≥ R^l(M_d).

5.4 Empirical Study

To obtain some indication of how often the single-crossover Unrooted Full-Decomposition Optimality Conjecture is violated in practice, we carried out an small simulation study using the program beagle (Lyngso et al., 2005) which implements a branch and bound strategy to exactly compute R¹(M).

We determine if a given set of sequences M is a counterexample to the conjecture as follows. We first find the tree T̅ from M, and then compute F^l(M) as detailed in Section 5.1. We use beagle to solve each of the rooted and unrooted problems that arise in that computation, and to compute R^l(M). As detailed in Section 5.1, the procedure for computing F^l(M) is correct, and so M is a counterexample to the single-crossover, Unrooted Full-Decomposition Optimality Conjecture if and only if the computed value F^l(M) is strictly greater than R^l(M).

Let ρ := 4 _ec, where _e denotes the effective population size and c the recombination rate per generation per sequence. For fixed n, m, and ρ, we used Hudson's program MS (Hudson, 2002) to generate 10,000 n by m simulated data sets generated under the coalescent model with recombination. Table 1 gives a summary of the number of times (out of 10,000) that a counterexample was identified. (Note that we could not consider large data sets since beagle cannot compute the minimum number of recombinations for large data sets.) As the table shows, counterexamples occur infrequently in the data that we examined. In these eight counterexamples, R¹(M) ranges from three to nine; F¹(M) is always R(M) + 1; and G(M) always has two non-trivial connected components. Of course, we do not know how robust these empirical results are in other ranges of data, or to multiple-crossover recombination, or when there is a fixed ancestral sequence.

Table 1.

The frequency of data sets (out of 10, 000) where a counterexample to the Full-Decomposition Optimality Conjecture was observed.

n	m	ρ	#datasets with k ≥ 2	#counterexamples
15	20	10	389	0
15	30	10	465	2
20	20	10	527	0
20	30	10	546	3
15	20	15	372	1
15	30	15	388	1
20	20	15	482	1
20	30	15	396	0

The variable k denotes the number of non-trivial connected components in the incompatibility graph. We used Hudson's MS (Hudson, 2002) to simulate n by m data sets for given recombination rate ρ.