Dimerization between aequorea fluorescent proteins does not affect interaction between tagged estrogen receptors in living cells

Abstract

Förster resonance energy transfer (FRET) detection of protein interaction in living cells is commonly measured following the expression of interacting proteins genetically fused to the cyan (CFP) and yellow (YFP) derivatives of the Aequorea victoria fluorescent protein (FP). These FPs can dimerize at mM concentrations, which may introduce artifacts into the measurement of interaction between proteins that are fused with the FPs. Here, FRET analysis of the interaction between estrogen receptors (alpha isoform, ERα) labeled with “wild-type” CFP and YFP is compared with that of ERα labeled with “monomeric” A206K mutants of CFP and YFP. The intracellular equilibrium dissociation constant for the hormone-induced ERα-ERα interaction is similar for ERα labeled with wild-type or monomeric FPs. However, the measurement of energy transfer measured for ERα-ERα interaction in each cell is less consistent with the monomeric FPs. Thus, dimerization of the FPs does not affect the kinetics of ERα-ERα interaction but, when brought close together via ERα-ERα interaction, FP dimerization modestly improves FRET measurement.

1 Introduction

Molecular interactions within the cell are a central component of life. Tracking those dynamic interactions and determining the activities, structure, and function of the subsequent complexes form the basis of modern biochemistry. Biochemical interactions between ligands and receptors, factors and cofactors, enzymes and substrates, or the myriad of sequential complexes formed throughout a biologic process, traditionally have been studied through analysis of the interactions and activities of purified proteins or complexes in test tubes. These reductionist approaches have been extremely valuable in identifying components of biologic pathways as well as important biochemical details about the processes themselves. However, there always is some concern that the processes identified will be substantively different in living cells, where the availability of still unknown factors and/or the physiologic environment or concentration of the factors will affect the biochemical response.

A key step toward tracking biochemical events in living cells was the cloning of the visible fluorescent proteins (FP).¹ Because these are fluorescent molecules that double as proteins, the cDNAs for the FPs can be spliced together with the cDNA for any protein of interest.² The spliced cDNA then can be introduced into any cell type and expressed as a “fusion” protein. Provided that the attachment of the FP does not affect the normal biologic function of the protein of interest, FP tagging enables the tracking, by fluorescence microscopy, of specific molecules within living cells.^2-5 Following an FP-tagged protein in a living cell over time has proved to be a tremendous asset in understanding the cell biology of a protein and, together with the development of fluorescence bleaching and fluorescence correlation techniques, has provided invaluable insight about the transit of the protein complexes through the cell.^3-7

The characterization of the first green FP was followed by the discovery and development of additional FPs with unique excitation and emission profiles.^8-15 These developments permitted multiple FP-tagged proteins to be tracked simultaneously within a single cell.^3-6 It also offered the opportunity to obtain genuine biochemical information about a complex in living cells through the application of Förster resonance energy Transfer (FRET) measurements between FPs attached to interacting proteins.^4,6,15-18 FRET measures energy transferred from a high energy “Donor” fluorophore [typically the cyan FP (CFP) or its derivatives] to a lower energy “Acceptor” fluorophore [typically the yellow FP (YFP) or its derivatives].^19-23 The amount of energy transfer drops dramatically with the sixth power of the distance between the fluorophores,^22,23 such that, for CFP and YFP, FRET can be detected efficiently only if the FPs are well within 80 Å of each other;²⁴ for comparison, a domain within a typical protein commonly is in the range of 25 to 50 Å across. Thus, FRET is detected if the FPs are attached to proteins that interact with each other or are present in a common complex or cell structure that places the FPs very close to each other.

The amount of FRET between two FP-tagged proteins will be affected by the distance between and alignment of the dipoles of the FP.^19-23 This provides information about the structure of the interacting complex. In addition, the amount of FRET will be affected by the extent to which the FP-tagged proteins interact.^4,25-31 Thus, the kinetics of interaction between the factors affects the FRET signal. Analytical methods have been developed that dissect the interactive and structural components of the FRET signal from each other.^4,25,27 These techniques apply standard biochemical concepts of the kinetics of interaction to the FRET output. The measurements obtained are analogous to biochemical parameters classically defined in the test tube, except they are measured in living cells.

Most of the native FPs isolated to date naturally exist as oligomeric complexes for which extensive mutagenesis has produced monomeric FPs.^8,31 The first FPs to be cloned, the aequorea FPs, are predominantly monomeric but also can dimerize at mM concentrations.³¹ Experience from many laboratories shows that the weak interaction between the aequorea FPs is not sufficient to drive their interaction in the cell in the absence of attaching them to interacting proteins or to proteins that cluster very tightly in the cell. However, recent reports suggest some benefit of the FP interaction: structural sensors consisting of CFP and YFP derivatives attached to the same molecule show higher levels of energy transfer if these aequorea-derived FPs retain their weak dimerization ability.^32,33 Thus, dimerization between the FPs may enhance the FRET signal. This raises a concern that, for FRET measurement of interactions between two FP-labeled factors, the interaction between two proteins may bring dimerization-competent FPs into a high enough local concentration to impact the kinetics of interaction between the proteins being studied.

To determine whether, and how, FP dimerization may affect the measurement of protein interaction via FRET, we directly compared the kinetics of interaction between two proteins labeled with dimerization-competent CFP and YFP and their strongly monomeric “A206K”³¹point mutants (mCFP and mYFP). For these studies, we investigated the interactions between the alpha isoform of the human estrogen receptor (ERα). We and others previously showed that the addition of estradiol (an estrogen) to cells coexpressing CFP and YFP-labeled ERα caused CFP and YFP to become close enough to permit energy transfer.^25,27,34 ERα dimerization was likely responsible for this energy transfer, since point mutation of three amino acids within the known ERα dimerization interface disrupted the estradiol-dependent acquisition of FRET.²⁵ The current studies show that the ERα interaction kinetics measured by FRET were not impacted by the use of dimeric or monomeric FPs.

2 Materials and Methods

2.1 Expression of Fluorescent-Protein-Tagged ERα and Calibration Standards in Living Cells

ERα was tagged at its carboxy terminus with enhanced CFP or with enhanced YFP as previously described.²⁵ The A206K mutation, which abrogates the weak dimerization interface in the aequorea-derived FPs³¹ was introduced into the ERα-CFP and ERα-YFP constructs using point mutagenesis. Throughout the text, ERα labeled with either wild-type (dimeric) or A206K (monomeric) ECFP and EYFP is abbreviated as ERα-CFP, ERα-YFP, ERα-mCFP, and ERα-mYFP, respectively. The cDNA expression vectors for the calibration standards, consisting of ECFP and EYFP fused to the amino and carboxy termini, respectively, of the androgen receptor (AR) were previously described.²⁷ The H874Y, T877A, and T877S mutants in this “CFP-AR-YFP” expression vector were previously described.²⁷ The V715M mutant was introduced by point mutagenesis. The ERα, AR, and FP cDNAs within the ERα-FP and CFP-AR-YFP expression vectors were sequenced to ensure that only the desired mutations were inserted.

Human cervical carcinoma HeLa cells were grown in six-well dishes on 22×22-mm number 1 borosilicate cover glasses in cell culture media stripped of small lipophilic hormones (including estrogens and androgens) by charcoal treatment.²⁵ Three wells of HeLa cells were transfected, using 10 μl of Lipofectamine 2000 (Invitrogen Corporation, Carlsbad, California), with a combined 1280 ng of the expression vector for ERα-CFP and with 2720 ng of the expression vector for ERα-YFP. Parallel cotransfection of the monomeric ERα-mCFP and ERα-mYFP expression vectors were conducted. Three wells of control cells were transfected with 1280 ng of one of the ERα-CFP, ERα-YFP, ERα-mCFP, and ERα-mYFP expression vectors together with 2720 ng of carrier vector (Rc-CMV, Invitrogen). 1000 ng of each CFP-AR-YFP calibration control, and their associated AR-CFP and AR-YFP bleed-through controls, similarly were transfected in HeLa cells using Effectene (Qiagen Incorporated, Valencia, California), then split into six wells for ligand treatment.

The transfected cells were grown overnight to allow expression of the ERα-FP or CFP-AR-YFP fusion proteins as previously described.^25,27 The next day, the coexpressing and control ERα-FP cells were treated with 10⁻⁸ M estradiol (two wells) or an equivalent amount of drug delivery vehicle (ethanol, one well). Cells were imaged live on the cover glass in a 10-min window from 30 to 40 min following estradiol or ethanol addition. Prior temporal FRET measurements in our laboratory showed that interaction between the ERs was complete within 15 min of estradiol addition (t_1/2 =4.7 mins).^25,27 Each of the six wells of CFP-AR-YFP-expressing cells were treated with one of 10⁻⁹ M dihydrotestosterone, 10⁻⁷ M hydroxyflutamide, 10⁻⁶ M casodex, 10⁻⁷ M estradiol, 10⁻⁷ M progesterone, or drug delivery vehicle (ethanol) for one hour prior to image collection. Prior temporal FRET studies showed that the conformation change of CFP-AR-YFP induced by ligand was complete within this time (t_1/2=3.5 mins).²⁷

2.2 Image Collection and Automated Object Identification

The microscope equipment and the “acceptor,” “donor” and “FRET” filter sets used for imaging were as previously described.^25,27-29 Four images [see Figs. 1(a)–1(d)] were collected at a 12-bit depth for each field using a 20× /0.75 NA air objective at the following integration times: Fig. 1(a), 1.00× acceptor image (200 ms); Fig. 1(b), 0.25× acceptor image (50 ms); Fig. 1(c), 1.00× donor image (200 ms); and Fig. 1(d), 0.50× FRET image (100 ms). Variable integration times for the acceptor channel permitted FRET to be examined under a wide range of acceptor amounts, which is a key consideration in FRET analysis of two interacting factors.^{4,25,27,28,35} Each image was background subtracted using a background image specific for each collection condition; the background images were created by averaging at least ten images of cover glasses containing only media (no cells). Imaging of the CFP-AR-YFP calibration controls was conducted similarly, except that the corresponding integration times were 300, 75, 300, and 150 ms (1.00× acceptor, 0.25×accceptor, 1.00× donor, and 0.50× FRET).

Fig. 1.

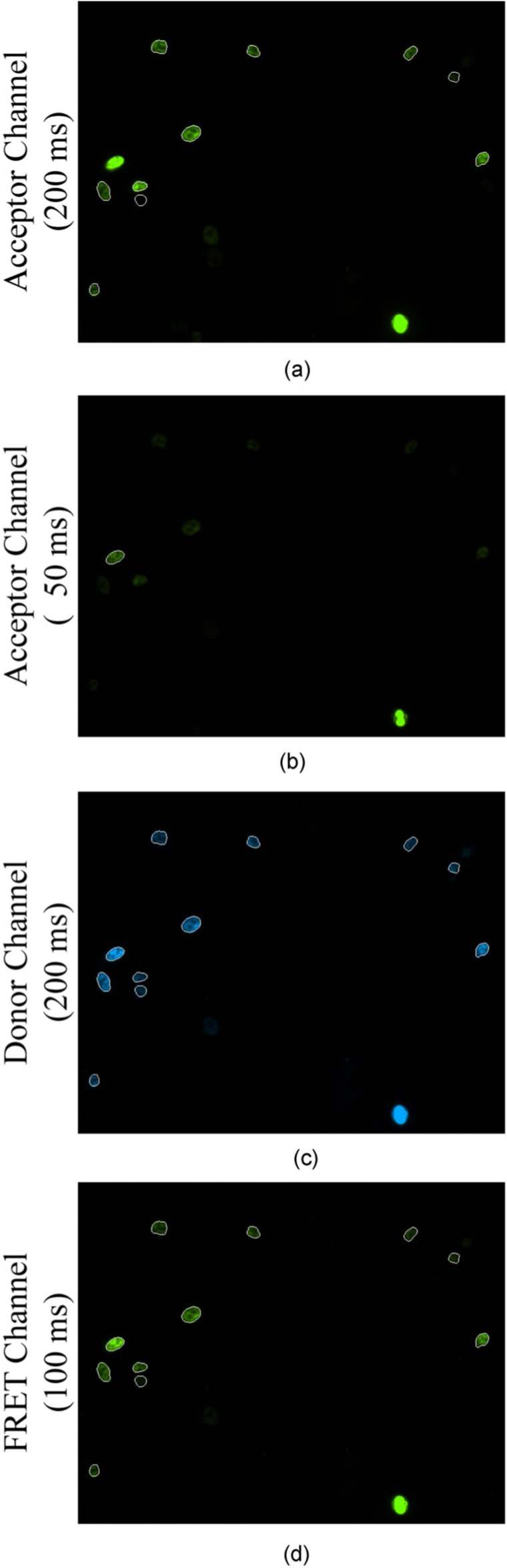
Image collection and region of interest assignment. Four channels were collected per field: (a) Acceptor channel collected at 200 ms. (b) Acceptor channel collected at 50 ms. (c) Donor channel collected at 200 ms. (d) FRET channel collected at 100 ms. ROIs containing any saturated pixels were deleted. The ROIs remaining are shown as white outlines in this example. ROIs were used from the 200-ms acceptor channel except when there were saturated pixels in that channel. In that case, acceptor ROIs were taken from the 50-ms acceptor channel and the associated intensity multiplied by four to obtain accurate acceptor measurements.

Background subtraction and all steps following were processed automatically using the Metamorph 7.0 imaging program (Molecular Devices, Downingtown, Pennsylvania). Objects containing contiguous donor fluorescence above background were identified using the Count Nuclei application in Metamorph (minimum and maximum object widths set at 12 and 24 μm; minimum intensity above local area set at 100 fluorescence units). Those regions of interest (ROI) were transferred to the original 1.00× acceptor, 0.25× acceptor, 1.00× donor and 0.50× FRET images. ROIs containing any saturated pixels in the 0.25× acceptor, 1.00× donor, or 0.50× FRET images were deleted. Of the nonsaturated ROIs, the average intensity in the background-subtracted 1.00× donor and 0.50× FRET images were downloaded into an Excel file (Microsoft Corporation, Redmond, Washington); the intensity in the FRET ROI was multiplied by two to describe fluorescence intensity for an equivalent integration time. The acceptor fluorescence amount was downloaded as the average ROI intensity in the background-subtracted 1.00× acceptor channel (if not saturated) or, if saturated, as four times the average ROI intensity in the 0.25× acceptor image.

The ratio of the average background-subtracted intensity in the 0.25× and 1.00× acceptor images serves as a quality control for image collection and appropriate background subtraction. As an example of the consistency of these quality control measurements, Table 1 shows the mean 0.25× /1.00× ratios (+SD) for all unsaturated ROIs detected in the five experiments presented in this study. This shows the quantitative linearity of the equipment with respect to integration time, the accuracy and robustness of the background subtraction protocol, and the overall consistency and accuracy of the intensity measurements.

Table 1.

0.25×/1.00× average acceptor intensity ratio measurements for studies in Fig. 5. For each experiment, average ratios are presented for each of the ER-YFP and ER-mYFP: −1, acceptor only control cells, −2, acceptor/donor coexpressing cells treated with drug vehicle, and −3, acceptor/donor coexpressing cells treated with estradiol.

	Experiment 1	Experiment 2	Experiment 3	Experiment 4	Experiment 5
ER-YFP-1	0.250±0.002	0.250±0.002	0.255±0.003	0.250±0.002	0.250±0.003
ER-YFP-2	0.250±0.002	0.250±0.002	0.251±0.002	0.247±0.002	0.247±0.002
ER-YFP-3	0.250±0.002	0.250±0.002	0.253±0.003	0.247±0.002	0.248±0.002
ER-mYFP-1	0.251±0.002	0.250±0.002	0.254±0.003	0.250±0.003	0.250±0.003
ER-mYFP-2	0.249±0.002	0.250±0.002	0.252±0.003	0.248±0.001	0.248±0.002
ER-mYFP-3	0.250±0.002	0.249±0.002	0.252±0.003	0.249±0.002	0.249±0.002

2.3 Simple Förster Resonance Energy Transfer Determination: Bleed-Through Control Values

The background-subtracted fluorescence intensities in the acceptor, donor, and FRET channels for each ROI were used to determine the amounts of energy transfer as described previously.^1-5 Briefly, the ERα-CFP, ERα-YFP, ERα-mCFP, and ERα-mYFP control cells establish the bleed-through contributions of the acceptor fluorophore (YFP) alone to the FRET and donor channels, and the contributions of the donor fluorophore (CFP) alone to the FRET and acceptor channels. An example of a bleed-through determination from one experiment is shown in Fig. 2(a). Cells expressing only the CFP-labeled ERα were used to determine the contribution of the CFP (donor fluorophore) into the FRET channel by plotting the average background-subtracted fluorescence intensities for all ROIs in the FRET channel (y axis) against the donor channel fluorescence intensity for the same ROIs (x axis). The good linear fit to this graph indicated the contribution of the donor to the FRET channel that is the value of the slope of that graph (curve fitting was conducted in Prism, GraphPad, San Diego, California). By contrast, the poor fit (low r² values) and zero slope of the graph of the acceptor and donor channel fluorescence intensities were indicative of zero contribution of the donor into the acceptor channel. Similar analysis with cells expressing only the YFP-labeled ER provides the contributions of the acceptor to the donor and FRET channels [Fig. 2(b)]. The slope and r² values from each of the five experiments analyzed in this study are shown in Table 2, which provides an example of the extent to which these control values are reproducible from experiment to experiment. The mean (±SD) bleed-through control values of all five measurements for the ERα, and of all six measurements for the AR calibration studies, are listed in the right-most columns of Table 2.

Fig. 2.

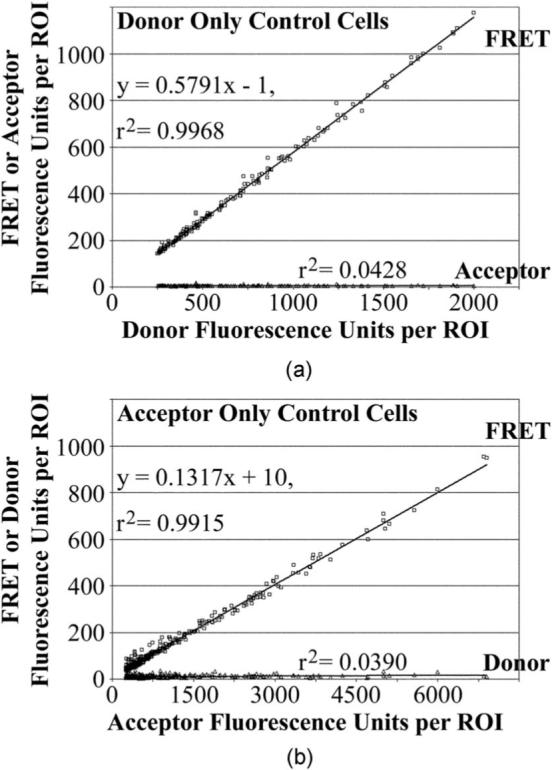
Bleed-through control values determined by linear regression. (a) The amounts of background-subtracted fluorescence from the donor-labeled ERα (CFP or mCFP) in the FRET or acceptor channel in relationship to the donor channel. The r² values indicate whether the data points fall along a straight line. For a linear relationship, the slope of the line represents the bleed-through contributions of the donor to each channel. (b) Similar analysis for the acceptor-labeled ERα (YFP or mYFP). The bleed-through and r² values for each of the five experiments are shown in Table 2.

Table 2.

Contributions of acceptor or donor to each collection channel determined from control cells for experimental studies in Figs. 4 and 5, calibration studies in Fig. 3. (A low r² value and zero slope indicates zero contributions of the fluorescent protein to that channel. Ratios established from plots with high r² values represent fluorescent contributions to the channels relative to that of the fluorescent protein in its cognate channel.)

	ER Experiment 1	ER Experiment 2	ER Experiment 3	ER Experiment 4	ER Experiment 5	Mean ± SD ER studies	Mean ± SD AR studies
	Ratio (r2)	Ratio (r2)	Ratio (r2)	Ratio (r2)	Ratio (r2)	Ratio (r2)	Ratio (r2)
Donor (ER-CFP)
to FRET channel	0.579 (0.997)	0.572 (0.996)	0.577 (0.996)	0.558 (0.997)	0.563 (0.997)	0.570 ± 0.009 (0.997 ± 0.001)	0.563 ± 0.011 (0.988 ± 0.009)
to Acceptor channel	0.001 (0.043)	0.001 (0.048)	0.001 (0.113)	0.000 (0.037)	0.001 (0.072)	0.001 ± 0.000 (0.062 ± 0.031)	0.002 ± 0.001 (0.096 ± 0.070)
Acceptor (ER-YFP)
to FRET channel	0.132 (0.992)	0.133 (0.992)	0.130 (0.983)	0.130 (0.990)	0.132 (0.989)	0.131 ± 0.001 (0.989 ± 0.004)	0.126 ± 0.009 (0.956 ± 0.043)
to Donor channel	0.001 (0.039)	0.003 (0.080)	0.002 (0.022)	0.002 (0.037)	0.001 (0.020)	0.002 ± 0.001 (0.040 ± 0.024)	−0.001 ± 0.002 (0.025 ± 0.035)
Donor (ER- mCFP)
to FRET channel	0.584 (0.996)	0.569 (0.997)	0.582 (0.998)	0.562 (0.996)	0.579 (0.998)	0.575 ± 0.009 (0.997 ± 0.001)
to Acceptor channel	0.001 (0.157)	0.001 (0.059)	0.001 (0.124)	0.000 (0.064)	0.001 (0.157)	0.001 ± 0.000 (0.112 ± 0.048)
Acceptor (ER- mYFP)
to FRET channel	0.127 (0.979)	0.127 (0.992)	0.129 (0.994)	0.127 (0.991)	0.128 (0.989)	0.128 ± 0.001 (0.989 ± 0.006)
to Donor channel	0.001 (0.006)	0.002 (0.047)	0.002 (0.044)	0.001 (0.010)	0.002 (0.031)	0.001 ± 0.001 (0.027 ± 0.019)

2.4 Simple Förster Resonance Energy Transfer Determination: Acceptor Bleed-Through Corrected F/D Ratios

Because the donor CFP does not contribute to the acceptor channel, the fluorescence intensity in the acceptor channel originates solely from YFP. Therefore, in cells expressing both the CFP- and YFP-labeled ERs (or the dual-labeled CFP-AR-YFP), the contribution of YFP to the donor and FRET channels to the ROI can be determined by multiplying the acceptor fluorescence intensity by the appropriate bleed-through control values (zero contribution to the donor channel and 0.1293±0.0022 to the FRET channel, mean ±SD of all ER control measurements). These acceptor bleed-through contributions then are subtracted from amounts of fluorescence in the donor and FRET channels of the same ROI. The remaining fluorescence in the donor and FRET channel originates from the excitation of CFP. If there is no FRET, the amount of fluorescence in the FRET channel relative to the donor channel is exactly the same as in the control cells expressing ERα-CFP alone (0.5725±0.0090). If the ERα-CFP interacts with ERα-YFP and energy is transferred from the CFP to the YFP, fluorescence in the donor channel decreases while fluorescence in the FRET channel increases. Thus, when energy is transferred, the acceptor bleed-through-corrected FRET/donor ratio (F/D) exceeds 0.5725.

2.5 Converting F/D into System-Independent, Energy Transfer Efficiencies

The F/D values are accurate and readily used to compare studies collected on the same equipment, but only when collection parameters such as objectives, camera, filters, mirrors, or excitation light source remain unchanged. The best cross-platform numerical indicator of energy transfer is the proportion of donor energy transferred to acceptor (E, the efficiency of energy transfer).^6-10 Conversion of the F/D ratios measured to E requires an understanding of the fluorescence values collected and correcting the fluorescence values detected in each channel to reflect equimolar amounts of each FP.

The conversion process is described next to facilitate the discussion of our calibrations in the Results in Sec. 3. The conversion process parallels that of Chen et al.,¹⁹ but is stated in modified terms. Acceptor bleed-through correction results in the F/D ratio being a property of the donor itself. Conversion of F/D to E therefore requires knowing the components of the donor contributions to the donor (D) and FRET (F) channels.

The amount of donor collected in the donor channel (D) represents the total amount of donor energy present (Dt) minus the fraction of Dt energy transferred (E). Thus, D=Dt −Dt·E.

The amount of donor detected in the FRET channel (F) has two components.

1. The amount of donor energy transferred to the acceptor (Dt·E) detected in the FRET channel. This is represented by Dt·E·kfaD, in which kfaD is the constant that reflects the ability of the equipment to detect donor energy transferred to the acceptor in the FRET channel relative to the equipment's ability to detect the same amount of donor in the donor channel.

2. The amount of donor energy not transferred to the acceptor (Dt−Dt·E) detected in the FRET channel. This is represented by (Dt−Dt·E)·kfD, in which kfD is the constant that reflects the ability of the equipment to detect donor energy in the FRET channel relative to the equipment's ability to detect the same amount of donor in the donor channel.

The previous considerations therefore describe the FRET/donor ratio measured as

$$F∕D=\frac{Dt\cdot E\cdot kfaD+(Dt-Dt\cdot E)\cdot kfD}{Dt-Dt\cdot E},$$ (1)

In our example [Fig. 2(a)], kfD is the FRET channel bleed-through value measured from the donor-only control cells (i.e., 0.5725, assuming Dt is 1.000). Thus, to use this kfD value, Dt is set as 1.000, which yields the relationship:

$$F∕D=\frac{E\cdot kfaD+(1-E)\cdot kfD}{(1-E)},$$ (2)

which can be rearranged to

$$E=\frac{(F∕D-kfD)}{(F∕D-kfD+KfaD)}.$$ (3)

Once the F/D ratio and kfD constant are known for a specific instrument, only the kfaD remains to be calibrated to calculate E. If E is known for a given set of donor- and acceptor-labeled reference standards, then that E value can be used, together with the measurement of F/D and kfD, to define the kfaD constant on any piece of equipment.³⁶ Such well-characterized FRET reference standards currently exist, at least for the Cerulean and Venus fluorescent proteins, and those standards can be used for calibration when using those two common fluorescent proteins.³⁶

For the studies here, we define a set of CFP- and YFP-labeled FRET reference standards based on a spectrum of FRET values obtained with the Androgen receptor in response to different drugs (Secs. 3.1 and 3.2). For calibration of those standards, we needed to establish kfaD without knowing E. This can be accomplished by using intensity-based methods as previously described¹⁹ and detailed later. For these calibrations, the standard proteins must be dual-labeled with both donor and acceptor (i.e., one CFP and one YFP molecule attached to each protein standard).

With a dual-labeled standard, the total molar amount of donor (Dt) equals the total molar amount of acceptor (At). The ability of an instrument to detect acceptor fluorescence in the acceptor channel relative to the ability to detect fluorescence from an equimolar amount of donor in the donor channel is described by a constant kaD. Therefore, the dual-labeled FRET standards contain equimolar amounts of donor and acceptor, such that the amounts of fluorescence measured in the acceptor channel relative to the donor channel (A/D) are described by:

$$A∕D=\frac{At}{(Dt-E)}\times kaD.$$ (4)

Since the measured acceptor fluorescence (A) is not affected by energy transfer from the donor, it is equivalent to At. By contrast, the measured donor fluorescence (D) decreases from the actual amount of donor (Dt) by the proportion of energy transferred. So, when energy transfer is present, A/D increases, even though the dual-labeled protein has equimolar amounts of acceptor and donor. When Dt is 1.0000 [as in Eq. (3)], At also is 1.000 for the dual-labeled standard and Eq. (4) becomes

$$A∕D=\frac{kaD}{(1-E)},$$ (5)

which can be rearranged to

$$E=\frac{A∕D-kaD}{A∕D}.$$ (6)

Equations (3) and (6) both describe E in terms of the readily measured F/D and A/D values obtained for a dual-labeled FRET standard. Since Eq. (3)=Eq. (6), we can rearrange those equations and define the unknown constants kfaD and kaD according to the equation:

$$F∕D=\frac{kfaD}{kaD}\cdot A∕D+(kfD-kfaD).$$ (7)

This describes a linear relationship (y =mx+b) for a graph of the measured F/D values (y axis) against the measured A/D values (x axis) from a series of FRET reference standards of varying energy transfer levels. This graph defines a line with a y intercept of (kfD−kfaD) and a slope of kfaD/kaD. Since kfD is established from the donor-only control cells (0.5725 in the current example only), kfaD can be readily determined from the y intercept b as:

$$kfaD=-(b-kfD).$$ (8)

Once kfaD is determined, kaD is readily determined from the slope m as:

$$kaD=\frac{kfaD}{m}.$$ (9)

With the calibration values determined using the CFP-AR-YFP calibration standards (Sec. 3.1), the F/D ratios determined for the interaction of ERα-CFP with ERα-YFP were converted into E values using Eq. (3). In our studies of ERα interaction, all amounts of acceptor fluorescence collected are reported after dividing A by kaD. This allows us, for example, to know that 1000 units of calibrated acceptor fluorescence and donor fluorescence (corrected for the amount of donor lost to energy transfer) represent equivalent numbers of molecules.

2.6 Determination of B Max and Kd of Interaction

For each of the five experiments collected, the data points were fit to the curve

$$Y=\frac{B\max \cdot X}{(Kd+X)},$$

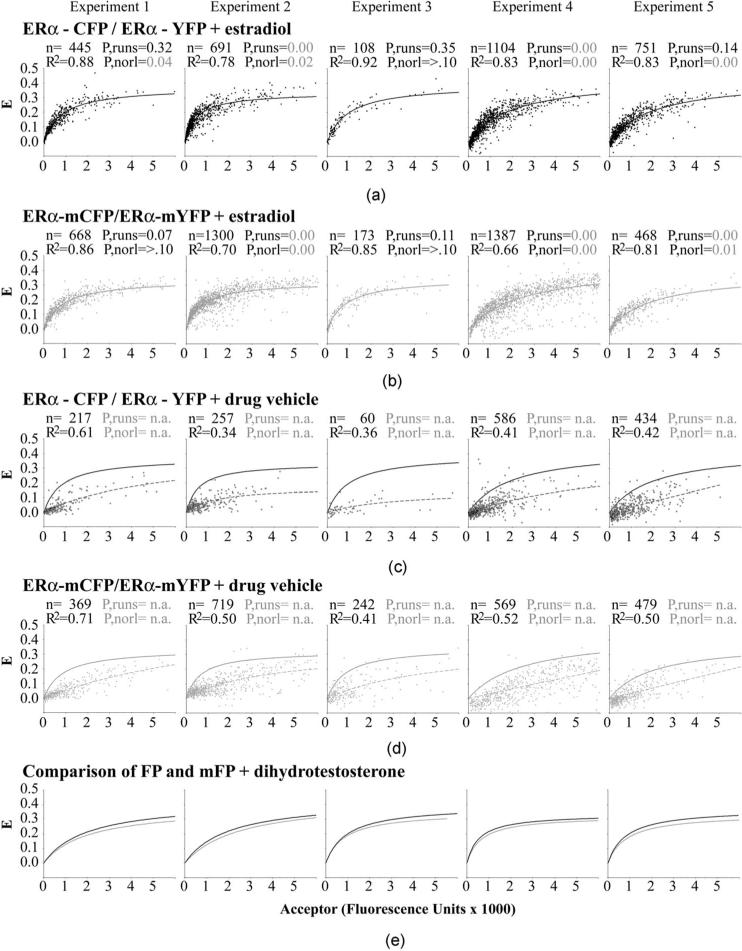
using the nonlinear regression function of Prism (GraphPad). Prism performs curve fitting by using the Marquardt method of nonlinear regression. Curve fitting was conducted (with equal weight to all points and no constrained variables) until the sum of squares from the vertical distance from the curve differed less than 0.0001% variation in three consecutive iterations. A high R² value indicates that the data points are close to the extrapolated curve. A runs test indicates whether there are more stretches of consecutive data points below the curve than predicted by random chance. The failure of a runs test (P, runs <0.05 in Fig. 5) suggests that the curve used does not precisely fit the data points, or that all of the data points are not represented by that single curve. A test for the latter possibility also is included in assessing whether the residuals of the data points (i.e., the distance of the data points from the curve) follows a Gaussian distribution. In Fig. 5, P, norl<0.05 is interpreted as a non-normal fit of the data to the curve.

Fig. 5.

FRET measurement of the dimerization kinetics of the estrogen receptor (ERα) labeled (a) and (c) with the dimer competent FPs or (b) and (d) with the monomeric A206K FP mutants. (a) and (b) Plotting the amount of complex formed (represented by E) against the concentration of acceptor present (x axis) shows that the data points fit well to a curve indicative of a one-site, bimolecular interaction, when the cells are grown in the presence of estradiol. The curve fitting values (R², P-values from runs test, P-values for normal distribution) are shown for each dataset, along with the number of cells analyzed (n). P-values of <0.05 (shown in gray) are considered to represent significant deviation from the expected number of runs or from a normal distribution of the data points around the best-fitting curve. The data from five separate experiments are shown in five different columns of data to assess data reproducibility. (c) and (d) Similar analysis for cells grown without the addition of estradiol; the curves obtained for the binding in the presence of estradiol are shown as solid lines to compare against the no estradiol control cells (dashed lines). (e) Direct comparison of the dimeric CFP/YFP and monomeric mCFP/mYFP binding curves obtained in parallel experiments.

3 Results

3.1 Calibration Standards for Measuring E

The goal of the current study is to establish whether weak dimerization of the FPs affects the interaction between two FP-labeled proteins. To describe FRET in terms of interaction between estrogen receptors (alpha isoform, ERα) tagged with the dimer-capable and monomeric forms of CFP and YFP, we must determine the proportion of the ERs in the interacting complex (Y) in relationship to the concentration of one of the interacting factors (X) according to the curve Y =(B max·X)/(Kd+X). As discussed in Sec. 4.4, Y can be represented by E (the proportion of donor energy lost to energy transfer), provided assumptions are met. By contrast, the acceptor bleed-through-corrected FRET/donor value (F/D) does not precisely describe Y, since the F/D values are nonlinear with respect to E. Inserting Eq. (5) into Eq. (7) shows that F/D is inversely proportional to (1–E). Therefore, measuring interaction between two interacting factors will be aided by converting the F/D values into E.

Converting F/D to E requires calibrating the equipment according to previously defined calibration parameters.^19,36 Calibration determines a series of instrument-specific constants (outlined in Sec. 2.4) that describe the relative abilities of different fluorescent outputs to be detected in different channels. Calibration is achieved by measuring the F/D values for a series of calibration standards of known E. The calibration standards described in this study were based on a series of dual-labeled androgen receptors (AR) containing CFP fused to the AR amino terminus and YFP fused to the AR carboxy terminus. We previously showed by using F/D measurements that there is almost no energy transfer within the CFP-AR-YFP fusion protein (hereafter listed simply as AR) when present in cells grown in the absence of hormone.²⁷ By contrast, energy transfer was detected in cells treated with the hormone dihydrotestosterone, which causes a conformational shift in the AR. We also found that a series of four AR point mutations, found in prostate cancer tumors that no longer responded clinically to androgen deprivation therapy, showed variable levels of energy transfer in response to no ligand, dihydrotestosterone, the antiandrogens hydroxyflutamide and Casodex, and two hormones that AR does not normally respond to: estradiol and progesterone (Ref. ²⁷, unpublished data). The different combinations of ligands and AR mutants created a series of thirty, almost identical, protein/ligand standards that provided a range of FRET responses with which to calibrate the equipment.

We first established that the CFP and YFP-tagged AR was an appropriate calibration control for the later studies of the CFP and YFP-tagged ERα. Bleed-through controls for the singly labeled ARs were not significantly different (p>0.05) from those obtained for the singly labeled ERs (Table 2). The similar behavior of CFP and YFP attached to the AR and ER validates the use of the AR standards for calibration of our ER studies.

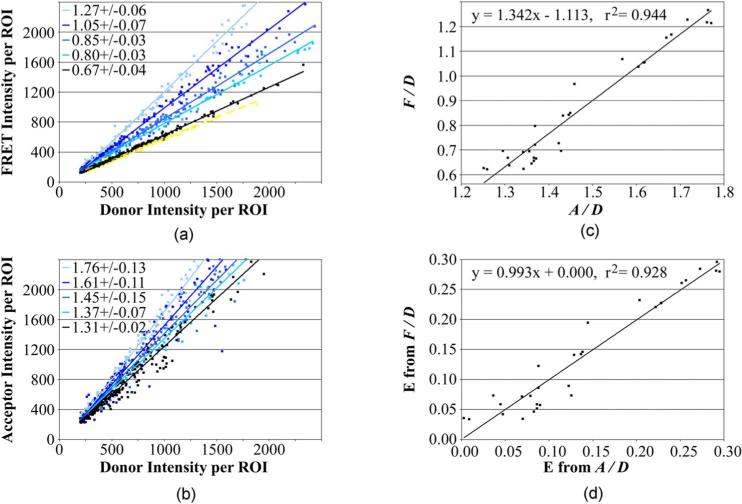
As outlined in Sec. 2.4, calibration required the collection of F/D and A/D measurements for all 30 different AR/ligand calibration standards. As an example, the F/D [Fig. 3(a)] and A/D [Fig. 3(b)] measurements are shown for cells treated with one of the ligands, 10⁻⁶ M progesterone. The F/D and A/D ratios were calculated for the wild-type AR (black line) and various mutant ARs (V715M cyan line; H874Y blue line; T877A dark blue line; T877A light blue line) as the slopes of the graphs of the (background-subtracted and acceptor bleed-through-corrected) FRET or acceptor channel fluorescence intensities, in each ROI, against the donor channel intensity. For a dual-labeled standard that contains the same relative levels of Donor and Acceptor, we observed that control values determined by linear regression (rather than simply averaging the ratios calculated for each individual ROI) minimized experiment-to-experiment variations in F/D or A/D measurement arising from experiment-to-experiment variations in background correction.

Fig. 3.

Establishment of calibration constants to convert acceptor-bleedthrough-corrected FRET/donor (F/D) measurements into the proportion of donor transferred to acceptor (E). Background-subtracted and acceptor bleed-through corrected intensity measurements in the acceptor (A), donor (D), and FRET (F) channels were collected from cells expressing a dual-labeled CFP-AR-YFP calibration standard. (a) F/D ratios for 30 different CFP-AR-YFP calibration standards (only five shown here) were collected by plotting F against D for a large number of cells. The F/D ratios for those five standards (mean ± SD from six independent studies) are shown in the inset. (b) A/D ratios from the same cells were collected by plotting A against D. (c) As outlined in Sec. 2.4, Eq. (7), plotting F/D against A/D, yields a curve with a y intercept that is the difference of the constants KfD and KfaD. The slope of that same curve represents KfaD divided by KaD (see Sec. 2.4 for definition of the constants). Establishment of the calibration constants enables E to be extrapolated from the easily and accurately measured F/D ratio [Eq. (3)]. (d) Comparison of E determined from the F/D ratios with E determined from the A/D ratios [Eq. (6)] for the 30 calibration standards. (Color online only.)

As we previously reported,²⁷ the F/D ratio of the wild-type AR in cells treated with progesterone [black slope in Fig. 3(a)] was only marginally increased above that obtained with the AR labeled only with the donor (yellow slope). This indicated little energy transfer within the dual-labeled wild-type AR. By contrast, the four mutants responded abnormally, and variably, to progesterone. As expected, the energy transfer detected as an increase in F/D [Fig. 3(a)] was paralleled by an increase in A/D [Fig. 3(b)].

The mean F/D and A/D ratios from the six independent calibration studies of the progesterone-treated cells are listed in Fig. 3 (insets). By F/D measurement, each of the different standards shown in Fig. 3(a) have significantly different (p>0.05) levels of energy transfer. By contrast, there was a much higher variation in the A/D measurements than in the F/D measurements. This variation also was visible in the much higher scatter of the A/D data points from the best fitting slope (see Fig. 3; r²=0.984±0.014 for F/D compared to 0.958±0.027 for A/D). We do not know the origin of the variation in the A/D measurement, but suspect that the F/D measurement, which incorporates two variables affected by FRET (F and D), may be less affected by random FRET measurement error than A/D, in which only the D variable is affected by FRET. It also is possible that the “sensitized emission” component of energy transfer, read in the FRET channel, may be more accurately detected than other components of the FRET signal. Regardless of origin, the F/D measurement is clearly a more reproducible indicator of energy transfer. For calibration, errors that might be introduced by the relatively inaccurate A/D measurement can be minimized by collecting a large number of data points in a number of independent experiments.

3.2 Calibration of kfD, kfaD, and kaD

For the current calibration studies, 19,178 different calibration ROIs, and 1030 bleed-through control ROIs, were collected in six independent studies. kfD, the ability of the equipment to detect Donor fluorescence in the FRET channel relative to the donor channel, is represented by the FRET channel bleed through from the control cells expressing AR-CFP only. In the six AR calibration studies, kfD averaged 0.5625 (95% CI from 0.5459 to 0.5795). kfaD (the ability of the equipment to detect donor energy transferred to the acceptor in the FRET channel) and kaD (the ability of the equipment to detect equimolar amounts of donor and acceptor) were calibrated, as described in Sec. 2.4, by plotting the F/D values obtained from the 30 calibration controls against A/D [Fig. 3(c)]. According to Eq. (8), the y intercept (−1.1129±0.0910) described kfaD as 1.6756 (95% CI from 1.4891 to 1.8617), when kfD is 0.5625. According to Eq. (9), the slope (1.3421±0.0616) described kaD as 1.2485 (95% CI from 1.2246 to 1.2682).

Using these equipment-specific calibration constants, E was determined from the F/D [Eq. (3)] and A/D [Eq. (6)] measurements for each of the 30 calibration standards. Plotting those E values against each other [Fig. 3(d)] provided a best-fitting straight line of slope of 0.993 with a y intercept of zero. This is near to the slope of 1.000 expected if, on average, the E values measured by F/D correspond to those measured by A/D. Since the values were generated from the same set of F/D and A/D data used to derive the constants, the near unity of the data is expected. More importantly, the distribution of the 30 calibration data points around the slope was normal (p>0.10), which provided some validation for the calibration values obtained despite the large scatter. As noted before, the significant scatter in the graph (r²=0.928) likely originates from the much lower statistical confidence in the A/D measurements than in the F/D measurements, which was compensated for by the use of large sets of calibration data.

3.3 Automated Removal of Cell Debris Artifacts

The measurements of interaction, described next, rely on the more accurate F/D ratio. Still, some form of quality control must be implemented to ensure that the data points are accurate. Images were collected from cells coexpressing ERα-CFP and ERα-YFP or coexpressing ERα-mCFP and ERα-mYFP (the monomeric variants). The cells were treated for 30 min either with 10⁻⁸ M estradiol or with an equivalent amount of ethanol (0.01%) before image collection. ROIs were drawn automatically around regions of contiguous ERα-CFP (or ERα-mCFP) fluorescence emitted from the cell nucleus. ROIs with donor intensity below 100 units (on a 12-bit scale) above background were excluded. ROIs also were excluded when the amount of background-subtracted fluorescence collected in the acceptor channel at 50-ms integration time was not between 0.235 to 0.265 that collected at 200 ms. This 0.25 exclusion was done only for ROIs with measurable amounts of acceptor fluorescence, defined as >200 fluorescent units on a 12-bit scale. These ROIs likely represented cells that moved during collection. Only 0.2% of cells were excluded by this criterion, as this intensity ratio was generally very close to 0.25 (see Table 1).

After the initial exclusions, a number of ROIs remain that do not represent real cells. Most of those false objects generally represent yellow autofluorescent debris excited by the same wavelengths of light used to excite CFP. This debris mimics fluorescent in the FRET channel and therefore shows artificially high E values. Retaining those false objects in the FRET analysis would introduce error, but removal of those false FRET objects by visual inspection of each image is impractical in large-scale analyses. For example, a total of 10,433 control and 11,929 experimental ERα-CFP-expressing ROIs were collected for the studies of Fig. 5.

The method used to mathematically remove the autofluorescent non-ERα objects incorporates other fluorescent properties of the autofluorescent debris. Since the autofluorescent debris is not well excited using the acceptor excitation wavelengths, these artifacts cluster at very low acceptor and high FRET amounts. Dividing the high E measurement by the low acceptor measurement should therefore result in very high q_c-value for the autofluorescent debris (high E, low acceptor), but a low q_c-value for cells expressing CFP. The q_c-value distribution is shown in Fig. 4(a) for one dataset. 108 of the 135 objects had a q_c-value between 0.8×10⁻³ and −0.8×10⁻³ (closed boxes, mean of 0.2±0.2×10⁻³) and were included in subsequent analyses. By contrast, the excluded objects (open boxes) showed a very high scatter in q_c-value with all of those objects localized in ROIs with very low acceptor levels. The excluded ROIs in Fig. 4(a) also are clear outliers of the curve in Fig. 4(b) (open boxes). As discussed in the next section, that curve is representative of the amount a complex formed between CFP-tagged and YFP-tagged ERα as a function of the amount of YFP-tagged ERα [Fig. 4(b)]. The failure of the excluded objects to fit to that curve confirms their designation as “debris.” Figure 4(b) also highlights that the retention of those points during analysis would introduce significant error into measurements based on accurate curve fitting to the data points. For all the studies listed in the following sections, 7.6% of objects identified were categorized as debris according to the prior criteria and excluded from further analysis.

Fig. 4.

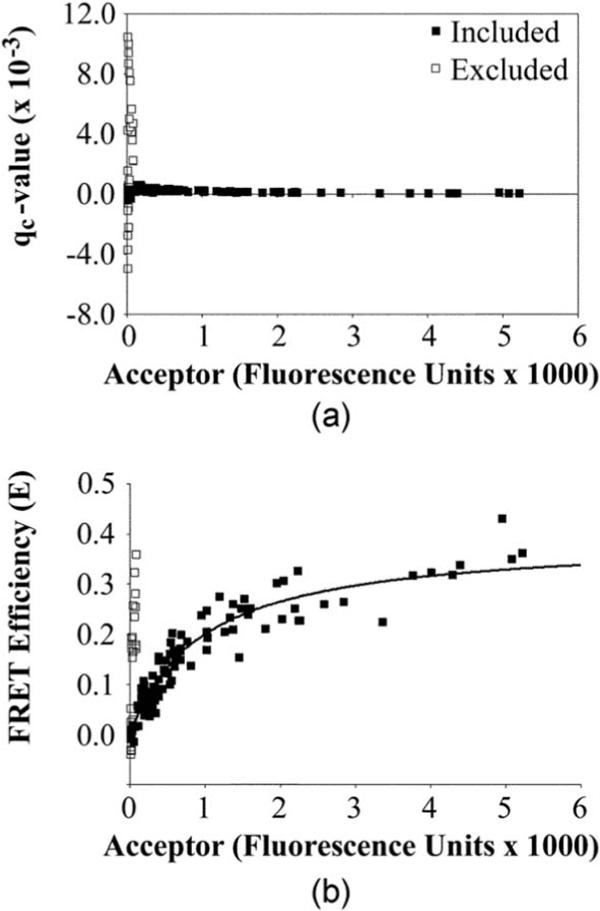
Removal of autofluorescent debris. (a) For high throughput analysis with no user intervention, a quality control (q_c) measurement was derived (Sec. 3.3) to identify ROIs (open boxes) that varied substantially from the ROIs representing actual cellular objects (closed boxes). In the current study, all objects with q_c values between −0.8 and 0.8×10⁻³ were retained for further analysis. Note that the corresponding acceptor fluorescence values here (x axis) and in the remaining graphs are all corrected by dividing A by KaD (the constant that describes how well acceptor fluorescence is collected relative to an equimolar amount of donor). Where helpful, this enables acceptor fluorescence values to be compared in relationship to an equal amount of fluorescence from an equimolar amount of donor. (b) Included data points fit well to the one-site binding bimolecular interaction curve (see Sec. 3.4), whereas most of the excluded data points do not.

3.4 Describing E in Relationship to Biochemical Interaction

As shown in the example [Fig. 4(b)], the E values for each ROI were graphed against the fluorescence intensity of the acceptor in the same ROI. The data points are expected to follow a biochemical relationship described by the formation of a complex at a constant amount of one factor (CFP-labeled in our example) with increasing amounts of the interacting factor (YFP-labeled in our example).^25,27,36 The formula for this relationship, Y =(B max·X)/(Kd+X), describes how the concentration of a complex (Y) increases as a function of increasing concentrations of one of the interacting factors (X). For FRET analysis, E is assumed to represent a surrogate measurement of the proportion of the YFP-labeled factor in the complex, whereas the intensity of the acceptor is assumed to represent the concentration of the YFP-labeled factor. The merits of these and other assumptions are discussed in Secs. 4.3 and 4.4.

In the example provided, the quality-controlled data [Fig. 4(b), closed boxes] fit to the binding curve with an R² value of 0.92. By contrast, inclusion of the debris in the data (open boxes) resulted in an R² value of questionable significance (0.51). For the quality-controlled data, a runs test showed that no portions of the data were nonrandomly distributed above or below the curve. This suggests that the use of the one-site binding model for fitting the data points was appropriate (note that a two-site binding model did not fit well to the data by this criterion). Thus, the FRET data indeed appear to fit the binding model, which enabled the extrapolation of biochemical data to compare interaction of ERα labeled with dimer-competent and monomeric FPs. Experiment-to-experiment variations in the extent to which the data points fit the curve are discussed in later sections.

3.5 Interaction of ERα with Dimer-Competent Fluorescent Proteins is Retained with Monomeric Fluorescent Proteins

We compared the interaction of ERα-CFP and ERα-YFP (dimer-capable FPs) with the interaction of ERα-mCFP and ERα-mYFP (monomeric FPs) in cells treated or not with 10⁻⁸ M estradiol. E was graphed against acceptor intensity for each of those four conditions. The data from each of the five independent experiments are shown in each column of graphs in Fig. 5 (experiment 1, 2, etc.). The studies of ERα-CFP/ERα-YFP and ERα-mCFP/ERα-mYFP interaction in the presence of estradiol are shown in Figs. 5(a) and 5(b). The parallel studies with no estradiol added are shown in Figs. 5(c) and 5(d). The side-by-side comparison of the curves of ERα interaction using the monomeric and dimeric FPs are shown in Fig. 5(e).

Within each plot, the data points were fit to the biochemical curve described earlier. Curve-fitting parameters are described in Sec. 2.5. The best-fitting curves for each dataset are shown as a solid line for the cells treated with estradiol [Figs. 5(a) and 5(b)] and as a dashed line for the cells treated with the drug vehicle [Figs. 5(c) and 5(d), in which the solid lines depicting interaction on estradiol treatment are displayed for comparison]. Values inserted into each graph show the number of ROIs used to draw the curve (n), the R² value describing the goodness of fit of those data points to that curve, the P-value that shows whether the data points deviate consistently in certain regions away from the curve by a runs test (“P,runs”), and the P-value that shows whether the data points are normally distributed around each curve (“P,norl”). P,runs and P,norl values of less than 0.05 [shown in gray in Figs. 5(a) and 5(b)] are considered to show significant deviations from the curves.

In the absence of estradiol [Figs. 5(c) and 5(d)], the data points did not fit well to the bimolecular interaction curve for either the dimer-competent FPs (R²=0.43±0.11, mean ± SD of all five experiments) or for the monomeric FPs (0.53±0.11). No P,runs or P,norl values are shown for these curves, since the R² values alone indicated that the data do not fit the curves. Visual inspection suggests a poorly fitting trend toward more FRET at higher acceptor levels. Thus, as a population of cells, dimer formation is inconsistent, at best, in the absence of estradiol.

By contrast, a good fit to the bimolecular interaction curve (Fig. 5, high R² values) was observed for all cells treated with estradiol, regardless of whether FRET was measured using the dimer-competent FPs [Fig. 5(a)] or the monomeric FPs [Fig. 5(b)]. Within each experiment, the data points fit somewhat better (p=0.04) to the curve when the dimer-competent FPs were used (R²=0.85±0.05, mean ±SD of all five experiments) than when the monomeric FPs were used (R²=0.78±0.09). However, the P values for the runs test and test for normalcy showed that there was substantive experiment-to-experiment variation in the extent to which the data points distributed randomly around the curves. Visual inspection suggested that the curve fit is appropriate in all experiments, but that larger amounts of noise in experiments 2 and 4 led to poorer runs tests and poorer tests for normalcy.

3.6 No Consequence of Fluorescent Protein Dimerization on ERα-ERα Interaction Kinetics

The fit to the bimolecular interaction curves in the presence of estradiol permitted the extrapolation of the equilibrium dissociation constant (Kd) and the maximal amount of energy transfer at saturated binding (B max) for ERα-ERα interaction with dimer-competent and monomeric FPs. The Kd, which describes the relative on and off-rates of ERα-ERα interaction, was not statistically different for interaction using the dimer-competent or monomeric FPs. The Kd (±95% confidence intervals) derived from each of the five studies is shown in Fig. 6(a) (experiment 1 to 5), together with the mean of all experiments. Experiment-to-experiment variation in the Kd was observed, which perhaps reflects day-to-day variation in some aspect of cell health or physiology. Still, on the same day, the Kds measured for both the FP- and mFP-tagged ERα interactions were the same.

Fig. 6.

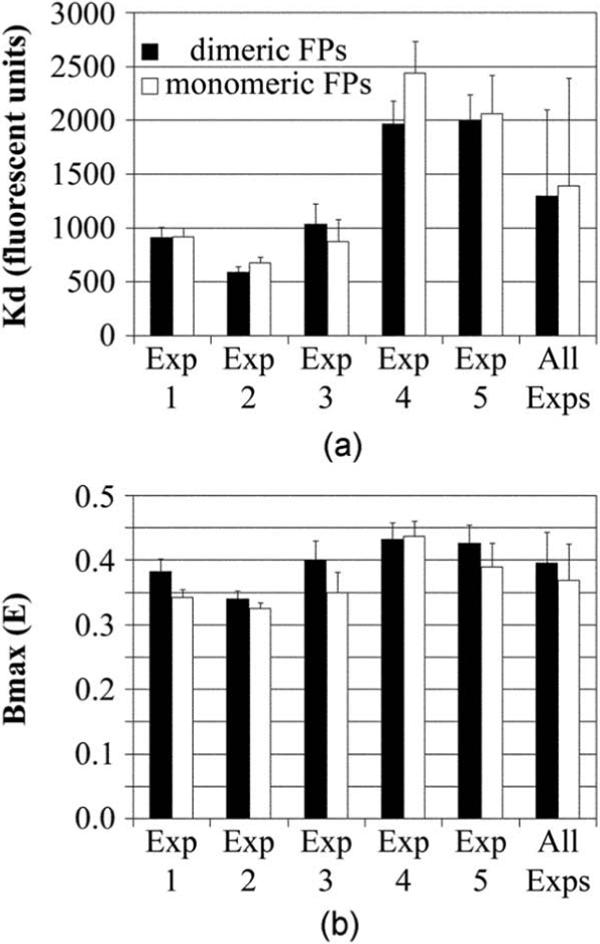
FP dimerization does not affect FRET measurement of the interaction kinetics of the estradiol-bound estrogen receptor (ERα) with itself. (a) For each of the five independent studies shown in Fig. 5, the amounts of acceptor required to reach half of B max (Kd) were no different for the interactions of ERα tagged with the dimer-competent (closed bars) or monomeric (open bars) FPs. (b) The associated B max measurements also showed no significant differences within most experiments, although there was a marginally significant (p=0.05) trend for the B max to be less for interactions measured with the monomeric FP. The mean ± standard deviation for all five experiments is shown for both graphs as the right-most bars.

The maximal amount of energy transfer (Bmax) tended to be lower for the dimerization of ERα tagged with the monomeric FPs [Fig. 6(b)](p=0.05, i.e., at the margin of statistical significance). However, the uncertainty in the fits to the curve (poor runs test and poor tests for normalcy on some days) introduced an element of uncertainty in the B max measurements. With the nonrandomness of the data fit to the curve, the marginally different B max levels may reflect nothing more than a higher number of poor quality data points collected with the monomeric FPs.

4 Discussion

4.1 Equipment Calibration

The methods for calibration essentially parallel those described by Chen et al. and Koushik et al.,^19,36 albeit derived and expressed somewhat differently here. Details of those calibrations, and the rationale behind them, are provided in Materials and Methods (Sec. 2). In short, the kfaD constant described here is the counterpart of the G-factor described by them and others.^36,37 The kaD constant is the inverse of their k-factor. The kfaD constant observed here for CFP and YFP (1.676±0.091) is not much different than the G-factor (1.815±0.067) observed by Chen et al.¹⁹ using the spectrally similar Cerulean and Venus FPs under somewhat similar filter conditions (excitation/emission wavelengths for the donor channel of 436±10/480±20 versus 436±10/470±15; for the FRET channel of 436±10/540±15 versus 436±10/535±15) but using different dichroic mirrors, objectives, and cameras. The large difference in the kaD constant (1.248, observed here) and the inverse of the k-factor (4.613, observed by Chen et al.¹⁹) reflects the better excitement of CFP on our system (with a 200-W Hg/Xe lamp containing a very strong peak at 436 nm) than on their system (75-W Hg lamp). These differences highlight the need to calibrate each instrument in each laboratory with each filter set and with each objective.

The major addition to the calibration procedure that we report is the use of large calibration datasets. The constants are described here in terms of the overall differences in measurements for each of the 30 calibration standards, and our equations have been cast to represent the calibration constants by the slopes and y intercepts of the graphs using this large number of standards. We believe this to be an improvement over extrapolating efficiencies from a more limited number of calibration data points. The large datasets used here also helps to provide an indication of the variation and consistencies in the measurement of energy transfer.

The calibration data showed that E derived from F/D [Eq. (3)] to be quite accurate, whereas the A/D measurements of E [Eq. (6), possible only when using a dual-labeled sensor] showed significant experimental variability. The uncertainties in A/D measurement have a strong potential to introduce an error into the measurement of the calibration constants, which would result in a systematic error when converting F/D into E values using those constants. We attempted to circumvent these errors by using very large datasets (30 different calibration standards with a total of almost 19,178 measurements) and by repeating the calibration studies six times. We also obtained very similar constants when conducting another calibration at a later date using a restricted subset of the calibration standards reported here, plus some newer standards in the intermediate FRET range (data not shown). We therefore are quite confident of the accuracy of the constants used for the subsequent studies of ERα interaction.

We caution that, if not conducting a large scale calibration as done here, the significant uncertainty observed for individual measurements can introduce inaccuracies in the calibration constants (and in experimental FRET measurements that rely on a limited number of data points). We therefore recommend most users to calibrate their equipment with known calibration standards in which E has been determined and validated by multiple independent means.³⁶ The calibration standards used here also require some level of familiarity and experience in androgen receptor studies, owing to the large amounts of hormone present in calf serum that must be removed prior to analysis. Laboratory to laboratory variations in the ability to strip testosterone from the serum likely will result in different amounts of energy transfer for the same CFP-AR-YFP standard when used in different laboratories. We strongly agree that useful, freely distributed standards, in which the user assumes the reported E value to be valid for their laboratory, must have a limited capability to vary with laboratory-specific conditions.³⁶

4.2 Debris Removal

We also report mathematical methods to remove a common form of debris encountered during FRET analysis using CFP and YFP or their derivatives. This q_c-value (Fig. 4) eliminates autofluorescent debris that is detected strongly in the FRET channel but poorly in the acceptor channel. As shown in Fig. 4(b), the elimination of this debris is a necessary prerequisite in obtaining data that fits with high confidence to the curve describing interaction between two proteins. It is also a necessary prerequisite for higher throughput FRET analysis in which data validation by visual inspection becomes impossible.

In our exclusion of debris by the q_c-value, a small number of bona fide CFP-expressing cells with low FRET signal and even lower acceptor signal were removed along with the debris. This exclusion of data may have a modest effect on curve fitting. In particular, runs tests and normalcy measurements may be skewed at low acceptor amounts and falsely report on a poor fit to the curve. Still, we prefer this form of data exclusion over, for example, the simple elimination of data points with high residuals (i.e., those that are greater than a specified distance away from the average curve), since the q_c-value targets objects with the specific fluorescence properties that we are trying to eliminate. In addition, we prefer not to incorporate any methods based on the assumption that all points should fit the curve, since, in a biologic system, cells that vary from the norm may be even more interesting than cells that fit the curve.

4.3 Applying Biochemical Kinetics to Förster Resonance Energy Transfer Data

The amount of energy transfer between two factors in a complex must be considered in relationship to how well those two factors interact. Interaction will be a function of their on- and off-rates (Kd), as well as the proportion of factors in a complex at equilibrium binding (B max). Since the concentration of those factors affects those biochemical parameters, the amount of energy transfer detected will be a function of the concentration of the donor and acceptor-labeled factors in the cell, as outlined in Secs. 2.6 and 3.4.

The question addressed in the current study is whether the FRET data points collected (Fig. 5) fit well to the curve that defines a one-site biochemical interaction between two proteins. The data collected tended to fit quite well to the hypothetical curve, whereas curves generated using other assumptions fit significantly less well (not shown). However, there remained some uncertainty about the randomness of the data points surrounding the curve (experiment-to-experiment inconsistencies in the runs tests and normal distributions). Visual inspection suggested that the experiments in which the data fit poorly to the curves (Fig. 5, experiments 2 and 4) showed a larger number of points falling below the curve. It is possible that measurement error is greater in some experiments than in others. In addition, the curve-fitting analysis operates under the assumption of an equivalent response by all cells, and the variable response may indicate that interaction is incomplete in a subpopulation of cells. Nevertheless, our data suggest that the dimerization of ERα measured in living cells generally follows the curve expected of an estrogen-dependent, one-site interaction between two proteins, and that the response is reasonably equivalent in most cells measured. As for all studies, it is important to understand the power of the FRET analysis while remaining cognizant of the limitations.

4.4 Technical Assumptions of the Kinetic Analysis of Förster Resonance Energy Transfer

Fitting the FRET data to the one-site interaction curve also depends on other assumptions. For curve fitting, the amounts of energy transfer from CFP to YFP were considered to be a surrogate indicator of the amount of complex formed. This assumption is true only if the FRET measurement is independent of the concentration of the complex. However, this may not be true if the structure or composition of the complex changes with increasing concentration of the interaction factors. Because of the uncertainties of knowing whether E is linear with complex concentration, an attractive future development may be the application of techniques that directly measure the proportion of donor-labeled proteins that are in a complex. This is possible through the analysis of FRET by fluorescence lifetime imaging microscopy (FLIM) using time-correlated single photon counting, in which the number of donor-labeled proteins in a complex with an acceptor-labeled protein can be directly compared with the number of free donor-labeled proteins.^38-40

In our study, the data fit best to a curve that described a one-site interaction of a donor-labeled protein with the acceptor-labeled protein. Attempts to fit the data to curves that assumed multisite interaction were not as successful. This suggested that the interaction measured indeed was representative of the binding of one CFP-labeled ERα, or ERα complex, with one YFP-labeled ERα, or ERα complex. Note that this does not exclude a stoichiometry of, for instance, a dimer of ERα-CFP interacting with a dimer of ERα-YFP. That scenario is unlikely in the current example, since the ERα-CFP and ERα-YFP would themselves be expected to form a dimer. However, we caution that all binding interactions are unique, and that for each interaction, the user is urged to consider all possibilities.

A further assumption in the analysis is that the fluorescence intensities collected for both the acceptor and donor-labeled receptors represent the concentration of that receptor. This would likely to be true for volume-limited confocal measurements, but is not necessarily true for the wide-field measurements used here. Nevertheless, we prefer to use wide-field measurements, since we routinely observe greater measurement variation using confocal than wide-field microscopy. The variations in confocal measurements with live cells likely arise from z-movements in the live cells during collection of the acceptor, donor, and FRET channels. The wider z-depth of the wide-field measurement tends to better average out that z-drift. A further confounding variable is the assumption that the fluorescence measured reflects the effective concentration of the interacting factors. This may not be true if the factors are predominantly constrained in microstructures that either limit the abilities of factors to interact, or that push noninteracting factors into a sufficiently high local concentration to permit energy transfer.^41,42

The analysis also assumes a constant amount of CFP-labeled factor, which will never be precisely realized in transiently transfected cells. In the five different experiments here, each with four different conditions (wild type and A206K CFP, each with or without estradiol) CFP fluorescence averaged 637±81 fluorescence units (following correction for energy transfer). This indicated little cross-condition or cross-experiment variation in average CFP amount. Within each condition, 25% of cells showed fluorescence intensities less than 310 units on average and 25% more than 830 units. These are essentially tracer amounts compared to the amount of acceptor-labeled factor expressed in the current studies (see the x axis in Figs. 4 and 5 in which the acceptor fluorescence intensities, corrected such that equal amounts of donor and acceptor fluorescence represent equal numbers of molecules, is measured in thousands of units).

Overall, FRET measurement of biochemical interactions in cells makes assumptions about the relationship between the FRET read-out and complex formation, about fluorescence intensities and factor concentration, and suffers from poorer control than an in vitro binding analysis over factor amounts introduced to the system. Even for in vitro binding analysis, derivation of Kd and B max is subject to assumptions that there is a single form of complex that does not change with concentration, that all molecules are equally available to interact/dissociate, and that binding does not irreversibly change the complex. Any of these conditions may not hold within the complex environment of living cells or in the test tube.

One goal of the current study was indeed to assess the reproducibility of measurements, and of the deviations from the binding curves, as a prelude to establishing response variations in different subregions of the cell or in different cellular subpopulations. Significant experiment-to-experiment variations in our Kd measurements [Fig. 6(a)] may reflect different cell growth or physiologic conditions at the time of measurement. By contrast, the B max measurements tended to be consistent from experiment to experiment. Since the maximal amount of energy transfer is an indirect read-out also of the orientation and distance between the fluorophore dipoles, the consistent B max measurements suggest very little change in the structure of the ERα complex in different experiments. Knowing these consistencies and variations are important as we apply the FRET analysis to high throughput measurements, in which well-to-well and day-to-day measurement consistency will be essential for the accurate identification of treatments that alter FRET measurements.

4.5 Choice of Dimer-Competent or Monomeric Fluorescent Proteins

The major purpose of the current study was to define whether the use of dimeric FPs affected interaction driven by the ERα. Our prior studies showed that energy transfer from ERα-CFP to ERα-YFP, expressed at physiologic levels, was eliminated by the mutation of three amino acids in the ERα dimer interface.^25,27 This demonstrated that there was no nonspecific FRET that would affect the conclusion, described next, that dimerization between the FPs impacted ERα dimerization. In general, we urge users of the FRET technique to express only tracer amounts of their FP-labeled factors, since the purpose of live cell studies is to define the interactions in the presence of the limiting number of other cellular factors.

The current studies showed a similar Kd of ERα-ERα interaction measured for complexes formed with the dimeric and monomeric FPs. This suggested that ERα interaction was not affected by any FP dimerization. The maximum amount of energy transfer for ERα-ERα interaction (B max) was marginally lower for the interaction measured with the monomeric FPs. Although uncertainties in this conclusion remain, owing to the deviations from normalcy and poor runs test, particularly with experiments 2 and 4, the lower B max observed with the monomeric FPs was consistent (p=0.05).

It is difficult with the current data to distinguish whether the marginally lower B max measurement obtained with the monomeric FPs originates from a structural difference (different positions or orientations of the monomeric and dimeric FPs) or an interactive difference (FP dimerization improving the actual biochemical B max). We currently favor the hypothesis that the decreased B max measured with the monomeric FPs was due to a less favorable (for FRET) average position or orientation of the monomer FPs in the ERα-ERα complex. This assessment is based on the assumption that the higher R² values measured for the complexes containing the dimeric FPs originate from the weak FP-FP interaction, which may somehow permit a more consistent registration in the average dipole orientation or FP location. That would lead to both improved data quality (higher R²) and, if the average FP distance or orientation is more favorable, a higher FRET amount (higher B max) for the dimeric FPs. We emphasize that this interpretation is highly speculative. Regardless of origin, the better R² values observed with the dimeric FPs suggest that there may be some advantage to the use of the dimer-competent FPs for the FRET measurements. Certainly the potential negative consequence that FP dimerization could affect ERα interaction was not observed in this study [Fig. 6(a), similar Kds for interaction with monomeric and dimeric FPs].

Some potential disadvantages to using dimeric FPs were not ruled out by the current study. Knowing the distance at which energy transfer between CFP and YFP is 50%⁵ and the relationship of E to fluorophore distance first defined by Förster,^6,7 the average B max values obtained for the dimeric (39.2%) and monomeric (36.7%) FPs suggest a distance between the FP dipoles of 52.9 Å or 53.9 Å, respectively, in the ERα-ERα complex. These distance estimates are notoriously inaccurate, since the relative orientations of the FPs in the ERα-ERα complex will affect E and the distance estimate derived from E. However, taken at face value, these distances suggest that the FPs are not in actual contact with each other in the ERα-ERα dimer. Thus, although FP-FP interaction did not affect the interaction of ERα with itself measured by FRET, a closer positioning of dimer-competent FPs in another complex may result in an FP interaction that may affect the interaction measured for those proteins. We recommend that others assess the merits of monomeric and dimeric FPs for their specific interactions. If there is no effect on interaction kinetics, then there may be some advantages to the dimeric FPs. If there is an effect on interaction kinetics, then the monomeric FPs are preferable.