Abstract
Despite its fundamental role in development, sex determination is highly diverse among animals. Approximately 20% of all animals are haplodiploid, with haploid males and diploid females. Haplodiploid species exhibit diverse but poorly understood mechanisms of sex determination. Some hymenopteran insect species exhibit single-locus complementary sex determination (sl-CSD), where heterozygosity at a polymorphic sex locus initiates female development. Diploid males are homozygous at the sex locus and represent a genetic load because they are inviable or sterile. Inbreeding depression associated with CSD is therefore expected to select for other modes of sex determination resulting in fewer or no diploid males. Here, we investigate an alternative, heretofore hypothetical, mode of sex determination: multiple-locus CSD (ml-CSD). Under ml-CSD, diploid males are predicted to develop only from zygotes that are homozygous at all sex loci. We show that inbreeding for eight generations in the parasitoid wasp Cotesia vestalis leads to increasing proportions of diploid males, a pattern that is consistent with ml-CSD but not sl-CSD. The proportion of diploid males (0.27 ± 0.036) produced in the first generation of inbreeding (mother–son cross) suggests that two loci are likely involved. We also modeled diploid male production under CSD with three linked loci. Our data visually resemble CSD with linked loci because diploid male production in the second generation was lower than that in the first. To our knowledge, our data provide the first experimental support for ml-CSD.
DIFFERENTIATION between males and females is a fundamental aspect of life for sexually reproducing animals. The underlying principle of sexual differentiation is similar in most animals: a primary signal that differs in males and females leads to differential expression of a key gene. This key gene directs expression of sex-differentiating genes, resulting in the sexual phenotype. Evolution has led to an astonishing diversity of primary signals of sex determination, including environmental, social, or genetic signals that can vary between closely related species and even within species (Bull 1983; Marin and Baker 1998; Schütt and Nöthiger 2000).
All sexually reproducing members of the insect order Hymenoptera are haplodiploid, with haploid males developing from unfertilized eggs and diploid females from fertilized eggs. This precludes a role for heteromorphic sex chromosomes as primary signals of sex determination. Instead, many hymenopterans exhibit complementary sex determination (CSD) (Whiting 1943; Beye et al. 2003; van Wilgenburg et al. 2006; Heimpel and de Boer 2008). Under single-locus (sl)-CSD, female development is initiated by heterozygosity at a single, highly polymorphic, sex locus. Homozygotes at the sex locus develop into inviable or sterile diploid males (Whiting 1943; Cook 1993b; Cook and Crozier 1995; Holloway et al. 1999; de Boer et al. 2007b), with the exception of the vespid wasp Euodynerus foraminatus, in which diploid males have near normal fertility (Cowan and Stahlhut 2004). The production of diploid males increases dramatically under conditions of inbreeding or low genetic diversity and represents a severe genetic load. The production of diploid males can reduce population growth rates (Stouthamer et al. 1992) and effective population size (Zayed 2004), and it can increase extinction risk (Zayed and Packer 2005). Because inbreeding levels are presumed to be high in many hymenopteran species, it is expected that the genetic load associated with CSD should select for modes of sex determination that do not result in the costly production of diploid males. Indeed, not all hymenopterans exhibit CSD, but sex determination in species without CSD is largely unknown. An alternative model, involving a maternal effect and genomic imprinting, has been proposed for the parasitoid wasp Nasonia vitripennis (Beukeboom et al. 2007; Kamping et al. 2007).
An extension of the sl-CSD model is multiple-locus (ml)-CSD (Snell 1935; Crozier 1971), where diploid males develop only from fertilized eggs that are homozygous at all of two or more independent sex loci. Compared to sl-CSD, ml-CSD should lead to significantly fewer diploid males, and the same genetic load should be reached at higher levels of inbreeding. To date, no evidence has been reported that conclusively supports this genetic model (van Wilgenburg et al. 2006), and very few studies have attempted to find evidence. We have argued elsewhere that evidence for ml-CSD may have been missed in previous studies due to ml-CSD collapsing to de facto sl-CSD under inbreeding (Heimpel and de Boer 2008). Cook first raised this issue in his experimental analysis of CSD in the bethylid parasitoid Goniozus nephantidis (Cook 1993a). Under ml-CSD, the proportion of diploid males among the fertilized offspring depends on the number of heterozygous sex loci (h) of the mother and is 1/2h for a cross between parents that share a sex allele at each putative locus. When only one sex locus is heterozygous (h = 1), ml-CSD collapses to sl-CSD. If studies on CSD are done using material that has been previously inbred or has a narrow genetic basis, a collapse from ml-CSD to sl-CSD may lead to an underestimation of the number of sex loci.
Here, we report results from a multiple-generation inbreeding experiment in which we maximized the chance of starting the experimental crosses with females that are heterozygous at each putative sex locus. We used the braconid wasp Cotesia vestalis [= C. plutellae (Shaw 2003)], a solitary endoparasitoid of diamondback moth larvae, for which we recently showed CSD based on the occurrence of diploid males in inbred but not in outbred crosses. We specifically test the ml-CSD model for this species because diploid male frequencies were lower than those expected under sl-CSD (de Boer et al. 2007a). An alternative multilocus model of sex determination was proposed by Battaglia for a copepod but was considered unlikely for Hymenoptera by Crozier (1975), and currently there are no other testable models that include development of diploid males under inbreeding.
We also modified the original ml-CSD model to predict the effect of linkage between putative sex loci on the proportion of diploid males produced under inbreeding. If additional sex loci arose through duplication, they may be linked to the original sex locus. For example, in Drosophila, 70% of recent gene duplications were found in tandem with the original gene (Clement et al. 2006). Similarly, many gene families occur in groups. We compare our data to the predictions of this new model.
METHODS
Experimental crosses:
We used two strains of C. vestalis: one started with material from a commercial supplier (Biofac Crop Care, Mathis, TX) and one started with wasps from a wild population in Benin (de Boer et al. 2007a). Ten experimental lines were started by outcrossing a haploid male from one strain with a female from the other strain to minimize the chance of fixed sex loci in the female offspring (Figure 1). Four lines were initiated with a male of the Biofac strain and a female of the strain from Benin; the other 6 lines were made in the other direction. One to four daughters from each of these lines were exposed to hosts as virgins to produce haploid sons. Approximately 2 weeks later, each of the 19 surviving females was crossed with one of her own sons. Subsequently, we established brother–sister crosses for seven generations. One to 4 replicates were done per original mother–son mating for a total of 22–26 replicates in each generation. We ensured using haploid males in each cross by allowing virgin females to oviposit in 10–15 second and third instar diamondback moth larvae before mating and using these male offspring in brother–sister matings of the next generation (de Boer et al. 2007b). To allow mating, pairs were kept together for 24 hr in a plastic vial (2.5 cm diameter, 6.5 cm high) with a piece of host-damaged cabbage leaf and a droplet of honey. After mating, females were exposed two times to ∼30 hosts on a piece of cabbage leaf for 24 hr in the same type of plastic vials with a droplet of honey. Three sets of hosts were offered in the mother–son generation because we anticipated lower parasitism and fertilization rates due to the age of females and keeping them at low temperatures for ∼12 days. Parasitized hosts were subsequently fed on cabbage for 2 days and then reared individually on artificial diet (modified from Shelton et al. 1991) in 1-oz. clear cups until cocoon formation, diamondback moth pupa formation, or death. Cocoons were transferred individually to microcentrifuge tubes with a small droplet of honey. Emerging wasps were sexed and then frozen at −30° for analyses of ploidy (see below). Mating and oviposition were done at 23° ± 1°, 30–50% relative humidity (rh), and 16 hr light (L):8 hr dark (D) in a climate-controlled room, and larval development was followed at 25° ± 1°, 30–50% rh, and 16 hr L:8 hr D in a growth chamber in the quarantine facility at the University of Minnesota. Data recorded in each generation were proportion of hosts that developed into C. vestalis cocoons or diamondback moth pupae, proportion of hosts that died, and secondary sex ratio (proportion of males).
Figure 1.—
Experimental design followed. As an example, genotypes for a ml-CSD model with two independent sex loci are shown (A indicates locus 1, with alleles i, j, and l; B indicates locus 2, with alleles k, m, and n). For all matings, haploid males are obtained via oviposition by virgin females. Genotypes in boldface type are homozygous at both sex loci and thus diploid males. In each mating, sex alleles that are shared by the female and her mate are underlined. Step 1 is an outcross between a female from one population and a haploid male from the other population. Within each population, one or more sex loci may be fixed for a single allele but assuming the populations carry different alleles at the same sex locus, all resulting diploid offspring will be heterozygous. In step 2, females from the outcross first produce haploid sons as virgins (A) and are then mated to one of their own sons (B), which reduces the number of possible alleles per sex locus to two. A mother and her own son always share an allele at each sex locus and, under two-locus CSD, result in 25% of the fertilized offspring developing as DM. In step 3, full-sib matings are established between the haploid males and diploid females resulting from step 2B. In this example of two-locus CSD, three different types of sibling matings can occur after a mother–son mating. In type A, one of the female's sex loci is fixed and her mate shares a sex allele at only one of the sex loci, which leads to all fertilized offspring being female. When the female is heterozygous for both loci and her mate shares sex alleles at each of these loci (type B), 25% of the fertilized offspring becomes DM. In type C, the female is heterozygous for one locus and her mate shares sex alleles at both loci, resulting in 50% of the fertilized offspring developing as DM. Type C matings represent a two-locus CSD system that has collapsed to sl-CSD. Continued sib mating in subsequent generations leads to an increasing fraction of type C matings and thus the ml-CSD system collapsing to functional sl-CSD.
Flow cytometry:
Ploidy of male offspring of replicates that produced at least one female was identified with flow cytometry, following methods described by de Boer et al. (2007b). In short, the head of an individual wasp was pulverized in Galbraith buffer (Galbraith et al. 1983) and DNA was stained with propidium iodide. The DNA content of 2500 nuclei was determined on a FACSCalibur flow cytometer (Becton Dickinson Immunocytometry Systems, San Jose, CA). Males were classified as haploid (h), diploid (d), or unknown by comparing their DNA histograms to those of known haploid males and diploid females. In total, ploidy of 186 of 2453 analyzed males remained unknown (7.6%). The number of haploid males (HM) and diploid males (DM) in each replicate was then estimated as HM = [total males × h/(d + h)] and DM = [total males × d/(d + h)], respectively. Using these data, we determined the proportion of diploid males [DM/(DM + females)] and the fertilization rate [(DM + females)/total adult offspring] per replicate family.
Model predictions:
Previous work on ml-CSD assumed that the sex loci were independent (Cook 1993a), following the model proposed by Crozier (1971). Here, we designed a new model to predict the fraction of diploid males under three-locus CSD with varying degrees of linkage between these loci. The model works as follows: The sex loci are indicated with A1, A2, A3 and B1, B2, B3, where 1–3 are the three sex loci, and A and B indicate (sets of) homologous chromosomes. Recombination between loci 1 and 2 occurs at rate “a,” and recombination between loci 2 and 3 at rate “b.” Because of the mother–son mating structure in the first generation of our experiment (Figure 1), only two different alleles at each locus are possible in the model (indicated by “1” and “2”). This leads to a maximum of eight different haploid gametes under three-locus CSD (i.e., 111, 112, 122, 121, 212, 211, 221, 222). Haploid males have a single allele at each sex locus, and thus there are eight different haploid male genotypes. Under three-locus CSD, there are 36 unique diploid genotypes. The 28 diploid genotypes with at least one heterozygous locus (i.e., A1 ≠ B1 or A2 ≠ B2 or A3 ≠ B3) are females, while the 8 genotypes with only homozygous loci (A1 = B1 and A2 = B2 and A3 = B3) are diploid males.
We first modeled the frequencies of each type of gamete produced by each of the 28 female genotypes. Parental gametes (no crossover) are produced at rate (1 − a) × (1 − b)/2, gametes in which a single crossover occurred between loci 1 and 2 at rate a × (1 − b)/2, gametes in which a single crossover occurred between loci 2 and 3 at rate b × (1 − a)/2, and gametes in which a double crossover occurred at rate a × b/2. Diploid males do not produce any gametes because they were not used in the experiment. No recombination occurs in haploid males.
Each female can potentially be paired with each of the 8 haploid male genotypes. The frequency at which each haploid male genotype occurs depends on the mother's genotype and is equal to the frequency of gametes she produces. There are thus 28 possible sets of haploid males, with different frequencies of genotypes for each set. Using these sets of haploid males, we modeled the frequencies of diploid genotypes (36) produced by each combination of female genotype (28) and a set of haploid males produced by a certain mother (28). In our inbreeding experiment, the first generation was a mother–son mating, so in the model, females were paired only with the set of haploid males produced by their own genotype. In subsequent generations of the experiment, females were crossed with their brothers, so in the model they were allowed to mate with the set of males produced by their mother's genotype (irrespective of which genotype their own father was). Per generation, we calculated the proportion of DM among all diploid genotypes and the sums of relative frequencies of each female genotype per mother's genotype, irrespective of the father's genotype. These frequencies were used as starting frequencies of mother–father combinations in the next generation. The model was written in R (R Development Core Team 2007) and is available from the authors upon request.
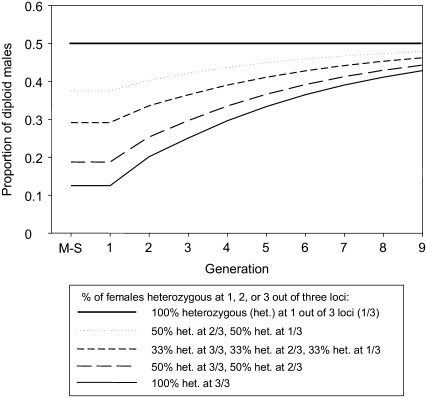
Assumptions in the model are that DM survival is equal to that of females and that iso-female lines were started with a female that was heterozygous at each sex locus. The latter assumption can be varied in our model and affects the level of DM production (Figure 2 shows the results for varying proportions of females being heterozygous at one, two, or three sex loci). To predict sex ratio under each CSD model for the sib-mating generations, the proportion of males was calculated as (1 − f + f × dmp), where dmp is the proportion of DM among the diploid offspring, and f is the proportion of eggs that is fertilized. We used the average fertilization rate across all generations in our experiment (0.57).
Figure 2.—
Effect of female genotypes at the beginning of an inbreeding experiment (mother–son mating followed by sib matings) on the predicted proportions of diploid males among fertilized offspring under CSD with three independent loci. All females are heterozygous at all three sex loci (bottom, solid line), which is the assumption made in our other predictions, or various fractions of the females used to start experiments are heterozygous at one or two of the three sex loci and homozygous at their other locus or loci (females must always be heterozygous at least at one locus because homozygosity at all three loci results in diploid male development). When 100% of females are heterozygous only at one of three sex loci, predictions are identical to those under sl-CSD (top, thick solid line).
Statistical analyses:
Statistical analyses were done on replicates with at least seven diploid offspring (DM + females) because when a mother produces fewer than seven diploid offspring we cannot accurately estimate the proportion of diploid males (Table 1).
TABLE 1.
Parameter values (mean ± SE) for the mother–son mating and seven subsequent sib-mating generations
| Generation
|
||||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | Mother–son | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| No. of replicates | 19 | 26 | 24 | 21 | 25 | 25 | 22 | 24 |
| No. of replicates with ≥1 daughter | 17 | 24 | 18 | 12 | 15 | 16 | 14 | 18 |
| No. of replicates with ≥7 diploid offspring | 13 | 19 | 12 | 10 | 12 | 10 | 12 | 16 |
| No. of hosts reared | 66.5 ± 2.2 | 55. 9 ± 2.7 | 49.7 ± 1.9 | 55.6 ± 2.1 | 59.4 ± 1.1 | 61.5 ± 2.4 | 59.6 ± 1.0 | 58.7 ± 1.4 |
| No. dead | 12.5 ± 2.3 | 10.8 ± 1.1 | 11.8 ± 1.6 | 7.0 ± 0.8 | 5.9 ± 0.9 | 13.5 ± 1.9 | 16.0 ± 2.0 | 13.1 ± 2.4 |
| No. of moth pupae | 4.1 ± 1.3 | 2.1 ± 0.5 | 1.7 ± 0.7 | 4.5 ± 1.4 | 5.4 ± 1.6 | 5.0 ± 1.7 | 5.8 ± 1.7 | 6.9 ± 1.3 |
| No. of cocoons | 49.9 ± 3.1 | 43.0 ± 2.9 | 36.3 ± 2.2 | 44.1 ± 2.6 | 48.1 ± 2.3 | 43.0 ± 2.7 | 37.8 ± 2.6 | 38.7 ± 2.8 |
| No. of haploid males | 17.3 ± 2.9 | 10.6 ± 1.0 | 11.0 ± 1.4 | 14.5 ± 1.4 | 13.9 ± 2.3 | 13.3 ± 1.3 | 12.3 ± 1.7 | 13.3 ± 1.7 |
| No. of females | 13.2 ± 1.5 | 14.8 ± 1.5 | 10.3 ± 1.3 | 9.3 ± 1.2 | 8.6 ± 1.1 | 10.9 ± 1.2 | 9.7 ± 1.4 | 10.1 ± 1.8 |
| No. of diploid males | 5.4 ± 1.1 | 3.4 ± 0.9 | 2.6 ± 0.7 | 7.3 ± 1.0 | 6.4 ± 1.2 | 6.9 ± 1.5 | 6.4 ± 1.1 | 10.7 ± 2.0 |
| No. not emerged | 14.1 ± 2.4 | 14.1 ± 1.9 | 12.4 ± 1.1 | 13.0 ± 2.5 | 19.2 ± 1.9 | 11.9 ± 0.8 | 9.5 ± 1.8 | 4.6 ± 1.0 |
Number of hosts reared to number not emerged are shown for replicates with at least seven diploid offspring (females and diploid males).
We compared our data on DM production by C. vestalis to the predictions of sl-CSD and ml-CSD with two independent loci, using a likelihood-ratio test. Under sl-CSD, the probability of producing DM is constant for all replicates over all generations of inbreeding because we started our experiment with a mother–son mating. Therefore, for each replicate, the distribution of the number of DM (x) is binomial with probability p, and n is equal to the number of offspring for that replicate, and
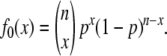 |
Under two-locus CSD, the distribution of the number of DM (x) for a particular replicate is a mixture of three binomial distributions, with probabilities pj (j = 1, 2, 3), where the mixing parameters αkj depend on the generation k following from our model (see Figures 1 and 3B),
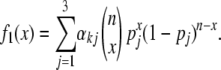 |
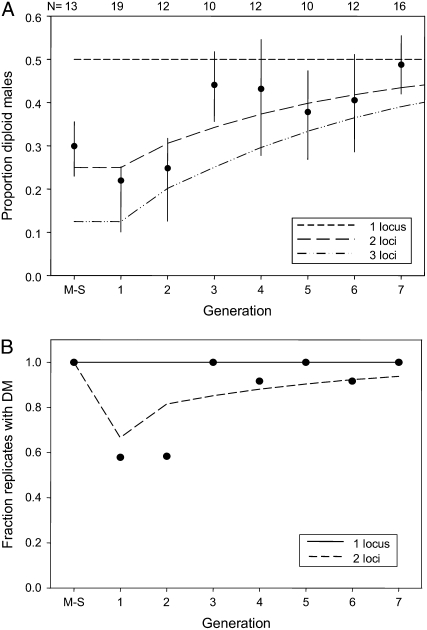
Figure 3.—
Diploid male production by C. vestalis upon a mother–son mating and seven subsequent generations of sib mating. (A) Proportion of DM among total fertilized offspring (vertical lines represent binomial 95% confidence intervals, which were calculated after adding 1 to all observations, and data points represent averages). Model predictions are given for sl-CSD and ml-CSD with two or three independent loci. (B) Fraction of replicates in which at least one DM was found, and predicted fractions of replicates with DM under sl-CSD and two-locus CSD.
We compared the two models using a likelihood-ratio test (Berry and Lindgren 1996), where the null hypothesis was that sl-CSD is true and the alternative hypothesis was that two-locus CSD is true. The negative log-likelihood ratio,
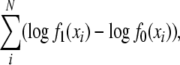 |
where N is the total number of replicates over all generations, was computed using the observed data. The significance of this ratio was obtained by comparing it to the distribution of the negative log-likelihood ratio, assuming the null hypothesis was correct. This distribution was estimated using R (R Development Core Team 2007) to simulate 1000 data sets from sl-CSD and computing the negative log-likelihood ratio for each. Simulated data sets were equal to the observed data set in terms of the number of replicates in each generation and the number of offspring per replicate.
We supplemented this analysis with a number of other tests of ml-CSD predictions. First, we tested for effects of the inbreeding level over the seven generations of brother–sister crosses on the following parameters using linear regression: the number of diploid males, the number of females, and the number of haploid males. The prediction from these analyses for ml-CSD is that the number of diploid males produced increases with inbreeding, the number of females decreases, and haploid males are unaffected by inbreeding. As a related test that corrects for family size, we analyzed the effect of inbreeding level on the ratio between DM and females, using logistic regression (under ml-CSD, this ratio should increase). To assess whether variation in this ratio could be caused by developmental mortality of DM or females or general developmental mortality, we determined Pearson's correlation coefficient for the ratio of DM to females and (1) total number of DM and females and (2) proportion of dead hosts. We also analyzed the effect of inbreeding on the fertilization rate ([diploid males + females]/all adults), using logistic regression (no effect is expected under ml-CSD).
The initial mother–son mating also affords an opportunity to compare the results to hypotheses related to different numbers of loci within ml-CSD. Assuming heterozygosity at all loci in the mother, expected proportions of diploids that are male are 0.5, 0.25, and 0.125 for sl-CSD, two-locus CSD, and three-locus CSD, respectively. We compared our diploid male data to all of these predictions, using t-tests (JMP 2007).
Finally, we used logistic regression to analyze the effect of inbreeding level on sex ratio ([haploid males + diploid males]/all adults) across brother–sister generations, treating sex ratio as a binary response variable using PROC LOGISTIC in SAS/STAT 2006. Here, the expectation under ml-CSD is an increase in the sex ratio (proportion of males) over generations of inbreeding. For all of the analyses that incorporate multiple generations of inbreeding, we used the inbreeding coefficient, F, as opposed to generations of inbreeding as the independent variable. The inbreeding coefficients are 0.5, 0.75, 0.875, 0.938, 0.969, 0.984, 0.992, and 0.996 for the mother–son mating and seven generations of sib mating, respectively (Crow 1986).
RESULTS
Diploid males:
We previously found that C. vestalis produces diploid males after inbreeding but not after outcrossing, thus demonstrating that it has CSD (de Boer et al. 2007a). Here, we inbred C. vestalis wasps for eight generations (a mother–son mating followed by seven generations of sib mating) to disentangle the effects of (1) the number of sex loci and (2) diploid male survivorship. When proportions of DM are low after one or a few generations of inbreeding, this may reflect sl-CSD with low DM survivorship or ml-CSD with high DM survivorship. Continued inbreeding is thus needed to distinguish between these two scenarios: under the first scenario, proportions of DM should remain low, while under the second they should increase, assuming that inbreeding has no effect on developmental survivorship itself (see below). Mother–son matings reduce the potential number of alleles per putative sex locus to two. Therefore, under sl-CSD, 50% of fertilized eggs will result in diploid males in every subsequent sibling generation but under ml-CSD, the proportion of DM will increase gradually with inbreeding (Cook 1993a; Heimpel and de Boer 2008). Our results show that DM production increased with inbreeding level (Figure 3A), a phenotypic pattern that is consistent with the predictions of ml-CSD. We used a likelihood-ratio test to statistically compare how well the predictions of sl-CSD and two-locus CSD fit our data. In this analysis, the sl-CSD scenario was designated as the null model and the two-locus case as the alternative model. The null model was rejected, indicating that the two-locus CSD model fits our data significantly better than does the sl-CSD model (observed negative log-likelihood ratio of 166.0, P < 0.001; the estimated distribution of the negative log-likelihood ratio is approximately normal with mean −63.4 and standard deviation 9.3).
sl-CSD and ml-CSD also differ clearly in the expected fraction of replicates per generation that produced at least one diploid male (Figure 3B). Under sl-CSD, each replicate female in every generation should produce DM. Under ml-CSD, however, each mother–son mating should result in the production of DM, but not every subsequent sibling cross results in the production of DM because some combinations of brothers and sisters are not matched in terms of sex alleles. Under two-locus CSD, three types of sib matings are possible, resulting in DM proportions of 0, 0.25, or 0.50 (Figure 1). Under CSD with three or more (linked) loci, an even wider range of mating types is possible. Our data show that all of the mother–son matings produced DM, but that in sibling generations 1 and 2, ∼60% of replicates produced DM, while >90% of replicates produced DM in sibling generations 3–8. This is consistent with expectations of ml-CSD but not with expectations of sl-CSD.
In addition, the proportion of DM in the mother–son generation can be used to estimate the number of loci involved in CSD because all females in this generation should produce the same proportion of DM, assuming that all of them are heterozygous for all putative sex loci. Given this, the expectation for the proportion of diploids that are male is 0.5 for sl-CSD, 0.25 for two-locus CSD, and 0.125 for three-locus CSD. In our experiment, 0.27 ± 0.036 (SEM) of diploids were male with a normal distribution (Shapiro–Wilks W = 0.92, P > 0.3). This mean differs significantly from expectations under sl-CSD (t-test; t12 = −6.5; one-tailed P < 0.0001) or 3 locus-CSD (t-test, t12 = 4.1, one-tailed P < 0.001) but not from expectations of two-locus CSD (t-test; t12 = 0.6, one-tailed P > 0.25).
Diploid male survival:
We define diploid male survival as the developmental survivorship of DM relative to that of females. Here we explore the possibility that the results in Figure 3A reflect an effect of inbreeding on developmental survivorship of DM or females rather than ml-CSD. An increase in the proportion of DM with inbreeding could still be consistent with sl-CSD either if developmental survival of females decreases with inbreeding or if developmental survival of DM increases with inbreeding. This should be reflected in an effect of inbreeding on the per-family proportion of diploid offspring. This proportion, which is the same as the fertilization rate, was 0.57 ± 0.02 averaged over all generations and was not affected by the level of inbreeding (logistic regression, Wald's χ2 = 1.23, P = 0.27; see also Table 1). A related prediction is that under ml-CSD, the number of diploid males should increase with inbreeding, the number of females should decrease with inbreeding, and the number of haploid males should not be affected by inbreeding. This is in contrast to predictions under sl-CSD, where all of these values should remain unchanged with increased inbreeding following a mother–son mating. Our data are consistent with the predictions for ml-CSD (linear regressions, haploid males, P > 0.05; diploid males, P < 0.001, r2 = 0.14, diploid males = −13.6 + 21.6F; females, P < 0.01, r2 = 0.11, females = 29.3 – 20.1F; F is the inbreeding coefficient). This shows that increasing DM production with inbreeding in C. vestalis results from an increase in diploid males at the expense of females as expected under ml-CSD rather than from changing developmental survivorship of females or DM.
As a related test that corrects for family size, we analyzed the effect of inbreeding level on the ratio between DM and females. This ratio significantly increased with inbreeding (logistic regression, Wald's χ2 = 28.9, P < 0.001; see Figure 3A), inconsistent with sl-CSD but consistent with ml-CSD. Variation in this ratio could still be consistent with sl-CSD if inbreeding affects developmental mortality of DM or females differentially or inbreeding affects general developmental mortality. However, we found no significant relationship between the total number of diploid offspring and the ratio of DM to females (Pearson's correlation, r = 0.14, P = 0.07) or between the proportion of hosts that died and the ratio of DM to females (Pearson's correlation, r = −0.02, P = 0.80).
On the basis of the ratio of DM to females in sibling generations 3–7, where the DM to female ratio was quite stable and >90% of replicates produced at least one diploid male (Figure 3 and Table 1), we estimate DM survivorship to be ∼0.92 ± 0.08. This validates our model assumption and confirms our previous findings (de Boer et al. 2007a).
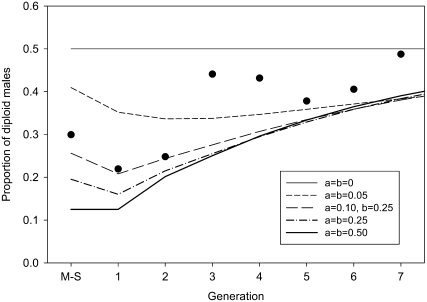
Linkage between the sex loci:
Snell's and Crozier's ml-CSD models assumed that the sex loci were independent (Snell 1935; Crozier 1971). Here, we investigated the effect of linkage between three putative complementary sex loci on the production of DM in our inbreeding experiment (Figure 4) (for the effects of linkage in a single generation of matched mating see Heimpel and de Boer 2008). Our model predictions show that linkage between the sex loci (dashed lines in Figure 4) is predicted to result in a higher proportion of DM in the mother–son mating compared to independent loci (thick solid line in Figure 4). When loci are independent, crossover gametes are produced as often as parental, noncrossover, gametes. When loci are linked, more parental gametes than crossover gametes are produced, with the extreme of only parental gametes when loci are fully linked and act as a single locus (top solid line in Figure 4). Since DM develop from zygotes formed by two identical gametes, the proportion of DM is higher when more parental gametes and fewer crossover gametes are produced.
Figure 4.—
Effect of linkage between three putative sex loci on the predicted proportion of DM among diploid offspring. Crossovers between loci 1 and 2 occur at rate “a” and between loci 2 and 3 at rate “b.” a and b can vary between 0 (fully linked) and 0.5 (independent). Data points represent the average proportion of DM in each generation (see Figure 1 for 95% confidence intervals).
In subsequent sib matings, all daughter genotypes produced by a single mother can potentially pair with the same set of haploid brothers, produced by the same mother. Because each of these daughter genotypes produces its own type of parental and crossover gametes, the initial bias toward a certain genotype of parental gametes is partially averaged out, leading to a lower fraction of DM in the first sib-mating generation than in the mother–son generation. Linkage also leads to a slightly slower approach of the asymptote of DM production than independent loci.
Our data show a reduction in the proportion of DM in the first sib-mating generation compared to the mother–son generation, which might indicate linkage between the putative sex loci in C. vestalis. The marked increase in the proportion of DM in the third sibling generation is not expected under CSD with linked loci. Perhaps this could be explained by differences in sex-determining strength between the sex loci (Crozier 1971). We did not statistically compare how well our data fit ml-CSD with linked loci compared to ml-CSD with independent loci because the variation in proportions of DM within generations in our data compromises the power of such a test.
Sex ratio:
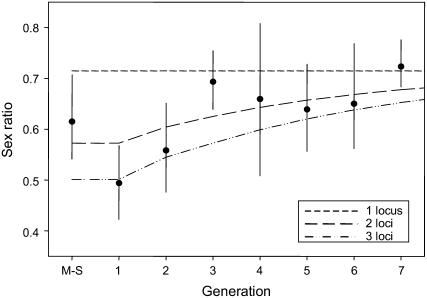
The presence of CSD is often detected or suspected on the basis of male-biased sex ratios that appear under conditions of inbreeding (Heimpel and Lundgren 2000) and we present sex ratio in Figure 5 to allow comparisons with other studies. The secondary sex ratio (proportion of males among adult progeny) is a result of the proportion of DM, the fertilization rate, and the relative survival of haploid males, diploid males, and females. Although C. vestalis can presumably manipulate sex ratio by preferentially withholding or allocating stored sperm, our results show no change in the fertilization rate over the course of eight generations of inbreeding (see above). Thus, the secondary sex ratio is directly related to the proportion of DM and is expected to become increasingly male biased over more than one generation of inbreeding under ml-CSD but not sl-CSD when generations of sib mating follow a mother–son mating. Indeed, the secondary sex ratio of C. vestalis follows a very similar pattern to DM production over eight generations of inbreeding (Figure 5). Sex ratio increased significantly with the level of inbreeding (logistic regression, Wald's χ2 = 17.79, P < 0.001), consistent with ml-CSD but not sl-CSD.
Figure 5.—
Secondary sex ratio (binomial 95% confidence intervals and averages) per generation and predictions under sl-CSD and ml-CSD with two or three independent loci. Predicted sex ratio was calculated as 1 − f + f × dmp, where f is the fertilization rate (we used the average of 0.57 found across all generations), and dmp is the generation-specific predicted proportion of DM following from our model.
DISCUSSION
Multiple locus-CSD was first proposed in 1935 but until now convincing experimental support was lacking. Several studies suggested their results might be better explained by ml-CSD rather than sl-CSD (Garofolo 1973; Kerr 1974; Naito et al. 2000), while others found no support for ml-CSD in a range of other species (Skinner and Werren 1980; Cook 1993a; Periquet et al. 1993; Butcher et al. 2000; Niyibigira et al. 2004a; Schrempf et al. 2006). Here, we show that inbreeding the braconid wasp C. vestalis for eight generations results in increasing proportions of DM and an increasingly male-biased sex ratio (Figures 3 and 4). This phenotype is consistent with predictions of ml-CSD but not with those of sl-CSD. However, an increase in the proportion of DM among diploid offspring might in principle also be explained by decreased survivorship of females with inbreeding or increased survivorship of DM with inbreeding. This should lead to a significant effect of inbreeding on the proportion of diploids among all offspring. Because we failed to find such a relationship, the pattern of DM increase with inbreeding is best explained by ml-CSD. Our data from the mother–son crosses allowed for a direct test of the number of loci involved and that suggests that two loci are more likely than more loci. To confirm that multiple complementary sex loci form the basis of sex determination in C. vestalis, genetic mapping studies are underway. Discovery of the ml-CSD phenotype leads to questions about the potential regulatory pathways and evolution of such a mechanism of sex determination. We discuss these questions here in light of our new data and the predictions of our revised ml-CSD model, which includes linkage between the putative loci.
How might multiple complementary sex loci result in the initiation of female and male development? In Crozier's original model, females would develop from zygotes that have at least one heterozygous sex locus, irrespective of which sex locus this is (Crozier 1971). Males develop from haploid zygotes and from diploid zygotes that are homozygous at each of the sex loci. When Crozier proposed ml-CSD, sl-CSD was not yet understood at the molecular level. Cloning and sequencing of the complementary sex determiner gene (csd) in honeybees provided a major breakthrough in this respect (Beye et al. 2003). Allelic variants in csd were detected (Hasselmann and Beye 2004) and on the basis of this information Beye developed three models that could explain how csd determines sex within the context of haplodiploidy (Beye 2004). All models are based upon the assumption of a single sex locus. In the first model, products of the two divergent sex alleles in females combine to form a heterodimer that activates the female-producing pathway while no dimer is formed in males. In the second model, homodimers are formed in both males and females, but the fact that females have two distinct types of homodimers initiates the female pathway. In the third model, the transcripts from the divergent alleles in females complement each other's activity to initiate female development. Beye's models are hypothetical and designed to be consistent with two observations: (i) haploid individuals are always male, and (ii) interference with the csd transcript (by RNAi) turns genetic females into males, but interference with csd transcripts in haploid males does not lead to the production of females (Beye et al. 2003; Beye 2004). But how do these models stand up to ml-CSD? If additional sex loci arose via duplication of the first locus (see below), and products of alleles from the first locus can interact with products of alleles from additional sex loci in a similar way to products of two different alleles at a single locus, then all three of Beye's models would predict the production of haploid females and no diploid males under ml-CSD. Haploid females have recently been found in N. vitripennis, but this species does not exhibit sl-CSD or ml-CSD, and haploid females were attributed to a failure in maternal imprinting of an unknown sex determination gene (Beukeboom et al. 2007; Kamping et al. 2007). Interaction between products of different sex loci similar to interaction between products of a single sex locus seems very unlikely because the female pathway would be activated in haploid individuals and males would be entirely absent. We therefore expect no interaction between the products of multiple complementary sex loci. To summarize this section, we currently have no clear explanation of how ml-CSD might function. More insight into the sex determination pathway in species with sl-CSD, especially the honeybee, could provide a basis upon which we can build hypotheses for ml-CSD.
How might ml-CSD have evolved? sl-CSD is generally thought to be ancestral within the Hymenoptera (Cook 1993b; van Wilgenburg et al. 2006). ml-CSD might have evolved from sl-CSD by one or more duplications of the sex locus. Duplications of genes occur quite frequently, through tandem duplication of the entire gene, segmental duplication of part of a gene, chromosome duplication, or global duplication of the entire genome (Graur and Li 1999). For example, a survey of the Drosophila melanogaster genome revealed the presence of 106 recently duplicated genes (Clement et al. 2006). Many duplicate genes become dysfunctional (pseudogenes) but genes can be retained by changes in the protein-coding domain, or by changes in regulatory elements, leading to different spatial or temporal gene expression (Force et al. 1999; Prince and Pickett 2002). For example, the Sex lethal gene in Drosophila probably arose by duplication and acquired its function in sex determination, while the ancestral gene (CG3056) continued to serve yet-unknown functions (Traut et al. 2006). In the honeybee Apis mellifera two sex determination genes have been identified, csd and fem, with csd alleles showing signatures of balancing selection (Hasselmann and Beye 2004). The gene fem (previously designated as “type II csd alelles”) appears to be the progenitor of csd, so that csd may represent a duplication event from fem (Hasselmann et al. 2008a). However, fem shows low variability and no signature of balancing selection (Hasselmann and Beye 2004, 2006; Hasselmann et al. 2008a,b) and does therefore not appear to function as a second csd locus as envisioned under ml-CSD.
In the case of duplication of the sex locus in species with sl-CSD, selection on retention of the duplicated gene is expected to be strong because a second functional locus should significantly reduce the genetic load under inbreeding. How strong this selection is depends on the level of linkage between the original gene and its duplicate (see below, Figure 4). Theoretically, ml-CSD may also evolve from sl-CSD if an unrelated locus acquires a function in the sex determination pathway in such a way that heterozygosity of the second locus is important in initiating female development. Interestingly, QTL analysis showed that several minor loci may be involved in sex determination in the parasitoid Habrobracon sp. near hebetor, a species with a clear sl-CSD phenotype (Holloway et al. 2000).
We investigated the effect of linkage between the putative sex loci on predicted DM production. Snell (1935) and later Crozier (1971) proposed independent sex loci under ml-CSD (Snell 1935; Crozier 1971) but this may be unlikely if additional loci arose through duplication(s). Compared to independent loci, linkage leads to higher predicted DM proportions in the mother–son mating and a drop in the subsequent sib-mating generation (Figure 4). Visually, our data follow this pattern, which may indicate that linkage between the putative sex loci indeed plays a role, but we did not statistically compare the fit of a linkage model to our data. An alternative explanation for the relatively high DM proportion in the mother–son mating may be that the females were kept at 10° for ∼12 days while their sons developed. Sex determination in N. vitripennis appears to be influenced by the age of the mother and by temperature (Beukeboom and Kamping 2006; Kamping et al. 2007), and some studies have suggested a temperature effect on DM production under CSD (Whiting and Anderson 1932; but see Weiser et al. 2004).
Our model also shows that three rather tightly linked sex loci result in a significant reduction in DM production, compared to fully linked loci acting as a single locus (Figure 4). Recombination rates around the sex locus in honeybees are much higher than the average recombination rate in the honeybee genome (Beye et al. 1999; Hasselmann and Beye 2006). This could be an important advantage if the sex locus were duplicated because it reduces the chance of the two genes inheriting as a single locus, defeating an advantage over a single csd gene. However, whether recombination rates around the sex locus are also high in other species with CSD is not known.
On the practical side, linkage between the sex loci makes distinguishing ml-CSD from sl-CSD more difficult because of the continuum of predicted DM levels for a single generation of inbreeding (Heimpel and de Boer 2008). We therefore stress the importance of employing multiple generations of inbreeding and of initiating experiments with genetically diverse material.
To conclude, we have confirmed that the pattern of DM production in C. vestalis is consistent with ml-CSD but not with sl-CSD. Further, our results are most consistent with two-locus CSD. This in itself does not prove the existence of ml-CSD, but it is a strong indication, with important implications for research on sex determination in the Hymenoptera. In particular, studying species that potentially possess ml-CSD might provide more insight into the mechanisms of CSD, and comparative studies on species with different modes of sex determination will provide insight into the evolution of this important trait in the Hymenoptera. The braconid genus Cotesia could provide a valuable system for comparative studies because it comprises species with presumed sl-CSD (C. glomerata), ml-CSD (C. vestalis), and no CSD (C. sesamiae, C. flavipes) (Gu and Dorn 2003; Niyibigira et al. 2004a,b; Zhou et al. 2006; de Boer et al. 2007a,b). A similar diversity of sex determining systems can be found more broadly in the Braconidae as well (Beukeboom et al. 2000; Wu et al. 2005; van Wilgenburg et al. 2006). Another interesting group is the ant family, Formicidae, because many species are believed to have sl-CSD (van Wilgenburg et al. 2006), but it appears to be absent in the inbreeding ant Cardiocondyla batesii (Schrempf et al. 2006). Also, a number of socially parasitic ants engage in inbreeding, bringing into question whether they have sl-CSD (Crozier and Pamilo 1996). Sex determination and inbreeding are intimately related in the Hymenoptera (Hamilton 1967), and population-level consequences of CSD are potentially severe (Zayed and Packer 2005). Fundamental knowledge on sex determination could be used to improve the effectiveness with which hymenopterans are used as biological control agents of pest insects and as pollinators (Stouthamer et al. 1992; Heimpel et al. 1999; Heimpel and Lundgren 2000; Antolin et al. 2003; Ode and Hardy 2008). In addition, knowledge of the genetics of sex determination could be used in conservation management of natural populations of pollinating hymenopterans, many of which are declining (Zayed and Packer 2005; Biesmeijer et al. 2006).
Acknowledgments
We thank Dominique Bordat for supplying C. vestalis from Benin; Lynn Knutson, Laura Stone, Dan Barta, Virginia Howick, and Beth Sandager for rearing assistance; Remco van Poecke for his help in modifying the ml-CSD model; Greg Veltri of the Flow Cytometry Core Lab at the University of Minnesota Cancer Center for his help in the flow cytometry analyses; Zhishan Wu for letting us use facilities at the University of Minnesota/Minnesota Department of Agriculture Quarantine Facility; and Leo Beukeboom for comments on a previous version of the manuscript. This study was supported by the National Science Foundation and the University of Minnesota Agricultural Experiment Station.
References
- Antolin, M. F., P. J. Ode, G. E. Heimpel, R. B. O'Hara and M. R. Strand, 2003. Population structure, mating system, and sex determining allele diversity of the parasitoid wasp Habrobracon hebetor. Heredity 91 373–381. [DOI] [PubMed] [Google Scholar]
- Berry, D. A., and B. W. Lindgren, 1996. Statistics: Theory and Methods. Duxbury Press, Belmont, CA.
- Beukeboom, L. W., and A. Kamping, 2006. No patrigenes required for femaleness in the haplodiploid wasp Nasonia vitripennis. Genetics 172 981–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beukeboom, L. W., J. Ellers and J. J. M. van Alphen, 2000. Absence of single-locus complementary sex determination in the braconid wasps Asobara tabida and Alysia manducator. Heredity 84 29–36. [DOI] [PubMed] [Google Scholar]
- Beukeboom, L. W., A. Kamping and L. van de Zande, 2007. Sex determination in the haplodiploid wasp Nasonia vitripennis (Hymenoptera: Chalcidoidea): a critical consideration of models and evidence. Semin. Cell Dev. Biol. 18 371–378. [DOI] [PubMed] [Google Scholar]
- Beye, M., 2004. The dice of fate: the csd gene and how its allelic composition regulates sexual development in the honey bee, Apis mellifera. BioEssays 26 1131–1139. [DOI] [PubMed] [Google Scholar]
- Beye, M., G. J. Hunt, R. E. Page, M. K. Fondrk, L. Grohmann et al., 1999. Unusually high recombination rate detected in the sex locus region of the honey bee (Apis mellifera). Genetics 153 1701–1708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beye, M., M. Hasselmann, M. K. Fondrk, R. E. Page and S. W. Omholt, 2003. The gene csd is the primary signal for sexual development in the honeybee and encodes an SR-type protein. Cell 114 419–429. [DOI] [PubMed] [Google Scholar]
- Biesmeijer, J. C., S. P. M. Roberts, M. Reemer, R. Ohlemuller, M. Edwards et al., 2006. Parallel declines in pollinators and insect-pollinated plants in Britain and the Netherlands. Science 313 351–354. [DOI] [PubMed] [Google Scholar]
- Bull, J. J., 1983. Evolution of Sex Determining Mechanisms. Benjamin/Cummings Publishing, Menlo Park, CA.
- Butcher, R. D. J., W. G. F. Whitfield and S. F. Hubbard, 2000. Complementary sex determination in the genus Diadegma (Hymenoptera: Ichneumonidae). J. Evol. Biol. 13 593–606. [DOI] [PubMed] [Google Scholar]
- Clement, Y., R. Tavares and G. A. B. Marais, 2006. Does lack of recombination enhance asymmetric evolution among duplicate genes? Insights from the Drosophila melanogaster genome. Gene 385 89–95. [DOI] [PubMed] [Google Scholar]
- Cook, J. M., 1993. a Experimental tests of sex determination in Goniozus nephantidis (Hymenoptera: Bethylidae). Heredity 71 130–137. [Google Scholar]
- Cook, J. M., 1993. b Sex determination in the Hymenoptera: a review of models and evidence. Heredity 71 421–435. [Google Scholar]
- Cook, J. M., and R. H. Crozier, 1995. Sex determination and population biology in the Hymenoptera. Trends Ecol. Evol. 10 281–286. [DOI] [PubMed] [Google Scholar]
- Cowan, D. P., and J. K. Stahlhut, 2004. Functionally reproductive diploid and haploid males in an inbreeding hymenopteran with complementary sex determination. Proc. Natl. Acad. Sci. USA 101 10374–10379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow, J. F., 1986. Basic Concepts in Population, Quantitative, and Evolutionary Genetics. W. H. Freeman, New York.
- Crozier, R. H., 1971. Heterozygosity and sex determination in haplo-diploidy. Am. Nat. 105 399–412. [Google Scholar]
- Crozier, R. H., 1975. Animal Cytogenetics 3. Insecta (7) Hymenoptera. Gebruder Borntraeger, Berlin/Stuttgart, Germany.
- Crozier, R. H., and P. Pamilo, 1996. Evolution of Social Insect Colonies: Sex Allocation and Kin Selection. Oxford University Press, Oxford.
- de Boer, J. G., P. J. Ode, L. E. M. Vet, J. Whitfield and G. E. Heimpel, 2007. a Complementary sex determination in the parasitoid wasp Cotesia vestalis (C. plutellae). J. Evol. Biol. 20 340–348. [DOI] [PubMed] [Google Scholar]
- de Boer, J. G., P. J. Ode, L. E. M. Vet, J. B. Whitfield and G. E. Heimpel, 2007. b Diploid males sire triploid daughters and sons in the parasitoid Cotesia vestalis. Heredity 99 288–294. [DOI] [PubMed] [Google Scholar]
- Force, A., M. Lynch, F. B. Pickett, A. Amores, Y. L. Yan et al., 1999. Preservation of duplicate genes by complementary, degenerative mutations. Genetics 151 1531–1545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galbraith, D. W., K. R. Harkins, J. M. Maddox, N. M. Ayres, D. P. Sharma et al., 1983. Rapid flow cytometric analysis of the cell cycle in intact plant tissues. Science 220 1049–1051. [DOI] [PubMed] [Google Scholar]
- Garofolo, C. A., 1973. Occurrence of diploid drones in a neotropical bumblebee. Experientia 29 726–727. [Google Scholar]
- Graur, D., and W. H. Li, 1999. Fundamentals of Molecular Evolution. Sinauer Associates, Sunderland, MA.
- Gu, H. N., and S. Dorn, 2003. Mating system and sex allocation in the gregarious parasitoid Cotesia glomerata. Anim. Behav. 66 259–264. [Google Scholar]
- Hamilton, W. D., 1967. Extraordinary sex ratios. Science 156 477–488. [DOI] [PubMed] [Google Scholar]
- Hasselmann, M., and M. Beye, 2004. Signatures of selection among sex-determining alleles of the honey bee. Proc. Natl. Acad. Sci. USA 101 4888–4893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmann, M., and M. Beye, 2006. Pronounced differences of recombination activity at the sex determination locus of the honeybee, a locus under strong balancing selection. Genetics 174 1469–1480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmann, M., T. Gempe, M. Schiott, C. G. Nunes-Silva, M. Otte et al., 2008. a Evidence for the evolutionary nascence of a novel sex determination pathway in honeybees. Nature 454 519–523. [DOI] [PubMed] [Google Scholar]
- Hasselmann, M., X. Vekemans, J. Pflugfelder, N. Koeniger, G. Koeniger et al., 2008. b Evidence for convergent nucleotide evolution and high allelic turnover rates at the complemetary sex determiner gene of western and Asian honeybees. Mol. Biol. Evol. 25 696–708. [DOI] [PubMed] [Google Scholar]
- Heimpel, G. E., and J. G. de Boer, 2008. Sex determination in the Hymenoptera. Annu. Rev. Entomol. 53 209–230. [DOI] [PubMed] [Google Scholar]
- Heimpel, G. E., and J. G. Lundgren, 2000. Sex ratios of commercially reared biological control agents. Biol. Control 19 77–93. [Google Scholar]
- Heimpel, G. E., M. F. Antolin and M. R. Strand, 1999. Diversity of sex-determining alleles in Bracon hebetor. Heredity 82 282–291. [DOI] [PubMed] [Google Scholar]
- Holloway, A. K., G. E. Heimpel, M. R. Strand and M. F. Antolin, 1999. Survival of diploid males in Bracon sp. near hebetor (Hymenoptera: Braconidae). Ann. Entomol. Soc. Am. 92 110–116. [Google Scholar]
- Holloway, A. K., M. R. Strand, W. C. Black and M. F. Antolin, 2000. Linkage analysis of sex determination in Bracon sp near hebetor (Hymenoptera: Braconidae). Genetics 154 205–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- JMP, 2007. JMP 2007. SAS Institute, Cary, NC.
- Kamping, A., V. Katju, L. W. Beukeboom and J. H. Werren, 2007. Inheritance of gynandromorphism in the parasitic wasp Nasonia vitripennis. Genetics 175 1321–1333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerr, W. E., 1974. Advances in cytology and genetics of bees. Annu. Rev. Entomol. 19 253–268. [Google Scholar]
- Marin, I., and B. S. Baker, 1998. The evolutionary dynamics of sex determination. Science 281 1990–1994. [DOI] [PubMed] [Google Scholar]
- Naito, T., M. Ishikawa and Y. Nishimoto, 2000. Two-locus multiple-allele sex determination in the rose sawfly Arge nigrinodosa. Third International Hymenopteran Congress, Canberra, Australia.
- Niyibigira, E. I., W. A. Overholt and P. Stouthamer, 2004. a Cotesia flavipes Cameron (Hymenoptera: Braconidae) does not exhibit complementary sex determination (ii): evidence from laboratory experiments. Appl. Entomol. Zool. 39 717–725. [Google Scholar]
- Niyibigira, E. I., W. A. Overholt and R. Stouthamer, 2004. b Cotesia flavipes Cameron and Cotesia sesamiae (Cameron) (Hymenoptera: Braconidae) do not exhibit complementary sex determination: evidence from field populations. Appl. Entomol. Zool. 39 705–715. [Google Scholar]
- Ode, P. J., and I. C. W. Hardy, 2008. Parasitoid sex ratios and biological control, pp. 253–291 in Behavioral Ecology of Insect Parasitoids, edited by E. Wajnberg, C. Bernstein and J. J. M. van Alpen. Blackwell Publishing, Oxford.
- Periquet, G., M. P. Hedderwick, M. Elagoze and M. Poirie, 1993. Sex determination in the hymenopteran Diadromus pulchellus (Ichneumonidae): validation of the one-locus multi-allele model. Heredity 70 420–427. [Google Scholar]
- Prince, V. E., and F. B. Pickett, 2002. Splitting pairs: the diverging fates of duplicated genes. Nat. Rev. Genet. 3 827–837. [DOI] [PubMed] [Google Scholar]
- R Development Core Team, 2007. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna.
- Schrempf, A., S. Aron and J. Heinze, 2006. Sex determination and inbreeding depression in an ant with regular sib-mating. Heredity 97 75–80. [DOI] [PubMed] [Google Scholar]
- Schütt, C., and R. Nöthiger, 2000. Structure, function and evolution of sex-determining systems in Dipteran insects. Development 127 667–677. [DOI] [PubMed] [Google Scholar]
- Shaw, M. R., 2003. Revised synonymy in the genus Cotesia (Hymenoptera: Braconidae: Microgastrinae): the identity of Microgaster vestalis Haliday, 1834, as a senior synonym of Apanteles plutellae Kurdjumov, 1912. Entomol. Gazette 54 187–189. [Google Scholar]
- Shelton, A. M., R. J. Cooley, M. K. Kroening, M. T. Wilsey and S. D. Eigenbrode, 1991. Comparative analysis of two rearing procedures for diamondback moth. J. Entomol. Sci. 26 17–26. [Google Scholar]
- Skinner, S. W., and J. H. Werren, 1980. The genetics of sex determination in Nasonia vitripennis (Hymenoptera, Pteromalidae). Genetics 94 s98. [Google Scholar]
- Snell, G. D., 1935. The determination of sex in Habrobracon. Proc. Natl. Acad. Sci. USA 21 446–453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stouthamer, R., R. F. Luck and J. H. Werren, 1992. Genetics of sex determination and the improvement of biological control using parasitoids. Environ. Entomol. 21 427–435. [Google Scholar]
- Traut, W., T. Mimi, K. Ikeo and K. Sahara, 2006. Phylogeny of the sex-determining gene Sex-lethal in insects. Genome 49 254–262. [DOI] [PubMed] [Google Scholar]
- van Wilgenburg, E., G. Driessen and L. W. Beukeboom, 2006. Single locus complementary sex determination in Hymenoptera: an “unintelligent” design? Front. Zool. 3 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiser, L., M. F. Antolin, Z. Wu and G. E. Heimpel, 2004. Does temperature affect diploid male production in Habrobracon hebetor (Say) (Hymenoptera: Braconidae)? J. Hymenopt. Res. 13 309–315. [Google Scholar]
- Whiting, P. W., 1943. Multiple alleles in complementary sex determination of Habrobracon. Genetics 28 365–382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whiting, P. W., and R. L. Anderson, 1932. Temperature and other factors concerned in male biparentalism in Habrobracon. Am. Nat. 56 420–432. [Google Scholar]
- Wu, Z., K. R. Hopper, P. J. Ode, R. Fuester, M. Tuda et al., 2005. Single-locus complementary sex determination absent in Heterospilus prosopidis (Hymenoptera: Braconidae). Heredity 95 228–234. [DOI] [PubMed] [Google Scholar]
- Zayed, A., 2004. Effective population size in Hymenoptera with complementary sex determination. Heredity 93 627–630. [DOI] [PubMed] [Google Scholar]
- Zayed, A., and L. Packer, 2005. Complementary sex determination substantially increases extinction proneness of haplodiploid populations. Proc. Natl. Acad. Sci. USA 102 10742–10746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou, Y., H. Gu and S. Dorn, 2006. Single-locus sex determination in the parasitoid wasp Cotesia glomerata (Hymenoptera: Braconidae). Heredity 96 487–492. [DOI] [PubMed] [Google Scholar]