Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2008 Nov;180(3):1679–1690. doi: 10.1534/genetics.108.090969

Selective Transcriptional Profiling and Data Analysis Strategies for Expression Quantitative Trait Loci Mapping in Outbred F2 Populations

Fernando F Cardoso *,†,1, Guilherme J M Rosa ‡, Juan P Steibel †, Catherine W Ernst †, Ronald O Bates †, Robert J Tempelman †
PMCID: PMC2581967  PMID: 18791244

Abstract

Genetic analysis of transcriptional profiling experiments is emerging as a promising approach for unraveling genes and pathways that underlie variation of complex biological traits. However, these genetical genomics approaches are currently limited by the high cost of microarrays. We studied five different strategies to optimally select subsets of individuals for transcriptional profiling, including (1) maximizing genetic dissimilarity between selected individuals, (2) maximizing the number of recombination events in selected individuals, (3) selecting phenotypic extremes within inferred genotypes of a previously identified quantitative trait locus (QTL), (4) purely random selection, and (5) profiling animals with the highest and lowest phenotypic values within each family–gender subclass. A simulation study was conducted on the basis of a linkage map and marker genotypes were derived from data on chromosome 6 for 510 F2 animals from an existing pig resource population and on a simulated biallelic QTL with pleiotropic effects on performance and gene expression traits. Bivariate analyses were conducted for selected subset sample sizes of 80, 160, and 240 individuals under three different correlation scenarios between the two traits. The genetic dissimilarity and phenotypic extremes within genotype methods had the smallest mean square error on QTL effects and maximum sensitivity on QTL detection, thereby outperforming all other selection strategies, particularly at the smallest proportion of samples selected for gene expression profiling (80/510).

GENETIC analysis of transcriptional profiling experiments has emerged as a promising approach to unravel genes and gene networks underlying variation of complex biological traits. This new field of study, also called genetical genomics (Jansen and Nap 2001), applies linkage analysis to gene expression data derived from microarray experiments as if they were classical quantitative traits. Hence DNA sequence variation is related to variation in gene expression in the search for a better understanding of transcriptional regulation (Brem et al. 2002; Schadt et al. 2003; Yvert et al. 2003). The genetic basis for transcriptional abundance is described by its association with locations of the linkage map, i.e., the expression quantitative trait loci (eQTL), and its polygenic heritability (Schadt et al. 2003; Gibson and Weir 2005). Because each transcript has a corresponding encoding gene with a known position in the genome, eQTL can be regarded as having “local” regulation, when mapped near the genomic location of the gene encoding the transcript, or “distant” regulation, when mapped elsewhere in the genome (Rockman and Kruglyak 2006). Combining information on local eQTL and coincident QTL for economically relevant traits (ERT) such as weight gain provides a compelling strategy to identify candidate genes (CG) for use in breeding programs (Nettleton and Wang 2006).

The design of genetical genomics experiments, nevertheless, is currently challenged by the high cost of microarrays, which limits the sample size for global genetic mapping of transcript abundance relative to what is possible for ERT. This is particularly true for eQTL mapping in large livestock studies with limited budgets. Conversely, the relative cost of genotyping is smaller, particularly with the use of high-throughput chips, such that the number of genotyped individuals available can be substantially larger than that used for gene expression profiling. Consequently, several methods based on the use of selective phenotyping (Darvasi 1998) have been proposed to determine optimally chosen subsets of individuals for microarray experiments when gene expression profiling requires substantially more resources than genotyping on a per subject basis.

The proposed methods differ in the nature and amount of prior information required and their intended purposes. The particular strategy proposed by Jin et al. (2004) uses genetic marker data to select a subset of individuals for expression profiling by maximizing their genotypic dissimilarity; they demonstrated substantial improvements with their strategy for the sensitivity of QTL detection compared to a random sample of equal size. Other selective phenotyping/profiling strategies use marker genotypes to select a subsample, on the basis of maximizing the balance and number of crossover events (Jannink 2005; Xu et al. 2005). These recombination-based methods are intended to improve the precision of QTL location compared to random subset selection, whereas selecting a subsample that is as dissimilar as possible between individuals with respect to marker genotypes flanking the QTL (as in Jin et al. 2004) should retain better power of QTL detection and precision of QTL effects estimates (Rosa et al. 2006a). Finally, Wang and Nettleton (2006) proposed a selective profiling strategy that utilizes information on a correlated quantitative ERT for which a QTL has been identified, based on a full set of ERT data and molecular markers flanking the QTL. This method involves selecting individuals with extreme ERT responses within each genotype of the identified QTL such that its primary goal is to find genes whose expression is associated with the pleiotropic QTL (i.e., eQTL = QTL) and/or correlated with the ERT itself (Nettleton and Wang 2006).

In this study, we investigate variations of formerly proposed selective phenotyping/profiling strategies, namely, the genetic dissimilarity method of Jin et al. (2004), the maximum-recombination (maxRec) method of Jannink (2005), and the method of Wang and Nettleton (2006) for use with outbred F2 resource populations as typical of livestock studies. Two additional selective profiling strategies were also examined, one being purely random selection of a subset of animals and the other based on profiling only animals with the highest and lowest trait values within subclasses (Rosa et al. 2006b). We compared the performance of these selective profiling strategies in terms of sensitivity and specificity of QTL detection and the precision of inference on the corresponding QTL location and effect. Moreover, we compare alternative statistical modeling approaches to analyze selectively profiled expression data that vary in the manner in which they utilize information on a completely recorded and correlated ERT. These analysis methods are (1) a bivariate mixed-model analysis of ERT and CG, (2) using the ERT as a covariate for CG expression, and (3) completely ignoring ERT in a conventional single-trait mixed-model analysis on CG expression. The comparisons were considered at different levels of correlations between the recorded ERT and CG expression and at different selection proportions of individuals chosen for selective profiling.

MATERIALS AND METHODS

Simulations:

This study was conducted assuming that ERT records were available on all animals and that a QTL scan has been conducted, leading to a putative QTL identified for a particular ERT (e.g., back fat 10th rib or loin muscle area in swine). Simulated data sets for each of two correlated phenotypes, the ERT and a correlated transcriptional abundance or expression of a particular CG, were generated on the basis of bivariate mixed-effects models. We were particularly interested in situations where the ERT and the CG expression were correlated and both were affected by the same segregating pleiotropic QTL. In this case, the corresponding probe would be a potential CG for the ERT QTL, thereby providing a powerful way of understanding the molecular genetic mechanisms underlying variation in a traditional quantitative trait (Nettleton and Wang 2006).

Linkage map and genetic marker data:

To mimic an ongoing genetical genomics experiment from an existing resource population, characterized by typical data features (uninformative genotypes, missing markers, unequally spaced markers, different number of marker alleles, etc.), we used the linkage map and marker genotypes derived from the Michigan State University pig resource population (MSUPRP). This population was based on an F2 design, originating from F0 Pietran females and Duroc males, and developed to discover genes associated with production and meat quality (Edwards et al. 2008a,b). Full details on this population development and structure are available in Edwards (2005). Chromosome 6 served as the basis for this simulation study. There were eight markers available in the linkage map, spaced between 5.8 and 31.8 cM from each other, as described in Table 1.

TABLE 1.

Genetics markers on pig chromosome 6 (SSC6) and their respective map locations (centimorgans) relative to marker S0099, the number of F2 individuals with missing genotypes, the number of alleles, and the polymorphism information content for each marker locus

Genetic marker Map location No. of missing F2 genotypes No. of alleles Polymorphism information content
S0099 0 42 5 0.7231
SW2406 22.4 6 5 0.5157
SW2525 50.6 10 4 0.5535
S0087 81.3 10 4 0.4781
S0220 98.1 13 2 0.2717
SW122 103.9 9 5 0.6357
SW1881 135.7 26 4 0.5809
SW322 164.8 3 7 0.7154
SW2419 181 12 7 0.7533
Open in a new tab

The polymorphism information content was obtained as proposed by Botstein et al. (1980).

A biallelic QTL located at position 92 cM, about two-thirds of the distance between markers S0087 and S0220, was simulated with pleiotropic effects, explaining 10% of the phenotypic variance for both CG expression and ERT. The two alleles were fixed within each base F0 founder breed, A and B. Using the actual microsatellite marker genotypes observed in 510 F2, 54 F1, and 19 F0 pigs, marker phase probabilities for the F0 were calculated using the MCMC algorithm available from QxPak (Perez-Enciso and Misztal 2004). These probabilities were used to simulate the phases of the F0, which were then used to determine the conditional probabilities to subsequently draw random samples of the F1 phases when they were deemed to be ambiguous from marker data. Finally, the phase simulation step was concluded by determining the probabilities used to subsequently draw random samples of the phases of the F2 individuals conditional upon the F0 and F1 sampled phases. Once all the marker phases were assigned, the probabilities of inheriting alternate alleles of the QTL were calculated on the basis of the observed marker distances and marker genotypes, simulated phases, and recombination based on the Haldane map function. These probabilities were in turn used to simulate the inheritance of the QTL alleles.

Data generation:

Data records were generated from a bivariate normal distribution with the model

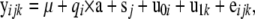graphic file with name M1.gif

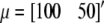where Inline graphic is the 2 × 1 vector of correlated records on the two responses (ERT phenotype and CG expression) of individual i having sex j and belonging to family k, Inline graphic is the overall mean vector, 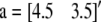Inline graphic is the vector of additive QTL allele substitution effects, sj is the vector of sex effects (j = 1 for males with 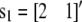Inline graphic and j = 2 for females with 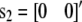Inline graphic), u0i is the vector of polygenic effects, 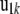Inline graphic is the vector of full-sib family effects, 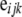Inline graphic is the vector of residual errors, and qi indicates the number of QTL alleles originating from breed A for individual i.

Distributional assumptions on the random effects were

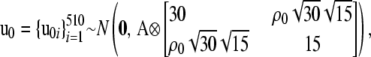graphic file with name M9.gif
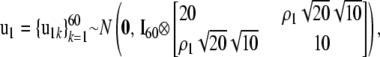graphic file with name M10.gif

and

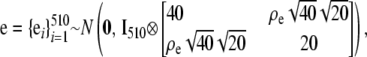graphic file with name M11.gif

where A is the numerator relationship matrix of the MSUPRP and and Ip represents an identity matrix of dimension p. Here, the dimension, p = 510, of u0 matches the number of F2 individuals whereas the dimension, p = 60, of u1 matches the number of full-sib families. Note that full-sib family effects specify environmental and maternal effects that might be common to sibs.

To check robustness of each selective profiling approach and data analysis strategy to differences in the correlations between trait and expression, three alternative scenarios were also simulated: a high correlation scenario (ρ0 = 0.71, ρ1 = 0.92, and ρe = 0.82), a medium correlation scenario (ρ0 = −0.47, ρ1 = −0.49, and ρe = 0.53), and a low correlation scenario (ρ0 = 0.19, ρ1 = 0.21, and ρe = 0.21). Negative correlations were considered in the medium correlation scenario as Sorensen et al. (2003) demonstrated that bivariate QTL mapping was particularly most efficient relative to the conventional univariate mapping when the contributions of the QTL and of the polygenic components to the genetic correlation between the two traits have opposite signs.

Two hundred replicates were generated for each of the three correlation scenarios.

Selective profiling strategies:

For each generated bivariate data set, five different selective profiling strategies based on three different proportions of animals selected were applied to retain a subset of records for the CG expression phenotype. These profiling strategies are listed as follows:

  • Strategy 1. Random selection of individuals across F2 families.

  • Strategy 2. Phenotypic within-family selection based on choosing the most extreme males and females for the ERT phenotype within each family: Again, family size and distribution of sexes within families were based on those actually observed from the MSUPRP. Not all of the 60 families (litters) had enough males and females for higher proportions of animals selected; therefore, in those cases where a larger average number of individuals per family were chosen for profiling, more individuals were selected from larger families than from smaller families.

  • Strategy 3. Line dissimilarity selection based on the proposal of Jin et al. (2004): Note, however, that because of our use of microsatellite markers on a cross between outbred lines, our similarity measure was based on the estimated line of origin probabilities rather than on the number of marker alleles shared at each locus. To compute the similarity between two individuals, we used the haplotype samples generated at each MCMC cycle by QxPak. We traced the line of origin of each marker allele in pig chromosome 6 (SSC6) as being either A or B for each cycle and assigned the shared number of alleles deriving from the same line of origin between two individuals as their similarity measure. A posterior mean similarity between each pair of individuals was based on 1000 cycles of the MCMC algorithm. The subsample with the lowest pairwise posterior mean similarities was used to selectively profile individuals of a certain subset size across the entire F2 population, as similar to Jin et al. (2004).

  • Strategy 4. Phenotypic within-genotype selection as proposed by Wang and Nettleton (2006): On the basis of the calculated line of origin probabilities from the MCMC algorithm of QxPak at position 92 cM (i.e., the QTL location), F2 individuals were assigned to the QTL genotype group (AA, AB, or BB) that they had the highest probability of belonging to. The most extreme individuals (highest and lowest observed values) for the ERT from groups AA and BB were selected. Individuals from the homozygous groups were preferred because these are the most informative groups when searching for QTL with additive effects (Rosa et al. 2006a). Nevertheless, some extreme individuals from AB were needed to complete the set when the sample size chosen for selective profiling exceeded the number of individuals assigned to the two homozygous genotype groups.

  • Strategy 5. Maximum-recombination selection based on maximizing the number of recombinant genotypes in the selected samples, using the principles of maxRec (Jannink 2005): Within each MCMC cycle, we considered a marker interval to be recombinant for an F2 individual if the two flanking markers derived from a different line of origin, assuming that the probability of multiple recombinations was zero. The sum of the posterior probabilities of recombination was used to identify and selectively profile individuals as having the greatest probability of inheriting recombinant gametes. These probabilities were obtained by summing the proportion of times that each of the 16 marker intervals (8 for each gamete) was recombinant over 1000 MCMC cycles.

Selected sample sizes:

Three alternative sample sizes (or selectively profiled proportions), namely 80 (15.7%), 160 (31.4%), or 240 (47.1%) individuals, were used to compare the different selective profiling strategies as used on the 510 F2's available. Moreover, a complete profiling analysis (i.e., complete records on CG expression for all 510 animals) was conducted to compare the efficiency of the five different strategies relative to the more informative, yet also more expensive, option of no selective profiling.

Analyses of simulated data:

All analyses were performed by QxPak, in part on the basis of the same mixed model used to generate the data with QTL effects specified as fixed. Three different deviations on a mixed-model analysis of this data were considered and are subsequently listed.

  • Analysis method 1. Bivariate analysis: In this case, all 510 records on the ERT were used to partially recover information due to selectively profiling on the CG expression by jointly modeling both ERT and CG expression in a bivariate mixed-model analysis. In agreement with the model used to generate the data, the QTL was assumed to have pleiotropic effects on both ERT and CG expression.

  • Analysis method 2. Covariate analysis: Here, a univariate mixed-model analysis was conducted on the selectively profiled CG expression data using the ERT as a covariate.

  • Analysis method 3. Univariate analysis: Here, a univariate mixed-model analysis was conducted on the selectively profiled CG expression data as in analysis method 2, but without the ERT covariate.

In all cases, the QTL scan was conducted every 2 cM throughout the linkage group.

Performance comparisons:

We compared the performance of the five different selective profiling strategies and the three different analysis methods for each of the three different correlation scenarios and three different selected sample size proportions considered. Performance criteria were based on measures of sensitivity and specificity of QTL detection and precision of QTL location and QTL effect inference. We adopted the following conventions on the basis of previous work conducted in this area (Jin et al. 2004; Xu et al. 2005). A peak was defined as a position where the likelihood-ratio (LR) value exceeded a threshold of statistical significance and the LR values of adjacent points. The range of the peak was taken to be the interval on either side of the peak bounded by either the end of the linkage group or by that point closest to the peak with an LR value equal to the significance threshold, whichever came first. If this range bracketed the true QTL position, then the peak was tallied as a true positive (TP); if not, it was determined to be a false positive (FP). If no peaks were found in regions of the linkage group without the QTL, the particular simulation run was counted as true negative (TN); however, if the true QTL position was not bracketed by any peak, then that run was counted as a false negative (FN). The threshold value of statistical significance was obtained as the LR value that yielded an expected proportion of false positives (PFP) (Fernando et al. 2004) of 5%. The algorithm of Nettleton et al. (2006) was used to estimate the number of true null hypotheses over all QTL scan tests for each of the 200 replicates generated under the three different levels of correlation, using each possible combination of selective profiling strategy (five), analysis method (three), and selected sample size proportions (three). Using these definitions, we had the following performance criteria:

  1. Sensitivity (Sn) = TP/(TP + FN).

  2. Specificity (Sp) = TN/(TN + FP).

  3. Mean squared error (MSE) of the QTL effect defined as the variance plus the squared bias of the QTL allele substitution effect estimated at the highest peak position for each simulation run: This included even analyses when this peak did not exceed the significance threshold level, since we postulate that a QTL has already been discovered for the ERT such that the objective is to identify the corresponding CG in the profiling experiment.

  4. Mean absolute distance (MAD) taken from the highest QTL peak to the simulated QTL location for each simulation run, even when this peak did not exceed the threshold level.

  5. QTL scan profile, represented by the negative base 10 logarithm of the likelihood-ratio test P-values averaged over the replicates for each combination of selective profiling strategy, analysis method, selected sample size, and correlation scenario as a function of scan location.

Analysis of variance was used to assess significance of MSE and MAD differences within each correlation scenario (high, medium, or low), using a factorial analysis based on selective profiling strategy (five levels), analysis method (three levels), and selected sample size (three levels). Overall mean differences between levels of any factor were tested using the Tukey adjustment.

RESULTS

QTL scan profiles:

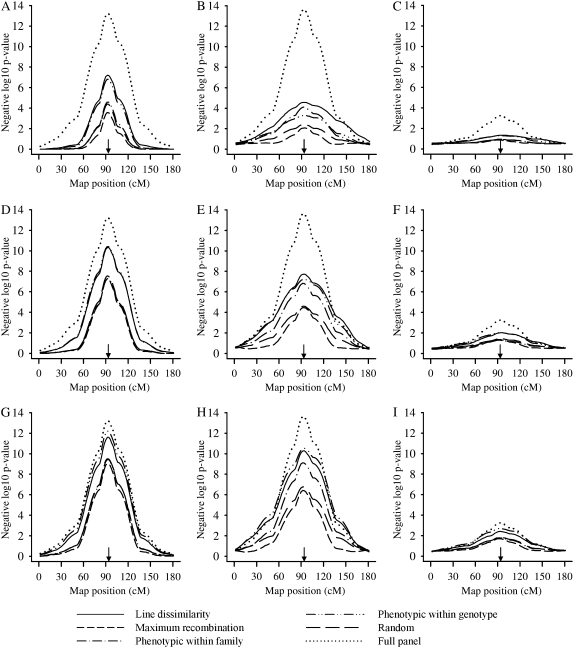
Figure 1 plots the negative logarithm base 10 of P-values (–Log10P) of the LR test profile, averaged across replicates, against each scanned position (2-cM intervals) within the correct linkage group for each combination of selective profiling strategy, selected sample size, and method of inference based on data generated under the high-correlation scenario. Figure 1 provides a visual assessment of the power for QTL detection as indicated by the relative height of the profile curve compared across strategies and of the precision for QTL location by the peak location and sharpness of the profile curve. The full-panel profile refers to a sample size of 510 animals in which all animals were profiled for gene expression; this curve serves as a positive control to illustrate the potential loss of information due to selectively profiling a subset of the population. All selective profiling strategies unbiasedly estimated the true location of the QTL, given no visually evident difference in average peak location across the various strategies as they all align over the true location. Line dissimilarity and phenotypic within-genotype selection were the two strategies providing the highest profiles throughout the scan, thereby indicating that they were more efficient relative to the other methods. As expected, increasing sample sizes elevated the profile curves for all selective phenotyping strategies, while retaining the relative rankings between them. We also observe from Figure 1 that bivariate analyses (Figure 1, A, D, and G) provided higher profiles and sharper peaks compared to univariate (Figure 1, B, E, and H) and covariate analyses (Figure 1, C, F, and I). That is, bivariate analyses provided a substantial gain of statistical power by conditioning inference on the correlated unselected ERT such that substantially more individuals would need to be profiled on the CG expression to achieve the same precision and power if using univariate analyses on the CG expression data only. Conversely, using the ERT as a covariate (Figure 1, C, F, and I) in the model for CG removes genetic variability for CG expression, particularly when the genetic correlation between the two traits is high as in Figure 1. Hence covariate analyses had poorer power and precision of QTL detection for all selective phenotyping methods as seen by the substantially flatter –Log10P profiles in Figure 1. These results indicate that using ERT as a covariate is an inappropriate analysis method for eQTL studies. Hence, additional results based on covariate analysis are not presented further in this article.

Figure 1.—

Figure 1.—

Open in a new tab

Negative logarithm base 10 of P-values of the likelihood-ratio test for scanned positions at linkage groups averaged over all the replicates for the different selective profiling strategies, analysis methods (A, D, and G, bivariate; B, E, and H, univariate; and C, F, and I, covariate analyses), and sample sizes (A–C, 80; D–F, 160; and G–I, 240) for the high-correlation scenario. Arrows point to the true QTL location.

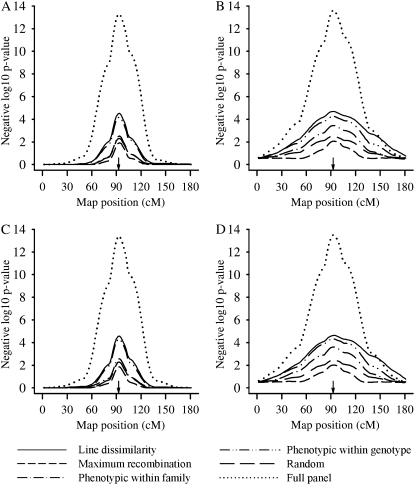
Additional scan profile results are presented for low and medium correlation scenarios for a selected sample size of 80 in Figure 2. Relative rankings for selected samples sizes of 160 and 240 were similar to that for 80 under these two scenarios; hence these results are not reported further. Figure 2 is similar to Figure 1 in terms of performance ranking of the different selective profiling methods for a selected sample size of 80 with results for low vs. medium correlation being virtually identical. Nevertheless, as expected, the relative advantage of using bivariate analyses compared to univariate analyses diminished because of the lower correlation between the two responses and hence less value for conditioning upon a completely recorded ERT. At any rate, univariate analyses still provided flatter QTL scan profiles compared to their bivariate counterparts.

Figure 2.—

Figure 2.—

Open in a new tab

Negative logarithm base 10 of P-values of the likelihood-ratio test for scanned positions at linkage groups averaged over all the replicates for the different selective profiling strategies at a selected sample size of 80, for bivariate (A and C) and univariate analysis methods (B and D), for the low- (A and B) and medium- (C and D) correlation scenarios. Arrows point to the true QTL location.

Mean squared error of the estimated QTL effect:

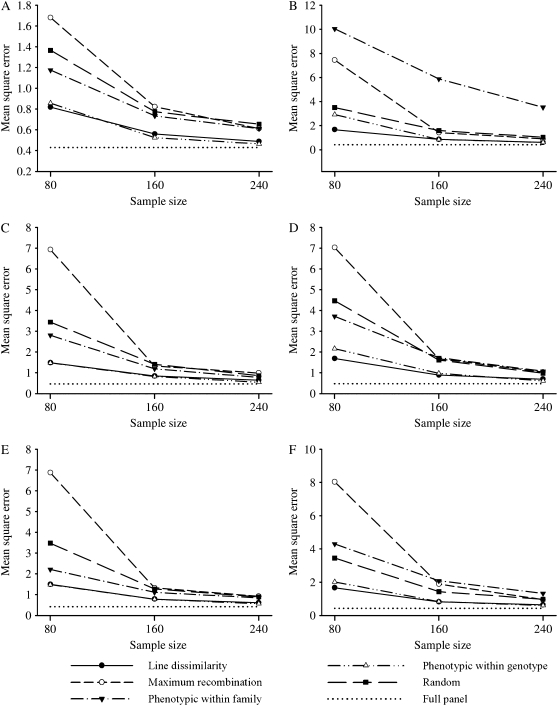
The precision of QTL effect estimates, based on the MSE across replicates, is presented for the different selective profiling strategies, selected sample sizes, and bivariate vs. univariate analyses in Figure 3. The full-panel MSE that corresponded to profiling all 510 animals is again plotted for reference. For the high-correlation scenario, as anticipated, the bivariate analyses (Figure 3A) had a much smaller magnitude of MSE compared to univariate analysis (Figure 3B), for all selective profiling strategies and selected sample sizes.

Figure 3.—

Figure 3.—

Open in a new tab

Mean squared error (MSE) of the quantitative trait locus effect estimation, as a function of the variance and squared bias of the estimator averaged over the replicates for the different selective profiling strategies and samples sizes, from bivariate (A, C, and E) and univariate analysis methods (B, D, and F), for the high- (A and B), low- (C and D), and medium- (E and F) correlation scenarios. The full-panel MSE corresponding to a sample size of 510 animals is plotted for reference.

On the basis of bivariate analyses for the smallest selected sample size (80 animals), the line dissimilarity and phenotypic within-genotype selections had no significant difference between their MSEs (P > 0.05) whereas both had much smaller MSEs than any of the other selective profiling strategies considered (P < 0.0001), regardless of level of correlation between the ERT and CG expression. The largest MSE was observed for maximum-recombination selection (P < 0.0001), with phenotypic within-family and random strategies having intermediate results. These last two strategies were not different from each other under the high-correlation scenario; however, the phenotypic within family had smaller MSE under the low- and medium-correlation scenarios (P < 0.01). The most striking difference among the profiling strategies is the much larger MSE for the phenotypic within-family method compared to other selective profiling strategies under the high-correlations scenario using univariate analyses (Figure 3B), although this problem dissipated when bivariate analyses were used (Figure 3A). Under univariate analysis and sample size of 80, the line dissimilarity strategy of selective phenotyping was the best among all methods of selection, outperforming the phenotypic within-genotype approach (Figure 3B). In the other situations of low and medium correlations, ranking of the selective strategies using univariate analyses (Figure 3, D and F, respectively) was similar to that of bivariate analyses (Figure 3, C and E, respectively). Moreover, in all cases as the selected sample sizes increased, particularly from 80/510 to 160/510, the difference between the selection strategies decreased as expected; yet their relative rankings were retained (see Figure 3). However, increasing selected sample sizes from 160/510 to 240/510 and from 240/510 to a full-panel analysis had no apparent pragmatic advantage on precision. These results suggest, as pointed out by Jin et al. (2004), that most of the power and precision relative to the full-panel analysis is retained by the first subsample fractions selected from the available animals; nevertheless, the appropriate size of the subsample depends on the eQTL effects or heritability levels.

Mean absolute distance of QTL location:

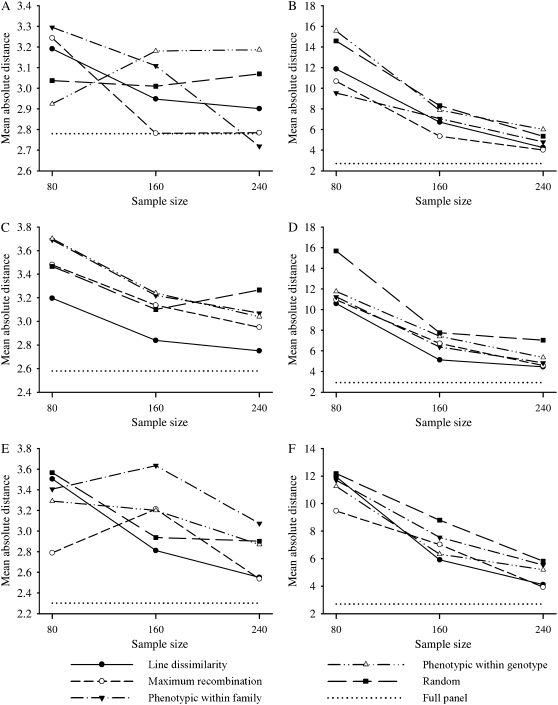
Figure 4 illustrates the precision of QTL mapping evaluated in terms of MAD averaged over the replicates for each of the different selective profiling strategies and selected sample sizes under each of the three different correlation scenarios for bivariate vs. univariate analyses. Once again, the MAD for the full panel is plotted for reference. The pleiotropic nature of the simulated QTL and the use of the ERT data in the bivariate analyses (Figure 4, A, C, and E) afforded much greater precision for mapping the QTL than its univariate counterpart based on the analysis of the selectively profiled CG data only (Figure 4, B, D, and F). This was noted for all selection strategies and selected samples sizes. For bivariate analyses, there was no clear trend for preference of any one particular selective profiling strategy as none of the MAD differences were significant at any selection proportion (Figure 4A). Conversely, we observed some significant differences among selection strategies and selected sample sizes based on univariate analyses (see Figure 4). For example, with a sample size 80/510, the random and the phenotypic within-genotype approaches had larger MAD compared to other selective profiling strategies at high correlation (Figure 4B), whereas random selection performed worst at low correlation (Figure 4D). There were no significant differences (P > 0.05) among selection strategies at the medium correlation (Figure 4, E and F). Naturally, as the selection proportion increased, the differences among selective phenotyping strategies tended to decrease in the univariate analysis, particularly under the high- and low-correlation scenarios (Figure 4, D and F).

Figure 4.—

Figure 4.—

Open in a new tab

Mean absolute distance (MAD) between the true and the estimated quantitative trait locus location averaged over the replicates for the different selective profiling strategies and sample sizes, from bivariate (A, C, and E) and univariate analysis methods (B, D, and F), for the high- (A and B), low- (C and D), and medium- (E and F) correlation scenarios. The MAD for the full panel (sample size 510) is plotted as a dotted line for reference.

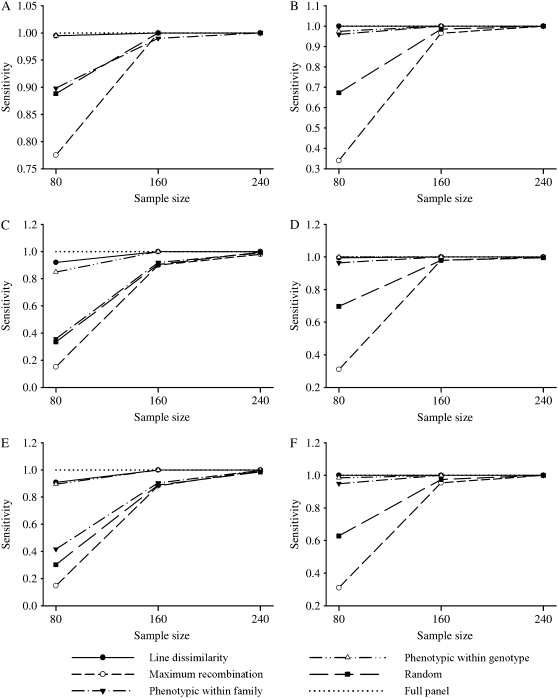
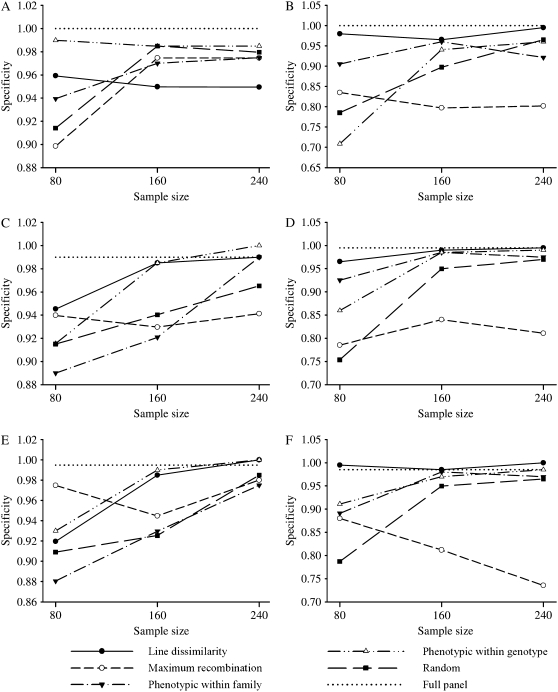
Specificity and sensitivity of QTL detection:

Sensitivity and specificity of QTL detection are presented in Figures 5 and 6 for the different selection strategies, selected sample sizes, and correlation scenarios, with bivariate analyses presented in Figure 5, A, C, and E, and Figure 6, A, C, and E, and univariate analyses presented in Figure 5, B, D and F, and Figure 6, B, D, and F. Sensitivity, as a numerical measure of power of QTL detection, followed the same trend of relative performance observed from the QTL scan profiles in Figures 1 and 2. For example, for the bivariate analyses under all levels of correlation, and when 80 of 510 animals were selected for profiling, the line dissimilarity and the phenotypic within-genotype strategies presented the greatest sensitivity whereas maximum-recombination selection had the worst. Under univariate analysis, the line dissimilarity, the phenotypic within-genotype, and the phenotypic within-family strategies had the best performance, while the maximum recombination had the lowest sensitivity at all three different levels of correlation. As the selected sample size increased, the differences diminished substantially, particularly when 240 animals were selected; this was true for both the bivariate and the univariate analyses and under all levels of correlation. Finally, it is worth noting that differences in sensitivity among selection methods were smaller under bivariate analyses and high correlation (Figure 5A). On the other hand, similarly to MAD for QTL location, there was no clear pattern in terms of specificity of QTL detection among the different selective profiling strategies (Figure 6). Nonetheless, there was some indication of better performance of the line dissimilarity profiling strategy in the univariate analyses (Figure 6, B, D, and F), although other researchers found similar specificities for genome-based genetic dissimilarity vs. random selective profiling of an F2 mice population (Jin et al. 2004).

Figure 5.—

Figure 5.—

Open in a new tab

Sensitivity of quantitative trait locus detection averaged over the replicates for the different selective phenotyping strategies and sample sizes, from bivariate (A, C, and E) and univariate analysis methods (B, D, and F), for the high- (A and B), low- (C and D), and medium- (E and F) correlation scenarios. The sensitivity for the full panel (sample size 510) is plotted as a dotted line for reference.

Figure 6.—

Figure 6.—

Open in a new tab

Specificity of quantitative trait locus detection averaged over the replicates for the different selective phenotyping strategies and sample sizes, from bivariate (A, C, and E) and univariate analysis methods (B, D, and F), for the high- (A and B), low- (C and D), and medium- (E and F) correlation scenarios. The specificity for the full panel (sample size 510) is plotted as a dotted line for reference.

DISCUSSION

In this study, we compared different selective profiling strategies for the efficient design of eQTL experiments with outbred F2 populations. These strategies are intended to conserve resources for the microarray experiment while maximizing power and precision of eQTL mapping as suited for expensive livestock studies focusing on identifying CG for particular ERT.

The five examined selective profiling strategies have different requirements and efficiency of use of prior information. The line dissimilarity and the maximum-recombination selection require a complete panel of genotyped individuals but no records on an ERT whereas these records would be required for the phenotypic within-family and the phenotypic within-genotype strategies. The latter selection strategy also requires the identification of a QTL for the performance trait and genotyped individuals for this QTL position, whereas the random selection does not require any prior information on ERT or genotypes.

The line dissimilarity strategy, following the proposal of Jin et al. (2004), aims to select a sample of individuals with maximum dissimilarity with respect to line of origin within a genomic region of particular interest or across the whole genome if there are no targeted segments. Since we used the number of alleles (0, 1, or 2) coming from the same line of origin as the measure of similarity, our deviation on their strategy favored the choice of homozygous individuals, thereby optimizing the detection of additive QTL effects. However, estimation of more general genetic effects (e.g., dominance) can be favored by specifying other genotypes as similar (code = 1) or dissimilar (code = 0), regardless if they share one or no alleles from the same line or origin (Jin et al. 2004; Bueno et al. 2006). This strategy along with the phenotypic within-genotype selection approach had the best performance for power of QTL detection and estimation of QTL effects as measured, respectively, by sensitivity and MSE across all selective profiling strategies.

In our simulations, we used chromosome-based line dissimilarity, calculated using all markers in the linkage group in which the QTL was detected for the ERT. This approach would be especially suitable in situations with sparse maps and wide confidence intervals for the putative QTL position. However, for denser marker maps with high precision for the putative QTL location, probably only one or a few markers closely linked to the QTL could be used to obtain a marker-based genetic dissimilarity, potentially resulting in higher sensitivity and precision of eQTL detection (Jin et al. 2004). Moreover, for two-color microarray platform experiments, the distant pairing of most genetically dissimilar individuals could further improve power and resolution in eQTL analyses (Fu and Jansen 2006).

The maximum-recombination strategy, analogous to the maxRec method of Jannink (2005), selected individuals with a larger expected number of crossover events. As such, this strategy is expected to improve the QTL mapping resolution, as observed in this and other studies (Jannink 2005; Xu et al. 2005), when compared to the random selection using the univariate analysis of CG expression data. However, this superior behavior was not seen in our simulation study for the bivariate analyses, as there were no clear patterns in the MAD graphs (Figure 5) in favor of any of the selective profiling strategies. Furthermore, the maximum-recombination method was outperformed by other selective profiling strategies in terms of sensitivity of QTL detection and MSE of QTL effect estimates. The F2 population structure had few recombinant gametes (the estimated mean number of recombinations with respect to line of origin across the 16 marker intervals for both gametes inherited by the 510 F2 individuals based on MCMC inference was 3.24), thereby not facilitating refined mapping resolution. Hence this may be one of the main reasons for poorer results for the maximum-recombination method, even though we observed crossover enrichment in the decreasing selected sample sizes of 240, 160, and 80 individuals, in which the estimated mean number of recombinations rose from 4.31 to 4.71 and 5.23, respectively.

The phenotypic within-genotype strategy of Wang and Nettleton (2006) required the previous detection of a QTL for the corresponding ERT as well as genotypes for this QTL or closely linked markers. This method improved sensitivity of QTL detection and precision of QTL effects estimation compared to the random, the maximum-recombination, and the phenotypic within-family strategies under the bivariate analysis and selected sample sizes of 80 and 160 individuals, whereas its performance was similar to that of the line dissimilarity approach. Therefore, this profiling strategy seems to be suitable, particularly when the microarray experiment targets gene(s) associated with a particular performance QTL of interest (Nettleton and Wang 2006). On the other hand, the phenotypic within-genotype and the line dissimilarity strategies were shown to have somewhat equivalent performance. This was true even when a QTL was present with pleiotropic effects on a highly correlated ERT and CG expression, thereby characterizing the ideal scenario for the phenotypic within-genotype selection. Hence, the line dissimilarity approach is a robust procedure suitable for most general cases, regardless of whether or not there are one, several, or no QTL of particular interest and available data on ERT.

The phenotypic within-family strategy that selected extreme individuals for ERT within family (Rosa et al. 2006b) can be applied, with some loss in precision and power of QTL detection compared to the line dissimilarity and the phenotypic within-genotype strategies. Nevertheless, no genotype data are required for this particular selective profiling strategy. However, it is vitally important for the phenotypic within-family strategy to use bivariate analysis conditional upon the ERT on which selection was based to avoid badly biased QTL effect estimates for the CG expression as seen in Figure 3B. Finally, random sampling is a resource-wasteful strategy for expensive microarray experiments and should be avoided. There are superior selective profiling strategies (Jin et al. 2004; Jannink 2005; Xu et al. 2005; Wang and Nettleton 2006) that could be chosen, depending on the information available, the goal of the experiment, and the inferential methods used (Rosa et al. 2006a).

In this study, bivariate mixed-model analysis was shown to be efficient in recovering information lost by selective profiling as noted by smaller MSE of effects (Figure 3) and MAD of location (Figure 4) for the pleiotropic QTL across all selective profiling strategies and hence should be preferred for the statistical analysis of such experiments (Wang and Nettleton 2006). Our recommendation holds despite the larger computational requirements of bivariate analyses and the fact that most selective profiling proposals have been based on univariate analyses (Jin et al. 2004; Jannink 2005; Xu et al. 2005). We have also demonstrated that using the ERT as a covariate for the CG data substantially decreases the power of eQTL detection (Figure 1) such that this analysis method should not be employed in genetical genomics studies. However, this strategy continues to be used in classical livestock QTL mapping, for example, when carcass weight is used as a covariate for other carcass traits (De Koning et al. 2001; Ovilo et al. 2002; Varona et al. 2002; Edwards et al. 2008a).

Finally, it is important to emphasize that selective profiling is a resource-efficient design strategy. In our simulation results, with the eQTL explaining 10% of the phenotypic variance we generally observed no practical advantage by increasing the selected sample size for profiling from 160/510 to 240/510. Therefore, selective phenotyping should be considered to increase power and precision of eQTL mapping experiments whenever resources are not abundant. In practice, the relative efficiency of selective phenotyping methods compared to a full-panel analysis will depend on several factors, notably magnitude of the eQTL effects, correlation between ERT and CG expression, population structure, marker density, and sample size.

Acknowledgments

This research was financially supported by the Michigan State University Department of Animal Science, by a National Research Initiative grant (no. 2004-35604-14580) from the United States Department of Agriculture Cooperative State Research, Education, and Extension Service, and by the Brazilian Agricultural Research Corporation Corporative Education Coordination.

References

  1. Botstein, D., R. L. White, M. Skolnick and R. W. Davis, 1980. Construction of a genetic-linkage map in man using restriction fragment length polymorphisms. Am. J. Hum. Genet. 32 314–331. [PMC free article] [PubMed] [Google Scholar]
  2. Brem, R. B., G. Yvert, R. Clinton and L. Kruglyak, 2002. Genetic dissection of transcriptional regulation in budding yeast. Science 296 752–755. [DOI] [PubMed] [Google Scholar]
  3. Bueno, J. S. S., S. G. Gilmour and G. J. M. Rosa, 2006. Design of microarray experiments for genetical genomics studies. Genetics 174 945–957. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Darvasi, A., 1998. Experimental strategies for the genetic dissection of complex traits in animal models. Nat. Genet. 18 19–24. [DOI] [PubMed] [Google Scholar]
  5. de Koning, D. J., B. Harlizius, A. P. Rattink, M. A. M. Groenen, E. W. Brascamp et al., 2001. Detection and characterization of quantitative trait loci for meat quality traits in pigs. J. Anim. Sci. 79 2812–2819. [DOI] [PubMed] [Google Scholar]
  6. Edwards, D. B., 2005. Analysis of a Duroc × Pietrain F2 pig resource population for quantitative trait loci affecting growth, body composition, and meat quality traits. Ph.D. Dissertation, Michigan State University, East Lansing, MI.
  7. Edwards, D. B., C. W. Ernst, N. E. Raney, M. E. Doumit, M. D. Hoge et al., 2008. a Quantitative trait locus mapping in an F-2 Duroc x Pietrain resource population: II. Carcass and meat quality traits. J. Anim. Sci. 86 254–266. [DOI] [PubMed] [Google Scholar]
  8. Edwards, D. B., C. W. Ernst, R. J. Tempelman, G. J. M. Rosa, N. E. Raney et al., 2008. b Quantitative trait loci mapping in an F-2 Duroc × Pietrain resource population: I. Growth traits. J. Anim. Sci. 86 241–253. [DOI] [PubMed] [Google Scholar]
  9. Fernando, R. L., D. Nettleton, B. R. Southey, J. C. M. Dekkers, M. F. Rothschild et al., 2004. Controlling the proportion of false positives in multiple dependent tests. Genetics 166 611–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Fu, J. Y., and R. C. Jansen, 2006. Optimal design and analysis of genetic studies on gene expression. Genetics 172 1993–1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gibson, G., and B. Weir, 2005. The quantitative genetics of transcription. Trends Genet. 21 616–623. [DOI] [PubMed] [Google Scholar]
  12. Jannink, J. L., 2005. Selective phenotyping to accurately map quantitative trait loci. Crop Sci. 45 901–908. [Google Scholar]
  13. Jansen, R. C., and J. P. Nap, 2001. Genetical genomics: the added value from segregation. Trends Genet. 17 388–391. [DOI] [PubMed] [Google Scholar]
  14. Jin, C. F., H. Lan, A. D. Attie, G. A. Churchill, D. Bulutuglo et al., 2004. Selective phenotyping for increased efficiency in genetic mapping studies. Genetics 168 2285–2293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Nettleton, D., and D. Wang, 2006. Selective transcriptional profiling for trait-based eQTL mapping. Anim. Genet. 37 13–17. [DOI] [PubMed] [Google Scholar]
  16. Nettleton, D., J. T. G. Hwang, R. A. Caldo and R. P. Wise, 2006. Estimating the number of true null hypotheses from a histogram of p values. J. Agric. Biol. Environ. Stat. 11 337–356. [Google Scholar]
  17. Ovilo, C., A. Clop, J. L. Noguera, M. A. Oliver, C. Barragan et al., 2002. Quantitative trait locus mapping for meat quality traits in an Iberian x Landrace F-2 pig population. J. Anim. Sci. 80 2801–2808. [DOI] [PubMed] [Google Scholar]
  18. Perez-Enciso, M., and I. Misztal, 2004. Qxpak: a versatile mixed model application for genetical genomics and QTL analyses. Bioinformatics 20 2792–2798. [DOI] [PubMed] [Google Scholar]
  19. Rockman, M. V., and L. Kruglyak, 2006. Genetics of global gene expression. Nat. Rev. Genet. 7 862–872. [DOI] [PubMed] [Google Scholar]
  20. Rosa, G. J. M., N. de Leon and A. J. M. Rosa, 2006. a Review of microarray experimental design strategies for genetical genomics studies. Physiol. Genomics 28 15–23. [DOI] [PubMed] [Google Scholar]
  21. Rosa, G. J. M., R. J. Tempelman, C. W. Ernst and R. O. Bates, 2006. b Combining molecular marker information and gene expression profiling for studying complex traits. 8th World Congress on Genetics Applied to Livestock Production, Belo Horizonte, MG, Brazil, communication no. 23-11.
  22. Schadt, E. E., S. A. Monks, T. A. Drake, A. J. Lusis, N. Che et al., 2003. Genetics of gene expression surveyed in maize, mouse and man. Nature 422 297–302. [DOI] [PubMed] [Google Scholar]
  23. Sorensen P., M. S. Lund, B. Guldbrandtsen, J. Jensen and D. Sorensen, 2003. A comparison of bivariate and univariate QTL mapping in livestock populations. Genet. Sel. Evol. 35 605–622. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Varona, L., C. Ovilo, A. Clop, J. L. Noguera, M. Perez-Enciso et al., 2002. QTL mapping for growth and carcass traits in an Iberian by Landrace pig intercross: additive, dominant and epistatic effects. Genet. Res. 80 145–154. [DOI] [PubMed] [Google Scholar]
  25. Wang, D., and D. Nettleton, 2006. Identifying genes associated with a quantitative trait or quantitative trait locus via selective transcriptional profiling. Biometrics 62 504–514. [DOI] [PubMed] [Google Scholar]
  26. Xu, Z. L., F. Zou and T. J. Vision, 2005. Improving quantitative trait loci mapping resolution in experimental crosses by the use of genotypically selected samples. Genetics 170 401–408. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Yvert, G., R. B. Brem, J. Whittle, J. M. Akey, E. Foss et al., 2003. Trans-acting regulatory variation in Saccharomyces cerevisiae and the role of transcription factors. Nat. Genet. 35 57–64. [DOI] [PubMed] [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES