Controlling Type-I Error of the McDonald–Kreitman Test in Genomewide Scans for Selection on Noncoding DNA

Abstract

Departures from the assumption of homogenously interdigitated neutral and putatively selected sites in the McDonald–Kreitman test can lead to false rejections of the neutral model in the presence of intermediate levels of recombination. This problem is exacerbated by small sample sizes, nonequilibrium demography, recombination rate variation, and in comparisons involving more recently diverged species. I propose that establishing significance levels by coalescent simulation with recombination can improve the fidelity of the test in genomewide scans for selection on noncoding DNA.

THE McDonald–Kreitman (MK) test is a widely used statistical test of neutral model of evolution originally proposed for nonrecombining protein sequences (McDonald and Kreitman 1991; Nielsen 2005). The test compares within-species polymorphism and between-species divergence for two distinct classes of sites: synonymous sites, which are assumed to be neutral and nonsynonymous sites, which are putative targets of selection. The null model assumes that some fraction, f, of nonsynonymous sites is strongly deleterious and contributes negligibly to polymorphism and divergence. For the remaining nonsynonymous sites, (1 − f), the ratio of polymorphism to divergence is expected to be identical to that for synonymous sites, if both behave according to the neutral model.

Departures from expectations under neutral model are expected if nonsynonymous sites experience negative or positive selection. If the evolution of (nonlethal) nonsynonymous sites in a particular gene is largely governed by negative (or purifying) selection, this will tend to decrease the level of divergence at nonsynonymous sites more strongly than levels of polymorphism (Kimura 1983). The result will be that nonsynonymous sites will exhibit a higher ratio of polymorphism to divergence than putatively neutral synonymous sites. In contrast, if the evolution of nonsynonymous sites is governed primarily by positive selection, this will tend to decrease the ratio of polymorphism to divergence relative to synonymous sites. A departure from the neutral expectation in either direction can be detected by applying a standard statistical test to a 2 × 2 contingency table of polymorphism and divergence counts for synonymous and nonsynonymous sites.

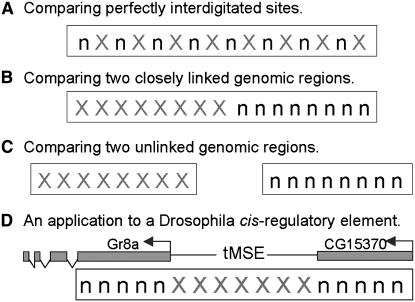
An attractive feature of the MK test is that the inference of selection, although not necessarily its mode, is remarkably robust to assumptions about nonequilibrium demography (Nielsen 2001; Eyre-Walker 2002) and recombination rates (Sawyer and Hartl 1992). In the absence of recombination, this robustness stems from the fact that all surveyed sites share the same genealogy and thus the entries of the 2 × 2 table are sufficient statistics (Nielsen 2001). In the presence of recombination, the robustness of the MK test is largely owed to the fact that nonsynonymous and synonymous sites are homogenously interdigitated in protein sequences (Figure 1A).

Figure 1.—

The MK test applied to genomic regions with different spatial organization of neutral (n) and selected (X) polymorphic and divergent mutations. D shows the spatial organization of neutral and selected sites in the study of Jeong et al. (2008). The tan gene cis-regulatory element, tMSE, regulates the expression of abdominal pigmentation in D. yakuba and is inferred to have an excess of divergence relative to polymorphism when compared to synonymous sites from two neighboring genes.

Using synonymous (or other neutral sites) to test for selection in linked noncoding DNA:

Although the MK test was originally applied to protein coding sequences, it can readily be generalized to test for departures from neutrality using any putatively neutral and putatively selected classes of mutations. For example, several recent studies have applied the MK test to putatively functionless (i.e., neutral) vs. putatively functional (i.e., selected) sites in noncoding DNA elements (Jenkins et al. 1995; Ludwig and Kreitman 1995; MacDonald and Long 2005; Ding and Kullo 2006; Casillas et al. 2007). Similarly, a wave of recent studies has used closely linked synonymous sites to test for departures in noncoding DNA (Kohn et al. 2004; Begun et al. 2007; Holloway et al. 2007; Egea et al. 2008; Jeong et al. 2008) or compared synonymous sites and noncoding sites from unlinked genomic regions (Andolfatto 2005; Casillas et al. 2007; Egea et al. 2008). These applications of the MK test are a departure from the standard assumption of the MK test—that neutral and selected sites are homogenously interdigitated (i.e., compare Figure 1A to Figures 1B and 1C).

Departures from the assumption of homogenously interdigitated neutral and selected sites make the MK test sensitive to assumptions about the recombination rate. Intuitively this problem arises because, in the presence of recombination, neutral sites in one part of a sequence no longer share the same genealogical history as selected sites in other parts of the sequence (Hudson 1983). As illustration of the problem, I used Hudson's (2002) coalescent program ms to simulate data that resemble the situation depicted in Figure 1B—a case in which linked synonymous sites are used to test for departures from neutrality in linked noncoding DNA. I simulated genealogies with intralocus recombination and generated MK test contingency tables with polymorphism and divergence counts from the first and second half of the simulated region. Since the MK test lacks power when table cell counts are low, I restricted tests to replicates that had a minimum of six mutations in each marginal row and column count [following Begun et al. (2007) and Holloway et al. (2007)].

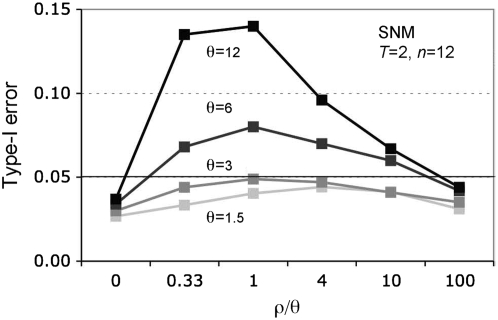
Figure 2 shows the performance of the MK test under the standard neutral model (SNM) (a large panmictic population at mutation-drift equilibrium; all sites are neutral). Note that when there is no recombination, or when recombination rates are high (i.e., ρ/θ = 100), the type-I error of the MK test is <5%. However, with recombination rates empirically estimated in humans (ρ/θ ∼ 1, Pritchard and Przeworski 2001) and Drosophila (ρ/θ ∼ 4–10, Andolfatto and Przeworski 2000), there is considerable false rejection of the neutral model when θ for the surveyed genomic region is large (i.e., >3 under the standard neutral model for sample size n = 12 and divergence time T = 8N_e generations ago). The inflation in the type-I error of the test is generally symmetrical on both tails of the test and the median 2 × 2 table is close to that expected under the SNM (results not shown). These features distinguish the linkage effect described here from linkage-selection effects described elsewhere (Smith and Eyre-Walker 2002; Welch 2006; Shapiro et al. 2007).

Figure 2.—

Performance of the MK test when comparing neutral sites to closely linked putatively selected sites (Figure 1B). Tests were only performed on MK tables where each marginal sum exceeded five counts. ρ/θ is the ratio of the population recombination rate ρ = 4N_erL to the population mutation rate, θ = 4N_eμL, where N_e is the species effective population size, L is the locus length in base pairs, and r and μ are the recombination and mutation rates per site per generation. The standard neutral model is simulated with θ = 1.5 (light shading), θ = 3 (shaded), θ = 6 (dark shading), and θ = 12 (solid). Sample size, n = 12 and the divergence time, T, were set to 2 (in units of 4N_e generations) in each case. All points are based on 10,000 replicates of the neutral coalescent with recombination implemented using the program ms, except θ = 1.5 (100,000 replicates).

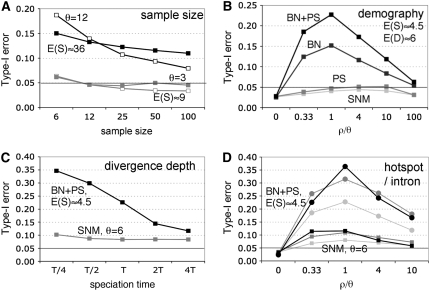
In Figure 3, I show how several other factors further exacerbate the problem outlined above. Figure 3A shows an effect due to sample size. The type-I error generally decreases with increasing sample size, although the effect is diminished as the number of polymorphisms increases (as suggested by Figure 2). In Figure 3B, I show examples of three nonequilibrium demographic departures from the SNM that increase levels of linkage disequilibrium, such as population structure or a recent bottleneck (or their combined effects). Note that under all demographic models simulated, θ and T vary; however, the average number of observed polymorphic and divergent mutations is the same and correspond to θ = 1.5, T = 2, and n = 12 under the SNM. These results suggest that nonequilibrium demography can considerably elevate type-I errors relative to the SNM. In Figure 3C, I show that the type-I error of the MK test also increases as speciation times become more recent (relative to within-species coalescence times).

Figure 3.—

The effect of various factors on the performance of the MK test in the context of Figure 1B. Tests were only performed on MK tables where each marginal sum exceeded five counts. (A) The effect of sample size. For open squares, θ = 3 (shaded line) and θ = 12 (solid line) are plotted for ρ/θ = 1. For solid squares, θ is adjusted with sample size such that the mean observed number of polymorphisms, E(S), is the same as for n = 12. (B) The effect of demography. The sample size, n = 12. θ and T are varied such that observed average number of polymorphic and divergent sites [E(S) ∼ 4.5 and E(D) ∼ 12, respectively] is similar for all models and corresponds to expectations for θ = 1.5 and T = 2 under the SNM. Models: SNM, the standard neutral model (light shading, ms command line –t 1.5); PS, a two-deme population structure model with all individuals sampled from one deme (shaded, ms command line –t 0.825–I 3 12 0 1–ma × 1 0 1 × 0 0 0 × –ej 4 2 1 –ej 4 3 1); BN, a bottleneck model (dark shading, ms command line –t 4.3 -en 1 0.0041 0.03 -en 1 0.019 1 –ej 0.45 2 1 –ej 0.45 3 1) based on parameters estimated for D. melanogaster by Thornton and Andolfatto (2006); BN + PS, a combined population structure and bottleneck model (solid, with parameters as above, except –t 2.4 –ej 0.7 2 1 –ej 0.7 3 1). (C) The effect of divergence depth. All parameters are as in B, except species divergence time is varied. For SNM, T = 2 and for BN + PS, T = 0.7. (D) The effect of an intron or a recombination hotspot. The two demographic models shown are the SNM with θ = 6 (squares) and the BN + PS model (circles) from B. For the intron model (solid lines), a 1-kb intron is added in the middle of a 1200-bp sequence. Note that recombination rate is uniform and the intron is not included in the MK test but changes the cumulative genetic distance between the tested regions. For the hotspot model (dark shaded lines), a 100-bp hotspot with 10-fold intensity relative to the background in the middle of the surveyed region was modeled (implemented with msHOT (Hellenthal and Stephens 2007), with locus length = 1200 bp and command line: -v 1 550 650 10). In the hotspot model, background levels of recombination were set such that the cumulative genetic distance of the surveyed region is the same in the presence and absence of the hotspot. For each demographic model, results for “no intron” and “no hotspot” are indicated with light shaded lines for comparison.

In Figure 3D, I show that the type-I error of the test can also be inflated by heterogeneity in recombination rates or the presence of an intervening intron. The elevation in recombination between the two halves of the sequence decreases the extent to which their genealogies are correlated, thus increasing the type-I error of the test (in fact, type-I error is maximized when the two regions compared are unlinked; results not shown). Recombination hotspots are a pervasive feature of yeast and mammalian genomes (Coop and Przeworski 2007) and evidence for small-scale spatial variation in recombination rates, though less extreme, is beginning to be documented in Drosophila (Cirulli et al. 2007). However, even in a uniform recombination environment, the presence of a large intron may effectively increase the recombination distance between two exons (for example one exon containing a UTR and the other synonymous sites to which it is compared) will look similar to recombination rate variation. Similarly, spatial variation in mutation rates, or levels of selective constraint, will also lead to patterns that look similar to recombination rate variation (Andolfatto and Przeworski 2000).

The results in Figures 2 and 3 suggest that caution should be used in interpreting the MK test in comparisons of noncoding DNA to synonymous or other putatively neutral sites. For example, in a genomewide application of this approach to detect noncoding DNA elements rejecting the neutral model, Begun et al. (2007) found that the proportion 5′-UTR, 3′-UTR, intron, and intergenic loci that deviated from neutrality with P < 0.05 was 0.13, 0.13, 0.12, and 0.17, respectively. In that study, the sample size was n = 6 (or smaller) and an average coding region (∼300 synonymous sites) has a 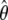∼ 6–10 while an average 300 bp noncoding region would have θ ∼ 3–6. In addition, synonymous site divergence along the Drosophila simulans lineage is particularly short (Begun et al. 2007). The results in Figures 2 and 3 suggest that the proportions of rejections observed by Begun et al. are not necessarily unexpected under neutrality particularly given estimated levels of recombination D. simulans (ρ/θ ∼ 1, Andolfatto and Przeworski 2000), the small sample size used, the relatively low levels of synonymous site divergence along the D. simulans lineage and evidence for population structure and recent bottlenecks in this species (Wall et al. 2002; Baudry et al. 2006).

Correcting for linkage effects by simulation:

Andolfatto (2005) previously noted that pooling data from unlinked regions (see Figure 1C) can lead to incorrect confidence limits for the MK test. He proposed to correct this problem by simulating data to determine an appropriate critical P-value (P_crit) that accounts for the effects of linkage on the confidence interval of the test. A similar approach can be taken when the MK test is applied in situations resembling Figure 1B. As an example, I use recent findings by Jeong et al. (2008), who used the MK test in a similar way to investigate the mode of selection operating on tMSE, an adult abdominal pigmentation-specific cis-regulatory element (CRE) of the tan locus in Drosophila (see Figure 1D). In this study, Jeong et al. (2008) conclude that there is highly significant evidence for adaptive evolution of tMSE in a D. yakuba–D. teissieri comparison (P = 0.001), but fail to detect evidence for adaptive evolution when using D. santomea, consistent with the recent inactivation of this CRE (associated with a loss of pigmentation) and subsequent accumulation of polymorphism in the latter species.

Table 1 shows a reanalysis of the data for the D. yakuba–D. teissieri comparison that incorporates effects of linkage. When ρ/θ = 1, the type-I error of the MK test is 14.1% and the true P-value (P_true) of the data is ∼0.016 rather than 0.001 as estimated assuming no recombination. If ρ/θ is 4, the type-I error of the test is 10% and the true P-value of the data is ∼0.008. Thus, it appears that, in this case, the conclusion of adaptive evolution is robust to the issue of linkage, particularly given that ρ/θ is estimated to be ∼15 on the basis of levels of intragenic linkage disequilibrium in this species group (Bachtrog et al. 2006).

TABLE 1.

A reanalysis of tMSE in the D. yakuba–D. teissieri comparison (Jeong et al. 2008) incorporating linkage

ρ/θ	Type-I error	P_crit	P_true
0 (standard MK)	0.040	0.062	0.001
1	0.141	0.009	0.016
4	0.100	0.019	0.008
15	0.063	0.037	0.003

See Figure 1D for a schematic of genomic region tested. Synonymous sites in two flanking protein-coding genes (positions 1–1125 and 1959–2799) were used in an MK test vs. the cis-regulatory element tMSE (positions 1126–1958). Based on 10,000 replicates of the neutral coalescent with recombination (ms) with θ = 26, with within-species sample size n = 24 alleles, and divergence time T = 2.5 (in units of 4N_e generations) to mimic polymorphism and divergence counts in the real data. P_true is the fraction of simulated data sets that had the observed P-value (0.0011) or smaller.

Conclusions:

The MK test assumes that polymorphic and divergent mutations within a locus are homogenously interdigitated. Some applications of the MK test, such as using synonymous sites to test for departures in noncoding DNA violate this assumption and result in spurious rejections of the neutral model in the presence of intralocus recombination. This problem is alleviated to some extent by very high levels of recombination, but can be exacerbated by any factor that increases the scale and the variance in levels of linkage disequilibrium, such as nonequilibrium demography, the presence of introns and small-scale spatial variation recombination rate, mutation rate, or variation in selective constraint. While this article has focused on the MK test, the same issues apply to estimating confidence limits on the fraction of adaptive divergence or the estimation of selection coefficients using similar statistical frameworks (Kohn et al. 2004; Andolfatto 2005; Begun et al. 2007; Casillas et al. 2007; Haddrill et al. 2008).

Perhaps a bigger concern is evaluating evidence for selection at individual genes or genomic regions, relative to others, using the MK test in genomewide scans for selection. Since the type-I error of the MK test (applied as in Figure 1, B or C) increases with increasing size of the regions surveyed (i.e., with increasing θ), type-I error is expected to be higher for tests involving longer genes or noncoding regions. As a result, it may be misleading to rank genomic regions of different sizes by their P-values without accounting for locus-specific propensities for error. Further, if gene ontology (GO) categories are associated with particular gene structures (such as long introns for example) or recombination hotspots (e.g., International HapMap Consortium 2007), this may also make it problematic to compare distributions of MK test P-values by GO category.

While the linkage effect described here is clearly an issue in Drosophila (discussed above), how important is this issue to species, such as primates, with smaller effective population sizes? In humans, an average protein-coding gene with 300 synonymous sites has ∼1.5 polymorphisms (SNPs) on average in a sample of 39 individuals (Bustamante et al. 2005). Figure 2 suggests that, for small genomic region sizes (i.e., on the scale of <6 kb in humans), excessive type-I error is not likely to be an issue in humans under the standard neutral model. On the other hand, Figure 3B suggests nonequilibrium demography can be an issue when average SNP density is as low as 4.5/region (keeping in mind we have limited analyses to 2 × 2 tables that have marginal sums of more than five mutations). This corresponds to ∼1 kb of noncoding DNA in a sample of 39 human individuals (assuming average diversity levels of ∼0.001 per site) (Zhao et al. 2006). Figure 3D further suggests that recombination rate variation may further exacerbate the problem in humans.

The examples outlined here are largely meant to be illustrative rather than quantitative. As illustrated in the above example of the tan CRE tMSE, it is straightforward enough to simulate genealogies with linkage to obtain more appropriate P-values for the MK test in particular cases. One can similarly establish more appropriate confidence intervals for the MK test and related methods to estimate selection parameters, using multilocus data sets (Andolfatto 2005). In the case of genomewide scans for selection using the MK test, one could incorporate more realistic details about how putatively neutral and selected sites are spatially organized across the genome to establish more appropriate critical P-values. Though coalescent programs such as ms and msHOT (http://home.uchicago.edu/∼rhudson1/source/mksamples.html) can implement a wide range of genome structures and demographic scenarios, accounting for uncertainty about the demographic history of populations, and complex sampling schemes used by researchers, present a formidable challenge. From the limited simulations carried out here, it is clear that caution should be used in interpreting the MK test when population samples come from recently bottlenecked or highly structured populations, unless it is clear that neutral and selected polymorphic and divergent mutations are close to evenly interdigitated.

An R script to determine type-I error, critical P-values, and true P-values from a list of MK tables is available from the author by request.