Abstract
The timed secretion of the luteinizing hormone (LH) and follicle stimulating hormone (FSH) from pituitary gonadotrophs during the estrous cycle is crucial for normal reproductive functioning. The release of LH and FSH is stimulated by gonadotropin releasing hormone (GnRH) secreted by hypothalamic GnRH neurons. It is controlled by the frequency of the GnRH signal that varies during the estrous cycle. Curiously, the secretion of LH and FSH is differentially regulated by the frequency of GnRH pulses. LH secretion increases as the frequency increases within a physiological range, and FSH secretion shows a biphasic response, with a peak at a lower frequency. There is considerable experimental evidence that one key factor in these differential responses is the autocrine/paracrine actions of the pituitary polypeptides activin and follistatin. Based on these data, we develop a mathematical model that incorporates the dynamics of these polypeptides. We show that a model that incorporates the actions of activin and follistatin is sufficient to generate the differential responses of LH and FSH secretion to changes in the frequency of GnRH pulses. In addition, it shows that the actions of these polypeptides, along with the ovarian polypeptide inhibin and the estrogen-mediated variations in the frequency of GnRH pulses, are sufficient to account for the time courses of LH and FSH plasma levels during the rat estrous cycle. That is, a single peak of LH on the afternoon of proestrus and a double peak of FSH on proestrus and early estrus. We also use the model to identify which regulation pathways are indispensable for the differential regulation of LH and FSH and their time courses during the estrous cycle. We conclude that the actions of activin, inhibin, and follistatin are consistent with LH/FSH secretion patterns, and likely complement other factors in the production of the characteristic secretion patterns in female rats.
Keywords: mathematical model, ovarian cycle, estrous cycle, hormone rhythms, gonadotroph
1. Introduction
The anterior lobe of the pituitary gland contains endocrine cells of several types, including lactotrophs, somatotrophs, gonadotrophs, thyrotrophs and corticotrophs. The gonadotroph is unique in that it secretes two hormones, luteinizing hormone (LH) and follicle stimulating hormone (FSH), both of which are crucial for reproductive function. Hormones secreted by the hypothalamus and the gonads regulate biosynthesis of the LH and FSH hormones and their secretion. Hypothalamic input is from neurons that secrete gonadotropin-releasing hormone (GnRH) into hypophysial portal blood vessels, through which the GnRH travels to bathe the cells of the anterior pituitary (see (Freeman, 2006) for review). Input from the gonads includes estrogen, progesterone, and testosterone, as well as the polypeptide inhibin. While the steroid hormones can have an amplifying influence on LH/FSH secretion, a primary target is hypothalamic GnRH neurons (Freeman, 2006). In particular, the rise in the plasma estrogen level that occurs on proestrus acts to increase the activity frequency of GnRH neurons (Freeman, 2006). Inhibin, on the other hand, acts directly on the pituitary gonadotrophs (Welt, 2002). GnRH secretion is pulsatile in all mammals studied to date and pulsatile GnRH signals within a physiological range of frequency and amplitude are both necessary and sufficient for maintaining a healthy level of LH and FSH in these species (Knobil, 1980). A model that incorporates a fast binding and slow desensitization of the GnRH receptors was proposed to explain such a frequency specificity (Li and Goldbeter, 1989), although the exact level at which desensitization occurs remains unknown.
GnRH secretion is pulsatile in both male and female rats, and the frequency and amplitude of this pulsatility change dynamically throughout the estrous cycle in the female rat (Levine and Ramirez, 1982). The frequency of GnRH pulses as well as its mean level in the portal blood rise throughout the estrous cycle, peaking on the afternoon of proestrus and declining rapidly on the morning of estrus (Levine and Ramirez, 1982). Direct measurement of GnRH in the portal blood is difficult, so measurements of the GnRH pulse frequency are often indirect, based on the frequency of pulsatile plasma LH levels. The LH pulse frequency was shown to range from 1 pulse every two hours during estrus (Gallo, 1981a) to as much as 3 pulses per hour during the afternoon of proestrus (Gallo, 1981b) in the rat. The amplitude of pulsatile LH has also been shown to change during the estrous cycle, and to increase during the afternoon of proestrus (Gallo, 1981b). Both oscillation amplitude and frequency appear to peak during the LH surge that occurs on the afternoon of proestrus and evokes ovulation (Pupkin et al., 1966). The plasma FSH level also peaks on the afternoon of proestrus, and has a second peak early on estrus (Pupkin et al., 1966).
Motivated by the pulsatility of LH secretion and its variation throughout the estrous cycle, in vitro studies on rat gonadotrophs have been performed to determine how LH and FSH secretion is affected by pulsatile GnRH over a range of frequencies. In one study (Kaiser et al., 1997b), it was shown that LH secretion is low at a low frequency of 1 pulse every 4 hours. It increases at increasing GnRH pulse frequencies, reaching a maximum at the highest frequency tested (2 pulses per hour). FSH secretion is quite different. It is low at a low frequency and increases as the frequency increases, reaching a maximum at an intermediate frequency of 1 pulse every 2 hours. It then decreases again at higher frequencies. Thus, within this range of GnRH frequencies, LH and FSH secretion are regulated differentially with LH secretion increasing monotonically with increasing GnRH frequency, while the FSH frequency response curve is biphasic, with maximal secretion at a lower frequency. More than one potential mechanism exists for this differential response pattern of LH and FSH to GnRH pulse frequency, and the various mechanisms may work together in a complementary fashion. For example, it has been shown that GnRH receptor expression is upregulated at high stimulus frequencies in gonadotrophs (Bédécarrats and Kaiser, 2003), and that this favors LH secretion from the GH3 pituitary cell line (Kaiser et al., 1997b). Another potential mechanism is the actions of activin, follistatin, and inhibin. The goal of this paper is to develop a simple dynamic model for the actions of these polypeptides, using known interaction pathways between the polypeptides and LH and FSH production and secretion. With this model, we demonstrate that polypeptide actions are consistent with differential LH and FSH secretion patterns from gonadotrophs. We also demonstrate that these differential frequency responses are sufficient to explain the difference in the patterns of LH and FSH secretion during the rat estrous cycle. That is, a single surge of LH during the afternoon of proestrus and a double-peaked surge of FSH on the afternoon of proestrus and early morning of estrus. Thus, the actions of activin, follistatin, and inhibin have the right dynamic properties to complementother actions of GnRH (such as upregulation of GnRH receptors) and the steroid hormones (such as sensitization of gonadotrophs to GnRH) in the production of the characteristic LH and FSH secretion patterns during the rat ovarian cycle.
2. Mathematical model of the in vitro system
The polypeptides activin, inhibin, and follistatin are key players in the expression of FSH mRNA in gonadotrophs (see (Welt et al., 2002) for review). Activin is secreted by gonadotrophs (as well as other cell types) and binds to activin receptors on gonadotrophs in an autocrine/paracrine fashion. Activation of these receptors leads to an increase in the biosynthesis of the β subunit of FSH. FSHβ biosynthesis is almost undetectable in the absence of activin (Weiss et al., 1992). Inhibin, released from the gonads, plays an endocrine role in the pituitary. It appears to bind to both an inhibin receptor (betaglycan) and an activin receptor (ActRII), forming a cross-linked complex that prohibits the binding of activin (Lewis et al., 2000). The primary result of inhibin receptor activation is a disruption of activin signal transduction (Chapman and Woodruff, 2001). Another inhibitor of activin action is follistatin. This is secreted from gonadotrophs and, unlike inhibin, binds almost irreversibly to extracellular activin molecules, making them nonfunctional (Welt et al., 2002). Our model incorporates the actions of all three polypeptides as illustrated in Fig. 1. Other key variables of the model include variables for the plasma levels of LH and FSH and the protein level of FSH, which is affected by the actions of the polypeptides.
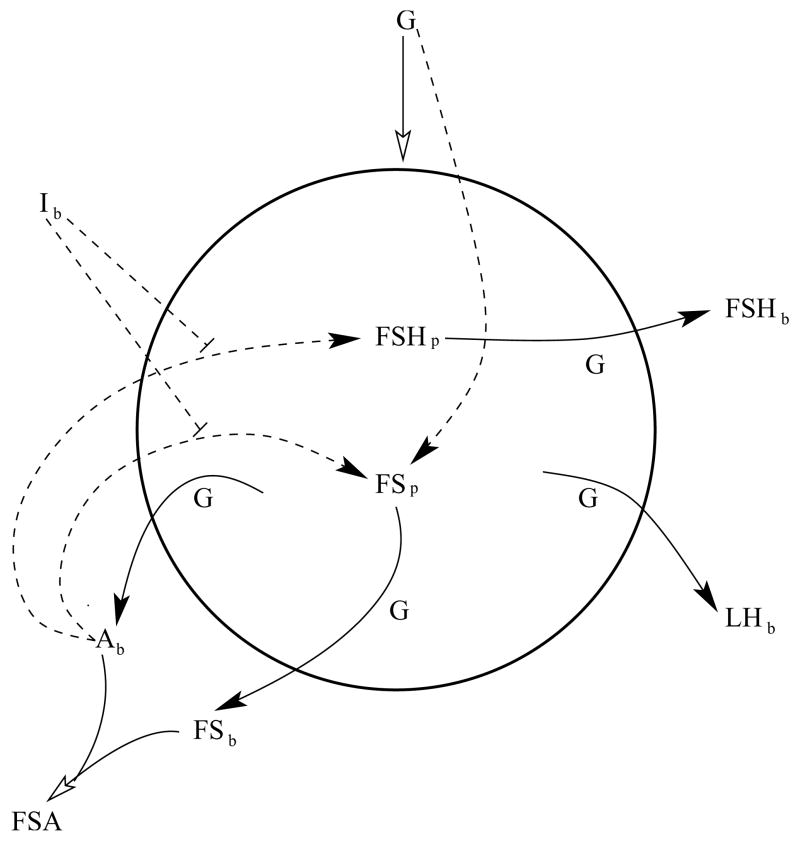
Figure 1.
Illustration of the variables in the mathematical model, and their interactions. The circle represents a gonadotroph. A solid arrow represents secretion, regulated by the GnRH frequency G. A dashed arrow represents effects on gene transcription. A closed arrowhead represents a positive action, while a short terminating line segment represents a negative action. An open arrowhead represents both the effects of G on secretion and the irreversible binding of activin and follistatin. FSH=follicle stimulating hormone, LH=luteinizing hormone, FS=follistatin, I=inhibin, A=activin, FSA=follistatin-activin complex, subscript b=plasma level, subscript p=intracellular protein level.
The endocrine system is very complex, and the secretion of hormones relating to reproduction is tightly regulated by numerous factors (Freeman, 2006). Our approach is to use a simple representation of the system that focuses on the interactions of the three polypeptides activin, inhibin, and folllistatin, in response to a pulsatile GnRH signal. While other factors are important in the regulation of gonadotropin secretion, our aim is to understand the interactions involving the polypeptides. For simplicity, we develop a mean field model in which each variable represents the spatial or population mean. For comparison with experimental data, these variables are quantified by units in ng/ml, except for time, which has units of hours. The primary input to the model is the normalized GnRH frequency (G). Such an input variable is adopted to avoid involving the complex mechanism of frequency specificity that happens at time scales faster than those considered here (a model for this has been developed previously, (Li and Goldbeter, 1989)). We assume the variable G is scaled by the maximum physiological frequency so that G is a dimensionless variable with a maximum that is equal to 1. We omit the time dynamics that occur on the time scale of GnRH oscillations (these dynamics have been described in previous models, (Khadra and Li, 2006) and (LeBeau et al., 2000)). In the in vitro model, GnRH input reflects exogenous application. The other input to the system, inhibin, is not included in the in vitro model since this factor is not secreted by gonadotrophs. Its role as an endocrine inhibitor is considered only in the in vivo model. Parameter values of the model were chosen to fit steady state response curves, as described later.
We begin with the FSH protein level in the gonadotroph, FSHp. It has been shown that FSHβ gene expression is upregulated by activin (Besecke et al., 1996; Kaiser et al., 1997b; Welt et al., 2002). We describe this positive effect of activin with a Michaelis-Menten function, v1 Ab/(k1 + Ab), where Ab is the level of activin in the blood. This function increases with Ab to a maximum value of v1. Half of the maximum value is attained when Ab = k1. This particular choice of the Michaelis-Menten function is aimed at achieving the simplest possible equations. Other types of monotonic saturating functions (such as a Hill or Boltzmann function) would yield similar results (see Appendix B). The differential equation for FSHp is:
| (1) |
where the second term represents first-order removal of FSH protein, with a rate constant of d. The values of the parameters v1, k1, and d, as well as other parameters, are listed in Table 1.
Table 1.
Parameter values used in the model.
| v1 = 10 ng/ml h−1 | v2 = 10 ng/ml h−1 | v3 = 4ng/ml h−1 | v4 =100 ng/ml h−1 | v5 = 10 ng/ml h−1 |
| v6 =15 ng/ml h−1 | k1 = 5 ng/ml | k2 = 0.1 | k3 = 5ng/ml | k4 = 1.5 |
| k5 = 0.5 ng/ml | k6 = 1 | k7 = 5 ng/ml | k8 = 0.1 | k9 = 1 |
| d =1h−1 | p =10ml2/ng2 h−1 | k̄1= 20ng/ml | k̄5 = 2ng/ml | kI = 3 ng/ml |
The FSH level in the blood, FSHb, is determined by the protein level of FSH in the gonadotrophs and the secretion rate. Hormone exocytosis is a Ca2+-mediated event that is increased by the presence of the cell stimulator GnRH. Protein kinases A and C are also activated by GnRH and play key roles in exocytosis of LH and FSH (Kile and Nett, 1994). We do not include the dynamics of Ca2+ and other second messengers in the model, but instead include an “exocytosis factor” that increases with the GnRH frequency. Since the amount of total FSH protein secreted is small compared to the amount produced, we neglect the effect of secretion on the FSH protein level. Both the increase of FSHb with protein level and the increase with GnRH frequency due to the exocytosis factor are described with Michaelis-Menten functions for simplicity. The differential equation for FSHb is:
| (2) |
As before, a first-order clearance term is included. There are at least 10 FSH isoforms, differing in their oligosaccharide structure (Ulloa-Aguirre et al., 1995). The breakdown rates of the various isoforms are different (Ulloa-Aguirre et al., 1992), illustrating the extreme complexity of the endocrine system. Likewise, the breakdown rates of other hormones and peptides differ from one to another. Incorporating this complexity into the model (e.g., using 10 variables for the various FSH isoforms with different degradation rates, rather than a single variable) would make the interpretation of the model results more complicated. For simplicity, we therefore use a single degradation rate, d, for all variables. Therefore, such a degradation rate should be considered as representing an average rate of many isoforms that participate in the interactions under consideration.
While activin upregulates FSHβ gene transcription, there is also evidence that it upregulates follistatin (FS) gene transcription. In one report, only FS secretion was measured, so it was not possible to determine if the increased secretion promoted by activin was due to increased exocytosis or increased FS protein levels (Bilezikjian et al., 1993). In another report, the FS mRNA level was measured directly, and it was shown that this was increased by activin (DePaolo et al., 1993). We therefore include a Michaelis-Menten term in the FS protein (FSp) equation for activin-mediated upregulation. In addition to this, there is evidence that FS mRNA levels are directly regulated by GnRH pulse frequency, such that the mRNA level is greater at a larger GnRH pulse frequency (Dalkin et al., 1999). We include a Michaelis-Menten factor to reflect this direct stimulatory action of G on FS protein levels. The differential equation for FSp is then:
| (3) |
The next equation describes the FS level in the blood, FSb. The first term is similar to the first term of Eq. 2, with Michaelis-Menten functions describing the exocytosis factor and the FSp factor. There is also a term for the removal of active FS from the blood due to irreversible binding of FS to activin, −p Ab FSb. The differential equation for FSb is:
| (4) |
The biosynthesis of activin protein does not appear to be modulated during the rat estrous cycle (Halvorson et al., 1994), so we do not include a variable for the activin protein level in the gonadotroph. Since the protein level is assumed to be constant, the secretion of activin depends only on the exocytosis factor. The differential equation for the level of activin in the blood, Ab, includes this factor, as well as the FS binding term and a clearance term:
| (5) |
The final equation describes the LH level in the blood (LHb). The LH protein level in the gonadotroph is not regulated by activin, but LH biosynthesis is increased with the GnRH pulse frequency (Bédécarrats and Kaiser, 2003; Kaiser et al., 1997b). The combination of this effect of GnRH on the LH protein level and the stimulatory effect of GnRH on exocytosis is included in the differential equation for LHb as a single Michaelis-Menten function:
| (6) |
In Eqs. 1–6, the production and/or secretion rates of the main variables are assumed to be regulated instantaneously by the variable G and/or by other variables. This is because the time scales that we consider in this model range from hours to days, which are significantly slower than the time scales of the regulations described in these equations.
The differential equations were solved numerically using the CVODE method implemented in the XPPAUT software package (Ermentrout, 2002). The tolerance was 10−9. Steady state curves of the full model were computed using numerical continuation as implemented in XPPAUT. For a minimal model (described later), explicit steady state functions were computed. Parameter values are listed in Table 1. Computer programs used to generate figures are freely available at www.math.fsu.edu/~bertram/software/pituitary.
3. Steady state response curves
Much of the in vitro data consists of measurements of mRNA or secretion levels after a relatively long period of pulsatile GnRH stimulation and over a range of GnRH pulse frequencies (Bédécarrats and Kaiser, 2003; Besecke et al., 1996; Dalkin et al., 1999; Kaiser et al., 1997b). We calculate similar response curves by computing the steady state values of the variables and plotting these values over a range of G from 0.01 to 1. The value G = 0.01 represents a very low frequency of stimulation while G = 1 represents a high stimulation frequency. These steady state response curves are shown in Fig. 2. The basic shapes of the curves are determined by the interaction terms in the differential equations. Parameter values were chosen to improve the qualitative fit to experimental data in the form of steady state response curves, where these data are available.
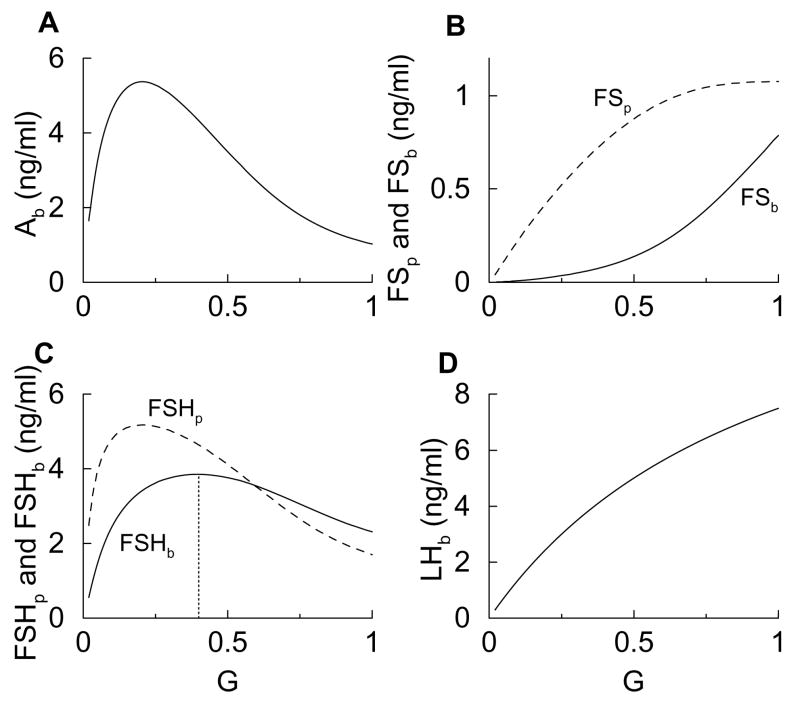
Figure 2.
Steady state response curves for G ranging from 0.01 (reflecting low-frequency stimulation) to 1 (high-frequency stimulation). The dotted vertical line in panel C marks the peak of FSHb.
Panel A shows that Ab first rises, due to the positive effect of the exocytosis factor in Eq. 5, and then declines, due to irreversible binding with FS. This biphasic response curve is crucial for the biphasic response in FSHp (dashed curve in Fig. 2C). This is indispensable for the differential response curves of LH and FSH secretion which shall be demonstrated by a minimal model later (Fig. 6). The FSb response curve continuously increases with G (Fig. 2B), in spite of the fact that much of the FS becomes bound to Ab. This continual increase in FSb is due largely to the continual increase in FSp (Fig. 2B) which overcomes the removal due to the binding with Ab. The increase in the FS protein levels is consistent with experimental data showing an increase in FS mRNA with GnRH pulse frequency (Besecke et al., 1996). The FSHp response curve (Fig. 2C) is similar to that of Ab, since FSH biosynthesis is regulated by activin, and is consistent with measurements of FSHβ mRNA levels (Kaiser et al., 1997a). The FSHb response curve is also biphasic but with a peak that is right shifted relative to that of FSHp (Fig. 2C). This is due both to the biphasic FSH protein level and to the G-dependent exocytosis factor, which accentuates the rising part of the curve and shifts the peak to the right. The biphasic FSHb response curve is consistent with measurements of FSH secretion (Kaiser et al., 1997b). Finally, Fig. 2D shows that LHb increases continually with G, due to the positive effects of G on both LH biosynthesis and exocytosis, and is consistent with secretion measurements (Kaiser et al., 1997b). Thus, the model generates steady state response curves that are consistent with experimental measurements. Most importantly, it reproduces the differential responses of LH and FSH secretion to GnRH stimulus frequencies.
Figure 6.
Steady state response curves and estrous cycle time courses computed with the minimal model. The removal of two feedback interactions from the full model to form the minimal model has little effect on the LH and FSH time courses.
4. Simulation of hormone levels during the rat estrous cycle
The hypothalamic GnRH neurons are key players in the four-day rat estrous cycle. Secretion levels from these neurons are largely regulated by ovarian hormones, and are low during most of the cycle, but increase dramatically on proestrus, followed by a rapid decline on estrus (Levine and Ramirez, 1982; Wise et al., 1981). The proestrus surge in both the frequency and amplitude of GnRH in portal blood results in surges in LH and FSH (Pupkin et al., 1966). We do not include variables for steroid hormone levels in the model, but do implicitly consider their effects on GnRH neurons by simulating the dynamics in G as shown in Fig. 3A (see Appendix A for equations). This shows G over a 4-day cycle, representing metestrus, diestrus, proestrus, and estrus (labels on x-axis). Notice that the sharp rise and fall in G occurs during one day, proestrus, as has been shown experimentally (Freeman, 2006; Levine and Ramirez, 1982; Wise et al., 1981). The time-varying G is input to Eqs. 1–6, resulting in time-varying values of the system variables. Our goal is to demonstrate that the combined actions of activin, inhibin and follistatin on the synthesis and secretion of LH and FSH is sufficient to account for the most important features of LHb and FSHb profiles during the simulated estrous cycle given the cyclic profile of G shown in Fig. 3A.
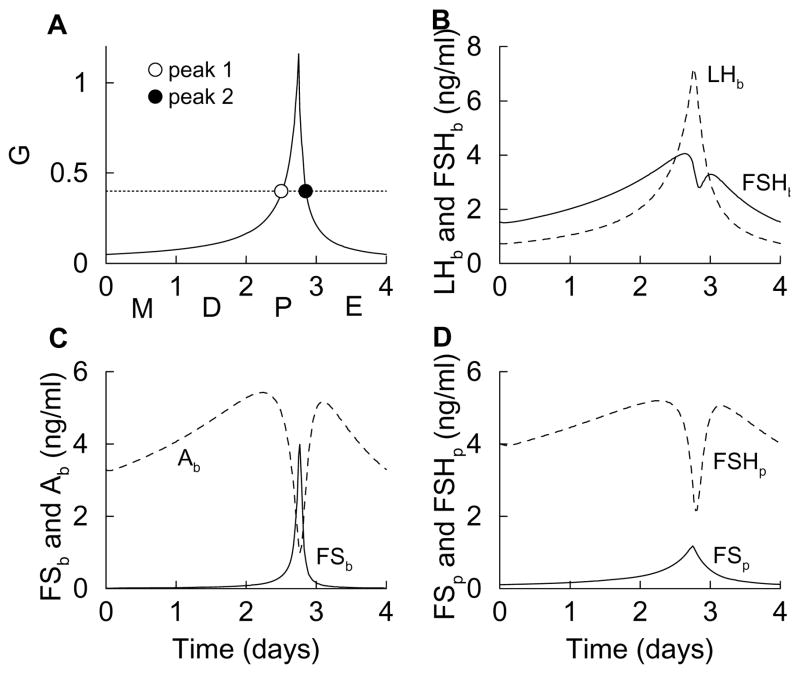
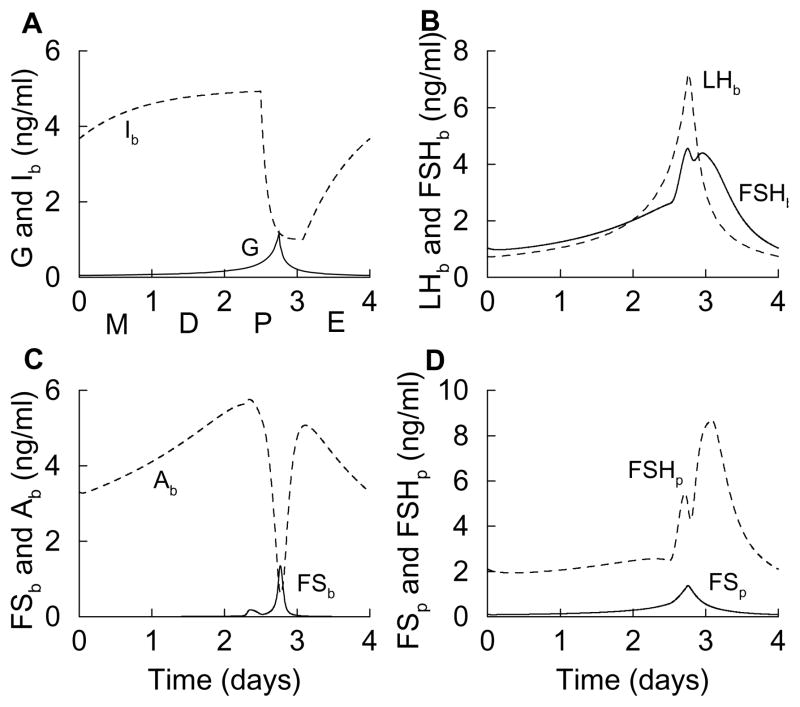
Figure 3.
Time courses of variables during the simulated estrous cycle, which is modeled as a surge in the GnRH level during the afternoon of proestrus (A). This results in a single surge of LH in the blood, and a double surge of FSH (B), due to the interactions of other variables (C and D).
Figure 3B shows LHb and FSHb during the simulated estrous cycle. There is a single surge of LH during the afternoon of proestrus, reflecting the surge of G. There is also a double surge in FSH; the first occurs during the afternoon of proestrus shortly before the LH surge and the second during the end of proestrus. The peak times and number of peaks in LH and FSH are similar to those observed in blood serum measurements of LH and FSH (Besecke et al., 1997; Pupkin et al., 1966).
While the LH surge in the model is easy to understand, the double FSH surge is subtler, but ultimately can be traced back to the activin time course. The activin level rises with G, but is quickly reduced by a surge in FS (Fig. 3C) that is coincident with the peak of G. That is, the irreversible binding of FS to activin causes free activin to decline when the FS level rises. When the FS level falls (coincident with the fall in G), the free activin level returns to a high value (a second peak) before declining due to the low level of G. The activin time course is similar to measurements of serum activin Ab during the estrous cycle (Besecke et al., 1997), and the peak of follistatin protein (Fig. 3D) in the afternoon of proestrus is similar to measurements of FS mRNA during the cycle (Halvorson et al., 1994). Since FSH biosynthesis is stimulated by activin, the FSHp time course (Fig. 3D) has a shape similar to that of Ab. Indeed, measurements of FSHβ mRNA during the estrous cycle have shown two peaks, one early in proestrus and one near the end of proestrus (Halvorson et al., 1994). The peaks in experimental measurements, however, tend to be more pronounced than those produced by the model (this is addressed later). Finally, the double-peaked FSH protein time course results in a double peaked FSHb time course, with one peak shortly before the LH surge and the other after, as has been shown in experimental measurements (Besecke et al., 1997; Pupkin et al., 1966). Again, the measured peaks in FSH plasma levels tend to be more pronounced than those produced by the model.
The dynamics of the variables during the simulated estrous cycle (Fig. 3) can also be understood in terms of the steady state response curves (Fig. 2). This is because the variables change much faster than does G during the cycle, so they are in a state of quasi-equilibrium. Using the response curves, we simply examine what happens to each variable as G is first increased from 0.01 to 1 (as occurs during the first three days of the simulated cycle), and then decreased back to near 0.01 (as occurs after the proestrus peak in G). For example, the steady state FSHb curve (Fig. 2C) is biphasic, so when G increases from 0.01 to 1 FSHb first increases, peaks, and then decreases. When G next decreases from 1 to 0.01 FSHb again increases, peaks, and then decreases. Hence, during the cycle FSHb will have two peaks; one is due to the increase in G leading up to proestrus, and the other is due to the decrease in G following proestrus. This is the double-peaked solid curve in Fig. 3B. Each peak in FSHb during the cycle occurs at a value of G where the FSHb response curve is at a maximum (dotted line in Fig. 2C). The first peak in FSHb occurs while G is rising during proestrus (open circle in Fig. 3A), and the second occurs while G is declining late in proestrus (closed circle in Fig. 3A).
A similar explanation applies to Ab and FSHp, since each has a biphasic steady state response curve. In contrast, the steady state LHb curve is monophasic. When G increases from 0.01 to 1 LHb increases, and when G decreases back to 0.01 LHb decreases. Thus, during the cycle LHb exhibits a single peak, which occurs at the peak of G. This is the single-peaked dashed curve in Fig. 3B. Other variables with monophasic response curves (FSp and FSb) exhibit similar single peaks during the simulated estrous cycle.
5. Interactions necessary for a double-peaked FSH time course
Many feedback interactions are included in Eqs. 1–6, based on evidence from experimental data. Which of these interactions are necessary and which are superfluous in producing the double-peaked FSH time course during the estrous cycle? We address these questions by iteratively removing a single interaction and recalculating steady state response and estrous cycle curves. The terms or factors that are examined are those multiplying the vj parameters in Eqs. 1–6. For example, to remove the feedback of Ab onto FSHp, the steady state value of Ab for a fixed value of G is used to calculate Ab/(k1 + Ab), and then this value is used in place of Ab/(k1 + Ab) in the calculation of response and estrous cycle curves. We focus first on two interactions that have almost opposite effects on the FSHb response curve: the direct feedback of G and the feedback of FSHp, both in Eq. 2.
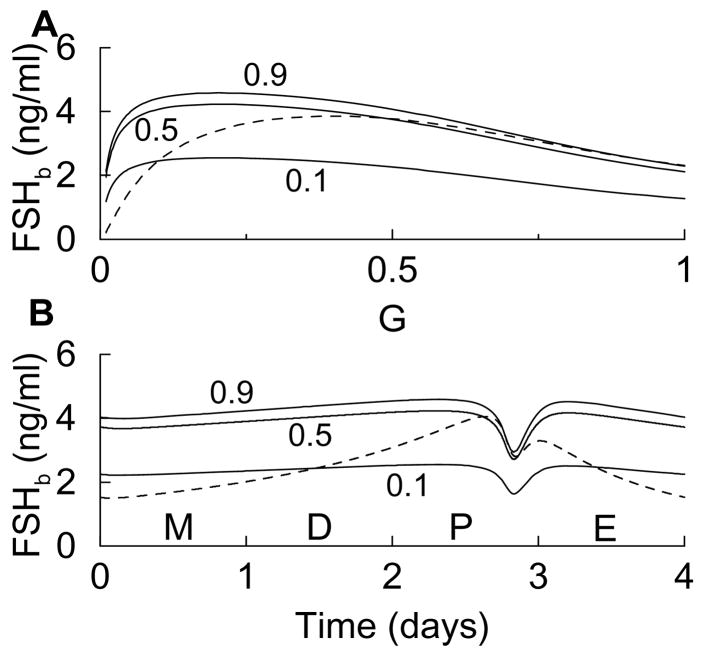
When the direct stimulatory feedback of G onto FSHb is removed by replacing G in the term G/(k2 + G) with three different values of G (0.1, 0.5, and 0.9) the FSHb steady state response curves peak at a much lower value of G than the original curve (Fig. 4A, solid and dashed, respectively). As a result, the FSHb time course during the simulated estrous cycle has only a very shallow rise leading up to proestrus and a shallow decline following proestrus (Fig. 4B). This is quite different from what one observes in the data, and demonstrates that the exocytosis factor is important to achieving an appropriate FSHb time course during the cycle.
Figure 4.
(A) FSHb steady state response calculated with Eqs. 1–6 (dashed) and with the direct stimulatory influence of G removed (solid) by replacing G in G (k2 + G) with the fixed values 0.1, 0.5, or 0.9 in Eq. 2. (B) When the stimulatory influence of G is removed, the rise in FSHb leading up to proestrus and the decline following proestrus are very shallow.
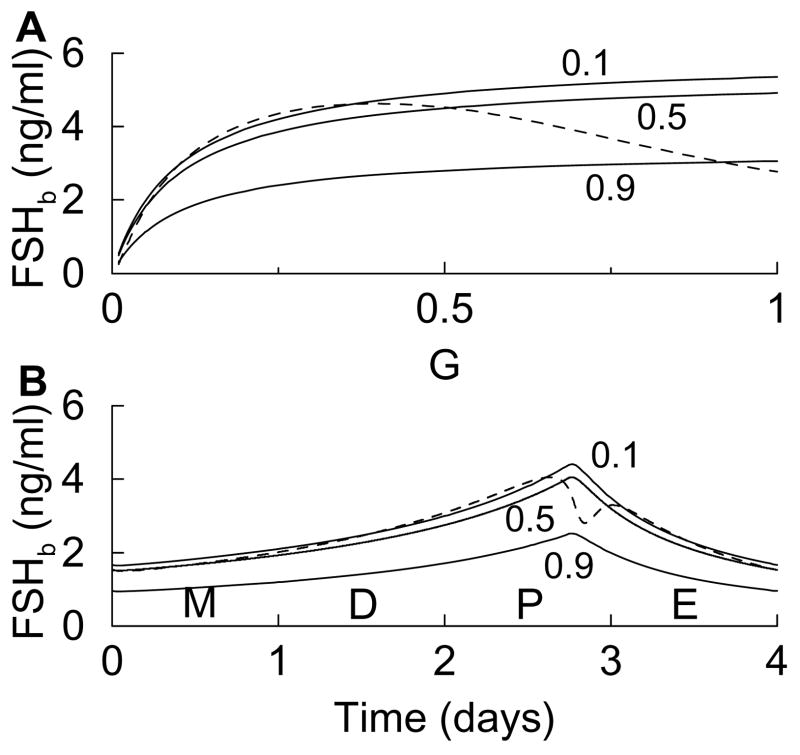
While the rising phase of the biphasic FSHb response curve is shortened by removing direct feedback of G, the falling phase of the curve is totally eliminated if, instead, the term FSHp/(k3 + FSHp) is replaced by 0.43, 0.45, or 0.28. (These are calculated using the steady state values of FSHp when G=0.1, 0.5, and 0.9, respectively.) That is, if the FSH protein biosynthesis proceeds at a constant rate, then FSHb will increase continually when G is increased (Fig. 5A). This is because the inhibiting effects of FS are factored out. The result during the simulated estrous cycle is an FSHb time course with a single peak on the afternoon of proestrus (Fig. 5B), contrary to experimental data.
Figure 5.
(A) FSHb steady state response calculated with Eqs. 1–6 (dashed) and with the effects of FSH biosynthesis removed (solid) by replacing FSHp (k3 + FSHp) with 0.49, 0.45, or 0.28 in Eq. 2. (B) When the influence of FSH biosynthesis is removed, the rise in the FSHb time course has a single peak on the afternoon of proestrus, rather than the characteristic double peak.
We have demonstrated that both feedback factors in the FSHb equation are necessary for achieving an appropriate double-peaked FSHb time course. Many other feedback factors in the model are also needed. Since it is clear from Figs. 4–5 that the results are similar regardless of the value at which G is fixed, we fixed G at 0.5 when subsequent interactions were removed. If Ab/(k1 + Ab) is replaced by 0.42 in Eq. 1, then the FSHp response curve is horizontal (no G dependence), so the FSHb response and estrous cycle curves are similar to those in Fig. 5. When G/(k4 + G) is replaced with 0.25 in Eq. 3 the FSHp response curve has a shallow declining phase, so the FSHb response curve has a negligible declining phase and the FSHb estrous cycle time course again has a single peak. The results are similar when G/(k6 + G) is replaced with 0.33 or when FSp/(k7 + FSp) is replaced with 0.15 in Eq. 4. In the latter case, FS secretion now depends only on G, so the FSb response curve has a much shallower rise. This results in a shallow declining phase of FSHp.
While each of the factors above is necessary for proper FSHb response and estrous cycle curves, there are two feedback factors that are superfluous. One is the stimulatory action of activin on FS biosynthesis. When Ab/(k5 + Ab) is replaced by 0.87 in Eq. 3 the FSp response curve continues to rise as G is increased, rather than saturating as it normally does (Fig. 2B). This greatly accentuates the increase of FSb with G, so that the biphasic profiles of FSHp and FSHb are enhanced. The other superfluous feedback factor is the exocytosis factor in the Ab equation, Eq. 5. Replacing G/(k8 + G) with 0.83 eliminates the rising phase of the Ab response curve, but this has little impact on FSHp and FSHb; it is the declining phase of the Ab response curve that is the key element in the production of biphasic FSH curves.
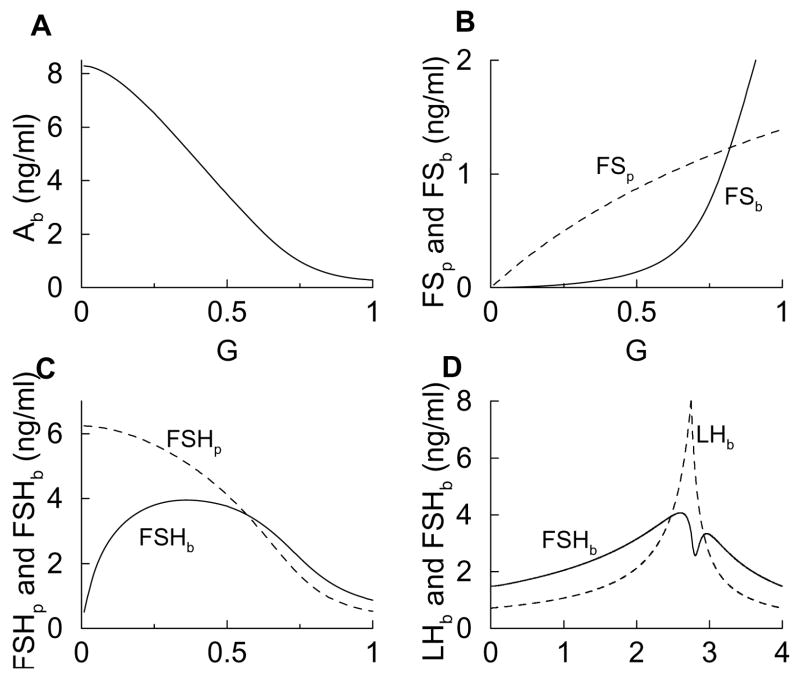
A “minimal model” can be formed by removing both of the superfluous feedback interactions, Ab/(k5 + Ab) in Eq. 3 and G/(k8 + G) in Eq. 5, and replacing them with constants. The extra simplicity of this model makes it possible to explicitly solve for the steady states. This calculation is demonstrated in Appendix B. Figure 6 shows steady-state response curves (panels A, B, C) and estrous cycle curves (panel D) for the minimal model. Unlike the response curves calculated with the full model (Fig. 2), the Ab curve now declines monotonically with G (Fig. 6A). Also, FSp does not saturate for G < 1, so FSb increases more rapidly with G (Fig. 6B). The result is an FSHp response curve that declines continually and a biphasic FSHb response curve whose declining phase is enhanced (Fig. 6C). The subsequent FSHb estrous cycle curve is double-peaked (Fig. 6D), just like that in the full model (Fig. 3B). Comparing panels A and C in Fig. 6 and in Fig. 2, we notice that the biphasic response in FSHp and Ab is not essential for the biphasic response in FSHb. The decline in Ab at higher levels of G is crucial. This decline is caused by the increase in FSb at higher G. Thus, removing the two superfluous feedback interactions while leaving these crucial mechanisms intact has little consequence on the FSH time course, but simplifies the model to the point where analytical calculations can be performed (Appendix B). From these calculations, for example, one can deduce by an examination of the steady state formulas whether a response curve is increasing, decreasing, or biphasic.
6. Inhibin accentuates the double-peaked FSH time course and improves the time courses of other variables
Thus far we have considered factors secreted from gonadotrophs and extrinsic forcing from GnRH neurons. We now incorporate the effects of inhibin, an important modulating polypeptide secreted by the ovaries. The primary action of inhibin on gonadotrophs is competition with activin for the activin binding site (Lewis et al., 2000). We therefore model the action of inhibin by varying the Michaelis constants for the activin feedback terms so that they increase with the inhibin blood level (reducing the effective activin feedback). That is, we replace parameter k1 in Eq. 1 and k5 in Eq. 3 with:
| (7) |
where kI, k̄1, and k̄5 are parameters (see Table 1) and Ib is the inhibin level in the blood. A third power is used to sharpen the response to inhibin. We then impose an inhibin estrous cycle time course that is similar to that measured for serum levels of inhibin B (or the sum of inhibin A and inhibin B) (Woodruff et al., 1996). That is, the inhibin level is high during the first two days of the cycle, it declines rapidly during the afternoon of proestrus, and it rises slowly during estrous (Fig. 7A).
Figure 7.
Estrous cycle time courses when the actions of inhibin are included in the model. (A) The time courses of inhibin (Ib) and GnRH are imposed on the system to qualitatively match experimental measurements. (B) The FSHb level during the first two days of the cycle is suppressed by inhibin action on FSHp, accentuating the proestrus surge. (C) The blood FS level now exhibits two small peaks, rather than the single large peak that it did without inhibin action. (D) The FSH protein time course, with two clear peaks on proestrus, is now a much better fit to experimental measurements.
When the inhibin action is added to the actions of GnRH, activin, and follistatin, the FSHb estrous cycle time course retains the features produced without inhibin, but now the FSHb level is suppressed prior to proestrus. This accentuates the surge in FSHb that occurs during proestrus, improving the fit of the FSHb time course with serum FSH measurements (Besecke et al., 1997; Pupkin et al., 1966). The way that inhibin affects FSHb is through its inhibitory action on the FSH protein level. Without inhibin there were two shallow peaks in FSHp separated by a large decline (Fig. 3D). With inhibin the FSHp level is kept low during the first two days of the cycle, and then exhibits two peaks, during the middle of proestrus and then late in proestrus (Fig. 7D). Also, the second peak is larger and broader than the first. This time course is a better fit to mRNA measurements (Halvorson et al., 1994) than the FSHp time course without inhibin action.
The final noticeable effect of inhibin is on the FS blood level. Without inhibin there is a single surge of FSb during the afternoon of proestrus (Fig. 3C). With inhibin there are two FSb peaks, a small one early on proestrus and a larger one on the afternoon of proestrus (Fig. 7C). The rapid decline in Ib on the afternoon of proestrus causes a small bump in Ab, which in turn disrupts the FSb proestrus surge. Thus, the single large peak present without inhibin is converted into two blunted peaks, with the second one larger than the first. There are data showing a similar FS time course, from measurements of both FS mRNA and pituitary content (Besecke et al., 1997). Thus, including the actions of inhibin in the model improves the overall fits of the model response and estrous cycle curves to the experimental data.
7. Discussion
The primary goal of this study was to determine which aspects of LH and FSH secretion could be accounted for, at least in part, by the known actions of activin, inhibin, and follistatin. We demonstrated that the actions of activin and follistatin can account for the differential responses of LH and FSH secretion to GnRH stimulation. Thus, the frequency response curves determined in vitro are reproduced by the model, which incorporates known feedback interaction terms. The model also produces time courses for LH, FSH, follistatin, and activin protein and blood levels that agree qualitatively with measurements of mRNA and plasma protein levels during the estrous cycle. The cycle is simulated here only through the cyclic changes in the GnRH frequency, which is a simplification that excludes the direct action of ovarian steroid hormones on gonadotrophs. Inhibin is not necessary to reproduce most of the basic features of the variable time courses during the estrous cycle, but inclusion of inhibin action sculpts the time courses of several variables to provide a better fit to experimental measurements. Results presented here not only illustrate that the autocrine/paracrine actions of the polypeptides on gonadotrophs are sufficient to cause the observed differential regulations of LH and FSH secretion, they also helped identify the key actions that are necessary for explaining the observed dose-response in FSH and the time courses for LH, FSH, follistatin, and activin protein.
While activin, follistatin, inhibin, and GnRH can reproduce the estrous cycle time courses, we note that both inhibin secretion from the ovaries and GnRH secretion from GnRH neurons are regulated by the ovarian hormones estrogen and progesterone. Both steroids inhibit the frequency and amplitude of GnRH pulses, and cause them to vary throughout the estrous cycle (Freeman, 2006). In addition, both estrogen and progesterone sensitize gonadotrophs to GnRH during proestrus (Baldwin and Downs, 1980). Other hormones also have modulating effects on gonadotrophs. For example, the hormones oxytocin (Robinson and Evans, 1990) and neuropeptide Y (Bauer-Dantoin et al., 1993) both potentiate the effects of GnRH on LH secretion. In addition, the GnRH receptor density in the gonadotroph is regulated by GnRH pulse frequency (Kaiser et al., 1997b). Finally, there are apparent differences in the exocytosis of the FSH and LH hormones (Kile and Nett, 1994). Thus, the reality of LH and FSH secretion during the rat estrous cycle is more complicated than the picture provided by our model, as one would expect for the secretion of such key reproductive hormones. However, the model does illustrate the roles played by some of the important factors, and demonstrates how gonadal peptides interact dynamically and may contribute to many of the key features of gonadotropin hormone levels during the rat estrous cycle.
Since the 1960s, mathematical models have been used to understand the rat ovarian cycle (Schwartz, 1969). There have also been models developed of the human menstrual cycle (Clark et al., 2003; Rasgon et al., 2003; Schlosser and Selgrade, 2000; Zeeman, 2003), some of which considered the dynamics and effects of inhibin (Clark et al., 2003; Schlosser and Selgrade, 2000). Although an LH surge occurs during the menstrual cycle, the FSH dynamics are quite different from those during the rat estrous cycle. Models have also been published that focus on GnRH-induced LH secretion from gonadotrophs (Blum et al., 2000; Heinze et al., 1998; Leng and Brown, 1997; Tien et al., 2005), and the origin of pulsatile GnRH release from (Khadra and Li, 2006) and electrical activity in (LeBeau et al., 2000) hypothalamic neurons. The model of Blum et al. (Blum et al., 2000) contains detailed signal transduction pathways for GnRH-mediated LH secretion; the model of Heinze et al. (Heinze et al., 1998) considers depletion of releasable LH and GnRH receptor desensitization as mechanisms for the ineffectiveness of continuous GnRH stimulation of gonadotrophs; the model of Tien et al. (Tien et al., 2005) considers desensitization of inositol trisphosphate receptors and their recovery as a mechanism for the LH surge; and the model of Scullion et al. (Scullion et al., 2004) considers self priming of GnRH as a mechanism for enhanced LH secretion during the LH surge. These are mechanistic models that focus on certain aspects of the ovarian cycle. Our model is, to our knowledge, the first that considers the interactions of activin, inhibin, and follistatin in the regulation of gonadotropin secretion. Clearly, many factors are involved in the dynamics of LH and FSH during the ovarian cycle of the rat, and mathematical modeling will likely continue to play a role in integrating these factors.
Acknowledgments
This work was supported by National Institutes of Health grant DA-19356 to R.B. and Natural Sciences and Engineering Research Council of Canada grants to Y. X. L.
APPENDIX A
Equations for G and Ib
In this appendix we describe how the estrous cycle time courses of G and Ib are computed. Unlike the other variables, which depend on each other as well as G and possibly Ib, these time courses are imposed and depend only on time.
The G time course is described by the following differential equation:
| (8) |
where μ is a parameter that has a positive value of 0.3 prior to proestrus and up until hour 18 of proestrus (so that G increases) and a negative value of −0.6 afterwards (so that G decreases).
The Ib time course is described by the differential equation:
| (9) |
where I∞ = 5 and τI = 20 h prior to proestrus and up until hour 12 of proestrus, I∞ = 1 and τI = 2 h during the next 14 h, then returning to I∞ = 5, τI = 20 for the remainder of the estrous cycle.
APPENDIX B
Steady state solution to a generalized minimal model
In the model described by Eqs. 1–6 we use Michaelis-Menten functions extensively. These are often used in modeling when an increasing and saturating function is needed. However, the behavior of our model is not limited by the use of Michaelis-Menten relations; any increasing and saturating function would work, with suitable readjustment of parameter values. In what follows we define fj (x, k) to be an increasing saturating function of the variable x, with half-maximal value when x = k. The subscript j is used to denote possibly different functions. For the Michaelis-Menten function, . The minimal model can then be written as:
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
where and (see text describing the minimal model for an explanation of these values).
The steady state solution can be obtained by setting all derivatives to 0 and solving (superscript “ss” denotes steady state):
| (16) |
| (17) |
| (18) |
where b = d + pq and . Then
| (19) |
| (20) |
| (21) |
From these steady state equations, one can deduce that both and are monotonic increasing functions of G, since they depend only on the increasing functions f4and f7. The expression depends on b, which is itself an increasing function of G. The derivative of with respect to b is negative, so the response curve will decrease with G. Since has increasing functions in the numerator and a decreasing variable in the denominator, it will increase monotonically with G. The variable will decrease with G, since the f1 function has as an argument, and decreases with G. Finally, the expression for contains the product of an increasing function (f2) and a decreasing function (f3) of G, so it is a biphasic function of G. These observations are all consistent with the response functions computed numerically for the minimal model in Fig. 6.
References
- Baldwin DM, Downs TR. Release of LH and FSH by anterior pituitary cell suspensions from female rats during the estrous cycle and from estrogen-treated ovariectomized rats. Biol Reprod. 1980;24:581–590. doi: 10.1095/biolreprod24.3.581. [DOI] [PubMed] [Google Scholar]
- Bauer-Dantoin AC, Knox KL, Schwartz NB, Levine JE. Estrous cycle stage-dependent effects of neuropeptide-Y on leuteinizing hormone (LH)-releasing hormone-stimulated LH and follicle-stimulating hormone secretion from anterior pituitary fragments in vitro. Endocrinology. 1993;133:2413–2417. doi: 10.1210/endo.133.6.8243258. [DOI] [PubMed] [Google Scholar]
- Bédécarrats GY, Kaiser UB. Differential regulation of gonadotropin subunit gene promoter activity by pulsatile gonadotropin-releasing hormone (GnRH) in perifused LβT2 cells: Role of GnRH receptor concentration. Endocrinology. 2003;144:1802–1811. doi: 10.1210/en.2002-221140. [DOI] [PubMed] [Google Scholar]
- Besecke LM, Guendner MJ, Schneyer AL, Bauer-Dantoin AC, Jameson JL, Weiss J. Gonadotropin-releasing hormone regulates follicle-stimulating hormone-B gene expression through an activin/follistatin autocrine or paracrine loop. Endocrinology. 1996;137:3667–3673. doi: 10.1210/endo.137.9.8756531. [DOI] [PubMed] [Google Scholar]
- Besecke LM, Guendner MJ, Sluss PA, Polak AG, Woodruff TK, Jameson JL, Bauer-Dantoin AC, Weiss J. Pituitary follistatin regulates activin-mediated production of follicle-stimulating hormone during the rat estrous cycle. Endocrinology. 1997;138:2841–2848. doi: 10.1210/endo.138.7.5279. [DOI] [PubMed] [Google Scholar]
- Bilezikjian LM, Corrigan AZ, Vaughan JM, Vale WM. Activin-A regulates follistatin secretion from cultured rat anterior pituitary cells. Endocrinology. 1993;133:2554–2560. doi: 10.1210/endo.133.6.8243277. [DOI] [PubMed] [Google Scholar]
- Blum JJ, Reed MC, Janovick JA, Conn PM. A mathematical model quantifying GnRH-induced LH secretion from gonadotropes. Am J Physiol. 2000;278:E263–E272. doi: 10.1152/ajpendo.2000.278.2.E263. [DOI] [PubMed] [Google Scholar]
- Chapman SC, Woodruff TK. Modulation of activin signal transduction by inhibin-B and inhibin-binding protein (InhBP) Mol Endocrinol. 2001;15:668–679. doi: 10.1210/mend.15.4.0616. [DOI] [PubMed] [Google Scholar]
- Clark LH, Schlosser PM, Selgrade JF. Multiple stable periodic solutions in a model for hormonal control of the menstrual cycle. Bull Math Biol. 2003;65:157–173. doi: 10.1006/bulm.2002.0326. [DOI] [PubMed] [Google Scholar]
- Dalkin AC, Haisenleder DJ, Gilrain JT, Aylor K, Yasin M, Marshall JC. Gonadotropin-releasing hormone regulation of gonadotropin subunit gene expression in female rats: Actions on follicle-stimulating hormone beta messenger ribonucleic acid (mRNA) involve differential expression of pituitary activin (beta-B) and follistatin mRNAs. Endocrinology. 1999;140:903–908. doi: 10.1210/endo.140.2.6483. [DOI] [PubMed] [Google Scholar]
- DePaolo LV, Mercado M, Guo Y, Ling N. Increased follistatin (activin-binding protein) gene expression in rat anterior pituitary tissue after ovariectomy may be mediated by pituitary activin. Endocrinology. 1993;132:2221–2228. doi: 10.1210/endo.132.5.8477666. [DOI] [PubMed] [Google Scholar]
- Ermentrout GB. Simulating, analyzing, and animating dynamical systems: A guide to XPPAUT for researchers and students. SIAM; Philadelphia: 2002. [Google Scholar]
- Freeman ME. Neuroendocrine control of the ovarian cycle of the rat. In: Neill JD, editor. Knobil and Neill’s Physiology of Reproduction. Elsevier; 2006. pp. 2327–2388. [Google Scholar]
- Gallo RV. Pulsatile LH release during periods of low level LH secretion in the rat estrous cycle. Biol Reprod. 1981a;24:771–777. doi: 10.1095/biolreprod24.4.771. [DOI] [PubMed] [Google Scholar]
- Gallo RV. Pulsatile LH release during the ovulatory LH surge on proestrus in the rat. Biol Reprod. 1981b;24:100–104. doi: 10.1095/biolreprod24.1.100. [DOI] [PubMed] [Google Scholar]
- Halvorson LM, Weiss J, Bauer-Dantoin AC, Jameson JL. Dynamic regulation of pituitary follistatin messenger ribonucleic acids during the rat estrous cycle. Endocrinology. 1994;134:1247–1253. doi: 10.1210/endo.134.3.8119165. [DOI] [PubMed] [Google Scholar]
- Heinze K, Keener RW, Midgley AR. A mathematical model of luteinizing hormone release from ovine pituitary cells in perfusion. Am J Physiol. 1998;275:E1061–E1071. doi: 10.1152/ajpendo.1998.275.6.E1061. [DOI] [PubMed] [Google Scholar]
- Kaiser UB, Conn PM, Chin WW. Studies of gonadotropin-releasing hormone (GnRH) action using GnRH receptor-expressing pituitary cell lines. Endocr Rev. 1997a;18:46–70. doi: 10.1210/edrv.18.1.0289. [DOI] [PubMed] [Google Scholar]
- Kaiser UB, Jakubowiak A, Steinberger A, Chin WW. Differential effects of gonadotropin-releasing hormone (GnRH) pulse frequency on gonadotropin subunit and GnRH receptor messenger ribonucleic acid levels in vitro. Endocrinology. 1997b;138:1224–1231. doi: 10.1210/endo.138.3.4968. [DOI] [PubMed] [Google Scholar]
- Khadra A, Li YX. A model for the pulsatile secretion of gonadotropin-releasing hormone from synchronized hypothalamic neurons. Biophys J. 2006;91:74–83. doi: 10.1529/biophysj.105.080630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kile JP, Nett TM. Differential secretion of follicle-stimulating hormone and luteinizing hormone from ovine pituitary cells following activation of protein kinase A, protein kinase C, or increased intracellular calcium. Biol Reprod. 1994;50:49–54. doi: 10.1095/biolreprod50.1.49. [DOI] [PubMed] [Google Scholar]
- Knobil E. The neuroendocrine control of the menstrual cycle. Res Progr Horm Hum Res. 1980;36:53–88. doi: 10.1016/b978-0-12-571136-4.50008-5. [DOI] [PubMed] [Google Scholar]
- LeBeau AP, Van Goor F, Stoijikovic SS, Sherman A. Modeling of membrane excitability in gonadotropin-releasing hormone-secreting hypothalamic neurons regulated by Ca2+-mobilizing and adenylyl cyclase-coupled receptors. J Neurosci. 2000;20:9290–9297. doi: 10.1523/JNEUROSCI.20-24-09290.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leng G, Brown D. The origins and significance of pulsatility in hormone secretion from the pituitary. J Neuroendocrinology. 1997;9:493–513. doi: 10.1046/j.1365-2826.1997.00615.x. [DOI] [PubMed] [Google Scholar]
- Levine JE, V, Ramirez D. LHRH release during the rat estrous cycle and after ovariectomy, as estimated with push-pull cannulae. Endocrinology. 1982;111:1439–1448. doi: 10.1210/endo-111-5-1439. [DOI] [PubMed] [Google Scholar]
- Lewis KA, Gray PC, Blount AL, MacConell LA, Wiater E, Bilezikjian LM, Vale W. Betaglycan binds inhibin and can mediate functional antagonism of activin signaling. Nature. 2000;404:411–414. doi: 10.1038/35006129. [DOI] [PubMed] [Google Scholar]
- Li YX, Goldbeter A. Frequency specificity in intercellular communication: influence of patterns of periodic signaling on target cell responsiveness. Biophys J. 1989;55:125–145. doi: 10.1016/S0006-3495(89)82785-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pupkin M, Bratt H, Weisz J, Lloyd CW, Balogh K., Jr Dehydrogenases in the rat ovary. I. A histochemical study of 5- 3 b-and 20 a-hydroxysteroid dehydrogenases and enzymes of carbohydrate oxidation during the estrous cycle. Endocrinology. 1966;79:316–327. doi: 10.1210/endo-79-2-316. [DOI] [PubMed] [Google Scholar]
- Rasgon NL, Prolo PLP, Elman S, Negrao AB, Licinio J, Garfinkel A. Emergent oscillations in mathematical model of the human menstrual cycle. CNS Spectr. 2003;8:805–814. doi: 10.1017/s1092852900019246. [DOI] [PubMed] [Google Scholar]
- Robinson G, Evans JJ. Oxytocin has a role in gonadotrophin regulation in rats. J Endocrinol. 1990;125:425–432. doi: 10.1677/joe.0.1250425. [DOI] [PubMed] [Google Scholar]
- Schlosser PM, Selgrade JF. A model of gonadotropin regulation during the menstrual cycle in women: qualitative features. Environ Health Perspect. 2000;108(suppl 5):873–881. doi: 10.1289/ehp.00108s5873. [DOI] [PubMed] [Google Scholar]
- Schwartz NB. A model for the regulation of ovulation in the rat. Recent Prog Horm Res. 1969;25:1–55. doi: 10.1016/b978-0-12-571125-8.50004-1. [DOI] [PubMed] [Google Scholar]
- Scullion S, Brown D, Leng G. Modelling the pituitary response to luteinizing hormone-releasing hormone. J Neuroendocrinology. 2004;16:265–271. doi: 10.1111/j.0953-8194.2004.01169.x. [DOI] [PubMed] [Google Scholar]
- Tien J, Lyles D, Zeeman ML. A potential role of modulating inositol 1,4,5-triphosphate receptor desensitization and recovery rates in regulating ovulation. J Theor Biol. 2005;232:105–117. doi: 10.1016/j.jtbi.2004.08.003. [DOI] [PubMed] [Google Scholar]
- Ulloa-Aguirre A, Cravioto A, Damian-Matsumura P, Jimenez M, Zambrano E, Diaz-Sanchez V. Biological characterization of the naturally occurring analogues of intrapituitary human follicle-stimulating hormone. Hum Reprod. 1992;7:23–30. doi: 10.1093/oxfordjournals.humrep.a137550. [DOI] [PubMed] [Google Scholar]
- Ulloa-Aguirre A, Midgley AR, Jr, Beitins I, Padmanabhan V. Follicle-stimulating isohormones: Characterization and physiological relevance. Endocrine Rev. 1995;16:765–787. doi: 10.1210/edrv-16-6-765. [DOI] [PubMed] [Google Scholar]
- Weiss J, Harris PE, Halvorson LM, Crowley WF, Jameson JL. Dynamic regulation of follicle-stimulating hormone-beta messinger ribonucleic acid levels by activin and gonadotropin-releasing hormone in perifused rat pituitary cells. Endocrinology. 1992;131:1403–1408. doi: 10.1210/endo.131.3.1505470. [DOI] [PubMed] [Google Scholar]
- Welt C, Sidis Y, Keutmann H, Schneyer A. Activins, inhibins, and follistatins: From endocrinology to signaling. A paradigm for the new millennium. Exp Biol Med. 2002;227:724–752. doi: 10.1177/153537020222700905. [DOI] [PubMed] [Google Scholar]
- Wise PM, Rance N, Selmanoff MK, Barraclough CA. Changes in radioimmunoassayable luteinizing hormone-releasing hormone in discrete brain areas of the rat at various times on proestrus, diestrus day 1, and after phenobarbital administration. Endocrinology. 1981;108:2179–2185. doi: 10.1210/endo-108-6-2179. [DOI] [PubMed] [Google Scholar]
- Woodruff TK, Besecke LM, Groome N, Draper LB, Schwartz NB, Weiss J. Inhibin A and inhibin B are inversely correlated to follicle-stimulating hormone, yet are discordant during the follicular phase of the rat estrous cycle, and inhibin A is expressed in a sexually dimorphic manner. Endocrinolgy. 1996;137:5463–5467. doi: 10.1210/endo.137.12.8940372. [DOI] [PubMed] [Google Scholar]
- Zeeman ML. Resonance in the menstrual cycle: a new model of the LH surge. Rep BioMed online. 2003;7:295–300. doi: 10.1016/s1472-6483(10)61867-6. [DOI] [PubMed] [Google Scholar]