A COMPUTATIONAL THEORY OF SELECTION BY CONSEQUENCES APPLIED TO CONCURRENT SCHEDULES

Abstract

Virtual organisms animated by a computational theory of selection by consequences responded on symmetrical and asymmetrical concurrent schedules of reinforcement. The theory instantiated Darwinian principles of selection, reproduction, and mutation such that a population of potential behaviors evolved under the selection pressure exerted by reinforcement from the environment. The virtual organisms' steady-state behavior was well described by the power function matching equation, and the parameters of the equation behaved in ways that were consistent with findings from experiments with live organisms. Together with previous research on single-alternative schedules (McDowell, 2004; McDowell & Caron, 2007) these results indicate that the equations of matching theory are emergent properties of the evolutionary dynamics of selection by consequences.

McDowell (2004) proposed a theory of behavior dynamics in the form of a computational model of selection by consequences. The theory uses Darwinian principles of selection, reproduction, and mutation to cause a population of potential behaviors to evolve under selection pressure exerted by reinforcement from the environment. A virtual organism animated by the theory emits a behavior from the population of potential behaviors every time tick, or generation, which creates a continuous stream of behavior that can be studied by standard behavior-analytic methods.

The computational theory operates in such a way that reinforcement tends to concentrate behavior in one or more target classes, which are analogous to key pecks or lever presses, while nonreinforcement and mutation tend to spread responding among all classes of behavior. At equilibrium these opposing tendencies cause a target response rate to vary around a steady-state value. McDowell (2004) and McDowell and Caron (2007) showed that when applied to single-alternative random interval (RI) schedules, the theory generated equilibrium response rates that were accurately described by forms of the Herrnstein (1970) hyperbola. In their experiments, repeated application of low-level rules of selection, reproduction, and mutation produced high-level quantitative order known to characterize the behavior of live organisms. In other words, the Herrnstein hyperbola was shown to be an emergent property of the dynamics of selection by consequences.

The computational theory can also be applied, without material modification, to responding on concurrent schedules. The behavior of live organisms on concurrent schedules has been studied extensively and is known to be governed by the power-function matching equation, which is

1

where the Bs refer to response rates, the Rs refer to reinforcement rates, and the numerical subscripts identify the two components of the concurrent schedule. The bias parameter, b, in this equation is known to vary from unity when there are asymmetries between the two alternatives of the concurrent schedule (Baum, 1974b, 1979; McDowell, 1989; Wearden & Burgess, 1982). The parameter, a, may also vary from unity in ways that are referred to as undermatching (a < 1) or overmatching (a > 1). Undermatching is the far more common outcome in experiments with live organisms, and a is usually found to vary around a value of about 0.8 (Baum, 1974b, 1979; McDowell, 1989; Myers & Myers, 1977; Wearden & Burgess, 1982).

The purpose of the present experiment was to study the responding of virtual organisms animated by the dynamic theory of selection by consequences on concurrent schedules of reinforcement. Before presenting details, the theory will be described in general terms.

The computational theory of selection by consequences consists of a genetic algorithm (Goldberg, 1989; Holland, 1992) that is used to cause a population of 100 potential behaviors to evolve under the selection pressure provided by reinforcement from the environment. Each behavior in the population is represented by a ten-character string of 0 s and 1 s that constitutes the behavior's genotype. The decimal integer represented by this binary string constitutes the behavior's phenotype. For example, a behavior might be represented by the string “0001101011”, which is the binary representation of the decimal integer, 107. Behaviors are sorted into classes based on their integer phenotypes. With ten-character binary strings, integer phenotypes can range from 0 (“0000000000”) through 1023 (“1111111111”). To arrange a concurrent schedule, one target class of behavior might be defined as the 41 integers from 471 through 511, and a second target class might be defined as the 41 integers from 512 through 552. The remaining 942 integers would then constitute a class of extraneous, or nontarget, behaviors. From every population of potential behaviors one behavior is emitted each generation or time tick. The class that is the source of the emitted behavior is determined by the relative frequencies of the behaviors in each class. For example, if 10 of the 100 potential behaviors are in the first target class, 25 of the potential behaviors are in the second target class, and the remaining 65 are in the extraneous class, then the probabilities of emission from the three classes are .10, .25, and .65.

Once a behavior is emitted, a new population of 100 potential behaviors is generated from 100 pairs of parent behaviors that are selected from the existing population. These parents are selected in one of two ways, depending on whether the emitted behavior was reinforced. If it was reinforced, then the behaviors in the population are assigned fitness values that indicate how similar they are to the reinforced behavior. A parental selection function is then used to choose parents such that fitter behaviors are more likely to be chosen as parents than less fit behaviors. As will be explained in detail later, the mean of the parental selection function determines the strength of the selection event. Stronger selection events result in fitter parents, which tend to produce fitter offspring, that is, behaviors more like the reinforced behavior. If, on the other hand, the emitted behavior did not produce reinforcement, then parents are selected at random from the existing population of potential behaviors.

Parent behaviors reproduce by contributing some of their bits to a child behavior. The 100 pairs of parent behaviors create 100 child behaviors, which constitute the new population of potential behaviors. A small amount of random mutation is then added to the population by, say, flipping a single, randomly selected bit in a percentage of behaviors selected at random from the population. The behaviors in the now-mutated population are then sorted into classes based on their phenotypes, and the next behavior to be emitted is determined as described earlier. This process of selection, reproduction, and mutation is then repeated, and the resulting continuous stream of behavior is recorded just as in an experiment with live organisms.

It is important to note that in this novel application to concurrent schedules, the genetic algorithm that implements the evolutionary theory is not materially different from the algorithm that was used in previous research with single schedules (Kulubekova & McDowell, 2008; McDowell, 2004; McDowell & Caron, 2007). The details of the algorithm are described in the Procedure section below.

The purpose of the first two phases of the present experiment was to compare behavior generated by the evolutionary dynamics of selection by consequences to the behavior of live organisms. In Phase 1, responding generated by the computational theory was studied on a series of symmetrical concurrent RI RI schedules. The schedules were symmetrical inasmuch as the forms and means of the parental selection functions were the same in both components of each schedule, as were the methods of implementing reproduction and mutation. This is the canonical concurrent schedule experiment. In Phase 2, responding was studied on a series of asymmetrical concurrent RI RI schedules. In these schedules, the forms of the parental selection functions were the same in both components, as were the methods of implementing reproduction and mutation, but the means of the parental selection functions differed in the two components. McDowell (2004) suggested that the mean of a parental selection function could be taken to represent the magnitude of a reinforcer ceteris paribus. Hence, these schedules can be seen as arranging different reinforcer magnitudes in the two components. The purpose of the third phase of the present series of experiments was to study quantitative properties of the computational theory. In this phase, the mutation rate and the mean of the parental selection function were varied over wide ranges in symmetrical concurrent RI RI schedules. The form of the parental selection function and the methods of implementing reproduction and mutation were the same for all components of all schedules in this phase of the project.

Method

Subjects

Virtual organisms having repertoires of 100 potential behaviors at each moment, or tick, of time served as subjects. Each behavior in a population of potential behaviors was represented by a 10-character string of 0 s and 1 s, which constituted the behavior's genotype. The decimal integer represented by the binary string constituted the behavior's phenotype. Ten-character binary strings decode into the 1024 possible integers from 0 through 1023. This range of integers was taken to be circular, which is to say that it wrapped back upon itself from 1023 to 0. For this circular segment of integers, the distance between two integer phenotypes, x and y, is |x − y| when going one way around the circle, and 1024 − |x − y| when going the other way. For example, the distance between 0 and 1023 is 1023 when going in the direction of increasing magnitude, and is 1 when going in the opposite direction. The difference between two integer phenotypes was defined as the smaller of these two distances. According to this definition, the difference between 0 and 1, to take an example, is the same as the difference between 0 and 1023.

The behaviors in a population were sorted into one of three classes based on their phenotypes. Two target classes were defined by the 41 integers from 471 through 511, and the 41 integers from 512 through 552. An extraneous class of behavior was defined by the remaining 942 integers. Each population of potential behaviors existed for one time tick, or generation, during which a behavior from one of the three classes was emitted. The probability of emission from each class was equal to the relative frequency of the behaviors in that class. For example, if a population consisted of 5 behaviors in the first target class, 10 in the second target class, and 85 in the extraneous class, then the probabilities of emission from the three classes were .05, .10, and .85. The fixed class structure of the population determined operant levels, or baseline probabilities of responding, for the three classes. These probabilities were .04 ( =  41/1024) for each of the target classes, and .92 ( =  942/1024) for the extraneous class.

Apparatus and Materials

Phases were conducted on computers with Intel Pentium III or better processors, running at 498-MHz or faster, with at least 184 MB of RAM installed. The genetic algorithm that created and animated the virtual organisms was a computer program written in VB .NET. The program implemented the algorithm described in the Procedure section below. The output of the organism program interacted with an environment program, also written in VB .NET, which ran on the same computer as the organism program and arranged the concurrent schedules. The resulting sequences of target and nontarget responses and their consequences were stored in standard databases and analyzed with standard software.

Procedure

All concurrent schedules arranged occasional reinforcement for behavior emitted from the two target classes according to independent RI schedules. Intervals for each RI schedule were drawn randomly with replacement from an exponential distribution of intervals with a specified mean value. Hence, the RI schedules were idealized Fleshler-Hoffman (Fleshler & Hoffman, 1962) variable-interval (VI) schedules. We have found that 20-interval Fleshler-Hoffman VI schedules produce nearly exponential distributions of intervals. The component RI schedules operated just as in an experiment with live organisms. Each generation the interval timers advanced one tick. If a behavior was emitted from a target class, then its associated RI schedule was queried; if a reinforcer was set up on that schedule, then it was delivered and a new interval was scheduled. Once a reinforcer was set up by a schedule it was held until obtained.

If a behavior was emitted from one of the target classes and it was reinforced, then a midpoint fitness method (McDowell, 2004) was used to assign fitness values to each behavior in the population of potential behaviors. According to the midpoint fitness method, the fitness of a behavior is the difference, as defined earlier, between the behavior's phenotype and the phenotype at the midpoint of the class from which the just-reinforced behavior was emitted. For example, if the just-reinforced behavior was emitted from the first target class (with phenotypes 471 through 511), then the midpoint used to assign fitness values was 491. A behavior in the population with a phenotype of 400 would therefore have a fitness value of |400–491|  =  91, and a behavior with a phenotype of 512 would have a fitness value of |512 − 491|  =  21. Because the latter behavior is less different than the criterion midpoint, it is the fitter behavior. It is helpful to keep in mind that this method assigns smaller fitness values to fitter behaviors.

Once fitness values were assigned to the behaviors in the population, a linear parental selection function was used to select parents for mating on the basis of their fitness. This function expresses the probability density, p(x), associated with a behavior of fitness, x, of becoming a parent as

2

for 0 ≤ x ≤ 3μ, where μ is the mean of the density function. Notice that probability density decreases as fitness decreases (i.e., as the fitness value, x, increases) until it reaches a value of 3μ. Behaviors with fitness values of 3μ and greater have no chance of becoming parents. This same parental selection function was used in previous research with single schedules (Kulubekova & McDowell, 2008; McDowell, 2004; McDowell & Caron, 2007; McDowell, Soto, Dallery & Kulubekova, 2006) and is the simplest linear density function that depends only on its mean. A father behavior was chosen from the population by drawing a fitness value at random from the distribution specified by Equation 2, and then searching the population for a behavior with that fitness. If none was found, then another fitness value was drawn from the distribution, and so on, until a father behavior was obtained. A mother behavior was chosen in the same way, but with the requirement that it be distinct from the father behavior. One hundred pairs of parents were obtained in this way. All parents were selected with replacement, which means that a behavior could be a parent more than once, and could have multiple partners. A detailed discussion of parental selection functions, including methods of drawing random values from them, can be found in McDowell (2004).

The process of assigning fitness values and selecting parents using Equation 2 occurred only if the emitted behavior was reinforced. If the emitted behavior came from one of the target classes but was not reinforced, or if it came from the extraneous class, then 100 pairs of parents were randomly selected with replacement from the population, with the requirement that the father and mother behaviors in a pair be distinct. Again, a given behavior could be a parent more than once and could have multiple partners.

A child behavior was created from each pair of parents by building a new 10-character bit string based on the parents' genotypes. Each bit in the child's string had a .5 probability of being identical to the bit in the same location of the father's bit string, and a .5 probability of being identical to the bit in the same location of the mother's bit string. This method of reproduction was used in previous research with single schedules (Kulubekova & McDowell, 2008; McDowell, 2004; McDowell & Caron, 2007), where it was referred to as bitwise reproduction. It generates children that resemble their parents to varying degrees, where resemblance refers to the difference, as defined earlier, between the phenotypes of parents and offspring. The 100 child behaviors created in this way constituted the new population of potential behaviors.

A small amount of mutation was added to the new population by flipping one randomly selected bit in a percentage of behaviors chosen at random from the population. This method of mutation was referred to as bitflip mutation in previous research with single schedules (Kulubekova & McDowell, 2008; McDowell, 2004; McDowell & Caron, 2007). The mutation rate specifies the probability that a behavior will mutate. For example, if the mutation rate is 1%, then each behavior in a population has a .01 probability of mutating. If a behavior does mutate, a location in the 10-character bit string is chosen at random and the bit at that location is changed from 0 to 1 or from 1 to 0. Using this method, a population of potential behaviors may have any number of mutants from 0 to 100, but across generations the mutation rate converges on the specified percentage.

Following mutation, the behaviors were sorted into classes and a behavior from one of the classes was emitted based on the relative frequencies of the behaviors in each class, as described earlier, and then the process of selection, reproduction and mutation was repeated for the duration of the experiment. Each population constituted a generation, and lasted one time tick.

The target classes of behavior were defined so as to have maximum Hamming distances (Russell & Norvig, 2003) at their boundaries. This introduced an effect similar to that introduced by a changeover delay (COD). The Hamming distance between two bit strings of equal length is the number of bits that must be changed to convert one string into the other. The Hamming distance between the upper boundary of the first target class (511  =  “0111111111”) and the lower boundary of the second target class (512  =  “1000000000”) was ten, which is the maximum Hamming distance for a 10-character string. The Hamming distance between the upper boundary of the second target class (552  =  “1000101000”) and the lower boundary of the first target class (471  =  “0111010111”) was also ten. This means that it was relatively difficult for recombination or mutation to cause a potential behavior to switch from one target class to the other. The result was responding that tended to be concentrated in bouts in a target class. Target classes with small Hamming distances at their boundaries tend to produce frequent switching between classes, just as often occurs in the absence of a COD in experiments with live organisms.

At the start of each concurrent schedule, artificial forced-choice shaping was implemented by preloading the population of potential behaviors with roughly equal numbers of behaviors in the two target classes. This ensured that at the start of exposure to each schedule, the probabilities of emitting behaviors from the target classes were roughly equal, and an order of magnitude larger than their baseline probabilities. This shaping was not necessary; it simply decreased the number of generations required to reach equilibrium.

Phase 1

Virtual organisms animated by the computational theory responded on 11 independent concurrent RI RI schedules of reinforcement. The RI values in one component of the schedule were 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, and 120 time ticks. These were paired with the same RI schedules in the second component, but in reverse order. Hence, the first schedule was a concurrent RI 20 RI 120, the second was a concurrent RI 30 RI 110, and so on. The mean of the linear parental selection function was 40 in both components of all schedules, and the mutation rate was 10% in all schedules. Sessions on each concurrent schedule continued for 20,500 generations, or time ticks. The series of 11 concurrent schedules was repeated 10 times, yielding about 2 × 10⁶ generations of responding.

Phase 2

Virtual organisms animated by the computational theory responded on 4 sets of 11 independent concurrent RI RI schedules of reinforcement. The mean of the linear parental selection function was 10, 25, 55, or 70 in one component of each set of schedules, and was 40 in the other component. The component RI schedules were the same as those used in Phase 1. The mutation rate was 10% in all schedules, and sessions on each schedule continued for 20,500 generations. Each of the four sets of 11 concurrent schedules was repeated four times, yielding about 4 × 10⁶ generations of responding.

Phase 3

Virtual organisms animated by the computational theory responded on sets of 11 independent concurrent RI RI schedules of reinforcement at all possible combinations of four parental selection function means and 10 mutation rates. The parental selection function means were the same in both components of each concurrent schedule and were 20, 40, 60 or 80. The mutation rates were 0.5, 1, 2, 3, 5, 7.5, 10, 12, 20, and 50%. The component RI schedules were the same as those used in Phase 1. Sessions on each schedule continued for 20,500 generations. Each set of 11 concurrent schedules was repeated 5 to 20 times, yielding a total of about 7 × 10⁷ generations of responding.

Results

Reinforcements and responses were accumulated in 500-generation blocks. The first 500-generation block on each schedule was discarded, and average reinforcement and response frequencies were calculated over the remaining forty 500-generation blocks. All analyses were conducted on these average frequencies. In what follows, the first alternative or component refers to the target class defined by the integers from 471 through 511; the second alternative or component refers to the other target class.

Phase 1

The logarithmic transformation of Equation 1,

3

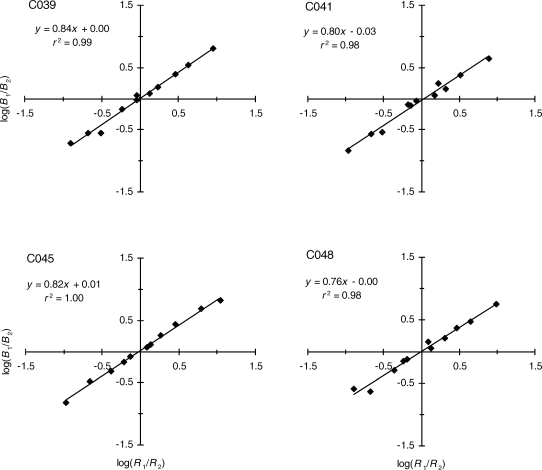
was fitted to the response ratios and reinforcement ratios from each of the 10 repetitions of the concurrent schedule experiment. Plots of the data and the least-squares fits for 4 of the repetitions are shown in Figure 1. Values of the exponents, a, and the bias parameters, b, for each fit, and the proportions of variance accounted for by the fit are listed in Table 1 for all repetitions of the experiment. The results shown in Figure 1 and Table 1 indicate that the power-function matching equation provided an excellent description of the steady-state behavior generated by the theory, accounting for between 97% and 100% of the variance, with a mean of 98% of the variance accounted for. The residuals for each fit were examined by plotting the standardized residuals against the log response ratios predicted by the best-fitting Equation 3. No consistent polynomial trends were evident across fits. When the residuals from all 10 fits were pooled, the same absence of polynomial trends was observed.

Fig 1.

Log response ratios plotted against log reinforcement ratios for four repetitions of the canonical concurrent schedule experiment. Straight lines are least-squares fits of Equation 3. The codes in the upper left of each panel identify the repetition. Equations of the best-fitting lines and the proportions of variance they account for (r²) are given in each panel.

Table 1.

Exponents, a, and bias parameters, b, from least-squares fits of Equation 3 to Phase 1 data, and the proportion of variance accounted for (pVAF) by the fits.

Rep. ID	a	b	pVAF
C039	0.84	1.01	0.99
C040	0.85	1.03	0.99
C041	0.80	0.92	0.98
C042	0.80	0.98	0.98
C043	0.87	1.03	0.98
C044	0.77	0.90	0.97
C045	0.82	1.03	1.00
C046	0.83	0.95	0.99
C048	0.76	0.99	0.98
C049	0.89	1.01	0.98
Mean	0.82	0.99	0.98

As shown in Table 1, the exponent, a, varied from 0.76 to 0.89 over the 10 fits, with an average of 0.82, which indicates a moderate degree of undermatching. The bias parameter, b, varied from 0.92 to 1.03, with a mean of 0.99, indicating the absence of bias in responding on these symmetrical concurrent schedules.

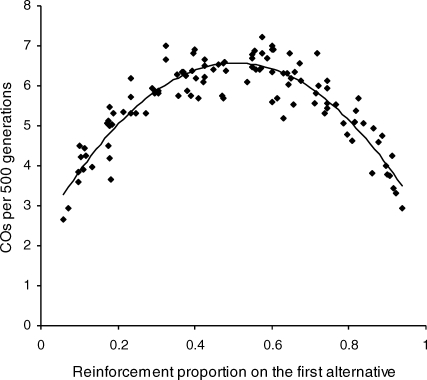
The average number of changeovers (COs) per 500 generations is plotted in Figure 2 as a function of the average reinforcement proportion obtained from the first alternative of the concurrent schedule. COs from all repetitions are pooled in the figure. Hence there is one data point for each of the 11 concurrent schedules in the canonical experiment, times 10 repetitions of the experiment. The smooth curve is the best-fitting quadratic polynomial, which simply illustrates the trend. As is clear from the figure, the CO rate was greatest when the two alternatives delivered similar proportions of reinforcement (around .5) and was least when they delivered very discrepant proportions of reinforcement (around .1 and .9). In general, the more discrepant the reinforcement rates in the two alternatives, the less frequent were the COs. Although the quadratic polynomial in Figure 2 is an arbitrary form, it in fact provided a good description of the CO data inasmuch as the standardized residuals plotted against the CO rates predicted by the fitted quadratic showed no polynomial trends.

Fig 2.

Average number of changeovers (COs) per 500 generations plotted against the average reinforcement proportion obtained from the first alternative. Data from all repetitions of the canonical experiment are plotted. The smooth curve is the best-fitting quadratic polynomial, which simply illustrates the trend.

Phase 2

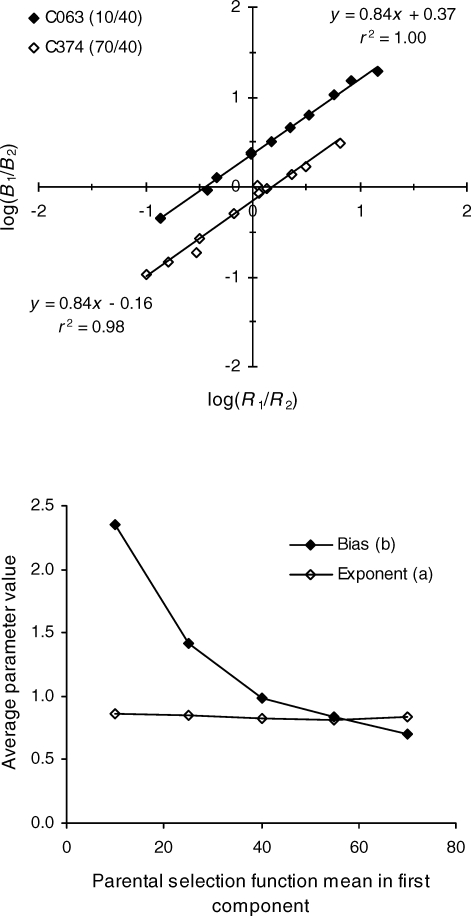
Equation 3 was fitted by the method of least squares to the 16 sets of concurrent schedule data, 4 each having parental selection function means of 10, 25, 55, and 70 in the first component, and all having parental selection function means of 40 in the second component. Recall that smaller means correspond to stronger selection events and consequently may be taken to represent larger reinforcer magnitudes ceteris paribus. Plots of 2 of the 16 sets of data, one with a parental selection function mean of 10 in the first component (C063) and one with a parental selection function mean of 70 in the first component (C374), are shown in the top panel of Figure 3, along with the best fitting straight lines, their equations, and the proportions of variance they account for. Evidently, Equation 3 described these data well. For C063 the stronger selection events arranged in the first alternative of the schedule produced biased responding in favor of that alternative, as indicated by the positive intercept of the best-fitting line. For C374 the stronger selection events arranged in the second alternative of the schedule produced responding biased in favor of that alternative, as indicated by the negative intercept of the best-fitting line.

Fig 3.

Top panel: Filled diamonds represent data from repetition C063, in which parental selection function means of 10 and 40 were arranged in the two components of the concurrent schedule. The best-fitting line is plotted through the points, and its equation and the proportion of variance it accounts for are given in the upper right of the panel. Unfilled diamonds represent data from repetition C374, in which parental selection function means of 70 and 40 were arranged in the two components of the concurrent schedule. The best fitting line is plotted through the points and its equation and the proportion of variance it accounts for are given in the lower left of the panel. Bottom panel: Average bias parameters (filled diamonds) and exponents (open diamonds) plotted against the mean of the parental selection function arranged in the first component of the schedule. Averages are across the individual parameter values listed in Tables 1 and 2.

The parameter values and proportions of variance accounted for are listed in Table 2 for all 16 data sets. The proportions of variance accounted for (pVAFs) in the table indicate that Equation 3 described the data well. In addition, residuals plotted as in Phase 1 showed no consistent polynomial trends for any fit, or when pooled across fits. The average bias parameters and exponents calculated from the individual values in Table 2 are plotted in the bottom panel of Figure 3 as a function of the parental selection function mean in the first component of the concurrent schedule. The averages for the parental selection function mean of 40 were taken from Table 1. As the plot shows, bias consistently favored the stronger selection event. The average bias declined from a high of 2.4 when the parental selection function means were 10 and 40, passed through 1.0 when the means were 40 and 40, and fell to 0.7 when the means were 70 and 40. Across this range, the average exponent of the best fitting lines remained constant at a value of about 0.83, as indicated by the unfilled diamonds in the bottom panel of Figure 3. Hence, the exponent remained constant even as the bias parameter changed by an order of magnitude.

Table 2.

Exponents, a, and bias parameters, b, from least-squares fits of Equation 3 to Phase 2 data, and the proportion of variance accounted for (pVAF) by the fits.

Rep. ID	a	b	pVAF
Linear 10/40
C063	0.84	2.35	1.00
C363	0.86	2.36	0.99
C364	0.83	2.29	0.98
C365	0.90	2.40	0.99
Linear 25/40
C064	0.75	1.41	0.99
C366	0.88	1.42	0.99
C367	0.88	1.41	1.00
C368	0.89	1.42	0.99
Linear 55/40
C065	0.81	0.84	0.99
C369	0.79	0.83	1.00
C370	0.81	0.85	0.99
C371	0.84	0.84	0.98
Linear 70/40
C066	0.86	0.66	0.98
C372	0.84	0.71	0.98
C373	0.80	0.75	0.98
C374	0.84	0.70	0.98

Phase 3

Equation 3 was fitted to each repetition of 11 concurrent schedules at all combinations of 10 mutation rates and four parental selection function means. The exponents, a, and bias parameters, b, averaged over repetitions at each combination of mutation rate and parental selection function mean are listed in Table 3, along with their standard errors. The numbers of repetitions, and the proportions of variance accounted for (pVAF) averaged over repetitions, are listed in the second and seventh columns of the table.

Table 3.

Mutation rate, number of repetitions, means and standard errors of exponents, a, and bias parameters, b, from least-squares fits of Equation 3, proportions of variance accounted for by the fits (pVAF), maximum changeover rate (CO_max), and the increase in changeover rate from the rate at a reinforcement proportion of zero to CO_max (ΔCO).

Mutation rate (%)	No. of repetitions	a		b		pVAF	COmax	ΔCO
		Mean	S.E.	Mean	S.E.	Mean
Linear 20/20
0.5	10	0.75	0.08	1.12	0.10	0.82	0.04	0.00
1	20	0.80	0.04	1.06	0.17	0.94	0.14	0.05
2	15	0.86	0.04	1.03	0.19	0.96	0.36	0.24
3	5	0.85	0.05	1.09	0.22	0.97	0.75	0.50
5	10	0.83	0.01	1.00	0.13	0.99	2.00	1.42
7.5	10	0.82	0.02	0.98	0.13	0.99	3.59	2.25
10	5	0.86	0.01	1.03	0.10	0.99	5.23	3.64
12	5	0.86	0.02	1.00	0.09	1.00	6.31	4.05
20	5	0.81	0.01	1.00	0.08	0.99	9.69	5.33
50	5	0.52	0.01	1.00	0.07	0.99	15.44	4.85
Linear 40/40
0.5	5	0.68	0.04	1.08	0.07	0.76	0.08	0.03
1	5	0.72	0.05	0.93	0.07	0.90	0.13	0.04
2	10	0.80	0.03	0.99	0.05	0.96	0.61	0.43
3	5	0.83	0.06	1.06	0.08	0.97	1.26	0.80
5	10	0.79	0.01	1.02	0.02	0.99	2.76	1.79
7.5	5	0.82	0.03	1.01	0.03	0.99	4.72	3.00
10	10	0.82	0.01	0.99	0.01	0.98	6.57	4.21
12	5	0.82	0.01	0.99	0.02	0.99	8.03	4.51
20	5	0.70	0.02	1.00	0.01	0.98	11.48	4.91
50	5	0.33	0.01	1.00	0.01	0.95	17.00	2.91
Linear 60/60
0.5	10	0.62	0.04	1.11	0.05	0.73	0.09	0.05
1	10	0.66	0.03	1.06	0.07	0.83	0.24	0.10
2	5	0.68	0.03	1.01	0.03	0.95	0.73	0.35
3	5	0.71	0.02	1.07	0.04	0.96	1.49	0.81
5	10	0.79	0.02	1.00	0.02	0.98	3.24	1.97
7.5	15	0.81	0.01	1.01	0.01	0.98	5.49	3.34
10	5	0.78	0.03	0.98	0.02	0.98	7.54	3.95
12	5	0.77	0.02	0.97	0.02	0.98	8.90	4.60
20	5	0.56	0.02	1.01	0.02	0.96	12.41	4.45
50	5	0.21	0.01	1.00	0.01	0.88	17.68	1.44
Linear 80/80
0.5	20	0.67	0.04	1.02	0.04	0.64	0.12	0.04
1	15	0.66	0.03	1.04	0.06	0.86	0.33	0.16
2	5	0.64	0.02	0.99	0.02	0.93	1.10	0.54
3	5	0.68	0.03	0.98	0.03	0.95	1.87	0.99
5	20	0.78	0.01	0.96	0.01	0.97	3.97	2.38
7.5	15	0.75	0.01	1.00	0.01	0.97	6.28	3.25
10	5	0.74	0.03	0.98	0.01	0.96	8.28	3.87
12	5	0.66	0.02	1.01	0.01	0.96	9.42	3.43
20	5	0.45	0.01	0.99	0.01	0.93	13.22	3.58
50	5	0.16	0.02	1.00	0.01	0.83	17.86	0.43

The pVAFs in Table 3 show that in most cases Equation 3 provided a good description of the data, accounting for between 65% and 100% of the variance in the log response ratios, with an average of 93% (median  =  96%) of the variance accounted for. The pVAFs tended to be slightly higher for stronger selection events (lower parental selection function means) across all mutation rates. In addition, the pVAFs were highest at mutation rates from about 5% to about 10%, regardless of parental selection function mean. At mutation rates below this range, the pVAFs fell, sometimes markedly, to a low of .65 when the parental selection function mean was 80. At mutation rates above this range, pVAFs fell more modestly, to a low of .83, again when the parental selection function mean was 80. Studies of the residuals indicated that the lower pVAFs were due to random variability around the least-squares fit of Equation 3 rather than to systematic deviations from the equation.

Across the 330 fits summarized in Table 3, plots of the standardized residuals against the log response ratios predicted by Equation 3 showed no consistent polynomial trends. In addition, when the standardized residuals were pooled across repetitions at each combination of mutation rate and parental selection function mean, no polynomial trends were evident. To test further the residuals for randomness the three statistical tests recommended by Reich (1992), and used in previous research (McDowell, 2004), were applied to each of the 330 sets of residuals. These include a test for the expected number of residuals of one sign, the expected number of runs of residuals of the same sign, and the expected lag-1 autocorrelation of the residuals, all given the null hypothesis of randomness. If a set of residuals failed one or more of these tests, that is, if for at least one test the null hypothesis of randomness was rejected at an α-level of .05, then that set of residuals was identified as nonrandom. Of the 330 sets of residuals, 39 were identified as nonrandom using this method. Applying the binomial test recommended by McDowell (2004), which takes into account the cumulative Type I error rate of the three Reich tests (cumulative α  =  .1426), the binomial probability of identifying 39 of 330 sets of residuals as nonrandom under the null hypothesis of randomness was .91. This indicates that the collection of 330 sets of residuals can be considered random.

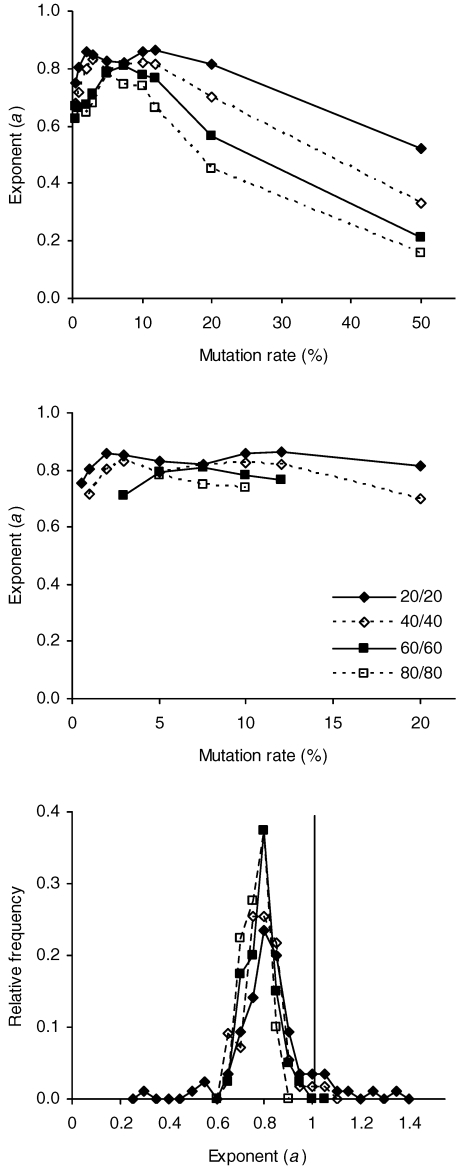
The average exponents listed in Table 3 are plotted in the top panel of Figure 4. Lower parental selection function means, which correspond to stronger selection events, tended to produce higher exponents across all mutation rates, with an upper boundary of about 0.85. In addition, exponents tended to cluster around 0.8 at mutation rates from about 5% to about 10%, regardless of parental selection function mean. At mutation rates below the 5–10% range, exponents tended to decline modestly; at mutation rates above this range, exponents declined markedly. In contrast to changes in the exponents, the average bias parameters remained roughly constant across mutation rates and parental selection function means, varying from 0.93–1.12 over the 40 combinations of mutation rate and parental selection function mean, with an overall mean of 1.01 (median  =  1.00). Although the bias parameters remained roughly constant, they tended to be more variable at lower mutation rates.

Fig 4.

Top panel: Average exponents, a, from Table 3 plotted against mutation rate. The legend in the middle panel, which applies to all panels, identifies the parental selection function means used in the components of the schedules. Middle panel: Average exponents from Table 3 having values from 0.7 through 0.9 plotted against mutation rate. Bottom panel: Relative frequency distributions of individual exponents, the means of which are plotted in the middle panel. The downrule marks an exponent of 1.

To obtain a better understanding of the joint effect of parental selection function mean and mutation rate on the exponents it is helpful to examine only those exponents with values from 0.7 through 0.9, which could be considered a range of more or less typical average exponents for live organisms. Exponents with values in this range are plotted in the middle panel of Figure 4. Higher exponents were still associated with stronger selection events in this subset of 25 exponents, although the effect was more muted than for the entire set of 40 exponents. Parental selection function means of 20, 40, 60, and 80 produced overall average exponents of 0.83, 0.79, 0.77, and 0.76 in this subset of the data. Notice also that the range of mutation rates yielding average exponents from 0.7 through 0.9 increased with the strength of the selection events. The ranges were 5–10%, 3–12%, 1–20%, and 0.5–20% for parental selection function means of 80, 60, 40, and 20. In other words, the stronger the selection event, the greater the range of mutation rates that produced average exponents roughly consistent with those from live organisms. The subset of fits represented in the middle panel of Figure 4 also tended to have the largest pVAFs, which varied from .82 to 1.00, with means of .96, .97, .98, and .97 for the four parental selection function means in increasing order. Similarly, the bias parameters for this subset of fits were well behaved, with averages of 1.04, 1.00, 1.01 and 0.98 for the four parental selection function means in increasing order.

It is also worthwhile to examine the individual exponents for the subset of average exponents shown in the middle panel of Figure 4. Relative frequency distributions of these exponents for each parental selection function mean are plotted in the bottom panel of the figure. All distributions had strong modes at or near 0.8. The distribution for the parental selection function mean of 20 (N  =  85) had the largest standard deviation (0.15). Exponents in this distribution varied from 0.31 to 1.37, the former value indicating severe undermatching, the latter indicating moderate overmatching. The distributions for the other parental selection function means had smaller Ns (from 40–55) and were less variable (standard deviations from 0.05–0.08), although the distribution for the parental selection function mean of 40 also included instances of overmatching.

The CO profiles for these concurrent schedules were studied by fitting a quadratic polynomial,

4

to the average COs per 500 generations for each combination of mutation rate and parental selection function mean, pooled across all repetitions of the set of 11 concurrent schedules. To obtain the fits, average COs (represented by y in Equation 4) were plotted against the proportion of reinforcement obtained from the first alternative of the schedule (represented by x in Equation 4), as was done in Figure 2. The vertex of the fitted parabola is an estimate of the maximum CO rate for a set of concurrent schedules and is given by

Values of CO_max for sets of concurrent schedules pooled across repetitions are listed in the penultimate column of Table 3. The increase in CO from its value at a reinforcement proportion of 0 to its maximum at CO_max is a measure of the parabola's curvature in the restricted domain of 0 to 1, and is given by

Small values of ΔCO indicate relatively flat parabolas whereas large values indicate relatively curved ones in the restricted domain. Values of ΔCO for sets of concurrent schedules pooled across repetitions are listed in the final column of Table 3.

The values of CO_max and ΔCO listed in the table indicate that these quantities were strongly affected by mutation rate. The former increased with mutation rate, while the latter increased and then decreased with mutation rate. Thus, COs were few and the CO profile was relatively flat at low mutation rates; COs increased and the CO profile became more curved at intermediate mutation rates; and COs increased further but the CO profile tended to flatten again at the highest mutation rates. Flattening at the highest mutation rates was more pronounced for the weaker than for the stronger selection events.

Discussion

The steady-state behavior of virtual organisms animated by the evolutionary dynamics of selection by consequences conformed to the power-function matching equation (Equation 1) in all of the present experiments. In addition, the parameters of the equation behaved in ways that were consistent with parameters obtained from experiments with live organisms. In symmetrical concurrent schedules (Phases 1 and 3), the bias parameter varied around a value of approximately 1, and in asymmetrical concurrent schedules (Phase 2) it tracked the magnitude of the asymmetry. The average exponent for the Phase 1 data was 0.82, which indicates a degree of undermatching that is typically found in experiments with live organisms (Baum, 1974a, 1979; McDowell, 1989; Myers & Myers, 1977; Wearden & Burgess, 1982). In Phase 2, the average exponents assumed similar values, varying between 0.81 and 0.86, and they remained roughly constant as the bias parameter changed by an order of magnitude. The independence of exponent and bias parameter has been observed in experiments with live organisms (e.g., Dallery, Soto & McDowell, 2005). In Phase 3, the average exponents again were similar in value, around 0.8, for all parental selection function means across a middle range of mutation rates, and for low parental selection function means (strong selection events) across a wider range of mutation rates. Conditions with low parental selection function means are probably most analogous to laboratory experiments with live organisms, which ensure strong reinforcer values by depriving animals of food or water. In these conditions, individual exponents in Phase 3 varied over a wide range, and included instances of severe undermatching and instances of overmatching, a result that is consistent with findings from live organisms (Baum, 1979; Wearden & Burgess, 1982).

The switching behavior observed in Phase 1 was also consistent with data from live organisms (Alsop & Elliffe, 1988; Baum, 1974a; Brownstein & Pliskoff, 1968; Herrnstein, 1961). Switching was greatest when the components of the schedule delivered roughly equal frequencies of reinforcement and was least when the components delivered the most discrepant frequencies of reinforcement. The same pattern of switching was observed in Phase 3 for most conditions that arranged low parental selection function means (strong selection events) and for all conditions over a middle range of mutation rates, from about 5% to about 10%. The CO profiles tended to flatten at the lowest and highest mutation rates.

To summarize, for conditions that arranged relatively low parental selection function means over a relatively wide range of mutation rates, and for all conditions over a middle range of mutation rates, in both symmetrical and asymmetrical concurrent schedules, the behavior generated by the computational theory was qualitatively and quantitatively indistinguishable from the behavior of live organisms.

An especially interesting agreement between theory and data in these experiments was the value of the exponent of Equation 1. A value of about 0.8 was found consistently over a middle range of mutation rates. At mutation rates below this range, behavior became perseverative, that is, it tended to get stuck in a particular class regardless of reinforcement. Evidently, genotype recombination during reproduction was not sufficient to counteract this effect of a low mutation rate; the consequence was behavior that was less sensitive to the reinforcement rate ratio. The opposite effect occurred at high mutation rates, where behavior became impulsive, that is, it tended to leave its current class regardless of reinforcement. This resulted in too much behavioral variability and, consequently, less sensitivity to the reinforcement rate ratio. That the limiting value of the exponent was in the neighborhood of 0.8 is noteworthy. McDowell and Caron (2007) found a similar limiting value for the exponent entailed by a form of Herrnstein's hyperbola derived from Equation 1 (McDowell, 2005), when it was fitted to data generated by virtual organisms responding on single-alternative RI schedules. This specific value itself must be an emergent property of the evolutionary dynamics of selection by consequences. The emergence of this specific value, together with the well known difficulty of identifying independent variables that affect it (e.g., Wearden & Burgess, 1982), suggest that it may be a biological constant, akin to physical constants like the constant of universal gravitation or Planck's constant, albeit with stochastic properties appropriate to a biological system.

Previous research showed that the computational dynamics of selection by consequences yielded behavior on single-alternative RI schedules that was accurately described by forms of the Herrnstein hyperbola (McDowell, 2004; McDowell & Caron, 2007). The present experiment shows that the theory, without material modification, produces behavior on concurrent RI RI schedules that is accurately described by the power-function matching equation (Equation 1). Evidently, the equations of matching theory are emergent properties of the evolutionary dynamics of selection by consequences. The quantitative accuracy of this result is noteworthy inasmuch as the computational theory consists entirely of low-level rules of selection, reproduction, and mutation. These rules govern the emission of behavior from moment to moment, but they in no way require the high-level properties of behavior to be quantitatively consistent with matching theory. That the outcome produced by the theory is quantitatively indistinguishable from outcomes produced by live organisms, lends support to the idea (McDowell, 2004; McDowell & Caron, 2007) that the material events responsible for instrumental behavior are computationally equivalent to selection by consequences (Wolfram, 2002; see also Staddon & Bueno, 1991). As noted by McDowell and Caron, this idea, when taken to its logical conclusion, suggests that evolution engineered a copy of itself in the nervous systems of biological organisms to regulate their behavior with respect to local environments during their individual lifetimes.

As was discussed earlier, and elsewhere (McDowell, 2004), it seems reasonable to consider the mean of the parental selection function to be related to reinforcer magnitude. The physical referent of mutation rate is less clear. It may be that this source of behavioral variability is a more or less fixed property of an evolved nervous system. An ideal mutation rate or range of mutation rates may produce enough variability in behavior to render it sensitive to a changing environment, while avoiding degrees of perseveration and impulsiveness that degrade this sensitivity. It seems likely that a more or less fixed mutation rate nevertheless could be affected by physiological abnormalities, and could be modified by neurosurgical or pharmacological insult. The possibility of modeling maladaptive perseverative or impulsive behavior by changing the mutation rate in the computational model is an interesting prospect.

The results of this experiment were reported in terms of response allocation, but they could just as well have been reported in terms of time allocation. The computational model does not distinguish between the two. Because the model allocates each time tick to a class of behavior, the more fundamental representation may be time allocation. This also makes sense for general theoretical reasons. Not all behaviors occur in brief discrete bouts that can be counted in a meaningful way, yet all behaviors can be timed (Baum & Rachlin, 1969). In the present analyses each time tick was assumed to contain a response, but it would be possible to permit dead time on an alternative during which no responding occurred, which would allow the separation of response and time allocation. An additional algorithm for determining responding while on an alternative would be required, which is a complication that may not be worth the extra degrees of freedom it would introduce. Because recent reviews indicate that the results of response- and time-allocation matching are the same (Wearden & Burgess, 1982), it may be prudent to take as fundamental the more general time-allocation representation. If it were deemed essential to have a response-allocation representation for discrete responses, then one could simply assert as an empirical fact that the probability of responding is constant while on an alternative, a fact established by the comparability of response- and time-allocation results.

Several features of the computational theory merit further investigation, such as the significance of the Hamming cliff that separates the target responses. There are smaller cliffs elsewhere among the integer phenotypes. For example, the Hamming distance between 127 (“0001111111”) and 128 (“0010000000”) is 8. Hamming distance may be analogous to the COD in experiments with live organisms; if so, then a minimal Hamming distance would be required to obtain matching with a reasonable exponent, and larger Hamming distances would have no further effect. An alternative would be to remove all Hamming cliffs and arrange a true COD. This could be accomplished by using binary-reflected Gray codes (Goldberg, 1989) to represent the integer phenotypes. Like binary codes, Gray codes represent integers using bit strings, but the Hamming distance between Gray-code representations of successive integers is always 1.

The evolutionary dynamics tested in this experiment, together with the descriptive statics of matching theory, constitute a mathematical mechanics of instrumental behavior. Although the descriptive account provided by matching theory is widely accepted (but cf. McDowell, 2005), there has been much disagreement about the correct approach to behavior dynamics. In 1992 an entire issue of the Journal of the Experimental Analysis of Behavior (volume 57, number 3) was devoted to various aspects of this problem. Proposed dynamic accounts have been based on a variety of principles and theories including molar optimality or maximization principles (e.g., Baum, 1981; Rachlin, Battalio, Kagel & Green, 1981), molecular maximization (Shimp, 1966), melioration (Herrnstein, 1982; Vaughan, 1981), regulatory principles (e.g., Hanson & Timberlake, 1983; Staddon, 1979), switching principles (Myerson & Hale, 1988), linear system theory (McDowell, Bass & Kessel, 1993), incentive theory (e.g., Killeen, 1982), and scalar expectancy theory (Gibbon, 1995). None of these accounts has been widely accepted. Many of them were developed using differential equations, which is a traditional continuous mathematical approach to dynamics that has worked well in science for several centuries. The differential equation approach usually entails stating a differential equation, which constitutes the dynamic theory, and then integrating it to obtain the equilibrium result. The computational theory of selection by consequences takes a different approach by specifying low-level rules, constituting the dynamic theory, that must be applied repeatedly to reveal the higher-level equilibrium outcome, if one exists. Just as the calculus was invented because existing algebraic methods were inadequate to the problems that interested natural philosophers of the time (e.g., Newton), so too some contemporary scientists have argued that computational approaches represent an advance of sorts over the calculus in that they may be able to solve problems, such as the description of turbulence in fluid flow, that have proved refractory to more traditional methods (Bentley, 2002; Wolfram, 2002). Computational approaches have been used to good effect in a variety of disciplines (see NOVA, July 2007, for a brief but broad popular survey), and they are not missing from the literature of behavior analysis (e.g., Donahoe, Burgos, & Palmer, 1993; Shimp, 1966, 1992; Staddon & Zhang, 1991). Staddon and Bueno (1991) have gone so far as to argue that some sort of computational theory is likely to be essential for a satisfactory account of behavior dynamics.

The computational theory of selection by consequences can be developed further. For example, McDowell, Soto, Dallery and Kulubekova (2006) proposed an extension of the theory that includes stimulus control and incorporates a mechanics of conditioned reinforcement. The latter consists of a statics based on Mazur's (1997) hyperbolic delay theory of conditioned reinforcement, and a dynamics based on the Rescorla-Wagner rule (Danks, 2003). Interestingly, the objective of these researchers was to propose an alternative solution to a canonical problem in artificial intelligence, namely, the problem of generating adaptive state–action sequences, or policies, for a virtual or mechanical agent. States in artificial intelligence are equivalent to discriminative stimuli in behavior analysis. Actions that may be taken in those states are equivalent to behaviors under the control of those discriminative stimuli. McDowell et al.'s work lies at the interface of behavior analysis and specialties in artificial intelligence, such as artificial life, machine learning, and robotics. Interestingly, a number of other researchers working in these areas, usually computer scientists, have turned to behavior analysis to inform their research (Daw & Touretzky, 2001; Delepoulle, Preux, & Darcheville, 1999; McDowell & Ansari, 2005; Seth, 1999, 2002; Touretzky & Saksida, 1997). Obviously, the development and verification of a reasonably comprehensive theory of behavior dynamics would be a boon to both behavior analysis and artificial intelligence, and is certainly worthy of focused research effort. But there are many hurdles to overcome. For example, on what data should a dynamic theory be tested? How do the many existing theories of behavior dynamics compare? How do their domains differ? Can they or parts of them be translated into any of the other theories or their parts? These are some of the difficult questions that will require careful study and debate. Indeed, the mere task of fully comprehending the various, sometimes quite complicated, theories (e.g., Gallistel et al., 2007) is daunting. Accordingly, it may be time in our discipline to welcome specialists in theoretical behavior analysis, just as there are specialists in theory in other fields, such as physics. This may seem a strange idea for a discipline founded on inductive experimentation. It goes without saying that this foundation has served our discipline well; the experimental analysis of behavior has generated a large body of data that establishes many important facts about behavior and the environmental variables that regulate it. But it may now be time to make a concerted effort to weave those facts into a coherent and reasonably comprehensive mathematical mechanics of adaptive behavior that can be widely accepted, and hence can take its place among the established theories of science. As this work progresses, and as our discipline matures, deductive experimentation, that is, experiments motivated by theory, will no doubt rise in importance as a second experimental tradition to complement our original tradition of inductive research.