Orthogonal dipolar interactions between amide carbonyl groups

Abstract

Orthogonal dipolar interactions between amide C=O bond dipoles are commonly found in crystal structures of small molecules, proteins, and protein–ligand complexes. We herein present the experimental quantification of such interactions by employing a model system based on a molecular torsion balance. Application of a thermodynamic double-mutant cycle allows for the determination of the incremental energetic contributions attributed to the dipolar contact between 2 amide C=O groups. The stabilizing free interaction enthalpies in various apolar and polar solvents amount to −2.73 kJ mol⁻¹ and lie in the same range as aromatic-aromatic C–H⋯π and π–π interactions. High-level intermolecular perturbation theory (IMPT) calculations on an orthogonal acetamide/N-acetylpyrrole complex in the gas phase at optimized contact distance predict a favorable interaction energy of −9.71 kJ mol⁻¹. The attractive dipolar contacts reported herein provide a promising tool for small-molecule crystal design and the enhancement of ligand–protein interactions during lead optimization in medicinal chemistry.

Dipolar contacts involving organic bond dipoles and a carbonyl group, or a pair of carbonyl groups are commonly found both in chemistry and biology (1). On the basis of an analysis of crystal structures of small molecules, proteins, and protein–ligand complexes, it is theorized that, owing to steric constraints, these dipoles preferentially adopt an orthogonal alignment at closest contact distance (Fig. 1). For their expected weakness, the contributions of these interactions have previously been neglected in the study of inter- and intramolecular contacts. Recently, we have been able to determine the free interaction enthalpy between a C–F and a C=O bond dipole ranging between −0.8 kJ mol⁻¹ and −1.2 kJ mol⁻¹ (2, 3). Despite the evident importance of orthogonal interactions between carbonyl dipoles for crystal packing (4–9), peptide secondary structure (10–12), and medicinal chemistry (13), no experimental quantification of the energetic contributions of such interactions has been reported so far. Intermolecular perturbation theory (IMPT) calculations performed by Allen et al. (9) assessed the interaction energy for a perpendicular propan-2-one dimer at an optimal contact distance of d_O⋯C=O = 3.02 Å to amount to −7.6 kJ mol⁻¹, comparable to the strength of weak hydrogen bonds. To provide experimental proof for the favorable energetic contributions attributed to orthogonal dipolar carbonyl–carbonyl interactions, we embarked on their determination. We chose to investigate a monomolecular model system, based on the Wilcox molecular torsion balance (14–16), providing for the determination of weak interactions with a greater accuracy and geometric control than given by the study of bimolecular chemical or biological complexes. The primary noncovalent interaction, an aromatic–aromatic edge-to-face C–H⋯π contact, prearranges the functional groups bearing the interacting carbonyl groups rather than enforcing a discrete geometry. The incremental energetic contribution attributed to the orthogonal dipolar C=O⋯C=O contact is subsequently dissected from the primary interaction by applying a chemical double-mutant cycle approach popularized by Hunter and coworkers (17). The work presented herein details the design, the synthesis, and the evaluation of a set of indole-extended molecular torsion balances ((±)-1 to (±)-4 in Fig. 2), mimicking the orthogonal amide carbonyl–amide carbonyl interaction geometries observed in protein and small-molecule crystal structures. The thermodynamic double-mutant cycle depicted in Fig. 2 is constructed and the individual folding free enthalpies were determined in C₆D₆, CDCl₃, C₂D₂Cl₄, and CD₂Cl₂ solution. The difference in folding free enthalpy between the vertical/horizontal mutations (Eq. 1) provides the incremental free enthalpy attributed to the interaction between the 2 amide carbonyl groups in (±)-1.

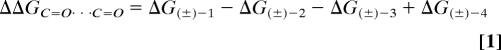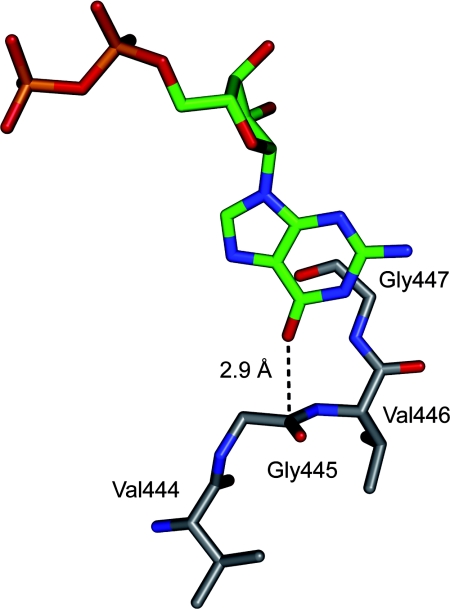
Fig. 1.

Section of the X-ray crystal structure of the complex between adenylosuccinate synthetase and GDP (PDB ID code 1lny; 2.20-Å resolution, EC 6.3.4.4) showing an orthogonal dipolar C=O⋯C=O interaction (18). Color code: ligand skeleton, green; C, gray; O, red; N, blue; P, orange.

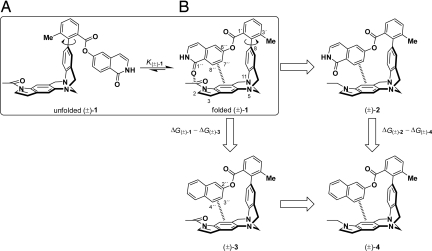
Fig. 2.

A set of indole-extended molecular torsion balances for the measurement of orthogonal dipolar C=O⋯C=O interactions. The numbering scheme used throughout this work is represented in (±)-1 and (±)-3. (A) Atropisomerism around a biaryl-type bond (C8–C2′) interconverts the unfolded into the folded conformation. (B) Thermodynamic double-mutant cycle used to assess the incremental contribution of the C=O⋯C=O interaction to the folding free enthalpy of (±)-1.

Results and Discussion

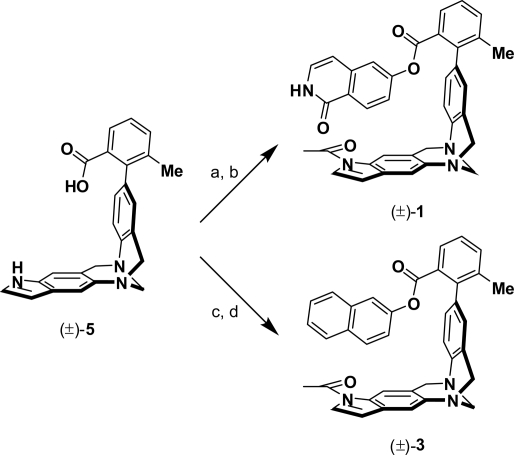
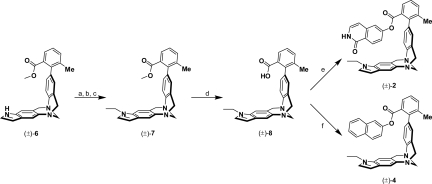
The molecular torsion balances (±)-1 and (±)-3 were synthesized starting from the common carboxylic acid precursor (±)-5 (Fig. 3 and supporting information (SI) Fig. S1) (3). Acylation of the indole N atom, followed by esterification (19) of the carboxylic acid with 6-hydroxyisoquinolin-1(2H)-one furnished a racemic mixture of (±)-1 bearing 2 amide C=O bond dipoles in an orthogonal alignment in the folded conformation. An inverted sequence comprising an esterification of (±)-5 with naphthalen-2-ol and a subsequent acylation of the indole provided the torsion balance (±)-3 in fair yields. To ensure the construction of a valid thermodynamic double-mutant cycle, the indole N atom in the mutant torsion balances (±)-2 and (±)-4 had to be substituted for a noninteracting alkyl chain. Standard protocols for the alkylation of the indole N atom by using various strong or moderate bases and alkyl halides gave predominantly mixtures of quaternary Tröger base (20) salts and the elimination products thereof. Thus, we relied on a stepwise procedure (Fig. 4 and Fig. S2) comprising a selective N-acylation of the methyl benzoate (±)-6, followed by treatment of the N-acetylindole with Lawesson reagent, and subsequent reduction of the thioamide to the N-ethylindole (±)-7 by using a surplus of Raney Nickel (RaNi) in dry THF. Saponification of the methyl ester provided the carboxylic acid (±)-8 which was coupled with 6-hydroxyisoquinolin-1(2H)-one or naphthalen-2-ol under Castro conditions (19) to give the desired molecules (±)-2 and (±)-4, respectively.

Fig. 3.

Synthesis of the molecular torsion balances (±)-1 and (±)-3 starting from the common carboxylic acid precursor (±)-5. (a) Ac₂O, DMAP, NEt₃, CH₂Cl₂, 24 °C, 72 h, 60%. (b) 6-Hydroxyisoquinolin-1(2H)-one, BOP, NEt₃, CH₂Cl₂, 24 °C, 45 h, 50%. (c) Naphthalen-2-ol, BOP, NEt₃, CH₂Cl₂, 24 °C, 72 h, 72%. (d) Ac₂O, DMAP, NEt₃, CH₂Cl₂, 24 °C, 72 h, 68%. DMAP, 4-N,N-(dimethylamino)pyridine; BOP, benzotriazol-1-yloxy-tris(dimethylamino)phosphonium hexafluorophosphate.

Fig. 4.

Synthesis of the molecular torsion balances (±)-2 and (±)-4 starting from the common methyl benzoate precursor (±)-6. (a) Ac₂O, DMAP, NEt₃, CH₂Cl₂, 24 °C, 16 h, 86%. (b) Lawesson reagent, PhMe, 100 °C, 20 h, 63%. (c) RaNi, THF, 24 °C, 25 min, 98%. (d) LiOH, MeOH, H₂O, 50 °C, 17 h, 93%. (e) 6-Hydroxyisoquinolin-1(2H)-one, BOP, NEt₃, CH₂Cl₂, 24 °C, 45 h, 29%. (f) Naphthalen-2-ol, BOP, NEt₃, CH₂Cl₂, 24 °C, 72 h, 48%. RaNi, Raney nickel.

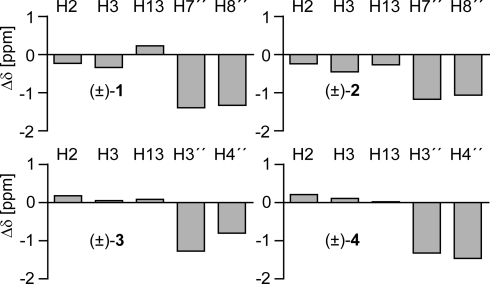
The structure of the molecular torsion balances in solution could be ascertained by extensive 1- and 2-dimensional NMR spectroscopy. In the folded conformation of all 4 torsion balances, the electron-rich indole moiety interacts with the 6-hydroxyisoquinolin-1(2H)-one moiety in (±)-1 and (±)-2 or the naphthalene-2-ol moiety in (±)-3 and (±)-4 in an aromatic edge-to-face C–H⋯π interaction. The H atoms on C7″ and C8″ in (±)-1 and (±)-2 and the respective protons adjacent to C3″ and C4″ in (±)-3 and (±)-4 come to rest within the shielding cone of the indole ring. Consistent with the observations in previous torsion balances, the respective ¹H NMR signals in C₆D₆ are shifted by Δδ = −0.8 to −1.5 ppm to higher field on folding (Fig. 5). The tautomeric 1-hydroxyisoquinoline/isoquinolin-1(2H)-one equilibrium lies predominantly on the side of the latter (21); thus, the anisotropic effect of the carbonyl group in (±)-1 and (±)-2 shifts the resonance signals of the protons on C2 and C3 of the indole to higher field with respect to the unfolded conformation. The deshielding cone of the naphthyl moiety instead induces a weak downfield shift in the indole hydrogens. The observation of a significant ¹H–¹H NOE between the protons of the acetyl group on the indole N atom in the folded conformation of torsion balance (±)-1 and the hydrogen on N2″ of the isoquinolin-1(2H)-one moiety (CH₃⋯HN distance <4.5 Å) indicates of a sub van der Waals contact distance between the interacting C=O bond dipoles (see Fig. S3). The overall geometry of the folded state is further corroborated by X-ray crystal structures of related torsion balances (2, 3).

Fig. 5.

Shifts of the ¹H NMR signals of selected protons in the folded conformation relative to the unfolded torsion balances.

On the NMR spectroscopy timescale, the interconversion between the rotational atropisomers is slow (ΔG^‡ ≥ 67 kJ mol⁻¹ at 273 K) (14), thus, 2 separate resonance signals for the methyl group on C3′ of the rotor, corresponding to the folded and the unfolded conformation of the torsion balances, can be observed. The ¹H NMR spectra recorded at 298 K in C₆D₆, CDCl₃, C₂D₂Cl₄, and CD₂Cl₂ (see Fig. S4) were line-fitted to Lorentz functions and integrated to determine the relative population of both conformations at thermodynamic equilibrium. The resulting folding free enthalpies derived from the equilibrium constants at 298 K are summarized in Table 1.

Table 1.

Folding free enthalpies ΔG of torsion balances (±)-1 to (±)-4 in C₆D_6, CDCl₃, C₂D₂Cl₄, and CD₂Cl₂

Compound	ΔG, kJ mol−1*
	C6D6	CDCl3	C2D2Cl4	CD2Cl2
(±)-1	−3.00	−1.15	−0.40	−1.54
(±)-2	−0.92	0.15	1.05	−0.40
(±)-3	−0.85	−0.48	−0.04	−0.84
(±)-4	−1.50	−0.69	−0.29	−0.93

*Determined by integration of line-fitted ¹H NMR (500 MHz) spectra of 2 mM solutions at 298 K. Uncertainty: ±0.12 kJ mol⁻¹. For an error analysis see the SI Text.

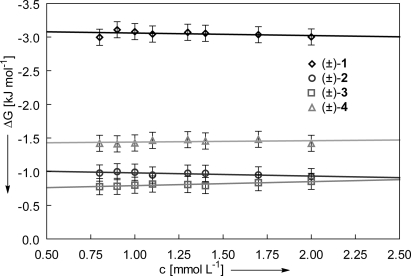
The atropisomeric equilibrium of all torsion balances in C₆D₆ and CD₂Cl₂ lies predominantly on the side of the folded conformation, reflected in the negative values of ΔG. In CDCl₃ and C₂D₂Cl₄, however, the population of the folded conformation is substantially decreased. We attribute this observation to interactions between solvent molecules and the Tröger base cleft, shifting the atropisomeric equilibrium toward the unfolded conformation of the torsion balances. The introduction of a functional group in (±)-1 and (±)-2, namely the isoquinolin-1(2H)-one moiety, capable of interacting via hydrogen bonds with the solvent or other solute molecules, imposes an uncertainty on the accuracy of the determination of the respective absolute folding free enthalpies. For steric reasons a dimerization of the torsion balances in solution is only possible in the unfolded conformation. As a consequence, the hydrogen bonding interaction would most certainly shift the atropisomeric equilibrium of (±)-1 and (±)-2 toward the unfolded conformation, thereby underestimating the interaction between the amide carbonyl dipoles. The effect should be particularly strong in C₆D₆ and weaker in CDCl₃, as observed for the dimerization of isoquinolin-1(2H)-one (K_dim = 333 L⁻¹ in C₆D₆, K_dim = 57 L⁻¹ in CDCl₃; see Fig. S5). To assess the influence of intermolecular hydrogen-bonding interactions on the folding free enthalpy ΔG of the torsion balances (±)-1 to (±)-4, a dilution study in C₆D₆ was performed (Fig. 6). Within the experimental errors, essentially no concentration dependence on the folding equilibrium could be observed.

Fig. 6.

Concentration dependence of the folding equilibrium of the torsion balances (±)-1 to (±)-4 in C₆D₆ solution acquired at 298 K.

With the differences in folding free enthalpy ΔG determined for each torsion balance, the double-mutant cycle depicted in Fig. 2 can be applied. The horizontal mutations [(±)-1→(±)-2 and (±)-3→(±)-4, respectively] account for the changes in electron density in the π-system of the indole moiety, on substitution of an electron-withdrawing acetyl group on N1 by an electron-donating ethyl residue. The vertical mutations (±)-1→(±)-3, and (±)-2→(±)-4 reflect the perturbation of the electronic structure of the edge component induced by the lactam moiety. The computed (Eq. 1) interaction free enthalpy ΔΔG^298K between 2 amide C=O bond-dipoles is strongest in C₆D₆ (−2.73 ± 0.25 kJ mol⁻¹). In chlorinated solvents, such as CDCl₃ (−1.50 ± 0.25 kJ mol⁻¹), C₂D₂Cl₄ (−1.70 ± 0.25 kJ mol⁻¹), and CD₂Cl₂ (−1.22 ± 0.25 kJ mol⁻¹), the dipolar interaction is substantially weaker. This observation can be attributed to a stronger interaction of dipolar solvents with both amide groups in (±)-1 shifting the thermodynamic equilibrium toward the unfolded conformation. A closer analysis of the thermodynamic data in Table 1 reveals that the mutation of an N-ethyl-substituted indole to an N-acylated indole [(±)-4→(±)-3] brings about a small unfavorable change in folding free enthalpy of +0.09 to +0.65 kJ mol⁻¹ in C₆D₆ and the chlorinated solvents. The electron density of the indole decreases because of the introduction of an electron-withdrawing substituent, and thus weakens the primary edge-to-face interaction. The vertical mutation [(±)-4→(±)-2] accounts for the difference in folding free energy between a naphthyl and an isoquinolin-1(2H)-one ester. On introduction of the latter, the folding free energy decreases. Despite the fact that the electron-withdrawing effect of the amide group stabilizes the C–H⋯π interaction, the repulsion between the lone pairs of the carbonyl O atom and the p-orbital of the indole N atom dominates the interaction. As a consequence, the equilibrium is shifted toward the unfolded conformation. The effect is weakest in C₆D₆ (+0.58 kJ mol⁻¹) and CD₂Cl₂ (+0.53 kJ mol⁻¹), whereas it amounts to +0.84 kJ mol⁻¹ and +1.34 kJ mol⁻¹ in CDCl₃ and C₂D₂Cl₄, respectively.

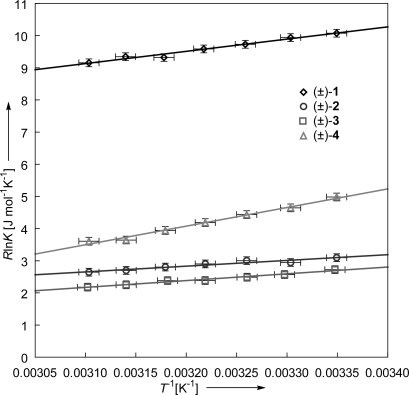
In an effort to gain a deeper insight into the driving force of the folding process, we dissected the overall folding free enthalpy ΔG into the enthalpic ΔH and the entropic ΔS components. Variable temperature ¹H NMR experiments in C₆D₆ were performed to determine the temperature dependence of the folding equilibrium in a range from 298 K to 322 K. On heating 2 mM solutions of the torsion balances (±)-1, (±)-2, (±)-3, and (±)-4 in C₆D₆ (see Fig. S6), a shift of the folding equilibrium toward the unfolded conformation can be observed in the ¹H NMR spectra. As a consequence, the folding free enthalpy ΔG at 322 K decreases by +0.06 kJ mol⁻¹ to +0.33 kJ mol⁻¹. The individual equilibrium constants at different temperatures were plotted as RlnK against T⁻¹ (van′t Hoff plot), and are depicted in Fig. 7. Both the enthalpy ΔH and the entropy ΔS were determined by fitting linear equations to the experimental data points. The goodness of fit (r²) exceeds 0.98 for (±)-1, (±)-3, (±)-4, and 0.93 for (±)-2.

Fig. 7.

Van′t Hoff plot of RlnK against T⁻¹ for the torsion balances (±)-1 to (±)-4 in C₆D₆. The goodness of fit (r²) for the linear equations exceeds 0.93 in all cases.

Table 2 summarizes the individual thermodynamic parameters. The folding process is enthalpy-driven for all torsion balances with the strongest contribution determined for (±)-1 and (±)-4 (ΔH = −3.81 kJ mol⁻¹ and ΔH = −5.79 kJ mol⁻¹, respectively). The folding enthalpy for (±)-2 and (±)-3 is weaker, reflecting the observations in the double-mutant cycle. The horizontal mutation (±)-4→(±)-3 reduces the electron density of the indole, therefore weakening the edge-to-face interaction, reflected in a decrease in folding enthalpy (δΔH = ΔH_(±)-3 − ΔH_(±)-4 = +3.68 kJ mol⁻¹). The opposite effect can be observed for the substitution of the ethyl residue on N1 in (±)-2 by an acetyl group ((±)-2→(±)-1). Despite the electron density in the indole being reduced on introduction of a COCH₃ group, the folding free enthalpy increases (δΔH = ΔH_(±)-1 − ΔH_(±)-2 = −2.03 kJ mol⁻¹). It is intriguing to relate this difference in enthalpy (ΔΔH = ΔH_(±)-1 − ΔH_(±)-2 − ΔH_(±)-3 + ΔH_(±)-4 = −5.71 kJ mol⁻¹) to the interaction between the orthogonal amide C=O bond-dipoles. However, it cannot be concluded from the data whether this is the unique contribution. Solvent–solvent, as well as solvent–solute interactions, or a cooperative effect enforcing an optimized primary edge-to-face interaction have to be considered. In the case of torsion balance (±)-4, the stronger enthalpic component ΔH is mirrored in a decrease in entropy ΔS, indicative of a tighter interaction in the folded conformation. This efficient enthalpy–entropy compensation levels out the overall differences in folding free enthalpy in Table 1.

Table 2.

Folding enthalpies ΔH and folding entropies ΔS determined graphically

Compound	ΔH, kJ mol−1*	ΔS, J mol−1 K−1*	TΔS298K, kJ mol−1
(±)-1	−3.81 ± 0.26	−2.67 ± 0.86	−0.80 ± 0.26
(±)-2	−1.78 ± 0.22	−2.86 ± 0.71	−0.85 ± 0.21
(±)-3	−2.11 ± 0.14	−4.36 ± 0.44	−1.30 ± 0.13
(±)-4	−5.79 ± 0.28	−12.46 ± 0.90	−4.31 ± 0.27

*Errors were determined graphically.

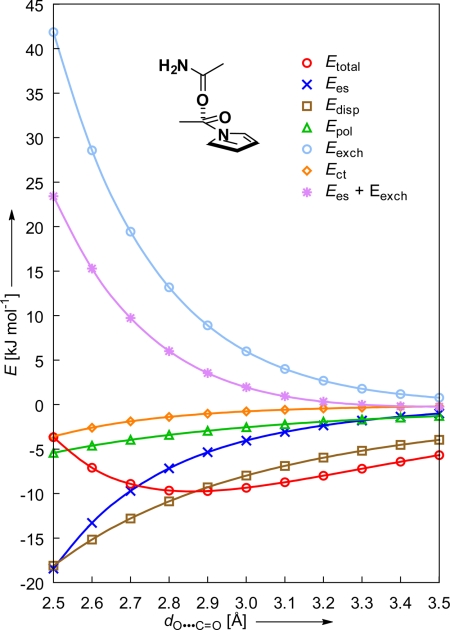
Intermolecular perturbation theory (IMPT) calculations (see Computational Methods for full details) were performed on an acetamide/N-acetylpyrrole model mimicking the orthogonal dipolar interaction geometry in (±)-1 (see Fig. S7). This geometry was chosen based on extensive analyses of C=O⋯C=O (9) and C≡N⋯C≡N (22) interactions in crystal structures obtained from the CSD (23). The E_total profile illustrated in Fig. 8 is dominated by attractive contributions from dispersion E_disp and electrostatic E_es interactions, counterbalanced by the exchange repulsion term E_exch. Both the polarization E_pol and the contributions attributed to charge transfer interactions E_ct are smaller in magnitude. The interaction energy E_total between the 2 amide groups is minimized (−9.71 kJ mol⁻¹) at a O⋯C=O contact distance of 2.9 Å. With respect to the propan-2-one dimer (E_total,min = −8.02 kJ mol⁻¹, d_O⋯C=O = 3.0 Å; see Fig. S8) both an increase in polarization and dispersion interactions can be observed for the acetamide/N-acetylpyrrole model. These changes can be accredited to an increase in dipole moment and the extended delocalization of the amide N atom lone pair with the C=O group.

Fig. 8.

Ab initio-based molecular orbital calculations (6–31G**) using intermolecular perturbation theory (IMPT) applied to an orthogonal interaction between an acetamide and an N-acetylpyrrole mimicking the dipolar interaction in torsion balance (±)-1.

In summary, we have presented the design, synthesis, and evaluation of a set of molecular torsion balances, providing experimental evidence for the existence of attractive orthogonal dipolar interactions between 2 amide carbonyl groups. The measured contributions of this dipolar contact to the overall folding free enthalpy ΔG of (±)-1 lie in the range of −2.73 kJ mol⁻¹ (C₆D₆) to −1.22 kJ mol⁻¹ (CD₂Cl₂). Because of crystal packing effects, solvent effects, and sterically constrained molecular geometries, an ideal interaction reflecting the calculated values will most certainly never be observed in crystal structures or in solution. Yet, the enthalpic (ΔΔH) contribution to the dipolar interaction of torsion balance (±)-1 in C₆D₆ amounts to almost 60% of the calculated interaction energy of an orthogonal acetamide/N-acetylpyrrole complex in the gas phase at optimized contact distance. Aside from providing a promising tool for the enhancement of small-molecule and ligand–protein interactions in crystal design as well as in medicinal chemistry, the study of attractive orthogonal dipolar interactions between carbonyl groups is expected to contribute new insights into the process of protein folding and the stabilization of secondary protein structures.

Materials and Methods

Protocols for the determination of the folding free enthalpy of the torsion balances, an error analysis, the procedures for the synthesis of (±)-1 to (±)-4, and the Figs. S1– S8 can be found in the SI Text.

Computational Methods.

The intermolecular perturbation theory (IMPT) of Hayes and Stone (24) as implemented in the CADPAC 6.5 program package (25) was used to calculate intermolecular interaction energies between orthogonal C=O dipoles. The IMPT methodology has been widely used to calculate interaction energies in a variety of systems (26–29). The model systems used in this study were the propan-2-one orthogonal dimer, as described by Allen et al. (9) and the analogous acetamide/N-acetylpyrrole dimer as shown in Fig. 8 and, in more detail, in Fig. S7. The IMPT methodology yields separate interaction energy components (first order, electrostatic and exchange-repulsion energies; second order, polarization, charge-transfer, and dispersion energies) which sum to a total interaction energy (E_total) that is free from basis-set superposition errors (30). In each set of calculations, the monomers were first geometry optimized separately by using the 6–31G** basis set. The dimer interaction energies were then calculated by using the resulting fixed intramolecular geometries at varying intermolecular C=O⋯C=O distances.