Structure of transmembrane pore induced by Bax-derived peptide: Evidence for lipidic pores

Abstract

The structures of transmembrane pores formed by a large family of pore-forming proteins and peptides are unknown. These proteins, whose secondary structures are predominantly α-helical segments, and many peptides form pores in membranes without a crystallizable protein assembly, contrary to the family of β-pore-forming proteins, which form crystallizable β-barrel pores. Nevertheless, a protein-induced pore in membranes is commonly assumed to be a protein channel. Here, we show a type of peptide-induced pore that is not framed by a peptide structure. Peptide-induced pores in multiple bilayers were long-range correlated into a periodically ordered lattice and analyzed by X-ray diffraction. We found the pores induced by Bax-derived helical peptides were at least partially framed by a lipid monolayer. Evidence suggests that the formation of such lipidic pores is a major mechanism for α-pore-forming proteins, including apoptosis-regulator Bax.

Pore-forming proteins and peptides are water soluble but also capable of spontaneously inserting into membranes and making stable transmembrane pores. These proteins and peptides have attracted a great deal of interest for their ability to regulate molecular transport across membranes, for their unusual sequence–structure relationships, and for biotechnological applications (1). Among the large number of pore-forming proteins discovered so far (2–4), those that have been investigated fall into 2 distinct classes. One class, whose secondary structures are predominantly β-sheets, form crystallizable porin-like transmembrane β-barrel pores. Another class, whose secondary structures are predominantly α-helical segments, and all of the known antimicrobial peptides (5) form pores without a crystallizable protein assembly (6). The pore structures for this latter class α-pore-forming proteins (α-PFPs) have long been a puzzle, because unlike β-strands, α-helices cannot hydrogen-bond side-by-side to form a bonded barrel structure. The most common assumption is that α-helical segments form a transmembrane barrel-stave assembly stabilized by hydrophobic interactions (7, 8). However there has been experimental evidence suggesting another type of pores whose walls were partially lined by lipid head groups rather than framed by a purely proteinaceous structure. Here, we present X-ray diffraction results confirming both types of pore structures induced by helical peptides. Significantly, the formation of lipidic pores is expected to be a common mechanism for α-PFPs including apoptosis-regulating proteins.

The best known β-pore-forming proteins are bacterial toxins, e.g., staphylococcal α-hemolysin (9). An increasing number of them have been crystallized and imaged in their prepore and pore forms (2–4). On the contrary, none of α-pore-forming toxins, such as colicins (10) and diphtheria toxin (11), have ever been crystallized in their pore forms. The class of α-PFPs now includes the Bcl-2 family of apoptosis-regulating proteins (12–14), notably Bax (15) that activates pore formation in the outer mitochondria membrane to release the apoptotic factor cytochrome c. Recent studies have shown that the pore forming properties of α-toxins (3, 10) and Bax (12, 14) are similar to that of antimicrobial peptides (5, 16, 17), the innate immune factors that kill microbes by forming pores in the cell membranes. In particular, peptide segments derived from the pore-forming domain of Bax, Bax-α5, reproduced the pore-forming activity of the parent full-length protein (18–20).

In the absence of evidence to the contrary, a membrane pore is traditionally presumed to be a protein channel, and the idea of peptide helices forming a barrel-stave assembly (Fig. 1A) (7, 8) was supported by the study of α-helical antibiotic peptide alamethicin (21–23). However, often not mentioned is the fact that alamethicin is distinct from almost all other pore-forming peptides (23): 8 of its 20 amino acids are the unusual residues α-aminoisobutyric acids; it is weakly charged and has low water solubility, and it produces well-defined, discrete single-channel conductance (22). The pores produced by highly charged, water-soluble peptides did not exhibit well-defined conductance levels (23), and their pore sizes were substantially larger than alamethicin's, such that the pores could not be fully lined by the peptides (23–25). Thus, it was proposed that the pores were formed by the merging of 2 lipid leaflets through the pore and that perhaps the edge of the pore was lined by both the peptides and lipid head groups (23, 24). This was called the toroidal (or wormhole) model (Fig. 1B) (24). This model implies that the curvature properties of the lipid would influence pore formation. Indeed, the pore-forming activities of antimicrobial peptide (26, 27), Bax-α5 (20), colicins (10), and full-length Bax (12, 14) all exhibited dependence on intrinsic monolayer curvature and enhanced transbilayer lipid flip–flop, consistent with forming toroidal pores. Nonetheless, lacking the structural evidence, the toroidal model has so far remained speculation.

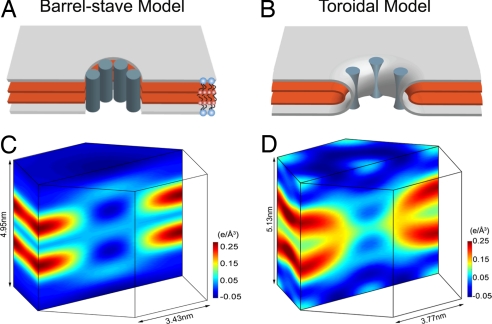
Fig. 1.

Two models of peptide-induced pores in membranes and the experimental proof for each. (A and B) Schematics of the barrel-stave model (A) and the toroidal model (B) are shown in a 3D view cut through the pores, showing only the layers representing the lipid headgroups (silver) and the Br atoms (red). Blue-gray cylinders represent peptide segments; the actual distribution and orientation of peptides are expected to vary with peptide and lipid. Schematic lipid molecules [1,2-distearoyl(9–10dibromo)-sn-glycero-3-phosphocholine] are shown in A, where the red dots represent the Br atoms on the chains. (C and D) The normalized electron density distributions of Br atoms in a unit cell of the R phase containing alamethicin and Bax-α5, respectively. (The data for C were reproduced from ref. 28.) Br atoms are distributed in the high-density (yellow-red-black) region. The nonuniformity in the low-density region (light blue to dark blue, which average to ≈0 e/ų) is due to the limited resolution (28).

We performed X-ray diffraction experiments to view the electron density distributions of peptide-induced pores. This was possible because the peptide-induced pores spontaneously formed a periodically ordered lattice of rhombohedral symmetry (the R phase) under a dehydrated multilamellar condition (28, 29). The diffraction from such lattices is of limited resolution (typically consisting of ≈15 Bragg peaks). To delineate the lipid structures, we used a lipid of brominated chains, 1,2-distearoyl(9–10dibromo)-sn-glycero-3-phosphocholine [abbreviated as di18:0(9,10Br)PC] and performed the Br-edge anomalous diffraction to single out the diffraction amplitudes of the Br atoms (30). Thus, we greatly simplified the complicated electron density distribution of lipids, peptides, and water molecules to that of Br atoms alone. Yet, because lipids always form continuous layers, this layer structure will be revealed by the Br distribution. We compare the unit cell structures of 2 R phases (Fig. 1), one induced by alamethicin (28) and the other by Bax-derived peptide segment, Bax-α5. Reassuringly, the electron density distribution of Br atoms in the alamethicin pore is consistent with the barrel-stave model—the Br layers (and therefore the lipid layers) are interrupted by an empty hole (Fig. 1C) as schematically predicted by the model (Fig. 1A). In contrast, the electron density distribution of Br atoms in the pore induced by Bax-α5 (Fig. 1D) is consistent with the toroidal model (Fig. 1B)—the top Br layer bends continuously into the bottom Br layer through the pore, proving that lipid molecules, at least partially, line the edge of the pore. This result validates the toroidal model, namely, the lining of the pore is an extension of the water–lipid chain interface. Previous experiments (23–25) have shown the correlation between the formation of pores and a change of peptide orientation (from parallel to the bilayer to perpendicular) [see supporting information (SI) Text]. This suggests that the lining of a toroidal pore includes a number of adsorbed peptides, because such a peptide–lipid composition tends to lower the free energy of the monolayer curvature (31). Unfortunately, the distribution of the peptides is not visible by the technique used in this experiment.

Note that the pores were first formed in multiple layers of fully hydrated lipid bilayers and then by dehydration correlated into a lattice. As a result, the central water channel of the toroidal pore (Fig. 1D) was reduced (dehydrated) to a diameter of ≈1.3 nm, judging from the Br–Br distance (≈3.8 nm; the Br–phosphate distance ≈1.25 nm Fig. S1). From an experiment measuring Bax-α5-induced leakage of 20- and 70-kDa dextrans from large unilamellar vesicles, the Bax-α5 pore size was estimated to have an upper limit of 11.6 nm in diameter (20). Previous neutron in-plane scattering from many different peptide-induced pores in fully hydrated lipid bilayers showed that the inner diameters of toroidal pores were in the range of 3.0–5.0 nm, depending on the peptide and lipid (23–25, 29, 32). Thus, the toroidal pore in the R phase is considerably smaller than its normal size in fully hydrated bilayers. In contrast, the alamethicin pores in the lattice (Fig. 1C) retained the same size (inner diameter 1.8 nm) as in fully hydrated lipid bilayers (33); the barrel-stave pore did not shrink by dehydration (28). This is consistent with toroidal pores being lipidic in nature, which is expected to be sensitive to hydration, whereas the alamethicin pore is framed by a peptide assembly that is less sensitive to hydration.

Discussion

Mechanism of Pore Formation.

Pore-forming peptides are amphipathic; they spontaneously bind to the water–lipid chain interface of the lipid bilayer. The resulting interfacial area increase stretches the hydrocarbon core of the bilayer (17). Thus, binding of amphipathic peptides causes an elastic strain in the lipid bilayer. The strain increases with the peptide concentration, and when it exceeds a threshold, pores are formed. Indeed, it has been demonstrated with lipid vesicle experiments that the binding of pore-forming peptides had the same effect as applying a mechanical tension; both resulted in pore formation when the membrane areas were stretched beyond a critical value of fractional area increase (17). The only difference was that mechanical tension enlarged the pore and ruptured the membrane, whereas the pores induced by peptides were of finite size and stable. This explains why antimicrobial peptides are active only if their concentrations exceed a threshold value known as the minimum inhibitory concentration or MIC (5). As we have shown here, pores can be either the barrel-stave type that requires the peptides to be compatible for a barrel-like aggregation, e.g., they must be weakly charged or neutral so as not to repel each other, or more generally the toroidal type that seems to place no condition on the peptides other than that it must be amphipathic. Either of these pores forms because the formation partially relieves the interfacial strain. The barrel-stave pores remove some peptides from the interface. The toroidal pores allow some extension of the interfacial area without stretching the hydrocarbon core. This negative feedback to the interfacial strain is the reason the pores are stable (34).

The great majority of pore-forming peptides discovered so far (5), including Bax-α5, are highly ionic (typically in 25% of their amino acids) and water soluble. As a group, their pore-forming activities are similar (5) and distinct from that of alamethicin-like peptides (16, 23). Thus, we expect the majority of the pores induced by peptides to be lipidic pores.

Possible Mechanism of α-PFPs.

The structure of Bax (35) is closely similar to the pore-forming domain of colicins (10) or diphtheria toxin (11). Each consists of 7 or more amphipathic α-helical segments. It is speculated that when an α-PFP binds to the membrane, most of these peptide segments are bound to the interface (10, 35). These bound peptide segments are confined to a small area because they are linked. Thus, in a local region of membrane, even a small number of α-PFPs can create the effect of a high concentration of pore-forming peptides, which is the condition for pore formation. For the reason given above, we expect α-PFPs to form lipidic pores. This could explain the similarity of pore-forming activity between peptides and α-PFPs (10, 18).

Methods

Materials and Sample Preparation.

Peptide Bax-α5 (Ac-DGNFN WGRVV ALFYF ASKLV LKALS TKVPE LIRT-NH₂) was derived from the pore-forming (α5 and part of α6 hairpin) domain (residues 102–135) of mouse Bax (20), synthesized by SynBioSci Corporation to HPLC purity >95%. When bound to lipids, Bax-α5 is largely α-helical according to its circular dichroism spectrum (20), probably consisting of 2 helical segments (102–126 and 130–135) according to the structure of the water-soluble form of Bax (36). Lipid 1,2-distearoyl(9–10dibromo)-sn-glycero-3-phosphocholine [abbreviated as di18:0(9,10Br)PC] was purchased from Avanti Polar Lipids.

The peptide and 0.8 mg of the lipid were codissolved at the peptide–lipid molar ratio 1:30 in trifluoroethanol (TFE)-chloroform (≈1:1) solvent and deposited on a thoroughly cleaned silicon wafer of 10 × 20 mm² (37). After the evaporation of the organic solvent in vacuum for at least 1 h, the sample was incubated in a temperature–humidity chamber with saturated water vapor at 35 °C for several hours, until the peptide–lipid mixture on the substrate was visibly smooth and uniform in thickness (≈4 μm). The sample was then cooled to room temperature.

Grazing-Angle X-Ray Anomalous Diffraction.

Grazing-angle diffraction was used to identify the structure of the peptide–lipid mixture. The experiment was performed at beamline X21 of the National Synchrotron Light Source, Brookhaven National Laboratory (Upton, NY). The experimental setup was described in ref. 28. The sample as prepared was in a well-oriented lamellar phase consisting of multiple layers of fully hydrated lipid bilayers all parallel to the surface of the substrate. Oriented circular dichroism [OCD (38)] of the sample (Fig. S2) showed that ≈30% of the helical components of the peptides were oriented normal to the plane of the bilayers (see SI Text). (Note that OCD cannot distinguish a mixture of normal and parallel helices from a tilted helix—see SI Text.) We have previously established the correlation between the OCD-containing normal helical components and the formation of pores in the bilayers by neutron in-plane scattering (23, 24, 33). When such a lamellar phase was gradually dehydrated, we could see by the changes of the diffraction pattern that the pores became correlated and developed into a periodically ordered lattice of the rhombohedral symmetry (R phase), where the unit cell contained a pore (25, 29, 32). The R phase of Bax-α5 in di18:0(9,10Br)PC appeared as the relative humidity (RH) of the sample chamber was lowered to <78% RH at 25 °C. Fig. 2 shows the grazing angle diffraction of this R phase at 60% RH and 25 °C.

Fig. 2.

Grazing-angle diffraction pattern from the R phase of a Bax-α5 and di18:0(9,10Br)PC mixture in the molar ratio of 1:30 at 60% RH, 25 °C. The vertical (q_z) is normal to the substrate. To show all peaks clearly, intensity attenuators were applied to the peaks on q_z and on the 2 columns next to q_z.

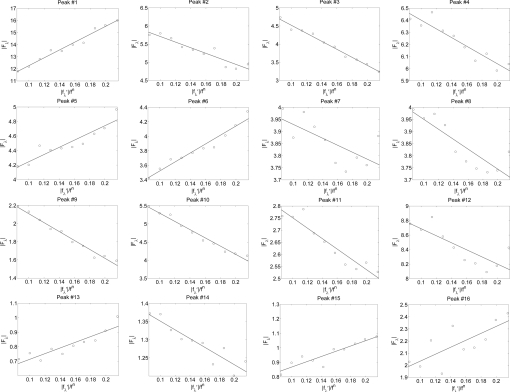
The rhombohedral diffraction pattern in Fig. 2 is on a lattice described by the set of reciprocal vectors B₁ = (1/a,1/$\sqrt{3}$a,0), B₂ = (0,2/$\sqrt{3}$a,0), and B₃ = (0,0,1/3c) indexed by (H, K, L) and the crystal axes A₁ = (a,0,0), A₂ = (−a/2,$\sqrt{3}$a/2,0), and A₃ = (0,0,3c) with lattice constants a = 6.53 nm and c = 5.13 nm. The cell defined by A₁,A₂,A₃ contains 3 primitive unit cells positioned at (0,0,0), (a/2,a/2$\sqrt{3}$,c), and (0,a/$\sqrt{3}$,2c). The diffraction pattern consisted of 16 independent Bragg peaks listed in Table 1, with all of the symmetry-related peaks counted as 1.

Table 1.

Data for the unit cell reconstruction

No.	(H, K, L)	∣F2∣	∣F0∣	−F0/F2	ε	F2 phase	F0 phase
1	(0,0,3)	32.53	9.01	0.28	0.987	+	−
2	(0,0,6)	7.74	6.48	−0.84	−0.938	−	−
3	(0,0,9)	11.07	5.63	−0.51	−0.992	−	−
4	(0,0,12)	3.60	6.76	−1.88	−0.934	−	−
5	(1,0,1)(−1,1,1)(0,–1,1)	4.97	3.75	0.75	0.927	−	+
6	(0,1,2)(−1,0,2)(1,−1,2)	6.19	2.91	0.47	0.974	−	+
7	(1,0,4)(−1,1,4)(0,−1,4)	1.43	4.07	−2.84	−0.680	+	+
8	(0,1,5)(−1,0,5)(1,−1,5)	2.05	4.16	−2.02	−0.861	+	+
9	(1,0,7)(−1,1,7)(0,−1,7)	4.91	2.60	−0.53	−0.989	−	−
10	(0,1,8)(−1,0,8)(1,−1,8)	11.37	6.44	−0.57	−0.988	+	+
11	(1,0,10)(−1,1,10)(0,−1,10)	2.15	2.97	−1.38	−0.945	−	−
12	(0,1,11)(−1,0,11)(1,−1,11)	4.86	9.17	−1.89	−0.803	+	+
13	(1,1,3)(−1,2,3)(−2,1,3)(−1,−1,3)(1,−2,3)(2,−1,3)	1.96	0.52	0.26	0.910	−	+
14	(1, 1,9)(−1,2,9)(−2,1,9)(−1,−1,9)(1,−2,9)(2,−1,9)	1.20	1.47	−1.23	−0.920	−	−
15	(1, 1,12)(−1,2,12)(−2,1,12)(−1,−1,12)(1,−2,12)(2,−1,12)	1.81	0.69	0.38	0.918	+	−
16	(0,2,10)(−2,0,10)(2,−2,10)	2.88	1.75	0.61	0.752	−	+

Results of multiwavelength anomalous diffraction analysis for the R phase of the mixture of Bax-α5 and di18:0(9,10Br)PC, in the molar ratio of 1:30 at 60% RH, 25 °C. Sixteen independent diffraction peaks, denoted by crystal indices (H,K,L), were detected. ∣F₂∣, ∣F₀∣, and −F₀/F₂ were obtained from the linear fits in Fig. 3. ε is the correlation coefficient of the linear fit.

The method of grazing-angle multiwavelength anomalous diffraction has been described in great detail previously (28, 30). We followed the same experimental procedure as described in the alamethicin experiment (28) that produced Fig. 1C. Briefly, we measured the real f′λ and imaginary f″λ parts of the bromine atom's anomalous scattering factor using the actual sample (instead of an arbitrary Br compound) at 10 X-ray energies below the bromine K-edge at 13.474 keV. Then we measured the diffraction patterns of the sample at these 10 subedge X-ray energies (28). The integrated intensities of the diffraction peaks were then reduced to the relative magnitudes of the diffraction amplitude F_λ(H,K,L) at 10 different X-ray wavelength λ. Denote the normal diffraction amplitudes of the Br atoms as F₂, the normal diffraction amplitudes of the whole system as F₀, and the anomalous scattering factor of Br as f = fⁿ + f′λ + if″λ. The lipidic structure under consideration arose spontaneously from a symmetric bilayer of the peptide–lipid mixture. Therefore, its average molecular distribution in the unit cell is most likely centrosymmetric. We assume that this is the case and the assumption will be justified by the result. [It has been shown by lipid vesicle experiments (17) that even when only 1 side of a lipid bilayer was exposed to peptides, the peptides would distribute symmetrically across the bilayer.] Then the amplitudes F₀ and F₂ are real quantities with a phase angle equal to either 0 or π. Under this condition, we have previously derived a well-justified approximate relation (30)

From Eq. 1 the magnitudes of F₀, F₂, and their relative phase can be obtained by a linear fit to ∣F_λ∣ vs. ∣f′λ∣/fⁿ as shown in Fig. 3. The result is shown in Table 1. The strong correlations of the linear fits (Table 1 and Fig. 3) indicate the excellent quality of the data and also justify the assumption of centrosymmetry (because the linear relation of Eq. 1 would not be valid without this assumption).

Fig. 3.

Multiwavelength anomalous diffraction analyses for the detected peaks. For each independent peak, the square root of the integrated intensity, ∣F_λ∣, is plotted as a function of ∣f′λ∣/fⁿ. The data are fit with a straight line, from which ∣F₀∣, ∣F₂∣, and the ratio ∣F₀∣/∣F₂∣ are obtained. The results are in Table 1.

Fig. 4.

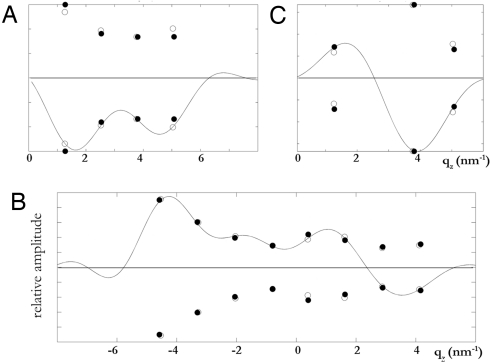
Three-dimensional swelling method for phase determination applied to the rhombohedral phase (42). Shown is the swelling method applied to different q_r series using the diffraction amplitudes obtained at 50% RH (open circles) and 60% RH (filled circles). (A) q_r = 0 nm⁻¹ series. (B) q_r = 1.11 nm⁻¹ series. (C) q_r = 1.92 nm⁻¹ series. The vertical scales are relative. The solid curves are F(q_H,K,q_z) of equation 12 in ref. 42 constructed from 1 set of data measured at 1 relative humidity (see details in ref. 42).

Phase Determination.

The swelling method (39, 40) for the rhombohedral phase has been described in great detail previously (41, 42). We made use of the lattice constant changes with the degree of hydration and collected diffraction patterns at 50% RH and 60% RH, where the vertical repeat spacing c was 5.10 and 5.13 nm, respectively. The swelling method was applied to the series of diffraction peaks at the same q_r (the reciprocal vector parallel to the hexagonal plane) (Fig. 3). The method determined the relative phases among the peaks of a series. That left the relative phases between different q_r series undetermined. There were 4 different q_r series (one of them had only 1 peak), so there were 8 (2³) possible different choices. We inspected all 8 possible choices and determined the one that made the physical sense (Table 1). The normalized electron density distribution of Br atoms in a unit cell (Fig. 1D) was constructed from F₂ (Table 1) by the method described in ref. 28.

This method worked for the following reasons: (i) Because each peak amplitude is either positive or negative, there is 1 correct phase combination among all possible choices. (This would not be case if the amplitudes were complex quantities; there would be infinite possible phase combinations.) (ii) Lipid assemblies follow the principle of continuous layers (43), that is, there should be no free edges for lipid monolayers unless the edge is anchored by amphipathic molecules such as the case of alamethicin pore (Fig. 1 A and C). This principle allows us to reject nonsensical lipid structures produced by incorrect phases (42). Being able to isolate the diffraction amplitudes for the Br atoms alone makes this method workable, because, despite the relative low resolution, the Br distribution is clear. The electron density distribution of the whole system, constructed from F₀ (see Fig. S1 and SI Text), is much less clear because of the limited resolution for a complex composition; most notably the peptides are not identifiable (28). This method has been successfully applied to many other lipid systems (28, 30, 44, 45).