Abstract
Biological pores regulate the cellular traffic of a large variety of solutes, often with high selectivity and fast flow rates. These pores share several common structural features: the inner surface of the pore is frequently lined with hydrophobic residues, and the selectivity filter regions often contain charged functional groups. Hydrophobic, narrow-diameter carbon nanotubes can provide a simplified model of membrane channels by reproducing these critical features in a simpler and more robust platform. Previous studies demonstrated that carbon nanotube pores can support a water flux comparable to natural aquaporin channels. Here, we investigate ion transport through these pores using a sub-2-nm, aligned carbon nanotube membrane nanofluidic platform. To mimic the charged groups at the selectivity region, we introduce negatively charged groups at the opening of the carbon nanotubes by plasma treatment. Pressure-driven filtration experiments, coupled with capillary electrophoresis analysis of the permeate and feed, are used to quantify ion exclusion in these membranes as a function of solution ionic strength, pH, and ion valence. We show that carbon nanotube membranes exhibit significant ion exclusion that can be as high as 98% under certain conditions. Our results strongly support a Donnan-type rejection mechanism, dominated by electrostatic interactions between fixed membrane charges and mobile ions, whereas steric and hydrodynamic effects appear to be less important.
Keywords: biomimetic platform, ion channel, ion transport, nanofiltration
Ion transport across cellular membranes is essential to many of life's processes, such as electrical signaling in nerves, muscles, and synapses or cell's maintenance of homeostatic balance. Biological systems achieve rapid, selective, and ultraefficient transmembrane mass transport by employing a large variety of specialized protein channels of nanometer or subnanometer size (1). High-resolution x-ray structures, protein sequencing, targeted mutations, and biophysical characterizations have provided new insight on the link between nanochannel protein architecture, transport rates, selectivity, and gating properties. Interestingly, these studies have shown that membrane nanochannels share several common features. For example, aquaporins (2, 3), proton channels (4, 5), and ion channels (6–11) all have relatively narrow and hydrophobic pore regions. By contrast, the selectivity filter regions of membrane ion channels are enriched with charged residues.
Despite the enormous progress made in recent decades, the complex macromolecular nature of these biological machines still complicates our understanding of the underlying mechanisms responsible for fast mass transport, selectivity, gating, and the functional role of hydrophobic pore lining and charged functionalities. Thus, it is important to create simplified, biomimetic nanochannels that could help to clarify the physics of ion permeation at the nanoscale, as well as create the next generation of membranes that employ efficient molecular transport for applications ranging from water purification to separations of biomolecules. Recent theoretical and experimental works have proposed carbon nanotubes (CNTs) as ideal candidates for such simplified models of biological channels. The graphitic walls of CNTs form hydrophobic pores with diameters close to those of biological channels. Molecular dynamics and theoretical studies have shown single-file transport for water along the nanotube axis (12–15) that is highly reminiscent of the water wires observed in aquaporins (2, 3). Predicted (13, 15) and experimentally measured (16, 17) water transport rates through CNTs are extremely large and comparable to measured values for aquaporins. MD simulations have revealed the importance of water ordering near the smooth hydrophobic walls to facilitate enhanced, frictionless water transport (52). In addition, the chemical inertness of the CNT sidewalls facilitates specific functionalization of the CNT pore entrance with different functionalities. This specificity provides an opportunity to create an artificial “selectivity filter” that could impart gating properties to a CNT (18–23).
We have recently demonstrated a model nanofluidic platform consisting of sub-2-nm CNT membranes fabricated by conformal deposition of silicon nitride on densely packed, vertically aligned CNT forests (Fig. 1 a–c) (16). The etching processes, used to expose and selectively uncap the CNTs, introduce hydroxyl (OH), carbonyl (C O), and carboxylic (COOH) functional groups at the nanotube entrance (24, 25). In particular, ionization of these carboxylic groups provides a ring of negative charges at the pore entrance that could affect the ion transport through the nanotube pore. In this study, we use nanofiltration experiments to quantify ion exclusion in the sub-2-nm CNT pores, and we investigate the fundamental mechanisms governing ion transport and ion exclusion in this system. Charged nanochannels can use both steric hindrance and electrostatic repulsion to achieve ion rejection (26–28). To understand the relative importance of these rejection mechanisms, we investigate ion exclusion and selectivity as a function of solution concentration, pH, ion valence, and ion size. Our measurements provide a strong indication that ion rejection in nanopores of this size is mostly governed by the electrostatic effects and demonstrate that Donnan's membrane equilibrium model (29, 30) accounts for most of the experimentally observed transport selectivities. Although it is not clear whether continuum models can be rigorously applied at the sub-2-nm scale relevant for this study, they provide an insight into the nature of the ion transport process.
O), and carboxylic (COOH) functional groups at the nanotube entrance (24, 25). In particular, ionization of these carboxylic groups provides a ring of negative charges at the pore entrance that could affect the ion transport through the nanotube pore. In this study, we use nanofiltration experiments to quantify ion exclusion in the sub-2-nm CNT pores, and we investigate the fundamental mechanisms governing ion transport and ion exclusion in this system. Charged nanochannels can use both steric hindrance and electrostatic repulsion to achieve ion rejection (26–28). To understand the relative importance of these rejection mechanisms, we investigate ion exclusion and selectivity as a function of solution concentration, pH, ion valence, and ion size. Our measurements provide a strong indication that ion rejection in nanopores of this size is mostly governed by the electrostatic effects and demonstrate that Donnan's membrane equilibrium model (29, 30) accounts for most of the experimentally observed transport selectivities. Although it is not clear whether continuum models can be rigorously applied at the sub-2-nm scale relevant for this study, they provide an insight into the nature of the ion transport process.
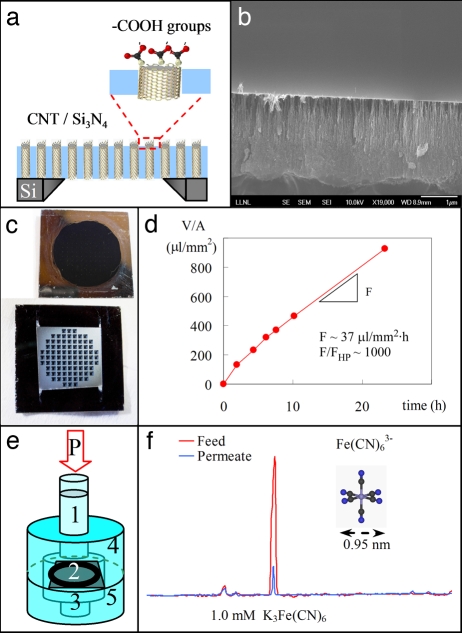
Fig. 1.
CNT/silicon nitride membrane platform for ultrafast nanofiltration of electrolytes. (a) Cross-section schematic of a CNT membrane representing the silicon support chip, the aligned DWNTs, the filling silicon nitride matrix, and the CNT tips functionalized with carboxylic groups. (b) Cross-section SEM image of the CNT/silicon nitride composite showing the gap-free coating of silicon nitride. (c) Photographs of the membrane sides exposed to the feed (Upper) and to the permeate (Lower). (d) Time variation of permeate volume per unit area of freestanding membrane during the filtration of 0.6 mM K3Fe(CN)6 solution. The resulting permeation flux, F, is ≈1,000 larger than the calculated value with the Hagen–Poiseuille equation, FHP. (e) Schematic of the nanofiltration cell showing the column of feed solution (1) pressurized at P = 0.69 bar, the CNT membrane (2), the permeate solution (3), and feed (4) and permeate (5) chambers. (f) Capillary electrophoresis chromatogram for feed (red) and permeate (blue) showing a 91% exclusion of the ferricyanide anion after nanofiltration of a 1.0 mM K3Fe(CN)6 solution.
Results and Discussion
To quantify ion rejection in CNT membranes, we use pressure-driven filtration of electrolyte solutions (Fig. 1e) followed by capillary electrophoresis (CE) analysis of the ion concentration in the permeate and feed solutions (Fig. 1f). Several observations emerge from these experiments. First, CNT membranes maintain the extraordinarily high rates of water flow reported in the previous study (Fig. 1d) (16). Filtering the ionic solutions through the membrane for extended periods of time does not result in the membrane's clogging. Second, CE measurements indicate that CNT membranes reproducibly [see supporting information (SI) Text and Fig. S1] exclude a large portion of the ionic species present in the feed solution. For example, passing of 1.0 mM potassium ferricyanide (K3FeCN6) solution under a 0.69-bar pressure differential across the membrane results in the exclusion of ≈91% of the anions and 79% of the cations. For a 1.0 mM potassium chloride (KCl) solution under 0.69 bar, CNT membranes exhibit smaller, yet still significant, rejection of Cl− (45%) and K+ (37%). These rejection ratios are comparable with the rejection ratios exhibited by a tight nanofiltration membrane (Filmtec NF90) tested under the same conditions (unpublished data). Note that our DWNT membranes have not been optimized for desalination yet, and that, remarkably, they provide an order of magnitude higher flux than the commercial nanofiltration membrane Filmtec NF90.
Modulation of the Electrostatic Field at the CNT Mouth by Solution pH.
The size of the CNT membrane pores is 1.3–2.5 times larger than the solvated radii of the ions used in our studies (Table 1). For these solute-to-pore size ratios, a sieving effect due to steric hindrance or hydrodynamic interactions with the pore wall may contribute to the observed ion rejection (31, 32). It is also likely that the rejection mechanism involves charge repulsion due to the interaction of the ions with the ionized carboxylic groups at the CNT mouth (24, 25). To test the importance of the electrostatic interaction, we measure the exclusion characteristics of the CNT membrane at two different solution pH values, one above the pKa of the COOH group on the surface (pKa = 5.5) (33) [and, also, on a CNT tip, pKa = 4.5 (34, 35)] and one below it. For these experiments we choose to use a 0.5 mM pyrenetetrasulfonic acid tetrasodium salt solution (Na4PTS) because the large PTS4− ion remains ionized over a wide range of solution pH values (36). Also, the selected low solution concentration minimizes possible screening of electrostatic interactions (see next section). As the solution pH changes from a high to a low value, the COO− groups become protonated and neutral, which should result in a sharp drop in the membrane rejection ratio. Indeed, at pH 7.2, PTS4− absorption in the permeated solution is nearly undetectable (Fig. 2a), indicating an almost complete exclusion (96% of anions; Fig. 2b). However, at pH 3.8, the rejection ratio drops sharply to only 60% (Fig. 2b). These results support a major role of electrostatic interactions in ion rejection.
Table 1.
Studied ionic species: valence z, hydrated radius rh, Stokes radius rs, and bulk diffusivity D∞
| Ion | z | rh, nm | rs, nm | D∞, 10−5 cm2/s |
|---|---|---|---|---|
| Fe(CN)63− | −3 | 0.475 | 0.273 | 0.896 |
| SO42− | −2 | 0.379 | 0.230 | 1.065 |
| Cl− | −1 | 0.332 | 0.121 | 2.032 |
| K+ | 1 | 0.331 | 0.125 | 1.957 |
| Ca2+ | 2 | 0.412 | 0.310 | 0.791 |
| Ru(bipy)32+ | 2 | 0.590 | 0.475 | 0.516 |
Fig. 2.
Effect of pH on measured rejection for a 0.5 mM Na4PTS solution. (a) UV spectra for feed (red) and permeate at pH 3.8 (blue) and pH 7.2 (green). (b) Anion (red) and cation (yellow) rejection at pH 3.8 and pH 7.2.
Ion Rejection and Electrostatic Screening at the CNT Mouth.
If electrostatic interactions at the nanotube mouth play a role in ion rejection, then the rejection properties of the membrane should be highly sensitive to the degree of electrostatic screening and, thus, to solution ionic strength. Indeed, we observe that variations in the electrolyte concentration of the solution produce large modulations of the membrane rejection ratio (Fig. 3 a and b). For K3Fe(CN)6 filtration, anion rejection is almost complete and independent of the solution ionic strength as long as the Debye length, λD,** is larger than the CNT diameter, dCNT (Fig. 3). However, when λD drops down close to dCNT, Fe(CN)63− exclusion rapidly decays to a value as low as a few percent. K+ rejection shows an identical trend, although it is somewhat (≈10%) lower than Fe(CN)63− rejection at low ionic strength, a difference that disappears with increasing salt concentration. Anion and cation rejections for KCl mirror the trends observed for K3Fe(CN)6 with the exception that the maximum measured rejection was ≈54% for Cl− and 41% for K+. Notably, KCl rejection decays less sharply with decreasing λD. Similar to the trend observed in the K3Fe(CN)6 rejection experiments, percent anion exclusion is slightly higher than percent cation exclusion (see SI Text for a possible explanation of this small difference).
Fig. 3.
Dependence of K3Fe(CN)6 (circles) and KCl (diamonds) rejections on solution concentration (a) and Debye length (b). Filled markers correspond to anions, and empty markers correspond to cations. The dashed black vertical line in b marks the average CNT diameter. Dashed green and orange lines show the rejection coefficients calculated using Donnan membrane equilibrium theory (Eq. 1) for a 1:3 and a 1:1 electrolyte, respectively. To illustrate the trends predicted by the Donnan theory, the membrane charge density is set equal to 3.0 mM.
We can rationalize these trends if we consider an exclusion mechanism that accounts for the effect of the Donnan membrane equilibrium. The Donnan model provides a well known classic description of the electrochemical equilibrium that is established when an ionic solution contacts a charged membrane. Because electrostatic forces with the fixed charges on the membrane counteract the tendency of the co-ions (ions having the same charge sign of the pore charges) to move in the direction of their concentration gradient, charged species distribute unequally between membrane and solution phase. This results in the membrane's being enriched with counterions and depleted of co-ions. As a consequence, a potential difference is established at the solution/membrane interphase (Donnan potential). When a pressure gradient is applied in a filtration experiment, the Donnan potential tends to exclude co-ions from the membrane. Because of the electroneutrality requirement, which arises from the energetic cost of charge separation, counterions have to be rejected as well. Donnan theory provides the following expression for the rejection coefficient, R, of ideal point-charge ions permeating through a charged membrane (26):
 |
where ci and cim are the concentrations of co-ions in the solution and in the membrane phase respectively, cxm is the membrane charge concentration, and subscripts i and j indicate co-ions and counterions, respectively. Eq. 1 indeed provides an ion-exclusion dependence on the Debye length that closely approximates the measured trend.††Eq. 1 also predicts that the rejection coefficient decreases faster by decreasing λD for a 1:3 salt (such as K3FeCN6) than for a 1:1 salt (such as KCl), which is exactly what the experimental data show (Fig. 3b). The decay of rejection with increasing salt concentration can be explained by the simple reasoning that follows. For a charged pore with diameter greater than the permeating ion, we expect significant exclusion of co-ions when the range of ion electrostatic interaction (λD) with the pore charges is much larger than the pore size, dCNT. With increasing salt concentration, as λD becomes comparable to dCNT, a rejection coefficient based on electrostatic interaction quickly decreases because the electrostatic potential decays rapidly with 1/λD away from a charged wall (37).‡‡
Ion Valence and Ion Exclusion.
One of the important consequences of the Donnan exclusion mechanism is the extreme sensitivity of the rejection ratio to the valency of the cationic (z+) and anionic (z−) species present in solution. Indeed, Eq. 1 predicts that the rejection should increase rapidly with the increase of the ratio of z−/z+. This is a consequence of the fact that, in this theory, the ion rejection exhibited by the membrane is due to the equilibrium partitioning of ions between the solution and membrane phase under the constraints of electroneutrality. Electrostatic forces repel anions from the negatively charged CNT tips while attracting cations. The electroneutrality condition prevents an independent migration of anions and cations. Thus, the overall rejection is determined by a balance between two opposite electrostatic forces: the larger the anion valence relative to the cation valence, the stronger the net repulsive force and, therefore, the salt rejection. On the contrary, a larger cation valence screens more effectively the carboxylic groups on the DWNT entrance, facilitating anion permeation.
To test whether ion rejection can be described by the Donnan model, we measure the ion exclusion by the CNT membrane for a series of salts differing in ion valence at the same equivalent solution concentration: K3Fe(CN)6 (cation–anion valence, z+–z−: 1–3), K2SO4 (1–2), CaSO4 (–2), KCl (–1), CaCl2 (–1), and Ru(bipy)3·Cl2 (–1). We chose to conduct these measurements at low ionic strength (λD ≫ dCNT) to ensure that the rejection coefficient stays nearly independent of concentration and close to its maximum for a 0.69-bar pressure differential used in our measurements. Remarkably, rejection coefficients measured in these experiments (Fig. 4) show a significant increase for larger z−/z+ ratios from negligible rejection [CaCl2 and Ru(bipy)3·Cl2] to nearly complete exclusion [K3Fe(CN)6]. Note also that the rejection of the symmetric salts CaSO4 and KCl (z−/z+ = 1) is about the same (≈37%), despite the larger charge and size of both the anion and cation of CaSO4 relative to KCl. Similarly, CaCl2 and Ru(bipy)3·Cl2 (z−/z+ = 0.5) permeate almost freely through the DWNT membrane. The measured rejection for Ru(bipy)3·Cl2 is slightly lower than that of calcium chloride, which is a somewhat striking result considering the much larger size of the Ru(bipy)32+ cation.
Fig. 4.
Rejection coefficients (bars) measured for six salt solutions that have the same equivalent concentration but different ion valence. Points (filled circles) indicate rejections calculated with the Donnan theory, Eq. 1, with a membrane charge density cxm = 2.0 mM [this value was chosen to fit K3Fe(CN)6 rejection]. This density corresponds to approximately seven charged groups per nanotube (see SI Text).
A comparison of the measured ion rejection rates with the prediction of the Donnan model using a reasonable membrane charge density (see SI Text) provides a strong argument for the claim that ion rejection in CNT membranes is dominated by electrostatic interactions (Fig. 4). Moreover, a comparison of the measured rejection ratios with the predictions of the hindered transport model that describes the effects of steric hindrance on the expected ion permeability shows poor correlation (see Fig. S2). Thus, the data strongly suggest that the underlying mechanism of ion exclusion in sub-2-nm CNT membranes is indeed dominated by electrostatic interactions, and that ion size (relative to our DWNT average diameter, 1.6 nm) is much less important.
Molecular dynamics (MD) simulations of uncharged CNTs (38–41, 53) also show that pores with diameters >1 nm pose little free-energy barrier for permeation of small ionic species such as Na+ or K+ and that these ions retain their hydration shell almost entirely in pores of these diameters. On the contrary, entrance into subnanometer CNT imposes a high energy penalty because it requires losing part of the hydration shell. MD simulations for other hydrophobic nanopores used as models for biological nanochannels (42, 43) reach similar conclusions. For charged CNTs, theoretical efforts have focused on understanding ion transport through subnanometer CNT and under an external electric field. Cases of both tip-localized charges (44) and distributed charges along the pore wall (38, 44, 45) have been considered. Unfortunately, a direct comparison with our experimental data is difficult because none of these studies considered pressure-driven filtration and ion valence effects. Moreover, the diameter of the simulated CNTs is significantly smaller than our CNT diameters, making confinement effects much more important in the simulated scenario.
Because gap junction (GJ) membrane channels have pore sizes similar to those of the CNTs used in this study (1–2 nm) (1), parallels can be drawn between ion rejection mechanisms of these channels and the CNTs used here. Interestingly, small ions are believed to transport through the GJ selectivity filter with little or no loss of their hydration shell. These channels often transport preferentially negatively or positively charged species, and their ion selectivity is also believed to be primarily determined by the presence of charged residues on the GJ pores (46, 47). For example, the cation selectivity of Cx46 hemichannels (1.15-nm-wide pores) has been demonstrated to be strongly influenced by fixed negative charges located toward the extracellular end of the hemichannel. Replacement of negatively charged residues with positively charged groups imparted anion selectivity to the hemichannel (46, 47). Previous studies of GJ pores, together with the data presented in this study, stress the importance of electrostatic interactions in ion rejection mechanisms of pores in the 1- to 2-nm regime.
Conclusions
We have shown that hydrophobic, 1- to 2-nm-wide CNT pores with negatively charged functionalities at their entrance exhibit significant ion rejection when aqueous electrolyte solutions pass through the pore. The observed sensitivity of the rejection to the solution pH and electrostatic screening length suggests that electrostatic interactions dominate over steric effects in governing ion rejection. The observed trends are in agreement with Donnan membrane equilibrium theory. Our conclusions are consistent with molecular dynamics studies for ion permeation in uncharged pores, as well as with experimental work on biological ion channels of similar pore sizes, such as gap junctions.
Biological pore channels share a number of structural and functional features with CNTs that make CNT nanofluidic platforms ideal candidates for the realization of a robust, biomimetic system that could exploit the fast transport, selectivity, and gating properties of biological pores. Possible applications range from controlled, nanoscale delivery of therapeutics to molecular sensing. The combination of ultrafast transport and ion exclusion demonstrated in this work could also lead the way toward efficient water desalination. Further reductions in CNT diameter (53), as well as careful control of the pore surface chemistry, may further improve the membrane performance.
Materials and Methods
Materials.
The salts used in this study were potassium ferricyanide [K3Fe(CN)6, 99+% purity; Aldrich], potassium chloride (KCl, 99.999%; Aldrich), potassium sulfate (K2SO4, 99%; Sigma), calcium sulfate dihydrate (CaSO4, 98%; Sigma), calcium chloride (CaCl2, 99.5%; EM Science), Tris(2,2′-bipyridyl)dichlororuthenium hexahydrate [Ru(bipy)3·Cl2; Fluka], and 1,3,6,8-pyrenetetrasulfonic acid tetrasodium salt (PTSNa4; Invitrogen). 4-Methylbenzylamine (97% purity) and α-hydroxyisobutyric acid (α-HIBA) were purchased from Sigma–Aldrich. All salt solutions and buffers were prepared using 18 MΩ water generated by a Milli-Q laboratory water purification system (Millipore) and subsequently filtered through a 0.1-μm PVDF filter (Millipore).
Membrane Fabrication.
Silicon nitride/CNT composite membranes were fabricated according to the previously reported method (16). Briefly, a dense, vertically aligned array of double-walled CNTs (DWNT) with sub-2-nm diameters was grown by catalytic chemical vapor deposition (CVD) on the surface of a silicon chip, using ethylene as the carbon source and Fe/Mo as the catalyst. Conformal encapsulation of the nanotubes by low-pressure silicon nitride deposition produced a gap-free matrix that filled the volume between DWNTs. Excess silicon nitride on both sides of the membrane and the catalyst particles were removed by argon ion milling. Reactive ion etching in an oxygen-containing plasma further exposed and opened the CNTs. The final result was a silicon nitride membrane with DWNT pores that span the entire membrane thickness and have carboxylic functional groups at their tips (24, 25). The free-standing membrane area was ≈0.175 mm2 with a DWNT density of ≈2.5 × 1011 cm−2 (16).
Nanofiltration Experiments.
A schematic of the filtration cell is shown in Fig. 1e. A 2 × 2-cm CNT membrane sandwiched between two O-rings divided the cell in two chambers. The top chamber (feed) was filled with ≈2 ml of salt solution, and the bottom chamber (permeate) was sealed with a small vial containing 1 ml of distilled water, the function of which was to minimize errors in the measured rejection by limiting permeate evaporation before the analysis of ion concentration. The feed solution was pressurized at 0.69 bar with a controlled nitrogen gas line, whereas the permeate was at atmospheric pressure. The permeate flow rate was measured as height variation of the column of salt solution in the top chamber with respect to time. When 100–150 μl of solution had permeated through the CNT membrane, the nanofiltration experiment was stopped, and solution samples from both feed and permeate were collected for subsequent analysis by either capillary electrophoresis or UV-vis spectroscopy. Samples that are not immediately analyzed were stored at 4°C in sealed vials to prevent evaporation. For testing Donnan prediction about the rejection dependence on ion valence, we used salt solutions with the same equivalent concentration: salt content was 0.5 mM for all solutions except KCl (1.0 mM) and K3Fe(CN)6 (0.3 mM).
Capillary Electrophoresis Analysis.
A Hewlett–Packard 3D CE capillary electrophoresis system (Agilent Technologies) was used to determine both the anion and cation concentration. Fused silica capillaries with 50-μm internal diameters and 40-cm lengths from injection point to detection window were purchased from Agilent Technologies. Samples were introduced into the capillary by a 5-s hydrodynamic injection at 50 mbar. Nonabsorbing ions were detected by the indirect UV method. For anion analysis, the running buffer was Agilent inorganic anion buffer (pH 7.7) containing 1,2,4,5-benzenetetracarboxylic acid as background electrolyte, the applied voltage was −25 kV, and the detection wavelength was 210 nm. For cation analysis, we used either IonPhor cation DDP buffer (pH 4.5) (Dionex) or UV Cat-1 buffer (48, 49) prepared in our laboratory [5 mM 4-methylbenzylamine, 6.5 mM α-hydroxyisobutyric acid (pH 4.3)]. The detection wavelengths were 225 and 214 nm for IonPhor and UV Cat-1 buffers, respectively, and the applied voltage was 30 kV. A direct detection method was used to measure Ru(bipy)32+ concentration because the cation strongly absorbs at 286 and 452 nm. Measurements for feed and permeate concentration (from peak area) were repeated at least three times and typically agreed within 2–3%. Average values were used for rejection calculations.
Experiments Testing Rejection Sensitivity to Solution pH.
Na4PTS rejection was measured at two different pHs, 7.2 (no pH adjustment) and 3.8. A few drops of 0.1 M HCl were used to reduce the pH of a 0.5 mM Na4PTS solution at the desired level while maintaining nearly constant ionic strength and osmotic pressure. The ionic strength, Debye length, and osmotic pressure were 5.0 mM, 4.34 nm, and 0.062 bar, respectively, for the experiment at neutral pH, and 5.16 mM, 4.28 nm, and 0.070 bar, respectively, for the experiment at acidic pH. Thus, the added hydrochloric acid for pH adjustment had minor impact on ionic strength, osmotic pressure, and Debye length.
The full PTS4− UV-spectrum was obtained with a Lambda 25 UV-vis spectrometer (PerkinElmer) after a 1:20 dilution with 18 MΩ water. The PTS4− concentration was measured at 244, 283, and 375 nm. Measured anion rejection coefficients were independent of the chosen wavelength. The Na+ concentration was obtained by capillary electrophoresis as explained above.
Acknowledgments.
We thank Gregory L. Klunder for advice regarding the capillary electrophoresis analysis and Matthew D. Hamtak for help in the experimental work. This work was partially supported by the Defense Advanced Research Planning Agency Defense Sciences Office and Lawrence Livermore National Laboratory. Lawrence Livermore National Laboratory is operated by Lawrence Livermore National Security, LLC, for the U.S. Department of Energy, National Nuclear Security Administration under Contract DE-AC52-07NA27344. C.P.G. and O.B. were partially supported by National Science Foundation NER Grant 0608964. A.N., C.P.G., and O.B. acknowledge support through National Science Foundation NIRT Grant CBET-0709090. O.B. also acknowledges support from the Center for Biophotonics, a National Science Foundation Science and Technology Center managed by the University of California, Davis, under Cooperative Agreement PHY 0120999.
Footnotes
This paper results from the Arthur M. Sackler Colloquium of the National Academy of Sciences, “Nanomaterials in Biology and Medicine: Promises and Perils,” held April 10–11, 2007, at the National Academy of Sciences in Washington, DC. The complete program and audio files of most presentations are available on the NAS web site at www.nasonline.org/nanoprobes.
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0710437105/DC1.
The Debye length is defined as 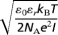 , where ε0 and εr are the vacuum and relative permittivity, respectively, kB is the Boltzmann constant, T is the absolute temperature, e is the elementary charge, NA is the Avogadro number, and I is the ionic strength of the solution. Because our feeds are single salt solutions, I is proportional to the feed concentration, c0, and λD ∝ c0−1/2.
, where ε0 and εr are the vacuum and relative permittivity, respectively, kB is the Boltzmann constant, T is the absolute temperature, e is the elementary charge, NA is the Avogadro number, and I is the ionic strength of the solution. Because our feeds are single salt solutions, I is proportional to the feed concentration, c0, and λD ∝ c0−1/2.
The explicit expression of the rejection coefficient dependence on λD can be easily obtained by substituting ci with α/λD2 in Eq. 1, where α is defined as  .
.
The observed concentration dependence of rejection coefficients alone does not provide a definitive proof that the charges on the CNT entrance are responsible for the reduced ion rejection at larger concentrations because the reduction of ion rejection may simply be a result of the variation of the driving forces for transport rather than a consequence of the reduced range of electrostatic interaction. Indeed, for both neutral and charged solutes at constant applied pressure, an increase in feed concentration reduces water permeation and increases the ion permeation rate. The effective driving force for water permeation is reduced because of the raising osmotic pressure, whereas the effective driving force for ion permeation is increased because of increased concentration gradient. However, a combination of the concentration dependence and the observed sensitivity of the rejection properties to the change of solution pH does provide a strong indication that electrostatic forces are one of dominant contributors to the ion rejection.
References
- 1.Hille B. Ion Channel of Excitable Membranes. Sunderland, MA: Sinauer; 2001. [Google Scholar]
- 2.Sui HX, Han B-G, Lee JK, Walian P, Jap BK. Structural basis of water-specific transport through the AQP1 water channel. Nature. 2001;414:872–878. doi: 10.1038/414872a. [DOI] [PubMed] [Google Scholar]
- 3.Murata K, et al. Structural determinants of water permeation through aquaporin-1. Nature. 2000;407:599–605. doi: 10.1038/35036519. [DOI] [PubMed] [Google Scholar]
- 4.Wikstrom M. Proton translocation by bacteriorhodopsin and heme-copper oxidases. Curr Opin Struct Biol. 1998;8:480–488. doi: 10.1016/s0959-440x(98)80127-9. [DOI] [PubMed] [Google Scholar]
- 5.Wikstrom M, Verkhovsky MI, Hummer G. Water-gated mechanism of proton translocation by cytochrome c oxidase. BBA Bioenergetics. 2003;1604:61–65. doi: 10.1016/s0005-2728(03)00041-0. [DOI] [PubMed] [Google Scholar]
- 6.Jiang YX, et al. Crystal structure and mechanism of a calcium-gated potassium channel. Nature. 2002;417:515–522. doi: 10.1038/417515a. [DOI] [PubMed] [Google Scholar]
- 7.Jiang YX, et al. The open pore conformation of potassium channels. Nature. 2002;417:523–526. doi: 10.1038/417523a. [DOI] [PubMed] [Google Scholar]
- 8.Bass RB, Strop P, Barclay M, Rees DC. Crystal structure of Escherichia coli MscS, a voltage-modulated and mechanosensitive channel. Science. 2002;298:1582–1587. doi: 10.1126/science.1077945. [DOI] [PubMed] [Google Scholar]
- 9.Doyle DA, et al. The structure of the potassium channel: Molecular basis of K+ conduction and selectivity. Science. 1998;280:69–77. doi: 10.1126/science.280.5360.69. [DOI] [PubMed] [Google Scholar]
- 10.Miyazawa A, Fujiyoshi Y, Unwin N. Structure and gating mechanism of the acetylcholine receptor pore. Nature. 2003;423:949–955. doi: 10.1038/nature01748. [DOI] [PubMed] [Google Scholar]
- 11.Kuo AL, et al. Crystal structure of the potassium channel KirBac1.1 in the closed state. Science. 2003;300:1922–1926. doi: 10.1126/science.1085028. [DOI] [PubMed] [Google Scholar]
- 12.Berezhkovskii A, Hummer G. Single-file transport of water molecules through a carbon nanotube. Phys Rev Lett. 2002;89:4. doi: 10.1103/PhysRevLett.89.064503. [DOI] [PubMed] [Google Scholar]
- 13.Hummer G, Rasaiah JC, Noworyta JP. Water conduction through the hydrophobic channel of a carbon nanotube. Nature. 2001;414:188–190. doi: 10.1038/35102535. [DOI] [PubMed] [Google Scholar]
- 14.Hummer G. Water, proton, and ion transport: From nanotubes to proteins. Mol Phys. 2007;105:201–207. [Google Scholar]
- 15.Kalra A, Garde S, Hummer G. Osmotic water transport through carbon nanotube membranes. Proc Natl Acad Sci USA. 2003;100:10175–10180. doi: 10.1073/pnas.1633354100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Holt JK, et al. Fast mass transport through sub-2-nanometer carbon nanotubes. Science. 2006;312:1034–1037. doi: 10.1126/science.1126298. [DOI] [PubMed] [Google Scholar]
- 17.Majumder M, Chopra N, Andrews R, Hinds BJ. Nanoscale hydrodynamics—Enhanced flow in carbon nanotubes. Nature. 2005;438:44. doi: 10.1038/43844a. [DOI] [PubMed] [Google Scholar]
- 18.Hinds BJ, et al. Aligned multiwalled carbon nanotube membranes. Science. 2004;303:62–65. doi: 10.1126/science.1092048. [DOI] [PubMed] [Google Scholar]
- 19.Majumder M, Chopra N, Hinds BJ. Effect of tip functionalization on transport through vertically oriented carbon nanotube membranes. J Am Chem Soc. 2005;127:9062–9070. doi: 10.1021/ja043013b. [DOI] [PubMed] [Google Scholar]
- 20.Majumder M, Zhan X, Andrews R, Hinds BJ. Voltage gated carbon nanotube membranes. Langmuir. 2007;23:8624–8631. doi: 10.1021/la700686k. [DOI] [PubMed] [Google Scholar]
- 21.Nednoor P, Chopra N, Gavalas V, Bachas LG, Hinds BJ. Reversible biochemical switching of ionic transport through aligned carbon nanotube membranes. Chem Mater. 2005;17:3595–3599. [Google Scholar]
- 22.Nednoor P, Gavalas VG, Chopra N, Hinds BJ, Bachas LG. Carbon nanotube based biomimetic membranes: Mimicking protein channels regulated by phosphorylation. J Mater Chem. 2007;17:1755–1757. [Google Scholar]
- 23.Chopra N, Majumder M, Hinds BJ. Bifunctional carbon nanotubes by sidewall protection. Adv Funct Mater. 2005;15:858–864. [Google Scholar]
- 24.Yang DQ, Rochette JF, Sacher E. Controlled chemical functionalization of multiwalled carbon nanotubes by kiloelectronvolt argon ion treatment and air exposure. Langmuir. 2005;21:8539–8545. doi: 10.1021/la0514922. [DOI] [PubMed] [Google Scholar]
- 25.Li PH, et al. Tailoring wettability change on aligned and patterned carbon nanotube films for selective assembly. J Phys Chem B. 2007;111:1672–1678. doi: 10.1021/jp066781t. [DOI] [PubMed] [Google Scholar]
- 26.Schaep J, Van der Bruggen B, Vandecasteele C, Wilms D. Influence of ion size and charge in nanofiltration. Sep Purif Technol. 1998;14:155–162. [Google Scholar]
- 27.Schaep J, Vandecasteele C, Mohammad AW, Bowen WR. Modelling the retention of ionic components for different nanofiltration membranes. Sep Purif Technol. 2001;22-3:169–179. [Google Scholar]
- 28.Childress AE, Elimelech M. Relating nanofiltration membrane performance to membrane charge (electrokinetic) characteristics. Environ Sci Technol. 2000;34:3710–3716. [Google Scholar]
- 29.Donnan FG. The theory of membrane equilibria. Chem Rev. 1924;1:73–90. [Google Scholar]
- 30.Donnan FG. Theory of membrane equilibria and membrane-potentials in the presence of non-dyalizing electrolytes—A contribution to physical-chemical physiology. J Membr Sci. 1995;100:45–55. [Google Scholar]
- 31.Dechadilok P, Deen WM. Hindrance factors for diffusion and convection in pores. Indian Eng Chem Res. 2006;45:6953–6959. [Google Scholar]
- 32.Deen WM. Hindered transport of large molecules in liquid-filled pores. AIChE J. 1987;33:1409–1425. [Google Scholar]
- 33.Vezenov DV, Noy A, Rozsnyai LF, Lieber CM. Force titrations and ionization state sensitive imaging of functional groups in aqueous solutions by chemical force microscopy. J Am Chem Soc. 1997;119:2006–2015. [Google Scholar]
- 34.Wong SS, Joselevich E, Woolley AT, Cheung CL, Lieber CM. Covalently functionalized nanotubes as nanometre-sized probes in chemistry and biology. Nature. 1998;394:52–55. doi: 10.1038/27873. [DOI] [PubMed] [Google Scholar]
- 35.Wong SS, Woolley AT, Joselevich E, Cheung CL, Lieber CM. Covalently-functionalized single-walled carbon nanotube probe tips for chemical force microscopy. J Am Chem Soc. 1998;120:8557–8558. [Google Scholar]
- 36.Nagai Y, Unsworth LD, Koutsopoulos S, Zhang S. Slow release of molecules in self-assembling peptide nanofiber scaffold. J Controlled Release. 2006;115:18–25. doi: 10.1016/j.jconrel.2006.06.031. [DOI] [PubMed] [Google Scholar]
- 37.Newman J, Thomas-Alyea KE. Electrochemical Systems. Hoboken, NJ: Wiley; 2004. [Google Scholar]
- 38.Park JH, Sinnott SB, Aluru NR. Ion separation using a Y-junction carbon nanotube. Nanotechnology. 2006;17:895–900. [Google Scholar]
- 39.Peter C, Hummer G. Ion transport through membrane-spanning nanopores studied by molecular dynamics simulations and continuum electrostatics calculations. Biophys J. 2005;89:2222–2234. doi: 10.1529/biophysj.105.065946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Leung K, Rempe SB, Lorenz CD. Salt permeation and exclusion in hydroxylated and functionalized silica pores. Phys Rev Lett. 2006;96:4. doi: 10.1103/PhysRevLett.96.095504. [DOI] [PubMed] [Google Scholar]
- 41.Liu HM, Murad S, Jameson CJ. Ion permeation dynamics in carbon nanotubes. J Chem Phys. 2006;125 doi: 10.1063/1.2337289. 084713. [DOI] [PubMed] [Google Scholar]
- 42.Beckstein O, Sansom MSP. The influence of geometry, surface character, and flexibility on the permeation of ions and water through biological pores. Phys Biol. 2004;1:42–52. doi: 10.1088/1478-3967/1/1/005. [DOI] [PubMed] [Google Scholar]
- 43.Beckstein O, Tai K, Sansom MSP. Not ions alone: Barriers to ion permeation in nanopores and channels. J Am Chem Soc. 2004;126:14694–14695. doi: 10.1021/ja045271e. [DOI] [PubMed] [Google Scholar]
- 44.Joseph S, Mashl RJ, Jakobsson E, Aluru NR. Electrolytic transport in modified carbon nanotubes. Nano Lett. 2003;3:1399–1403. [Google Scholar]
- 45.Sumikama T, Saito S, Ohmine I. Mechanism of ion permeation in a model channel: Free energy surface and dynamics of K+ ion transport in an anion-doped carbon nanotube. J Phys Chem B. 2006;110:20671–20677. doi: 10.1021/jp062547r. [DOI] [PubMed] [Google Scholar]
- 46.Kronengold J, Trexler EB, Bukauskas FF, Bargiello TA, Verselis VK. Single-channel SCAM identifies pore-lining residues in the first extracellular loop and first transmembrane domains of cx46 hemichannels. J Gen Physiol. 2003;122:389–405. doi: 10.1085/jgp.200308861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Trexler EB, Bukauskas FF, Kronengold J, Bargiello TA, Verselis VK. The first extracellular loop domain is a major determinant of charge selectivity in connexin46 channels. Biophys J. 2000;79:3036–3051. doi: 10.1016/S0006-3495(00)76539-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Weston A, Brown PR, Heckenberg AL, Jandik P, Jones WR. Effect of electrolyte-composition on the separation of inorganic metal-cations by capillary ion electrophoresis. J Chromatogr. 1992;602:249–256. [Google Scholar]
- 49.Weston A, Brown PR, Jandik P, Jones WR, Heckenberg AL. Factors affecting the separation of inorganic metal-cations by capillary electrophoresis. J Chromatogr. 1992;593:289–295. [Google Scholar]
- 50.Nightingale ER. Phenomenological theory of ion solvation—Effective radii of hydrated ions. J Phys Chem. 1959;63:1381–1387. [Google Scholar]
- 51.Carter DJ, Ogden MI, Rohl AL. Incorporation of cyano transition metal complexes in KCl crystals—Experimental and computational studies. Aust J Chem. 2003;56:675–678. [Google Scholar]
- 52.Joseph S, Aluru NR. Why are carbon nanotubes fast transporters of water? Nano Lett. 2008;8:452–458. doi: 10.1021/nl072385q. [DOI] [PubMed] [Google Scholar]
- 53.Corry B. Designing carbon nanotube membranes for efficient water desalination. J Phys Chem B. 2008;112:1427–1434. doi: 10.1021/jp709845u. [DOI] [PubMed] [Google Scholar]