Microscale Heat Transfer Transduced by Surface Plasmon Resonant Gold Nanoparticles

Abstract

Visible radiation at resonant frequencies is transduced to thermal energy by surface plasmons on gold nanoparticles. Temperature in ≤10-microliter aqueous suspensions of 20-nanometer gold particles irradiated by a continuous wave Ar+ ion laser at 514 nm increased to a maximum equilibrium value. This value increased in proportion to incident laser power and in proportion to nanoparticle content at low concentration. Heat input to the system by nanoparticle transduction of resonant irradiation equaled heat flux outward by conduction and radiation at thermal equilibrium. The efficiency of transducing incident resonant light to heat by microvolume suspensions of gold nanoparticles was determined by applying an energy balance to obtain a microscale heat-transfer time constant from the transient temperature profile. Measured values of transduction efficiency were increased from 3.4% to 9.9% by modulating the incident continuous wave irradiation.

1. Introduction

Microscale thermal transport in colloidal noble metal nanoparticle suspensions is important in novel heat transfer fluids,^1–3 laser-induced transformation of nanoparticle size, shape and phase,^4–6 optothermal imaging,^7–8 and targeted photothermal medical therapies⁹ such as photothermally activated drug delivery¹⁰ and photothermolysis of mammalian^11–13 and bacterial¹⁴ cells. Suspended nanoparticles irradiated at resonant frequencies dissipate heat to the matrix in a cascade of events.^15,16 Resonant irradiation induces a non-thermal electron distribution that thermalizes in ~500 femtoseconds via elastic electron-electron scattering to an equilibrium Fermi electron distribution that corresponds to a higher electron temperature.¹⁷ The Fermi distribution or ‘electron gas’. cools by electron-phonon coupling with the noble metal lattice at a timescale of 2–5 picoseconds and by phonon-phonon interactions with surrounding medium at timescales between 100–380 picoseconds. Phonon-phonon interactions dissipate heat across a particle-matrix interface to an adjacent shell of matrix medium at a rate dependent on matrix, particle size and pump power as nanoparticles return to their initial electron temperature.^6,18,19 Similar dynamics are observed in thin noble metal films.^20,21

High-power nano-, pico- and femto-second pump-probe spectroscopies that are used to excite nanoparticles and examine electron relaxation processes in noble metal nanoparticles^6,22–24 and gold-silica nanoshells²⁵ produce dynamic structural changes such as lattice vibration²⁶ as well as interrelated proximal phenomena including particle melting and solvent vaporization that depend on laser intensity and duration and particle size. High-powered pulses shorter than a relaxation time of τ_r = r_p ²/6.75α_p for spheres of radius r_p and thermal diffusivity α_p rapidly heat individual NPs⁹ which exhibit negligible conductive/convective and radiative heat loss on timescales <τ_r.²⁷ Heating thus confined to a nanoparticle (NP) subsequently superheats a thin layer of adjacent fluid. At temperatures ~85% of Tcritical, pressure due to fluid surface tension, σ, given by p_s = 2σ/r_p, is overcome and adjacent fluid vaporizes.²⁴ This creates a rapidly expanding vapor microbubble²⁸ that implodes and collapses at 1–1.5 microns.¹⁴ Solvent vaporization further insulates the rapidly heated particle, which reduces particle cooling and melts gold (Au) NPs at lattice temperatures >529K.⁶ Explosive vaporization coincides with cavitation -- strong localized pressure transients associated with irreversible fragmentation and reduced particle size^24,27,29 as well as damage to adjacent proteins^11,30–31 and cells.¹⁴ Nanoparticles may become transparent at resonant frequencies due to intense photoexcitation and ultimately vaporize.³² Nanoparticle suspensions must be replaced between successive laser shots in experiments to avoid accumulation of damage from the laser.⁶

Rather than dissipate heat using high-intensity laser pulses, we evaluated heat transfer by continuous wave irradiation of NP suspensions at fluence values which are 10⁸ to 10¹¹-fold lower. We used contact times >τ_r to heat particle and adjacent media in isolated microvolumes to temperatures that were below threshold values for explosive vaporization, melting or fragmentation. Continuous wave (cw), low-intensity, resonant irradiation of Au NP at long contact times has been used to image cells by polarization interference,⁷ to measure optothermal properties of nanorods,³³ and to inactive tumor cells with Au-shell Si-core nanoshells,¹² but microscale heat transport from NP suspensions and effects of NP concentration or laser power on temperature rise were not examined and optothermal transduction efficiencies were not determined. We monitored temperatures of aqueous suspensions of 20-nanometer Au particles <10 microliters in volume that were irradiated in a vacuum by continuous wave Ar+ ion laser at 514 nm as laser power and NP concentration were varied. We determined microscale time constants for conductive and radiative heat transfer from thermally isolated NP suspensions using the transient temperature profile. Time constants were correlated to a linearized heat transfer coefficient. This allowed determination of efficiency of NP transduction of continuous-wave, low-intensity light to bulk microvolume heat for the first time. We found that modulating the incident irradiation increased transduction efficiency ≥2.1-fold. Our linearized heat transfer model predicted equilibrium temperature increases proportional to NP concentration at low absorbance values and to applied laser power, consistent with data. These results support development of thermalfluid meso-, micro- and nano-scale systems that incorporate NPs to transduce light to heat, including miniaturized fabricated analytical and manufacturing devices. NP transducers in such systems must be capable of efficient, repeated excitation to reproducibly generate heat over multiple cycles. In particular, there has been recent interest in nanofluids -- NPs suspended in base heat transfer fluids that exhibit higher, temperature-dependent thermal conductivities^34,35 and critical heat fluxes relative to base fluids.³⁶

2. Experimental Section

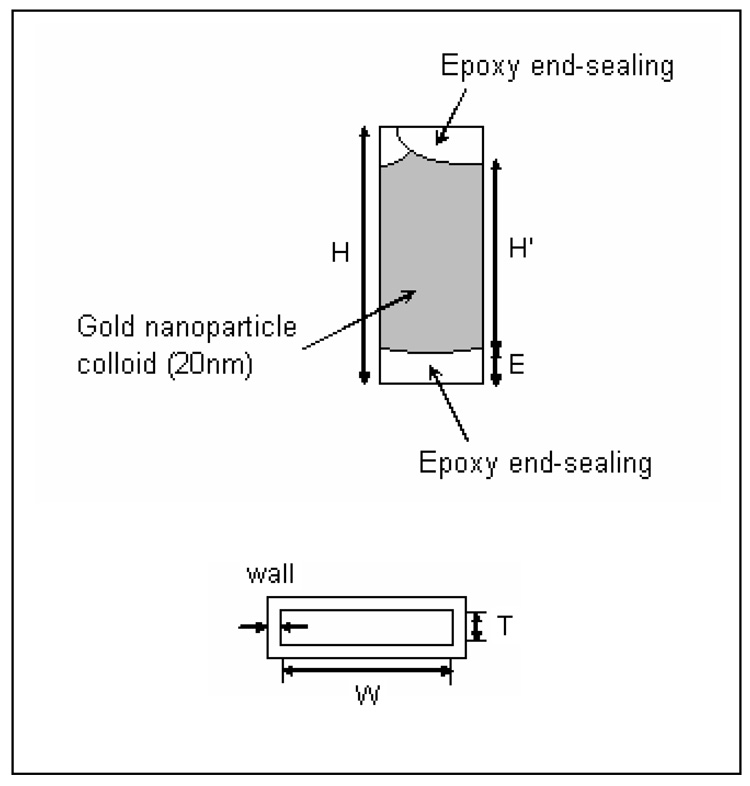
Gold colloid purchased from Sigma (G 1652, St. Louis, MO, USA) 20 nm in diameter and ~0.01% w/v HAuCl₄ (0.0046% w/v Au NP) was used. Colloid was concentrated by centrifugation at 12,000 rpm for 15–20 minutes (Marathon Model 13K/M, Fisher Scientific, Hampton, NH, USA) and resuspended in distilled, deionized (18 MΩ, Millipore Corp, Bedford, MA, USA), vacuum-degassed water. Vacuum-resistant sample cells, shown in Schematic 1, were fabricated from borosilicate glass rectangle tubing (Fiber Optic Center, New Bedford, MA, USA). Tubing had inner dimensions of 0.2 × 4.0 × 15.9 mm (thickness × width × height) with a wall thickness of 0.2 mm. Cells were cleaned with ethanol (Aaper Alcohol and Chemical Co., Shelbyville, KY, USA) prior to use. One end of the glass tubing was sealed with 5 Minute Epoxy and Hardener (Devcon, Danvers, MA, USA), to a depth of ~3.0 mm. The opposite end was partially sealed to allow insertion of Au colloid solution through a small opening with a pipette after drying the epoxy. Injected colloid completely displaced air in the cell and the opening was sealed with epoxy.

Scheme 1.

A schematic representation of the gold NP suspension sample cell and its cross section. The cell has the following dimensions: thickness (T) of 0.2 millimeters (mm); width (W) of 4.0 mm; wall thickness (wall) of 0.2 mm; and total height (H) of 15.9 millimeters that included two 3-millimeter lengths of epoxy end seal (E) and 9.9 millimeters (H’) of colloid sample.

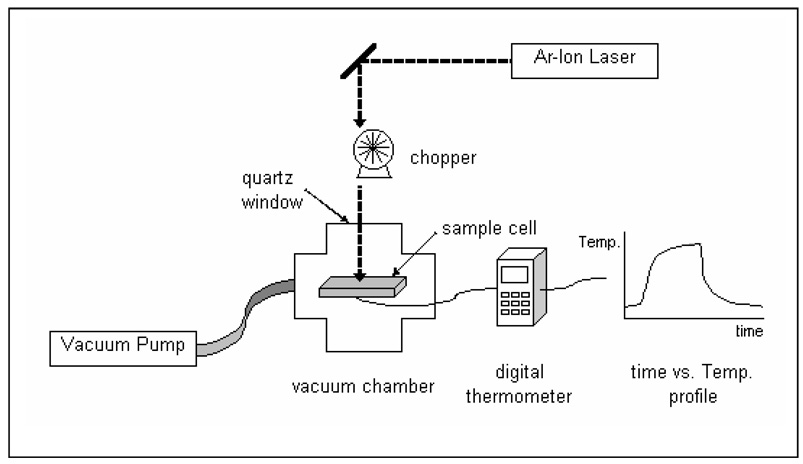
Schematic 2 shows the experimental layout. A cw Ar-Ion laser (514 nm and 488 nm, BeamLok™ 2060&2080, Spectra-physics, Mountain View, CA, USA) was used to irradiate the sample through a quartz window in the vacuum chamber. A sample cell was suspended inside the vacuum chamber by a K-type chrom-alumel thermocouple (0.003 inches, Omega, Stamford, CT, USA) connected to a digital thermometer (Omega HH509R, Stamford, CT, USA). Pressure in the chamber was reduced to <1 Torr to eliminate convective heat transfer from the surface of the sample cell. A mechanical chopper (HMS model 220) with 60 slots and frequency control from 0 to 6000 rpm was used to modulate irradiation in some experiments. UV-vis absorbance spectra of samples were obtained using a Perkin-Elmer spectrophotometer (Lambda-9, Wellesley, MA, USA). Data presented graphically are average values ± one standard deviation (error bars).

Scheme 2.

Experimental setup used to measure temperature changes in irradiated Au NP suspensions. An Ar⁺ ion laser irradiates the sample cell inside a vacuum chamber evacuated to <1 Torr. Laser may be mechanically chopped. A thermocouple attached to the cell measures temperature. Data is collected via a digital thermometer using a computer.

3. Results and Discussion

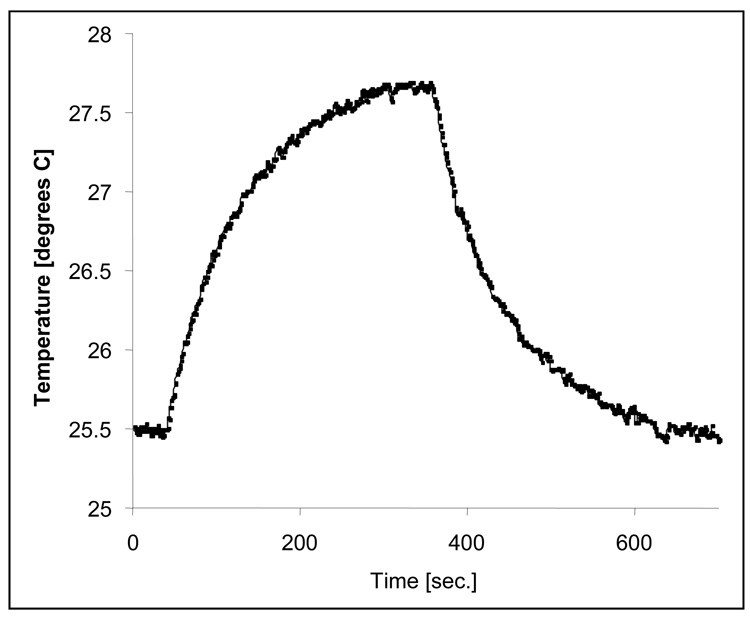
A typical plot of temperature versus time obtained from cw irradiation of an optically transparent microliter sample cell filled with NP suspension and thermally isolated inside a vacuum chamber is shown in Figure 1. The sample was a rectangular borosilicate glass cell containing a volume of 7.9 microliters consisting of 0.092 g of 20-nm Au NPs per 100 milliliters of distilled, deionized, degassed water. The cell was epoxy sealed and suspended in a vacuum chamber by a 2”-long, 0.003”-OD chrom-alumel thermocouple (TC). The sample thermally equilibrated with the surrounding vacuum chamber before exposure to the laser during a minimum delay period of 30 seconds. Resonant irradiation at a wavelength of 514 nm at a nominal power of 0.17 W in a spot size of 3 mm diameter (fluence of 2.4 W/cm²) was applied using a cw Ar⁺ ion laser. The laser beam was mechanically chopped at a rate of 6000 rpm, reducing the incident power from a nominal value of 170 mW to an effective value of 85 mW. Temperature increased in this experiment from an ambient value of T_amb=25.5°C to a maximum equilibrium value of T_max=27.7°C after 320 seconds of exposure. After a short equilibration period at T_max, irradiation by the cw laser was discontinued and the sample was allowed to cool, returning to a value of T_amb=25.5°C in equilibrium with its surroundings. Temperature data were fit to a linearized energy balance derived from a description of microscale thermal dynamics in the NP suspension to determine the efficiency of transducing light to heat in bulk suspensions of Au NPs.

Figure 1.

Temperature in a sample cell containing a 7.9-microliter suspension of Au NPs at 920 g Au/m³ increases from an ambient value of 25.5°C to an equilibrium value of 27.7°C during a 320-second continuous-irradiation period by a 0.17-watt beam at 514 nanometers.Temperature returns to its ambient value at thermal equilibrium with the surroundings after discontinuing irradiation.

3.1 Thermal dynamics in irradiated NP suspensions

NP temperature, T_p, during excitation increases with NP diameter from 5 to 50 nm in proportion to pump laser flux (intensity, I_o / spot size, σ), relative energy absorption calculated from sample absorbance (A) by Beers Law and inversely proportional to sample heat capacity, C_p, Au concentration, [Au], and cell pathlength, l:

$$\mathrm{\Delta }T\propto \frac{I_o(1-{10}^{-A})}{\sigma [Au]C_{p}l}$$ (1)

High-power regeneratively amplified Ti:sapphire lasing yielded ΔT from 40 to 160 K in 15-nm Au NP with a single 120 fs pulse²³; whereas low-intensity cw irradiation of Au NP yielded ΔT from 15°C⁷ to about 30°C in times ranging from 5 seconds³³ to 6 minutes.¹² Resonant energy absorbed by NP electrons dissipates in pico- to nanoseconds across the particle-matrix interface to a surrounding adjacent medium layer at temperature T_s, at a rate dependent on particle-size, pump-power and environmental conditions^6,18,23 according to:

$$\frac{T_p(t)-T_s}{T_i-T_s}=\text{exp}\left\{-{\left(t/{\tau }_d\right)}^{\beta }\right\}$$ (2)

In eq 2, T_i is initial particle temperature, τ_d is a characteristic time scale for temperature dissipation, and β is a phenomenological constant. For negligible heat-transfer resistance across the particle-matrix interface, τ_d, is estimated by equating heat capacity of radius r_p particles (4/3πr_p³C_pρ_p) to heat capacity of adjoining thermal diffusion layer (4πr_p²l_dC_fρ_f) of thickness l_d=(α_fτ_d)^1/2, where α_f is fluid thermal diffusivity, α_f≡k_f/ρ_fC_f:¹⁹

$${\tau }_d=\frac{r_p^2{C}_p^2{\rho }_p^2}{9C_f{\rho }_f{K}_f}$$ (3)

Hu and Hartland²³ observed β=0.6 for 2r_p= 5 to 15 nm and β=0.7 for 2r_p = 26 to 50 nm particles, respectively, and reported τ_d=0.64 picoseconds nm⁻² × r_p ² for r_p in nm at high pump power, consistent with quadratic dependence of cooling time on particle radius given by eq 3. In the limit of negligible interface resistance, estimated temperature dissipation rate for the system shown in Figure 3 is between 27 picoseconds (eq. 3) and 64 picoseconds.

Figure 3.

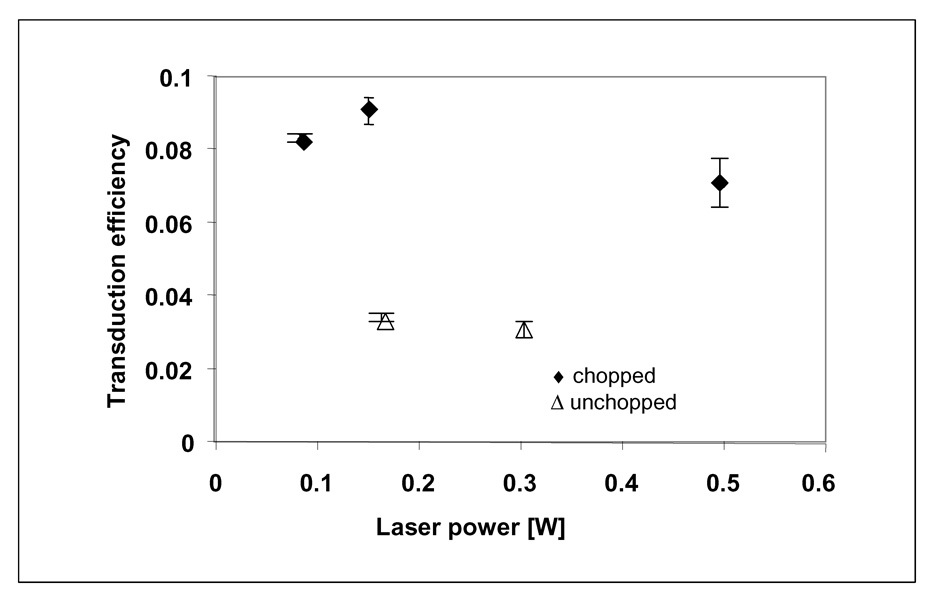
Efficiency of transducing resonant irradiation to heat in a 7.9-microliter aqueous sample of suspended 20-nanometer gold NPs with (◆) and without (Δ) mechanically chopping the incident radiation at a frequency of 6000 cycles per second.

When interface thermal conductance, G, which has units of Wm⁻²K⁻¹, is much slower than conductance in the adjacent medium, i.e. G<<3C_f ρ_fk_f/(r_pC_pρ_p), β reduces to unity and the controlling interface thermal conductance replaces conductance by the adjacent medium in eq 3:^6,19

$${\tau }_d=\frac{r_p{\rho }_p{C}_p}{3G}$$ (4)

Wilson et al.¹⁹ reported that dodecanethiol-terminated Au NP with 2r_p =3–5 nm exhibited G~20 MW m⁻²K⁻¹, which delayed energy exchange between surface Au atoms and surrounding molecules. Plech et al.⁶ obtained G=105±15 MW m⁻²K⁻¹ for an aqueous sol of Au NP excited at low power (14.7 mW or 529 K) by fitting decay of lattice expansion measured by time-resolved x-ray scattering T_p(t). This was consistent with nanosecond-scale values of τ_d ∝ r_p ^1.46 which were intermediate between adjacent medium-limited and interface-limited conduction. Fragmentation, melting, and gas-layer formation at NP surfaces induced by high-power irradiation were postulated to decrease heat transfer rates. For slow interface conductance in the absence of these effects, estimated temperature dissipation rate for our system using G=105±15 MW m⁻²K⁻¹ is 79 picoseconds.

3.2 Energy balance on irradiated sample

A continuum energy balance on the system in Figure 1 consisting of an aqueous Au NP suspension within a borosilicate glass sample cell inside a vacuum chamber that is irradiated by a laser gives

$${\displaystyle \sum _i{m}_i{C}_{p,i}\frac{dT}{dt}}={\displaystyle \sum _j{Q}_j}$$ (5)

where the i terms m_iC_p,i are products of mass and heat capacity of system components (AuNP suspension, sample cell and epoxy), T is aggregate system temperature and t is time. The j energy terms Q_j include laser-induced energy source term, Q_I and Q_o as well as conduction, Q_cond, and radiation, Q_rad, energy outputs. Eq 5 is valid when thermal equilibrium within the system is attained much faster than energy exchange with surroundings. This is confirmed later by showing a time constant for internal thermal equilibration is substantially smaller than the equilibrium time constant for heat transfer with the surroundings that will be obtained from eq 5.

Laser-induced source term Q_I represents heat dissipated by electron-phonon relaxation of plasmons on the Au surface induced by laser irradiation of Au NP at resonant wavelength λ:

$$Q_I=I\left(1-{10}^{-A_{\lambda }}\right){\eta }_T$$ (6)

where I is incident laser power, η_T represents the efficiency of transducing incident resonant absorbance to thermal energy via plasmons, and A_λ is absorbance of NP in the borosilicate glass sample cell at wavelength λ given by Beer-Lambert’s Law, A_λ=ε_λL_c, where ε_λ is wavelength-dependent molar absorptivity, L is pathlength and c is molar concentration. Source term Q_o represents heat dissipated from light absorbed by the quartz sample cell itself. It was measured independently to be Q_o=(5.4×10⁻⁴)I in J s⁻¹ using borosilicate glass cell containing aqueous samples without NP.

Conduction energy outputs Q_cond,air and Q_cond,TC correspond to heat conduction away from the system surface by air and thermocouple (TC) wires, respectively, given in general for a single dimension by:

$$Q_{\mathit{\text{cond}}}=\frac{kA}{L}(T-T_{\mathit{\text{amb}}})$$ (7)

where k is thermal conductivity, A is area cross-section perpendicular to conduction, L is the conduction length between system and surroundings, and T_amb is the ambient temperature of the surroundings. Radiation energy output term Q_rad corresponds to energy radiation from the surface:³⁶

$$Q_{\mathit{\text{rad}}}=A\epsilon \sigma (T^4-T_{\mathit{\text{amb}}}^4)$$ (8)

where ε is emissivity, σ is Stefan-Boltzman constant, and A is surface area for radiative heat transfer. The transduction efficiency, η_T, may be obtained by numerically fitting eq 5–eq 8 to the temperature distribution in Figure 1. However, for temperature increases ≤11K examined in this study, the ratio Q_rad/(T-T_amb) factored out from eq 8 remains constant to within 2.8%. This fact allows a convenient linearization of the energy balance using a heat transfer model with a relatively constant coefficient of Aεσ(T+T_amb)(T²+T²_amb) for the radiation term. The heat transfer model permits straightforward analytical determination of η_T.

3.3 Heat transfer equation for sample cell and contents

External heat flux in the system, Q_ext, is nearly proportional to linear thermal driving force, with a heat transfer coefficient, h, as the proportionality constant:

$$Q_{\mathit{\text{ext}}}=hA(T-T_{\mathit{\text{amb}}})$$ (9)

In this case the energy balance in Eq 5 simplifies to:

$${\displaystyle \sum _i{m}_i{C}_{p,i}\frac{dT}{dt}=}{Q}_I+Q_o-Q_{\mathit{\text{ext}}}$$ (10)

Introducing a dimensionless driving force temperature, θ, scaled using the maximum system temperature, T_max,

$$\theta \equiv \frac{T_{\mathit{\text{amb}}}-T}{T_{\mathit{\text{amb}}}-T_{\text{max}}}$$ (11)

and a sample system time constant τ_s

$${\tau }_s\equiv \frac{{\displaystyle \sum _i{m}_i{C}_{p,i}}}{hA}$$ (12)

which are substituted into eq 10 and rearranged to yield

$$\frac{d\theta }{dt}=\frac{1}{{\tau }_s}\left[\frac{Q_I+Q_o}{hA(T_{\text{max}}-T_{\mathit{\text{amb}}})}-\theta \right]$$ (13)

When laser irradiation ceases, Q_I+Q_o =0 and the system cools, reducing eq 13 to

$$\frac{d\theta }{dt}=\frac{-\theta }{{\tau }_s}$$ (14)

Eq 14 may be solved using the initial condition θ = 1 at t = 0 to give

$$\theta =\text{exp}\left(\raisebox{1ex}{$-t$}\!\left/ \!\raisebox{-1ex}{${\tau }_s$}\right.\right)$$ (15)

During laser irradiation, Q_I+Q_o is finite and system temperature rises to a maximum value when external heat flux given by eq 9 equals heat input via laser transduction given by eq 6:

$$Q_I+Q_o=hA(T_{\text{max}}-T_{\mathit{\text{amb}}})$$ (16)

Substituting eq 16 into eq 13 gives

$$\frac{d\theta }{dt}=\frac{1}{{\tau }_s}(1-\theta )$$ (17)

Eq 17 can be solved using the initial condition θ = 0 at t = 0 to give

$$\theta =1-\text{exp}\left(\raisebox{1ex}{$-t$}\!\left/ \!\raisebox{-1ex}{${\tau }_s$}\right.\right)$$ (18)

3.4 Determine thermal equilibrium time constant and heat transfer coefficient of the system

The linear temperature driving force approximation in eq 9–eq 13 permits system equilibration time, τ_s, and heat transfer coefficient, h, to be estimated using system parameters from cooling data (via eq 15) and/or heating data (via eq 18). Parameter values for our system were: A_rad = A_cond,cell = 164 mm²; ε = 0.8;³⁷ σ = 5.67×10⁻⁸ W/m²K⁴; L_TC = 0.05 m; A_TC = 9×10⁻⁹ m²; k_air^1Torr = 2.63×10⁻² W/mK; k_air ^0.3Torr=7.89×10⁻³ W/mK; k_chrom = 93.7 W/mK; k_alum = 237 W/mK; x_Au = 46 g Au per m³ aqueous suspension at 1x concentration or 920 g Au per m³ at 20x concentration; r_P = 10 nm; r_L = 1.5 mm; λ= 514 nm; A_λ = 0.186 at 920 g Au/m³; ∑_im_iC_p,i = 0.0946 J/K; and ρ_Au=19.3 g/cm³.

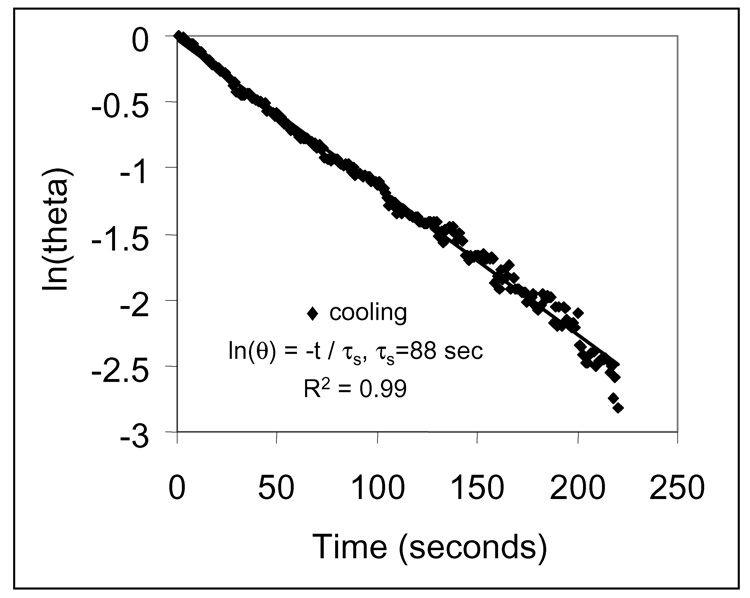
Figure 2 shows a time constant for heat transfer of τ_s=88 seconds determined as the negative reciprocal slope of ln(θ) vs. t (eq 15) using temperature versus time data recorded during cooling in Figure 1. Data were truncated at 220 seconds to avoid scatter as the logarithmic operand approached zero. Evaluating time constants with cooling data avoided effects of thermal gradients during heating. Temperature in the system dissipated at a rate inversely proportional to the internal equilibration time, τ_internal = (L²/α)_int. During cooling, a value of τ_internal = 4.5 seconds was determined for internal equilibration time using L = 2 mm (half the cell width) and α_glass = 8.8×10⁻⁷ m²s⁻¹, since α_glass/α_H2O = 6 for a thermal conductivity of k_NP~1.01*k_H2O for our 0.0048% v/v Au NP suspension.³⁵ Since τ_internal/τ_s ~0.05, the temperature remains essentially uniform across the heat transfer surface area, A, which validates use of eq 5.

Figure 2.

The time constant for heat transfer from the system is determined to be τ_s = 88 seconds by applying the linearized energy balance to temperature vs. time data from the cooling period of Figure 1 (◆).

An average time constant of τ_s = 86.3 ± 8.61 seconds (N=37) was obtained for thermal equilibration with the surroundings via conductive and radiative heat transfer. This value is 10¹²-fold larger than equilibration times for heat dissipation from thermally excited NPs calculated using eq 3–eq 4, which tells us that monitored changes in the system temperature are representative of irradiated NP temperatures which are equilibrated with surrounding fluid. The time constant value of τ_s = 86.3 ± 8.61 seconds was substituted into eq 12 to estimate an average heat transfer coefficient for our sample cell of h = 7.02 ± 0.6 Wm⁻² K⁻¹. This value is 37% larger than an effective heat transfer coefficient of 5.1 Wm⁻¹ K⁻¹ calculated for radiation alone in our system,³⁸ because of added heat transfer by conduction (eq 7) which occurs at a rate about half that of radiation (eq 8).

3.5 Determine efficiency of transducing resonant light to heat using suspended nanoparticles

From measured values of h, the transduction efficiency, η_T, may be determined by substituting eq 6 for Q_I into eq 16 and rearranging to get

$${\eta }_T=\frac{hA(T_{\text{max}}-T_{\mathit{\text{amb}}})-Q_o}{I\left(1-{10}^{-A_{\lambda }}\right)}$$ (19)

where Q_o was measured independently to be Q_o = (5.4×10⁻⁴)I in J s⁻¹ using borosilicate glass cells containing aqueous samples without NP. Figure 3 shows values of transduction efficiency calculated using eq 19 for data obtained with (◆) and without (Δ) mechanically chopping the irradiation laser beam at a frequency, ν, of 6000 cycles per second. Error bars for each data point correspond to ± 1 standard deviation. Chopping the laser increased transduction efficiencies ≥2.1-fold.

Irradiation at 514 nm, rather than 525 nm, in our system decreases the likelihood that plasmon bleaching might decrease laser-to-heat transduction and reduces convolution of measured efficiency by NP aggregation. Plasmon bleach exhibited by excited electrons^17–19 transiently lowers the Au NP absorption spectra at its maximum, ~524 nm, while raising absorption at its wings, ~475 and 575, respectively. The value of A₅₁₄ falls between the maximum and the wings at a point where transient absorption remains relatively constant. Irradiation at 514 nm also yields monotonically decreasing absorption in the event of NP aggregation. Because aggregration both broadens and red-shifts the spectra, absorption between 524 and 575 nm can fluctuate nonmonotonically in proportion to the degree of aggregation.

Continuous-wave irradiation of aqueous Au NP suspensions at low power allows even heating with reproducible efficiencies at temperatures within physiological limits, whereas high-power nano-, pico- and femto-second pulses produce large particle-to-matrix temperature gradients that cause vaporization and concomitant cavitation and NP fragmentation, which are incompatible with biological or steady-state applications, and yield variable efficiencies. Resonant plasmon decay by radiative or scattering processes that divert laser light absorbed by NP from producing heat are minimized by using spherical NP between about 10 and 20 nm in diameter. Only dipole oscillations contribute significantly to extinction in this size range, so localized surface plasmon resonance is independent of particle size. In this size range electron-surface scattering also increases the overall electron-phonon cross-section by 10%.¹⁹ Certain irradiation frequencies can enhance photoluminescence in nanorods or clusters <5 nm to lower heating efficiencies relative to spheres. On the other hand, broad spectral absorbances characteristic of nanorods and nanoshells can increase absorption magnitudes across a broader range of incident wavelengths, allowing excitation within the near-infrared ‘water window’, for example. The extensive parameter space provided by this rich set of variables is useful to optimize laser-to-heat transduction via NP in non-homogeneous suspensions, solids or gases where variations due to lattice-induced changes in interface thermal conductance are anticipated. Measuring transduction efficiencies can identify underlying physical phenomena that effect microscale thermal transport, permitting optimization, and allow prediction of heat flux from incident irradiation and NP concentration.

3.6 Modulating irradiation reduces nanoparticle aggregation

Mechanically chopping the incident irradation decreases NP-NP aggregation, which increases laser-to-heat transduction. Negatively-charged ions on NP surfaces form an electric double layer that produces a repulsive electrostatic potential, which stabilizes NP at interparticle distances (surface to surface) over a few nanometers. Resonant cw irradiation accelerates aggregation of 10-nm colloidal Au in aqueous⁴⁰ and organic^41,42 suspensions. Aggregation is more likely to arise in our experiments from photoionization of NP, which reduces Derjaguin-Landau-Verwey-Overbeek electrostatic stabilization,⁴³ than from induction of optical attractive forces, which occurs at applied intensities >10⁶ W/cm².⁴⁴ Coagulation of NPs without coalescence is reported at radiation wavelengths of 514 nanometers.⁴¹ We measured spectral broadening, red-shifting and lowered absorbance at 514 nm after unmodulated cw laser irradiation, consistent with previous reports.^40–42 Delivering eight times as much laser power to a modulated sample lowered its relative absorbance by just one-third of the unmodulated amount.

Reducing aggregation by chopping incident light is also consistent with time constants in our system. The diffusive time constant, τ_D, for coagulative interactions between neighboring³⁹ Au NP with Stokes-Einstein diffusivity D_p=κT/(6πr_pμ) separated by a diffusion length L_D = r_p (ρ_p/x_Au)^1/3 may be estimated from τ_D = L_D²/D_p as:⁴⁵

$${\tau }_D=\frac{6\pi \mu r_p^3{\left(\raisebox{1ex}{${\rho }_p$}\!\left/ \!\raisebox{-1ex}{$x_{Au}$}\right.\right)}^{2/3}}{\kappa T}$$ (20)

where κ is Boltzmann’s constant and μ is matrix viscosity. NP suspensions at x_Au = 920 g m⁻³ have a diffusive interaction time of τ_D = 0.35 milliseconds, which corresponds to ~1×10⁶ interactions per particle per 320-second irradiation period, T_I. At ν=6000 cycles per second, the chopping frequency is 0.167 milliseconds – less than half the diffusive interaction time at x_Au = 920 g m⁻³. Between successive chopped pulses, NP temperatures relax rapidly with short thermal dissipation times of τ_d~ 27–79 picoseconds (eq 3–eq 4). Therefore, when laser light is chopped, NP-NP interactions are less likely to result in coagulation. Slower chopping frequencies decrease transducion efficiency, as expected. Aggregation does not influence the system heat transfer time constant, τ_s, since values of mass, heat capacity, heat transfer area and radiative/conductive heat transfer coefficient in eq 12 are system properties that are unaffected by NP aggregation. When absorbance at the incident wavelength of 514 nm, A₅₁₄, is reduced by aggregation, the fraction of incident light absorbed, (1–10^−A), in eq 6 is decreased. This decreases transduction of incident laser light, I, to heat ,Q_I. This appears in Fig 3 as a decrease in transduction efficiency.

3.7 Laser power and nanoparticle concentration increase equilibrium heat flux

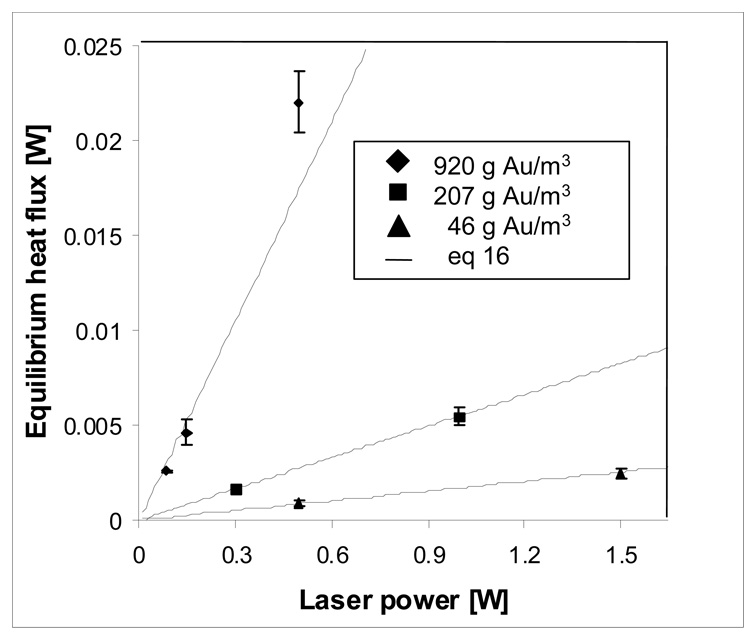
The maximum attainable heat flux due to incident radiation on a NP suspension, Q_max = hA(T_max–T_amb), may be predicted as a function of laser power and NP concentration by substituting eq 6 into eq 16 and solving for Q_max. Figure 4 compares measured increases in maximum attainable heat flux of irradiated NP suspensions at 46 g Au per cubic meter (◆) and at 920 g Au per cubic meter (Δ) with predicted values (—) from eq 6 and eq 16. Maximum heat flux rises in proportion to applied laser power and nearly in proportion to concentration up to absorbance values of about ~0.1. Above absorbance values of 0.1, increasing concentration produces less than proportional increases in Q_max, due to the logarithmic absorbance dependence of the fraction of incident radiation that is absorbed, 1–10^−A.

Figure 4.

Maximum equilibrium heat flux from 7.9-microliter suspensions of Au NPs increases in proportion to laser power from 0.085 to 1.5 W and NP concentration from 46 g Au/m³ (Δ) to 920 g Au/m³ (◆).

4. Conclusions

The efficiency of transducing resonant, continuous wave irradiation to bulk heat by a gold nanoparticle suspension has been analyzing thermal energy in a thermally isolated system and applying a description of linearized heat transfer by radiation and conduction. The description accounts for transient temperature changes during heating and cooling in an experimental system and allows maximum attainable equilibrium temperatures to be predicted as a function of laser power and nanoparticle concentration. The description was derived and validated by analyzing internal and external timescales for thermal equilibration. Modulating the incident continuous wave irradiation at a frequency shorter than the timescale for coagulative particle-particle interactions increased the transduction efficiency.