Abstract
A small-world network has been suggested to be an efficient solution for achieving both modular and global processing—a property highly desirable for brain computations. Here, we investigated functional networks of cortical neurons using correlation analysis to identify functional connectivity. To reconstruct the interaction network, we applied the Ising model based on the principle of maximum entropy. This allowed us to assess the interactions by measuring pairwise correlations and to assess the strength of coupling from the degree of synchrony. Visual responses were recorded in visual cortex of anesthetized cats, simultaneously from up to 24 neurons. First, pairwise correlations captured most of the patterns in the population's activity and, therefore, provided a reliable basis for the reconstruction of the interaction networks. Second, and most importantly, the resulting networks had small-world properties; the average path lengths were as short as in simulated random networks, but the clustering coefficients were larger. Neurons differed considerably with respect to the number and strength of interactions, suggesting the existence of “hubs” in the network. Notably, there was no evidence for scale-free properties. These results suggest that cortical networks are optimized for the coexistence of local and global computations: feature detection and feature integration or binding.
Keywords: Ising model, maximum entropy, orientation selectivity, parallel recording, scale free, visual cortex
Introduction
The cerebral cortex is a complex network of densely connected, interactive computational units, the neurons. Therefore, the activity of individual neurons is often correlated. In the visual system, for example, synchronized firing has been observed at all processing levels, the retina (Neuenschwander and Singer 1996; Castelo-Branco et al. 1998; Schnitzer and Meister 2003), the lateral geniculate nucleus (Neuenschwander and Singer 1996; Castelo-Branco et al. 1998; Dan et al. 1998), and the cortex (Toyama et al. 1981; Gray and Singer 1989; Fries et al. 1997; Castelo-Branco et al. 1998; Biederlack et al. 2006). These synchronization processes are believed to play an important role for information processing in the brain (for review, see Gray 1999; Singer 1999; Fries 2005; Fries et al. 2007). The understanding of this phenomenon at the level of neuronal populations can be approached best from the perspective of network theory. The recently developed theoretical tools for studying the structure and dynamics of networks—systems of interacting units—have been quite successful in identifying characteristic features of social, biological, and technical networks (Boccaletti et al. 2006). An important finding was that many of these networks have so-called “small-world” properties. A small-world network exhibits a connectivity that constitutes a compromise between random and nearest neighbor regimes resulting in a short average path length despite the predominance of local connections (Watts and Strogatz 1998; Sporns et al. 2004; Bassett and Bullmore 2006). Thus, a small-world network has many local interactions, indicated by the high clustering property inherent to regular networks and short average path length among any pair of nodes, which is a property inherent to random networks. This organization optimizes the network for both local and global interactions (Sporns et al. 2004; Bassett and Bullmore 2006). Another important feature shared by some of the networks is that they are “scale free.” Scale-free networks are characterized by the fact that nodes with differing degrees of connectivity distribute according to a power law. Nodes with a high degree, the so-called “hubs,” are rare, whereas weakly connected nodes are frequent (Barabasi and Albert 1999). A small-world network need not be scale free, whereas a scale-free network always has small-world property (Amaral et al. 2000). Small-world and scale-free properties of networks have important implications for the efficiency with which information can be processed and exchanged (Watts and Strogatz 1998; Lago-Fernandez et al. 2000; Simard et al. 2005), for the robustness (vulnerability) of the network in case of malfunction of its nodes (Albert et al. 2000; Achard et al. 2006), and for the emergence of synchronization (Watts and Strogatz 1998; Lago-Fernandez et al. 2000).
So far, only a few studies provided evidence that brain networks could be scale free (Eguiluz et al. 2005; Kaiser et al. 2007). A power law distribution of nodes’ connectivity has been found for the coherence among activated voxels using functional magnetic resonance imaging (fMRI) (Eguiluz et al. 2005). In addition, the robustness against simulated lesions of anatomic cortical networks was found to be most similar to that of a scale-free network (Kaiser et al. 2007). In contrast, numerous studies suggest that brain connectivity has small-world properties. Some of these studies are based on anatomy (Watts and Strogatz 1998; Sporns et al. 2000; Stephan et al. 2000; Hilgetag and Kaiser 2004; Sporns and Zwi 2004; Humphries et al. 2006; He et al. 2007), others on functional analyses of electroencephalographic (EEG) and magnetoencephalographic or fMRI signals, reflecting the activity of large populations of neurons (Stam 2004; Achard et al. 2006; Bassett et al. 2006; Micheloyannis et al. 2006; Achard and Bullmore 2007; Stam et al. 2007). Only 1 study investigated the structure of a neuronal network by analyzing functional interactions among individual neurons. In this case, coupling was assessed from the spontaneous activity of a neuronal culture and the results suggested a small-world property (Bettencourt et al. 2007). Here, we investigate the organization of functional cortical networks in vivo by evaluating correlations between single cell responses to physiological stimuli. We recorded simultaneously the spiking activity of up to 24 neurons that were distributed within and across several microcolumns of cat primary visual cortex. This allowed us to relate network properties to some of the characteristic features of visual neurons such as their orientation tuning.
When using correlation analysis for the identification of network properties, one needs to consider that synchronization among pairs of neurons does not necessarily imply that they interact directly because correlated firing can also be caused by common input (Schneidman et al. 2006). Therefore, additional computations are required to consider the possibility that the actual network architecture differs from the directly measurable correlation data (Fingelkurts et al. 2005). To this end, we applied the Ising model, which has been recently introduced in the studies of neuronal synchrony by Schneidman et al. (2006) (but see also Cowan and Friedman 1990). This model is capable of identifying and removing correlations caused by common inputs and of adding instead the estimated paths of interactions that are not directly visible in the correlation network. Applying the Ising model also allows one to test whether the complex activity patterns can be accounted for by the measured pairwise correlations. Only if this is the case, can realistic interaction architectures be derived from analyses of pairwise correlations (Schneidman et al. 2003, 2006; Shlens et al. 2006).
Materials and Methods
Experimental Preparation
All the experiments were conducted according to the guidelines of the Society for Neuroscience and the German law for the protection of animals, approved by the local government's ethical committee and overseen by a veterinarian.
Adult cats (n = 2) were anaesthetized with ketamine (Ketanest, Parke-Davis, Berlin, Germany. 10 mg/kg, intramuscularly [i.m.]) and xylazine (Rompun, Bayer, Leverkusen, Germany. 2 mg/kg, i.m.). After tracheotomy, the animals were placed in a stereotactic frame and all pressure points and incisions were infiltrated with a long-acting anesthetic (2% lidocaine HCl). Then animals were ventilated, and anesthesia was maintained with a mixture of 70% N2O and 30% O2, supplemented with halothane (0.5–1.2%). EEG and electrocardiogram were monitored continuously. A craniotomy was performed, and the skull was cemented to a metal rod. After completion of all surgical procedures, the ear and eye bars were removed, and the halothane level was reduced from 1.2% to 0.5–0.6%. After assuring that the level of anesthesia was stable and sufficiently deep to prevent any vegetative reactions to somatic stimulation, the animals were paralyzed with pancuronium bromide (Pancuronium, Organon, Roseland, NJ. 0.15 mg/kg/h). Glucose and electrolytes were supplemented intravenously and through a gastric catheter. The end-tidal CO2 and rectal temperature were kept in the range of 3–4% and 37–38 °C, respectively. The value of 0.5–0.6% halothane was kept constant throughout the experiment with the exception of potentially painful procedures (e.g., intramuscular injection of antibiotic) in which case the level of halothane was increased to 1.2% 10 min prior to the procedure and then returned immediately back to 0.5–0.6%. After this procedure, no new recordings were made for a period of at least 20 min. The nictitating membrane was retracted with neosynephrine, the pupils were dilated with Atropine, and the eyes were protected from desiccation by contact lenses containing artificial pupils.
Visual Stimulation
Stimuli were presented binocularly on a 21” computer screen (100 Hz refresh rate; HITACHI CM813ET) that was positioned at the distance of 57 cm in front of the eye plane. To obtain binocular fusion, the optical axes of the 2 eyes were 1st determined by mapping the borders of binocular receptive fields (RFs) from responses to moving single bars and then the optical axes were aligned on the computer screen with adjustable prisms placed in front of 1 eye. The software for visual stimulation was the stimulation tool ActiveSTIM (www.ActiveSTIM.com). The visual stimuli were full-contrast drifting sinusoidal gratings, whose spatial and temporal frequencies were adjusted to activate a maximal number of cells. The motion direction of the grating was orthogonal to its orientation. In 1 cat, we presented grating stimuli with the movement directions chosen randomly from a set of 12 directions changing in steps of 30°, ranging from 0° to 360°. Each stimulus condition was presented 60 times, 3 s in duration. The responses to these gratings were also used to compute the orientation tuning curves of the cells. In the other cat, in addition to these 12 stimulus conditions, another set of 14 stimuli was presented that consisted of center gratings, adjusted to evoke strong rate responses in the majority of the cells, which were embedded in surround gratings of varying orientations and sizes. In this cat, each of the 26 stimulation conditions was presented 19 times for 4 s. Presentation of the full set of stimuli required 33 and 36 min in the 2 cats, respectively. The intertrial intervals lasted about 2 s. The average luminance of the gratings matched that of the screen background. For analysis, responses had to be pooled across all stimuli in order to ensure a sufficient sample size. We consider this pooling as appropriate in the present context because different stimulation conditions are likely to elicit different activation patterns, thus increasing the chances to fully determine the role of neurons with different stimulus preferences within the networks (e.g., the role of a network hub).
Recordings
Multiunit activity (MUA) was recorded from cells in cat area 17 with eccentricities less than 18°. In order to record simultaneously at different cortical depths and from different cortical columns, we used 16-channel silicon probes provided by the Center for Neural Communication Technology at the University of Michigan. Each probe consisted of four 3-mm long shanks that were separated by 200 μm and contained 4 electrode contacts each (1250 μm2 area, 0.3–0.5 MΩ impedance at 1000 Hz, intercontact distance 200 μm). The probe was positioned such that it would enter the cortex approximately perpendicular to the surface. In 1 cat, 2 probes were inserted simultaneously at a distance of about 3 mm, which allowed us to investigate the neuronal activity in different cortical depths and columns simultaneously as well as the interactions across shorter (within probe) or longer (between probes) distances.
MUA signals were amplified ×10 000 and band-pass filtered between 300 Hz and 3 kHz. The signals were then sent to an analog-to-digital converter and recorded by a customized LabView program running on a PC. Both the time stamps and the waveforms of the detected spikes were recorded (32 kHz sampling frequency), which allowed for later application of off-line spike-sorting techniques.
Analysis
Spike Sorting
Spike sorting was performed by customized software. Spike waveforms of multiunit were 1st subjected to principal component analysis (PCA). A single unit was isolated if, in the 3-dimensional PCA space of the 1st 3 component, we found a cluster of waveforms that was segregated from all the remaining waveforms. Spike sorting was based on the waveforms recorded by individual electrode. We can exclude the possibility that some of the multiple recording sites picked up activity from the same cells because such stereo recordings should have the properties of autocorrelation, that is, very high values of Pearson's r. All the presently measured values were smaller than r = 0.10, which are values typical of cross-correlation. This indicates that the spatial separation of the recording sites (minimum 200 μm) is sufficiently large to prevent contamination of the results by stereo recordings. The average firing rate of the sorted units was 10.9 spikes/s.
Orientation Selectivity
Orientation selectivity was calculated for each single unit with the methods described elsewhere (Leventhal et al. 1995). The responses to the different stimulus orientations were represented as vectors, which were 1st added and then divided by the sum of their absolute values. The angle of the resulting vector indicated the preferred stimulus orientation for that unit. The length of the resulting vector was named the orientation bias (OB) and represented a quantitative measure of the orientation sensitivity (taking values between 0 and 1). Zero indicates that the neuron responded equally to all orientations and 1 means that the neuron responded only to 1 stimulus orientation.
Ising Model and Examination of Predominance of Pairwise Correlations
The simultaneously recorded spike trains of neural populations were converted into a binary variable (1 for spike and −1 for no spike, within 2-ms windows). Let vector σ = (σ1, σ2, …, σN) represent the state of the selected population, where σi equals 1 or −1, representing the state of the ith neuron. In our analysis, N, the number of neurons, always equaled 10. P(σ) represents the probability of the system to enter the arbitrary state σ. The Shannon entropy of the system is then calculated by
| (1) |
The actual entropy (S) is computed by using the observed probability for individual σ. The entropy of the system, if constrained only by firing rates (S1), is computed by using the expected P(σ), which is determined on the basis of observed firing rates under the assumption of independent firing.
To estimate the entropy of the system that is constrained both by firing rates and pairwise correlation (S2), we used the Ising model, as proposed in a previous study (Schneidman et al. 2006). The P(σ) provided by the Ising model could be expressed as follows:
| (2) |
where Z indicates a normalization factor, h indicates the intrinsic property of cell i, and J indicates the exchange interaction between cells i and j. Z, h, and J could be determined according to the experimentally observed averages <σi> and <σiσj>. The entropy decrease due to pairwise correlations is denoted by I2 = S1 − S2, whereas the entropy decrease due to all possible correlations is denoted by I = S1 − S. Therefore, the ratio I2/I represents the relative importance of pairwise correlations in determining the population activity. As a quantity based on estimation of entropy, the ratio I2/I is subject to systematic errors caused by the finite sample size (Schneidman et al. 2006). To estimate this error, we computed the ratio I2/I with different sample sizes amounting to 25%, 50%, 75%, and 100% of the total recording length. The values for the ratio increased systematically, but for the 2 largest samples the difference became very small, the averages for different sample sizes being 0.868, 0.910, 0.926, and 0.933, respectively (a positively decelerated curve). This result suggests that the present estimates of I2/I, although biased toward underestimation, produce bias of a very small magnitude.
Examination of the Network Properties
The interaction matrix obtained by applying the Ising model to individual 10-neuron groups defined an undirected graph with 10 nodes. After applying thresholds, r, to the strength of interaction |J|, we converted the graph either to a binary graph (nodes were either connected or not) for analyzing the small-world property or to a weighted graph (weights defined by interaction strength were assigned to individual connections) for analyzing the properties associated with the connection strength of the nodes. Two different thresholds were chosen for each of the 3 datasets according to the following criteria: 1) At least 1 threshold should keep the majority (>50%) of 10-neuron networks connected, and both thresholds should keep the large networks (i.e., those that contain all the recorded neurons) connected. 2) All connected networks should have an average degree (k) larger than ln(10) = 2.3 to allow for the analysis of small-world properties. We applied the 2 chosen thresholds uniformly to all 10-neuron subnetworks chosen from the given dataset. This provided sufficient statistics to allow for a robust estimate of the small-world property.
The average path length, L, was defined as the average length of the shortest path connecting any pair of nodes in a network. The clustering coefficient for individual nodes was defined as the ratio of the number of connections between the neighbors of this node and the number of all the possible connections between its neighbors. The clustering coefficient of a network, C, was the mean value of the clustering coefficients of all nodes. The average path length, L, and clustering coefficient, C, were then compared with those of 100 random networks, which preserved the same number of nodes and connections as the actual network but, in contrast to the studies with much larger networks, could not preserve the degrees of individual nodes. Despite this limitation, both the original and random networks lacked scale-free properties, showing single-scale degree distributions. The same procedure was applied to analyze the small-world property of correlation networks, in which case the graph was defined by correlation coefficients between the neurons’ activities. The network graphs shown in Figures 4 and 5 and Supplementary Figure 2 were produced by using Pajek software (http://vlado.fmf.uni-lj.si/pub/networks/pajek/).
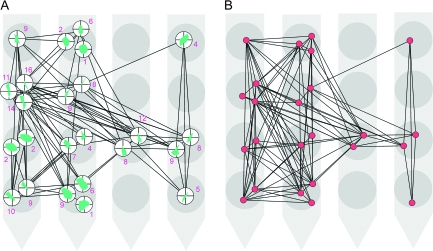
Figure 4.
The connection matrices for 24 units are shown in a spatial constellation that depicts the relative positions of the units as defined by the positions of the corresponding electrode contacts on a 16-channel (4-shank) Michigan probe. Contacts at the lower parts of the figure were recorded from deeper layers of the cortex. (A) The interaction matrix is thresholded at |J| = 0.15 (see Table 1). The orientation tuning curves are indicated for each unit by the small polar plots. The number associated to each unit indicates its degree. (B) A network obtained from the correlation matrix from which the interactions in (A) are extracted. This network is thresholded at r = 0.012 (see Supplementary Table 3).
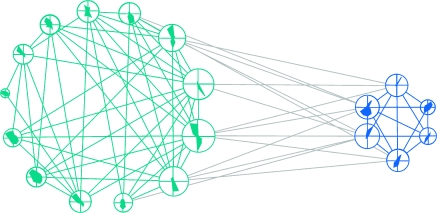
Figure 5.
The connection matrix from Figure 4A rearranged such that the units with similar orientation preferences form a group: One group comprises units with preferred orientations between 0° and 90° (blue) and the other between 90° and 180° (green). Five units with weakest orientation preferences could not be classified accurately and were, thus, removed from the plot. The size of each node is proportional to the number of its connections (i.e., its degree). Gray: intercluster connections. Note the higher interconnectivity within than between the groups (quantitative analysis is reported in the main text).
We also made a control analysis to investigate whether the total connection strength of a node depended on the node's firing rate to the most preferred stimulus direction, and the analysis revealed no significant correlation (r = 0.23; P > 0.05). This indicates that the hub property of a unit was not a confound of the spike-sorting procedure such that the quality with which the unit was isolated would, in some correlated manner, affect both orientation tuning of the unit and the strength of its synchrony with other units.
Mutual Information
The mutual information between the state of neuron i, σi, and the state of the rest of network, σ′, was computed as
| (3) |
where P indicates the probability to observe an event. σi can only take the value of 1 or −1, whereas σ′ can take 29 = 512 different values. To overcome a systematic error caused by limited sample size, these values of mutual information were corrected by a method introduced in Panzeri and Treves (1996).
Results
We obtained data from a total of 63 neurons, whereby 24, 17, and 22 neurons had been recorded in parallel from a single 16-channel Michigan probe. Results from these 3 datasets were very similar, and therefore, unless specified otherwise, data are documented for the largest set with 24 simultaneously recorded cells.
Correlation Analysis
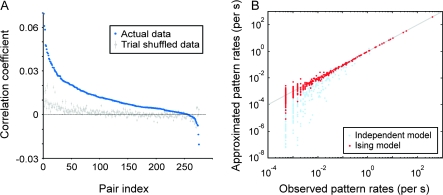
Spike trains were binned in windows of 2 ms and digitized, yielding time series of zeros and ones. We computed Pearson’s correlation coefficients for pairs of such binary series (i.e., phi-coefficient; 2nd-order correlation), which corresponded to the height of the central peak (zero-shift) in an appropriately normalized cross-correlation histogram. These coefficients were larger than zero and got strongly reduced by shuffling the trials in which the identical stimuli were presented (Fig. 1A). If the observed correlations were due to neuronal responses being tightly time locked to the stimuli, the strength of the correlations would have stayed unchanged after the trial shuffling. The finding that the correlations largely disappeared after the shuffling procedure indicates that those correlations originated mostly from the synchronization generated internally and not from the temporal dynamics of the stimulus.
Figure 1.
Correlations in neuronal activity and model approximation of the firing patterns. (A) Distribution of correlation coefficients between neuronal pairs computed from their original spiking activity (blue) and from trial-shuffled activity (50 repetitions of shuffling; gray). Error bars represent the SD. Neuronal pairs (pair index) are sorted by the magnitude of the correlation coefficient obtained for the actual (nonshuffled) data. (B) For an example of a 10-neuron group, the observed frequency of individual firing patterns is plotted against the frequency predicted by the Ising model (2nd-order correlation; red dots) and the predictions from the independent model (no correlation; light-blue dots). The solid line indicates equality.
Pairwise versus Higher-order Correlations
To examine the relative contribution of pairwise correlations to the overall coupling, that is, to determine the extent to which complex activity patterns could be accounted for by pairwise correlations, we used an entropy-based approach introduced in a previous study (Schneidman et al. 2006). For this analysis, the number of samples required for reliable statistics increases exponentially with the size of the network. Because of the limited period during which neuronal responses could be recorded, we had to confine this analysis to subnetworks of 10 neurons, as in Schneidman et al. We randomly chose with replacement 10 neurons from the entire set of simultaneously recorded neurons (17–24 in our case) and analyzed 300–500 such subnetworks per dataset.
Within the chosen 2-ms bin, neurons either fired once or were silent. These binary states of individual neurons lead to a total of 210 = 1024 possible states of the 10-neuron systems, that is, firing patterns. To investigate whether the pairwise correlations (interactions) explained the activity of the network, we investigated how well the empirically obtained distribution of patterns, which contained correlations up to the 10th order, could be approximated by the distribution reconstructed from a model that considered firing rates and pairwise interactions and that was based on the Ising model (see Materials and Methods). For a typical group of 10 neurons the comparison is shown in Figure 1B (red dots). The data points scattered around the diagonal, indicating a close approximation of the original data. As a control and as in Schneidman et al. (2006), we also computed the pattern distribution predicted by a model based only on neuronal firing rates and not on correlations. This model matched the original distribution much less well (light-blue dots).
These results were quantified by an information-theoretic approach (see Materials and Methods and Schneidman et al. [2006] for details). This analysis revealed that 93% of the network's activity (standard deviation [SD] across all 10-neuron groups = 3%) could be explained by 2nd-order correlations and the firing rates, whereas at most 7% required for the explanation coupling of higher order. Similar results were obtained by using bin sizes other than 2 ms (ranging form 1 to 5 ms, results not shown) and for the other 2 datasets (93% and 92%, with SD = 3% and 1%, for 17 and 22 neuron groups, respectively).
These findings are highly consistent with previous reports from the isolated retina (Schneidman et al. 2006; Shlens et al. 2006), cultured networks (Schneidman et al. 2006; Tang et al. 2008), and acute cortical slices (Tang et al. 2008), suggesting that, in visual cortex too, most of the patterns of neuronal activity can be explained by taking into account the contributions of only 2 components: 1) the firing rates of individual neurons and 2) 2nd-order neuronal interactions (pairwise synchronization). This finding was a prerequisite for all subsequent analyses because it allowed us to extract the network of interactions solely on the basis of pairwise correlations and to disregard the higher-order correlations.
Networks of interactions
To extract the networks of interactions, we used the parameter J of the fitted Ising model (eq. [2] in Materials and Methods), which, in its original application in statistical mechanics, represents exchange interactions between pairs of spins. In the present application, as introduced in Schneidman et al. (2006), it is related to the likelihood that a spike occurring in 1 neuron will “cause” a spike in another neuron or vice versa (the directions of interactions are not estimated by this model). A similar parameter was used to estimate gene interactions (Lezon et al. 2006). It has been shown that the Ising model (Schneidman et al. 2006) and other similar maximum entropy models (Lezon et al. 2006) can efficiently distinguish between correlations caused by shared inputs, for example, from a 3rd driving unit, and correlations caused by direct mutual interactions.
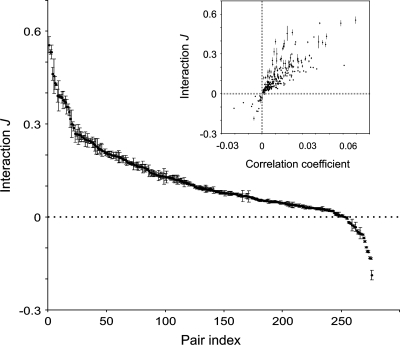
Figure 2 (inset) shows a comparison of the model-based interaction strengths with the original, experimentally determined Pearson's correlation coefficients. The 2 measures are correlated positively because strongly correlated units are more likely to interact strongly, but this relation, as in previous studies (Schneidman et al. 2006; Tang et al. 2008), is not straightforward: Some neuronal pairs with strong correlations have weak interactions and vice versa.
Figure 2.
The stability of interactions estimated across different 10-neuron groups and their nontrivial relation to correlation coefficients. Distribution of interaction, J, for all 276 investigated neuronal pairs. Neuronal pairs (pair index) are sorted according to the mean interaction value. Inset: interactions, J, for pairs of units plotted against the corresponding correlation coefficients. Error bars represent SD of J across all estimates made for the same pair embedded into different 10-neuron groups.
The interaction networks resulting from this model-based reconstruction agreed well with the functional organization of the visual cortex. The values of the interaction strength, |J|, were highly consistent with the known layout of association connections in the primary visual cortex. Neuronal pairs with similar orientation preferences were estimated to have stronger interactions than pairs preferring different stimulus orientations. Similarly, interactions were stronger between narrowly spaced than between widely spaced pairs (in this latter case, we analyzed neuronal synchrony across 2 Michigan probes; see Supplementary Fig. 1 for more details on these analyses). This agrees with the topology and spatial extent of tangential intracortical connections (Gray et al. 1989; Schmidt et al. 1997).
As a further test for the reliability of our network reconstruction, we analyzed the variability of the interaction index, J, for all possible 276 pairs and across all investigated 10-neuron groups, that is, over a total of 300 different 10-neuron groups. For the 24-neuron network, each pair appeared on average in 49 ± 10 (mean ± SD) groups. The variability of J for individual pairs was much smaller (SD = 0.008) than the variability across different pairs of neurons (SD = 0.12), indicating that the reconstruction of the interaction graph contained no spurious interactions and was to a large extend independent of the particular subsample of the entire network that had been assessed (Fig. 2, main graph).
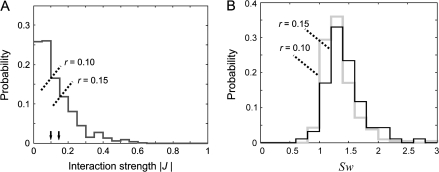
To test whether the reconstructed networks had small-world and maybe also scale-free properties, we 1st set a threshold by which the scalar J was converted into a binary value indicating whether the connection was present or not. For each network, we set 2 different thresholds (see Materials and Methods for details on the criteria used to determine the thresholds). Then, we computed for each 10-neuron group the ratio λ between the average of the empirically determined path lengths (numerator) and the path lengths of a random network (denominator). A random network is constructed by randomly repositioning the connections of the original empirical network and has thus the same number of nodes and connections as the empirical network. In addition, a similar ratio γ was computed for the networks’ clustering coefficients (see Materials and Methods for the computation procedure of the average path length and the clustering coefficient). A small-world property was inferred if the 2 networks had the same average path lengths, λ ≈ 1, and if the empirical network had a larger clustering coefficient than the random network, γ > 1, or, equivalently, if the ratio Sw = γ/λ > 1 (Montoya and Sol 2002; Achard et al. 2006; Humphries et al. 2006; He et al. 2007).
The results of this analysis were highly consistent across the 3 datasets. Most of the networks had short path lengths (all average λs ≤ 1.05 and all SDs ≤ 0.06) and larger clustering coefficients than the random networks (average γs reaching values of up to 1.48 with all SDs ≤ 0.33). As a result, 79–96% of networks had Sw > 1. These results were largely independent of the value chosen for thresholding |J| (Fig. 3, see also Table 1 for more details on this analysis). Therefore, the analyzed networks fulfilled all criteria of small-world networks.
Figure 3.
Distributions of interaction strength, |J|, and the measures of small-world property, Sw. (A) Distribution of interaction strength |J| and the positions of the 2 different thresholds, r. (B) Distributions of Sw obtained for the 2 different thresholds in (A).
Table 1.
Characteristics of interaction networks extracted by applying the Ising model
| |J| | r | k | ED | L | C | λ | γ | Sw | % | n | |
| R1 | 0.13 | 0.10 | 4.56 ± 0.82 | 0.51 ± 0.09 | 1.59 ± 0.16 | 0.66 ± 0.11 | 1.03 ± 0.04 | 1.36 ± 0.26 | 1.33 ± 0.27 | 96 | 211 |
| 0.15 | 3.44 ± 0.69 | 0.38 ± 0.08 | 1.89 ± 0.21 | 0.51 ± 0.14 | 1.04 ± 0.06 | 1.48 ± 0.32 | 1.43 ± 0.31 | 96 | 94 | ||
| R2 | 0.08 | 0.06 | 4.49 ± 0.55 | 0.50 ± 0.06 | 1.57 ± 0.11 | 0.56 ± 0.10 | 1.02 ± 0.02 | 1.15 ± 0.18 | 1.14 ± 0.17 | 79 | 493 |
| 0.09 | 3.44 ± 0.60 | 0.38 ± 0.07 | 1.85 ± 0.20 | 0.45 ± 0.13 | 1.02 ± 0.04 | 1.30 ± 0.33 | 1.27 ± 0.32 | 82 | 223 | ||
| R3 | 0.13 | 0.10 | 5.20 ± 0.90 | 0.57 ± 0.10 | 1.47 ± 0.16 | 0.69 ± 0.10 | 1.02 ± 0.03 | 1.23 ± 0.19 | 1.21 ± 0.19 | 94 | 434 |
| 0.15 | 3.85 ± 0.78 | 0.43 ± 0.09 | 1.79 ± 0.21 | 0.48 ± 0.13 | 1.05 ± 0.05 | 1.18 ± 0.19 | 1.12 ± 0.18 | 81 | 98 |
Note: R1–R3 indicate different datasets. |J| indicates the average interaction strength, r the threshold, and k the mean degree (i.e., number of connections per node). ED, edge density; L and C indicate the average path length and clustering coefficient, respectively. λ and γ indicate the ratios obtained for the values of L and C, respectively, computed for the empirical and the corresponding random networks (λ = L/LRandom; γ = C/CRandom). Sw stands for small-world index, which is defined as the ratio between γ and λ. The % indicates the percentage of networks that have Sw > 1. n is the number of networks that could be used for further analysis (valid networks) as they remained connected after thresholding and had k > ln(10). For each threshold, we analyzed all the connected networks out of the total 300–500. All results are shown as mean ± SD.
As the estimates of the interactions across the 10-neuron groups were stable, we considered it justified to calculate their averages and to reconstruct the entire networks, and an example of such a network is shown in Figure 4A. These networks had again small-world properties. The path lengths for the 24-neuron network were short with λ = 1.05 and 1.12 for thresholds of 0.10 and 0.15, respectively, and the clustering coefficients were even higher than those for the 10-neuron networks, (γ = 1.49 and 2.00), resulting in stronger small-world properties (Sw = 1.42 and 1.79). The results for the other 2 datasets were similar (see Supplementary Table 1). The architecture by which the small-world property is achieved in these networks is illustrated in Figure 5, in which the units from Figure 4A are grouped according to the similarity of their orientation preferences. By this grouping, the edge density (ED), defined as the number of actual connections divided by the total number of possible connections, was much smaller between the groups than within each of the 2 groups (ED = 0.19 vs. 0.60 and 0.93, respectively). Thus, the small-worldness is formed by strong clustering around similar orientation preferences and by a smaller number of “long-distance” interactions that bridge the groups of different orientation preferences. It is noteworthy that the analyses of the entire networks have to be regarded with care: They are based on fitting Ising models, and those assume that essentially all network activity can be explained by pairwise interactions. Whereas we had been able to demonstrate this for networks of up to 10 neurons, experimental limitations prevented the tests for the entire networks of up to 24 neurons.
Correlation Networks
We also analyzed the functional network architecture defined directly by the raw correlation coefficients (an example is shown in Fig. 4B) using the same method and found again small-world properties both for the 10-neuron networks and for the larger networks containing all neurons recorded from a probe (Supplementary Tables 2 and 3). This finding was expected but without the complementary results from the Ising model would not have allowed us to infer a small-world property. The correlations were dominated by positive values (Fig. 1) and, therefore, could have resulted from shared inputs (redundant connections). In this case, the interaction network need not have a small-world property (see Supplementary Fig. 2 for an example of such a network). However, our converging results from the 2 approaches suggested that the analyzed cortical networks did indeed have small-world properties and hence that they could capitalize on all the advantages of such architecture, in particular the ability to handle equally well-local and global interactions (Bassett and Bullmore 2006). It needs to be noted that small-world properties cannot be compared quantitatively across correlation and interaction networks because critical values such as γ depend on thresholds, the choice of which cannot be standardized across the 2 types of networks.
Degree Distribution
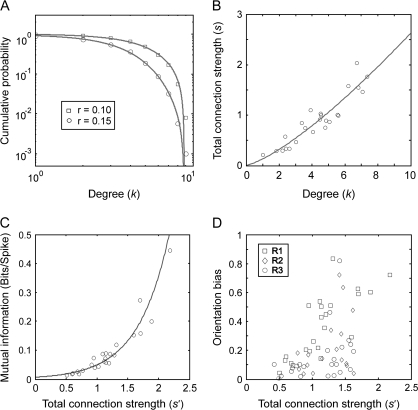
A small-world network can, but does not have to be scale free (Amaral et al. 2000). In order to examine whether the present networks were scale free, we counted the number of connections for each node. For a given node, the number of its connections is its so-called “degree” and across nodes, one can determine the so-called “degree distribution”. The average cumulative degree distributions across all 10-neuron networks revealed some heterogeneity but did not suggest a scale-free structure. In log–log plots relating the number of nodes with the degree of connectedness, expressed as cumulative probability, the empirical distribution deviated from a straight line (Fig. 6A) as the frequency of nodes with large numbers of connections was lower than expected for scale-free networks. Instead, the observed cumulative degree distributions were approximated well by Gaussian functions for all 3 datasets and for different thresholds (for an example, see Fig. 6A). The same analysis was made for degree distributions of individual networks, and these results also did not support a scale-free property (for examples of degree distributions see Supplementary Fig. 3).
Figure 6.
Various properties of interaction networks. (A) Average cumulative degree distribution (P|Degree ≥ k) for networks computed for the 2 values of thresholds, r (log–log plot). (B) The average degree values of individual neurons plotted against the neuron's average total connection strengths. (C) The average total connection strength of individual neurons plotted against the average mutual information between the activity of the corresponding neuron (spike present or not) and the activity of the remaining part of the investigated network (the pattern of spikes in other neurons). (D) The average total connection strength of individual neurons plotted against their OB. In A, B, and C, the results are shown only for the 24-neuron dataset and in D for all 63 neurons investigated in the present study and acquired across the 3 recording probes (R1–R3). Solid lines: best-fitting Gaussian function (A), best-fitting power law function (B), and best-fitting exponential function (C).
Weighted Networks
So far, we have not considered the strength of interactions but only whether pairs of neurons were connected or not. In the so-called “weighted” networks, each connection is assigned a weight, |J|, and the relation between the degree k and the total connection strength s = ∑jaij|Jij| is usually expressed well by the equation: s(k) ∼ kα, where a takes values 1 and 0, indicating respectively the presence and absence of connections, and i and j are the indices of the nodes (Barrat et al. 2004). If α = 1, the average strength of the connection is independent of the node's degree, and if α > 1, the nodes with strong connections are more likely to have high degrees. For the 24-neuron dataset, we calculated the average s and k for individual neurons across all 10-neuron networks for threshold r = 0.10 and found that the relationship between a node's degree and connection strength could be fitted best with s(k) ∼ k1.32 (Fig. 6B), that is, with an α value >1. For other thresholds and other datasets, α ranged between 1.2 and 1.6. This indicates that nodes with more connections are also more likely to have stronger connections.
Nodes rich in connections are addressed as hubs as their activity shares more mutual information with the rest of the network than does the activity of weakly connected nodes (see Fig. 6C). The mutual information, I, between a neuron i and the network increases as a function of the neuron's total connection strength, s′ = ∑j|Jij|. We calculated the relation between mutual information and total connection strength and in this case did not eliminate any connections by thresholding—but included all connections no matter how weak. Interestingly, in all datasets this relation followed an exponential function. Thus, the high mutual information and the strong connections of the nodes with high degree indicate that the present networks, although they are not scale free, posses hubs—neurons that are particularly well connected and likely to play a special role in cortical processing.
Orientation Tuning and Network Connectivity
In order to examine whether there was a relation between the neurons’ functional properties and their position in the network, we quantified the orientation tuning of cells and related it to their strength of connectivity. We used orientation selectivity as variable because this property is believed to be influenced by intracortical interactions (Sompolinsky and Shapley 1997; Ferster and Miller 2000). The hypothesized relation is already suggested by the example network shown in Figures 4 and 5, where sharply tuned units have predominantly a higher degree. Those units appear also more likely to connect to the units of different orientation preferences. The same conclusions were reached by the quantitative analysis. Neurons with strong OB (see Materials and Methods for calculations) were also strongly connected: Most of the neurons (93%, 26/28) with narrow orientation tuning (OB ≥ 0.2) had also strong interactions with the network (s′ ≥ 1.0) (Fig. 6D) and, as one would expect from the correlation shown in Figure 2 (inset), were also strongly synchronized with the rest of the network (result not shown). However, the association between connectedness and tuning was not as strong in the other direction: not all strongly connected neurons were also sharply tuned (note the triangle-shaped scatter in Fig. 6D).
Intrinsic Properties
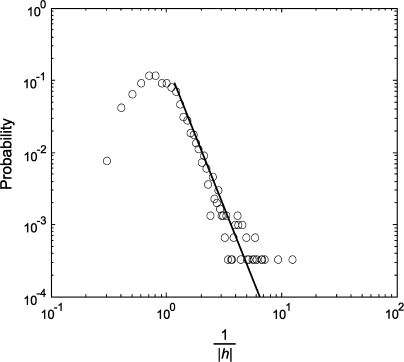
Nodes can have intrinsic properties that influence the dynamics of the network (e.g., see Huang 2005; Huang and Pipa 2007). The Ising model estimates such intrinsic properties by the parameter h (see eq. [2] in Materials and Methods). In the present case, such an intrinsic property is related to the probability of generating an action potential in the absence of all interactions with the considered network. A large value of |h| indicates that the neuron's activity is caused only to a small degree by the considered network. As shown in Figure 7, the reciprocal of |h| showed an exponential distribution with a right tail that follows a power law, that is, P(|h|−1) ∼ (|h|−1)β. The value of β was −4.0 for the 24-neuron dataset and −3.2 and −4.4 for the other 2 datasets. This result indicates that there is a large pool of neurons whose activity depends to a substantial extent on input from other sources than the considered network. Thus, as expected, a relatively small proportion of investigated neurons interact strongly with the analyzed networks.
Figure 7.
Distribution of the reciprocal of the absolute value of neuronal intrinsic property, |h|, estimated by the Ising model and shown in a log–log plot. Solid line: best-fitting power law function for the right tail of the distribution.
Discussion
Methodological Considerations
When interpreting the present results, several limitations need to be considered. First, we analyzed an arbitrary sample of neurons, ignoring their laminar positions and their anatomical connectivity. Second, the network was activated with a simple set of stimuli, and it cannot be excluded that other stimuli would have disclosed different functional networks. Third, interaction analysis was based solely on precise neuronal synchrony defined on a millisecond time scale. Although precise synchrony is thought to be important for information processing (Gray 1999; Singer 1999; Fries et al. 2007), it is possible that important interactions occur also at longer time scales and differ from those investigated in the present study. Unfortunately, the Ising model used in the present study could be applied only for short-time windows because it was based on the assumption of a binary procedure (spike or nonspike), which would have been violated if more than 1 spike had fallen often into the same window. Due to the typical response properties of visual cortical neurons, this violation started occurring already with windows larger than about 5 ms. Thus, for an analysis of larger windows, a different maximum entropy model should be used (e.g., Lezon et al. 2006). Finally, and this is the most important limitation, the number of cells used for network reconstruction was very small. The decision to restrict the analysis to networks of 10 neurons was the result of a trade-off between the rigorous analysis of correlation/interaction structures and the amount of data (the length of recordings) that could be acquired. Thus, we cannot exclude that analysis of larger networks would have revealed an important role of higher-order correlations or scale-free properties. In a related study of the interaction networks of genes (Lezon et al. 2006), larger networks have been studied, but this required that the trade-off between the rigor of analysis, controlling, for example, for the relevance of higher-order correlations, and the size of the treatable network had been biased towards the network size. Despite these limitations, we are confident that the reconstructed interaction networks reflect essential features of cortical organization: The strength of the identified interactions corresponds very well with the known layout of anatomical connectivity across cells with different orientation preferences and cortical distances. In addition, our results obtained from different cell samples were highly consistent.
Features of Cortical Interaction Networks
In the present study, we demonstrate, for the 1st time, that pairwise correlations capture most of the patterns found in the population activity of the visual cortex in vivo. Thus, our results extend previous in vitro studies (Schneidman et al. 2006; Shlens et al. 2006; Tang et al. 2008) that have come to the same conclusion. Considering the structural and functional differences between retina and cortex, this finding is significant and suggests that different types of neural networks such as retina and cortex obey certain basic rules. This conclusion may not be generalizable to large networks with reentry loops because a similar analysis, which would then require much longer recordings, might reveal higher-order couplings. However, even if this were the case, the high consistency of the results obtained from the 10-neuron groups (Fig. 2) suggests that the analysis of 2nd-order correlations still reveals basic features of cortical network architecture. This finding imposes a strong constraint on the possible mechanisms for the generation of neuronal synchrony. Thus, it remains to be investigated which types of neuronal architectures are capable of generating spike trains with such stochastic properties and how well they agree with the known anatomy and the functional organization of the brain.
After having extracted the interaction networks by applying the Ising model, we found that the functional networks of cortical neurons exhibit a small-world property. This result held for small 10-neuron networks as well as for larger reconstructed networks of up to 24 neurons. Consistent with these results from the interaction networks, we found that the correlation networks had also small-world properties. To the best of our knowledge, this is the 1st demonstration of small-world properties of cortical networks in vivo at the scale of singe cell interactions. This implies that the organization of cortical networks is ideally suited to support, within the same network, both local and global processing. At the scale investigated in the present study, local processes would correspond to interactions within and global processes to interactions across orientation columns.
Another interesting finding was the existence of neurons with many and strong connections that share much mutual information with the rest of the network—neurons that could be described as hubs. Their strong interactions correlated with narrow orientation tuning, suggesting an important functional role of these interactions for the formation of cells’ RF properties. Further studies, preferably in combination with the imaging of functional maps and morphological identification of the cells, are required in order to make inferences on a possible special function of these cells. One possibility is that these cells are more than others controlled by inhibitory networks. This could account for the sharp tuning of these cells and the fact that they are particularly well synchronized with other neurons in the network. This follows from the evidence that inhibitory interactions are both responsible for sharpening the neurons’ orientation selectivity (e.g., Sompolinsky and Shapley 1997) and for the synchronization of their discharges (e.g., Fries et al. 2007).
Consistent with the majority of other reports on brain connectivity (Achard et al. 2006; Humphries et al. 2006; He et al. 2007), the networks analyzed in the present study were not scale free. Instead, the degree distributions followed Gaussian decay. One possible reason is that constraints such as the limited dynamical range of neurons and/or space restrictions confine the number of connections per node and thereby prevent the implementation of very large hubs (Amaral et al. 2000). However, it is also conceivable that evolutionary selection has favored an architecture with a decay faster than power law because such networks are likely to be more resistant to the malfunction of nodes than scale-free networks (Achard et al. 2006). Importantly, the lack of scale-free property of the small-sized networks reported here cannot be simply extrapolated to larger networks, as Stumpf et al. (2005) have shown that subnetworks of a scale-free network are not necessarily scale free. Thus, we cannot exclude that a similar analysis of larger networks would have revealed scale-free properties.
Finally, the present results have important implications for the hypothesis that synchronization supports the perceptual organization of visual scenes (Gray 1999; Singer 1999; Fries et al. 2007). This study shows for the 1st time how patterns of synchronous firing are distributed across neurons and demonstrates a small-world organization of these synchronization patterns as well as of the underlying interaction skeleton that gives rise to these synchronization patterns. Thus, if synchronization serves to group responses to related features, the interaction network mediating synchronization is suited equally well to support both short- and long-distance synchronization or, in other words, binding functions at both local and global scales.
Funding
The Max-Planck Society; The Hertie Foundation; Deutsche Forschungsgemeinschaft (NI 708/2-1); The Alexander von Humboldt Foundation; National Natural Science Foundation of China (10572080); Shanghai Rising-Star Program (05QMX1422); and Dawn Project of the Education Committee of Shanghai Municipality (05SG41; 04YQHB089) to D.H.
Supplementary Material
Supplementary material can be found at: http://www.cercor.oxfordjournals.org/.
Supplementary Material
Acknowledgments
The authors would like to thank Diek Wheeler, Pascal Fries, and Raul Muresan for fruitful discussions; Martha Havenith and Julia Biederlack for help in data collection; and Nan-Hui Chen for providing the software for spike sorting. Debin Huang deceased on 31 August 2007. Conflict of Interest: None declared.
References
- Achard S, Bullmore E. Efficiency and cost of economical brain functional networks. PLoS Comput Biol. 2007;3(2):e17. doi: 10.1371/journal.pcbi.0030017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J Neurosci. 2006;26(1):63–72. doi: 10.1523/JNEUROSCI.3874-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albert R, Jeong H, Barabasi AL. Error and attack tolerance of complex networks. Nature. 2000;406(6794):378–382. doi: 10.1038/35019019. [DOI] [PubMed] [Google Scholar]
- Amaral LAN, Scala A, Barthelemy M, Stanley HE. Classes of small-world networks. Proc Natl Acad Sci USA. 2000;97(21):11149–11152. doi: 10.1073/pnas.200327197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barabasi AL, Albert R. Emergence of scaling in random networks. Science. 1999;286(5439):509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- Barrat A, Barthelemy M, Pastor-Satorras R, Vespignani A. The architecture of complex weighted networks. Proc Natl Acad Sci USA. 2004;101(11):3747–3752. doi: 10.1073/pnas.0400087101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Bullmore E. Small-world brain networks. Neuroscientist. 2006;12(6):512–523. doi: 10.1177/1073858406293182. [DOI] [PubMed] [Google Scholar]
- Bassett DS, Meyer-Lindenberg A, Achard S, Duke T, Bullmore E. Adaptive reconfiguration of fractal small-world human brain functional networks. Proc Natl Acad Sci USA. 2006;103(51):19518–19523. doi: 10.1073/pnas.0606005103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bettencourt LMA, Stephens GJ, Ham MI, Gross GW. Functional structure of cortical neuronal networks grown in vitro. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;75(2):021915. doi: 10.1103/PhysRevE.75.021915. [DOI] [PubMed] [Google Scholar]
- Biederlack J, Castelo-Branco M, Neuenschwander S, Wheeler DW, Singer W, Nikolić D. Brightness induction: rate enhancement and neuronal synchronization as complementary codes. Neuron. 2006;52(6):1073–1083. doi: 10.1016/j.neuron.2006.11.012. [DOI] [PubMed] [Google Scholar]
- Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang DU. Complex networks: structure and dynamics. Phys Rep. 2006;424(4–5):175–308. [Google Scholar]
- Castelo-Branco M, Neuenschwander S, Singer W. Synchronization of visual responses between the cortex, lateral geniculate nucleus, and retina in the anesthetized cat. J Neurosci. 1998;18(16):6395–6410. doi: 10.1523/JNEUROSCI.18-16-06395.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan JD, Friedman AE. Simple spin models for the development of ocular dominance columns and iso-orientation patches. In: Lippmann RP, Moody JE, Touretzky DS, editors. Proceedings of the 1990 Conference on Advances in Neural information Processing Systems 3. San Francisco: Morgan Kaufmann Publishers; 1990. pp. 26–31. [Google Scholar]
- Dan Y, Alonso JM, Usrey WM, Reid RC. Coding of visual information by precisely correlated spikes in the lateral geniculate nucleus. Nat Neurosci. 1998;1(6):501–507. doi: 10.1038/2217. [DOI] [PubMed] [Google Scholar]
- Eguiluz VM, Chialvo DR, Cecchi GA, Baliki M, Apkarian AV. Scale-free brain functional networks. Phys Rev Lett. 2005;94(1):018102. doi: 10.1103/PhysRevLett.94.018102. [DOI] [PubMed] [Google Scholar]
- Ferster D, Miller KD. Neural mechanisms of orientation selectivity in the visual cortex. Annu Rev Neurosci. 2000;23:441–471. doi: 10.1146/annurev.neuro.23.1.441. [DOI] [PubMed] [Google Scholar]
- Fingelkurts AA, Fingelkurts AA, Kahkonen S. Functional connectivity in the brain—is it an elusive concept? Neurosci Biobehav Rev. 2005;28(8):827–836. doi: 10.1016/j.neubiorev.2004.10.009. [DOI] [PubMed] [Google Scholar]
- Fries P. A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn Sci. 2005;9(10):474–480. doi: 10.1016/j.tics.2005.08.011. [DOI] [PubMed] [Google Scholar]
- Fries P, Nikolić D, Singer W. The gamma cycle. Trends Neurosci. 2007;30(7):309–316. doi: 10.1016/j.tins.2007.05.005. [DOI] [PubMed] [Google Scholar]
- Fries P, Roelfsema PR, Engel AK, Konig P, Singer W. Synchronization of oscillatory responses in visual cortex correlates with perception in interocular rivalry. Proc Natl Acad Sci USA. 1997;94(23):12699–12704. doi: 10.1073/pnas.94.23.12699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray CM. The temporal correlation hypothesis of visual feature integration: still alive and well. Neuron. 1999;24(1):31–47. doi: 10.1016/s0896-6273(00)80820-x. [DOI] [PubMed] [Google Scholar]
- Gray CM, Konig P, Engel AK, Singer W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature. 1989;338(6213):334–337. doi: 10.1038/338334a0. [DOI] [PubMed] [Google Scholar]
- Gray CM, Singer W. Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc Natl Acad Sci USA. 1989;86(5):1698–1702. doi: 10.1073/pnas.86.5.1698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y, Chen ZJ, Evans AC. Small-world anatomical networks in the human brain revealed by cortical thickness from MRI. Cereb Cortex. 2007;17(10):2407–2419. doi: 10.1093/cercor/bhl149. [DOI] [PubMed] [Google Scholar]
- Hilgetag CC, Kaiser M. Clustered organization of cortical connectivity. Neuroinformatics. 2004;2(3):353–360. doi: 10.1385/NI:2:3:353. [DOI] [PubMed] [Google Scholar]
- Huang D, Pipa G. Achieving synchronization of networks by an auxiliary hub. Europhys Lett. 2007;77(5):50010. [Google Scholar]
- Huang DB. Simple adaptive-feedback controller for identical chaos synchronization. Phys Rev E. Stat Nonlin Soft Matter Phys. 2005;E 71(3):037203–037207. doi: 10.1103/PhysRevE.71.037203. [DOI] [PubMed] [Google Scholar]
- Humphries MD, Gurney K, Prescott TJ. The brainstem reticular formation is a small-world, not scale-free, network. Proc Biol Sci. 2006;273(1585):503–511. doi: 10.1098/rspb.2005.3354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser M, Martin R, Andras P, Young MP. Simulation of robustness against lesions of cortical networks. Eur J Neurosci. 2007;25(10):3185–3192. doi: 10.1111/j.1460-9568.2007.05574.x. [DOI] [PubMed] [Google Scholar]
- Lago-Fernandez LF, Huerta R, Corbacho F, Siguenza JA. Fast response and temporal coherent oscillations in small-world networks. Phys Rev Lett. 2000;84(12):2758–2761. doi: 10.1103/PhysRevLett.84.2758. [DOI] [PubMed] [Google Scholar]
- Leventhal AG, Thompson KG, Liu D, Zhou Y, Ault SJ. Concomitant sensitivity to orientation, direction, and color of cells in layers 2, 3, and 4 of monkey striate cortex. J Neurosci. 1995;15(3):1808–1818. doi: 10.1523/JNEUROSCI.15-03-01808.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lezon TR, Banavar JR, Cieplak M, Maritan A, Fedoroff NV. Using the principle of entropy maximization to infer genetic interaction networks from gene expression patterns. Proc Natl Acad Sci USA. 2006;103(50):19033–19038. doi: 10.1073/pnas.0609152103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micheloyannis S, Pachou E, Stam CJ, Breakspear M, Bitsios P, Vourkas M, Erimaki S, Zervakis M. Small-world networks and disturbed functional connectivity in schizophrenia. Schizophr Res. 2006;87(1–3):60–66. doi: 10.1016/j.schres.2006.06.028. [DOI] [PubMed] [Google Scholar]
- Montoya JM, Sol RV. Small world patterns in food webs. J Theor Biol. 2002;214(3):405–412. doi: 10.1006/jtbi.2001.2460. [DOI] [PubMed] [Google Scholar]
- Neuenschwander S, Singer W. Long-range synchronization of oscillatory light responses in the cat retina and lateral geniculate nucleus. Nature. 1996;379(6567):728–733. doi: 10.1038/379728a0. [DOI] [PubMed] [Google Scholar]
- Panzeri S, Treves A. Analytical estimates of limited sampling biases in different information measures. Network Comput Neural Syst. 1996;7(1):87–107. doi: 10.1080/0954898X.1996.11978656. [DOI] [PubMed] [Google Scholar]
- Schmidt KE, Goebel R, Lowel S, Singer W. The perceptual grouping criterion of colinearity is reflected by anisotropies of connections in the primary visual cortex. Eur J Neurosci. 1997;9(5):1083–1089. doi: 10.1111/j.1460-9568.1997.tb01459.x. [DOI] [PubMed] [Google Scholar]
- Schneidman E, Berry MJ, Segev R, Bialek W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature. 2006;440(7087):1007–1012. doi: 10.1038/nature04701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneidman E, Still S, Berry MJ, Bialek W. Network information and connected correlations. Phys Rev Lett. 2003;91(23):238701. doi: 10.1103/PhysRevLett.91.238701. [DOI] [PubMed] [Google Scholar]
- Schnitzer MJ, Meister M. Multineuronal firing patterns in the signal from eye to brain. Neuron. 2003;37(3):499–511. doi: 10.1016/s0896-6273(03)00004-7. [DOI] [PubMed] [Google Scholar]
- Shlens J, Field GD, Gauthier JL, Grivich MI, Petrusca D, Sher A, Litke AM, Chichilnisky EJ. The structure of multi-neuron firing patterns in primate retina. J Neurosci. 2006;26(32):8254–8266. doi: 10.1523/JNEUROSCI.1282-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simard D, Nadeau L, Kroger H. Fastest learning in small-world neural networks. Phys Lett A. 2005;336(1):8–15. [Google Scholar]
- Singer W. Neuronal synchrony: a versatile code for the definition of relations? Neuron. 1999;24(1):49–65. doi: 10.1016/s0896-6273(00)80821-1. [DOI] [PubMed] [Google Scholar]
- Sompolinsky H, Shapley R. New perspectives on the mechanisms for orientation selectivity. Curr Opin Neurobiol. 1997;7:514–522. doi: 10.1016/s0959-4388(97)80031-1. [DOI] [PubMed] [Google Scholar]
- Sporns O, Chialvo DR, Kaiser M, Hilgetag CC. Organization, development and function of complex brain networks. Trends Cogn Sci. 2004;8(9):418–425. doi: 10.1016/j.tics.2004.07.008. [DOI] [PubMed] [Google Scholar]
- Sporns O, Tononi G, Edelman GM. Theoretical neuroanatomy: relating anatomical and functional connectivity in graphs and cortical connection matrices. Cereb Cortex. 2000;10(2):127–141. doi: 10.1093/cercor/10.2.127. [DOI] [PubMed] [Google Scholar]
- Sporns O, Zwi JD. The small world of the cerebral cortex. Neuroinformatics. 2004;2(2):145–162. doi: 10.1385/NI:2:2:145. [DOI] [PubMed] [Google Scholar]
- Stam CJ. Functional connectivity patterns of human magnetoencephalographic recordings: a ‘small-world’ network? Neurosci Lett. 2004;355(1–2):25–28. doi: 10.1016/j.neulet.2003.10.063. [DOI] [PubMed] [Google Scholar]
- Stam CJ, Jones BF, Nolte G, Breakspear M, Scheltens P. Small-world networks and functional connectivity in Alzheimer's disease. Cereb Cortex. 2007;17(1):92–99. doi: 10.1093/cercor/bhj127. [DOI] [PubMed] [Google Scholar]
- Stephan KE, Hilgetag CC, Burns GA, O'Neill MA, Young MP, Kotter R. Computational analysis of functional connectivity between areas of primate cerebral cortex. Philos Trans R Soc Lond B Biol Sci. 2000;355(1393):111–126. doi: 10.1098/rstb.2000.0552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stumpf MP, Wiuf C, May RM. Subnets of scale-free networks are not scale-free: sampling properties of networks. Proc Natl Acad Sci USA. 2005;102(12):4221–4224. doi: 10.1073/pnas.0501179102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang A, Jackson D, Hobbs J, Chen W, Smith JL, Patel H, Prieto A, Petrusca D, Grivich MI, Sher A, et al. A maximum entropy model applied to spatial and temporal correlations from cortical networks in vitro. J Neurosci. 2008;28(2):505–518. doi: 10.1523/JNEUROSCI.3359-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toyama K, Kimura M, Tanaka K. Cross-correlation analysis of interneuronal connectivity in cat visual-cortex. J Neurophysiol. 1981;46(2):191–201. doi: 10.1152/jn.1981.46.2.191. [DOI] [PubMed] [Google Scholar]
- Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature. 1998;393(6684):440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.