Cortical Dynamics Subserving Visual Apparent Motion

Abstract

Motion can be perceived when static images are successively presented with a spatial shift. This type of motion is an illusion and is termed apparent motion (AM). Here we show, with a voltage sensitive dye applied to the visual cortex of the ferret, that presentation of a sequence of stationary, short duration, stimuli which are perceived to produce AM are, initially, mapped in areas 17 and 18 as separate stationary representations. But time locked to the offset of the 1st stimulus, a sequence of signals are elicited. First, an activation traverses cortical areas 19 and 21 in the direction of AM. Simultaneously, a motion dependent feedback signal from these areas activates neurons between areas 19/21 and areas 17/18. Finally, an activation is recorded, traveling always from the representation of the 1st to the representation of the next or succeeding stimuli. This activation elicits spikes from neurons situated between these stimulus representations in areas 17/18. This sequence forms a physiological mechanism of motion computation which could bind populations of neurons in the visual areas to interpret motion out of stationary stimuli.

Introduction

The detection of motion is an integral part of vision (Nakayama 1985). Although there has been some progress in the physiological mechanisms the visual system uses to detect the position and motion of objects (Motter and Mountcastle 1981; Steinmetz et al. 1987; Albright and Stoner 1995), we are still far from understanding the computation of object motion. Motter et al. (1987) showed that moving objects in the parietal cortex were represented by a traveling (wave of) inhibition and excitation. Still, however it is not known how moving objects are represented in early and intermediate visual areas. Intuitively and logically, the visual system must use information related to the disappearance of a stimulus at one position and its reappearance at an adjacent position to compute motion: a result that tells the brain that an object has spatially shifted within the visual field. The topic however is more complicated, because one can perceive motion from a brief sequence of stationary images presented in different positions. This illusion is called apparent motion (AM) (Exner 1875; Wertheimer 1912). During continuous motion there is evidence that a retinal contribution to motion may exist as a time locked wave of ganglion cell spike discharge across the retina ahead of the position of a continuously moving object (Berry et al. 1999). Hence, it is difficult to discern the contributions of the brain in motion perception from the contributions of the retina. For this reason we examined AM in order to establish how early and intermediate visual areas compute motion out of a sequence of stationary objects. AM exists in primates (Newsome et al. 1986; Muckli et al. 2002; Claeys et al. 2003; Merchant et al. 2003; Zhou et al. 2003), carnivores (Pasternak 1987; van Wezel et al. 1997), and probably in all mammals.

A sequence of stationary images which induce AM can be presented over a short-range (less than a degree of the visual field) or over a longer range (several degrees). Short-range AM depends on stimulus conditions different from those causing long-range AM (Braddick 1980; Anstis and Mather 1985; Chubb and Sperling 1988). Both of these illusions are very robust in their basic form: it is impossible by conscious effort or attention to inhibit or change the direction, speed and vividness with which the stationary stimuli appear to move (Palmer 1992). As the stimuli producing AM are stationary on the retina, the brain must compute the perception of motion. It is known that neurons in early and intermediate visual areas react to long-range AM (Newsome et al. 1986; Muckli et al. 2002; Claeys et al. 2003; Merchant et al. 2003; Zhou et al. 2003). We expected long-range AM, therefore, to depend on communication within area 17 as well as long-range communication between several visual areas. As long-range corticocortical axons are excitatory (Maunsell and Van Essen 1983; Loewenstein and Somogyi 1991; Rockland and Drash 1996; Anderson and Martin 2002), one may be able to detect increases in excitation of the target neurons elicited by long-range axons (Roland et al. 2006).

We, therefore, examined the physiological basis of AM by staining 4 visual cortical areas (areas 17,18, 19, and 21) of the ferret with a voltage sensitive dye and recorded the signals from these areas under stimulus conditions that lead to long-range AM. This revealed that the long-range AM conditions tested were always associated with activations in the cortex moving in the direction of the AM. In addition, we found that these activations were always preceded by a feedback from areas 21 and 19.

Materials and Methods

All experimental procedures were approved by the Institutional Animal Care and Use Committee of Karolinska Institute and were performed according to Swedish and European Community guidelines for the care and use of animals in scientific experiments and the policies of the use of animals in neuroscience research of the Society for Neuroscience, 1995.

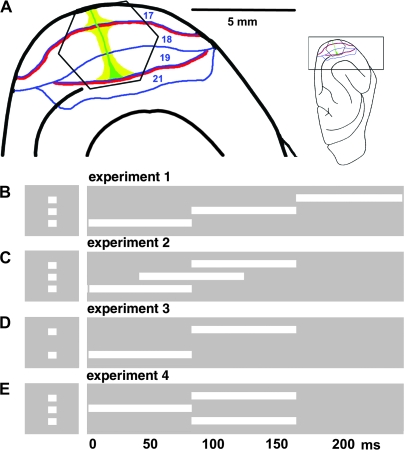
Ten fully anaesthetized adult female ferrets (isoflurane 1%, N₂O:O₂, 50:50) were paralyzed (pancuronium bromide 0.6 mg/kg/h, i.v.) and artificially ventilated, expiratory CO₂ and body temperature were maintained between, respectively, 3.3–4% and 37°C. The pupil was dilated (1% atropine sulfate eye drops) and a contact lens was placed over one eye, the other eye was occluded. After a right-sided craniotomy and dural resection, the animal was equipped with a pressure chamber (Optical Imaging, Rehevot, Israel) and the exposed visual cortex was stained for 2 h with the voltage sensitive dye RH 795 (Molecular Probes, Leyden, The Netherlands) at 0.5 mg/ml. Figure 1A shows the cortical region used for the optical recording.

Figure 1.

Experimental setup. (A) The insert shows the orientation of ferret brain. The visual cortex is enlarged at the left. The hexagonal photodiode array monitor visual areas 17, 18, 19, and 21. Each channel of the array picks up the signal from a cortical area with a diameter of approximately 150 μm. The representations of the vertical meridians of the field of view are red, the horizontal meridian is green and the representation of the 5° center of field of view, yellow (after Manger et al. 2002). In all experiments 2 × 2° white squares were presented for 83 ms along the vertical meridian. The baseline condition was a homogenous gray background of the same average luminance as the stimulus conditions. (B) Experiment 1, 1 square appears 1st 3.5° below, then at 83 ms at the center of field of view, and at 166 ms 3.5° above the horizontal meridian. Control stimuli: a single stationary square displayed in 1 of these 3 positions. (C) Experiment 2: As in (B) but the onset times are 0, 42, and 83 ms. (D) Experiment 3: onset times 0 and 83 ms, distance 7° between 1st and last square. (E) Experiment 4: split motion, central square presented at 0 ms, at 83 ms 1 square in top + 3.5° and 1 in lower position −3.5° from the central square. Controls (not shown) at 0 ms single square in central position, at 83 ms the top and lower square simultaneously.

Visual Stimuli

Visual stimuli were presented on a computer display (Cambridge Research Systems, Cambridge, UK), refreshed at 120 Hz, placed at a distance of 57 cm from the animal. The right eye was occluded and all stimuli were delivered to the left eye. The stimulus was a white square (2° by 2°, duration 83 ms, and 120 cd/m²) presented on a uniform gray background (30 cd/m²). The square was always presented in the following positions along the vertical meridian (checked by electrophysiology) 3.5° below the horizontal meridian (lower square), at the crossing of the vertical and horizontal meridian (center square), and 3.5° above the horizontal meridian. For the stationary control conditions, the square was presented in 1 of the 3 positions at the onset time matching the AM condition (experiment 1). Figure 1B–E illustrates the 4 different stimulus conditions for AM. In experiment 1 the square is displayed successively at the 3 positions: lower, central, and top. In experiment 2, the exposure of the central and lower square and the top and central square overlaps in time (Fig. 1C). In experiment 3, the distance between the successive square positions is increased to 7°, such that 1st the lower is displayed, then the top square (Fig. 1D). In experiment 4, 1st a central square is presented, then the lower and top square is presented simultaneously. This induces a perception of the single square being split into 2 (Fig. 1D). Each stimulus trial had a 200 ms prestimulus period. A gray screen of the same average luminance as in the stimulus and control conditions was used as a baseline for the creation of difference images. The AM conditions are shown in Figure 1.

Voltage Sensitive Dye Measurements

A Wu-Tech H469-IV^R camera with an array of hexagonally arranged 464 photodiode detectors and a RedShirtImaging^R macroscope (RedShirtImaging, Fairfield, CT) with 2× objective were used for optical imaging. The frame rate was 1 frame every 0.61 ms. The photodiode array measured from a hexagonal cortical area of diagonal length 4.2 mm (Fig. 1A). The excitation filter was a 530 nm narrow band filter (Schott 530 VG6, Scott AG, Mainz, Deutschland) and the acquisition a long pass 610-nm filter (Schott RG 610, Scott AG). The stimulus presentation was synchronized with the electrocardiogram (ECG) signal, and respiration was stopped during stimulus presentation. During recordings the animal was placed on a vibration free table (Minus K Technology, Inglewood CA). The voltage sensitive dye RH 795 stains all layers of the cerebral cortex. Due to attenuation of the photons the signal reaching the detectors will stem mainly from the upper, supragranular layers (Kleinfeld and Delaney 1996; de Curtis et al. 1999). The pulse artifact of RH 795 is much larger than that of the new blue dyes (e.g., RH 1691) especially near pial vessels, but the signal to noise ratios of the 2 dyes are comparable in cortex away from the vessels (Civillico and Contreras 2005). The laminar staining of RH 795 is strongest for layer I of the cortex and diminishes exponentially with depth (Kleinfeld and Delaney 1996; de Curtis et al. 1999), whereas RH 1691 stains layer II the strongest (Petersen et al. 2003a; Lippert et al. 2007). Thus RH 795 might have an advantage for detecting activations in layer I, such as those that could be caused by feedback axons terminating here (Rockland and Drash 1996). Each detector channel monitored a small circular cortical area of 150 μm in diameter.

Electrophysiology and Anatomy

The action potentials of single/multiple neurons were recorded with thin tungsten electrodes (impedance range: 0.8–1.1 MΩ; FHC, Boudain, ME) mainly from the upper (supragranular) layers of the visual cortex. A total of 59 units responded statistically significantly to one or more of the stimuli in the AM condition. The electrode positions were marked and occasional coagulation marks were left to calibrate the depth measurements from the microdrive. A Poisson distribution was fitted to the spike trains in the prestimulus period and spikes from the background trial. Spike trains passing both the criterion of having significantly increased discharge rate compared with the prestimulus period of P < 0.01 and increased rate compared with the background condition of P < 0.01, were considered statistically significant periods of firing.

After recordings, the brain was sectioned, stained (Nissl and cytochrome oxidase) and cytoarchitectonic areal borders were marked and electrode marks identified (Innocenti et al. 2002). The sections were reconstructed and fitted to the pictures of the operative field and voltage sensitive dye recording sites, to match the electrode penetrations. The reconstruction provided a mapping of the cytoarchitectural borders between the 4 visual areas 17, 18, 19, and 21. As the cytoarchitectural border between areas 17 and 18 marks the position of the vertical meridian, we could by this independent information evaluate whether the initial electrode penetrations, for the localization of the crossing between the vertical and horizontal meridian (Fig. 1), indeed were localized along the vertical meridian. Similarly, we evaluated whether the retinotopic sites of the square stimulus (see below) were overlapping the cytoarchitectural border between areas 17 and 18.

Data Processing

The voltage sensitive dye signal from the background condition was subtracted from that of the stimulus condition trial by trial. This subtraction was done in order to remove pulse artifacts. Although the stimulus presentation was synchronized with the ECG signal, this does only guarantee that the 1st ECG spike is aligned for the stimulus and background trial, as the later ECG spikes may diverge more and more. In order for the pulse artifact subtraction to work during the whole trial, the voltage sensitive dye signal for the background condition was modified as follows. If the ECG spike for the stimulus condition arrived prior to the ECG spike in the background condition then the frames at certain time points were removed from the background condition such as to compress the background condition in time, and hence align the ECG spikes for the 2 conditions. The exact time points at which to remove the single frames were decided with linear interpolation. If the ECG spike for the stimulus condition arrived after the ECG spike in the background condition then frames were inserted in the background file in order to expand the background condition in time. If an image had to be inserted at time point t_n then the actual frame inserted was the frame at time point t_n–1, that is, the frame at t_n–1 is copied such as to be on position t_n and the following frames are shifted forward by 0.616 ms. This procedure efficiently removed the pulse artifact as seen in the data and autocorrelation in Supplementary Figure 1.

ΔV(t)_xy is the difference in fluorescence to the stimulus minus the fluorescence to the baseline gray screen, divided by the fluorescence obtained in darkness F_0,xy . For 1 detector channel x,y:

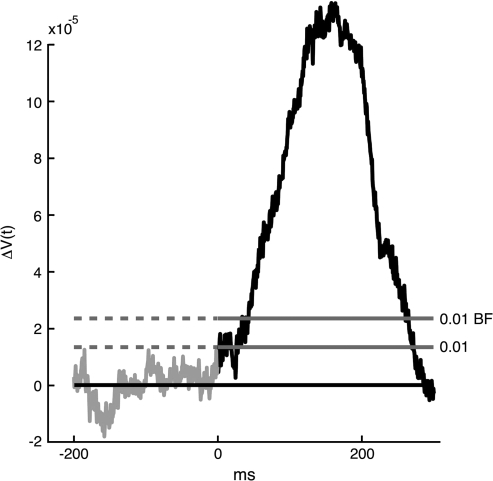
in which stim is a stimulus condition, ctl is the condition with only the gray screen presented. As the voltage sensitive dye signal V(t) depends on the amount of stain, one must normalize the signal by dividing with the fluorescence recorded with the animal in total darkness (screen off). Usually, 10–16 ΔV(t)_xy were averaged by adding the files and dividing by the number of files (averaging of the temporal course of the ΔV(t)_xy). In the text this average is referred to as simply ΔV(t)_. Using the amplitude fluctuations in the prestimulus interval to define the noise level for each channel, the ΔV(t)_xy was thresholded at P < 0.01 of being noise (P < 0.01 1-sided, as only ΔV(t) increases occurred in response to the stimulus conditions). In this we assumed the amplitude fluctuations to be not significantly different from a Gaussian distribution. A threshold of estimated P < 0.01 was set for each photodiode detector channel and divided by the number of channels (464) to give the Bonferroni corrected value of P < 0.01 (Fig. 2) which is used for determining the statistical significance.

Figure 2.

Statistics of the ΔV(t)_xy. The voltage sensitive dye signal from 1 channel, ΔV(t)_xy, after 12 averages (Animal 89). The lower threshold is the 0.01 threshold uncorrected for multiple comparisons. The upper threshold labeled 0.01 BF is the Bonferroni corrected threshold.

The relative amplitude was calculated for the poststimulus interval, that is, from 0 to 400 ms after the start of the stimulus as the (ΔV(t)_xy − ΔV(t)_xymin) divided by the overall maximal amplitude − minimal amplitude (ΔV(t)_xymax − ΔV(t)_xymin), that is,

in which ΔV(t)_xymin is the minimum value of ΔV(t)_xy in the poststimulus interval up to 400 ms. In the text, the index xy is suppressed and ΔV(t)_xy,_relative is referred to simply as ΔV(t)rel.

In vitro the dye signal, V(t), is a linear function of the membrane potential (Davila et al. 1973; Salzberg et al. 1973; Cohen et al. 1974; Grinvald and Hildesheim 2004). However, as the absolute dye signal depends on the amount of staining one divides the raw signal by F_{0, xy.} Further, the dye signal must be calibrated by intracellular recordings/patch clamping. This is not possible in vivo where large populations of neurons and glia cells are stained. Furthermore, in vivo, the photons from deeper layers of cortex are attenuated and those from the upper layers are scattered. In addition, the in vivo signals, V(t)_xy,stim and V(t)_xy,ctl have a pulse artifact. The pulse artifact can in practice be removed (see above). Still given this, the signal may also be subjected to equipment noise and fluctuations in the number of photons due to variations in the illumination source.

Still if one assumes the noise sources are invariant and the pulsation artifact removed, it is not possible to measure depolarization and hyperpolarization in vivo. In the strict sense depolarization is an increase in the absolute value of the membrane potential of a cell. This means that depolarization is defined from the resting potential, that is the membrane potential of a neuron without any synaptic input. Consequently the definition of depolarization and hyperpolarization will not work in vivo. The ΔV(t)_xy is a difference signal between the signal introduced by the background and the square + background that is made relative due to the division by the resting light intensity, F₀. If the ΔV(t) is >0 it means that the cortex from which the signal originates is relatively more depolarized during the stimulus condition, than during the condition when only the background is exposed to the animal. If the ΔV(t) < 0 the cortex during background condition is relatively more depolarized than it is during the AM condition. The ΔV(t)_xy will consequently indicate changes in the deporalization direction and changes in the hyperpolarizing direction, provided that the pulse artifact is removed and the noise is identical in the 2 conditions. Furthermore as the component from glia cells is moderate and has a much slower time course compared with the neuronal changes in membrane potentials (Konnerth and Orkand 1986; Lev-Ram and Grinvald 1986; Konnerth et al. 1988; Bergles and Jahr 1997), fast changes of ΔV(t) may be ascribed to the neurons. That the ΔV(t) is a reliable measurement of the relative changes in population membrane potentials of supragranular neurons is also verified by simultaneous in vivo measurements of the V(t) and the membrane potentials of neurons in layers II and III (Petersen et al. 2003a, 2003b; Ferezou et al. 2006). Therefore, we use the term relative depolarization for ΔV(t) increases under the above conditions.

Retinotopic sites were defined as the 4–7 coherent small cortical areas (corresponding to the cortex monitored by 4–7 photodiode detector channels) having the maximal amplitude of ΔV(t) close to or at the cytoarchitectonic defined borders between areas 17/18 or 19/21. The criterion was that at least 1 small area overlapped the reconstructed cytoarchitectural border. The cortical size of the retinotopic sites were estimated based on the magnification factors provided by (Manger et al. 2002; see also Fig. 1).

Detection of Wave-Fronts

The results showed that ΔV(t) increases in the shapes of wave-fronts in amplitude plots of the cortex were associated with all conditions of AM. A wave-front is just a surface of points having the same phase. The algorithm described in Figure 3 was made to detect such wave-fronts. All wave-fronts progressed from one retinotopic site to the next retinotopic site.

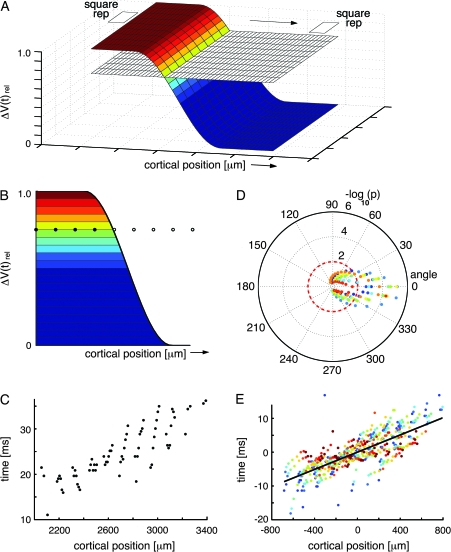
Figure 3.

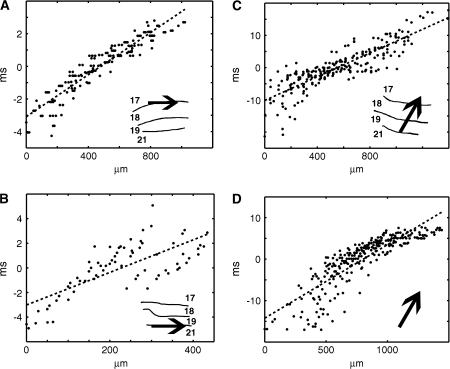
Statistical estimation of the progress of the wave-fronts. (A) A schematic of the depolarization wave-front progressing from the cortical retinotopic site of one square to the retinotopic site of the next square. During its passage between these sites, the wave-front passes cortical positions monitored by the photodiode detector array channels, symbolized by the plane with the small squares. For the time interval of the sliding time window, the mean values of the ΔV(t)rel were calculated across the width of the wave-front. This mean level is indicated on the wave-front as the transition of the dark blue to the slightly lighter blue color. Then the amplitude from ΔV(t)rel mean to the maximum value 1.0 was divided into 10 levels of amplitudes. This allowed visualization of the wave-front as it passed over a given cortical point on its path by exhibiting successively higher levels of amplitudes. These 10 levels of the wave-front are illustrated by the 10 different colors deviating from the dark blue. (B) One section of the wave-front at a given time point. If the wave-front progresses in 1 direction, 1 amplitude level of the wave-front will pass successive points of the cortex with increasing time. The same applies for any other amplitude level represented by a different color. Note that wave-fronts, in contrasts to traveling waves do not need to progress with constant velocity and amplitude. (C) Plot of real data from animal 60, showing the progression of the yellow amplitude level in (B) across the cortex from the retinotopic site of the lower square to the retinotopic site of the central square. Time zero indicates 100 ms after the start of the lower square stimulus. (D) Polar plot of the direction and significance of the wave-front progression for all amplitude levels. The color coding of the amplitude levels is seen in (B). The rings 2,4.6 show the −log₁₀P values of the slope of the regression of each amplitude level being equal to zero. The polar plot also shows that the most significant direction of progress is 0°. (E) Regressions of position versus time for all 10 amplitude levels for the optimal direction of progress aligned by their centers of gravity. This regression has R² = 0.85 and a −log₁₀P > 7. The P values of the regressions for each animal are shown in Table 2. The slope of the regression of the aligned points will underestimate the velocity with which the wave-front progresses (see Fig. 6).

The wave-fronts appeared in 3 places of the visual cortex: 1) along the cytoarchitectural border of areas 17 and 18, and between the retinotopic site of one square and the next square; 2) along the cytoarchitectural border of areas 21 and 19, and between the retinotopic site of one square and the next; and 3) between the retinotopic site of the square at the area 19/21 border and the retinotopic site of the square at the area 17/18 border. For each of these paths, approximately 600–800 μm wide, we examined whether there was a wave-front of increased ΔV(t) moving between these defined sites which was time locked to the offset of the square at 1 position (30–60 ms after the offset). During its passage between these sites, the wave-front passes cortical positions monitored by the photodiode detector array channels, symbolized by the plane with the small squares in Figure 3A. To distinguish wave-front propagation from an iceberg effect, that is, progression of a general increase in all directions, we calculated the ΔV(t)rel showing the phase of ΔV(t). The algorithm for wave-front detection has a sliding time window of 30 ms during which it, for each amplitude level of ΔV(t)rel above mean, plots the relation between time of arrival and distance over cortex for any progression over cortex in any direction (Fig. 3B). It then calculates the regression of time of arrival versus cortical position of progress for each of the amplitude levels (Fig. 3C) and plots the −log₁₀P values for the slope of the regression being = 0 for all tested directions (Fig. 3D). Finally, the −log₁₀P value is calculated for all tested levels together with the direction giving the highest −log₁₀P value (Fig. 3E). The algorithm automatically examines all directions 0–360° in steps of 10°. For each step the −log₁₀P value is plotted for that direction. The final direction of wave-front motion is that giving the highest −log₁₀P value. This is the best estimate of the direction of propagation of the wave-front. As the algorithm examines each amplitude level (Fig. 3C) the positions of the wave-front surface points for that level are mapped in cortical space in time steps of 0.6 ms. If the progress/time-step is approximately identical from step to step, the points will be close to the regression line. For other directions the progress/time-step will deviate more from the regression line and, hence, will give a lower −log10P value. This will apply to any wave-front irrespective of its profile.

The time derivative of a ΔV(t) iceberg is a wave progressing in all directions outward from the edge of the iceberg, whereas the time derivative of a directed wave-front is a unidirectional moving wave. Note that wave-fronts, in contrast to traveling waves, do not need to progress with constant velocity and amplitude. Note also that a lateral spreading depolarization out from a retinotopic site per definition is also a shallow wave-front. In this case the wave-front is circular with new amplitude levels appearing from the center or edge of the retinotopic site. For the iceberg, this is not the case, as the outward wave when the time derivative is taken of the emerging iceberg is located only where the iceberg breaks the surface, that is, at the edge of the iceberg.

Calculation of the speed of the wave-front was done from the time derivative of ΔV(t), that is, d(ΔV(t))/dt was calculated and then the slope of the overall regression (as in Fig. 3E) was estimated with the wave-front detection algorithm. Calculating the speed of the wave-front from the ΔV(t) or ΔV(t)rel tends to underestimate the velocity of propagation as higher amplitude levels tended to move more slowly.

The contribution of the wave-fronts to the total signal was calculated using a similar strategy. The ΔV(t) was divided into 10 levels. The lowest level, showing a motion from one retinotopic site of the square to the next retinotopic site, was the magnitude that separated the wave-front from the underlying depolarization (as the wave-front was superimposed on the lateral spreading depolarization, see Results). This was done for all animals and gave a mean value of 34 ± 12%. The mean velocity of the wave-fronts was calculated from the slope of the regression line of the d(ΔV(t))/dt from the path of the wave-front.

The differences in dynamics between an AM condition signal and the control conditions was calculated by adding the ΔV(t)'s from the 3 control conditions in which the squares were presented individually, to form ∑ΔV(t). Then the ΔV(t) from AM and the ∑ΔV(t) was normalized as described under the calculation of ΔV(t)rel. Then the difference ΔV(t)rel, AM − ΔV(t)rel,sum was calculated. This difference was then differentiated, that is,

Results

We calculated ΔV(t), that is, the difference in the voltage sensitive dye signal between luminance contrast square stimuli and the condition in which only the gray screen was shown, from the upper layers of the ferret visual cortex (Salzberg et al. 1973; Cohen et al. 1974; Grinvald and Hildesheim 2004). This signal, V(t), was sampled at a rate of 0.61 ms per frame. In this report we focus on the dynamics of the voltage sensitive dye signals associated with long-range AM elicited by a small square shown in successively different positions (Fig. 1).

In experiment 1, the ferrets were shown a short display of a static square in 1 of 3 different positions, separated by 3.5° along the vertical meridian in independent trials: lower, center, and top. This served as a control for the AM condition. In the 4th trial of experiment 1, 3 squares were shown in identical positions, but in quick succession lower–center–top (Fig. 1B). This produces a clear perception of (apparent) object motion in humans (Supplementary Video 1). The last trial was a blank screen at the same average luminance, which served as the baseline condition. The signal from this baseline condition was subtracted from the signal of the stimulus conditions to produce the voltage sensitive dye signal ΔV(t) (see Methods). The analysis reported here was restricted to the period during which the signal was statistically significant (P < 0.01 after Bonferroni correction; see Methods). First we examined how these squares were mapped in the upper layers of the visual cortex in terms of a high ΔV(t) increase.

As the stimuli in all experimental conditions were stationary on the retina (the animals were anaesthetized and the eye muscles paralyzed), the AM must be produced by the brain. To investigate how, one must examine the dynamics of the neuron populations in the visual areas. This is done here by measurements of relative changes in the membrane potentials of populations of neurons in the supragranular layers, ΔV(t), of the visual areas (see Methods). There are only 3 papers dealing with the spatial and temporal dynamics in visual areas in mammals after stimulation with transient stimuli (Jancke et al. 2004; Chen et al. 2006; Roland et al . 2006). From the paper of Jancke et al. (2004) one may predict that the expected dynamics of stimulating with 2 stationary stimuli, one after another, could be approximated by a linear combination of the dynamics to the single stimuli in area 17. Directly following this, our null hypothesis is that the AM dynamics could be described in areas 17 and 18 by

in which, ΔV_L(t) is the relative change in the population membrane following stimulation with the lower square (Fig. 1); ΔV_C(t) is the relative change in the population membrane following stimulation with the center square; ΔV_T(t) is the relative change in the population membrane following stimulation with the top square. Therefore we 1st examined the dynamics by presenting only 1 square in 1 of the 3 positions: lower, center, and top.

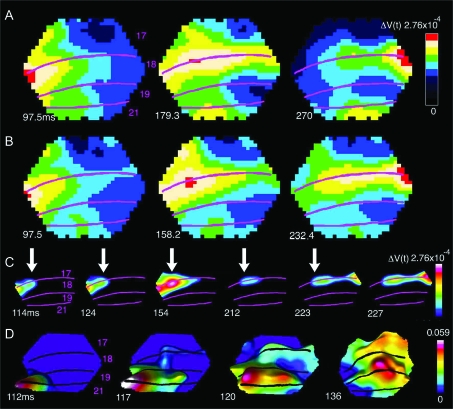
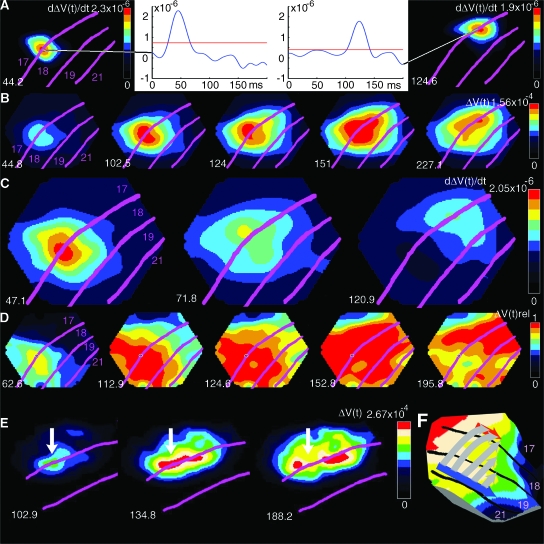
The 83 ms display of 1 static square produced a ΔV(t) increase, an activation, starting at 36 ± 2 ms (mean ± SD, n = 10) following the onset of the stimulus. The activation became maximal at a site where it 1st appeared, at the location of the border between areas 17 and 18. That site was the retinotopic site of the square in the visual cortex at the area 17/18 border (Fig. 4A, Methods). With the single static square at the 3 different positions, the respective retinotopic sites were mapped along the border between areas 17 and 18, that is, along the cortex where the vertical meridian of the field of view was represented. The ΔV(t) increase also spread out spatially from the retinotopic site such that the activation covered a larger area of the visual cortex (Fig. 4A). This lateral spread of the activation outside the immediate location of the retinotopic site has been observed for visual stimuli, even to very small ones, and has been described in detail earlier (Grinvald et al. 1994; Roland et al. 2006). Inevitably, the activation in supragranular layers, therefore, spreads to cover most of areas 17 and 18 (Roland et al. 2006). In addition, there is a weaker activation at the retinotopic site for the square at the border of areas 19/21 (yellow in Fig. 4A, middle and right). Here one can see some spatial overlap between the retinotopic sites as expected from earlier multiunit recordings in these areas (Manger et al. 2002; Cantone et al. 2005).

Figure 4.

The dynamics of AM in Experiment 1 (see Fig. 1b for stimulus presentation; Animal 60). (A) Control trials for experiment 1. The absolute depolarization ΔV(t) in response to a single square at the time when the ΔV(t) is maximum. Panel shows 3 different trials. From the left: square in position 3.5° below the horizontal meridian, square in central position, square 3.5° above horizontal meridian. In the control trials, the times of stimulus presentation of the single squares at these 3 positions were identical to those in the AM trials (lower square presented at 0 ms, central square presented in isolation at 83 ms, and top square presented in isolation at 166 ms). The time after start of 1st stimulus is shown as well as cytoarchitectural areal borders. (B) AM, ΔV(t) as a function of time after the start of the 1st square stimulus. Note the distinct representations of the square as in (A) and also the earlier time for the maximal depolarization compared with (A). (C) AM, only the strongly depolarized parts of cortex are shown corresponding to the retinotopic position of the square stimulus. (D) AM, the dynamics of the motion feedback depolarization from areas 19/21 to area 17. Time derivative of difference between ΔV(t)rel AM and sum of ΔV(t)rel from 3 single square presentations (control). Note motion feedback depolarization at 117–120 ms and the subsequent start of the moving depolarization wave-fronts at 17/18 from 126 ms, and the motion of the position of the square in area 19/21, 117–136 ms. In (C) and (D), the data have been filtered in time with a 20 ms Gaussian filter.

When the same 3 squares, each of 83 ms duration, were presented in rapid succession (Fig. 1B), the maximal ΔV(t) developed at the identical retinotopic sites (Fig. 4B). However, within the time intervals between the absolute maximal ΔV(t)s, there was a strong ΔV(t) increase, moving from the retinotopic site of the lower stimulus toward the retinotopic site of the center stimulus (Fig. 4C). Some 34 ms after the offset of the lower square, this activation progressed from the site of the lower square toward the retinotopic site of the center square after which the ΔV(t) at the retinotopic site for the lower square decreased (Supplementary Video 2). Similarly, after the offset of the center square, a strong ΔV(t) increase moved from the retinotopic site of the center square toward the retinotopic site of the top square (Supplementary Video 2; Fig. 4C). The shape of these activations moving from one retinotopic site to the next, may formally be described as wave-fronts (see Methods). This description is neutral with respect to the underlying causes of these ΔV(t) increases. The wave-fronts traversed, along the border between areas 17 and 18, from the retinotopic site of the lower square (medially) to the retinotopic site of the upper square (laterally) in the time interval in which the square appeared to move (Fig. 4C; Supplementary Videos 1 and 2). For this reason we refer to this wave-front as the 17/18 wave-front. There were no such wave-fronts in response to the stationary stimuli. The timing of the motion of this 17/18 wave-front was rather sharp, it started 34.3 ± 2.3 ms after the offset of the lower or the center square (Table 1).

Table 1.

Onset times and velocities (±SD) of the motion feedback signal

	Experiment 1, n = 4	Experiment 2, n = 6	Experiment 3, n = 4	Experiment 4, n = 6
Area 19/21 ms	34.3 ± 2.3	33.9 ± 5.2	32.8 ± 2.1	33.0 ± 3.7
Area 17/18 ms	38.0 ± 4.3	37.9 ± 3.5	35.0 ± 2.8	36.0 ± 4.4
Velocity 17/18 mm/ms	0.213 ± 0.075	0.227 ± 0.061	0.227 ± 0.075	0.220 ± 0.075

In areas 19/21, the offset of the lower square/center square also evoked an activation to the next retinotopic site of the center/top square. Although the activation here was noisier, a wave-front could be detected in most animals. This wave-front moved along the border between areas 19 and 21 as shown in Figures 2D and 7D. The wave-front in area 19/21 started 34.3 ± 2.3 ms after the offset of the lower or the center square (Table 1). In the text this wave-front is referred to as the 19/21 wave-front.

Figure 7.

Experiments 2, 3, and 4. (A) Experiment 3 (Fig. 1C; Animal 106), time derivatives of ΔV(t) to the appearance of the 2 squares. Note the temporal and spatial separation at the retinotopic sites of the squares at the times for the maximal d(ΔV(t))/dt. Onset of lower square was at 0 ms and of top square at 83 ms. (B) Same experiment as in (A), same animal; ΔV(t) shows a smooth motion of the maximum of the wave-front after starting at 116 ms (between the 102.5 ms and the 124 ms) and continuing up to 230 ms. (C) Experiment 2, d(ΔV(t))/dt, shown at 47.1 ms after the onset of the lower square, at 71.8 ms (30.3 ms after the onset of the central square, and at 120.9 ms (37.9 ms after the onset of the top square; Animal 106). (D) Experiment 2, same animal as in (C). ΔV(t)rel, showing the phase relations over the 4 cortical areas. Note the start of the wave-fronts propagation between 112.9 ms and 124 ms and again at 152.8 ms (29 ms after the offset of the central square). (E) Experiment 4, split motion, (see Fig. 1E; Animal 101), note the split of depolarization. (F) Proposed mechanism of AM. Cartoon illustrating the time order of changes in the membrane potentials of the neurons in the supragranular layers of areas 21,19,18, and 17 at the time interval of the AM wave-fronts. The wave-front in 19/21 traverses to the next retinotopic site. Simultaneously the neurons in 19/21 send a motion feedback toward the corresponding retinotopic site at the 17/18 border. The motion feedback may also depolarize the space between these borders as the iso-elevation domains of the retinotopic map in the ferret are in the direction of the motion feedback (Manger et al. 2002). Arriving at the retinotopic site and depolarizing the neurons at 17/18, these neurons start the 17/18 wave-front which then would lag the 19/21 wave-front. This cartoon could explain the dynamics as seen in (D).

The 19/21 wave-front and the 17/18 wave-front were associated in time with yet another moving activation emanating from the retinotopic site at the area 19/21 border and moving toward the area 17/18 retinotopic site of the square (Fig. 5 at 116–132 ms and again at 206–213 ms). This ΔV(t) increase appeared from the retinotopic site of area 19/21 as a feedback signal toward the area 17/18 border where it activated the path to the next retinotopic site along the area 17/18 border (Figs 4D and 5, Supplementary Movie 3). To characterize the phase relations of these activations over the cortex, we calculated ΔV(t)rel (see Methods). This showed that the feedback to areas 17/18 started simultaneously with the onset of the 19/21 wave-front and prior to the 17/18 wave-front (Table 1; see also Fig. 7D). We refer to this wave-front as the motion feedback. Experiment 1, thus revealed that associated with AM, there was a 19/21 wave-front, a motion feedback to 17/18, and a 17/18 wave-front moving in the direction of AM.

Figure 5.

Motion feedback and the 17/18 wave-front. Snapshots of the ΔV(t) at the times after the onset of the lower square in experiment 1. Note the simultaneous progress of the 19/21 wave-front at the motion feedback at 116–124 ms and the full progression of the (overshooting) wave-front just below the 17/18 area border. At 206–213 ms, the feedback repeats, albeit this time with minimal progress of the 19/21 wave-front (Animal 98). That the motion feedback indeed has direction toward the area 17/18 border is shown in Figure 6C.

Different Forms of AM Produced Activation Wave-Fronts Moving at Different Onset Times and in Different Directions

As shown in Figure 1, our experimental protocol included a number of conditions that produced AM in humans. All conditions associated with AM were associated with statistically significant moving wave-fronts, moving from one retinotopic site to the next and with a motion feedback (wave-front detection in methods, Fig. 3 and Table 2). Figure 6A,B show further examples of the progressions of the wave-fronts calculated from the path taken by the wave-fronts from the retinotopic site of the square at its offset to the retinotopic site of the next square at its onset. It is apparent from these examples that the leading edge of the wave-fronts, that is, the d(ΔV(t))/dt, progressed with almost constant velocity and only in this direction. Similarly, the motion feedback moved from areas 19/21 to areas 17/18, and not in the reverse direction (Fig. 6C,D; Table 2). The wave-fronts and the motion feedback could be detected in the ΔV(t) or the d(ΔV(t))/dt (see Methods). All 10 animals had statistically significant 17/18 wave-fronts moving in the direction of AM (P < 0.01 per animal or better, Table 2). Furthermore, in all animals, there was a statistically significant feedback from the retinotopic site in areas 19/21 toward the edge of the retinotopic site at the area 17/18 border at 29.3 ± 4.0 ms after the offset of the lower/center square (Figs 4D, 5, and 6; P < 0.01 per animal or better, Table 2). In 9 animals we confirmed that 19/21 wave-fronts progressed along the area 19/21 cytoarchitectural border (P < 0.01 per animal or better, Table 2, in 1 animal the area 19/21 cytoarchitectural border was outside the cortex monitored by the photodiode array).

Table 2.

Statistical significance of wave-fronts, that is, significance of the slope of regression for motion in direction of next retinotopic site

	Animal	17/18, P	19/21, P	Feedback, P
Experiment 1	60	<0.0000001	<0.00001	<0.00001
	62	<0.0002	<0.00001	<0.00001
	70	<0.0001	<0.00001	<0.001
	98	<0.000002	<0.00001	<0.00001
Experiment 2	79	<0.0000001	<0.00001	<0.00001
	89	<0.0000002	<0.001	<0.0001
	101	<0.01	*	<0.00001
	106	<0.0000001	<0.00001	<0.01
	116	<0.0000001	<0.00001	<0.00001
	130	<0.005	<0.00001	<0.0001
Experiment 3	101	<0.002	*	<0.00001
	106	<0.0000001	<0.00001	<0.0001
	116	<0.0000001	<0.00001	<0.00001
	130	<0.0000001	<0.001	<0.001
Experiment 4	79	<0.01
	89	<0.000005
	101	<0.01
	106	<0.01
	116	<0.001
	130	<0.000005

^*area 19/21 border was outside of region monitored by the photodiode array.

Figure 6.

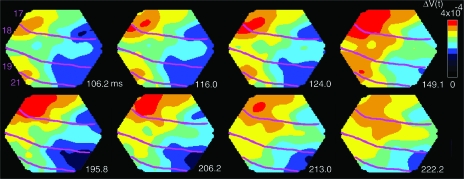
Examples of the wave-fronts and motion feedback during AM. The examples show the regression on the point clouds obtained from each point of the cortex along the paths taken by the wave-fronts in the direction found by the wave-front algorithm (Fig. 3). (A) The 1st motion of the 17/18 wave-front, in experiment 1, 31–40 ms after the offset of the lower square. The abscissa shows the distance form the retinotopic site of the lower square. The ordinate shows the time in ms centered as in Figure 3. The arrow shows the direction found by the algorithm (data d(ΔV(t))/dt; Animal 60). Estimated mean velocity 0.21 mm/ms. (B) The motion of the 19/21 wave-front 31–43 ms after the offset of the central square (data d(ΔV(t))/dt; Animal 98). Abscissa distance from center square retinotopic site. (C) motion feedback in the time interval 22–62 ms after the offset of the lower square in experiment 1 (data: ΔV(t); Animal 98). Abscissa: distance from the retinotopic site in area 19/21. (D) Motion feedback in experiment 3, 31–56 ms after offset of lower square (data: ΔV(t); Animal 116). Abscissa: distance from the retinotopic site in area 19/21.

As the eye position was fixed, the squares appeared and disappeared, instantaneously, from one spatial position to the next. Accordingly, the initial on-responses of ΔV(t) and the retinotopic site of the squares in areas 17/18 appeared distinct. This is apparent if the time derivative of ΔV(t), d(ΔV(t))/dt is calculated. Figure 7A shows that the time derivatives for the 2 positions in experiment 3 are spatially and temporally separated at the area 17/18 border. That the relative depolarization at each retinotopic site at the area 17/18 border is stable in its position until the wave-fronts begin can also be demonstrated by marking the point of maximal depolarization for each time frame after the start of the stimulus (Fig. 7B). Taken over all animals and all experiments the point of maximum depolarization at the 17/18 border remained stationary within ± 150 μm until 37.1 ± 4.6 ms after the offset of the lower/center square (all experiments, mean ± SD; n = 20).

In experiment 1, the offset of one square was timed to the onset of the next square at the new position. This did not allow one to distinguish whether it was the onset of the new square or the offset of the former square that initiated the wave-fronts. In experiment 2 our protocol allowed us to distinguish between these possibilities. The onset of the center square was timed to occur 42 ms after the onset of the lower square. Consequently, the 2 squares remained ON for 41 ms before offset of the lower square. Similarly, the onset of the top square was timed to remain ON for 42 ms before the offset of the center square (see Fig. 1C). These temporal changes in the timing of the sequence of presentations as seen in Figure 1C, had no effect on the appearance of the wave-fronts seen in Figure 7D. The wave-fronts from the retinotopic site of the lower square appeared exactly as in the 1st experiment, some 36 ms after the offset of the lower square (Table 1, Fig. 7D). Similarly, the wave-fronts traveling toward the retinotopic site of the top square, appeared on average 33 ms after the offset of the center square (Fig. 7D, Table 1). Thus the wave-fronts were time locked to the offsets and not the onsets. This is in accordance with psychophysical observations in humans (Giashi and Antis 1989).

In the 1st and 2nd experiments, the wave-fronts traversed across the cortex at the same velocity of 0.21 to 0.23 mm/ms (P > 0.5 2 tailed t-test n₁ = 4, n₂ = 6, Table 1). As the distance between the positions of the squares were identical in both experiments, this is perhaps not surprising. In experiment 3 we examined whether the velocity of the wave-fronts could be altered. We left out the center square and presented only the lower and upper squares with the offset of the lower square exactly timed to the onset of the top square (Fig. 1D). The result was that the wave-fronts were initiated as usual after the offset of the lower square at 33 ms and traveled in a single sweep directly to the retinotopic site of the top square (Fig. 7B). Surprisingly, the velocity of the 17/18 wave-fronts, was still 0.227 mm/ms (Table 1). There were no significant differences in wave velocities between experiments 1, 2, 3, and 4 (Table 1, analysis of variance P> 0.9).

If AM is always dependent on the visual cortex computing an activation wave-front from the retinotopic site of one stimulus to the next, a stimulation in which 1 square is followed by 2 oppositely positioned squares (experiment 4; Fig. 1E), should produce 2 wave-fronts, each traveling in opposite directions but toward the retinotopic sites of the 2 new squares. Indeed this was our finding. At 36 ms after the offset of the center square, 2 oppositely directed wave-fronts progressed in this divergent manner (Fig. 7E, Table 1). In the V(t)rel domain, 2 oppositely directed wave-fronts traveled to the retinotopic site of the lower and the top square. Although the data were noisy, a similar divergence could be seen at the area 19/21 border again preceding the 17/18 wave-fronts (Table 1; Supplementary Video 4). Thus, if a single stimulus was briefly presented and at its offset was followed by the onset of 2 stimuli but located on either side, the cortex computed 2 wave-fronts which traveled over the cortex to the retinotopic sites of the diametrically opposed stimuli. In humans this is associated with the perception of 1 object moving while being split into 2.

The initial on-responses of ΔV(t) to the squares in areas 17/18 appeared distinct and stationary (Fig. 7A). Notably, in all conditions of AM the wave-fronts appeared 1st after the offset of the squares and moved fast between the retinotopic sites of the squares. The peak depolarization in contrast moved only slowly and after a delay vanished at the former retinotopic site, whereas the new peak increased at the next retinotopic site (Figs 4C, 5, 7B–E; Supplementary Videos 2–4).

Interarea Dynamics of AM

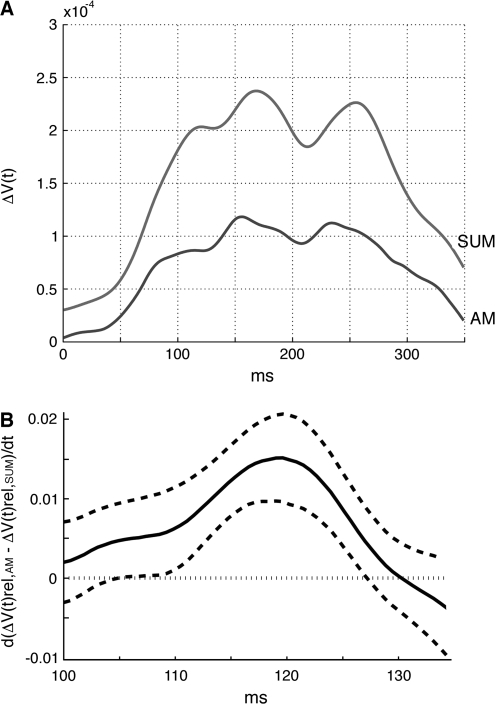
In experiments 1 and 4, we included control conditions in which single squares were presented in isolation at the same positions where they were presented as a sequence during the AM conditions (see Fig. 4A and Methods). When we calculated the sum of the depolarizations evoked by each of the 3 squares when presented singly, that is, the sum of the 3 files similar to those depicted in Figure 4A, the calculated amplitude of the signal ΔV(t) for this sum in each animal was considerably larger than the ΔV(t) for the AM after 100 ms (Fig. 8A). In order to remove the local amplitude differences, but preserve the spatial dynamics we computed the time derivative of the difference, that is, d(ΔV(t)rel,AM − ΔV(t)rel,sum)/dt. This difference, between the 2 conditions, showed that the AM condition was associated with a significant feedback to the area 17/18 border in the interval from 32 to 47 ms after the offset of the lower square (Figs 4D and 8B; Supplementary Video 5; Table 2).

Figure 8.

Comparison of the ΔV(t) of AM with the ΔV(t) of the sum of the individual presentations. (A) The mean signal ΔV(t) for all channels covering areas 17 and 18. Experiment 1. Gray curve: ΔV(t)sum, that is, the arithmetical sum of the signals to the lower square, the center square and the top square when presented singly. Dark curve: AM condition. Note the stronger and longer lasting signal ΔV(t)sum and the earlier appearance of the peak depolarizations in AM (Animal 60). (B) Comparison of the ΔV(t)rel of AM with the ΔV(t)rel of the sum of the individual presentations. The time relation of the motion feedback depolarization, from areas 19/21 toward the area 17/18 border. The time derivative from the path of the feedback depolarization of the difference in signal between AM and the sum of the signals to stationary squares, that is, d(ΔV(t)rel,AM − ΔV(t)rel,sum)/dt is on the ordinate. Abscissa: time after start of 1st stimulus in the AM condition. The curve shows the mean d(ΔV(t)rel,AM − ΔV(t)rel,sum)/dt for all animals, The stippled lines show the standard errors.

Relation between the Wave-Fronts and Neuronal Firing

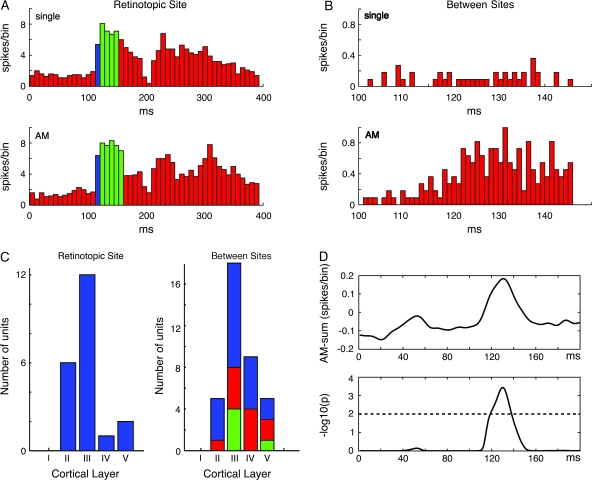
The membrane activations in the form of the wave-fronts should be capable of firing neurons between the retinotopic sites of the squares. We, therefore, recorded electrophysiologically from 59 multiunits in areas 17 and 18. These units were significantly activated by the AM conditions (P < 0.01, see Methods). Neurons at the retinotopic sites, at the area 17/18 border (n = 22) faithfully fired an on-response in the control condition with single stimuli and in the AM conditions with no differences in onset latencies (P > 0.3, paired t-test, n = 22; Fig. 9A). For units (n = 37) located between the retinotopic sites of the lower and center squares and between the center and upper squares in areas 17/18, the spike responses were sparse or nonsignificant to the single square conditions (Fig. 9B). However, these 37 units fired significantly more in the AM condition during the time interval 110–140 ms than in any of the single square conditions (Fig. 9B; P < 0.05). For these 37 units, we compared the sum of spike trains to the AM condition with the sum of spike trains from the 3 conditions in which the squares were shown individually. This revealed that the 37 units fired significantly higher spike rates in the AM condition but only for the duration of the time interval during the passage of the wave-front (Fig. 9D; P < 0.01). Moreover, 21 of the 37 units had a mean spike rate in the AM condition which was significantly and positively correlated to the averaged ΔV(t)rel overlying the electrode penetration. Thus, they fired in the time interval during the passage of the wave-fronts with a lag of 1–2 ms (Spearman rank correlation coefficient, r, significant at P < 0.05 or less per unit). The responses of 11 of the 37 units were negatively correlated with the wave-front ΔV(t)rel (P < 0.05 or less per unit). Thus, the neurons at the retinotopic sites fired almost identically in the AM conditions and the single square conditions. The neurons between the retinotopic sites, mostly fired only in the AM conditions and their responses were either positively correlated or negatively correlated to the average wave-front amplitude in the time interval during its passage from one retinotopic site to the next.

Figure 9.

Responses from neurons within retinotopic sites and between retinotopic sites. (A) Layer III multiunit recorded at the border between areas 17/18. Top: on-response (blue) at 115 ms, 32 ms after stimulus onset to the presentation of the single square at center position. Bottom: responses during AM, onset at 115 ms. The 80% of maximal firing rate is shown in green. Note no differences in onset latency, but on-response decays faster. Experiment 1 (Animal 62). (B) Multiunit, layer II area 18, between lower and center square retinotopic site. Top: Response to the presentation of the single center square (not significant). Bottom; significantly correlated responses from the same multiunit during the passage of the moving depolarization wave-fronts at 116–144 ms, Experiment 4 (Animal 106). (C) Left: Histogram of responsive units at retinotopic sites according to cortical layer. Right: idem for units located between retinotopic sites. Blue: significantly and positively correlated to average ΔV(t) at time of passage of moving depolarization wave-fronts; red: significantly and negatively correlated; green: not significantly correlated. (D) Top: mean difference in firing rate of between site units in AM versus sum of single responses. Bottom: These units fired statistically significantly more spikes in the interval 120–145 ms during AM as compared with the firing in the single square conditions (P < 0.01, n = 37).

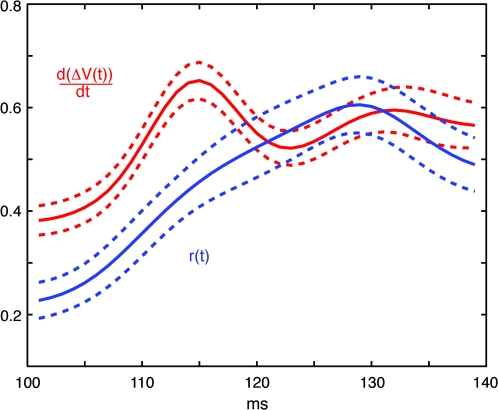
Assuming that the ΔV(t) originates mainly from the dendrites (Grinvald and Hildesheim 2004), the time derivative d(ΔV(t)/dt can be regarded as proportional to the relative input driving force for the populations of neurons in the supragranular layers. For the neurons populating the space between the retinotopic sites of the square stimuli, we compared the time course of the d(ΔV(t))/dt with the instantaneous firing rates of the neurons located here in the time interval of the wave-front passage 100–140 ms. The result was that the relative drive, that is, the mean d(ΔV(t))/dt increase preceded the mean instantaneous firing rate increase (Fig. 10). We also compared the time of peak firing in this interval to the peak d(ΔV(t))/dt. The result was that the peak d(ΔV(t))/dt came statistically in advance of the peak firing (P < 0.0005; paired comparison; n = 20; the remaining neurons had no detectable peak of firing rates in this interval). These results are consistent with the idea that the wave-front passage drives the firing of the neurons in between the retinotopic sites.

Figure 10.

Time relation between the relative drive and the firing of the neurons in between the retinotopic sites at the area 17/18 border at the time interval of the passage of the wave-front. The d(ΔV(t))/dt is the relative input driving force (see text). For all electrode penetration sites the maximum value in the interval 100–140 ms of the d(ΔV(t))/dt of the corresponding supragranular cortex was normalized to 1.0. A similar normalization was done for the instantaneous firing rate r(t). Thereafter the individual files were summed and divided by the number of penetration sites for d(ΔV(t))/dt, and divided by the number of multiunits (n = 37) for r(t) to give the values shown on the ordinate. The abcissa is the time from the start of the preceding stimulus. This result is consistent with the idea that the moving wave-front ΔV(t) increase drives the neurons to fire in between the retinotopic sites of the square stimuli.

Furthermore, the neurons at the retinotopic sites of the squares at the 17/18 border fired with onset latencies not significantly different from those in the single square conditions (Fig. 9A). Thus at onset of the 2nd or 3rd square, the firing of neurons at this retinotopic site in area 17/18 did not significantly alter the spike firing of neurons at the retinotopic site of the former square.

Discussion

In summary, the results showed that after the offset of the 1st stimulus, a moving activation wave-front appears in areas 19/21 and a motion feedback is sent to areas 17/18. Immediately, the area 17/18 wave-front starts and progresses together with the area 19/21 wave-front in the direction of AM. In the time interval during which the 17/18 wave-front traverses from one retinotopic to the next retinotopic site, the neurons located between these retinotopic sites generate spike responses. The 4 conditions that produced AM in humans, in the ferret visual cortex invariably were associated with such wave-fronts and these were triggered by the offset of the stimulus. The wave-fronts appear to correspond to the time interval eliciting AM and to the predicted speed of the AM (Supplementary Video 1; Giaschi and Anstis 1989; Chavane et al. 2000).

A number of possibilities were examined as possible explanations for our results. First, could the wave-fronts arise from the fact that retinal ganglion cells fire slightly ahead of a continuously moving object (Berry et al. 1999) and, 2nd, could they in fact not be wave-fronts, but motion streaks. A motion streak is a “smeared contour, a tail of the cortical position of a moving object caused by temporal integration in the visual system” (Geisler 1999; Geisler et al. 2001). As our stimuli were stationary, they were unlikely to have set up a wave of excitation between successive spatial locations within the retina. Also we recorded only localized on-responses both with the voltage sensitive dye signal and electrophysiologically by recording action potentials in areas 17/18 (Figs 4–7 and 9). Finally, the squares were transiently presented with a separation of 3.5°, and the AM wave-fronts started with a 35–40 ms delay after the offset of the 1st square stimulus and not the onset of the next stimulus. A streak is defined as being behind the object moving with respect to the direction of movement. In contrast, in our case the new square had already appeared (experiment 2) when the wave-front emerged from the retinotopic site of the lower/center square and moved to the retinotopic site of the next square (Supplementary Video 3; Fig. 5).

Excluding retinal causes for the activation wave-fronts, the question is whether the physiological mechanisms of AM can be explained by a feed-forward depolarization of the supragranular layers at the area 17/18 border in accordance with our null hypothesis. From our results, the wave-fronts appeared immediately after the offset of the lower square, and not after the onset of the center square. This makes it unlikely that the On-response from the lateral geniculate nucleus via layer IV spiny stellate neurons should have produced the wave-fronts. Secondly, the sum of the signal computed from single square presentation, ∑ΔV(t), was consistently larger than the ΔV(t) of the AM condition. Third, the neurons between the retinotopic sites fired significantly more during AM when compared with all single square presentation conditions (Fig. 9D). To this we have to add the statistically significant feedback (Figs 4D, 5, 7D; Supplementary Videos 3–5; Table 2). Furthermore, the direction of the increases in ΔV(t) and ΔV(t)rel of the motion feedback signal was toward the area 17/18 border. Moreover, this feedback signal is only present in the AM condition, and absent in the control conditions as well as the individual sum of the 3 ΔV(t) signals (Figs 4D and 8B; and Supplementary Video 5). All these results are against the null hypothesis and hence against linear and feed-forward mechanisms. These results are also incompatible with feed-forward models of (apparent) motion (Reichardt 1961; Barlow and Levick 1965; Carandini et al. 1997).

The statistics, the accurate timing, the speed, and the averaging of the ΔV(t) make it unlikely that the wave-fronts and the motion feedback signal could be explained as spontaneous moving depolarizations or “up-states” (Prechtl et al. 2000; Petersen et al. 2003b). These factors taken together with the fact that the ferrets were anaesthetized with their eye muscles paralyzed, make it very unlikely that the source of the wave-fronts and motion feedback signal could be the result of attention, arousal or eye movements.

The arrival of a new stimulus on the retina is associated with a feed-forward depolarization of the corresponding retinotopic site in the visual cortex and this is followed by a laterally spreading depolarization (Grinvald et al. 1994; Roland et al. 2006). The laterally spreading depolarization spreads out in all directions from the retinotopic site and attenuates after some 70 ms (Roland 2006). In experiments 1, 2, and 3, the wave-fronts associated with AM moved in the opposite direction to the initial laterally spreading depolarization caused by the onset of the next square (Figs 4–7). This was also true for experiment 4, in which the wave-fronts moved from the retinotopic position of the 1st square at offset toward the retinotopic positions of the 2 new squares, that is, again against the direction of the laterally spreading depolarizations from the new squares (Supplementary Movie 4).

Each wave-front always was unidirectional moving in the direction of AM, and also unidirectional when converted to a wave as d(ΔV(t))/dt. This evidence suggests that it cannot be explained by a combination of feed-forward depolarization and lateral spreading depolarization, and nor can it be explained by an off-response. Although the wave-fronts in areas 19/21 may be triggered by an off-response, the wave-fronts moved in different directions depending on the type of AM and, therefore, were unlikely to be due to off-responses. In any case, off-responses are localized to the retinotopic sites albeit with some laterally spreading depolarization. In addition, the wave-fronts cannot be interpreted as local increases of the ΔV(t) (as an iceberg effect, or a standing wave) as such increases will give a d(ΔV(t))/dt signal that spreads outward in all directions from the retinotopic site, while the center of the increase will remain stationary.

The Nature of Wave-Fronts

The activations, that is the ΔV(t) increases, can be interpreted as relative increases in the membrane potentials of large population of cells and axons in the supragranular layers in excess of that provided when only the gray screen is displayed (see Methods). In other words, the ΔV(t) increases could be interpreted as an increase in excitation from the level prevailing when only the background gray screen is displayed. As further argued in the methods section and elsewhere, the glia contribution to the voltage sensitive dye signal, V(t) is small and very slow (Konnert and Orkand 1986; Lev-Ram and Grinvald 1986; Konnerth et al. 1988; Bergels and Jahr 1997; Petersen et al. 2003a, 2003b; Grinvald and Hildesheim 2004; Ferezou et al. 2006). This means that the fast changes in the relative depolarizations of the cells of the supragranular layers that were formally described as wave-fronts in the results section, mainly stem from neurons (axons, dendrites, cell bodies) (Petersen et al. 2003a, 2003b; Grinvald and Hildesheim 2004; Ferezou et al. 2006). The wave-fronts then are fast, directional, progressions of relative excitation from sites already excited over the level prevailing when only the gray screen is shown. The area 17/18 excitation progresses between the retinotopic sites of the squares with an amplitude slightly less than the maximal amplitude at the retinotopic site of the lower/center square (Figs 4B,C, 5, and 7B,C). This, however, is sufficient for the neurons to fire significantly more at the path connecting the retinotopic sites during the time of passage. As the ΔV(t) increase must originate in the supragranular layers (Kleinfeld and Delaney 1996; de Curtis et al. 1999; Petersen et al. 2003a), the neurons, axons from elsewhere and glia in these layers must have been more depolarized. The progress of the wave-front excitation was fast, 0.22 mm/ms, which is likely to exclude a progression through gap-junctions (Haas et al. 2006). This is also twice as fast as the lateral spreading depolarization that spreads out from the retinotopic site when a new stimulus is introduced (Roland et al. 2006). The fast excitatory directional spread, that by analogy was described as wave-fronts, then is likely to be induced by synaptic activity. This could either be by axons from neurons having their cell bodies elsewhere or by local, multisynaptic propagation through neighboring neurons in the supragranular layers, or both. The high speed of the progression speaks against multisynaptic propagation through large populations of neurons (Tanifuji et al. 1994; Pinto et al. 2005). The observation that the relative excitation in the direction of AM (wave-front) started after the off-response of the lower/center square, speaks against any thalamocortical connectivity. One possibility then is that the fast progressing excitatory activity is cortical and hence dependent on cortical connectivity. The pyramidal neurons in layers II and III have axons which arborize in all directions. The horizontal axons further make synapses with other supragranular neurons along their course in layers II and III (Gilbert and Wiesel 1979; Martin and Whitteridge 1984; Yoshioka et al. 1992; Lund et al. 1993; Kisvarday et al. 1997). This would be the analogy with the mechanism initially suggested to underlie laterally spreading depolarization (Grinvald et al. 1994; Roland et al. 2006). Indeed large parts of areas 17 and 18 outside the retinotopic site of the square become relatively depolarized after the onset of a new square as expected (Bringuier et al. 1999) (Figs 4A,B, 5, 7; Supplementary Movies 3, 4). This means that the cortex along the vertical meridian in the direction of the AM also becomes relatively predepolarized just after the on-response to the lower square (Figs 4A,B, 5, and 7B,C). Then later, after the off-response of the square, the wave-front progresses at double the speed and fired the neurons on the path to the next retinotopic site. Seemingly this progress in areas 17/18 was induced by the feedback signal from area 19/21.

Perhaps puzzling is the observation of a consistent motion feedback which relatively depolarizes the cortex along the whole path between the area 19/21 retinotopic site and the area 17/18 retinotopic site of the square (Figs 4D and 5; Supplementary Videos 3–5). However, from areas 21 and 19 there are direct retinotopically ordered feedback axons to areas 18 and 17 in the ferret (Cantone et al. 2005, 2006). Also there are feedback axons from areas 19 and 18 to area 17 (Cantone et al. 2005, 2006). It is not known whether in ferrets these feedback axons make synapses in areas 19 and 18 on their way to area 17 as feedback axons do in primates (Rockland and Drash 1996; Anderson and Martin 2002). From our consistent observations in 10 animals, the motion feedback signal was a relative depolarization between areas and was probably related to the iso-elevation retinotopy in the ferret (Manger et al. 2002). We have no systematic electrophysiology to determine whether neurons located between areas 19/21 and 17/18 and outside the retinotopic sites of the square are activated.

Physiological Mechanisms Subserving AM

In 1986 Newsome et al., after a series of electrophysiological recordings in V1 and MT to AM stimuli, concluded that “the neural substrate for AM is distributed over more than 1 cortical visual area depending on the speed and interflash intervals of the stimulus”. Our results are in accordance with this, and extend this conclusion. The consistency, timing, direction and constant speed of the evoked membrane potential dynamics of the neuron populations in areas 17, 18, 19, and 21 suggest that the motion feedback and depolarization wave-fronts may play a role in inducing AM. The electrophysiological recordings of the spike trains gave no support for any spatial and temporal integration of the on-responses to the squares in the AM conditions. This is consistent with the observation that it is the offset of the square event that triggered the AM computation. This is also logical as the requirement for movement of an object must be that it disappears at one position and is detected at another position (for example, if the lower square persisted 2 squares would be detected). This strict stationary retinotopic mapping of the squares at the area 17/18 border is then eliminated by the subsequent wave-front here which may drive the firing in between the retinotopic sites (Fig. 10).

Figure 7F schematically illustrates a simple explanation of the results as depending on a feedback from areas 21 and 19 toward the area 17/18 border in parallel with the wave-front progression in areas 19/21. The model is speculative, as the results, albeit showing tight coincidence in time of the feedback and the wave-fronts, provide no evidence of causal relations. As in primates (Chen et al. 2006), the area 19/21 neurons may react fast to motion and even AM, due to their larger receptive fields (Philipp et al. 2006). The 19/21 feedback was a relative increase in the membrane potentials of the cells along the path to the next retinotopic site in areas 17/18. Once this was achieved, the wave-front began to move in the direction of AM, and the neurons along this path were activated, that is, the stationary retinotopic mapping in areas 17/18 was transformed into AM of the squares. If the feedback is a computed motion signal from areas 21 and 19 following the presentation of the sequence of squares at different positions, the network of visual areas would have a conflict as the mapping in areas 17 and 18 is that of stationary squares. However, after the wave-front and the firing of the neurons between the retinotopic sites, there would be no conflict between the computations undertaken by the 19/21 (suprasylvian) neurons and the area 17/18 neurons. The network of working populations of neurons then may unambiguously signal (apparent) motion (see also Deco and Lee 2004). The population membrane dynamics and firing described in this report seems sufficiently robust even under anesthesia. This is in accordance with the observations that the types of long-range AM examined in this report are insensitive to changes in attention and that the neurons in the suprasylvian area react readily to motion under similar anaesthetic conditions (Philipp et al. 2006).

In a broader context, the wave-fronts and the motion feedback from areas 19/21 represent examples of long-range communication within areas and across areas addressing large populations of neurons by driving the membrane potentials in the direction of depolarization. Spike trains however, may change their information content during perception in an orderly way reflecting different phases of the computation of sensory data (Romo et al. 2002). The causes of these changes, that is, the dendritic input, may be difficult to detect in the individual spike trains, leaving uncertainty as to how the neuronal populations communicate to achieve solutions to perceptual problems. Recently it was shown that long-range communication between neuronal populations in different cortical areas could address large populations of neurons in early visual areas within a few ms (Roland et al. 2006). The present study adds 2 new examples of this type of communication dynamics, the moving wave-fronts and the motion feedback signal from areas 19/21 engaging large populations of neurons in both higher and lower order visual areas.

Supplementary Material

Supplementary material can be found at: http://www.cercor.oxfordjournals.org/

Funding

Swedish Science Council (K2004-33X-09456-14A); and the Wallenberg Foundation to P.E.R.