Volumetric Interpretation of Protein Adsorption: Kinetic Consequences of a Slowly-Concentrating Interphase

Abstract

Time-dependent energetics of blood-protein adsorption are interpreted in terms of a slowly-concentrating three-dimensional interphase volume initially formed by rapid diffusion of protein molecules into an interfacial region spontaneously formed by bringing a protein solution into contact with a physical surface. This modification of standard adsorption theory is motivated by the experimental observation that interfacial tensions of protein-containing solutions decrease slowly over the first hour to a steady-state value while, over this same period, the total adsorbed-protein mass is constant (for lysozyme, 15 kDa; albumin, 66 kDa; prothrombin, 72 kDa; IgG, 160 kDa; fibrinogen, 341 kDa studied in this work). These seemingly divergent observations are rationalized by the fact that interfacial energetics (tensions) are explicit functions of solute chemical potential (concentration), not adsorbed mass. Hence, rates-of-interfacial-tension-change parallel a slow interphase concentration effect whereas solution depletion detects a constant interphase composition within the time frame of experiment. A straightforward mathematical model approximating the perceived physical situation leads to an analytic formulation that is used to compute time-varying interphase volume and protein concentration from experimentally-measured interfacial tensions. Derivation from the fundamental thermodynamic adsorption equation verifies that protein adsorption from dilute solution is controlled by a partition coefficient at equilibrium, as is observed experimentally at steady state. Implications of the alternative interpretation of adsorption kinetics on biomaterials and biocompatibility are discussed.

1.0 Introduction

Protein-adsorption kinetics are of practical importance in biomaterials because adsorption rates have been implicated as a cause of selective protein adsorption. For example, the so-called Vroman Effect is commonly thought to occur because low-molecular-weight proteins presumably arriving first at a surface immersed in a multi-component solution are displaced by higher-molecular-weight proteins arriving later (see refs. [1–24] and citations therein). The final adsorbed-protein composition is thus purported to be achieved through a complex series of time-dependent, adsorption-displacement steps. Adsorption kinetics is also of fundamental importance in surface science, which subsumes the field of biomaterials surface science, because adsorption rates provide important insights into adsorption mechanism(s). As a consequence, adsorption kinetics has been an active area of scientific investigation for decades. Fig. 1 is a timeline summary of selected papers that have appeared over the last century, first among which appears to be Milner’s pioneering work published in 1907 [1] using Fick’s core theory [2] to pursue subsequent observations of Marangoni and Rayleigh (cited in ref. [1]).

Figure 1.

Timeline summary of selected papers on the subject of adsorption kinetics illustrating more than a century of continuous scientific inquiry. An important conclusion drawn from early work was that diffusion alone cannot account for experimentally-observed slow kinetics.

One of the early conclusions drawn from the work of Fig. 1 was that adsorption rates were not, in general, controlled solely by mass transfer/diffusion from stagnant solution to the surface region. This conclusion was based on the observation that the rate-of-appearance of surfactants (meant here to include surface-active compounds such as detergents, soaps, and proteins) at surfaces brought into contact with bulk solution was orders-of-magnitude too slow to be controlled by diffusion. For example, simple calculations presented in Appendix A based on Bond and Puls analysis [3] or Fick’s law reveal that protein adsorption should come to equilibrium within milliseconds under purely diffusion control. By contrast, the interfacial tensions that are exquisitely-sensitive measures of surfactant adsorption are observed to decay over tens-of-minutes or even hours (see refs. [4–11] for recent work on a broad selection of purified blood proteins as well as serum derived from different species).

In view of this discrepancy between measured rates and diffusion theory, physical chemists proposed that surfactant molecules must overcome an energy barrier to become adsorbed and that the height of this putative energy barrier controlled adsorption rates. Fig. 2 diagrams a typical description of the physical situation (adapted from ref. [12]) in which surfactant molecules are proposed to quickly diffuse to, and collect within, a subsurface region separated from the physical surface by an energy barrier. This energy barrier is sometimes referred to as a reflecting plane [13] because it can repel surfactant molecules arriving from bulk solution. A rate-limiting process is presumed to bring surfactant to the surface region where these now-adsorbed molecules can participate in surface phenomena such as reduction of interfacial tensions. Effectively, the energy barrier to adsorption accounts for the fact that not every encounter with the surface leads to adsorption so that the surface is semi-adsorbing (reflecting), as opposed to a perfectly-adsorbing sink [13]. The Random Sequential Adsorption (RSA) model [14–16], and the venerable Langmuir adsorption isotherm [17–20] from which RSA models ultimately originate, are implicitly energy-barrier models as well. Here, net adsorption is controlled by opposing adsorption/desorption rates which, according to activated-rate theory, are moderated by activation energy barriers, with lower barriers corresponding to faster rates.

Figure 2.

Sketch of a 2D adsorption paradigm in which protein molecules (spheroids) adsorb to a planar interface separating the physical (air or solid) surface from bulk solution. The thickness dimension is effectively ignored in the 2D paradigm. Proteins are thought to arrive at a sub-surface region by diffusion from which rate-limiting adsorption to the authentic interface occurs. Adsorption rate is controlled by energy required to cross the energy barrier/reflecting plane. Molecules within sub-surface region are not construed to be in the adsorbed state whereas molecules within the interface are adsorbed and contribute to reduction of interfacial energetics.

Our recent work has focused on energy-and-mass-balance in protein adsorption from stagnant solutions [5–8, 10, 21–26], motivated by the idea that these complimentary measures of adsorption for a broad range of proteins should clarify unresolved mechanistic issues such as adsorption reversibility, formation of adsorbed multilayers, and applicability of thermodynamic models. This work has emphasized that adsorption is a partitioning process [27, 28] distributing both protein and water molecules between the bulk-solution phase and a three-dimensional (3D) interphase region (Guggenheim surface construction [28, 29]). The interphase paradigm is not new to surface science but is quite different from the more conventional view of adsorption as occurring at a two-dimensional (2D) plane (see Fig. 2) that typically does not include the role of water in the adsorption process in an explicit way. We use the 3D model (so-called “volumetric interpretation” of protein adsorption [22–25]) herein to reexamine protein-adsorption kinetics and to formulate an alternative interpretive physical model that rationalizes rapid rates of protein diffusion and slow rates of time-dependent interfacial energetics. Implications for biomaterials is discussed in light of these findings.

2. Methods and Materials

2.1 Proteins and Adsorbent Particles

Proteins were used as received from the vendor without further purification. Table 1 lists relevant details. Protein solutions were prepared by 80:20 dilution in PBS. SDS-PAGE of protein solutions yielded single bands. Octyl Sepharose™ 4 Fast Flow adsorbent (ODS) was obtained from Amersham Biosciences (75% by volume of 90 µm nominal-diameter sepharose-based particles dispersed in 20% aqueous ethanol solution). The actual surface area of these hydrogel particles was not measured because accurate knowledge of adsorbent surface area is not necessary in volumetric analysis of protein adsorption [22–24] and because analytical difficulties encountered in working with relatively low-nominal-surface-area, hydrated-hydrogel particles precluded accurate surface-area determinations at a size scale relevant to proteins. ODS was freshly prepared just before each depletion experiment by 3× washing in PBS (to remove ethanol) using a sequential centrifugation/resuspension protocol (40 RPM for 1 min in a Hettick microtube fixed-rotor centrifuge, VWR) that processed 1 mL of as-received suspension (750 µL beads, 250 µL fluid). After each of 3 centrifugations, 1 mL of supernate was replaced with 1 mL PBS, ending with a 75:25 v/v stock suspension in PBS. For each depletion experiment, 20 µL stock (5 µL fluid, 15 µL beads) was pipetted into a 0.5 mL microtube (~ 65 cm² adsorbent surface area or a 97:3 adsorbent-to-tube surface area ratio). Beads were re-suspended by gentle pipette aspiration in 25 µL protein solution prepared in advance to the desired protein composition or concentration so that the final depletion volume V_B = 30 µL . In all depletion experiments, adsorbent settled to the bottom of the conical test tube, allowing particle-free supernate to be sampled without centrifugation.

Table 1.

Purified Protein Source and Purity

Name of protein (Origin)	Molecular weight (kDa)	As-received form	Purity (electrophoresis) or activity	Vendor
Lysozyme (Human Neutrophils)	15	powder	>95%	Sigma Aldrich
α-Amylase (Human Saliva)	51	powder	1,920 units/mg	Sigma Aldrich
Human serum Albumin (Human Blood)	66.3	powder	96–99%	Sigma Aldrich
Prothrombin (Human Blood)	72	powder	90 µg/unit	Enzyme Research
Human IgG (Human Blood)	160	powder	>95%	Sigma Aldrich
Fibrinogen (Human Blood)	341	powder	80% clottable protein	Sigma Aldrich

2.2 Depletion Measurements

Experimental details for the SDS-electrophoresis implementation of the depletion method have been disclosed elsewhere [22–24]. Briefly, protein solutions (25 µL) in phosphate-buffered-saline (PBS; Sigma; 0.14 M NaCl, 3mM KCL prepared in 18 MΩ water) at varying concentrations were mixed with a fixed amount (surface area) of washed sepharose particles (20 µL; see below) by gentle pipette aspiration and allowed to stand undisturbed in 0.5 mL conical microtubes (Safe-lock micro centrifuge tubes, Eppendorf; approximately 2 cm² internal surface area) every 5 min. for 90 min. before analysis. No correction was made for the small-but-measurable adsorption to tube surfaces [23] (see further Computational Methods below). Control experiments in which tube contents were continuously mixed on a hematology rocker did not yield significantly different results than unmixed experiments (see Table 2 and Section 3). Consequently, continuous mixing of low-volume solutions with adsorbent was abandoned as an unnecessary inconvenience that invited experimental error related to solution/particle hang-up within the plastic microtube and in advertent loading of adsorbent particles onto electrophoresis gels.

Table 2.

Time-Average Protein Adsorption to Octadecyl Sepharose Particles by Solution Depletion

Concentration (mg/ml)	Experimental Condition	Mean Depletion ± Standard Deviation (mg/ml, N ≤ 20)
		Human Serum Albumin	Human IgG	Lysozyme	α - Amylase	Prothrombin	Fibrinogen
0.8	Stagnant Solution	0.44 ± 0.11	0.37 ± 0.06	0.51 ± 0.06
1.6	Stagnant Solution	0.96 ± 0.15	0.71 ± 0.08		0.57 ± 0.06
	Continuous Mixing	0.81 ± 0.08	0.71 ± 0.07
	Radiometry Stagnant Solution	0.58 ± 0.04	0.52 ± 0.03
2.4	Stagnant Solution	1.18 ± 0.26	0.98 ± 0.10			0.90 ± 0.12
	Continuous Mixing	1.06 ± 0.17	1.00 ± 0.07
	Radiometry Stagnant Solution	0.83 ± 0.11	0.83 ± 0.04
3.2	Stagnant Solution	1.75 ± 0.25	1.47 ± 0.12				1.30 ± 0.14
3.9	Stagnant Solution	2.01 ± 0.43	1.75 ± 0.17

2.3 SDS-PAGE Electrophoresis

26 lane NuPAGE® Novex Tris-Acetate precast gels (Invitrogen; 500 kDa capacity) were used to separate and quantify proteins. NuPAGE® Novex Bis-Tris gels were used for the low-MW protein lysozyme. Electrophoresis was carried out for 70 min. at 150 V (Tris-Acetate) or 35 min. at 220V (Bis-Tris) using an XCell SureLock™ Cell (Invitrogen). Gels were stained with SimplyBlue™ SafeStain (Invitrogen) for 1 hour and destained with de-ionized (18 MΩ) water for several hours while mixing on a standard hematology rocker. Band intensity was quantified using the Gel-doc system (Bio-Rad Laboratories) that employed a highly-sensitive CCD camera to read optical density (OD). A standard curve was prepared for each protein and each gel using the first 6–8 lanes by applying solutions of known concentration of the probe protein(s). Linear calibration curves were obtained (R² > 98%) within the concentration range 0.1 < $W_B^o$ < 4 mg/mL (single-protein experiments) for gels of all proteins listed in Table 1. Each different protein required a separate calibration curve on the same gel to account for differences in staining density.

2.4 Radiometry

Radiometric assessment of solution depletion was carried out basically as described above except that depletion of a radioactively-labeled protein was used to quantify depletion rather than electrophoresis. Standard methods of radiometry were applied [30]. Iodine-125 was purchased from Perkin Elmer (Waltham, MA). Proteins were labeled using the Cholromine T (Sigma) method [31, 32] for 30 seconds to yield specific activity of 30.4 $\raisebox{1ex}{$\mu \mathit{\text{Ci}}$}\!\left/ \!\raisebox{-1ex}{$g$}\right.$ for HSA and 36.4 $\raisebox{1ex}{$\mu \mathit{\text{Ci}}$}\!\left/ \!\raisebox{-1ex}{$g$}\right.$ (Wallac 1470 Wizard Automatic Gamma Counter, PerkinElmer). Free Iodine was separated from the labeled protein using a G 50 chromatographic column (Sigma). Stock labeled protein was stored at 2° C and used within 2 days over which protein degradation was assessed by chromatography on a on a G 100 column (Sigma) and judged to be less than 5% of labeled protein. Test protein solutions were prepared by mixing 3 µL of stock labeled protein solution with 1.5 mL unlabelled protein solution prepared at the desired concentration to yield 0.8 µCi/mL.

2.5 Computational Methods

Computational and statistical methods have been disclosed in detail in ref. [22]. Briefly reiterating essential details for the purposes of this paper, amount of protein adsorbed to ODS adsorbent was calculated by difference D in protein-solution concentrations before $W_B^o$ and after W_B adsorption to particulates $(D=\left[W_B^o-W_B\right])$. In the absence of particulate adsorbent, D < 0.1 mg/mL for all proteins at surface-saturating bulk-solution concentrations ${\left(W_B^o\right)}^{\text{max}}$ and decreased in proportion to decreasing $W_B^o$. This background adsorption, due to all sources of protein loss to tubes and pipette tips in handling procedures, represented less than 1–2% of experimental D measured in the presence of particulate adsorbent. Thus, it was concluded that background correction of depletion measurements was unnecessary within the $W_B^o$ range explored in this work [22]. Solution depletion by radiometry at a given elapsed contact time was measured in triplicate using empty vials as a measure of background counts.

3. Results

3.1 Protein Adsorption Kinetics Measured Using the Solution Depletion Method

The basic idea behind the depletion method was to measure the w/v concentration (mg/mL) of protein in solution before $W_B^o$ and after W_B contact with test particulate adsorbents. Loss in solution concentration at any time t due to adsorption was calculated by difference (mass balance) as the solution depletion $D\equiv \left(W_B^o-W_B\right)$ for each of the proteins listed in Table 1, where D is expressed as mass lost per-unit-volume bulk solution (mg/mL). Effectively then, depletion is a gravimetric method measuring mass of protein adsorbed. Solution depletion occurred because protein adsorbed from solution into the interphase region surrounding the adsorbate particles which, according to the volumetric interpretation of adsorption, had a discrete volume V_I and concentration W_I so that $D=\left[W_I\left(\frac{V_I}{V_B}\right)\right]$; where V_B was the volume of the bulk-solution phase. We implemented the depletion method two ways in this work using either gel electrophoresis or radiometry as the means of quantifying adsorption.

The gel-electrophoresis implementation of the standard depletion method described in Section 2 met the need for unambiguous interpretation in a manner that was largely free of experimental artifacts; such as solute labeling, rinsing/drying, or complicated instrumentation. This method was sensitive to about 0.1–0.2 mg/mL (estimated to be equivalent to 0.3 mg/m² [23] or approximately 10% CV). Previous work “certified” method and theory applied to steady-state adsorption (t → 1 hr.) by first studying adsorption of a broad range of single proteins to hydrophobic [22] surfaces (ODS and silanized glass) from aqueous-buffer solution, showing that results comported with thermochemically-measured free energies of adsorption and interfacial energetics measured by tensiometry (contact angle and wettability methods). Subsequently, HSA adsorption to silanized-glass adsorbent particles with incrementally-increasing hydrophilicity was measured [23], showing here that mass and energy balances for HSA adsorption were in full agreement. Consistent mass-and-energy balance obtained using very different analytical methods engendered confidence that this gel-electrophoresis implementation of the depletion method provided internally-consistent and accurate results; at least for proteins adsorbing to surfaces from stagnant fluids at steady state. We have also demonstrated utility of these results in studying protein-adsorption competition to the same adsorbent surface immersed in multi-component solutions [24]. Standard radiometric methods were used as a check on the electrophoresis method described above for two of the proteins listed in Table 1, HSA and IgG. Methods outlined in Section 2 were sensitive to about 0.05–0.1 mg/mL (approximately 5% CV). Methods outlined in Section 2 could not be reliably executed by our hands in less than about 3 min., yielding a minimum reproducible elapsed time resolution of about 5 min. (which was small compared to the 15–60 min. time span over which significant adsorption kinetics was observed using tensiometry [5–11]; see below).

Fig. 3 documents adsorption kinetics of IgG to octadecyl sepharose chromatography particles (ODS) at various solution concentrations measured by the depletion method. All proteins of Table 1 exhibited similar adsorption kinetics in that (i) there was no statistically-significant variation observed in total adsorbed protein mass with time t over the range 5 ≤ t ≤ 90 min. and (ii) the amount adsorbed increased in proportion to solution concentration. Fig. 4 compares three methods of measuring adsorption of HSA to ODS from a 2.4 mg/mL solution. Panel A shows electrophoresis adsorption results from stagnant solution, Panel B electrophoresis results obtained under continuous mixing using an inverting hematology rocker, and Panel C radiometric assessment of adsorption from stagnant solution. As reported previously [22–25], mixing did not significantly influence adsorption outcomes (compare Panels A,B) and continuous mixing of low-volume solutions with adsorbent was abandoned as an unnecessary inconvenience that invited experimental error related to solution/particle hang-up within the plastic microtube. Radiometry results confirmed constant adsorbed protein mass with time t over the range 5 ≤ t ≤ 90 min., but the total amount of radio-labeled HAS was about 15–20% lower than that obtained with unlabeled protein (using the electrophoresis method at 2.4 mg/mL, see Table 2). We attribute this difference to the influence of the radiolabel on protein amphilicity [33–37]. Table 2 compiles experimental results obtained for the proteins listed in Table 1.

Figure 3.

Adsorption kinetics of IgG to octadecyl sepharose from buffer solution measured by the depletion method. Note that the depletion (ordinate) is in proportion to initial bulk concentration (filled circles = 0.8 mg/mL, open circles = 1.6 mg/mL, filled inverted triangles = 2.4 mg/mL, open triangles = 3.2 mg/mL, filled squares = 3.9 mg/L ) and does not vary (mean ± standard deviation) with time in the experimentally-accessible range 5 ≤ t ≤ 90 min.

Figure 4.

Comparison of results using different methods of quantifying adsorption of HSA to octadecyl sepharose from buffer solution. Panel A and B show that statistically-identical results are obtained using stagnant or continuously-mixed solutions, respectively. Quantification by radiometry (Panel C) yields lower estimates by about 65% (for this particular protein and concentration) but the same kinetic trend. Lower adsorption estimates by radiometry is attributed to the influence of the radiolabel on protein amphilicity (see Table 2 for comparison of radiolabel effect on HSA and IgG).

3.2 Protein Adsorption Kinetics Measured Using Tensiometry

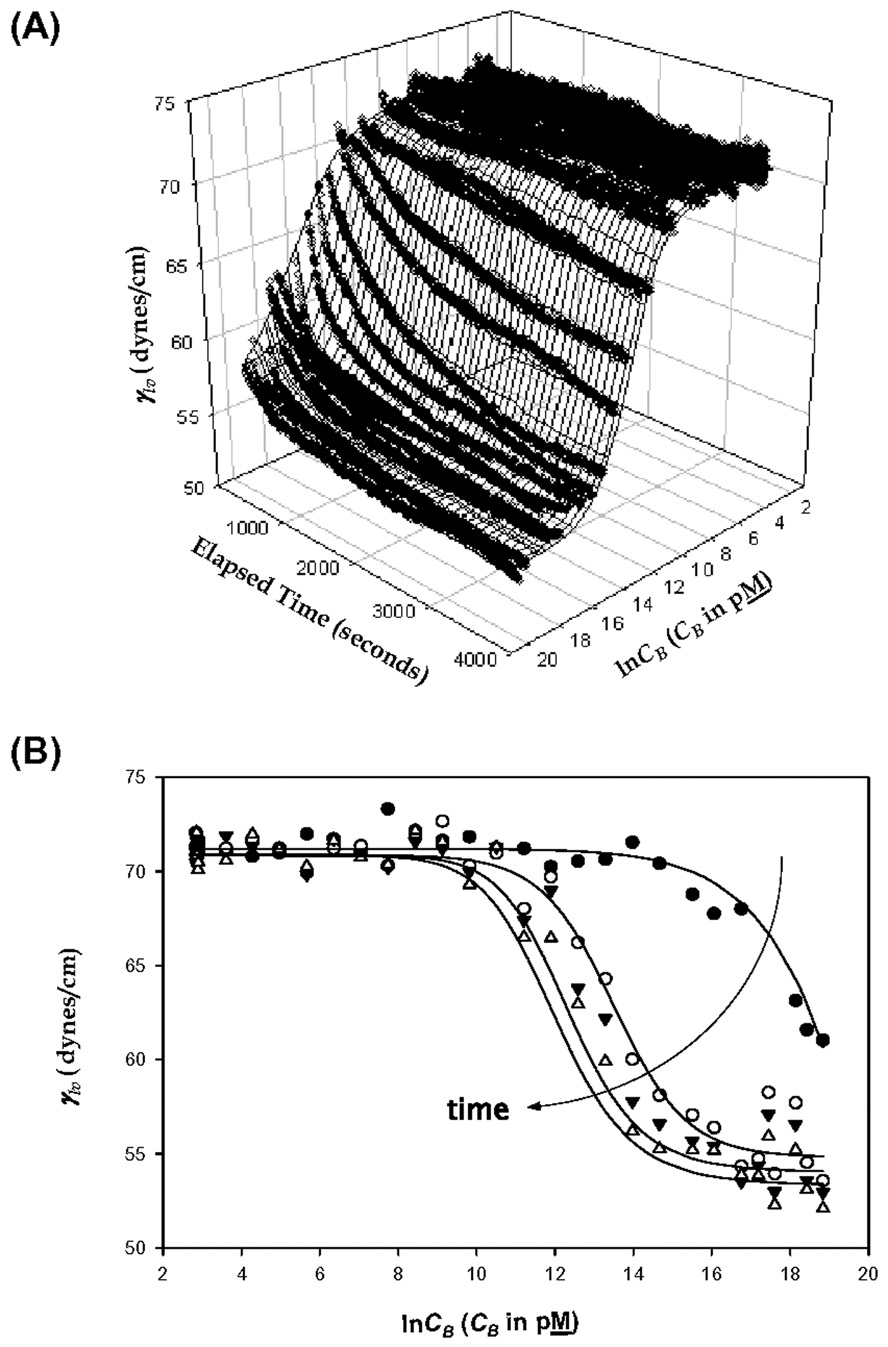
Time-and-concentration dependent buffer/air interfacial tensions and contact angles for proteins of Table 1 have been reported and extensively discussed elsewhere [5–11]. Fig. 5 is example data for HSA (taken from ref. [6]) showing measurable changes in buffer/air interfacial tension γ_lv over 15–30 min. Panel A shows the combined effect of solution concentration and time. Panel B compares time slices taken from Panel A. It is apparent from Fig. 5A,B that adsorption kinetics reach steady state within about 30 min. for HSA. Higher molecular weight proteins such as IgM (1000 kDa, not studied in this work) required up to an hour to achieve or asymptotically approach steady state. These results are to be contrasted with the constant protein mass measured within 5 min. by depletion, as shown in Fig. 3,Fig. 4 and summarized in Table 2.

Figure 5.

Interfacial tension profile of HSA adsorbing to the buffer/air (liquid-vapor, lv) interface in 3D (Panel A, lv interfacial tension γ_lv in dyne/cm as a function of elapsed time and natural logarithmic solution concentration C_B) and 2D (Panel B, γ_lv as a function of natural logarithmic solution concentration C_B at selected elapsed times). The symbols in the 2D panel represent time slices through the 3D representation (filled circle = 0.25 sec, open circle = 900 sec, filled triangles = 1800 sec, and open triangles = 3594 sec). Notice that interfacial energetics exhibit significant kinetics within the range 5 < t ≤ 60 min. whereas mass adsorption does not (Fig. 3,Fig. 4).

3.3 Interpretation of Kinetic Data

The model used to interpret experimental data comparing mass (depletion measurements) and energy (tensiometric measurements) balance in adsorption was predicated on the idea that proteins rapidly move from bulk solution by Fickian diffusion into an interphase with time-dependent volume V_I(t) that was spontaneously formed by bringing protein solution into contact with a physical surface (forming a buffer/air interface or immersing particulate ODS adsorbent into solution in this work), as further elaborated in Section 4. The mathematical model outlined in Appendix B assumed that time-dependent interfacial tension γ(t) arises from time-dependent interphase concentration C_I(t) according to the differential Eq. (3) stating that $\frac{d\gamma (t)}{dt}=\left(\frac{d\gamma (t)}{d{C}_I(t)}\right)·\left(\frac{d{C}_I(t)}{dt}\right)$.

The fundamental surface thermodynamic adsorption Eq. (4) was solved in terms of equilibrium interphase concentration $C_I^E$ for dilute solutions and was applied to the kinetics problem by proposing that, at any instant in time, a quasi-equilibrium (microscopic partitioning equilibrium) exists between interphase and bulk solution. This assumption was justified on the basis that protein adsorption from stagnant solutions follows expectations of a reversible partitioning between interphase and bulk solution and has been shown to be inconsistent with irreversible adsorption ([22–24] and refs. [11, 21] for more discussion). In accordance with experimental observations, it was proposed that C_I(t) increased with time because a fixed mass of protein was trapped within an interphase volume that was decreasing with time to an equilibrium value $V_I^E$. Eq. (3) was then solved in terms of interfacial tension reduction (spreading pressure) Π(t) ≡ (γ^o − γ(t)), where γ^o is the initial interfacial tension and γ(t) is the interfacial tension at any time t. Finally, solution for the ratios $\left[\frac{V_I(t)}{V_I^E}\right]\text{and}\left[\frac{C_I(t)}{C_I^E}\right]$ was obtained in terms of experimental parameters by assuming that the total protein mass adsorbed to buffer/air and buffer/ODS interfaces was approximately the same, so that the apparent Gibbs’ surface excess Γ_app measured at the liquid-vapor (lv) surface approximated that at the hydrophobic ODS solid-liquid (sl) surface (see further Appendix B). This assumption was justified on the basis that concentration-dependent tensiometry has shown that Gibbs’ surface excess at buffer/air and buffer/hydrophobic surfaces (such as methyl-terminated self-assembled monolayers) were not measurably different (i.e. Γ_lv = [Γ_sl − Γ_sv] ≈ Γ_sl; where (sv) refers to the solid-vapor interface; see refs. [9, 21] for more discussion). Associated with this, it was further assumed that spreading pressures were similar at (lv) and (sl) interfaces. These latter simplifications avoided the complexity of interpreting (sl) interfacial tensions in terms of time-dependent contact angles [9–11, 21] and were deemed adequate for the limited purpose of semi-quantitative demonstration of core ideas contained within this paper. Assumptions and simplifications embodied by the model were made in full recognition of the facts that these were not general, did not apply to more hydrophilic surfaces, and that a more general approach was required for the development of a rigorous protein-adsorption kinetics theory beyond the scope of this work.

Fig. 6 used Eq. (13) to calculate $\left[\frac{V_I(t)}{V_I^E}\right]$ (left-hand ordinate) and $\left[\frac{C_I(t)}{C_I^E}\right]$ (left-hand ordinate) as a function of t and Π(t)for prothrombin (blood factor FII, 2.2 mg/mL) using time-dependent (lv) interfacial tension γ_lv reported in ref. [6] as input experimental data. The vertical line annotation marks 5 min. corresponding to the first observation of adsorption by depletion. Values for $\left[\frac{V_I(t)}{V_I^E}\right]\text{and}\left[\frac{C_I(t)}{C_I^E}\right]$ to the left of this vertical line extrapolate theory back in time before it is securely known that mass adsorption was constant and should be accepted only as speculation. Values for $\left[\frac{V_I(t)}{V_I^E}\right]\text{and}\left[\frac{C_I(t)}{C_I^E}\right]$ to the right of the vertical line apply theory within the time interval during which it is securely known by experiment that mass adsorption was constant. The reciprocal relationship between V_I(t) and C_I(t) (by model construction) corresponding to nearly 10-fold reduction in V_I(t) was plainly evident from Fig. 6. Effectively, $\left[\frac{V_I(t)}{V_I^E}\right]\text{and}\left[\frac{C_I(t)}{C_I^E}\right]$ measured time-dependent packing efficiency of protein rapidly adsorbed within the interphase region.

Figure 6.

Interphase volume (left axis, closed circles) and concentration (right axis, open circles) ratios computed from interfacial tension data for prothrombin (FII, 2.2 mg/mL). Interphase concentration occurs because a fixed protein mass is trapped in a volume V_I(t) that is shrinking with time to an equilibrium value $V_I^E$ by the exclusion of water from the interphase to fulfill demands of an equilibrium partition coefficient.

4.0 Discussion

4.1 Interpretation of Principal Experimental Observations

The two principal experimental observations of this work are that:

1. Total mass of protein adsorbed from solution to hydrophobic ODS surfaces measured by solution depletion exhibits no detectable change as a function of time over 5 ≤ t ≤ 90 min for all proteins listed in Table 1 at any solution concentration examined (see Fig. 3–Fig. 4 for examples).

2. Interfacial energetics of adsorption (interfacial tensions measured by buffer/air interfacial tension γ_lv and advancing contact angles) exhibit significant concentration-dependent kinetics over 0.25 sec ≤ t ≤ 60 min (see Fig. 5 for example and refs. [5–11, 21] for more details).

We take observations (i) and (ii) as strong evidence that these two venerable methods of measuring protein adsorption are sensitive to two different rate-determining steps. That is to say, mass transfer to the surface region (a.k.a. interphase) is not directly related to reduction of interfacial energetics. Observations (i) and (ii) are together inconsistent with the popular notion that interfacial energetics decrease with time because protein adsorbs to the surface at a proportional rate. This inconsistency can be resolved by recognizing that, according to conventional Gibbsian (or Guggenheim) surface thermodynamics (see, for example, ref. [28]), interfacial energetics are explicit functions of solute chemical potential (protein concentration) - not the absolute mass of adsorbed solute. In other words, interfacial tensions decrease because protein concentration within the surface region increases, not necessarily just because the absolute adsorbate mass increases. In fact, there are three ways interphase concentration can increase: (a) total adsorbed mass within a fixed interphase volume can increase, (b) the interphase volume containing a fixed total adsorbed mass can decrease, or (c) both (a) and (b) can simultaneously occur.

Solution depletion is basically a gravimetric method that measures mass lost from solution upon adsorption. Principal observation (i) shows that, over the time interval sampled in this work, total adsorbed mass is constant, thereby eliminating both options (a) and (c) as an explanation of increasing interphase protein concentration (decreasing interfacial tensions). It is concluded, therefore, that constant adsorbed mass and decreasing interfacial tensions over the same time interval must mean that interphase volume V_I(t) decreases with time, presumably due to the loss of interphase water (time-dependent protein concentration by interphase dehydration).

Principal observations (i) and (ii) are not entirely unique to this work and do not necessarily establish precedence in the literature. Using a novel resonant elastomeric surface tension (REST) sensor, Clark et al. recently measured rapid mass accumulation of hen egg-white lysozyme associated with much more gradual change in surface energy (tension of adsorbed protein) [38]. Clark et al. thus capture the essence of observation (i); relatively fast mass adsorption that is not directly coupled to slow change in interfacial tension. And of course tensiometry has been applied to measure protein-adsorption kinetics by many investigators over the last few decades, including our own extensive survey of blood-protein adsorption to various surfaces reported over the last few years [5–11, 21]. Obviously, we make no priority claim to surface thermodynamics showing that interfacial tensions scale by concentration, not mass (see Appendix B). However, use of the standard depletion method in the measurement purified human-blood protein-adsorption kinetics to reveal instantaneous (within the time frame of experiment) adsorption of protein mass in proportion to solution concentration does appear to be new. Likewise, our interpretation that the comparatively slow change in interfacial energetics arises from the concentration effect of moving water out of the interphase, not protein into the interphase, seems to be novel. This latter interpretation is completely consistent with our general interpretation of a variety of experimental evidence [5–11, 22–24, 39–41] that water controls the essential aspects of protein adsorption. The conclusion that protein mass adsorption rates are much faster than otherwise inferred from interfacial energetics has a number of ramifications in the interpretation of the biological response to materials, as will be discussed further in section 4.4.

In summary, according to the above rationalization of principal experimental observations, a fixed mass of protein in proportion to bulk solution concentration diffuses promptly into an interface that is spontaneously formed by bringing protein solution into contact with a physical surface (see section 4.3 below for more detail). The total mass of adsorbed protein measured by depletion is thus constant within the time resolution of experiment (which is long compared to diffusion but short compared to decay in interfacial tensions). The initially-formed interphase volume shrinks continuously with time to an equilibrium volume, concentrating the fixed adsorbed protein mass to satisfy an equilibrium ratio of interphase (I) and bulk solution (B) concentrations (a partition coefficient $P(t\to \infty )\equiv \left(\raisebox{1ex}{$W_I$}\!\left/ \!\raisebox{-1ex}{$W_B$}\right.\right)=\left(\raisebox{1ex}{$C_I$}\!\left/ \!\raisebox{-1ex}{$C_B$}\right.\right)$; where W and C are weight or molar concentrations). This partition coefficient is controlled by the overall free energy of adsorption $\mathrm{\Delta }{G}_{\mathit{\text{ads}}}^o=-RT\text{ln}P$, which itself may be the sum of several components [22, 23]. Interfacial tensions slowly decrease in response to slowly increasing interphase concentrations. Section 4.3 articulates this qualitative mechanism in terms of a mathematical model that allows calculation of $\left[\frac{V_I(t)}{V_I^E}\right]\text{and}\left[\frac{C_I(t)}{C_I^E}\right]$ from tensiometric data.

4.2 An Examination of Interface and Interphase Models

Principal observation (i) and the findings of Clark et al. discussed above are inconsistent with standard adsorption-kinetic theories briefly outlined in Section 1 that are responsible, in whole or in part, for the general expectation that interfacial energetics decrease with time because protein adsorbs to the surface at a proportional rate. It is thus of interest to critically reexamine the conceptual basis of these theories as a means of identifying the source of inconsistency between theoretical expectation and experimental reality.

It is our contention that the 2D model of the surface region is an inadequate conceptual basis for the formulation of protein adsorption theories [27, 40] because it ignores the thickness dimension. In so doing, the 2D interpretation effectively forgoes the concept of chemical activity (concentration) so essential to a complete understanding of mass and energy balances in protein adsorption. Indeed, interphase thickness is not negligible because blood-protein dimensions are quite large in comparison to low-molecular-weight amphiphiles for which the 2D surface interpretation seems to work quite well. Blood proteins exhibit a partial specific volume v^o that falls within a surprisingly conserved range of 0.70 ≤ v^o ≤ 0.75 cm³/g protein [42] (see refs. [43–49] for basic information regarding spherical dimensions and molecular packing of proteins). Thus, the interphase separating a physical surface from bulk-protein solution (e.g. solution/air or solution/solid interface) must have a volume no less than v^o, and can be expected to be significantly larger when packing efficiencies, hydration spheres, and protein multilayering are taken into account (see ref. [6] and citations therein for more discussion). And yet, examination of theories ranging from Fick’s law [2] to the Langmuir adsorption isotherm [2], through to the more modern embellishments of Varoqui and Pefferkorn [13] or the RSA model in all of its various editions (Fig. 1; see also refs. [14–16, 38, 50–54]) reveals a pervasive predilection to strictly interpret “adsorbed” as bound to a 2D surface. Molecules residing below this interface are not construed to be in the adsorbed state, even if only separated from that surface by an invisible reflecting plane (see Fig. 2) introduced to the literature as a theoretical expedient rather than an experimental actuality. We further find this 2D perspective not to be in general accord with Gibbs or Guggenheim theories which define a surface as a boundary region (interphase) between immiscible contacting phases having a composition that is different than either of these bulk phases (see, for example, ref. [28] for a lucid discussion of Gibbs and Guggenheim models). Accordingly, the subsurface region diagrammed in Fig. 2 must be an essential part of this interphase and molecules contained therein in excess of bulk solution (positive or negative) must be thus regarded as (positively or negatively) adsorbed. In other words, the interface (interphase) should properly regarded as a volume comprised of both 2D surface and subsurface region - not just 2D surface alone. This distinction between 2D and 3D becomes particularly important in the event of multilayer adsorption, as has been shown to occur for proteins by a number of investigators using a variety of experimental methods over the last twenty years or so [5, 6, 10, 22, 24, 26, 55–64].

A primary issue with the 2D model applied to the interpretation of principal observations (i) and (ii) of the preceding section is that it eliminates an important degree-of-freedom that allows adsorbate concentration to vary independent of adsorbed mass. Partly because of this, we suspect, modern embellishments of RSA theory are forced to embrace an ever-increasing number of variables to explain all experimental outcomes (see, as a recent example, ref. [38]). We speculate (but do not show herein) that simpler protein-adsorption kinetic models can be assembled by linking diffusion-based theories (such as that of Varoqui and Pefferkorn [13]) with a 3D interphase model in a way that that fills an expanding interphase volume by diffusion at a rate and extent that is dependent on bulk-solution concentration, followed by relatively slow interphase concentration by the elimination of interphase water.

4.3 Time-Dependent Interphase Volume

Appendix B implements a mathematical model embracing the core concepts outlined in the preceding sections that are proposed to control adsorption kinetics. Specifically, the model proposes that protein adsorption occurs in at least three sequential stages, presented here as discrete steps for the sake of clarity but recognizing that the process is more likely quite concerted in nature:

1. Spontaneous movement of water and ions to accommodate the energetic perturbation induced by creation of the interface formed by bringing protein solution into contact with a physical surface [65]. In this work, hydrophobic buffer/air or buffer/ODS adsorbent-particle interfaces are specifically considered, wherein the buffer contains varying concentrations of the purified proteins listed in Table 1. It is presumed that this initial surface region, possibly only a few water molecules thick in the fleeting moments after creation [40, 66], is depleted in protein relative to bulk concentrations because objects the size of protein do not fit within this initial interphase volume.

2. Fickian diffusion of protein from bulk solution into the newly-formed interface due to the concentration gradient formed by Step 1. Influx of protein forms a 3D interphase scaling with protein-molecule dimensions that thickens with time to accommodate newly-arrived protein. Initially, the interface is a perfect sink for protein but adsorption efficiency decreases with time due to back diffusion of protein molecules (reflection) in the manner contemplated by Varoqui and Pefferkorn [13]. This initial interphase concentration C_I(t → 0) is much lower than that dictated by the steady-state partition coefficient P_t→1hr that can require interphase concentrations between 100–500× higher than bulk-solution concentration [6, 22].

3. Resolution of the concentration disequilibrium established in step (2) by movement of water (not necessarily proteins) out of the interphase. This interphase dehydration step is slow relative to diffusion of protein into the interphase (step 2) because it requires organization, interaction, and concentration of protein molecules into a loose interfacial network like that inferred from various studies including neutron reflectometry [67, 68] , interfacial rheology [26], and interfacial tensiometry [6] (see also citations in ref. [40]).

Steps 1 and 2 are essentially common to all diffusion-based theories of adsorption [69] and it is herein assumed these steps are complete within the timeframe of depletion measurements (5 ≤ t ≤ 90 min for all proteins listed in Table 1 at any solution concentration examined; see Fig. 3–4 for examples). It is important to stress that this assumption is particular only to proteins at the relatively-high solution concentrations studied herein. It is known that mass-adsorption kinetics can be observed for proteins at low concentrations (≤ 1 mg/mL) by sensitive techniques with good time resolution [34, 38].

The model of Appendix B implements step (3) with assumptions and simplifications discussed in Section 3.3. Solution of the fundamental surface thermodynamic adsorption Eq. (4) in terms in terms of time-dependent interphase concentration C_I(t) for dilute solutions predicts that protein adsorption at equilibrium should be governed by a partition coefficient P, as has been observed experimentally for various blood proteins adsorbing to surfaces spanning a full range of water wettability [22–24]. Protein-adsorption experiments that do not comply with such a partitioning process must thus fall outside the range of applicability of the fundamental adsorption equation and, conversely, protein-adsorption experiments exhibiting such behavior probably approximate conditions contemplated by reversible thermodynamics, including reversible partition of protein between interphase and bulk solution [9, 21].

Fig. 6 illustrates the reciprocal relationship between interphase volume and concentration. Early stages of adsorption t < 5 min. falling to the left of the vertical line annotation are purely speculation because it is not known with experimental certainty that mass adsorption is constant within this time period. However, if events outlined in steps (1)–(3) above capture the general trends, it can be expected that $\left[\frac{V_I(t)}{V_I^E}\right]$ rises sharply from essentially zero within the first moments of interphase formation to a peak value within the first few µsec in which Step (2) dominates adsorption (see Appendix A). Presumably, Fig. 6 captures the falling edge of this volume peak as Step (3) becomes manifest. Thereafter, relatively minor changes in interphase volume are responsible for slow changes in interphase concentration.

4.4 Implications for the Biological Response to Materials

Biocompatibility is controlled by the acute and chronic biological response to materials [70–73]. A working hypothesis that has emerged as a fundamental biomaterials-surface-science tenet from more than three decades of biomaterials research is that protein adsorption is among the first steps [24] in the acute biological response to artificial materials [5, 65, 74–77]. Hence, biocompatibility is presumed to be directly related to protein adsorption. Understanding how protein arrives at, and adsorbs to, biomaterial surfaces is thus one of the most fundamental problems of biomaterials surface science. It is of practical interest therefore, to consider how this work might impact understanding of the fundamentals of biocompatibility.

Based on the findings of this and recent work on protein adsorption [22–24, 38], we conclude that immersion of a hydrophobic surface into a concentrated, multi-component protein solution such as blood [78, 79] leads to virtually instantaneous accumulation of protein molecules from the proximal fluid phase (relative to the timescale of the observable acute biological responses to materials; see Appendix A). Given that (i) surface capacity for protein is actually quite small (in the range of 2–3 mg/m² or µmoles/m² for kDa-size proteins), (ii) the total blood-protein concentration is large (50–60 mg/mL, [78, 79]), and that (iii) proteins exhibit surprisingly little difference in adsorption energetics across a broad range of blood protein types (3 decades in molecular weight, see refs. [6–11, 21–24, 26] for more discussion), we see little reason to suspect that this proximal solution is significantly depleted by adsorption and no readily-apparent physical rational for significant surface-selective adsorption of one protein over another in this early phase (say, within the first few minutes of surface-solution contact). Rather, it seems more likely that the concentration profile of initially-adsorbed protein resembles that of the contacting solution phase so that “…in mixtures such as blood, the proteins would be adsorbed simply in proportion to their surface collision frequency or concentrations…”; as argued by Brash and Lyman in the early 1960’s [80] and supported by more recent studies of protein-adsorption competition [24]. The qualitative explanation for the Vroman based on relative arrival rates of low-and high-molecular-weight proteins articulated in Section 1 thus seems untenable because proteins traverse only short distances from concentrated solutions to arrive at a rapidly-filled surface region, arguably only a few protein-molecule diameters thick (see Appendix A.1). Hence, there seems simply too little time and space for mass transfer to exert a significant adsorption-discrimination effect from concentrated protein solution. However, if physical circumstances permit equilibration of the initially-adsorbed protein layer with bulk solution, as might occur in a simple test-tube experiment or perhaps by continuous contact of a stagnant interphase with flowing solution [81] as examples, then sorting of proteins based on relative size and/or adsorption affinity that results in selective adsorption might occur; as has been shown to occur in at least stagnant solutions using both depletion and tensiometric methods [7, 24].

Interpreting the above in terms of blood-contact phenomena as a single example of practical importance to cardiovascular biomaterials, we propose that the relative concentration of blood proteins initially adsorbed to a surface immersed in plasma is substantially equivalent to whole plasma (irrespective of surface energy but excluding surfaces with ion-exchange functionalities or immobilized ligands). If the surface is relatively hydrophobic (using a water contact angle greater than about 60° as a useful demarcation between hydrophobic and hydrophilic types [39, 40, 82]), then the interphase-concentration effect can lead to time-dependent, selective concentration of relatively small proteins (such as Hageman Factor, FXII) at the expense of larger proteins [24] because protein adsorbs to hydrophobic materials with characteristic partition coefficients P ≥ 100[6, 21, 22]. By contrast, no such interphase concentration effect occurs at hydrophilic materials (water contact angle less than 60° according to above) because protein does not adsorb at concentrations greater than solution concentration (P = 1, see citations above). Perhaps these events partially account for the sluggish coagulation of plasma in contact with hydrophobic materials compared to hydrophilic analogs [83, 84], even though FXII activation in neat solutions is found to be nearly surface-energy independent [85]. Clearly the significance of such interpretation warrants considerable investigation and verification before it is incorporated into general biomaterials thinking. But it seems clearly evident from the data at hand that the reality of fast mass adsorption followed by slow interphase concentration will have significant ramifications in understanding biocompatibility.

5.0 Conclusions

This study shows that a fixed mass of protein in proportion to solution concentration promptly adsorbs to a hydrophobic surface immersed in concentrated protein solution. The interphase region separating the physical surface from bulk solution undergoes significant time-dependent decrease in volume. Interphase concentration of adsorbed protein increases commensurately over this time frame to satisfy an equilibrium partition coefficient by moving water out of the interphase. This revision of standard adsorption theory has important ramifications in the interpretation of biocompatibility and emphasizes an important role of water in protein adsorption.

Appendix A

Appendix A. 1 Bond and Puls Analysis

Bond and Puls state that the depth of solution that would hypothetically be depleted to fill a surface region to the equilibrium value of Gibbs’ surface excess Γ (mass/surface area) is Γ/C, where Γ has units of mass/surface area and solution concentration C is solution concentration in mass/volume. At Γ = 2 mg/m² for example, and a blood protein concentration of 50 mg/mL, Γ/C = 40 nm; or about 10× the diameter of albumin (see refs. [43–49] for basic information regarding spherical dimensions and molecular packing of proteins). Although adsorption is unlikely to deplete surrounding solution in the manner contemplated by such as simple calculation, it is evident that the depth of solution surrounding an adsorbent significantly affected by adsorption will be only a few protein molecules in depth when the solution phase is concentrated.

Bond and Puls further estimate the half-time τ required to fill this surface region to be $\tau =\left[\frac{{\left(\mathrm{\Gamma }/C\right)}^2}{D}\right]$, where D is the diffusion coefficient. Using D ~ 10⁻⁶ cm²/sec appropriate for proteins [86], τ ≈ 1.6 msec, anticipating that equilibrium would be achieved within a few milliseconds.

Appendix A.2 Simple Diffusion Theory

The solution to Fick’s’ law for diffusion of a solute “2” in solvent “1” reads [81]:

$${\mathrm{\Gamma }}_2(t)=2C_B^o{\left(\frac{Dt}{\pi }\right)}^{1/2}$$ (1)

where Γ₂ ≡ (n_I,2/ A) measures the number of solute moles within the interphase n_I,2 per-unit-area (moles/cm²), $C_{B,2}^o$ is the initial bulk-solution concentration of 2, D is the solute diffusion constant in solvent 1, and t is time. Eq. (1) can be expressed in terms of solute interphase concentration C_I,2(t) = Γ(t)/Ω(t) where Ω(t) is the time-dependent thickness of the interphase region and solved for time:

$$t=\left(\frac{\pi }{D}\right){\left[\left(\frac{C_{I,2}(t)}{C_{B,2}^o}\right)\left(\frac{\mathrm{\Omega }(t)}{2}\right)\right]}^2$$ (2)

For spheroidal blood proteins with diameters falling between, say, 5 to 10 nm, 10⁻¹⁴ ≤ Ω(t)² ≤ 10⁻¹² cm (see refs. [43–49] for basic information regarding spherical dimensions and molecular packing of proteins). Combined with D ~ 10⁻⁶ cm²/sec appropriate for such proteins (compared to 10⁻⁵ cm²/sec for water [87]), this implies that ${10}^{-7}<\left[t{\left(\frac{C_{B,2}^o}{C_{I,2}(t)}\right)}^2\right]<{10}^{-6}\text{sec}$ and that diffusion will approach the equilibrium dictated by $\left(\frac{C_{I,2}(t)}{C_{B,2}^o}\right)\to 1$ within a few microseconds if purely Fickian diffusion prevailed over the entire adsorption process.

Appendix B

We adopt the practical idea that time-dependent interfacial tension γ(dyne/cm) follows time-dependent interphase concentration C_I(t) (molarity) [88] which, as discussed in section 4.1 and section 4.3, decreases with time due to interphase dehydration:

$$\frac{d\gamma (t)}{dt}=\left(\frac{d\gamma (t)}{d{C}_I(t)}\right)·\left(\frac{d{C}_I(t)}{dt}\right)$$ (3)

The objective of the model is to solve Eq. (3) in terms of time-dependent interphase volume V_I(t) by finding approximate analytical relationships for the two terms on the right hand side (RHS). C_I(t) follows immediately from V_I(t) because the total mass adsorbed within the interphase is constant within the time interval considered by the model.

Appendix B.1 $\left(\frac{d\gamma (t)}{d{C}_I(t)}\right)$

The fundamental equilibrium adsorption equation for a two component system (solvent component “1”, solute component “2”; water and protein, respectively) according to the Guggenheim surface construction [28, 29] reads:

$$d\gamma =-\left[{\mathrm{\Gamma }}_2-\left(\frac{n_{B,2}}{n_{B,1}}\right){\mathrm{\Gamma }}_1\right]d{\mu }_2$$ (4)

where γ is interfacial tension (ergs/cm² = mJ/m²), Γ ≡ (n_I/ A) measures the number of moles within the interphase n_I per-unit-area (moles/cm²), and n_B is the mole number within bulk solution. At equilibrium, the solute chemical potential μ₂ in bulk solution is equal to that within the interphase so that $d{\mu }_{B,2}=RTd\text{ln}{A}_{B,2}=\left(\frac{RT}{A_{B,2}}\right)d{A}_{B,2}=d{\mu }_{I,2}=RTd\text{ln}{A}_{I,2}=\left(\frac{RT}{A_{I,2}}\right)d{A}_{I,2}$; where A is solute activity and B or I denotes bulk phase or interphase, respectively. Neglecting the $\left(\frac{n_{B,2}}{n_{B,1}}\right)$ term in Eq. (4) in view of the fact that n_B,1 ≫ n_B,2 for dilute solutions, allows the fundamental adsorption equation to be rewritten as:

$$d\gamma =-\left(\frac{RT{\mathrm{\Gamma }}_2}{A_{I,2}}\right)d{A}_{I,2}=-\left(\frac{RT{\mathrm{\Gamma }}_2}{A_{B,2}}\right)d{A}_{B,2}$$ (5)

Eq. (5) thus leads to the conclusion that $\left(\frac{d{A}_{I,2}}{d{A}_{B,2}}\right)=\left(\frac{A_{I,2}}{A_{B,2}}\right),$or that an incremental change in solution activity leads to an incremental change in interfacial activity governed by the ratio of activities. This is the essence of solute partitioning. The relevance of this observation becomes clearer when activity is converted to concentration using A_I,2 ≡ σ_I,2X_I,2 and $X_{I,2}\approx \left(\frac{n_{I,2}}{n_{I,1}}\right)=\left(\frac{C_{I,2}}{C_{I,1}}\right)$, where σ_I,2 is an activity (fugacity) coefficient and the approximation is appropriate to dilute solute solutions. Accordingly, $A_{I,2}={\sigma }_{I,2}\left(\frac{C_{I,2}}{C_{I,1}}\right)$ and it becomes evident that:

$$\begin{array}{c}\left(\frac{A_{I,2}}{A_{B,2}}\right)=\left(\frac{{\sigma }_{I,2}}{{\sigma }_{B,2}}\right)\left(\frac{C_{I,2}}{C_{B,2}}\right)\left(\frac{C_{B,1}}{C_{I,1}}\right)=\left(\frac{{\sigma }_{I,2}}{{\sigma }_{B,2}}\right)\left(\frac{p_2}{p_1}\right)=\left(\frac{{\sigma }_{I,2}}{{\sigma }_{B,2}}\right)P_2\\ \text{or}\\ P_2=\left(\frac{A_{I,2}}{A_{B,2}}\right)\left(\frac{{\sigma }_{B,2}}{{\sigma }_{I,2}}\right)\end{array}$$ (6)

where the partition coefficient $p\equiv \raisebox{1ex}{$C_I$}\!\left/ \!\raisebox{-1ex}{$C_B$}\right.$ measures relative concentrations within the interphase and bulk-solution phase. The term $\left(\frac{p_2}{p_1}\right)$ is the ratio of these partition coefficients for solute and solvent. As the relative solute interphase concentration increases (p₂ > 1), the relative solvent concentration must decrease commensurately (p₁ < 1) because two things cannot occupy the same space at the same time. In fact, for any particular protein, the amount of water displaced from the interphase upon adsorption will principally depend on size of the protein (excluded volume). Consequently, the ratio of partition coefficients will be particular to, and characteristic of, the protein defining a net partition coefficient such that $P_2=\left(\frac{p_2}{p_1}\right)$. Eq. (6) thus predicts that adsorption from dilute solutions of purified proteins can be expected to be controlled by a characteristic partition coefficient P₂. In fact, this kind of adsorption behavior is observed experimentally, up to surface saturation for various blood proteins adsorbing to surfaces spanning a full range of water wettability [22–24]. Thus, experiment vindicates the assumptions leading to Eq. (5) and first-principles theory explains why protein adsorption from dilute solutions is controlled by a partition coefficient at equilibrium (steady state). Failure of a real protein system to follow expectations of partitioning is diagnostic that protein does not adsorb reversibly and, conversely, it can be expected that protein partitioning is diagnostic of reversible protein adsorption.

Returning now to the relationship $A_{I,2}={\sigma }_{I,2}\left(\frac{C_{I,2}}{C_{I,1}}\right)$, it is evident that $d{A}_{I,2}=\left[\left(\frac{{\sigma }_{I,2}d{C}_{I,2}}{C_{I,1}}\right)+\left(\frac{C_{I,2}d{\sigma }_{I,2}}{C_{I,1}}\right)\right]$ for dilute solutions in which the change in solvent concentration accompanying an incremental change in solute concentration is small (C_I,1 approximately constant). Insertion of this relationship into Eq. (5) leads to:

$$\begin{array}{c}d\gamma =-\left(\frac{C_{I,1}}{C_{I,2}}\right)\left(\frac{RT{\Gamma }_2}{{\sigma }_{I,2}}\right)\left[\left(\frac{{\sigma }_{I,2}d{C}_{I,2}}{C_{I,1}}\right)+\left(\frac{C_{I,2}d{\sigma }_{I,2}}{C_{I,1}}\right)\right]=-\left(\frac{RT{\Gamma }_2}{{\sigma }_{I,2}{C}_{I,2}}\right)\left[{\sigma }_{I,2}d{C}_{I,2}+C_{I,2}d{\sigma }_{I,2}\right]\\ \text{or}\\ d\gamma =-RT{\Gamma }_{2}d\text{ln}\left[{\sigma }_{I,2}{C}_{I,2}\right]\end{array}$$ (7)

The model applies the equilibrium adsorption equation (7) to adsorption kinetics by proposing that, at any instant in time, a quasi-equilibrium exists between protein within the interphase and bulk solution. In other words, the distribution of protein between interphase and bulk solution is controlled by a time-dependent partition coefficient P₂(t) and interfacial tension is a function of time because interphase concentration is a function of time. Writing Eq. (7) explicitly in terms of time-dependent interfacial tension γ(t) and interphase concentration C_I,2(t) and expanding the differential leads to:

$$\frac{d\gamma (t)}{d{C}_{I,2}(t)}=-\left(\frac{RT{\Gamma }_2}{{\sigma }_{I,2}{C}_{I,2}(t)}\right)\left(\frac{d}{d{C}_{I,2}(t)}\right)\left({\sigma }_{I,2}{C}_{I,2}(t)\right)=-\left(\frac{RT{\Gamma }_2}{C_{I,2}(t)}\right)\left[\left(\frac{1}{{\sigma }_{I,2}}\right)\frac{d}{d{C}_{I,2}(t)}\left({\sigma }_{I,2}{C}_{I,2}(t)\right)\right]$$ (8)

Appendix B.2 $\left(\frac{d{C}_I(t)}{dt}\right)$

Under experimental conditions explored in this work when the mass of protein adsorbed from solution is constant (depletion does not change with time or $\frac{dD}{dt}=0$), then it is apparent that time-dependent interphase concentration $\left(\frac{d{C}_{I,2}(t)}{dt}\right)$ must be due only to change in time-dependent interphase volume V_I(t) because n_I,2 is constant and:

$$\left(\frac{d{C}_{I,2}\mathit{\left(}t\mathit{\right)}}{dt}\right)=\left[n_{I,2}\frac{d}{dt}\left(\frac{1}{V_I\mathit{\left(}t\mathit{\right)}}\right)\right]=-\left[\left(\frac{n_{I,2}}{V_I{\mathit{\left(}t\mathit{\right)}}^2}\right)\left(\frac{d{V}_I\mathit{(}t)}{dt}\right)\right]=-\left[\left(\frac{C_{I,2}\mathit{\left(}t\mathit{\right)}}{V_I\mathit{\left(}t\mathit{\right)}}\right)\left(\frac{d{V}_I\mathit{\left(}t\mathit{\right)}}{dt}\right)\right]$$ (9)

Appendix B.3 $\left(\frac{d\gamma (t)}{dt}\right)$

Eq. (8) and Eq. (9) can be combined in accordance with Eq. (3) and solved for time-dependent interfacial tension γ(t) due to time-dependent interphase volume V_I(t):

$$\begin{array}{c}\frac{d\gamma \mathit{\left(}t\mathit{\right)}}{dt}=\left(\frac{d\gamma \mathit{\left(}t\mathit{\right)}}{d{C}_{I,2}\mathit{\left(}t\mathit{\right)}}\right)·\left(\frac{d{C}_{I,2}\mathit{\left(}t\mathit{\right)}}{dt}\right)=-\left(\frac{RT{\Gamma }_2}{C_{I,2}\mathit{\left(}t\mathit{\right)}}\right)\left[\left(\frac{1}{{\sigma }_{I,2}}\right)\frac{d}{d{C}_{I,2}\mathit{\left(}t\mathit{\right)}}\left({\sigma }_{I,2}{C}_{I,2}\mathit{\left(}t\mathit{\right)}\right)\right]·\left[-\left(\frac{C_{I,2}\mathit{\left(}t\mathit{\right)}}{V_I\mathit{\left(}t\mathit{\right)}}\right)\left(\frac{d{V}_I\mathit{\left(}t\mathit{\right)}}{dt}\right)\right]\\ \text{or}\\ \frac{d\gamma \mathit{\left(}t\mathit{\right)}}{dt}=RT{\Gamma }_2\left[\left(\frac{1}{{\sigma }_{I,2}}\right)\frac{d}{d{C}_{I,2}\mathit{\left(}t\mathit{\right)}}\left({\sigma }_{I,2}{C}_{I,2}\mathit{\left(}t\mathit{\right)}\right)\right]·\left[\left(\frac{1}{V_I(t)}\right)\left(\frac{d{V}_I\mathit{\left(}t\mathit{\right)}}{dt}\right)\right]\end{array}$$ (10)

Eq. (10) is not experimentally useful in the present form due to unknown parameters appearing in the RHS, especially including Γ₂. In principle, Γ₂ can be calculated from depletion data for a particular protein with molecular weight MW through ${\Gamma }_2=\left(\frac{D{V}_B}{aMW}\right)$; where V_B is the volume of the bulk solution phase (see ref. [23] for details of depletion arithmetic). Unfortunately, surface area a of ODS hydrogel adsorbent materials used in this work is not known with precision, introducing considerable uncertainty in such calculations. Apparent Gibbs’ surface excess Γ_app is, however, known from concentration-dependent γ_lv [6, 11, 21] within 10–20% and is a good measure of Γ₂ for dilute solutions, as discussed above, if proper correction for the non-ideality proteins is made (and assuming that γ_lv is a good surrogate for γ_sl of ODS adsorbent particles, see section 3.3). Noting that ${\Gamma }_2=-\left(\frac{A_{B,2}}{RT}\right)\left(\frac{d{\gamma }_{lv}}{d{A}_{B,2}}\right)\text{and}{\mathrm{\Gamma }}_{\mathit{\text{app}}}=-\left(\frac{X_{B,2}}{RT}\right)\left(\frac{d{\gamma }_{lv}}{d{X}_{B,2}}\right)$, it is evident that $\left(\frac{{\mathrm{\Gamma }}_{\mathit{\text{app}}}}{{\mathrm{\Gamma }}_2}\right)=\frac{\left[\left(\frac{X_2}{RT}\right)\left(\frac{d{\gamma }_{lv}}{d{X}_2}\right)\right]}{\left[\left(\frac{A_2}{RT}\right)\left(\frac{d{\gamma }_{lv}}{d{A}_2}\right)\right]}=\left(\frac{X_2}{A_2}\right)\left(\frac{d{A}_2}{d{X}_2}\right)$. Inserting relationships among mole fraction, activity, and activity coefficients, it is found that:

$$\begin{array}{c}\left(\frac{{\mathrm{\Gamma }}_{\mathit{\text{app}}}}{{\mathrm{\Gamma }}_2}\right)=\frac{\left[\left(\frac{C_{I,2}}{C_{I,1}}\right)d\left({\sigma }_{I,2}\frac{C_{I,2}}{C_{I,1}}\right)\right]}{\left[{\sigma }_{I,2}\left(\frac{C_{I,2}}{C_{I,1}}\right)d\left(\frac{C_{I,2}}{C_{I,1}}\right)\right]}=\left(\frac{1}{{\sigma }_{I,2}}\right)\frac{d}{d{C}_{I,2}}\left({\sigma }_{I,2}{C}_{I,2}\right)\\ \text{or}\\ {\mathrm{\Gamma }}_{\mathit{\text{app}}}={\mathrm{\Gamma }}_2\left[\left(\frac{1}{{\sigma }_{I,2}}\right)\frac{d}{d{C}_{I,2}}\left({\sigma }_{I,2}{C}_{I,2}\right)\right]\end{array}$$ (11)

Using this relationship in Eq. (10) leads to the relationship sought between time-dependent interfacial tension γ(t) and interphase volume V_I(t):

$$\begin{array}{c}\frac{d\gamma \mathit{\left(}t\mathit{\right)}}{dt}=RT{\mathrm{\Gamma }}_{\mathit{\text{app}}}·\left[\left(\frac{1}{V_I\mathit{\left(}t\mathit{\right)}}\right)\left(\frac{d{V}_I\mathit{\left(}t\mathit{\right)}}{dt}\right)\right]\Rightarrow d\gamma \mathit{\left(}t\mathit{\right)}=RT{\mathrm{\Gamma }}_{\mathit{\text{app}}}\left[\frac{d{V}_I\mathit{\left(}t\mathit{\right)}}{V_I\mathit{\left(}t\mathit{\right)}}\right]\\ \text{or}\\ \gamma \mathit{\left(}t\mathit{\right)}=RT{\mathrm{\Gamma }}_{\mathit{\text{app}}}\mathit{\text{ln}}\left[k_1{V}_I\mathit{\left(}t\mathit{\right)}\right]\end{array}$$ (12)

where k₁ is a combination integration constants. It is important to stress that Γ_app is not a function of time when $\frac{dD}{dt}=0$ because both n_I,2 and adsorbent surface area are constants. At equilibrium, Eq. (12) becomes ${\gamma }^E=RT{\mathrm{\Gamma }}_{\mathit{\text{app}}}\mathit{\text{ln}}\left[k_1{V}_I^E\right]$, where γ^E is the steady-state interfacial tension at the particular bulk solution concentration under consideration and $V_I^E$ is the corresponding steady-state interphase volume. The equilibrium spreading pressure Π^E ≡ (γ^o − γ^E) can be related to the time-dependent spreading pressure Π(t) ≡ (γ^o − γ(t)) by the parameter ΔΠ(t) ≡ (Π^E − Π(t)), allowing Eq. (12) to be written in terms of ΔΠ(t):

$$\left[\frac{V_I(t)}{V_I^E}\right]=e^{\left(\raisebox{1ex}{$\mathrm{\Delta }\Pi (t)$}\!\left/ \!\raisebox{-1ex}{$RT{\mathrm{\Gamma }}_{\mathit{\text{app}}}$}\right.\right)}\text{and}\left[\frac{C_I(t)}{C_I^E}\right]=e^{-\left(\raisebox{1ex}{$\mathrm{\Delta }\Pi (t)$}\!\left/ \!\raisebox{-1ex}{$RT{\mathrm{\Gamma }}_{\mathit{\text{app}}}$}\right.\right)}$$ (13)