Inverse radiation dose-rate effects on somatic and germ-line mutations and DNA damage rates

Abstract

The mutagenic effect of low linear energy transfer ionizing radiation is reduced for a given dose as the dose rate (DR) is reduced to a low level, a phenomenon known as the direct DR effect. Our reanalysis of published data shows that for both somatic and germ-line mutations there is an opposite, inverse DR effect, with reduction from low to very low DR, the overall dependence of induced mutations being parabolically related to DR, with a minimum in the range of 0.1 to 1.0 cGy/min (rule 1). This general pattern can be attributed to an optimal induction of error-free DNA repair in a DR region of minimal mutability (MMDR region). The diminished activation of repair at very low DRs may reflect a low ratio of induced (“signal”) to spontaneous background DNA damage (“noise”). Because two common DNA lesions, 8-oxoguanine and thymine glycol, were already known to activate repair in irradiated mammalian cells, we estimated how their rates of production are altered upon radiation exposure in the MMDR region. For these and other abundant lesions (abasic sites and single-strand breaks), the DNA damage rate increment in the MMDR region is in the range of 10% to 100% (rule 2). These estimates suggest a genetically programmed optimatization of response to radiation in the MMDR region.

The dose-rate effect (DRE) on mutation has important implications for genetics and radioprotection. The risk of genetic effects of ionizing radiation for both somatic and germ cells decreases with reduction of dose rate (DR). This phenomenon is called the direct DRE (reviewed in refs. 1 and 2). But some somatic cell lines show inverse DREs, with higher sensitivity to mutation induced by low linear energy transfer (LET) radiation (3–12) or to oncogenic transformation induced by fission neutrons (2) at very low DRs than at low DRs. However, some investigators have reported a direct DRE (1, 12) or no DRE (13, 14), at very low DRs of continuous (13) or fractionated (14) low LET radiation. With respect to mutational DREs in germ cells, Lyon and coworkers (15) have suggested a similar inverse effect at very low DRs, whereas Russell and coworkers (16) concluded that their data did not confirm such an effect. The general view is that germ-line mutations do not show an inverse DRE (reviewed in ref. 1). Here we reanalyze these data, together with recent low LET data on DREs, and conclude that there is indeed a general pattern of inverse effects at very low DRs for both somatic and germ cells.

Evidence for Inverse DREs

Somatic HPRT Mutation in Mammalian Cells in Vitro.

Although there are data on other genetic DREs than HPRT mutation in somatic mammalian cells (for review see refs. 1, 5, and 17), we limited our analysis to HPRT mutations because they have been the most studied. For the most part, the data were obtained by using low LET radiation, i.e., x-rays and γ-rays. The low DR somatic mutation data that we plot in Fig. 1 all were evaluated and reviewed in at least four reviews published in the 1990s (1, 4–6) with one exception for a radiosensitive mutant of the L5178Y cell line, because this cell line is probably DNA repair deficient.

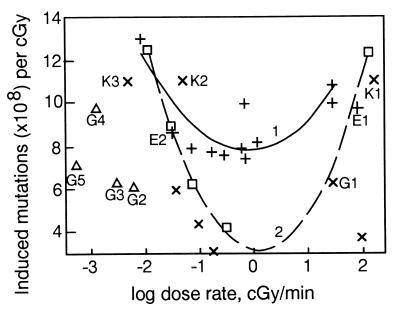
Figure 1.

DREs of low LET radiation upon HPRT mutations (×10⁸). + and 1, mouse L5178Y cells, per cGy (refs. 5 and 7–10, and reviewed in refs. 1, 4, and 5). Points E1 and E2 are Evans and coworkers' data (13). □ and 2, Chinese hamster V-79, subline 85 cells, per 4 cGy (6). × and ▵, Human TK6 lymphoblastoid cells, per cGy. ×, refs. 3 and 12. Points K1, K2, and K3 are König's and Kiefer's data (18). Points G1–G5 are from Grosovsky and Little (14). Points ▵ G2–G5 resulted from irradiation at multiple acute doses (see text). Curves 1 and 2 are of the parabolic form, y = ax² + bx + c.

In mouse lymphoma L5178Y cells, also designated (LY-R) (13), the induced mutant frequency was lower after irradiation at 0.33 cGy/min than at high DR; thus a direct DRE was observed. After irradiation at 0.01 cGy/min, however, the mutant frequency was higher than at 0.33 cGy/min (7) in contradiction to the common conclusion that there is a leveling off at low rates with no further change at very low DRs (reviewed in ref. 1). Moreover, data on Hprt mutant frequencies in different somatic rodent cells [mouse LY cells (7–10]; Chinese hamster V79 cells, subline V79-S85 and other sublines (6), and the human TK6 lymphoblastoid cell line (3, 12, 14) corroborate this curvilinear relationship, which we approximated by using a second-order polynomial (parabolic) model (Fig. 1). In fact, these different somatic cell lines show higher mutant frequencies at DRs lower than 0.1–1 cGy/min, than at rates of 1 cGy/min, or even higher. The observations of Crompton and coworkers (6) further indicate that neither changes in duration of very low DR exposure nor the contribution of background mutation rate and growth and radiosensitivity changes (including the effect on mutation of doubling time, plating efficiency, and cell cycle distribution) could account for the observed effects. The increase of mutagenic efficiency of low LET ionizing radiation with the reduction of DR below 0.1 cGy/min is not artefactual. Until recently it was commonly stated that the frequency of mutation at the HPRT locus in human TK6 cells does not depend on DR (1, 18). But at very low DRs of continuous irradiation, there is indeed a similar inverse effect on mutant frequencies in TK6 cells (3) (Fig. 1).

König and Kiefer (18) reported that there is no difference between the HPRT mutation yields induced by 90 cGy/min x-ray exposure and either 0.27 or 2.7 cGy/h, that is 0.0045 and 0.045 cGy/min, respectively; in each case, the mutant frequency in TK6 cells was slightly higher than 10 per 10⁸-surviving cells/cGy. These data, taken together with the HPRT mutation data for TK6 cells reported by two other groups (3, 12, 14), who measured mutant frequencies at three or more low and very low DRs or after multiple daily exposure of cells to x-rays, do not contradict a parabolic dependence of the mutation yield, with the transition from direct to inverse DRE in the 0.1–1 cGy/min DR region (Fig. 1). Evans' group (13) also reported absence of any DRE for mouse L5178Y cells, but, here again, the DRs were high (96 cGy/min) or very low (0.033 cGy/min). In fact, the Evans' group data correspond almost exactly to the parabolic dependence of mutation frequency on DRE for Hprt mutations in L5178Y cells. The TK6 mutation data of Grosovsky and Little (ref. 14, Fig. 1) are not in good agreement, but they were obtained under different conditions; the x-ray doses were not continuous but rather small daily acute doses of 1, 2.5, 5, or 10 cGy. Total doses were accumulated over many days, up to 1 mo.

A few observations indicate that mammalian cells indeed may not show inverse DRE under certain conditions (19, 20). In particular, an inverse DRE was not found in m5S mouse cells exposed to radiation under resting conditions in the confluent state, whereas in the exponential state of growth, they showed a small inverse DRE for Hprt mutation (19), supporting a suggestion published almost 30 years ago that an inverse DRE for mouse male germ cells (15) may depend on cell replication. This theme of the relationship of inverse DREs to the cell cycle has provided the basis for a mathematical model of inverse DREs in somatic cells by Brenner and coworkers (12).

There are very few studies of DREs on HPRT mutations in vivo in the very low DR range (21), so it is difficult to decide whether there is an inverse DRE. However, mutant frequencies were elevated in lymphocytes of humans exposed to low doses of ionizing radiation at low and/or very low DRs (22–25), relative to high DRs. There may, therefore, be an inverse effect at very low DRs, but a synergistic effect with chemical mutagens cannot be ruled out (26, 27).

Genetic Effects in Mouse Spermatogonial Stem Cells.

The most comprehensive genetic data are those on specific locus mutations in mouse male germ cells, stem spermatogonia (for excellent reviews see refs. 15 and 16, as well as refs. 1, 5, and 28–32). Forty years ago Russell and coworkers (31) reported that a dogma of radiation genetics, formulated by investigators of Drosophila, that frequency of radiation-induced mutations is independent of DR, is in contradiction with their experiments with mouse spermatogonia. Since that time, direct DREs on mutation frequencies in male spermatogonia have been well documented and reviewed by Russell and coworkers (16) and others (1, 15, 29, 30, 32). On the other hand, Lyon and coworkers (15) found some evidence for an inverse DRE in the very low DR region, whereas 10 years later, Russell and coworkers concluded that “the mutation frequencies in the new data continue to support, or at least are not in conflict with, the view that radiation-induced mutation frequency in spermatogonia is independent of dose rate at dose rates below approximately 0.8 R/min” (ref. 28, page 541). This carefully weighed statement usually is interpreted in the literature and in private communications as meaning that there is only a direct DRE or no DRE on locus-specific mutations in spermatogonia below 0.8 R/min. As a result, to the best of our knowledge, Lyon and coworkers' (16, 28) suggestion has neither been experimentally tested further since the early 1980s (although those authors clearly stated the need for further research on inverse DREs for mouse spermatogonia), nor analyzed theoretically since 1993 (1, 5, 29).

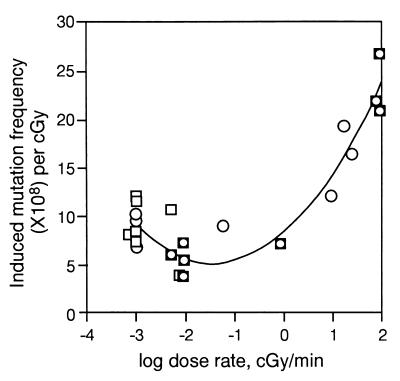
With these different opinions in mind, we have re-examined the data of both groups. The relevant data on induced specific-locus mutation rates (per cGy per locus) in mouse spermatogonia are summarized in Table 1 and Fig. 2. Because Russell and coworkers published data (16) for mutation rates that included spontaneous rates, we recalculated the data to estimate the yield of induced mutations per unit of dose. To do this, the average spontaneous mutation rates have been estimated by using the relevant published data from laboratories that include Russell's (16, 28, 31) and other laboratories (refs. 15 and 30; reviewed in ref. 32). Fortunately the values of these rates are in very good agreement. The data sets for germ-line mutations (shown in Table 1) were analyzed by using the same second-order polynomial model as for somatic cells (Fig. 1). A parabolic relationship is again suggested, from both sets of data (published by Russell's and Lyon's groups). As seen in Figs. 1 and 2, the dependence of mutation on DR in mouse spermatogonia is comparable to that in somatic mouse and Chinese hamster cells and in the human lymphoblastoid cell line TK6. We conclude from these figures that there is an inverse DRE on mutation rate at very low DRs in both mouse male germ cells and at least some somatic cells, as originally proposed by Lyon and coworkers for germ cells (15). Furthermore, these inverse effects are part of a parabolic pattern of DREs over a broad range of DRs. We refer to this relationship as rule 1 for DREs.

Table 1.

DREs of ionizing radiation on mutation frequencies in mouse spermatogonial stem cells

Dose, Gy	Dose rate, cGy/min	Induced rate per cGy (×108)
		Ref. 15	Ref. 16
3	0.0007	—	8.2
0.38	0.001	9.6	12.2
0.86	0.001	7.0	7.3
3	0.001	11.7	11.7
6	0.001	8.5	8.5
3	0.005	—	10.9
6.41	0.005	6.3	—
6.71	0.005	—	6.1
6.18	0.008	3.9	3.8
3	0.009	5.3	4.8
5.16	0.009	3.7	3.7
8.61	0.009	7.3	7.3
6.15	0.06	8.9	—
6	0.8	7.2	7.2
6	9	12.2	—
6.36	17	19.3	—
6	24	16.3	—
6.7	72	21.8	21.8
3	90	26.3	26.5
6	90	20.8	20.8

Figure 2.

DREs on specific locus mutations induced by low LET ionizing radiation in mouse spermatogonia. Data in Table 1: ○, ref. 15; □, ref. 16. The curve fitted to the data are y = 1.55x² + 4.5x + 8.53.

Dependence of DREs on the Rate of DNA Damage.

Here we examine the possibility that the observed optimal region for DR response reflects a program of DNA repair whose induction depends on a comparison of the rates of endogenous and radiation-induced DNA lesions. Such activation may not occur at very low DRs of radiation and, therefore, very low rates of production of DNA damage, i.e., at a very low rate of “signal” to “noise.” We, therefore, examine here the rates of spontaneous occurrence of certain DNA lesions in mammalian cells and how their rates of production may be changed upon irradiation, particularly in the DR range of 0.1 to 1.0 cGy/min. For this purpose, we shall quantitate the kinds of changes in DNA that are induced under spontaneous background conditions and in cells irradiated in the region of the parabolic minimum of DR, 0.1–1.0 cGy/min.

Thermodynamic Instability of Primary Structure of DNA.

DNA-decaying processes are counteracted by DNA repair processes (refs. 33–37 and references cited in Table 2), some of which were measured in nonreplicating rat brain cells of adult rats in vivo by one of us (35, 36) and confirmed by other investigators (reviewed in ref. 38). The probability of spontaneous cleavage of a covalent bond in DNA caused by spontaneous fluctuations in thermal energy at physiological temperatures is very low but finite. Such molecular transition is activated when the vibrational energy of a covalent bond reaches a critical energy level, E_a, necessary for cleavage of the bond. The rate at which this energy distribution can be achieved spontaneously follows the equation

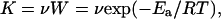1

where R is the universal gas constant, T is the absolute temperature, and ν is the characteristic vibrational frequency of a covalent bond at which the transition is activated or, in chemical terms, a bond is cleaved. This frequency with which the system passes from one microstate to the next at physiological temperatures is of the order of magnitude of 10¹³/sec (39).

Table 2.

Yields of DNA damage at 37°C

Type of DNA damage	Induced yield per cell per cGy	Refs.	Spontaneous rate per cell per min	Refs.
Bases	≈10	27, 44, 45	≈10	33–37, 40, 42
8-oxoG	≈10	50, 55	3–21	51, 54
Thymine glycol	3	49, 56	2–30	57, 58
Single-strand breaks	≈10	1, 29, 43, 46–48	10–50	27, 29, 33

One of the weakest bonds in DNA is the purine-deoxyribose glycosyl bond (33, 34, 37, 40). The most probable value of E_a for cleavage of this bond (DNA depurination in vitro), is ≈32 kcal/mol (27, 34), from which we estimate that K = 10¹³ × exp (−32,000/1.987 × 310) = 10^−9.6/sec. This value is of the same order of magnitude as the depurination constant estimated here (Fig. 3, Table 2). These approximations, compared to estimated depurination rates of lyophilized DNA, also reveal that covalent bonds can be cleaved in DNA even under conditions of very limited accessibility of DNA to water with about the same E_a (27, 33, 36). Thus, truly spontaneous (“heat-induced”) DNA damage could contribute significantly to the mechanisms of production of endogenous DNA damage at physiological temperatures.

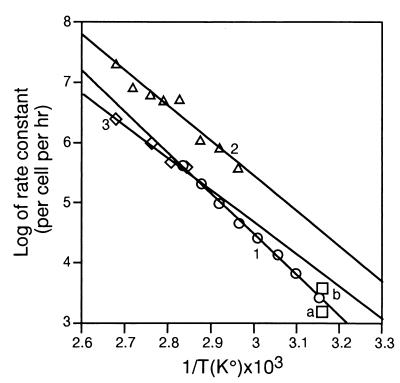
Figure 3.

Arrhenius plots. The rate of spontaneous production of AP sites and single-strand breaks in DNA exposed to different temperatures in vitro or in vivo. 1, (○), Spontaneous loss of purines from native Bacillus subtilis DNA heated in buffer at pH 5. The low pH experimental values (34) have been recalculated here for conditions of incubation in the same buffer at pH 7.4 based on the published dependence of DNA depurination on pH (34), to permit comparison of rates of spontaneous production of different DNA lesions at physiological pH. 2, (▵), Spontaneous loss of adenine from native calf thymus DNA in 0.005 M phosphate buffer (pH 6.8) (data from refs. 33 and 40). 3, (◊), Spontaneous hydrolysis of the phosphate-diester bond in single-stranded bacterial DNA in 0.0025 M phosphate buffer, pH 6.8 (data from ref. 41). Points a and b, rates of induction by mild hyperthermia of alkali-labile sites, including AP sites, in DNA of human diploid fibroblasts of strains 18J, L3, and D3. The values of the rate constants for strains 18J and L3 were about the same (data from refs. 33 and 26), and, therefore, these values are shown as one point, b. The plotted data were reviewed in ref. 33.

Production of Abasic Sites and Strand Breaks in Mammalian Cells.

Single-strand breaks and abasic (apurinic, apyrimidinic; AP) sites are among the most frequent spontaneous and induced DNA lesions (Table 2). The rate coefficient (K) of their production at a given temperature can be estimated by plotting log₁₀K vs 1/T (Arrhenius plot). The relationship between ln K and T⁻¹ is linear (Fig. 3), thus permitting ready comparisons of K at different temperatures. This relationship includes that between temperature and depurination rate of native DNA in different buffers (data from refs. 27, 33, 34, and 40) or between temperature and spontaneous rate of hydrolysis of phosphate-diester bonds in single-stranded DNA (data from ref. 41).

There are, however, difficult problems in the measurement of endogenous DNA damage rates in vivo, because of the presence of ubiquitous DNA repair enzymes. Therefore, estimations of DNA instability in vivo usually are made assuming that the rate of DNA hydrolysis in vivo is similar to that which occurs under normal conditions in aqueous solution in vitro (34, 37, 42, 43). To test whether this assumption is correct, an improved alkaline sucrose gradient sedimentation method was used to measure AP sites and other alkali-labile DNA sites in diploid human fibroblasts in vitro and/or in vivo (33). The rates of formation of AP sites and alkali-labile sites were measured directly in diploid human fibroblasts after culture in vitro and exposure to mild hyperthermic conditions (details in ref. 33). The temperatures and times of treatment were selected to reversibly inhibit DNA repair mechanisms, without killing the cells, after the felicitous observation that human fibroblasts are relatively resistant to hyperthermia (27). The rates of spontaneous formation of DNA damage in human cells are plotted in Fig. 3 (points a and b). From these data the spontaneous rate of production of alkali-labile sites (per 6 × 10⁹ bp/h) at 37°C can be estimated, using the Arrhenius plot in the following form,

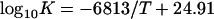2

to be approximately 800 lesions per cell per h. For comparison, Swenberg and coworkers (42) recently reported estimates of rates of formation of AP sites in DNA in vitro, under physiological conditions, of 1.54 per 10⁶ nt per day, which is equivalent to 770 AP sites per 6 × 10⁹ bp per cell per h, in remarkable agreement with the estimate of 800 noted above. Together these estimates suggest that the spontaneous DNA damage rate in mammalian cells could be at a level of several hundreds to 1,000 DNA lesions/cell per h (≈10–15/cell per min) at 37°C. under normal conditions. This rate approximates the yield (per cell per cGy) of the most abundant, simple, not difficult to repair, radiation-induced single-strand breaks and base damage, including abasic sites and oxidative damage (43–49) (Table 2).

Major Products of Oxidative DNA Damage.

A significant part of endogenous and radiation-induced damage is mediated by reactive oxygen species (ROS) (Table 2) (36, 37, 49–64). Data published by Kasai (50), who discovered that the formation of 8-hydroxyguanine [now called 8-oxoguanine (8-oxo G)] is one of the principal products of radiation-induced damage in cells, suggest that in irradiated human HeLa cells and mouse liver, one to several tens of 8-oxoG are induced per cell per cGy. It was reported (51, 54) that the spontaneous production rates of 8-oxo G by the human cell line IMR-90 varied from 15 to 52.5 pmol/10⁹ cells/day, depending on the age of cultured cells; i.e., the “oxidant hits” rate varied from 9,000 (15 × 10⁻¹² × 6 × 10²³ × 10⁻⁹) to 31,500 hits/cell per day, or ≈6–22/cell per min. We call attention to the fact that 8-oxo G can be excised through two different DNA repair pathways, the major one, base excision (37), and nucleotide excision (44), whereas the usual measurement in urine reflects only nucleotide excision. However, any underestimate may be countered at least in part by overestimation caused by DNA oxidation during analysis.

The rates of excision of another abundant oxidative DNA damage product, thymine glycol (TG), also have been reported. In rat tissues, the rate of spontaneous production of TG varied from 2 to 30 TG/cell per min (58). For comparison, ≈3 TGs are induced per 1 cGy of low LET ionizing radiation (56) (Table 2). Thus, 0.6–10 cGy of low LET ionizing radiation induces an amount of TG approximately equivalent to that produced spontaneously per min. According to other recent estimates, the daily rate of spontaneous production of TG damage is equivalent to that added by irradiation at a DR of 4.7 Gy/day (reviewed in ref. 59), or 0.33 cGy/min.

Taken together, these data (Table 2) show that different DNA lesions, such as single-strand breaks, AP sites, and oxidative DNA damage of different kinds, all are produced spontaneously per cell at a rate, per min, that is roughly equivalent to the rate of their induction in different mammalian cells by low LET ionizing radiation at DRs in a relatively narrow range, ≈1 cGy/min, which corresponds approximately to the range of minima in the dependence of the mutagenic action of low LET ionizing radiation on DR. Thus, irradiation in this range increases the damage rate by 10–100% over the spontaneous background rate (rule 2 for DREs).

DNA Damage, DR, and the Radioadaptive Response.

Although the oxidative damage products 8-oxo G and TG are radiotoxic (61) and premutagenic lesions (56, 60, 62), they also can activate DNA repair (49, 63, 64), which is part of the general phenomenon of the adaptive response to both ionizing radiation and oxidative stress of different types (63–71). Adapted cells exhibit higher survival (survival adaptive response) and lower frequencies of chromosomal aberrations and gene mutations than do nonadapted cells, upon subsequent exposure to a challenging high dose of ionizing radiation (65–71). The adapting (priming) dose is usually at a level of one or several cGy and/or is delivered at a low DR, e.g., 1 cGy/min. There is evidence for the dependence of an adaptive response on DR with an optimal response of somatic cells, at some (but not all) conditions (69, 71), near 1 cGy/min, i.e., at a minimum value of mutation rate. This minimum could be a mutational signature of the antimutagenic radioadaptive response, as supported by studies of factors that can inhibit both radioadaptation and mutational DREs (e.g., ref. 65). Protection against induced mutations decreases with further decrease in the DR of the priming dose into a very low DR range (70). Thus, there is also an inverse DRE for the adaptive response in this very low DR range, whereas it also can be decreased if the priming dose is delivered at high DR (ref. 69 and references cited therein). Therefore, the pattern of the DREs shown in Figs. 1 and 2 can be explained by the optimal induction of DNA repair and other defense mechanism(s) in the DR range of 0.1 to 1.0 cGy/min, and at certain doses (the interplay between doses and DREs is not considered here). This is compatible with the suggestion that direct mutational DREs also depend on efficient DNA repair mechanisms (reviewed in refs. 1 and 5).

All abundant radiation-induced DNA lesions also are produced spontaneously (Table 2 and Fig. 3). Therefore, a signal for induction of the antimutagenic radioadaptive response must be recognized by a cell against a “noisy” background. Such recognition should be most effective in the presence of a relatively low (but probably not too low) background. If our explanation of the DR pattern in Figs. 1 and 2 is correct, then such a maximum would be realized in the region of minimally mutagenic DRs (MMDR). Thus, the DREs on mutation suggest a “law,”

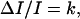3

where ΔI/I is the fractional increase in DNA damage rate and ΔI is the difference between the damage rate in exposed and nonexposed cells that is required for induction of an antimutagenic radioadaptive response.

The Parabolic Minimum: A Signature of Stochastic Resonance?

Here we estimate values of ΔI and I, and derive k for somatic and germ cells separately. The value of I is given by the rates of spontaneous production of 8-oxo G, TG, abasic sites, and single DNA strand breaks, which are each at an average level of 10–15 DNA lesions per somatic diploid cell per min (Table 2) and, therefore, 5–7 DNA lesions per haploid genome of mouse spermatogonia. Minimal-induced mutational yields are seen in somatic cell line L5178Y (Fig. 1) and mouse spermatogonia (Fig. 2), for which there are the most comprehensive data, at DRs ≈0.5 cGy/min and 0.07 cGy/min, respectively. The yields of single-strand breaks, oxidative damage to DNA, and probably AP sites, induced in somatic and germ-line mammalian genomes by low LET radiation delivered at MMDRs of 0.5 and 0.07 cGy/min, respectively, are each approximately (10–15) × 0.5, or ≈6; and 5–7 × 0.07, or ≈0.4/cell per min, respectively. If the minima in the curves shown in Figs. 1 and 2 reflect a law that a certain ratio of “signal” to “noise” is required to induce an optimal antimutagenic radioadaptive response, then the values of k would be most probably in the region from ≈6/15 = 0.4 to 6/10 = 0.6 for somatic cells and from 0.4/7 = 0.06 to 0.4/5 = 0.08 for germ cells. The latter values are uncertain because spontaneous DNA damage rates have not been measured for germ cells.

The rules of DREs on mutation and their mechanism(s) resemble fundamental quantitative rules for sensation and perception, which are derived from analyses on both cellular (for example, chemotropism) (72) and organismic (73, 74) levels. In particular, the psychophysical rule, which is known since Weber's study of sensation and perception in humans (therefore called Weber's law, refs. 73 and 74), usually is given in a form of equation similar to Eq. 3; that is, ΔI/I = k or ΔI = kI, where ΔI is the change required for a just noticeable difference in stimulation; I is the stimulus magnitude, and k is a constant for a particular sense, called the Weber ratio. This ratio has been calculated for brightness (0.02–0.05); auditory frequency (up to 0.03); loudness (intensity measure) (0.1–0.2); cutaneous pressure (0.14–0.16); and taste (salt) (0.15–0.25) (73). These ratios are similar to those for induced to endogenous damage rate in the MMDR.

Mammalian cells have evolved signaling systems to respond to different physical and chemical stresses. Among them, the universal intracellular type of stress is oxidative, which is induced by many environmental agents, including ionizing radiation, which induces and activates endogenous production of ROS. At least some of the ROS that are responsible for the stress are induced by low LET ionizing radiation at a level that is a linear function of the dose, and, therefore, at a rate that is a linear function of the DR. Thus, the cell can “measure” the DR of the exposure through “sensing” of rate of induction of both oxidative DNA damage and/or ROS. Our estimates of the ratio between the radiation-induced yields (per cGy) to the spontaneous production rates (per min) of ROS suggest that in many types of mammalian cells, this ratio for some, but not all, ROS is at a level ≈0.1–1 (data not shown). These values of k are also in the range of those listed above for the Weber ratio for various senses (73).

We conclude that the minima shown in Figs. 1 and 2 reflect the existence in somatic and germ cells of adaptive signaling pathways that respond to an increase of rate of production of ROS and/or oxidative DNA damage. The cell may sense not only a rate of induced DNA damage but also perhaps a rate of induction of certain ROS. This suggestion already has some direct experimental support: an increase of defense mechanisms against both ROS and DNA damage was registered in cells that were exposed to different forms of oxidative stress, including that connected with exposure to ionizing radiation (49, 64, 75, 76). One result of our study is that it predicts on a quantitative level that induction of DNA repair and/or antioxidant enzymes by radiation depends not only on the level, but also on the rate of production, of certain DNA lesions and ROS, with an optimal response to an increase of 10–100% above the “spontaneous” background rates. This phenomenon resembles that of “stochastic resonance” observed for signal-to-noise relationships in physics and physiology (77), whereby an optimal noise level exists for signal transduction.

Discussion

Unfortunately, we do not have Hprt mutation data for DR in the range of 10⁻⁷ to 10⁻⁴ cGy/min for low LET radiation. However, the data of Russell's group (ref. 15 and Table 1) suggest a maximum or leveling off of DREs near 7 × 10⁻⁴ cGy/min. It is interesting that a transition from inverse DRE to direct DRE also has been reported for high LET radiation (radon) for lung cancer induction (more exactly on the first mutation, “first hit,” initiating carcinogenesis) in rats exposed to radon at different DRs, or more correctly at different exposure rates. Indeed, an inverse DRE on the risk of cancer induction was reported at radon exposure levels above 20 working levels, whereas below an exposure rate of 10 working levels the cancer risk (per unit of dose) decreased with increasing duration of exposure (78). (One working level radon exposure rate to the rat lung is equivalent to an absorbed DR of ≈1.4 × 10⁻⁵ cGy/min or 1.4 × 10⁻⁴ cSv/min, taking into account a quality factor for radon-induced cancer of ≈10.) We suggest, therefore, that these data indicate an inverse DRE on induction of the first hit at DRs higher than 1.4 × 10⁻⁴ × 20, that is, 2.8 × 10⁻³ cSv/min, but a direct DRE at DRs lower than 1.4 × 10⁻⁴ × 10, i.e., 1.4 × 10⁻³ cSv/min; this narrow range corresponds approximately to 10⁻³ cGy per min for x-rays and gamma rays, the region of inverse DRE for low LET radiation. A region for inverse DRE (transformation of mouse cells) also has been observed with fission neutrons (intermediate LET), but in a range of 0.01 to 1 cGy/min (reviewed in refs. 1 and 2). The best interpretation of the overall mutational effects from radiation DRs from 10⁻⁷ (approximate background rate) to 10³ cGy/min would appear to be that, as the DR increases, DREs do not change or increase to a maximum, then decrease to a minimum in the MMDR, as a program of DNA repair is induced; above this DR level the repair system becomes less effective, showing a direct DRE.

The existence of rules 1 and 2 evokes a principle that the ratio of signal to noise is a determinant of the response of a cell to a signal such as that produced by damaged DNA. This conclusion could have consequences for DREs of cancer cells because it is apparent that they are characterized by increased noise in terms of oxidative stress or deregulated signaling, thereby reducing their sensitivity to extracellular signals.

What might be the mechanism of a system for inducible repairs of DREs as a function of DRs? Because this DRE pattern is observed in replicating but not resting cells, it seems to be connected with mechanisms of cell cycle control. Attention has been focused on the TP53 gene, because its level is increased after radiation of cells in the G₁ phase of the cell cycle. Furthermore, cells from patients with the Li-Fraumeni syndrome that harbor a TP53 mutation are evidently more resistant than normal cells to low, but not high, DR radiation (79). Another critical regulator of the cell cycle, the RB1 gene, also is involved in the response to ionizing radiation and other agents that damage DNA or induce ROS, through its protein checkpoint function, and thus could play a major role in determining the shape of the mutational responses to DRs and the location of the MMDR. We conclude that the responses to radiation-induced damage are inducible, of high fidelity, and adaptive. They apparently are connected to the regulation of cell cycle checkpoints that are very sensitive to DNA damage (80, 81). The molecular analysis of DREs on mutation should be connected with DREs for cell killing (reviewed in refs. 2 and 82), which we have not considered here but which could have significant implications for radiotherapy.

The MMDR is approximately one million-fold higher than the background radiation level. Why and how was this high level of 0.1–1.0 cGy/min for the MMDR selected during evolution? Could it be that selection for protection against DNA damage occurred as a result of exposure to radiation delivered at such high DRs during some earlier age, or that it resulted from coselection by another, perhaps chemical, agent? This is a problem for further research.

Abbreviations

LET

linear energy transfer

DR

dose rate

DRE

dose-rate effect

MMDR

minimal mutability dose rate

AP

apurinic, apyrimidinic

8-oxo G

8-oxoguanine

TG

thymine glycol

ROS

reactive oxygen species