Diffusion Tensor Imaging at Low SNR: Non-monotonic behaviors of tensor contrasts

Abstract

Diffusion tensor imaging (DTI) provides measurements of directional diffusivities and has been widely used to characterize changes in tissue micro-architecture in the brain. DTI is gaining prominence in applications outside of the brain where resolution, motion, and short T2’s often limit the achievable SNR. Consequently, it is important to revisit the topic of tensor estimation in low SNR regimes. A theoretical framework is developed to model noise in DTI, and by using simulations based on this theory, the degree to which the noise, tensor estimation method, and acquisition protocol affects tensor-derived quantities, such as fractional anisotropy and apparent diffusion coefficient, is clarified. These results are then validated against clinical data. It is shown that reliability of tensor contrasts depends on the noise level, estimation method, diffusion weighting scheme, and underlying anatomy. The propensity for bias and errors is not monotonically increasing with noise. Comparative results are shown in both graphical and tabular form so that decisions about suitable acquisition protocols and processing methods can be made on a case-by-case basis without exhaustive experimentation.

Introduction

Diffusion tensor imaging (DTI) is a magnetic resonance (MR) imaging technique that is sensitive to the random thermal motions of water.¹ DTI has proven especially useful in providing insight into intra-voxel microarchitecture of brain white matter tracts.² Previous studies have shown that the diffusivity in the direction of the fiber bundle is larger than across the bundle because there are comparatively few barriers to water diffusion.² DTI provides measurements of these directional diffusivities, which enables inferences about white matter structural integrity and connectivity.³ DTI has been widely used to characterize changes in micro-architecture associated with stroke,^4,5 white matter damage,⁶ and edema.^7,8

The estimation process used in DTI has been shown to be sensitive to noise.^9–11 At low SNR’s, the derived diffusivities (i.e., eigenvalues of the estimated diffusion tensor) tend to systematically diverge from their true values, subsequently altering the estimated diffusion anisotropy while leaving measures of the mean diffusivity relatively less affected.^9–12 The SNR,^9–11 diffusion weighting scheme,^7,8 and tensor estimation method^13,14 have all been shown to affect derived tensor contrasts such as fractional anisotropy (FA) and mean diffusivity (MD). Fortunately, DTI can be readily accomplished in vivo in the human brain at sufficient SNR to avoid severe problems related to noise contamination.^15,16

DTI is gaining prominence in applications outside of the brain such as the spinal cord,¹⁷ optic nerve,¹⁸ and musculature¹⁹ (including the tongue²⁰). These regions are small, prone to motion, or have substantially shorter T2’s than typical brain tissue. To achieve sufficient resolution in small structures while simultaneously maintaining high SNR, long acquisition times may be necessary. However, tissue motion may cause undesirable image artifacts or blurring in such cases. Additionally, when T2 is short or when the field strength is low (e.g., 0.4T-1.0T) the available signal is reduced, which drives the SNR further down. Despite these significant limitations, a substantial amount of DTI research is being conducted with data at much lower SNR than is typical for brain research at 1.5T or 3T, and DTI images are being generated with relevant and interesting structure under these conditions. However, a detailed study of the effects of noise in this low SNR regime has yet to have been undertaken.

This manuscript develops a theoretical framework to explain how noise propagates from acquired diffusion weighted images to tensor-derived quantities. Using this model, we present simulations that utilize data from an in vivo DTI study and provide insight into the qualitative and quantitative properties of noise propagation. These simulations demonstrate how seemingly innocuous differences in estimation method at low SNR can lead to very different behaviors. Overall, this study clarifies the relative degree to which the noise, tensor estimation method, and acquisition protocol influence the derived tensor contrasts.

A careful reading of the existing literature permits one to arrive at many conclusions that are presented herein; in this sense, our study reiterates important points presented previously. However, rather than simply duplicating previous work, we feel that our article contributes in two significant ways. Firstly, it presents relevant results in a comprehensive single body of work, which can serve as an effective resource. The need for this is clear given the multitude of articles that tackle individual pieces of the DTI-SNR relationship. Effectively comparing results across studies is always challenging, even more so given the intricacies of the DTI-SNR relationship. Secondly, our study provides a comprehensive framework based on a theoretical model which enables characterization of FA and MD measurements over a wide range of SNR’s. This treatment enables the effects of different parameters to be compared side by side, which has important consequences for experiment design and optimization. Through multiple simulations at closely spaced SNR’s, the bias and variability of FA and MD are mapped, and non-monotonic trends in low SNR behavior are well exposed. Finally, a suggested error metric provides a simple method for evaluating the tradeoffs of using various DTI approaches in specific anatomical contexts.

Theory

Estimation of diffusion tensor contrasts from diffusion weighted (DW) images is a complicated, multi-step process. It is therefore difficult to conceptually connect noise properties in the image domain with those of tensor-derived contrasts. This section presents four simplified examples followed by a generalized tensor estimation model to explain how noise propagates from the image domain into the FA contrast.

The eigenvalues of random matrices have been explored in other contexts.^21–23 In the limit of large matrices with normally distributed coefficients, the eigenvalues converge to a distribution with mass primarily on unit circle in the complex plane (e.g., to a complex number with unit magnitude and phase drawn uniformly at random). However, general theory on the distribution of eigenvalues remains an open problem for finite matrices (e.g., the 3×3 matrices of symmetric diffusion tensors). The remainder of this section develops general expressions for the distribution of diffusion tensor derived contrasts (which may not be analytically evaluated in closed form) and presents numerical methods for specific experimental designs.

In the Stejskal-Tanner model of diffusion,²⁴ the signal observed when diffusion weighting is applied is proportional to a reference signal by

$$S_{\text{obs}}=S_{\text{ref}}{e}^{-b{g}^T\mathrm{D}g}+\mathit{\eta }$$ (1)

where S_obs is the observed signal, S_ref is a reference signal, b is the b-value attenuation constant (a chosen experimental parameter), g is a unit vector in ℜ³, D is the symmetric diffusion tensor, and η is a noise term. The apparent diffusion coefficient (ADC) is computed as the logarithm of the ratio of the observed and reference signals. Without loss of generality for diffusion anisotropy calculations, let b be absorbed into D. If observations are made along N non-collinear g (and not mutually co-planar), then the tensor is well determined when 6 or more ADC’s are observed:

$${[AD{C}_i]}_{\mathrm{N}\times 1}=-{[{\{g_x^{2}2g_x{g}_{y}2g_x{g}_z{g}_y^{2}2g_y{g}_z{g}_z^2\}}_i]}_{\mathrm{N}\times 6}{[{\mathrm{D}}_{1,1}{\mathrm{D}}_{1,2}{\mathrm{D}}_{1,3}{\mathrm{D}}_{2,2}{\mathrm{D}}_{2,3}{\mathrm{D}}_{3,3}]}_{1\times 6,}^T$$ (2)

where g_x,g_y and g_z are the components of the unit vector g. The components of D may be estimated, for example, under minimum least squared error criteria with a pseudoinverse (i.e., the log-linear minimum mean square error method). FA is a nonlinear function of the eigenvalues,

$$FA=\sqrt{\frac{3}{2}\frac{{({\mathrm{\lambda }}_1-\overline{\mathrm{\lambda }})}^2+{({\mathrm{\lambda }}_2-\overline{\mathrm{\lambda }})}^2+{({\mathrm{\lambda }}_3-\overline{\mathrm{\lambda }})}^2}{{\mathrm{\lambda }}_1^2+{\mathrm{\lambda }}_2^2+{\mathrm{\lambda }}_3^2}}$$ (3)

where λ₁,λ₂, and λ₃ are the eigenvalues of D and $\overline{\mathrm{\lambda }}$ is the mean of the three eigenvalues. With non-negative eigenvalues, FA ranges from zero to unity, where zero is when diffusion is not oriented (e.g., isotropic), and one is when diffusion in one direction is infinitely larger than the other two directions (e.g., high anisotropy). When negative eigenvalues are permitted, FA ranges from zero to $\sqrt{\frac{3}{2}}$.

In the absence of artifact, MRI noise on Fourier coefficients is well known to be identically independently distributed (i.i.d.) normal (Gaussian).^25,26 Fourier reconstruction of these coefficients to complex-valued images preserves the noise structure. A magnitude operation produces real-valued images from complex-valued images, which transforms the normally distributed noise in complex-valued images to Rician distributed noise in real-valued images. As the signal intensity goes to zero and noise level remains fixed, Rician distributions converge to Rayleigh distributions,

$$p\mathrm{x}(x;\mathrm{\sigma })=\frac{x}{{\mathrm{\sigma }}^2}{e}^{-\frac{x^2}{2{\mathrm{\sigma }}^2}}$$ (4)

where σ is the standard deviation of the noise in the complex domain prior to the magnitude operation.

Example Framework

Consider a simplified DTI experiment in a limiting low SNR regime in which (1) there is no signal, (2) there is finite noise, (3) a separate reference is acquired for each diffusion weighted direction, and (4) tensor orientation is assumed known. In this situation, the SNR is -∞ dB (0:1); ADC’s along each diffusion weighting direction are i.i.d. as the logarithm of the ratio between two identical Rayleigh random variables. Three orthogonal orientations are required to estimate the tensor eigenvalues. Integration reveals that that distribution of the ratio, q, of two i.i.d. Rayleigh random variables does not depend on the noise level (σ),

$$\begin{array}{cc}p\mathrm{Q}\left(q;\mathrm{\sigma }\right)\hfill & ={\displaystyle {\int }_0^{\infty }x[\frac{x}{{\mathrm{\sigma }}^2}{e}^{-\frac{x^2}{2{\mathrm{\sigma }}^2}}][\frac{qx}{{\mathrm{\sigma }}^2}{e}^{-\frac{q^2{x}^2}{2{\mathrm{\sigma }}^2}}]dx}\hfill \\ \hfill & =\frac{2q}{{\left(1+q^2\right)}^2}.\hfill \end{array}$$ (5)

This result can then be transformed by manipulation of the corresponding cumulative distribution function to find the distribution of the ADC,

$$p_{\text{ADC}}(x;\mathrm{\sigma })=\frac{2e^{2x}}{1+e^{2x}}-\frac{2e^{4x}}{{(1+e^{2x})}^2.}$$ (6)

Without further loss of generality, we orient the reference frame such that tensor’s eigenvectors correspond to the Cartesian axes. The numerical integrations that follow in this section were performed with the quasi-Monte Carlo method with four significant digits in Mathematica (Wolfram Research, Inc., Champaign, IL).

Example 1

Consider an experiment in which we independently observe the eigenvalues in the simplified model. Suppose that three diffusion weighting directions are chosen to correspond to the Cartesian axes: g₁=[100]^T, g₂=[010]^T, and g₂=[001]^T By assumption, the off-diagonal entries of the tensor are zero, so Eq. (2) simplifies to

$$\left[\begin{array}{c}{\text{ADC}}_1\\ {\text{ADC}}_2\\ {\text{ADC}}_3\end{array}\right]=-\left[\begin{array}{c}100\\ 010\\ 001\end{array}\right]\left[\begin{array}{c}{\mathrm{\lambda }}_1\\ {\mathrm{\lambda }}_2\\ {\mathrm{\lambda }}_3\end{array}\right]⟹{\mathrm{\lambda }}_i=-{\text{ADC}}_i.$$ (7)

The expected value and variance of FA may be computed by integrating over the joint probability of observations,

$$E[FA]={\displaystyle {\iint }_{{\text{ADC}}_{1:3}}p({\text{ADC}}_1,{\text{ADC}}_2,{\text{ADC}}_3)f_{\text{FA}}({\text{ADC}}_1,{\text{ADC}}_2,{\text{ADC}}_3,)d{\text{ADC}}_{1:3}}$$ (8)

where f_FA is the function that computes the FA from observed ADC’s. Note that Eq. (8) could have equivalently been integrated over signal observations if the probability distribution, p , were taken over the combined observations. Since ADC’s are independent (by model assumptions), Eq. (6) provides a convenient form for the joint probability distribution of p(ADC₁, ADC₂, ADC₃). Numerical integration of the joint probability of FA demonstrates that the expected value of FA is 0.964. Thus, when the eigenvalues are independently observed according to the ratio of Rayleigh distributions, the expected FA is approximately unity.

Example 2

Now consider an experiment in which the eigenvalues are modified by post-processing. Suppose that negative eigenvalues are set to zero prior to calculating FA (also known as “censoring” of eigenvalues). This type of approach might be taken to try to mitigate the impact of “non-physical,” negative eigenvalues. When f_FA in Eq. (7) is modified to reflect the censoring of eigenvalues, numerical integration of the modified joint probability distribution reveals that the expected value of FA is 0.883. Thus, manipulation of derived eigenvalues alters the expected FA.

Example 3

Now consider an experiment in which there is statistical dependence between the distributions of observed eigenvalues. In particular, suppose that the three diffusion weighting directions are chosen in a “dual gradient” scheme:$g_1=\frac{1}{\sqrt{2}}{[110]}^T,g_2=\frac{1}{\sqrt{2}}{[011]}^T,\text{and}{g}_3=\frac{1}{\sqrt{2}}{[101]}^T.$ Again, following a simplified Eq. (2) yeilds,

$$\left[\begin{array}{c}{\text{ADC}}_1\\ {\text{ADC}}_2\\ {\text{ADC}}_3\end{array}\right]=-\frac{1}{2}\left[\begin{array}{c}110\\ 011\\ 101\end{array}\right]\left[\begin{array}{c}{\mathrm{\lambda }}_1\\ {\mathrm{\lambda }}_2\\ {\mathrm{\lambda }}_3\end{array}\right]⟹\begin{array}{c}{\mathrm{\lambda }}_1=\left[-{\text{ADC}}_1+{\text{ADC}}_2-{\text{ADC}}_3\right]\\ {\mathrm{\lambda }}_2=\left[-{\text{ADC}}_1-{\text{ADC}}_2{\text{+ADC}}_3\right]\\ {\mathrm{\lambda }}_3=\left[{\text{ADC}}_1-{\text{ADC}}_2-{\text{ADC}}_3\right]\end{array}$$ (9)

The eigenvalues are no longer independent, but the ADC’s remain i.i.d., and f_FAis updated to reflect the altered diffusion weighting directions and computation of the eigenvalues. Numerical integration of the modified joint probability distribution (with explicit dependence between the eigenvalues) reveals that the expected value of FA is 1.101.

Example 4

Finally, consider an experiment with the dual gradient scheme as in Example 3 and the eigenvalues are censored as in Example 2. Numerical integration of the modified joint probability distribution reveals that the expected value of FA is 0.969.

Summary

From these examples, we can appreciate that the tensor estimation process is essentially a projection process: the high-dimensional imaging data is projected onto a tensor space. To compute contrasts, one projects the tensor space onto a scalar space. Censoring eigenvalues or altering the tensor estimation method changes the projection function, and thus changes the resulting contrasts.

In the first example, small changes due to noise in the observed data directly translate into small changes in the eigenvalues. The FA computation function is smooth except when all eigenvalues are zero [Eq. (3)], so small changes in eigenvalues generally result in small changes in FA. Censoring eigenvalues (as in Examples 2 and 4) introduces a crease in the projection from eigenvalues to FA, so that all of the sets of eigenvalues that would map to an FA greater than one map to one or less. Therefore, censoring eigenvalues causes a notable drop in the expected FA. The dependence structure in Example 3 increases the frequency of negative eigenvalues because it generates a strong correlation between large eigenvalues and negative eigenvalues [Eq. (9)], which leads to FA greater than one. The expected FA with this type of correlation is greatly increased over the independent measurements. We note that the impact of negative eigenvalues can be both varied and substantial at low SNR.

Generalized Framework

While numeric evaluation of the FA expectation integrals is presented above for simplified cases, the methodology is equally applicable to more realistic situations; so long as the expectation integrals exist. For a general diffusion tensor experiment with N ADC observations, we may write

$$E[FA]={\displaystyle {\iint }_{{\text{ADC}}_{1:N}}p(AD{C}_{1:N})f_{\text{FA}}({\text{ADC}}_{1:N})}d{\text{ADC}}_{1:N}.$$ (10)

The following sections use simulations to evaluate the distribution of contrast values over a field of empirically derived diffusion tensors. Equivalently, this approach may be interpreted as Monte Carlo numerical integration of contrast values against the joint probability of observing a dataset [i.e., as in Eq. (10)] for each SNR. In a realistic model, the probability distribution of observations depends both on the noise model and the assumed field of tensors. The connection between these approaches may be made explicit by expanding Eq. (10) to reveal dependence on the assumed distribution of underlying tensors,

$$E[FA]={\displaystyle {\int }_{T\in \mathrm{\Theta }}{\displaystyle {\iint }_{{\text{ADC}}_{1:N}}p({\text{ADC}}_{1:N}|T)p(T)f_{FA}({\text{ADC}}_{1:N})d{\text{ADC}}_{1:N}}}d\mathrm{\Theta },$$ (11)

where T is a tensor in the assumed tensor field,θ, and p(T) is probability density function of T over θ. In others, in order to compute the expected FA value we posit a distribution for the likelihood of a certain true tensor to be observed; this is denoted p(T). The distribution could be derived from a theoretical tissue model, or, as in the following examples, empirically derived from a high SNR dataset.

Henceforth, simulation will be used to interpret the results. The impacts of tensor estimation method and diffusion weighting directions are studied as a function of SNR. Findings are reported as the expected value and variance of contrasts at each SNR.

Materials and Methods

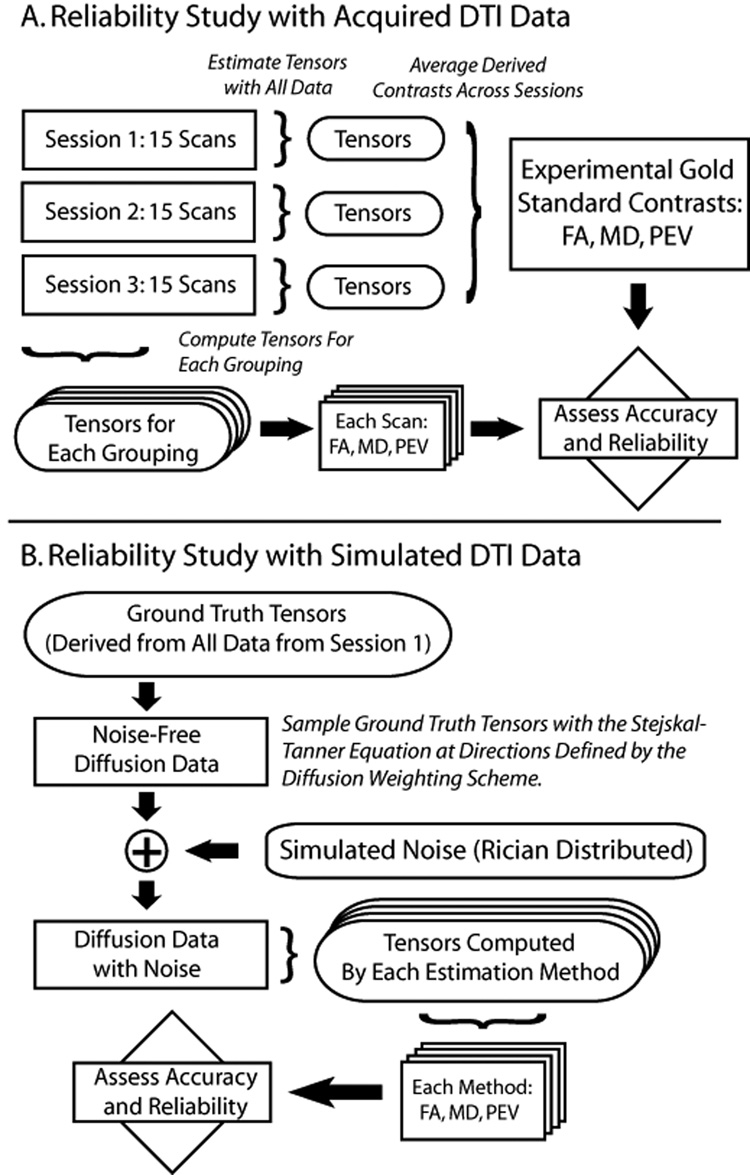
The theoretical model presented above demonstrates how small changes in analysis method can generate large differences in the expected tensor contrasts. However, the effect size and relative importance of each of the choices in diffusion tensor estimation cannot be readily appreciated from the simple examples. Utilizing this framework we continue with an in vivo empirical and simulation study on the effects of using different common DTI protocols. This study is based on high quality, publically available data from the Biomedical Informatics Research Network (BIRN, http://www.nbirn.net). Figure 1 illustrates a flow diagram for the analysis scheme.

Figure 1.

Schematic of reliability estimation with experimental data (upper panel) and simulated data (lower panel).

Data acquisition

Tensors estimated from a high SNR dataset^15,16 were used as ground truth to assess the effects of low SNR and tensor fitting method. Briefly, the dataset consists of 15 DTI scans of a healthy 24 year old male volunteer acquired using a 1.5T MR scanner (Intera, Philips Medical Systems, Best, The Netherlands) with body coil excitation and a six channel phased array SENSE head-coil for reception. Each DTI dataset was acquired with the following imaging protocol. A multi-slice, single-shot EPI (SENSE factor = 2.0), spin echo sequence (90° flip angle, TR/TE = 3632/100 ms) was used to acquire 25 transverse slices parallel to the line connecting the anterior and posterior commissures, with no slice gap and 2.5 mm nominal isotropic resolution (FOV = 240 × 240 mm, data matrix = 96 × 96, reconstructed to 256 × 256). Diffusion weighting was applied along 30 directions using the Jones30 scheme⁸ with a b-factor of 1000 s/mm². Five minimally weighted images (5 b₀s) were acquired and averaged on the scanner as part of each DTI dataset. The total scan time to acquire one DTI dataset was 2 min 18s. Local institutional review board approval and informed consent were obtained prior to data acquisition.

Image Processing

The DTI data from three imaging sessions were coregistered and processed with CATNAP (Coregistration, Adjustment and Tensor-solving, a Nicely Automated Program, Johns Hopkins University, 2006). High SNR tensors were computed at each voxel using a standard, unrestricted log-linear minimum mean squared error estimator that used all 450 diffusion weighting directions and 75 b₀ effective volumes (e.g., 15 repetitions of 30 diffusion weighting directions and 5 b₀s) for each scan session. This estimation method was chosen for consistency with previously published methods. The diffusion tensor in each voxel was diagonalized, and FA and MD were computed. The high SNR DTI contrasts from each session were then averaged to yield gold standard contrasts.

By analyzing the groupings of scans¹⁵, empirical reliability of contrasts was determined as a function of SNR for the 30 direction diffusion weighting scheme. An optimized subset of 6 of the 30 total directions was selected and used to empirically assess reliability of a 6 directions diffusion weighting scheme as a function of SNR¹⁶. An axial slice at the level of the lateral ventricles was selected for analysis (see Figure 2 inlays).

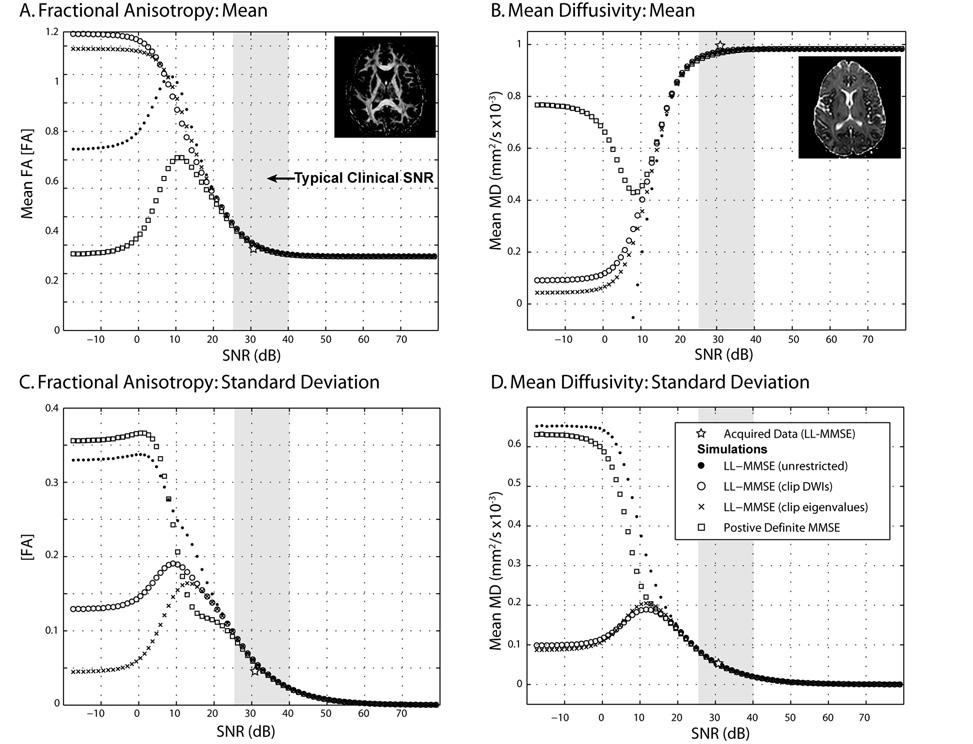
Figure 2.

Simulated contrasts by SNR with tensor fitting method. Both the FA (left) and MD (right) exhibit substantial non-monotonic bias (top row) and variability (lower row) with SNR. Symbols show the within-slice mean FA (Panel A), mean MD (Panel B), standard deviation of FA (Panel C), and standard deviation of MD (Panel D) using the indicated tensor fitting method on 50 data sets with a given SNR on the minimally weighted (b₀) image. Inlaid images show the high SNR contrasts derived with the LL-MMSE method. Gray region shows an approximate range of mean SNR on the representative b₀ slice.

Simulation Studies

In a similar approach to Koay et al.,¹³ four methods of tensor estimation were compared. First, we considered direct application of the Stejskal-Tanner tensor model²⁴ to the estimation of tensor coefficients by applying the pseudoinverse of analytical imaging equations in matrix form, referred to as the multivariate log-linear minimum mean squared error methods, or “LL-MMSE (unrestricted).” Using this fitting method, non-physical solutions to the tensor model may occur (e.g., negative eigenvalues), especially when there is a large contribution of noise. One situation that can lead to negative eigenvalues is when the DW images are of greater intensity than the minimally weighted volume due to noise or artifact. Our second estimation method, denoted “LL-MMSE (clip DWI)”, implements a partial solution to this problem by replacing any DW values that are greater than the minimally weighted value with the minimally weighted value prior to LL-MMSE tensor estimation. Another way to avoid non-physical solutions is to replace negative eigenvalues with zero-values; this is our third tensor estimation method, and is denoted “LL-MMSE (clip eigenvalues).”

Another approach to produce physically reasonable tensors is to limit the estimation procedure to search the space of positive definite tensors. Several nonlinear frameworks are available that can process clinical datasets in a few minutes with modern computer hardware.^13,14,27,28 We selected the method provided with the freely available AFNI toolkit (National Institutes of Health, Bethesda, MD).¹⁴ Analyses were performed with a combination of custom Matlab (MathWorks, Natick, MA) scripts and AFNI tools. This method is denoted “Positive Definite MMSE”. For each method, the resulting diffusion tensors (D) were diagonalized, which resulted in three eigenvalues and three eigenvectors. The FA and MD diffusion contrasts were computed from the eigenvalues.²⁹

Simulation

SNR was measured and simulated relative to the b₀ volumes, which were scanner averages of five k-space acquisitions. The SNR on a single b₀ would be approximately 7 dB lower than the k-spaced averaged volumes. SNR is reported in power decibels; 25 dB is approximately equivalent to a ratio of 18:1 while 40 dB is 100:1. To provide quantitative measures of the differences between tensor estimation methods, the average root mean square error (RMSE), bias and standard deviation in the SNR interval from 25 dB to 40 dB are computed. This interval roughly corresponds to achievable ranges of SNR in in vivo clinical DTI settings of the brain (approximately one acquisition at 1.5T up to eight repeated acquisitions at 3T¹⁵).

The effects of both SNR and tensor estimation method on DTI derived contrasts were assessed through Monte Carlo (MC) simulation.³⁰ Ground truth imaging data were derived from the ground truth tensors with the Skejstal-Tanner equation. For each of 75 noise levels (standard deviations of noise in logarithmic steps between 1 and 1x10⁶ arbitrary intensity units), Gaussian noise with the chosen standard deviation was added to the real and imaginary channels of the ground truth data (e.g., in quadrature). The magnitude of the combined complex signal was taken to produce simulated datasets. To replicate the noise characteristics of the acquired b₀s, five b₀s were simulated and averaged. For each noise level, the SNR of the simulated averaged b₀s was calculated for each voxel, and the mean SNR over all voxels was reported as the SNR for the specific noise level. Note that no attempt was made to replicate the spatially varying SNR that occurs in vivo. Tensor estimation was performed on the simulated data using each of the previously described tensor fitting methods. FA and MD were derived from the simulated results and reported by tensor fitting method and SNR.

Two experiments on the impact of SNR were performed with the same framework. First, the average behaviors within a slice of the derived contrasts were assessed with 50 MC iterations at each noise level. The simulation was repeated for both the 30 and 6 direction diffusion weighting schemes, and the data were analyzed with each of the four tensor estimation methods. Second, the SNR characteristics of a low (0.06), moderate (0.40), and high (0.82) FA tensor were simulated to expose the differences in reliability based on the underlying tensor. To improve accuracy of the reliability measures, 65,536 MC iterations were performed at each noise level.

Results

Impact of SNR

The low-SNR limiting values of FA and MD are dependent on the tensor estimation method (Figure 2A and 2B). At high SNR (>40 dB), there was little change with SNR or dependence on estimation method. At moderate SNR (20–40 dB), the bias in underlying contrasts increased with decreasing SNR, while the rate of change was greatest at low SNR (0–20 dB). At very low SNR (<0 dB), the contrast values showed little relationship to the underlying ground truth data.

The variability patterns of FA and MD estimation are also well categorized by high, moderate, low, and very low SNR regimes (Figure 2C and 2D). At high and moderate SNR, variability decreases with increased SNR but there is little dependence on tensor estimation method. At low SNR, there are rapid changes in variability with increasing dependence on estimation method with decreasing SNR. At very low SNR, variability is approximately constant and dependent on the tensor estimation method.

The effects in the range of clinical SNR were further examined by computing the area between the ground truth and the respective curves (Table 1). RMSE observations were fit with sigmoid with nonlinear gradient descent between 20 and 45 dB (Table 2). The positive definite method showed reduced bias in FA, but increased bias in MD. The three LL-MMSE methods performed better for MD and less well for FA. The relative performance of FA bias with LL-MMSE and variants was dependent on SNR. For comparison, the mean SNR and FA from the actual data acquisition are shown in Figure 2 (labeled “Acquired Data (LL-MMSE)”).

Table 1.

Mean Tensor Estimation Error (25 to 40 dB)

	RMS Error		Bias		Std. Dev.		CPU Time
	FA		FA		FA
	[FA]	MD	[FA]	MD	[FA]	MD
Estimation Methods	(x10−3)	[um2/s]	(x10−3)	[um2/s]	(x10−3)	[um2/s]	Relative
LL-MMSE (unrestricted)	69.31	44.59	43.84	−7.67	55.84	46.97	1
LL-MMSE (clip DWI)	67.34	44.09	41.30	−6.79	55.18	46.56	1
LL-MMSE (clip eigenvalues)	69.27	44.58	43.83	−7.67	55.79	46.96	1
Positive Definite MMSE	62.69	44.15	35.56	−11.01	53.86	45.65	11.5

Notation: Multiply values in each column by (•) to achieve [•] units.

Table 2.

Sigmoid Fit to RMSE (20 to 45 dB)

	FA [FA]				MD [×10−3 um2/s] (× 1000)
Estimation Methods	a (×10−3)	b (×103)	c	d	a (×10−7)	b (×102)	c	d
LL-MMSE 1	8.98	1.65	15.9	5.87	6.82	12.6	−2.12	10.4
LL-MMSE (clip DWI) 1	10.2	1.90	27.6	5.56	7.90	12.6	−1.53	10.0
LL-MMSE (clip eigenvalues) 1	9.62	1.80	21.8	5.71	9.87	9.69	−1.88	10.1
Positive Definite MMSE 1	9.71	1.67	26.9	5.68	10.5	12.0	−1.28	9.39

Definition of sigmoid form:$\text{RMSE}=a\frac{1+b{e}^{-\text{SNR}/d}}{1+c{e}^{-\text{SNR}/d}}$

Notation: Multiply values in each column by (•) to achieve [•] units.

Impact of Diffusion Weighting Scheme

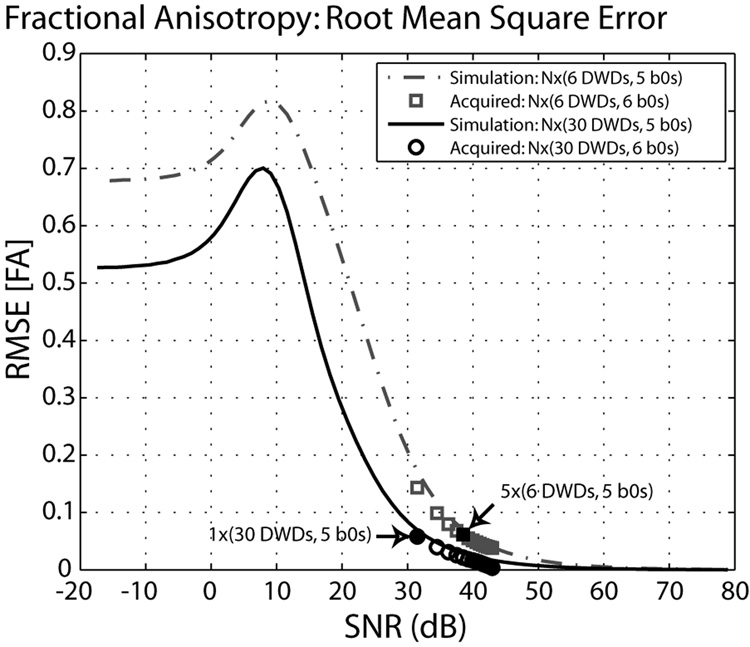
The effect of the diffusion weighting scheme was investigated for the LL-MMSE (unrestricted) method. When six diffusion weighting directions were used, both the low-SNR limiting value and the path of convergence were different, in comparison to the results with the 30 direction scheme (Figure 3). Analyses based on integer repetitions of the baseline protocol are represented by the individual markers and show a good correspondence with the simulated results. Note that the results of the 6 and 30 direction schemes are not time-normalized (with the same SNR, the 30 direction scheme has five times more DWIs to calculate a tensor), which leads to the shift of the SNR-FA curve to the right. For comparison, approximately time-normalized time points (5 repeated datasets × 6 direction scheme vs. 1 dataset × 30 direction scheme) are indicated in Figure 3, which only differ in RMS FA error by 0.003. The empirical data closely follow the simulated curves.

Figure 3.

Fractional anisotropy root mean square error (RMSE) by SNR with LL-MMSE (unrestricted) tensor fitting. Analyses from differing diffusion weighting schemes (dashed versus solid lines) converge to distinct levels of RMS error. At high SNR, this is effectively a horizontal shift, but the low SNR behaviors are different. Highlighted symbols (arrows) indicated analyses with diffusion weighted volumes.

Single Tensor Simulations

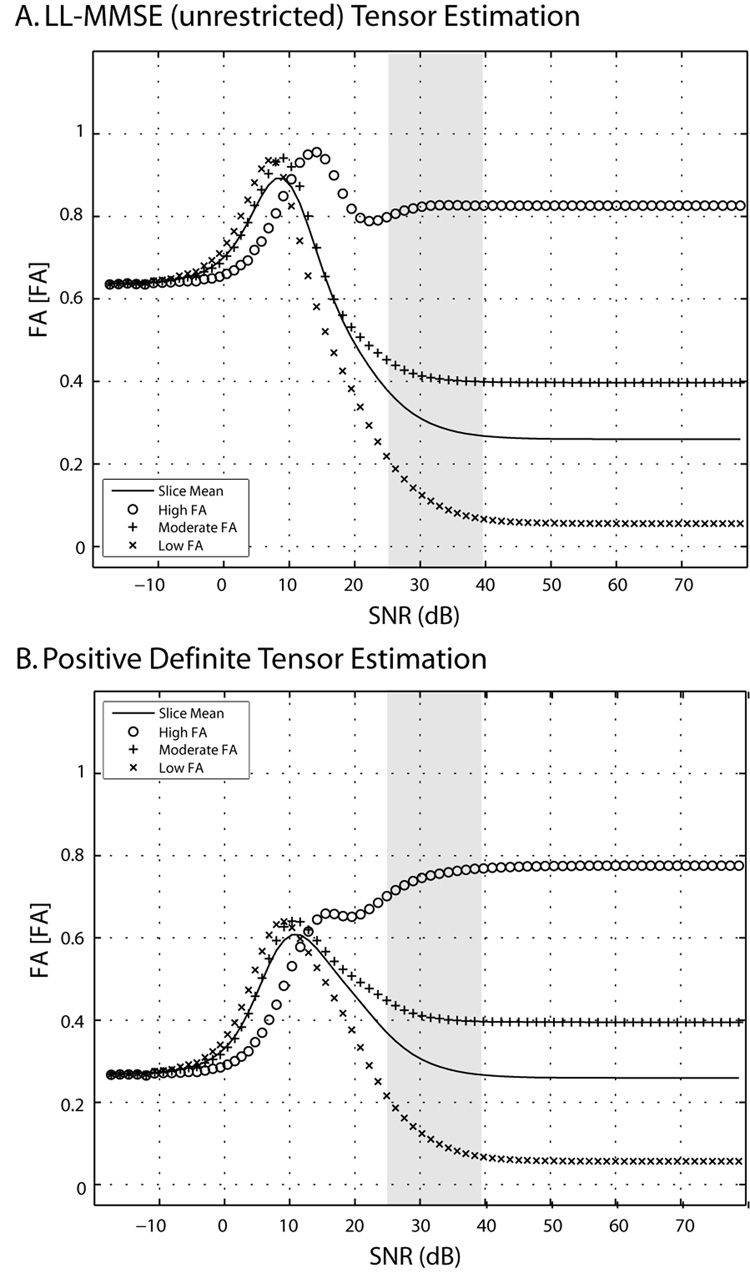
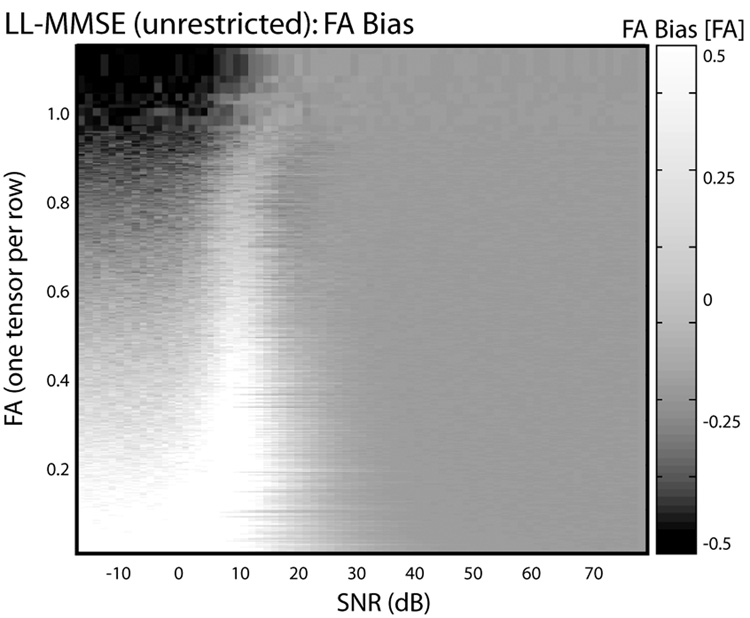
Simulations for representative single tensors chosen from the experimental data with low (0.06), moderate (0.40) and high (0.82) FA demonstrate that the direction and magnitude of bias were dependent on the underlying tensor (Figure 4). At high SNR, FA and MD are largely insensitive to SNR, however, at low and moderate SNR the observed values drift towards the unique values (~0.62 for LL-MMSE (unrestricted) and ~0.25 for positive definite tensor estimation) at low-SNR limits, with larger effects observed for lower FA tensors. FA does not always go up monotonically, this is evident in the case of the high FA tensor in the neighborhood of 20dB where the computed FA first decreases, then increase as SNR is reduced further. At very low SNR, FA showed little dependence on underlying ground truth tensor. A comprehensive view of the relationship between FA bias and SNR as a function of different FA values is shown in Figure 5. The top right hand corner in Figure 5 represents a tensor with very high FA at very high SNR. As one moves from right to left along the row, the intensity indicates bias in FA. Notably, at very low SNR, FA has a downward bias for a high FA tensor. Overall, the bias landscape is not monotonic and a complex relationship between SNR and tensor anisotropy may be appreciated.

Figure 4.

Simulated single tensor contrasts by tensor fitting method at differing SNR. Both the mean and the individual tensor behaviors vary by tensor estimation method at low SNR. Symbols show the mean FA of 65536 simulations using LL-MMSE (Panel A) and Positive Definite (Panel B) tensor fitting methods for three representative tensors.

Figure 5.

Representative impact of fitting method on individual tensor contrasts by SNR. Each row in the image corresponds to FA derived from a single tensor. Rows are sorted by FA at high SNR, and height is adjusted to so that vertical axis is linear with FA. Gray scale intensity indicates the bias for the corresponding tensor between the high SNR FA and the mean contrast from 50 simulations at the indicated SNR. Dark regions correspond to negative bias while bright regions correspond to positive bias.

Discussion

Noise propagation in DTI can be considered from a theoretical perspective as the integration of a biophysical model that describes the phase loss due to spin displacement or from an engineering perspective as the simulation of a random process. For practical DTI experiments, the two approaches are equivalent when viewed in terms of Monte Carlo integration. By producing simulations at closely spaced SNR, one can readily appreciate the sensitivity of each method to SNR. For example, some previous studies seem to indicate that bias and error (e.g., eigenvalue divergence) increases monotonically at low SNR.^9,10 However, investigation of DTI contrast estimations at closely spaced SNR’s that span a wide range reveals that neither the bias and variability (Figure 2) nor the combined RMSE (Figure 3) need be monotonic. The immediate consequence of these results are that one can neither tacitly expect that FA is elevated at low SNR nor that the errors are greater at lower SNR.

In contrast to some previous approaches comparing tensor estimation methods (e.g., ¹³), we present results across a broad range of SNR. We do not advocate imaging at 0 dB or 75 dB, but rather show these results so that one can appreciate the complex behavior of the contrasts as well as the sensitivity of each approach to the noise level. For example, if one only examined Figure 4 at 15 dB and 30 dB, one might conclude that low SNR increased FA for high FA tensors with LL-MMSE and decreased FA for the positive definite method. With this approach, one would miss the (potentially) clinically important finding that both methods show negative bias for high FA tensors at the lower end of clinically relevant SNR regime (Figure 4, gray box). It is much easier to compare results across studies and appropriately scale SNR of different diffusion weighting scheme if simulations are presented over a range that is “too large” rather than at only few “clinically relevant” SNR points. As DTI is applied beyond the brain, at different field strengths, the range of relevant SNR’s may change substantially.

The convergence, at low SNR, of the contrast estimates from the high, moderate and low FA single tensor simulations clearly demonstrates the “squashing peanuts and smashing pumpkins” effect of the noise floor.¹² Note that the low SNR behaviors with the LL-MMSE and positive definite tensor estimation methods are very different. Perhaps counter intuitively, the LL-MMSE method preserves more contrast between the tensors than the positive definite method at low SNR. For some applications, preserving contrast between tissue types may be more important than reducing absolute error.

The choice of diffusion weighting scheme and tensor estimation method can significantly alter the accuracy and variability of DTI contrasts over a wide range of SNR, including clinical SNR regimes (e.g., 25–40 dB). The simulations presented in this study generally agree with previous results. In summary we show that: (1) bias and variability are dependent upon tensor estimation methods and ground truth data; (2) expansion of the low SNR regimes demonstrates that FA does not necessarily converge to a fixed value; and (3) the progression towards low-SNR limiting values need not be monotonic; and in some cases, the FA of high anisotropy tensors can decrease within the clinically practical SNR range. Estimation errors for FA and MD depend on both tensor estimation method (Figure 2),^13,31,32 diffusion weighting scheme (Figure 3),^33,34 and underlying anatomy (Figure 4 and Figure 5).^10,32,35 FA tends to be positively biased in regions of low FA at low SNR,³⁶ while regions of high FA may be negatively or positively biased (Figure 3 and Figure 4). The largest methodological differences occur with very low SNR (<10 dB) where the mean bias in FA is already greater than 0.2 and in MD greater than 0.2×10⁻³ mm²/s. While the dramatic low SNR benefits of the advanced methods are of theoretical interest, the typical clinical differences are much smaller. The error metrics (Table 1) provide a quantitative system for comparing and ranking tensor estimation methods over a range of clinically feasible SNR. Table 2 provides functional fits to the RMSE so that one may estimate the error at a specific SNR. The tabular comparisons provide combined error measures as well as an indication of the relative tradeoffs between bias (systematic mean differences) and variability (random spread of observations) that may be achievable. Furthermore, FA and MD biases at low SNR can be negative or positive, depending on the underlying tensor and the noise level.

Unfortunately, analytic identification of the distributions of tensor eigenvalues is not possible for a generic DTI study, so we cannot provide a simple recommendation regarding the differences between two diffusion weighting schemes. However, the dataset used in this study is publically available and numeric integration/simulation of the tensor estimation process is readily accomplished using consumer hardware. The authors advocate a brief comparison study of each tensor estimation method and DW scheme used within a laboratory so that one may be aware of its benefits and shortcomings. The applicable range of SNR used to define the integrated error metrics can be readily updated to reflect the needs of a particular protocol and/or anatomy. The close agreement between empirical and simulation results serves to validate this approach and increase confidence in simulation findings related to tensor noise (Figure 4).

The closed form integration view of the problem presents an appealing target for optimizing selection of diffusion weighting protocols. We constructed tables (Table 1 and Table 2) that summarize the relative performance of four methods over an interesting range of SNR. This approach could be readily replicated with new anatomies in order to provide a quantitative basis for deciding which approach is most suitable for a particular application. We note the selection of a tensor estimation procedure depends on practical considerations such as algorithm availability and computational time. The methods presented in this study are publicly available as both source code and executable programs for common platforms. The nonlinear method is approximately 10 times slower than the linear-based methods (Table 1); however, whole brain analysis can still be performed in several minutes using modern computers.

DTI may be viewed as an estimation process, where each design choice (tensor estimation method, diffusion weighting scheme, and anatomical target) affects the accuracy and precision of the results. One could conceive of a tensor estimation approach where one wished to minimize the expected bias or expected mean squared error in a statistical context. The described framework provides a numeric mechanism to evaluate the expected performance of a particular set of choices, so one may envision optimizing DTI estimation methods and protocols based on these error criteria which take into account the noise distribution. Although the theoretical framework is described for the estimation of expected FA, one may readily compute the expected value of statistics on any other tensor contrasts of by replacing f_FAin Eq. (11) with the appropriate function of the observed data. Initial results with maximum likelihood tensor estimation methods have been successful both with simplified criteria and with the full statistical model.³⁷ As more computational power and creative numerical methods are developed, it is conceivable that one could jointly optimize a DTI protocol and analysis method for a particular anatomical target.