Materials and noncoplanar mesh designs for integrated circuits with linear elastic responses to extreme mechanical deformations

Abstract

Electronic systems that offer elastic mechanical responses to high-strain deformations are of growing interest because of their ability to enable new biomedical devices and other applications whose requirements are impossible to satisfy with conventional wafer-based technologies or even with those that offer simple bendability. This article introduces materials and mechanical design strategies for classes of electronic circuits that offer extremely high stretchability, enabling them to accommodate even demanding configurations such as corkscrew twists with tight pitch (e.g., 90° in ≈1 cm) and linear stretching to “rubber-band” levels of strain (e.g., up to ≈140%). The use of single crystalline silicon nanomaterials for the semiconductor provides performance in stretchable complementary metal-oxide-semiconductor (CMOS) integrated circuits approaching that of conventional devices with comparable feature sizes formed on silicon wafers. Comprehensive theoretical studies of the mechanics reveal the way in which the structural designs enable these extreme mechanical properties without fracturing the intrinsically brittle active materials or even inducing significant changes in their electrical properties. The results, as demonstrated through electrical measurements of arrays of transistors, CMOS inverters, ring oscillators, and differential amplifiers, suggest a valuable route to high-performance stretchable electronics.

Increasingly important classes of application exist for electronic systems that cannot be formed in the usual way, on semiconductor wafers. The most prominent example is in large-area electronics (e.g., back planes for liquid crystal displays), where overall system size rather than operating speed or integration density, is the most important metric. Similar systems that use flexible substrates are presently the subject of widespread research and commercialization efforts because of advantages that they offer in durability, weight, and ease of transport/use (1, 2). Stretchable electronics represents a fundamentally different and even more challenging technology, of interest for its unique ability to flex and conform to complex curvilinear surfaces such as those of the human body. Several promising approaches exist, ranging from the use of stretchable interconnects between rigid amorphous silicon devices (3) to “wavy” layouts in single-crystalline silicon CMOS circuits (4), both on elastomeric substrates, to net-shaped structures in organic electronics on plastic sheets (5). None offers, however, the combination of electrical performance (high electron and hole mobility), scalability (with relatively modest modifications to conventional microelectronic technologies), integrated circuit applicability in complementary designs and mechanical properties required of some of the most demanding, and most interesting, systems. Here, we introduce design concepts for stretchable electronics that exploit semiconductor nanomaterials (i.e., silicon ribbons) in ultrathin, mechanically neutral circuit layouts integrated on elastomeric substrates in noncoplanar mesh designs, with certain features inspired by methods recently reported for transforming planar optoelectronics into hemispherical shapes for electronic-eye cameras (6). The noncoplanar structure, combined with deformable serpentine bridge designs, can accomplish much higher stretchability (i.e., up to ≈140%) compared with previous reports of related systems (3–6). This increased stretchability enables much wider application possibilities, including electronic circuits on complex surfaces with high curvature. As demonstrated in diverse circuit examples, these ideas accomplish a form of stretchable electronics that uniquely offers both high performance and an ability to accommodate nearly any type of mechanical deformation to high levels of strain. Experimental and theoretical studies of the electrical and mechanical responses illuminate the key materials and physics aspects associated with this type of technology.

Results and Discussion

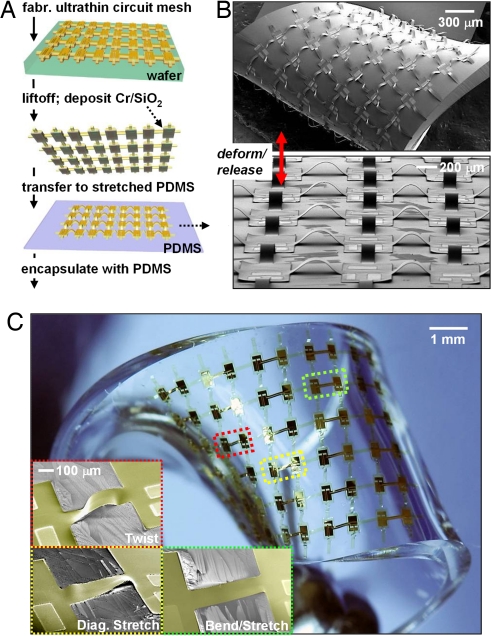
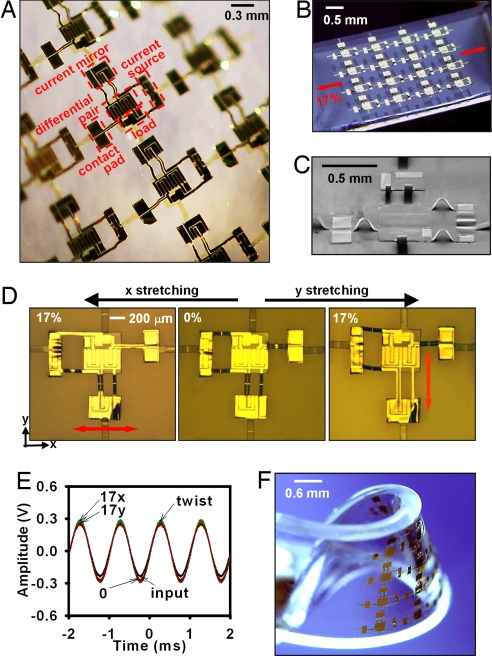
Fig. 1 A schematically illustrates steps for fabricating a representative system that consists of a square array of CMOS inverters. The overall process can be divided into 2 parts. The first defines CMOS circuits on ultrathin plastic substrates by using printing methods and single-crystalline silicon ribbons, according to procedures described previously (7). For all of the results reported here, the ribbons had thicknesses of 260 nm and 290 nm for p-channel and n-channel metal oxide semiconductor field effect transistors (MOSFETs), respectively. The gate dielectric consisted of a 50-nm-thick layer of SiO₂ deposited by plasma-enhanced chemical-vapor deposition. The same type of film formed an interlayer dielectric for metal (Ti:5 nm/Au:150 nm) interconnect lines and electrodes. The plastic substrate consisted of a thin layer (1.2 μm) of polyimide (PI) supported by a carrier wafer (test grade silicon) coated with a film (100 nm) of poly(methylmethacrylate) (PMMA) (8). A thin top coating of PI (1.2 μm), with etched (reactive ion etching; RIE) holes for electrical access, protected the circuits and placed the most fragile components near the neutral mechanical plane (4). Individual devices fabricated in this manner exhibited device mobilities of ≈130 and ≈370 cm²/Vs for p-channel and n-channel MOSFETs, respectively, with on/off ratios >10⁶ and operating voltages in the range of <5 V. These fabrication procedures are useful but have some disadvantages. For example, conventional self-aligned processes for defining the channel and gate cannot be implemented easily. The polymer materials restrict the processing temperatures and prevent, as an example, the use of dry oxide for the gate dielectric. A modified procedure, in which most or all of the device or circuit block processing occurs on the mother silicon wafer, before transfer to the polymer substrate, can avoid these limitations. Exploring this possibility represents a focus of current work.

Fig. 1.

Fabrication of noncoplanar stretchable electronics and responses to deformation. (A) Schematic overview of the fabrication process for representative circuits that accomplish high levels of stretchability through the use of noncoplanar mesh designs integrated with elastomeric substrates [for the case shown here, PDMS]. (B) SEM images of an array of CMOS inverters that result from this process, in an undeformed state (Lower; ≈20% prestrain) and in a corresponding configuration that results from a complex twisting motion (Upper). (C) Optical image of a freely deformed stretchable array of CMOS inverters, highlighting 3 different classes of deformation: diagonal stretching, twisting, and bending. The Insets provide SEM images for each case (colorized for ease of viewing).

The second part of the fabrication process involves structuring the circuits into noncoplanar layouts intimately integrated with elastomeric substrates to yield systems with reversible, elastic responses to extreme mechanical deformations. In the first step toward achieving this outcome, certain regions of the PI/PMMA between the electronic components of the system were removed by RIE through a patterned layer of photoresist. The result was a segmented mesh with active device islands connected electrically and/or mechanically by thin polymer bridges with or without metal-interconnect lines, respectively. Immersion in acetone washed away the PMMA layer to release the system from the carrier. Lifting off the patterned circuit sheet onto a slab of poly(dimethylsiloxane) (PDMS) exposed its underside for deposition of a thin layer of Cr/SiO₂ (3 nm/30 nm) at the locations of the islands by electron beam evaporation through an aligned shadow mask. Delivering the circuit to a biaxially prestrained substrate of PDMS with its surface activated by exposure to ozone led to the formation of strong mechanical bonds at the positions of the islands. The interface chemistry responsible for this bonding involves condensation reactions between hydroxyl groups on the SiO₂ and PDMS (4) to form O–Si–O linkages, similar to that described recently for controlled buckling in collections of semiconductor ribbons (8). Releasing the prestrain resulted in compressive forces that caused the connecting bridges to lift vertically off the PDMS, thereby forming arc-shaped structures. We refer to this layout as a noncoplanar mesh design. The localization of this out-of-plane mechanical response to the bridges results partly from their poor adhesion to the PDMS and partly from their narrow geometries and low bending stiffnesses compared with the device islands. (This latter aspect allows similar structures to be formed even without the patterned SiO₂ adhesion layer.) The bottom frames of Fig. 1 A and B show schematic illustrations and scanning electron microscope (SEM) images. In this format, the system can be stretched or compressed to high levels of strain (up to 100%, and in some cases higher, as described subsequently), in any direction or combination of directions both in and out of the plane of the circuit, as might be required to allow complex twisting, shearing, and other classes of deformation. Fig. 1B Upper and Fig. 1C Upper show images that illustrate some of these capabilities in circuits that use a PDMS substrate with thickness ≈1 mm and a prestrain of ≈17%, as defined by the change in separation between inner edges of adjacent device islands. For practical applications, such systems are coated with a protective layer of PDMS in a way that does not alter significantly the mechanical properties, as argued subsequently. For ease of imaging and electrical probing, the circuits described in the following are all unencapsulated.

The physics of deformation associated with applying tensile or compressive forces oriented along the directions of the bridges is similar to that involved in relaxing the prestrain in the circuit-fabrication process of Fig. 1. The bridges move up or down (corresponding to decreases or increases in end-to-end lengths, respectively) as the system is compressed or stretched, respectively. Another, less obvious, feature is that the thin, narrow construction of these bridges also enables them to twist and shear in ways that can accommodate more complex distributions of strain. Fig. 1C shows some representative cases, described in more detail subsequently, for different regions of a system under a complex, twisting deformation. The basic mechanics is similar to that of systems that are encapsulated by PDMS. For example, calculation indicates that the maximum strain that can be applied to the system, as shown in Fig. 1B Lower, reduces by only ≈2.5% because of the addition of a ≈1-mm-thick overcoat of PDMS [supporting information (SI) Fig. S1].

These designs lead to electronic properties that are largely independent of strain, even in extreme configurations such as those illustrated in Fig. 1 B and C. This feature can be demonstrated explicitly through device and circuit measurements on systems for various, well-defined mechanical deformations induced with custom assemblies of mechanical stages. The simplest case corresponds to in-plane stretching in directions parallel to the bridges. Testing of this deformation mode was performed by using 3-stage ring oscillators, in which each island supports an n channel and a p channel MOSFET (channel widths of 100 μm and 300 μm, respectively; channel lengths of 13 μm). Metal electrodes on the bridges form the required interconnects. Fig. 2A shows optical micrographs of a typical response, for a system fabricated with a prestrain of ≈17%. With stretching in the x direction, the bridges oriented along x progressively flatten, whereas those along y rise up slightly, because the Poisson effect, and vice versa. A critical aspect of the strategy outlined in Fig. 1 is the ability of the noncoplanar structures to absorb nearly all of the strains associated with the fabrication process and with deformations that can occur during use.

Fig. 2.

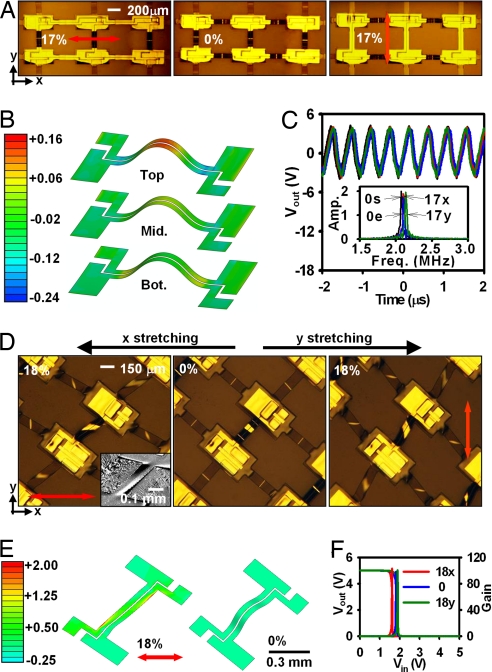
Mechanical and electrical responses of noncoplanar stretchable electronics to in-plane strains. (A) Optical images of stretchable, 3-stage CMOS ring oscillators with noncoplanar mesh designs, for stretching along the bridges (x and y). (B) FEM modeling of the strain distributions at the top surface of the circuit (Top) and at the midpoint of the metal layer (Mid.) and bottom surface (Bot.). (C) Electrical characteristics of the oscillators as represented in the time and frequency (Inset) domains in the different strain configurations illustrated in A. Here, 0s and 0e refer to 0% strains at the start and end of the testing, respectively; 17x and 17y refer to 17% tensile strains along the x and y directions indicated in A, respectively. (D) Optical images of stretchable CMOS inverters with noncoplanar mesh designs, for stretching at 45° to the directions of the bridges (x and y). (E) FEM simulations of these motions. (F) Transfer characteristics of the inverters (output voltage, V_out, and gain as a function of input voltage, V_in). The notations 18x and 18y refer to 18% tensile strains along the x and y directions indicated in D, respectively.

This mechanical isolation can be seen clearly through finite element modeling (FEM) analysis of the tensile strain distribution at the top and bottom surface and midpoint through the thickness of the metal layer in the circuit (Fig. 2B). For the middle layer, all areas experience almost zero strain because of the neutral mechanical plane design. Negligible strains throughout the thickness and in all regions of the islands derive from strain relaxation provided by the bridges/interconnects in the noncoplanar mesh layout. For this example, the change in separation of islands (i.e., prestrain) is ≈17%, which corresponds to the system-level strain of ≈11% as defined by the change of the distances from the outer edges of adjacent device islands. Mechanics analysis based on energy minimization (Figs. S2 and S3) gives an amplitude of 116.3 μm for the 445-μm-long bridge, which agrees well with the experimental value of ≈115 μm. The maximum tensile strains calculated for the metal layer in the bridges and islands are ≈0.11% and ≈0.01%, respectively, whereas that in the Si layer of the islands is ≈0.01%. These values are all much smaller than the fracture strains (≈1%) in these materials. This neutral mechanical plane layout and noncoplanar mesh design also reduce the strain at the interface between silicon and gate oxide to less than ≈0.05% for applied strains of ≈20% (SI Text). The corresponding changes in the electron and hole mobilities are expected be <5%, based on separate studies of the influence of strain on electronic properties of silicon (9). The finite element analysis results of Fig. 2B are consistent with this analysis. For applied strains between −40% (i.e., compressive) and 17% (tensile), which corresponds to a strain range of 57%, the mechanical advantage provided by the noncoplanar mesh layout, as defined by the ratio of the system-level strain to the peak material strain, is ≈180. Measurements on these oscillators show well-behaved responses at these strain conditions and others in between. The observed frequencies (≈2 MHz, Fig. 2C) and other properties of the circuits and individual devices reported here and elsewhere in this article are comparable with those measured in the initial, planar configurations before removal from the carrier substrate (Fig. 1A).

A somewhat more complex deformation mode that involves in-plane stretching along an axis not aligned to the bridges illustrates additional capabilities of the noncoplanar design. Such applied strains cause the bridges not only to flatten, as for the case of Fig. 2 A–C, but also to rotate and twist out of the plane (Fig. 2D). This deformation is referred to as lateral buckling (11) and can be characterized by a Bessel function (for tilting) and a sinusoidal function (for flattening) to accommodate off-axis stretching (SI Text). Because this type of stretching involves significant shear, the principal strain, which combines the tensile and shear strains (see SI Text), replaces the tensile strain to describe the extent of deformation. For off-axis stretching that results in 14% stretching in the bridge and 7.5% shear, minimization of energy (including the twisting energy) gives a maximum principal strain of 2% and 0.8% in the metal layer of the bridges and islands, respectively, and 0.6% in the Si layer of islands. FEM simulation of these systems, as illustrated in Fig. 2E, further quantifies the underlying mechanics. The ability of the bridges to absorb nearly all of these off-axis strains enables excellent device and circuit performance, with little dependence on strain. Fig. 2F shows, as an example, transfer characteristics and gains (up to ≈100) measured on CMOS inverters formed by electrical interconnects on bridges between adjacent islands that each support one p channel and one n channel MOSFET. Also, electrical simulation of the inverters, using individual transistor data, agrees with the measurement results (see Fig. S4). These transistors have layouts identical to those in the ring oscillators of Fig. 2A. Although the deformation modes of Fig. 2 are also possible with recently reported wavy designs (4), the noncoplanar mesh layouts increase the levels of strain that can be accommodated by >5 times, and they substantially reduce the sensitivity of electrical response to strain (i.e., to values close to measurement repeatability limits for the cases of Fig. 2). In all cases, the deterministic, linear elastic nature of the underlying mechanics, which arises from the small strains in the electronic materials and the linear response of the PDMS (up to strains of 110%) (9), leads to little change in properties even on extensive mechanical cycling, as demonstrated subsequently (see Fig. 5E).

Fig. 5.

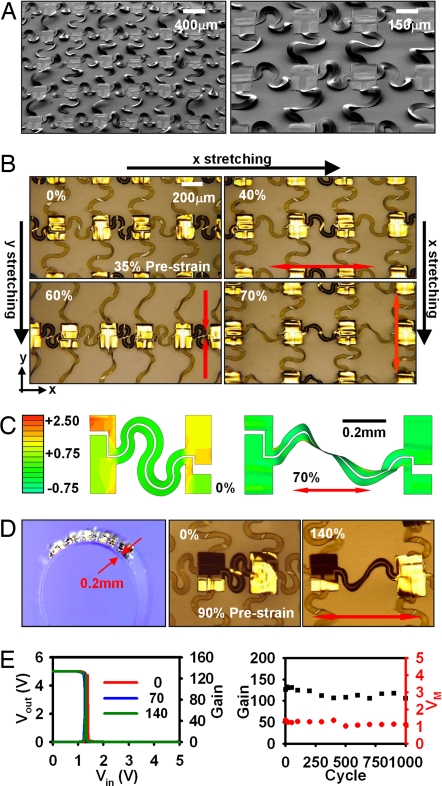
Extreme stretchability in noncoplanar electronics with serpentine bridge designs. (A) SEM image of an array of stretchable CMOS inverters with noncoplanar bridges that have serpentine layouts (Left) and magnified view (Right). (B) Optical images of stretching tests in the x and y directions. (C) FEM simulation before (35% prestrain) and after (70% applied strain) stretching. (D) Arrays of inverters on a thin PDMS substrate (0.2 mm) (Left) and images in unstretched (middle; 90% prestrain) and stretched (Right; 140% tensile strain) states. (E) Transfer characteristics and gain for a representative inverter under stretching (Left) and plot of gain and voltage at maximum gain (V_M) for a similar device as a function of stretching cycles (Right).

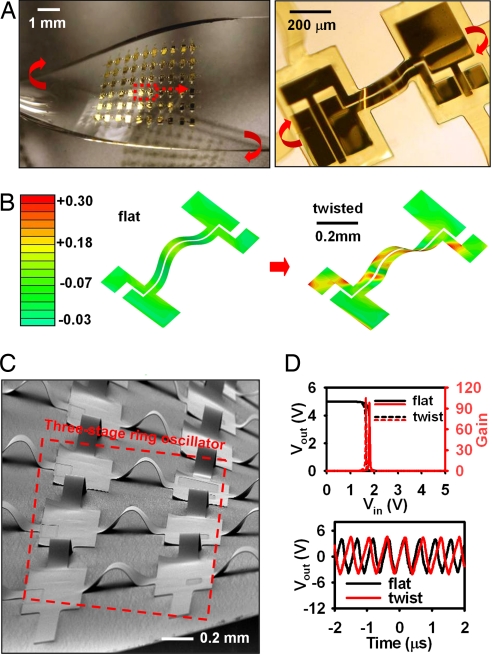
An extreme type of deformation, which is partly involved in the configuration shown in Fig. 1, involves twisting into corkscrew shapes with tight pitch. Under such applied strain, the bridges deform due mainly to in-plane shear with a magnitude on the order of the ratio of (bridge or island) thickness to length times the rotation angle (see SI Text for details). Such twisting deformation is different from off-axis stretching because it does not involve buckling and is therefore amenable to linear analysis. For a 90° rotation over a distance corresponding to a pair of bridges and an island, the maximum shear strains in the metal and Si layers are 0.08% and 0.02%, respectively, for the 445-μm-long bridge and 260-μm-long island. Fig. 3A Left shows an image of a circuit on thin PDMS, in a twisted geometry; Fig. 3A Right shows a magnified view of a CMOS inverter in this system. As for the previously described cases, FEM simulation (Fig. 3B) supports the experimental observations and reveals the level of principal strain to be 0.3% in the metal layer of the bridge and the island. A SEM image of an interconnected array of inverters for a ring oscillator (Fig. 3C) shows the shape of the twisted bridges. Electrical measurements indicate stable electrical performance before and after twisting, both for inverters (Fig. 3D Upper) and ring oscillators (Fig. 3D Lower). The electrical properties, in all cases, are comparable with those described previously. In other words, the systems are, to within experimental uncertainty, agnostic to deformation mode for all configurations studied here.

Fig. 3.

Mechanical and electrical responses of noncoplanar stretchable electronics to twisting deformations. (A) Optical images of an array of stretchable CMOS inverters in a twisted configuration (Left) and magnified view of a single inverter, illustrating the nature of the deformation (Right). (B) FEM simulation of the mechanics of twisting on the bridge structures. (C) SEM image of an array of stretchable, 3-stage CMOS ring oscillators in a twisted configuration. (D) Electrical characteristics of the inverters (Upper; gain and output voltage, V_out, as a function of input voltage, V_in) and oscillators (Lower; output voltage, V_out, as a function of time) in planar and twisted states.

Figs. 1–3 illustrate examples for circuits, such as inverters and ring oscillators, that are straightforward to implement in repetitive, arrayed layouts. More complex, irregular designs might be required in many cases of practical importance; these can also be implemented in noncoplanar mesh designs. We demonstrated this concept for a differential amplifier (10), in which we divided the circuit into 4 sections, each of which forms an island connected by metal lines on pop-up bridges. The red dotted boxes in Fig. 4A Left highlight these 4 regions; an angled view SEM image in the Inset shows the structure. The bridges provide a mechanics that is conceptually similar to those in the regular array layouts, even though the details are somewhat different. As a result, this irregular circuit can be stretched or twisted reversibly, as shown in Fig. 4 B and C, respectively. Fig. 4D shows magnified images of stretching in the x and y directions. Electrical measurements verify that the amplifiers work well under these deformations. The gains for 0%, 17% x stretching, 17% y stretching, and twisting to a full 180° rotation of a PDMS substrate with a length of ≈2 cm were 1.15, 1.12, 1.15, and 1.09 (design value ≈1.2), respectively. Such systems can also be freely deformed, as shown in Fig. 4F.

Fig. 4.

Noncoplanar stretchable electronics with asymmetric layouts. (A and B) Optical images of an array of stretchable differential amplifiers in twisted (A) and planar stretched (B) layouts. (C) Tilted view SEM of a representative amplifier, showing the noncoplanar layout. (D and E) Optical images under stretching along the x and y directions (D) and corresponding electrical output as a function of time for a sinusoidal input (E). (F) Optical image of a device in a complex deformation mode. Here, 17x and 17y refer to 17% tensile strains along the x and y directions indicated in D, respectively.

Although the materials and mechanical designs described previously can accommodate larger strains and in more diverse configurations compared with previous demonstrations, they might not satisfy requirements for certain advanced device concepts, such as electronics for “smart” surgical gloves or hemispherical focal plane arrays with large, double curvature, where truly “rubber band-like” stretchability (e.g., to >50% strain) is needed. A simple method to increase the stretchability, without changing the materials or layouts in the stacks that make up the circuits, involves increasing the separations between the device islands and decreasing the thicknesses of the bridges. The quantitative effects of these parameters on the peak material strain can be represented by a simple analytical relation, presented in the SI, for the approximate case that the islands are strictly rigid and remain planar (Fig. S5). To expand the deformability even further, without increasing the sparseness of the distribution of islands, serpentine bridges can be used. Fig. 5A shows SEM images of such a design after executing the fabrication procedures of Fig. 1. When external strain is applied along the x or y directions, these noncoplanar serpentine bridges effectively compensate the applied strain not only through changes in height but also by changes in geometry of the serpentine shape. Fig. 5B shows images of the response of a representative device to on-axis stretching strains up to 70%, for a system built with 35% prestrain, in which deformations of the serpentine bridges exhibit changes in configurations that might be expected intuitively. Remarkably, finite-element modeling reveals that, even to stretching strains of 70%, the peak strains in the metal layer in the bridges and islands are 0.2% and 0.5%, respectively, and the strain in silicon is 0.15% as indicated in Fig. 5C. (The strains reach ≈3% in certain locations of the PI.) To explore the limits, we used thin PDMS substrates (0.2 mm) to facilitate stretching to even larger strains. Fig. 5D shows a case corresponding to ≈90% prestrain, which allows stretching to ≈140% strain and corresponds to ≈100% system strain. The large prestrain improves the stretchability, and it also increases the active-area density in the circuit by decreasing the lengths of the interconnecting bridges. For example, in the designs illustrated here, the active-area density for a prestrain of ≈35% (Fig. 5B, ≈70% stretchability) and ≈90% (Fig. 5D, ≈140% stretchability) is ≈19% and ≈34%, respectively. The essential strategy of bridge-type interconnects, however, requires a tradeoff between degree of stretchability and area consumed by the interconnects. Consistent with the small strains in the active materials revealed by FEM, the electrical properties approach those of the corresponding unstrained, planar systems; the operation is also stable over many cycles (up to 1,000, evaluated here) of stretching, as indicated in Fig. 5E.

Finally, the practical application of pop-up circuits requires an additional encapsulation layer on top of devices to protect active regions from unwanted damage. To this end, we coated the circuits with a liquid prepolymer PDMS and cured it after all bridges and islands were embedded. A dual neutral mechanical plane design can be implemented by controlling the top and bottom PDMS thickness to provide additional mechanical strength for deformation (4). This encapsulation has relatively minor effects on the essential mechanics, primarily through slight increases in the strain in the bridges due to restricted deformation inside the PDMS. Pop-up inverters with straight (Movie S1 and Movie S2) and S-shaped (Movie S3 and Movie S4) bridges show these behaviors (see also SI Text).

Conclusions

Collectively, the results presented here provide design rules for circuits that offer both excellent electrical performance and capacities to be elastically deformed in diverse configurations to high levels of strain. The same ideas can, in many cases, be used to advantage in other conventionally rigid, planar technologies such as photovoltaics, microfluidics, sensor networks, photonics, and others. These and related types of systems might enable many important new applications that cannot be addressed with other approaches. Exploring these possibilities represents a fruitful area for future work.

Materials and Methods

Preparation of Doped Silicon Ribbons.

Preparation of doped silicon ribbons starts with the doping of the top silicon on silicon-on-insulator (SOI) wafers: nMOS source/drain doping with p-type SOI wafers (SOITEC) and pMOS source/drain doping with n-type SOI wafers (SOITEC). This process uses plasma-enhanced chemical-vapor deposition (PECVD) of silicon dioxide (SiO₂) for a diffusion mask, photolithography, and RIE with CF₄/O₂ gas for patterning, spin coating, and high-temperature diffusion of boron spin-on dopant (B153; Filmtronics) at 1,000 °C to ≈1,050 °C for p-type and phosphorous spin-on dopant (P509; Filmtronics) at 950 °C to ≈1,000 °C for n-type. The typical surface doping concentrations using phosphorous and boron spin-on dopants are ≈2 × 10²⁰ cm⁻³ and ≈10²⁰ cm⁻³, respectively (13, 14). After doping, ribbons are defined by photolithography and RIE; they are released from the mother wafer by removing the buried oxide layer of the SOI wafers. These doped ribbons are picked up by PDMS and transfer-printed to a carrier wafer for circuit integration.

Fabrication of Stretchable Circuits.

Doped n-type and p-type nanoribbons are sequentially transfer printed to a carrier wafer coated with thin layers of PMMA (≈100 nm) as a sacrificial layer and PI (≈1.2 μm) as an ultrathin substrate. After transfer printing, 50 nm of PECVD SiO₂ is deposited for the gate dielectric. Contact windows for source and drain are etched with buffered oxide etchant, 150-nm metal electrodes are evaporated and patterned, and another PI layer is spin-cast for passivation and control of neutral mechanical plane location. After circuit fabrication, oxygen RIE defines the mesh format. Dissolution of the PMMA layer with acetone releases the circuits from the carrier wafer. Such circuits are transferred to mechanically prestrained PDMS for the formation of noncoplanar, pop-up layouts. To help define the locations of the pop-up regions, thin layers of Cr and SiO₂ are selectively deposited on the bottoms of active islands by evaporation through a shadow mask to enhance the adhesion between these regions of the circuit and PDMS.

Stretching Tests and Electrical Measurements.

Stretching tests are performed with automated assemblies of translations stages, capable of applying tensile or compressive strains in x, y, or diagonal directions. For twisting, edges of the PDMS are mechanically clamped with a twist angle of 180°. Electrical measurement are performed with a probe station (5155C; Agilent), directly while under stretching or twisting deformations.

Analytical Calculations of the Noncoplanar Bridge Structures.

The bridge is modeled as a composite beam. Its out-of-plane displacement has a sinusoidal form, with the amplitude determined by energy minimization. The island is modeled as a composite plate. Its out-of-plane displacement is expanded as a Fourier series, with the coefficients determined by energy minimization. The PDMS substrate is modeled as a semiinfinite solid subjected to a surface displacement, which is the same as the out-of-pane displacement of islands. The total energy of the system consists of the membrane and bending energy in the bridges, membrane and bending energy in the islands, and strain energy in the substrate. Minimizing the total energy gives the displacements and strain distributions in bridges and islands.

Finite Element Modeling.

Three-dimensional finite element models of the systems have been developed by using the commercial ABAQUS package. Eight-node, hexahedral brick elements with 4-node multilayer shell elements are used for the substrate and the thin film, respectively. The multilayer shell is bonded to the substrate by sharing the nodes. Each layer of thin film is modeled as a linear elastic material; the soft, elastomeric substrate is modeled as an incompressible hyperelastic material. We first determine the eigenvalues and eigenmodes of the system. The eigenmodes are then used as initial small geometrical imperfections to trigger the buckling of the system. The imperfections are always small enough to ensure that the solution is accurate. The simulations are performed in the same procedure as the key fabrication steps of integrated circuits system. These simulations give an insight to the formation of buckling patterns, the mechanics behavior of the thin film, and the nested hierarchy of the structure.