Abstract
Impulse response functions (IRFs) were obtained from two-pulse detection thresholds using isoluminant stimuli that produced increments or decrements in S-cone excitation. The pulses were chromatically modulated at constant luminance (based on 18 Hz heterochromatic flicker photometry). Chromatic stimuli were presented as a Gaussian patch (±1 SD = 2.3°) in one of four quadrants around a central fixation cross on a CRT screen. Each of the two pulses (6.67 ms) was separated by an inter-stimulus interval (ISI) from 20 to 360 ms. Chromaticity of the pulses was changed from the equal-energy white of the background to a bluish or yellowish color along individually determined tritan lines (based on color matching under strong S-cone adaptation from a 420 nm background superimposed in Maxwellian view). Chromatic detection thresholds were determined by a four-alternative forced-choice method with staircases for each ISI interleaved in each session. Measurements were repeated in at least four sessions for each observer. IRFs were calculated by varying four parameters of an exponentially-damped sinewave. Both S-cone increment and decrement IRFs are characterized by a single excitatory phase and a much longer time course compared with IRFs derived for luminance modulation using the same apparatus and observers. S-cone increment IRFs are faster than S-cone decrement IRFs; the time to peak amplitude of S-cone increment and decrement IRFs is 50–70 and 100–120 ms, respectively. These results were used to derive the temporal contrast sensitivity for human observers of putative ON- and OFF-channels carrying signals from S-cones.
Keywords: S-cones, Koniocellular pathway, Temporal vision, Impulse response, ON- and OFF-pathways
1. Introduction
The impulse response function represents a theoretical response to a flash of infinitely short duration. This function can be used to predict response to any temporally modulated stimulus. To the extent that the visual system is linear, the impulse-response function (IRF) is related to the temporal contrast sensitivity function (tCSF) by the inverse Fourier transform. Psychophysical methods have been used extensively to derive an impulse-response function from two-pulse thresholds (separated by varying inter-stimulus intervals) using achromatic (e.g., Ikeda, 1965) and chromatic modulation (e.g., Uchikawa & Yoshizawa, 1993), but have only recently been used to characterize the isolated S-cone responses to increments (Shinomori & Werner, 2006). The purpose of this paper is to compare responses of isolated S-cone pathways mediating detection of increments and decrements, and thereby characterize putative ON- and OFF-channels of S-cone (koniocellular) pathway(s) (Kaplan, 2004).
There are numerous oddities of the S-cone system (Mollon, 1982), but apart from the sparse distribution of S-cones within the receptor mosaic, their distinctive spatio-temporal properties seem primarily due to their post-receptoral pathways. Individual S-cones do not differ in their temporal properties from M- and L-cones (Schnapf et al., 1990), but at a systems level, the S-cone pathway has been characterized as sluggish, with critical flicker fusion at low temporal frequencies (Brindley et al., 1966). Cottaris and DeValois (1998) estimate that S-opponent signals reach cortical area V1 of the Macaque monkey about 30 to 40 ms after the arrival of signals from M/L-opponent pathways. This could be due to smaller fibers carrying S-cone signals and/or to more complex synaptic circuitry in processing S-cone signals in the cortex (DeValois et al., 2000).
There have been only a few attempts to isolate psychophysically the separate ON- and OFF-responses of S-cone pathways (Shinomori et al., 1999: McLellan & Eskew, 2000; Vassilev et al., 2003), perhaps because OFF-cells receiving S-cone input are so rare in those neurophysiological studies that have found them (Derrington et al., 1984; Valberg et al., 1986) that their existence has been questioned (Malpeli & Schiller, 1978). More recent studies have identified the retinal origins of an S-cone ON (M/L cone OFF) response in bistratified ganglion cells (Dacey & Lee, 1994) and an S-cone OFF (M/L-cone ON) response in larger and sparser monostratified ganglion cells (Dacey et al., 2002, 2003; see also Klug et al., 2003). The small bistratified cells are known to project to the koniocellular layers of the LGN (Hendry & Yoshioka, 1994) and then directly to cytochrome-oxidase rich regions, or blobs, of layers 2 and 3 of striate cortex. At the level of the lateral geniculate nucleus, there are many more S-ON than S-OFF cells, but at the cortex their numbers are similar (DeValois et al., 2000). The cortical synaptic transformations adding to the S-cone OFF cortical representation, along with small fibers carrying S-cone signals to cortex, could contribute to a slower time course for an S-cone IRF compared to an IRF with luminance modulation (Shinomori & Werner, 2003, 2006), and potentially to differences between S-cone IRFs for isoluminant increments and decrements. The purpose of this study was to compare impulse response functions of putative ON- and OFF-channels using increments and decrements in stimulation of isolated S-cone pathways.
2. Materials and methods
Impulse response functions were derived from thresholds for a series of double-pulses that were chromatically modulated along individual tritan lines at constant luminance. Changing the pulses from a white point toward short wavelengths at constant luminance produced S-cone increments while changing the pulses from a white point toward middle/long wavelengths at constant luminance produced an S-cone decrement.
2.1. Observers
Four observers (three males and one female), ranging in age from 21.3 to 40.1 years, participated in these experiments. Each observer was a normal trichromat according to several screening criteria (Neitz anomaloscope, HRR pseudoisochromatic plates, the Farnsworth F-2 plate, and the Cambridge Colour Test). All had normal visual acuity. The presence of retinal or optic nerve disease, or abnormal ocular media, was ruled out by ophthalmological exam. Written informed consent was obtained following the Tenets of Helsinki, and with approval of the Office of Human Research Protection of the University of California, Davis, School of Medicine.
2.2. Apparatus, stimuli, and calibrations
The stimuli were presented on a CRT display (Sony GDM-200 PS) operating at a 150 Hz frame rate that was controlled by a video board with 15-bit resolution (Cambridge Research Systems, VSG 2/4) using a Dell Pentium computer. The CRT monitor was viewed through a 2.16× astronomical telescope. A beam-splitter combined the CRT optical path with a Maxwellian-view optical channel to present a superimposed adapting field. The latter system used a 300 W xenon lamp and regulated direct current supply. A neutral density wedge and neutral density filters were placed in a focal plane and collimated section of the beam, respectively. This system was calibrated at 420 nm, the central wavelength (8 nm bandwidth at half peak amplitude) of an interference filter placed in a collimated beam. An aperture was placed before the telescope to form a 2.5 mm exit pupil in the plane of the eye pupil; the Maxwellian-view image was 1.5 mm in the plane of the eye pupil. The eye and head were stabilized with a dental-impression bite-bar assembly that could be aligned by viewing the pupil with an auxiliary optical channel.
Two-pulse thresholds were measured for stimuli modulated in chromaticity along a tritan line, changing from the white background (CIE x, y = 0.33, 0.33; 10 cd/m2, 1.69 log Td) toward the short-wavelength or long-wavelength spectrum locus. S-cone increments were measured with a double pulse (6.7 ms with inter-stimulus intervals from 20 to 360 ms) in which the two flashes were modulated equally in chromaticity at constant luminance toward short wavelengths. S-cone decrements used essentially the same procedure except that six frames instead of one frame were used for each pulse modulation toward long-wavelengths, yielding a “pulse” duration of 40.2 ms. This was due to insufficient chromatic change toward yellow in a single frame. Control experiments using one, three, and six frames demonstrate that this did not affect the results.
Each pulse was presented as a Gaussian patch, 2.26° diameter at 1 SD (106 pixels on a 640 × 480 pixel display), in one of four quadrants located 1.70° to one side or the other, and 1.70° above or below a central fixation cross. Heterochromatic flicker photometry used to determine isoluminance was carried out with an annulus encompassing the regions in which Gaussian patches were presented.
The CRT phosphors were calibrated spectrally using a spectro-radiometer/photometer (Photo Research, Model PR703-A) and radiometrically using a p-i-n 10 silicon photodiode and linear read-out system (United Detector technology, Optometer 81). Luminance was measured with a chromameter (Minolta, CS-100). The relation between phosphor radiance and voltage was linearized based on tables generated using a photodiode and calibration software in the VSG software (Cambridge Research Systems, OptiCal). Rise and fall times of the CRT phosphors were measured with a photodiode and digital oscilloscope and found to be ∼1.2 ms for all phosphors. Peak-to-peak timing error of the inter-stimulus intervals was ≤3%.
2.3. Procedures
The stimuli were presented on a background of fixed luminance for all subjects, but the chromatic modulation of the IRF test probes was based on individual measures of isoluminance using 18 Hz heterochromatic flicker photometry with an annular stimulus (0.64°–2.77°, inner-outer diameter). The retinal illuminance ratio was measured for each of the three CRT phosphor combinations (R-G, G-B, B-R). To evaluate the accuracy of the observer's settings, each measured isoluminant phosphor combination was compared with that predicted from the other two combinations. The difference between the measured and predicted ratios was <10% for all observers. These phosphor values, in combination with fixed exit pupil size in the plane of the eye pupil, equated retinal illuminance across observers.
Individual tritan lines were determined by a color match under strong adaptation to S-cones by the 420 nm light presented in Maxwellian view. Following 5 min adaptation to a 420 nm field (12°), the observer was asked to find a match between bipartite rectangular patches (combined subtense 1.2 × 0.6°) falling near a nominal tritan line by adjusting the angle of the line around the white point, and the intensity of one of the two half-fields. The stimulus was an array of four bipartite fields each corresponding to the approximate locations and size of the test stimuli used for two-pulse threshold measurements. The observer viewed a central fixation cross. Without S-cone adaptation, these patches did not match regardless of the angle of the line. Under the S-cone adaptation, however, all observers reported that they were able to find a metameric match between the squares. This match was determined five times and the mean defined the coordinates of the tritan line.
Two-pulse thresholds began after 5 min dark adaptation and 5 min adaptation to a 10 cd/m2 equal-energy white background. Two pulses were presented on the screen, preceded by a high-pitched tone and followed by a low-pitched tone. The observer's task was to indicate in which of four quadrants the stimulus was detected by pressing one of four correspondingly arranged buttons. The stimulus was a chromaticity change in one Gaussian patch from equal-energy white along the individually determined tritan line. The four-alternative forced-choice task was combined with a two-down, one-up staircase in which staircases for each ISI were interleaved. Thresholds for each ISI were based on the last four of six reversals corresponding to a 70.7% probability of detection. This was repeated in at least 4–6 sessions per observer.
3. Results
3.1. Double-pulse thresholds and calculation of the impulse response function
The double-pulse method is based on the assumption that the pulses sum to contribute to threshold provided the inter-stimulus interval is short enough to be integrated within the excitatory period of the mechanism. If the inter-stimulus interval is longer than a critical duration, the response of the two pulses will not sum to contribute to threshold, or the second pulse may produce a response that is combined during an inhibitory phase of the response to the first flash. As a result, threshold for this double-pulse pair will increase. From the threshold change as a function of inter-stimulus interval, the shape of the IRF can be estimated. We modeled the IRF as an exponentially damped frequency modulated sine-wave as proposed by Burr and Morrone (1993) using the following equation:
| (1) |
where I(t) is the impulse response as a function of time (t), parameters a0-3 are positive with a0 defining the overall gain, a1 the fundamental frequency of oscillation, a2 the modulation frequency over time, and a3 the steepness of the decay. H(t) is the Heaviside function to assure that I(t) begins with a value of 0 when t < 0. Four parameters, a0-3, were varied using a least-squares criterion and in this way the IRF could be fitted without any assumptions about the number of excitatory or inhibitory phases. Other computational details are described elsewhere (Shinomori & Werner, 2003, 2006).
3.2. S-cone increment and decrement impulse response functions
Fig. 1 (left column) shows one observer's thresholds as a function of ISI for S-cone increments (top) and S-cone decrements (bottom). The right panels show the corresponding IRFs derived from these functions. Both S-cone IRFs are monophasic and the durations are protracted compared to the biphasic and triphasic IRFs that characterize response to an achromatic double pulse. The rise time to the peak is 64 ms for the S-cone increment IRF and 145 ms for S-cone decrement IRF, compared with 21.3 ms with luminance modulation (Shinomori & Werner, 2003, Fig. 7). With luminance modulation, the first excitatory phase is followed by an inhibitory phase making the excitatory duration easy to define. For the S-cone IRF, the duration of the excitatory phase is operationally defined as the value on the descending slope corresponding to 5% of the peak amplitude.
Fig.1.
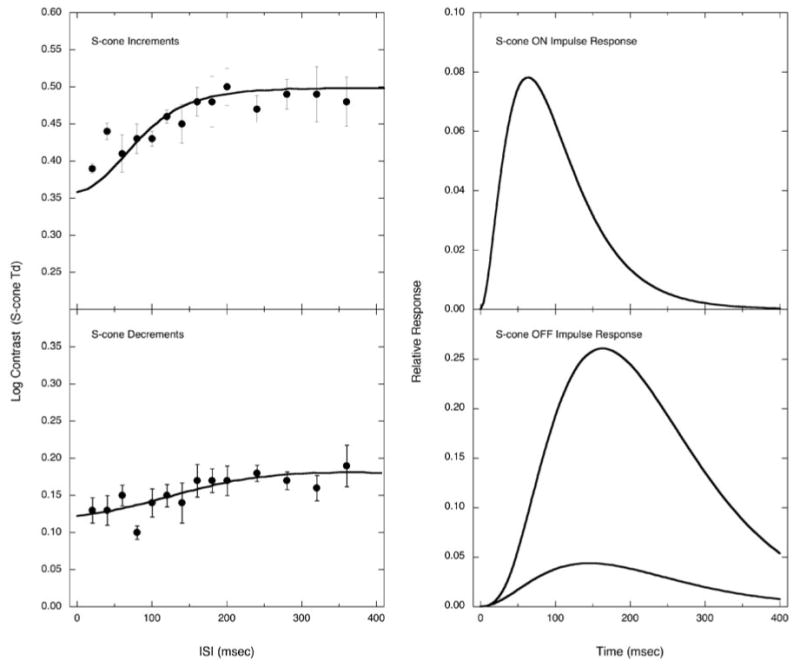
Threshold data with the model fit (smooth curve) are shown on the left; impulse response functions (IRFs) calculated by the model for one observer (AS) are shown on the right. Top panels are for S-cone increment detection and bottom panels are for S-cone decrement detection. In the case of the S-cone decrement IRF, because one pulse consisted of six frames, linear summation of six response functions with 6.67 ms delay each was used to calculate the expected threshold curve from the shape of the IRF (denoted by the curve in the threshold data panel).
As mentioned, it was not always possible to obtain sufficient S-cone modulation in a double-pulse defined by single frames because of the luminance limit of the CRT phosphors. However, because the S-cone IRF is slow, it was possible to use multiple frames (typically six frames) to define each pulse without affecting the shape of the IRF. In this case, we defined each pulse as one series of successive frames of the IRF calculated as the summation of S-cone IRFs with a time delay by each frame (6.67 ms frame rate). In Fig. 1, this IRF for S-cone decrements is shown by the curve with lower amplitude in which each pulse was defined by six frames for S-cone decrement IRF measurement. This method of measurement and calculation assuming linear summation is justified because the double-pulse method itself has to employ this assumption to obtain the IRFs.
3.3. Individual variation in the S-cone impulse response
Fig. 2 shows S-cone increment IRFs (smooth curves) and S-cone decrement IRFs (dotted curves) for each observer in separate panels. S-cone increment IRFs have consistently higher amplitude and less sluggish response than S-cone decrement IRFs. The mean amplitude for S-cone increment IRFs are 0.077 (SEM = 0.004), compared to a mean 0.038 (SEM = 0.005) for S-cone decrement IRFs. Thus, S-cone increment IRFs is stronger by 2.03 times in terms of S-cone stimulation contrast. S-cone increment IRFs are also faster than S-cone decrement IRFs. The mean time to the peak is 59.7 ms (SEM = 8.3 ms) for S-cone increment IRFs, compared to a mean time of 116.0 ms (SEM = 11.7 ms) for S-cone decrement IRFs. Not only the time to the peak, but also the IRF duration, is much longer for S-cone decrement IRFs. The mean duration corresponding to 5% of the peak amplitude is 251 ms (SEM = 37 ms) for S-cone increment IRFs, compared to the mean duration for S-cone decrement IRFs of 438 ms (SEM = 40 ms).
Fig.2.
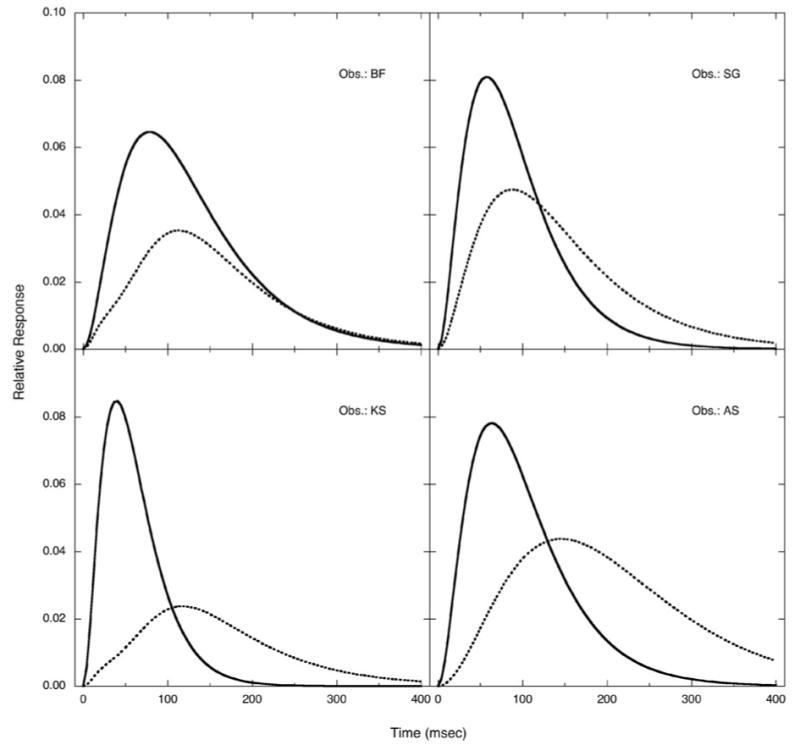
S-cone increment IRFs (smooth curves) and S-cone decrement IRFs (dotted curves) for four observers. S-cone increment IRFs have higher amplitude and faster rise time than S-cone decrement IRFs for all observers.
Fig. 3 shows the difference between S-cone increment and decrement IRFs in terms of: (1) relative peak amplitude, (2), peak time, and (3) duration. Despite individual variation, differences in all characteristics are statistically significant (paired t-tests; p < 0.05).
Fig.3.
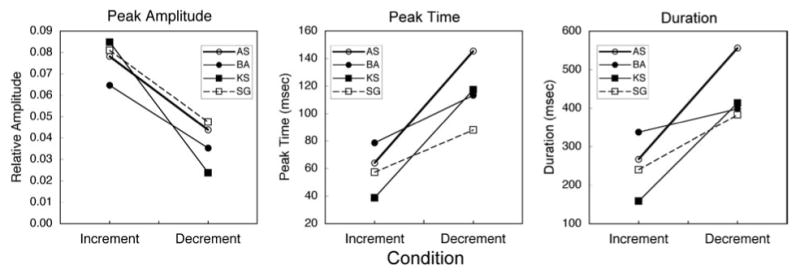
S-cone increment and decrement IRFs compared for each observer in terms of relative peak amplitude (left), peak time (middle), and duration (right).
4. Discussion
Fig. 4 summarizes the S-cone increment (solid curve) and decrement (dotted curve) IRFs for the observers of this study and compares them to the average IRFs obtained with luminance modulation (scaled by 20% in the figure) for young observers using the same procedures and apparatus (Shinomori & Werner, 2003). We have suggested that the latter function is likely to be mediated by a magnocellular pathway due to conditions of measurement (brief achromatic flashes) and the presence of three response modes. The lack of IRF inhibition in the S-cone IRFs contributes to the protracted response but does not explain the sluggish rise time. The longer rise time in the psychophysical S-cone IRF is consistent with slower conduction velocity in the smaller koniocellular fibers and possibly more complex cortical circuitry, especially for processing by S-cone OFF cells (DeValois et al., 2000). While these differences between temporal ON- and OFF channels may originate in the retina, they are maintained and possibly elaborated through higher-level processing stages to permit their measurement psychophysically.
Fig.4.
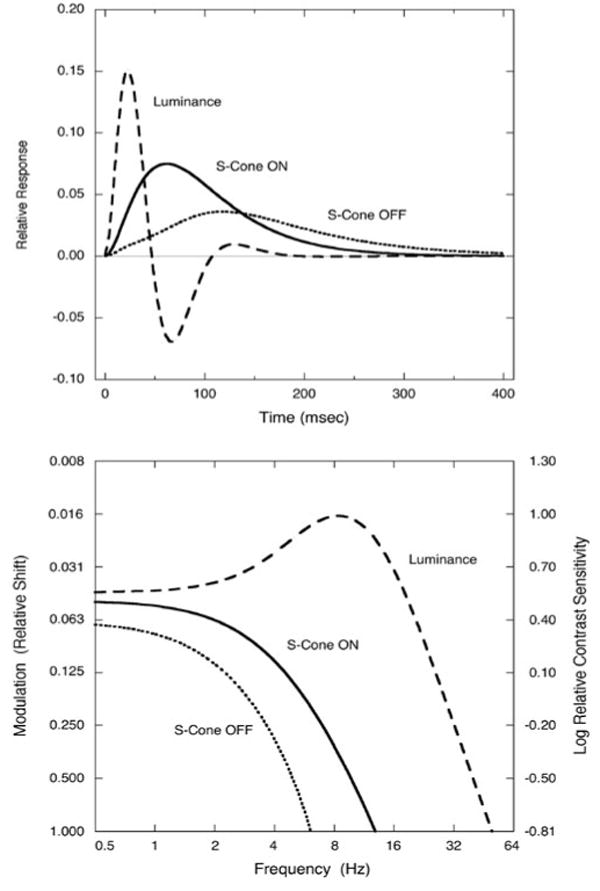
Average IRFs (top panel) for S-cone increments (solid curve) and decrements (dotted curve) compared with previously published IRFs from young observers with luminance modulation (dashed curve). For purposes of illustration, the amplitude of the luminance IRF is reduced by a factor of 5. Lower panel shows calculated temporal contrast sensitivity functions. The contrast sensitivity resulting in a 50 Hz cut-off for luminance modulation was used to estimate modulation (as 100%) and cut-OFF's for S-cone increment and S-cone decrement functions. The modulation was defined as the amplitude of the flicker sine wave divided by the mean luminance or chromaticity of the flicker (= ΔL/Lmean or ΔC/Cmean).
It is important to emphasize that, unlike previous studies using short-wave stimuli with the two-pulse method (Uchikawa & Ikeda, 1986; Uchikawa & Yoshizawa, 1993), the stimuli were modulated along individually determined tritan lines at isoluminance and hence restrict response to an S-cone pathway. These studies that did not use tritan stimuli, and others (Smith et al., 1984), have not clearly revealed differences among chromatic pathways. For this reason, it is perhaps not surprising that the IRF for an isoluminant yellow flash measured previously (Uchikawa & Ikeda, 1986) was faster and had a higher amplitude for two of three observers compared to IRFs for red, green, or blue flashes. In small bistratified cells, the (L + M) OFF response is slower than the S-cone ON response (Field et al., 2007). Thus, an alternative interpretation to our S-cone decrement data is that the slow time course is not due to a putative S-cone OFF pathway per se, but to its opponent yellow-ON response. There are two reasons for challenging this interpretation: First, the stimuli were modulated on a tritan line which means that M- and L-cone modulation are held constant. Second, if the response were mediated by inputs from M- and L-cones, the IRF would be expected to have completely different temporal dynamics (i.e., it would be faster) as shown by the red-green chromatic responses of Burr and Morrone (1993) and the isoluminant yellow response reported by Uchikawa and Ikeda (1986).
Two recent studies compared reaction times for isoluminant stimuli varied along L-M and S-(L + M) cone axes (McKeefry et al., 2003; Smithson & Mollon, 2004). Both studies support an earlier reaction-time study (Mollon & Krauskopf, 1973) indicating that the S-cone pathway is sluggish. While McKeefry et al. (2003) report an S-cone lag of ∼40 ms calculated from reaction-time data, Smithson and Mollon (2004) find that the difference between L-M and S-(L + M) pathways does not exceed 20–30 ms. The difference between our S-cone increment IRFs (Shinomori & Werner, 2006) and Burr and Morrone's (1993) red-green chromatic IRFs is ∼32 ms. To compare our data to the reaction time data, we calculated the theoretical time to reach the detection threshold assuming that when the luminous or chromatic modulation of a stimulus is increased by multiples of the modulation at the detection threshold, the time needed to reach the accumulated response for threshold is no longer the sum of all stimulation, but must be shorter depending on the total response calculated by the IRF for that stimulus condition and the profile of the stimulus, and the assumption of probability summation (Watson, 1979) as used for our calculation of IRFs. This permits an estimate of the difference in reaction times between luminance increments, S-cone increments and S-cone decrements as shown in Table 1. The calculated differences between luminance increments and S-cone decrements are about 100–170 ms and the differences between S-cone increments and S-cone decrements are about 35–60 ms. These values are close to the differences in measured reaction times (McKeefry et al., 2003). There is, however, less agreement between the reaction time study of McKeefry et al. (2003) and the data presented here based upon two-pulse thresholds for S-cone increments and decrements. Our data imply that S-cone OFF signals are substantially slower than S-cone ON, while McKeefry et al. (2003) find the opposite. The reason for this discrepancy is unclear, although it may be noted that while they measured individual observer's isoluminance settings, they did not measure individual tritan lines. If there are minor deviations in the angle of the tritan line for an individual compared to a standard observer, intrusion of L- and M-cone response cannot be excluded. If this were to occur, reaction times would be reduced as they are for L- and M-cone conditions.
Table 1. Theoretical time (ms) to reach detection threshold.
| Stimulus condition | |||
|---|---|---|---|
| Stimulus intensity | Luminance | S-cone increment | S-cone decrement |
| 2 × threshold | 137 | 247 | 303 |
| 4 × threshold | 93.3 | 180 | 227 |
| 8 × threshold | 73.3 | 143 | 183 |
| 12 × threshold | 63.3 | 127 | 163 |
Stimulus temporal profile was assumed to be 190 ms sinusoidal increment, 190 ms constant in the maximum modulation and 190 ms sinusoidal decrement, as in McKeefry et al. (2003). Impulse response functions in Fig. 4 were used and the temporal step size in this calculation was 3.33 ms. Zero time is defined as the stimulus onset (no delay, reaction latency or time for motor response is included).
The IRFs in the upper panel of Fig. 4 were transformed to temporal contrast sensitivity functions (tCSF) by the inverse Fourier transform. These derived tCSFs are shown in the bottom panel of Fig. 4. As expected, and consistent with previous measurements, the tCSFs for S-cone modulation are low-pass (Wisowaty & Boynton, 1980) while the tCSF's for luminance modulation are band-pass. The major difference between S-cone increment and S-cone decrement IRFs is the higher sensitivity and less steep high-frequency fall-off of the former function. This results in a shift in the high temporal frequency cutoff. The modulation in Fig. 4 was arbitrarily shifted to yield a 50 Hz high-frequency cut-off for luminance modulation (Kelly, 1974) and provides a contrast sensitivity value for estimating cut-offs for the other curves. Although there are no direct comparison measures in the literature, these theoretical tCSFs imply temporal cut-offs of 13 and 6.1 Hz for detection of increments and decrements, respectively, by the human S-cone pathways.
Acknowledgments
This work was supported by a National Institute of Health grant (NIA AG04058) to J.S. Werner and the Special Subsidies in Subsidies for ordinary expenses for private schools from the Promotion and Mutual Aid Corporation for Private Schools of Japan to K. Shinomori.
References
- Brindley GS, Du Croz JJ, Rushton WAH. The flicker fusion frequency of the blue-sensitive mechanism of colour vision. Journal of Physiology (London) 1966;183:497–500. doi: 10.1113/jphysiol.1966.sp007879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burr DC, Morrone MC. Impulse-response functions for chromatic and achromatic stimuli. Journal of Optical Society of America A. 1993;10:1706–1713. [Google Scholar]
- Cottaris NP, DeValois RL. Temporal dynamics of chromatic tuning in macaque primary visual cortex. Nature. 1998;395:845–846. doi: 10.1038/27666. [DOI] [PubMed] [Google Scholar]
- Dacey DM, Lee BB. The ‘blue-on’ opponent pathway in primate retina originates from a distinct bistratified ganglion cell type. Nature. 1994;367:731–735. doi: 10.1038/367731a0. [DOI] [PubMed] [Google Scholar]
- Dacey DM, Peterson BB, Robinson FR. Identification of an S-cone opponent OFF pathway in the macaque monkey retina: Morphology, physiology and possible circuitry. Investigative Ophthalmology & Visual Science. 2002;43:2983. E-abstract. [Google Scholar]
- Dacey DM, Peterson BB, Robinson FR, Gamlin PD. Neurotechnique. Fireworks in the primate retina: In vitro photodynamics reveals diverse LGN-projecting ganglion cell types. Neuron. 2003;37:15–27. doi: 10.1016/s0896-6273(02)01143-1. [DOI] [PubMed] [Google Scholar]
- Derrington AM, Krauskopf J, Lennie P. Chromatic mechanisms in lateral geniculate nucleus of Macaque. Journal of Physiology (London) 1984;357:241–265. doi: 10.1113/jphysiol.1984.sp015499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeValois RL, Cottaris NP, Elfar SD, Mahon LE, Wilson JA. Some transformations of color information from lateral geniculate nucleus to striate cortex. Proceedings of the National Academy of Sciences. 2000;97:4997–5002. doi: 10.1073/pnas.97.9.4997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Field GD, Sher A, Gauthier JL, Greschner M, Shlens J, Litke AM, Chichilnisky EJ. Spatial properties and functional organization of small bistratified ganglion cells in primate retina. Journal of Neuroscience. 2007;27:13261–13272. doi: 10.1523/JNEUROSCI.3437-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hendry SHC, Yoshioka T. A neurochemically distinct third channel in the macaque dorsal lateral geniculate nucleus. Science. 1994;264:575–577. doi: 10.1126/science.8160015. [DOI] [PubMed] [Google Scholar]
- Ikeda M. Temporal summation of positive and negative flashes in the visual system. Journal of the Optical Society of America. 1965;55:1527–1534. doi: 10.1364/josa.55.000560. [DOI] [PubMed] [Google Scholar]
- Kaplan E. The M, P, and K pathways of the primate visual system. In: Chalupa LM, Werner JS, editors. The Visual Neurosciences. Cambridge, MA: MIT Press; 2004. pp. 481–493. [Google Scholar]
- Kelly DH. Spatio-temporal frequency characteristics of color-vision mechanisms. Journal of the Optical Society of America. 1974;64:983–990. doi: 10.1364/josa.64.000983. [DOI] [PubMed] [Google Scholar]
- Klug K, Herr S, Ngo IT, Sterling P, Schein S. Macaque retina contains an S-cone OFF midget pathway. Journal of Neuroscience. 2003;23:9881–9887. doi: 10.1523/JNEUROSCI.23-30-09881.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malpeli JG, Schiller PH. Lack of blue OFF-center cells in the visual system of the monkey. Brain Research. 1978;141:385–389. doi: 10.1016/0006-8993(78)90211-1. [DOI] [PubMed] [Google Scholar]
- McKeefry DJ, Parry NRA, Murray IJ. Simple reaction times in color space: The influence of chromaticity, contrast, and cone opponency. Investigative Ophthalmology & Visual Science. 2003;44:2267–2276. doi: 10.1167/iovs.02-0772. [DOI] [PubMed] [Google Scholar]
- McLellan JS, Eskew RT. ON and OFF S-cone pathways have different long-wave cone inputs. Vision Research. 2000;40:2449–2465. doi: 10.1016/s0042-6989(00)00107-3. [DOI] [PubMed] [Google Scholar]
- Mollon JD. A taxonomy of tritanopia. Documenta Ophthalmologica. 1982;33:87–101. [Google Scholar]
- Mollon JD, Krauskopf J. Reaction time as a measure of the temporal response properties of individual colour mechanisms. Vision Research. 1973;13:27–40. doi: 10.1016/0042-6989(73)90162-4. [DOI] [PubMed] [Google Scholar]
- Schnapf JL, Nunn BJ, Meister M, Baylor DW. Visual transduction in cones of the monkey Macaca Fascicularis. Journal of Physiology (London) 1990;427:681–713. doi: 10.1113/jphysiol.1990.sp018193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinomori K, Spillmann L, Werner JS. S-cone signals to temporal OFF-channels: Asymmetrical connections to postreceptoral chromatic mechanisms. Vision Research. 1999;39:39–49. doi: 10.1016/s0042-6989(97)00460-4. [DOI] [PubMed] [Google Scholar]
- Shinomori K, Werner JS. Senescence of the temporal impulse response to a luminous pulse. Vision Research. 2003;43:617–627. doi: 10.1016/S0042-6989(03)00009-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinomori K, Werner JS. Impulse response of an S-cone pathway in the aging visual system. Journal of the Optical Society of America A. 2006;23:1570–1577. doi: 10.1364/josaa.23.001570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith VC, Bowen RW, Pokorny VC. Threshold temporal integration of chromatic stimuli. Vision Research. 1984;24:653–660. doi: 10.1016/0042-6989(84)90206-2. [DOI] [PubMed] [Google Scholar]
- Smithson HE, Mollon JD. Is the S-opponent chromatic sub-system sluggish? Vision Research. 2004;44:2919–2929. doi: 10.1016/j.visres.2004.06.022. [DOI] [PubMed] [Google Scholar]
- Uchikawa K, Ikeda M. Temporal integration of chromatic double pulses for detection of equal-luminance wavelength changes. Journal of Optical Society of America A. 1986;3:2109–2115. doi: 10.1364/josaa.3.002109. [DOI] [PubMed] [Google Scholar]
- Uchikawa K, Yoshizawa T. Temporal responses to chromatic and achromatic change inferred from temporal double-pulse integration. Journal of the Optical Society of America A. 1993;10:1697–1705. [Google Scholar]
- Valberg A, Lee BB, Tigwell DA. Neurones with strong inhibitory S-cone inputs in the macaque lateral geniculate nucleus. Vision Research. 1986;26:1061–1064. doi: 10.1016/0042-6989(86)90040-4. [DOI] [PubMed] [Google Scholar]
- Vassilev A, Mihaylova MS, Racheva K, Zlatkova M, Anderson R. Spatial summation of S-cone ON and OFF signals: Effects of retinal eccentricity. Vision Research. 2003;43:2875–2884. doi: 10.1016/j.visres.2003.08.002. [DOI] [PubMed] [Google Scholar]
- Watson AB. Probability summation over time. Vision Research. 1979;19:515–522. doi: 10.1016/0042-6989(79)90136-6. [DOI] [PubMed] [Google Scholar]
- Wisowaty JJ, Boynton RM. Temporal modulation sensitivity of the blue mechanism: Measurements made without chromatic adaptation. Vision Research. 1980;20:895–909. doi: 10.1016/0042-6989(80)90071-1. [DOI] [PubMed] [Google Scholar]


