Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2008 Nov 10;105(46):17676–17681. doi: 10.1073/pnas.0809654105

Environmental signatures associated with cholera epidemics

Guillaume Constantin de Magny a, Raghu Murtugudde b, Mathew R P Sapiano b, Azhar Nizam c, Christopher W Brown b,d, Antonio J Busalacchi b, Mohammad Yunus e, G Balakrish Nair f, Ana I Gil g, Claudio F Lanata g,h, John Calkins i, Byomkesh Manna f, Krishnan Rajendran f, Mihir Kumar Bhattacharya f, Anwar Huq j, R Bradley Sack k, Rita R Colwell a,j,l,1
PMCID: PMC2584748  PMID: 19001267

Abstract

The causative agent of cholera, Vibrio cholerae, has been shown to be autochthonous to riverine, estuarine, and coastal waters along with its host, the copepod, a significant member of the zooplankton community. Temperature, salinity, rainfall and plankton have proven to be important factors in the ecology of V. cholerae, influencing the transmission of the disease in those regions of the world where the human population relies on untreated water as a source of drinking water. In this study, the pattern of cholera outbreaks during 1998–2006 in Kolkata, India, and Matlab, Bangladesh, and the earth observation data were analyzed with the objective of developing a prediction model for cholera. Satellite sensors were used to measure chlorophyll a concentration (CHL) and sea surface temperature (SST). In addition, rainfall data were obtained from both satellite and in situ gauge measurements. From the analyses, a statistically significant relationship between the time series for cholera in Kolkata, India, and CHL and rainfall anomalies was determined. A statistically significant one month lag was observed between CHL anomaly and number of cholera cases in Matlab, Bangladesh. From the results of the study, it is concluded that ocean and climate patterns are useful predictors of cholera epidemics, with the dynamics of endemic cholera being related to climate and/or changes in the aquatic ecosystem. When the ecology of V. cholerae is considered in predictive models, a robust early warning system for cholera in endemic regions of the world can be developed for public health planning and decision making.

Keywords: ecology, epidemiology, microbiology, remote sensing

Vibrio cholerae, a serious pathogen for humans, has been the subject of intense study for more than a century, yet the discovery that this bacterium is a natural inhabitant of riverine, estuarine, and coastal waters throughout both temperate and tropical regions of the world was made only relatively recently (1). Before the late 1970s, transmission of cholera was believed to occur exclusively by person-to-person contact, with epidemics initiated by contaminated water and food. In 1855, Sir John Snow hypothesized that devastating epidemics of cholera are caused by contaminated drinking water (2). In his time, the germ theory of disease had not been proven nor accepted and, obviously, it was not understood that the epidemic strain of V. cholerae was a bacterium naturally occurring in the aquatic environment (1, 3).

It is now recognized that V. cholerae is a component of coastal and estuarine microbial ecosystems, with the copepod species of zooplankton that comprise the aquatic fauna of rivers, bays, estuaries and the open ocean serving as host for the bacterium (4–7). V. cholerae can be found attached to the carapace and in the gut of copepods in large numbers, the copepod essentially serving as a vector for this human pathogen (1, 8, 9). A single copepod, for example, can contain as many as 103–105 V. cholerae cells (10). Because a concentration of 109 ml−1 V. cholerae comprises an infective dose, ingestion of untreated water containing a relatively small number of copepods carrying V. cholerae can initiate the disease (11). Therefore, conditions favorable for multiplication of copepods and related chitinous zooplankton species for which V. cholerae is commensal or symbiotic will result in an increase in the number of V. cholerae. The importance of copepods in cholera transmission was demonstrated in a study showing that the number of cholera cases in Bangladeshi villages was significantly reduced when a simple filtration method that effectively removed the plankton and particulate matter was used to treat drinking water (12, 13).

Another advance in understanding cholera epidemics was made with the discovery that the epidemics are significantly influenced by climatic factors (1, 13–17). Several environmental drivers of the seasonal cycle of cholera in India and Bangladesh where cholera is endemic have been identified (1, 18). Ocean surveillance by satellite remote sensing was used to monitor changes in sea surface temperature (SST) and sea surface height (SSH) in the Bay of Bengal. The pattern of changes in these parameters were shown to be related to V. cholerae dynamics in coastal, estuarine, and riverine waters of the Bay of Bengal and to the cholera epidemics caused by these bacteria in that region of the world (14). That is, the distinct seasonal pattern of cholera, in countries where the disease is endemic has been correlated with environmental factors and climate that drive both copepod population dynamics and the seasonal peaks in abundance of V. cholerae in the aquatic ecosystem of the Bay of Bengal. Given this relationship, it is concluded that the variables related to copepod population dynamics can serve as a proxy for the estimation of V. cholerae abundance in the environment.

Lobitz et al. (14) were the first to explore the now well recognized relationship between SST, SSH and cholera incidence using remote sensing, describing changes in coastal ecosystems significantly related to the annual cyclic pattern of cholera epidemics. Significant progress has since been made in modeling interannual variability of cholera epidemics in Bangladesh, employing mathematical models to reproduce the seasonal cycle of cholera (19, 20). In one such study, a significant correlation was found between selected environmental variables, namely precipitation, SST, and CHL, with cholera cases in a single epidemic during 2000–2001 in KwaZulu-Natal, South Africa (21). In that analysis, SST and CHL data were estimated from satellite sensor measurements, and a conclusive finding was that robust predictive associations require multiyear analyses (21).

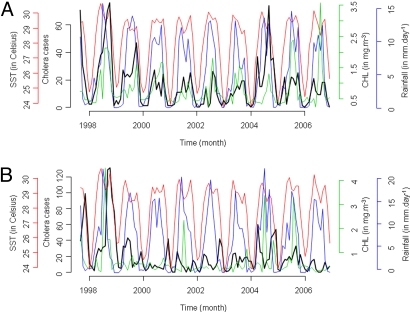
Here, we report on the association between selected environmental variables and confirmed cholera cases in two separate human populations resident in Kolkata, India, and Matlab, Bangladesh, in the northern Bay of Bengal, a marginal sea of the Indian Ocean (Fig. 1). Different satellite-derived data (CHL and SST) for the nearest coastal environment for each of the two geographical areas, and local rainfall during a nine year period (Fig. 2), September 1997–December 2006, for which all three environmental datasets were available, were analyzed. To determine which environmental signatures were associated with cholera epidemics in Kolkata and in Matlab, and to demonstrate the capacity to predict cholera, a historical approach was taken in modeling the relationship between the dynamics of the cholera epidemics and related environmental factors.

Fig. 1.

Fig. 1.

Open in a new tab

Map showing the region from which the environmental and epidemiological data were obtained. Locations for extraction of the monthly mean values for CHL and SST are indicated by (i) one degree resolution squares, orange for Kolkata (centered in 20.5N/88.5E) and white for Matlab (centered in 20.5N/90.5E), and for (ii) the five degree box average for both sites by the black solid line square (centered in 18.5N/89.5E). Locations where monthly mean rainfall values were obtained are indicated as follows: (i) two and half degree resolution points for Kolkata are delimited by a red dashed line square (centered in 23.75N/88.75E) and for Matlab by a red solid line square (centered in 23.75N/91.25E), and (ii) for the five degree box average for Kolkata by the yellow dashed line square (centered in 22.5N/87.5E) and for Matlab by the black dashed square (centered in 22.5N/90.0E). Background image represents the ground elevation coded from dark green, the lowest value, to white, the highest [The Global Land One-kilometer Base Elevation (GLOBE) NOAA, NGDC; (http://www.ngdc.noaa.gov/mgg/topo/globe.html); (48)].

Fig. 2.

Fig. 2.

Open in a new tab

Epidemiological and environmental dynamics for (A) Kolkata, India, and (B) Matlab, Bangladesh. The cholera cases, the CHL, the SST and the rainfall are shown in black, green, red and blue lines, respectively.

Results

For Kolkata, a positive relationship was observed between the number of cholera cases and CHL anomaly (CHLano) for both the single grid-point and the box-averaged values (see Materials and Methods and Fig. 1 for details). A 1 mg/m3 increase in monthly mean CHLano for the single grid-point value was associated with an increase of 32.5% [95% confidence interval (CI) = 8.3%–62.0%] in the number of cholera cases, after controlling for the annual cycle and the “persistence” effect arising from density dependence in cholera transmission.

The relationship described above for CHLano was also observed for the single grid-point value of rainfall anomaly (PREano) and the number of cholera cases in Kolkata. A 1 mm/day increase in monthly mean PREano was associated with an increase of 6.5% [95% CI = 1.6%–11.7%] in the number of cholera cases, after controlling for the annual cycle and the “persistence” effect.

The final model for Kolkata is

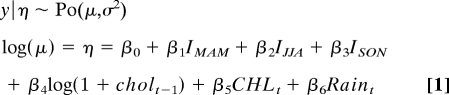graphic file with name zpq04608-5532-m01.jpg

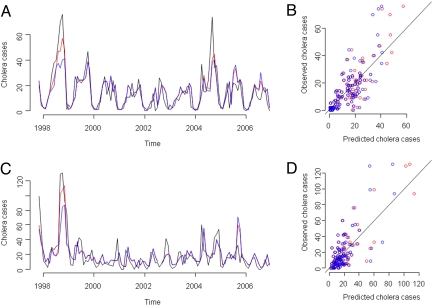
where coefficients are detailed in Table 1. Observed cholera case time-series and the prediction of both the fitted model and the fitted cross-validation model are displayed in Fig. 3A. The comparison of observed cholera cases against the prediction of the fitted models (Fig. 3B) shows that the cross-validation model tends to underestimate more of the highest values of cholera cases than the fitted model. The pseudo R2 value for the fitted model is equal to 88.17%.

Table 1.

Summary of the model obtained for Kolkata, India, and Matlab, Bangladesh

Model parameters
Intercept IMAM* IJJA* ISON* Log(cholt-1)* CHLt Raint CHLt-1 Df
Kolkata 103
Coefficient −0.264 1.597 1.524 1.476 0.578 0.281 0.063
P value 0.39 1.10−7 4.10−7 1.10−6 9.10−12 7.10−3 9.10−3
SE 0.31 0.28 0.28 0.29 0.07 0.10 0.02
Matlab 103
Coefficient 0.676 0.674 0.168 0.659 0.637 0.273
P value 2.10−2 2.10−3 0.44 9.10−4 2.10−14 5.10−4
SE 0.29 0.22 0.22 0.19 0.07 0.08
Open in a new tab

*As described in Materials and Methods, this parameter was maintained in the model without considering the P value.

Fig. 3.

Fig. 3.

Open in a new tab

Observed epidemiological data and prediction of fitted models. For Kolkata, (A) temporal dynamics of observed cholera cases, fitted model and cross-validation model shown in black, red and blue, respectively. (B) Scatterplot of observed cholera cases against (i) predicted cholera cases by fitted model in red circles, and (ii) predicted cholera cases by cross-validation model in blue circles. Black line represents perfect agreement between predicted and observed cases. For Matlab, C same as A. D same as B.

In contrast to CHLano, the PREano five degree grid box average was not retained in the model, suggesting that the major effects of precipitation occur locally rather than at a large scale, reflecting localized precipitation, even in a large scale monsoon system (22). SST was not retained in the model, either with the single grid point anomaly or with the five degree grid box average. It could be because of collinearity between the variables, most of the variance likely being already explained by CHLano and PREano.

For Matlab, a positive relationship was observed between number of cholera cases and the single grid-point data for CHLano, with a one month lag. A 1 mg/m3 increase in the monthly mean CHLano was related to the number of cholera cases increasing by 31.4% [95% CI = 13.0%–52.7%], after controlling for the annual cycle and the “persistence” arising from density dependence in cholera transmission. When the model was run using a five degree box for the averaged data, a positive relationship was observed between CHLano and the number of cholera cases. Upwelling occurs mainly along the coast of the Bay of Bengal, thus the five degree box yielded a significantly weakened coastal upwelling signal. As for Kolkata, SST was not retained in the model presumably because of the same reasons.

The final model for Matlab is

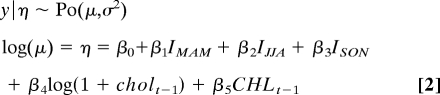graphic file with name zpq04608-5532-m02.jpg

where coefficients are detailed in Table 1. Observed cholera case time series and the prediction of both the fitted model, and the fitted cross-validation model are displayed in Fig. 3C. The contrast of observed cholera cases against the prediction of the fitted models (Fig. 3D) shows that the cross-validation model tends to underestimate more of the peak cholera case values than the fitted model, with both models overestimating the low number of cholera cases. The pseudo R2 value for the fitted model is equal to 71.46%.

Discussion

Environmental factors were found to be statistically significant in two different geographical locations of the Indian continent in directly influencing the dynamics of cholera epidemics. A relationship between the short time lag (one month), coincident environmental conditions, and cholera epidemics was observed. Interestingly, despite the geographical proximity of Kolkata and Matlab, the effect of the environmental variables examined in this study was clearly different. These regional differences strongly indicate an important effect of the local environment and local zooplankton populations on the dynamics of cholera epidemics.

Indeed for Kolkata, higher values of CHLano reflected the more intense algal blooms than normal that occurred and led to larger zooplankton populations that were comprised mainly of crustacean copepods, a natural aquatic host for V. cholerae (1, 8, 9). From the analyses of the Dhaka, Bangladesh data, it was concluded that the tidal intrusion of coastal water carrying plankton into inland water could initiate increased human contact with the cholera vibrio (14), because water used for daily hygiene, personal consumption, and religious rites (e.g., ablutions) in rural areas of Bangladesh and India is taken directly from local rivers or ponds essentially untreated (13, 23, 24). The relationship observed for PREano similarly reflects the effect of unusually heavy precipitation influencing cholera transmission by feeding surface runoff into streams and rivers flooding the water supply (15, 16). It also can have a direct role in cholera dynamics by increasing nutrient runoff, inducing river enrichment responsible for local algal blooms (25, 26). During intense rainfall events, the tidal intrusion of coastal water carrying plankton into inland water influencing cholera transmission may be minimized by the increase of the river flows. We concluded that both factors are influencing cholera transmission independently.

For Matlab, the relationship between number of cholera cases and CHLano was as expected. Matlab comprises a densely populated cluster of villages in a flat, low altitude region representing a dense, natural hydrological system intersected by the Dhanagona River and having a strong tidal influence. The relative proximity of Matlab to the coastal region of the Bay of Bengal can explain both the significant relationship of CHLano with cholera and the one month lag for Matlab, because Matlab lies further inland than Kolkata.

It is evident that each location requires a different model because of local or regional specificity. While CHL was determined to be important in influencing the dynamics of cholera epidemics in both locations within the same month or with one month lag, a longer lead time was found to be necessary for the environmental factors to be useful in predicting epidemics of cholera and give health workers time to formulate plans, disseminate warnings and recommendations to the public. Nevertheless, even a short lead time, at the submonthly time scale, can provide sufficient warning so that precautionary measures can be taken to save lives. In this context, the robust results obtained in this study indicate that increasing the lead time for prediction in dynamic or statistical regional climate and/or ocean forecast models, will provide a valuable tool for public health purposes. A functional model for an early warning system will require finer temporal resolution of acquired data, particularly for Kolkata where the relationship appears to be submonthly although most likely a data-limitation issue at present. For practical applications of these models, environmental as well as epidemiological data need to be collected and compiled expediently to provide useful and reliable predictions of the onset, epidemics, and trends of cholera based on environmental variability. The environmental variables related to cholera dynamics in this study, rainfall and CHL, as well as predictable phenomena, such as the Madden-Julian Oscillation, El Niño-Southern Oscillation, and the more recently proposed Indian Ocean Dipole/Zonal mode (27–31), clearly point to the potential for prediction of cholera with a significant lead time. A simple statistical model presented here that incorporates only local environmental conditions, nevertheless, yielded significant statistical association between cholera and selected environmental factors.

Obviously, not all of the variance in the number of cholera cases in each region can be explained by this method alone, because cholera epidemics involve a complex and critical interplay of intrinsic dynamics with extrinsic drivers (20). For example, cholera is no longer a disease threat for developed countries, including the United States, even though the presence of V. cholerae O1 in the waters of the Chesapeake Bay and coastal states of the Gulf of Mexico has long been known (32–34). Because good sanitation is practiced and safe drinking water is available to the populations of the region, cholera epidemics no longer occur. However, V. cholerae does remain as a naturally occurring inhabitant year round in those aquatic environments, with the same spring and fall peaks in number of the cholera bacteria, and a similar relationship with its copepod host (32, 35). The results of this study provide a foundation on which to build a predictive capacity for cholera epidemics, hence, an early warning system for enhancing public health measures, especially for developing countries and areas of the world undergoing social disruption or climate change. Better spatial resolutions of the satellite datasets as well as finer temporal resolution, i.e., ground based network stations, will improve our ability to predict cholera outbreaks. It will also allow a continued environmental data validation as well as alleviate the problem of missing satellite data because of clouds or other potential technical issues. Selected environmental factors serve effectively as indicators for cholera, but an integrative, mechanistic and interdisciplinary model combining satellite and ground observations will be required. The Aquarius (http://aquarius.gsfc.nasa.gov/index.php) satellite mission, designed to measure global sea surface salinity, to be launched in 2009, will provide additional useful information because salinity has a critical influence on the ecology of V. cholerae (15, 36–38).

Subseasonal-to-interannual time-scale operational forecast systems that employ statistical forecasting tools and combine local ecosystem, coastal, and ocean data, including SST, SSH, CHL, and zooplankton concentration, from mechanistic hydrodynamic and ecosystem modeling to analysis of climate parameters from coupled climate forecast models (rainfall, river runoff, air temperature, and humidity) may prove more useful for Kolkata, where time-resolved environmental parameters to obtain submonthly lead times are needed, compared with Bangladesh, where the environmental lead time appears to be longer.

A fully integrated model for cholera prediction that takes into account the demographic components of human populations exposed to endemic cholera and the complexity of cholera epidemiology, as well as climate, and the environment, ecology and the genomics of V. cholerae will continue to be a focus of our research. Interannual variability of cholera (15, 20, 39, 40) and the strong El Niño that occurred in 1998 were found to be associated with the largest number of cholera cases for both Kolkata and Matlab and offer challenging examples of cholera and climate interaction.

Materials and Methods

Data for Matlab, Bangladesh, and Kolkata, India, included in the analyses correspond to the monthly number of admitted patients for cholera symptoms individually confirmed by culture. The clinical specimens from which V. cholerae was isolated were from patients admitted either to the International Center for Diarrhoeal Diseases Research, Bangladesh (ICCDR, B) or to the Infectious Diseases Hospital of the National Institute of Cholera and Enteric Diseases (NICED) in Kolkata, India. Methods used for isolation and culture of V. cholerae have been reported elsewhere (41, 42). Additional computations detailed in supporting information (SI) Text showed no differences in using the monthly accumulation of cholera cases as a response variable in models instead of incidence.

Rainfall data used in the analyses were taken from the monthly merged satellite/gauge estimates of the Global Precipitation Climatology Project (GPCP) Version 2 (43). These data provide merged ocean/land estimates. Source of the monthly SSTs was Reynolds and Smith (44), generated from the NOAA Optimally Interpolated (v2) product provided by the National Climatic Data Center (www.ncdc.noaa.gov). CHL estimates were derived from the Sea-viewing Wide Field of View (SeaWiFS) sensor launched in 1997 (45), and provided by the NASA Goddard Distributed Active Archive Center (http://daac.gsfc.nasa.gov). CHL data are available by month from September, 1997 to the present. The spatial resolution of CHL and SST was a one degree grid and that for the rainfall data comprised a two-and-a-half degree grid. CHL and SST data were extracted from the measurements taken off the coast of the Bay of Bengal, whereas rainfall data (over land and ocean) were extracted coincident with the study locations (see Fig. 1). To evaluate potential differences at local or regional scale in the relationships between cholera cases and environmental variables, we also computed a five degree box-average for the environmental variables. For CHL and SST, it corresponds to the mean computed over a five by five square of data at one degree resolution, i.e., a mean of twenty five pixels (Fig. 1). For PRECIP, it corresponds to a parameter mean computed over a five by five square of data at two-and-half degree grid resolution, i.e., a mean of four pixels (Fig. 1). Because the three environmental datasets show a strong seasonal pattern (Fig. S1), anomalies were computed to remove the effect of the annual cycle, which can result in spurious relationships between cotrending variables. The anomalies were constructed by calculating the climatological mean for each month and subtracting these means from each corresponding month from the original data.

Environmental factors for the months preceding the cholera outbreaks proved to be important. That is, for CHL, phytoplankton biomass increases followed by an increase in the zooplankton population, the latter harboring V. cholerae, both associated with an increase in SST. This process, however, is not instantaneous and a lag time of one to two months was used for an increase in the V. cholerae population after the increase in SST and CHL had occurred. A time lag after precipitation is mechanistically justified because precipitation during months preceding a cholera outbreak feeds streams and rivers with surface runoff, thereby playing its unique role in the initiation of cholera outbreaks, especially when flooding occurs (15, 16). The chain of these climate events and their lead times provide the basis for prediction of cholera outbreaks, and were exploited to demonstrate feasibility of prediction, hence an early warning system.

There is a mechanistic basis for expecting up to two months lag for CHL, SST, and rainfall peaks in these drivers of cholera. A mechanistic approach allows translation of an empirical predictive understanding into quantitative prediction for cholera. To exploit the process empirically, variables included in the model were taken from both the coincident month and a one-month lag (t-1). CHL data also included a two-month lag (t-2). Indicator variables for quarterly means of cholera cases representing the annual cycle were included in the model as well as log number of cholera cases for the previous month. The latter is analogous to the differencing technique commonly used in an ordinary least squares linear regression (adapted for generalized linear models on a log scale), removing the “persistence” effect arising from density-dependence in cholera transmission (19). Both variables were included as fixed parameters in the models to remove residual autocorrelation.

A generalized linear model (GLM) with a Poisson distribution and a log link was used to model the data (46). As is common with such data, strong over-dispersion was apparent and was accommodated by using a quasi-Poisson GLM fitted using the R software package. This model estimates the degree of overdispersion and inflates standard errors accordingly. For the quasi-Poisson model, the constraint of equal mean and variance is relaxed so that the variance of the response is related to the mean μ by

graphic file with name zpq04608-5532-m03.jpg

where σ2 is the (constant) dispersion parameter. Our model for counts in the presence of overdispersion can thus be written as

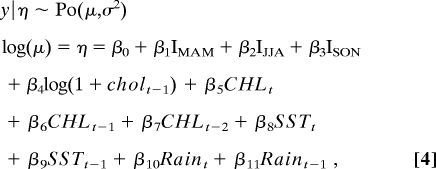graphic file with name zpq04608-5532-m04.jpg

where y represents the observed counts, η is the fitted model, Po represents the Poisson distribution, the βj are the model parameters, and IMAM, IJJA, and ISON represent the quarterly mean of cholera case index for March–April–May, June–July–August, and September–October–November, respectively and were used to remove any remaining annual cycle. Hypotheses of environmental factors driving cholera dynamics in the two locations was tested by using a 5% rejection range for significant variables. To evaluate the models computed on the whole dataset, cross-validations predictions were also made from the model by predicting cholera cases for each year using the final model structure, i.e., with only significant parameters, but estimating coefficients on the data set without data for the year under consideration. Then we assembled each predicted year to construct the cross-validation predictions for the whole period. The pseudo R2 proposed by (47) was used as a model diagnostic estimate adapted for quasi-Poisson model. Like the estimate of R2 commonly used for ordinary least squares linear regression, this statistical can be interpreted as the percentage of variability explained by the model.

SI.

Further information is available in SI Text and Fig. S2.

Supplementary Material

Supporting Information
supp_105_46_17676__index.html (590B, html)

Acknowledgments.

We thank the donor countries and agencies that provide unrestricted support to the International Centre for Diarrhoeal Disease Research, Bangladesh, for its operation and research; and the three referees for their constructive remarks and useful comments. This work was supported by National Oceanic and Atmospheric Administration Grant S0660009, Oceans and Human Health Initiative, and National Institutes of Health Grant 1 R01 AI39129.

Footnotes

The authors declare no conflict of interest.

This article contains supporting information online at www.pnas.org/cgi/content/full/0809654105/DCSupplemental.

References

  • 1.Colwell RR. Global climate and infectious disease: The cholera paradigm. Science. 1996;274:2025–2031. doi: 10.1126/science.274.5295.2025. [DOI] [PubMed] [Google Scholar]
  • 2.Snow J. On the Mode of Communication of Cholera. 2nd Ed. London: J. Churchill; 1855. pp. 1–162. [Google Scholar]
  • 3.Johnson S. The Ghost Map: The Story of London's Most Terrifying Epidemic–And How It Changed Science, Cities, and the Modern World. New York: Riverhead Books; 2006. p. 320. [Google Scholar]
  • 4.Colwell RR, Kaper J, Joseph SW. Vibrio cholerae, Vibrio parahaemolyticus, and other vibrios: Occurrence and distribution in Chesapeake Bay. Science. 1977;198:394–396. [PubMed] [Google Scholar]
  • 5.Huq A, et al. Ecological relationships between Vibrio cholerae and planktonic crustacean copepods. Appl Environ Microbiol. 1983;45:275–283. doi: 10.1128/aem.45.1.275-283.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Islam MS, Drasar BS, Sack RB. The aquatic flora and fauna as reservoirs of Vibrio cholerae: A review. J Diarr Dis Res. 1994;12:87–96. [PubMed] [Google Scholar]
  • 7.Kaper JB, Morris JG, Jr, Levine MM. Cholera. Clin Microbiol Rev. 1995;8:48–86. doi: 10.1128/cmr.8.1.48. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Nalin DR, Daya V, Reid A, Levine MM, Cisneros L. Adsorption and growth of Vibrio cholerae on chitin. Infect Immun. 1979;25:768–770. doi: 10.1128/iai.25.2.768-770.1979. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Rawlings TK, Ruiz GM, Colwell RR. Association of Vibrio cholerae O1 El Tor and O139 Bengal with the copepods Acartia tonsa and Eurytemora affinis. Appl Environ Microbiol. 2007;73:7926–7933. doi: 10.1128/AEM.01238-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Colwell RR, Spira WM. The ecology of Vibrio cholera. In: Barua D, Greenough WB, editors. Cholera. 3rd Ed. New York: Plenum Medical Book Co.; 1992. pp. 107–127. [Google Scholar]
  • 11.Cash RA, et al. Response of man to infection with Vibrio cholerae. I. Clinical, serologic, and bacteriologic responses to a known inoculum. J Infect Dis. 1974;129:45–52. doi: 10.1093/infdis/129.1.45. [DOI] [PubMed] [Google Scholar]
  • 12.Huq A, et al. A simple filtration method to remove plankton-associated Vibrio cholerae in raw water supplies in developing countries. Appl Environ Microbiol. 1996;62:2508–2512. doi: 10.1128/aem.62.7.2508-2512.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Colwell RR, et al. Reduction of cholera in Bangladeshi villages by simple filtration. Proc Natl Acad Sci USA. 2003;100:1051–1055. doi: 10.1073/pnas.0237386100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Lobitz B, et al. Climate and infectious disease: Use of remote sensing for detection of Vibrio cholerae by indirect measurement. Proc Natl Acad Sci USA. 2000;97:1438–1443. doi: 10.1073/pnas.97.4.1438. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Lipp EK, Huq A, Colwell RR. Effects of global climate on infectious disease: The cholera model. Clin Microbiol Rev. 2002;15:757–770. doi: 10.1128/CMR.15.4.757-770.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Pascual M, Bouma MJ, Dobson AP. Cholera and climate: Revisiting the quantitative evidence. Microbes Infect. 2002;4:237–245. doi: 10.1016/s1286-4579(01)01533-7. [DOI] [PubMed] [Google Scholar]
  • 17.Ruiz-Moreno D, Pascual M, Bouma M, Dobson A, Cash B. Cholera seasonality in Madras (1901–1940): Dual role for rainfall in endemic and epidemic regions. Ecohealth. 2007;4:52–62. [Google Scholar]
  • 18.Bouma MJ, Pascual M. Seasonal and interannual cycles of endemic cholera in Bengal 1891–1940 in relation to climate and geography. Hydrobiologia. 2001;460:147–156. [Google Scholar]
  • 19.Pascual M, Rodo X, Ellner SP, Colwell R, Bouma MJ. Cholera dynamics and El Nino-Southern Oscillation. Science. 2000;289:1766–1769. doi: 10.1126/science.289.5485.1766. [DOI] [PubMed] [Google Scholar]
  • 20.Koelle K, Rodo X, Pascual M, Yunus M, Mostafa G. Refractory periods and climate forcing in cholera dynamics. Nature. 2005;436:696–700. doi: 10.1038/nature03820. [DOI] [PubMed] [Google Scholar]
  • 21.Mendelsohn J, Dawson T. Climate and cholera in KwaZulu-Natal, South Africa: The role of environmental factors and implications for epidemic preparedness. Int J Hyg Environ Health. 2007;211:156–162. doi: 10.1016/j.ijheh.2006.12.002. [DOI] [PubMed] [Google Scholar]
  • 22.Goswami BN, Venugopal V, Sengupta D, Madhusoodanan MS, Xavier PK. Increasing trend of extreme rain events over India in a warming environment. Science. 2006;314:1442–1445. doi: 10.1126/science.1132027. [DOI] [PubMed] [Google Scholar]
  • 23.Huq A, et al. Critical factors influencing the occurrence of Vibrio cholerae in the environment of Bangladesh. Appl Environ Microbiol. 2005;71:4645–4654. doi: 10.1128/AEM.71.8.4645-4654.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Sack RB, et al. A 4-year study of the epidemiology of Vibrio cholerae in four rural areas of Bangladesh. J Infect Dis. 2003;187:96–101. doi: 10.1086/345865. [DOI] [PubMed] [Google Scholar]
  • 25.Rao DVS. Effects of environmental perturbations on short-term phytoplankton production off Lawsons-Bay, a tropical coastal embayment. Hydrobiologia. 1973;43:77–91. [Google Scholar]
  • 26.Valsaraj CP, Rao VNR. Nitrogen limitation in the tropical waters of the Bay of Bengal. Hydrobiologia. 1994;286:139–148. [Google Scholar]
  • 27.Chen D, Cane MA. El Nino prediction and predictability. J Computational Phys. 2008;227:3625–3640. [Google Scholar]
  • 28.Saji NH, Goswami BN, Vinayachandran PN, Yamagata T. A dipole mode in the tropical Indian Ocean. Nature. 1999;401:360–363. doi: 10.1038/43854. [DOI] [PubMed] [Google Scholar]
  • 29.Webster PJ, Moore AM, Loschnigg JP, Leben RR. Coupled ocean-atmosphere dynamics in the Indian Ocean during 1997–98. Nature. 1999;401:356–360. doi: 10.1038/43848. [DOI] [PubMed] [Google Scholar]
  • 30.Murtugudde R, McCreary JP, Busalacchi AJ. Oceanic processes associated with anomalous events in the Indian Ocean with relevance to 1997–1998. J Geophy Res Oceans. 2000;105:3295–3306. [Google Scholar]
  • 31.Waliser D, et al. The experimental MJO prediction project. Bull Amer Meteo Soc. 2006;87:425–431. [Google Scholar]
  • 32.Heidelberg JF, Heidelberg KB, Colwell RR. Seasonality of Chesapeake Bay bacterioplankton species. Appl Environ Microbiol. 2002;68:5488–5497. doi: 10.1128/AEM.68.11.5488-5497.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Louis VR, et al. Predictability of Vibrio cholerae in Chesapeake Bay. Appl Environ Microbiol. 2003;69:2773–2785. doi: 10.1128/AEM.69.5.2773-2785.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Castaneda Chavez Mdel R, Pardio Sedas V, Orrantia Borunda E, Lango Reynoso F. Influence of water temperature and salinity on seasonal occurrences of Vibrio cholerae and enteric bacteria in oyster-producing areas of Veracruz, Mexico. Mar Pollut Bull. 2005;50:1641–1648. doi: 10.1016/j.marpolbul.2005.06.036. [DOI] [PubMed] [Google Scholar]
  • 35.Heidelberg JF, Heidelberg KB, Colwell RR. Bacteria of the gamma-subclass Proteobacteria associated with zooplankton in Chesapeake Bay. Appl Environ Microbiol. 2002;68:5498–5507. doi: 10.1128/AEM.68.11.5498-5507.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Singleton FL, Attwell R, Jangi S, Colwell RR. Effects of temperature and salinity on Vibrio cholerae growth. Appl Environ Microbiol. 1982;44:1047–1058. doi: 10.1128/aem.44.5.1047-1058.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Huq A, West PA, Small EB, Huq MI, Colwell RR. Influence of water temperature, salinity, and pH on survival and growth of toxigenic Vibrio cholerae serovar O1 associated with live copepods in a laboratory microcosms. Appl Environ Microbiol. 1984;48:420–424. doi: 10.1128/aem.48.2.420-424.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Colwell RR. Viable but nonculturable bacteria: A survival strategy. J Infect Chemother. 2000;6:121–125. doi: 10.1007/pl00012151. [DOI] [PubMed] [Google Scholar]
  • 39.Constantin de Magny G, Guégan JF, Petit M, Cazelles B. Regional-scale climate-variability synchrony of cholera epidemics in West Africa. BMC Infect Dis. 2007;7:20. doi: 10.1186/1471-2334-7-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Constantin de Magny G, Cazelles B, Guégan JF. The cholera threat to humans in Ghana is influenced by both global and regional climatic variability. EcoHealth. 2006;3:223–231. [Google Scholar]
  • 41.Basu A, et al. Vibrio cholerae O139 in Calcutta, 1992–1998: Incidence, antibiograms, and genotypes. Emerg Infect Dis. 2000;6:139–147. doi: 10.3201/eid0602.000206. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Longini IM, Jr, et al. Epidemic and endemic cholera trends over a 33-year period in Bangladesh. J Infect Dis. 2002;186:246–251. doi: 10.1086/341206. [DOI] [PubMed] [Google Scholar]
  • 43.Adler RF, et al. The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979-Present) J Hydrometeo. 2003;4:1147–1167. doi: 10.3390/atmos9040138. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Reynolds RW, Rayner NA, Smith TM, Stokes DC, Wang WQ. An improved in situ and satellite SST analysis for climate. J Climate. 2002;15:1609–1625. [Google Scholar]
  • 45.McClain CR, et al. Science quality SeaWiFS data for global biosphere research. Sea Techn. 1998;39:10–16. [Google Scholar]
  • 46.McCullagh P, Nelder JA. Generalized linear models. 2nd Ed. Boca Raton: Chapman & Hall/CRC; 1998. p. xix.p. 511. [Google Scholar]
  • 47.Nagelkerke NJD. A note on a general definition of the coefficient of determination. Biometrika. 1991;78:691–692. [Google Scholar]
  • 48.Hastings DA, Dunbar Paula K., Elphingstone Gerald M., Bootz Mark, Murakami Hiroshi, Maruyama Hiroshi, Masaharu Hiroshi, Holland Peter, Payne John, Bryant Nevin A., Logan Thomas L., Muller J.-P., Schreier Gunter, MacDonald John S. GLOBE Task Team and others. National Oceanic and Atmospheric Administration, National Geophysical Data Center; 1999. The Global Land One-kilometer Base Elevation (GLOBE) Digital Elevation Model, Version 1.0. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_105_46_17676__index.html (590B, html)
0809654105_0809654105SI.pdf (399.2KB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES