A mathematical model of distal nephron acidification: diuretic effects

Abstract

Through their action on the distal nephron (DN), diuretics may produce systemic acid-base disturbances: metabolic alkalosis with thiazides or loop diuretics and metabolic acidosis with amiloride. Enhanced acid excretion may be due to a local effect on the diuretic target cell (a shift of Na⁺ reabsorption from NaCl transport to Na⁺/H⁺ exchange), or an effect at a distance: namely, increases in luminal fluid flow or luminal Na⁺ concentration may enhance more distal proton secretion. Both local and distance effects are supported by micropuncture data. In the present work, mathematical models of the distal convoluted tubule (DCT)/connecting tubule (CNT) (Weinstein AM, Am J Physiol Renal Physiol 289: F721–F741, 2005), and cortical and medullary collecting ducts (CD) (Weinstein AM, Am J Physiol Renal Physiol 283: F1237–F1251, 2002) have been concatenated to yield a model of rat DN. Among the segments of this DN, the DCT-CNT is responsible for the major portion of distal acidification. Predictions from the model calculations include the following. 1) With increasing distal Na⁺ delivery, there is little change in net acid excretion, but a shift in acidification locus from shared DCT and CNT contributions, to DCT prominence. 2) Urinary acidification by thiazides is primarily local (in the DCT) via the shift in Na⁺ reabsorption from NaCl cotransport to entry via NHE2. Increased NaCl delivery to the CNT increases β-cell HCO₃⁻ secretion, and thus blunts urine acidification. 3) In contrast to conclusions drawn from the isolated CD model, inclusion of the CNT now reproduces the observed distal acidification defect found with ENaC block, so that this action of amiloride appears to be sufficient to produce “voltage-dependent” distal renal tubular acidosis. 4) The effect of furosemide to enhance distal urinary acidification is not reproduced by the model without major upregulation of CNT α-cell transport, perhaps as a result of increased luminal flow.

concomitant with diuretic-induced natriuresis, there may be disturbances of acid-base metabolism: metabolic alkalosis with thiazides or loop diuretics and metabolic acidosis with amiloride (11). Indeed, beyond its being an inconvenient side effect, advantage is often taken of furosemide-enhanced acid excretion as a clinical test of renal acidification (2), alone or in concert with mineralocorticoid stimulation (18). A number of mechanisms have been advanced to rationalize diuretic-enhancement of net acid excretion. One possibility is the local effect on the diuretic target cell: for both ascending Henle limb (AHL) and distal convoluted tubule (DCT), the NaCl entry transporter sits within the luminal membrane in parallel with a Na⁺/H⁺ exchanger (NHE); inhibition of NaCl entry depresses cytosolic Na⁺, thus enhancing NHE flux, and with it, luminal acidification. Another possibility is an effect at a distance: namely, increases in luminal fluid flow or luminal Na⁺ concentration increase more distal reabsorption of Na⁺ (15), and this may enhance proton secretion. Both local and distal enhancement of acidification are supported by micropuncture data (7). Beyond such tubular events, thiazides or loop diuretics can produce volume depletion, hyperaldosteronism, and hypokalemia, which all augment distal proton secretion. Amiloride acts to block channel-mediated distal Na⁺ reabsorption and has been used as an experimental model of distal renal tubular acidosis in the rat. This classic observation was thought to implicate the distal nephron (DN) epithelial Na⁺ channel (ENaC) function as necessary for normal acid excretion. More recently, the precise location of the requisite ENaC has been addressed with the observation that ENaC knockout in cortical and medullary collecting ducts does not impair urine acidification (8). This prompted the indirect conclusion that intact connecting tubule function is sufficient for normal urinary acidification.

Mathematical models had been developed for rat cortical, outer medullary, and inner medullary collecting duct segments (CCD, OMCD, and IMCD, respectively), and acid excretion by these tubules in series has been examined in a model of a full collecting duct system (20, 21, 22). The model components were scaled to whole-kidney anatomy so that model output could be directly compared with ureteral urine flow and composition. Observations from that study included the prediction that increases in CD tubular flow would act to simultaneously increase urine HCO₃⁻ and NH₄⁺, leaving net acid excretion relatively unperturbed. An attempt was made to use that model to simulate the putative defects of distal renal tubular acidosis (DRTA), but it was found that isolated ENaC inhibition along the CD had a negligible impact on acidification. This result provided no support for the “voltage-dependent” DRTA, and called attention to other tubular effects of amiloride (on ATPases) that might have contributed to the acidification defect. Since that work, models of rat DCT and connecting segment (CNT) have been developed and examined in series in a study of K⁺ secretion (23, 24). In the present work, the DCT-CNT and CD models are conjoined to yield a mathematical model of rat DN, and the focus is on urinary acidification. The model displays the components of net acid excretion within each tubule segment in the context of the DN and thus provides a tool for estimating both the local diuretic action plus the effect at a distance. In this model, both the DCT and CNT are revealed as the dominant sites for acidification, depending on urine Na⁺ concentration. Once the CNT effect is included in the amiloride simulation, the possibility of an amiloride-induced DRTA is captured by the model. The action of furosemide, however, to increase net acid excretion remains enigmatic.

MODEL FORMULATION

Figure 1 displays a schematic of the model DN: 36,000 DCT (all 1 mm in length) lead to the CNT, which coalesce over 2 mm to 7,200 CCD (2 mm in length), then 7,200 OMCD (2 mm in length), and finally the IMCD, which coalesce over 5 mm to 113 papillary collecting ducts emptying into the renal pelvis. The DCT shown here is identical to the published model (23). The prior DCT-CNT model (24) had a CNT that was a straight cylinder 1 mm in length. In the present model, the coalescing of CNT segments is represented as tubules of constant radius, for which the aggregate circumference and area decline exponentially according to the formula

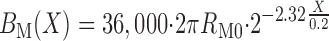(1)

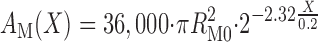(2)

Fig. 1.

Schematic of distal nephron (DN), consisting of a 1-mm distal convoluted tubule (DCT), 2-mm connecting tubule (CNT), 2-mm cortical collecting duct (CCD), 2-mm outer medullary collecting duct (OMCD), and 5-mm inner medullary collecting duct (IMCD). Within the CNT, the 36,000 tubules coalesce to form 7,200 CCD. Within the IMCD, the tubules coalesce exponentially so that final urine flows through only 113 papillary collecting ducts.

In Eq. 1, X is the distance along the CNT, ranging from 0.0 to 0.2 cm, B_M and A_M are CNT circumference and area, R_M0 is the tubule radius, and the factor 2.32 is chosen to yield the 80% reduction in tubule number at X = 0.2 cm. Parenthetically,

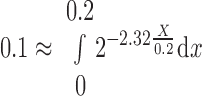so that the total luminal surface area within this coalescing 2-mm CNT system is nearly identical to that of the 36,000 CNT (all 1 mm in length) in the prior model (24). Thus, by using the same CNT transport parameters as those previously published, overall CNT transport will be comparable with that of the published model. With respect to CCD parameters, only three changes were made from prior values (20). In this DN model, fluid delivered to the CCD is more dilute than had been previously assumed, and this tended to swell the principal cells. Accordingly, principal cell peritubular P_f has been increased by a factor of 3. The dilute luminal solution also increased tight junction electrical resistance, so in this model, all tight junction permeabilities have been increased by a factor of 2. Finally, the presence of a relatively large luminal acid disequilibrium pH, imported from the CNT, acts to decrease α-intercalated cell proton secretion, thus depolarizing the cell, and increasing cell Cl⁻ and cell volume. This was remedied by decreasing the density of the peritubular Cl⁻/HCO₃⁻ exchanger (AE1) to 20% of its original value in CCD α-cells. With respect to the method of solving the model equations, the CCD in the past had used a centered difference scheme, but in the context as a DN component, this scheme produced oscillations. In the present model, the CCD equations are solved using a first-order backward scheme, so that with 80 mesh points for the 2-mm CCD, the fourth decimal place for luminal Na⁺ concentration is accurate. All OMCD and IMCD parameters are unchanged from the prior model (20).

MODEL CALCULATIONS

Table 1 displays the luminal and peritubular composition assumed for the baseline condition of the model DN. With the exception of a slightly higher Pco₂ (50 mmHg, rather than 40 mmHg), these are the same perfusion conditions as used previously (23). For a luminal flow of 6 nl/min (and an assumed single nephron glomerular filtration rate of 30 nl/min), 20% of filtered fluid reaches this point of the nephron. Thus, just under 10% of the filtered load of the important electrolytes (Na⁺, K⁺, Cl⁻, and HCO₃⁻) reaches the start of the DN. About 30% of filtered phosphate is present; with a luminal pH comparable to the pK of phosphate; this is ∼6.8 pmol/min of titratable acid (0.24 μmol/min for the 36,000 nephron DN). The peritubular conditions are those that have been used previously (20), modified with a more realistic renal venous NH₄⁺ concentration (0.2 mM, decreased from 1.0 mM) (23), and a slightly lower blood phosphate concentration (26). These conditions are intended to suggest a mildly antidiuretic kidney with substantial Na⁺ excretion (as might be encountered in a micropuncture experiment); the solution of the model equations is displayed in Figs. 2 and 3, and numerical results are in Table 2. In Fig. 2, the abscissa for all panels is distance along the DN; on the left are intensive variables: lumen PD (mV), and the concentrations of Na⁺, K⁺, and Cl⁻ (mM); on the right are axial flows of volume (μl/min), and Na⁺, K⁺, and Cl⁻ (μmol/min) for the ensemble of DN tubules at any given level. The figure indicates that most DN Na⁺ reabsorption occurs in the cortex, in DCT and CNT, with a minor contribution by IMCD. With reference to Table 2, DCT, CNT, and IMCD all reabsorb ∼40% of the Na⁺ delivered to those segments, while relative to the entering DN load, Na⁺ reabsorption by these segments is 40, 25, and 15%, respectively. Of note, Na⁺ entering the CCD is 4.8 μmol/min, compared with 3.8 μmol/min, which had been assumed for the CD model (20). K⁺ secretion is primarily a CNT phenomenon and amounts to over four times the entering DN K⁺ load. The CCD K⁺ concentration is ∼37 mM, a value that shuts off additional secretion by this segment. In this model, CCD K⁺ delivery is 2.8 μmol/min, about twice the value in the prior CD model (1.3 μmol/min). Over the remainder of the CD, the increase in luminal K⁺ concentration drives diffusive K⁺ reabsorption, and this reabsorption is augmented by H-K-ATPase activity. Overall, K⁺ excretion is 1.3 μmol/min, so that about half of the secreted K⁺ is reabsorbed before the final urine, an amount consistent with the micropuncture observations of Malnic et al. (9).

Table 1.

Luminal and peritubular composition

	Luminal Fluid			Peritubular Interstitium
	Concentration, mM	Delivered Load,a μmol/min	% Filtrateb	Cortex, mM	OIMJ,c mM	Papillary Tip, mM
Na+	65.0	14.04	9.0	144.0	284.0	284.0
K+	2.0	0.43	8.0	5.0	10.0	20.0
Cl−	56.1	12.12	9.4	119.6	266.0	280.9
HCO3−	8.0	1.73	6.4	25.0	25.0	25.0
H2CO3, μM	4.4			4.4	4.4	4.4
CO2	1.5			1.5	1.5	1.5
HPO42−	2.1			2.0	3.0	3.0
H2PO4−	1.9			0.6	0.9	0.9
Total PO4	4.0	0.86	30.8	2.6	3.9	3.9
Urea	30.0	6.48	120.0	5.0	20.0	500.0
NH3, μM	15.1			2.9	58.0	131.4
NH4+	3.2	0.69	320.0	0.2	3.9	8.8
pH	6.828			7.323	7.323	7.323
Imp	0.0			2.0	2.0	2.0
Osm	169.8			304.9	616	1126

^aAssumes distal flow = 6 nl·min⁻¹·tubule⁻¹ = 216 μl/min for distal convoluted tubule (DCT).

^bAssumes cortical blood concentrations and glomerular filtration rate = 30 nl/min = 1,080 μl/min for DCT.

^cOuter-inner medullary junction.

Fig. 2.

DN electrolyte transport under baseline conditions. The abcissa for all panels is distance along the DN (cm), and elongated tic marks denote boundaries of the DCT, CNT, CCD, OMCD, and IMCD. Panels on the left include transepithelial potential difference (PD), and the lumen concentrations of Na⁺, K⁺, and Cl⁻ on the right are axial flows of volume (μl/min) and solutes (μmol/min) for the whole ensemble of nephrons.

Fig. 3.

DN acid/base transport under baseline conditions. The abcissa for all panels is distance along the DN (cm), and elongated tic marks denote boundaries of the DCT, CNT, CCD, OMCD, and IMCD. Panels on the left include lumen pH and the concentrations of HCO₃⁻, titratable acid (TA), and NH₄⁺; on the right are axial flows of these species for the nephron ensemble. Net acid flow is the sum of TA and NH₄⁺, less HCO₃⁻ flow.

Table 2.

DN solute transport under baseline conditions (entering flow = 6 nl/min, Na⁺ = 65, K⁺ = 2.0, HCO₃⁻ = 8.0)

	DCT	CNT	CCD	OMCD	IMCD	Total
Absolute delivery, μmol/min
Na+	14.04	8.42	4.79	4.57	5.37	3.22
K+	0.43	0.80	2.70	2.53	1.92	1.30
Cl−	12.12	8.02	6.42	5.94	6.42	3.96
HCO3−	1.73	0.79	0.64	0.50	0.31	0.09
TA	0.24	0.48	0.60	0.42	0.41	0.41
NH4+	0.68	0.66	0.49	0.42	0.51	0.53
Net acid	−0.80	0.35	0.45	0.34	0.60	0.85
Absolute reabsorption, μmol/min
Na+	5.62	3.63	0.22	−0.80	2.15	10.82
K+	−0.37	−1.90	0.17	0.60	0.62	−0.87
Cl−	4.10	1.60	0.48	−0.47	2.46	8.16
HCO3−	0.94	0.15	0.14	0.19	0.22	1.64
TA	−0.23	−0.12	0.18	0.02	−0.00	−0.17
NH4+	0.02	0.18	0.06	−0.09	−0.02	0.16
Net acid	1.15	0.10	−0.10	0.26	0.25	1.65

DN, distal nephron; CNT, connecting tubule; CCD, cortical collecting duct; OMCD, outer medullary duct; IMCD, inner medullary collecting duct; TA, titratable acid.

Acid-base transport by the model DN is displayed in Figs. 3 and 4. The abscissa of Fig. 3 is distance along the nephron; intensive variables are in the left panels, flows on the right. HCO₃⁻ is reabsorbed along the entire DN, with over half in the DCT and ∼10% in each of the remaining segments. Lumen pH falls promptly in the DCT from 6.8 to 6.3 and then in the CNT to 5.8, due to a disequilibrium pH of 0.6 units. Along the remainder of the DN, the disequilibrium pH is <0.2 units and declines over distance, so that lumen pH is stable at 6.3. The flows of both titratable acid (TA) and NH₄⁺ are nearly constant over the DN, and each contributes a relatively equal portion to net acid flow. By the end of DN, net acid excretion is 0.85 μmol/min (0.53 from NH₄⁺ and 0.41 from TA, less 0.09 HCO₃⁻ excretion). The components of urinary acidification along the DN are displayed in Fig. 4, where the ordinate is μmol/min. The first set of four bars, from left to right, represents DN delivery of HCO₃⁻, TA, NH₄⁺, and net acid (TA+NH₄⁺ − HCO₃⁻ = −0.80 μmol/min). Each of the following five sets of bars depicts the contribution of each of the nephron segments to urinary acidification (with increases in acid excretion plotted as positive): segmental HCO₃⁻ reabsorption, segmental TA exit less TA delivery, segmental NH₄⁺ exit less NH₄⁺ delivery, and segmental net acid exit less net acid delivery. The final set of bars shows DN excretion of HCO₃⁻, TA, NH₄⁺, and net acid. The utility of this figure is the easy appreciation of the relative contribution of each segment to overall DN acid secretion (1.65 μmol/min), and it is clear that for these baseline conditions, DCT is most important.

Fig. 4.

DN acid/base transport under baseline conditions. For the calculations of Fig. 3, segmental contributions to urinary acidification are displayed (μmol/min). Each set of 4 bars includes (from left to right) flows or fluxes of HCO₃⁻ (open bars), of TA (left hatched bars), of NH₄⁺ (right hatched bars), and of net acid (crosshatched bars). The first set of bars shows DN delivery of acid/base species; the next 5 are segmental reabsorption and secretion; and the last set shows excretory flows. The convention is that positive values are additions to net acid excretion, HCO₃⁻ reabsorption, or secretion of TA or NH₄⁺; negative values correspond to HCO₃⁻ flow or secretion, or reabsorptive fluxes of TA or NH₄⁺. Starting with the bars on the left, the cumulative effect of the middle 5 sets of bars yields the set of bars on the right.

In view of the generous Na⁺ inflow at baseline, it is important to examine the impact of Na⁺ delivery on DN acidification. Table 3 and Fig. 5 display the extremes of inlet Na⁺ concentration (as addition or subtraction of NaCl), with no change in other solute concentrations or in the inlet volume flow of 6 nl/min. When inlet Na⁺ is 25 mM, delivery is 5.4 μmol/min and excretion falls to 0.42 μmol/min; at this flow rate, distal K⁺ excretion is severely compromised and falls to 0.17 μmol/min. When inlet Na⁺ is 135 mM, Na⁺ and K⁺ excretion are 14.8 and 2.7 μmol/min, respectively, so that K⁺ excretion varies over the full range of Na⁺ delivery. DN acidification is shown in Fig. 5, which has the same bar graph format as Fig. 4. In the top panel, inlet Na⁺ is 25 mM, and the pattern has changed from Fig. 4, insofar as the major contributions to acidification are now shared between the DCT and CNT. (With the decrease in luminal Na⁺, there is diminished Na⁺/H⁺ exchange in the DCT.) By the DN terminus, all HCO₃⁻ is gone (with urine pH 5.44); however, NH₄⁺ excretion is also diminished, due to increased cortical reabsorption. (Increased water removal increases cortical ammonia concentrations, favoring reabsorptive flux.) Overall, compared with baseline, low Na⁺ delivery produces only mild reductions in net acid excretion (0.67 μmol/min) and overall DN acid secretion (1.47 μmol/min). When inlet Na⁺ is high, almost all DN acid secretion occurs in the DCT, and in this case the CNT actually becomes a base secretor by virtue of β-intercalated cell Cl⁻/HCO₃⁻ exchange. With higher luminal flows, both bicarbonaturia and NH₄⁺ excretion are enhanced, so that overall net acid excretion and DN acid secretion are only mildly increased from baseline, 0.99 and 1.79 μmol/min, respectively. In sum, over the 5.4-fold increase in DN Na⁺ delivery, K⁺ excretion increases 16-fold, but net acid excretion increases only 45%, corresponding to a 22% increase in DN acid secretion. With respect to acidification, changes in Na⁺ delivery and axial fluid flow tend to affect both HCO₃⁻ and NH₄⁺ excretion in parallel, with each opposing the effect of the other on net acid excretion. This observation had been made previously, examining the CD in isolation (20).

Fig. 5.

DN acid/base transport with variation in DCT delivery of NaCl. The top panel summarizes urinary acidification when luminal Na⁺ is reduced (from 65 mM) to 25 mM, and for the bottom panel luminal Na⁺ was 135 mM. The significance of each bar is as in Fig. 4, with each set showing fluxes of HCO₃⁻, TA, NH₄⁺, and net acid, and with positive deflections denoting increases in urinary acidification.

To simulate the effect of hydrochlorothiazide (HCTZ) on DN function, baseline perfusion conditions were used, and the density of the NaCl cotransporter in the DCT was reduced to 1% of its value. It should be emphasized that this is a simulation of acute diuretic administration and does not attempt to represent the adaptive changes that accrue with prolonged use. The results are summarized in Table 4 and Fig. 6. In the model, the impact of HCTZ on Na⁺ transport is a reduction in DCT reabsorption from 40 to 15% of delivered load, only a modest compensatory increase in the CNT, from 26 to 30%, and virtually no change more distally. Overall, Na⁺ excretion nearly doubles from 3.2 to 5.8 μmol/min. The increase in CNT Na⁺ reabsorption enhances K⁺ secretion by this segment, and the increase in axial flow along the CD blunts K⁺ reabsorption along the remainder of the DN. Overall, K⁺ excretion increases from 1.3 to 1.8 μmol/min. The predicted impact on acid-base transport is shown in Fig. 6, where the most striking change is the increase in proton secretion by the DCT. This is manifest as an increase in HCO₃⁻ reabsorption from 0.94 to 1.44 μmol/min, an increase in TA secretion from 0.23 to 0.36 μmol/min, and even a shift from NH₄⁺ reabsorption (0.02 μmol/min) to secretion (0.04 μmol/min). In sum, DCT net acid secretion increases from 1.15 to 1.85 μmol/min. This increase in urine acidification is blunted as a consequence of increased CNT Cl⁻ delivery, which drives β-cell HCO₃⁻ secretion, turning the CNT from an acid-secreting to a base-secreting segment (0.10 to −0.35 μmol/min). In the remainder of the CD, acid-base fluxes following HCTZ are comparable to baseline (Fig. 4). Overall, DN acid excretion increases modestly, from 0.85 to 1.07 μmol/min, corresponding to an increase in DN acid secretion from 1.65 to 1.87 μmol/min.

Table 4.

DN solute transport with a thiazide (entering flow = 6 nl/min, Na⁺ = 65, K⁺ =2.0, HCO₃⁻ = 8.0)

	DCT	CNT	CCD	OMCD	IMCD	Total
Absolute delivery, μmol/min
Na+	14.04	11.90	7.68	7.33	8.05	5.81
K+	0.43	0.84	3.04	2.94	2.38	1.83
Cl−	12.12	12.24	9.90	9.34	9.75	7.26
HCO3−	1.73	0.29	0.50	0.44	0.31	0.12
TA	0.24	0.60	0.62	0.46	0.45	0.47
NH4+	0.68	0.73	0.58	0.55	0.68	0.72
Net acid	−0.80	1.05	0.70	0.57	0.81	1.07
Absolute reabsorption, μmol/min
Na+	2.14	4.22	0.35	−0.71	2.23	8.23
K+	−0.41	−2.20	0.10	0.56	0.55	−1.40
Cl−	−0.12	2.33	0.57	−0.41	2.48	4.85
HCO3−	1.44	−0.21	0.06	0.13	0.19	1.61
TA	−0.36	−0.02	0.16	0.02	−0.02	−0.23
NH4+	−0.04	0.15	0.03	−0.13	−0.05	−0.04
Net acid	1.85	−0.35	−0.13	0.24	0.26	1.87

Fig. 6.

DN acid/base transport with application of a thiazide. Using baseline conditions for DCT delivery and peritubular solute concentrations, DCT NaCl cotransport has been reduced by 99%. The significance of each bar is as in Fig. 4, with each set showing fluxes of HCO₃⁻, TA, NH₄⁺, and net acid, and with positive deflections denoting increases in urinary acidification.

Table 5 and Figs. 7 and 8 simulate the DN under acidosis, with and without the presence of amiloride. Metabolic acidosis has been represented as a halving of initial luminal and peritubular HCO₃⁻ from 8 and 25 to 4 and 12 mM, along with a decrease in ambient CO₂ from 1.5 (Pco₂ = 50 mmHg) to 1.1 mM (Pco₂ = 37 mmHg). It must be acknowledged that in this simulation, there has been no attempt to represent associated adaptive changes (e.g., enhanced delivery of phosphate and ammonium to DN). With acidosis, there is no significant change in DN Na⁺ transport (reabsorption of 10.5 μmol/min, compared with 10.8 in control), and only a minor increase in overall K⁺ secretion from 0.87 to 0.95 μmol/min, due entirely to an increase in CNT K⁺ transport. With acidosis, entering acid flow is 0.15 μmol/min and net acid excretion is 1.17 μmol/min, so that compared with baseline, there is enhanced acid excretion but overall decreased proton secretion along the DN. With regard to the top panel of Fig. 7, the decrease in DN acidification is due to a blunting of proton secretion in the DCT along with a small HCO₃⁻ secretory flux in the CNT. NH₄⁺ excretion is identical to baseline, so that the overall increase in net acid excretion is achieved by increasing TA, while eliminating the small amount of urinary HCO₃⁻. In Fig. 8, the left panels show the tubule fluid pH and the concentrations of HCO₃⁻, TA, and NH₄⁺ and may be compared with the panels in Fig. 3. In acidosis, the lower luminal HCO₃⁻ is sufficiently low that even with water reabsorption in the CNT, luminal HCO₃⁻ concentration remains <4 mM and can start to decrease in the OMCD. In the IMCD, the lumen is cleared of HCO₃⁻, and the pH can fall to its limiting value (pH = 3.76); TA and NH₄⁺ concentrations increase to ∼30 mM each, due to water abstraction, and with a final urine flow of 20 μl/min, each contributes ∼0.6 μmol/min to net acid excretion.

Fig. 7.

DN acid/base transport during metabolic acidosis (top) and with application of amiloride (bottom). Acidosis corresponds to a decrease in peritubular HCO₃⁻ from 25 to 12 mM, a decrease in luminal HCO₃⁻ from 8 to 4 mM, and a decrease in ambient CO₂ from 1.2 to 1.1 mM. These conditions apply to the calculations of both the top and bottom panels. Application of amiloride corresponds to a 99% reduction in the permeability of luminal Na⁺ entry channels in athe CNT, CCD, and IMCD. The significance of each bar is as in Fig. 4, with each set showing fluxes of HCO₃⁻, TA, NH₄⁺, and net acid, and with positive deflections denoting increases in urinary acidification. The striking finding is the decrement to net acid flow within the CNT.

Fig. 8.

DN acid/base transport during metabolic acidosis (left) and with application of amiloride (right). For the calculations of Fig. 7, the luminal pH and concentrations of HCO₃⁻, TA, and NH₄⁺ are displayed as a function of distance along the DN. With application of amiloride, there is increased tubule fluid pH along the entire DN, and a decrease in all 3 components of net acid excretion.

To simulate amiloride, luminal membrane Na⁺ permeabilities of the CNT, CCD, and IMCD were all reduced to 1% of their baseline values (along with a comparable reduction in IMCD luminal K⁺ permeability, recognizing that the IMCD luminal membrane Na⁺ channel is a nonselective cation channel). With these parameter changes, final urine flow increased to 30 μl/min, Na⁺ reabsorption decreased to 6.4 μmol/min, and Na⁺ excretion approximately doubled, to 7.7 μmol/min (Table 5). In the absence of CNT Na⁺ reabsorption, CNT K⁺ secretion ceases and becomes reabsorptive due to the action of the luminal H⁺-K⁺-ATPase in α-intercalated cells. Overall, DN K⁺ transport becomes reabsorptive, 0.39 μmol/min, and urinary K⁺ excretion is virtually abolished (0.04 μmol/min, compared with 1.39 under acidotic control). With respect to acid/base transport, it is apparent from Fig. 7 that the major impact of amiloride on urinary acidification is in the CNT, where the small HCO₃⁻ secretory flux increases (from −0.07 to −0.33 μmol/min), as does the small reabsorptive NH₄⁺ flux (from 0.19 to 0.30 μmol/min), so that net base secretion by CNT increases from −0.18 to −0.59 μmol/min. Acid/base transport in the remaining CD segments appears relatively unaltered. Overall, DN proton secretion is decreased from 1.01 to 0.68 μmol/min, and net acid excretion falls to 0.83 μmol/min. Although the effect of amiloride on acid excretion does not seem large, the impact on luminal pH is striking (Fig. 8). With amiloride, there is increased HCO₃⁻ delivery to the OMCD, so that with water reabsorption, there is an increase in OMCD HCO₃⁻ concentration. The HCO₃⁻ load delivered to the IMCD is thus too great to be completely cleared, and lumen pH remains above 6.2. This would be interpreted as a distal renal tubular acidosis, and it stands in contrast to the calculations using only the model CD, in which the impact of amiloride on CNT function was not included (22).

Compared with baseline conditions, application of furosemide produces a sharp increase in early DCT luminal Na⁺ concentration (nearly that of plasma Na⁺), an increase in luminal K⁺, and a decrease in luminal pH (7). In the model simulation of furosemide administration, entering Na⁺ has been increased to 135 mM (along with an increase in Cl⁻), entering K⁺ has been increased to 8 mM, and entering HCO₃⁻ is decreased to 4 mM. In contrast to the simulation of metabolic acidosis, peritubular HCO₃⁻ and CO₂ remain at their baseline values, 25 and 1.5 mM, respectively. Table 6 and Figs. 9 and 10 display the results of these calculations. Compared with acidosis, Na⁺ delivery has increased from 14.0 to 29.2 μmol/min, and DN Na⁺ reabsorption increases from 10.5 to 13.2 μmol/min, a decline in fractional reabsorption from 75 to 45%. Compared with acidosis, K⁺ delivery has increased from 0.43 to 1.73 μmol/min, secretion has increased from 0.95 to 1.43 μmol/min, and excretion has increased from 1.39 to 3.16 μmol/min. Both the increase in Na⁺ reabsorption and the dilution of luminal K⁺ contribute to this enhanced K⁺ secretion. Net acid delivery is 0.21 μmol/min, and overall net acid excretion is 1.09 μmol/min, slightly less than in the case of metabolic acidosis (1.16 μmol/min). The difference between these two conditions can be seen by comparing Figs. 7 and 9: Entering profiles are identical, and the transport patterns of the DCT are nearly identical. The major difference is in the CNT, where the high luminal NaCl with furosemide drives substantial HCO₃⁻ secretion. Transport differences are relatively small throughout the remainder of the CD. The most striking differences between acidosis and furosemide appear in comparison of Figs. 8 and 10, showing luminal acid/base profiles. In the case of furosemide, CNT HCO₃⁻ secretion increases HCO₃⁻ concentration in the CCD, OMCD, and into the IMCD, so that the luminal pH is never <5.5 and end-luminal pH is 6.23.

Fig. 9.

DN acid/base transport with application of furosemide (top) and with furosemide plus a 3-fold increase in α-cell transport in the CNT, CCD, and OMCD (bottom). Peritubular conditions are those of baseline, but the DCT-entering Na⁺ and K⁺ have been increased to 135 and 8 mM, and HCO₃⁻ concentration has been reduced to 4 mM. The significance of each bar is as Fig. 4, with each set showing fluxes of HCO₃⁻, TA, NH₄⁺, and net acid, and with positive deflections denoting increases in urinary acidification. In the top panel, furosemide has produced a decrease in net acid flow, localized primarily to the CNT; the bottom panel shows that this was reversed by CNT α-cell activity, and net acid excretion is augmented in the OMCD.

Fig. 10.

DN acid/base transport with furosemide, and with furosemide plus increased α-cell transport. For the calculations of Fig. 9, the luminal pH and concentrations of HCO₃⁻, TA, and NH₄⁺ are displayed as a function of distance along the DN. With application of furosemide, the increase in CNT HCO₃⁻ propagates along the remainder of the nephron. The increase in α-cell transport is just sufficient to overcome this base secretion.

This high urinary pH with furosemide is contrary to observation (pH = 5.16) (7), so one must ask what in the model formulation can be amended to obtain more congruence with the data. Table 7 displays the net acid excretion, net acid secretion, and end-luminal pH from a number of attempts to achieve suitable urinary acidification. With a decrease in DCT entering HCO₃⁻ concentration from 4.0 to 2.0 mM, there is still ample HCO₃⁻ secretion by CNT β-cells that end-luminal pH is little different. Increasing entering TA increases net acid excretion, and to some extent promotes proton secretion, but does little to acidify the final urine. It is known that CCD principal cells respond to increases in flow, with increases in Na⁺ reabsorption and K⁺ secretion (15). Conceivably, if principal cell transport were activated by furosemide-induced flow increases, it could hyperpolarize the epithelium, and thus enhance proton secretion. However, when all transport components of principal cells of both CNT and CCD were doubled (doubling CNT and CCD Na⁺ fluxes), there was little change in proton secretion, and end-luminal pH remained high. (Of note, even when there is flow stimulation of CCD Na⁺ reabsorption, the epithelium is not hyperpolarized.) (10). There is no experimental basis on which to suppose that increases in luminal flow, or that of furosemide itself, would act to suppress β-cell activity. Nevertheless, reducing β-cell transport components to 10% of their baseline value does increase acidification by 50% and produces an end-luminal pH that comes closer to observation. A comparable increase in urinary acidification can be achieved by increasing α-intercalated cell transport to 200% of baseline in the CNT, CCD, and OMCD (with or without a comparable increase in principal cell transport). However, with β-cells intact, this scaling up of α-cell activity failed to lower final urine pH. Only an increase in α-cell activity to 300% of baseline (in CNT, CCD, and OMCD) was sufficient to lower urine pH to 5.15, and this occurred with a doubling of net acid excretion. The model results with this parameter set are displayed in Table 6 and in Figs. 9 and 10. Compared with furosemide alone, this increase in α-cell activity was sufficient to neutralize CNT base secretion; the CCD remained relatively unimportant; but the increase in OMCD α-cells was sufficient to acidify the lumen to pH 5.5 and create an ammonia trap. Ultimately, nearly all remaining HCO₃⁻ was cleared in the IMCD.

Table 7.

DN transport with furosemide: maneuvers to enhance urine acidification

	HCO3−	TA	NH4+	Net Acid	Urine pH
Absolute excretion, μmol/min
HCO3− = 4 mM (Table 6)	0.37	0.49	0.97	1.09	6.23
HCO3− = 2 mM	0.36	0.50	0.99	1.12	6.22
Phosphate = 8 mM	0.32	1.02	0.99	1.68	6.16
Principal cell × 2	0.34	0.47	0.92	1.06	6.27
β-Cell × 10%	0.04	0.63	1.05	1.64	5.47
α-Cell × 2	0.13	0.58	1.24	1.68	5.88
Principal and α × 2	0.12	0.57	1.19	1.64	5.90
α-Cell × 3	0.02	0.65	1.50	2.13	5.15
Absolute reabsorption, μmol/min
HCO3− = 4 mM (Table 6)	0.49	−0.10	−0.29	0.88
HCO3− = 2 mM	0.07	0.01	−0.30	0.36
Phosphate = 8 mM	0.54	−0.24	−0.30	1.08
Principal cell × 2	0.53	−0.08	−0.24	0.85
β-Cell × 10%	0.82	−0.24	−0.37	1.43
α-Cell × 2	0.73	−0.19	−0.55	1.47
Principal and α × 2	0.75	−0.18	−0.50	1.43
α-Cell × 3	0.85	−0.26	−0.81	1.92

DISCUSSION

The model that has been considered here is a concatenation of the previously published DCT-CNT and the CD system (20, 24). Whereas the original CNT was a 1-mm tubule, the current segment is a 2-mm structure with coalescing tubules, so that the number of CCDs is one-fifth of the nephron number. With this geometry, the present CNT has the same luminal surface area as the original 1-mm segment, so that CNT cellular parameters from that earlier model have been maintained. As previously, the interstitial conditions have been taken to suggest moderate antidiuresis, and the sodium transport rates are compatible with tubules stimulated by ADH and aldosterone. The entering luminal flow, ∼20% of the glomerular filtration rate, and entering luminal Na⁺, ∼9% of filtered load, are both generous, but are well within the scope of micropuncture observation. Indeed, this is the first model that is sufficiently comprehensive to simulate distal micropuncture, yielding predictions of both DCT flows and urinary excretion rates. The format chosen for model output (Figs. 2 and 3) allow for direct appreciation of the magnitudes of cortical and medullary transport by the DN. Notably, most of the action is cortical, where about two-thirds of delivered Na⁺ is reabsorbed, and about two-thirds of this is within the DCT. Despite parameters suggesting an aldosterone-stimulated CCD, luminal conditions are such that there is negligible Na⁺ transport within the CCD (∼1.5% of distal delivery). Since the original formulation of the model OMCD, there has been no Na⁺ transport ascribed to OMCD principal cells, respecting the absence of discernible Na⁺ fluxes by the isolated perfused tubule (17). More recently, however, whole cell patch clamp of rat OMCD has documented functional luminal ENaC, with Na⁺ transport rates comparable to those for the CCD (6). In light of the fluxes in Table 2 and Fig. 3, an OMCD with CCD-like Na⁺ transport might be expected to change the final Na⁺ excretion from 23% of distal delivery to 21%, so the impact of such transport would not be expected to be substantial. The other salient observation from Fig. 2 is that the CNT is the locus of K⁺ secretion, increasing luminal K⁺ flow to about five times the delivered load; ultimately, about half of this is lost to medullary reabsorption.

The DCT-CNT is also the principal locus for net acid secretion, responsible for ∼70% of the increase in net acid flow from the DCT to final urine. One prediction from this model is that the relative contributions of the DCT and CNT to urinary acidification depend on DN Na⁺ delivery. High Na⁺ loads favor DCT acidification, and lower Na⁺ concentrations shift the balance more equally (Fig. 5). This follows directly from the activity of the luminal membrane Na⁺/H⁺ exchanger (NHE2) in the DCT (3, 5, 19). Of note, the model DCT proton secretory rates, 1.15 μmol/min at baseline (Table 2), increasing to 2.13 μmol/min with high Na⁺ (Table 3), translate into individual tubule fluxes of 32 and 59 pmol·mm⁻¹·min⁻¹, well within the values reported for early DCT (19). One limitation of this model is the absence of a specific kinetic representation of NHE2 function and reliance on the representation of NHE3 to simulate DCT Na⁺/H⁺ activity. Another critical aspect of model performance with respect to acid/base transport is that both α- and β-intercalated cells are functioning simultaneously. Together, proton secretion with Cl⁻/HCO₃⁻ exchange combine to yield electrogenic Cl⁻ reabsorption, which proceeds relatively uninfluenced by transepithelial potential difference. In rats, the impact of low luminal Cl⁻ to enhance net HCO₃⁻ reabsorption has long been noted, both in control and alkalotic animals (25), and that enhanced reabsorption has been specifically localized to “late DCT” (19). In perfused mouse CCD, this β-cell component of Cl⁻ reabsorption could be stimulated by angiotensin II, and accounted for about half of the reabsorptive Cl⁻ flux (12).

With simultaneous activity of α- and β-cells, variation in distal NaCl delivery is predicted to have a minor impact on net acid excretion (Figs. 4 and 5): with increasing NaCl delivery, there is increasing excretion of both HCO₃⁻ and NH₄⁺, and little change in TA. In the model tubule, going from Na⁺ excretion of 0.3 to 9.5% of estimated filtered load, there was an increase in HCO₃⁻ excretion from 0 to 0.40 μmol/min, an increase in NH₄⁺ excretion from 0.20 to 0.93 μmol/min, and no change in TA excretion of 0.47 μmol/min (Table 3). Wilcox et al. (26) examined the impact of saline infusion on rat urinary acidification, and their low- and high-saline infusion control groups showed urine Na⁺ excretion rates 0.4 and 8.9% of filtered load. For these two groups, the calculated HCO₃⁻ excretion (based on a Pco₂ = 50 mmHg) increased from 0 to 0.37 μmol/min, NH₄⁺ excretion increased from 0.65 to 0.99 μmol/min, and TA showed no change at 0.27 μmol/min. At least in this aspect of distal acidification, the model appears to be concordant with observations. When flow-enhanced NH₄⁺ excretion was identified in the CD model, it was due to luminal dilution of NH₄⁺, and the maintenance of a favorable concentration gradient for continued NH₄⁺ secretion (20).

The scope of the present model makes it suitable for modeling the acute impact of distal diuretics on solute excretion and urinary acidification. The most straightforward application is the action of thiazides to inhibit the NaCl cotransporter of the DCT. In these simulations, peritubular conditions and luminal delivery were unchanged from baseline. Cotransporter inhibition produced Na⁺ excretion of 41% of the Na⁺ delivered to the DCT, up from 23% at baseline, and comparable to the 45% of DCT delivery, observed in the acute study of Hropot et al. (7). With respect to K⁺, in the thiazide simulation, model excretion is 34% of estimated filtered load, up from 24% of filtered load at baseline. Measured values with HCTZ are K⁺ excretion 19% of filtered load, up from the control value 11% of filtered load (7). The difference between the experiments and the model is a more active model CNT: in the model with thiazide, late CNT K⁺ flow is 56% of filtered load, compared with a measured value of 34%; model K⁺ excretion was 60% of late distal K⁺ flow, compared with the measured value of 57% (7). The impact of thiazides on acid excretion is predicted to be local, namely, an increase in Na⁺/H⁺ exchange within the DCT and relatively minor perturbation of acid secretion in the remainder of the nephron. In the model, acid excretion by the DCT is predicted to increase from 1.15 to 1.84 μmol/min from baseline to thiazide, while net acid excretion by the CD is little changed (0.41–0.37). Overall, the change in DN acid excretion is only from 1.65 to 1.87 μmol/min, actually less than in the DCT. This is due to a model prediction that with the increase in Cl⁻ delivery to the CNT, that segment shifts from acid secretion to robust HCO₃⁻ secretion, and this derives from the activity of CNT β-cells. Unfortunately, there are no micropuncture studies of DN acid/base transport with thiazides with which to evaluate this prediction.

The action of amiloride has been simulated as a 99% reduction in luminal membrane Na⁺ channels in the CNT, CCD, and IMCD. Ambient conditions were taken to represent metabolic acidosis, to see whether the defective ENaC could be responsible for a distal renal tubular acidosis. The acidotic condition, per se, did little to change Na⁺ excretion (26% of distal delivery) and K⁺ excretion (26% of estimated filtered load); although DN proton secretion was diminished, net acid excretion increased above baseline, and final urine pH was low. With abolition of ENaC, Na⁺ excretion doubled to 53% of distal delivery, and K⁺ excretion vanished. This was comparable to the finding of Duarte et al. (4) with amiloride infusion, namely, urine Na⁺ increasing from 2.9 to 5.3% of filtered load (roughly 29 to 53% of delivered load, since DN Na⁺ delivery was ∼10% of filtered load); K⁺ excretion fell from 43 to 8% of filtered load. Arruda et al. (1) studied chronically acidotic rats and found that amiloride increased urine Na⁺ from 0.5 to 6.2% of filtered load, and dropped K⁺ excretion from 20 to 8% of filtered load. With respect to urinary acidification, the model prediction is that amiloride produces an increase in urine pH (6.27) and decreases all aspects of net acid excretion, namely, the appearance of urinary HCO₃⁻ (3.5 mM), along with decreases in TA and NH₄⁺ (Table 5). In the study of Arruda et al., only the amiloride-induced increase in pH and the appearance of urinary HCO₃⁻ achieved statistical significance.

What is notable about the current model prediction of urinary acidification failure with amiloride is that it is different from the conclusion drawn from the CD model in isolation, in which ENaC elimination failed to yield a voltage-dependent distal renal tubular acidosis (22). The findings in the CD model had prompted other explanations of the experimental observations with amiloride, namely, studies documenting inhibition of CD ATPases by amiloride. More recently, Kovacikova et al. (8) have investigated the role of ENaC in urinary acidification by mice. These workers confirmed that, as in rats and humans, mice acidified their urine following furosemide administration and ENaC inhibition (with amiloride or benzamil) blocked this acidification. They went on to create an ENaC α-subunit knockout, in which the deletion was restricted to cortical and medullary collecting ducts. These knockout mice, acidified normally (minimal urine pH and net acid excretion) following furosemide. The authors concluded that the CNT must be the main site of urinary acidification. The model calculations of this work are concordant with that conclusion.

In the model, furosemide administration has been represented as an increase in distal delivery of Na⁺ and K⁺, and a decrease in HCO₃⁻ delivery, as has been documented in micropuncture experiments (7). In the model, distal Na⁺ delivery was increased to 19% of estimated filtered load and the predicted Na⁺ excretion was 52% of distal delivery; the experimental findings were distal delivery of 18.5%, with Na⁺ excretion 44% of distal delivery. Among the possibilities for higher Na⁺ excretion in the model is the absence of flow-dependent enhancement of principal cell Na⁺ reabsorption in model tubules. With respect to K⁺, distal delivery in the model was increased to 32% of estimated filtered load and the predicted K⁺ excretion was 59% of filtered load; the experimental findings were distal delivery of 28% of filtered load and excretion of 46% of filtered load. An important experimental finding with furosemide was that tubule fluid reaching the DN had already been subject to increased acidification: a decrease in entering luminal pH from 6.55 to 6.03, with a 58% increase in TA and little change in NH₄⁺ (Table 6 in Ref. 7). In the model calculations, entering luminal HCO₃⁻ was reduced from 8 to 4 mM, TA increased by 60%, and NH₄⁺ was unchanged from baseline (Table 6); overall, net acid delivery to the DN was 0.21 μmol/min, compared with −0.80 μmol/min under control conditions. What the model predicted was a small increase in net acid excretion, 1.09 μmol/min, compared with 0.85 μmol/min at baseline. Most notable, however, was that the increase in NaCl delivery to the CNT produced significant HCO₃⁻ secretion by β-cells that resulted in bicarbonaturia and an increase in urine pH to 6.23. Thus net urinary acidification by DN actually decreased from 1.65 to 0.88 μmol/min in this simulation. Experimentally, the findings were very different: with furosemide, urine pH fell to 5.16 and both TA and NH₄⁺ excretion increased, so that net acid excretion increased to 2.9 μmol/min for a 250-g rat (Table 4 in Ref. 7).

The discrepant response to furosemide between model and tubule is substantial. Attempts to achieve concordance by modifying model parameters included enhanced acid delivery (as a decrease in delivered HCO₃⁻ or increase in phosphate) or doubling CNT and CCD principal cell activity (conceivably, in response to flow), and these did nothing to bring final urine pH closer to observations. Reducing CNT and CCD β-cell function gave substantial improvement, but there is little physiological justification. An increase in α-cell activity following furosemide seems most likely. Quantitatively, doubling of CNT, CCD, and OMCD α-cell transport (with or without doubling principal cell transport) was not quite sufficient to reproduce observations; however, tripling the activity of these α-cells dropped urine pH to 5.15 and increased net acid excretion to 2.13 μmol/min. The impact of furosemide on renal acid excretion is known to be time dependent. In studies in humans, the initial response to furosemide was bicarbonaturia (13, 16), and only after 2 h did urine pH drop below 5.5 (14). Even with prior administration of fludrocortisone, it required 3 h to attain minimal urine pH (18). These findings suggest an adaptive response of the nephron to furosemide diuresis, something outside the scope of the physical factors embodied in the model. Although principal cell adaptation to changes in flow has been documented (15), there has not been comparable examination of α-cell activity. If increased α-cell function in response to flow were responsible for the observed furosemide effect, the model prediction is that this effect would not be subtle.

In sum, a model of rat DN has been constructed from existing DCT-CNT and CD models, with minor modification of the components. With respect to acid/base transport, there is reasonable agreement between model performance and micropuncture observations obtained during hydropenia and with saline diuresis. Among the segments of this DN, the DCT-CNT is recognized as responsible for the major portion of distal acidification. Predictions from the model calculations include the following. 1) With increasing distal Na⁺ delivery, there is little change in net acid excretion, but a shift in acidification locus from shared DCT and CNT contributions, to DCT prominence. 2) Urinary acidification by thiazides is primarily local (in the DCT) via the shift in Na⁺ reabsorption from NaCl cotransport to entry via NHE2. Increased NaCl delivery to the CNT increases β-cell HCO₃⁻ secretion, and thus blunts the DCT effect. 3) In contrast to the isolated CD model, inclusion of the CNT now reproduces the observed distal acidification defect found with ENaC block, so that this action of amiloride appears to be sufficient to produce voltage-dependent distal RTA. (4) The effect of furosemide to enhance distal urinary acidification is not reproduced by the model without major upregulation of CNT α-cell transport, perhaps as a result of increased luminal flow.

GRANTS

This investigation was supported by Public Health Service Grant R01-DK-29857 from the National Institute of Arthritis, Diabetes, and Digestive, and Kidney Diseases.

Table 3a.

DN solute transport with low-sodium delivery (entering flow = 6 nl/min, Na⁺ = 25, K⁺ = 2.0, HCO₃⁻ = 8.0)

	DCT	CNT	CCD	OMCD	IMCD	Total
Absolute delivery, μmol/min
Na+	5.40	2.42	1.04	1.18	2.17	0.42
K+	0.43	0.76	1.60	1.37	0.76	0.17
Cl−	3.48	1.44	1.51	1.38	2.07	0.15
HCO3−	1.73	1.14	0.52	0.30	0.10	0.00
TA	0.24	0.40	0.57	0.39	0.40	0.47
NH4+	0.68	0.56	0.31	0.21	0.25	0.20
Net acid	−0.80	−0.18	0.36	0.30	0.55	0.67
Absolute reabsorption, μmol/min
Na+	2.98	1.37	−0.13	−0.99	1.75	4.98
K+	−0.32	−0.84	0.23	0.61	0.59	0.27
Cl−	2.04	−0.07	0.13	−0.69	1.92	3.33
HCO3−	0.59	0.63	0.21	0.20	0.10	1.73
TA	−0.15	−0.17	0.18	−0.01	−0.06	−0.22
NH4+	0.12	0.25	0.10	−0.04	0.04	0.48
Net acid	0.62	0.55	−0.07	0.25	0.12	1.47

Table 3b.

DN solute transport with high-sodium delivery (entering flow = 6 nl/min, Na⁺ = 135, K⁺ = 2.0, HCO₃⁻ = 8.0)

	DCT	CNT	CCD	OMCD	IMCD	Total
Absolute delivery, μmol/min
Na+	29.16	22.62	17.13	16.55	17.11	14.84
K+	0.43	0.84	3.46	3.52	3.07	2.68
Cl−	27.24	22.80	19.60	18.97	19.36	17.01
HCO3−	1.73	0.43	0.71	0.69	0.60	0.40
TA	0.24	0.57	0.62	0.46	0.44	0.47
NH4+	0.68	0.74	0.63	0.64	0.85	0.93
Net acid	−0.80	0.88	0.54	0.41	0.69	0.99
Absolute reabsorption, μmol/min
Na+	6.53	5.50	0.58	−0.56	2.28	14.32
K+	−0.41	−2.61	−0.07	0.45	0.39	−2.25
Cl−	4.44	3.20	0.63	−0.39	2.35	10.23
HCO3−	1.30	−0.29	0.02	0.10	0.20	1.33
TA	−0.33	−0.05	0.16	0.02	−0.03	−0.22
NH4+	−0.05	0.11	−0.01	−0.20	−0.08	−0.24
Net acid	1.68	−0.34	−0.13	0.28	0.30	1.79

Table 5a.

DN solute transport under metabolic acidosis (entering flow = 6 nl/min, Na⁺ = 65, K⁺ = 2.0, HCO₃⁻ = 4.0)

	DCT	CNT	CCD	OMCD	IMCD	Total
Absolute delivery, μmol/min
Na+	14.04	8.77	5.14	4.91	5.72	3.57
K+	0.43	0.80	2.78	2.62	2.03	1.39
Cl−	13.07	9.00	7.20	6.70	7.18	4.70
HCO3−	0.86	0.28	0.34	0.27	0.11	0.00
TA	0.33	0.55	0.62	0.49	0.51	0.63
NH4+	0.69	0.70	0.51	0.45	0.51	0.53
Net acid	0.15	0.97	0.79	0.67	0.91	1.17
Absolute reabsorption, μmol/min
Na+	5.26	3.63	0.23	−0.82	2.16	10.47
K+	−0.37	−1.98	0.17	0.59	0.64	−0.95
Cl−	4.07	1.80	0.50	−0.48	2.48	8.36
HCO3−	0.59	−0.07	0.07	0.15	0.11	0.86
TA	−0.23	−0.07	0.14	−0.02	−0.12	−0.30
NH4+	−0.01	0.19	0.06	−0.06	−0.03	0.15
Net acid	0.82	−0.18	−0.12	0.24	0.26	1.02

Table 5b.

DN solute transport under metabolic acidosis, with amiloride (entering flow = 6 nl/min, Na⁺ = 65, K⁺ = 2.0, HCO₃⁻ = 4.0)

	DCT	CNT	CCD	OMCD	IMCD	Total
Absolute delivery, μmol/min
Na+	14.04	8.77	9.36	9.47	9.97	7.68
K+	0.43	0.80	0.64	0.62	0.35	0.04
Cl−	13.07	9.00	8.85	8.79	9.32	7.05
HCO3−	0.86	0.28	0.61	0.53	0.34	0.11
TA	0.33	0.55	0.59	0.43	0.44	0.47
NH4+	0.69	0.70	0.39	0.33	0.42	0.46
Net acid	0.15	0.97	0.38	0.23	0.53	0.82
Absolute reabsorption, μmol/min
Na+	5.26	−0.59	−0.11	−0.49	2.29	6.36
K+	−0.37	0.16	0.03	0.27	0.31	0.39
Cl−	4.07	0.15	0.06	−0.54	2.27	6.01
HCO3−	0.59	−0.33	0.08	0.19	0.23	0.76
TA	−0.23	−0.04	0.17	−0.01	−0.03	−0.15
NH4+	−0.01	0.30	0.06	−0.09	−0.03	0.23
Net acid	0.82	−0.59	−0.15	0.29	0.30	0.68

Table 6a.

DN solute transport with furosemide (entering flow = 6 nl/min, Na⁺ =135, K⁺ = 8.0, HCO₃⁻ = 4.0)

	DCT	CNT	CCD	OMCD	IMCD	Total
Absolute delivery, μmol/min
Na+	29.16	23.42	18.14	17.59	18.16	15.92
K+	1.73	1.78	4.01	4.04	3.57	3.16
Cl−	29.55	24.74	21.28	20.62	21.00	18.67
HCO3−	0.86	0.27	0.64	0.63	0.55	0.37
TA	0.39	0.59	0.63	0.48	0.46	0.49
NH4+	0.69	0.76	0.66	0.68	0.89	0.97
Net acid	0.21	1.08	0.65	0.52	0.79	1.09
Absolute reabsorption, μmol/min
Na+	5.74	5.28	0.56	−0.57	2.24	13.24
K+	−0.06	−2.23	−0.03	0.47	0.41	−1.43
Cl−	4.81	3.46	0.65	−0.38	2.33	10.88
HCO3−	0.60	−0.37	0.00	0.08	0.18	0.49
TA	−0.20	−0.04	0.15	0.02	−0.03	−0.10
NH4+	−0.07	0.10	−0.02	−0.21	−0.08	−0.29
Net acid	0.86	−0.43	−0.13	0.27	0.30	0.88

Table 6b.

DN solute transport with furosemide and threefold α-cell fluxes (entering flow = 6 nl/min, Na⁺ = 135, K⁺ = 8.0, HCO₃⁻ = 4.0)

	DCT	CNT	CCD	OMCD	IMCD	Total
Absolute delivery, μmol/min
Na+	29.16	23.42	18.15	17.55	18.09	15.77
K+	1.73	1.78	3.54	3.57	2.52	2.16
Cl−	29.55	24.74	21.25	20.60	20.96	18.55
HCO3−	0.86	0.27	0.26	0.30	0.14	0.02
TA	0.39	0.59	0.66	0.56	0.58	0.65
NH4+	0.69	0.76	0.69	0.75	1.43	1.50
Net acid	0.21	1.08	1.09	1.01	1.87	2.13
Absolute reabsorption, μmol/min
Na+	5.74	5.28	0.60	−0.55	2.33	13.39
K+	−0.06	−1.75	−0.03	1.05	0.35	−0.44
Cl−	4.81	3.49	0.65	−0.36	2.40	10.99
HCO3−	0.60	0.01	−0.04	0.16	0.12	0.85
TA	−0.20	−0.08	0.11	−0.02	−0.08	−0.26
NH4+	−0.07	0.07	−0.06	−0.68	−0.07	−0.81
Net acid	0.86	0.02	−0.09	0.86	0.26	1.92