Human neutrophil surface protrusion under a point load: location independence and viscoelasticity

Abstract

Mechanical properties of neutrophils have been recognized as key contributors to stabilizing neutrophil rolling on the endothelium during the inflammatory response. In particular, accumulating evidence suggests that surface protrusion and tether extraction from neutrophils facilitate stable rolling by relieving the disruptive forces on adhesive bonds. Using a customized optical trap setup, we applied piconewton-level pulling forces on targeted receptors that were located either on the microvillus tip (CD162) or intermicrovillus surface of neutrophils (CD18 and CD44). Under a constant force-loading rate, there always occurred an initial tent-like surface protrusion that was terminated either by rupture of the adhesion or by a “yield” or “crossover” to tether extraction. The corresponding protrusional stiffness of neutrophils was found to be between 0.06 and 0.11 pN/nm, depending on the force-loading rate and the cytoskeletal integrity, but not on the force location, the medium osmolality, nor the temperature increase from 22°C to 37°C. More importantly, we found that neutrophil surface protrusion was accompanied by force relaxation and hysteresis. In addition, the crossover force did not change much in the range of force-loading rates studied, and the protrusional stiffness of lymphocytes was similar to that of neutrophils. These results show that neutrophil surface protrusion is essentially viscoelastic, with a protrusional stiffness that stems primarily from the actin cortex, and the crossover force is independent of the receptor-cytoskeleton interaction.

to fight against invading bacteria during the inflammatory response, human neutrophils leave circulating blood and migrate to infected tissues. This is a well-coordinated multistep journey that starts with weak rolling adhesion along the endothelial lining of the blood vessel, followed by firm adhesion and diapedesis. Stable rolling is an indispensable step to expose neutrophils to locally expressed signaling molecules that eventually activate the integrin-mediated firm adhesion. Driven by shear stress, neutrophil rolling is a highly complex and dynamic process mediated primarily by selectins and their ligands, including L-selectin and P-selectin glycoprotein ligand-1 (PSGL-1 or CD162) on neutrophils (37). L-selectin and PSGL-1 are selectively concentrated on the tips of neutrophil microvilli (1, 4, 21, 42), which are actin-dependent, tiny surface protrusions that disappear when neutrophils are treated with actin-sequestering drugs such as latrunculin A and cytochalasin D (16, 38). On the contrary, β₂-integrins (CD18), which mediate firm adhesion after rolling, are confined to the intermicrovillus region of the neutrophil surface (4). This special arrangement of adhesion molecules helps coordinate the initiation of rolling adhesion and the subsequent firm adhesion.

The capability of selectins and their ligands in mediating neutrophil rolling under physiological shear stress relies on their distinct kinetic and mechanical features, which are modulated by the pulling force exerted by the blood flow (2, 7, 19, 20). This pulling force also generates dynamic surface protrusion and membrane nanotube (i.e., tether) extraction, which facilitate stable neutrophil rolling under various shear stresses (22, 25, 30, 34, 45). The dynamic surface protrusion, which is very likely a tentlike local surface deformation, always precedes tether extraction, which only occurs after the pulling force exceeds the crossover force. Using the micropipette aspiration technique (MAT), Shao et al. (34) applied small pulling forces (<45 pN) on PSGL-1 and determined the neutrophil protrusional stiffness to be ∼0.043 pN/nm. More recently, Evans et al. (5) applied larger pulling forces on PSGL-1 and β₂-integrins (from ∼50 to ∼150 pN) by using the biomembrane force probe (BFP). In the latter study, the protrusional stiffness of the neutrophil surface was determined under hypotonic conditions to range from ∼0.15 to 0.3 pN/nm, showing its dependence on the force-loading rate (from 240 to 38,000 pN/s) but not on the adhesion molecules on which the forces were applied. The smaller protrusional stiffness measured with the MAT is likely due to the relatively longer time of force application in that measurement (a few seconds). Consequently, these different stiffness values indicate that neutrophil surface deformation under a point or concentrated load may be viscoelastic. However, no direct study of this viscoelastic property has been conducted.

In the BFP study (5), tether extraction was rarely observed when β₂-integrins were pulled, probably because the bond lifetime between inactivated β₂-integrins and its ligand, intercellular adhesion molecule-1, is short. As a result, the crossover force was reported only for the tethers extracted via PSGL-1. Nevertheless, tether extraction via β₂-integrins is still likely in vivo, especially in the later stage of neutrophil rolling when β₂-integrins become activated. With the MAT, the threshold force for neutrophil tether extraction, i.e., the intercept of a linear regression of the force versus tether velocity data, was measured using L-selectin, PSGL-1, or β₂-integrin as the force handles, and its value did not depend on which receptor was pulled as long as neutrophils were not activated (33, 35, 44). The threshold force and the crossover force are inherently different because the crossover force includes the contribution from rupturing the receptor-cytoskeleton connection, whereas the threshold force does not. Therefore, it remains unknown whether the crossover force at the conclusion of neutrophil surface protrusion depends on which receptor is being pulled.

In this paper, we aim to examine the viscoelastic behavior and the mechanical origin of neutrophil surface protrusion under a point load and to explore the crossover force with different receptors. With the optical trap (OT) method, we imposed pulling forces on single membrane receptors located either on the microvillus tip (CD162) or in the intermicrovillus region (CD18 and CD44) of the neutrophil surface. We found that neutrophil surface protrusion was indeed viscoelastic as manifested by force relaxation and hysteresis. The protrusional stiffness of the neutrophil surface was ∼0.06 to 0.11 pN/nm under the protrusional rates of ∼300–4,000 nm/s, which can be translated into the force-loading rates of ∼20 to 400 pN/s. These results agree very well with the predictions from the three-parameter solid model. We also found that both the protrusional stiffness and the tether crossover force did not depend on the particular receptor being pulled. These findings not only show substantial cytoskeletal involvement in neutrophil surface protrusion, but also point to the direction that the major contributor to the crossover force may not be the linkage between the receptor and the cytoskeleton.

MATERIALS AND METHODS

Cell isolation and treatment.

A few drops of blood from healthy donors were collected by finger prick into a heparinized capillary glass tube (Fisher Scientific, Pittsburgh, PA). To isolate neutrophils, the blood was immediately layered onto 0.2-ml monopoly-resolving medium (MP Biomedicals, Irvine, CA) and centrifuged at 300 g for 15 min at room temperature (∼22°C). Afterwards, 0.1 ml of the neutrophil layer between the plasma fraction and the erythrocyte pellet was collected and washed in 1-ml HBSS solution (modified endotoxin-free Hanks' Balanced Salt Solution without Ca²⁺ or Mg²⁺, buffered with 25 mM HEPES; Sigma, St. Louis, MO) and again centrifuged at 300 g for 5 min at room temperature. After being washed, neutrophils were resuspended in 0.1-ml 50% autologous plasma (diluted with HBSS). Only a small fraction of the neutrophil suspension was transferred into the experimental chamber to avoid an excessive number of cells around the OT. All the samples were obtained with the protocol approved by the IRB at Washington University and voluntary written permission was obtained from all donors.

In this paper, lymphocytes were studied for comparison. To isolate lymphocytes, the collected blood was immediately layered onto 0.2-ml Histopaque 1077 gradient medium (Sigma) and centrifuged at 300 g for 10 min at room temperature. Then 0.1 ml of the top layer containing lymphocytes was collected, washed in 1-ml HBSS solution (Sigma), and spun at 200 g for 5 min at room temperature. After being washed, the lymphocytes were resuspended in 0.1-ml 50% autologous plasma (diluted with HBSS), a small fraction of which was transferred into the experimental chamber.

Unless otherwise specified, our experiments with passive neutrophils were performed at room temperature in the experimental chamber containing 50% autologous plasma of which the osmolality was ∼310 mosmol/kg, measured with a freezing-point osmometer (Advanced Instruments, Norwood, MA). The effect of temperature was examined in a custom-built heating chamber that can maintain the medium temperature at 37°C (15). In addition, the effect of osmolality on neutrophil surface protrusion was examined in a hypotonic buffer (25% autologous plasma, 25% HBSS, and 50% water) of which the osmolality was measured to be ∼156 mosmol/kg.

To examine the role of the actin cortex in neutrophil surface protrusion under point-pulling forces, isolated neutrophils were incubated in 50% autologous plasma containing 1 μM latrunculin A (Molecular Probes, Eugene, OR) at 37°C for 15 min and then introduced into the experimental chamber that contained the same concentration of the drug. Latrunculin A at the selected concentration is known to have a potent effect on neutrophil morphology and mechanics of tether extraction (16, 18).

Bead preparation.

Polystyrene beads of ∼4.5 μm in diameter (coated with goat anti-mouse IgG antibodies; Bangs Laboratories, Fishers, IN) were washed twice in phosphate-buffered saline (PBS without Ca²⁺ or Mg²⁺; Cambrex, Walkersville, MD) and incubated in PBS at 37°C for 1 h with either mouse anti-human CD162 (PharMingen, San Diego, CA) for pulling the microvillus tip (21) or mouse anti-human CD18 or CD44 (PharMingen) for pulling the nonmicrovillar neutrophil surface (4, 42). As a control, the same beads coated with purified general-type mouse IgG (Sigma) were used to verify the specificity of antibody interaction with the targeted molecules on the cell surface. All beads were stored at 4°C and washed twice with PBS before use.

OT setup and calibration.

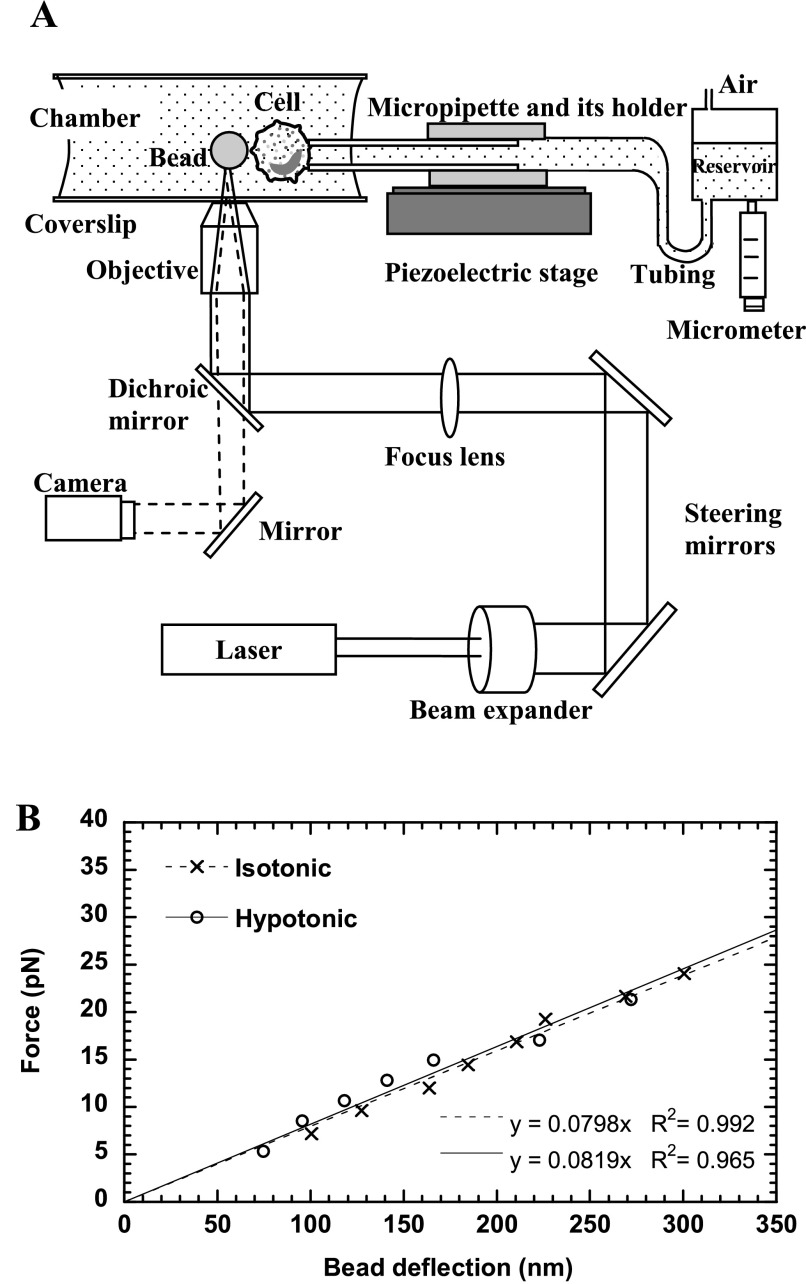
The OT was built around an inverted microscope (Zeiss 200M, Jena, Germany). As shown in Fig. 1A, a beam of infrared Nd:YVO₄ laser (wavelength 1,064 nm; Spectra-Physics, Mountain View, CA) was expanded 10 times by a beam expander (Newport, Irvine, CA) and directed by two steering mirrors toward the epifluorescence port of the microscope. In addition, a focusing lens (Chroma Technology, Brattleboro, VT) was placed in the laser beam path in front of the epifluorescence port to control the divergence of the laser beam and thus the vertical position of the trap. The laser beam was then reflected by a dichroic mirror in the reflector turret (Chroma Technology) into the back aperture of an oil-immersion objective (numerical aperture = 1.3, ×100; Zeiss) and focused into a tiny focal spot in the medium-filled chamber. An antibody-coated polystyrene bead can be trapped by the focused laser and function as a mechanical spring. The emitted visible light from the sample was transmitted through the dichroic mirror and directed toward an analog camera (model WV-BP330; Panasonic System Solutions, Suzhou, China) or a high-speed digital camera (Phantom v4.2; Vision Research, Wayne, NJ) mounted on the side port of the microscope. The image from the analog camera was then recorded by a DVD recorder, and the image from the digital camera was stored directly on a computer hard drive.

Fig. 1.

The optical trap (OT) setup and calibration. A: schematic of the OT setup combined with a micropipette manipulation system (not drawn to scale). Solid lines represent the laser beam path, and dashed lines represent the imaging light path. The laser was expanded and directed into the back aperture of the objective of the microscope. The laser focused by the objective can trap a latex bead and function as a soft mechanical spring, whereas the micropipette can hold a cell with suction pressure applied by adjusting the height of the reservoir. The motion of the piezoelectric stage where the micropipette is affixed is controlled by a computer. B: calibration of the OT stiffness in isotonic or hypotonic media. The slope of the fitted lines gave the trap stiffness of ∼0.08 pN/nm.

For our measurement, the OT was combined with a micropipette manipulation system. As shown in Fig. 1A, a micropipette in its holder was mounted on a piezoelectric stage (Physik Instrumente), of which its movement was controlled by LabView (National Instruments, Austin, TX). The pressure inside the micropipette can be precisely controlled by adjusting the height of the reservoir connected to the pipette with plastic tubing, so a cell can be held by small suction pressure with the micropipette. The position and the motion of the cell can be precisely controlled with the piezoelectric stage, so the cell-bead contact and the ensuing stretch between the cell and the bead were accomplished by moving the micropipette with the piezoelectric stage.

The effective “spring constant” of the OT was calibrated against viscous drag in the transverse plane (perpendicular to the laser propagation direction). By moving a customized chamber attached to the piezoelectric stage at a certain speed (v), we can impose a constant viscous drag force (F) on the trapped bead that can be calculated by (10)

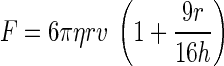(1)

where η is the medium viscosity, r is the bead radius, and h is the distance between the bead center and the bottom coverslip above the objective. Equation 1 is a modified version of Stokes' law when a sphere moving in a viscous fluid is close to the substrate. To control the height of the trapped bead above the coverslip (h), a bead on the coverslip was first focused and trapped (initially h = r). Then the trap was raised by the motorized objective of which its vertical position can be precisely controlled. The eventual height of the trapped bead above the coverslip would be the sum of the bead radius and the relative rise of the objective's vertical position.

At the laser output power of 1.8 W, the horizontal bead deflection was recorded at different medium velocities generating different viscous drag forces (Eq. 1). The corresponding digital movie, from either processed DVD video (at 30 frames/s) or digital camera (at 100–1,000 frames/s), was then analyzed frame by frame with a MatLab script, NanoTrack, written in our laboratory from which the bead position in each frame can be obtained. NanoTrack was adapted from the method developed by Gelles et al. (9). Shown in Fig. 1B was the calculated viscous drag as a function of the bead deflection from the trap center for a 4.5-μm bead placed at a height of ∼8.2 μm above the coverslip. The viscosities (η) of the media at room temperature (∼22°C) were measured by a rheometer (Brookfield Engineering Laboratories, Middleboro, MA). The trap stiffness in 50% plasma-HBSS (η = ∼1.24 cP) was ∼0.08 pN/nm (Fig. 1B), which would remain constant at different temperatures (17). The trap stiffness in the hypotonic buffer (η = ∼1.1 cP) was about the same (Fig. 1B). According to Eq. 1 and the parameters used in our calculation, the relative error of the force should be less than 3% even for a 20% variation in the bead height estimation.

Experimental procedure.

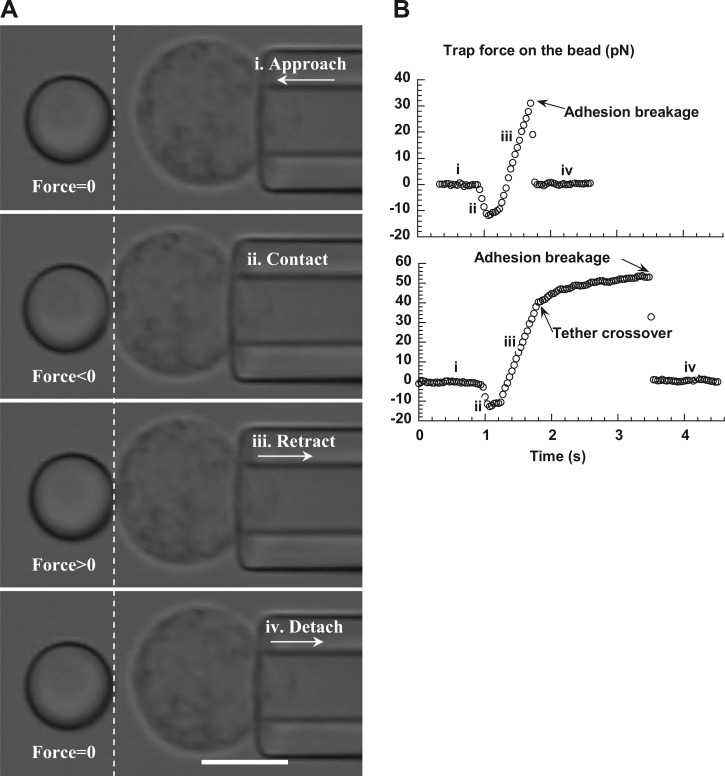
A neutrophil held with micropipette suction was driven by the piezoelectric stage shown in Fig. 1A to approach the trapped bead at the speed of 2,500 nm/s (Fig. 2 A-i) and gently contact the bead (Fig. 2A-ii), resulting in a compressive force on the cell and the bead. After a short pause, the cell was driven to retract from the bead at a constant speed (Fig. 2A-iii). If an antibody-receptor bond formed between the cell and the bead, the bead would be pulled away from the trap center and an increasing trap force would be applied on the bead. In the meantime, a pulling force would be applied on the cell surface as shown in Fig. 2A-iii. After the adhesion was broken, the bead would detach from the cell and return quickly to its initial trapped position (Fig. 2A-iv). Then this whole process of approach and retraction was repeated many times before a new cell-bead pair was used. The trap force imposed on the bead at any moment was calculated as the product of the trap stiffness and the bead deflection (Fig. 2B). The cell surface deformation, of which its increase over time yields the protrusional rate, was calculated by subtracting the bead deflection from the cell displacement, starting from the instant when the bead was deflected. The experiments were performed at various cell retraction speeds (500–8,000 nm/s) to achieve a range of protrusional rates and force-loading rates. The neutrophil protrusional stiffness in each adhesion event was calculated as the ratio of the force-loading rate to the protrusional rate.

Fig. 2.

A: video micrograph sequences of a trapped bead (left of the dashed line) and a neutrophil (right of the dashed line) during an experiment. From the top, these micrographs show consecutively the neutrophil approach (i), contact (ii), retraction (iii), and detachment (iv) to/from the trapped bead. Dashed line was superimposed to indicate the initial position of the right edge of the trapped bead. Scale bar represents 5 μm. B: typical force-time curves obtained during the neutrophil approach and retraction when there was adhesion between the bead and the neutrophil. The neutrophil retraction speed was 2 μm/s. The periods of approach (i), contact (ii), retraction (iii), and detachment (iv) were marked accordingly. The extent of the initial apparently linear response was limited by either of the following two events: the adhesion breakage at the interface of the bead and the cell (top) and the abrupt crossover to membrane tether extraction before the adhesion was broken (bottom).

For force relaxation during neutrophil surface protrusion, the piezoelectric stage shown in Fig. 1A was programmed to stop at ∼300 nm away from the trapped bead after retraction. If there was adhesion between the cell and the bead, force relaxation could be measured with the OT. To demonstrate hysteresis, the piezoelectric stage was programmed to drive the cell to approach the bead at 200 nm/s immediately after retraction at the same speed.

RESULTS

Apparently linear neutrophil surface protrusion under a point-pulling force.

If a bond formed between an antibody on the bead and a targeted receptor on a passive neutrophil during neutrophil retraction, there was always an initial apparently linear deformation of the neutrophil surface. The bead was displaced from the trap center and followed the neutrophil retraction at a constant speed that was smaller than the neutrophil retraction speed. Correspondingly, the neutrophil was deformed at a constant protrusional rate under a constant force-loading rate. Typical force histories during neutrophil approach and retraction are shown in Fig. 2B. For historical reasons, this deformation will be referred to as surface protrusion, not surface extension (15). The extent of the initial neutrophil surface protrusion was limited by two events. One was the breakage of the adhesion at the interface of the bead and the neutrophil (Fig. 2B, top). The other was the abrupt crossover to a viscous membranous tether flow (Fig. 2B, bottom; also see Fig. 5A for a video micrograph of a membrane tether extracted from a passive neutrophil). In general, there is a linear relationship between the pulling force and tether extraction velocity that has been well documented for many cell types, including neutrophils and lymphocytes (33, 35, 44). Therefore, depending on the force magnitude when the crossover occurred, the force would then increase or decrease gradually toward a plateau that was needed to maintain the tether growth at the neutrophil retraction speed (Fig. 2B, bottom). The tether extraction could be terminated at any moment due to the breakage of the adhesion between the neutrophil and the bead. In either case, after the adhesion between the neutrophil and the bead was broken, the bead was pulled back quickly to the trap center by the focused laser (Fig. 2B).

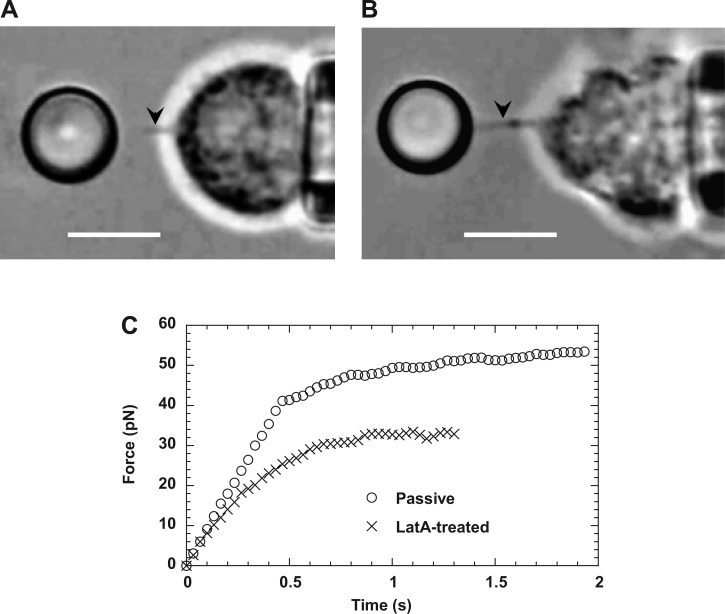
Fig. 5.

Crossover from apparently linear deformation to tether extraction. Two video micrographs show membrane tethers extracted from normal (A) and latrunculin-A-treated neutrophils (B), respectively. Tethers are the faint shadows between the cell and the bead (marked by the arrows in the video frames). In both cases, pulling forces were applied on CD162, and the cell retraction speed was 2,000 nm/s. Scale bars in both A and B represent 5 μm. C: typical force histories of apparently linear deformation and tether extraction from passive and latrunculin A-treated neutrophils.

The adhesion specificity between the cell and the bead was confirmed by a dramatic decrease in adhesion frequency (defined as the ratio of the number of adhesion events to the total number of contacts between a cell-bead pair) from ∼15–35% for the beads coated with specific antibodies to <5% for the beads coated with general type IgG. Since an adhesion frequency of <30% indicates that a single bond is present in most of the adhesion events (3, 24, 31, 32), we assumed that only a single microvillus or a single receptor on the cell surface was pulled in all adhesion events. This assumption is also supported by the single adhesion breakage following the cell deformation (Fig. 2B). Occasionally, we obtained force histories clearly from two separate adhesive points, one broken after the other with two distinctive force-loading rates (data not shown), which was indicative of surface protrusion from two separate locales (the overall stiffness for this kind of double surface protrusion was nearly twice as large as that for a single surface protrusion).

As another control experiment, a plastic bead was used in place of the neutrophil in the experiment and brought to contact the bead in the laser trap. Occasionally, these two beads adhered to each other by nonspecific adhesion. We obtained several adhesion events between these two beads at different retraction speeds. As expected for two nearly rigid beads, the corresponding force-loading rates were nearly the same as the maximum force-loading rates that can be achieved when the trapped bead was displaced at the retraction speeds of the piezo stage.

Protrusional stiffness and crossover force of neutrophil surface protrusion.

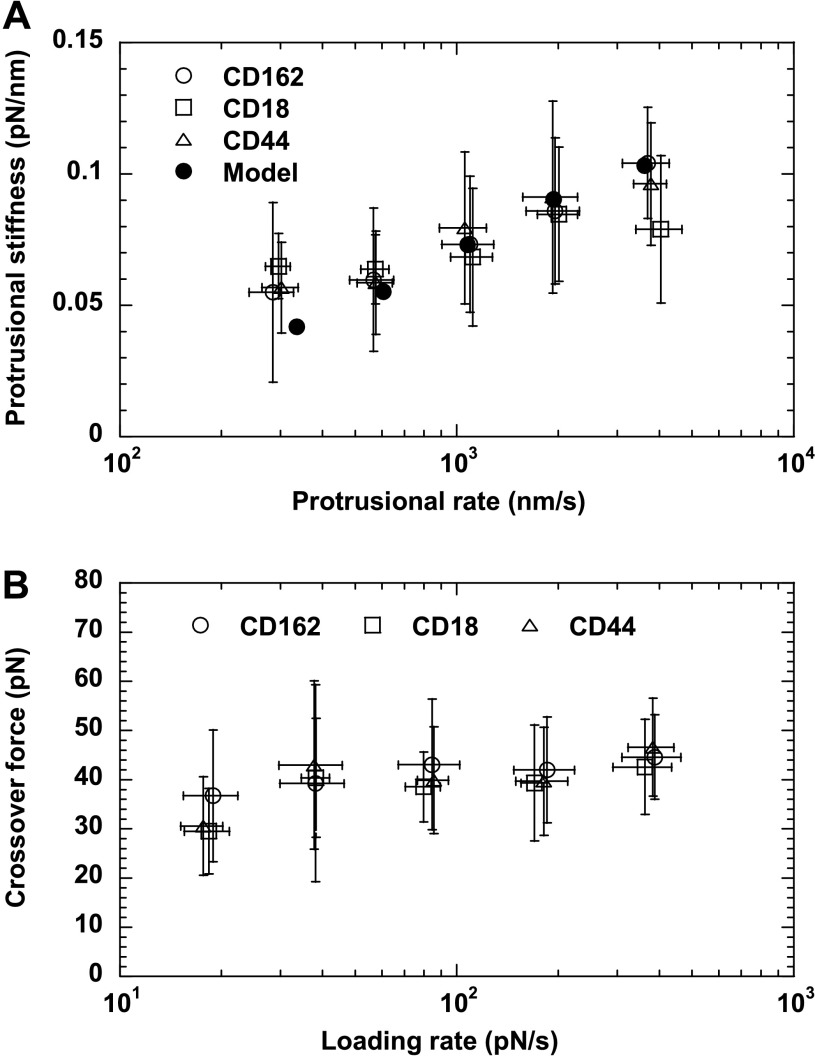
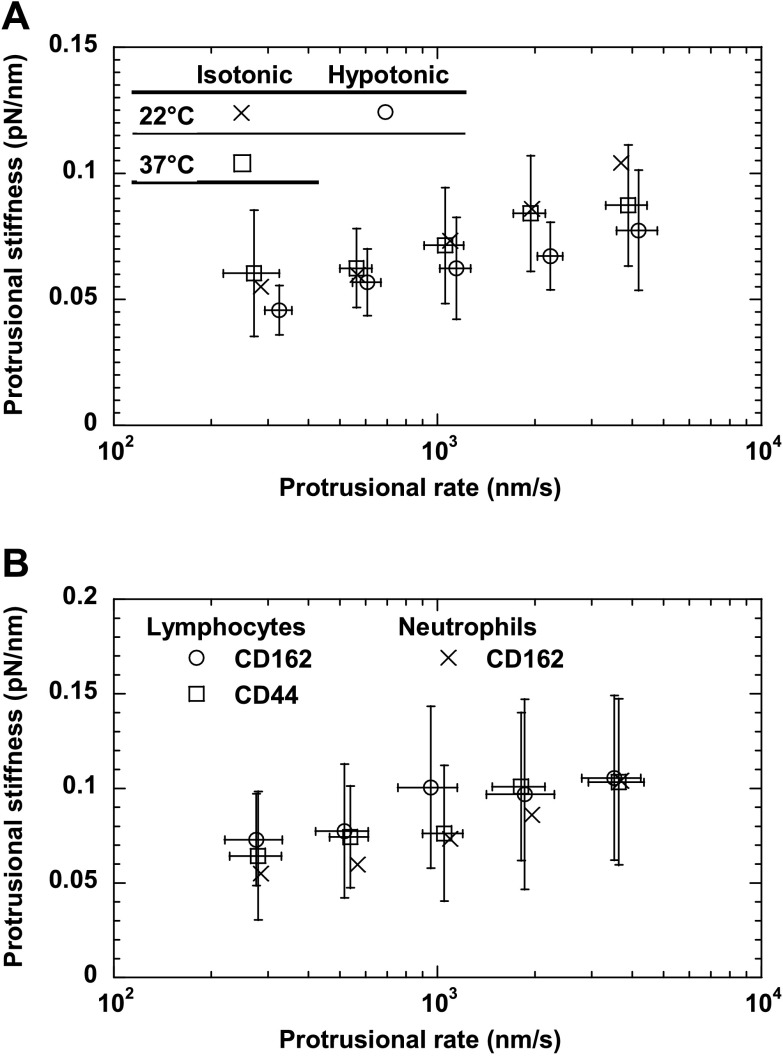
During the initial neutrophil surface protrusion, both the protrusional rate (∼300–4,000 nm/s) and the force-loading rate (∼20–400 pN/s) increased with the retraction speed of the neutrophil (500–8,000 nm/s). The neutrophil protrusional stiffness measured at several protrusional rates is shown in Fig. 3A. On average, the protrusional stiffness was between 0.06 and 0.1 pN/nm, showing dependence on the protrusional rate of ∼300–4,000 nm/s or the force-loading rate of ∼20–400 pN/s. At the protrusional rate of ∼300 nm/s, the protrusional stiffness is close to the stiffness of microvillus extension measured with the MAT in a previous study, 0.043 pN/nm (34). However, the fact that the protrusional stiffness is independent of the type of receptor used in this study strongly indicates that the so-called microvillus extension is not caused by the increase in the microvillar length. Instead it is probably caused by an overall cellular deformation that came from the composite of membrane and cytoskeleton. As shown in the Appendix, the neutrophil surface protrusion can be described by the three-parameter solid model. The stiffness calculated from the model is shown in Fig. 3A for comparison.

Fig. 3.

The protrusional stiffness (A) and the crossover force (B) of neutrophil surface protrusion. Different symbols correspond to different receptors as marked. The error bars signify the standard deviations. Also shown in A is the protrusional stiffness calculated from the three-parameter solid model (see appendix). Each point in A was the average of 14–108 events from 7 to 16 neutrophils. Each point in B was the average of 6–21 tethers from 5 to 9 neutrophils.

The extent of neutrophil surface protrusion was limited by either adhesion breakage or sudden crossover to membrane tether extraction (Fig. 2B). Shown in Fig. 3B are the crossover forces measured under several force-loading rates from ∼20 to 400 pN/s. The average crossover forces were always ∼30–45 pN when CD162, CD18, or CD44 was pulled. This is very close to the reported threshold force for extracting single tethers from neutrophils determined with the MAT (∼45 pN) (33, 34). Both CD162 and CD44 bind to the actin-rich neutrophil cytoskeleton via the ezrin-radixin-moesin complex (14, 36, 48), whereas inactivated and activated CD18 bind to the cytoskeleton via talin and α-actinin, respectively (23, 29). The independence of the crossover force as to how these receptors are linked to the cytoskeleton suggests that the linkage played a minor or equal role in its contribution to the crossover force.

Force relaxation.

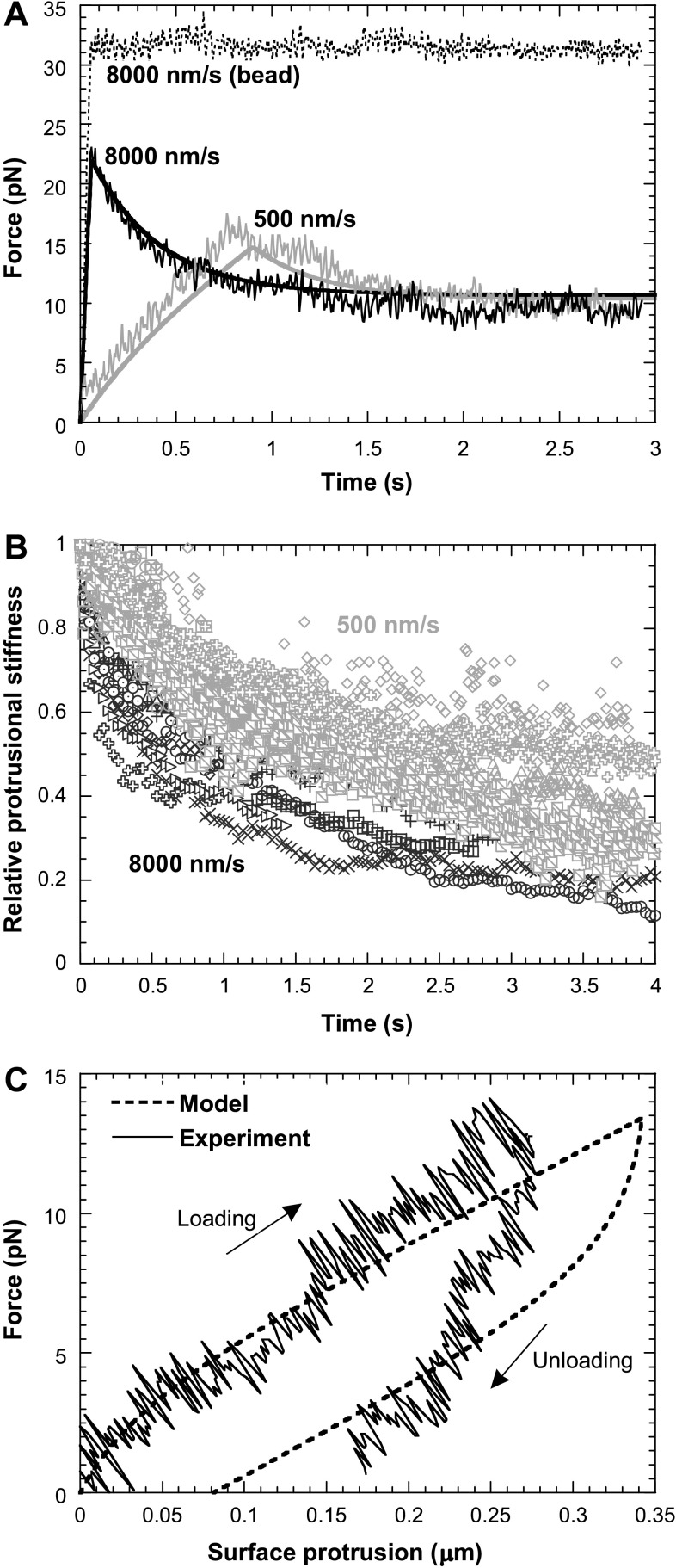
The dependence of the protrusional stiffness on the force-loading rate indicates that neutrophil surface protrusion under a point load is viscoelastic. To examine this possibility directly, we first performed force-relaxation experiments. Before the cell-bead adhesion was broken, the neutrophil retraction was stopped ∼300 nm away from the trapped bead, and the pulling force on the neutrophil was measured by the OT. We found that the pulling force decreased continuously toward a constant magnitude. Figure 4A shows two typical force-relaxation histories when the neutrophil was pulled at two different initial retraction speeds, 500 and 8,000 nm/s. The larger the initial retraction speed, the faster and larger the force relaxation. As a control, a latex bead was also used in place of the neutrophil in the same experiment. As expected, we found that, when there was adhesion between this bead and the bead in the trap, the trapped bead would follow the retracting bead at about the same speed, and the force remained constant after the bead retraction stopped (Fig. 4A). Although our force-relaxation experiment was not an ideal one, in which an instantaneous deformation is generated, we were able to simulate our experiments with the three-parameter solid model and predict the behavior shown in Fig. 4A. The prediction from the model agrees very well with our experimental measurements.

Fig. 4.

Viscoelasticity of neutrophil surface protrusion under a point-pulling force. All pulling forces were applied on CD162. A: force relaxation when a neutrophil was retracted at 500 and 8,000 nm/s. As a control, a bead was also retracted at 8,000 nm/s, and no force relaxation was observed. The smooth continuous curves were the predicted results from the three-parameter solid model (see appendix). B: after the initial cell retraction at 8,000 nm/s (n = 9 from 4 neutrophils; dark symbols) or 500 nm/s (n = 10 from 7 neutrophils; grey symbols) stopped, the corresponding stiffness, normalized by the stiffness at the instant when the cell retraction was just stopped, decreased with time. C: a typical hysteresis curve for passive neutrophils during a cycle of force loading and unloading. The speed of neutrophil retraction (loading) and approach (unloading) from/to the trapped bead was 200 nm/s. The predicted results from the three-parameter solid model are shown as the dashed line.

Because of force relaxation, the bead in the trap would gradually move closer to the trap center. As a result, the neutrophil surface protrusion increased gradually and this, in addition to the force decrease, caused further gradual decrease in the apparent protrusional stiffness (force/deformation). Figure 4B shows the protrusional stiffness (normalized according to the initial stiffness) over the course of force relaxation, starting from the instant when the neutrophil retraction was just stopped. The protrusional stiffness corresponding to the same initial retraction speed showed a similar decreasing trend toward a lower level in just several seconds (Fig. 4B). Similar to the typical force relaxation (Fig. 4A), the decrease in the protrusional stiffness after the slower initial cell retraction (500 nm/s) was slower than the one after the faster initial cell retraction (8,000 nm/s).

Hysteresis.

When the adherent neutrophil was retracted away from the bead in the trap, the pulling force increased with a certain loading rate. Before the adhesion was broken by the increasing load, the neutrophil could also be driven to approach the bead to unload the force. A typical force-deformation curve during one cycle of this loading and unloading was shown in Fig. 4C. Hysteresis, i.e., the lag of the unloading curve below the loading curve, was clearly present. Both the neutrophil retraction and approach speed were 200 nm/s (note: 500 nm/s was also used in the tests and similar hysteresis curves were obtained; data not shown). Neutrophil surface protrusion usually did not recover to its nondeformed state when the pulling force was unloaded to zero (except in one case out of eight, data not shown). The dissipated energy due to hysteresis can be calculated as the difference between the areas under the loading and unloading curves. Based on eight cases obtained from five different neutrophils, the energy loss due to the hysteresis in this process was 0.70 ± 0.38 pN·μm (or ×10⁻¹⁸ J) for the maximum surface protrusion of 0.21 ± 0.05 μm. The corresponding percentage of the dissipated energy relative to the work done during the force-loading phase was 53 ± 15%. Consistent with the force-relaxation experiment and simulation (Fig. 4A), the hysteresis can also be predicted with the three-parameter solid model, and the prediction agrees reasonably well with our experimental findings (Fig. 4C).

Role of actin cortex.

Filamentous actin and its peripheral cortical network have proven to be critical to the morphology, mechanics, and function of neutrophils (41). Local pulling forces imposed on receptors in different regions of the neutrophil surface most likely result in similar local deformation of the underlying actin cortex, as indicated by the independence of the protrusional stiffness on receptor type (Fig. 3). To examine the role of actin cortex in neutrophil surface protrusion, we treated neutrophils with latrunculin A, which is known to bind actin monomers and lead to actin depolymerization. After treatment with 1-μM latrunculin A, neutrophils were no longer spherical and showed very irregular shapes (Fig. 5B). Pulling forces on CD162 on treated neutrophils always extracted a membrane tether (Fig. 5B) nearly instantaneously without the initial surface protrusion and a clear crossover as seen in normal neutrophils (Fig. 5C), which is consistent with previous findings under hypotonic conditions (5). Therefore, under physiological conditions, the initial neutrophil surface protrusion also requires the integrity of the actin cortex. In addition, the asymptotic tether force for a latrunculin A-treated neutrophil (∼30 pN) at the cell retraction speed of 2,000 nm/s was much smaller than that for a normal neutrophil (∼60 pN) at the same retraction speed (Fig. 5C), which agrees well with the previous results for normal (∼65 pN) and latrunculin A-treated neutrophils (∼23 pN) at the same tether extraction speed (18, 33, 44).

Effect of osmolality, temperature, and cell type.

Osmolality, temperature, and cell type (e.g., lymphocyte) can all affect biochemical and biomechanical properties of living cells. Hypotonic buffer, which is required in the BFP study so that swollen erythrocytes can function as the force transducer, might alter neutrophil properties. To examine this possible alteration, we performed the neutrophil surface protrusion experiments in a buffer with an osmolality of ∼150 mosmol/kg. We found that the protrusional stiffness measured with CD162 was ∼0.05 to 0.08 pN/nm corresponding to the protrusional rates ranging from ∼320 to 4,200 nm/s, which is close to the range measured in isotonic media (Fig. 6A). Therefore, the protrusional stiffness did recover after the initial hypotonic shock in the BFP study by Evans et al. (5).

Fig. 6.

A: effect of osmolality and temperature on neutrophil surface protrusion under a point-pulling force. The forces were applied to CD162. B: protrusional stiffness of normal lymphocytes when pulling forces were applied to CD162 or CD44 individually. In both A and B, the protrusional stiffness of neutrophils in isotonic media at room temperature is also plotted for comparison. The error bars signify the standard deviations.

With a custom-built heating chamber that can maintain the medium temperature at 37°C (15), we applied pulling forces on neutrophils via CD162 with the OT. At 37°C, the protrusional stiffness was ∼0.06 to 0.09 pN/nm corresponding to the protrusional rates of ∼270 to 3,800 nm/s, which is similar to the values measured at room temperature at comparable protrusional rates (Fig. 6A).

Lymphocytes are similar to neutrophils in mechanical properties such as cortical tension (43) and membrane tether extraction (44). For comparison, we applied pulling forces on passive human lymphocytes via CD162 and CD44. As found in neutrophils, lymphocytes had apparently linear surface protrusion under constant force-loading rates corresponding to a range of cell retraction speeds (500 to 8,000 nm/s). The corresponding protrusional stiffness values were ∼0.06 to 0.11 pN/nm, and the corresponding protrusional rates were ∼280 to 3,600 nm/s, which are independent of receptor type and similar to the range of values for neutrophils (Fig. 6B).

DISCUSSION

Both surface protrusion and tether extraction from neutrophils have been visualized in flow chamber studies and recognized as key cellular features for stabilized neutrophil rolling (22, 25, 30, 45). Quantification of these features is therefore important to understanding the rolling process. Although surface protrusion may not contribute much to the adhesive force decline during neutrophil rolling, it is a critical step that precedes tether extraction and determines whether tether extraction can occur. Applying piconewton-level forces on specific adhesion receptors located either on the microvillus tip or in the nonmicrovillar region of neutrophils, we probed the protrusional stiffness, the crossover force, and the viscoelastic properties of neutrophil surface protrusion. The viscoelastic behavior of neutrophil surface protrusion was shown directly by force relaxation and hysteresis and indirectly by the dependence of the protrusional stiffness on the protrusional rate and the force-loading rate. The predictions from the three-parameter solid model for neutrophil surface protrusion are in excellent agreement with these experimental findings. In addition, we found that the protrusional stiffness and the crossover force were about the same no matter where the pulling forces were applied: the microvillus tip or the inte-microvillus region. These results indicate that, for the three receptors studied here, there is a common structural basis for the surface deformation generated by them and their cytoplasmic interactions with the actin cortex are comparable mechanically.

We found that disrupting F-actin in neutrophils abrogated the initial apparently linear response and led to direct tether extraction (zero crossover force), which indicates that the initial surface protrusion and the crossover force are dependent on the integral actin cortex. This is consistent with previous findings from similar experiments under hypotonic conditions (5). The actin cortex has been shown to be the most important cytoskeletal component for maintaining the morphology and mechanical properties of neutrophils (16, 18, 35, 38, 42, 49). Indeed, the membrane-cytoskeleton complex and the receptor-actin linkage both can contribute to the crossover force. We found that the crossover force did not depend on which receptor was pulled (Fig. 3B). Therefore, the linkages of CD162, CD44, and CD18 by moesin, ezrin, and talin, respectively (14, 29, 36, 48), to the cytoskeleton either did not contribute much to the crossover force or contributed almost equally at the force-loading rates used in this study.

We found that the protrusional stiffness did not depend on which receptor was pulled. This strongly indicates that surface protrusion was from a common structure, likely the composite of membrane and cytoskeleton. Some simple estimation based on the mechanics of actin filaments and cortex may also shed some light on the origin of surface protrusion. On the one hand, if the actin filaments inside the neutrophil microvilli are in parallel bundles like those in lymphocytes (16), the estimated protrusional stiffness of single microvilli with an average length of ∼0.35 μm (39) would be at least 20 pN/nm, calculated with the protrusional stiffness of single actin filaments with the same microvillar length (12). On the other hand, if we treat the actin cortex as an isotropic elastic spherical shell, the protrusional stiffness (k_a) corresponding to the initial tentlike deformation of this shell under a point load can be estimated by (27, 28)

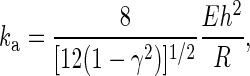(2)

where E, γ, R, h are the Young's modulus, Poisson's ratio, radius, and thickness of the actin cortex, respectively. Assume the bending rigidity of the actin cortex is B. Substituting the following relationship between E and B for E in Eq. 2 (13),

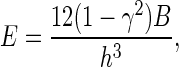(3)

we obtain

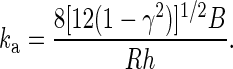(4)

On average, human neutrophils are ∼8.3 μm in diameter (34) and their actin cortex has a bending rigidity of ∼1 pN·μm and a thickness of ∼0.1 μm (49). The bending modulus of the lipid membrane is not likely to be the major contributor to the protrusional stiffness because it is one order of magnitude smaller than that of the actin cortex (11). Using these typical values for neutrophils in Eq. 4, we calculated the protrusional stiffness of the actin cortex under a point force at its apex to be ∼0.06 pN/nm, which is close to our measured protrusional stiffness at small pulling speeds and is much softer than that of a single actin filament in the microvillus. Therefore, when point piconewton-level pulling forces are applied on the tip of a microvillus, the microvillus itself would have negligible deformation relative to the deflection of the underlying actin cortex. The so-called microvillus extension is actually the local deflection of the underlying actin cortex rather than the extension of the microvillus itself. The excellent agreement between the estimated protrusional stiffness of the actin cortex and the measured value for neutrophil surface protrusion indicates that the initial surface protrusion is mainly due to the deformation of the cytoskeleton, especially the actin cortex. Since the number of microvilli on a neutrophil surface can be dramatically reduced by hypotonic swelling (8), forces applied on CD162 of neutrophils in hypotonic buffer were most likely applied to the intermicrovillus region. This supports our claim that the protrusional stiffness of neutrophils is mainly determined by the overall mechanical properties of the actin cortex, particularly its local cytoskeletal deformation. Our results from lymphocytes (Fig. 6B) further support this claim since most microvilli on lymphocytes have regular finger-like shapes (16). Nevertheless, the deflection around the surface receptor due to an applied pulling force can be quite localized as no deformation during surface protrusion was observable under an optical microscope.

In addition to the bending rigidity discussed above, the cortical tension of neutrophils might be another major determinant of the protrusional stiffness for neutrophil surface protrusion. It is well known that large neutrophil deformation is primarily regulated by the cortical tension (6). Recently, Liu et al. (15) found that higher temperature (∼37°C) resulted in a fourfold decrease in neutrophil cortical tension from ∼0.023 pN/nm at room temperature (∼22°C) to ∼0.006 pN/nm. However, they found only a slight decrease in the protrusional stiffness from ∼0.056 to ∼0.04 pN/nm with the method employed by Shao et al. (34). In this work, we found that neutrophils had about the same protrusional stiffness at these two different temperatures (Fig. 6A). Therefore, the bending rigidity of the actin cortex is very likely the one that dominates the local neutrophil surface protrusion under a point-pulling force, as in an elastic shell (13, 27, 28). Cellular tension or prestress likely involves the action of motor proteins; whereas the bending of the cytoskeletal components may be entirely structural, this may be why little change in the protrusional stiffness was detected at 37°C. Moreover, the structure of the actin cortex might be regulated by the neutrophil under different conditions so that its bending rigidity does not change.

Overall, our results agree well with the previous measurements of neutrophil protrusional stiffness with the MAT (34) and the BFP (5). In the MAT study, neutrophil surface protrusion was generated with pulling forces over longer time periods (several seconds), which naturally resulted in smaller stiffness because of apparent viscoelastic effects (∼0.043 pN/nm). Although the smallest protrusional rate (∼300 nm/s) used in the BFP study was comparable to that used in the MAT study (∼400 nm/s), a stiffer response was found (∼0.15 pN/nm). We suspected that the hypotonic buffer used in the BFP study might have caused this difference. Figure 6A has shown that this is not the case. We obtained more or less the same protrusional stiffness when using P-selectin-coated microspheres in the OT (J. Ying and J. Y. Shao, unpublished observations), so the difference in these two studies was not caused by the usage of ligand-decorated or antibody-coated probes either. Nevertheless, our data seem to agree well with the MAT measurement at small force-loading rates (∼20 pN/s) and with the BFP measurement at large force-loading rates (∼400 pN/s), which shows that it is really the force-loading rate that causes different cellular mechanical responses. Although faster cell retraction speeds are desired to achieve higher force-loading rates, nonspecific hydrodynamic suction forces can become significant enough to drag the bead to follow the cell retraction and thus lead to an apparently stiffer cell response (5). In the BFP study, a similar linear viscoelastic model for neutrophil surface protrusion was proposed to accommodate the discrepancy between the MAT and the BFP measurements of the protrusional stiffness (5). In this model, the parameters were obtained by fitting either the force or the deformation to the experimental measurements, which resulted in quite different parameters from the data obtained with different techniques, i.e., the characteristic time (t_c) = 0.5 s from the MAT data and t_c = 1.2–1.4 s from the BFP data (5). In the present study, the parameters were directly estimated from both the MAT and the OT measurements, and the same set of parameters accurately predicted the outcome of the viscoelastic experiments. Therefore, the parameters presented here can better represent neutrophil surface protrusion under a point-pulling force.

We focused on passive neutrophils in this study because they are more relevant to the rolling phenomenon. Coincidentally, the protrusional stiffness of passive neutrophils measured here is very close in magnitude to the intracellular uniaxial stiffness of crawling neutrophils measured by Yanai et al. (47). Furthermore, the characteristic relaxation time shown in Fig. 4 is very close to the ratio of viscosity to stiffness found by Yanai et al. In a later study (46), Yanai et al. found that the k value in the structural damping model was ∼0.5 (with k → 0 representing more elastic and k → 1 representing more viscous), which is strikingly close to the percentage of energy loss in our hysteresis measurement. Although the structural damping model fitted the data better than the viscoelastic model in the study by Yanai et al., the three-parameter solid model presented here precisely predicted our findings in relaxation and hysteresis and it is convenient to employ in numerical simulations. The structural basis for the three components in the three-parameter solid model is still unclear, although the rheological properties of passive neutrophils have been well studied by large cellular deformation and morphological recovery (6, 40, 43).

The extent of neutrophil surface protrusion was limited by either the rupture of the cell-bead adhesion or the crossover to tether extraction. Several mechanisms are possible for the rupture of the cell-bead adhesion: 1) breakage of the antibody-receptor bond, 2) breakage of the primary and secondary antibody bond on the bead surface, or 3) extraction of the receptor from the cell membrane. In a similar experimental setting, a detailed MAT study on the adhesion frequency and unbinding forces has shown that receptors were most likely extracted from the membrane in the event of adhesion rupture (32). The crossover from surface protrusion to tether extraction around the receptor site in the membrane is very intriguing. In general, there is little doubt that the tether is a lipid membrane cylinder, and there are no actin filaments inside the tether (26), therefore, no actin stretching is involved. However, the crossover to tether extraction could be caused by either direct membrane unbinding from the underlying actin cortex around the receptor site, or indirect membrane unbinding resulting from certain actin structural failure (the weakest link in the actin network). Either case of membrane unbinding would be consistent with our finding that the crossover force (∼30–45 pN) was independent of the receptor type. On the other hand, Evans et al. (5) showed that by pulling CD162 with the force-loading rates of ∼250 to 40,000 pN/s, the crossover force increased from ∼50 to 150 pN, showing the characteristic of a specific membrane-receptor (CD162)-cytoskeleton linkage (5). Therefore, these results together suggest that a phase transition might exist for the overall neutrophil membrane-receptor-cytoskeleton association for CD162-mediated tether extraction, i.e., from an adhesion apparently insensitive to small force-loading rates to one that is dependent on large force-loading rates. For future studies, it would be interesting to examine the crossover forces obtained by pulling other receptors (e.g., CD18 and CD44) at large force-loading rates and to compare with the crossover forces obtained with receptors that lack the cytoplasmic tails.

During the inflammatory response, neutrophil rolling on the endothelium is subjected to both hydrodynamic forces and molecular adhesive forces. The ultimate force balance and thus rolling dynamics can be greatly affected by the local surface deformation of the cell. The initial local apparently linear protrusion followed by membrane unbinding and tether extraction not only prevents large deformation of the cell body but also quickly lowers the forces on the adhesive bonds. This process has now been recognized as a key cellular feature that facilitates stable neutrophil rolling over a large range of shear stresses (22, 25, 30, 34, 45). With detailed knowledge of the mechanical properties of neutrophils, including surface protrusion, tether extraction, and their transition or crossover, we can establish accurate mathematical models to better understand the dynamic rolling process, which will eventually lead to rational intervention or control of this critical step in the inflammatory response under either physiological or pathological conditions.

GRANTS

This work was supported by the National Institutes of Health Grants R01 HL-069947 and R21/R33 RR-017014.

APPENDIX

Three-Parameter Solid Model for Neutrophil Surface Protrusion Under a Point Load

Similar to the phenomenological model proposed by Evans et al. (5) for neutrophil surface protrusion, we show here that the three-parameter solid model can describe neutrophil surface protrusion under a point load very well. More importantly, we show that this model can accurately predict force relaxation and hysteresis during neutrophil surface protrusion. The three-parameter solid model consists of a spring element connected in series to a Kelvin-Voigt element. The Kelvin-Voigt element that consists of a spring (k_c) in parallel with a viscous damper (η_c) is used to describe the slow neutrophil surface protrusion at long time scales (34), which can be represented well by these two parameters: k_c = 0.043 pN/nm and η_c 0.033 pN·s/nm, It has been shown by the OT and the BFP that the stiffness of neutrophil surface protrusion increases with the force-loading rate. Consequently, another stiffer elastic spring (k_m) is added in series with the Kelvin-Voigt element to describe the initial instantaneous apparently linear deformation at large force-loading rates.

The laser trap can also be described by a Kelvin-Voigt model consisting of a mechanical spring with calibrated stiffness (k_o = ∼0.08 pN/nm) and a viscous damper (η_o) imposed on the bead by the surrounding medium. The effective damping coefficient (η_o = ∼3.2×10⁻⁴ pN·s/nm) was estimated from the fast recovery of the bead deflection to the trap center. Since all the pulling speeds used in this study were <8,000 nm/s, the effect of this small retardation on the bead is negligible. Therefore, the trapped bead is considered simply as a spring of which its deformation was not impeded by any viscous drag. The OT spring is connected in series with the three-parameter solid model of the neutrophil that is pulled at a constant speed, u. Thus the force on the neutrophil (f) and the resulting neutrophil surface protrusion (ΔL) are given, respectively, by

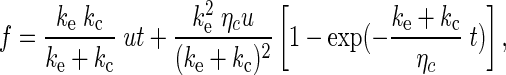(A1)

and

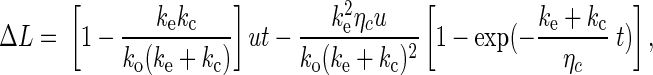(A2)

where

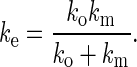The protrusional stiffness data in this study (Fig. 3A) can be represented well by assigning a value of 0.12 pN/nm to k_m. With these parameters, the same model can be used to predict force relaxation and hysteresis. If the pulling is done for only a short period of time as in the OT study, the neutrophil surface protrusion will appear to be linear elastic; if the pulling is done for a longer period of time as in the MAT study, the neutrophil surface protrusion will appear to be viscoelastic.