Analysis of Case-Control Studies of Genetic and Environmental Factors With Missing Genetic Information and Haplotype-phase Ambiguity

Abstract

Case-control studies of unrelated subjects are now widely used to study the role of genetic susceptibility and gene-environment interactions in the etiology of complex diseases. Exploiting an assumption of gene-environment independence, and treating the distribution of the environmental exposures to be completely nonparametric, Chatterjee and Carroll (2005) recently developed an efficient retrospective maximum-likelihood method for analysis of case-control studies. In this article, we develop an extension of the retrospective maximum-likelihood approach to studies where genetic information may be missing on some study subjects. In particular, special emphasis is given to haplotype-based studies where missing data arises due to linkage-phase ambiguity of genotype data. We use a profile likelihood technique and an appropriate EM algorithm to derive a relatively simple procedure for parameter estimation, with or without a rare disease assumption, and possibly incorporating information on the marginal probability of the disease for the underlying population. We also describe two alternative robust approaches that are less sensitive to the underlying gene-environment independence and Hardy-Weinberg-Equilibrium assumptions. The performance of the proposed methods are studied using simulation studies in the context of haplotype-based studies of gene-environment interaction. An application of the proposed method is illustrated using a case-control study of ovarian cancer designed to study the interaction between BRCA1/2 mutations and reproductive risk factors in the etiology of ovarian cancer.

1 Introduction

Risks of complex diseases, such as cancers, are determined by both genetic and environmental factors. Advances in human genome research have thus led to epidemiologic investigations not only of the effects of genes alone, but also of their effects in combination with environmental exposures. The case-control study design, which has been widely used in classical questionnaire based epidemiologic studies, is now being increasingly used to study the role of genes and gene-environment interactions in the etiology of complex diseases.

The traditional approach for analysis of case-control studies is prospective logistic regression. Here the basis of inference is formed by the likelihood of the disease (D) outcome data conditional on covariate information (X) ignoring the fact that under the case-control sampling design data are observed on X conditional on D. Andersen (1970) and Prentice and Pyke (1979) showed that such a prospective approach is actually equivalent to the retrospective maximum likelihood analysis that properly accounts for the case-control sampling design, provided that the distribution of the covariates are treated completely nonparametrically. Roeder et al. (1996) generalized these results to show that even in the presence of covariate missing data or/and measurement error, the prospective and retrospective maximum-likelihood methods for analyzing case-control studies are equivalent as long as the underlying model for the covariate distribution is nonparametric.

In studies of genetic epidemiology, it often may be reasonable to assume certain parametric or semi-parametric models for the covariate distribution in the underlying source population. For example, if G represents one of the three possible genotypes a subject can have at a particular bi-allelic locus, the population frequencies of the three genotypes could be specified in terms of the allele frequency of one of the alleles under the Hardy-Weinberg Equilibrium (HWE) assumption. Another assumption that is commonly invoked in practice is that genetic susceptibility and environmental exposures are independently distributed in the population. The prospective logistic regression analysis, being the semiparametric maximum likelihood solution for the problem that allows an arbitrary covariate distribution, clearly remains a valid option for analyzing case-control studies in such setting. However, retrospective methods that can exploit these various covariate distributional assumptions can be more efficient (Epstein and Satten, 2003; Satten and Epstein, 2004; Chatterjee and Carroll, 2005).

Chatterjee and Carroll (2005) developed a retrospective maximum-likelihood approach for analysis of case-control studies exploiting the gene-environment independence and possibly the HWE assumption. In this article, we extend this approach for dealing with missing data on genetic risk factors (G). Missing data on genetic factors could arise due to incomplete genotyping information. Moreover, in haplotype-based studies, where the effect of a gene is studied in terms of ‘haplotypes’, the combination of alleles at multiple loci along individual chromosome, missing data arises due to intrinsic “phase ambiguity” of the locus-specific genotype data. For example, if A/a and B/b denote the major/minor alleles in two bi-allelic loci, then subjects with genotypes (Aa) and (Bb) at the first and the second locus, respectively, are considered “phase ambiguous”: their genotypes could arise from either the haplotype-pair (A-B,a-b) or the haplotype-pair (A-b, a-B).

As haplotype-based association studies are becoming increasingly popular, a number of researchers have developed methods for logistic regression analysis of case-control studies in the presence of phase ambiguity. Zhao et al. (2003) described an estimating-equation approach where the logistic regression parameters are estimated based on score-equations derived from a prospective likelihood of the disease outcome data given covariates. The estimates of the haplotype frequencies, which are required for evaluation of the prospective score-equations, were proposed to be estimated using an EM algorithm (Excoffier and Slatkin, 1995) applied to the genotype data of the controls. Lake et al (2003) described a similar prospective approach, except that they proposed estimating the haplotype-frequencies jointly with the regression parameters from the prospective likelihood itself. Incorporation of environmental factors is straightforward in these approaches under the assumption of gene-environment independence.

Epstein and Satten (2003) described an alternative approach for haplotype-based analysis of case-control studies that jointly estimates the regression parameters and haplotype-frequencies by maximizing the proper retrospective likelihood of the data under the case-control sampling design. The authors observed that the retrospective likelihood approach yielded more efficient estimates of the regression parameters than the previously proposed prospective methods, a consequence of the fact that the former approach fully exploited the HWE assumption for the underlying population. Incorporation of environmental factors, however, is complicated in this approach because the retrospective likelihood involves potentially high dimensional nuisance parameters that specify the distribution of the environmental factors in the underlying population. Stram et al (2003) described yet another approach based on the joint likelihood of the disease and genotype data, after accounting for the ascertainment scheme that cases and control are selected with differential probabilities from the underlying population. We will show later that an extension of this ascertainment-corrected-joint-likelihood method, which can incorporate environmental covariates, is equivalent to the retrospective-maximum likelihood method we propose in this article.

In this article, we extend the profile likelihood approach of Chatterjee and Carroll (2005) to develop a relatively simple algorithm for obtaining the efficient retrospective maximum-likelihood estimator for case-control studies that can incorporate both genetic and environmental factors and can account for the presence of missing data in the genetic factors. In Section 2, we first describe the key results for derivation of the profile likelihood and related asymptotic theory in a general missing data setting. In Section 3.1 we describe a representation of the profile likelihood that links the retrospective-maximum-likelihood procedure to the ascertainment-corrected joint likelihood approach of Stram et al. (2003). In Sections 3.2–3.3, we describe a computational algorithm for implementation of the profile likelihood method in the context of haplotype-based gene-environment interaction studies. Further simplification of the proposed methodologies under the rare disease assumption is also described.

In Section 3.4, we describe extension of the methods to account for possible correlation between genetic and environmental factors that may arise due to their dependence on other common factors, such as ethnicity. In Section 3.5, we describe a modified prospective estimating equation approach that is fairly robust to violation of the gene-environment independence and HWE assumptions. We discuss how this latter approach contrasts with some of the recently proposed “prospective” method that could be inconsistent under the case-control design, even if the true haplotype-frequencies were known and the model assumptions were valid. In Section 4, we study the performance of the proposed estimators using simulated data in the context of gene-environment interaction studies involving haplotypes. In Section 5, we illustrate the application of the proposed method based on a case-control study of ovarian cancer aiming to study the interaction of reproductive risk factors and BRCA1/2 mutation.

2 Methods: The General Setting

2.1 Notations and model assumptions

Let D be the binary indicator of the presence, D = 1, or the absence, D = 0, of a disease. Suppose the prospective risk model for the disease given a subject’s genetic covariate of interest, H, and environmental risk factors, X, is given by the logistic regression model pr(D = 1|H, X) = ℒ{β₀ + m(H, X; β₁)} is the logistic, where ℒ(u) = {1 + exp(−u)}⁻¹ distribution function and m(·) is a known but arbitrary function. We assume H and X are independently distributed in the underlying population and their joint distribution is given by the product form V (H, X) = Q(H)F(X), where Q and F are the marginal distribution functions of H and X, respectively. We assume H is discrete with pr(H = H_j) = q(H_j; θ) where q(·) is a known function and θ is a vector of parameters. The environmental covariates X can be of arbitrary type, possibly including both continuous and discrete components. The corresponding distribution F(x) is left completely unspecified.

Suppose that the true genetic covariate of interest, H, may not be always directly observed. Let G denote all the genetic information for a subject that is directly observed. We assume that G is independent of (D, X) given H, i.e., G does not contain any additional information on D and X given H. Let Δ be a variable whose values indicate what sort of genetic information is measured in G. For example, in a haplotype-based study, we could have

$$\mathrm{\Delta }=\{\begin{array}{ll}1\hfill & \text{if}\text{no}\text{genetic}\text{information}\text{is}\text{measured};\hfill \\ 2\hfill & \text{if}\text{unphased}\text{genotypes}\text{are}\text{measured};\hfill \\ 3\hfill & \text{if}\text{phased}\text{haplotypes}\text{are}\text{measured}.\hfill \end{array}$$

Suppose that N₀ controls and N₁ cases are sampled from the conditional distributions pr(Δ, G, X|D = 1) and pr(Δ, G, X|D = 0), respectively, and let ${(G_i,X_i)}_{i=1}^{N_0+N_1}$ denote the corresponding covariate data of the N₀ + N₁ study subjects. We assume pr(Δ|D, X, H) = pr(Δ|D, X, G), i.e., the type of genetic information measured does not depend upon the individual’s true genetic covariate (H) given the disease status (D), environmental covariates (X) and the measured genetic information (G).

Define ℋ to be the set of all possible values of H and ℋ_G = {h_j:h_j is consistent with G} to be the set of all possible values of H that are consistent with the observable genetic information G. Then,

$$\begin{array}{l}\text{pr}(D\mid X,G)=\sum _{h\in {\mathcal{H}}_G}\text{pr}(D\mid X,H=h,G)\text{pr}(H=h\mid X,G)\\ =\sum _{h\in {\mathcal{H}}_G}\text{pr}(D\mid X,H=h)\text{pr}(H=h\mid G)=\sum _{h\in {\mathcal{H}}_G}\frac{\text{pr}(D\mid X,H=h)q(h;\theta )}{{\sum }_{h^{\prime }\in {\mathcal{H}}_G}q(h^{\prime },\theta )}.\end{array}$$

The log-likelihood of the data under the case-control sampling scheme assuming the above model is given by

$$L=\sum _{i=1}^{N_0+N_1}log\{\text{pr}(G_i,X_i\mid D_i)\}=\sum _{i=1}^{N_0+N_1}log\{\text{pr}(D_i\mid G_i,X_i)\text{pr}(G_i\text{)pr}(X_i)/\text{pr}(D_i)\},$$ (1)

where

$$\text{pr}(D_i)={\int }_x\sum _{h\in \mathcal{H}}\text{pr}(D_i\mid X=x,H=h)\text{pr}(H=h)dF(x).$$

2.2 Identifiability

In a nonparametric setting, where no assumption is made about the form of the covariate distribution V (h, x), it is well known that neither V (·) nor the intercept parameter β₀ is identifiable from case-control data (Prentice and Pyke, 1979). In contrast, under the assumption of gene-environment independence, Chatterjee and Carroll (2005) noted that except for some boundary situations, the intercept parameter β₀ and the covariate distribution V (·) are identifiable from the retrospective case-control likelihood. In general, the identifiability of β₀ is intrinsically related to the class of V (·) that is under consideration.

In the presence of missing data on H, the identifiability of the parameter estimates also depends on the nature of missing data and the form of the functions m(H, X, β₁) and q(H, θ). In haplotype-based studies, for example, where H reflects the pair of haplotypes (diplotypes) a subject carries in two homologous chromosomes, certain diplotypes may never be directly observable from the unphased genotype data. In such a situation, identifiability of parameter estimates requires specifying the distribution q(H, θ) using the HWE assumption (see Section 3) and restricting the model m(H, E, β₁) so that it does not involve interaction between pairs of haplotypes which are never directly observed together. For the subsequent calculations, we will assume that depending on the missing data structure of H, the model q(H; θ) and m(H, X, β₁) are chosen in such a way that all of the parameters β₀, β₁, θ and the nonparametric distribution function F(x) are identifiable from prospective studies. In what follows, we state easily verifiable conditions for identifiability of parameters of a prospective model from retrospective studies.

We will assume X to be discrete with K possible values. Although the results we state below can be expected to hold for continuous X, a rigorous proof would require a more sophisticated argument. Let q(G) and f(X) denote the marginal probability mass functions for G and X in the underlying population. Further define

$$\phi (G,X)=log\frac{\text{pr}(D=1\mid G,X)\text{pr}(D=0\mid G_0,X_0)}{\text{pr}(D=0\mid G,X)\text{pr}(D=1\mid G_0,X_0)}$$

to be the log-odds-ratio of the disease associated with the joint-exposure (G, X) in reference to a chosen baseline value (G₀, X₀) and let α = logit{pr(D = 1|G₀, X₀)}, so that α is the corresponding baseline odds of the disease. With slight abuse of notation, let f, q and φ denote the vectors that contain the values of f(X), q(G) and φ(G, X), respectively, for distinct values of X and G. We note that the parameter vector ϑ = (α, φ^T, ψ^T, f^T)^T completely characterizes the joint distribution pr(D, G, X). It is clear that φ is identifiable from retrospective studies because prospective and retrospective odds-ratios are equivalent. In the following Lemma, we state conditions under which the other components of ϑ are identifiable from retrospective studies.

Lemma 1

Define α^* = α + log[{N₁pr_ϑ(D = 0)}/{N₀pr_ϑ(D = 1)}]. Let ℬ₀ ⊂ ℬ be the subspace for the parameter vector ϑ that satisfies the constraint

$$V^{\ast }(G,X)\equiv \frac{[1+exp\{{\alpha }^{\ast }+\phi (G,X)\}]{[1+exp\{\alpha +\phi (G,X)\}]}^{-1}q(G)f(X)}{{\sum }_{g,x}[1+exp\{{\alpha }^{\ast }+\phi (g,x)\}]{[1+exp\{\alpha +\phi (g,x)\}]}^{-1}q(g)f(x)}=q^{\ast }(G)f^{\ast }(x)$$ (2)

for some probability mass functions q^*(G) and f^*(X). Then, for all ϑ ∉ ℬ₀,

$${\text{pr}}_{\vartheta }(X=x,G=g\mid D=d)={\text{pr}}_{\vartheta \ast }(E=e,G=g\mid D=d)$$

if and only if ϑ = ϑ^*. Moreover, if the model q(H; θ) and m(H, X, β₁) are chosen in such a way that γ = (β₀, β₁, θ) are uniquely identifiable from the prospective-likelihood pr(D, G, X), then for all γ ∉ Γ₀ ≡ {γ:ϑ(γ) ∈ Θ₀},

$${\text{pr}}_{\gamma }(X=x,G=g\mid D=d)={\text{pr}}_{\gamma \ast }(E=e,G=g\mid D=d)$$

if and only if γ = γ^*

Lemma 1 first ensures the conditions under which the joint distribution pr(D, G, X) of the observable variables (D, G, X) can be nonparametrically identified from retrospective studies. Further, it states the condition under which the parameters β₀, β₁, θ, that characterizes the joint distribution pr(D, H, X) involving the potentially unobservable variable H, can be identified from the retrospective studies. The proof of our Lemma 1 follows from Lemma 1 of Roeder, et al (1996), which states that the V^*(G, X) is the only distribution of (G, X) that can yield the same value of the retrospective-likelihood as the true distribution V (G, X) = q(G)f(X). Now, for ϑ ∉ ℬ₀, V^*(G, X) lies outside the model-space under consideration that assumes G and X are independent. Thus, for ϑ ∉ ℬ₀, the retrospective-likelihood uniquely identifies the joint distribution V (G, X), which together with the odds-ratio parameters φ(G, X) further identifies the intercept parameter α.

Consider the hypothetical population 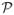^* that could be obtained by sampling each subject from the original population 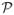according to a Bernoulli sampling with the selection probability for the cases and controls being proportional to N₁/pr(D = 1) and N₀/pr(D = 1). A case-control sample from the population 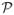can be viewed as a random sample from the population 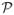^*. Moreover, with some algebra it can be seen that V^*(G, X) represents the distribution of (G, X) for the selected population 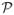^*. Thus the constraint (2) can be checked in the data by testing for independence of G and X in the combined case-control sample. The boundary condition (2) implies that if G and X are assumed to be independently distributed in the underlying population, then the departure of the distribution of (G, X) in the case-control sample from independence is informative for estimation of V (G, X) and α. Similarly, if certain parametric models, such as HWE, are assumed to hold for q(G) in the underlying population, then the departure of the distribution of G in the case-control sample from the assumed parametric models is informative for estimation of q(G) and α.

2.3 Estimation

Now we consider maximization of L with respect to the underlying parameters of the model,β₀, β₁, θ, and the nonparametric distribution function F(x). We consider the restricted nonparametric maximum likelihood estimator of F that allows positive masses only within the set 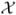= {x₁, …, x_K} that represents the unique values of X that are observed in the case-control sample of N = N₀ + N₁ study subjects. Thus, for obtaining the maximum likelihood estimator it is sufficient to consider the class of discrete F that have support points within the set 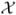. Any F in this class can be parameterized with respect to the probability masses {δ₁, …, δ_K} that it assigns to the points {x₁, …, x_K}.

Since the dimension of δ could easily becomes very large when X consists of multiple covariates, possibly including continuous ones, direct maximization of the log-likelihood with respect to (β₀, β₁, θ, δ) may be complex or even infeasible. Following Chatterjee and Carroll (2005) we consider deriving the profile likelihood for the lower dimensional parameters γ = (β₀, β₁, θ) by maximizing the likelihood with respect to δ for fixed values of γ. The result in the following lemma shows that the profile likelihood L{γ, δ̂(γ)} can be obtained in a closed form up to only one additional parameter κ and thus numeric maximization of the likelihood L(γ, δ) with respect to the potentially high-dimensional nuisance parameter δ can be avoided.

Lemma 2

Let κ = β₀+log[{N₁pr(D = 0)}/{N₀pr(D = 1)}], Ω = (γ, κ) and S(D, X, H, Ω) = q(H, θ) exp[D{κ + m(X, H, β₁)}]/[1 + exp{β₀ + m(X, H, β₁)}]. The profile loglikelihood L{γ, δ̂(γ)} can be computed as L^*{γ, κ̂(γ)} where

$$L^{\ast }(\gamma ,\kappa )=\sum _{i=1}^N[log\{\sum _{h_j\in {\mathcal{H}}_{G_i}}S(D_i,X_i,h_j,\mathrm{\Omega })\}-log\{\sum _{d=0}^1\sum _{h_j\in \mathcal{H}}S(d,X_i,h_j,\mathrm{\Omega })\}]$$ (3)

and κ̂(γ) is defined by the solution of the equation ∂L^*(κ, γ)/∂κ = 0 for fixed γ.

The proof of the Lemma is given in the Appendix.

In the above approach, for rare diseases, the estimate of the parameter β₀ itself can be expected to be imprecise because of intrinsic noninformativeness of the retrospective likelihood. Much more precise estimation of β₀ is possible when the marginal probability of the disease, pr(D = 1) = p₁, for the underlying population is known, which is often the case for case-control studies conducted within a well defined population or an established cohort. In this case, we observe that κ and β₀ are uniquely determined from each other based on the formula

$$\kappa ={\beta }_0+log\frac{N_1}{N_0}-log\frac{p_1}{1-p_1}.$$ (4)

Thus the profile-likelihood can be defined in terms of the reduced set of parameters Ω = (β₀, β₁, θ). Hereafter, we will use the generic notation Ω so that our results are valid for both the cases of pr(D = 1) being known and pr(D = 1) being unknown, with the convention that Ω = (β₀, β₁, θ) in the former case and Ω = (β₀, κ, β₁, θ) in the latter case.

The score function is given by $\partial L^{\ast }(\mathrm{\Omega })/\partial \mathrm{\Omega }={\sum }_{i=1}^N\mathrm{\Psi }(D_i,X_i,G_i,\mathrm{\Omega })$ where

$$\mathrm{\Psi }(D_i,X_i,G_i,\mathrm{\Omega })=\frac{{\sum }_{h\in {\mathcal{H}}_{G_i}}{S}_{\mathrm{\Omega }}(D_i,X_i,h,\mathrm{\Omega })}{{\sum }_{h\in {\mathcal{H}}_{G_i}}S(D_i,X_i,h,\mathrm{\Omega })}-\frac{{\sum }_{d=0,1}{\sum }_{h_j\in \mathcal{H}}{S}_{\mathrm{\Omega }}(d,X_i,h_j,\mathrm{\Omega })}{{\sum }_{d=0,1}{\sum }_{h_j\in \mathcal{H}}S(d,X_i,h_j,\mathrm{\Omega })}$$

and S_Ω(D_i, X_i, H, Ω) = ∂S_Ω(D_i, X_i, H, Ω)/∂Ω. Further define I = −N⁻¹E{∂²L^*(Ω)/∂Ω∂Ω^T}, with the expectation being taken under the case-control sampling design. Let

$$\mathrm{\Lambda }=\sum _{d=0}^1(N_d/N)\text{E}\{\mathrm{\Psi }(\mathrm{\Delta },D,X,G,\mathrm{\Omega })\mid D=d\}{[\text{E}\{\mathrm{\Psi }(\mathrm{\Delta },D,X,G,\mathrm{\Omega })\mid D=d\}]}^{\text{T}}.$$

In the following lemma we state the main asymptotic result, which in turn is used to obtain estimates of the asymptotic variance-covariance matrix of the parameter estimates.

Theorem 1

Under suitable regularity conditions, the following results hold:

1. The estimating equations $\partial L^{\ast }/\partial \mathrm{\Omega }\equiv {\sum }_{i=1}^N\mathrm{\Psi }({\mathrm{\Delta }}_i,D_i,X_i,G_i,\mathrm{\Omega })=0$ have a unique, consistent sequence of solutions, {Ω̂}^N _N≥1;

2. Moreover, N^1/2 (Ω̂^N − Ω₀) → Normal(0, Σ) in distribution, with Σ = I⁻¹ − I⁻¹ΛI⁻¹.

3 Haplotype-Based Gene-Environment Studies

3.1 Background, Notation and Model

For haplotype-based studies, the underlying genetic factor (H) of interest for a subject is defined by “diplotypes”, that is, the two haplotypes the individual carries in his/her pair of homologous chromosomes, where each “haplotype” is the combination of alleles at the loci of interest along an individual chromosome within the genomic region of interest. We denote the diplotype data for subject by H^d = (H₁, H₂) where H₁ and H₂ denote the constituent haplotypes. The diplotype data however, is not directly observable using standard PCR methods. Instead, for each subject, the multi-locus genotype data G is observed, which contain information on the pair of alleles the subject carries on the pair of homologous chromosomes at each locus, but does not provide the “phase information”, that is which combination of alleles appears along each of the individual chromosomes. Thus, the same genotype data G could be consistent with multiple diplotypes. We will denote ${\mathcal{H}}_{\mathbf{G}}^d$ to be the set of all possible diplotypes that are consistent with the genotype data G. We observe that for subjects who carry two copies of the same allele (homozygous genotype) at all loci or all but one locus, the diplotype information is uniquely identifiable. It is for the subjects who are heterozygous at two or more loci that the phase remains ambiguous.

Given the diplotype data H^d and environmental covariate X, we assume the risk of the disease is given by the logistic regression model

$$\text{logit}\{\text{pr}(D=1\mid H^d,X)\}={\beta }_0+m(H^d,X;{\beta }_1).$$

Often, one imposes structural assumptions on the risk associated with H^d by modelling its effect through the constituent haplotypes according to a dominant, additive or recessive model (Wallenstein, Hodge, and Weston, 1998). Such modelling may be necessary due to identifiability considerations (Epstein and Satten, 2003). Such modelling may also be desirable when the effects of the haplotypes themselves are of direct scientific interest. For example, a logistic regression model which assumes an additive effect for each copy of a haplotype (additive model) corresponds to

$$m\left\{H^d=(h_1,h_2),X;{\beta }_1\right\}={\beta }_{X}X+{\beta }_{h_1}+{\beta }_{h_2}+{\beta }_{h_1:X}X+{\beta }_{h_2:X}X,$$

where β_X is the main effect of X, β_hi is the main effects of haplotypes h_i, i = 1, 2 and β_hiX is the interaction effect of X with haplotype h_i, i = 1, 2.

We assume that H^d is independent of X in the population. Moreover, we assume that the distribution of the diplotypes is specified by the Hardy-Weinberg-Equilibrium (HWE)

$$\begin{array}{l}{\text{pr}}_{\theta }\left\{H^d=(H_i,H_j)\right\}={\theta }_i^2\text{if}{H}_i=H_j\\ =2{\theta }_i{\theta }_j\text{if}{H}_i\ne H_j,\end{array}$$ (5)

where θ_i denotes the frequency for haplotype H_i.

In the following, we present an alternative representation of L^*that links the retrospective-maximum-likelihood approach to an extension of the approach of Stram et al. (2003) to account for environmental covariates. For algebraic convenience we now introduce some further notations. Define

$$r_{\mathrm{\Omega }}(h^d,X)=\frac{1+exp\{\kappa +m(h^d,x,{\beta }_1)\}}{1+exp\{{\beta }_0+m(h^d,x,{\beta }_1)\}}.$$

Consider a sampling scenario where each subject from the underlying population is selected into the case-control study using a Bernoulli sampling scheme where the selection probability for a subject given his/her disease status D = d is proportional to μ_d = N_d/pr(D = d). Let R = 1 denote the indicator of whether a subject is selected in the case-control sample under the above Bernoulli sampling scheme. We observe the following probability equalities

$$S(D,H^d,X,\mathrm{\Omega })=\text{pr}(D\mid H^d,X,R=1)q(H^d;\theta )r_{\mathrm{\Omega }}(H^d,X),$$ (6)

$$\text{pr}(D=1\mid H^d,X,R=1)={[1+exp\{-\kappa -m(H^d,X,{\beta }_1)\}]}^{-1},$$ (7)

$$\text{pr}(H^d\mid D,G,X,R=1)=\frac{\text{pr}(D\mid H^d,X,R=1)\text{pr}(H^d\mid X,R=1)}{{\sum }_{h^d\in {\mathcal{H}}_G}\text{pr}(D\mid H^d=h^d,X,R=1)\text{pr}(H^d=h^d\mid X,R=1)}$$ (8)

and

$$\text{pr}(H^d\mid X,R=1)=\frac{q(H^d;\theta )r_{\mathrm{\Omega }}(H^d,X)}{{\sum }_{h^d}q(h^d,\theta )r_{\mathrm{\Omega }}(h^d,X)}.$$ (9)

With some algebra, one can now show that the log-profile-likelihood given in Lemma 1 can be expressed in the form

$$\begin{array}{l}{L}^{\ast }=\sum _{i=1}^{N}log[\sum _{h^d\in {\mathcal{H}}_{G_i}^d}\text{pr}(D_i\mid H_i^d=h^d,X_i,R_i=1)\text{pr}(H_i^d=h^d\mid X_i,R_i=1)]\\ =\sum _{i=1}^{N}log[\sum _{h^d\in {\mathcal{H}}_{G_i}^d}\text{pr}(D_i,H_i^d=h^d\mid X_i,R_i=1)]\\ =\sum _{i=1}^{N}log\{\text{pr}(D_i,G_i\mid X_i,R_i=1)\}.\end{array}$$ (10)

When no environmental factors are involved, Stram et al. (2003) proposed analysis of haplotype-based case-control studies using an “ascertainment corrected joint-likelihood” of the form Π_i pr(Y_i, G_i|R_i = 1). The representation of the profile likelihood L^* given in (10) suggests that when F(x) is treated completely nonparametrically, the efficient retrospective maximum-likelihood estimate of the haplotype frequency and the regression parameters can be obtained by conditioning on X in the approach of Stram et al (2003).

In the next two sections we develop an algorithm for estimating Ω = (κ, β₁, θ) using L^* assuming pr(D = 1) is known. Then we describe modification of the methods required when pr(D = 1) is unknown.

3.2 Estimation of Haplotype Frequencies

Here, we describe an estimation method for the haplotype-frequency parameters (θ) for fixed (κ, β). Let N_k(H^d) be the number of copies of haplotype H_k contained in the diplotype H^d. Note N_k(H^d) could be 0,1 or 2. The value of θ that maximizes L^* with the constraints ${\sum }_{k=1}^K{\theta }_k=1$ will satisfy the equation

$$\frac{\partial }{\partial {\theta }_k}\left\{L^{\ast }+\lambda \sum _k{\theta }_k\right\}=0.$$

The resulting estimating equation can be shown to be

$$0=\sum _{i=1}^N{E}_{\mathrm{\Omega }}[\frac{\partial log\{q(H;\theta )\}}{\partial {\theta }_k}\mid D_i,G_i,X_i,R=1]-\sum _{i=1}^N{E}_{\mathrm{\Omega }}[\frac{\partial log\{q(H;\theta )\}}{\partial {\theta }_k}\mid X_i,R=1]+\lambda ,$$ (11)

where ∂log{pr_θ(H)}/∂θ_k = N_k(H)/θ_k and the expectations in the first and second terms are taken with respect to the distribution pr(H^d|D, G, X, R = 1) (see formula 8) and pr(H^d|X, R = 1) (see formula 9), respectively. Now multiplying the estimating equation (11) by θ_k, summing it over k, and using the fact that ${\sum }_{k=1}^K{N}_k(H^d)=2$ we can show that λ = 2N − 2N = 0. Thus, we have shown that the estimating function for θ is given by

$$\sum _{i=1}^N{E}_{\mathrm{\Omega }}\left\{N_k(H^d)\mid D_i,G_i,X_i,R=1\right\}-\sum _{i=1}^N{E}_{\mathrm{\Omega }}\left\{N_k(H^d)\mid X_i,R=1\right\}.$$ (12)

Now we notice that

$$\sum _{i=1}^N{E}_{\mathrm{\Omega }}\left\{N_k(H^d)\mid X_i,R=1\right\}={\theta }_k\sum _{i=1}^N\frac{{\sum }_{h_k^{\prime }}2{\theta }_{k^{\prime }}{r}_{\mathrm{\Omega }}\{H^d=(h_k,h_k^{\prime }),X_i\}}{{\sum }_{h^d}{\text{pr}}_{\theta }(H^d=h^d)r_{\mathrm{\Omega }}(h^d,X_i)}.$$

This representation suggests the following iterative approach for solving (12) in terms of θ:

$${\theta }_k^{(s+1)}=N_k^{(s)}{\left\{\sum _{i=1}^N\frac{{\sum }_{h_k^{\prime }}2{\theta }_{k^{\prime }}^{(s)}{r}_{\mathrm{\Omega }}\{H^d=(h_k,h_k^{\prime }),X_i\}}{{\sum }_{h^d}{\text{pr}}_{{\theta }^{(s)}}(H^d=h^d)r_{\mathrm{\Omega }}(h^d,X_i)}\right\}}^{-1}$$ (13)

where $N_k^{(s)}={\sum }_{i=1}^N{E}_{\mathrm{\Omega }=(\kappa ,\beta ,{\theta }^{(s)})}\left\{N_k(H^d)\mid D_i,G_i,X_i,R=1\right\}$ is the expected count for the k^th haplotype under the current parameter estimates. We observe that by definition, ${\theta }_k^{(s)}>0$. Further, in each iteration we will normalize ${\theta }_k^{(s+1)}={\theta }_k^{(s+1)}/{\sum }_{k^{\prime }=1}^K{\theta }_k^{(s+1)}$. Thus, we note that the estimate of haplotype-frequencies using formula (13) is given by the expected haplotype-count as a ratio of an “effective sample-size” formula.

3.3 Estimation of β₁ and κ

Define β^*= (κ, β₁). The estimating equation corresponding to ∂L^*/∂β^* = 0 can be written in the form (B1) + (B2) + (B3) = 0, where

$$\begin{array}{l}(B1)=\sum _i{E}_{\mathrm{\Omega }}\left[\frac{\partial }{\partial {\beta }^{\ast }}log\{{\text{pr}}_{{\beta }^{\ast }}(D_i\mid H^d,X_i,R=1)\}\mid D_i,G_i,X_i,R_i=1\right];\\ (B2)=\sum _i{E}_{\mathrm{\Omega }}\left[\frac{\partial }{\partial {\beta }^{\ast }}log\{r_{\mathrm{\Omega }}(H^d,X_i)\}\mid D_i,G_i,X_i,R=1\right];\\ (B3)=-\sum _i{E}_{\mathrm{\Omega }}\left[\frac{\partial }{\partial {\beta }^{\ast }}log\{r_{\mathrm{\Omega }}(H^d,X_i)\}\mid X_i,R_i=1\right].\end{array}$$

Let V_β^*(Ω) = (B2) + (B3) We propose to estimate β^* by iteratively solving

$$\sum _{i=1}^N{E}_{{\mathrm{\Omega }}^{(t-1)}}\left[\frac{\partial }{\partial {\beta }^{\ast }}log\{{\text{pr}}_{{\beta }^{\ast }}(D_i\mid H,X_i,R=1)\}\mid D_i,G_i,X_i,R=1\right]=-V_{{\beta }^{\ast }}({\mathrm{\Omega }}^{(t-1)}),$$ (14)

We observe that the estimating equations given in (14) are similar to the corresponding estimating equations for β₀ and β₁ in a logistic regression model in the presence of missing data, except that we are equating them to a non-zero term. Because of the similarity with the parameter estimation in standard logistic regression model, we can get a fairly stable algorithm for solving these equations.

Unknown pr(D = 1)

We observe that in the calculations given above, the value of pr(D = 1) is only needed to get an estimate β₀ from the estimate of κ. Moreover, the parameter β₀ enters into computation only through the function r_Ω(H, X). If we assume rare disease, then we have

$$r_{\mathrm{\Omega }}(H,X)\approx 1+exp\{\kappa +m(H,X;{\beta }_1)\}.$$ (15)

Thus, if one assumes rare disease, β₀ need not be estimated and hence pr(D = 1) need not be known. Under this rare disease approximation, the proposed retrospective maximum-likelihood method reduces to that of Epstein and Satten (2003) in the absence of environmental covariates. If one is not willing to make the rare disease assumption, we propose to estimate θ, κ and β₁ by maximizing L^* for fixed values of β₀ and then do a one-dimensional grid-search to find the estimate of β₀ that maximizes the profile likelihood L^*(β₀, β̂^*(β₀), θ̂(β₀)). We have found that the grid-search method performs very well for unbiased estimation of the odds-ratio parameters (β₁) of interest, see Table 2, unknown pr(D = 1). The estimates of the intercept parameter β₀, however, are typically imprecise. Gains in precision are possible if one places reasonable bounds on pr(D = 1).

Table 2.

The results from 1000 simulated case-control studies from a population under HWE, with independent distributions for haplotypes (H) and environmental covariates (X). Each replicate contains 1000 cases and 1000 controls and is analyzed using the proposed retrospective maximum-likelihood method assuming HWE and H-X independence. Estimates are shown (a) using the known probability of the disease in the population and (b) estimating the probability from the data using the grid-search method.

pr(D=1)	Parameter	Value	Bias	Observed Standard Error	Estimated Standard Error	Coverage Probability
Known	βX	0.10	−0.009	0.053	0.054	0.961
	βH	0.15	−0.013	0.119	0.122	0.945
		0	0.006	0.171	0.172	0.951
		0	−0.007	0.147	0.145	0.948
	βHX	0.20	0.009	0.036	0.037	0.939
		0	−0.001	0.049	0.050	0.953
		0	0.001	0.041	0.042	0.964
	θ	0.25	0.001	0.009	0.009	0.954
		.15	< 0.001	0.009	0.009	0.954
		.05	< 0.001	0.004	0.004	0.938
Unknown	βX	0.10	−0.006	0.054	0.056	0.961
	βH	0.15	−0.008	0.123	0.129	0.961
		0	0.006	0.171	0.172	0.951
		0	−0.007	0.147	0.145	0.949
	βHX	0.20	0.007	0.040	0.043	0.964
		0	−0.001	0.049	0.049	0.953
		0	0.001	0.041	0.042	0.963
	θ	0.25	< 0.001	0.010	0.011	0.967
		.15	< 0.001	0.009	0.009	0.956
		.05	< 0.001	0.004	0.004	0.939

3.4 Population Stratification

Although in many situations genetic susceptibility and environmental exposures are unlikely to be causally related at an individual level, these factors may be correlated at a population level due to their dependence on other factors. A classic example is “population stratification” due to ethnicity. Allele frequencies for many genes vary widely across different races. Moreover, environmental covariates such as life-style or dietary factors also often have different distributions for people of different races. Thus, although the genetic and environmental factors may be independently distributed within an ethnic group, there could be spurious correlation between these factors when ethnicity is ignored. In this section, we will briefly describe how to generalize our methods to handle such “population stratification”.

We assume there is a set of co-factors W so that gene-environment independence and HWE holds conditional on W. We consider a polytomous logistic regression model for specifying the haplotype-frequencies given W as

$$log\{\text{pr}(H=h_k\mid W)/\text{pr}(H=h_0\mid W)\}=log\{{\theta }_k(W)/{\theta }_0(W)\}={\gamma }_{k0}+{\gamma }_{k1}^{\text{T}}W,$$

for k = 1, …, K, where h₀ is a reference haplotype, typically chosen to be the most common haplotype. We further assume HWE conditional on W, that is,

$$\begin{array}{l}{\text{pr}}_{\gamma }\left\{H^d=(H_i,H_j)\mid W\right\}={\{{\theta }_i(W)\}}^2\text{if}{H}_i=H_j\\ =2{\theta }_i(W){\theta }_j(W)\text{if}{H}_i\ne H_j,\end{array}$$

We also allow W to be potential risk factors for the disease by simply extending the disease-risk-model to be

$$\text{logit}\{\text{pr}(D=1\mid H^d,X,W)\}={\beta }_0+m(H^d,X,W;{\beta }_1).$$

Define

$$r_{\mathrm{\Omega }}(H^d,X,W)=\frac{1+exp\left\{\kappa +m(H^d,X,W;{\beta }_1)\right\}}{1+exp\{{\beta }_0+m(H^d,X,W;{\beta }_1)\}}.$$

Following previous arguments, the estimating equation for γ_k that corresponds to maximization of the profile likelihood L^*= Σ_iΣ _H^d∈ℋGi log{pr(D_i, H^d|X_i, W_i, R = 1)} can be shown to be

$$\begin{array}{l}0=\sum _{i=1}^N{E}_{\mathrm{\Omega }}\left[\frac{\partial log\{{\text{pr}}_{\gamma }(H^d\mid W)\}}{\partial {\gamma }_k}\mid D_i,G_i,X_i,W_i,R=1\right]\\ -\sum _{i=1}^N{E}_{\mathrm{\Omega }}\left[\frac{\partial log\{{\text{pr}}_{\gamma }(H^d)\}}{\partial {\gamma }_k}\mid X_i,W_i,R=1\right],\end{array}$$ (16)

where

$$\frac{\partial log\{{\text{pr}}_{\gamma }(H\mid W)\}}{\partial {\gamma }_k}=W\{N_k(H)-2{\theta }_k(W)\}.$$ (17)

One can get a fairly stable Newton-Raphson or related algorithm for solving (16) by exploiting the GLM form of (17). Finally, the updating procedures for κ and β₁ remain the same as before, except that throughout we condition on W.

3.5 Alternative Robust Estimation of β

Although exploitation of the gene-environment independence and the HWE assumptions can lead to major efficiency gains for analysis of case-control studies, we recommend cautious use of these assumptions, because violation of them can lead to major bias in parameter estimation (Albert et al., 2001; Satten and Epstein, 2004; Chatterjee and Carroll, 2005). The gene-environment independence assumption, for example, is likely to be satisfied in a wide range of studies involving external environmental agents, exposure to which is not directly controlled by an individual’s own behavior. When an exposure depends on subject’s individual behavior, on the other hand, the independence assumption could be violated due to direct or indirect association. Family history of a disease, for example, which is associated with genetic risk factors, may influence a subject to change his/her behavior regarding established environmental risk factors such as smoking for lung cancer. In Section 3.3, we have proposed a possible remedy for accounting for such indirect association between G and E due to their dependence on other common factors S. There could be also direct association. Genetic polymorphisms in the smoking metabolism pathway, for example, may not only modify a subject’s risk from smoking, but may also influence a subject’s degree of addiction to smoking.

When violation of the HWE or/and the gene-environment independence assumption seems plausible, it is important to consider alternative methods for analysis of case-control studies that are less sensitive to these assumptions. In the absence of missing data, it is well known that the standard prospective logistic regression analysis is such an option because it does not rely on any assumption on the covariate distribution. In the presence of missing data, a prospective likelihood-based method that treats the distribution of the cofactors to be completely nonparametric will be also such a robust option (see e.g. Roeder et al, 1996). For haplotype-based studies, however, complete nonparametric treatment of the covariate distribution may not be possible because of a lack of parameter identifiability. Nevertheless, when no environmental factors are involved, Satten and Epstein (2004) showed that methods that estimate the regression parameters from the prospective likelihood of the data are less sensitive to the violation of the HWE assumption than those based on the true retrospective likelihood. Following, we point out a problem for use of prospective estimating equation for analysis of case-control study and propose an appropriate remedy.

For fixed values of the haplotype-frequency parameter θ, the score-equations for the regression parameters β^*= (κ, β₁) corresponding to the prospective likelihood of the data is given by

$$0=\sum _{i=1}^N\frac{{\sum }_{h^d\in {\mathcal{H}}_{G_i}^d}\frac{\partial }{\partial {\beta }^{\ast }}log\{{\text{pr}}_{{\beta }^{\ast }}(D_i\mid h^d,X_i)\}{\text{pr}}_{{\beta }^{\ast }}(D_i\mid h^d,X_i)q(h^d;\theta )}{{\sum }_{h^d\in {\mathcal{H}}_{G_i}^d}{\text{pr}}_{{\beta }^{\ast }}(D_i\mid h^d,X_i)q(h^d;\theta )};$$ (18)

We argue in the appendix that this “purely prospective” score-equation (18) is biased under the case-control sampling design due to the underlying covariate distributional assumptions. In other words, even if the true haplotype-frequencies were known and the underlying HWE and gene-environment independence assumptions were valid, the estimator of the regression parameter β₁ based on solving the score-equation (18) is not consistent. We, however, show that the following simple modification of the prospective score equation is unbiased:

$$0=\sum _{i=1}^N\frac{{\sum }_{h^d\in {\mathcal{H}}_{G_i}^d}\frac{\partial }{\partial {\beta }^{\ast }}log\{{\text{pr}}_{{\beta }^{\ast }}(D_i\mid h^d,X_i)\}{\text{pr}}_{{\beta }^{\ast }}(D_i\mid h^d,X_i)r_{\mathrm{\Omega }}(h^d,X_i)q(h^d;\theta )}{{\sum }_{h^d\in {\mathcal{H}}_{G_i}^d}{\text{pr}}_{{\beta }^{\ast }}(D_i\mid h^d,X_i)r_{\mathrm{\Omega }}(h^d,X_i)q(h^d;\theta )}.$$ (19)

The only structural difference between the two sets of score-equations is that (19) is obtained from (18) by replacing q(h^d, θ) with r_Ω(h^d, X_i)q(h^d; θ). The unbiasedness of the modified prospective-score equations under the case-control sampling design is shown in the appendix. We also show that with an appropriate rare disease approximation, the proposed method is equivalent to the estimating equation approach proposed by Zhao et al. (2003). However, we note that the proof of the asymptotic unbiasedness of the estimating equation approach that is given in Zhao et al (2003) assumes random sampling of subjects and does not properly account for the case-control sampling design. Thus our derivation justifies the validity of the procedure of Zhao et al (2003) under the case-control sampling design. Moreover, it shows how one can avoid the rare disease approximation by using the exact score-equation (19) itself.

We observe that evaluation of the score-function (19) requires knowing θ and β₀. Similar to Satten and Epstein, we propose estimating θ for fixed value of β^*and β₀ by maximization of the retrospective likelihood, the algorithm for which we have described in Section 3.2. As before, we observe that if pr(D = 1) is known, then β₀ could be evaluated as a function of κ using the relationship (4). If pr(D = 1) is unknown, one can use the rare disease approximation given in equation (15) so that evaluation of (19) does not require knowing β₀. Alternatively, one can estimate θ and β for fixed values of β₀ following above procedures and then do a one-dimensional grid-search to estimate β₀ as the maximizer of the profile likelihood L^*{β₀, β̂^*(β₀), θ̂(β₀)}. Finally, we observe that the functional form of the right hand side of the score-equations (19) is equivalent to that of B₁, the first of the three terms of the score-equations corresponding to the retrospective likelihood that are given in Section 3.3. Thus, the proposed prospective estimation method can be implemented with minimal modification of the algorithm for the retrospective method and vice versa. A sandwich variance estimator, that properly accounts for the case-control design, can be also easily obtained based on estimating equation theory. A general formula for the variance estimator is given in the Appendix.

4 Simulation Studies

4.1 H and X are Independent

In the first set of simulation studies, we examined the performance of the proposed retrospective semiparametric maximum-likelihood method in haplotype-based studies of gene-environment interaction. We simulated data in a setting similar to that of Lake et al (2003). We considered the first five of the six SNPs listed in Table 1 of Lake et al. The corresponding haplotypes and their frequencies are listed in Table 1. Given these haplotype frequencies, we generated diplotypes for each subject under the assumption of Hardy-Weinberg Equilibrium. Additionally, we generated an environmental covariate for each subject independent of the subject’s diplotype status, from a lognormal distribution, where the underlying normal distribution has mean and variance 0 and 1, respectively. The environmental covariate was truncated above at 10. Given the diplotype status H^d and environment covariate X, we generated the binary disease status for each subject according to the model

Table 1.

The haplotypes and associated frequencies used to generate case-control data for the simulation studies reported in Section 4.1.

Haplotype	Frequency
h1 = (0, 0, 0, 0, 0)	0.25
h2 = (0, 0, 0, 1, 0)	0.15
h3 = (0, 1, 1, 0, 1)	0.25
h4 = (0, 1, 1, 1, 0)	0.10
h5 = (1, 0, 0, 0, 0)	0.10
h6 = (1, 0, 0, 1, 0)	0.05
h7 = (1, 0, 1, 1, 1)	0.05
h8 = (1, 1, 1, 0, 0)	0.05

$$\text{logit}\{\text{pr}(\text{D}\mid \text{H},\text{X})\}={\beta }_0+{\beta }_{\text{X}}+{\beta }_{\text{H}}{\text{N}}_3({\text{H}}^{\text{d}})+{\beta }_{\text{HX}}{\text{N}}_3({\text{H}}^{\text{d}})\text{X},$$

where N₃(H^d) denote the number of copies of h₃ contained in H^d and (β₀, β_X, β_H, β_HX) = (−3.5, 0.1, 0.15, 0.20). For each replicate of our simulation, we first generated data for a large random sample of subjects, which was then treated as the underlying study base for selection of 1000 cases and 1000 controls. For analysis of each data, we assume only the unphased genotype data are observed. Further, to examine the influence of missing genotype data, we deleted genotype information for the 4th and the 5th SNP in a randomly selected subset of subjects. The proportion of subjects who can have missing genotypes for both of the SNPs was chosen to be 20% and that of the subjects who can have missing genotypes only for one but not the other was chosen to be 10% and vice versa.

We analyzed each dataset using the retrospective maximum-likelihood method under the assumption that H^d and X are independent in the population, with pr(D = 1) being known and unknown, the algorithms for which are described in Section 3.1–3.3. In the case of pr(D = 1) being unknown, we used the grid search method for estimation of β₀ that we described earlier. Although we know that there are eight true haplotypes in the underlying population, for analysis of each data, we allowed all possible 32 haplotypes to arise and let the algorithm estimate the frequencies of each of the haplotypes separately. For estimation of the regression parameters (β₁), we pooled three rare haplotypes h₆, h₇, h₈ and all of the artificial haplotypes which may appear in a given data to have non-zero, but small, frequencies. The performance of the proposed method for estimation of the haplotype-frequency (θ) and the regression parameters (β) are shown in Table 2. For convenience of presentation, the frequency estimates are shown for the non-null haplotype H₃ which is known to be associated with the disease, for one null “common” (f = 15%) haplotype and for one null “rare” (f = 5%) haplotype. The estimates of the regression parameters are shown for the non-null haplotype (h₃), for one “common” haplotype (h₂) and for the pooled category of rare haplotypes.

Using the results shown in Table 2, we observe that the proposed method performed very well in estimating both the regression parameters (β) and the haplotype-frequencies (θ). The proposed standard error estimator also performed very well and the corresponding 95% confidence intervals had coverage that is very close their nominal values. Estimates of the interaction parameter β_HX for the non-null haplotype h₃ were more precise when pr(D = 1) known than when pr(D = 1) was unknown.

4.2 H are X are independent given S

In the second simulation study, we examined the robustness of alternative methods in a scenario where the assumptions of gene-environment independence and HWE hold only within subpopulations. We consider a population comprised of two strata, with frequencies 0.40 (S = 1) and 0.60 (S = 2), which differed in their distribution of both haplotypes and environmental factors. We assumed a simple scenario involving four haplotypes constructed from two binary SNPs with the haplotypes {(0, 0), (0, 1), (1, 0), (1, 1)} having frequencies (.35, .30, .15, .20) and (.35, .20, .30, .15) in strata 1 and 2, respectively. We chose the frequencies for the larger stratum (stratum 2) to correspond to the haplotypes defined by the 3rd and the 4th SNP listed in Table 1. The values of $R_h^2$, a popular measure for haplotypes-phase uncertainty (Stram et al, 2003), for the haplotypes {(0, 0), (0, 1), (1, 0), (1, 1)} were (0.88, 0.87, 0.79, 0.83) for stratum 1 and were (0.88, 0.83, 0.87, 0.78) for stratum 2. Thus, in this setting, the degree of phase-uncertainty was modest, but not negligible.

We generated the environmental covariate from a lognormal distribution with the mean and variance for the underlying normal distribution to be .67 and 1 for stratum 1 and 0 and 1 for stratum 2. Again, we truncated the environmental exposure above at 10 for both strata. Additionally, we assumed that the stratification variable, S, is a risk factor for disease. In particular, the disease status for each subject was generated according to the model

$$\text{logit}\{\text{pr}(\text{D}\mid {\text{H}}^{\text{d}},\text{X},\text{S})\}={\beta }_0+{\beta }_{\text{X}}+{\beta }_{\text{H}}{\text{N}}_2({\text{H}}^{\text{d}})+{\beta }_{\text{HX}}{\text{N}}_2({\text{H}}^{\text{d}})\text{X}+{\beta }_{\text{S}}+{\beta }_{\text{HS}}{\text{N}}_2({\text{H}}^{\text{d}})\text{S},$$

where N₂(H^d) denotes the number of copies of h₂ = (0, 1) contained in H^d and where the parameters (β₀, β_X, β_H, β_HX, β_S, β_HS) = (−3.5, 0.1, 0.15, 0.20, 0.69, 1.10). For each replicate of our simulation, we first generated data for a large random sample of subjects, which was then treated as the underlying study base for selection of 1000 cases and 1000 controls.

During analysis of each data set, as before, we assumed only that the locus-specific genotype data were available, but the phase information was unknown. Each data set was analyzed using (a) the retrospective maximum-likelihood method under the assumption that H^d and (X, S) are independently distributed in the population; (b) the retrospective maximum-likelihood method under the assumption that H^d and X are independent conditional on S (see Section 3.4) and (c) using the modified prospective estimating equation method (see Section 3.5). We assumed pr(D = 1) to be known for this set of simulations.

The results shown in Table 3 suggest the following important observations. First, when the true model assumed that H^d and X are independent conditional on S, but we analyzed the data as though H^d and (X, S) are independent in the entire population, we induced substantial bias in estimating the parameters β_H,β_S, and β_HS. Neither the prospective method nor the method which accounts for the population stratification suffered from such bias. Secondly, the prospective method had the largest variance of the three methods, while the maximum-likelihood method under the unconditional independence assumption had the smallest. The method which takes the populations stratification into account provided both small bias and relatively small variance. These observations suggest that when gene-environment dependence is suspected, the use of the retrospective maximum-likelihood method under the conditional gene-environment independence model could be optimal, assuming the factors which may induce such dependence are observable. If such factors are not observable, or if direct association between genetic and environmental factors may exist, then the use of the modified prospective method should be considered.

Table 3.

The results from 1000 simulated case-control studies from a population where HWE and the independence between haplotypes (H) and environmental covariate (X) holds within strata defined by S. Each replicate contains 1000 cases and 1000 controls and is analyzed using (a) the proposed unconditional retrospective maximum-likelihood (RML) method that assumes HWE and H – X independence hold in the entire population; (b) the proposed conditional RML method assuming HWE and H-X independence hold conditional on S and (c) the proposed modified prospective score-equation (PSE) method

		βX	βH	βHX	βS	βHS
(a) Unconditional RML
	Bias	0.009	−0.547	−0.033	−0.102	0.755
	Empirical SE	0.059	0.290	0.064	0.305	0.264
	Estimated SE	0.062	0.303	0.063	0.318	0.281
	Covergage Prob	0.956	0.551	0.897	0.941	0.223
(b) Conditional RML
	Bias	−0.004	−0.012	0.010	0.008	0.002
	Empirical SE	0.061	0.313	0.065	0.331	0.307
	Estimated SE	0.063	0.327	0.067	0.339	0.317
	Covergage Prob	0.955	0.963	0.954	0.957	0.965
(c) Modified PSE
	Bias	0.001	−0.022	−0.003	0.010	0.029
	Empirical SE	0.070	0.326	0.075	0.337	0.302
	Estimated SE	0.069	0.350	0.076	0.349	0.330
	Covergage Prob	0.942	0.966	0.947	0.960	0.972

4.3 Bias of alternative prospective methods

Stram et al. (2003) observed that although a naive prospective-method which ignores the case-control sampling design may not be strictly correct, the bias in such a method is typically small unless the predictability of haplotypes given the genotypes, as measured by the $R_h^2$ statistics, is low and the magnitudes of the true risk-parameters are high. We evaluated the bias of alternative prospective methods in a situation where the bias of a naive prospective method is expected to be high. We implemented three procedures:(a) the naive prospective method based on cohort likelihood (Lake et al., 2003); (b) the estimating equation approach of Zhao et al (2003) assuming rare disease; (c) the proposed modified prospective-score-equation approach assuming Pr(D = 1) to be known. We considered a simulation scenario involving three SNPs. To generate maximal amount of phase ambiguity, we assumed all of the 2³ = 8 haplotypes are equally likely. We generated diplotypes for each subject under the assumption of Hardy-Weinberg Equilibrium. We generated a continuous environmental covariate for each subject, independent of the subject’s diplotype status, using a log-normal model as before (see Section 4.1). We assumed one of the eight haplotypes were associated with the disease, with the mode of the effect being dominant. The true values of the parameters for the underlying logistic regression model were (β₀, β_X, β_H, β_HX) = (−3.5, 0.1, 0.69, 1.60), which corresponded to an overall disease rate of 10.7%. In each replication, we generated data for 1000 cases and 1000 controls.

We implemented all of the three methods to estimate the regression parameters associated the known “risk haplotype”. From the results shown in Table 4, we observe that while the proposed modified prospective method was unbiased in estimating all of the three parameters, both the naive prospective method and the estimating equation approach of Zhao et al (2003) produced substantial bias for estimation of the parameters β_H and β_HX. The large bias in the approach of Zhao et al. was likely to have been caused by the violation of the underlying rare disease assumption. In the current simulation setting, although the overall disease rate for the population is low (10.7%), the risk of the disease could become very high for those subjects who carried the risk haplotype and also had a high value of the environmental exposure. It is, however, important to note that the example reflects a fairly extreme scenario involving large amount of phase ambiguity and strong genetic effects on risk of the disease. In many other examples, that involved less extreme parameter settings, the bias for both the naive prospective method and the estimating equation approach of Zhao et al. were found to be very small or negligible.

Table 4.

Bias and standard errors for regression parameters estimated using three alternative prospective methods: (a) the naive prospective method based on cohort likelihood (Lake et al., 2003); (b) the estimating equation approach of Zhao et al (2003) assuming rare disease; (c) the proposed modified prospective-score-equation approach assuming Pr(D = 1) to be known

		βX	βH	βHX
(a) Naive prospective
	Bias	0.055	−0.198	0.181
	Empirical SE	0.040	0.252	0.216
(b) Zhao et al.
	Bias	−0.022	0.692	−0.705
	Empirical SE	0.042	0.216	0.119
(c) Modified PSE
	Bias	−0.002	0.004	0.017
	Empirical SE	0.044	0.250	0.200

5 Data Analysis: Israeli Ovarian Cancer Study

Chatterjee and Carroll (2005) described an application of their proposed methodology on a case-control study of ovarian cancer in Israeli women that was performed to investigate the interaction between the BRCA1/BRCA2 mutations and oral contraceptive use and parity (Modan et al.,2001). Briefly, this study consisted of all ovarian cancer cases identified in Israel between March 1, 1994 and June 30, 1999. For each case, two controls were selected. The selected cases and controls provided blood samples for testing mutations in the BRCA1 and BRCA2 genes. In addition, data were collected on reproductive/gynaecological history such as parity, number of years of oral contraceptive use and gynaecological surgery.

Chatterjee and Carroll (2005) restricted their analysis to 832 cases and 747 controls who were genotyped for BRCA1/2 mutations, leaving out 50 cases and 763 controls for whom BRCA1/2 status was missing, but data on all other risk factors were available. We reanalyzed the data using the proposed retrospective maximum-likelihood method including the subjects with missing genotype information. Similar to Chatterjee and Carroll (2005) we considered the following logistic regression model for risk of ovarian cancer:

$$\begin{array}{l}\text{logit}\{\text{pr}(D=1)\}={\beta }_0+{\beta }_{\mathit{BRCA}1/2}I(\text{BRCA}1/2)+{\beta }_{OC}\text{OC}+{\beta }_{\mathit{parity}}\text{Parity}\\ +{\beta }_{\mathit{BRCA}1/2\ast OC}I(\text{BRCA}1/2)\ast \text{OC}\\ +{\beta }_{\mathit{BRCA}1/2\ast \text{Parity}}I(\text{BRCA}1/2)\ast \text{Parity}+Z^{\text{T}}\gamma ,\end{array}$$

where I(BRCA1/2) denotes the 0–1 indicator of carrying at least one BRCA1/2 mutation, OC denotes years of oral contraceptive use, Parity denotes the number of children and Z denotes the set of all cofactors that Modan et al. (2001) used to adjust their regression analysis. Moreover, similar to Chatterjee and Carroll (2005) we assumed the independence between presence of mutation and reproductive risk factors conditional on Age, Ethnicity, Personal history of breast cancer (PHB) and Family history of breast and ovarian cancer (FHBO). The genotype frequencies were modelled as a function of these four factors using the parametric model

$$\begin{array}{l}\text{logit}\{\text{pr}(G=1\mid S)\}={\theta }_0+{\theta }_{\mathit{Age}}I(\text{Age}\ge 50)+{\theta }_{\mathit{Eth}}I(\text{Non}-\text{Ashkenazi})\\ +{\theta }_{PH}I(\text{PHB}=1)+{\theta }_{1FH}I(\text{FHBO}=1)+{\theta }_{2FH}I(\text{FHBO}=2).\end{array}$$

The results of our analysis for the main covariates of interest, parity, oral contraceptive use, BRCA1/2 mutation, and the interactions between the mutations and each of the two reproductive risk factors, are presented in Table 5. Compared to the analysis of Chatterjee and Carroll (2005) that included only those individuals with complete genotype information, we observe that there were important reduction in the standard errors for the main effects of the two environmental factors, OC use and Parity. This result is intuitive given that the additional subjects who were incorporated in the new analysis provided data on these two risk factors. In addition, the new analysis confirms the original finding of Modan et al. (2001) which suggested an interaction between BRCA1/2 mutation and OC use. In particular, the results suggest that, unlike for non-carriers, the risk of ovarian cancer for carriers did not decrease with increasing oral contraceptive use.

Table 5.

Parameter estimates and estimated standard errors for the parameters of interest for the Israeli ovarian cancer study. The current analysis includes all individuals available for study, regardless of whether or not they have BRCA1/2 status measured.

	Current Analysis		Chatterjee and Carroll (2005)
Parameter	Estimate	St. Error	Estimate	St. Error
βmut	3.183	0.337	3.154	0.329
βpar	−0.051	0.024	−0.061	0.032
βoc	−0.068	0.020	−0.051	0.026
βmut;par	−0.046	0.060	−0.036	0.053
βmut;oc	0.092	0.030	0.086	0.033

6 Discussion

We have developed a method for retrospective maximum-likelihood analysis of case-control studies of genetic and environmental factors that can account for missing genetic information. Particular emphasis has been given to haplotype-based studies where missing data arises due to phase ambiguity of available genotype data. By utilizing a profile likelihood of the data under the assumption of gene-environment independence and HWE, we were able to develop a relatively simple computational algorithm for obtaining the estimator. We also showed how this profile likelihood approach established a connection between two seemingly different methods for haplotype-based association analysis of case-control studies: the ascertainment corrected joint-likelihood approach of Stram et al. (2003) and the retrospective maximum-likelihood approach. Further simplifications of the methodology under a rare disease assumption were also described.

Simulation studies in this current article as well as those reported in Epstein and Satten (2003), Satten and Epstein (2004) and Chatterjee and Carroll (2005) show that retrospective methods that can exploit various covariate distributional assumptions, such as HWE and gene-environment independence, can lead to major efficiency gains for analysis of case-control studies. However, caution is needed in practical use of these methods because these simulation studies also demonstrate the possibility of major bias in the retrospective methods when the underlying covariate distributional assumptions are violated in truth. In this article, we proposed two alternative methods for relaxing the covariate distributional assumptions. In one, we proposed explicitly accounting for those factors, such as ethnicity, which could be both related to allele frequencies and environmental factors, possibly inducing association between these factors in the population. In the second, we propose a variation of prospective-estimating equation which we showed to be asymptotically consistent under the retrospective case-control design, assuming the underlying covariate distributional assumptions are valid. Moreover, in simulation studies we showed that the method produced very little bias in parameter estimates even when the covariate distributional assumptions were violated.

A novel finding of our simulation studies as well as those reported in Chatterjee and Carroll (2005) is that when the G-E independence assumption holds, incorporation of external information on the marginal probability of disease in the population can lead to further efficiency in the estimation of regression parameters of interest. In traditional logistic regression analysis, knowing the marginal probability of disease allows one to estimate the intercept term of the regression model, but otherwise does not have any effect on the estimation of the other regression parameters of interest. The marginal probability of the disease, possibly stratified by basic demographic factors such as age, sex, race, is often available or can be estimated precisely in population based case-control studies as well as in case-control studies that are nested within a larger cohort study. The proposed methodology allows incorporation of such additional information into the analysis and hence can lead to further precision gain in the estimation of regression parameters under the G-E independence model.

When a study involves a large number of haplotypes, estimation of their frequencies as well as the associated regression parameters could become unstable due to the presence of rare haplotypes. Schaid (2004) gives an excellent review for various currently available techniques for tackling this problem. In principle, in our setting, the parametric model pr_θ(H^d) can incorporate genetic models based on evolutionary history, thus specifying the haplotype frequencies in terms of a reduced set of genetic parameters. Similarly, hierarchical modelling techniques can be used to specify the regression parameters β in terms of a set of lower dimensional parameters. This and other extensions of the proposed methodology will be pursued in future.

Appendix

A.1 Proof of Lemma 2

Recall that ζ_m is the probability mass function for X = x_m, m = 1, …K. For fixed γ = (β₀, β₁, θ), and except for constants, the log-likelihood function for ζ has the form

$$\ell (\zeta \mid \gamma )=\sum _{i=1}^{N}log\{\sum _{m=1}^K{\zeta }_{m}I(X_i=x_m)\}-\sum _{i=1}^{N}log\left\{\sum _k\sum _{h_j\in \mathcal{H}}\text{pr}(D=D_i\mid X=x_k,H=h_j)q(h_j,\theta ){\zeta }_k\right\}.$$

Taking derivatives with respect to each ζ_m and solving, we find that

$${\zeta }_m=\sum _{i}I(X_i=x_m)/\sum _{i=1}^N\frac{{\sum }_{h_j\in \mathcal{H}}\text{pr}(D=D_i\mid X=x_m,H=h_j)q(h_j,\theta )}{{\sum }_k{\sum }_{h_j\in \mathcal{H}}\text{pr}(D=D_i\mid X=x_k,H=h_j)q(h_j,\theta ){\zeta }_k}.$$

However, notice that pr(D = d) = Σ_kΣ_hj∈ℋ pr(D = d|X = x_k, H = H_j)q(H_j, θ)ζ_k, and define μ(d) = N_d/{N pr(D = d)}. This implies that pr(D = d) = N_d/{Nμ(d)} and

$${\zeta }_m=\frac{{\sum }_{i}I(X_i=x_m)}{N{\sum }_d{\sum }_{h_j\in \mathcal{H}}\text{pr}(D=d\mid X=x_m,H=h_j)\mu (d)q(h_j,\theta )}.$$

It is easily shown that Σ_m ζ_m = 1. Substituting, and except for constants, the profile log-likelihood function has the form

$$\begin{array}{l}L\{\gamma ,\zeta (\gamma )\}=\sum _{i=1}^N[log\{\sum _{h\in {\mathcal{H}}_{G_i}}\text{pr}(D_i\mid X_i,h)q(h,\theta )\}+log\{\mu (D_i)\}\\ -log\{\sum _d\sum _{h_j\in \mathcal{H}}\text{pr}(D=d\mid X_i,h_j)\mu (d)q(h_j,\theta )\}].\end{array}$$

Now, define κ so that log{μ(1)} = log{μ(0)} + κ − β₀. Then,

$$\begin{array}{l}\ell \{\gamma ,\zeta (\gamma )\}=\sum _{i=1}^{N}log\left[\sum _{h\in {\mathcal{H}}_{G_i}}\text{pr}(D_i\mid X_i,h)q(h_j,\theta )exp\{D_i(\kappa -{\beta }_0)\}\right]\\ -\sum _{i=1}^{N}log\left[\sum _d\sum _{h_j\in \mathcal{H}}\text{pr}(D=d\mid X_i,h_j)q(h_j,\theta )exp\{d(\kappa -{\beta }_0)\}\right].\end{array}$$

Defining Ω = (γ, κ), and recalling the definition of S(d, x, H, Ω), simple algebra completes the proof.

A.2 Proof of Theorem 1

Let subscripted Ω denote partial derivatives, e.g., S_Ω(•) and S_{Ω Ω} (•) are the vector and matrix of first and second partial derivatives of S(•) with respect to Ω, respectively. Obviously, the semiparametric likelihood score is

$$L_{\mathrm{\Omega }}(\mathrm{\Omega })=\sum _{i=1}^N\frac{{\sum }_{h\in {\mathcal{H}}_{G_i}}{S}_{\mathrm{\Omega }}(D_i,X_i,h,\mathrm{\Omega })}{{\sum }_{h\in {\mathcal{H}}_{G_i}}S(D_i,X_i,h,\mathrm{\Omega })}-\sum _{i=1}^N\frac{{\sum }_d{\sum }_{h_j\in \mathcal{H}}{S}_{\mathrm{\Omega }}(d,X_i,h_j,\mathrm{\Omega })}{{\sum }_d{\sum }_{h_j\in \mathcal{H}}S(d,X_i,h_j,\mathrm{\Omega })}.$$

That L_Ω(Ω) is an unbiased estimating equation is a simple consequence of the following easily proved result. Let f_X(•) be the probability density function of X. Let the distinct values of G be (g₁, …, g_M), and let ℋ_gj be the values of h consistent with g_j. Recall the definition of μ(0) = N₀/{N pr(D = 0)}.

Lemma A.1

For any function R(D, X, G), and any function R^*(D, X, H),

$$\begin{array}{l}E\{N^{-1}\sum _{i=1}^{N}R(D_i,X_i,G_i)\}=\mu (0){\int }_x{f}_X(x)\sum _d\sum _{j=1}^{M}R(d,x,g_j)\sum _{h\in {\mathcal{H}}_{g_j}}S(d,x,h,\mathrm{\Omega })dx;\\ E\{N^{-1}\sum _{i=1}^N{R}_{\ast }(D_i,X_i,H_i)\}=\mu (0){\int }_x{f}_X(x)\sum _d\sum _{h_j\in \mathcal{H}}{R}_{\ast }(d,x,h_j)S(d,x,h_j,\mathrm{\Omega })dx.\end{array}$$

In addition, assuming that N₀/{N pr(D = 0)} = μ(0) converges to a finite, positive constant, the obvious law of large numbers applies to the sums in the expectations.

Lemma A.1 can be used to compute the expectations of the matrix of second partial derivatives (the so-called “bread of the sandwich”) and the variance of the score.

A.2.1 The Matrix of Second Partial Derivatives

Note that

$$\begin{array}{l}{N}^{-1}{L}_{\mathrm{\Omega }{\mathrm{\Omega }}^{\text{T}}}(\mathrm{\Omega })=N^{-1}\sum _{i=1}^N[\frac{{\sum }_{h\in {\mathcal{G}}_i}{S}_{\mathrm{\Omega }{\mathrm{\Omega }}^{\text{T}}}(D_i,X_i,h,\mathrm{\Omega })}{{\sum }_{h\in {\mathcal{G}}_i}S(D_i,X_i,h,\mathrm{\Omega })}-\frac{{\sum }_d{\sum }_{h_j\in \mathcal{H}}{S}_{\mathrm{\Omega }{\mathrm{\Omega }}^{\text{T}}}(d,X_i,h_j,\mathrm{\Omega })}{{\sum }_d{\sum }_{h_j\in \mathcal{H}}S(d,X_i,h_j,\mathrm{\Omega })}\\ -\frac{{\sum }_{h\in {\mathcal{G}}_i}{S}_{\mathrm{\Omega }}(D_i,X_i,h,\mathrm{\Omega }){\{{\sum }_{h\in {\mathcal{G}}_i}{S}_{\mathrm{\Omega }}(D_i,X_i,h,\mathrm{\Omega })\}}^{\text{T}}}{{\{{\sum }_{h\in {\mathcal{G}}_i}S(D_i,X_i,h,\mathrm{\Omega })\}}^2}\\ +\frac{{\sum }_d{\sum }_{h_j\in \mathcal{H}}{S}_{\mathrm{\Omega }}(d,X_i,h_j,\mathrm{\Omega }){\{{\sum }_d{\sum }_{h_j\in \mathcal{H}}{S}_{\mathrm{\Omega }}(d,X_i,h_j,\mathrm{\Omega })\}}^{\text{T}}}{{\{{\sum }_d{\sum }_{h_j\in \mathcal{H}}S(d,X_i,h_j,\mathrm{\Omega })\}}^2}]\\ =S_{N1}-S_{N2}-S_{N3}+S_{N4}.\end{array}$$

It is easy to show using Lemma A.1 that

$$E(S_{N1})=E(S_{N2})=\mu (0){\int }_x{f}_X(x)\sum _d\sum _{h_j\in \mathcal{H}}{S}_{\mathrm{\Omega }{\mathrm{\Omega }}^T}(d,x,h_j,\mathrm{\Omega })dx,$$

and that S_N1−S_N2 = o_p(1). A further application of Lemma A.1 shows that the expectations, and hence the probability limits of S_N3 and S_N4 are given by

$$\begin{array}{l}E(S_{N3})={\eta }_3=\mu (0){\int }_x\sum _d\sum _{j=1}^M\frac{{\sum }_{h\in {\mathcal{H}}_{g_j}}{S}_{\mathrm{\Omega }}(d,x,h,\mathrm{\Omega }){\{{\sum }_{h\in {\mathcal{H}}_{g_j}}{S}_{\mathrm{\Omega }}(d,x,h,\mathrm{\Omega })\}}^{\text{T}}}{{\sum }_{h\in {\mathcal{H}}_{g_j}}S(d,x,h,\mathrm{\Omega })}{f}_X(x)dx\\ E(S_{N4})={\eta }_4=\mu (0){\int }_x\frac{{\sum }_d{\sum }_{h_j\in \mathcal{H}}{S}_{\mathrm{\Omega }}(d,x,h_j,\mathrm{\Omega }){\{{\sum }_d{\sum }_{h_j\in \mathcal{H}}{S}_{\mathrm{\Omega }}(d,x,h_j,\mathrm{\Omega })\}}^{\text{T}}}{{\sum }_d{\sum }_{h_j\in \mathcal{H}}S(d,x,h_j,\mathrm{\Omega })}{f}_X(x)dx.\end{array}$$

Hence, the matrix I defined in Theorem 1 is η₃ − η₄.

A.2.2 The Variance of the Score

Recall that

$$\begin{array}{l}{L}_{\mathrm{\Omega }}(\mathrm{\Omega })=\sum _{i=1}^N\left\{\frac{{\sum }_{h\in {\mathcal{G}}_i}{S}_{\mathrm{\Omega }}(D_i,X_i,h,\mathrm{\Omega })}{{\sum }_{h\in {\mathcal{G}}_i}S(D_i,X_i,h,\mathrm{\Omega })}-\frac{{\sum }_d{\sum }_{h_j\in \mathcal{H}}{S}_{\mathrm{\Omega }}(d,X_i,h_j,\mathrm{\Omega })}{{\sum }_d{\sum }_{h_j\in \mathcal{H}}S(d,X_i,h_j,\mathrm{\Omega })}\right\}\\ =\sum _{i=1}^N\{A_1({\mathrm{\Delta }}_i,D_i,X_i,G_i,\mathrm{\Omega })-A_2(X_i,\mathrm{\Omega })\}.\end{array}$$

Define A₃(d, Ω) = E{A₁(Δ, D, X, G, Ω) − A₂(X, Ω)|D = d}. Then, ${\sum }_{i=1}^N{A}_3(D_i,\mathrm{\Omega })=0$, because the score is unbiased. Thus we can write,

$$L_{\mathrm{\Omega }}(\mathrm{\Omega })=\sum _{i=1}^N\{A_1({\mathrm{\Delta }}_i,D_i,X_i,G_i,\mathrm{\Omega })-A_2(X_i,\mathrm{\Omega })-A_3(D_i,\mathrm{\Omega })\}.$$

Notice that each of the terms in this sum is independent with zero mean. Then,

$$\begin{array}{l}{N}^{-1}\text{E}\{L_{\mathrm{\Omega }}(\mathrm{\Omega })L_{\mathrm{\Omega }}^{\text{T}}(\mathrm{\Omega })\}=N^{-1}\sum _{i=1}^N\text{E}\left[\{A_1({\mathrm{\Delta }}_i,D_i,X_i,G_i,\mathrm{\Omega })-A_2(X_i,\mathrm{\Omega })\}{\{•\}}^{\text{T}}\right]\\ -N^{-1}\sum _{i=1}^N{A}_3(D_i,\mathrm{\Omega })A_3{(D_i,\mathrm{\Omega })}^{\text{T}},\end{array}$$

where the expression {•} here means a repetition of the previous argument. The first term can be written as $D_1-D_2-D_2^{\text{T}}+D_3$, where by Lemma A.1, D₂ = D₃ and

$$\begin{array}{l}{D}_1=\mu (0){\int }_x\sum _d\sum _{j=1}^M\frac{{\sum }_{h\in {\mathcal{H}}_{g_j}}{S}_{\mathrm{\Omega }}(d,x,h,\mathrm{\Omega }){\{{\sum }_{h\in {\mathcal{H}}_{g_j}}{S}_{\mathrm{\Omega }}(d,x,h,\mathrm{\Omega })\}}^{\text{T}}}{{\sum }_{h\in {\mathcal{H}}_{g_j}}S(d,x,h,\mathrm{\Omega })}{f}_X(x)dx\\ D_3=\mu (0){\int }_x\frac{{\sum }_d{\sum }_{h_j\in \mathcal{H}}{S}_{\mathrm{\Omega }}(d,x,h_j,\mathrm{\Omega }){\{{\sum }_d{\sum }_{h_j\in \mathcal{H}}{S}_{\mathrm{\Omega }}(d,x,h_j,\mathrm{\Omega })\}}^{\text{T}}}{{\sum }_d{\sum }_{h_j\in \mathcal{H}}S(d,x,h_j,\mathrm{\Omega })}{f}_X(x)dx.\end{array}$$

Since D₁ − D₃ = −N⁻¹E{L_{Ω Ω}T(Ω)]}, we have shown that

$$N^{-1}\text{E}\{L_{\mathrm{\Omega }}(\mathrm{\Omega })L_{\mathrm{\Omega }}^{\text{T}}(\mathrm{\Omega })\}=I-\mathrm{\Lambda }.$$

Application of the Central Limit Theorem yields Theorem 1.

A.3 Consistency Issue for Prospective Estimating Equations

We first prove that the modified prospective score-equation (19) is unbiased for estimation of κ and β₁, assuming θ and β₀ are fixed at their true values. We note that the joint distribution of D, H^d and X in the underlying population is characterized by the parameters β₀, β₁ and the distribution function V (h^d, x) = q_θ(h^d) × F(x). Using Lemma 1 of Roeder et al. (1996), we observe that for any given value of the parameters β₀, β₁ and any given function V (·), one can chose β₀ ^*and a distribution function V ^*(·) such that,

$${\text{pr}}_{{\beta }_0,{\beta }_1,V}(H^d,X\mid D)={\text{pr}}_{{\beta }_0^{\ast },{\beta }_1,V^{\ast }}(H^d,X\mid D),$$

and

$${\text{pr}}_{{\beta }_0^{\ast },{\beta }_1,V^{\ast }}(D=1)=N_1/N.$$

In particular, by construction the authors showed that ${\beta }_0^{\ast }=\kappa$ and

$$V^{\ast }(h^d,x)\propto r_{\mathrm{\Omega }}(h^d,x)V(h^d,x).$$

Let P and P^*denote the probability law for (D, H^d, X) under (β₀, β₁, V) and (κ, β₁, V^*), respectively. Let E and E^*denote expectations under the probability law P and P^*. Now, the right hand side of equation (19) when evaluated at true values of κ, β₁, θ and β₀ can be expressed as

$$\begin{array}{l}\sum _{i=1}^{N_1}{E}^{\ast }\left[\frac{\partial }{\partial \beta }log\{{\text{pr}}_{\kappa ,{\beta }_1}(D_i\mid H^d,X_i)\}\mid D_i=1,G_i,X_i\right]\\ +\sum _{i=1}^{N_0}{E}^{\ast }\left[\frac{\partial }{\partial \beta }log\{{\text{pr}}_{\kappa ,{\beta }_1}(D_i\mid H^d,X_i)\}\mid D_i=0,G_i,X_i\right],\end{array}$$ (A.1)

Let

$$q_{\kappa ,{\beta }_1}^{\ast }(D,G,X)=E^{\ast }\left[\frac{\partial }{\partial \beta }log\{{\text{pr}}_{\kappa ,{\beta }_1}(D\mid H^d,X)\}\mid D,G,X\right].$$

Thus, under the case-control sampling design, the asymptotic limit of (19) divided by the total sample size N = N₀ + N₁ can be written as

$$\frac{N_1}{N}{E}_{G,X}\left[q_{\kappa ,\beta 1}^{\ast }(D,G,X)\mid D=1\right]+\frac{N_0}{N}{E}_{G,X}\left[q_{\kappa ,{\beta }_1}^{\ast }(D,G,X)\mid D=0\right].$$ (A.2)

Since P^*(D = 1) = N₁/N and P^*(G, X|D) = P(G, X|D), we can write (A.2) as

$$E_D^{\ast }{E}_{G,X}^{\ast }\left[q_{\kappa ,\beta 1}^{\ast }(D,G,X)\mid D\right]=E_{D,H,X}^{\ast }\left[\frac{\partial }{\partial \beta }log\{{\text{pr}}_{\kappa ,{\beta }_1}(D\mid H^d,X)\}\right]$$ (A.3)

which in turn can be shown to be zero by following standard theory of unbiasedness of the prospective-score equations under random sampling.

To see why the proof of consistency fails for the ordinary prospective-estimating-equation we note that each individual term of the equation (18) when evaluated at true values of κ,β₁ and θ can be written as

$$\frac{{\sum }_{h^d\in {\mathcal{H}}_{G_i}^d}\frac{\partial }{\partial \beta }log\{{\text{pr}}_{\kappa ,{\beta }_1}(D_i\mid h^d,X_i)\}{\text{pr}}_{\kappa ,{\beta }_1}(D_i\mid h^d,X_i)q(h^d;\theta )}{{\sum }_{h^d\in {\mathcal{H}}_{G_i}^d}{\text{pr}}_{\kappa ,{\beta }_1}(D_i\mid h^d,X_i)q(h^d;\theta )}.$$

The above, however, cannot be written in the usual expectation form because while pr_κ,β1(D_i|h^d, X_i) correspond to the probability law of [D|H, X] under P^*, q(h^d; θ) correspond to the probability law of [H|X] = [H] under P. Thus, the ordinary prospective-score equation, when evaluated at κ, β₁, θ, does not have a conditional expectation form, which was key to the proof given in Zhao (2003). Nevertheless, we observe that

$${\text{pr}}_{\kappa ,{\beta }_1}(D\mid H^d,X)r_{\mathrm{\Omega }}(H^d,X)=\frac{exp\left[D\{\kappa +m({\beta }_1,H^d,X)\}\right]}{1+exp[{\beta }_0+m({\beta }_1,H^d,X)]}.$$

Assuming the disease is rare in the population for all combination of H^d and X, one can make the approximation [1 + exp{β₀ + m(β₁, H^d, X)}]⁻¹ ≈ 1, which, when substituted in equation (19) yields the approximate estimating function of Zhao (2003).

A.4 Sandwich variance estimator under case-control design

Let Ω̂ = (β̂^*, θ̂) be the estimate of Ω = (β̂^*, θ̂) that solves the estimating equation ${\sum }_{i=1}^N{\mathrm{\Psi }}_{\mathrm{\Omega }}(D_i,G_i,X_i)=0$ for a vector-valued kernel function Ψ_Ω (D_i, G_i, X_i) that has the same dimension as Ω. Using standard estimating equation theory, it follows that under suitable regularity conditions,

$$N^{1/2}(\widehat{\mathrm{\Omega }}-{\mathrm{\Omega }}_0)\Rightarrow \text{Normal}\{0,\mathrm{\sum }={\mathrm{\Psi }}_{\mathrm{\Omega }\mathrm{\Omega }}^{-1}(A-B){({\mathrm{\Psi }}_{\mathrm{\Omega }\mathrm{\Omega }}^{-1})}^{\text{T}}\},$$

where

$$\begin{array}{l}{\mathrm{\Psi }}_{\mathrm{\Omega }\mathrm{\Omega }}=\underset{N\to \infty }{lim}{N}^{-1}\sum _{i=1}^{N_0+N_1}\partial {\mathrm{\Psi }}_{\mathrm{\Omega }}(D_i,G_i,X_i)/\partial \mathrm{\Omega };\\ A=\underset{N\to \infty }{lim}{N}^{-1}\sum _{i=1}^{N_0+N_1}{\mathrm{\Psi }}_{\mathrm{\Omega }}(D_i,G_i,X_i){\mathrm{\Psi }}_{\mathrm{\Omega }}^{\text{T}}(D_i,G_i,X_i);\\ B=\underset{N\to \infty }{lim}\sum _{d=0}^1(N_d/N)\text{E}\{\mathrm{\Psi }(D,X,G,\mathrm{\Omega })\mid D=d\}{[\text{E}\{\mathrm{\Psi }(D,X,G,\mathrm{\Omega })\mid D=d\}]}^{\text{T}}.\end{array}$$

A consistent variance estimator can be obtained by based on the above sandwich formula by estimating Ψ_{Ω Ω}, A and B with their respective empirical versions.