Deep Brain Stimulation Reduces Neuronal Entropy in the MPTP-Primate Model of Parkinson's Disease

Abstract

High-frequency stimulation (HFS) of the subthalamic nucleus (STN) or internal segment of the globus pallidus is a clinically successful treatment for the motor symptoms of Parkinson's disease. However, the mechanisms by which HFS alleviates these symptoms are not understood. Whereas initial studies focused on HFS-induced changes in neuronal firing rates, recent studies suggest that changes in patterns of neuronal activity may correlate with symptom alleviation. We hypothesized that effective STN HFS reduces the disorder of neuronal firing patterns in the basal ganglia thalamic circuit, minimizing the pathological activity associated with parkinsonism. Stimulating leads were implanted in the STN of two rhesus monkeys rendered parkinsonian by 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine (MPTP). Action potentials were recorded from neurons of the internal and external globus pallidus and the motor thalamus (ventralis anterior, ventralis lateralis pars oralis, and ventralis posterior lateralis pars oralis) during HFS that reduced motor symptoms and during clinically ineffective low-frequency stimulation (LFS). Firing pattern entropy was calculated from the recorded spike times to quantify the disorder of the neuronal activity. The firing pattern entropy of neurons within each region of the pallidum and motor thalamus decreased in response to HFS (n ≥ 18 and P ≤ 0.02 in each region), whereas firing rate changes were specific to pallidal neurons only. In response to LFS, firing rates were unchanged, but firing pattern entropy increased throughout the circuit (n ≥ 24 and P ≤ 10⁻⁴ in each region). These data suggest that the clinical effectiveness of HFS is correlated with, and potentially mediated by, a regularization of the pattern of neuronal activity throughout the basal ganglia thalamic circuit.

INTRODUCTION

Deep brain stimulation (DBS) at high frequencies (>80 Hz) is an increasingly common and successful treatment for a variety of movement disorders. In particular, high-frequency stimulation (HFS) of the subthalamic nucleus (STN) or the internal segment of the globus pallidus (GPi) alleviates the cardinal motor signs of Parkinson's disease (PD): rigidity, tremor, and bradykinesia. The mechanisms by which HFS alleviates motor symptoms are not fully understood. The effects of HFS resemble the symptom alleviation that follows ablative lesions of GPi or STN, and it was hypothesized that HFS inhibits neuronal activity and reduces output from the stimulated region. In this HFS-induced inhibition model, stimulation results in a disinhibition of the motor thalamus, either directly by reducing inhibitory outflow from GPi or indirectly by reducing excitatory inputs to GPi from STN. Several lines of research support the HFS-induced inhibition hypothesis, including slice recordings (Beurrier et al. 2001), in vivo recordings in rodents (Benazzouz et al. 2000) and primates (Boraud et al. 1996), and recordings in human patients (Benabid et al. 1998; Filali et al. 2004).

Multiple studies using a variety of approaches, however, have yielded contradictory results, suggesting that rather than inhibiting neurons and suppressing output, HFS increases output from the site of stimulation. In vivo studies in rodents (Windels et al. 2000) and primates (Anderson et al. 2003; Hashimoto et al. 2003) suggest that HFS excites axons projecting from the stimulated region, whereas functional MRI (fMRI) (Jech et al. 2001) and PET (Perlmutter et al. 2002; Hershey et al. 2003) studies in humans show changes consistent with increased activation of the output of the stimulated regions. Computational studies provide a resolution to these apparently contradictory results by showing that extracellular stimulation inhibits somatic action potentials while simultaneously evoking action potentials in the axon of the same neuron (McIntyre et al. 2004a). Thus efferent excitation seems to underlie the therapeutic benefit associated with stimulation. However, this axonal activation hypothesis does not explain why increased neuronal output during stimulation and presumably reduced output following ablative therapy both improve motor symptoms.

A number of groups have described regularization in the pattern of neuronal activity leaving the site of HFS (Anderson et al. 2003; Bar-Gad et al. 2004; Brown et al. 2004; Degos et al. 2005; Grill et al. 2004; Hashimoto et al. 2003; Meissner et al. 2005) and explored how HFS-regularized activity in the globus pallidus may enable thalamic neurons to respond to motor commands with higher fidelity (Guo et al. 2008; Rubin and Terman 2004). To evaluate further the change in the patterns of neuronal activity, data recorded from 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine (MPTP)-treated monkeys (Hashimoto et al. 2003) were used to estimate the firing pattern entropy of neurons in the globus pallidus and motor thalamus. Firing pattern entropy is an upper bound on the information embedded within a firing pattern and was used to quantify changes in firing patterns in the basal ganglia thalamic circuit during HFS, which improves motor symptoms, and LFS, which does not. While HFS increased mean neuronal firing rates in the globus pallidus, overall mean thalamic firing rates were largely unaffected and LFS did not change firing rates in any examined region. In contrast, entropy changes were robust and universal. Our results suggest that HFS-induced reductions in firing pattern entropy, and thus the removal of disease-associated pathological activity, may play a critical role in symptom alleviation by HFS.

METHODS

All surgical and behavioral protocols were approved by the Institutional Animal Care and Use Committee of Emory University and complied with U.S. Public Health Service policy on the humane care and use of laboratory animals.

Surgical procedures

Experiments were conducted in two rhesus monkeys (Macaca mulatta) weighing 5.2 and 6.9 kg. These were the same monkeys used in a previous study of STN DBS (Hashimoto et al. 2003). Both monkeys were treated with MPTP via injection through the internal carotid artery and developed a stable parkinsonian state characterized by contralateral rigidity and bradykinesia. After the stable hemiparkinsonian state was achieved, two craniotomies were trephined, and recording chambers were implanted over the craniotomies in a subsequent aseptic procedure under isoflurane anesthesia with the head held in a primate stereotaxic instrument. Stainless steel screws were secured to the skull, and the implant system consisting of screws, recording chamber, and head stabilization receptacle was bonded together with dental acrylic. During a 2-wk postoperative recovery period, the monkeys were given unlimited food and water, analgesics, and extra fruit. Prophylactic antibiotics were given preoperatively and continued postoperatively for 10 days.

A chronic stimulating electrode was implanted in the STN through one recording chamber. The stimulating electrode was a scaled-down version of the electrode used in humans (Model 3387, Medtronic) and consisted of four platinum-iridium contacts each with a cylindrical diameter of 0.76 mm, height of 0.50 mm, and separation between contacts of 0.50 mm. Each contact displaced 0.6–0.8% of the STN (0.23 mm³ per contact; assumed STN volume of 34 ± 6 mm³) (Hardman et al. 2002), matching 0.7–0.9% displacement in human patients (1.99 mm³ per contact; assumed human STN volume of 240 ± 6 mm³) (Hardman et al. 2002). The contacts were connected to a programmable pulse generator (Itrel II, Medtronic) implanted subcutaneously in the monkey's back.

Neuronal recordings

After permanently implanting the stimulating electrode, single neuron activity in the ipsilateral pallidum and thalamus was recorded through the second recording chamber while the monkeys were seated in a primate chair with the head restrained. Glass-insulated platinum-iridium microelectrodes (impedance, 0.4–0.8 MΩ at 2 kHz) were advanced by a microdrive (MO-95-lp, Narishige Scientific Instruments) attached to the recording chamber. Spontaneous neuronal activity was recorded before, during, and after stimulation using a predefined set of stimulation parameters. The analog neuronal signal was amplified, band-pass filtered at 300–10,000 Hz, sampled at 50 kHz with 12-bit resolution, and saved on computer disk for later off-line analysis. After testing with stimulation, neuronal activity was examined for responses to passive manipulations of the limbs and orofacial structures before the microelectrode was moved to find another neuron. The pallidal recording sites and stimulating lead locations were identified histologically and have been reported elsewhere (Hashimoto et al. 2003).

Stimulation artifacts were removed by template averaging and subsequent subtraction from the analog signal (Hashimoto et al. 2002). For most recordings, a brief (<0.5 ms) portion of the stimulus artifact could not be reliably subtracted because the recording amplifier became saturated. These digital samples were replaced with the average of the two samples adjoining the removed time period. To insure this process did not bias action potential discrimination during the stimulation period, segments of the control recording of equal duration (<0.5 ms) and frequency were set to the average of the adjoining samples. The entire data stream was digitally band-pass filtered 500−5,000 Hz, and the times of action potentials from single units were determined using off-line time-amplitude window discrimination.

Behavioral assessment

Symptom alleviation was identified by observers blinded to the stimulation condition and occurred with bipolar stimulation between the clinically identified optimal contacts, at pulse durations of 90→140 μs, voltages of 2.4→4.0 V, and frequencies of 136 Hz. As a control, to verify that observed changes in neuronal activity were the result of the high-frequency aspect of stimulation, we also applied LFS to the STN. The pulse widths and amplitudes identified as clinically effective for HFS in that animal were used, and the stimulation frequency was reduced to 2.0 Hz. One monkey was assessed for symptom severity in response to LFS. In that monkey, LFS did not alleviate parkinsonian symptoms.

Data analysis

Sensory stimuli, motor commands, and internal brain states are encoded to patterns of action potentials across neuronal membranes. There is an increased incidence of burst-like activity—firing patterns in which many spikes are compressed into very short intervals—in GPi in the parkinsonian state (Bergman et al. 1994; Magnin et al. 2000; Soares et al. 2004; Wichmann et al. 1999). Because we hypothesize that bursts and other irregular activity underlie motor symptoms, we calculated firing pattern entropy, which is a direct and quantifiable measure of disorder (Shannon and Weaver 1949). The entropy of a neuronal firing pattern is an upper bound to the information that its spike times can convey.

The class of entropy estimation techniques we used required transforming the interspike intervals (ISIs) into discrete probability distributions. Although others have binned ISIs linearly in time (Dayan and Abbott 2001; Rieke et al. 1993), we constructed our probability distributions in logarithmic time (Dorval 2008). Logarithmic bins enabled sampling the ISI distributions such that very long ISIs and very short ISIs (e.g., those within bursts) can contribute equally to the entropy estimate and have been used to quantitatively separate bursts from nonbursts (Selinger et al. 2007). Because spike time variability typically scales with mean firing rate, this logarithmic transformation isolates the subsequent entropy estimates from firing rate (Dorval 2008). For example, doubling of the absolute time between each pair of spikes in a dataset would halve the firing rate yet leave the entropy unaffected. Conversely, a dataset of the same duration with the same number of perfectly periodic spikes would have the same firing rate but zero entropy. We adapted the direct entropy estimate technique corrected for finite data size (Strong et al. 1998) to the logarithmically transformed ISIs(Dorval 2008).

ENTROPY ESTIMATION.

We assumed each spike train to be statistically stationary over the recording period. Each train of N spikes was converted into a series of N-1 ISIs. Probability histograms of ISIs were generated by rounding the ISIs into bins of logarithmic time. The right edge of the kth bin was defined as ISI_k = ISI₀ × 10^k/k, where k went from 1 to K. The 0th time ISI₀, the left edge of the first bin, was set below the shortest observed ISI and ISI_K was set such that ISI_K was larger than the longest ISI. Particular choices of ISI₀ and K did not alter significantly subsequent calculations. The important parameter is κ: the number of discrete time bins per ISI decade. Results reported here were generated with κ = 20, but the results were qualitatively unchanged over a wide range (5 ≤ κ ≤ 30). For a complete description, justification, and demonstration of the benefits of using logarithmically binned ISIs to estimate firing pattern entropy see Dorval (2008).

Probability distributions were constructed over all ISIs (Fig. 1C) and higher-dimensional trains of ISIs. For the two-dimensional case, for example, P(ISI_b |ISI_a) and P(ISI_b,ISI_a) were found as the number of times ISI_b followed ISI_a divided by the number of times ISI_a occurred or the total number of ISI pairs (i.e., N-2), respectively (Fig. 1D). From these probability distributions, the maximum likelihood estimates of entropy H^MLE were calculated in each dimension as (Rieke et al. 1993)

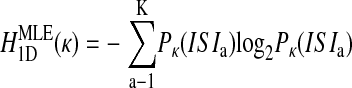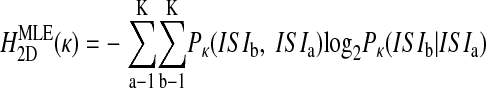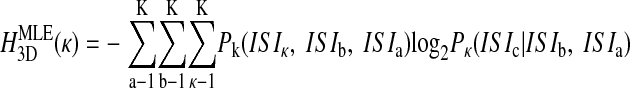and so on, where the parenthetical κ (omitted elsewhere for clarity) reminds us that the probability distributions are fundamentally dependent on the chosen bin size. These definitions of entropy define the Jth dimensional entropy (H_JD) as the average additional entropy introduced by each ISI, given the J-1 previous ISIs.

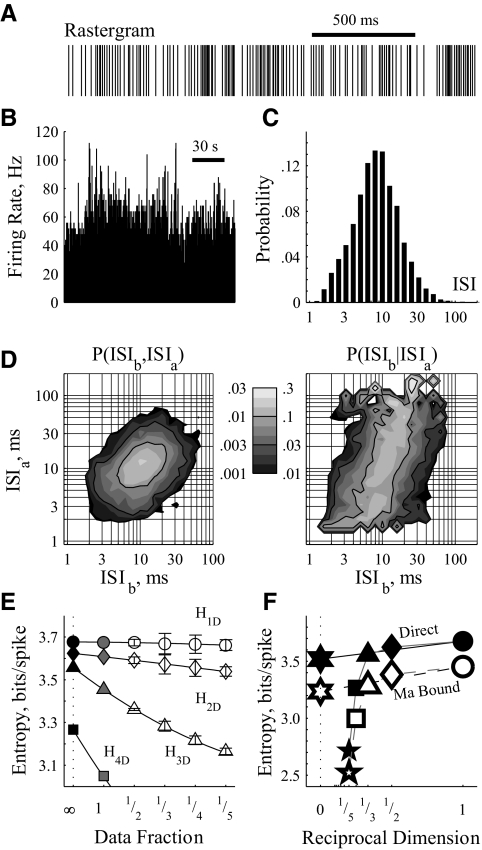
FIG. 1.

Estimating entropy from neuronal spike trains. Extracellularly recorded data from 1 trial of an internal segment of the globus pallidus (GPi) neuron without stimulation. A: rastergram of spike times displays interspike interval (ISI) irregularity on short time scales (ones to hundreds of milliseconds). B: firing rate as a function of time displays frequency irregularity on long time scales (ones to tens of seconds). C: probability distribution histogram of ISIs, constructed to have 10 bins per ISI decade. Most of these ISIs are between 3 and 30 ms. D: probability distribution histograms of consecutive ISIs, where ISI_b follows ISI_a. Left: joint probability distribution, P(ISI_b,ISI_a), i.e., the probability that 2 subsequent ISIs are ISI_a followed by ISI_b. The left column of the color bar denotes probability color map; the sum of the entire field is 1.0. The distribution is centered on 12-ms ISI pairs with a principal axis along the diagonal denoting correlated durations of consecutive ISIs. Right: dependent probability distribution, P(ISI_b|ISI_a), i.e., the probability of observing ISI_b given a previous ISI of ISI_a. The right column of the color bar denotes probability color map; the sum of each horizontal line is 1.0. E: entropy estimates from various fractions of the available data considering lone ISIs (H_1D; ○), pairs (H_2D; ⋄), triplets (H_3D; ▵), and quartets (H_4D; □). The axes have been set to show the relative independence of dataset fraction on H_1D and H_2D, leaving most of the H_4D estimates off the plot. Where appropriate, error bars denote SE measure, calculated by considering all available nonoverlapping data sections. Gray filled symbols denote the maximum likelihood estimates, calculated from the entire dataset (e.g., the filled gray diamond was calculated directly from the distributions in d via the H_2D^MLE equation in the text). A 2nd-order polynomial was fit to the data for each dimension. Extrapolations to infinity constitute the bias-corrected estimates, denoted as filled black symbols. F: the bias-corrected (filled) and Ma bound (open) estimates, plotted against the reciprocal of their dimension (e.g., H_5D; five-point star; plotted at 1/5). The precipitous drop off above H_3D indicates undersampling of the higher dimensional space: those entropies are ignored. The 0 crossings of the linear fits to the 1st 2 estimates were taken as the direct entropy (H_Dir; filled six-point star) and the Ma lower bound (H_Low; open six-point star).

To correct for undersampling bias, the entropy estimates for each dimension were extrapolated from data subsets (Fig. 1E) (Dorval 2008; Strong et al. 1998; Treves and Panzeri 1995). Specifically, the full dataset was partitioned into fractions (i.e., the dataset was split in half to yield 2 one-half datasets; split in thirds to yield 3 one-third datasets, etc.). Entropies calculated from equally sized subsets were lumped together to yield an entropy estimate (mean ± SE) for that data fraction size. Those estimates were plotted against their data fraction size reciprocal, i.e., the estimate from the entire data set (H^MLE) at 1, the mean estimate from the one-half datasets at 2, the mean estimate from the one-third datasets at 3, and so on. Those points were fit with a quadratic function. The value of that function at zero, corresponding to an estimate of the entropy were the dataset infinitely large, was taken as the bias-corrected entropy estimate. For the data examined, the maximum likelihood estimates (Fig. 1E, gray filled symbols) were typically within 2% of the bias-corrected estimate (Fig. 1E, black filled symbols) for only the first two dimensions (H_1D and H_2D), indicating that the dataset was not large enough to estimate accurately third or higher dimensional entropies.

Bias-corrected estimates were plotted versus the reciprocal of their dimension (Fig. 1F). Because each ISI typically affects (i.e., provides information about) subsequent ISIs, entropy estimates decrease as dimension increases. Beyond H_3D, however, the estimates drop off precipitously because of undersampling of the true distribution by our finite dataset. We desire an estimate of the firing pattern entropy accounting for infinite consecutive ISIs, but we can trust consistently only the bias-corrected estimates for the one- and two-dimensional cases. Hence, we found the zero crossing of a linear fit to those bias-corrected estimates as the direct entropy estimate H_Dir (Dorval 2008; Strong et al. 1998). In some conditions, our extrapolation from only two points (i.e., H_Dir = 2H_2D − H_1D) may underestimate the entropy. During burst firing, for example, (H_1D –H_2D) ≫ (H_2D –H_3D), suggesting that the actual entropy may be closer to H_2D than to H_Dir. In the example figures, we show both estimates, along with the Ma entropy estimate (Fig. 1F, open symbols), a widely accepted lower bound (Ma 1981).

When contrasting the effects of two stimulus conditions within a neuron (e.g., control vs. HFS), we used the same number of ISIs for each condition: N equaled the number of ISIs in the trial with the fewer ISIs. This manipulation removed all differential effects of the undersampling bias, enabling a perfectly fair comparison between conditions. For trials with extra ISIs, we found the entropy as the average of repeated estimates made from N ISIs, which minimizes the variance of our estimate without affecting the sampling bias. Thus entropy estimates from neurons with very low firing rates will be biased toward zero, but for a given neuron, firing pattern entropy should be equally biased across conditions. Regardless, using all recorded ISIs did not change qualitatively the results.

In the example figures, we show both the direct estimates (H_Dir, thick dark bars), the extrapolated Ma lower bounds (H_Low, thin light bars), and the two-dimensional bias-corrected estimates (H_2D, filled diamonds as in Fig. 1F). However, in the summary, population data and statistical analyses (Figs. 7 and 8), we use only the estimate least likely to confirm our hypotheses, H_Dir. Estimates were verified (data not shown) for qualitative similarity with results using the Miller-Madow bias correction (Miller 1955; Paninski 2003) and the Nemenman-Shafee-Bialek estimate (Nemenman et al. 2002).

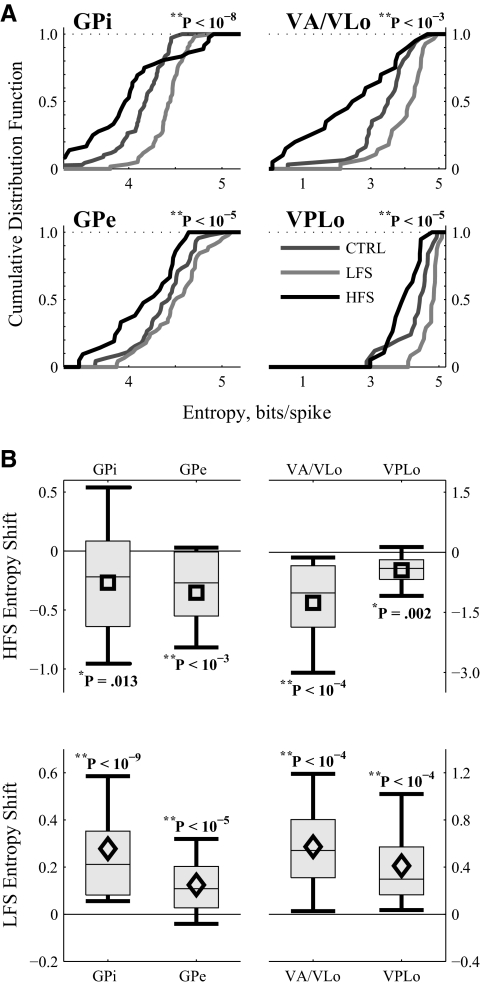
FIG. 7.

Summary of firing pattern entropy changes by region in response to LFS and HFS of STN. A: cumulative distributions of the firing pattern entropy in the 4 examined regions in the 3 conditions. One-way ANOVAs indicate that stimulus frequency is a factor in determining firing pattern entropy in all 4 regions. B: average entropy changes across the populations of all neurons from a region for which HFS (top) or LFS (bottom) data were recorded. Symbols report the mean; boxes cover the middle 2 quartiles split by a thin line denoting the median; thick lines stretch from 10th to 90th percentiles. Statistics from a 2-tailed pairwise t-test indicate that HFS decreases and LFS increases firing pattern entropy in all 4 regions. VA/VLo neurons with HFS-induced firing rate suppression to <2.0 Hz were omitted from this analysis.

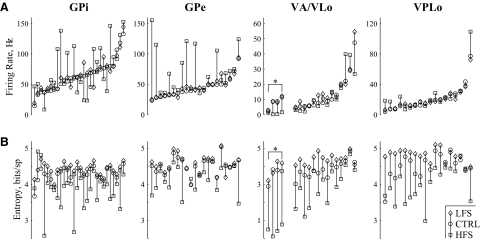
FIG. 8.

Summary of rate and entropy changes for individual neurons recorded in response to both LFS and HFS of STN. A: firing rates for each neuron recorded without stimulation (circle) and in response to LFS (diamond) and HFS (square). The units have been sorted by control condition firing rate to ease viewing. B: firing pattern entropies for the same neurons, in the same conditions, depicted in the same order as above to enable direct comparisons of firing rate (top) and entropy (bottom) changes in individual neurons. Entropy increases with LFS and decreases with HFS were nearly universal. *These 4 units in VA/VLo had HFS-induced firing rates <2.0 Hz and thus were omitted from the firing pattern entropy statistics reported in Fig. 7.

PALLIDAL MULTIMODAL RESPONSES.

In the globus pallidus, neurons often responded to HFS by firing phase-locked to the stimulation pulses (Fig. 3D, top). This phase-locking lead to regularly spaced action potentials with ISIs of ∼7 ms, corresponding to the interpulse interval of stimulation. Simple integer harmonics and subharmonics of the interpulse interval were also common (Fig. 2B), as neurons fired, for example, twice each stimulus pulse (2:1) or once every other pulse (1:2). We used the ISI probabilities at these integer ratios of the HFS frequency to determine whether or not a neuron exhibited multimodal ISIs. We found the highest probability mode (almost always 1:1) and its neighboring mode with the next highest probability. We compared the peak probabilities of the two chosen modes with the minimum probability of the trough between them. If the trough was <2/3 of the primary peak and <3/4 of the secondary peak, we classified the cell as multimodal. If the trough was <1/4 of the primary peak and <1/2 of the secondary peak, we additionally classified the cell as highly multimodal.

FIG. 3.

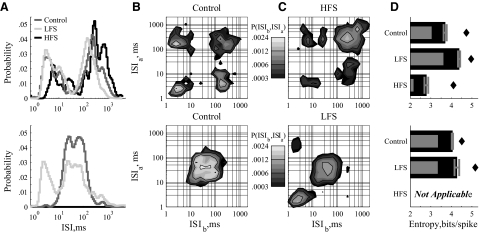
Example responses of external segment of the globus pallidus (GPe) neurons to LFS and HFS of STN. Two example units (top and bottom) that typify GPe responses. In response to HFS, GPe neurons were harmonically phase locked to the stimulation pulse (top) and/or exhibited increased firing rates (bottom). A: ISI distributions show harmonic phase-locking or shortened ISIs. B: in response to HFS, joint distributions show multimodal, structured phase locking (top) or unimodal distributions with minimal periodicity (bottom). C: entropy estimates show that both responses to HFS reduced the firing pattern entropy from the control. D: poststimulus instantaneous firing rate histograms in response to HFS, normalized by the average firing rate in the control case. The HFS-induced rate of the phase-locked neuron is only slightly increased, with the normalized rate histogram oscillating from ∼0 to ∼5 (top). The HFS-induced rate of the other example is always well above the control case, staying between ∼2 and ∼10 (bottom). Gray bars denote time period of the stimulus artifact.

FIG. 2.

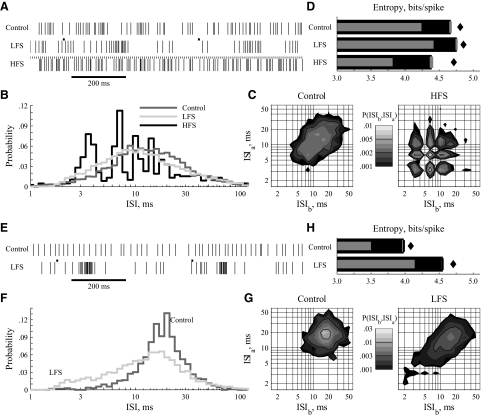
Example responses of GPi neurons to low-frequency stimulation (LFS) and high-frequency stimulation (HFS) of subthalamic nucleus (STN). Two example units (A–D and E–H) that typify GPi responses. A and E: rastergrams with and without stimulation. The small bars depict the occurrence of stimulus pulses. B and F: ISI histograms as line rather than bar graphs so that the distributions can be drawn on the same axis for visual clarity. The HFS-induced distribution in B shows harmonic phase-locking to the stimulating pulses. C and G: joint probability distribution, P(ISI_b,ISI_a), in control (left) and in response to deep brain stimulation (DBS) (right). In C, HFS generates a strong tendency to phase-lock. In G, LFS broadens the distribution, reduces its peak value, and induces burst-like, consecutive short ISIs. Note the logarithmic color maps. D and H: entropies calculated from the ISI distributions as described in methods. The primary thick bars are direct entropy estimates H_Dir with SE. The lighter thin bars are the Ma lower bounds H_Low. The filled diamonds are bias-corrected estimates from the 2-dimensional distributions, H_2D. Entropy reduction in response to HFS follows from the highly regular phase-locking visible in the ISI distributions.

THALAMIC BURSTS.

Neurons in the motor thalamus often burst, firing several action potentials in a brief time period followed by a longer pause. When plotted with a logarithmic abscissa, the ISI distributions of the recorded thalamic neurons exhibited two well-defined modes of ISI duration, consistent with burst identification (Selinger et al. 2007). Across all of our thalamic cells with two ISI modes, the short mode was 1–15 ms and the long mode was 10–1,000 ms (Fig. 4A). To identify burst events conservatively, ISIs <10 ms were classified as burst ISIs. Thalamic neurons with ≥10% burst ISIs were labeled as having a prominent burst mode, solely to enable quantitative discussions of bursting neurons. Within a reasonable range, neither the precise criterion (10%) nor the minimum number of spikes per burst (1 ISI → 2 spikes) affected the results qualitatively.

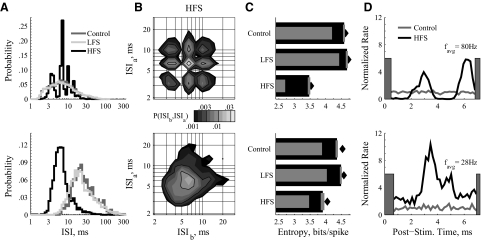
FIG. 4.

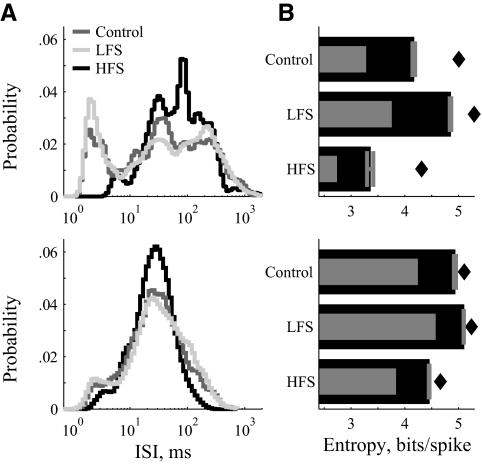
Example responses of ventralis anterior (VA)/ventralis lateralis pars oralis (VLo) neurons to LFS and HFS of STN. Two example units (top and bottom) that typify VA/VLo responses. A: ISI distributions show a prominent short-interval burst mode (<10 ms) strengthened by LFS but reduced by HFS. B: without stimulation, some neurons exhibited both irregular spiking and true bursting (top), identified in the joint distributions by a broad slow mode (top right) and a narrow fast mode (bottom left), and the 2 transition modes that connect them (top left, bottom right). Some cells did not exhibit the burst-related modes under control conditions (bottom). C: in bursting cells, HFS greatly reduced the power of the burst and transition modes (top). In nonbursting cells, LFS induced burst and transition modes (bottom). D: LFS increased and HFS decreased firing pattern entropy. Entropy analysis in the HFS condition was not performed on cells that stopped firing in response to HFS (bottom).

RESULTS

Action potentials were recorded extracellularly from single units in the globus pallidus or motor thalamus of the MPTP-treated monkey in the presence and absence of DBS. Each trial included a 30-s control recording period followed by 30–120 s of recording during stimulation of the STN with either LFS (2 Hz) or HFS (136 Hz). All epochs of the same condition in a given neuron were used to estimate the firing pattern entropy of that neuron under that condition. In many neurons, action potentials occasionally occurred in bursts of brief-duration ISIs during control conditions (Fig. 2A), consistent with previous reports in MPTP monkeys (Bergman et al. 1994; Raz et al. 2000) and persons with PD (Magnin et al. 2000). Other neurons fired action potentials at more regular intervals (Fig. 2E), behavior more often associated with neurons in the nonparkinsonian state (DeLong 1971). The majority of neurons fell between these two extremes, and for our analysis, we grouped all neurons together by region. We estimated spike train entropy of all neurons in the absence of stimulation (control) and in response to LFS and HFS. In Figs. 2–5, we show data from two example neurons from each region whose behaviors typify the response patterns we observed. We highlight how firing patterns and ISI distributions were modified by LFS and HFS and show the impact of those modifications on firing pattern entropy. The final three figures show population data, summarizing the impact of LFS and HFS on spike rate and firing pattern entropy in all regions.

FIG. 5.

Example responses of VPLo neurons to LFS and HFS of STN. Two example VPLo neurons (top and bottom) that typify VPLo responses. B: ISI distributions of regularly bursting (top) and minimally bursting (bottom) VPLo neurons. LFS enhanced bursting; HFS reduced bursting and narrowed the distribution. B: LFS increased and HFS decreased firing pattern entropy.

GPi

From GPi, 68 neurons were examined: 60 in response to LFS and 36 in response to HFS, i.e., 28 in response to both. We show two example neurons that in control conditions span the range of activity observed across the population, from fairly irregular (Fig. 2, top) to fairly regular (Fig. 2, bottom). The LFS-induced changes in the top example were quantitatively typical for the population. Changes in the bottom example are larger and more illustrative. Some degree of the highly regular HFS-induced activity shown in the top example was seen in the 31/36 GPi neurons.

LFS typically made the spike times visibly more burst-like (Fig. 2, A and E) with the ISI distributions pushed leftward, commensurate with more brief, intraburst duration ISIs (Fig. 2, B and F). The leftward shift had minimal effect on the mean ISI, because the probability of very long ISIs consistently increased as well (e.g., Fig. 2F, right tail). The ISI distributions of nearly all GPi neurons were broader with lower peak probabilities, typified by the examples (Fig. 2, B, F, and G). The spike pattern entropy increased in response to LFS (Fig. 2, D and H), as a reflection of the broader ISI distribution. The link between short-duration burst-like ISIs, distribution shape, and entropy is shown in the bottom example (Fig. 2, E–H). The down and leftward skew of the joint distribution reflects LFS-induced trains of short, intraburst ISIs (Fig. 2G).

In direct contrast to LFS effects, HFS made spike patterns less burst-like (Fig. 2A). The spike times were highly synchronous with the HFS pulses (Fig. 2B), and the example distribution had at least five identifiable modes, with ISIs of ∼3.5, 7, 10.5, 14, and 18–21 ms. These modes corresponded to spike-to-pulse phase locking with ratios of: 2:1, 1:1, 2:3, 1:2, and 2:5–1:3. The joint distribution shows that the phase-locked modes persisted over multiple ISIs (Fig. 2C, right). The example (Fig. 2, A–D) is typical of the highly multimodal responding neurons (13/36, highly multimodal as defined in methods). The majority of GPi neurons showed multimodal responses to HFS (26/36, multimodal as defined in methods), whereas a few showed regular, unimodal phase-locking (i.e., 1:1 in 5/36). The spike pattern entropy of GPi neurons was reduced in response to HFS, commensurate with spikes occurring at predictable times relative to the stimulation pulse (Fig. 2D).

External segment of the globus pallidus

From the external segment of the globus pallidus (GPe), 45 neurons were examined: all 45 in response to LFS and 21 in response to HFS. We show two example neurons with control condition responses that span the population results from rapidly firing (Fig. 3, top) to slowly firing (Fig. 3, bottom). The LFS-induced changes in both examples were nearly universal across the population. HFS responses could be divided into two classes evenly, which we show with a typical example from each class.

In response to LFS, nearly every GPe neuron exhibited the marginally broadened ISI distributions with smaller peak probabilities (Fig. 3A) that slightly increased firing pattern entropy (Fig. 3C) depicted in both examples. The joint distributions of the control and LFS cases, both in these examples and across the population, exhibited analogous changes to the one-dimensional distributions and were visually similar to the joint distributions of the GPi neurons in control conditions (Fig. 2, C and G).

In response to HFS, GPe neuronal ISI distributions formed two classes of behavior. The first class (Fig. 3, top) exhibited multimodal phase locking to the stimulus frequency, similar to the behavior of most GPi neurons (9/21 multimodal; 4/21 highly multimodal). The second class (9/21; Fig. 3, bottom) exhibited a left-shifted (>1/5 decade, which corresponds to ∼18%) and significantly narrowed ISI distribution, consistent with increased firing rates. Responses in both classes reduced spike pattern entropy (Fig. 3C). The remaining GPe neurons had HFS induced ISI distributions similar to their control, but with either slightly increased firing rates (<1/5 decade) or tendencies toward multiple modes that did not reach our criteria for multimodality.

The differences in response class are more evident in the joint distributions (Fig. 3B). Phase-locked cells exhibit many high-peak low-variance modes, whereas cells with only one mode were most likely those that also showed an increase in rate. From the poststimulus time normalized instantaneous firing rate histograms (Fig. 3D), both classes showed some degree of correlation with stimulus pulse times and increased rates. The difference between the classes is mostly in the troughs of the histograms. The phase-locked class exhibits intervals following stimulus pulses in which spikes rarely occurred (Fig. 3D, top, troughs), whereas the minimum instantaneous rate of the increased rate class was still twice the control rate (Fig. 3D, bottom, troughs).

Pallidal thalamus

From the pallidal receiving area of the motor thalamus, ventralis anterior (VA) and ventralis lateralis pars oralis (VLo), 31 neurons were examined: 27 in response to LFS and 22 in response to HFS, i.e., 18 in response to both. We show two example neurons that typify or show the changes observed across the population (Fig. 4). The top example is representative of the population in control, LFS, and HFS conditions. The bottom example shows the LFS-induced changes with an extreme example and shows one of the small number of neurons that ceased spiking altogether in response to HFS.

In most VA/VLo neurons, the time between spikes was bimodally distributed, consistent with two different spiking mechanisms (Fig. 4A, top). Short intervals (ISI < 10 ms) represent spikes within a burst, whereas long intervals (ISI > 10 ms) represent isolated spikes or interburst intervals. In control conditions, all VA/VLo distributions exhibited an isolated spike mode, and most (22/31) exhibited a prominent burst mode. In other words, in control conditions, most cells exhibited both modes (Fig. 4, top), whereas a few cells exhibited only isolated spikes (Fig. 4, bottom), consistent with recordings in humans (Sarnthein and Jeanmonod 2007). The ISI joint probability distributions of bursting neurons in control conditions exhibited four modes (Fig. 4B, top): the first two, isolated spiking (top right) and bursting (bottom left), correspond to modes in the one-dimensional ISI distribution, and the other two modes reflect the transitions from isolated spiking to bursting (top left) and bursting to isolated spiking (bottom right).

LFS made the isolated spike mode less prominent and/or broadened burst mode of the ISI distributions in most VA/VLo neurons (17/27; Fig. 4). In many neurons (13/27), LFS increased the relative probability of the burst mode—in some cases creating a burst mode where one had not existed (Fig. 4, A–C, bottom). In the LFS-induced joint distribution of this example, neither the burst mode (bottom left) nor the transition mode (top left) was present in the control condition, but both developed with LFS. These LFS-induced distribution modifications increased firing pattern entropy (Fig. 4D).

In VA/VLo neurons with burst mode activity (17/22), HFS shifted the ISI distribution toward the isolated spike mode (12/17). For example, in Fig. 4C (top), the isolated spike mode increased at the expense of the other three modes that all include burst duration ISIs. Weakening or abolishing the burst spikes decreased firing pattern entropy. In some cases, cell activity was suppressed completely during HFS, tantamount to inducing a zero entropy state. However, because we report entropy in units of bits per spike, our measure of entropy is technically undefined for neurons that stopped spiking. Thus cases with firing rate suppression to <2.0 Hz were not analyzed for HFS-induced effects on firing pattern entropy (4/22; Fig. 4, bottom).

Cerebellar thalamus

From the cerebellar receiving area of the motor thalamus, ventralis posterior lateralis pars oralis (VPLo), 25 neurons were examined: 24 in response to LFS and 19 in response to HFS, i.e., 18 in response to both. We show two example neurons with distributions and stimulation induced changes that span the ranges observed. In general, ISI distributions were more variable in VPLo than the other regions examined. We detail the fractions of neurons exhibiting the described changes in the paragraphs below.

As in VA/VLo, these neurons exhibited two distinct modes of ISIs with the burst mode (19/25) slightly less common than the isolated spike mode (24/25) in control conditions. Similar to VA/VLo and as depicted by both representative examples (Fig. 5A), LFS made the isolated spikes mode less prominent (14/24) and shifted the distribution toward the burst mode (14/24), particularly in VPLo neurons with few burst-interval ISIs [e.g., LFS increased burst spikes in all cells (6/6) with <10% burst-interval ISIs in control]. Both changes in the distribution increased firing pattern entropy (Fig. 5B). In response to HFS, VPLo neurons showed decreases in burst spikes (10/15 neurons with >10% burst-interval ISIs in control; Fig. 5A, top) and a narrowing of the ISI distribution that translated into a more periodic firing pattern (12/19; Fig, 5A, bottom). Both changes correspond to reductions in firing pattern entropy (Fig. 5B).

Summary

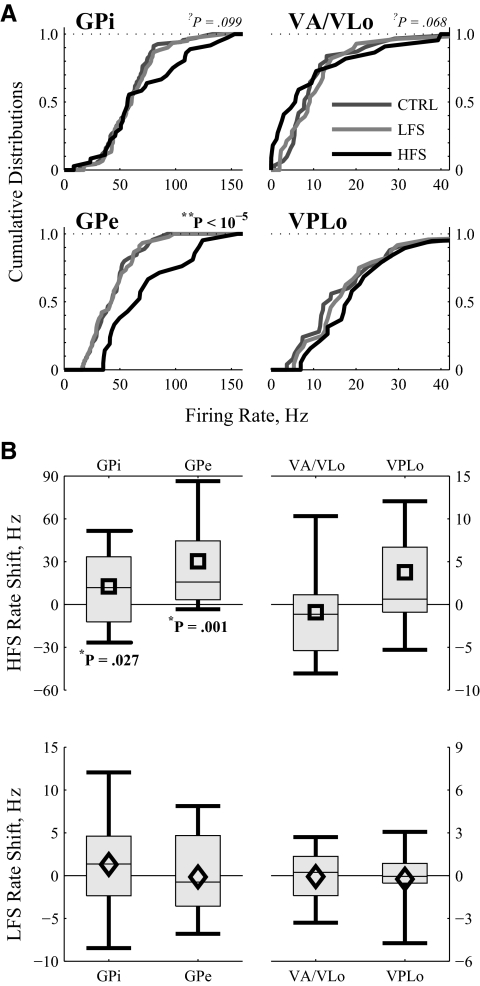
The number of cells recorded/analyzed in each area in each condition are listed in Table 1. Although LFS had no significant effect on firing rate in any region, HFS increased mean neuronal firing rates in GPe and GPi (Fig. 6), although there was a wide degree of variability in individual cell responses in GPi, visible in the boxes that depict the distribution intervals (Fig. 6B). HFS tended to decrease VA/VLo firing rates, although that trend was not statistically significant.

TABLE 1.

Number of cells used in each condition in summary

	GPi	GPe	VA/VLo	VPLo
Control	68	45	31	25
LFS	60	45	27	24
HFS	36	21	22 (18)	19
Both	28	21	18 (14)	18

The split numbers in VA/VLo responses to HFS (and Both) correspond to the number of cells recorded vs. analyzed for entropy changes in parentheses. The 4 cells missing from the entropy analysis had HFS-induced firing rates <2.0 Hz, and are highlighted (*) in Fig. 8. GP: internal segment of the globus pallidus; GPe, external segment of the globus pallidus; VA/VLo, ventralis anterior/ventralis lateralis pars oralis; VPLo, ventralis posterior lateralis pars oralis; LFS, low-frequency stimulation; HFS, high-frequency stimulation.

FIG. 6.

Summary of firing rate changes by region in response to LFS and HFS of STN. A: cumulative distributions of the neuronal firing rates in the 4 examined regions in the 3 conditions. Statistics from a 1-way ANOVA test whether stimulus frequency contributes to observed firing rate. B: the average firing rate changes across the populations of all neurons from a region for which HFS (top) or LFS (bottom) data were recorded. Symbols (diamonds and squares) report the mean; boxes cover the middle 2 quartiles split by a thin line denoting the median; thick lines stretch from 10th to 90th percentiles. Statistics from a 2-tailed pairwise t-test indicate that HFS increased firing rate in GPi and GPe, whereas LFS had no effect. Neither stimulus frequency affected firing rate in motor thalamus.

In contrast to the limited firing rate changes, both LFS and HFS had significant effects on the firing pattern entropy in each brain region (Fig. 7). The cumulative probability distributions of firing pattern entropy were consistently left-shifted by HFS and right-shifted by LFS (Fig. 7A). One-way ANOVAs confirmed, independently in each region, that stimulus frequency was a highly significant contributor to resultant firing pattern entropy. Similarly, pairwise differences (2-sided paired t-test) confirmed that in all regions, LFS increased and HFS decreased firing pattern entropy (Fig. 7B). Despite the universality of these findings across regions, a small subset of neurons in GPi experienced large increases in firing pattern entropy, seen in the top right tail of the HFS cumulative distribution function (Fig. 7A) and in the positive-going tail of the distribution interval for the entropy shift seen in GPi responses to HFS (Fig. 7B).

To quantify the differential effects of LFS versus HFS on individual cells, we compared DBS-induced firing rate changes with entropy changes in only those neurons for which responses to both LFS and HFS had been recorded (Fig. 8). The data have been sorted by control firing rate to ease viewing. Note the monotonic progression of the circles from left to right (Fig. 8A). For visual comparisons, entropy estimates in Fig. 8B come from the same cell as the firing rate data directly above them. On a cell-by-cell basis, LFS raised and HFS lowered firing pattern entropy in the vast majority of neurons in each region (Fig. 8B). In contrast, the only rate change with similar robustness was an HFS-induced increase in GPe (Fig. 8A).

DISCUSSION

Recent computational (Grill and McIntyre 2001; McIntyre et al. 2004b), and experimental studies (Anderson et al. 2003; Degos et al. 2005; Hashimoto et al. 2003) suggest that, despite inhibition of the cell bodies in the stimulated site, the efferent axons of the neurons surrounding the DBS electrode increase their firing rate in response to HFS. Previously, we reported the increased mean discharge rate and regularization of neuronal activity in the GPi and GPe during STN HFS in the MPTP monkey model of parkinsonism (Hashimoto et al. 2003). In this study, we extended that work by quantifying changes in firing pattern entropy in both GPi and GPe cells and by expanding the analysis to neurons in the pallidal- and cerebellar- receiving areas of the motor thalamus. We found that HFS decreased, and LFS increased, entropy in all examined neural structures. Our results suggest that reductions in firing pattern entropy by HFS may play a critical role in symptom alleviation by DBS.

Previous studies in animal models and human subjects have found that neurons in the basal ganglia thalamic circuit exhibit less regular firing patterns with more bursts and synchronized oscillatory activity in the parkinsonian state than in the nonparkinsonian state (Bergman et al. 1994; Brown et al. 2004; Lenz et al. 1994; Magnin et al. 2000; Molnar et al. 2005; Raz et al. 2000; Soares et al. 2004; Wichmann and DeLong 2003). Even in the nonparkinsonian state, however, activity in the basal ganglia is more disordered than would be expected by chance (Darbin et al. 2006), and pallidal and cerebellar receiving areas of the motor thalamus exhibit irregular patterns of activity, including bursts (Elder and Vitek 2001; Molnar et al. 2005). These findings suggest that firing patterns in the healthy state convey information above and beyond that carried by spike rate alone.

However, firing patterns change after parkinsonism onset, likely disrupting the transmission of information through the basal ganglia thalamic circuit. These changes in firing patterns do not necessarily require a change in entropy, and because we did not assess entropy before MPTP exposure, we do not know whether parkinsonism is associated with any changes in firing pattern entropy. Regardless of whether entropy levels increase or decrease as an animal moves from the healthy-normal to parkinsonian condition, substantial neuronal firing pattern entropy exists in the parkinsonian state. Many recent studies have reported a decrease in disordered activity in response to effective DBS (Anderson et al. 2003; Bar-Gad et al. 2004; Brown et al. 2004; Degos et al. 2005; Grill et al. 2004; Hashimoto et al. 2003; Meissner et al. 2005). We hypothesize that the irregular firing patterns present in the parkinsonian condition inhibit and slow intentional movements (i.e., akinesia and bradykinesia) and generate unwanted movements (e.g., tremor). To alleviate symptoms, a treatment must eliminate or mask these patterns pharmacologically (e.g., L-DOPA), surgically (i.e., GPi or STN lesion), or physiologically (i.e., HFS of GPi or STN). In this study, we tested the hypothesis that the effect of STN HFS is to reduce the firing pattern entropy and thus regularize neuronal firing within the pallidothalamic circuit.

LFS increases entropy

In the globus pallidus, LFS of the STN increased entropy in the neuronal spike trains by raising the proportion of very short and very long ISIs (Figs. 2 and 3). In VA/VLo, a broadening of the ISI distribution modes (61% of neurons) and an increase in the burst mode (75% of neurons) led to more irregular, burst-dominated firing patterns that decreased the fidelity of thalamic throughput (Pare et al. 1990; Rubin and Terman 2004). The increase in pallidal entropy was amplified in the pallidal-receiving area of the motor thalamus. Specifically, in response to STN LFS, entropy (mean ± SE bits/spike) increased by 0.28 ± 0.03 in GPi versus 0.57 ± 0.11 in VA/VLo (Fig. 6B). The exaggerated effect follows from the propensity of thalamic cells to burst and may be driven by a confluence of information—many GPi neurons, all with slightly elevated firing pattern entropies, likely project onto each VA/VLo neuron (Rubin and Terman 2004). Changes to VPLo firing pattern entropy were similar to those in the pallidal receiving area: a global increase (0.41 ± 0.08 bits/spike) mediated through increased bursts (Fig. 5, top) and broader ISI distributions (Fig. 5, bottom).

In response to STN LFS, entropy increased in globus pallidus and motor thalamus. Although we made no attempt to assess symptom exacerbation in these animals during LFS, data collected from human subjects suggest that LFS exacerbates parkinsonian symptoms (Moro et al. 2002; Timmermann et al. 2004). An LFS-induced entropy increase coupled with symptom exacerbation would provide compelling evidence to support the hypothesis that the irregularity of neuronal activity in the parkinsonian basal ganglia is related to the development or amelioration of parkinsonian motor signs.

HFS decreases entropy

In contrast to LFS responses, HFS of the STN generated orderly patterns of neuronal activity, reflected by a decrease in firing pattern entropy of pallidal neurons (Figs. 2, 3, 7, and 8). Tightly locked, typically multimodal ISI distributions were observed in 86% of GPi neurons (Fig. 2B) and 43% of GPe neurons (Fig. 3, top) responding to STN HFS. These highly peaked, multimodal distributions, which correspond to very low firing pattern entropies, indicate that pallidal spikes were phase-locked to the stimulation pulse (Fig. 4D). The simplest explanation is that pallidal cells fired in response to synchronized barrages of excitatory synaptic input from STN. However, STN stimulation desynchronizes activity of STN cell bodies (Meissner et al. 2005). Thus for synchronized synaptic input to be the mechanism of pallidal phase-locking, STN axons would have to be electrically isolated from their cell bodies, a possibility supported by computational work (McIntyre et al. 2004a). An alternative mechanism is that pallidal neurons were stimulated antidromically by efferents that pass near the DBS electrodes. These two mechanisms are not mutually exclusive and both have been argued to play a role in mediating the changes in pallidal neuron firing patterns (Miocinovic et al. 2006; Montgomery and Gale 2008).

Pallidal synchronization has been considered an underlying cause of parkinsonian symptoms (Raz et al. 2000). These data show that during symptom-alleviating HFS, pallidal neuronal activity was phase-locked to the HFS pulses (Fig. 4D), and widespread phase-locking implies tight synchronization between pallidal neurons. Thus synchronization of pallidal neurons would not seem to be a sufficient condition for motor symptom generation, and only synchronized activity that is highly entropic (e.g., parkinsonism-associated bursts and pauses) may underlie the development and worsening of motor symptoms, whereas synchronized activity that is regularized into a low entropy state (e.g., HFS-induced phase-locked spiking) improves motor symptoms.

Distinct from the pallidal phase-locked cells, 43% of GPe neurons exhibited shorter average ISIs with a narrower distribution that could not be attributed to tight phase locking with the stimulation pulse (Fig. 3, bottom). Although these cells did exhibit some degree of correlation with the HFS pulses, the firing pattern changes were dominated by the large increases in firing rate, consistent with that reported by others (Kita et al. 2005). The asynchronous firing rate increases suggest that, in addition to rhythmic excitatory synaptic inputs or antidromic excitation, HFS induces an excitatory, or suppresses an inhibitory, tonic drive to GPe. However, the scope of firing rate changes was less universal than firing pattern changes. Combining all pallidal cells, 70% exhibited phase-locked responses and 19% phase-independent increased firing rates. These results parallel findings by Bar-Gad et al. (2004) in response to pallidal microstimulation in which they found 70% phase-locked responses and 18% nonlocked responses. The similarity suggests that, whatever the underlying cellular mechanisms, the network effects of GPi and STN stimulation on firing pattern entropy, and presumably symptom alleviation, are similar.

Mirroring the relationship seen in responses to LFS, reductions in firing pattern entropy by HFS in the GPi (0.27 ± 0.10 bits/spike) were amplified in VA/VLo (1.26 ± 0.27 bits/spike). This entropy amplification is further evidence that the information in GPi efferent firing patterns consolidates in VA/VLo cells and supports computational findings that the effects of HFS are mediated through changes in the patterns of GPi activity altering thalamic fidelity (Guo et al. 2008). In 77% of VA/VLo neurons that exhibited burst behavior, HFS reduced the number of bursts either by shifting activity to longer duration ISIs (Fig. 4, top) or by eliminating firing completely (Fig. 4, bottom). Similarly, even in the nonparkinsonian primate, VLo cells had lower burst rates in response to HFS of GPi (Anderson et al. 2003).

Although VPLo is not within the pallidothalamic circuit, previous studies have reported a change in mean discharge rate and pattern of neuronal activity in VPLo in the parkinsonian monkey (Elder and Vitek 2001). More recent work has also shown a decrease in metabolic activity of the cerebellar receiving area of the motor thalamus in the parkinsonian state (Rolland et al. 2007). Whatever the change from healthy to parkinsonian, we did not observe significant firing rate changes in response to HFS. However, changes to VPLo firing pattern entropy were similar to those in the pallidal receiving area. HFS reduced the burst-duration ISIs in 67% of bursting cells (Fig. 5, top) and narrowed the ISI distribution in 64% of VPLo neurons. Because our entropy estimates were independent of firing rate (Dorval 2008), we would not expect changes in metabolic activity to follow from changes in firing pattern entropy.

Changes in VPLo firing pattern entropy indicate that the local circuit regularization effects of STN stimulation spread to a brain region larger than merely the pallidothalamic circuit. This spread may be mediated through multiple pathways affected by parkinsonism (Vitek 1997) including GPi efferents projecting to the pendunculopontine nucleus or midbrain extrapyramidal area that project to nucleus reticularis and other portions of motor thalamus (Levey et al. 1987; Steriade et al. 1988); GPe efferents projecting to nucleus reticularis (Asanuma 1994; Hazrati and Parent 1991); activation of cerebellothalamic fibers that run near the posterior portion of the STN (Stover et al. 2005); or by a more global regularization of motor output.

Conclusions

Recent circuit models of PD argue for changes in neuronal firing patterns as the mechanisms underlying development of parkinsonian motor symptoms. Pathological patterns associated with PD include neuronal bursting, synchronization between neurons, local oscillatory activity, and a widening of receptive fields (for review, see Filion et al. 2001), and these patterns of neuronal activity are associated with motor symptoms. On the single cell level, irregular firing patterns and frequent bursts in the parkinsonian state carry pathological information through the basal ganglia thalamic circuit. In response to HFS of the STN, pallidal neurons fired action potentials phase locked to the HFS pulses. The resulting multimodal ISI distributions show that simple statistics, such as mean rate and CV, may mask important underlying changes in neuronal firing patterns. Thus we used entropy to quantify firing pattern changes.

We found that, in the MPTP model of PD, HFS of the STN decreased entropy (reduced disorder), whereas LFS increased entropy (heightened disorder) in the neuronal firing patterns of the globus pallidus and motor thalamus. The disordered activity in GPi that occurs in PD likely propagates to the motor thalamus through the primary pallidal efferents and brain stem projections. If some of these efferents were silenced, as they are following GPi ablation, we would expect changes in firing patterns of the pallidal-receiving area of the motor thalamus that, while distinct from the changes seen during DBS, nonetheless constitute an abolition of disorder and a regularization of thalamic activity. If the disordered firing patterns of the motor thalamus contribute to the development of parkinsonian motor symptoms, treatments via lesion and HFS of the GPi or STN share the common mechanism of replacing the parkinsonism-induced disordered activity with firing patterns that are less disordered and less disruptive to motor function.

GRANTS

This work was supported by funding from National Institute of Neurological Disorders and Stroke Grants K25-NS-0535444 to A. D. Dorval, R01-NS-43450 to W. M. Grill, and R01-NS-37019 to J. L. Vitek.