Endpoint Force Fluctuations Reveal Flexible Rather Than Synergistic Patterns of Muscle Cooperation

Abstract

We developed a new approach to investigate how the nervous system activates multiple redundant muscles by studying the endpoint force fluctuations during isometric force generation at a multi-degree-of-freedom joint. We hypothesized that, due to signal-dependent muscle force noise, endpoint force fluctuations would depend on the target direction of index finger force and that this dependence could be used to distinguish flexible from synergistic activation of the musculature. We made high-gain measurements of isometric forces generated to different target magnitudes and directions, in the plane of index finger metacarpophalangeal joint abduction–adduction/flexion–extension. Force fluctuations from each target were used to calculate a covariance ellipse, the shape of which varied as a function of target direction. Directions with narrow ellipses were approximately aligned with the estimated mechanical actions of key muscles. For example, targets directed along the mechanical action of the first dorsal interosseous (FDI) yielded narrow ellipses, with 88% of the variance directed along those target directions. It follows the FDI is likely a prime mover in this target direction and that, at most, 12% of the force variance could be explained by synergistic coupling with other muscles. In contrast, other target directions exhibited broader covariance ellipses with as little as 30% of force variance directed along those target directions. This is the result of cooperation among multiple muscles, based on independent electromyographic recordings. However, the pattern of cooperation across target directions indicates that muscles are recruited flexibly in accordance with their mechanical action, rather than in fixed groupings.

INTRODUCTION

The CNS can typically utilize many different muscle combinations when controlling multiple degrees of freedom (DOF) of the body. To simplify task control (Bernstein 1967), it has been proposed that the CNS enforces muscle synergies: fixed patterns of activation among multiple muscles acting about the relevant DOF (d'Avella et al. 2003; Drew et al. 2008; Giszter et al. 2007; Ivanenko et al. 2006; Overduin et al. 2008; Saltiel et al. 2001; Ting and Macpherson 2005; Tresch et al. 2006). Alternatively, the CNS could use a task-specific muscle coordination pattern without requiring fixed patterns, perhaps reflecting the optimization of movement according to some suitable performance criteria (Buchanan and Shreeve 1996; Harris and Wolpert 1998; Kuo 1994; Todorov and Jordan 2002; Valero-Cuevas 2000; Valero-Cuevas et al. 1998). It is also unclear whether some force in some directions is generated by a “prime mover” muscle (Thomas et al. 1986) or whether all force generation involves the cooperation of multiple muscles (Buchanan et al. 1986; Keenan et al. 2006). These questions remain unresolved, in spite of multiple attempts to characterize muscle activation patterns across multiple DOFs.

The synergistic activation hypotheses and the task-specific flexible activation hypotheses are not incompatible; strategies could apply to voluntary skilled tasks different from those applying to stereotypical reflexive tasks. To separate these hypotheses in voluntary tasks, we introduce a new method for assessing muscle force contributions to net force generation at a multiple DOF joint: the metacarpophalangeal (MCP) joint of the index finger. This method uses high-gain force measurements recorded at the finger tip to estimate the various muscle contributions to net joint force. In contrast, most prior studies investigating muscle coordination across multiple DOFs have focused on the use of electromyographic (EMG) recordings. Although such EMG recordings provide valuable information about muscle activity, they offer significant disadvantages for studying muscle coordination in multiple muscle systems. For example, it is not always possible to record EMGs from all muscles that may contribute to a task. Also, the identification of muscle-level synergies from EMGs in natural behaviors may also be complicated by the existence of biomechanical or task-planning constraints unrelated to muscle synergies. If the CNS chooses to generate force in stereotypical ways, it may cause muscle activation patterns to appear to obey simplifying activation constraints, even if other activation patterns are possible.

An alternative approach to studying muscle coordination involves mapping isometric endpoint force variability for an array of targets distributed uniformly across the endpoint force space. Stochastic effects may enter such tasks in several ways, but one of the most significant is signal-dependent noise (SDN) (Enoka et al. 1999; Galganski et al. 1993; Laidlaw et al. 2000; Schmidt et al. 1979; Slifkin and Newell 1999), where isometric force variability increases with average isometric force. Such SDN may arise from the sequential recruitment of motor units with larger twitch forces as the muscle force requirement increases (Jones et al. 2002). If muscle force variability increases with average muscle force, then differing neuromotor control strategies can generate different patterns of endpoint force variability. For example, one muscle acting alone will induce variability that not only increases with signal magnitude but is also directionally aligned with the muscle's action direction in endpoint force space. Alternatively, cooperation among multiple muscles, each with different action directions, will induce endpoint variability that reflects the multiple directions of muscle action. It follows that the overall endpoint force covariance caused by a muscle synergy will be composed of individual covariances from the constituent muscles, but will not be aligned with the covariance of any one muscle. Noise may occur at other levels in the motor cascade, such as at the level of synergy commands, and where noise is generated may have an impact on the structure of endpoint force fluctuations.

In light of these possibilities, the aim of the present study was to determine, using multidirectional forces generated by the human index finger, whether the covariance of multidirectional isometric force exhibits significant differences as a function of target force direction. Furthermore, we argue that such force covariance maps provide strong clues about the ways in which the nervous system controls muscle combinations or synergies, acting about multiple DOFs.

METHODS

We developed a method to use the variability of isometric forces exerted by the index finger as an indicator of underlying muscle coordination. The method uses the pattern of this force variability as a function of target force direction and magnitude, termed the force covariance map, to quantify the relative amount of variability that occurs in the target direction itself, termed the target-directed variance fraction (η). Muscle coordination strategies may constrain how η varies with the target direction. In the following text we describe the theoretical basis for the force covariance map, our means of experimentally measuring it, and the techniques used for relating the force covariance map to muscle action direction and activity.

Force covariance map

The variability of endpoint forces will likely be influenced by how muscles are activated. In the present study, we define the task as the exertion of isometric forces by the tip of the index finger (i.e., the endpoint), with a specified direction and magnitude in the plane perpendicular to the finger. We define the axes of this plane as flexion–extension and abduction–adduction, corresponding to vertical and horizontal forces, respectively, when the palm of the hand faces down. The relation between the pattern of endpoint force variability—the force covariance map—and hypothetical muscle coordination is based on three assumptions of muscle force production: linear superposition, signal-dependent noise, and low correlation of noise-like forces between muscles. When these assumptions are valid, the force covariance map may be used to study muscle coordination and muscle synergies.

Linear superposition provides a means to examine muscle coordination in endpoint force space. Superposition is the assumption that the endpoint force is the linear sum of individual contributions of force from each muscle. These individual contributions occur along directions in the endpoint force space, or muscle mechanical actions (illustrated hypothetically in Fig. 1 A) that depend on the musculoskeletal geometry, such as the lengths of body segments and moment arms about the degrees of freedom of joints (Kuo 1994, 2000). Action directions have been empirically quantified for cat hindlimb muscles contributing to multidirectional ankle force (Lawrence et al. 1993), monkey forearm muscles contributing to multidirectional wrist force (Hoffman and Strick 1999), and human thenar motor units contributing to thumb abduction and flexion (Westling et al. 1990). Superposition does not always apply, for example, if a single muscle also pulls on neighboring muscles. However, these effects are usually small, even among motor units within a muscle (Sandercock 2005). Mechanical actions have been measured for the muscles controlling the human index finger and the forces from individual tendons have been found to superpose linearly at the fingertip (Valero-Cuevas et al. 2000). Superposition of isometric force has been found to apply well in other biomechanical systems such as the frog hindlimb (Mussa-Ivaldi et al. 1994).

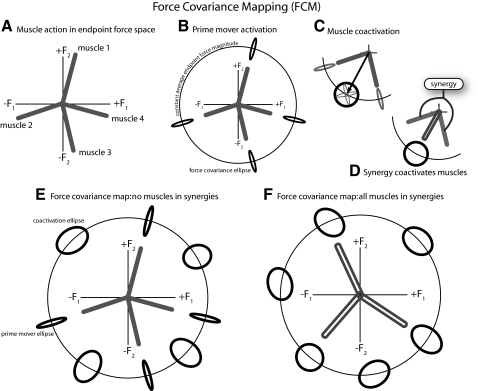
FIG. 1.

Conceptual basis for force covariance mapping. A: muscles have biomechanical actions in endpoint force space, represented hypothetically as action vectors in the endpoint force space of isometric abduction/adduction (F₁) and flexion/extension (F₂) forces exerted by the index finger. B: activation of any single muscle alone, as a prime mover, will generate an average force vector in endpoint force space, with force covariance due to signal-dependent noise. Four such covariances are illustrated, each largely aligned with one muscle's action direction. We refer to this type of covariance as target-directed. C: ≥2 muscles may be coactivated, for example, to generate a force (arrow) with direction between the individual muscle action directions. Coactivation produces a much broader covariance, representing the combined effect of the individual muscles (see appendix). We refer to this type of covariance as non-target-directed. D: if the coactivation of multiple muscles is fixed by a synergy, the synergy produces a similar net action, with a similar covariance to C. E: the force covariance map summarizes the covariances for a variety of target directions, at fixed levels of endpoint force magnitude. If muscles are not in fixed synergies, both target-directed and non-target-directed covariance may be observed. F: if all muscles are in fixed synergies, only non-target-directed covariance will be observed.

Signal-dependent noise will induce variability in endpoint forces, dependent on muscle action directions and how muscles are coordinated. We consider first the hypothetical case of a muscle activated as a prime mover, when the target force direction is aligned with a particular muscle's mechanical action. The endpoint force would be expected to fluctuate (e.g., Galganski et al. 1993; Thomas et al. 1991) along the action direction, with force variability increasing with activation magnitude (e.g., Jones et al. 2002; Moritz et al. 2005). The force covariance may be thought of as an ellipse aligned with the principal axis aligned with the target direction (Fig. 1B). In general, the force covariance ellipse may be thought of as the region of force space that contains a large proportion of the force data points for a given target. For example, if force variability is Gaussian distributed, a 2σ force covariance ellipse would contain about 87% of force data points.

We next consider the more typical case where muscles are activated together, for example, to produce a force not aligned with a single muscle's action. The individual muscle covariances then approximately add together to determine the total force covariance. The force covariance ellipse will then be aligned with neither muscle action (Fig. 1C). A single muscle synergy combines multiple muscles together (Fig. 1D) and will therefore produce a covariance ellipse in the direction of synergy action that is the same covariance as the coactivation case. Here it is important to assume that noise-like fluctuations in the individual muscle forces are relatively uncorrelated. Correlation is a concern because, for instance, very highly correlated force fluctuations between two antagonistic muscles would cancel from the measurable endpoint force variance, hiding their activation from the force covariance map. Correlation has been observed across muscles (Bremner et al. 1991a,b) and may vary depending on the training of an individual (Semmler 2002; Semmler and Nordstrom 1998b). However, the correlation across muscles is weak and its functional significance during the production of smooth force has been questioned (Deluca et al. 1993; Schieber and Santello 2004). Coherence between surface EMG pairs has been shown to be modest (<10%) at low frequencies, with higher values (30–50%) only in upper frequencies of 15–30 Hz (Farmer et al. 2007; Fisher et al. 2002; Kilner et al. 1999). Joint force contains a significant signal only in the 6- to 12-Hz range due to unfused motor unit twitches, but relatively little signal at higher frequencies due to the slow time course of muscle contraction (see Galganski et al. 1993). Therefore even if there is significant coherence in muscle electrical activity, it occurs at frequencies unlikely to produce significant muscle forces.

The force covariance map is a set of force covariances measured at equally spaced points around a constant average endpoint force magnitude. A force covariance map when no muscles are in synergies may contain two types of force covariance ellipses: 1) narrow ellipses aligned with the target direction in directions of muscle action (target-directed ellipses), indicating muscles behaving as prime movers; and 2) broad nonaligned ellipses (non-target-directed ellipses) in directions involving coactivation of multiple muscles with different action directions (Fig. 1E). Alternatively, if all muscles are grouped into synergies with muscles having different action directions, only coactivation ellipses will be observed because multiple muscles will always contribute in some fixed amount (Fig. 1F).

Experimental procedures

We experimentally measured the force covariance map for endpoint forces produced by the MCP joint of the human index finger. We also measured surface EMG from three muscles to compare with the force covariances and also to form rough estimates of muscle recruitment curves and action directions. Seven unimpaired subjects (two female, five male) participated in the study. All subjects were right-handed and used their dominant index finger to produce isometric forces in different directions and magnitudes in the flexion–extension/abduction–adduction (FEAA) force plane. The Northwestern University Institutional Review Board approved the study protocol and informed consent was obtained from each subject prior to participation.

The experimental apparatus was designed to mechanically isolate the index finger (Fig. 2). Subjects were seated upright in an adjustable chair with the shoulder abducted about 15°, with the elbow resting on a padded support. The elbow joint was flexed to 90° and the forearm was casted and secured in a plastic orthosis, in a pronated position with the palm facing down. The index finger was casted and placed in a fixed cylindrical tube, so that forces were exerted against the inside of the tube and about an “endpoint” just distal to the distal interphalangeal (DIP) joint. These forces were transmitted to the tube by three screws 120° apart that centered the finger in the tube. The screws were gently pushed into the cast while it hardened, making a secure but comfortable connection with the index finger. One subject repeated the experiment with the screws rotated to different positions relative to the finger and it was found that the screw positions did not affect the results. This setup maintained both interphalangeal joints extended and approximately aligned the MCP extension axis with the vertical load cell axis. Digits 3–5 were secured in a resting position that was slightly adducted away from the index finger. The thumb was abducted to 50° and casted with the wrist. One Velcro strap was placed around the subject's waist and two Velcro straps were placed in a crisscross fashion over each shoulder to restrain the subject and to minimize shoulder movement.

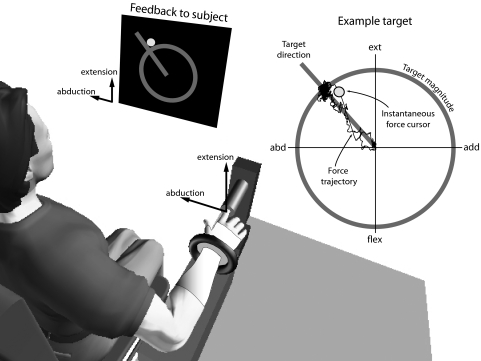
FIG. 2.

Experimental setup for measuring isometric forces exerted by the index finger. The subject is configured with the shoulder abducted about 15° and the elbow flexed to 90° and positioned in full pronation. The wrist is immobilized with rigid casting tape and secured within a fixture. The right index finger is similarly immobilized and secured just distally to the distal interphalangeal joint, connected to a 6 degree-of-freedom load cell through a rigid tube. Visual feedback of abduction–adduction (left–right direction) and flexion–extension (down–up) forces is displayed to the subject on a computer screen, with instantaneous force and the target direction and magnitude displayed in polar coordinates. The subject exerts forces to move the cursor (indicated by a dot) toward the target force (intersection of ray with circle). The example shows the force trace recorded over a trial.

Isometric index finger forces in the FEAA plane were measured using a sensitive six-axis load cell (Model 20E12A-I25 9N.5, JR3, Woodland, CA). In the configuration it was used, this load cell had a bandwidth of 0–250 Hz. Forces were low-pass filtered by an analog fourth-order Butterworth filter with a 926-Hz cutoff frequency. The index finger exerted forces on one end of the tube and the other end transmitted and amplified these forces to the load cell. The length of the tube (10 cm) was designed to amplify potentially small endpoint forces and to allow them to be recorded by both translational forces and rotational moments on the load cell. We estimated the load cell's resolution (smallest measurable force) to be 1 mN. These forces were also presented visually to subjects in real time. We displayed a dynamic cursor representing the instantaneous two-dimensional force in the FEAA plane (see Fig. 2) on a computer screen. Forces were sampled at 1,000 Hz.

We also recorded surface EMGs from several finger muscles, so that EMG activity regions could be compared with force covariances. EMGs were recorded using miniature electrode/preamplifiers (Delsys, Boston, MA) with two silver recording surfaces, 5 mm long and 10 mm apart. The preamplifiers have bandwidth 20–450 Hz for surface recordings, with gains set to 100. EMG electrodes were placed according to standard anatomical landmarks and verified with the recommended test maneuvers (Perotto 2005). EMG signals were sampled at 2,000 Hz.

Electromyograms were recorded from the first dorsal interosseous (FDI), extensor digitorum communis (EDC), and extensor indicis proprius (EIP), but not in all subjects. EMG activity was recorded from the FDI in six subjects. Additional activity was recorded from the EDC in three of these subjects and the EIP from the other three. We used the EMGs to estimate recruitment curves as a function of target direction and to estimate muscle action directions. These were then compared qualitatively to force covariance results. We found the small number of subjects acceptable for such qualitative comparisons.

The experimental protocol called for the exertion of endpoint forces in 24 different directions and at three different magnitudes. The directions were generally distributed equally over the plane at 15° increments. One subject performed a slightly different protocol, with tighter distribution between pure abduction and pure flexion, but the same number of directions overall. A rest trial was collected for each subject to establish EMG baseline levels. For each trial, the subject viewed the desired force as a target on the visual display (Fig. 2), represented in polar coordinates by a static ray for target direction, and a static circle for target magnitude. The subject was instructed to gradually exert force in the target direction and then to hold the target force as precisely as possible for about 10–20 s, the goal being to generate a stationary time series of forces with constant magnitude and direction on average. The experimenter examined the time-domain force traces on-line. Trials were repeated if forces were found not to be approximately constant. The force feedback display was zeroed, with the subject at rest, before each set of trials. Subjects were asked to rest for ≥10 s between each trial and ≥1 min after each group of 10 trials.

The force magnitudes were also equally distributed at three levels, chosen to require very minimal effort for all subjects. Because these magnitudes were at discrete levels, we refer to them as target levels 1–3. These target levels were distributed at equal intervals, with the highest magnitude level, task level 3, at about 2 N in magnitude.

Data analysis

The experimental data were analyzed to quantify endpoint force variability, to determine regions of activity in task space for key muscles, and to estimate the action direction of these muscles.

Quantifying force variability

We used measured forces to compute force covariance maps. We first cropped each trial to isolate relatively constant forces of ≥10 s in duration (Fig. 3 A). The time series forces, F_AA(t) in the adduction–abduction direction and F_FE(t) in the flexion–extension direction, were combined in a vector time series F(t). The empirical target force vector F_target was defined to be equal to the average force vector F̄, with F̂_target defined as the unit vector in that direction. Target direction can also be expressed as an angle θ in endpoint force space, measured counterclockwise from the adduction axis. To reduce the voluntary contribution to force variability, we filtered both force components (Fig. 3B) with a zero-phase-lag eighth-order Butterworth band-pass filter with 3-dB cutoffs at 5 and 30 Hz (Filter Design and Analysis Toolbox of MATLAB, The MathWorks, Natick, MA). We found substantial voluntary contribution below 5 Hz and nonphysiological noise >30 Hz. The choice of cutoff frequencies was found to have no qualitative effect on the results. Filtered force data F̃ were then used to compute the force covariance (Fig. 3, C–E). The covariances, plotted as ellipses centered at the target force for each trial, constitute the force covariance map (Fig. 3F).

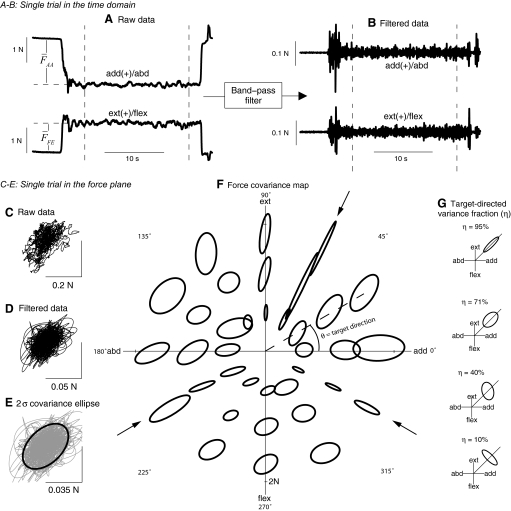
FIG. 3.

Construction of force covariance map with representative data. A: raw force traces in abduction/adduction and flexion/extension. Subjects produced ramp-and-hold forces to a specified magnitude and direction, holding for 10–20 s. B: noise-like fluctuations were emphasized by band-pass filtering data. Data were cropped to include only the steady hold interval, indicated between the vertical lines in A and B. C: raw force fluctuations during the hold interval, plotted in the abduction–adduction/flexion–extension plane. D: band-pass filtered force fluctuations. E: covariance of force variability, plotted as a σ ellipse, representing the data covariance matrix. F: covariance ellipses plotted for every trial from one representative subject. The center of the ellipse indicates the average force vector produced during the trial; the target direction θ is the angle between the average force vector direction and the adduction axis. The ellipses are magnified by a factor of 25 for visualization. G: alignment between ellipse and target direction is quantified using the target-directed variance fraction η, the fraction of total variance that occurs in the direction of the target force. Various hypothetical force covariance ellipses are shown along with the corresponding η value, where the diagonal ray indicates the target direction.

To determine whether endpoint force variability could be used as an indicator of muscle activity, we examined endpoint force variability for signal-dependent noise (SDN), which should manifest itself in recordings of multidirectional force variability as a scaling of variability as a function of target magnitude level (see appendix). We tested this hypothesis by computing the total variance of force as the trace of the force covariance matrix. The total variance was averaged across all target directions for each task level and subject. Within each subject, the total variance was normalized by dividing by the total variance of task level 1. A linear regression analysis was performed (regress in MATLAB) using the equation: Normalized total variance = a × Task level + b, where a and b are coefficients to be determined.

We quantified the degree to which the covariance for each trial was aligned with that trial's target force direction. We refer to this quantity as the target-directed variance fraction (η), defined as the fraction of the total variance (in both force components) that occurs in the direction of the target force (Fig. 3G). For example, η is 100% if force fluctuates only in the target direction, 50% if it fluctuates equally in all directions, and 0% if it fluctuates entirely in a direction orthogonal to the target direction. We refer to the covariance matrix of filtered forces as cov [F̃], so that

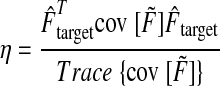where the numerator quantifies the amount of variance occurring in the target direction and the denominator summarizes the amount of total variance as a scalar.

Assuming that SDN applies to each individual muscle's force and that there is little correlation between these forces, the target-directed variance fraction η can be used as a bound on synergistic behavior among muscles. Suppose that the force covariance map exhibits a high target-directed variance in a muscle A's action direction. If η = 0.9 in this target direction, then at most 10% of the force variance is generated by the combined effect of muscles acting in different directions than muscle A. Such a relatively low contribution to force variability from muscles in other directions suggests that muscle A is not strongly synergistically linked to muscles that act in different directions: 1 − η is an upper bound on synergistic behavior because muscle A may contain motor units with slightly different mechanical actions, thereby generating variance outside the target direction without any synergistic coupling with other muscles.

Statistical regularities in the force covariance map were quantified using a one-way ANOVA of the target-directed variance fraction using task direction as the factor. Target direction θ was a continuous variable. To make it a discrete factor for ANOVA analysis, target direction was separated into 15° bins, corresponding to the increment of target directions presented to the subject.

Regions of muscle activity in endpoint force space

Muscle recruitment curves were computed from EMG data and plotted as a function of target direction. Raw EMG traces were first rectified and averaged across the hold period of each trial and the corresponding rest period, with the difference between the two serving as the net EMG. We fit a cosine tuning curve (Hoffman and Strick 1999; Todorov 2002) to net EMG data within each subject and target level (24 values for each target level), minimizing the sum-squared error. The EMG data for each target level and subject were then normalized to the maximum of the fit, thus avoiding normalization to a spurious maximum in the data. Once the EMG data were normalized, comparisons of directional tuning could be made across target levels and subjects. To summarize the EMG data for each muscle across target levels and subjects, a single cosine tuning curve was fit to the normalized EMG data.

Estimates of muscle activity correlation

Due to its potential effects on inferences drawn from the force covariance map, we estimated muscle activity correlation. The correlation coefficient between EMG signals during the steady portion of the contraction was calculated for the FDI–EIP and FDI–EDC pair. Correlation coefficients are reported only for target directions exhibiting significant average EMG activity in both muscles.

Estimates of muscle action in endpoint force space

We estimated the directions of muscle actions, in the endpoint force space of abduction–adduction and flexion–extension, with a cross-correlation of force and EMG data. This is a generalization of the spike-triggered averaging method, normally applied to single motor unit EMGs, to surface EMGs. Spike-triggered averaging correlates intramuscular EMGs to a single motor unit's spike waveform, to yield spike times, and then correlates spike times to endpoint force to yield an estimate of a single motor unit's mechanical action. Our method correlates surface EMGs directly to endpoint force to yield an estimate of a muscle's action. Referring to muscle i's EMG time series (normalized to its mean) as E_i[n], with n for discrete time, the cross-correlation z_i[n] is defined as

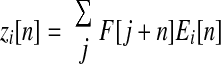where the sum was computed across the hold period of each trial. This equation quantifies the average trajectory that occurs in endpoint force space subsequent to increases in the EMG signal from muscle i. The action direction estimate α_i was derived by computing the direction of the average vector z̄_i[n] over a range of time shifts between force and EMG (EMG and force simultaneous to EMG leading force by 100 ms). The direction of α_i is the direction of change for isometric force when the rectified EMG in muscle i is increasing, averaged across the hold period. When E_i[n] is a spike train, the preceding process reduces to spike-triggered averaging. We have recently shown on theoretical grounds that the direction α_i may accurately represent muscle mechanical action despite the fact that z_i[n] may not accurately represent the muscle activation magnitude or time course (Kutch et al. 2007). This analysis produced action estimates, specific to our experimental setup, for the FDI, EDC, and EIP. For muscles from which we did not record EMGs, we estimated actions from moment arm data in the literature. We used published data for index finger muscles derived from magnetic resonance imaging (MRI) data (Fowler et al. 2001), for finger postures that corresponded to those used here. The literature estimates were: flexor digitorum profundus (FDP) 296.5°, flexor digitorum superficialis (FDS) 292.7°, first lumbrical (LUM) 247.9°, and first palmar interosseous (FPI) 347.5°.

Computational hypothesis analysis

We examined the ability of FCM to distinguish muscle activation strategies by mathematically describing the assumptions of superposition of muscle forces, signal-dependent noise, and modest muscle force correlation. The synergistic activation hypothesis was described mathematically as a linear coupling among muscle activations (d'Avella et al. 2003; Ting and Macpherson 2005; Tresch et al. 2006). The flexible activation hypothesis was described mathematically as a minimization of the sum of squared muscle forces (Buchanan and Shreeve 1996; Todorov and Jordan 2002; van Bolhuis and Gielen 1999). This minimization produces flexible muscle activation because it can appropriately activate single muscles or muscle groups depending on the target direction, whereas the synergistic activation hypothesis can activate muscle groups only. Simulations of both hypotheses were performed across unknown parameter values unknown noise source (synergy-level vs. muscle-level noise). The computational analysis permitted a rigorous assessment of the ability of FCM to distinguish competing hypotheses (see the appendix for mathematical details).

RESULTS

We will describe results supporting the hypothesis that patterns of isometric endpoint force variability contain significant information about neuromotor control strategies. Subjects produced fairly constant average endpoint forces in all directions and magnitudes. The residual variability yielded force covariance maps with considerable dependence on target direction (see representative data in Fig. 3F). For most target directions, the covariance ellipses were relatively broad with little alignment with the target direction (non-target-directed ellipses). These likely represent cases where multiple muscles cooperate to produce the endpoint force. However, for three particular directions, covariance ellipses were quite narrow and well aligned with the target direction (target-directed ellipses), indicating cases where a single muscle potentially acted as a prime mover. This pattern was also quite consistent across subjects, as quantified by high target-directed variance fractions η in those few directions. As a test of the FCM methodology, we found a positive correlation between force magnitude and total force variance, indicating that much of the variance can indeed be attributed to signal-dependent noise, as hypothesized. EMG tuning curves showed preferred directions of recruitment that corresponded with the directions of high target-directed variance, supporting the interpretation of target-directed covariances as indication of prime-mover activity. Estimates of mechanical action also indicated that these prime mover directions corresponded to the action induced by a single muscle. The quantitative data for these results are presented in the following text.

Testing assumptions of SDN and muscle activity correlation

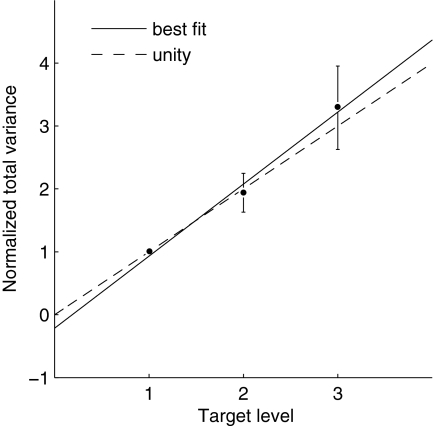
Total force variance generally scaled with target level, indicating that SDN was responsible for much of the observed endpoint force variability (Fig. 4). A linear regression analysis applied to the normalized total variance showed a significant increase in total variance as a function of target level (P = 0.00001), in accordance with the scaling assumption for SDN (see the appendix for mathematical details). The data also indicated a roughly linear scaling of variance with target magnitude level (slope), without a significant amount of “signal-independent noise” (intercept). The regression coefficients were a = 1.19 ± 0.16 and b = −0.19 ± 0.34 (mean ± 95% confidence interval).

FIG. 4.

Endpoint force variability exhibits signal-dependent noise. Total force variance, normalized to the lowest target level, plotted vs. target magnitude level. Variance increased with target level (P = 0.00001), as would be expected with signal-dependent noise. Error bars indicate 95% confidence intervals for the mean and the best-fit line, determined by linear regression, is shown.

The EMG–EMG correlation coefficients for the muscle pairs FDI–EIP and FDI–EDC were found to be very modest. Across target directions exhibiting significant EMG activity in both muscles of the pair, the FDI–EIP correlation coefficient was found to be 0.0078 ± 0.0122] (mean ± SD) and the FDI–EDC correlation coefficient was found to be 0.0055 ± 0.0144 (variation across targets and subjects). These correlations clearly do not represent all muscle pairings relevant to the experiment, but they are congruent with modest amounts of muscle activity correlation previously reported in the literature (Bremner et al. 1991a; Farmer et al. 2007; Fisher et al. 2002; Kilner et al. 1999). These correlations were not used to adjust the force covariance ellipses.

EMG tuning curves and directions of muscle mechanical action

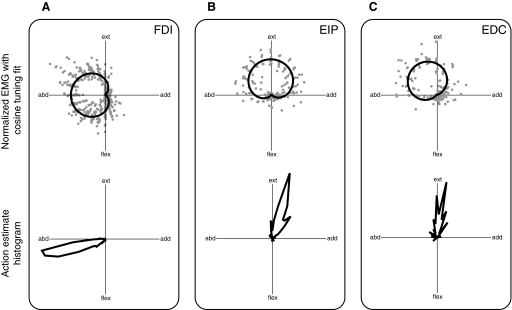
Each muscle had a distinct EMG tuning curve (Fig. 5, top) and mechanical action (Fig. 5, bottom). Cosine tuning curves used for EMG data normalization generally provided a good description of how EMG activity varied with direction. R² values for the cosine tuning fit to EMG activity were (mean ± SD) 0.82 ± 0.11 for the FDI, 0.75 ± 0.16 for the EDC, and 0.87 ± 0.05 for the EIP (variation is across subjects and target levels). When cosine tuning fits were produced for the normalized EMG data grouped across subject and target level, R² values were 0.74 for FDI, 0.68 for EDC, and 0.74 for EIP, indicating the consistency of directional tuning in these muscles across subject and target level (Fig. 5, top). FDI was recruited in the left half of the endpoint force plane, with a peak activity in the pure abduction direction. EDC was recruited primarily in combined abduction–extension target force directions, with a peak at 122°, as measured counterclockwise from the positive adduction axis. EIP was recruited primarily in the upper half of the endpoint force plane, with peak activity in the pure extension direction.

FIG. 5.

Regions of muscle activity and muscle action direction estimates in endpoint force plane. Top panels: normalized electromyographic data across all subjects, target directions, and target magnitudes, with a single cosine tuning fit to the grouped data. Bottom panels: polar histogram of action direction estimates across all subjects, target directions, and target magnitudes. A: the first dorsal interosseous (FDI) muscle is active in the left half of the endpoint force plane between extension and flexion and has an action direction of mostly abduction with some flexion (196°). B: the extensor indicis propius (EIP) muscle is active in the upper half of the endpoint force plane between adduction and abduction, and has an action direction of mostly extension with some adduction (70°). C: the extensor digitorum communis (EDC) muscle was active largely in the second quadrant of the endpoint force plane between extension, and has an action direction of mostly extension (90°).

The mechanical action directions (Fig. 5, bottom) were roughly aligned with the peak recruitment directions. The directions were (mean ± SD) 196.2 ± 20.1° for FDI, 90.5 ± 31.4° for EDC, and 70.5 ± 20.7° for EIP, measured counterclockwise with respect to the adduction axis.

Force covariance map relates to muscle activity and muscle action directions

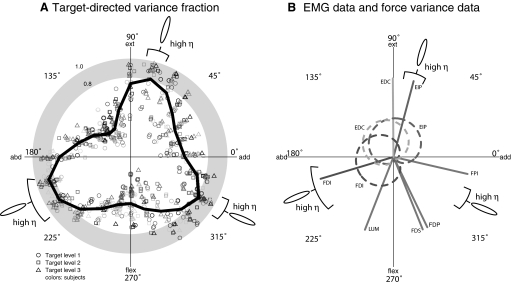
The shape and alignment of force covariance ellipses were nonuniform as a function of target direction. The target-directed variance fraction η varied significantly with target direction (ANOVA, P = 0.000001), with peaks in three distinct target directions that cross a threshold of 0.8 (Fig. 6 A). Peaks occurred in directions of 195, 75, and 330°, with average η values of 0.88, 0.80, and 0.82, respectively. These values were averaged to define the target directedness of the data, a value of 0.83, which is used to compare hypotheses in the next section. Intersubject variability was low, with an overall η SD of 0.099 across subjects, averaging over all target directions.

FIG. 6.

Force covariance map relates to muscle activity and action direction. A: relation between force covariance ellipses and the target force direction, as quantified by the target-aligned variance fraction (η). Each point represents a target, with direction given by the target direction, and magnitude given by η. Different target magnitude levels are represented by different symbols, whereas different subjects are represented by different colors. On top of the subject population data is a thick curve showing η averaged across subjects and target levels within each 15° bins of target direction. Averaged η exceeds a 0.8 threshold in 3 ranges of target directions, giving target direction ranges that had “high” η corresponding to target-directed covariance ellipses. B: the regions of target directions exhibiting target-directed and non-target-directed covariance were compared with muscle activity tuning curves for muscles recorded from and action directions from all muscles (lines).

We found that directions of target-directed ellipses corresponded closely to muscle action directions (Fig. 6B). The peak direction of 195° aligned well with the FDI action of 196.2° and the direction of 75° aligned well with the EIP action of 70.5°, both estimated from EMG–force cross-correlations (Fig. 6B). The peak direction of 330° aligned reasonably well with the FPI action of 347.5°, considering that the latter was obtained from MRI-based estimates obtained from the literature rather than the specific configuration and anatomy of our subjects. Configuration differences such as the greater MCP flexion angle in our setup could cause the FPI to have a greater flexion moment arm (An et al. 1983), sufficient to potentially explain any discrepancy with the anatomical studies. The close alignment between directions of target-directed ellipses and muscle actions suggests that these muscles may act as prime movers for those force targets that they are mechanically well suited.

For target directions between regions of high η and muscle mechanical actions, data indicate a greater amount of coactivation with no evidence of prime movers (Fig. 6B). For example, target directions ranging from 105 to 180° are aligned with none of the mechanical actions and were characterized by lower η. These same directions showed significant EMG coactivation in FDI, EDC, and EIP, with no clear prime mover. Evidence for other target directions is less direct but also indicates coactivation. For example, directions ranging from 225 to 300° showed significant FDI activity, even though the FDI produces too much abduction force to perform these target forces alone. These target forces could be performed with the coactivation of muscles with more flexor action, such as LUM, FDS, and FDP, although we did not collect EMG data from these muscles. Similarly, targets in the range 0–45° showed significant activity of EIP, implying the coactivation of other muscles such as FPI. Thus directions with low η corresponded to cases where either direct or indirect evidence supported the cooperation between multiple muscles with different action directions.

Analysis of endpoint force fluctuations from synergistic and flexible activation

We observed target-directed covariance for targets aligned with the action direction of several key muscles controlling the index finger, but non-target-directed covariance in other target directions. This observation suggests a flexible muscle coordination strategy, rather than the coordination of synergistic muscle groups that couple muscles with distinct action directions. We analyzed the ability of FCM to distinguish synergistic from flexible in the context of our assumptions, to estimate the conditions in which our conclusions are valid.

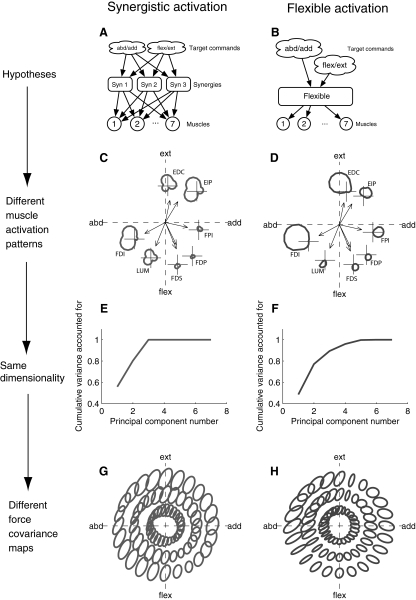
Synergy activation involves forming groups of muscles and then having the target commands activate these groups rather than activate muscles directly (Fig. 7 A). Flexible activation involves transforming target force commands into muscle control signals in a target-dependent way (Fig. 7B). Given the muscle action vectors, different hypotheses predict different directional tuning functions for the muscles (Fig. 7, C and D). Both hypotheses begin with two-dimensional target force commands, so both will produce low-dimensional muscle forces, regardless of whether there are synergies among the muscles (Fig. 7, E and F). Using the synergistic activation hypothesis, the first two principal components account for 80% of the total variance. Using the flexible activation hypothesis, the first two principal components account for 77% of the variance. Even though the synergy hypothesis is explicitly forming muscle groups, a dimensionality-reduction technique such as principal-components analysis (PCA) will be unable to distinguish these hypotheses because of the low target force dimensionality. However, since different hypotheses produce different directional tuning functions, and muscle force noise is assumed to be signal-dependent, the pattern of endpoint force fluctuations will be different for the two hypotheses. Synergy activation will produce non-target-directed ellipses for all tasks because the synergies require that each target force be performed by muscles with different action directions (Fig. 7G). Flexible activation will produce target-dependent force fluctuations, with target-directed ellipses in some target directions and non-target-directed ellipses in other target directions (Fig. 7H).

FIG. 7.

Different activation hypotheses produce the same muscle force dimensionality, but different force covariance maps. A: in the synergistic activation hypothesis, the nervous system forms groups of muscles called synergies. To achieve force targets, the target force commands are used to coordinate the synergies, rather than the muscles directly. B: in the flexible activation hypothesis, there is a target-dependent function that chooses an appropriate activation for each muscle given the target. C and D: given a particular choice for unknown parameters, directional tuning curves (average muscle force as a function of target direction) are calculated for each muscle using the synergistic (C) and flexible (D) hypotheses. The action directions (measured experimentally) are shown in the endpoint force space and the directional tuning curve in endpoint force space is shown for each muscle offset from the origin for clarity. E and F: the average force in the 7 muscles as a function of target is subjected to principal components analysis and the resulting variance fraction accounted for as a function of number of principal components used is shown for the synergistic (E) and flexible (F) hypotheses. Notice that a large percentage of the total variance in average muscle force across targets is accounted for by the first few principal components, regardless of whether there are muscle synergies. G and H: the predicted force covariance maps are shown for the synergistic (G) and flexible (H) hypothesis. Notice that under the synergistic hypothesis, muscles are coupled, so producing any target force involves the cooperation of multiple muscles, generating non-target-directed covariance for all targets in the plane. However, the flexible activation hypothesis is capable of generating target-directed ellipses when performing a target with a single muscle is appropriate and non-target-directed ellipses when muscle cooperation is appropriate.

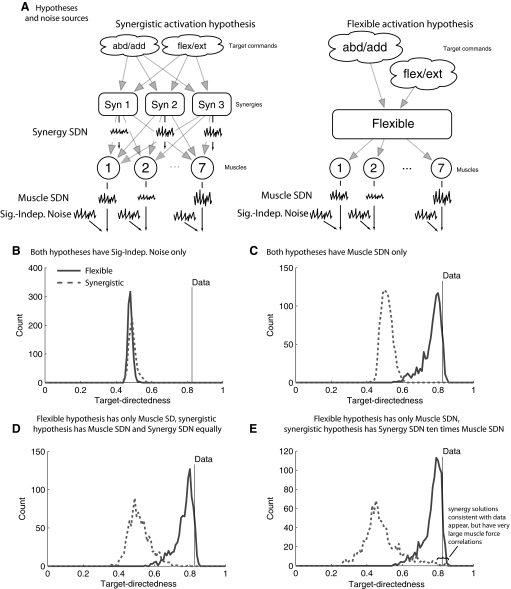
The source and type of noise will have an impact on FCM, so we analyzed noise occurring at the muscle level versus that at the synergy activation level (Fig. 8). As a baseline, FCM will not distinguish flexible activation from synergistic activation when noise is signal independent. When signal-dependent noise occurs at the muscle level, flexible activation produces much higher target directedness compared with synergistic activation, and certain parameter values can be found for flexible activation that describe the data, although no parameter values can be found that describe the data for synergistic activation (Fig. 8B).

FIG. 8.

Sensitivity analysis of force covariance mapping to noise source and strength. The ability of the different hypotheses to generate target-directedness as high, as observed, was analyzed by varying unknown parameters. A: signal-independent noise (Sig.-Indep. Noise) at the muscle level forces both hypotheses to generate low values of target directedness. B: under the assumption of signal-dependent noise at the muscle level (Muscle SDN), parameter values exist for the flexible activation hypothesis that are consistent with the data, but no parameter values were found for the synergistic activation hypothesis that can reproduce the target directedness of the data. C: a similar pattern emerges if there are equal amounts of SDN at the synergy (Synergy SDN) and muscle levels. D: if the synergy-level SDN is generating 10 times more variance in muscle force than the muscle-level SDN, some parameter values can be found so that the target directedness of the synergistic activation hypothesis is consistent with the data. However, the synergistic activation simulations consistent with the data also have much stronger correlations (average 0.75, maximum 0.95, minimum 0.41, averaged across all muscle pairs).

This same result occurs when synergy-level SDN is made to be as strong as the muscle-level SDN (Fig. 8C). When synergy-level noise is made tenfold stronger than muscle-level noise, some parameter sets appear for which synergistic activation is consistent with the data (Fig. 8D), but these parameter sets induce large correlations in muscle force. The grand average of correlation across data-consistent synergy simulations and muscle pairs was 0.75. The average correlation across muscle pairs of the maximum across data-consistent synergy simulations was 0.96. The average correlation across muscle pairs of the minimum across data-consistent synergy simulations was 0.41. The muscle force correlations required for the synergy-level noise to reproduce the data are much larger than our estimates for FDI–EDC and FDI–EIP EMG correlation or values reported in the literature for peak EMG coherence that range from 0.1 to 0.5 (Farmer et al. 2007; Fisher et al. 2002; Kilner et al. 1999), with 0.5 occurring only at 20 Hz, which is outside the frequency range of muscle force production (Galganski et al. 1993).

DISCUSSION

We have introduced force covariance mapping (FCM) as a means of studying muscle coordination through variability of endpoint forces. We applied this to forces exerted by the human index finger to examine cooperation of muscles acting about the metacarpophalangeal (MCP) joint. One outcome was that endpoint force covariance varies with the net direction of endpoint force, indicating that muscles make varying force contributions that depend on target direction. A muscle may act as a prime mover when the target is well aligned with that muscle's mechanical action and as part of a group of coactivated muscles for other targets. These variations in contribution indicate that muscles do not always act in fixed synergies, but can act in less rigid groupings that weight each muscle's mechanical action according to the target force. The FCM approach is also helpful for indicating the degree to which multiple muscles contribute to generating a particular force, even in the absence of a full set of EMG recordings. To integrate these findings with previous literature, we first discuss the relevance of our results to theories of muscle coordination such as the muscle synergy hypothesis, prime mover activation, and optimization. We then compare the FCM technique to other methods such as uncontrolled manifold and PCA. Finally, we conclude with a discussion of potential limitations of FCM and of this study.

Implications for muscle coordination

The target-dependent alignment of force covariance ellipses has implications for coupling of muscle activations. There were three target directions with highly target-directed force covariances, indicating cases where individual muscles dominated the net endpoint force and were consequently not strongly coupled with other muscles. The variation of the FCM with target direction also indicates that muscles were not activated in fixed-ratio synergies. For example, we found highly target-directed covariance (η ≃ 0.9) for the 195° target direction, which matches well with the action of first dorsal interosseous (FDI). If the FDI were activated in synergies with other muscles, we would expect the other muscles to contribute substantially to this force in this target direction, resulting in lower η. A possible explanation is that the FDI and other index finger muscles are activated flexibly for each target force and are not in synergies.

These results also offer insight regarding the apparent conflict between individual muscles acting as prime movers and multiple muscles acting cooperatively. For example, the FDI is often assumed to be a prime mover for MCP abduction (Flament et al. 1993; Semmler and Nordstrom 1998a; Thomas et al. 1986), but this has recently been challenged by observations of substantial coactivation of extensor muscles, which are required to mechanically cancel FDI flexion moments and successfully abduct the MCP joint (Keenan et al. 2006; see also Fig. 6B). Our results show that FDI is indeed the prime mover in target forces in the 195° direction, that is, along its mechanical action (An et al. 1983; Fowler et al. 2001; Thomas et al. 1986). However, other directions, such as pure abduction (180°), necessitate the coactivation of other muscles such as EDC and EIP. Conflicting observations might therefore depend on small changes in the target direction. Given freedom to do so, subjects might perform varying degrees of flexion or extension along with the abduction target force, with varying contributions from other muscles. Subtle differences such as a 15° change in target direction could therefore make the difference between the FDI acting as a prime mover as opposed to cooperating with other muscles. Target-dependent muscle activation implies that it is helpful to measure or control for the flexion–extension direction even during a simple abduction target force.

We have shown that, if its assumptions are valid, FCM does not provide sufficient evidence to reject the flexible activation hypothesis in favor of the synergistic activation hypothesis. The term synergy has many uses in the motor control literature. Most broadly, a synergy may refer to the cooperation among a group of muscles to achieve a particular task. A synergy could also refer to a group of muscles such that each muscle belongs to only one synergy (Buchanan et al. 1986; Lee 1984; Macpherson 1991; Soechting and Lacquaniti 1989). More recently, muscle synergies have been viewed as a mechanism to reduce the number of command signals needed to activate a set of muscles—a view that allows a single muscle to belong to multiple synergies (d'Avella et al. 2003; Ting and Macpherson 2005; Tresch et al. 2006). As far as the assumptions we have made explicit are valid, FCM analysis shows that this last type of muscle synergy does not describe the muscular control of the index finger for the isometric forces we examined, thus providing a counterexample for critical analysis of the muscle synergy hypothesis.

It is unknown whether the nonsynergistic patterns we identified apply to stereotypical or involuntary tasks, such as postural reactions (e.g., Ting and Macpherson 2005), where spatiotemporal synergies are found. Physiologically, synergistic muscle activation patterns have been observed from electrical stimulation of specific anatomical structures (d'Avella and Bizzi 1998; Giszter et al. 1993; Saltiel et al. 2001) and in reflex behaviors (Hart and Giszter 2004; Kargo and Giszter 2000, 2008), but there may be other contributions to net muscle activation. For example, it is also unknown whether the flexible patterns we observed arise from inhibitory interactions or from lateral feedback between motor groups (Kuo 1994), as well as a variety of central or sensory feedback mechanisms (Cheung et al. 2005; Lockhart and Ting 2007). Many reflexes have multiple feedback sources (Wilmink and Nichols 2003) that could increase the flexibility of muscle activation patterns.

Comparison with other approaches

The FCM potentially complements other methods for studying muscle coordination. Although EMGs certainly provide the most direct measurements of muscle activity, they have some limitations. First, it may be inconvenient or difficult to record EMGs from all relevant muscles that might contribute to potential synergies. Second, EMGs alone do not quantify how active muscles contribute to the net force (Zhou et al. 2007) in muscle or endpoint force space. The FCM complements EMGs by indicating when a single muscle acts alone or nearly alone and, conversely, when multiple, distinct muscles contribute to a net force. Another powerful approach for examining synergies is to access the anatomical structures directly, for example, through stimulation of the frog spinal cord, which has also revealed evidence for dimensionality reduction (Bizzi et al. 1991; Giszter et al. 1993; Saltiel et al. 2001). The FCM could potentially complement this method by indicating individual muscle force contributions to a net action in joint torque or endpoint force space. It could also be used to determine whether actions produced through microstimulation resemble those observed during normal behavior of the animal.

The FCM approach bears some similarity to uncontrolled manifold (UCM) analysis (Latash et al. 2002), but serves a different purpose. UCM analysis exploits a mismatch between joint and task DOF to determine how the CNS coordinates redundant kinematics. An example is the task of exerting vertical force by the index and middle fingers (with one-task DOF and two-finger DOF), where the CNS distributes force between the fingers to balance the moment about a point between them, at the expense of stabilizing total force (Latash et al. 2001). This shows that the CNS has implicit control demands that resolve the joint or finger redundancy during a task of relatively lower dimensionality. In contrast, the FCM approach attempts to explicitly match kinematic and task DOF, thereby eliminating kinematic redundancy. Force covariance mapping therefore indicates how the CNS uses the remaining muscle redundancy to satisfy implicit control demands. Variability provides insight to the control of redundancy in both analyses, but the FCM focuses on muscle rather than joint redundancy.

Another class of methods for studying coordination comprises mathematical techniques that seek to represent EMG activity in different muscles as combinations of simple elements. These techniques include PCA (Ivanenko et al. 2004), independent components analysis (Hart and Giszter 2004), nonnegative matrix factorization (Ting and Macpherson 2005; Tresch et al. 2006), and cluster analysis (Krouchev et al. 2006), to cite but a few. These studies generally show that EMG signals from multiple muscles can be represented using a smaller number of variables than there are muscles, which may be reflective of neural constraints simplifying the problem of coordination. However, one issue highlighted here is low dimensionality in muscle activation space that may originate during task planning. This observation provides an explanation for how muscles could be activated flexibly and constraints in the activity among muscles could still be observed (see Fig. 7, A–C). It therefore becomes difficult to determine whether low dimensionality of EMGs is indicative of a fixed neural constraint or merely the outcome of a low-dimensional task that is resolved at the muscle level with flexible neural constraints. This difficulty can be addressed by variations in task that can enrich its dimensionality (Ting and Macpherson 2005) or to examine natural behaviors (Hart and Giszter 2004), although the issue of task planning dimension compared with muscle activity dimension is of primary importance. The FCM approach cannot answer this question directly, but our results do demonstrate how isometric force variability may contain information that goes beyond the dimensionality of EMG signals across multiple muscles.

Limitations of the force covariance map

The force covariance map is based on two assumptions that, if incorrect, could lead to erroneous conclusions. The primary assumption is one of signal-dependent noise (SDN). If a muscle's force fluctuations scaled not with its average force but according to either a systematic but nonmonotonic or a random relationship, the force covariance would reflect these other phenomena instead. In the present study, force variance scaled in direct proportion to net force and almost all of this variance indeed appeared to be signal dependent (as indicated by the slope and intercept of the SDN fit in Fig. 4).

Another assumption is that there is little correlation between force fluctuations of distinct muscles. Significant correlation has been observed in surface EMG activity of distinct muscles, with coherence values as high as 0.5 (Kilner et al. 1999). High correlations in force fluctuations would be expected to produce distortions in the force covariance map. Target-directed covariance (high η) might overestimate the actual degree to which a muscle acts alone. However, correlation would also typically cause η to peak in directions not aligned with muscle actions, in poor agreement with our results. In addition, EMG correlation occurs at relatively high-frequency ranges compared with force fluctuations in muscle, acting as a low-pass filter. Indeed, for muscle pairs examined in this study, EMG correlation, in the frequency range of interest for force generation, was generally <2%. Although cancellation of surface-detected electrical potentials influences the estimation of force correlation from EMG correlation (Keenan et al. 2007), and EMG signals from multitendon muscles such as EDC might not reflect the compartment of interest, we expect that force fluctuations would have relatively low correlation. In addition, our rigorous analysis of hypotheses (Fig. 8) indicated that the ability of FCM to distinguish between synergistic and flexible activation of the musculature is robust to modest amounts of correlation in the SDN among muscles (examined ≤10%). Nonetheless, it is important to consider correlation in the time-varying forces exerted by different muscles when considering the force covariance map.

It was our intention in this study to demonstrate that significant information exists in the pattern of multidirectional endpoint force fluctuations. EMG recordings were used in this study to show that coactivity among muscles with different action directions were associated with non-target-directed ellipses. We did not, however, record intramuscular EMG from a complete set of muscles that could contribute force to the endpoint. Follow-up studies with EMG recordings from a complete muscle set will be needed to look in more detail at three remaining issues: 1) Are target-directed force covariance ellipses associated with a large amount of electrical activity in one muscle compared with another? 2) Do any target-directed force covariance ellipses arise from the correlated activity of multiple muscles with different action directions? 3) Can the FCM be predicted from the EMG-estimated muscle coordination pattern and vice versa?

The force covariance map is most applicable to experiments where the task is defined and constrained as explicitly as possible. For example, we constrained all DOFs other than the MCP and both measured and controlled the remaining force vector. The alternative to isolating a single joint is to allow multiple kinematic DOFs to remain unconstrained and to measure them fully, for example with a multiaxis load cell. This also necessitates that force directions be controlled to span the space of possible forces. The FCM approach is therefore ill-suited to the broader question of how the CNS coordinates joints for general tasks. The CNS appears to prefer stereotypical motor strategies of low dimension and these strategies might sensibly use certain muscles, either individually or in groups, that have actions suitable to the task. For example, postural reactions that accelerate the body center of mass can utilize arbitrary combinations of joints, but intersegemental coupling is such that very fast accelerations can be achieved by coordinating the joints in a relatively fixed ratio (Kuo and Zajac 1993). Some movements might therefore favor certain combinations of muscles, not because they are coordinated in fixed synergies, but merely as an outcome of task selection.

The FCM approach is also not limited to forces involving a single joint. If multiple joints are involved, the matrix that maps muscle forces to endpoint forces will be more complex, but each muscle will still have an action vector in endpoint force space and different action vectors will add together linearly (Valero-Cuevas et al. 2000), thus satisfying the superposition assumptions of FCM.

Although we have discussed how the FCM approach may be used to infer the pattern of muscle activity from endpoint force fluctuation, it should be noted that the inference of activation may be complicated by large differences in muscle moment arms and cross-sectional areas. A muscle with a larger moment arm would transmit more force fluctuation for a given level of activity than a muscle with a smaller moment arm. Thus inferences from FCM more properly describe patterns of muscle activity corrected for moment arm and cross-sectional area.

For simplicity, we performed our hypothesis analysis on a single set of moment arm data from the literature (Fowler et al. 2001). Several authors have used different approaches to quantify these moment arms including cadaveric measurements (An et al. 1983; Valero-Cuevas et al. 2000), electrical stimulation (Kamper et al. 2006), and MRI measurements (Fowler et al. 2001). We chose to analyze the MRI data for the following reasons. The measurements of Valero-Cuevas et al. (2000) were made from a finger posture different from that in our experiment. The cadaveric data of An et al. (1983) appeared to be rotated clockwise in the endpoint force plane relative to our estimates for FDI, EIP, and EDC. Moreover, this study reported that FPI had a pure adduction moment, which is inconsistent with other studies (Fowler et al. 2001; Kamper et al. 2006) and the fact that it lays on the palmar side of the MCP joint (Brand and Hollister 1993). The MRI data (Fowler et al. 2001) and electrical stimulation data (Kamper et al. 2006) were very consistent with each other, our moment arm estimates, and the target directions exhibiting target-directed covariance ellipses. We analyzed the MRI data of Fowler et al. (2001) because relative moment arm magnitude was reported that can affect the simulated force covariance map. Nonetheless, it is important to consider the exact distribution of moment arms for a set of muscles when comparing hypotheses using force covariance mapping. For example, we used a cost function that minimized the sum of squared muscle forces to simulate the flexible activation hypothesis. Using this cost function, muscles will be dominant for targets in their action direction if there are not muscles within 90° on both sides in the endpoint force plane. Thus using this cost function, relatively small changes in a muscle's action direction could make the difference between whether a muscle is dominant for targets in its action direction. Indeed, given MRI moment arm estimates for the seven finger muscles, it is clear that the flexors have the FDI and FPI both within 90°. The flexible activation strategy would then predict that the flexors would not appear as prime movers for targets in the direction of their action. This prediction is supported by our EMG data (Fig. 6) and previous work (Thomas et al. 1986), showing activation of the FDI for target forces in flexion.

Conclusion

We hypothesized that signal-dependent noise would transform the pattern of relative activity in various muscles to the pattern of multidirectional endpoint force variability. Mapping the endpoint force variability across a set of target forces spanning a set of two-dimensional forces generated about the MCP joint of the index finger, we established that force covariance was highly dependent on target direction. We showed that the covariance dependence on target direction was consistent with different muscle coordination strategies. non-target-directed force covariance, predicted to result from activation of multiple muscles with distinct action directions, occurs for target directions that provide EMG evidence of muscle coactivation. Conversely, target-directed force covariance, predicted to result from activation of one muscle much more than others, occurs for target forces in the action direction of several muscles. The latter observation suggests that, since several index finger muscles can dominate force production for certain target directions, index finger muscles may not group into muscle synergies that are active for all target force directions. The mapping of endpoint variance—that we have termed force covariance mapping—may provide a straightforward approach for discriminating theories of neuromotor coordination.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke/National Research Service Award Training Grant 1F31NS-057855-01 to J. J. Kutch and W. Z. Rymer and National Science Foundation Grants DMS-0604307 and CMS-0408542 to A. M. Bloch.

APPENDIX

We analyzed the ability of the FCM approach to distinguish competing hypotheses for the coordination of multiple muscles in the presence of signal-dependent noise (SDN). We began with estimates of muscle action vectors, made from MRI measurements, of all seven muscles of the index finger (Fowler et al. 2001). Muscle action vectors were placed as columns in a 2 × 7 matrix A. As described earlier, using FCM to infer muscle activation from force variability relies on three assumptions. These assumptions are described mathematically here.

ASSUMPTION 1.

Muscles act along fixed directions in endpoint space and contributions from different muscles add linearly in endpoint space

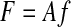(A1)

where the muscle forces are listed in vector f, endpoints forces are listed in vector F, and the muscle action matrix A performs the transformation.

CONSEQUENCE 1.

Since the average of a sum is the sum of the averages, we can use Equation A1 to calculate the average endpoint forces given the average muscle forces

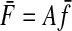(A2)

This equation converts the average muscle force vector to the average endpoint force vector, which is the center of the force covariance ellipse.

CONSEQUENCE 2.

Equation A1 also dictates that the covariance of endpoint force is

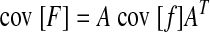(A3)

Since the force covariance map is described completely by F̄ and cov [F], all that remains is to calculate cov [f], which will be determined by SDN and muscle force correlation.

ASSUMPTION 2.

Muscle force variability is proportional to average muscle force. For muscle i, f = f̄_i + ɛ_i, where ɛ_i is the SDN with variance

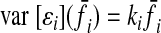(A4)

CONSEQUENCE 1.

If there is no muscle force correlation and the muscle activity pattern linearly scales with increasing force demands, the trace of the endpoint force covariance matrix will indicate how muscle force variability scales with average muscle force, on average across the muscles. If there is no muscle force correlation, then

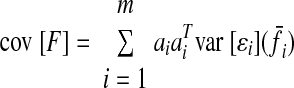(A5)

(A6)

where m is the number of muscles. Thus Trace {cov [F]}/m indicates the average of ‖a_i‖²k_if̄_i across all muscles. The average muscle force will be a function of the required average endpoint force: f̄_i = f̄_i(F̄). If we assume that the muscle coordination pattern simply scales for increasing endpoint force demands (Valero-Cuevas 2000), then f̄_i(αF̄) = αf̄_i(F̄). Thus if SDN variance scales linearly with average muscle force (on average across the set of muscles), the trace of the endpoint force covariance matrix will scale linearly with the magnitude of the average endpoint force. Since we observed this scaling experimentally, we chose to model SDN variance as a linear function of average muscle force.

ASSUMPTION 3.

Noise correlations among muscles are modest. The ijth element of the noise covariance matrix cov [ɛ](f̄) can be expressed as

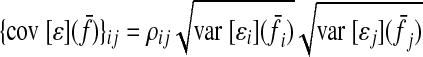(A7)

where ρ_ij is the correlation between noise in muscle i and j.

The goal for each target was to calculate the average amount of force in each muscle so that the average endpoint force vector equaled a given target vector. For each simulation, target vectors were distributed at 15° increments along the unit circle. Average muscle forces were simulated using two hypotheses: synergistic activation and flexible activation. Flexible activation served as the null hypothesis and we analyzed evidence for rejecting it in favor of the synergistic activation.

Flexible activation hypothesis (there are no synergies).

Under this hypothesis, a target-dependent vector of average muscle forces f̄^sel was selected so that

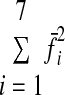(A8)

was minimized subject to the constraint that Af̄^sel = F_d, where F_d is the desired endpoint force vector for the given target force. The force covariance map under flexible activation is then given by

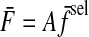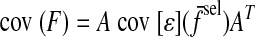(A9)

Synergistic activation hypothesis.

Under this hypothesis, constraints are introduced among the components of the average muscle force vector so as to reduce its dimensionality. This is accomplished by expressing the muscle force vector as f = Wc + ɛ, where the columns of W encode the relative strength of each muscle in a given synergy, c is a vector of synergy weighting coefficients, and ɛ is muscle-level SDN. Since noise may also arise at the synergy level, c = c̄ + γ, where γ is synergy-level SDN

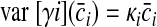(A10)

We chose to analyze this dependence of synergy-level noise because, if there were no SDN at the muscle level, this signal-dependent synergy-level noise would be required to produce the noise scaling in our data (see results). The object of synergies is to generate independently controllable muscle groups, so we did not consider cross-correlations in the synergy noise vector. Thus the synergy noise covariance matrix was diagonal with {cov [γ](c̄)}_ii = var [γ_i](c̄_i) = κ_ic̄_i. A target-dependent vector of average synergy coefficients c̄^sel was selected so that

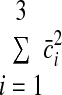(A11)

was minimized subject to the constraint AWc̄ = F_d for each target force. Simulations were performed using three synergies because this is the minimum number in a two-dimensional endpoint force space so that all target forces can be produced using the same set of synergies. The force covariance map under the synergistic activation is then given by

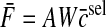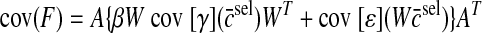(A12)

where β is a parameter used to control the strength of the force fluctuations due to synergy-level noise relative to force fluctuations due to muscle-level noise.

Unknown parameters

For each simulation, a random set of unknown parameter values were chosen from uniform distributions within specified ranges. Muscle-level noise scaling coefficients k were varied between 0 and 1, the synergy-level noise scaling coefficients κ were varied between 0 and 1, and the muscle-level noise correlation coefficients were varied between 0 and 0.1. The synergy coupling matrix for each simulation was generated as follows. A matrix W_temp was generated with elements chosen uniformly between 0 and 1. The mechanical actions of the synergies were then calculated: S_temp = AW_temp. W_temp was accepted and became the actual synergy matrix W if 1) the second strongest muscle in each synergy had action direction was ≥30° away from the action direction of the strongest muscle in that synergy and 2) the columns of S_temp spanned the endpoint force space with positive coefficients. These requirements ensured that synergies were not trivial (i.e., muscles with different mechanical actions were coupled) and could be activated to achieve all targets in the endpoint plane.

Hypothesis comparison

Each simulation generated a force covariance map for each hypothesis given the chosen parameters. The target-directed variance fraction η was calculated for each force covariance map in exactly the same way as for the data. We evaluated the hypotheses in their ability to generate high η when the data exhibited large η (on average across subjects and target magnitude levels). A set of target directions was identified when η peaked in the data. Average η in directions of data peaks was calculated for each simulation—we refer to this quantity as target directedness. Histograms of target directedness were generated across simulations (different parameter values) for each hypothesis and compared with the actual value of target directedness calculated from the observed data averaged across subjects and target magnitude levels.