Understanding Detection Performance in Public Health Surveillance: Modeling Aberrancy-detection Algorithms

Abstract

Objective

Statistical aberrancy-detection algorithms play a central role in automated public health systems, analyzing large volumes of clinical and administrative data in real-time with the goal of detecting disease outbreaks rapidly and accurately. Not all algorithms perform equally well in terms of sensitivity, specificity, and timeliness in detecting disease outbreaks and the evidence describing the relative performance of different methods is fragmented and mainly qualitative.

Design

We developed and evaluated a unified model of aberrancy-detection algorithms and a software infrastructure that uses this model to conduct studies to evaluate detection performance. We used a task-analytic methodology to identify the common features and meaningful distinctions among different algorithms and to provide an extensible framework for gathering evidence about the relative performance of these algorithms using a number of evaluation metrics. We implemented our model as part of a modular software infrastructure (Biological Space-Time Outbreak Reasoning Module, or BioSTORM) that allows configuration, deployment, and evaluation of aberrancy-detection algorithms in a systematic manner.

Measurement

We assessed the ability of our model to encode the commonly used EARS algorithms and the ability of the BioSTORM software to reproduce an existing evaluation study of these algorithms.

Results

Using our unified model of aberrancy-detection algorithms, we successfully encoded the EARS algorithms, deployed these algorithms using BioSTORM, and were able to reproduce and extend previously published evaluation results.

Conclusion

The validated model of aberrancy-detection algorithms and its software implementation will enable principled comparison of algorithms, synthesis of results from evaluation studies, and identification of surveillance algorithms for use in specific public health settings.

Introduction

New threats and advances in the capture and transmission of electronic health data are transforming public health surveillance. Many public health agencies now have real-time access to large volumes of data from clinical and other settings. While these data offer great potential to address public health threats, they pose new challenges for analysis. For example, clinical data, such as patients' initial chief complaints as recorded by emergency departments, are noisy and of much higher volume than the data historically available to public health. ^1,2

To take advantage of these novel data sources, many public health agencies now operate automated surveillance systems that monitor clinical data with the goal of detecting disease outbreaks rapidly and accurately. ^3–5 Due to the volume of data, surveillance analysts are not able to manually review all data, so aberrancy-detection algorithms play a key role, screening large volumes of data and issuing alerts to draw an epidemiologist's attention to statistical anomalies, or aberrations, that may indicate a localized outbreak. ^6,7 Aberrancy-detection algorithms, therefore, provide important input into public health decision-making around outbreak detection and management.

The last decade has seen the introduction of many aberrancy-detection algorithms. Some were developed specifically for surveillance, though most were adapted from other fields, such as econometrics, ^8,9 industrial process control, ^10,11 and cancer epidemiology. ^12,13 Theoretical considerations and empirical results suggest that not all algorithms perform equally well in terms of desirable characteristics such as accuracy and timeliness. ¹⁴ Researchers and practitioners have noted variations in performance when two different algorithms are applied to the same data, and when the same algorithm is applied to different data sets. ¹⁵

While performance differences are acknowledged, the evidence for describing how surveillance algorithms differ is fragmented and difficult to interpret due to the absence of a conceptual framework to support a consistent synthesis of the reasons for performance variations. ^7,16 This fragmented evidence hinders research, leads to confusion and variation in surveillance practice, ¹⁷ and threatens to reduce the return on the considerable investment in surveillance systems and aberrancy-detection algorithms. ¹⁸

Our present work addresses the need to consistently identify the precise reasons for variations in algorithm performance by developing an explicit model of aberrancy-detection algorithms and by developing a software infrastructure for rapidly conducting evaluations. The model clarifies the common features of, and meaningful distinctions among, algorithms and provides an extensible framework for gathering evidence about the relative performance of these algorithms. In this paper, we describe our model and validate it by using it to encode commonly used algorithms. We also review briefly the software implementation of our model, and validate the implementation by replicating and extending a study assessing the performance of the Early Aberration Reporting System (EARS) algorithms developed at the Centers for Disease Control and Prevention (CDC). ¹⁹

Background

Evaluating Aberrancy-detection Algorithms in Public Health Surveillance

Surveillance is a core public health activity that measures population health status to inform health protection and promotion efforts. Procedurally, surveillance involves collecting data, analyzing data, interpreting results, and conveying information to guide action. ²⁰ Automated surveillance systems are a recent innovation in public health. ¹ These systems monitor in real-time electronic data collected in clinical (e.g., emergency departments) and other (e.g., call-in advice centers) settings. While a variety of factors can be considered when evaluating automated surveillance systems, ²¹ evaluation guidelines developed by the CDC focus on outbreak detection. ²²

Researchers who evaluate aberrancy-detection algorithms for use in automated surveillance systems rely upon historical or simulated outbreaks ^14,21 and tend to evaluate only one or two algorithms at a time, ¹⁵ mainly because of the extensive resources required to concurrently evaluate multiple algorithms. More recently, some researchers have conducted evaluation studies that compare the performance of multiple algorithms systematically within a single study, applying each algorithm to a common data set. ^19,23,24 Such controlled comparisons are more valuable than single-algorithm studies because they provide direct evidence about the relative performance of algorithms. Still, authors of these multi-algorithm studies do not explicitly attribute observed performance differences to properties of the algorithms, so generalizations cannot be made regarding the performance characteristics of other algorithms in the same class. For example, if a particular regression method performs poorly in a certain setting, it is important to understand if all regression methods are likely to perform poorly in the same setting.

Previous Work in Describing Aberrancy-detection Algorithms: Existing Limitations

No universally recognized classification of public health surveillance algorithms exists, although a few researchers have attempted to develop informal groupings of data-analytic techniques used in public health. ^25–27 Existing groupings disagree about algorithm inclusion, naming, and how algorithms are categorized. Among the most commonly described algorithm classes are control charts, regression models, time-series methods, and scan statistics. Not surprisingly, algorithms within each class may vary considerably in terms of both their behavior and performance, while members of different classes may occasionally exhibit very similar characteristics. Classification schemes based on the historical origins of algorithms that do not consider how these algorithms function are not very helpful in understanding and describing the factors that underlie their performance.

Despite the lack of a universally recognized classification scheme, some authors have used functional and procedural distinctions between algorithms to explain their relative performance. For instance, researchers have emphasized the distinction between adaptive and non-adaptive algorithms, ²⁸ the use of theoretical versus empirical alerting thresholds, ¹⁶ and the amount of historical data required by an algorithm. ¹⁹ While none of these distinctions is sufficient for classification, they suggest that a comprehensive model of aberrancy-detection algorithms can be built using these and other characteristics, and that various aspects of performance can be linked to these characteristics.

Previous attempts to identify the meaningful functional characteristics of aberrancy-detection algorithms have tended to view these algorithms as atomic, indivisible units. However, such a “black-box” representation makes it difficult to understand the relationships among different algorithms because it obscures their procedural structure. The study by Murphy and Burkom ²⁴ is a notable exception to this tendency. The authors identify two major stages in the procedure of temporal aberrancy detection and demonstrate that decomposing algorithms into steps, even at a coarse level of granularity, allows for meaningful conclusions about the general determinants of performance. ²⁴

Task-analytic Methodology for Modeling Algorithms

While the surveillance community has not focused on modeling aberrancy-detection algorithms explicitly, several areas within computer science, most notably the knowledge modeling community, have developed approaches to declaratively represent the procedural structure of algorithms. ^29–32 These approaches model knowledge about systems with respect to their goal or the task that they perform, and most share a methodology referred to as task analysis. ³³ This methodology has been used successfully to model such complex processes as medical diagnosis ³⁴ and design problem-solving, ³⁵ and is also used extensively in software engineering. ³⁶

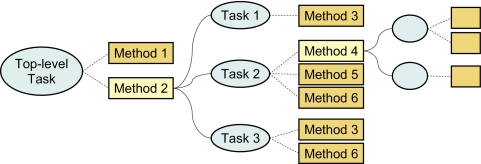
Within the task-analytic methodology, a task defines “what has to be done.” Tasks are accomplished by application of a method, which defines “how to perform a task.” A method can either perform a task directly (a primitive method), or decompose a task into subtasks with constraints on their execution order, and delegate their execution to other methods (a task-decomposition method, or TDM). This recursive decomposition process creates a tree-like structure representing the modeled process (▶). Since there can be many ways to accomplish a task there can be multiple eligible methods that may decompose the same task into different sets of subtasks. Also, a single method may be reused to accomplish multiple tasks. Methods are typically described in terms of their operators (steps), the objects they operate on, the specification of their preconditions and effects, and any additional knowledge that is required to accomplish the task. ³³

Figure 1.

Example Task Decomposition Tree Tasks (shown as ellipses) are accomplished by application of methods (rectangles). More than one eligible method may exist for each task. Methods can be either primitive (dark rectangles) or complex (light rectangles). Complex methods (also called task-decomposition methods) break down a task into subtasks. Solid lines on the graph read as “method decomposes a task into” (AND-relationship); dashed lines connect tasks with their eligible methods (OR-relationship).

The task-analytic methodology is desirable for modeling aberrancy detection because it makes explicit the structural similarities and differences among algorithms that may have implications for their performance, and it also clarifies the roles of different individual methods in the overall detection process. It identifies, for example, when a single method can be used for multiple tasks. In the following section, we describe how we use task analysis to extend our previous work modeling surveillance methods ^37,38 and to develop an explicit representation of aberrancy-detection algorithms. We have focused our modeling efforts on temporal aberrancy-detection algorithms. The proposed model, however, is extensible to include other algorithms.

Model Formulation

There are an infinite number of ways to use a task-analytic methodology to model a particular process. In our work, we were guided by four requirements: generality, modularity, extensibility, and human readability. Generality implies that the model must be able to describe multiple algorithms using the same core representation. This requirement imposes constraints on identifying subtasks at each level of task decomposition and on grouping of methods into categories. Modularity is important to support the reuse and parallel execution of the software components that implement the model. The implication of modularity for model formulation is that the atomic units of decomposition must be chosen without unnecessarily complicating the model and negatively affecting configurability and the execution of the model's implementation. Extensibility is essential because public health surveillance is an actively evolving field with new aberrancy-detection algorithms reported regularly. The task model must be extensible with new subtasks and methods, while maintaining a compact representation. Finally, human-readability is necessary so that the model can serve as a conceptual framework for gathering, interpreting, and synthesizing evidence about the performance of aberrancy detection algorithms. The model must therefore be compact and strike a balance between depth and breadth of decomposition structure while being intuitively clear to statisticians, epidemiologists and public health practitioners.

Our task-analytic model of aberrancy-detection algorithms includes three major parts. First, we identify the hierarchical task structure of the aberrancy-detection process and show how it applies to algorithms used in public health surveillance. We then augment this structural representation with control and data flow concepts, which are used to specify subtask ordering, repetitions and input-output relations among tasks. Finally, we identify the properties that characterize individual methods used to accomplish various tasks in our model.

Task Structure of Aberrancy-detection Algorithms

The surveillance literature consistently describes temporal aberrancy-detection algorithms as algorithms that sequentially evaluate the departure of the observed rate of health events from what would be expected based on previous experience. 2,7,16,20,26 In task-analytic terms, these algorithms can be viewed as instances of a single task-decomposition method, which performs the task of detecting aberrations in surveillance data. We refer to this task-decomposition method as the Temporal Aberrancy Detection method. Spatial and spatiotemporal algorithms are examples of other task-decomposition methods.

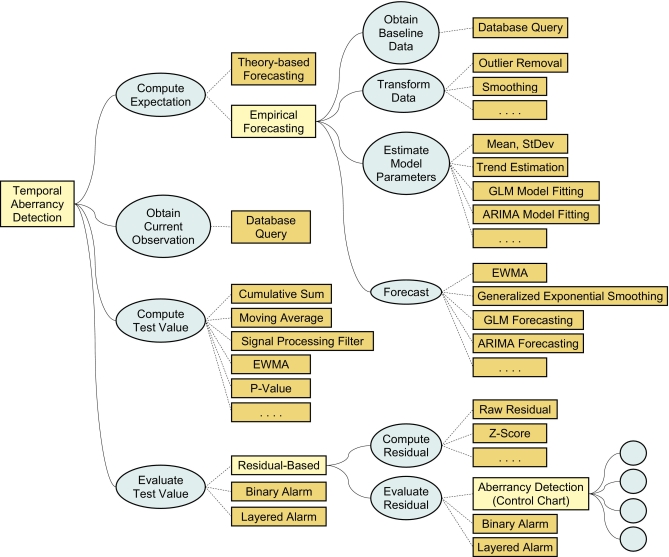
Following from the general definition above, aberrancy detection necessarily involves at least three key steps: obtaining the measure of expectation, obtaining data pertinent to the current rate of the health event, and evaluating whether the current rate deviates from expectation enough to indicate an alarm. These steps constitute three subtasks of the top-level aberrancy-detection task as performed by the Temporal Aberrancy Detection method. We include one additional subtask, since many algorithms compute a test value or detection statistic from the current observation instead of using the observation directly. For example, an exponentially weighted moving average computes a test value that is a weighted average of the current and previous observations. Thus the four generic subtasks of aberrancy detection within our model are: Compute Expectation, Obtain Current Observation, Compute Test Value, and Evaluate Test Value ^∗ (▶).

Figure 2.

General Task Structure of Temporal Aberrancy-detection Algorithms Temporal algorithms are represented as instances of a task-decomposition method (denoted on the graph as Temporal Aberrancy Detection) that performs the task of detecting aberrations in the surveillance data by decomposing this task into four subtasks (ellipses). Each subtask can be accomplished by different methods (rectangles), some of which perform the task directly (primitive methods shown as dark rectangles), and some further decompose the task into subtasks (task-decomposition methods shown as light rectangles). For instance, the Compute Expectation task, which constitutes one of the steps (subtasks) of aberrancy detection, can in turn be decomposed into four subtasks, if Empirical Forecasting method is used. Alternatively, this task can be accomplished directly by a primitive method—Theory-based Forecasting. Similar alternatives exist for Evaluate Test Value task.

In addition to aberrancy detection subtasks, ▶ displays methods eligible to perform each subtask. For readers unfamiliar with these methods, we recommend recent reviews. ^7,16,27 Obtain Current Observation is a straightforward step that is typically performed by querying a database. For the three other high-level subtasks, multiple primitive and complex eligible methods exist. For example, the Evaluate Test Value task, which is responsible for generating alarms, can be accomplished directly by comparing an observed value to an expected value using some predefined threshold (primitive method Binary Alarm), or by passing the residual of such a comparison through a control chart (task-decomposition method Residual-Based). The Compute Expectation task and Evaluate Test Value task can be further decomposed into subtasks.

To represent an algorithm, a single method must be selected for each task from the list of eligible methods, producing a sub-tree of the general structure depicted in ▶. These differences in method selection allow one to model the observed variety in aberrancy-detection algorithms: all of the algorithms perform similar steps, but may perform these steps using different methods. Theoretically, a large number of structurally different algorithms can be constructed using all possible bindings between tasks and eligible methods. In practice, however, the choice of a method for one task often imposes constraints on the method selection for other tasks, which limits the number of possible meaningful combinations. For example, in regression-based approaches, “matching” methods must be used for Estimate Model Parameters and Forecast tasks (▶).

The eligible methods noted in ▶ do not constitute an exhaustive list. Moreover, it is conceivable that newly developed aberrancy-detection algorithms may use previously undocumented methods for performing the tasks identified in our model. The extensible nature of task-decomposition representation allows for inclusion of such methods.

We also note that not all identified tasks are explicitly present in every aberrancy-detection algorithm. For instance, some algorithms use raw observations as a detection statistic, and thus omit the Compute Test Value task. In these cases, the output of Obtain Current Observation task is directed as an input to Evaluate Test Value task. Another example of an “optional task” is the Transform Data task, part of Compute Expectation.

Representation of Data and Control Flow

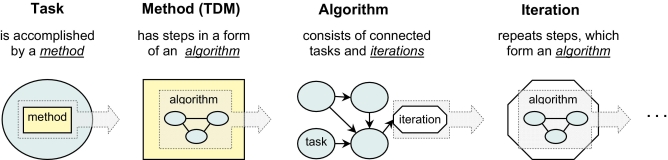
The structure depicted in ▶ is an incomplete representation of aberrancy detection, as it does not specify data flow or subtask ordering. We therefore extend our model to include concepts for encoding data and control flow. These concepts are applicable only to task-decomposition methods (TDMs): although primitive methods also have internal algorithmic flow, we do not model it.

A key concept in representing flow inside of TDMs is an algorithm ^† —a collection of tasks and control elements in the form of a directed graph. For the purpose of modeling aberrancy-detection, we distinguish between two types of graph nodes: subtasks and iterations. Subtasks are basic steps that the task-decomposition method performs to accomplish a higher-level task. Iteration is introduced to represent control flow when a set of subtasks in a TDM should be repeated multiple times. For example, the same sequence of computations and alerting decisions are usually repeated daily in a surveillance time series. A sequence of subtasks inside an iteration generates a set of intermediate results that are aggregated with the intermediate results from other repetitions of the same subtasks. ▶ illustrates the relations among algorithms, tasks, iterations, and methods.

Figure 3.

Relationship among Tasks, Methods, Iterations and Algorithms When a task is accomplished by a task-decomposition method (TDM), this implies that the method performs several steps in a particular order, i.e., the method has an algorithm associated with it. An algorithm, in turn, consists of interconnected tasks (these are the subtasks of the original, higher-level task) and iterations. An iteration specifies repetition of a sequence of tasks (or other, nested iterations); this sequence is, again, represented by an algorithm.

The arcs of a graph are called connectors, and they represent data flow throughout tasks and iterations. More specifically, a connector between two nodes indicates that the output of the predecessor node is used as input by the successor node. Even though connectors are not intended to model control flow directly, they do represent data dependencies between tasks and iteration units, and thus provide the information necessary for inferring control flow knowledge.

Characteristics of Individual Methods

To complete the representation, we encode additional knowledge about individual methods performing various tasks as properties of methods. One important property of a method is its role in the overall aberrancy-detection process. This role can be inferred directly from the location of the method in the task-decomposition structure. While some methods are relatively specialized, others may have multiple roles. An example of a method capable of accomplishing multiple tasks is the exponentially-weighted moving average (EWMA) method, which may function as a forecasting technique, or as a means to transform raw observations into test values.

Another group of properties relates to the objects and data that the method operates on, the results of method computations and, sometimes, internal state information. For example, the primitive method Cumulative Sum (CUSUM) takes an observation as an incoming data object and uses it and the sum from the previous step to compute the values of the upper and lower running sums; it thus operates on four objects.

Configuration properties, or parameters, provide control over how the task should be performed by a method. These properties can characterize both primitive and task decomposition methods, but they apply only to methods that allow variations in their internal procedures. Finally, some non-functional properties can be useful, such as those describing method performance characteristics (time and space requirements, etc.) or any helpful meta-information. ³⁹

Model Validation through Example

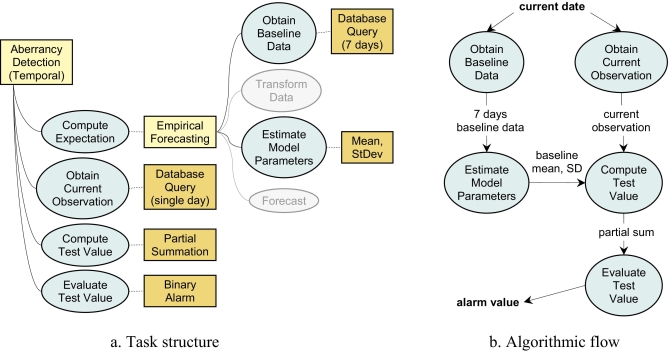
We illustrate the representation of aberrancy-detection algorithms within our model by encoding the C-family algorithms from the CDC Early Aberration Reporting System (EARS). The algorithms C1, C2 and C3 are adaptive algorithms based on a CUSUM control chart concept. ⁶ These algorithms are encoded in the EARS software developed by the CDC and used widely for public health surveillance. All three algorithms have identical task structures (▶a), and the differences are limited to variations in two configuration parameters used by primitive methods.

Figure 4.

Representation of EARS C-family Algorithms a) The task structure of C-family algorithms is based on the general task structure of temporal aberrancy detection algorithms (see ▶). A single eligible method is selected for each task. Omitted tasks are grayed out. b) The five tasks constituting C-family algorithms are connected to each other so that the outputs from one task are used as inputs by other task(s). Note that the current date is not produced by any task and must be specified externally; in our case it is provided by a containing iteration structure (not shown here), which increments the date at each step of algorithm execution. The alarm value is not consumed by any other task—this is a final result of the detection algorithm for a single day. Individual alarm values are aggregated into a vector by the iteration structure.

The C-algorithms compute expected values by analyzing a short sliding period of historical data, which is characteristic of an Empirical Forecasting method. This method decomposes the Compute Expectation task into several subtasks. First, seven consecutive observations from the recent history are retrieved to serve as baseline data. For C1, these are observations immediately preceding the current observation; C2 and C3 use baseline data separated from the current observation by two days. This difference can be encoded by manipulating the value of a configuration property of the Database Query method used to perform Obtain Baseline Data task, and these manipulations do not change the overall task structure, method selection, or procedural flow. The Estimate Model Parameters task for the C-algorithms entails computing a seven-day mean and standard deviation. None of the C-algorithms performs any data transformation, such as outlier removal, so the Transform Data task is not performed. The same is true for the Forecast task, since the baseline mean computed by a previous task is used directly as the expected value. The Obtain Current Observed Data task retrieves a single observation from the current test period.

C-algorithms are defined as variants of single-sided cumulative summation, ^10,11 which implies that the current observation is replaced with the value of a cumulative sum by the Compute Test Value task. However, the computation of a test statistic for these algorithms is different from traditional cumulative summation: C1 and C2 use only the current observation, which makes them more similar to Shewhart charts ⁴⁰ than to a true CUSUM; ¹¹ the C3 algorithm sums two previous observations and the current one. A true cumulative sum, on the other hand, can be influenced by an infinite number of prior observations. ¹¹ To reflect this important distinction and to avoid confusion, we have labeled the method for computing a test statistic in C-family algorithms as Partial Summation and supplied it with a configuration property (depth-of-memory) to specify how many values are considered.

Finally, a primitive Binary Alarm method is used to make an alerting decision in the Evaluate Test Value task. This method compares the previously computed detection statistic (partial sum) to the value of the alerting threshold, specified as the number of standard deviations above the expected mean.

▶b shows a data-flow diagram representing how subtasks of aberrancy detection using C-algorithms are interconnected. The knowledge required by the higher-level task decomposition method (Aberrancy Detection (Temporal)) to sequence the subtasks can be unambiguously inferred from this diagram by analyzing data dependencies. For instance, there are no ordering constraints between the Estimate Model Parameters task and the Obtain Current Observation task; however both tasks must be completed before the Compute Test Value task can be accomplished.

As adaptive algorithms, C1, C2, and C3 repeat all the steps listed above at each observation period. ▶b displays flow within a single step of execution and does not reflect the adaptive nature of the algorithms. To represent step repetition in C-algorithms, we place all five tasks into an iteration container, a control structure responsible for supplying dynamically changing data and configuration information to the enclosed tasks and their methods. In this particular case, current date, which is needed by data query methods of both the Obtain Current Observation and the Obtain Baseline Data tasks, must change at each execution step.

Software Implementation: BioSTORM Infrastructure

We have implemented our surveillance model in a modular system called BioSTORM, which provides a software infrastructure for deployment of aberrancy-detection algorithms. The software incorporates: (1) an ontology that formally encodes our model of aberrancy-detection algorithms, and (2) several ontology-driven software components to support the automated deployment and execution control of aberrancy-detection algorithms.

The BioSTORM Ontology

We have encoded our model of aberrancy-detection algorithms in an ontology—a formal, reusable description of the surveillance domain in a machine-interpretable form. This ontology was represented in the Web Ontology Language (OWL). ⁴¹ The ontology: a) defines a typology of tasks and methods as a hierarchy of classes; b) identifies eligible methods for each task; c) describes salient characteristics of individual methods as their properties; and, d) includes concepts related to control and data flow to represent algorithms, iterations and input-output connections among the tasks. In order to integrate aberrancy-detection algorithms with other operational components of the system we have extended our ontology to include concepts describing properties of the surveillance data and the configuration of an evaluation analysis.

The BioSTORM Software Components

Most aberrancy-detection evaluations have significant processing requirements due to the need to analyze multiple data sets, often over a range of algorithm settings. These evaluations often contain many tasks that can be executed in parallel, and surveillance evaluations can often benefit from task distribution.

To meet these processing requirements, we have implemented a software system that supports the distributed deployment of tasks in an evaluation. We implemented this system using the Java Agent Development Framework (JADE), ⁴² an open source platform for developing distributed applications. The basic unit of distribution in the JADE platform is an agent, which is typically a standalone module that performs a particular job. Agents are assigned to a platform, which is a logical space that can be distributed across machines, and communicate with each other using messages.

We have implemented the tasks involved in the aberrancy-detection algorithms as JADE agents. These task agents are created during an evaluation run and are configured to use a particular implementation of a method to perform their respective tasks. We developed an extensible software library of methods in Java to be used in our system. The BioSTORM methods use the R open-source statistical software ⁴³ for any non-trivial statistical computations. A controller agent was developed to deploy an aberrancy-detection algorithm by creating and configuring all the relevant task agents. We also developed a variety of data integration and communication agents to deal with the raw surveillance data and the flow of information between tasks.

Empirical Validation

To operationally validate our work, we used BioSTORM to replicate and extend a published study of aberration detection methods. This work entailed encoding the algorithms in our model; configuring and running the evaluation study using BioSTORM; and comparing our results to the study results. The goal was to demonstrate that our model can faithfully represent a typical evaluation study and that BioSTORM can deploy that study automatically and produce results that agree with published figures.

Study Design

We replicated and extended a study by Hutwagner, et al., who compared three algorithms from the CDC's Early Aberration Reporting System (EARS): C1, C2, and C3. ¹⁹ The original study used simulated data to estimate the sensitivity, specificity, and time to detection for the C algorithms. In our study, we used the same simulated surveillance data and followed the same evaluation steps as the original study. Briefly, we applied each of the C algorithms to each simulated data series and calculated the sensitivity, specificity, and timeliness of each algorithm by comparing the timing of algorithm alarms to the true timing of the outbreaks. One important change in our study was that, for selected data sets, we computed a receiver operating characteristics (ROC) curve for each algorithm by systematically varying the value of the alerting threshold and applying the algorithm at each threshold to the selected data sets. In the original study, only a single alerting threshold was used, and calculating the ROC curve allowed us to characterize the relative performance of not just three configurations, but the whole family of algorithms using a more general metric. The original simulated data included 56 distinct sets with varying baseline characteristics. We evaluated our performance against a randomly selected subset of 10 datasets. We further randomly sampled 2 of these datasets to compute the full ROC curve.

Results of Empirical Validation

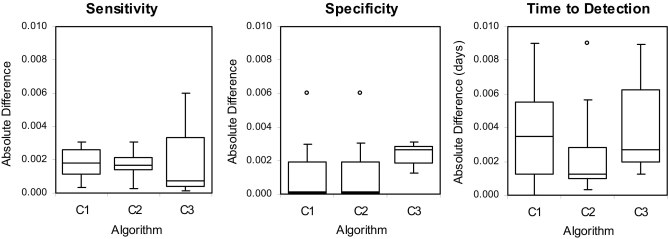
The comparative results for sensitivity, specificity, and time to detection for selected datasets are presented in ▶. The absolute deviations between the values computed using BioSTORM and those reported in the original study do not exceed 0.006 for sensitivity and specificity and 0.01 days for time to detection. A manual comparison of selected alarm vectors revealed that discrepancies in generated alarms occurred around missing data points. Discussion with the authors of the original study revealed minor differences in the handling of missing values between our implementation and the EARS implementation (Personal Communication with L. Hutwagner).

Figure 5.

Differences between CDC and BioSTORM Results for Selected Datasets The plots display the absolute differences between the sensitivity, specificity and time to detection computed in the original CDC study and those obtained in our validation study using BioSTORM. The boxes display median, upper and lower quartile differences for each of the algorithms across selected datasets. Minimal and maximal differences are shown by whiskers, and the outliers by circles.

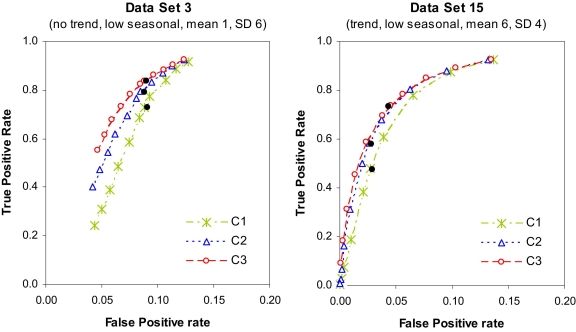
The ROC curves obtained in an extended analysis using 11 threshold values for two data sets are shown in ▶, which demonstrates the close match between the originally reported results and our corresponding results. The ROC curve also suggests that the current operating threshold used in the EARS software may not be the optimal operating point for all types of data, which has direct implications for public health surveillance practice.

Figure 6.

ROC Plots for Data Sets 3 and 15 The ROC curves were obtained in an extended analysis using 11 threshold values. The points corresponding to the results reported in the original CDC study for each of the algorithms are added to the plots as bold dots.

Discussion

We have developed and validated a model of aberrancy-detection algorithms used in public health surveillance and software that enables evaluation of algorithms encoded in terms of our model. The model and the software form an extensible framework for generating, gathering, and synthesizing evidence about the performance characteristics surveillance algorithms. This type of evidence is currently limited, but is crucial for ensuring effective public health practice and for guiding research in surveillance systems. In our validation study, we demonstrated that we can encode widely used algorithms in our model, and match published results with high precision.

The current work represents the foundation of a unified model of aberrancy-detection algorithms, in which distinct classes of algorithms share the same core representation schema, and thus can be analyzed and compared in a formal, systematic way. By clarifying the structural and procedural similarities and distinctions among algorithms, this model addresses an existing lack of understanding about how different aberrancy-detection algorithms are related to each other. Our choice of the task-analytic methodology for modeling purposes has allowed us to explicate the complex structure of aberrancy-detection algorithms and to clarify the roles of individual components in the overall aberrancy-detection process. We believe that the resulting modular representation facilitates understanding of the functional aspects of aberrancy detection and is extensible to accommodate a broad range of detection algorithms.

In addition to extending our own earlier work in this area, ^37,38 our research builds on work by others. A small number of researchers have performed systematic evaluation studies of multiple aberrancy-detection algorithms, ^19,23,44 but they have tended to view algorithms monolithically and not report results in a manner that allows attribution of performance to specific algorithm characteristics. Others have decomposed algorithms into sub-components in an attempt to better understand the determinants of algorithm performance. In particular, Murphy and Burkom divided a selection of algorithms into two component methods, forecasting and detection, and then evaluated the performance of different combinations of the methods. ²⁴ This high-level, informal decomposition allowed them to identify promising new combinations of methods. Our approach is distinct from earlier work due to our greater depth of decomposition of the aberrancy-detection task and our specification of a formal model that distinguishes between fundamental characteristics of methods and parameters of methods. Both of these features increase the precision with which it is possible to explain differences in method performance, and we believe that our deeper decomposition using a formal modeling approach is an important advance over earlier studies. The additional detail included in our model should enable the identification of the precise characteristics of algorithms that determine their performance and thereby support the generation of evidence about detection performance.

The present work is necessarily limited in scope, focusing on temporal aberrancy-detection methods, and leaving modeling of spatial and space-time algorithms for future work. A key requirement of our modeling effort, however, is to develop a model that can be extended to include other classes of algorithms. For example, space–time detection algorithms can be added naturally to our current model as a new task-decomposition method for aberrancy detection, using, as appropriate, the tasks and methods already defined for use in temporal aberrancy detection. Due to space limitations, we have been able to provide a detailed example of how only one type of aberrancy-detection algorithm can be represented using our model. We have, however, also successfully modeled several other algorithms (e.g., regression-based forecasting, hybrid regression and control-chart algorithms, and Holt-Winters forecasting) and these examples are available from the authors. We have also presented empirical validation of the model for only one published study, although this validation did entail examining our results for multiple types of data sets and outbreak signals. Finally, there are aspects of the BioSTORM software infrastructure, such as efficiency, robustness and usability, which we have yet to analyze. The software is built on a well-understood approach to scalable and distributed data processing, however, so it is reasonable to expect that it will scale well to larger volume of data processing.

In the future, we intend to make the BioSTORM software freely available and to use this system to populate a database with evaluation results that describe the relative performance of aberrancy-detection algorithms operating on different types of data sources in different surveillance contexts. Development of this database will entail encoding a number of algorithms in BioSTORM and then performing a large number of evaluations. Researchers, including us, will then be able to mine the results systematically to identify fundamental characteristics of the data and the methods that determine aberrancy detection performance, thereby producing empirical evidence to guide public health practitioners and researchers. We have begun this work for the C algorithms. ⁴⁵ This evidence may also be used in the future to guide automated algorithm selection. For example, it may be possible to use classification or planning algorithms in conjunction with the evidence about algorithm performance to suggest the best possible algorithm for a specific surveillance context.