Robust stability of genetic regulatory networks with distributed delay

Abstract

This paper investigates robust stability of genetic regulatory networks with distributed delay. Different from other papers, distributed delay is induced. It says that the concentration of macromolecule depends on an integral of the regulatory function of over a specified range of previous time, which is more realistic. Based on Lyapunov stability theory and linear matrix inequality (LMI), sufficient conditions for genetic regulatory networks to be global asymptotic stability and robust stability are derived in terms of LMI. Two numerical examples are given to illustrate the effectiveness of our theoretical results.

Introduction

In recent years, genetic regulatory networks have received more and more attention in the biological and biomedical sciences, few results have been done in this area (Becskei and Serrano 2000; Cao and Ren 2008; Chen and Arihara 2002; De Jong 2002; Elowitz and Leibler 2000; Gardner et al. 2000; Grammaticos et al. 2006; MacDonald 1989; Smolen 2000a, 2000b; Wei et al. 2007). As we all known, in order to understand the functioning of organisms on the molecular level, we need to know which genes are expressed, when and where in the organism, and to which extent. In fact, gene expression is a complex process regulated at several stages in the synthesis of proteins. The central dogma of molecular biology states that gene expression consists of two main processes, namely, transcription and translation. So the expression of a gene may be controlled during RNA processing and transport (in eukaryotes), RNA translation. The proteins fulfilling the above regulatory functions are produced by other genes. Typically a gene is subject to the regulatory effect of a few other genes which can act on it in either an activating or a suppressing way. How does genes and proteins produced by other genes interact to perform complicated biological functions? How to regulate the expression of genes? These questions makes us fell obliged to investigate genetic regulatory networks.

The study of genetic regulatory network requires large amounts of experimental data by gene expression assays. But only experimental data is not enough, a framework for deriving and expressing the biochemical architecture of genetic systems, using experimental data, is also required. The precision of mathematical language makes it a useful tool to model a useful framework for conceptualizing and understanding complex biochemical systems. Some theoretical results have made development based on mathematical models (Cao and Ren 2008; Chen and Arihara 2002; Grammaticos et al. 2006; Smolen 2000a, 2000b; Wei et al. 2007). In fact, there are many formalisms to describe genetic regulatory networks, such as Bayesian networks, Boolean network, ordinary differential equations (ODEs) and Piecewise-linear differential equation (PLDE) and so on. Among them, ODEs is the most widespread formalism to model the dynamics of genetic regulatory systems. Several simple genetic networks have been constructed and verified by experiments (Becskei and Serrano 2000; Elowitz and Leibler 2000; Gardner et al. 2000).

When modelling the genetic networks, time delay is an important factor, due to slow biochemical reactions such as gene transcription and translation, which should be considered. Nicholas (2003) showed that the observed oscillatory expression and activity of three proteins is most likely to be driven by transcriptional delays. Smolen et al. (2002) found time delays were essential for simulation of circadian oscillations with this model. Time delays in gene networks could strongly affect stimulus responses (MacDonald 1989), and also have an effect on synchronized spike-burst networks (Jirsa 2008). Therefore, it is necessary to take delay into consideration when modelling genetic networks. There are several theoretical analysis of different mathematical models with and without time delay. Chen and Arihara (2002) proposed a delayed genetic regulatory networks and analyzed nonlinear properties of the model in terms of local stability and bifurcation. Later, Li et al. (2006) investigated the stability of genetic regulatory networks with random perturbation. They further considered the stochastic stability of genetic network with disturbance attenuation (Li et al. 2007). Time delays are either discrete or continuous with the derivative less than 1. Improved on it, Ren and Cao (2008) discussed the robust stability of genetic network with time-varying delay, only bounded is required for the time-varying delays. We can see that time delays all of above are discrete. In fact, transport can be modelled as diffusive or active in nature. If active it can be modelled with a time delay. The time delay can be discrete, which assumes each macromolecule takes the same length of time to translocate from its place of synthesis to the location where it exerts an effect. However, this simplification may be too drastic, another approach is to assume a distributed delay (De Jong 2002; MacDonald 1989; Smolen 2000a). In principle, this approach is general enough to model any mechanism of macromolecular transport. For example, if movement of mRNA from a transcription site to translation sites is an active process with a significant range of transport times for individual molecules, a distributed delay would be the proper modelling framework. However, there are little work about the stability with distributed delays.

In the design of networks, such as genetic networks and neural networks, a common problem is that parameters acquired are inaccurate. There might also be some fluctuations in the parameters, which might lead to complex dynamical behavior. Therefore, it is essential to investigate the globally robust stability of such networks with uncertainties. There have been some studies on the robust stability or distributed delays analysis for neural networks (Lien and Chung 2007; Wang et al. 2006; Yang and Chu 2007). In fact, the biologic networks can show robust character under perturbation (Kwok et al. 2007). However, few works are done on the robust stability of genetic regulatory networks. Inspired by the above work, this paper aims to investigate robust stability of genetic regulatory networks with distributed delay by using Lyapunov functional and linear matrix inequality (LMI) technique which is used frequently for its easily being verified. Several criteria are derived to guarantee the asymptotic and robust stability of such networks. Two numerical examples are also given to verify the effectiveness of our obtained results.

Notation: Throughout this paper, A^T denotes the transpose of a matrix A. 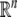denotes the n dimensional Euclidean space. 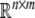is the set of all n × m real matrices. I denotes the identity matrix with appropriate dimensions. diag{…} denotes the diagonal matrix. The notation X > 0 (respectively, X < 0) means that the matrix X is positive (negative) definite, that is the eigenvalues of X are positive (respectively, negative).

Methods

Model description and preliminaries

A genetic regulatory network (GRN) is composed of a number of genes that interact and regulate the expression of other genes by proteins (the gene product). The dynamic behavior of a genetic regulatory networks with variable delays can be described by the following state equations (Cao and Ren 2008; Chen and Arihara 2002; Elowitz and Leibler 2000; Li et al. 2006, 2007; Ren and Cao 2008):

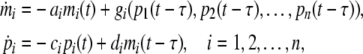1

where m_i(t), p_i(t) denote the concentration of mRNA and protein of the ith node at time t. a_i and c_i are positive real numbers that present the degradation rates of mRNA and protein, respectively. d_i is the translation rate. τ is the node delay, and the functions g_i denotes the feedback regulation of the protein on the transcription, which is generally nonlinear function but has a form of monotonicity of each variable (De Jong 2002; Smolen 2000b). In most existed paper, function g_i is of the SUM logic form (Cao and Ren 2008; Chen and Arihara 2002; Li et al. 2006, 2007), which is g_i = ∑ⁿ_j=1G_ij(p_j(t)). The functions G_ij(p_j(t)) are usually expressed by the Hill form

where H_j is the Hill coefficients, β_j is positive constants, α_ij are bounded constants, while are the dimensionless transcription rate of transcription factor j to i. From this, one can rewrite Eq. (1) as follows:

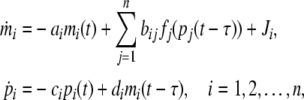2

where 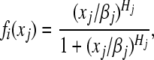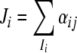and I_i is the set of all the j which is a repressor of gene i, B = (b_ij) is defined as follows:

Most paper considered the model (2) with discrete time delay (Cao and Ren 2008; Chen and Arihara 2002; Li et al. 2006, 2007). In fact, this simplification maybe too drastic. Here we consider the genetic regulatory networks with distributed delay. The derivative of mRNA and protein depends on an integral of a function of one or more variables over a specified range of previous time. A general distributed delay take the forms

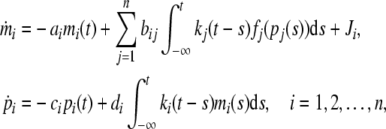3

where k_j is the delay kernel, which is a real value non-negative continuous function defined on [0, + ∞] satisfying

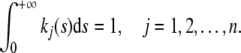Rewrite the system (3) into compact matrix form, we obtain:

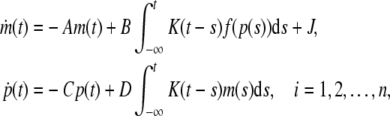4

where m(t) = [m₁(t), m₂(t), …, m_n(t)]^T, p(t) = [p₁(t), p₂(t) ,   …,  p_n(t)]^T, K(t−s) = diag{k₁(t−s), k₂(t−s), …, k_n(t−s)}, f(p(t)) = [f₁(p₁(t)),f₂(p₂(t)),   …, f_n(p_n(s))]^T, A = diag{a₁, a₂, …, a_n}, C = diag{c₁, c₂, …,  c_n}, D = diag{d₁, d₂, …, d_n}. In principle, this approach is general enough to model any mechanism of macromolecular transport (Smolen 2000a). Let ((m*)^T,(p*)^T)^T be an equilibrium point of Eq. (4), i.e. it is the solution of equation

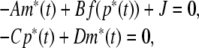Next we will shift an intended equilibrium point ((m*)^T, (p*)^T)^T of system (4) to the origin. Using the following transformation

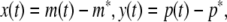the model (4) can be transformed into the following form:

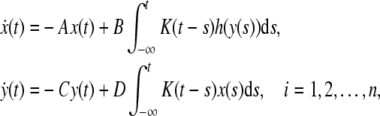5

where x(t) = [x₁(t), x₂(t), …, x_n(t)]^T, y(t) = [y₁(t), y₂(t), …, y_n(t)]^T, h(y(s)) = [h₁(y_i(s)), h₂(y_i(s)), …,  h_n(y_i(s))]^T, h_i(y_i(s)) = f_i(y_i(s) + 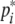) − f_i(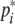). Since f_i is a monotonically increasing function with saturation, it satisfies

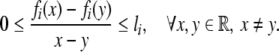Clearly, the function h_i(x) satisfies the sector condition

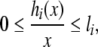which is equivalent to the following one

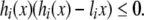6

Results

In this section, we give two main theorems to ensure the asymptotic and robust stability of genetic regulatory networks. First, we analyze the asymptotic stability of system (5).

Asymptotic stability for GRN

Theorem 1 If there exists positive definite matricesP, Q and diagonal positive definite matrices K, R = diag{r₁, r₂, …, r_n}, E = diag{e₁, e₂, …, e_n} with appropriate dimensions respectively, such that

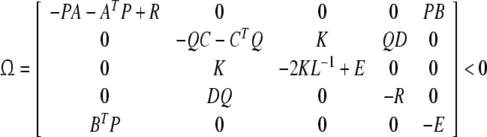7

where L⁻¹ = diag{l⁻¹₁, l⁻¹₂, …, l⁻¹_n}, then system (5) is asymptotically stable.

Proof Based on the system (5), we construct the following Lyapunov functional:

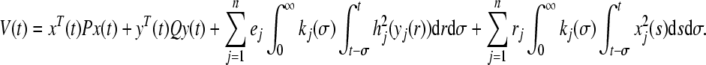8

Differentiating V with respect to time along the solution of (5) yield:

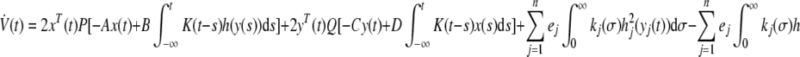It follows from Hölder inequality that

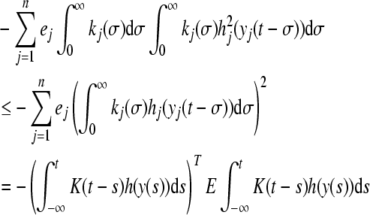9

and

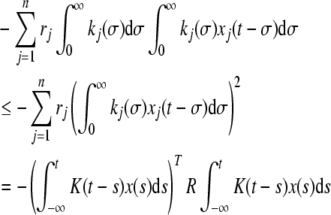10

By Eq. (6), for any diagonal positive matrix K one can get

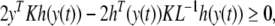11

where L⁻¹ = diag{l⁻¹₁, l⁻¹₂ ,  …,  l⁻¹_n}.

Combining Eqs. (9–11), we can get

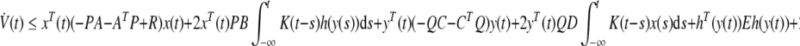where ξ(t) = [x^T(t),y^T(t),h^T(y(t)), (∫^t_−∞K(t−s)x(s)ds)^T, (∫^t_−∞K(t−s)h(y(s))ds)^T]^T. Ω is defined as Eq. (7). Clearly, if condition (7) holds, then 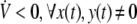. It follows from Lyapunov–Krasovskii theorem (Hale and Verduyn-Lunel 1993) that the genetic regulatory network (5) with distributed delay is asymptotically stable. □

Robust stability of uncertain GRN

Consider the following uncertain GRN

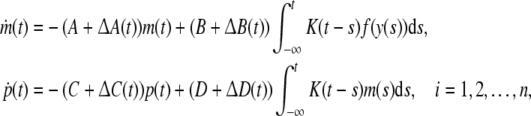12

where ΔA(t), ΔB(t), ΔC(t), ΔD(t) are parametric uncertainties satisfying

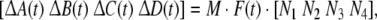M, N_i, i ∈ [1, 2, 3, 4] are some given constant matrices, F(t) is an unknown real time-varying function with appropriate dimensions and bounded as follows:

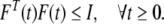Next, let us give the following lemma which will be used in the proof of our main results.

Lemma 1 (Singh 2004) LetU, V, W and X be real matrices of appropriate dimension with X satisfying X = X^T, then

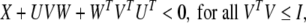if and only if there exists a scalar ɛ > 0 such that

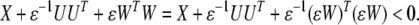Lemma 2 (Boyd et al. 1994) (Schur complement) For a given matrix

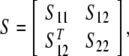withS₁₁ = S^T₁₁, S₂₂ = S^T₂₂, then the following conditions are equivalent:

1. S < 0,

2. S₂₂ < 0, S₁₁−S₁₂S⁻¹₂₂S^T₁₂ < 0.

Theorem 2 System (12) is robust stable if there exist some positive definite matricesP, Q, diagonal positive definite matricesK, R, E and a constant ɛ > 0 satisfying

13

where Ω is defined in Theorem 1 and

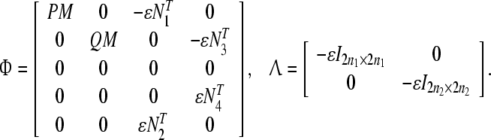whereM is n × n₁, N_i, i = 1, 2, 3, 4 are n₂ × n.

Proof Take the same Lyapunov functional as that in the proof of Theorem 1 and replace A,B,C, and D by A + MF(t)N₁, B + MF(t)N₂, C + MF(t)N₃, and D + MF(t)N₄, the sufficient condition to guarantee the asymptotic stability of system (12) can be obtained.

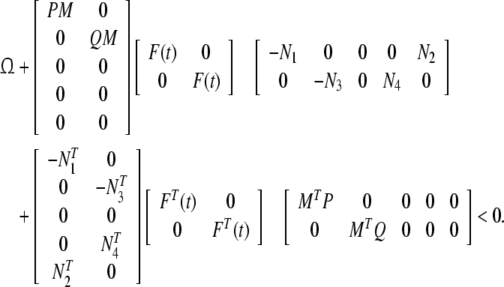14

From lemma 1 and 2, conditions (13) and (14) are equivalent, we can conclude that system (12) is robust stable. □

Computer simulation

In this section, we will give two examples to illustrate the correctness of our results.

Example 1 Consider a genetic regulatory network with distributed delay described by the following equations:

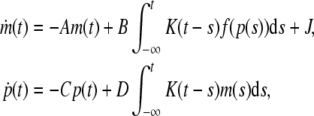15

where A = diag{3, 4, 5}, C = diag{1.5, 3, 4}, D = diag{4.5, 1, 5}, J = [2.5, 2.6, 2.4]^T,

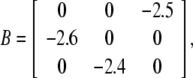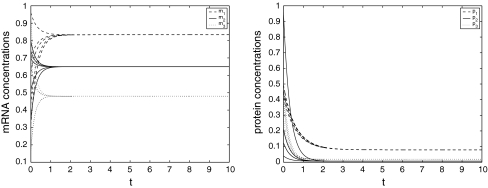
τ = 2, f_i(x) = x²_i/(1 + x²_i), i.e., the Hill coefficient is 2. The maximal value of the derivation of f_i(x) is < 0.65, so let l_i = 0.65, i = 1, 2, 3. k_j(s) = e^−s, j = 1, 2, 3. By using the Matlab LMI Toolbox, we solve the LMI (7) for P > 0, Q > 0, R > 0, E > 0, K = I and obtain P = diag{ 1.3759, 0.4549, 2.5304}, Q = diag{0.2861, 4.9528, 1.8482}, R = diag{3.8981, 1.3271, 10.0111}, E = diag{0.7113, 2.7313, 2.8210}. Therefore, it follows from Theorem 1 that the genetic regulatory network (15) is globally asymptotically stable. Figure 1 depicts the temporal evolution of each variable of the genetic regulatory network m_i, p_i, i = 1, 2, 3 with five random initial conditions, respectively.

Fig. 1.

Trajectories of m₁, m₂, m₃ and p₁, p₂, p₃, for (15)

Example 2 Consider the following uncertain genetic regulatory network:

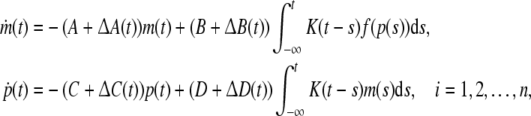16

where ΔA(t), ΔB(t), ΔC(t), ΔD(t) are parametric uncertainties satisfying

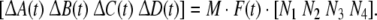For simplicity, let M = diag{0.1, 0.1, 0.2}, N₁ = diag{0.1, 0.2, 0.1}, N₂ = diag{0.05, 0.11, 0.25}, N₃ = diag{0.12, 0.01, 0.53}, N₄ = diag{0.1, 0.15, 0.08}.F(t) = diag{sin(t), cos(2t), sin(t)}. Again, by solving the LMI (12) for ɛ > 0, P > 0, Q > 0, R > 0, E > 0, K = I, we obtain

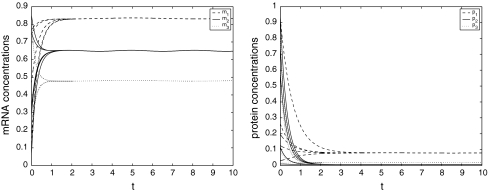
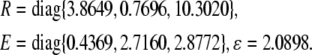which indicates that system (16) is globally asymptotically stable. Figure 2 depicts the temporal evolution of each variable of the genetic regulatory network m_i,p_i, i = 1,2,3. We can see that the curves are not smooth as in Fig. 2, especially for m_i, i = 1, 2, 3. It shows that the uncertain parameters do have an effect on system (15), but not obviously. The numerical simulation verifies the effectiveness of Theorem 2.

Fig. 2.

Trajectories of m₁, m₂, m₃ and p₁, p₂, p₃ for (16)

Discussion

In this paper, we discussed the robust stability of genetic regulatory network with distributed time delay. To the best of our knowledge, there are rare results above this issue. It is a more realistic model when taking distributed delay into account. In principle, this approach is general enough to model any mechanism of macromolecular transport. The analytical results obtained in this paper may therefore give new insights on the dynamics of genetic regulatory networks.