Wave-Block Due to a Threshold Gradient Underlies Limited Coordination in Pancreatic Islets

Abstract

Two models for coupled pancreatic β cells are used to investigate excited wave propagation in spatially inhomogeneous islets of Langerhans. The application concerns spatial variation of glucose concentration across the islet. A comprehensive model of coupled cells shows that wave blocking occurs as the conductance of adenosine triphosphate regulated potassium channels increases, corresponding to spatially decreasing glucose concentration. A simplified model based on a perturbed version of Fisher’s equation has been investigated using perturbation theory. We show that the perturbed Fisher’s equation likewise can exhibit wave blocking.

Introduction

Malfunctioning of the insulin secretory system is a major factor in diabetes. The pancreatic islets of Langerhans consist of thousands of coupled cells; among these are the β cells, which secrete insulin in response to several stimuli, with glucose being the physiologically most important. In order to function properly and secrete insulin, it is of great importance that the β cells cooperate in a synchronized manner, and the coupling between cells made of gap junctions seems to be crucial for this synchronization ([1–3] and references herein).

An increased intracellular calcium concentration is the signal that triggers insulin release, and thus, synchronized insulin secretion would be expected to be a result of synchronized Ca^2 + levels. In [4], it was shown experimentally that calcium waves could provide a way to synchronize the cells. Using a mathematical model of β cells, the authors showed that gap junctions indeed could result in waves of the observed kind. Moreover, it was suggested that active cells could activate less responsive cells by means of the waves.

In an elegant experiment [5], it was shown that such an activation signal from active to silent cells is only able to travel short distances. The authors imposed a glucose gradient across an islet such that cells in one part of the islet would feel a glucose concentration high enough to promote calcium influx and insulin secretion, while the rest of the islet sensed a lower glucose stimulus, below the activation threshold. Calcium wave propagation starting from the cells in high glucose was seen, but these waves did not travel into the region with a glucose concentration below the threshold, activating none or, at most, very few of the otherwise silent cells. In this article, we shall elucidate these findings, invoking mathematical modelling of pancreatic β cells.

Mathematical Models and Fisher’s Equation

Almost all mathematical models of β cell electrical activity and calcium dynamics are of the form

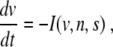1

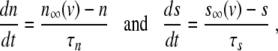2

where v = v(t) models the membrane potential as function of time t, and n = n(t) and s = s(t) are fast and slow gating variables, respectively, i.e., τ_n ≪ τ_s. I is the sum of the ion currents flowing through the cell membrane gates [6]. It has been argued that, on the front of an excitation wave, we can assume n = n_∞(v) and s = s^* to be constant [4]. Then, (1) becomes

3

where F = F(v; s^*) has three simple zeros v₀  <  v_a  <  v₁ and is negative on the interval ]v₀; v_a[. When we consider a line of N coupled cells, this becomes

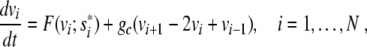4

where i counts the cells. We use open-end boundary conditions equivalent to v₀ = v₁, v_N + 1 = v_N. The coupling between cells is due to gap junctions and we assume a resistive ion current coupling with conductivity g_c. The continuum limit of the discrete equation (4) yields [4]

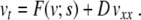Here, subscripts denote differentiation with respect to the subscript variable. Note that s is allowed to be a function of x. After a suitable change of variables (see [7] for details), this equation can be transformed into Fisher’s equation

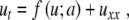5

where f = f (u; a) has three simple zeros when varying the variable u, for the parameter a belonging to the interval 0  <  a  <  1 and f (u; a) is negative for u ∈ [0; a]. The prototype is the cubic f (u) = u(1 − u)(u − a). It is well known [8, 9] that, for constant a = a₀ and 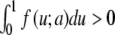, (5) has a traveling wave solution

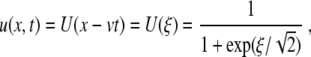6

where ξ = x − vt with lim_{ξ→ − ∞}U(ξ) = 1, lim_ξ→ ∞U(ξ) = 0, and 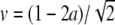. This means the solution has a kink shape.

The present work investigates the experiments described in [5] with a glucose gradient across the islet following the ideas above. Because an imposed glucose gradient corresponds to the threshold changing across the islet, we perturb the threshold a in (5), as well as the equation itself:

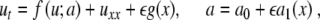7

where we require 0  <  a  <  1 and a₁ and g sufficiently smooth. Using perturbation theory much in the spirit of Keener’s investigation of the homogenized equation (5) [8], we show that a space varying parameter a = a(x) leads to a change in the propagation velocity v of the kink type solution in (6). This may result in a halt of the wave (wave blocking). We conjecture that a varying a(x) can model a glucose gradient through an islet of Langerhans leading to the observed wave block phenomena observed experimentally in [5].

Wave Propagation and Wave Block

We set [8, 9]

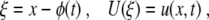such that (7) becomes

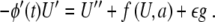8

In the following, we let f_u(u, a) denote the partial derivative of f (u, a) with respect to u, similarly for f_a(u, a). Introducing

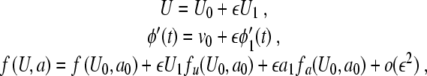in (8) and collecting terms with the same order in ε yields for ε⁰ and ε¹,

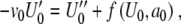9

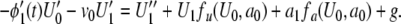10

From (9), we see that the zero-order solution U₀ and speed v₀ are given from the standard solution of (5). Equation 10 can then be written

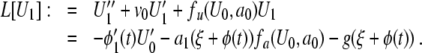11

By differentiating (9) with respect to ξ, we find L[U₀′] = 0. The adjoint operator L^† [9], defined by 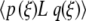= 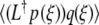, then has L^†[W ] = 0 for 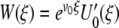. Here, 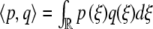. In order to have a solution of (11), we therefore must demand

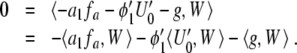12

From (12) we obtain

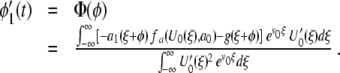13

Hence, we have an ordinary differential equation (ODE) for the instantaneous position ϕ, or, in other words, the instantaneous velocity ϕ′ is given by

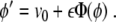From this equation, we can find the location ϕ when the wave front stops, that is, at ϕ′ = 0.

Example

To illustrate the theory introduced above, we look closer at a case where explicit calculation can be done. Let us consider the cubic

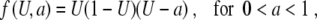in (7), and from (6), the solution U₀=U₀(ξ) of (9) becomes

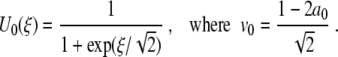Note that 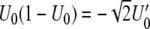, so that the denominator of (13) becomes

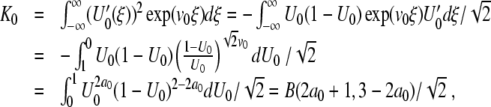where we have used the substitution 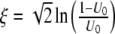, and introduced the Beta function B. Assume g = 0 and

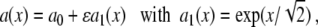14

where a₀ is a constant and ε ≪ 1. The partial derivative of f with respect to a is f_a(U₀,a₀)=− U₀(1 − U₀) and the numerator K₀ Φ(ϕ) in (13) becomes

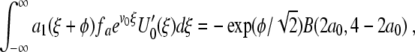15

from which we calculate, using the properties of the B - and Γ-functions,

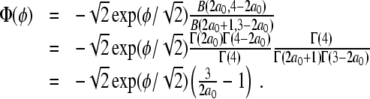This result finally yields the simple ODE for ϕ

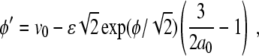possessing the analytical solution

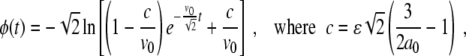16

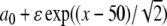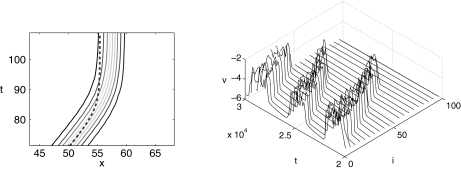
for the initial condition ϕ(0) = 0. In Fig. 1 (left), we show a contour plot of a full numerical simulation of the perturbed Fisher’s equation (7) with the space-dependent parameter given by a(x)= [see (14)] and with the initial conditions given by 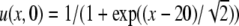. The perturbation term g is set to zero. From these formulas, we observe that the initial kink is positioned at x = 20 and a(x) is “positioned” at x = 50. The kink propagation is blocked at position x ≈ 57.7, a little after the “center position” of a(x). The simulation is compared to the results from the approximation in (16), which provide the trajectory of the kink. The trajectory determined from (16) is shown in Fig. 1 (left) as the dashed line, predicting a wave block at the position x ≈ 55.2. The approximate analysis predicts a slightly earlier wave block, and also the curvature of the kink trajectory is larger than the results from the full numerical simulation predict. Apart from this, the perturbation analysis seems to give a fair approximation of the full simulation results of (7) with g  =  0.

Fig. 1.

Left: Comparison between the full numerical simulation of the wave block of the perturbed Fisher’s equation (7) (contour plot) and the approximate solution in (16) (dashed line). The parameter values are a₀ = 0.2, ε = 0.001, 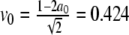, g = 0. Right: Simulation of a linear chain of coupled beta cells illustrating wave blocking. The voltage is shown as a function of time and cell position for linearly increasing g_K(ATP). Number of cells N = 100. Time is measured in units of k_t = 5.3 ms and the voltage is measured in units of k_v = s_m = 12 mV

Wave Block in Coupled Beta Cells: Discrete Model

We now return to the original model of β cell bursting given in (1–2), and this time, we shall be specific about the ion currents I. We consider a model of coupled cells in a line and include an adenosine triphosphate (ATP) regulated calcium gate. Following [6], we consider the model below adapted for coupled β cells

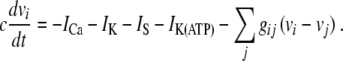17

The notation follows that in (4). The membrane capacitance is denoted by c. The currents I_Ca and I_K are voltage-dependent inward calcium and outward potassium currents, respectively, which are responsible for fast oscillations during the active phase. The current I_S is a slow current responsible for the depolarization of the membrane and I_K(ATP) is an ATP-regulated outward potassium current that is high at low ATP/glucose concentrations and low at high ATP/glucose concentrations, thus describing external control of the ion current activity by glucose metabolism. The final term models the gap junctions, interconnecting nearest neighbor cells, as linear passive electric conductors. The ion currents for cell i are given by [6]

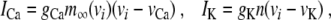18

19

The voltage-dependent coefficients m_∞(v_i), n = n(v_i,t), and s = s(v_i, t) are gating variables controlling the closing and opening of the associated ion channels. The dynamics of the gating variables are governed by (2). Each of the variables m_∞, n_∞, and s_∞ are given by formulas of the same form

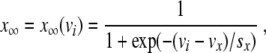20

where x represents m, n, and s, respectively. Representative parameter values are selected from references [4, 6] and given in Table 1. For the study of the wave front, s can be set to a constant value s = s^*, because it is a slow variable, and it can be assumed that the fast-gating variable n attains its equilibrium value n = n_∞. Under these assumptions, the total current then possesses three zeros with the parameter values used here [4], as explained in Section 2. This motivates the study of Fisher’s equation in Section 3.1.

Table 1.

Parameter values used in the models

gCa = 1000 pS

vCa = 25 mV

vm = − 20 mV

sm = 12 mV

c = 5300 fF

gK = 2700 pS

vK = − 75 mV

vn = − 16 mV

sn = 5.6 mV

τn = 20 ms

gs = 200 pS

gij = gc = 20 pS

vs = − 52 mV

ss = 5 mV

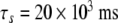pS = pico Siemens, mV = millivolt, ms = milliseconds, fF = femto Farad

With the above model, we are now in a position where we can address the experimental results of wave blocking. A linear glucose gradient was imposed across an islet of Langerhans in a microfluidic cavity setup [5]. In our model, this corresponds to varying g_K(ATP) along the cell sites of the linear chain model, and we shall assume a linear spatial variation of g_K(ATP) according to

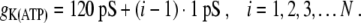21

For single cell dynamics with g_ij = 0, the model in (17) exhibits continuous spiking for 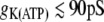, bursting behavior for 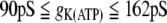, and silence for 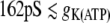. From (21), we will expect that an excitation wave can propagate along the cell chain from i = 1 until, at most, 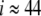. The model equations in (17–19) have been implemented on a computer in a scaled version. Time has been scaled in terms of k_t = c/g_Ca = 5.3 ms; that is, time is measured in units of k_t. Similarly, the voltage is scaled according to k_v = s_m = 12 mV and, hence, measured in units of k_v. Conductivities are measured in units of k_g = c/k_t = 1000 pS. Note that, in (21), we have given the variation of g_K(ATP) in physical units.

We have conducted a simulation in a scaled time interval from t = 0 to t = 3 · 10⁴ (corresponding to 159 s). In Fig. 1 (right), we show the scaled voltage v_i(t) as a function of cell position i and time t for the time interval t = 2 · 10⁴ (106 s) to t = 3 · 10⁴ (159 s). The figure shows how fronts form of cells changing from the resting state to the bursting state, and propagate analogous to the front solutions of Fisher’s equation (Fig. 1 left). Similarly, we see fronts corresponding to cells changing from the excited state to the silent state. The irregular shape is typically observed in coupled cell dynamics and may be due to chaotic dynamics or irregular synchronisation. At a fixed value of the cell position i less than about 60–80, we observe the characteristic bursting phenomena with decreasing burst period as g_K(ATP) increases as a function of i. For cells at position i larger than about 80, the bursting behavior disappears and the cells are silent. This means we have excitation wave propagation until, at most, cell number 80, and here, wave blocking occurs. We can conclude that the simulation confirms the wave blocking phenomena observed in the experiments from [5].

At cell number 44, the parameter g_K(ATP) equals 163 pS and the single-cell bursting disappears. Therefore, we would expect the excitation wave stops at about i = 44. However, the simulations show that the excitation waves propagate further into the region with silent cells leading to an induced bursting of otherwise silent cells. In other words, the coupling can induce excitation, leading to propagation of an excitation wave further into a region with depleted glucose concentration. This wave penetration is enhanced when increasing the coupling constant g_ij  = g_c.

Conclusion

Using mathematical modelling, we have investigated coupled pancreatic β cell dynamics with a focus on inhomogeneous spatial variation of parameters. The purpose is to investigate the occurrence of blocking of excitation waves observed in experiments, where a glucose gradient is imposed across an islet of Langerhans.

An excitation wave can propagate from high glucose concentration toward low glucose concentrations but will be stopped or blocked when entering the low glucose concentration region where the β cells are not excited. Our model shows that wave blocking occurs for spatial variation of the ATP-regulated potassium ion channel gate. In addition, we observe that the gap junction coupling leads to enhanced excitation of otherwise silent cells.

A simplified mathematical model for the wave blocking phenomenon has been suggested in terms of a perturbed Fisher’s equation. In the normalized Fisher’s equation, there is one parameter a, which gives the propagation velocity of a travelling wave solution. By letting a be a function of space x, perturbation theory shows that increasing a gives rise to blocking of wave propagation.