Numerical simulations of localized high field ¹H MR spectroscopy

Abstract

The limited bandwidths of volume selective RF pulses in localized in vivo MRS experiments introduce spatial artifacts that complicate spectral quantification of J-coupled metabolites. These effects are commonly referred to as a spatial interference or “4 compartment” artifacts and are more pronounced at higher field strengths. The main focus of this study is to develop a generalized approach to numerical simulations that combines full density matrix calculations with 3D localization to investigate the spatial artifacts and to provide accurate prior knowledge for spectral fitting. Full density matrix calculations with 3D localization using experimental pulses were carried out for PRESS (TE=20, 70 ms), STEAM (TE=20, 70 ms) and LASER (TE=70 ms) pulse sequences and compared to non-localized simulations and to phantom solution data at 4 Tesla. Additional simulations at 1.5 and 7 Tesla were carried out for STEAM and PRESS (TE=20 ms). Four brain metabolites that represented a range from weak to strong J-coupling networks were included in the simulations (lactate, N-acetylaspartate, glutamate and myo-inositol). For longer TE, full 3D localization was necessary to achieve agreement between the simulations and phantom solution spectra for the majority of cases in all pulse sequence simulations. For short echo time (TE=20 ms), ideal pulses without localizing gradients gave results that were in agreement with phantom results at 4 T for STEAM, but not for PRESS (TE=20). Numerical simulations that incorporate volume localization using experimental RF pulses are shown to be a powerful tool for generation of accurate metabolic basis sets for spectral fitting and for optimization of experimental parameters.

1. Introduction

Localized ¹H MR Spectroscopy (MRS) has been used extensively for the non-invasive detection of various metabolites under healthy and pathological conditions in the human brain in vivo. The increasing availability of high field MR scanners opens up new possibilities for improved characterization of the rich spectral information of in vivo MRS data. For example, up to 18 metabolites were quantified at 9.4 Tesla in a rat brain spectrum [1]. At higher fields the increased spectral dispersion reduces the spectral overlap between the resonances, facilitating the process of spectral fitting and quantification. However, the limited RF pulse bandwidths also create artifacts that complicate spectral quantification at higher fields due to the increase in spectral dispersion. In addition to creating spatial offsets of resonances with different chemical shifts (known as the chemical shift artifact), limited RF bandwidth can also alter the amplitudes and phases of J-coupled resonances. This effect is referred to as spatial interference or the “4 compartment” artifact due to the presence of different spatial compartments in the localized volume [2]. The relative contributions of these compartments to the overall spectral yield depend on the RF bandwidth and the frequency separation between coupled spins. Therefore, accurate quantification of localized in vivo data collected at high fields requires prior knowledge that takes these effects into account.

Prior knowledge for spectral fitting of the J-coupled resonances detected in vivo is generated either from metabolite solution spectra in vitro [3,4] or from numerical simulations with full density matrix calculations [5,6]. The former approach is used in the MRS community mostly in conjunction with the commercially available LC-Model software [7], although LC-Model can also use numerical simulations as basis sets [8]. Use of solution spectra has one major advantage over the simulation approach, which is the inclusion of exact experimental conditions into the basis sets used for fitting in vivo data, including localization artifacts associated with J-coupled resonances. This advantage is even more important at higher fields, since instrumental limitations are much more pronounced at higher fields. The disadvantage of this approach is the requirement of preparing metabolic solutions at physiological pH, an expensive and non-trivial procedure, and acquiring new basis sets at physiological temperature whenever experimental parameters are changed. The simulation method offers an elegant alternative to this approach, since basis sets from a “virtual spectrometer” are easily generated without using expensive chemicals/wet lab equipment and MR scanner time, which is often limited. Young et al. [6] have demonstrated a parametric spectral analysis procedure that utilizes the simulation method for generating a priori information. This approach has been incorporated into freely available SI TOOLS [9], GAVA [10] and MIDAS [11] software and has been used successfully to fit in vivo data [12,13]. Previously, Thompson et al. demonstrated that numerical simulations using a weak coupling approximation and ideal pulses are not adequate for description of J-coupled metabolites detected with PRESS [14] and STEAM [15]. These simulations demonstrated that it is possible to construct 2D parameter maps, showing the effects of echo-mixing times (TE-TM) in STEAM and (TE₁, TE₂) in PRESS on the strongly coupled spins. These parametric maps can provide the optimized detection timings or aid in developing a strategy for the multiple quantum filters to target a specific metabolite [16]. Several schemes for practical implementation of the simulations of PRESS-localized spectroscopy to obtain the “4 compartment” distribution of the lactate signal were also investigated with a specific focus on realistic experimental pulses and localization [17]. Taken together, these studies provide convincing evidence of the additional advantages that are inherent in using an extended numerical simulation approach for quantifying the metabolic resonances detected in vivo.

The main goal of this study is to demonstrate that simulations extended to 3D localization (achieved with actual RF pulse shapes) are fully capable of generating accurate a priori information in commonly employed MRS localization experiments at high fields. A generalized numerical simulation method is developed for three of the most popular localized sequences used in the MRS community: point-resolved spectroscopy (PRESS) [18,19], localization by adiabatic selective refocusing (LASER) [20], and stimulated-echo acquisition mode (STEAM) [21]. Basis sets generated using simulations with ideal RF pulses without localization (referred to as ideal simulations), 2D and 3D spatial localization with experimental pulses are compared to phantom solutions collected at 4.0 Tesla at TE=20 and 70 ms. In addition, short echo time (TE=20 ms) simulations are also performed at 2 field strengths: 1.5 and 7.0 Tesla. Pseudo-code for the 3D LASER simulations is provided (see Appendix) and the efficiency of calculations is discussed. While the importance of including localization and realistic pulse shapes for generating prior information via simulation for quantification of J-coupled metabolites has been pointed out elsewhere [14, 17], to the best of the authors’ knowledge this work constitutes the first attempt to outline and utilize a detailed, generalized methodology.

2. Methods

2.1. Spin Systems

For all simulations, the following coupled spin systems (all relevant to clinical studies of the central nervous system with ¹H MRS) were used: Lactate (Lac), N-acetylaspartate (NAA), glutamate (Glu), and myo-inositol (mI). An uncoupled spin system of creatine (Cr) with 2 singlet resonances was chosen to serve as a reference signal. At 4.0 Tesla, Lac (at 1.3 ppm) and Glu (at 3.7 ppm) represent the weakly coupled spin systems, with 465 Hz and 285 Hz separation between coupled spins respectively, while NAA (at 2.5–2.7 ppm) and mI (at 3.5 ppm) represent the metabolites with more closely spaced coupled resonances (although NAA spins are also weakly coupled to another spin at 4.5 ppm). The chemical shifts and J-coupling values were obtained from the literature [22].

2.2. Simulations Implementation

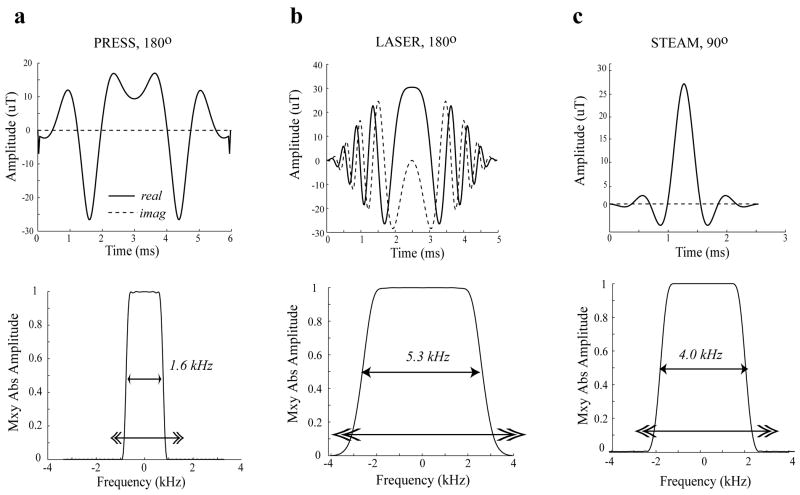
All simulations were written in C++ using GAMMA [23] library subroutines. Two types of simulations with full density matrix computations were performed: 1) simulations using ideal pulses without localization and 2) simulations using experimental RF pulses with spatial localization. RF pulses were generated using the MATPULSE software [24] developed in-house and available for downloading at http://www.cind.research.va.gov. Figure 1 shows the RF pulse shapes, their bandwidths and corresponding localization profiles for the refocusing 180° pulses used for PRESS and LASER and the 90° pulse used both for the STEAM sequence and for the excitation pulse in PRESS. The shape of the PRESS 180° pulse was obtained by root reflection of a conventional pulse (a routine available in MATPULSE) in order to lower the maximum B₁ (B_1max) amplitude needed for the pulse. All three pulse shapes were defined using 200 time points. The maximum amplitude strength for all the generated pulses was ~30 microtesla (uT). For the typical RF volume head coils this value can be achieved with a 7 kW amplifier, which represents the higher end of available B_1max strengths for human brain studies. In a majority of MR clinical research laboratories 3–4 kW amplifiers are much more common for higher field systems, and therefore B_1max is limited to approximately 20 uT. For those cases the localization effects are expected to be more severe. The localization gradient for N^3 points (where N is the number of points in 1D) was simulated as a frequency shift of the spin systems, ω_{spinsystem(0)}, during the pulse at nth spatial point, with n varying between [0, N-1]

Figure 1.

RF pulse shapes and corresponding magnetization profiles of the RF pulses used in the simulations and experiments at 4 Tesla a) 180° refocusing pulse based on root-reflection algorithm [24] for lowering B_1max requirements for use in the PRESS sequence (duration = 6 ms), b) adiabatic full passage 180° pulse for the LASER sequence (duration = 5 ms), and c) Shinnar-Le Roux [33] 90° excitation pulse used in STEAM and PRESS sequences (duration = 2.5 ms). The double-headed arrows indicate the “spatial” extent of the frequency sweep in the simulations.

$${\omega }_{\mathit{spinsystem}(n)}={\omega }_{\mathit{spinsystem}(0)}-({\omega }_{\mathit{offset}\_\mathit{start}}+n\ast ({\omega }_{\mathit{offset}\_\mathit{end}}-{\omega }_{\mathit{offset}\_\mathit{start}})/N),$$ (1)

The endpoints of the frequency sweep (ω_{offset _ end}, ω_{offset _ start}) were dependent on the widest part of the bandwidth of the RF pulse (the base of the localization profile, BW_base). In addition, these endpoints were shifted to adjust for the lowest and the highest detected chemical shifts in Hz of the metabolites of interest. As a result, those endpoints are defined for all simulations at 4 Tesla as follows:

$${\omega }_{\mathit{offset}\_\mathit{start}}=-B{W}_{\mathit{base}}/2+200Hz,{\omega }_{\mathit{offset}\_\mathit{end}}=B{W}_{\mathit{base}}+750Hz,$$ (2)

where the values of 200 Hz and 750 Hz correspond to the range between 1.3 and 4.5 ppm. The crusher gradients in all 3 pulse sequences were implemented similar to the procedure outlined previously by Young et al. [5]. The density matrix was split into four parts and the simulations were replicated four times with phase rotations of 0, π/2, π, and 3π/2, both prior to, and following, each localization RF pulse application. The four density matrix components were recombined at the end of the simulation, prior to the detection period. For STEAM, in addition to localization gradients, TE and TM crusher gradients were implemented in a manner similar to the procedure outlined by Young et al [5]. As a result, STEAM simulations took a significantly longer time (e.g. 1.3 seconds per 1 spatial point for Glu) compared to PRESS (0.2 seconds per spatial location for Glu). Since LASER required 6 localization pulses (two for each spatial direction), the laser simulation time was twice as long as for PRESS (0.4 seconds per spatial location for Glu). Ideal and 3D localized simulations used N=1 and N=40 steps, respectively (resulting for the 3D case in generation of 64,000 localized spectra). All simulations were performed on a 21 node Beowulf cluster with 3GHz dual processors on each node using Message Passing Interface (MPI) routines. The MPI implementation decreased the computation time by approximately a factor of 20 compared to a single PC with an equivalent processor. For the PRESS sequence, two echo times (TE=20ms and TE=70 ms) were used. The time between the first 90° excitation pulse and the first 180° refocusing pulse was made as short as possible (6 ms). For the STEAM simulations, two echo times (TE=20ms and TE=70 ms) were used, with mixing time (TM) of 20 ms for both. In addition, the STEAM gradient refocusing for the 90° pulses was implemented using additional phase evolution (φ_n) of the density matrix after each localization pulse at the nth spatial point:

$${\phi }_n=2\ast \pi \ast {\tau }_{\mathit{pulse}}/2\ast {\omega }_{\mathit{spinsystem}(n)},$$ (3)

where τ_pulse is the 90° pulse length and ω_{spinsystem(n)} is as defined in Eq. [1].

In LASER, an ideal pulse was used as the 90° excitation pulse. The six refocusing 180° pulses corresponded to the pulse shape depicted in Fig. 1b, with bandwidth of 5.3 kHz. This large bandwidth can be achieved via the use of the adiabatic pulses as described by Garwood et al [20]. The MATPULSE software has the capability to produce this type of pulse in the specific spectrometer tailored format [24]. In addition to the large bandwidth, these pulses are relatively B₁-insensitive, a feature important at higher fields and especially in combination with surface RF coils. One drawback to these pulses is that they have to be used twice for the selection of each orthogonal slice to refocus unwanted phase evolutions produced during application of a single RF pulse. As a result, short echo times (e.g. 20 ms) can not be realistically achieved due to the exceedingly high B_1max requirements (since RF pulses would have to be shortened significantly to fit all 6 localization pulses into short TE sequence). Therefore the simulations were only carried out at TE=70 ms.

2.3. Experimental

Metabolic solutions buffered at pH=7.2 were prepared with the following metabolites (concentration = 50 mM): NAA, mI, Cr, Glu (Sigma Aldrich) and D-Lactate (Fisher Scientific). All phantom solution spectra were acquired out on a Bruker MedSpec 4.0 Tesla system, which used an adaptation of the Siemens Trio software for acquisition, display, and processing. Experiments were performed using an 8-channel volume head coil. All experiments on phantom solutions were performed using 3D localization with PRESS, STEAM and LASER sequences, using timing parameters and RF pulses identical to those for the 3D simulations outlined above.

The water resonance linewidth measured in the phantom was 2 Hz. The data processing steps were performed on the phantom spectra using Matlab^™ based in-house software routines in the following order: 1) dc correction, 2) eddy current correction based on an unsuppressed water spectrum, 3) zero-filling of 2048 points to 8192 points, 4) Gaussian apodization (2 Hz), 5) Fourier Transformation.

3. Results

3.1. PRESS

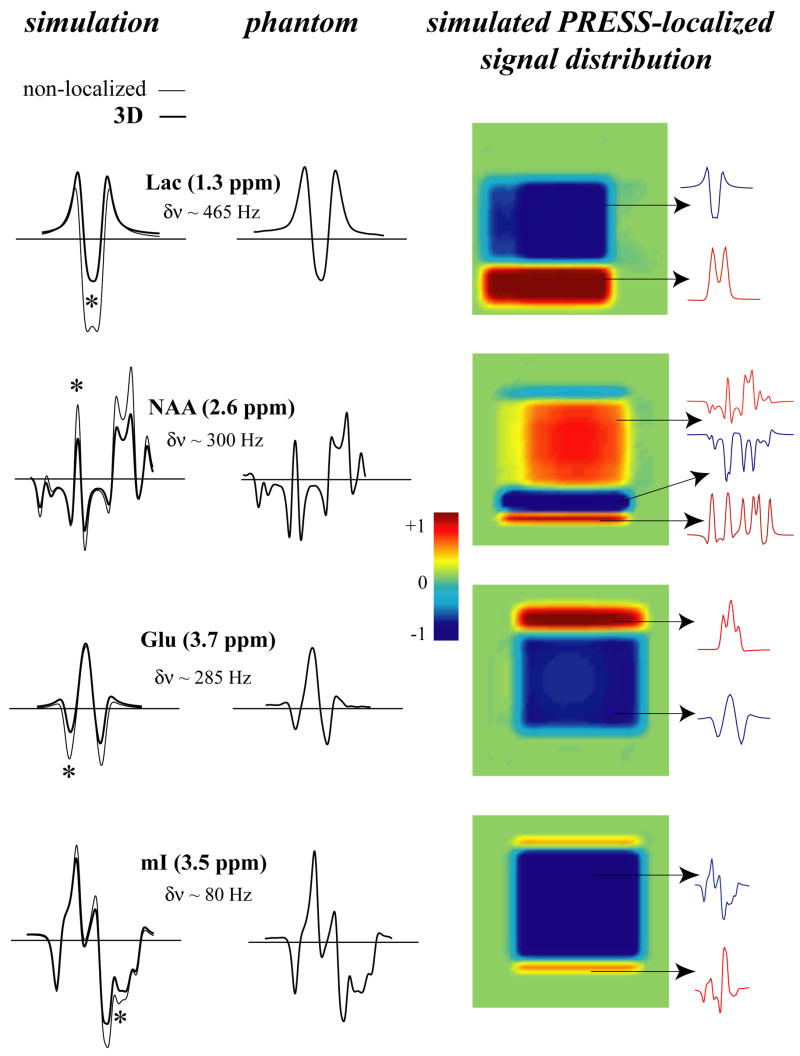
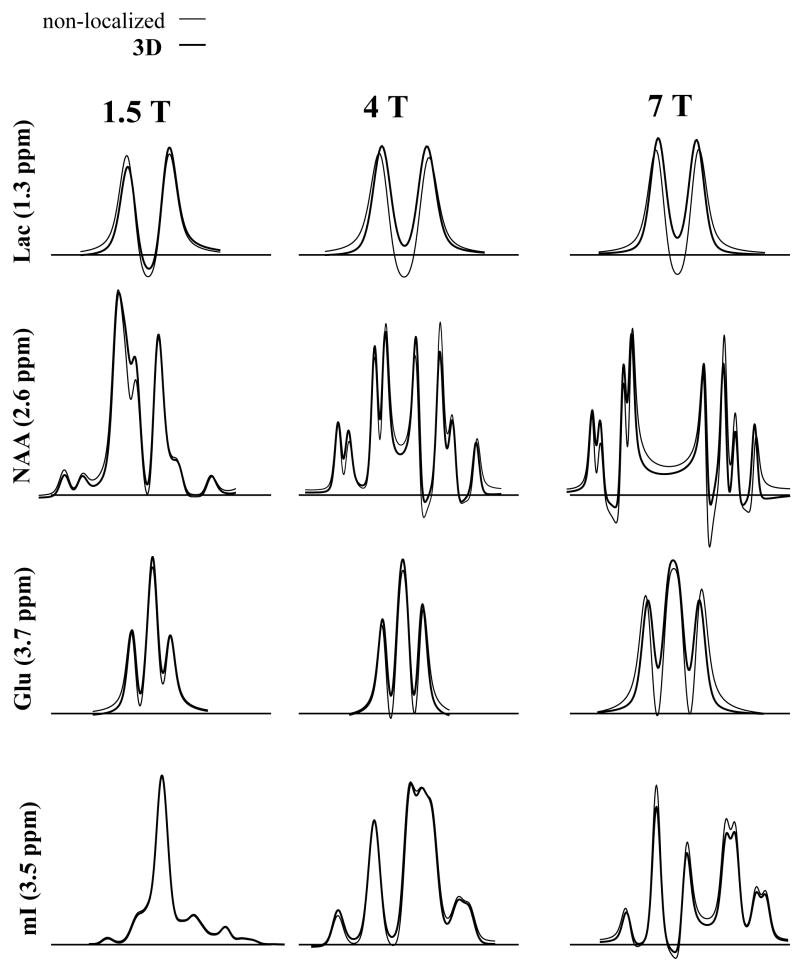
Figure 2 shows the simulation results of PRESS at TE=70 ms for Lac, NAA, Glu and mI. The metabolites are arranged in order of decreasing spectral separation between coupled spins. Lac (at 1.3 and 4.1 ppm) and Glu (at 2.1 and 3.7 ppm) are examples of weakly J-coupled systems, whereas NAA (at 2.5–2.7 ppm) and mI (at 3.3–3.6 ppm) are strongly coupled spin systems at 4 Tesla (although NAA spins are also weakly coupled to another spin at 4.5 ppm). The first column shows ideal (thin line) and 3D (thick line) simulations and the second column shows a corresponding phantom spectrum. Note that the 3D simulated spectra are the results of summed spectra over the entire 3D volume. The third column shows the middle 2D slice from the 3D simulations, where the color intensity represents the integration over the spectral region (10 Hz wide) marked by the asterisk in the simulated spectra. Spectra from the various locations within the localized area are also shown on the right hand side. The weakly coupled spin systems of lactate and NAA form a typical “4 compartment” signal distribution, while NAA and mI contain more compartments. The largest deviation between ideal and localized simulations is observed for lactate and the least for mI. Since the separation between the J-coupled spins relative to the volume selective 180° pulse bandwidth is the largest for Lac and smallest for mI, this is the expected result. The spectra obtained experimentally from the phantom solution are in good agreement with the 3D simulations. The spectra from the 2D simulations, where the excitation 90° pulse is ideal and only the localization effects from the 180° pulses are included, yield very similar results to the 3D simulations (spectra not shown). Figure 3 shows the results of the short echo (TE=20 ms) PRESS simulations at 1.5 Tesla (first column), 4.0 Tesla (second column) and 7.0 Tesla (third column). For short echo time at 4 Tesla, the differences between ideal and localized simulations are still present, but are not as dramatic as compared to the long echo time simulations, especially for mI. This is because J-coupled spins accumulate larger phase differences in the various compartments during J-evolution at longer echo times. However, at the higher field strength of 7 Tesla, the differences between ideal and 3D simulations become more pronounced, even for mI. On the other hand, at 1.5 Tesla, the differences are essentially negligible for all 4 metabolites, providing evidence of why templates generated from ideal simulations worked well for spectral fitting at lower fields for PRESS at short TE.

Figure 2.

Left: A comparison of ideal (thin line) and 3D localized (thick line) PRESS (TE=70 ms) simulations with experimental 3D PRESS-localized phantom spectra of Lac, NAA, Glu and mI. Right: Corresponding signal distribution in a slice from the 3D localized volume. The asterisk (*) denotes the spectral location (10 Hz wide) of the localized signal distribution. The spectral separation between coupled spins is indicated by δν for each metabolite.

Figure 3.

A comparison of ideal (thin line) and 3D localized (thick line) PRESS (TE=20 ms) simulations at different field strengths: 1.5 Tesla (first column), 4.0 Tesla (second column) and 7.0 Tesla (third column).

3.2. LASER

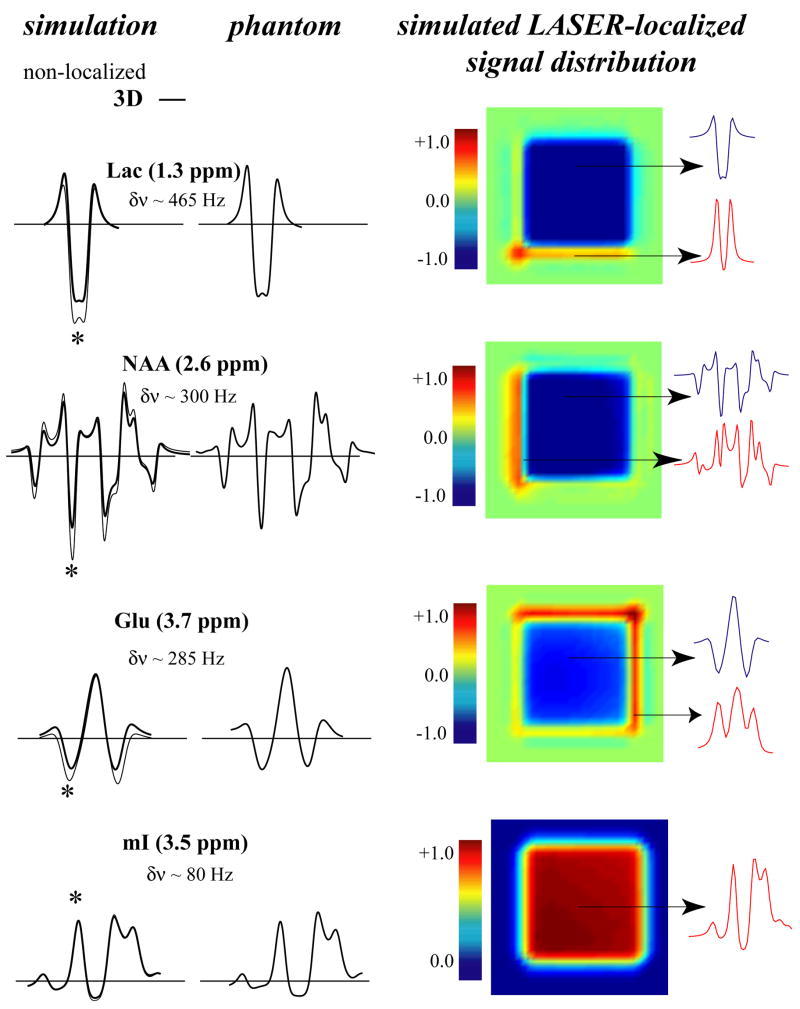
Figure 4 shows the results of the LASER simulations at TE=70 ms. Similar to the PRESS results at TE=70 ms, there are discrepancies between 3D and ideal simulations for Lac, NAA and Glu, but not for mI. The discrepancies between the ideal and localized simulations are not as pronounced as in the case of PRESS. The sizes of the compartments with different spectral phases are also much smaller compared to PRESS, because much higher bandwidth 180° RF pulse are used for localization. The 3D simulations agree very well with the phantom spectra. However when the first two localization 180° pulses were replaced with ideal 180° pulses, to create a 2D localized area, there were slight discrepancies between the phantom and simulations. This is because the first two 180 pulses in LASER (e.g., along the X direction) create additional compartments not observed in PRESS localization which uses a 90° excitation pulse for the first slice selection. In general, the LASER compartment distribution also follows the same trend as observed in PRESS: The higher the spectral separation in Hz between the coupled spins, the larger the compartment sizes and therefore the larger the discrepancy between ideal and localized simulations. For example, between the two strongly coupled spin systems of NAA and mI, only mI does not seem to be affected by the LASER localization, since all coupled spins are in close spectral proximity. However, the strongly coupled spins of NAA in the 2.6 ppm region are affected by the localization, since they are also coupled to the spin at 4.4 ppm, with ~ 300 Hz separation at 4 Tesla.

Figure 4.

Left: A comparison of ideal (thin line) and 3D localized (thick line) LASER (TE=70 ms) simulations with experimental 3D LASER-localized phantom spectra of Lac, NAA, Glu and mI. Right: The corresponding signal distribution in a slice from the 3D localized volume. The asterisk (*) denotes the spectral location (10 Hz wide) of the localized signal distribution. The spectral separation between coupled spins is indicated by δν for each metabolite.

Note also the predominantly “upright” phase of the LASER-localized mI signal compared to PRESS-localized mI at the same echo time. Although LASER localization cannot be performed at short echo times, several J-coupled resonances yield signal intensities and phases closer to short TE spectra (compare with Figure 3, middle column). This is due to refocusing (preservation) of the coupled metabolite patterns by the closely spaced 180° pulses. As originally discussed by Allerhand [25] and more recently demonstrated in localized MRS [26,27], the closely spaced spin echo train can preserve the pattern of J-coupled resonances, provided that the separation of the coupled spins is not too large. Therefore, in contrast to the mI pattern, the Glu spin at 3.7 ppm was not refocused by the LASER pulses (Fig. 4) (and neither was the lactate resonance at 1.3 ppm), exhibiting a similar spectral pattern to PRESS localization at TE=70 ms. However, the Glu resonance at 2.3 ppm was refocused completely in the phantom and simulations exhibited an “upright triplet” signal pattern (not shown). While the region of refocusing is dependent on the separation times between RF pulses relative to the J values and the spectral separation of the coupled spins [25], the results demonstrate that a generalized observation can be made: weakly coupled resonances with large frequency separation are not affected by the train of refocusing pulses, whereas the evolution due to J coupling in strongly coupled resonances is suppressed by LASER and they retain signal patterns typical of shorter TE sequences.

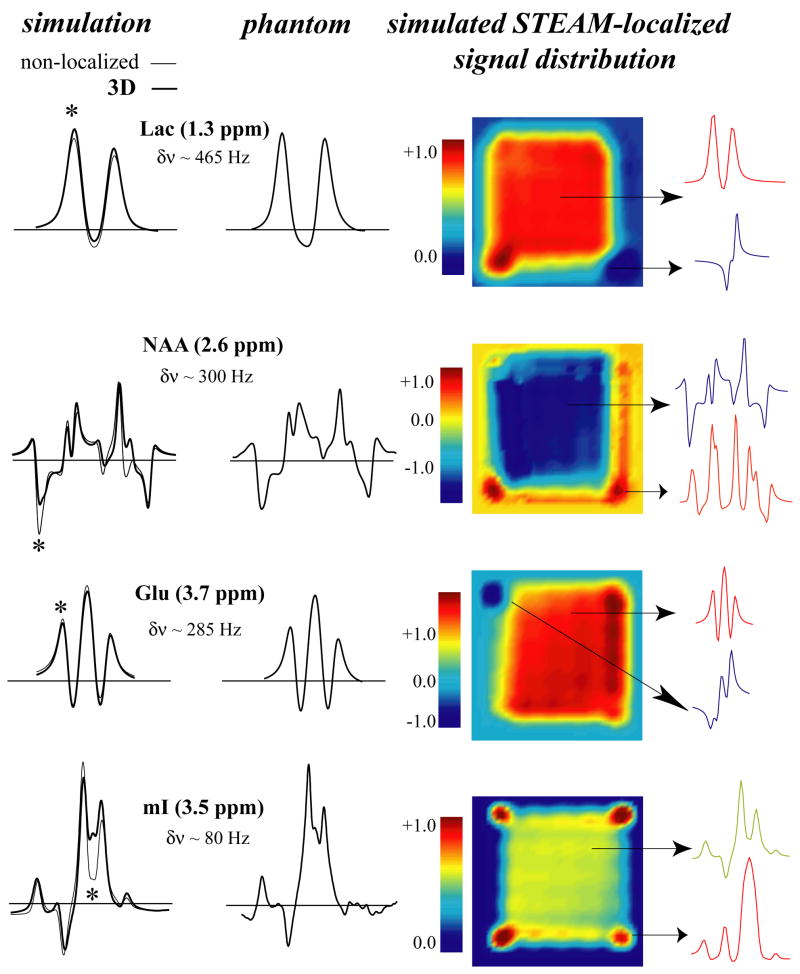
3.3. STEAM

Figure 5 compares simulations and phantom results for STEAM (TE=70 ms) at 4.0 Tesla. The strongly coupled spins of NAA and mI showed a non-negligible difference between ideal and 3D simulations, while for the weakly coupled resonances of Lac and Glu (despite a large separation for Lac coupled spins) the differences were minute. Therefore, there is almost an opposite trend compared with PRESS and LASER, with the smaller spectral separation in Hz between coupled spins (regime of strong coupling) contributing most to the STEAM localization artifacts observed in Fig. 5. The distribution of different compartments for all metabolites localized by 90° pulses was also strikingly different from the PRESS and LASER distributions due to 180° pulses. Especially striking is the asymmetric or “patchy” signal intensity distribution, even in the middle of the localized area. This is primarily due to the non-refocusing nature of the 90° pulses. Short echo time (TE=20 ms) 3D and ideal simulations were essentially in complete agreement with each other and phantom spectra and therefore not shown.

Figure 5.

Left: A comparison of ideal (thin line) and 3D localized (thick line) STEAM (TE=70 ms) simulations with 3D STEAM-localized experimental phantom spectra of Lac, NAA, Glu and mI. Right: The corresponding signal distribution in a slice from the 3D localized volume. The asterisk (*) denotes the spectral location (10 Hz wide) of the localized signal distribution. The spectral separation between coupled spins is indicated by δν for each metabolite.

4. Discussion

This study explored numerical simulations for different cases of localized spectroscopy and compared the results with the experimental solution spectra. The results indicate that the simulation approach extended to experimental pulse shapes and localization provides accurate representation of the resultant spectral amplitudes and phases for fitting of MRS spectra. The factors that exacerbate the phase and amplitude distortion during localization include limited bandwidths of the volume selective pulses, large spectral separations between coupled spins in sequences that use 180° pulses for localization, and longer echo times. While non-localized simulations are sufficient at 1.5 Tesla, the density matrix formalism approach needs to encompass localization effects to generate more accurate a priori information for spectral fitting of high field MRS data.

Among all three sequences at TE=70 ms at 4.0 Tesla, the PRESS sequence showed the greatest spectral variability within the localized volume, resulting in substantial discrepancies between the ideal and localized simulations. The STEAM simulations demonstrated fewer localization artifacts, since 90° pulses can be used with almost 3 times higher bandwidths for the same B_1max as for 180° pulses. The STEAM localization contribution was evident for the strongly coupled spin systems of NAA and mI, but did not affect the weakly coupled systems of Lac and Glu. This is in agreement with STEAM results shown previously by Thompson et al. [15]. At TE=20 ms (TM= 20 ms), STEAM simulations did not demonstrate any localization artifacts, but PRESS-localized spectra contained discrepancies between ideal and localized conditions. Those discrepancies were not as dramatic as at longer TE, but still need to be taken into account. Additional simulations of short TE PRESS at 7.0 Tesla demonstrated that those discrepancies become more severe at higher fields, while PRESS localization at 1.5 Tesla created negligible spatial effects.

The quantification of the J-coupled resonances in vivo requires prior knowledge, which is generated either from metabolite solution spectra or from simulations. Initially, both approaches were shown to be successful at lower fields (at 0.5–2 Tesla), especially after the software libraries (i.e. the GAMMA C++ package, which was used in this study) providing full density matrix capabilities became available. Also, the availability of J-coupling and chemical shift values for a large number of metabolites in the literature further enhanced the value of numerical simulations [15,22]. Early in vivo MRS data collected at higher fields was processed with the LC-Model solution spectra approach [1], most likely due to its ability to capture exact experimental conditions in the basis sets used for fitting, an important feature at higher fields where instrumental limitations can impact the final spectral outcome. However measurement of basis sets from phantom solutions is very time consuming even for experienced spectroscopists, requiring preparation of numerous solutions of metabolites with a precise concentration and pH, and subsequent measurement of spectra from each phantom at a precisely adjusted temperature. The ability of simulations to incorporate realistic experimental conditions and yield spectral patterns in good agreement with phantom solutions as demonstrated in this study makes it a very valuable tool in the arsenal of in vivo MRS researchers, especially for studies at higher field.

There are at least two areas of numerical simulation methods that merit discussion: computing efficiency and consolidation of various J-coupling values and chemical shifts reported in the literature. The full 3D localized simulations demonstrated in this study utilized the power of a multi-processors system and required several hours of computing time for metabolites with more than 4 spins. The required processing time is partially the result of the inefficient matrix routines implemented in the original GAMMA libraries. While the increased availability of reasonably priced multiprocessor/multicore systems provides broader access to such computer intensive simulations, some increase in efficiency of the core operations would be beneficial. The authors are aware of at least two other currently available packages that provide full density matrix simulation capabilities and that were written in a more efficient manner [28,29]. In addition, 2D localized simulations of STEAM and PRESS (using the initial excitation pulse as an ideal 90°) were in excellent agreement with full 3D simulations. In the case of LASER, which uses six 180° pulses for localization, 2D localization simulations were not as accurate as 3D, since the first two 180° pulses along a single gradient axis created additional non-negligible volume compartments. Therefore, in the sequences that use an initial 90° degree pulse for excitation and localization, the simulations can be reduced to 2D localized cases, significantly reducing computing time. Another component of simulations that can be further improved is the consolidation of some discrepancies between J-coupling and chemical shift values reported in the literature. In some cases there are disagreements between various sources, especially with longer echo time simulations, when extensive phase evolution due to J-coupling accentuates even small discrepancies [30]. Additionally, some metabolites undergo fast oxidation (i.e. glutathione, glutamine) when liquid solutions are prepared, rendering extracted J-coupling and chemical shift values inaccurate. In those cases, prior knowledge generated via solution spectra could also be adversely affected. Perhaps a consolidation of the various literature values can be obtained for each metabolite via direct fitting of in vivo data and not from metabolic solutions (e.g. rat brain spectra collected at higher fields). In this particular context, a technique demonstrated by de Graaf et al. [31] in a rat brain in vivo at 11.7 Tesla confirmed all chemical shifts and all but one J-value of NAA resonances reported previously [22]. A small correction (on the order of ~2 Hz, based on the experimental data and simulations) was made to the J-coupling value of the NAA resonance located in the downfield region of the spectrum. This confirms that further improvements in generation of prior knowledge may be made to further enhance the accuracy of simulations of in vivo spectroscopy.

The increased availability of the higher magnetic field strength scanners opens up new possibilities for various localized MRS experiments in vivo and at the same time imposes challenges due to hardware limitations. The localization effects on J-coupled resonances (as originally described by Yablonskiy et al. [2], Slotboom et al. [32]) are further exacerbated at higher fields and affect all localized MR sequences to various degrees. Numerical simulations with full density matrix formalism that incorporate 3D localization can account for these effects which would facilitate generation of accurate prior knowledge for quantification of in vivo metabolites at various magnetic fields strengths. The generalized approach demonstrated in this study applies to various MR sequences (to both weakly and strongly coupled spins) and it is fully compatible with a prior knowledge collected via phantom solutions at physiological pH and temperature. Additional efforts are needed to reduce computation times (while maintaining the generality of the approach) and to consolidate different J-values and chemical shifts reported in the literature.

APPENDIX

Pseudocode for full 3D numerical simulation of LASER, based on GAMMA simulation code

double specfreq = 170.0;//4T Tesla frequency in MHz

int Points1 = 40;//Number of spatial points in X

int Points2 = 40;//Number of spatial points in Y

int Points3 = 40;//Number of spatial points in Z

double bw_pulse_bottom = 7000;//Bandwidth of localization pulse in Hz at the base

double freqoff =-bw_pulse_bottom/2+200;//Start of sweep where 200 Hz is the lowest spin frequency

double freqfinal=bw_pulse_bottom/2+750;//End of sweep where 750 Hz is the highest spin frequency

double Step=(Points1*specfreq)/(freqfinal-freqoff);//Define gradient step

spin_system sys (“SpinSystems/lactate.sys”);//Set up the spin system and operators.

//Begin spatial simulation

for (nss1=0;nss1<Points1;nss1++)//Slice

 {

 for (nss2=0;nss2<Points2;nss2++)

  {

  for (nss3=0;nss3<Points3;nss3++)

   {

   sigma = Iypuls(sys,sigma,90);//Apply an ideal 90

   Udelay = prop(H, ipdhalf);//

   sigma = evolve(sigma,Udelay);//Evolve spins for tau=ipdhalf

   for (int pulse_number = 1;pulse_number < 7;pulse_number++)

    {

    //************* Begin 180 pulses ***************//

  if(pulse_number < 3)

      sys.offsetShifts(freqoff+nss1*specfreq/Step);//Gradient offset in Hz

    if((pulse_number >2) & (pulse_number < 5))

      sys.offsetShifts(freqoff+nss2*specfreq/Step);//Gradient offset in Hz

     if((pulse_number > 4 )

      sys.offsetShifts(freqoff+nss3*specfreq/Step);

      Vol1 = pulse_wave_form.GetUsum(−1);//Propagator for all steps of 180

      sigma = Apply_Crushed_Pulse_y(sys,sigma,Vol1,180)//Apply crushed pulse

     if(pulse_number < 3)

     sys.offsetShifts(-freqoff-nss1*specfreq/Step);//Gradient offset in Hz

    if((2 pulse_number > 2) & (pulse_number < 5))

     sys.offsetShifts(-freqoff-nss2*specfreq/Step);

   if((pulse_number > 4)

     sys.offsetShifts(-freqoff-nss3*specfreq/Step);

   //*************** End of 180s *****************//

   if(pulse_number < 6)

    {Udelay = prop(H, ipdfull);//Interpulse evolution

    sigma = evolve(sigma,Udelay);}//Evolve spins for tau=ipdfull

   else

    {Udelay = prop(H, ipdhalf);//Evolve spins after last pulse

    sigma = evolve(sigma,Udelay);}//Evolve spins for tau=ipdhalf

    }//end pulse_number loop

   }//end nss3 loop

  }//end nss2 loop

 }//end nss1 loop