A context-based theory of recency and contiguity in free recall

Abstract

We present a new model of free recall based on Howard and Kahana’s (2002) temporal context model and Usher and McClelland’s (2001) leaky-accumulator decision model. In this model, contextual drift gives rise to both short-term and long-term recency effects, and contextual retrieval gives rise to short-term and long-term contiguity effects, Recall decisions are controlled by a race between competitive leaky-accumulators. The model captures the dynamics of immediate, delayed, and continual distractor free recall, demonstrating that dissociations between short- and long-term recency can naturally arise from a model that uses an internal contextual state as the sole cue for retrieval across time scales.

The Law of Recency refers to the observation that memories of recent experiences come to mind more easily than memories from the distant past (T. Brown, 1824; Calkins, 1896). Given the ubiquitous nature of recency across time-scales, memory tasks, and stimulus materials, it is not surprising that it has occupied center stage in theoretical analyses of memory over many decades (Crowder, 1976).

Whereas some students of memory have sought a common cause for the varied manifestations of recency (Crowder, 1982; Greene, 1986) others have posited distinct mechanisms for the recency effects observed at short and at long time scales (Atkinson & Shiffrin, 1968). In support of a dual-store explanation of recency, Davelaar, Goshen-Gottstein, Ashkeriazi, Haarmann, and Usher (2005) identified several striking differences between the recency effects observed in immediate free recall and continual distractor free recall. In immediate free recall, participants are asked to recall the list items, in any order, immediately following the last item presentation. In continual distractor free recall, participants are given a demanding distractor task following each list item. After the last period of distraction they are asked to recall the items in any order (see Figure 1 for a graphical description of the free recall tasks).

Figure 1. Graphical illustration of immediate, delayed, and continual distractor free recall.

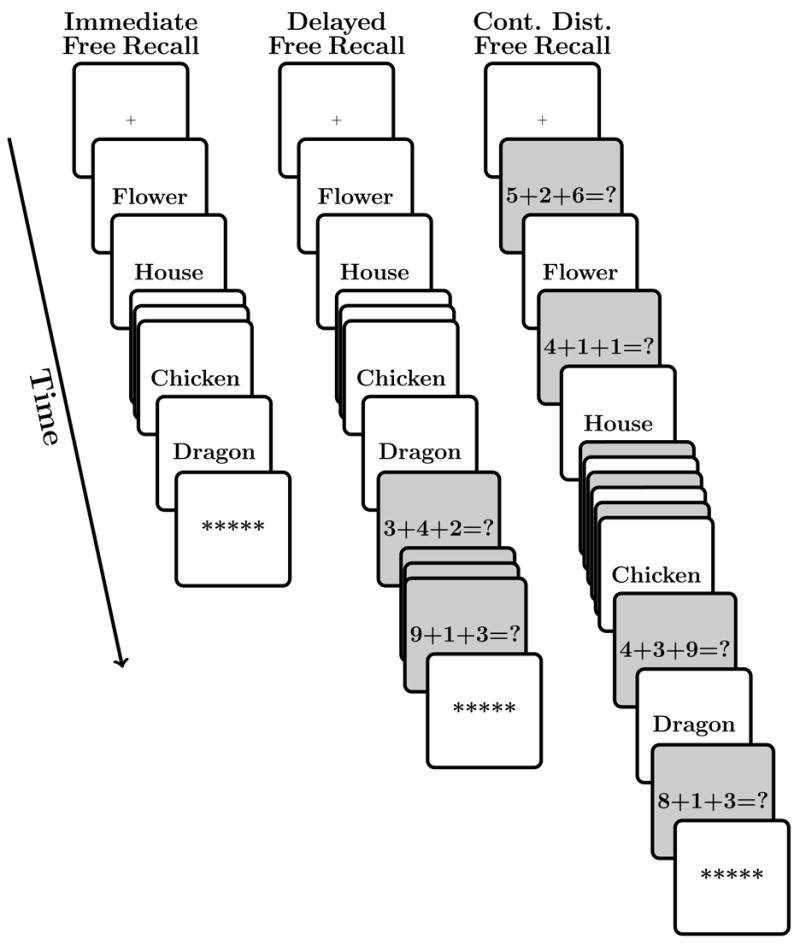
Each trial begins with a fixation cross. A row of asterisks signals participants to recall the items in any order.

Davelaar et al. (2005) suggest that the existence of dissociations between short- and long-term recency calls into question models that hypothesize a general forgetting process underlying recency phenomena observed at different time scales. One popular class of general forgetting models assumes that a time-varying internal context signal gives rise to recency in both short-term and long-term recall tasks (see Kahana, Howard, & Polyn, 2008, for a review). Davelaar et al. (2005) instead propose a model of free recall in which an activation-based short-term store (STS) produces recency in immediate free recall, and a time-varying context signal produces long-term recency via a weight-based long-term store (LTS) in continual distractor free recall.

We next review some of the major empirical phenomena observed in free recall and their relevance for single- and dual-store theories of episodic memory. We conclude the introduction with a discussion of dissociations between immediate and long-term recency effects.

Single- versus dual-store accounts of free recall

In delayed free recall, a filled distractor interval intervenes between the last item and the test, resulting in a dramatic reduction in the short-term recency effect observed in immediate free recall (Glanzer & Cunitz, 1966; Postman & Phillips, 1965). According to dual-store models (e.g., Atkinson & Shiffrin, 1968; Raaijmakers & Shiflrm, 1980; Davelaar et al., 2005), the recency effect in immediate free recall is due to a direct read-out from STS, which has a capacity of approximately 2 to 5 items. When no additional items can be retrieved from STS, recall continues with retrieval from LTS. Although easily accessible, items in STS are extremely sensitive to retroactive interference from incoming information. Consequently, the distractor interval clears items from STS and retrieval in delayed free recall is based only upon LTS.

Because in free recall the order of recall reflects the order in which items come to mind, recall transitions from one item to the next presumably reflect the organization of memory for the list items. To examine the effects of the temporal organization of the list on free recall transitions, Kahana (1996) measured the conditional response probability as a function of lag (lag-CRP). Given that the participant has just recalled the item from serial position i, the lag-CRP indicates the probability that the next item recalled comes from serial position i + lag. Lag-CRP analyses have shown that the contiguity effect, a tendency for participants to recall items from nearby in the list to the just-recalled item, and the asymmetry effect, a tendency for participants to recall items in the forward direction, are extremely robust properties of free recall (see Kahana et al., 2008, for a review).

In much the same way that dual-store models provide a natural account of recency effects in immediate and delayed recall, they also provide a natural explanation of the contiguity effect in immediate and delayed recall. The search of associative memory model (SAM, Raaijmakers & Shiffrin, 1980, 1981; Mensink & Raaijmakers, 1988, 1989; Sirotin, Kimball, & Kahana, 2005; Kimball, Smith, & Kahana, 2007), a detailed implementation of a dual-store model, postulates that connections are strengthened in long-term memory between items that are simultaneously active in STS. 4 contiguity effect arises because items from nearby positions in the list are likely to be co-active in STS. The inter-item associations then provide a boost in the probability of transitioning to a nearby item during retrieval from LTS (Kahana, 1996). It should be noted (that the cooccurance of items in STS does not by itself explain the ubiquitous asymmetrfy observed in the lag-CRP—this asymmetry must be added to SAM as an external constraint.

The ease with which the dual-store model addresses recency and contiguity effects in immediate and delayed free recall would give rise to an almost unquestioned adoption of dual-store models of memory were it not for the discovery of the long-term recency effect in continual distractor free recall (Bjork & Whitten, 1974). In continual distractor free recall, there is a filled distractor interval not only between the last item and the recall test, as in delayed free recall, but also in the interval between the study of each list item. Buffer models of STS cannot account for recency in continual distractor free recall; if the end-of-list distractor in delayed free recall is sufficient to clear STS, then it should also be sufficient to clear STS in continual distractor free recall. Nonetheless, long-term recency effects are robustly observed in continual distractor free recall (Bjork & Whitten, 1974; Tzeng, 1973; Glenberg et al., 1980; Glenberg, Bradley, Kraus, & Renzaglia, 1983; Howard & Kahana, 1999; Thapar & Greene, 1993; Watkins, Neath, & Sechler, 1989; Neath, 1993).

The discovery of long-term recency effects led Crowder (1982) and Greene (1986) to conclude that STS could not sufficiently explain recency effects in free recall. Whereas it is easy to postulate an additional recency mechanism in LTS to account for the long-term recency effect¹, similarities between immediate and long-term recency made it appealing to develop single-store models of memory that account for recency across time scales with a common mechanism.

Temporal distinctiveness models (Murdock, 1960; Neath & Crowder, 1990; Glenberg & Swanson, 1986; G. D. A. Brown, Neath, & Chater. 2007; Nairne, Neath, Serra, & Byun, 1997; Neath & Crowder, 1996) assume that recall of an; item depends not on its absolute recency, but on its relative recency to other list items. According to this view, continual distractor free recall results in larger recency than delayed free recall because the last item in the list is more distinctive in continual distractor free recall due to the fact that the delay in the inter-stimulus interval has placed the other items further into the past. Because the relative spacing of the list is similar in immediate and continual distractor free recall, temporal distinctiveness models can account for the existence of both immediate and long-term recency using the same mechanism. Temporal distinctiveness models often leave the mechanism by which a temporally-varying signal is implemented as an abstract concept; time tags (Yntema & Trask, 1963) or a randomly-varying temporal context (Estes, 1955; Bower, 1972; Murdock, 1997) are two hypothesized candidates. The idea of a time-varying context representation has also been used to explain a wide range of interference phenomena (e.g., Mensink & Raaijmakers, 1988; Kahana, in press).

Like the recency effect, the contiguity effect also persists when items are separated by an interval of distracting activity (Howard & Kahana, 1999, see also Howard, Youker, & Venkatadass, 2008). Following similar logic to that employed in our discussion of the long-term recency effect, STS cannot simultaneously account for the contiguity effect observed in continual distractor free recall and the effect of a delay on the recency effect—if the inter-item distractor is effective at clearing items from STS then adjacent items would never be in STS at the same time in continual distractor free recall.

Howard and Kahana (2002a) proposed the temporal context model (TCM) to account for the pattern of results observed for recency and contiguity effects in free recall across presentation schedules. During study, items are associated with the current state of a gradually-changing representation of temporal context. The recency effect follows because items that were studied more recently are more similar to the time-of-test context. TCM employed a probabilistic rule for selecting which item to recall that was sensitive to the relative activation of the items in the list. The contextual coding process along with the probabilistic choice rule enabled TCM to account for immediate and long-term recency using the same logic as distinctiveness models of long-term recency.

According to Howard and Kahana (2002a), temporal context is not independent of the items being presented. Rather than drifting randomly, as in stimulus fluctuation models (e.g. Estes, 1955; Mensink & Raaijmakers, 1989), context changes from moment to moment in TCM because the items, themselves, drive the evolution of context. This property provides a natural account of contiguity effects—when an item is recovered at test, it reinstates the temporal context active when that item was studied. Because this context overlaps with the encoding context of the items’ neighbors, a contiguity effect results. Because the retrieval rule is sensitive to the relative activation of the list items, TCM predicts a long-term contiguity effect for the same reason as it predicts the long-term recency effect.

Howard and Kahana (2002a) focused on modeling the contextual evolution and retrieval process, noting that TCM lacked much of the machinery needed to account for the major phenomena observed in free recall. To account for these phenomena, additional mechanisms would be needed. For instance, TCM lacked a stopping rule that would determine when recall terminates. It also lacked mechanisms to account for recall latency, as well as rules to avoid repetition of already-recalled items.

The assertion, made by both TCM and the distinctiveness models, that short- and long-term recency could share a common source is not universally accepted. A number of experimental dissociations between short- and long-term recency have been observed. Davelaar et al. (2005) argued that these dissociations could not be readily accounted for by single-store models in general, and TCM in particular.

Here we show that dissociations between short- and long-term recency can be addressed within the framework of context-based recency models without postulating separate short-term and long-term memory stores. Building on Howard and Kahana’s model of temporal context, we present a model of free recall in which cuing with context produces both short-term and long-term recency effects. Our model uses a retrieval rule based on the dynamic decision model of Usher and McClelland (2001). According to this model, each item accumulates strength based on its activation and competes with the other items for recall via lateral inhibition. Using this retrieval rule, recall of an item depends on both its absolute level of activation and its level of activation relative to other list items. As in the classic stimulus sampling theory of Estes (1955, 1959), evolved context in our model can be seen as an activation-based memory representation. However, it is the retrieval of weight-based associations between context arid items that determines retrieval of memories at both short and long time scales.

We start by reviewing the empirical dissociations between short- and long-term recency. We then present an overview of the TCM framework and TCM-A, a model of free recall that uses competing accumulators to retrieve particular items given a contextual cue (Usher & McClelland, 2001). A series of simulations demonstrate that TCM-A can address key dissociations between short- and long-term recency despite the fact that temporal context is the sole cue for recall in both short- and long-term recency experiments. More theoretical concerns about activation-based and weight-based memory are postponed until the General Discussion.

Dissociations between short- and long-term recency

Although there are many commonalities between short- and long-term recency in free recall (e.g. Greene, 1986), there are also a number of empirical dissociations between recency in these tasks. Two dissociations between recency in immediate and continual distractor free recall can be seen by examining the timing and order of participants’ recalls. Although participants exhibit a similar tendency to begin recall at the end of the list in both tasks, they take longer to initiate recall in continual distractor free recall. Second, participants tend to recall several end-of-list items in succession in immediate free recall whereas in continual distractor free recall they tend to jump to earlier list items after recalling one or two items from the end of the list. This dissociation can be seen in the lag-CRP functions: In immediate free recall, the lag-CRP exhibits much stronger contiguity in early than in late output positions (Kahana, 1996). This is not the case in delayed or continual distractor free recall where the contiguity effect is approximately constant across output positions (Howard & Kahana, 1999). A third dissociation can be seen in studies of proactive interference. Whereas the recency effect in immediate free recall is relatively insensitive to proactive interference (Murdock, 1962; Craik & Birtwistle, 1971), the recency effect in continual distractor free recall is reduced under conditions of high proactive interference (Davelaar et al., 2005). Finally, the long-term recency effect, but not the immediate recency effect, is disrupted in patients with ariterograde amnesia (Carlesimo, Marfia, Loasses, & Caltagirone, 1996). Below we discuss each of these dissociations.

Dissociation: Time to first recall

A dissociation between immediate and continual distractor free recall can be seen in the time participants take to initiate recall. In immediate free recall, recall starts quickly with a burst of several items, typically from the end of the list (Kahana, 1996; Nilsson, Wright, & Murdock, 1975). As recall proceeds, interresponse times (IRTs) increase with output position (Murdock & Okada, 1970). Continual distractor free recall does not start with a quick burst of items, but starts slowly in a way that appears to require an effortful search. Analysis of response times from Howard and Kahana (1999) shows that the mean time to initiate recall was 1.04 s in immediate and 2.15 s in continual distract or free recall.

Dissociation: Changes in the contiguity effect with output position

Davelaar et al. (2005) noted that in immediate free recall the contiguity effect measured for the first few recalls Is much more pronounced than the contiguity effect; observed at later output positions (Kahana, 1996; Howard & Kahana, 1999; Kahana, Howard, Zaromb, & Wingfield, 2002), but that this decrease in the contiguity effect with output position is not observed in delayed or continual distractor free recall (Kahana et al., 2002; Howard & Kahana, 1999). According to buffer models, the change in the contiguity effect with output position occurs because participants begin recall by reporting all of the items available in STS (Kahana, 1996; Davelaar et al., 2005). The items in STS at the time of test tend to be from the end of the list. In immediate free recall, these adjacent items are recalled first. Later in recall, responses depend on retrieval from LTS, resulting in a reduced contiguity effect. According to two-store models, retrieval in continual distractor free recall takes place entirely from LTS, so there would be no reason for the contiguity effect to change with output position (Davelaar et al., 2005).

Dissociation: Proactive interference

The short-term recency effect observed in immediate free recall is remarkably insensitive to proactive interference. This point was nicely illustrated by Murdock (1962) who showed that the magnitude of the recency effect in immediate free recall was the same for lists of 20, 30 and 40 items (Murdock, 1974). One might have expected that recall would decrease with increasing list length due to the buildup of proactive interference. In fact, the robustness of short-term recency to proactive interference may be the single most compelling rationale for a short-term memory buffer—no matter how much information a participant has been exposed to over the course of their lives, information presented in the last couple of seconds remains accessible².

Davelaar et al. (2005) presented an experiment in which they observed a reduction in the magnitude of the recency effect in continual distractor, but not in immediate free recall, due to proactive interference from semantically similar items on a previous list. It is reasonable to assume that presenting two lists of semantically similar items effectively increases the list length of the second list, and thus increases proactive interference, due to the semantic associations with the prior list items (e.g.. Underwood, 1983).

Dissociation: Anterograde amnesia

Carlesimo et al. (1996) reported a dissociation between short- and long-term recency, as measured by two tasks given to amnesic and control participants. They tested immediate recency by means of a standard immediate free recall procedure with each of 10 list items presented for 5 seconds. The test for long-term recency was quite different; they had participants solve lists of 10 anagrams with 30 seconds for each anagram. Each anagram was preceded by a 10 second distractor of backwards counting arid the last item was followed by 30 seconds of backwards counting. The behavioral results revealed no difference in recall for the last serial position in immediate free recall, but a decrease in recall relative to controls at all positions in their variant of continual distractor free recall. These results were taken as support for dual-store models of free recall because the amnesics’ presumably intact STS supports recall of recency items in immediate free recall whereas their damaged LTS impairs recall of recency items in continual distractor.

Because the critical comparison of Carlesimo et al. (1996) is between two very different tasks, it is difficult to make strong inferences from their reported dissociation. Furthermore, their use of a very slow presentation rate would allow participants to engage in extensive rehearsal, thus further confounding the relationship between the items’ nominal and functional serial positions (Brodie & Murdock, 1977; Tan & Ward, 2000; Ward, Woodward, Stevens, & Stinson, 2003; G. Brown, Sala, Foster, & Vousden, 2007). Nonetheless, the data are sufficiently interesting to warrant further theoretical investigation.

Overview

Howard and Kahana’s implementation of TCM lacked the mechanisms needed to account for a number of free recall phenomenon, including the key short- versus long-term recency dissociations outlined above. We present a new model that combines the associative framework of TCM with a dynamical decision component. The new model, called TCM-A, replaces the old retrieval rule in TCM with a set of leaky, competitive accumulators representing the activations of the words in the list (Usher & McClelland, 2001). As part of the general class of diffusion models (e.g., Ratcliff, 1978, 2006), the Usher and McClelland (2001) decision model has gained considerable currency in both psychology and neuroscience, providing realistic accounts of behavioral reaction times and neural activity during a wide variety of tasks (McMillen & Holmes, In press; Bogacz, 2007; Bogacz, Usher, Zhang, & McClelland, 2007).

The novel property of TCM-A that enables it to account for the key dissociations between short- and long-term recency is that the accumulator retrieval rule is sensitive both to the relative and absolute activation of items in selecting a candidate item to recall. This, coupled with the gradual change of temporal context across output positions, ensures that the recency effect in immediate free recall extends over several output positions, whereas the recency effect in continual distractor free recall falls off more steeply, affecting primarily the last item.

The next sections provide an overview of the TCM framework arid describe the implementation of TCM-A in detail, followed by the results of simulations compared to data from Howard and Kahana (1999). These simulations show that our elaborated version of TCM can account for the four dissociations described above. We conclude that while a separate working memory buffer may serve other useful cognitive functions (Jonides et al., 2007), it does not appear necessary to propose a mechanism in addition to a gradually-changing state of temporal context to account for the recency and contiguity effects observed in free recall.

TCM with accumulating retrieval dynamics

Howard and Kahana’s (2002) temporal context model (TCM) describes how context is represented and how it evolves as a consequence of item encoding and retrieval. It also describes an associative architecture that links items to context and context to items. In this section we describe TCM-A, a model of free recall which implements the basic assumptions of TCM in a neural network that can flexibly store and retrieve episodic memories. A key component of TCM-A is a retrieval rule based on the Usher and McClelland (2001) competitive leaky-accumulator choice model. We first provide a non-mathematical walkthrough TCM-A’s assumptions and their implications for modeling free recall data. We then provide a more formal treatment of the model and its implementation. In our description of TCM-A below, we will note aspects of the model that differ from the original TCM (Howard & Kahana, 2002a; Howard, Kahana, & Wingfield, 2006).³

Overview of the TCM framework

At the heart of TCM is a representation of temporal context, which is composed of a set of feature values slowly drifting through a high-dimensional feature space. Whereas early theorists modeled temporal context as feature values that change over time due to random fluctuations in the input (Estes, 1955; Anderson & Bower, 1972), in TCM activation of item representations, either during presentation or retrieval, drives the evolution of context.

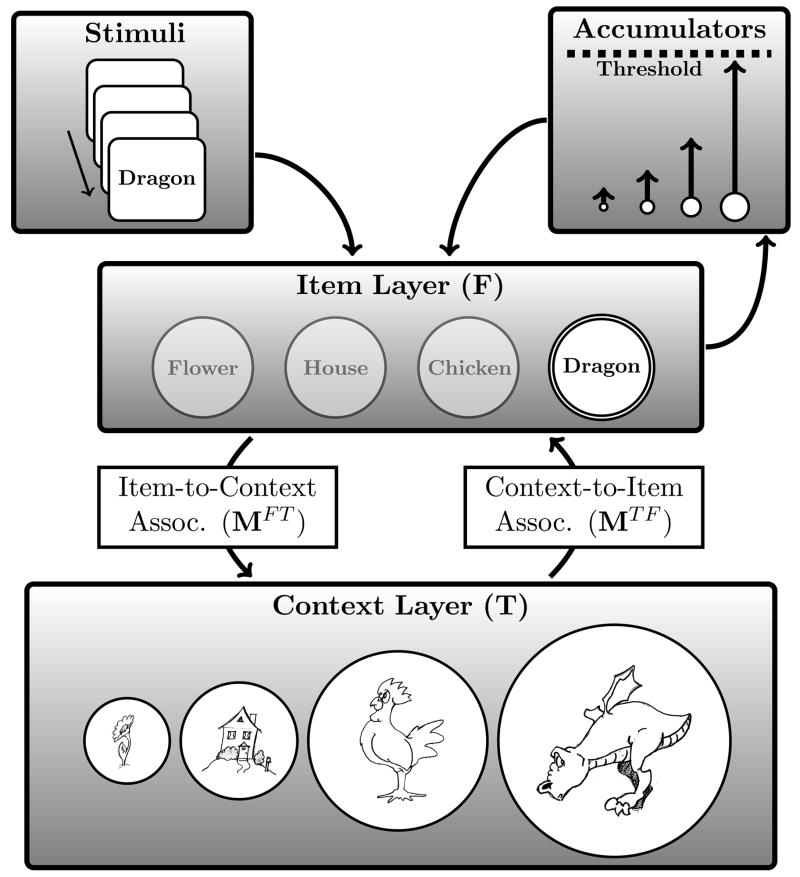
Prior to studying a list, TCM assumes that each list item is associated with a pre-experimental contextual representation. This contextual representation would in general be an amalgam of many prior contexts in which the item has appeared, but for the sake of simplicity, we will assume that all prior contexts combine into a single aggregate representation. As a participant studies each list item, the item activates its pre-experimental context via the stored item-to-context associative connections (see Figure 2).⁴ This pre-experimental context representation is then added to the current state of temporal context, which must first decay to make room for the newly-inserted item. This process, whereby each studied item activates its pre-experimental context, which in turn is combined with the current context, causes the contextual mechanism to drift as each new item is encoded. Because previous states of context are not completely obliterated by incoming information, this induces a correlation in successive states of context.

Figure 2.

TCM-A: Temporal context model with an accumulator-based retrieval rule. TCM-A is composed of three main layers: an item and a context layer, which are connected by associative matrices, and a layer of accumulators that provide a competitive retrieval mechanism. See the main text for a complete description of how these layers interact to store and retrieve episodic memories

To make this more concrete, suppose that a participant studied the list flower, house, chicken, and dragon. When flower is studied, it would activate flower-related information in memory (i.e., its pre-experimental context). This information would enter the current context, indicated by the picture of a flower in the context layer of Figure 2. When house is studied, it would activate house-related contextual information, which would enter the current state of context, weakening the strength of the flower-related information in the evolving context representation. This would continue for each item presentation, so that by the time dragon is studied (as indicated by the double-circle in the item layer of Figure 2), the current state of context would include the pre-experimental contexts of flower, house, chicken, and dragon, with the dragon context being represented more strongly than the chicken context, which in turn would be represented more strongly than the house context, etc (see the context layer at the bottom of Figure 2). By this mechanism, the contexts or thoughts evoked by each studied item push the internal context signal through a high-dimensional space.

As context evolves, the current state of context becomes associated with each studied item. This learning involves the creation of a new association between the state of context when that item was presented and its item representation. This enables subsequent states of context to cue for the item to the extent that it overlaps with this encoding state. In addition, an association is updated between the item representation and the contextual state, such that repeating an item will enable it to recover this newly-learned state of context. As described in more detail below, these context-to-item and item-to-context associations are represented as networks of Hebbian connections in our neural network implementation.

At the beginning of the recall period, the time-of-test context serves as a retrieval cue, activating items via the context-to-item associations stored in memory. By this point, each studied item has been associated with an experimental list context in addition to a pre-experimental context. Because recent list items (e.g., dragon] are most strongly represented in the time-of-test context, cuing with time-of-test context gives rise to greater activation of end-of-list items, which gives rise to the recency effect.

Although many items are activated to some extent by the contextual cue, only one item may be recalled at a, time. The process by which an individual item is selected for recall involves a competition among a set of leaky accumulators that correspond to the items. As suggested by the top-right of Figure 2, each item accumulates strength in the presence of noise based on the degree to which it is activated by the cue context. Item accumulators inhibit other accumulators, until an accumulator corresponding to a not-yet-recalled item crosses a threshold. In this example, the items near the end of the list have the greatest activation, which is indicated by the size of each circle representing an item. Consequently, the accumulators corresponding to end-of-list items grow faster than those corresponding to earlier list items, and have an increased chance of crossing threshold first.

Once recalled, an item is re-presented to the item layer and used to update the current state of temporal context. The retrieval of an item also retrieves the state of temporal context that was present when it was first studied. Consequently, context is updated with a combination of the pre-experimental and newly-learned contextual representations of the just-recalled item. This new state of context now serves as the cue to recall further items.

The pre-experimental contextual features for the just-recalled item provide a forward-asymmetric cue for nearby list items because they were present in context only after that item was presented during encoding. The newly-learned contextual features that were encoded when that item was studied provide a bidirectional cue for nearby list items because those features were part of temporal context both before and after the item was presented. The combined forward-asymmetric and bidirectional cue for subsequent recalls gives rise to the characteristic asymmetric contiguity effect.

This recall process, where the just-recalled item updates the current state of temporal context, which then provides a cue for the subsequent recall, continues until all the items are recalled or time runs out.

Formal description of TCM-A

The evolution of context

The state of context at time step i, t_i, evolves due to the information that is currently being processed by the memory system. Mathematically, TCM-A models the context vector as evolving according to the equation:

$${\mathbf{t}}_i={\rho }_i{\mathbf{t}}_{i-1}+\beta {\mathbf{t}}_i^{IN},$$ (1)

where β is a parameter that determines the rate of contextual drift during encoding, ρ_i is a scaling parameter chosen at each time step such that t_i is always of unit length, and ${\mathbf{t}}_i^{IN}$ is the input at time step i (throughout this article we use bold face letters to denote vectors and matrices), t₀ is the state of context prevailing when the first item, f₁, is presented for study. In TCM-A, as in prior work on TCM, we assume that the vectors representing the studied items, denoted as f_i, are orthonormal. As we will explain below, the input pattern ${\mathbf{t}}_1^{IN}$ is the contextual information retrieved by item f₁. Thus, after f₁ has been studied, ${\mathbf{t}}_1={\rho }_1{\mathbf{t}}_0+\beta {\mathbf{t}}_1^{IN}$. This is the context that prevails when the subsequent item, f₂, is presented.

Hebbian associative memory

TCM-A uses matrices to represent item-to-context and context-to-item associations (see Figure 2). The context-to-item associations are stored in a matrix, M^TF, which allows contextual states to cue items. The item-to-context matrix, M^FT, allows items to recover previous states of context. The input pattern ${\mathbf{t}}_i^{IN}$ that drives the evolution of context in Eq. 1 is calculated from M^FT and the item f_i as:

$${\mathbf{t}}_i^{IN}\propto {\mathbf{M}}^{FT}{\mathbf{f}}_i,$$ (2)

where the proportionality symbol reflects the fact that ${\mathbf{t}}_i^{IN}$ is normalized to be of unit length before contributing to Eq. 1.

In TCM-A we distinguish between pre-experimental and experimentally-learned item-to-context associations, which we denote as ${\mathbf{M}}_{\mathit{pre}}^{FT}$ and ${\mathbf{M}}_{\mathit{exp}}^{FT}$, respectively. These terms are weighted by a parameter γ_FT:

$${\mathbf{M}}^{FT}=(1-{\gamma }_{FT}){\mathbf{M}}_{\mathit{pre}}^{FT}+{\gamma }_{FT}{\mathbf{M}}_{\mathit{exp}}^{FT}$$ (3)

We also distinguish between pre-experimental and experimentally-learned context-to-item associations via ${\mathbf{M}}_{\mathit{pre}}^{TF}$ and ${\mathbf{M}}_{\mathit{exp}}^{TF}$, weighted similarly by a parameter γ_TF:

$${\mathbf{M}}^{TF}=(1-{\gamma }_{TF}){\mathbf{M}}_{\mathit{pre}}^{TF}+{\gamma }_{TF}{\mathbf{M}}_{\mathit{exp}}^{TF}.$$ (4)

This distinction between new (episodic) learning and longstanding (semantic) knowledge enables TCM-A to simulate performance in situations where the mechanisms responsible for new associative learning have been damaged (Carlesimo et al, 1996). A similar assumption made in the eSAM and fSAM models proved crucial for simulating the interacting effects of pre-experimental and new learning in categorized free recall (Sirotin et al., 2005) and in the Deese-Roediger-McDermott false memory paradigm (Kimball et al., 2007).

For simplicity, we fix ${\mathbf{M}}_{\mathit{pre}}^{FT}$ and ${\mathbf{M}}_{\mathit{pre}}^{TF}$ as identity matrices that do not change during the encoding and recall of a simulated list. Clearly, these pre-experimental weight matrices must change over time, but at a much slower time scale than the course of a single simulated list. The use of identity matrices for the pre-experimental weights implies that there is no semantic similarity between items in the list. While pre-experimental inter-item similarity does affect memory retrieval in free recall (Howard & Kahana, 2002b), it is not necessary to build semantic similarity into the model to illustrate differences between short-term and long-term recency effects. Finally, the matrices representing experimental item-to-context associations, ${\mathbf{M}}_{\mathit{exp}}^{FT}$ and ${\mathbf{M}}_{\mathit{exp}}^{TF}$, are set to zero at the beginning of each simulated list and updated to learn the associations between items and context during the list presentation ⁵.

Associations between context and items

TCM-A assumes that items become associated with context. We update a Hebbian outer-product matrix, ${\mathbf{M}}_{\mathit{exp}}^{TF}$, that associates the prevailing context with the presented item’s representation. This follows the equation:

$$\mathrm{\Delta }{\mathbf{M}}_{\mathit{exp}}^{TF}={\phi }_i{\mathbf{f}}_i{\mathbf{t}}_{i-1}^{\top },$$ (5)

where ⊤ denotes the transpose operator (note that the transpose operator bears no relation to our use of t to denote the state of temporal context) ⁶. As described in the Modeling primacy section below, φ_i biases learning depending on the item’s serial position in the list such that items from early serial positions are more strongly encoded. Similar assumptions have been used by computational models to describe primacy effects in serial recall (e.g., G. D. A. Brown, Preece, & Hulme, 2000; Burgess & Hitch, 1999).

Associations between items and context

As with the context-to-item associations, we also increment the Hebbian outer-product matrix, ${\mathbf{M}}_{\mathit{exp}}^{FT}$, that associates the active item to the state of context when that item was presented:

$$\mathrm{\Delta }{\mathbf{M}}_{\mathit{exp}}^{FT}={\mathbf{t}}_{i-1}{\mathbf{f}}_i^{\top }.$$ (6)

As a consequence of this learning in ${\mathbf{M}}_{\mathit{exp}}^{FT}$, recalling an item recovers the state of context prevailing just prior to its initial presentation.

While storing the newly-learned associations between t₀ and f₁, we update the current state of temporal context according to Equation 1. Specifically, ${\mathbf{t}}_1={\rho }_1{\mathbf{t}}_0+\beta {\mathbf{t}}_1^{IN}$. The first time an item is presented, only ${\mathbf{M}}_{\mathit{pre}}^{FT}$ contributes to the retrieved context because the newly-learned association between that item and the experimental context has yet to be stored. For instance, ${\mathbf{t}}_1^{IN}$ will be given by the equation:

$${\mathbf{t}}_1^{IN}={\mathbf{M}}_{\mathit{pre}}^{FT}{\mathbf{f}}_1.$$ (7)

Because ${\mathbf{M}}_{\mathit{pre}}^{FT}$ is an identity matrix and the f_is are orthonorrnal, this means that the input patterns caused by a list of unique items will also be orthonormal. Thus, the state of context following the presentation of f₁ is simply a weighted sum of the prior state of context, t₀, and the representation of f₁. Following the presentation of f₂ we would have ${\mathbf{t}}_2={\rho }_2{\mathbf{t}}_1+\beta {\mathbf{t}}_2^{IN}={\rho }_2{\rho }_1{\mathbf{t}}_0+{\rho }_2\beta {\mathbf{t}}_1^{IN}+\beta {\mathbf{t}}_2^{IN}$. Note that ${\mathbf{t}}_2^{IN}$ will have a larger weight than ${\mathbf{t}}_1^{IN}$ because ρ_i < 1.

The order of encoding operations

In our simulations, when an item is presented during study, we first store the context-to-item association in ${\mathbf{M}}_{\mathit{exp}}^{TF}$ based on the prevailing state of context when that item was presented (Eq. 5). We next calculate t^IN according to Eq. 2, but then update the item-to-context association in ${\mathbf{M}}_{\mathit{exp}}^{FT}$ (Eq. 6) prior to using the t^IN calculated in the previous step to update context (Eq. 1). That is, we do not allow the item-to-context weights to bind an item to the context that it has just retrieved. To some extent, this is simply a matter of convenience—there would be essentially no effect on the simulations we report here if this were not the case.⁷ One potential mechanism whereby items could avoid being bound to their own retrieved context is offered by the hypothesis that theta oscillations give rise to separate encoding and retrieval phases at region CA1 of the hippocampus (Hasselmo, Bodelon, & Wyble, 2002), Siekmeier, Hasselmo, Howard, and Coyle (2007) showed how this mechanism could be used to modulate encoding and retrieval of temporal context in much the same way we describe here.

Contextual states are used to retrieve item representations

According to dual-store models of free recall, retrieval begins by first reporting the items in STS, or those items whose activations exceed a threshold (Raaijmakers & Shiffrin, 1981; Sirotin et al., 2005; Davelaar et al., 2005). It is this buffer mechanism that is responsible for the recency effect in immediate free recall and the recency dissociations between immediate and continual distractor free recall. Unlike these models, TCM-A assumes that recall begins by using the time-of-test context as a retrieval cue. The time-of-test context serves as a cue for recall of items via M^TF.

Multiplying M^TF by the context vector, t_test, retrieves a superposition of the items f_i, each activated to the extent that the time-of-test context overlaps with both their encoding and pre-experimental contexts stored in M^TF:

$$\begin{array}{ll}\stackrel{\sim }{\mathbf{f}}& ={\mathbf{M}}^{TF}{\mathbf{t}}_{\text{test}}\\ & =(1-{\gamma }_{TF})({\mathbf{M}}_{\mathit{pre}}^{FT}{\mathbf{t}}_{\text{test}})+{\gamma }_{TF}({\mathbf{M}}_{\mathit{exp}}^{TF}{\mathbf{t}}_{\text{test}}),\end{array}$$ (8)

where the second line follows from the decomposition of M^TF (Eq. 4). Multiplying Eq. 8 from the left with ${\mathbf{f}}_i^{\top }$ we find that the activation of each item f̃_i is

$${\stackrel{\sim }{f}}_i=(1-{\gamma }_{TF})({\mathbf{t}}_i^{IN}·{\mathbf{t}}_{\text{test}})+{\gamma }_{TF}({\mathbf{t}}_{i-1}·{\mathbf{t}}_{\text{test}})$$ (9)

because ${\mathbf{f}}_i^{\top }{\mathbf{M}}_{\mathit{pre}}^{TF}={\mathbf{t}}_i^{IN}$ and ${\mathbf{f}}_i^{\top }{\mathbf{M}}_{\mathit{exp}}^{TF}={\mathbf{t}}_{i-1}$. Thus, items that were originally seen in a study context (t_i−1) is similar to the time-of-test context will be more strongly activated than those that were originally seen in a completely dissimilar context. Similarly, recently-studied items will be more strongly activated because they will have greater representation (via ${\mathbf{t}}_i^{IN}$) than early list items in the time-of-test context vector. This latter mechanism enables a recency effect in the absence of new learning at either ${\mathbf{M}}_{\mathit{exp}}^{TF}$ or ${\mathbf{M}}_{\mathit{exp}}^{FT}$. This property will turn out to be crucial in our account of anterograde amnesia.

We fixed γ_TF at 0.8 (except for the amnesia simulations), which indicates that the item activations derived from the time-of-test context are based more on the newly-learned experimental context-to-item associations than on the pre-experimental associations. Although one could imagine that participants might dynamically bias retrieval to favor pre-experimental/sernaritic or newly-learned experimental/temporal associations, which would be equivalent to changing γ_TF during the recall period, we do not consider such biasing effects in this manuscript.

Accumulator-based retrieval mechanism

In TCM-A, we replaced the Luce choice retrieval rule used in previous implementations of TCM with a set of competitive, leaky accumulators as described in the Usher-McClelland model of perceptual decision making (Usher & McClelland, 2001). The Usher-McClelland accumulator model has a number of desirable properties, including the ability to model competitive choice processes with realistic reaction times.

The item activations f̃ derived from the current state of context (Equation 8) provide the input to the accumulators, scaled by the coefficient of variation (C_V) of the item activations, defined as the standard deviation divided by the mean. The C_V serves as a measure of dispersion in the input to the accumulators, scaling the input so the accumulators can optimally decide between the retrieval choices. To ensure that only relevant inputs are considered in the determination of the input dispersion, items whose activations are below a minimum activation (f̃_i < α_min) are not included in the calculation of the C_V. If the C_V is greater than one, then the input is of high variance relative to its mean (i.e., the input is highly dispersed) and is scaled up to allow the accumulators to make a faster decision. Conversely, if the C_V is less than 1, then the input’s variance is low relative to its mean (i.e. the input is less dispersed) and item activations are scaled down, giving the accumulators more time to differentiate between the items. In our simulations of immediate and delayed free recall, the C_V factor is typically less than one and scales the inputs down at the start of recall, whereas in simulations of continual distractor free recall, the C_V factor scales the inputs up at the start of recall. Finally, if the C_V is undefined or zero, as is the case when the standard deviation or mean across item activations is zero, the C_V remains unchanged from the previous recall or is set to 1 if there have been no previous responses.

At the start of recall, the accumulators x are initialized to zero. They then evolve over the course of a retrieval attempt according to the following equations:

$$\begin{array}{l}{\mathbf{x}}_s=(1-\tau \kappa -\tau \lambda \mathbf{L}){\mathbf{x}}_{s-1}+\tau C_V\stackrel{\sim }{\mathbf{f}}+\epsilon \\ {\mathbf{x}}_s\to \mathit{max}({\mathbf{x}}_s,0),\end{array}$$ (10)

where x_s is the new state of the vector of accumulators across all list items at retrieval time step s, C_Vf̃ is the scaled vector of inputs to these accumulators (provided by TCM-A from the current state of context), κ is a constant controlling the strength of recurrent inhibition, λ is a constant controlling the strength of lateral inhibition, L is a lateral inhibition matrix with components L_ij = (1 − δ_ij), where δ_ij is the Kronecker delta, which equals 1 if i = j and 0 otherwise, ε is a vector of normally-distributed, random variables with mean zero and standard deviation σ, and τ scales the rate of growth of the accumulators at each time step. The second line reflects a component-wise comparison between x_s and zero such that none of the components of x can go below zero to prevent negative activations. The equations for the accumulators are exactly as presented in Usher and McClelland (2001) with the exception that rather than a two-choice response, we have l accumulators corresponding to the l items in the list.

The accumulators grow according to Equation 10 until an accumulator crosses a threshold Θ when this happens, the item corresponding to the accumulator that crosses threshold is recalled. The recalled item is used to update the contextual cue and thus C_V and f̃. Although all accumulators continue to compete across the course of recall, if an accumulator for a recalled item crosses threshold it is reset to zero without being recalled, thus precluding it from being repeated.⁸

The retrieval process for subsequent recalls

When an item f_i is recalled, TCM-A retrieves a combination of that item’s pre-experimental context via ${\mathbf{M}}_{\mathit{pre}}^{FT}$, as well as the item’s experimental context (the state of context when the item was presented) via ${\mathbf{M}}_{\mathit{exp}}^{FT}$. These two contextual representations combine by means of Eqs. 2 and 3 to form the input

$${\mathbf{t}}_i^{IN}=\left[(1-{\gamma }_{FT}){\mathbf{M}}_{\mathit{pre}}^{FT}{\mathbf{f}}_i+{\gamma }_{FT}{\mathbf{M}}_{\mathit{exp}}^{FT}{\mathbf{f}}_i\right]$$ (11)

that contributes to the new state of context calculated via Eq. 1.

Depending on the value γ_FT, ${\mathbf{t}}_i^{IN}$ can be biased towards the newly-learned experimental context, which provides a bidirectional cue to items from a similar temporal context, or towards the pre-experimental context, which provides a forward-asymmetric cue for words that were studied after the recalled item. Consequently, the bidirectional and forward-asymmetric cues for recall, which give rise to TCM-A’s ability to capture contiguity effects in the data, are mediated through associations between items and context and not direct item-to-item associations. Once updated, the new context then serves as the cue for the next recall in the same way that time-of-test context served as the cue for the first recall.

Stopping rule

The criterion for terminating recall is an essential ingredient for modeling serial position effects that was absent from the original TCM implementation. In TCM-A, the accumulators provide a natural stopping rule that is analogous to the time-limits imposed on participants in free recall experiments. Specifically, we assume that recall ends after a fixed number of accumulator time steps. In the subsequent simulations, this value is fixed at 600 time steps.

Modeling distractors

The arithmetic distractors employed in delayed and continual distractor free recall are modeled as orthogonal vectors that cause context to drift at a rate β_dist. Although distractor items drive context, we assume that they do not give rise to any modification of the ${\mathbf{M}}_{\mathit{exp}}^{FT}$ and ${\mathbf{M}}_{\mathit{exp}}^{TF}$ weight matrices. This assumption seems reasonable as participants have no reason to learn the distractors. Distractor intervals also differ from item presentations and recalls both in their duration and in the amount and/or type of information being processed. For instance, during a 30 second distractor interval participants may be solving ~15–20 arithmetic problems, which in turn could produce a larger change in context than a single item presentation.

Modeling primacy

Numerous studies have demonstrated that the two main sources of primacy effects in free recall are an increased tendency to rehearse items from early serial positions throughout the list presentation (Rundus, 1971; Murdock & Metcalfe, 1978; Tan & Ward, 2000) and increased attention or decreased competition during the study of early list items giving rise to better encoding (Sederberg et al., 2006). Howard and Kahana (1999) employed fast presentation rates and orienting tasks during encoding, which presumably attenuated rehearsal and, in turn, the primacy effect. Still, small primacy effects remained, which often manifested as an increase in the probability of initiating recall with the first item in the list and a higher probability of recalling items from early serial positions, both with respect to middle list items. Not wanting to complicate TCM-A by including a rehearsal mechanism during encoding, we chose to model primacy as an exponentially decaying boost in the learning rate for early serial positions. This encoding boost, is folded into the learning rate φ_i in Equation 5:

$${\phi }_i={\phi }_s{e}^{-{\phi }_d(i-1)}+1,$$ (12)

where φ_s + 1 determines the size of the primacy effect at the first serial position and φ_d controls the rate of decay of the primacy effect with each additional list item.

Simulations of experimental data

Table 1 provides a summary of the free and fixed parameters in TCM-A, organized into three categories. The Base category contains the parameters relevant to the theoretical foundation of TCM. The Primacy category lists the parameters specific to our implementation of primacy in the model. Finally, the Accumulator category lists the parameters from the Usher and McClelland (2001) decision model that determines which item is recalled given a set of activations. We allowed the free parameters to vary over a wide range that, based on the equations of the model, encompassed the range of observed behaviors. Similarly, the fixed parameters were selected prior to simulations to be of reasonable values based on the model equations.

Table 1. Summary of free, and fixed parameters in TCM-A.

Fixed parameters have only a single value denoted in the Range column.

Category	Parameter	Description	Range
TCM Base	β	Rate of contextual drift at item encoding and retrieval.	0.0–1.0
	βdist	Rate of contextual drift due to a distractor.	0.1–1.0
	γFT	Relative weight of pre-exp. to exp. context (item-to-context).	0.0–1.0
	γTF	Relative weight of pre-exp. to exp. context (context- to- item).	0.8
Primacy	φs	Primacy scale factor.	0.0–5.0
	φd	Primacy decay rate.	0.0–5.0
Accumulator	κ	Strength of recurrent inhibition.	0.0–0.9
	λ	Strength of lateral inhibition	0.0–0.9
	σ	Standard deviation of accumulator noise.	0.0–0.8
	θ	Recall threshold.	1.0
	τ	Rate of growth at each time step.	0.5
	αmin	Minimum item activation for inclusion in CV scaling.	.0001

Our goal was to produce a reasonable qualitative description of dissociations between short- and long-term recency. This approach has several advantages over attempting to find excellent quantitative fits by separately estimating parameters for each experimental condition being studied. First, it avoids the tendency to overfit the model to certain phenomena, which would would prevent the model from simultaneously capturing the trends observed across multiple experiments. In addition, it ensures that the model and not the parameters are doing the work in producing the pattern of dissociations observed across multiple experimental conditions.

We employed a genetic algorithm (GA) to fit the immediate, delayed, and continual distractor free recall conditions of Experiments 1 and 2 in Howard and Kahana (1999). The genetic algorithm starts with a large population of candidate model parameter sets (that span the entire free parameter space in a multidimensional grid), and, thus, is largely immune to local minima. At each generation, the GA simulates the individual parameter sets and calculates the root mean squared deviation (RMSD) from the behavioral data. These data include the serial position curve, the probability of first recall, and the contiguity effect as seen in the lag-CRP functions from both the immediate and delayed free recall conditions of Experiment 1 and from both the delayed and continual distractor free recall conditions from Experiment 2. The best fitting parameter sets from each generation evolve to form the next generation until reaching a stable state. We evolved a population made up of 8000 individuals, which we culled to 1000 individuals after 50 generations. These 1000 runs typically took 50 additional generations to stabilize at a single set of parameters that provided approximate fits to all critical conditions. We then performed minor adjustment of the parameters by hand to achieve a better qualitative description of aspects of the data missed by the genetic algorithm.

Modeling short-term and long-term recency

Our simulation results are organized as follows. First, we fit TCM-A to serial position curves, recency effects, and contiguity effects from immediate, delayed, and continual distractor free recall tasks reported in Experiments 1 and 2 of Howard and Kahana (1999). Using a single parameterization to fit data from all three tasks and from both experiments, we show that TCM-A also accounts for dissociations between immediate and long-term recency, including the dissociation in the contiguity effect (see Davelaar et al., 2005). Further simulations using the same parameter values account for the differential effect of proactive interference on immediate and long-term recency (Davelaar et al., 2005). Finally, we show that TCM-A can account for the differential effect of amnesia on immediate and long-term recency (Carlesimo et al., 1996).

Simulating recency and contiguity in immediate, delayed, and continual distractor free recall

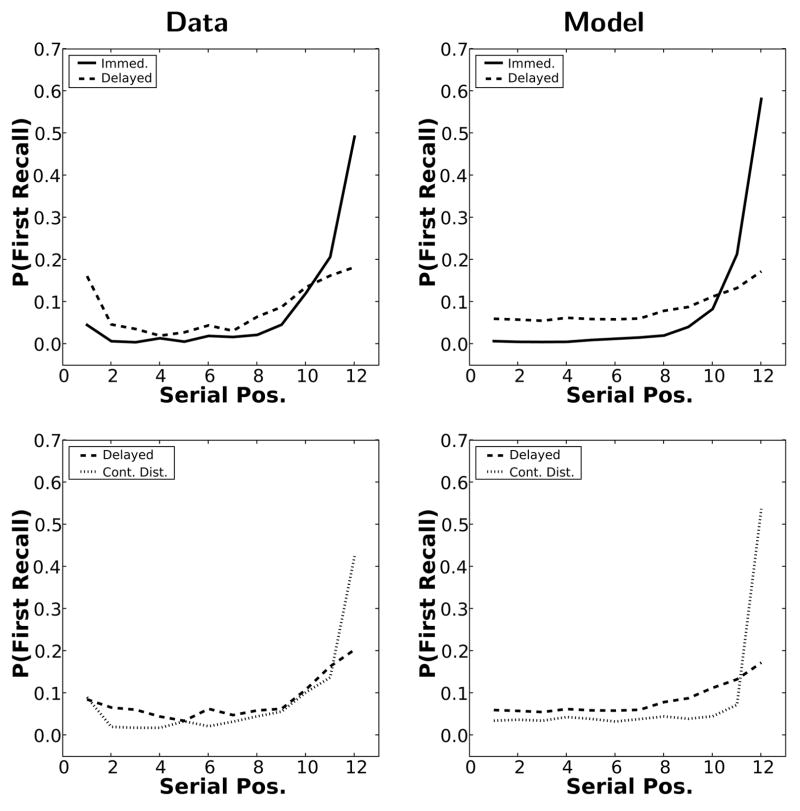
Our first goal was to assess whether TCM-A could reproduce the basic features of the serial position curve across immediate, delayed, and continual distractor free recall. Figure 3 shows the probability of recall as a function of serial position for the behavioral data and model simulation. TCM-A reproduces the major features of the serial position curve in immediate free recall (top row, Figure 3 solid line), illustrating a strong recency effect and a modest primacy effect. By simulating a distractor following the study list, TCM-A was able to capture the attenuated recency observed in delayed free recall (Figure 3 dashed line). Notably, the difference between immediate and delayed free recall is much greater at the end than at the beginning of the serial position curve. Although the model parameters were fixed between experiments, we plot the delayed condition (dashed line) to provide a point of reference between experiments (top and bottom). In fitting data from Experiment 2, TCM-A captured the relative behavior of the serial position curve in both delayed (Figure 3, bottom row, dashed line) and continual distractor free recall (Figure 3, bottom row, dotted line). TCM-A illustrates both the reduced overall level of recall at early serial positions in the continual distractor paradigm and the increased recency effect.

Figure 3. Serial position curves.

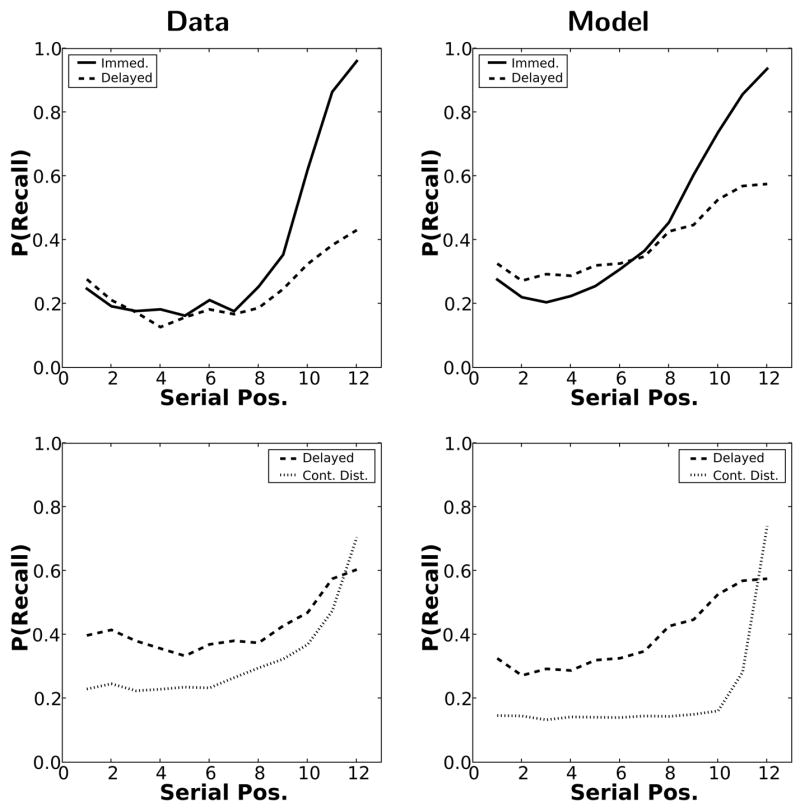
Behavioral data (left) from Howard & Kahana (1999) and model simulations (right) of the corresponding free recall conditions. Top: Immediate (solid line) and delayed (dashed line) free recall from Exp. 1. Bottom: Delayed (dashed line) and continual distractor (dotted line) free recall from Exp. 2. Note that the simulated fits to the delayed condition (dashed line) are repeated in the top and bottom because we did not allow parameters to change between experiments.

Whereas the serial position curve collapses data over the dynamics of the retrieval process, one can separately examine the way participants initiate recall and the way they make transitions. The probability of first recall (PFR Hogan, 1975; Laming, 1999), a serial position curve calculated only for the first item recalled, illustrates participants’ tendency to initiate recall with one of the terminal list items. As first shown by Deese and Kaufman (1957) the recency effect is closely related to participants’ tendency to begin recall at the end of the list (see also Kahana, 1996; Howard & Kahana, 1999). Figure 4 shows PFR curves generated by the same simulations used to generate the serial position curves in Figure 3. These curves illustrate that participants’ tendency to initiate recall at the end of the list was very strong in both immediate and continual distractor free recall, but much weaker in delayed free recall. As the PFR functions are strikingly similar in both immediate and continual distractor free recall, this analysis illustrates the persistence of recency across time-scales. TCM-A provides a good qualitative fit to both the overall form of the PFR and to the changes in the PFR across distractor schedules.

Figure 4. Probability of first recall.

Behavioral data (left) from Howard & Kahana (1999) and model simulations (right) of the corresponding free recall conditions. Top: Immediate (solid line) and delayed (dashed line) free recall from Exp. 1. Bottom: Delayed (dashed line) and continual distractor (dotted line) free recall from Exp. 2.

The foregoing analyses show that TCM-A successfully accounts for the qualitative form of both the serial position and PFR functions across immediate and delayed free recall. TCM-A was also able to predict the recovery of recency (both in relative and absolute levels) in continual distractor free recall.

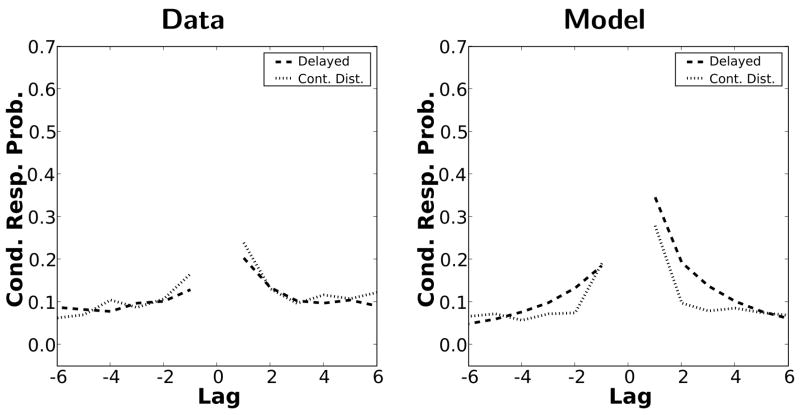
Another striking feature of free recall is the contiguity effect as seen in the lag-CRP analysis of Kahana (1996). Whereas dual store models account for contiguity based on the co-occurrence of items in STS, contiguity in TCM arises because recall of an item recovers its associated temporal context, which is similar to neighboring list items. Because retrieval is competitive, TCM predicts contiguity across time scales so long as the distractors separating the list items are unrelated to the list items (Howard & Kahana, 2002a). As shown in Figure 5, the lag-CRP curves generated from the same simulations depicted in Figures 3 and 4 account for similar levels of contiguity and asymmetry seen in both delayed and continual distractor free recall.

Figure 5. Conditioned response probability.

Behavioral data (left) from Howard & Kahana (1999) and model simulations (right) of delayed (dashed line) and continual distractor (dotted line) free recall from Exp. 2.

Summary of parameters

Table 2 reports the model parameters (eight free) that produced the fits shown in Figures 3, 4, and 5. The contextual drift rate during item presentations and retrievals (β) is moderately fast, which gives rise to the sharp contiguity effect observed in Figure 5. Similarly, the contextual drift during a distractor interval (β_dist) is quite large, meaning that the distractor interval, which may contain multiple math problems, has as large an effect on the previous context vector as several item presentations would have. The value of γ_FT indicates that the relative contributions of pre-experimental and experimental item-to-context associations are nearly equivalent (there is a slight bias towards pre-experimental context.) The scale and decay of primacy (ϕ_s and ϕ_d) provide a strong boost for the first item in the list, but this boost decays quite quickly for subsequent serial positions, dropping from ~ 2.66 for the first item to ~ 1.23 for the second item, which is close to the asymptotic value of 1. For the accumulator, we required the lateral inhibition λ to be equal to the leak (decay) rate κ resulting in accumulators that follow a drift diffusion process (Ratcliff, 1978); this has been shown to be desirable when fitting reaction times of decision processes (Bogacz, Brown, Moehlis, Holmes, & Cohen, 2006; McMillen & Holmes, In press; Smith & Ratcliff, 2004). Finally, the relatively high variance of the accumulator’s noise parameter enables remote transitions during recall as this is the only source of variability included in our simulations.

Table 2. Best fitting parameters for TCM-A simulations.

Parameters marked with an * were fixed. Parameters in parentheses were used for the amnesic simulations.

Category	Parameter	Value
TCM Base	β	0.62676
	βdist	0.97607
	γFT	0.44542 (0.0)
	γTF	0.8 (0.0) *
Primacy	φs	1.65538
	φd	1.98112
Accumulator	κ	0.62000
	λ	0.62000
	σ	0.29934 (0.28284)
	Θ	1.0*
	τ	0.5*
	αmin	.0001*

Dissociations between short- and long-term recency

The preceding simulations demonstrate that TCM-A can explain the basic recency and contiguity phenomena across conditions with a single set of parameters. In particular, TCM-A is able to describe the commonalities between short- and long-term recency, and the analogous similarity between contiguity effects observed in delayed and continual distractor free recall; both of which are expressed in relative probabilities of recall. Using the same model, and the same set of parameters, we now demonstrate that TCM-A is also able to account for the major dissociations between short- and long-term recency. The following sections demonstrate TCM-A’s ability to capture these dissociations using gradually-changing temporal context as the sole retrieval cue to initiate recall across conditions. In fact, temporal context, governed by the equations described above, is the sole retrieval cue at all recall attempts.

Time to first recall

Although it has not been explicitly reported before, it is well-known to investigators examining immediate and continual distractor free recall that the recall latency to the first response differs across these conditions. Figure 6 illustrates the model’s ability to capture this dissociation with the latencies to initiate recall in the immediate, delayed, and continual distractor free recall conditions for both the, behavioral data from Howard and Kahana (1999) and the simulations. Although the immediate and continual distractor free recall data are taken from different experiments, the delayed free recall conditions from Experiments 1 and 2 of Howard and Kahana (1999) provide a reference point for the comparison. The fact that the delayed free recall conditions exhibit comparable response times suggests that there is a meaningful difference between latencies in the immediate and continual distractor free recall conditions.

Figure 6. Time to first recall.

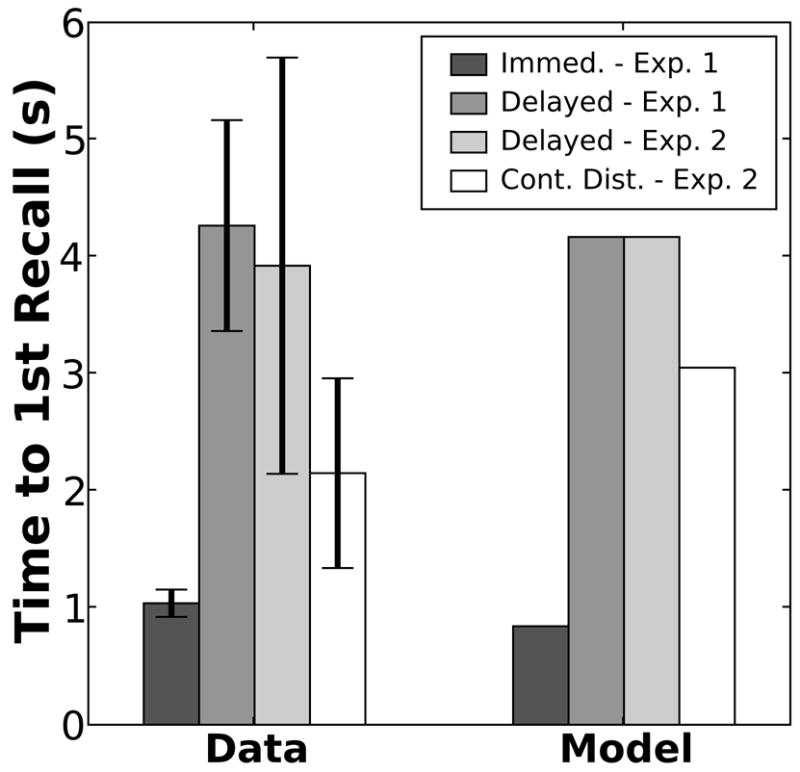
Data and model fits of the time, in seconds, until the first recalled item. White bars indicate the time to the first recall in continual distractor free recall, while dark grey bars provide the time to the first recall in immediate free recall. The intermediate grey bars show the time to first recall in the delayed free recall conditions of Exps. 1 and 2 from Howard & Kahana (1999) as a reference. Note, model output is in time steps, scaled by 40 to match the behavioral data. Error bars are 95% confidence intervals.

This finding reflects a key advantage of TCM-A. The accumulators are sensitive to both the relative activations of the list items and to their absolute level of activation. In particular, the greater overall level of activation for end-of-list items in immediate free recall causes the accumulators to reach threshold more quickly than in continual distractor free recall. Note that if there is a limited amount of time for recall, faster recall latencies translate into a higher probability that some item is recalled within the time limit.

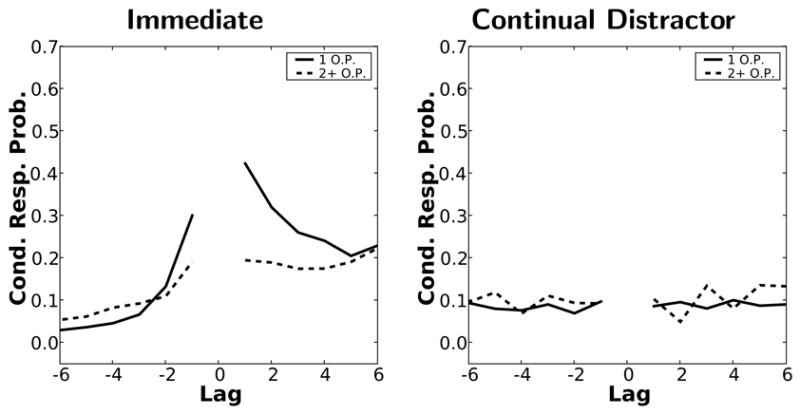
Contiguity effects in early output positions

The contiguity effect in immediate free recall is much stronger at the first couple of output positions than it is later in recall (Kahana, 1996). This change in the shape of the lag-CRP with output position is not observed in either delayed or continual distractor free recall (Howard & Kahana, 1999), Figure 7 demonstrates that TCM-A can account for the decline in the contiguity effect across output positions seen in immediate free recall and the lack of such a change in the contiguity effect across output positions in continual distractor free recall. The top row of Figure 7 shows that TCM-A captures the reduction in the contiguity effect between the first output position (solid line) and later output positions (dashed line) in immediate free recall. Figure 7 (bottom) shows that TCM-A correctly predicts the absence of any change in the contiguity effect across output positions in continual distractor free recall. The dissociation. was observed in the same simulations that generated the serial position curves, PFRs and lag-CRPs above.

Figure 7. Conditional response probability by output position.

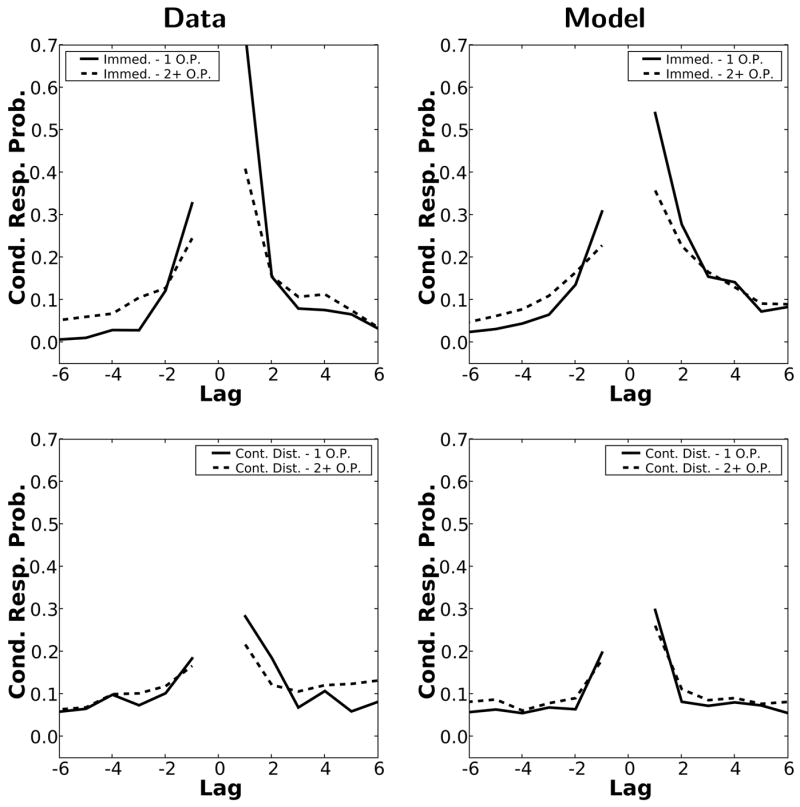
Lag-CRPs of the first (solid line) and then remaining (dashed line) output transitions for behavioral data (left) from Howard & Kahana (1999) and model simulations (right) in the immediate free recall condition of Exp. 1 (top) and the continual distractor free recall condition of Exp. 2 (bottom).

Proactive interference

Davelaar et al. (2005) showed that although the short-term recency effect, as measured by the probability of recall of end-of-list items, was not sensitive to proactive interference, the long-term recency effect was. We examined whether TCM-A. can account for the dissociation between the effect of proactive interference on short-and long-term recency by re-running the simulations reported above with lists of varying length. The items at the end of the longer lists are subject to more proactive interference from preceding list items than items at the end of shorter lists. As illustrated in Figure 8, TCM-A correctly predicts that the probability of recall for the recency part of the serial position curve remains relatively constant in immediate free recall (left) but declines with the same increase in list length in continual distractor free recall (right).

Figure 8. Proactive interference effect.

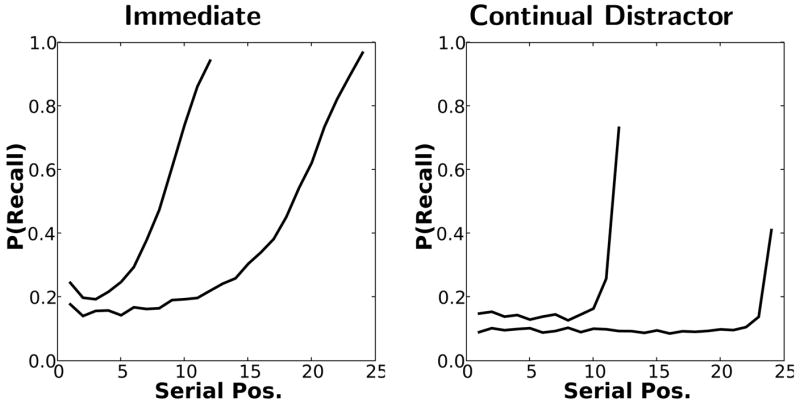
Model simulations of serial position curves illustrating the effect of increasing the list length in immediate free recall (left) versus continual distractor free recall (right).

Anterograde amnesia

Carlesimo et al. (1996) examined the effect of anterograde amnesia, on both immediate and continual distractor free recall Both amnesics and controls exhibited strong recency effects in both tasks. Although amnesics recalled substantially fewer words in both tasks, their recall of recency items was comparable to that of controls in immediate free recall. In continual distractor free recall, however, amnesics recalled fewer words than controls at all serial positions.

We hypothesize that the effect of anterograde amnesia on memory can be described by a disruption in the ability to associate an item with its temporal context and for an item to recover its temporal context when repeated. In other words, we assumed that no learning took place at $M_{\mathit{exp}}^{FT}$ and $M_{\mathit{exp}}^{TF}$, i.e. γTF = γFT = 0, for our simulated amnesia patients. In addition, we assumed that the accumulator-based retrieval process would exhibit less variability in amnesics than in controls. Decreasing the variability of the accumulators (i.e., reducing the standard deviation of the noise, σ, in Equation 10) reduces the probability of spontaneous fluctuations above threshold in the absence of a real memory signal. Consequently, it will take longer, on average, for any item to jump above the recall threshold for amnesics. The assumption that amnesics exhibit decreased accumulator noise relative to controls makes sense if one assumes that at least some of the noise is the consequence of variability in the strength of the memory signal. Because we have not yet expanded TCM-A to include variability in item-to-context or context-to-item associations, or in the structural similarity among items in semantic memory, the stochastic nature of the retrieval process is the only source of variability in our model. As such, increasing variability in the accumulators is functionally analogous to increasing variability in goodness-of-encoding or semantic structure within the list. In the General Discussion we discuss enhancements to TCM-A that include encoding variability and pre-experimerital semantic associations between items, either of which might account for the explicit noise decrease in our simulations.

Besides the changes to the learning and variability parameters, all other aspects of the model—the gradual change of temporal context from moment-to-moment, the pre-experimerital weights (i.e. $M_{\mathit{pre}}^{FT}$ and $M_{\mathit{pre}}^{TF}$), and the retrieval dynamics of the accumulators—were left intact. Notably, we hypothesize that the rate of contextual drift, parameterized by β, is unchanged in amnesia patients. The equivalence of the rate of contextual drift, coupled with intact pre-experimental context-to-item associations, means that there will be little to no difference in the effectiveness of the test context as a cue for recall between amnesics and controls. As a result, amnesics should exhibit recency effects that are similar to that of controls in both immediate and continual distractor free recall.

In contrast, our model predicts that contiguity effects are dependent on contextual retrieval and the formation of new context-to-item associations. Because these processes are hypothesized to be disrupted in amnesics, this predicts that the lag-CRP should be flat for amnesics in both continual distractor free recall and at later output positions in immediate free recall. Our account of short-term recency exploits the fact that the accumulators are sensitive to the absolute magnitude of activation, allowing the strong end-of-list cue available in immediate recall to cause the recall of several recency items. This immediate recall of multiple recency items results in a boost to the contiguity effect at early output positions in immediate free recall Because contextual drift is unchanged in amnesics, the time-of-test context is identical to that of controls. Given that multiple recency items are strongly represented in the end-of-list context in immediate free recall, this will give rise to a boost in the probability of recalling more than one item from the end of the list at the start of recall. Thus, even in the absence of contextual retrieval, we expect that amnesics would also exhibit a peaked contiguity effect at early output positions in immediate recall.

Although probability of first recall and lag-CRP curves are not available for the Carlesimo et al. (1996) study, we generated them for our simulated amnesics. Because we are not attempting a quantitative fit of the Carlesimo et al. (1996) data, we have left all experimental parameters (list length, delay intervals, etc.) unchanged from our simulations of the Howard and Kahana (1999) data. The curves shown for simulated control subjects are identical to those shown in Figures 3 and 4.

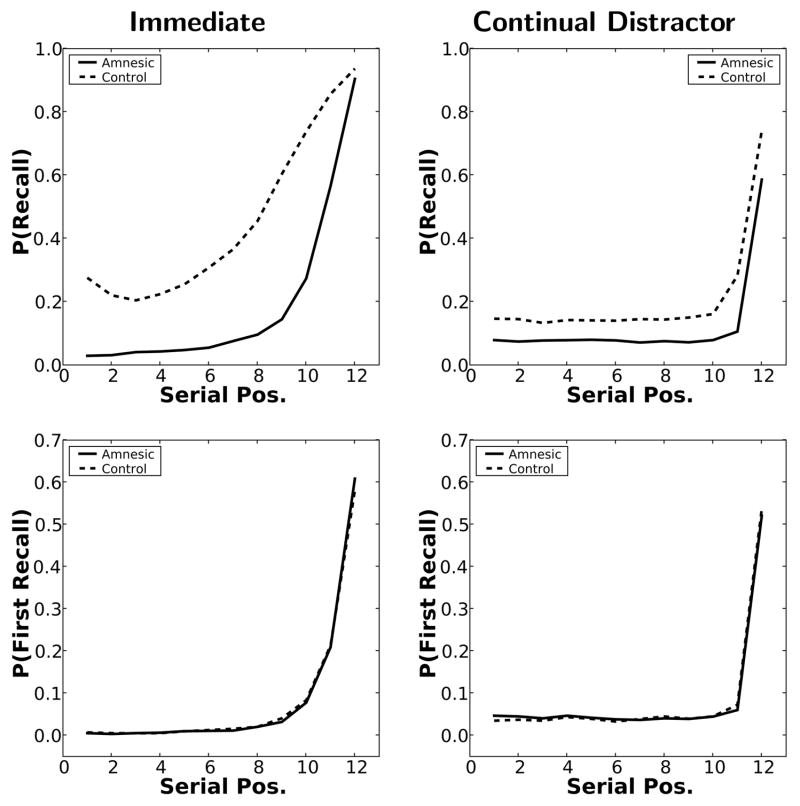
As can be seen from the top panel of Figure 9, TCM-A correctly predicts that the overall level of recall drops for amnesics in both immediate and continual distractor free recall. Although the recency effect, as measured by the PFR curves in the bottom panel of Figure 9, is nearly identical for controls and amnesics in both immediate and continual distractor free recall, the probability of recalling the last item in the list decreases only in the continual distractor simulations. As outlined above, this pattern of results is consistent with previous studies (Carlesimo et al., 1996; Marks & Cermak, 1998), which have shown that recency persists in amnesic participants, but that the overall probability of recall drops at all serial positions in continual distractor free recall.

Figure 9. Effects of amnesia on probability of recall.

Serial position curves (top) and probability of first recall (bottom) showing simulated effects of amnesia (solid) versus controls (dashed) in immediate free recall (left) and continual distractor free recall (right).

In contrast with the predictions for both overall recall levels and the probability of first recall, TCM-A produced dramatic differences in the lag-CRP in the simulated amnesics across distractor conditions. The simulated amnesics showed a peaked lag-CRP at the first output position in immediate free recall but a flat lag-CRP at later output positions (Figure 10, left). In contrast, the contiguity effect persisted across output positions in the simulated control participants (see Figure 7, right). In continual distractor free recall, the simulated amnesics showed a flat lag-CRP both early and late in output.

Figure 10. Effects of amnesia on conditional response probability.

Conditional response probability by output position curves showing simulated effects of amnesia in immediate free recall (left) and continual distractor free recall (right). Just as in Figure 7, these panels compare the lag-CRP from the first output position (solid) to all other output positions (dashed), but for the simulated amnesics.

The fact that our amnesia simulations resulted in a peaked lag-CRP early in immediate, but not in continual distractor free recall reflects an important dissociation between short- and long-term recency. The greater absolute levels of activation resulting from end-of-list context in immediate free recall is sufficient to drive recall of several end-of-list items. In contrast, the absolute level of activation due to end-of-list context in continual distractor free recall is relatively weaker, such that it does not affect multiple retrieval attempts.

Essential properties of the retrieval rule

TCM-A’s ability to capture the dissociations between short- and long-term recency results from the retrieval rule generating several fast recalls from the end of the list in response to the strong end-of-list cue in immediate free recall. Here we describe how our parameterization of TCM-A produces the dissociations described above.

Figure 11 displays the input to the accumulators (C_Vf̃) derived from the time-of-test context for each item as a function of serial position (see Equations 9 and 10). The inputs in both immediate and continual distractor free recall show a strong recency effect. However, the absolute magnitude of the inputs is smaller in the continual distractor condition. This difference in magnitude is due to the distractor delay in continual distractor free recall, which gives rise to a smaller overlap between the time of test context and the encoding context of the list items (Howard, 2004).⁹ The overall scale of the accumulator growth due to the input is largely determined by the standard deviation of the noise term, σ, which took on a value of ~ 0.3 in our simulations (see Table 2). Given that the only sources of accumulator growth are the input and the noise (see Equation 10), if the noise is much larger than the input it will mask the effect of the input. Inspection of Figure 11 shows that while the activation of several items is near or above σ when immediate recall is initiated, only the last item in the list has an activation on the order of σ in continual distractor free recall.

Figure 11. Accumulator input as a function of serial position.

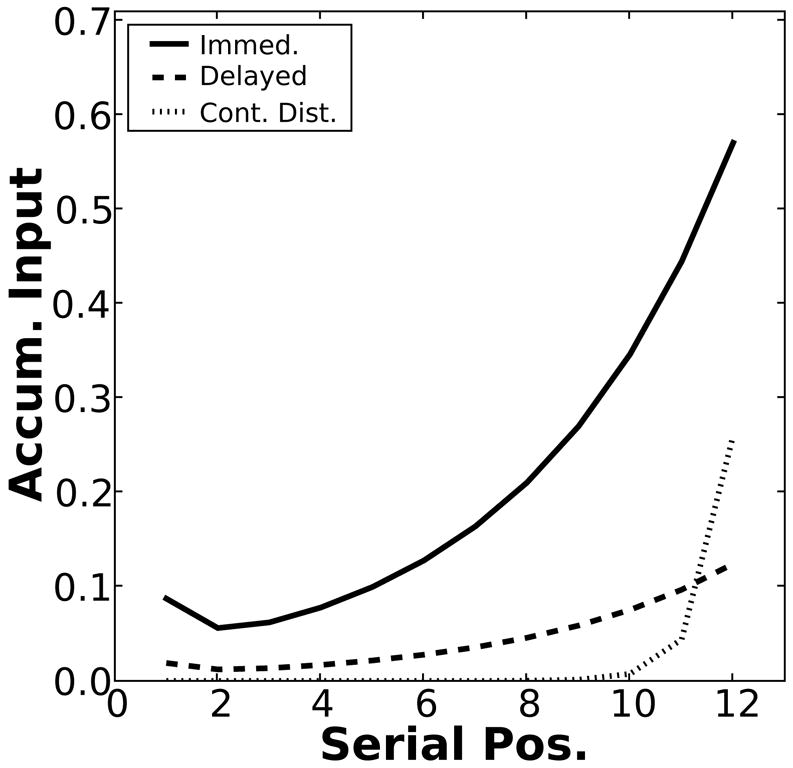
Accumulator input for immediate, delayed, and continual distractor free recall conditions for the first output position.

The absolute difference in the level of activation at the initiation of immediate compared to continual distractor free recall leads to the predicted differences between the short-and long-term recency effects. For instance, the greater magnitude of the activations in immediate free recall means that the accumulators reach threshold more quickly, accounting for the difference in time to initiate recall. Critically, the greater absolute level of activation of several end-of-list items in immediate free recall enables TCM-A to recall several end-of-list items at the start of the retrieval period. Although context is assumed to evolve during retrieval as well as during list presentation, the strong end-of-list cue that is present when immediate recall is initiated persists, weighted by ρ, as part of the cue for the second recall. Consequently, the strong residual activation from the end-of-the list items in immediate free recall combines with the reinstated context to provide a stronger cue for recall than retrieved context would alone. Thus, the average input to the accumulators for the second output in immediate free recall is still higher for items from the end of the list than for other items, giving rise to the enhanced recall probability for end-of-list items.

For the parameters used in these simulations, residual activation in the accumulators between responses is not contributing to the recency dissociations. The original motivation for using the accumulators in TCM-A was the expectation that non-recalled recency items in immediate free recall would have an increased probability of being recalled in quick succession because they would all be close to threshold when any one of them was recalled. However, for the parameters used in these simulations, resetting all the accumulators to zero following each recall had no effect on the simulated results.¹⁰ The dissociations between short- and long-term recency observed in the simulations thus do not depend on persistent activation of items across retrieval attempts, but rather reflect properties inherited from the rules for contextual evolution and recovery provided by TCM.

General Discussion

The TCM-A model assumes that a gradually-changing context representation serves as the sole retrieval cue throughout immediate, delayed, and continual distract or free recall We have shown how TCM-A not only captures the standard serial position, recency, and contiguity effects (Figures 3 to 5), but also accounts for several key dissociations between short- and long-term recency. These dissociations include the findings of faster recall initiation in immediate as compared with continual distractor free recall (Figure 6), more local recall transitions among recently studied items in immediate than in continual distractor free recall (Figure 7), significantly greater proactive interference in continual distractor than in immediate free recall (Figure 8), and differing effects of anterograde amnesia on immediate and continual distractor free recall (Figures 9 and 10).

The gradually-changing context representation in TCM-A cues recall of items using a combination of pre-experimental (e.g. $M_{\mathit{pre}}^{TF}$) and newly-learned (e.g. $M_{\mathit{exp}}^{TF}$) weight-based memories. Due to the temporal evolution of this context representation, and its associations with the studied items, recent items are activated more than remote items when cued with time-of-test context. This relative advantage for recent items gives rise to the recency effect observed both in immediate and continual distractor free recall tasks. Although the relative activations of recent as compared with remote items depends primarily on the relative timing of item presentations (which is constant across immediate and continual distractor free recall) the absolute magnitude of the activations is substantially greater in immediate than in continual distractor free recall. It is this difference in absolute activations that enables TCM-A to account for the dissociations between immediate and long-term recency.

The associative framework of TCM-A

Following study or recall of an item, the retrieval of pre-experimentally learned and newly-learned associations combine to update the current state of context. During recall the current state of context acts as the sole cue for retrieval of its associated item representations. As items are presented for study, TCM-A stores new experimental associations between items and context, but pre-experimental associations are not updated. Although these encoding and retrieval processes have separate components, it is overly simplistic to think of any piece in isolation as a store that holds memory traces.

Consider what would happen if we were to follow the process of learning far beyond the time scale of a single list. In this case, learning of item-to-context and context-to-item associations would build up over time to describe the set of contexts in which an item has been presented. However, at some point, it would seem necessary for the labile “experimental” component of these associative matrices to become the fixed “pre-experimental” component of the associative matrices. This would allow the model to account for the finding that in amnesics some “long-term memories” are intact, although the formation of new “long-term memories” is impaired.

In this sense, the associative framework of TCM-A may fit well with the theory of complementary learning systems, which posits that there are fast and slow learning mechanisms in the brain, working in concert to learn and store information (McClelland, McNaughton, &; O’Reilly, 1995). The fast system, which is comprised of the hippocampus and other medial temporal lobe structures, is able to learn associations quickly, but is unable to store these representations for long periods of time. Over time, learned associations are transferred to the cortical system, which learns slowly, but holds lasting representations of our experience. This type of model (see also Alvarez & Squire, 1994) has often been proposed to account for the standard model of consolidation in amnesia (Eichenbaum, Otto, & Cohen, 1994; Squire, 1992, but see Nadel & Moscovitch, 1997, 2001).

Short-term memory and temporal context

The equation describing the change of context from moment-to-moment in TCM-A (Eq. 1) is reminiscent of the correlated contextual fluctuations of variable context models (Anderson & Bower, 1972; Mensink & Raaijmakers, 1988; Murdock, 1997). These correlated vector states can be seen as an activation-based memory in the sense Davelaar et al. (2005) used the term. Indeed, Howard, Fotedar, Datey, and Hasselmo (2005) noted that a very close analogue of Eq. 1, with persistent neural activity representing the current state of context, could be implemented in a neurally realistic simulation that relied on known properties of cells in the entorhinal cortex (Egorov, Hamam, Fransen, Hasselmo, & Alonso, 2002; Fransén, Tahvildari, Egorov, Hasselmo, & Alonso, 2006) and cortical networks (Chance, Abbott, & Reyes, 2002; Chance & Abbott, 2000).

In TCM-A, fluctuations in temporal context are not random, but are caused by the sequence of presented and recalled items and the retrieval of their associated contexts. Thus, one might view context as being conceptually analogous to an activation-based memory. To see why this is so, consider what would happen if contextual learning were turned off (mathematically, suppose γFT = 0) so that each time an item is presented it causes the same pattern of input to the temporal context vector. Because there is a one-to-one correspondence between this input pattern and the item being presented, we can think of these patterns as a representation of the item itself. In this case, the temporal context vector contains a weighted sum of the patterns of recently presented items.

There are two salient differences between t_i; and traditional buffer models. One difference is that in TCM-A, the input patterns do not drop out in an all-or-none fashion, but decay gradually as more information comes in. This property enables TCM-A to describe recency and contiguity effects over different time scales with a single retrieval mechanism (see also Howard & Kahana, 2002a). The other salient difference is that in TCM-A, the patterns caused by an item do not, in general, stay constant over multiple repetitions of the item, but rather change to reflect the changing contexts in which the item has been presented. It is this latter property that enables TCM-A to describe contiguity effects (see also Howard et al., 2006), including those observed in short-term recency (Howard, Vankatadass, Norman, & Kahana, 2007). Viewed in this light, the distinction between a temporal context vector and a traditional STS is not so much about a fundamental distinction between activity-based storage vs something else, but rather about the way activity-based storage actually works. Of course this is not to suggest that these particular distinctions do not have important implications for how we understand memory, but that they do not have a direct bearing on the question of whether activity-based storage contributes to the recency effect. Indeed, TCM-A and traditional buffer models make distinct predictions about how memory should behave at both short- and long-time scales. In the next section we review some of the evidence in support of contextual-based memory from both behavioral and electrophysiological studies.

Evaluating predictions of temporal context across time scales

Howard et al. (2007) compared behavioral predictions of TCM-A with those of buffer models in describing associative effects in the early stages of the immediate recency effect. In this study, some lists contained an item from the middle of the list that was repeated just before the test. Howard et al. (2007) observed a boost for neighbors of the original presentation of the repeated item in early recall transitions, and even in the initiation of immediate recall. While TCM-A predicts these associative effects as a natural outcome of using temporal context as the cue to initiate immediate recall, buffer models of immediate recency would predict no such effect. One would not expect the predictions of TCM-A about immediate recency to be borne out over those of a buffer model if gradually-changing temporal context was not the cue for the initiation of immediate free recall.

Whereas Howard et al. (2007) confirmed behavioral predictions of TCM over a few seconds, Howard et al. (2008) evaluated behavioral predictions over a much longer time scale. Participants were presented with forty-eight lists one at a time for immediate free recall. At the end of the session, they were given a surprise final free recall test in which they were instructed to recall as many items as possible from all the lists in any order they came to mind. In examining the final free recall data, Howard et al. observed a recency effect that extended six to eight lists into the past. Moreover, Howard et al. observed a contiguity effect across lists in the final free recall data that extended about ten lists in each direction. A particularly striking feature of these data was the similar functional form observed for the recency and contiguity effects across time scales, suggesting that a similar cuing mechanism operates over short and long time scales, as predicted by TCM-A.

TCM-A naturally explains the findings of Howard et al. (2008) if the temporal context vector is allowed to change gradually across lists in addition to changing gradually within each list. If the temporal context vector is an activation-based memory in the medial temporal lobe, as hypothesized by Howard et al. (2005), this means that there should be neural activity in the medial temporal lobe that persists across lists.

Manns, Howard, and Eichenbaum (2007) examined the ensemble firing patterns of cells in the hippocampus while rats performed a judgment of recency task on lists of odors. In their experiment, rats were given “lists” of five odors. At the end of each list, the animals were presented with two odors from the list and rewarded for approaching the one that was presented earlier in the list. The rats were implanted with electrodes in the hippocampus that were able to record simultaneously from multiple, as many as several dozen, hippocampal neurons. Manns et al. (2007) treated these ensembles as vectors of neural activity and examined the way the ensemble firing pattern changed across time periods when the animal was “studying” the list odors. Manns et al. (2007) showed that the neural activity vector was more similar for study events that occurred closer together in time than for events that occurred further apart in time (see Eq. 1). That is, all other things being equal, the ensemble patterns for study events corresponding to nearby serial positions within a particular list were more similar to each other than ensemble patterns corresponding to study events from serial positions further apart in the list. Remarkably, Manns et al. (2007) also observed that the neural ensemble response changed gradually across lists as well, with measurable changes in the ensemble vector extending over essentially the entire recording session. This long-range correlation observed in the neural activity vector across lists in the rat hippocampus parallels the long-range correlations predicted for the temporal context vector across lists of words based on behavioral results from humans (Howard et al., 2008). These recent findings suggest that the TCM framework captures some basic insights about how episodic memory is encoded and retrieved at both short and long time scales.

Ingredients for a more complete model of free recall

Although TCM-A can account for many of the major findings in free recall, the model is still missing a number of mechanisms that would be required to explain the full range of benchmark phenomena. Specifically, TCM-A does not have the necessary machinery to explain semantic similarity, category clustering, and false-memory effects. TCM-A is also missing a realistic model of encoding and rehearsal processes, which have been shown to be related to several important recall phenomena such as the primacy effect. Below we discuss potential extensions of TCM-A that would make it a more complete description of free recall.

Semantic retrieval effects

Semantic relations between words have been demonstrated to influence behavior during memory tasks, giving rise to category clustering (Bousfield, 1953; Shuell, 1969) and semantic proximity effects (e.g., Howard & Kahana, 2002b; Romney, Brewer, & Batchelder, 1993). Computational models of semantic structure have exploited the fact that words with similar meaning occur in similar temporal contexts (Lund & Burgess, 1996; Landauer & Dumais, 1997; Griffiths, Steyvers, & Tenenbaum, 2007; Jones & Mewhort, 2007).

Zaromb et al. (2006) demonstrated that participants’ prior list intrusions—incorrect recalls of items from earlier lists tend to be semantically related to the correct recall that occurred just before the intrusion. This finding in recall of random word lists is reminiscent of the more striking demonstrations of false recall when lists are composed of items that are all strong associates of a critical non-presented item, as in the Deese-Roediger-McDermott false memory paradigm (Deese, 1959; Roediger & McDermott, 1995; Kimball et al., 2007). The TCM framework would suggest that prior list intrusions arise due to an interaction between the slowly-drifting temporal context cue and semantic associations between items as expressed in the item-to-context and context-to-item matrices. In other words, the current state of temporal context would weakly activate items in prior lists to the extent that the items occurred recently and would provide an additional boost to items that are semantically similar to the current context.

Based on these findings, one possible way to include semantic associations in the TCM framework is to have off-diagonal terms of the pre-experimental context-to-item association matrix code for the semantic representation of an item. This could allow for contextually-mediated semantic retrieval effects, such as prior list intrusions and false memory.

Encoding variability

Currently, the only source of variability in TCM-A is the stochastic noise in the accumulators. Although having a single source of variability does simplify analysis of the model, this is clearly not the case for actual memory. Numerous studies have reported that variability in brain activity during item encoding predicts which items will be recalled later (Paller & Wagner, 2002; Sederberg, Kahana, Howard, Donner, & Madsen, 2003; Sederberg et al., 2007, 2007). Such subsequent memory effects suggest that the level of encoding varies during the study-list and that this affects subsequent memorability. In TCM-A, encoding variability could be implemented by treating γTF and/or γFT as a random variable that varies from item to item.¹¹ In other words, the weight of newly-learned experimental item-to-context associations would change for each item presentation. Theoretically, it should be possible to set the degree of encoding based on neural activity recorded from participants performing the task, thus providing a link between the computational theory of episodic memory and brain data.

Rehearsal

Rehearsal processes have been implicated in a number of free recall phenomena, including primacy effects and spacing effects (e.g. Rundus, 1971). Rehearsal could be implemented in TCM-A by allowing item retrievals during study, with recalled items receiving an encoding boost. This would allow for a direct comparison with overt rehearsal paradigms and the relationship between rehearsals and recalls (Laming, 2006, see also Tan & Ward, 2000), as well as provide an explanation for why primacy effects are greatly diminished in studies that limit rehearsal (Howard & Kahana, 1999). Given that rehearsals would follow the same process as retrievals in TCM-A, it may be possible to map primacy effects to neural mechanisms, as well.

Going beyond temporal context

In the current implementation of TCM-A, temporal context evolves solely as a result of items being activated during presentation or retrieval. Although this appears to be adequate for simulating encoding and retrieval of a standard free recall list, items alone do not reflect the rich temporal context that we experience while encoding new experiences, even while in a controlled lab environment. One could envision an extension of TCM-A whereby additional sources of context would be represented in the model. Other contextual features could include the participants’ task during encoding, the modality or source information of each item, ordinal information, list information, spatial information including the location of a word on the screen and the spatial environment of the participant during the experiment, and even the participant’s affective state. An extension of TCM-A incorporating this broader view of context might allow the model to account for a far richer array of cognitive phenomena.

Conclusions

We have shown how TCM-A—a contextual-cuing model of episodic memory—can account for a wide range of recall phenomena including recency and contiguity effects in immediate, delayed and continual distractor free recall. In addition, TCM-A was able to account for a number of major empirical dissociations between recency effects observed in immediate and continual distractor free recall, including the longer time to first recall in continual distractor free recall, changes in the contiguity effect with output position in immediate free recall, as well as the resistance of recency in immediate free recall to both proactive interference and amnesia. The ability to account for these dissociations is striking because the model assumes that the same retrieval process supports recency and contiguity in both short-term and long-term memory tasks. Thus, we would argue that the universal phenomenon of recency in memory tasks may reflect a single basic forgetting mechanism, and that mechanism may be the fluctuating internal contextual state of the organism (e.g., McGeoch, 1932; Estes, 1950).