An approach to joint analysis of longitudinal measurements and competing risks failure time data

SUMMARY

Joint analysis of longitudinal measurements and survival data has received much attention in recent years. However, previous work has primarily focused on a single failure type for the event time. In this paper we consider joint modelling of repeated measurements and competing risks failure time data to allow for more than one distinct failure type in the survival endpoint which occurs frequently in clinical trials. Our model uses latent random variables and common covariates to link together the sub-models for the longitudinal measurements and competing risks failure time data, respectively. An EM-based algorithm is derived to obtain the parameter estimates, and a profile likelihood method is proposed to estimate their standard errors. Our method enables one to make joint inference on multiple outcomes which is often necessary in analyses of clinical trials. Furthermore, joint analysis has several advantages compared with separate analysis of either the longitudinal data or competing risks survival data. By modelling the event time, the analysis of longitudinal measurements is adjusted to allow for non-ignorable missing data due to informative dropout, which cannot be appropriately handled by the standard linear mixed effects models alone. In addition, the joint model utilizes information from both outcomes, and could be substantially more efficient than the separate analysis of the competing risk survival data as shown in our simulation study. The performance of our method is evaluated and compared with separate analyses using both simulated data and a clinical trial for the scleroderma lung disease.

1. INTRODUCTION

In clinical trials and other follow-up studies, it is common that a response variable (e.g. a biomarker) is repeatedly measured during follow-up and the occurrence of some key event, which could cause non-ignorable missing data for the biomarker, is also monitored. Often, the occurrence of the event is censored by some competing risks such as disease-related dropout. A typical example is the scleroderma lung study (SLS) [1] which has motivated this research. The SLS is a double-blinded, randomized controlled study on 162 patients, with 81 in each group. The goal of the SLS is to evaluate the effectiveness of oral cyclophosphamide (CYC) versus placebo in the treatment of active, symptomatic lung disease due to scleroderma. One outcome variable is forced vital capacity (FVC, as per cent predicted), a measure of lung function determined longitudinally at 3-month intervals. Another important measure is a clinical outcome variable—the time to treatment failure or death. Here a treatment failure occurs when %FVC of a patient in either group falls by ≥15 per cent after 6 months in the study. In addition, there are also considerable disease-related dropouts during the follow-up. Note that both death and dropout would cause non-ignorable missing data for the longitudinal measurements of %FVC.

Separate analysis for each of these endpoints has been studied extensively. For the time to event data, Cox’s [2] proportional hazards model is popular, while mixed effects models and the GEE method are widely used for longitudinal measurements [3–6]. However, joint analysis of both outcomes is often needed. This is the case for the SLS for two primary reasons. First, we are interested in evaluating the effects of CYC treatment on the two endpoints, %FVC and the time to treatment failure or death, simultaneously, since CYC is considered effective if it can either improve the %FVC of the patients in the study or lower the risk of treatment failure or death. Thus, it is necessary to build a more inclusive model which links the two aspects together. Secondly, the procedure of estimating the effects of CYC on the longitudinal outcome %FVC can be complicated by the disease-related dropout process or death, in which patients with worse scleroderma lung disease prognoses tend to withdraw from the study early or die, and hence are lost to follow up. Such non-ignorable missing data may lead to biased inferences if a separate analysis is performed on the longitudinal data using the mixed effects model or the GEE method [7, 8].

Joint modelling of the two different types of endpoints simultaneously has received considerable attention in recent years [9–20]. Tsiatis and Davidian provided a nice overview of joint models [21]. A joint model enables one to evaluate effects of factors of interest on both endpoints at the same time [9, 10], and also, it can be used to adjust inferences about longitudinal data for outcome-dependent missing values, of which the assumption of missing data mechanism can be non-ignorable non-response (NINR) [11–13]. In addition, we expect to gain more efficiency in statistical inferences with a joint model since information from both endpoints is utilized. A fourth advantage of joint modelling stems from scientific investigations such as AIDS studies, in which the interest is to characterize the relationship between CD4 count and the time to AIDS. One common procedure is that the true underlying trajectory of the CD4 count can be first modelled, and then be incorporated into a Cox model for the time to AIDS [14, 15], or into an accelerated failure time model in other applications if the proportional hazards assumption fails [16]. Non-likelihood-based approaches include the work of Robins and his colleagues [22–24] who used augmented inverse probability of censoring weighted estimating equations. The approach was supplemented by a sensitivity analysis for the parameter associated with longitudinal measurements in the non-response model.

However, previous joint models only deal with a single failure type with non-informative censorship for the time to event, and thus are not applicable to survival data with competing risks or informative censoring. In our SLS data, disease-related dropout should be taken into account along with treatment failure or death in a joint analysis with %FVC for two reasons. First, disease-related dropout is regarded as informative censoring for treatment failure or death, since it is recognized that both events are related to patient disease condition. Secondly, disease-related dropout generates non-ignorable missing values in %FVC. One possible way of handling such a complicated situation is to treat disease-related dropout as a competing risk for treatment failure or death.

This paper extends the work of Henderson et al. [9] by considering simultaneous analysis of longitudinal measurements and competing risks failure times to allow for more than one distinct failure type. Our model enables one to handle informative censoring by treating it as a competing risk. It also allows non-ignorable missingness after event times. We adopt a linear mixed effects sub-model for the longitudinal measurements and a mixture sub-model for competing risks survival data which is similar to that of Larson and Dinse [25] and Ng and McLachlan [26]. The mixture model for competing risks enables one to evaluate the effects of some factors on both the marginal probabilities of occurrence of the risks and the conditional cause-specific hazards. One major difference of our mixture model from their approach is that we introduce frailties which are linear in the random effects for the longitudinal measurements. Therefore, conditional on common covariates, the correlation between the two endpoints is characterized by latent random effects. An EM-based algorithm is derived to estimate the parameters in both sub-models, and inverse of the empirical Fisher information from the profile likelihood is used to approximate the variance–covariance matrix of the estimators. It is worth noting that the estimation procedure for joint analysis of longitudinal measurements and competing risks failure time data is more complicated than that for longitudinal measurements and survival data with a single failure type. With the two-step mixture sub-model for competing risks event times, we must introduce additional hidden variables to simplify the EM algorithm. Another commonly used model for competing risks is the cause-specific hazards proposed by Prentice et al. [27, 28]. Joint modelling of longitudinal data and competing risks using cause-specific hazards will be studied in a sequel paper.

This article is organized as follows. The model and the estimation procedure are described in Section 2. In Section 3, a real data application is illustrated by the SLS clinical trial. In Section 4, the performance of the joint model is examined by simulation studies, and the joint model is compared to separate analyses in terms of the bias, the empirical standard error, the estimated standard error, and the power of the tests for factors of interest. We also examined the estimates from the joint model with a single failure type in the presence of informative censoring. Some concluding remarks and possible future directions are given in Section 5.

2. MODEL AND ESTIMATION

2.1. The joint model

Suppose there are n subjects in the study. Let Y_i(t) be the measurement of a response variable for subject i at time t, where i =1, 2, …, n. During follow-up, each subject may experience one of g distinct failure types or could be right censored. Let C_i =(T_i, D_i) be the competing risks data on subject i, where T_i is the failure time or censoring time, and D_i takes value from {0, 1, …, g}, with D_i = 0 indicating a censored event and D_i = k showing that subject i fails from the kth type of failure, where k = 1, …, g. Throughout, the censoring mechanism is assumed to be non-informative. As stated before, informative censoring can be treated as one of the g types of failures. We also assume that each subject in the study will eventually fail from one of the g possible failure types.

Our joint model for Y (t) and C consists of the following three components:

$$Y_i(t)={\beta }_0+{\beta }_1^T{X}_i^{(1)}(t)+U_{0i}+U_{1i}^T{\tilde{X}}_i^{(1)}(t)+{\epsilon }_i(t)$$ (1)

$${\pi }_k(X_i^{(2)},W_{ki};\alpha )=\frac{\text{exp}({\alpha }_{0k}+{\alpha }_{1k}^T{X}_i^{(2)}+W_{ki})}{1+{\displaystyle {\sum }_{l=1}^{g-1}\text{exp}({\alpha }_{0l}+{\alpha }_{1l}^T{X}_i^{(2)}+W_{li})}}\text{for}k=1,\dots ,g-1$$ (2)

$$\begin{array}{ccc}{\lambda }_k(t;X_i^{(3)}(t),V_{ki},\gamma )\hfill & =\hfill & \underset{h\to 0}{\text{lim}}{h}^{-1}P[t\le T_i<t+h|T_i\ge t,D_i=k,X_i^{(3)}(t),V_{ki}]\hfill \\ \hfill & =\hfill & {\lambda }_{0k}(t)\text{exp}\{{\gamma }_k^{\mathrm{T}}{X}_i^{(3)}(t)+V_{ki}\}\text{for}k=1,\dots ,g\hfill \end{array}$$ (3)

where we denote ${\alpha }_k={({\alpha }_{0k},{\alpha }_{1k}^{\mathrm{T}})}^{\mathrm{T}},\alpha ={({\alpha }_1^{\mathrm{T}},\dots ,{\alpha }_{g-1}^{\mathrm{T}})}^{\mathrm{T}},\text{and}\gamma ={({\gamma }_1^{\mathrm{T}},\dots ,{\gamma }_g^{\mathrm{T}})}^{\mathrm{T}}$. Sub-model (1) is the linear mixed effects model for the longitudinal outcome Y_i (t), and sub-model (2)–(3) specifies the distribution of the competing risks survival data with ${\pi }_k(X_i^{(2)},W_{ki};\alpha )$ being the marginal probability of subject i failing from risk k, and ${\lambda }_k(t;X_i^{(3)}(t),V_{ki};\gamma )$ the conditional cause-specific hazard for risk k, also referred to as the component hazard [25, 26], in which λ_0k (t) is a completely unspecified baseline hazard function for risk k, where k =1, …, g.

To be more specific, in sub-model (1), $X_i^{(1)}(t)$ is a vector of covariates associated with the longitudinal trajectory Y_i(t) and is allowed to change over time, β1 represents the fixed effects of $X_i^{(1)}(t),$ U_0i is a random intercept, U_1i is subject-specific effects of ${\tilde{X}}_i^{(1)}(t),$ a vector of covariates which may or may not be the same as $X_i^{(1)}(t),$ and ε_i (t) ~ N(0, σ²) for all t ≥ 0 is the measurement error. We assume that $U_i={(U_{0i},U_{1i}^{\mathrm{T}})}^{\mathrm{T}}\sim \mathrm{N}(0,{\displaystyle \Sigma )}$ and is independent of ε_i (t). We further assume that ε_i (t₁) is independent of ε_i (t₂) for any t₁ ≠ t₂.We write $\beta ={({\beta }_0,{\beta }_1^{\mathrm{T}})}^{\mathrm{T}}.$ In sub-model (2)–(3)), $X_i^{(2)}\text{and}{X}_i^{(3)}(t)$ are vectors of covariates associated with the marginal probability and the conditional cause-specific hazards, respectively, and α and γ are the corresponding unknown coefficients. The sub-model incorporates random effects W_ki and V_ki, and the V_ki′s are usually referred to as frailties in regression models for survival data. It is reasonable to assume that U_i, W_ki, and V_ki for the same i are correlated. The simplest form is $W_{ki}={\theta }_k^{\mathrm{T}}{U}_i\text{and}{V}_{ki}={\nu }_k^{\mathrm{T}}{U}_i,$ with θ_k and ν_k being unknown parameters. We use this type of formulation in our joint model. Therefore, we need to rewrite ${\pi }_k(X_i^{(2)},W_{ki};\alpha )\text{as}{\pi }_k(X_i^{(2)},U_i;\alpha ,\theta )\text{and}{\lambda }_k(t;X_i^{(3)}(t),V_{ki},\gamma )$ as ${\lambda }_k(t;X_i^{(3)}(t),U_i,\gamma ,\nu ),$ where $\theta ={({\theta }_1^{\mathrm{T}},\dots ,{\theta }_{g-1}^{\mathrm{T}})}^{\mathrm{T}}\text{and}\nu ={({\nu }_1^{\mathrm{T}},\dots ,{\nu }_g^{\mathrm{T}})}^{\mathrm{T}}.$ Sub-model (2)–(3) is an extension of the mixture model for competing risks survival data described by Larson and Dinse [25] and Ng and McLachlan [26] which consists of a logistic model for the marginal distribution of failure types and a proportional hazards model for the conditional cause-specific hazard without any random effects. At last, we assume that the longitudinal measurements are independent of the competing risks survival data, conditional on all the covariates and random effects. Through (1)–(3), we adopt the most generic notation for the covariates which are used in different parts of the model. In practice, the vectors $X_i^{(1)}(t),X_i^{(2)}(t),\text{and}{X}_i^{(3)}(t)$ may have components in common. In the SLS data example as illustrated in Section 3, the three vectors are identical, containing the baseline %FVC, the degree of fibrosis in the lung, the treatment CYC, and an interaction between fibrosis and CYC.

We have the following remarks on our joint model.

Remark 1

We note that the characteristics of the study subjects are represented by two aspects: the observable covariates X and the hidden subject-specific effects U. Both X and U are responsible for characterizing the sub-models and introducing dependence between Y and C, if there are common covariates in (1)–(3). The parameters θ and ν measure the latent association from the random effects.

Remark 2

Our joint model belongs to the class of random-effects selection models, which assume the missing data in longitudinal measurements after dropout are non-ignorable [12]. This type of missing data in longitudinal measurements cannot be correctly analysed using usual linear mixed effectsmodels that require missingness to be missing at random (MAR) when some assumptions are satisfied [29, 30]. Let Y^(o) and Y^(m) denote the observed and missing components, respectively, for the longitudinal response variable Y, and let M denote the missing data indicator vector for Y. According to Little and Rubin [29], missing completely at random (MCAR) occurs when f (M|Y,ϕ) = f (M|ϕ) for all Y and ϕ, where ϕ is an unknown parameter. Missing at random (MAR) occurs when f (M|Y,ϕ)= f (M|Y^(o),ϕ). A missing mechanism is said to be ignorable if it is MCAR or MAR; and non-ignorable otherwise. In the study of longitudinal data with informative dropout, the time to dropout T has direct correspondence with M if there are no missing data before dropout. Under random-effects selection models, T is assumed to be independent of Y given random effects U. Therefore,

$$\begin{array}{ccc}f(T|Y)\hfill & =\hfill & {\displaystyle \int f(T|U,Y^{(o)},Y^{(m)})f(U|Y^{(o)},Y^{(m)})\mathrm{d}U}\hfill \\ \hfill & =\hfill & {\displaystyle \int f(T|U)f(U|Y^{(o)},Y^{(m)})\mathrm{d}U}\hfill \end{array}$$ (4)

Each density f here should be indexed by some unknown parameters which have been left out for simplicity. The above equation indicates that the conditional distribution of T given Y depends on both Y^(o) and Y^(m), which indicates that the missing mechanism is non-ignorable. However, for the missing data in longitudinal measurements before dropout, we need to assume the missing mechanism is MAR. If the informative dropout is one of the competing risks in the follow-up, and it is related to both the longitudinal outcome and the time to event of interest, a competing risks framework should be considered. It is necessary to take into account the correlation between the informative dropout and the event of interest, and more importantly, to adjust the inference on longitudinal measurements for non-ignorable missing values after the informative dropout.

2.2. Parameter estimation

Let Ψ=(β, Σ, σ², α, θ, γ, ν, λ₀₁(t), …, λ_0g(t)) be the vector containing all the unknown parameters from (1) to (3). Suppose the longitudinal outcome Y_i(t) is observed at time points t_{i j} for j = 1, …, n_i, and is denoted as Y_i = (Y_i1, …, Y_ini ). Note that the set (t_i1, …, t_ini) can be different among subjects, due to different dropout times and the fact that some patients may miss one or more visits. We assume that the missing values in the longitudinal measurements caused by reasons other than occurrence of events are MAR. Recall that the competing risks endpoint on subject i is C_i = (T_i, D_i). It is important to note that the joint distribution of (Y,C) is completely determined by f (Y|U), f (C|U), and f(U), which are specified in models (1)–(3). The full likelihood function for Ψ, conditional on the observed data (Y_i, C_i) for i = 1, …, n and the covariates, is thus

$$\begin{array}{ccc}L(\mathrm{\Psi };Y,C)\hfill & \propto \hfill & {\displaystyle \prod _{i=1}^{n}f(Y_i,C_i|\mathrm{\Psi })}\hfill \\ \hfill & =\hfill & {\displaystyle \prod _{i=1}^n{\displaystyle {\int }_{U}f(C_i|Y_i,U,\mathrm{\Psi })f(Y_i|U,\mathrm{\Psi })f(U|\mathrm{\Psi })\mathrm{d}U}}\hfill \\ \hfill & =\hfill & {\displaystyle \prod _{i=1}^n{\displaystyle {\int }_{U}f(C_i|U,\mathrm{\Psi })f(Y_i|U,\mathrm{\Psi })f(U|\mathrm{\Psi })\mathrm{d}U}}\hfill \\ \hfill & =\hfill & {\displaystyle \prod _{i=1}^n{\displaystyle {\int }_U\{{\displaystyle \prod _{k=1}^g[{\pi }_k(X_i^{(2)},U;\alpha ,\theta )f_k{(T_i;X_i^{(3)}(T_i),U,\gamma ,\nu )]}^{I(D_i=k)}}}}\hfill \\ \hfill & \hfill & \times S{(T_i;X_i^{(2)},{\overline{X}}_i^{(3)}(T_i),U,\alpha ,\theta ,\gamma ,\nu )}^{I(D_i=0)}\hfill \\ \hfill & \hfill & \times {\displaystyle \prod _{j=1}^{n_i}\frac{1}{\sqrt{2\pi {\sigma }^2}}\text{exp}[-\frac{1}{2{\sigma }^2}(Y_{ij}-{\beta }_0-{\beta }_1^{\mathrm{T}}{X}_i^{(1)}(t_{ij})-U_0}\hfill \\ \hfill & \hfill & -U_1^{\mathrm{T}}{\tilde{X}}_i^{(1)}(t_{ij}){)}^2]\times \frac{1}{\sqrt{2\pi |\sum |}}\text{exp}\left(-\frac{1}{2}{U}^{\mathrm{T}}{\sum }^{-1}U\right)\}\mathrm{d}U\hfill \end{array}$$ (5)

where the second equality follows from the assumption that Y and C are independent conditional on all the covariates and random effects. In the above expression, for a censored subject with censoring time T_i, we have

$$S(T_i;X_i^{(2)},{\overline{X}}_i^{(3)}(T_i),U_i,\alpha ,\theta ,\gamma ,\nu )={\displaystyle \sum _{k=1}^g{\pi }_k(X_i^{(2)},U_i;\alpha ,\theta )S_k(T_i;{\overline{X}}_i^{(3)}(T_i),U_i,\gamma ,\nu )}$$ (6)

Here, S_k(t) and f_k(t) are the conditional cause-specific survival and density functions for risk k, respectively, derived from λ_k(t) in (3), and ${\overline{X}}_i^{(3)}(T_i)=\{X_i^{(3)}(t):0\le t\le T_i\}$.

To maximize the above likelihood, the cumulative baseline hazard functions are assumed to be step functions with jumps at observed event times. It is obvious that the observed-data likelihood is difficult to maximize in the presence of integration. We may treat random effects U as missing data and use the EM algorithm to maximize the conditional likelihood in which the functions of U are replaced by their expectations given the observed data. However, for censored subjects, the term ${\displaystyle {\sum }_{k=1}^g{\pi }_k(X_i^{(2)},U_i;\alpha ,\theta )S_k(T_i;{\overline{X}}_i^{(3)}(T_i),U_i,\gamma ,\nu )}$ becomes non-linear in the logarithm of the conditional likelihood. To further simplify the estimation procedure, we introduce a latent vector τ_i = (τ_i1, …, τ_ig)^T for subject i if censoring occurs, where τ_ik is 1 or 0 indicating whether or not the ith subject would have eventually failed from cause k if the follow-up time is sufficiently long, where k = 1, …, g. This is similar to what Ng and McLachlan [26] postulated. The posterior distribution of τ_i given Y_i, C_i, and U_i is multinomial with probability τ_ik = 1 equal to

$$E({\tau }_{ik}|U_i,Y_i,C_i,\mathrm{\Psi })=\frac{{\pi }_k(X_i^{(2)},U_i;\alpha ,\theta )S_k(T_i;{\overline{X}}_i^{(3)}(T_i),U_i,\gamma ,\nu )}{{\displaystyle {\sum }_{l=1}^g{\pi }_l(X_i^{(2)},U_i;\alpha ,\theta )S_l(T_i;{\overline{X}}_i^{(3)}(T_i),U_i,\gamma ,\nu )}}$$ (7)

Given U and τ, the complete-data likelihood is

$$\begin{array}{ccc}L(\mathrm{\Psi };Y,C,U,\tau )\hfill & \propto \hfill & {\displaystyle \prod _{i=1}^n\{{\displaystyle \prod _{k=1}^g{[{\pi }_k(X_i^{(2)},U_i;\alpha ,\theta )f_k(T_i;{\overline{X}}_i^{(3)}(T_i),U_i,\gamma ,\nu )]}^{I(D_i=k)}}}\hfill \\ \hfill & \hfill & \times {\displaystyle \prod _{k=1}^g{[{\pi }_k(X_i^{(2)},U_i;\alpha ,\theta )S_k(T_i;{\overline{X}}_i^{(3)}(T_i),U_i,\gamma ,\nu )]}^{I(D_i=0){\tau }_{ik}}}\hfill \\ \hfill & \hfill & \times {\displaystyle \prod _{j=1}^{n_i}\frac{1}{\sqrt{2\pi {\sigma }^2}}\text{exp}[-\frac{1}{2{\sigma }^2}(Y_{ij}-{\beta }_0-{\beta }_1^{\mathrm{T}}{X}_i^{(1)}(t_{ij})-U_{0i}}\hfill \\ \hfill & \hfill & -U_{1i}^{\mathrm{T}}{\tilde{X}}_i^{(1)}(t_{ij}){)}^2]\times \frac{1}{\sqrt{2\pi |\sum |}}\text{exp}\left(-\frac{1}{2}{U}_i^{\mathrm{T}}{\sum }^{-1}{U}_i\right)\}\hfill \end{array}$$ (8)

It is clear that the complete-data log-likelihood is linear in the components π_k, f_k, and S_k, so that the parameters α and θ can be well separated from γ and ν.

The maximum likelihood estimate of Ψ is obtained via an EM-based algorithm, which involves iterations between an E-step and an M-step. In the E-step of the (m + 1)th iteration, we need to evaluate the expectation of the complete-data log-likelihood conditional on the observed data (Y,C) and the current parameter estimate, say Ψ^(m). This is equivalent to calculating the expected values of all the functions of U and τ that appear in the complete-data log-likelihood. We write l(Ψ;U, τ)= log L(Ψ; Y,C,U, τ) with L as defined in (8), where we drop Y and C to simplify the notation. We have

$$\begin{array}{ccc}{E}_{U,\tau |Y,C,{\mathrm{\Psi }}^{(m)}}[l(\mathrm{\Psi };U,\tau )]\hfill & =\hfill & E_{U|Y,C,{\mathrm{\Psi }}^{(m)}}[E_{\tau |U,Y,C,{\mathrm{\Psi }}^{(m)}}[l(\mathrm{\Psi };U,\tau )]]\hfill \\ \hfill & =\hfill & E_{U|Y,C,{\mathrm{\Psi }}^{(m)}}[l(\mathrm{\Psi };U,E_{\tau |U,Y,C,{\mathrm{\Psi }}^{(m)}}(\tau ))]\hfill \end{array}$$ (9)

The second equality holds because l(Ψ;U, τ) is a linear function of τ. Therefore, the only hidden variable in l(Ψ;U, E_τ|U,Y,C,Ψ^(m) (τ)) is U, and computation of the conditional expectation of complete-date log-likelihood is reduced to evaluating the expectation of all the functions of U, say, h(U) in l(Ψ;U, E_τ|U,Y,C,Ψ^(m) (τ)) conditional on (Y,C,Ψ^(m)), and we can write

$$E_{U|Y,C,{\mathrm{\Psi }}^{(m)}}[h(U)]={\displaystyle \int h(U)f(U|Y,C,{\mathrm{\Psi }}^{(m)})\mathrm{d}U}$$ (10)

In the M-step, E_U,τ|Y,C,Ψ^(m) [l(Ψ;U, τ)] is maximized with respect to Ψ, so that we can update the estimate of Ψ to get Ψ^(m+1). We write Q(Ψ; Ψ^(m)) = E_U,τ|Y,C,Ψ^(m) [l(Ψ; U, τ)] and have

$${\mathrm{\Psi }}^{(m+1)}=\underset{\mathrm{\Psi }}{\text{argmax}}Q(\mathrm{\Psi };{\mathrm{\Psi }}^{(m)})$$ (11)

Recall that Ψ=(β,Σ, σ², α, θ, γ, ν, λ₀₁(t), …, λ_0g(t)). In Appendix A we show that β, Σ, σ², and the cumulative baseline hazard functions H_0k(t) can be updated with closed forms (A5)–(A8), where H_0k(t) is a step function with jumps at observed event times due to risk k, k = 1, …, g. No closed-form solutions exist for α, θ, γ, and ν, which need to be updated using a one-step Newton–Raphson algorithm in each iteration as given in (A13)–(A24). Then Ψ^(m+1) will be the input for the E-step in the next iteration. The algorithm stops when the convergence criteria are satisfied. Technical details of the algorithm are deferred to Appendix A.

2.3. Standard error estimation

Louis [31] proposed a method for computing the observed information matrix together with the EM algorithm. However, this method is computationally unattractive and time-consuming for our model in which the non-parametric baseline hazards are involved. Here we develop a method similar to that of Lin et al. [32]. We split the parameter vector Ψ into two components, the parametric component Ω = (β,Σ, σ², α, θ, γ, ν) and the collection of non-parametric baseline hazard functions Λ=(λ₀₁(t), …, λ_0g(t)). Since we are only interested in making inference on Ω, calculating the entire information matrix with the baseline functions is unnecessary. The variance–covariance matrix of Ω can be approximated by the inverse of the empirical Fisher information obtained from the profile likelihood where the baseline hazards functions have been profiled out. Let l⁽ⁱ⁾ (Ω̂; Y, C) denote the observed score vector from the profile likelihood on the ith subject evaluated at Ω̂. The observed information matrix of Ω can be approximated by

$${\displaystyle \sum _{i=1}^n{l}^{(i)}(\widehat{\mathrm{\Omega }};Y,C)}{l}^{(i)}{(\widehat{\mathrm{\Omega }};Y,C)}^{\mathrm{T}}$$ (12)

Wald’s test can then be performed based on the estimated variance–covariance matrix (12).

3. THE SCLERODERMA LUNG STUDY

The proposed joint model for longitudinal measurements and competing risks failure time data is illustrated with the SLS clinical trial. We are interested in evaluating if treatment CYC is effective on at least one of the two endpoints, that is, if the treatment can either improve the %FVC level of a patient or decrease the risk of treatment failure or death. Initially patients were only given a partial dose, and the dose was gradually increased to the target level within the first 6 months. The treatment was given for 12 months from the baseline and there was an additional year of follow-up. The primary analysis has been based on the first 12 months data. In addition to treatment failure or death, there are considerable dropouts during the follow-up. Specifically, as summarized in Table I, we have observed the following during the 24 months follow-up: (1) 16 treatment failures or deaths; (2) 32 informative dropouts due to adverse event (AE), serious adverse event (SAE), or worsening disease; (3) 10 non-informative dropouts with no evidence showing that the dropouts were related to the disease. For example, the patient may have moved out of the city before completion of the study. The informative dropout not only causes non-ignorable missing data in %FVC which indicates linear mixed effects models are not applicable, but also introduces informatively censored events for treatment failure or death. Therefore, we have to take into account this type of events when evaluating the treatment effects on %FVC outcome and the risk of treatment failure or death.

Table I.

Three types of events in the scleroderma lung study.

Category	CYC	Placebo	Total
Treatment failure or death	6	10	16
Informative dropout
(AE, SAE, worsening disease)	19	13	32
Non-informative dropout
(Other reasons)	4	6	10

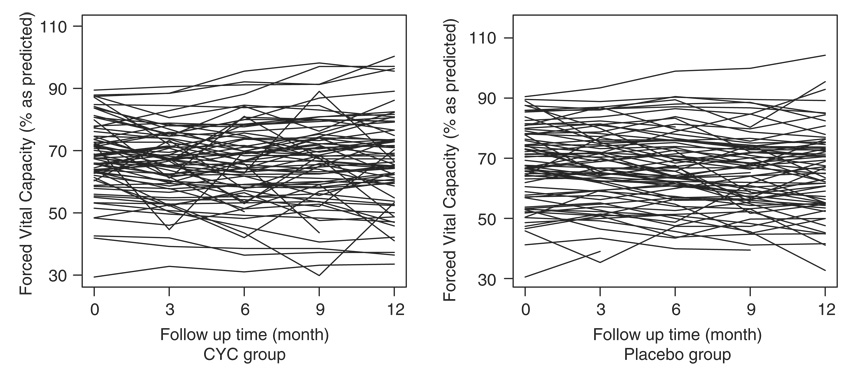
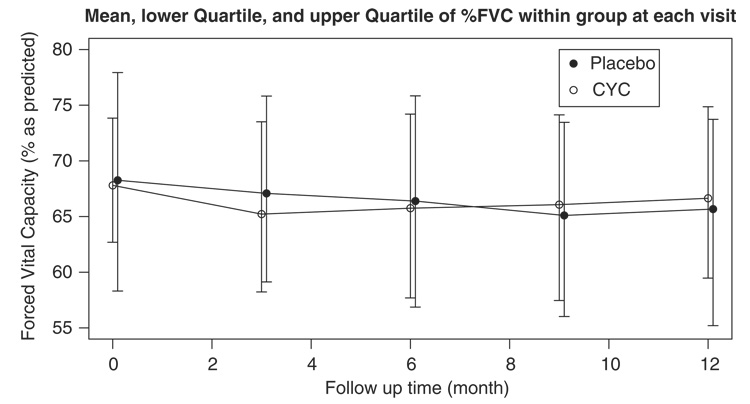
Figure 1 shows the longitudinal profile of %FVC over time for the CYC group versus the placebo. We observe a large variation in the baseline %FVC. There is no apparent time trend for both groups. Figure 2 shows the average, the lower quartile, and the upper quartile of %FVC within each group at months 0, 3, 6, 9, and 12. These quantities were calculated on those who had not dropped out by the time. It is observed that the average %FVC initially decreases in the CYC group. One explanation may be that prior to month 6 patients were only given partial doses, not allowing sufficient time or dosing for the treatment to take effect. To account for this, we only used data from month 6 and thereafter in the subsequent analysis. There were 10 patients with follow up ≤3 months, so they were not included in the analysis. The figure also shows that the CYC group tends to have a higher %FVC on average than the placebo group from month 9. However, no significant between-group difference is identified by the t-test at each visit (results not shown), and the figure indicates that the two groups have about the same interquartile ranges. We should note that both curves could be biased due to non-ignorable missing data in %FVC. Since patients with lower %FVC are more likely to dropout due to AE, SAE, worsening disease, or death, the observed curves for %FVC would be higher than the true population mean.

Figure 1.

Longitudinal profile of %FVC for the CYC group and the placebo group.

Figure 2.

The mean, the lower quartile, and the upper quartile of %FVC within each group during follow-up. At months 0, 3, 6, 9, and 12, the numbers at risk are 81, 72, 70, 68, and 70 for CYC group, and 80, 72, 70, 65, and 65 for the placebo group.

For illustrative purposes, we considered two confounding factors in our model when assessing CYC treatment effects: baseline %FVC and degree of fibrosis in the lung. These elements were stated for the primary analysis in the recorded manual of operations. No statistical selection procedure was used. We also considered the interaction between treatment CYC and fibrosis, which was indicated to be significant for %FVC measurements in preliminary analyses. Thus, we applied the joint model to the SLS data with three covariates: baseline %FVC, fibrosis, and the treatment group indicator, as well as the interaction between CYC and fibrosis. In the sub-model for %FVC, we fitted a linear mixed effects model with a random intercept and fixed effects for the three factors along with the interaction between CYC and fibrosis, and these terms were also considered in the mixture sub-model for the competing risks event times. Two competing risks, treatment failure or death and disease-related dropout, were analysed together with %FVC using the following joint model. In the sub-model for %FVC, we assume, for subject i at visit j

$$\%{\text{FVC}}_{ij}={\beta }_0+{\beta }_1{\text{FVC}}_{0i}+{\beta }_2{\text{FIB}}_i+{\beta }_3{\text{CYC}}_i+{\beta }_4{\text{CYC}}_i\times {\text{FIB}}_i+U_i+{\epsilon }_{ij}$$ (13)

where FVC_0i is the baseline %FVC, FIB_i is the degree of fibrosis in the lung, CYC_i is 1 or 0 as a group indicator for the CYC treatment or placebo, U_i is the random intercept with a mean zero normal distribution, and the ε_ij ’s are the mutually independent normal measurement errors. The normality assumption seems to be reasonable for this data set by diagnostics of residuals. For the competing risks survival data, we formulate the probability of treatment failure or death by the following:

$$\begin{array}{c}{\pi }_1({\text{FVC}}_{0i},{\text{FIB}}_i,{\text{CYC}}_i,U_i;\alpha ,\theta )\hfill \\ \hfill =\text{exp}({\alpha }_0+{\alpha }_1{\text{FVC}}_{0i}+{\alpha }_2{\text{FIB}}_i+{\alpha }_3{\text{CYC}}_i+{\alpha }_4{\text{CYC}}_i\times {\text{FIB}}_i+{\theta }_1{U}_i)/\hfill \\ \hfill (1+\text{exp}({\alpha }_0+{\alpha }_1{\text{FVC}}_{0i}+{\alpha }_2{\text{FIB}}_i+{\alpha }_3{\text{CYC}}_i+{\alpha }_4{\text{CYC}}_i\times {\text{FIB}}_i+{\theta }_1{U}_i))\end{array}$$ (14)

and the conditional cause-specific hazards for treatment failure or death (risk 1) and disease-related dropout (risk 2) are specified as

$$\begin{array}{c}{\lambda }_1(t;{\text{FVC}}_{0i},{\text{FIB}}_i,{\text{CYC}}_i,U_i,\gamma ,\nu )\hfill \\ \hfill ={\lambda }_{01}(t)\text{exp}\{{\gamma }_{11}{\text{FVC}}_{0i}+{\gamma }_{12}{\text{FIB}}_i+{\gamma }_{13}{\text{CYC}}_i+{\gamma }_{14}{\text{CYC}}_i\times {\text{FIB}}_i+{\nu }_1{U}_i\}\end{array}$$ (15)

$$\begin{array}{c}{\lambda }_2(t;{\text{FVC}}_{0i},{\text{FIB}}_i,{\text{CYC}}_i,U_i,\gamma ,\nu )\hfill \\ \hfill ={\lambda }_{02}(t)\text{exp}\{{\gamma }_{21}{\text{FVC}}_{0i}+{\gamma }_{22}{\text{FIB}}_i+{\gamma }_{23}{\text{CYC}}_i+{\gamma }_{24}{\text{CYC}}_i\times {\text{FIB}}_i+{\nu }_2{U}_i\}\end{array}$$ (16)

respectively.

The results of such a joint analysis are summarized in Table II, together with those from a linear random intercept model for the longitudinal outcome %FVC alone, and those from a mixture model for the competing risks failure time data. In the joint analysis, the interaction between CYC treatment and fibrosis is 1.79 with p-value 0.006, which suggests that the treatment CYC is more effective for the patient with a higher degree of fibrosis in the lung. However, the linear mixed effects model for %FVC alone failed to detect this effect. The test for the overall effects of treatment CYC can be done by jointly testing the two terms, the main effect and the interaction with fibrosis. The test gives p-value 0.0010 and 0.13 in the joint model and the separate analysis, respectively. In the joint model the inference for the effect of CYC has been adjusted for the non-ignorable missing data in %FVC, but we fail to do so in the analysis for %FVC alone. Finally, no treatment effects are identified for the competing risks failure time data, either with the joint model or the separate analysis. Possible reasons include the facts that the follow-up time is not long enough to detect any difference between the two groups and that the number of treatment failure or death is small.

Table II.

Comparison of the joint model versus the separate analysis for %FVC measurements alone using 6–12 month SLS data.

	Joint analysis		Separate analysis
	Estimate (SE)	p-value	Estimate (SE)	p-value
Longitudinal outcome %FVC
Baseline %FVC (β1)	0.96 (0.02)	<0.0001	0.96 (0.04)	<0.0001
Fibrosis (β2)	−1.66 (0.50)	0.001	−1.69 (0.85)	0.05
CYC group (β3)	−2.26 (1.50)	0.13	−2.51 (2.43)	0.30
CYC × Fibrosis (β4)	1.79 (0.66)	0.006	1.83 (1.11)	0.10
Effect of CYC (H0 : β3 = β4 =0)*		0.001		0.13
Cause-specific probability (treatment failure or death)
Baseline %FVC (α1)	−0.10 (0.14)	0.49	−0.03 (0.13)	0.83
Fibrosis (α2)	−0.45 (1.47)	0.76	0.30 (1.39)	0.83
CYC group (α3)	0.91 (6.71)	0.89	−0.86 (7.56)	0.91
CYC × Fibrosis (α4)	0.01 (2.82)	1.00	0.32 (3.30)	0.92
Effect of CYC (H0 : α3 = α4 = 0)*		0.93		0.99
Conditional cause-specific hazards (time to treatment failure or death)
Baseline %FVC (γ11)	0.01 (0.06)	0.85	0.04 (0.26)	0.87
Fibrosis (γ12)	0.001 (0.88)	1.00	−0.46 (2.88)	0.87
CYC group (γ13)	−0.34 (3.30)	0.92	2.72 (9.09)	0.76
CYC × Fibrosis γ14)	−0.28 (1.52)	0.85	−1.49 (3.68)	0.68
Effect of CYC (H0 : γ13 = γ14 = 0)*		0.64		0.86
Conditional cause-specific hazards (time to disease-related dropout)
Baseline %FVC (γ21)	−0.05 (0.05)	0.25	−0.01 (0.05)	0.76
Fibrosis (γ22)	0.24 (0.75)	0.75	0.45 (0.58)	0.44
CYC group (γ23)	1.61 (3.03)	0.60	1.06 (1.46)	0.47
CYC × Fibrosis (γ24)	−0.41 (1.27)	0.75	−0.36 (0.62)	0.56
Effect of CYC (H0 : γ23 = γ24 = 0)*		0.75		0.75

^*The p-values are based on Wald test with 2 degrees of freedom.

4. SIMULATION STUDY

We examined the finite sample performance of our joint model and the proposed estimation procedure using simulated data. We primarily looked at three aspects: first, we investigated for the joint model the simulated coverage probability of the 95 per cent confidence intervals which were obtained based on the estimated standard errors using the method described in Section 2.3; second, the joint model was compared to the separate analysis of either the longitudinal data or the competing risks survival data in terms of the bias, the empirical standard error, the estimated standard error, and the power of the tests for the effects of some factors; third, we examined the parameter estimates from a joint model with a single failure type in the presence of informative censoring, and the results were compared to our joint model which treated the informative censoring as a competing risk.

The longitudinal measurements were simulated from the following random slope model:

$$Y_{ij}={\beta }_0+{\beta }_1{t}_{ij}+{\beta }_2{X}_{2i}+U_i{t}_{ij}+{\epsilon }_{ij}$$ (17)

where t_{i j} = 0, 0.5, 1, …, 5 represents the scheduled visiting times and X_2i ~ Bernoulli(0.5) acts as a treatment group indicator in randomized trials. The random intercept U_i ~ N(0, 0.5) was independent of the measurement error ε_{i j}, which was distributed as N(0, 0.25). We simulated two competing risks for event times, say risk 1 and risk 2, with the marginal probability for risk 1 specified as

$${\pi }_1(X_{1i},X_{2i},U_i;\alpha ,\theta )=\frac{\text{exp}({\alpha }_{10}+{\alpha }_{11}{X}_{1i}+{\alpha }_{12}{X}_{2i}+{\theta }_1{U}_i)}{1+\text{exp}({\alpha }_{10}+{\alpha }_{11}{X}_{1i}+{\alpha }_{12}{X}_{2i}+{\theta }_1{U}_i)}$$ (18)

and the following conditional hazards for the two risks:

$${\lambda }_1(t;X_{1i},X_{2i},U_i,\gamma ,\nu )={\lambda }_{01}(t)\text{exp}\{{\gamma }_{11}{X}_{1i}+{\gamma }_{12}{X}_{2i}+{\nu }_1{U}_i\}$$ (19)

$${\lambda }_2(t;X_{1i},X_{2i},U_i,\gamma ,\nu )={\lambda }_{02}(t)\text{exp}\{{\gamma }_{21}{X}_{1i}+{\gamma }_{22}{X}_{2i}+{\nu }_2{U}_i\}$$ (20)

where X_1i ~ N(2, 0.1). The baseline hazards were held constant at 0.1 and 0.2 for risk 1 and 2, respectively, so that the time to each risk forms an exponential distribution. The censoring time was set to an exponential random variable with mean 15, to obtain average censoring rate at about 17 per cent, the events of risk 1 at about 33 per cent, and the events of risk 2 at about 50 per cent. The longitudinal outcome was missing after the observed or censored event times. The proportions of subjects with 1, 2, 3, …, 11 measurements are, respectively, 0.28, 0.20, 0.13, 0.10, 0.07, 0.05, 0.04, 0.03, 0.02, 0.02, and 0.06. Table III shows the simulated coverage probability of the 95 per cent confidence intervals from such a joint model at two sample sizes, 200 and 500, with 500 Monte Carlo samples for each. In the table we write ${\sigma }_u^2$ for the variance of the random intercept U_i. It is shown that the simulated coverage probability of confidence intervals is close to the nominal value 0.95.

Table III.

Simulated coverage probability of the 95 per cent confidence intervals for the joint model (each entry is calculated based on 500 Monte Carlo samples).

		N =200	N =500
Parameter	True value	95 per cent CI coverage rate	95 per cent CI coverage rate
β0	10	0.974	0.946
β1	1	0.934	0.944
β2	−1.5	0.960	0.948
σ2	0.25	0.958	0.932
${\sigma }_u^2$	0.5	0.926	0.954
α10	−0.5	0.948	0.934
α11	0.2	0.946	0.934
α12	−0.5	0.956	0.956
γ11	0.8	0.970	0.950
γ12	−0.5	0.940	0.948
γ21	0.5	0.940	0.940
γ22	0.5	0.934	0.946
ν1	0.7	0.938	0.928
ν2	0.5	0.954	0.944

Next we compared the joint model to the separate analysis of either endpoint on the following items: the bias of the point estimates, the empirical standard error, the estimated standard error, and the mean square error. The Monte Carlo samples were simulated from model (17)–(20) and analysed in two ways: the joint model as specified in (17)–(20), and the separate analysis of the two endpoints. The separate analysis was done by fitting a random slope linear model (17) for the longitudinal outcome and a mixture model for the competing risks failure time data with random effect Ũ_i as follows:

$${\pi }_1(X_{1i},X_{2i},{\tilde{U}}_i;\alpha ,\theta )=\frac{\text{exp}({\alpha }_{10}+{\alpha }_{11}{X}_{1i}+{\alpha }_{12}{X}_{2i}+{\tilde{U}}_i)}{1+\text{exp}({\alpha }_{10}+{\alpha }_{11}{X}_{1i}+{\alpha }_{12}{X}_{2i}+{\tilde{U}}_i)}$$ (21)

$${\lambda }_1(t;X_{1i},X_{2i},{\tilde{U}}_i,\gamma ,\tilde{\nu })={\lambda }_{01}(t)\text{exp}\{{\gamma }_{11}{X}_{1i}+{\gamma }_{12}{X}_{2i}+{\tilde{\nu }}_1{\tilde{U}}_i\}$$ (22)

$${\lambda }_2(t;X_{1i},X_{2i},{\tilde{U}}_i,\gamma ,\tilde{\nu })={\lambda }_{02}(t)\text{exp}\{{\gamma }_{21}{X}_{1i}+{\gamma }_{22}{X}_{2i}+{\tilde{\nu }}_2{\tilde{U}}_i\}$$ (23)

where Ũ_i was assumed to be a zero-mean Gaussian random variable with variance ${\tilde{\sigma }}_u^2.$ It is worth noting that for the separate competing risks model (21)–(23), there is no longer a coefficient θ₁ for the random effect Ũ_i in (21) to ensure identifiability. It is easy to see that ${\tilde{\sigma }}_u^2={\theta }_1^2{\sigma }_u^2,{\tilde{\nu }}_1={\nu }_1/{\theta }_1,\text{and}{\tilde{\nu }}_2={\nu }_2/{\theta }_1,\text{where}{\sigma }_u^2,$ ν₁ and ν₂ are the parameters associated with U_i in the competing risk data component (19)–(20) of the joint model. In this simulation, θ₁ was set to 1, and thus ${\tilde{\nu }}_1={\nu }_1,{\tilde{\nu }}_2={\nu }_2\text{and}{\tilde{\sigma }}_u^2={\sigma }_u^2.$ We used a similar approach as proposed in Section 2.3 to compute the variance–covariance matrix for the parameters in (21)–(23). The simulation was based on 500 Monte Carlo samples, and two sample sizes were considered (n =200 and 500; see Tables IV(A) and (B). We label the empirical standard error as SE, the median of estimated standard error as Est. SE, and the mean square error as MSE_J and MSE_S for the joint model and the separate analysis, respectively.

Table IV.

Comparison of the bias, the standard error (SE), the estimated standard error (Est. SE), and the mean square error (MSE) between the joint model and the separate analysis (A) sample size=200 and (B) sample size=500.

		Separate			Joint
Parameter	True	Bias	SE	Est. SE	Bias	SE	Est. SE	MSES/MSEJ
(A)
Longitudinal
Fixed effects
β0	10	0.011	0.039	0.040	−0.0003	0.040	0.041	1.026
β1	1	−0.126	0.070	0.073	−0.004	0.085	0.081	2.869
β2	−1.5	0.001	0.051	0.055	−0.002	0.055	0.057	0.859
Random effects
σ2	0.25	0.0002	0.014	0.015	−0.0004	0.014	0.015	1.001
${\sigma }_u^2$	0.5	−0.039	0.076	0.074	−0.002	0.093	0.087	0.843
Competing risks
Fixed effects
α10	−0.5	−0.159	1.281	6.698	−0.264	1.322	1.230	0.917
α11	0.2	0.065	0.629	2.948	0.115	0.650	0.596	0.918
α12	−0.5	−0.037	0.381	2.830	−0.042	0.375	0.366	1.029
γ11	0.8	−0.084	0.531	6.982	0.026	0.480	0.518	1.251
γ12	−0.5	0.037	0.360	6.504	−0.081	0.352	0.320	1.004
γ21	0.5	<0.0001	0.474	2.798	0.043	0.426	0.416	1.226
γ22	0.5	−0.002	0.282	2.804	0.023	0.277	0.257	1.029
Random effects
ν1	0.7	−0.664	0.210	132.2	0.025	0.419	0.373	2.753
ν2	0.5	−0.440	0.223	55.33	0.029	0.301	0.288	2.661
${\sigma }_u^2$	0.5	0.093	0.076	36.75	−0.002	0.093	0.087	1.667
(B)
Longitudinal
Fixed effects
β0	10	0.013	0.024	0.025	0.001	0.026	0.025	1.102
β1	1	−0.127	0.046	0.046	−0.002	0.054	0.051	6.248
β2	−1.5	−0.002	0.032	0.035	−0.002	0.035	0.035	0.836
Random effects
σ2	0.25	0.0001	0.010	0.009	−0.0003	0.009	0.009	1.234
${\sigma }_u^2$	0.5	−0.035	0.047	0.046	0.0004	0.055	0.054	1.135
Competing risks
Fixed effects
α10	−0.5	−0.128	0.825	0.995	−0.149	0.811	0.753	1.025
α11	0.2	0.052	0.395	0.442	0.063	0.386	0.364	1.038
α12	−0.5	−0.020	0.229	0.513	−0.011	0.222	0.228	1.070
γ11	0.8	−0.083	0.363	1.231	−0.0002	0.303	0.302	1.510
γ12	−0.5	0.023	0.248	1.901	−0.031	0.196	0.190	1.575
γ21	0.5	0.012	0.285	0.803	0.009	0.265	0.251	1.157
γ22	0.5	0.018	0.181	1.210	−0.002	0.170	0.159	1.145
Random effects
ν1	0.7	−0.541	0.368	31.34	−0.013	0.224	0.210	8.503
ν2	0.5	−0.358	0.321	23.29	0.016	0.182	0.170	2.005
${\sigma }_u^2$	0.5	0.086	0.038	6.601	0.0004	0.055	0.054	6.926

Note The separate analysis for longitudinal data used the linear mixed effects model (17) which is not able to handle non-ignorable missing data and results in considerable biases. The competing risks survival data were analysed using the mixture model (21)–(23). The joint analysis was based on the model (17)–(20).

The results can be summarized as follows. First of all, the time trend β₁ of the longitudinal measurements is severely underestimated in the separate analysis for both sample sizes. The variance of the time trend, ${\sigma }_u^2,$ is also negatively biased. This is the consequence of the informative dropout process in which with positive coefficients ν₁ and ν₂, we observe a higher risk of dropout for those subjects with greater than average increasing rates over time in the longitudinal out-come. The resultant non-ignorable missing values after dropout cannot be accounted for in the linear mixed effects model alone and thus biases in the estimated time trend and its variance are observed. However, we are able to obtain almost unbiased estimates for these quantities in the joint analysis, where the informative dropout process has been modelled together with the longitudinal measurements. Our results are consistent with the findings of Henderson et al. [9]. Second, it is observed that the joint model provides much more accurate estimates for ν₁ and ν₂, the coefficients of the random effects in the hazards, than those from the mixture model alone which produces even worse estimates when the sample size is not that large (say, 200). This finding indicates that we can improve the efficiency of frailty estimation in the survival endpoint by combining the information of the longitudinal outcome, if the latter is correlated with the frailty and the correlation is correctly modelled. This is analogous to frailty models for multivariate survival data, in which frailty measures association among multiple event times. The frailty is easier to estimate and identify in multivariate survival analysis than in univariate survival analysis for heterogeneity [33]. Third, in the separate analysis for the competing risks survival data, the standard errors are overestimated for all the parameters compared to the empirical ones, especially for ν₁ and ν₂. In contrast, we can obtain more accurate standard error estimates from the joint model. Overall, the joint model performs better than the separate analysis with smaller MSE for most parameters. We note that for parameters α₁₀, α₁₁ and ${\sigma }_u^2$ at the competing risks endpoint, the biases and/or variances are larger for the joint model than the separate at the current sample sizes (n =200 and 500). However, in our simulation with n =1000, smaller biases and variances are observed for the joint model compared to the separate.

We did further simulations to compare the power of detecting treatment effects on the competing risks failure time data between the joint model and the separate analysis. Here we did not compare the power for the longitudinal measurements since in the separate analysis, the linear mixed effects model is not valid in the presence of non-ignorable missing values. For simplicity, the longitudinal measurements were simulated from a random intercept linear model

$$Y_{ij}={\beta }_0+{\beta }_1{X}_{1i}+{\beta }_2{X}_{2i}+U_i+{\epsilon }_{ij}$$ (24)

and the competing risks failure times were simulated from model (18)–(20). The binary covariate X_2i acts as a treatment group indicator in randomized trials, so the test for treatment effects on competing risks would have the following null hypothesis and the alternative:

$$\begin{array}{cc}{H}_0:\hfill & {\alpha }_{12}=0\hfill \\ \hfill & {\gamma }_{12}=0\hfill \\ \hfill & {\gamma }_{22}=0\hfill \\ H_A:\hfill & \text{at least one of them}\ne 0\hfill \end{array}$$

Wald’s tests were performed on 200 Monte Carlo samples. The rejection rates under different sample sizes are summarized in Table V. There are four sets of coefficients for X₂. Model I is the null model, where α₁₂ =γ₁₂ =γ₂₂ =0. Under Model I, the rejection rate in the joint model is close to the significance level of 0.05 when the sample size is large enough, but the analysis for competing risks data alone tends to be conservative. Models II, III, and IV are different alternatives, where the true values for α₁₂, γ₁₂, and γ₂₂ are 0, 1.0, and −1.0 in Model II, 1.0, 1.0, and 0 in Model III, and 0.8, 0.8, and −0.8 in Model IV, respectively. It is shown that the analysis for competing risks alone has much lower power than the joint model in Models II, III, and IV for almost all sample sizes. It is the consequence of inflated variance estimates for competing risks failure time data in the separate analysis. We have observed similar results under model (17)–(20) (see Tables IV(A) and (B).

Table V.

Comparison of the power of the tests for treatment effects on the competing risks failure time data based on 200 Monte Carlo samples.

	Model I		Model II		Model III		Model IV
Sample size	Joint	Separate	Joint	Separate	Joint	Separate	Joint	Separate
50	0.025	<0.001	0.180	0.020	0.340	0.025	0.150	0.010
100	0.055	<0.001	0.740	0.080	0.920	0.155	0.745	0.090
200	0.040	0.005	0.990	0.525	1.000	0.255	1.000	0.235
500	0.060	0.015	1.000	0.950	1.000	0.630	1.000	0.680

We finally examined the behaviour of the joint analysis of longitudinal measurements and survival data with a single failure type in the presence of informative censoring. The Monte Carlo samples were generated from the joint model (17)–(20), and were analysed by the following joint model in which risk 1 is the event of interest, and failures due to risk 2 were incorrectly treated as non-informatively censored events

$$Y_{ij}={\beta }_0+{\beta }_1{t}_{ij}+{\beta }_2{X}_{2i}+U_i{t}_{ij}+{\epsilon }_{ij}$$ (25)

$${\lambda }_1(t;X_{1i},X_{2i},U_i;\gamma ,\nu )={\lambda }_{01}(t)\text{exp}\{{\gamma }_{11}{X}_{1i}+{\gamma }_{12}{X}_{2i}+{\nu }_1{U}_i\}$$ (26)

Tables VI(A) and (B) summarize the results for sample sizes 200 and 500, respectively, both of which are based on 500 Monte Carlo samples. Considerable bias occurs for the parameter ν₁ in the joint model with a single failure type, treating the correlated competing risk as non-informative censoring. This results in very low confidence interval coverage probabilities especially when the sample size increases to 500. No such bias is observed for the joint model in which the informatively censored events have been modelled together with risk 1 as failures due to a competing risk. In addition, we note that larger bias also occurs for the parameters ${\sigma }_u^2,$ γ₁₁, and γ₁₂ in the single failure type joint model with the correlated competing risk treated as independent censoring as the sample size goes up to 500.

Table VI.

Comparison of the bias, the standard error (SE), the estimated standard error (Est. SE), and the simulated coverage probability (CP) of the 95 per cent confidence intervals between a joint model with competing risks versus that with a single failure type where the other failure is treated as independent censoring (A) sample size=200 and (B) sample size=500.

		Ignoring the competing risk				Competing risks
Parameter	True	Bias	SE	Est. SE	CP	Bias	SE	Est. SE	CP
(A)
Longitudinal
Fixed effects
β0	10	0.001	0.039	0.041	0.952	−0.0003	0.040	0.041	0.974
β1	1	−0.002	0.079	0.073	0.928	−0.004	0.085	0.081	0.934
β2	−1.5	−0.004	0.053	0.056	0.968	−0.002	0.055	0.057	0.960
Random effects
σ2	0.25	−0.0005	0.014	0.015	0.962	−0.0004	0.014	0.015	0.958
${\sigma }_u^2$	0.5	0.031	0.090	0.092	0.954	−0.002	0.093	0.087	0.926
Survival
Fixed effects
γ11	0.8	0.085	0.436	0.447	0.960	0.026	0.480	0.518	0.970
γ12	−0.5	0.068	0.265	0.282	0.958	−0.081	0.352	0.320	0.940
Random effects
ν1	0.7	0.477	0.287	0.307	0.714	0.025	0.419	0.373	0.938
(B)
Longitudinal
Fixed effects
β0	10	0.003	0.024	0.025	0.958	0.001	0.026	0.025	0.946
β1	1	−0.005	0.049	0.046	0.934	−0.002	0.054	0.051	0.944
β2	−1.5	−0.005	0.034	0.035	0.956	−0.002	0.035	0.035	0.948
Random effects
σ2	0.25	−0.001	0.009	0.009	0.956	−0.0003	0.009	0.009	0.932
${\sigma }_u^2$	0.5	0.029	0.058	0.057	0.946	0.0004	0.055	0.054	0.954
Survival
Fixed effects
γ11	0.8	0.092	0.269	0.265	0.924	−0.0002	0.303	0.302	0.950
γ12	−0.5	0.079	0.165	0.169	0.944	−0.031	0.196	0.190	0.948
Random effects
ν1	0.7	0.435	0.178	0.180	0.304	−0.013	0.224	0.210	0.928

5. DISCUSSION

In clinical trials, it is very common that both longitudinal measurements and event times are recorded on the study subjects during follow-up. Previous methods for joint modelling of these two endpoints have focused on a single failure type for the event times with non-informative censoring, which may not be applicable in the presence of informative censoring or competing risks. In this article, we have proposed a joint model for longitudinal measurements and competing risks failure time data, which can be used to handle informative censoring by treating it as a competing risk for the event of interest. Our approach accommodates the mixed effects sub-model for the longitudinal outcome and the two-step mixture sub-model for competing risks. Besides the random effects U, we need to introduce an additional hidden variable τ to simplify the estimation procedure in the mixture sub-model. An EM-based algorithm has been developed to estimate the parameters of interest, and their variance–covariance matrix can be approximated by inverting the empirical Fisher information derived from the profile likelihood. Our joint model not only provides a framework for joint inference on longitudinal outcome and time to event data with competing risks, but also a means to analyse longitudinal outcome with non-ignorable missing mechanisms (discussed in Remark 2 of Section 2.1). In addition, our simulation studies show that the joint model improves the efficiency of frailty estimation in the survival endpoint, and is able to produce accurate estimates of the standard errors using the profile likelihood method. Our joint model also is shown to have more power in statistical tests for effects of factors at the survival endpoint. Finally, we point out that since we need to evaluate integrals of various functions of U in the E-step of each iteration, computational burden increases dramatically with growth of the dimension of the random effects U. This is a common issue in all likelihood-based approaches involving random effects.

Because we discretize the baseline hazards, the dimension of the parameter space increases with the sample size. It is a challenging task to establish the asymptotic properties of the estimators from such a complex semi-parametric model. Recently Zeng and Cai [34] derived the asymptotic distributions of the maximum likelihood estimators from their joint model in which they considered a single failure type for the time to event. A rigorous treatment of the asymptotic properties of the MLE’s under our model with competing risks warrants future research.

Our method can be further extended to robust inference for joint analysis of longitudinal measurements and survival data to handle outlying observations in the longitudinal outcome. One possible approach is to use the idea of Richardson [35] by incorporating weight functions in maximum likelihood and restricted maximum likelihood estimating equations. In a sequel we develop a robust procedure by replacing the normal distribution assumption for measurement errors with the t distribution to take into account longer-than-normal tails. Another issue is about the robustness to the normality assumption of the random effects. It has been noted by Song et al. [19] and Hsieh et al. [36] that the estimation procedure is robust to the normality assumption in some joint models of longitudinal and survival data with a single failure type. We have not investigated this issue in this paper although we expect similar conclusions.

APPENDIX A: THE EM-BASED ALGORITHM

E-step

Because the complete-data log-likelihood is linear in τ, we can write E_U,τ|Y,C,Ψ^(m)[l(Ψ;U, τ)] = E_U|Y,C,Ψ^(m)[l(Ψ;U, E_τ|U,Y,C,Ψ^(m)(τ))], where m indicates that the parameter estimates are from the mth iteration of the EM algorithm. In the E-step of the (m + 1)th iteration, for the censored subject i, we have

$$E_{{\tau }_{ik}|U,Y,C,{\Psi }^{(m)}}({\tau }_{ik})=\frac{{\pi }_k(X_i^{(2)},U_i;{\alpha }^{(m)},{\theta }^{(m)})S_k(T_i;{\overline{X}}_i^{(3)}(T_i),U_i,{\gamma }^{(m)},{\nu }^{(m)})}{{\displaystyle {\sum }_{l=1}^g{\pi }_l(X_i^{(2)},U_i;{\alpha }^{(m)},{\theta }^{(m)})S_l(T_i;{\overline{X}}_i^{(3)}(T_i),U_i,{\gamma }^{(m)},{\nu }^{(m)})}}$$ (A1)

which is a function of the hidden variable U. Therefore, we need to evaluate the expected values of all functions of U, say h(U), in l(Ψ;U, E_τ|U,Y,C,Ψ^(m) (τ)), conditional on the observed data and the current parameter estimates. We have

$$\begin{array}{ccc}{E}_{U|Y,C,{\mathrm{\Psi }}^{(m)}}[h(U)]\hfill & ={\displaystyle \int h(U)f(U|Y,C,{\mathrm{\Psi }}^{(m)})\mathrm{d}U}\hfill & \hfill \\ \hfill & =\frac{{\displaystyle \int h(U)f(U|Y,{\mathrm{\Psi }}^{(m)})f(C|U,{\mathrm{\Psi }}^{(m)})\mathrm{d}U}}{f(C|Y,{\mathrm{\Psi }}^{(m)})}\hfill & \hfill \\ \hfill & =\frac{{\displaystyle \int h(U)f(U|Y,{\mathrm{\Psi }}^{(m)})f(C|U,{\mathrm{\Psi }}^{(m)})\mathrm{d}U}}{{\displaystyle \int f(C|U,{\mathrm{\Psi }}^{(m)})f(U|Y,{\mathrm{\Psi }}^{(m)})\mathrm{d}U}}\hfill & \hfill \end{array}$$ (A2)

where we use the fact

$$\begin{array}{cc}f(U|Y,C,{\mathrm{\Psi }}^{(m)})\hfill & =\frac{f(U|Y,{\mathrm{\Psi }}^{(m)})f(C|U,{\mathrm{\Psi }}^{(m)})}{f(C|Y,{\mathrm{\Psi }}^{(m)})}\hfill \\ \hfill & =\frac{f(U|Y,{\mathrm{\Psi }}^{(m)})f(C|U,{\mathrm{\Psi }}^{(m)})}{{\displaystyle \int f(C|U,{\mathrm{\Psi }}^{(m)})f(U|Y,{\mathrm{\Psi }}^{(m)})\mathrm{d}U}}\hfill \end{array}$$ (A3)

The distribution of U|Y,Ψ^(m) is multivariate normal with an easily derived mean and variance covariance matrix, and

$$\begin{array}{cc}f(C|U,{\mathrm{\Psi }}^{(m)})=\hfill & {\displaystyle \prod _{k=1}^g{[{\pi }_k(X_i^{(2)},U_i;{\alpha }^{(m)},{\theta }^{(m)})f_k(T_i;X_i^{(3)}(T_i),U_i,{\gamma }^{(m)},{\nu }^{(m)})]}^{I(D_i=k)}}\hfill \\ \hfill & \times [{\displaystyle \sum _{l=1}^g{{\pi }_l(X_i^{(2)},U_i;{\alpha }^{(m)},{\theta }^{(m)})S_l(T_i;{\overline{X}}_i^{(3)}(T_i),U_i,{\gamma }^{(m)},{\nu }^{(m)})]}^{I(D_i=0)}}\hfill \end{array}$$ (A4)

for the i th subject. Note that our method requires integration with respect to U in (A2) and (A3). The integrals can be evaluated using numerical integration (quadrature) [37].

M-step

The vector of parameters Ψ is updated by maximizing Q(Ψ; Ψ^(m)) = E_U,τ|Y,C,Ψ^(m) [l(Ψ;U, τ)]. In the formula below, we use E to stand for E_U,τ|Y,C,Ψ^(m). Closed-form estimates are available for β, Σ, σ², and baseline hazards λ_0k(t) for k = 1, …, g, whose cumulative function H_0k (t) is shown below. We write vector $X_{ij}^{(1)}=(1,X_i^{(1)}{(t_{ij})}^{\mathrm{T}}{)}^{\mathrm{T}}$ and have

$${\beta }^{(m+1)}={\left[{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{n_i}{X}_{ij}^{(1)}{X}_{ij}^{(1)\mathrm{T}}}}\right]}^{-1}\left\{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{n_i}[Y_{ij}-E(U_{0i}+U_{1i}^{\mathrm{T}}{\tilde{X}}_i^{(1)}(t_{ij}))]}{X}_{ij}^{(1)}}\right\}$$ (A5)

$${\sigma }^{2(m+1)}=\frac{1}{{\displaystyle {\sum }_{i=1}^n{n}_i}}\left\{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{n_i}E(Y_{ij}-{\beta }^{(m+1)\mathrm{T}}{X}_{ij}^{(1)}-U_{0i}-U_{1i}^{\mathrm{T}}{\tilde{X}}_i^{(1)}{(t_{ij}))}^2}}\right\}$$ (A6)

and

$${\sum }^{(m+1)}=\frac{1}{n}\left\{{\displaystyle \sum _{i=1}^{n}E(U_i{U}_i^{\mathrm{T}})}\right\}$$ (A7)

In calculation of the baseline hazards, the failure time observations are firstly ordered from the smallest to the largest. If there are q_k distinct failure times due to the kth cause, then we write t_k1 ≤ …, ≤ t_kqk for k = 1, …, g. The cumulative baseline hazard function for cause k is denoted by H_0k(t). Let R(t_kj) be the risk set at time t_kj, and d_kj be the number of failures due to cause k at time t_kj. We have

$$\begin{array}{ccc}{H}_{0k}{(t)}^{(m+1)}\hfill & =\hfill & {\displaystyle \sum _{t_{kj}\le t}{\lambda }_{0k}{(t_{kj})}^{(m+1)}}\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{t_{kj}\le t}\{\raisebox{1ex}{$d_{kj}$}\!\left/ \!\raisebox{-1ex}{${\displaystyle \sum _{r\in R(t_{kj})}\text{exp}({\gamma }_k^{(m)\mathrm{T}}{X}_r^{(3)}(t_{kj}))[I(D_r=k)E(\text{exp}({\nu }_k^{(m)\mathrm{T}}{U}_r))}$}\right.}\hfill \\ \hfill & \hfill & +I(D_r=0)E({\tau }_{rk}\text{exp}({\nu }_k^{(m)\mathrm{T}}{U}_r))]\}\hfill \end{array}$$ (A8)

No closed-form solutions exist for α, θ, γ, and ν. They satisfy the following score equations, respectively

$${\displaystyle \sum _{i=1}^n\{I(D_i=k)+I(D_i=0)E({\tau }_{ik})-E({\pi }_k(X_i^{(2)},U_i;\alpha ,{\theta }^{(m)}))\}}{(1,X_i^{(2)\mathrm{T}})}^{\mathrm{T}}=0$$ (A9)

for k =1, …, g − 1

$${\displaystyle \sum _{i=1}^n\{I(D_i=k)E(U_i)+I(D_i=0)E({\tau }_{ik}{U}_i)-E(U_i{\pi }_k(X_i^{(2)},U_i;{\alpha }^{(m+1)},\theta ))\}}=0$$ (A10)

for k = 1, …, g − 1

$$\begin{array}{c}{\displaystyle \sum _{i=1}^n\{I(D_i=k)X_i^{(3)}(T_i)-{\displaystyle \sum _{t_{kj}\le T_i}{\lambda }_{0k}{(t_{kj})}^{(m+1)}\text{exp}({\gamma }_k^{\mathrm{T}}{X}_i^{(3)}(t_{kj}))[I(D_i=k)}}\\ \times E(\text{exp}({\nu }_k^{(m)\mathrm{T}}{U}_i))+I(D_i=0)E({\tau }_{ik}\exp ({\nu }_k^{(m)\mathrm{T}}{U}_i))]X_i^{(3)}(t_{kj})\}=0\end{array}$$ (A11)

for k = 1, …, g, and

$$\begin{array}{c}{\displaystyle \sum _{i=1}^n\{I(D_i=k)E(U_i)-{\displaystyle \sum _{t_{kj}\le T_i}{\lambda }_{0k}{(t_{kj})}^{(m+1)}\text{exp}({\gamma }_k^{(m+1)\mathrm{T}}{X}_i^{(3)}(t_{kj}))[I(D_i=k)}}\\ \times E({\text{U}}_i\text{exp}({\nu }_k^{\mathrm{T}}{U}_i))+I(D_i=0)E(U_i{\tau }_{ik}\exp ({\nu }_k^{\mathrm{T}}{U}_i))]\}=0\end{array}$$ (A12)

for k = 1, …, g, where t_{k j} and λ_0k (t_{k j}) are the same as in (A8). We do not need to solve the above equations, and the parameters α, θ, γ, and ν can be updated using the following one-step Newton–Raphson algorithm in each iteration. Letting ${\tilde{X}}_i^{(2)}=(1,X_i^{(2)\mathrm{T}}{)}^{\mathrm{T}},$ we have

$${\alpha }_k^{(m+1)}={\alpha }_k^{(m)}+I_{{\alpha }_k}^{(m)-1}{S}_{{\alpha }_k}^{(m)}$$ (A13)

for k =1, …, g − 1, where the matrix $I_{{\alpha }_k}^{(m)}$ and the vector $S_{{\alpha }_k}^{(m)}$ are

$$I_{{\alpha }_k}^{(m)}={\displaystyle \sum _{i=1}^{n}E({\pi }_k(X_i^{(2)},U_i;{\alpha }^{(m)},{\theta }^{(m)})-{\pi }_k^2(X_i^{(2)},U_i;{\alpha }^{(m)},{\theta }^{(m)})){\tilde{X}}_i^{(2)}{\tilde{X}}_i^{(2)\mathrm{T}}}$$ (A14)

$$S_{{\alpha }_k}^{(m)}={\displaystyle \sum _{i=1}^n\{I(D_i=k)+I(D_i=0)E({\tau }_{ik})-E({\pi }_k(X_i^{(2)},U_i;{\alpha }^{(m)},{\theta }^{(m)}))}\}{\tilde{X}}_i^{(2)}$$ (A15)

$${\theta }_k^{(m+1)}={\theta }_k^{(m)}+I_{{\theta }_k}^{(m)-1}{S}_{{\theta }_k}^{(m)}$$ (A16)

for k = 1, …, g − 1, where the matrix $I_{{\theta }_k}^{(m)}$ and the vector $S_{{\theta }_k}^{(m)}$ are

$$I_{{\theta }_k}^{(m)}={\displaystyle \sum _{i=1}^{n}E[U_i{U}_i^{\mathrm{T}}({\pi }_k(X_i^{(2)},U_i;{\alpha }^{(m+1)},{\theta }^{(m)})-{\pi }_k^2(X_i^{(2)},U_i;{\alpha }^{(m+1)},{\theta }^{(m)}))]}$$ (A17)

$$\begin{array}{ccc}{S}_{{\theta }_k}^{(m)}\hfill & =\hfill & {\displaystyle \sum _{i=1}^n[I(D_i=k)E(U_i)+I(D_i=0)E({\tau }_{ik}{U}_i)}\hfill \\ \hfill & \hfill & -E({\text{U}}_i{\pi }_k(X_i^{(2)},U_i;{\alpha }^{(m+1)},{\theta }^{(m)}))]\hfill \end{array}$$ (A18)

$${\gamma }_k^{(m+1)}={\gamma }_k^{(m)}+I_{{\gamma }_k}^{(m)-1}{S}_{{\gamma }_k}^{(m)}$$ (A19)

for k = 1, …, g, where the matrix $I_{{\gamma }_k}^{(m)}$ and the vector $S_{{\gamma }_k}^{(m)}$ are

$$\begin{array}{cc}{I}_{{\gamma }_k}^{(m)}=\hfill & {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{t_{kj}\le T_i}{\lambda }_{0k}{(t_{kj})}^{(m+1)}\text{exp}({\gamma }_k^{(m)\mathrm{T}}{X}_i^{(3)}(t_{kj}))[I(D_i=k)}}E(\text{exp}({\nu }_k^{(m)\mathrm{T}}{U}_i))\hfill \\ \hfill & +I(D_i=0)E({\tau }_{ik}\text{exp}({\nu }_k^{(m)\mathrm{T}}{U}_i))]X_i^{(3)}(t_{kj})X_i^{(3)}{(t_{kj})}^{\mathrm{T}}\hfill \\ \hfill & \hfill \end{array}$$ (A20)

$$\begin{array}{c}{S}_{{\gamma }_k}^{(m)}={\displaystyle \sum _{i=1}^n\{I(D_i=k)X_i^{(3)}(T_i)-{\displaystyle \sum _{t_{kj}\le T_i}{\lambda }_{0k}{(t_{kj})}^{(m+1)}\text{exp}({\gamma }_k^{(m)\mathrm{T}}{X}_i^{(3)}(t_{kj}))[I(D_i=k)}}\\ \times E(\text{exp}({\nu }_k^{(m)\mathrm{T}}{U}_i))+I(D_i=0)E({\tau }_{ik}\exp ({\nu }_k^{(m)\mathrm{T}}{U}_i))]X_i^{(3)}(t_{kj})\}\end{array}$$ (A21)

and finally

$${\nu }_k^{(m+1)}={\nu }_k^{(m)}+I_{{\nu }_k}^{(m)-1}{S}_{{\nu }_k}^{(m)}$$ (A22)

for k = 1, …, g, where the matrix $I_{{\nu }_k}^{(m)}$ and the vector $S_{{\nu }_k}^{(m)}$ are

$$\begin{array}{cc}{I}_{{\nu }_k}^{(m)}=\hfill & {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{t_{kj}\le T_i}{\lambda }_{0k}{(t_{kj})}^{(m+1)}\text{exp}({\gamma }_k^{(m+1)\mathrm{T}}{X}_i^{(3)}(t_{kj}))[I(D_i=k)}}E(U_i{\text{U}}_i^{\mathrm{T}}\text{exp}({\nu }_k^{(m)\mathrm{T}}{U}_i))\hfill \\ \hfill & +I(D_i=0)E(U_i{\text{U}}_i^{\mathrm{T}}{\tau }_{ik}\text{exp}({\nu }_k^{(m)\mathrm{T}}{U}_i))]\hfill \\ \hfill & \hfill \end{array}$$ (A23)

$$\begin{array}{c}{S}_{{\nu }_k}^{(m)}={\displaystyle \sum _{i=1}^n\{I(D_i=k)E(U_i)-{\displaystyle \sum _{t_{kj}\le T_i}{\lambda }_{0k}{(t_{kj})}^{(m+1)}\text{exp}({\gamma }_k^{(m+1)\mathrm{T}}{X}_i^{(3)}(t_{kj}))[I(D_i=k)}}\\ \times E(U_i\text{exp}({\nu }_k^{(m)\mathrm{T}}{U}_i))+I(D_i=0)E(U_i{\tau }_{ik}\exp ({\nu }_k^{(m)\mathrm{T}}{U}_i))]\}\end{array}$$ (A24)

It should be noted that in the M-step, some parameters are calculated conditional on the most updated values of other parameters. For example, we use β^(m+1) instead of β^(m) when updating σ² in (A6) and α^(m+1) instead of α^(m) when obtaining θ^(m+1) from (A10). This is similar for ${\lambda }_{0k}^{(m+1)}$ in (A11) and (A12), and γ^(m+1) in (A12). This is the modified version of EM algorithm called the expectation-conditional maximization (ECM) algorithm [38]. By the ECM algorithm, the maximization procedure is much simplified conditional on some parameters being estimated, due to the difficulty of maximizing the likelihood with respect to α, θ, γ, and ν simultaneously in our joint model formulation. In addition, it is shown that the ECM algorithm has the same convergence features as the EM algorithm.