Direct Comparison of the Task-Dependent Discharge of M1 in Hand Space and Muscle Space

Abstract

Since its introduction in the early 1980s, the concept of a “preferred direction” for neuronal discharge has proven to be a powerful means of studying motor areas of the brain. In the current paper, we introduce the concept of a “muscle-space”–preferred direction (PD_M) that is analogous to the familiar hand-space–preferred direction (PD_H). PD_M reflects the similarity between the discharge of a given neuron and the activity of each muscle in much the way that PD_H reflects the similarity of discharge with motion along each of the three Cartesian coordinate axes. We used PD_M to analyze the data recorded from neurons in the primary motor cortex (M1) of three different monkeys. The monkeys performed center-out movements within two different cubical workspaces centered either to the left or right of the monkey’s shoulder while we simultaneously recorded neuronal discharge, muscle activity, and limb orientation. We calculated preferred directions in both hand space and muscle space, and computed the angles between these vectors under a variety of conditions. PDs for different neurons were broadly distributed throughout both hand space and muscle space, but the muscle-space vectors appeared to form clusters of functionally similar neurons. In general, repeated estimates of PD_M were more stable over time than were similar estimates of PD_H. Likewise, there was less change in PD_M than in PD_H for data recorded from the two different workspaces. However, although a majority of neurons had this muscle-like property, a significant minority was more stable in Cartesian hand space, reflecting a heterogeneity of function within M1.

INTRODUCTION

It is widely accepted from a host of different types of experiments that primary motor cortex (M1) provides important signals for movement generation. However, it has proven surprisingly difficult to determine the nature of the information contained in the discharge of single M1 neurons and to identify the particular variables that they presumably control. Many movement-related variables covary with M1 discharge (Ashe 1997; Ashe and Georgopoulos 1994; Cheney et al. 1988; Evarts 1968; Fu et al. 1995; Thach 1978). Yet this covariation alone is not sufficient to prove that M1 controls any one in particular. The problem occurs, in large part, because each recorded neuron is actually part of a very large network of correlated neurons and many of the putative controlled variables are well correlated with one another during normal movements (Fu et al. 1995; Graham et al. 2003).

Classic studies of M1 discharge during whole limb movement revealed a striking relationship between neuronal firing rate and the direction of hand movement (Georgopoulos et al. 1983, 1986, 1988). The maximal discharge rate of many cells is associated with a “preferred direction” (PD) of hand movement. Movements in other directions elicit discharge that is proportional to the component of the movement along the PD axis. Other early experiments showed that the modulation of discharge rate is well correlated to the velocity and, to a lesser extent, position of the hand (Ashe and Georgopoulos 1994; Flament and Hore 1988; Hamada 1981; Humphrey et al. 1970; Paninski et al. 2004). These observations led to the suggestion that M1 discharge “encodes” the velocity of hand movement. Accordingly, these hand-movement command signals would then be transformed into appropriate muscle signals by propriospinal and segmental interneurons.

Although much of the descending input to the cord terminates on interneurons, there is abundant anatomical (Landgren et al. 1962; Lawrence et al. 1985) and physiological (Buys et al. 1986; Cheney et al. 1985) evidence of a system of corticomotorneuronal (CM) projections directly to motor neurons, including those of the proximal limb (McKiernan et al. 1998). This system would seem to allow for relatively little signal transformation between M1 discharge and muscle activity. It seems unlikely that it would coexist in parallel with a system encoding hand movement.

Beginning with Evarts (1968), numerous experiments were carried out using added weights (Kalaska et al. 1989), altered postures (Kakei et al. 1999; Scott and Kalaska 1997), or different workspaces (Caminiti et al. 1990) to change the relation between muscle activity and movement. The goal of such experiments is to alter the mutual correlations among the movement-related signals and to determine whether the relation between neuronal discharge and the kinematics of movement remains unchanged. If so, a stronger case could be made that that particular relation is a causal one. The experimental manipulations in each of the cited experiments caused significant alteration in neuronal discharge, despite the fact that the monkey produced very similar hand movements.

M1 discharge has also been compared with various kinetic signals for whole arm movement tasks. Experiments in which movements were constrained to the horizontal plane by a robotic exoskeleton showed that the activity in M1 is modulated in response to shoulder and elbow torque in much the same way as are the major proximal limb muscles (Cabel et al. 2001). The same was found to be true of both isometric forces and movements against load forces applied to the hand (Sergio and Kalaska 2003; Sergio et al. 2005). In contrast, however, an earlier study found distinct differences between the representation by M1 of the static and dynamic components of isometric forces. In this respect, the discharge differed from the general behavior of muscles (Georgopoulos et al. 1992). That observation may be explained by a recent observation of significant task dependency in M1, with respect to the representation of postural and movement commands (Kurtzer et al. 2005).

This combination of anatomical and physiological observations led us and others to hypothesize that M1 may control limb movement by specifying patterns of muscle activation rather than hand movement per se. Unfortunately, in relatively few experiments have neuronal discharge and electromyographic (EMG) activity been measured simultaneously during whole arm movements, such that they could be compared directly (although see McKiernan et al. 2000; Schwartz and Adams 1995). Often, M1 and EMG activity were measured and analyzed separately and comparisons made of the general characteristics of their timing and modulation (Cabel et al. 2001; Crammond and Kalaska 1996; Kakei et al. 1999; Moran and Schwartz 1999b; Scott 1997; Sergio and Kalaska 1998). There is also a significant literature describing the postspike effects of single action potentials on EMG (Fetz et al. 1976; Lemon et al. 1986; McKiernan et al. 1998; Poliakov and Schieber 1998). However, there have been no studies of which we are aware, in which relations between neuronal discharge and both EMG and limb movement were compared across conditions using simultaneously recorded data.

Our experiment is based on the design of a classic study of the changes in preferred direction that occurred for hand movements made in different workspaces. In that study, monkeys were trained to make center-out reaches to targets in three different workspaces: one centered in front of the shoulder, one to the left, and one to the right (Caminiti et al. 1990). The workspaces were designed and the monkeys were trained to produce approximately parallel trajectories in each of the three workspaces. Despite the similar movements, the neuronal preferred directions tended to rotate with the center of the workspace, although for any given neuron, this change was rather unpredictable. In addition to M1 discharge, the activity of most proximal arm muscles was also significantly different across the workspaces. However, because EMG was not measured together with neuronal discharge, it was impossible to determine whether the changes in EMG activity corresponded directly to the changes in neuronal discharge.

Using the same basic design, while simultaneously measuring neuronal discharge, EMG activity, and limb orientation, we calculated preferred directions using a novel method based on patterns of cross-correlations between neuronal firing rate and hand velocity. We also used this method to calculate preferred directions in muscle space, by comparing neuronal discharge to EMG signals rather than hand velocity. The majority of these muscle-space–preferred directions (PD_Ms) appeared to suggest groups of functionally similar neurons controlling synergistically related muscles. For most neurons, PD_M was more stable across both time and different workspaces than was the corresponding preferred direction in hand-movement space (PD_H). This suggests that the principal encoding scheme of M1 discharge is that of muscle activity patterns rather than kinematic hand-movement variables.

METHODS

Task and training

Neuronal activity, EMG activity, and limb-related kinematic signals were simultaneously recorded from each of three macaque monkeys. Neuronal activity was recorded from single units in the arm area of primary motor cortex, along with EMG signals from between 10 and 17 arm and hand muscles. Table 1 indicates the EMGs recorded from each monkey. A system of magnetic sensor coils (Nocher et al. 1996) was used to record limb segment orientation, from which hand-movement speed and direction were calculated. For monkey Q, three coils were implanted on the humerus, ulna, and first metacarpal; this allowed us to track the position in space of the first metacarpal–intraphalangeal joint. For monkeys Gn and Gv, two coils were fixed to the surface of the upper arm and the forearm at the beginning of each experimental session. For these two monkeys, we tracked the position of the wrist.

TABLE 1.

Muscles recorded for each monkey

Subject	EMG
	Trap	Inf	Rhm	Lat	Ter	Pec	PDl	MDl	ADl	Tri	Bic	Pro	Brd	FCR	FCU	ECR	ECU	FDS	EDC	E45	AbPL	AdP	1DI
Gn	●						●		●	●	●		●			●	●	●	●	●	●	●	●
Gv	●	●	●	●	●	●	●	●	●	●	●			●		●	●	●	●				●
Q	●				●		●	●		●		●	●		●	●		●

Abbreviations (left to right): Trap, trapezius; Inf, infraspinatus; Rhm, rhomboid; Lat, latissimus dorsi; Ter, teres major; Pec, pectoralis; PDl, posterior deltoid; MDl, medial deltoid; ADl, anterior deltoid; Tri, triceps; Bic, biceps; Pro, pronator teres; Brd, brachioradialis; FCR, flexor carpi radialis; FCU, flexor carpi ulnaris; ECR, extensor carpi radialis; ECU, extensor carpi ulnaris; FDS, flexor digitorum superficialis; EDC, extensor digitorum communis; E45, extensor digiti 4,5; AbPL, abductor pollicis longus; AdP, adductor pollicis; 1DI, 1st dorsal interosseous.

Each monkey performed a three-dimensional (3D) center-out limb movement task within a cubical workspace 20 cm on a side. A sensor was located at the center of the workspace and in each corner of the cube. In the “left” condition, the cube was placed in front of the monkey, about 10 cm to the left of the monkey’s shoulder, and in the “right” condition, 10 cm to the right. At the beginning of a trial, the monkey activated the sensor at the center of the workspace. One of the outer sensors was then illuminated, and a subsequent “go” tone signaled the animal to move. The monkey was required to move to and activate the outer sensor for a variable time between 500 and 1,000 ms, at the end of which a reward tone and a liquid reward were given and the monkey returned its hand to the center. The next trial was initiated after a random interval of 2–4 s. The monkey performed 15–30 trials in one of the two workspaces, typically without any interruptions. If the monkey stopped working for any significant length of time, the partial data file was discarded and data collection resumed when the monkey began working again. Data files were collected alternately from the two workspaces.

There were minor differences in the devices used for the three monkeys. Whereas monkeys Gn and Gv pressed a button during the time that the hand was in the center position, monkey Q rested its hand on a touch pad. For monkeys Gn and Gv, the outer targets were affixed to the ends of plastic rods and the monkeys were required to press the button for the duration of the target hold time. For monkey Q, the device was modified so that the outer target buttons were replaced with infrared (IR) sensors. The monkey was required to move its hand to a position where the IR sensor detected the hand and maintain that position for the required time interval. Monkey Q performed the task with a short delay (200–500 ms) between the time the target was lighted and the go tone. This task variation was introduced to allow us to study delay-period activity in M1 and premotor cortex. Those data are not discussed in this report.

Surgery

After training, a recording chamber was implanted over the arm area of the right M1, contralateral to the hand used for the tasks. In the same surgery, a halo-type head-restraint system was implanted. In a separate surgery, bipolar, epimysial electrodes were implanted on numerous muscles of the arm and hand. The electrode leads were tunneled from a connector implanted in the skin of the monkey’s back to the sites of implantation (Miller et al. 1993). In each monkey, a subset of the following muscles was implanted: upper trapezius (Trap); infraspinatus (Inf); rhomboid (Rhm); latissimus dorsi (Lat); teres major (Ter); pectoralis (Pec); posterior, medial, and anterior heads of deltoid (PDl, MDl, ADl); triceps (Tri); biceps (Bic); pronator teres (Pro); brachioradialis (Brd); flexor and extensor carpi radialis and ulnaris (FCR, FCU, ECR, ECU); flexor digitorum superficialis (FDS); extensor digitorum communis and quarti et quinti proprius (EDC, E45); abductor pollicis longus (AbPL); adductor pollicis (AdP); and 1st dorsal interosseous (1DI). Table 1 shows the muscles that were recorded from each monkey.

For monkey Q, the coils for detecting limb orientation were implanted during the EMG surgery. These sensor coils were implanted on the humerus, the ulna, and the second (index) metacarpal and are similar to although smaller than the scleral coils used for tracking eye movements (Robinson 1963).

All animal care, surgery, and experimental procedures were approved by the Institutional Animal Care and Use Committee of Northwestern University.

Data collection and experimental procedures

During each experiment, neuronal recordings were made along a single electrode track, using glass-coated, platinum–iridium electrodes. At each recording site, one or two neurons were isolated on-line using a digital neuronal acquisition processing system (either Tucker-Davis Technologies or Plexon). Spike times were saved with 100-μs precision. EMG signals, amplified and band-pass filtered (130–1,200 Hz), were sampled at either 1,500 or 2,200 Hz. In most cases, we characterized the nature of the motor response to intracortical trains of microstimulation (11 biphasic pulses at 400 Hz, 5–40 μA) at least once during each electrode penetration, typically when cortical responses to medullary pyramidal tract antidromic stimulation and/or cellular characteristics indicated that the microelectrode was in layer V of cortex. This allowed us to distinguish regions of M1 that corresponded to the proximal and distal limb. The experiments recorded here were restricted to the proximal arm areas of M1. EMG activity and limb position activity were recorded simultaneously with neuronal activity.

For each isolated neuron, several data files were recorded. In all cases, data were collected continuously as the monkey repeatedly performed the reaching task. Consequently, the correlations based on these data are the result of all the monkey’s movements, not just a limited subset. Furthermore, the variation in timing between trials (both natural and that imposed by the experimental design) was preserved. These factors are thought to be useful because they may help to diminish fixed, behavior-related correlations among the signals. Any given data file was recorded while the animal performed the center-out task in either the left or right workspace. The workspace location was alternated for each subsequent file and recording continued until the neuron was lost or until two files had been recorded in each workspace. The order of the task conditions was varied from one neuron to the next and comparisons were made within and across these conditions.

Histology and confirmation of recording sites

After recordings were completed, monkeys were administered a lethal dose of sodium pentobarbitone and perfused with physiological saline followed by 10% neutral-buffered formalin. We confirmed that our recording sites were located on the portion of precentral gyrus corresponding to M1 and determined the location of the central sulcus within the recording chamber coordinates.

Calculation of muscle-space– and hand-space–preferred directions

The discharge of each neuron was characterized for each data file by calculating perievent histograms synchronized to the monkey’s hand leaving the center sensor. The overall depth of modulation (DOM) was defined as the difference between the maximum and minimum firing rates within these event-related histograms. For each neuron, we calculated an instantaneous neuronal firing rate signal by computing the inverse of the interspike intervals, binned in 5-ms bins. A four-pole, 20-Hz digital low-pass filter was used to extract the modulation envelope from the EMG signals, which were subsequently resampled at 200 Hz.

The concept of a neuronal “muscle-space–preferred direction” (PD_M) is analogous to the more common concept of preferred direction for hand movement (PD_H). The preferred direction is typically thought of as representing the direction of hand motion associated with maximum discharge. PD_H can also be thought of as representing the relative magnitude of discharge associated with movements along each of the three axes of the Cartesian coordinate system. In the same sense, PD_M represents the relative discharge associated with the activity of each of the recorded muscles. By analogy, it can be thought of as the direction in n-dimensional muscle space that is associated with the greatest discharge.

We introduce a novel method for determining both PD_H and PD_M, entailing calculating cross-correlations between neuronal firing rate and either of two sets of signals. To determine PD_H, we correlate neuronal firing rate with the three components of hand velocity. To determine PD_M, we correlate neuronal firing rate with the n EMG signals. By using an identical method to calculate both PD_M and PD_H, we were able to directly compare the relative stabilities of the two coordinate systems. All cross-correlations were calculated using the formula

$${\mathrm{R}}_{\mathrm{nm}}\left(\tau \right)=\frac{1}{T}{\int }_{\text{0}}^{\mathrm{T}}\left[\frac{\mathrm{n}\left(\mathrm{t}\right)-\overline{\mathrm{n}}}{{\sigma }_{\mathrm{n}}}\right]\left[\frac{\mathrm{m}\left(t+\tau \right)-\overline{\mathrm{m}}}{{\sigma }_{\mathrm{m}}}\right]\mathrm{d}t$$ (1)

where n(t) is the time-varying neuronal discharge and m(t) is either the time-varying muscle activity or the limb velocity signals, each of which is sampled for a time interval of length T. n̄, m̄ and σ_n, σ_m represent the mean and variance of the corresponding signals. The cross-correlation is a function of τ, the time lag between the two signals. In this analysis we considered time lags from 0 to 150 ms. This interval was chosen because it incorporates the shortest possible latencies corresponding to the conduction delay and also to the longer latency that is characteristic of the delay between bursts of M1 activity and the onset of movement.

The peak cross-correlation within this range of lags for any muscle i was used as the ith element of an n-dimensional PD_M vector. Likewise, the three correlation peaks with the three components of velocity were used to form PD_H. The direction of the PD vector was determined in either case by the relative strength of correlation between the neuron’s discharge rate and each of the other signals. As such, it represents the “preference” of a given neuron for the different signals. PD_H represents the neuronal preference for hand movement along each of the three coordinate axes, whereas PD_M represents the neuronal preference for activation of each of the recorded muscles. Various factors, including the amount of filtering applied to the signals, can affect the magnitude of all the correlations that constitute the vector (Miller and Houk 1995). For all analyses reported here, the PD vectors have been converted to unit direction vectors to minimize these effects.

We made comparisons between any two PDs by calculating the angle between the vectors. The angle between two vectors was obtained from their dot product, calculated from the sum of the products of their individual components. The dot product between the two n-dimensional vectors X and Y is given by

$$\mathrm{X}·\mathrm{Y}=\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{i}}{\mathrm{y}}_{\mathrm{i}}={\mathrm{x}}_1{\mathrm{y}}_1+\dots +{\mathrm{x}}_{\mathrm{n}}{\mathrm{y}}_{\mathrm{n}}$$ (2)

If X and Y are unit vectors, the cosine of the angle between X and Y is equal to X·Y. Thus in general, θ is defined as

$$\theta ={\cos }^{-1}\left(\mathrm{X}·\mathrm{Y}/\left|\mathrm{X}\right|\left|\mathrm{Y}\right|\right)$$ (3)

We assumed all angles fell between 0 and 180°.

RESULTS

Calculation of hand-space–preferred direction

Many different kinematic reference frames might be considered in which to express neuronal discharge. We chose to use an extrinsic, as opposed to intrinsic, frame to provide the greatest possible contrast with the muscle system. Motion of the endpoint of the limb thus becomes an obvious choice. There is considerable evidence that the strongest M1 neuronal correlations with hand motion are found with velocity, rather than position or acceleration (Ashe and Georgopoulos 1994; Flament and Hore 1988; Hamada 1981; Humphrey et al. 1970). Therefore we chose to use the three components of hand velocity as the kinematic reference frame.

SIMULATED NEURAL DISCHARGE

In this study, we have introduced a new method to calculate the preferred directions (PDs) of neurons that relies on the cross-correlation between neuronal discharge and the speed of hand movement along each of the three coordinate axes. For some time we have used an analogous approach to study the relation between neural discharge and muscle activity (Holdefer and Miller 2002; Miller and Sinkjaer 1998; Miller et al. 1993; Stuphorn et al. 1999). By using a unified method of data analysis, we can more directly compare the stability of the neuronal discharge with respect to these two different coordinate systems.

To validate the cross-correlation method, we first performed a study in which we evaluated the spike trains generated by simulated neurons with known PDs. Figure 1A shows several seconds of the X, Y, and Z components of the hand velocity collected during execution of the center-out task by monkey Q. The full duration of the data file was 76 s. Most of the movements in this example have the roughly bell-shaped profile typical of simple, point-to-point movements, but there were exceptions that resulted from errors and small corrections (e.g., the movements at 3 and 9 s). This recorded trajectory was used to generate a spike train, in which the instantaneous discharge rate at time t was proportional to the dot product between the velocity at t + 0.1 s, and a randomly chosen preferred direction vector. The instantaneous rate R(t) was calculated as shown in the following equation and included an additive spontaneous rate component, n(t)

FIG. 1.

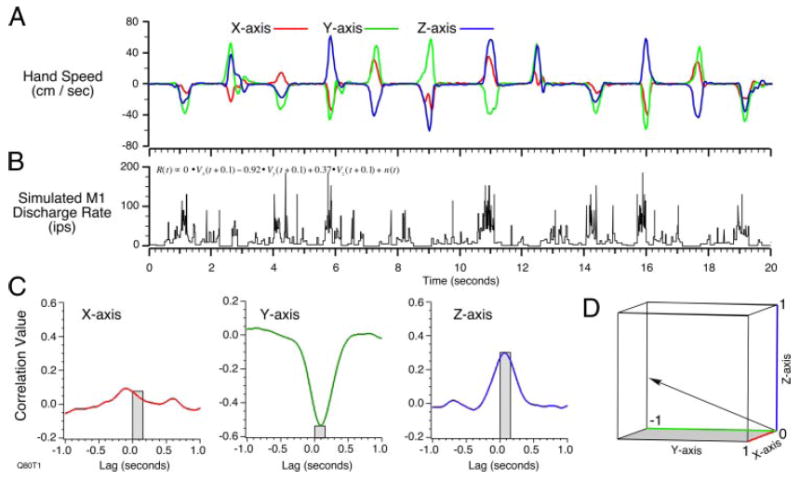
A: X, Y, and Z components of the hand velocity generated during a series of hand movements. B: simulated spike discharge conforming to a known preferred direction (PD) (0.0, −0.92, 0.37) and the trajectory in A. C: cross-correlations between discharge rate (B) and each component of hand velocity (A), where the 0- to 150-ms time lags are indicated by the gray boxes. D: vectors representing original PD and 2 estimates, ${\widehat{\mathrm{PD}}}_1$ (regression over target direction) and ${\widehat{\mathrm{PD}}}_2$ (cross correlations). This projection preserves the size of the 3-dimensional (3D) angular error for both estimates.

$$\mathrm{R}\left(\mathrm{t}\right)\propto {\mathrm{PD}}_{\mathrm{x}}·{\mathrm{V}}_{\mathrm{x}}\left(\mathrm{t}+0.1\right)+{\mathrm{PD}}_{\mathrm{y}}·{\mathrm{V}}_{\mathrm{y}}\left(\mathrm{t}+0.1\right)+{\mathrm{PD}}_{\mathrm{z}}·{\mathrm{V}}_{\mathrm{z}}\left(\mathrm{t}+0.1\right)+\mathrm{n}\left(\mathrm{t}\right)$$ (4)

R(t) was used as the input to a nonhomogeneous Poisson process used to generate spikes. Figure 1B shows the discharge rate of the spikes generated by a PD vector with components (0.0, −0.92, 0.37). This simulated spike train was processed as if it had been recorded from a neuron and two different estimates of the kinematic preferred direction were made. To compare the directions of these two estimates with the original randomly chosen PD, all of the vectors were normalized to unit direction vectors. One estimate was made using the methods described in the original studies of Georgopoulos and colleagues (Georgopoulos et al. 1982; Schwartz et al. 1988). In brief, this method involves regressing the mean discharge rate during a series of movements to each of the eight targets against the X, Y, and Z components of the targets. This operation yielded an estimate of (0.29, −0.87, 0.41) for the PD, which was 17° from the actual PD. A second estimate of PD was made by calculating cross-correlations between the time-varying firing rate and the hand-movement velocity signals. Figure 1C shows the resulting cross-correlations; the peaks within the 0- to 150-ms range of lags were 0.08, −0.54, and 0.29. When normalized, the resulting PD estimate was (0.13, −0.87, 0.47), differing from the actual PD by 10°. The original PD and both estimates are shown graphically in Fig. 1D.

Ten representative hand-movement trajectories were selected from the recordings made from monkey Q. One of these included the segment shown in Fig. 1A. For each of these 10 different trajectories, 10 spike trains were generated, each using a different, randomly selected PD. From these 100 data sets, estimates were made of PDs using both the multiple regression and cross-correlation methods outlined above. As a test of the reliability of both methods, the components of the estimated PD vectors were plotted against those of the PDs used to generate the spike trains. Results of this comparison are shown in Fig. 2. Figure 2A shows the results from the linear regression estimate, whereas Fig. 2B shows the results based on the cross-correlation method. Perfect estimation of the underlying preferred direction would have resulted in a diagonal line from the bottom left to the top right corner of the graph. The regression method shown in Fig. 2A had slope = 0.84 and R² = 0.80. The fit in Fig. 2B with slope = 1.05 and R² = 0.94 was significantly better (paired, two-tailed t-test of angles between actual and estimated PDs; P < 10⁻⁴).

FIG. 2.

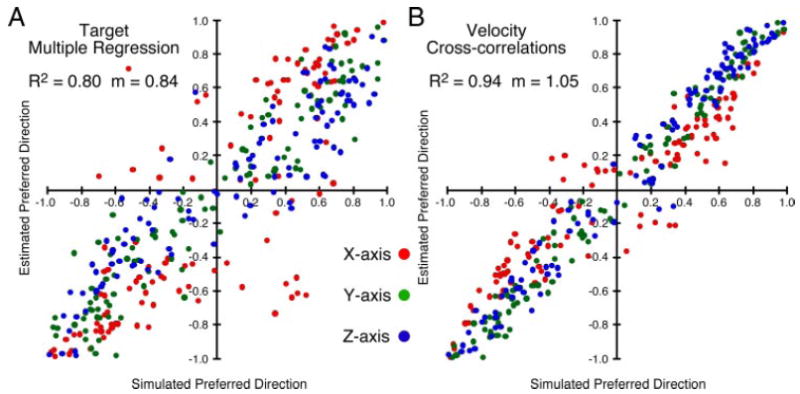
Summary of the linear regression (A) and cross-correlation (B) approaches to the estimation of PD: 100 different data sets of the type shown in Fig. 1 were generated and used to estimate PD. Estimated components of each of the PDs are plotted against the corresponding known components. Better estimates provided by the cross-correlations probably resulted because many of the hand trajectories did not follow the straight lines to the intended targets implicitly assumed by the regression method.

The more accurate results with the cross-correlation measure are probably explained by the nonideal properties in the actual hand trajectory. If deviations from an idealized straight-line path to a given target are reflected in altered discharge, the least-squares fit will become noisier, and could even be biased, if the deviations are systematic. In contrast, to the extent that the discharge reliably reflects the altered hand trajectory, the cross-correlation would be essentially unaffected. In confirmation of this interpretation, a similar analysis using idealized straight-line movements with bell-shape speed profiles yielded a slope of 1.0 and R² in excess of 0.98 for both methods (not shown).

In this simulation we assumed that neuronal discharge was entirely determined by the velocity of hand movement, with no position component. There is good evidence (reviewed above) that M1 discharge is dominated by a phasic component, but many neurons have a significant tonic component as well. Because cross-correlation is a linear operation, correlated signals will remain correlated after one is integrated or differentiated, although the shape of the cross-correlation will change. Consequently, position-related discharge will also influence the shape and magnitude of the cross-correlations (Miller and Houk 1995; Miller and Sinkjaer 1998). We repeated this analysis in the extreme case in which spike discharge was generated by movement position rather than velocity. The mean R² between the actual PD and the PD determined by velocity cross-correlations decreased only slightly, from 0.94 to 0.90.

RECORDED NEURAL DISCHARGE

We analyzed 87 neurons from the arm area of M1 across both left and right workspaces. Fifty-eight neurons were recorded from monkey Q, located between 0 and 2.1 mm from the central sulcus (mean 1.0 ± 0.7 mm); 23 were recorded from monkey Gv, ranging between 0 and 3.1 mm from CS (mean 1.8 ± 0.8 mm); and six were recorded from monkey Gn, in a narrow band between 2.0 and 2.5 mm from the sulcus. An additional nine neurons from monkey Q were recorded in only a single workspace and were used only for the cross-time comparisons. All neurons used in our analyses met a minimum DOM criterion of 20 impulses per second in both workspaces.

Figure 3 illustrates the data used for the calculation of preferred directions from actual neuronal data. The procedure is identical to that described above for the simulated firing rate data. Neuronal discharge, movement velocity, and proximal muscle EMG signals are shown for five repetitions of the center-out task taken from a longer data file. In this particular example, the kinematic data represent motion of the wrist because the forearm was the most distal segment of the arm for which movement data were collected. The bottom traces show the times of center and outer button presses. For many of the movements in this example, the velocity signals were more strongly biphasic than were those in Fig. 1. This was largely the result of a different behavior on the part of the two monkeys. Monkey Gv tended to pull its arm back and then thrust it forward to reach to the target, whereas monkey Q moved somewhat more slowly and directly to each target. This behavioral difference may also have arisen in part from the different apparatus sets used for each monkey.

FIG. 3.

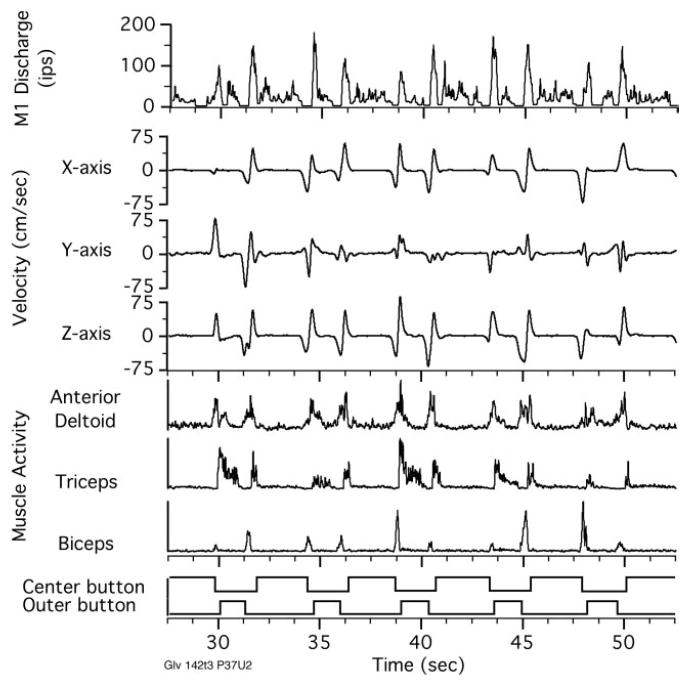
Simultaneously recorded neuronal, hand velocity, and EMG signals recorded as the monkey made a sequence of reaches in 5 different directions within a single workspace. Typical data files were several times this length. These signals were used to calculate the muscle- (PD_M) and hand-space–preferred direction (PD_H) vectors described below.

The entire file was used to calculate cross-correlations between neuronal discharge and each component of the velocity (Fig. 4A). The peak values within the 0- to 150-ms range (gray bars) were used to construct the PD vector shown in Fig. 4C, top. It pointed most strongly toward the X and Z axes because neuronal discharge correlated with velocity along these axes with a strength of 0.60 and 0.62, respectively. The Y component of velocity was much more weakly correlated (0.22). Vectors of this type were calculated for movements in both the left and right workspaces. Angles between the PD vectors provided a measure of the stability of the preferred directions across these workspaces, as well as for repeated estimates within a single workspace.

FIG. 4.

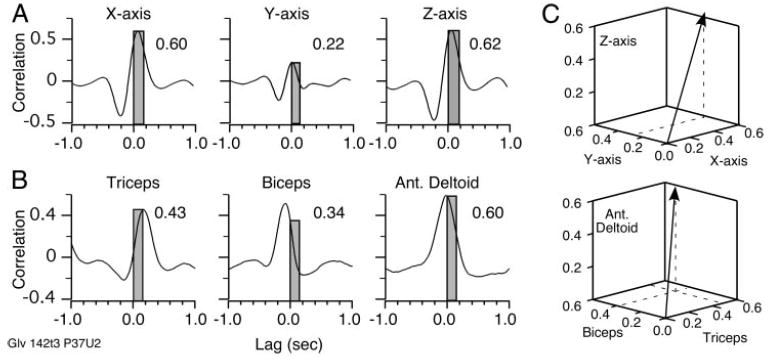
Cross-correlations between discharge rate and hand velocity components (A) and EMG signals (B). Peak strength of each correlation within the 0- to 150-ms range of lags was the basis for one of the components of the PD vector (C). PD_M was actually constructed from more muscles than the 3 that can be conveniently displayed.

Calculation of muscle-space–preferred direction

Cross-correlations between the discharge rate of neurons and muscle activity were previously used to quantify the motor behavior of individual neurons (Burton and Onoda 1978; Holdefer and Miller 2002; McKiernan et al. 2000; Miller et al. 1993). For the most part, these correlations were used to characterize each muscle independently. However, the CNS must control muscles in a well-coordinated fashion. Nearly all corticospinal neurons branch to multiple muscles (Fetz and Cheney 1980; Shinoda et al. 1981). For this reason, we chose to examine the relationship between a neuron and a group of muscles, rather than a single muscle.

Figure 3 shows a set of three EMG signals: anterior deltoid, triceps, and biceps, recorded simultaneously with neuronal discharge and movement. The similarity between EMG activity and neuronal firing rate can be seen in the raw data traces. Anterior deltoid activity, in particular, follows the neuronal activity quite closely. Although only three muscle signals are shown here, a larger number were recorded and used for subsequent calculations. Recordings from monkey Gv, from which this example comes, included 17 muscles (Table 1). Because the number of recorded muscles was greater than the three axes in the Cartesian coordinate system, PD_M can be thought of as lying in a much higher-dimensional space than PD_H. Despite the difference in dimensionality, we can use the same calculations to characterize the stability of either type of vector.

The cross-correlations in Fig. 4B were calculated between neuronal firing rate and the three muscles shown in Fig. 3. The peak value within the 0- to 150-ms range is shown for each cross-correlation and the resulting 3D PD_M vector is shown in Fig. 4C, bottom. In this example, the PD_M vector pointed most strongly along the anterior deltoid axis, with lesser components along the triceps and biceps axes. Biceps contributed the least to determining the direction of this PD_M vector, despite the fact that its cross-correlation had a greater overall magnitude than that of triceps because the biceps’ cross-correlation peak occurred at a lag of −100 ms. Its correlation within the causal range was actually rather small.

Figure 5 summarizes the overall strength of correlation for both hand-movement and muscle signals from the three monkeys. The filled bars indicate the mean and SDs of the correlation magnitude for the different types of signals. Although only the magnitude is summarized here, it should be noted that most of the EMG correlations were positive because both neuronal discharge and muscle activity tended to increase during movement. For monkey Gv, the magnitude of EMG and hand velocity correlations were statistically indistinguishable. For the other two monkeys, the mean EMG correlation was significantly stronger than the hand velocity correlations. For the EMG signals in particular, a number of muscles were often quite poorly correlated despite strong correlations with other muscles. As a means of summarizing this effect, we also found the single best EMG and hand velocity correlation for each neuron. The average magnitude of these best correlations is shown by the open bars in this figure and were very similar for all monkeys.

FIG. 5.

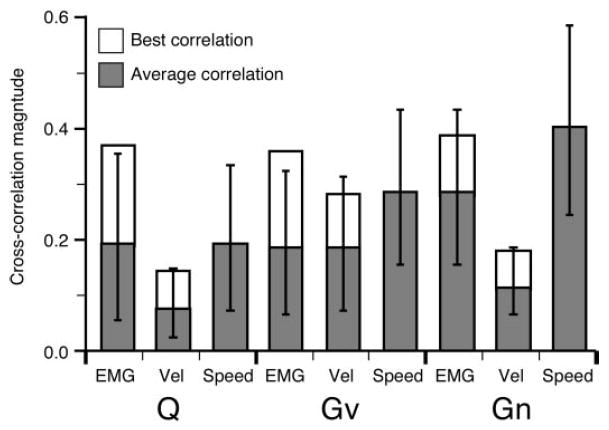
Distribution of mean cross-correlation magnitudes for both muscle and movement signals. Means were calculated from the absolute values of the cross-correlations because there were many negative correlations for velocity. Negative correlations resulted when a neuron increased its activity for movements in the negative direction along a given axis. For each neuron, the single, best EMG and velocity component (excluding speed) cross-correlation was determined. Open bars show the average of these best correlations.

Finally, we computed the correlation with hand speed as well as the individual components of velocity. A neuron might have a relatively large speed correlation without strong velocity correlations, if its bursts of activity during movement were not strongly related to the direction of movement. For example, the large difference between speed and velocity correlations for monkey Gn suggests that the discharge rates for this monkey were less directionally dependent than those of the other monkeys. Because only velocity components, and not speed, were included in the analysis of the best-correlated kinematic signals, it was possible for the average speed correlation to be higher than the best of the velocity correlations (as was the case for monkey Gn).

Variation in preferred direction across neurons and time

PD_M and PD_H measured from different neurons varied widely. As an index of this variation within the high-order space, we measured angles between all possible pairs of preferred direction vectors. Distribution of these angles is shown in Fig. 6A, which includes data from all three monkeys. In this figure comparisons of PD vectors were made between all combinations of neurons recorded from either the left or right workspace from a given monkey. Both workspaces are represented in the figure, although angles were calculated only within, not across, workspaces. Small angles reflect neurons with similar preferred directions in either hand space or muscle space, whereas large angles result from comparisons of two dissimilar vectors. Black bars indicate angles measured between pairs of hand-space–preferred directions (PD_H), whereas gray bars represent angles between muscle-space–preferred directions (PD_M). The angles that result between a set of uniformly distributed vectors will not be distributed uniformly, but rather will be distributed sinusoidally with a peak at 90°. That is essentially the form of the distribution of angles among the PD_H vectors, suggesting that these vectors were, indeed, uniformly distributed. However, although the means of the PD_H and PD_M distributions (89 and 71°, respectively) did not differ, small angles were significantly more common between PD_Ms than between PD_Hs [Kolmogorov–Smirnov (K-S) test; P < 0.01)]. This preponderance of small angles is consistent with the idea that the neurons are grouped into functionally similar clusters.

FIG. 6.

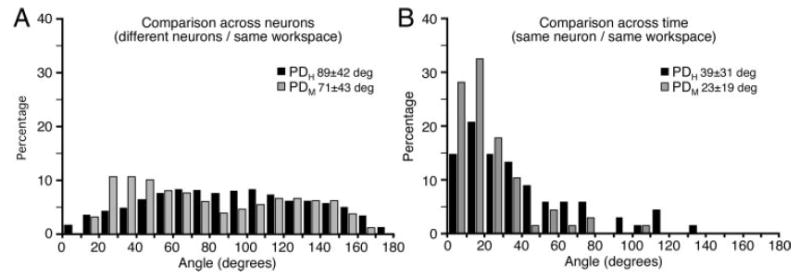
Distribution of angles measured between pairs of PD_H (black) or PD_M (gray) vectors. A: angles between the PDs of all possible combinations of neurons measured within a single workspace. There were somewhat more small angles (similar PDs) within muscle space than hand space, perhaps reflecting clusters of functionally similar neurons. B: angles between repeated estimates of the PD of a given neuron over time within the same workspace. PD_M vectors were significantly more stable over time than were PD_H vectors.

We also examined the stability of a given neuron’s preferred direction across time by measuring the angle between two estimates of its preferred direction made from data collected at two different times within a given workspace. In each case, the two data files collected from a given workspace were separated in time by a data file collected from the other workspace. Figure 6B shows results of this analysis. PD_M varied somewhat less across time than did PD_H, as reflected by the means of the two distributions (23 and 39°, respectively). With respect to PD_Ms 60% varied <30°, compared with only 30% of PD_Hs. These distributions were significantly different, according to both a Wilcoxon rank-sum test and a K-S test (P < 0.01).

Variation in preferred direction across workspaces

To determine the relative stability of hand- and muscle-space representation across workspaces, we examined changes in PD_H and PD_M across data collected from the left and right workspaces. Figure 7 shows the distribution of angles between PD vectors for a given neuron calculated in the left and right workspaces. PD_M was significantly more stable than PD_H for two of the three monkeys individually (P ≤ 0.05; Wilcoxon rank-sum/Mann–Whitney U test for matched pairs). The six cells from the third monkey (Gn) were too few to provide a meaningful statistical test. When the data for all three monkeys were combined, the difference was highly significant; the average change in PD_M was 33°, whereas the average change in PD_H was 53° (P < 0.001). With respect to PD_Ms 43% varied <30°, compared with only 17% of PD_Hs.

FIG. 7.

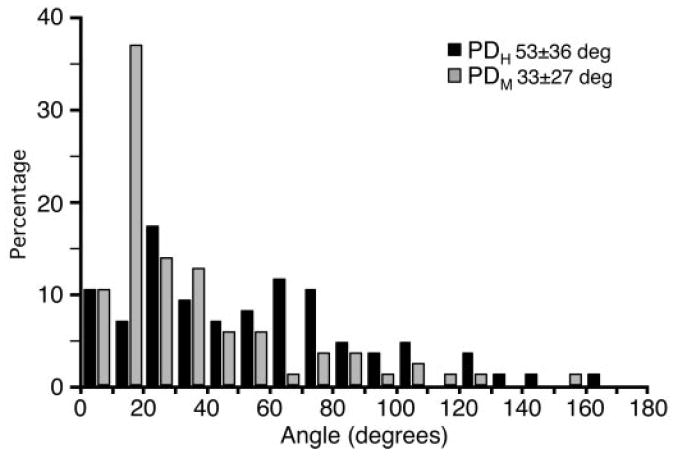
Distribution of angles between PDs for the same neuron in different workspaces. As was true for repeated estimates over time (Fig. 6B) PD_Ms were more stable across workspaces than were PD_Hs. However, both types of PDs were significantly less stable across workspaces than across time.

The ability to measure stability of neuronal discharge in both hand space and muscle space allows us to determine the extent to which a given neuron’s function is muscle-like or movement-like. Figure 8A represents the cross-workspace stability of each neuron as a single point, the angle between its PD_H vectors shown on the horizontal axis, and between its PD_M vectors on the vertical axis. The closer a point is to the horizontal axis (small change in PD_M) the more muscle-like its properties. Conversely, points lying close to the vertical axis represent movement-like neurons. With the exception of the small number of neurons collected from monkey Gn, which were all strongly muscle-like, there was a fairly broad scatter of points throughout this plane. A line drawn from the origin to any point provides an index of this property. As the angle to the horizontal axis decreases, the more muscle-like is the corresponding neuron. Over 70% of the neurons fell below a 45° line, in the half of the plot corresponding to neurons that were more stable in muscle space than hand space. Figure 8B summarizes the distribution of the muscle/movement index for all recorded neurons.

FIG. 8.

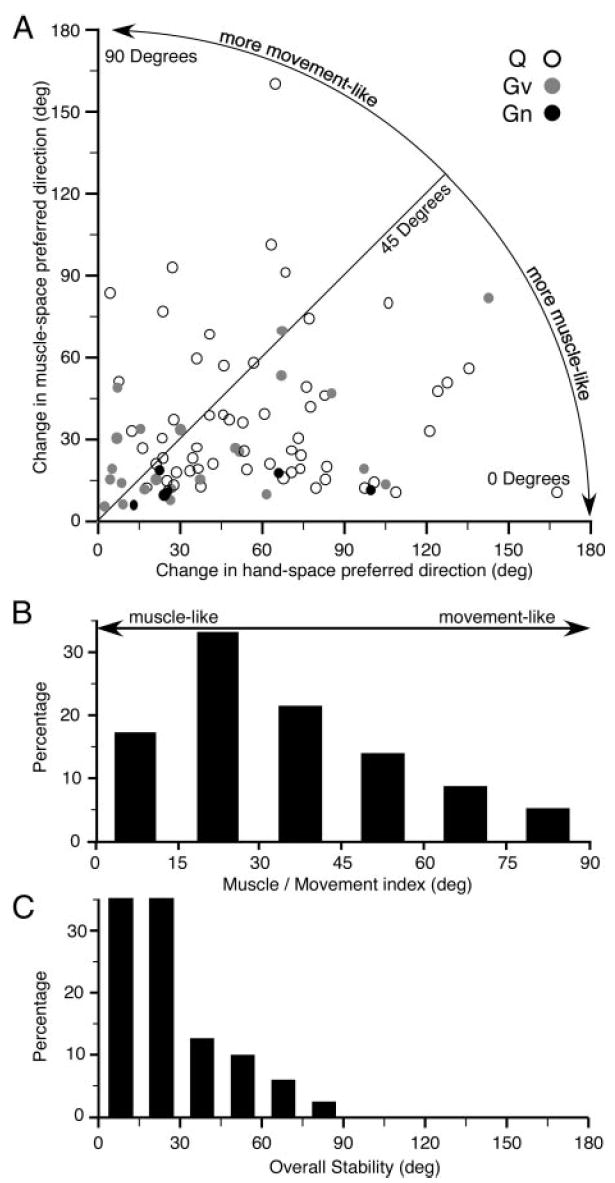
A: scatterplot comparing cross-workspace stability of PDs in muscle space against that of hand space Each point represents a single neuron. Neurons falling below the 45° line were more muscle-like than movement-like. B: angle that a given neuron made with respect to the horizontal axis in A determined the extent to which its workspace dependency was muscle-like or movement-like. C: overall workspace-related stability for a given neuron was determined by taking the smaller of the workspace-dependent change in PD_M or PD_H.

We also tested for a dependency of the muscle/movement index on the distance from the central sulcus at which a given neuron was recorded. There was no correlation between the two measures for either Gv or Q (R² <0.01; P > 0.88). There were too few points available to be meaningful for Gn. Finally, Fig. 8C is a distribution of the overall stability (whether muscle- or movement-like) for all neurons. It simply reflects the smaller of the workspace-related changes of either PD_M or PD_H. For 70% of the neurons, the more stable PD varied <30°. In no case was this angle >90°.

DISCUSSION

Summary of significant findings

In this study we have developed methods that allow us to characterize the discharge of M1 neurons with respect to two different frames of reference: the time course of hand movement through space and the time course of movement-related muscle activity. We used the strength of the cross-correlation between discharge rate and either hand velocity or EMG signals to calculate preferred direction vectors in either hand space (PD_H) or muscle space (PD_M). We found that for a given neuron, the relation between discharge rate and muscle activity (indicated by the direction of the PD_M vector) was quite stable over time. Across neurons, the direction of PD_M was distributed throughout muscle space in a nonuniform manner, consistent with the presence of several distinct clusters of functionally similar neurons. Although the direction of PD_M changed somewhat across workspaces, these changes were smaller than the corresponding changes in PD_H. Finally, despite workspace-related changes, PD_M returned more nearly to its original direction when movements were resumed in the original workspace than did PD_H.

Neuronal discharge and the kinematics and kinetics of movement

The control that M1 exerts over movement is highly redundant. There are many orders of magnitude more neurons than there are controlled degrees of freedom in the limb. Consequently, a given movement can in principle be produced by a variety of patterns of neuronal discharge. However, in practice, the nervous system appears to follow rules that guide the selection of a particular neuronal discharge “solution,” for a given movement. These rules might be reflected in a consistent pattern of covariation between the time course of neuronal discharge and some signal related to the movement. Such a signal is said to be “encoded” in the neuronal discharge. The implication is that this signal (or others like it) may form the basis for the rules underlyng neuronal modulation. Studies of neuronal encoding of movement signals are made complicated by the fact that the mechanics of the limb cause most of these signals to be well correlated with each other during normal movement. Consequently, it is useful to make measurements during different behavioral tasks. The use of different tasks introduces variations in such mutual correlations, potentially revealing stable correlations between discharge and a particular class of movement-related signals.

Extensive research has addressed the nature of the covariation between firing rate of M1 neurons and a variety of kinematic and kinetic signals related to limb movement. These studies typically examined the mean discharge measured during particular periods of repeated movements. The classic studies of Georgopoulos found that the discharge of many neurons in M1 varies systematically with target location in both two (Georgopoulos et al. 1982) and three dimensions (Schwartz et al. 1988). The direction of greatest discharge is described as the neuron’s preferred direction (PD). Discharge for other movement directions is proportional to the cosine of the angle between the PD and the actual hand-movement direction.

Using many sequentially recorded neurons and a preferred direction model, Schwartz and colleagues were able to reconstruct averaged hand-movement trajectories with remarkable accuracy (Moran and Schwartz 1999a; Schwartz and Moran 1999). However, the lag between discharge and movement varied systematically with the curvature of the path. At points of high curvature, the best correlation occurred with movement-leading discharge, suggesting that speed and direction alone could not sufficiently account for the modulation in neuronal firing rate.

In fact, the discharge of most M1 neurons is also influenced by forces that pull the hand in a particular direction (Evarts 1968; Kalaska et al. 1989). The direction of greatest force effect is typically opposite to a given neuron’s PD, suggesting that the neuron’s discharge reflects the force necessary to move the limb, rather than the direction of motion per se.

An early study that attempted to make real predictions based on simultaneous recordings from a small number of neurons found velocity to be predicted somewhat better than position (Humphrey et al. 1970). However, in the same study, force proved to be the signal most highly correlated with the time course of neuronal discharge. Quite recently several groups within the brain–machine interface (BMI) field have begun to use chronically implanted electrodes to make predictions of movement-related signals using much larger numbers of neurons (Serruya et al. 2002; Taylor et al. 2002; Wessberg et al. 2000). Most of these studies exclusively examined kinematic signals, although in one case about 60 M1 neurons were used to predict both Cartesian hand position and grasp force. The grasp predictions proved to be significantly more accurate than those of hand position (Carmena et al. 2003). The value of R² calculated between actual and predicted signals was about 0.6 for position and 0.8 for force.

Relation between discharge and muscle activity

Unlike the large number of studies of movement-related kinematic and kinetic signals, relatively few examined the relation between simultaneously recorded discharge rate and the activity of proximal limb muscles. One exception is the finding of a moderate linear correlation between mean biceps activity and discharge rate during elbow flexion, in a study with a very small number of neurons (Lamarre et al. 1981). Two others studies described changes in the relation between either discharge (Schwartz and Adams 1995) or local field potentials (Baker et al. 1997) and EMG during movement. However, both of these studies focused on changes that occurred within single trials, a time course much shorter than what we studied. It is difficult to relate these findings to the workspace-related variation in PD_M that we described for some neurons.

At least one group in addition to our own has now used recordings from electrodes chronically implanted in M1 to predict muscle activity. The average prediction R² for several different muscles in both the studies ranged from 0.5 to 0.7 (Santucci et al. 2005; Westwick et al. 2006). Comparisons across these BMI studies is a bit difficult because of the different tasks performed by the monkeys and the different numbers of neurons used for the predictions. However, it is noteworthy that in both these studies, EMG prediction accuracy was nearly the same as that of movement kinematics, despite the fact that EMG is a considerably noisier signal with a greater dynamic range than that of position.

A relatively large body of literature addresses the nature of the “postspike facilitation,” a short-latency correlation between individual spikes and fluctuations in EMG (Fetz et al. 1976; Lemon et al. 1986; McKiernan et al. 1998). The PD_M is also based on a measure of correlation between neuronal discharge and the activity of a set of muscles. Despite the apparent similarity, however, there is relatively little correspondence between the strength of the discharge rate cross-correlation and the strength of postspike effects for a given neuron and muscle, beyond a tendency for the signs of the two measures to be the same (McKiernan et al. 2000). This correspondence may be somewhat greater for the intrinsic hand musculature (Bennett and Lemon 1996). A critical difference between the two methods is the frequency range of interest. Postspike effects are calculated from unfiltered data and based on very short latency (5–10 ms) effects. Any slower background fluctuations are typically subtracted out. On the other hand, it is precisely these slower fluctuations that are important in the PD_M analysis. The correlation strength is essentially determined by the relative shape, scaling, and timing of the corresponding bursts of activity in the two signals.

Although the spike-triggered average (STA) is commonly used as an indication of a direct synaptic connection between neuron and muscle, an apparent postspike effect can also be caused by synchronous input from nonrecorded neurons without there actually being a connection between the recorded neuron and muscle. This effect has been referred to as “synchrony facilitation” (Poliakov and Schieber 1998). Neurons with overlapping muscle fields were previously shown to exhibit somewhat greater synchrony (Jackson et al. 2003). Significant modeling effort has been devoted to distinguishing the presumed causal component from the synchrony component (Baker and Lemon 1998). Because there is considerably greater coherence among neurons at the lower frequencies used to calculate PD_Ms (Baker et al. 2003), such common input effects will be more frequent in PD_Ms than STAs. As a result, PD_Ms are not an appropriate means of determining synaptic connections to particular muscles, any more than kinematic preferred directions would be considered “connections” to the associated part of the limb. On the other hand, PD_M is a useful means of quantifying the functional relationship between activation patterns in M1 neurons and corresponding patterns in EMGs.

Variation in preferred direction across neurons, time, and tasks

The broad distribution of angles between PD_Ms of different neurons is an important indication of the sensitivity of this method to neurons with differing functional properties. The gray bars in Figs. 6A and 7 included angles as large as 160–180°. Although the mean angle between PD_Ms was not significantly different from that among PD_Hs, the shape of the two distributions clearly differed. Most obvious was a significantly greater tendency to find small angles among PD_Ms than PD_Hs, consistent with an earlier finding from our group, in which PD_Ms tended to cluster within restricted regions of the muscle space (Holdefer and Miller 2002). In that study, neurons within any given cluster were thought to control a particular synergistic set of muscles. Angles measured between the PD_Ms of neurons within any given cluster would tend to be small. There was also a slight overrepresentation of large angles (>140°). These may well reflect the tendency for there to be muscle synergies with antagonistic function, yielding widely separated PD_Ms.

Preferred directions were relatively stable across time in both muscle space and hand space—an important if not surprising finding. Because of the redundancy in the descending motor system, it need not have been true. Furthermore, despite the attempt to hold behavior constant, some variation in trajectory, limb posture, and muscle activation is inevitable. Even within a single workspace, these small variations in PD may help to address the central question of which signals are “encoded” by M1. In this respect, it is worth noting from Fig. 6B that M1 representation was significantly more stable over time in muscle space than it was in hand space. Another recent study measured the direction of PDs in shoulder/elbow torque space for movements made in a plane. In that study, the PD varied by about 20° across repeated measurements, very close to the mean variation of PD_M in our study (Kurtzer et al. 2005). In that same study, there was a much larger difference between PDs (50°) when comparisons were made between movement and isometric tasks. This was nearly equivalent to the change in mean PD_H across workspaces in our study. A second study comparing discharge during an isometric task with that of movements against a significant inertial load found the PDs of roughly 45% of neurons differed by ≥90° (Sergio et al. 2005). This unexpected result was explained by the fact that during the movement task, many neurons had early and late bursts of activity for movements in one direction, with an intermediate latency burst for movements in the opposite direction. The pattern closely resembled the triphasic activity typical of many arm muscles and presumably served to accelerate, decelerate, and stabilize the load, thereby causing PD to change abruptly and dramatically.

Muscle-like neurons in primary motor cortex

The two-workspace center-out task that we adopted for our study was initially used by Caminiti and colleagues (1990). Their study used three separate workspaces, but hand trajectory and muscle activity were measured in separate sessions from the neural recordings. They reported that on average, the PD rotated to reflect the location of the workspace relative to the monkey’s shoulder. However, the PD rotation was quite noisy and difficult to appreciate for any given neuron.

Although the trajectories differed more across workspaces than within a workspace, the differences (by design) were rather small. Consequently, the workspace-related changes in preferred direction had to have been the result of significant changes in the patterns of neural discharge. The authors noted that like neural discharge, EMG activity patterns also changed as the shoulder joint angle changed. They stated that EMG activity differed for all muscles, “in intensity, sign of modulation, and temporal relations to movement onset.”

Quite similar preferred direction rotations occurred during isometric contractions as a function of hand position (Sergio and Kalaska 2003). For hand positions left of center, PDs tended to rotate counterclockwise, whereas positions right of center caused clockwise rotations. The shifts were relatively small during the reaction time period compared with the later phasic and tonic force application periods. The timing, direction, and magnitude of tuning shifts for most M1 neurons were broadly comparable to those of the main proximal limb muscles.

However, because neuronal discharge and EMG activity were measured only in separate sessions in both of these studies, it was impossible to say with confidence whether the two changes paralleled one another. Caminiti commented, “The orientation of such a [muscle] synergy vector will not remain constant with respect to an extrapersonal coordinate system but will rotate with the position of the arm in space. Our data are consistent with the hypothesis that motor cortical cells command muscle synergies” (Caminiti et al. 1990). Our current results confirm this hypothesis: most M1 neurons are more stable across different workspaces when the discharge is expressed relative to muscle space than to hand space. This finding suggests that for most M1 neurons, muscle activation information is a more important determinant of discharge than is kinematic information.

Nonmuscle-like neurons in primary motor cortex

Although the majority of neurons in our study were more muscle-like than movement-like, there was a significant minority (roughly 30%; Fig. 8B) with preferred directions that were more stable in hand space. This is not a surprising outcome because there is ample evidence that the physiological properties of M1 neurons are not completely homogeneous. An older study of wrist movements against a variety of different load forces found roughly equally sized groups of neurons whose patterns of discharge most nearly resembled patterns of muscle activity (36%), direction of intended movement (36%), and current position (27%) (Thach 1978). The proportions of these different properties appeared to be randomly distributed across different neurons, with no real suggestion that there were distinct populations of neurons. This is consistent with our own results, which suggest a continuum of discharge properties rather than distinct subpopulations.

More recently, investigators measured PDs during wrist movement and their dependency on forearm rotation (Kakei et al. 1999). Because the pulling direction of most muscles rotates as the forearm is supinated or pronated, the different orientations served to dissociate an intrinsic coordinate system from the extrinsic system. There were several groups of M1 neurons: an “extrinsic” group in which the PD remained relatively fixed in space (constituting 50% of the neurons); an “intrinsic” group in which PDs rotated in a fashion similar to that of most muscles (32%); and a third group in which PDs rotated significantly, but not in the systematic fashion characteristic of most muscles (18%). Within the extrinsic group, 60% had significant changes in the spatial pattern of discharge, despite the fact that the overall PD did not change direction. These were referred to as “modulated” by forearm orientation. Unlike our own, and the Thach study, the extrinsic and intrinsic groups of neurons formed two distinct modes.

In our study, we found a somewhat larger proportion of muscle-like cells than did either of these previous studies. However, neither of those studies measured EMG together with neuronal discharge. In the Kakei study, in particular, it is difficult to speculate just how the different categories of neurons—from the large number of modulated neurons to the smallest group that rotated in a nonsystematic manner—might have been related to the activity of particular groups of muscles. The difference is unlikely to have arisen from a difference between proximal and distal limb control. If anything, one would expect fewer muscle-like neurons controlling the shoulder because it receives fewer direct cortical projections than do the more distal muscles (McKiernan et al. 1998). Neurons in the Kakei study were initially selected on the basis of significant spatial tuning. This selection may well have led to a bias that was not present in our study. Finally, measurements in the Kakei study were made exclusively during the reaction time period, when posture-related effects in M1 neurons have been shown to be minimized (Sergio and Kalaska 2003).

Our study also found a small number of neurons that were not stable across workspaces in either hand space or muscle space: about 15% varied by >45° and 8% by >60°. These relatively large changes could represent neurons that encode a parameter other than muscle activity or hand movement. It is possible, for example, that a representation of joint angles or joint torques would have proved more stable for these neurons. Alternatively, if M1 is a site of transformation between coordinate systems, as the continuous distribution of Fig. 8 suggests, these less-stable outliers may simply represent combinations of muscle-space and hand-space signals that are not stable in either system.

Alternatively, the nonstable neurons could be a consequence of a control system that is genuinely task dependent. For example, the discharge rate of some M1 neurons that caused postspike effects in digit flexor muscles differed rather dramatically depending on whether those muscles were activated by a power grip as opposed to a precision grip (Muir and Lemon 1983). Indeed, a recent modeling study was able to reproduce the results of Kakai using a network of neurons with direct connections to muscles and fixed sinusoidal tuning, provided there was significant task-related modulation in the magnitude of each cell’s discharge rate (Shah et al. 2004). In the extreme, one can imagine two sets of neurons, each with a different set of fixed connections to a given set of muscles. The first set would be active for one condition, the second for the other. In practice, such groups of neurons would probably be largely overlapping; individual neurons would likely be active to varying extents across different postures.

Relation between muscle and hand spaces

The classic preferred direction is essentially an estimate of the direction of hand movement that is most likely to follow a burst of activity in a given neuron. By combining information from many neurons, an accurate estimate of hand movement can be made, at least within a given dynamical condition. PD_M can be thought of as an estimate of the most probable pattern of activity across a group of muscles after a burst of activity in the neuron. The activity of populations of M1 neurons might then encode the activity of synergistic groups of muscles in a manner that would generalize broadly across conditions. Calculation of PDs using identical methods for both hand space and muscle space allowed us to make a direct comparison of these two frames of reference, which suggests that the muscle-space representation is, indeed, more stable.

It is important to note, however, that the muscle space we measured is not perfectly analogous to Cartesian space, in at least two respects. It is a higher-order space, in the sense that in all cases, we incorporated more than three muscles. It can easily be demonstrated that one effect of increasingly higher-order spaces is that the angles between randomly chosen vectors become more tightly clustered around 90°. This effect would, if anything, have tended to increase the size of the angles between PD_Ms (which were virtually all <90), compared with PD_Hs.

More important, perhaps, the X, Y, and Z axes of Cartesian space are mutually orthogonal. Equally distributed movements to the eight targets within the cube yield velocity component signals that are uncorrelated. This is not typically true of the muscle signals. Close agonist muscles have very similar pulling directions and their EMG signals are often well correlated. Across the population of neurons, the correlation strengths measured for each of two agonist muscles will almost certainly be less independent than would be those for two more distantly related muscles. Thus this muscle space, unlike Cartesian space, is nonorthogonal.

A nonorthogonal space is not a “metric” space, which is to say, it may not have a well-defined notion of distance between points in different parts of the space. The errors introduced by measurements in different regions could cause a small and insignificant linear transformation or they might lead to significant distortions of distance measurements. To test the extent of any such distortion, we remapped a set of 18 representative vectors from monkey Gn into an orthogonal coordinate system, the axes of which were the principal components of the original data set. We repeated the cross-time analysis using both the original and the remapped vectors. The result was a linear relation between the two sets of angles: large angles remained large in both coordinate systems and small angles remained small. We concluded that there was no significant distortion caused by the nonorthogonality of the original coordinate system. Although it would have been possible to transform all of the muscle-space data, this process would have had the distinct disadvantage that the axes would no longer have represented real muscles. Consequently, because the effect of the nonorthogonality was small, we chose not to transform the data.

In summary, we have developed a novel form of the familiar preferred direction vector that expresses the discharge of neurons in muscle space rather than in hand-movement space. We found a range of large and small angles between pairs of PDs for different neurons in both muscle space and hand space, although there were disproportionately more small angles between the PD_M vectors measured between neurons. This may reflect a clustering of functionally similar neurons, controlling the activity of particular muscle synergies. Preferred directions were more stable over time and less dependent on workspace location in muscle space than in hand space for about two thirds of M1 neurons. However, M1 neurons appeared to be distributed along a continuum in this respect, rather than into two discrete groups. Although these data were collected during a typical center-out movement task, there is no reason, in principle, why the same methods could not be used to analyze data recorded during more natural, aperiodic movements, perhaps from a naïve, untrained animal. It would also be possible to analyze PD_Ms consisting of distal muscles during hand use rather than arm movement, conditions under which kinematic data are quite difficult to obtain.