NONLINEAR MODEL-BASED ESTIMATES OF IC₅₀ FOR STUDIES INVOLVING CONTINUOUS THERAPEUTIC DOSE-RESPONSE DATA

1. Introduction

A common objective at pre-clinical or phase I trial stages is to estimate an IC₅₀, i.e., the concentration of an experimental compound required to achieve 50% in vitro response inhibition. IC₅₀ is closely related to and sometimes confused with EC₅₀, the half-maximal effective concentration, which is the analogous quantity of interest when the response is increasing with dose. Although these parameters are commonly estimated, there is great variation in the techniques used and they are not always based upon sound statistical principles or accompanied by valid standard error estimates to properly reflect uncertainty.

Models for dose response upon which estimation of IC₅₀ and EC₅₀ has been based range from simple (e.g., linear) to more complex (e.g., three- or four-parameter nonlinear models). Prior authors (e.g., [1]) have emphasized the use of sigmoidal curves based on nonlinear regression techniques, with the logistic function forming the basis for some of the popular choices (e.g., [2]). It is clear that effective estimation of an IC₅₀ must properly account for random variation and be based upon a model that not only matches the nature of the response variable, but adequately characterizes the observed dose-response pattern.

In this article, we demonstrate the comparative fit of several nonlinear statistical models to continuous absorbance response data on bone marrow endothelial cell lines, replicated at various doses of an inhibitory agent. Our purpose is to outline a general process for defining IC₅₀ based on a specified model, fitting the model via maximum likelihood, and estimating IC₅₀ and its standard error. Other considerations raised by the motivating examples include model reparameterization, adjustment of the dose scale for more reliable model fitting, and extensions to allow for heterogeneous residual variance across doses. While experimental conditions, the nature of the response data, and the class of candidate dose-response curves necessarily vary in practice, it is hoped that the methods illustrated here will provide a useful reference contributing to valid IC₅₀ estimation in clinical practice. Thus, while most aspects of the techniques discussed here tie in with existing statistical strategies, our aim is to clearly and thoroughly illustrate the details of the analytic considerations motivated by the data described in the following section.

2. Motivating Study Data

Two independently established bone-marrow endothelial cell lines which demonstrate characteristic behavior were used for this study. Human bone-marrow endothelial cells (BMEC) [3] and transformed human bone-marrow endothelial cells (TrHBMEC) [4] are of particular interest given their ability to express specific surface receptors when treated with pro-inflammatory cytokines and their ability to form tubular networking when grown on Matrigel®. Breast and prostate cancer bone metastasis [5–7] are among the pathologic conditions that induce marrow angiogenesis, which requires proliferation of endothelial cells to create a tumor blood vessel system. Without an adequate blood supply, tumors will shrink in size and subsequently in clinical significance. Due to the diversity of microvascular endothelial cells, those derived from bone marrow are the model for determining the therapeutic potential of new anti-angiogenic compounds being considered for bone metastasis therapy. In the motivating study, we tested the ability of SC-2-71, a quinazoline-related compound derived from thalidomide, to inhibit growth of BMECs in vitro.

For this experiment, BMEC and TrHBMEC were grown to confluence in T-75 flasks (Corning), trypsinized, counted and plated in 48-well plates (Corning). For the data collected in this study, cells were plated in triplicate for each thalidomide analog dose concentration: control media, vehicle, 10um, 30uM, 50uM, 70uM and 90uM. The control media for BMECs contains Delbecco’s Modified Eagle Medium (Gibco) with 10% fetal bovine serum, 1% penicillin streptomycin and 100 ul antiobiotic. A 100 uM stock solution of SC-2-71 was made with a vehicle of 10% dimethyl sulfoxide and 90% ethanol and then diluted to final testing concentrations.

After one day incubation at 37°C in the control media, the media was changed every 48 hrs for 6 days with 250 ul/well of the treatment solutions. On day 7 the cells were washed with 300ul of a 1% Gluteraldehyde solution (4ml/996mL 1X-PBS) by gentle rocking for 15 min. The gluteraldehyde was then removed and the cells were fixed with 300ul of a 0.5% Crystal Violet solution (5g/1L ddH2O) by gentle rocking for 15 min. Plates were then rinsed in distilled water for 10 minutes, inverted, and allowed to let dry for 24 hours. In order to get an initial qualitative analysis, the dry 48-well plates were scanned. The crystal violet was next solublized in 750ul of Sorensen’s Solution (8.967g Tri-sodium citrate/305mL dH2O, 19.5mL 1N HCL/17.5mL dH2O, 500mL 90% ethanol) for 15 minutes of gentle rocking. The absorbance values constituting the response data for the current study were then obtained by reading the plates at 560 – 590 nm in an OPTIMA Fluorostar plate reader. For the purposes of this study, the vehicle was deemed to represent the appropriate “0-dose” condition, and the control media data were excluded.

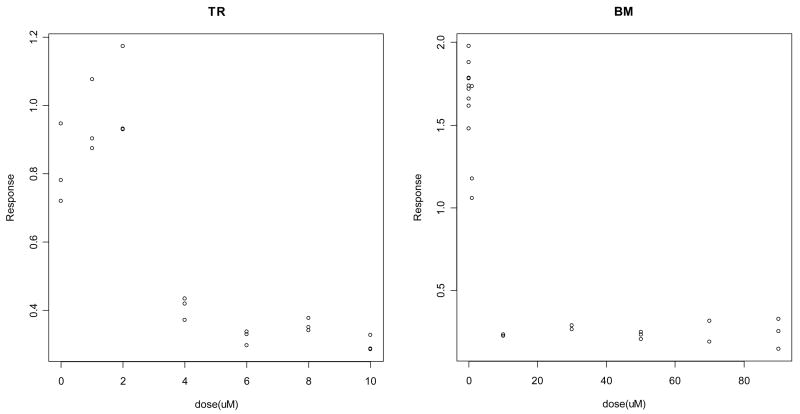
The goal of the motivating experiment is to estimate IC₅₀s (in units of uM) for the two sets of endothelial cell line data. Figure 1 displays the raw data for TrHBMEC and BMEC (hereafter referred to as TR and BM), with the dose axis displayed in the desired units. Note that for TR, doses measured in uM correspond to a natural scale for plotting and modeling the response data. For BM, however, the following doses were applied: 0, 0.01, 0.1, 1, 10, 30, 50, 70, and 90 uM. This scaling is as unappealing for modeling as it is for visual purposes (Figure 1), due to the lack of distance between doses at the lower end of the range. We address this issue of dose scaling further in section 3.4. Also of note in Figure 1 is a tendency for response observations to be more tightly distributed for higher doses, both for TR and BM cell line data. This invites considerations of variance heterogeneity, discussed in section 3.5. Despite the specific nature of the motivating endothelial cell line example, we note that the statistical models and methods discussed in section 3 are applicable in a wide variety of continuous dose-response data analytic settings that are often relevant to pre-clinical or early-stage clinical research.

Figure 1.

Plots of raw response data for TR (first panel) and BM (second panel) endothelial cell lines, using the desired dose scale units of uM.

3. Statistical Methods

The motivating data consist of multiple independent observations of a continuous response, generally with replicates at each of several doses of the inhibitor of interest. As a foundation for maximum likelihood analysis, we initially assume independent and identically distributed normal random errors with mean 0 and common variance σ². The mean (μ_i) of a given response (Y_i) is modeled as a nonlinear function of the dose (dose_i) that produced that response. Thus, the basic likelihood function upon which statistical analysis is based is expressed as follows:

$$\ell (\mathbf{\theta };\mathbf{y})=\prod _{\text{i}=1}^{\text{n}}\left\{\frac{1}{\sqrt{2\pi }\sigma }exp\left[-{({\text{y}}_{\text{i}}-{\mu }_{\text{i}})}^2/(2{\sigma }^2)\right]\right\},$$ (3.1)

where θ is a vector of model parameters to be estimated, n is the total number of observations, and μ_i = g(dose_i) is the smooth function of dose dictated by a particular nonlinear model. Maximum likelihood estimates derived under (3.1) are identical to least squares estimates. Standard error estimates based on the two methods are asymptotically equivalent, though there tends to be some discrepancy in relatively small samples such as those obtained in our motivating studies.

3.1 Models Considered

Based on the motivating endothelial cell line data, the primary models considered herein are as follows:

$$\begin{array}{ll}\text{1) Exponential}:\hfill & {\mu }_{\text{i}}=\text{g}(\mathit{dos}{e}_{\text{i}})={\text{e}}^{(\alpha +\beta \mathit{dos}{e}_{\text{i}})}\hfill \\ \text{2) Three}-\text{parameter}\text{logistic}:\hfill & {\mu }_{\text{i}}=\text{g}(\mathit{dos}{e}_{\text{i}})=\text{C}/[1+{\text{e}}^{(\alpha +\beta \mathit{dos}{e}_{\text{i}})}]\hfill \\ \text{3) Three}-\text{parameter}\text{Gompertz}:\hfill & {\mu }_{\text{i}}=\text{g}(\mathit{dos}{e}_{\text{i}})=\text{C}\text{exp}[-{\text{e}}^{(\alpha +\beta \mathit{dos}{e}_{\text{i}})}]\hfill \end{array}$$ (3.2)

The exponential model is clearly the most restrictive and incorporates the fewest parameters.

Versions of model 2) above are often used to account for a sigmoidal dose-response pattern. The three-parameter Gompertz curve described here also accommodates sigmoidal patterns and has connections with the Gompertz distribution, which underlies a model more commonly encountered in survival analysis (e.g., [9]). Allowing the linear function (α+ βdose_i) to vary freely over the real line, note that the theoretical range of the response (Y_i) based on the exponential model is (0, ∞). This is in contrast to the range of (0, C) based on the three-parameter logistic and Gompertz models, where the extra parameter C is a scaling constant that is needed to allow for mean responses exceeding one. While the response will generally be decreasing with dose when the objective is IC₅₀ estimation, each of these models can be used just as readily for estimating EC₅₀ based on a response that increases with dose.

3.2 Defining IC₅₀

We define IC₅₀ as the dose concentration that results in a mean response that is 50% of that achieved at the lowest (usually 0) dose, although this definition is typically adjusted when fitting models that assume a minimal response greater than zero (see section 3.6). A general process for determining a parametric expression for IC₅₀ is easily demonstrated via the exponential model. First, use model 1) in the previous section to define the mean response at dose 0, i.e., exp(α). Set the expression for μ = g(dose) based on model 1), i.e., exp(α+ βdose), equal to exp(α)/2, which is half of the 0-dose mean. Solving for dose based on the resulting equality yields the model-based IC₅₀. Following this process for each of the three models in section 3.1 produces the following functional expressions for IC₅₀:

$$\begin{array}{ll}\text{1) Exponential}:\hfill & {\text{IC}}_{50}=\text{h}(\beta )=-ln(2)/\beta \hfill \\ \text{2)}\text{Three}-\text{parameter}\text{logistic}:\hfill & {\text{IC}}_{50}=\text{h}(\alpha ,\beta )=[ln(2{\text{e}}^{\alpha }+1)-\alpha ]/\beta \hfill \\ \text{3) Three}\text{parameter}\text{Gompertz}:\hfill & {\text{IC}}_{50}=\text{h}(\alpha ,\beta )=\{ln[ln(2)+{\text{e}}^{\alpha }]-\alpha \}/\beta \hfill \end{array}$$ (3.3)

3.3 Maximum likelihood computation and standard errors

A variety of statistical software packages can be used to fit nonlinear models of the type discussed here, yielding numerically-derived maximum likelihood estimates (MLEs) and corresponding standard errors based on inverting the estimated observed information matrix. The MLEs for IC₅₀ under the exponential, three-parameter logistic, and three-parameter Gompertz models follow by inserting the MLEs for α and β into the expressions from section 3.2.

As IC₅₀ is a function of one or more of the original model parameters in each case, we may approximate the standard error of its MLE by means of the multivariate delta method (e.g., [9]). We express this conveniently in matrix terms by defining Σ̂ as the estimated variance-covariance matrix of the MLE for the model parameters involved in the IC₅₀ expression, and by defining D̂ as the vector of estimated first derivatives of the IC₅₀ function [h(.)] with respect to those parameters. Σ̂, obtained directly from the statistical software, is equal to the scalar Vâr(β̂) for the exponential model, and is the 2×2 matrix $\text{V}\widehat{\text{a}}\text{r}\left(\begin{array}{c}\widehat{\alpha }\\ \widehat{\beta }\end{array}\right)$ in the case of the three-parameter logistic and Gompertz models. The corresponding vectors D̂ are obtained by inserting the MLEs for α and β into analytical expressions (D) for the vectors of first derivatives, which are readily obtained (Appendix 1). The estimated standard error of the MLE for IC₅₀ is the square root of its delta method-based variance estimate, which is given by $V\widehat{a}r\left(\widehat{I{C}_{50}}\right)=\widehat{\mathbf{D}}\widehat{\mathbf{\sum }}{\widehat{\mathbf{D}}}^{\prime }$.

While the delta method is valid and generally produces equivalent results, a more transparent approach to facilitate standard errors for the IC₅₀ estimates relies upon rewriting the models for mean response (section 3.1) specifically in terms of IC₅₀. The appeal of this strategy is that the IC₅₀ estimate and its standard error may then be obtained directly from commercial statistical software, making such reparameterizations relatively common in similar dose-response modeling applications [10, 11]. To do so here, we use the formulae for IC₅₀ in section 3.2 to express β in terms of IC₅₀ and, where applicable, α. Inserting the resulting expression for β into the corresponding mean response functions yields the following equivalent models:

$$\begin{array}{ll}\text{1) Exponential}:\hfill & {\mu }_{\text{i}}=\text{g}(\mathit{dos}{e}_{\text{i}})={\text{e}}^{\{\alpha -\mathit{dos}{e}_{\text{i}}[ln(2)/{\text{IC}}_{50}]\}}\hfill \\ \text{2)}\text{Three}-\text{parameter}\text{logistic}:\hfill & {\mu }_{\text{i}}=\text{g}(\mathit{dos}{e}_{\text{i}})=\text{C}/[1+{\text{e}}^{\{\alpha +\mathit{dos}{e}_{\text{i}}\{ln[2exp(\alpha )+1]-\alpha \}/{\text{IC}}_{50}\}}]\hfill \\ \text{3)}\text{Three}-\text{parameter}\text{Gompertz}:\hfill & {\mu }_{\text{i}}=\text{g}(\mathit{dos}{e}_{\text{i}})=\text{Cexp}\{-{\text{e}}^{\{\alpha +\mathit{dos}{e}_{\text{i}}\{ln[ln(2)+exp(\alpha )]-\alpha \}/{\text{IC}}_{50}\}}\}\hfill \end{array}$$ (3.4)

Note that the scaling parameter C is the same as it was under the original parameterization in (3.2). Asymptotically valid statistical inferences about IC₅₀ via the ratio of the estimate to its standard error can be based on Student’s t distribution with (n−p) degrees of freedom, where p is the number of parameters used to characterize the mean response.

For all model fits illustrated in the Results section, we used SAS software package version 9.1 [12] for the calculation of MLEs and the estimated observed information matrix. Specifically, we fit each model via the user-specified likelihood facility available in the SAS NLMIXED procedure. Simple matrix manipulations to obtain delta-method based standard error estimates to accompany MLEs for IC₅₀ under the original model parameterizations were conducted using the SAS IML package [13]. As these yielded essentially identical standard errors to those obtained directly based upon the alternative model formulations given in this section, standard errors reported in section 4 are based on the reparameterized models as implemented via NLMIXED.

3.4 Dose axis scaling

While no adjustment of the dose axis is necessary for the TR cell line data, a rescaling to spread out the lower doses is required in order to promote stability in models fit to the BM data (Figure 1). For this purpose, we use the following transformation: dose_i* = ln(1000×dose_i + 1), where dose_i is measured in uM. This yields a range of approximately 0 to 11 for dose_i*, similar to the uM scale for the TR data. The exponential, logistic, and Gompertz models were then fit to the BM data with dose_i* replacing dose_i in the respective expressions for mean response given in sections 3.1 and 3.3. The resulting MLEs for IC₅₀ were then transformed back to the uM scale as follows:

$$\widehat{{\text{IC}}_{50}}=\frac{exp\left(\widehat{{\text{IC}}_{50}^{\ast }}\right)-1}{1000},$$ (3.5)

Where $\widehat{{\text{IC}}_{50}^{\ast }}$ represents the estimated IC₅₀ on the dose_i* scale. Standard errors on the uM scale were obtained via the following delta-method estimator, based on the preceding function of $\widehat{{\text{IC}}_{50}^{\ast }}$:

$$\widehat{\text{SE}}\left(\widehat{{\text{IC}}_{50}}\right)\frac{exp\left(\widehat{{\text{IC}}_{50}^{\ast }}\right)\times \widehat{\text{SE}}\left(\widehat{{\text{IC}}_{50}^{\ast }}\right)}{1000},$$ (3.6)

where $\widehat{\text{SE}}\left(\widehat{{\text{IC}}_{50}^{\ast }}\right)$ is obtained as described in section 3.3 based on models fit on the dose_i* scale.

3.5 Accounting for variance heterogeneity

As previously mentioned, Figure 1 suggests some indication of lower variance at higher doses when examining the response data from both the TR and BM cell lines. To accommodate such tendencies, the residual variance (σ²) in model (3.1) can be modeled as a function of dose in its own right, or simply assumed to be different for certain dose subgroups (e.g., high vs. low). This process is completely analogous to a weighted least squares approach (e.g., [14]), the purpose of which is generally to improve statistical efficiency. Though it adds little complexity to the model fitting process itself, it can lead to numerical instability depending on the amount of data available. We illustrate an analysis allowing for heterogeneous residual variance according to high or low dose in section 4, and programs to implement this approach as well as an exponential model for increasing or decreasing variability with dose are available from the authors.

3.6 More flexible models

When a sufficient number of doses and observations per dose are available, more complex models including extensions of the three-parameter curves introduced in section 3.3 may be desirable. For example, a four-parameter logistic model is emphasized in recent software developments devoted toward the estimation of sigmoidal dose-response patterns [15]. Here, we consider such natural extensions of the scaled logistic and Gompertz models introduced previously:

$$\begin{array}{l}\text{Four}-\text{parameter}\text{logistic}:{\mu }_{\text{i}}=\text{g}(\mathit{dos}{e}_{\text{i}})=\text{D}+\text{C}/[1+{\text{e}}^{(\alpha +\beta \mathit{dos}{e}_{\text{i}})}]\\ \text{Four}-\text{parameter}\text{Gompertz}:{\mu }_{\text{i}}=\text{g}(\mathit{dos}{e}_{\text{i}})=\text{D}+\text{C}\text{exp}/[-{\text{e}}^{(\alpha +\beta \mathit{dos}{e}_{\text{i}})}]\end{array}$$ (3.7)

The additional parameter (D) in each model is an additive scaling parameter that allows the curve to “bottom out” at a point distinct from 0. Given sufficient data, this can provide desirable flexibility and potentially improved fit. Because IC₅₀ is most generally defined as the dose that achieves a response halfway between the minimal theoretical response and the maximal (i.e., dose 0) response [e.g., between D and D + Cexp(−e^α), respectively, based on the Gompertz model in (3.7)], the parametric definitions of IC₅₀ for the four-parameter logistic and Gompertz models remain identical to their counterparts under the corresponding three-parameter models in (3.3). Thus, the models in (3.7) reparameterize in terms of IC₅₀ exactly as in (3.4), except with the addition of D to the mean response function.

Another type of extension that is sometimes warranted is to account for hormesis, which in the case of IC₅₀ estimation implies a mean response function that may be expected to increase over low doses before settling into a pattern of decreasing response with dose. The following is a four-parameter extension of the scaled logistic model in (3.2) that is an alternate form of a model proposed by Brain and Cousens [16], versions of which were further studied by others [10, 17]:

$$\text{Logistic}\text{model}\text{with}\text{hormesis}:{\mu }_{\text{i}}=\text{g}(\mathit{dos}{e}_{\text{i}})=\text{C}(1+{\text{fe}}^{{\text{dose}}_{\text{i}}})/[1+{\text{e}}^{(\alpha +\beta {\text{dose}}_{\text{i}})}]$$ (3.8)

The parameter f in (3.8) allows for hormesis, and (3.8) becomes equivalent to the logistic model in (3.2) when f = 0. Although (3.8) does not admit a closed-form expression for IC₅₀, similar logic to that employed in section 3.2 reveals that it implies the following equation:

$$(1+\text{f})[1+{\text{e}}^{(\alpha +\beta {\text{IC}}_{50})}]=2(1+{\text{e}}^{\alpha })(1+{\text{fe}}^{{\text{IC}}_{50}}),$$

where IC₅₀ is defined as the dose yielding 50% of the 0-dose response. By solving the above for β and inserting the resulting expression into (3.8), we obtain the following equivalent parameterization directly in terms of IC₅₀:

$${\mu }_{\text{i}}=\text{g}(\mathit{dos}{e}_{\text{i}})=\text{C}(1+{\text{fe}}^{{\text{dose}}_{\text{i}}})/\left\{1+exp\left[\alpha +{\text{dose}}_{\text{i}}\times ln\left(\frac{2(1+{\text{e}}^{-\alpha })(1+{\text{fe}}^{{\text{IC}}_{50}})}{1+\text{f}}-{\text{e}}^{-\alpha }\right)/{\text{IC}}_{50}\right]\right\}$$ (3.9)

When f = 0, equation (3.9) becomes equivalent to the corresponding expression for the three-parameter logistic model given in equation (3.4).

While we do not study it here in detail, note that a Gompertz model potentially allowing for hormesis, analogous to model (3.8), can be contemplated by multiplying the Gompertz curve expression in (3.2) by the factor (1+fe^dose_i). Sample programs for conducting all analyses described in Section 3 are available from the authors. As a specific example, Appendix 2 contains a straightforward program for fitting model (3.9) via the SAS NLMIXED procedure [12].

3.7 Assessment of model fit

One obvious measure of model fit that can be used to select among candidate nonlinear models is the average of the squared residuals, or mean squared error (MSE). For the models discussed here with homogeneous variance, this is equivalent to the square of the MLE for the residual standard deviation (σ̂). In addition, one can conduct a classical statistical test for “lack of fit” as discussed in many linear regression texts, which remains valid in the normal-error nonlinear model setting with replicates [18]. This test compares the observed mean response at each dose against the predicted mean based on the fitted model to determine whether the model provides an adequate representation of the data. The test statistic is a ratio of lack-of-fit and pure error mean squares and is distributed as a central F random variable with (c−p) and (n−c) degrees of freedom under the null hypothesis of adequate fit, where c is the number of distinct doses in the experiment, n is the total number of (dose, response) data pairs, and p is the number of parameters used to model the mean response. Details of this standard test are widely available (e.g., [14]).

4. Results

The observed data consist of 3 observations per dose in each case, for a total of 21 and 27 observations for the TR and BM cell lines, respectively. While these are relatively small numbers, numerically stable estimates of IC₅₀ and its standard error were obtained for all models discussed in section 3.1, with equivalent results based on the alternative parameterizations in section 3.3.

Table 1 provides MLEs and corresponding standard errors for all model parameters, including IC₅₀, based on fitting each of the three models in section 3.1 to the TR and BM cell line data. Note that the IC₅₀ estimate and its standard error are very similar across models for TR. In contrast, estimates of IC₅₀ and their standard errors for the BM data are quite different, with those based on the two-parameter exponential model vastly distinct from those derived via the three-parameter models. Table 1 also displays the MSEs for each model, which are all nearly identical for the TR data but are very different for BM. In the latter case, the exponential model clearly provides a poor fit, while the three-parameter logistic appears to fit slightly better than the Gompertz model.

Table 1.

Summary of models fit to endothelial cell line data ^a

		ML estimates (standard errors in parentheses)					MSE
Cell line	Model	C	α	β	σ	IC50 (uM)
TR	Exponential	--	−0.022 (0.069)	−0.136 (0.022)	0.160 (0.025)	5.11 (0.83)	0.026
	Three-parameter logistic	1.705 (1.279)	−0.249 (1.637)	0.221 (0.109)	0.158 (0.024)	5.38 (0.83)	0.025
	Three-parameter Gompertz	13.993 (90.320)	0.983 (2.403)	0.043 (0.089)	0.159 (0.025)	5.33 (0.91)	0.025
BM	Exponential	--	0.729 (0.091)	−0.133 (0.018)	0.398 (0.054)	0.18 (0.13)	0.158
	Three-parameter logistic	1.773 (0.065)	−6.889 (1.107)	0.862 (0.130)	0.175 (0.024)	2.98 (0.70)	0.031
	Three-parameter Gompertz	1.836 (0.096)	−4.287 (0.863)	0.486 (0.095)	0.205 (0.028)	3.31 (1.01)	0.042

^aModels for BM fit to scaled [dose_i* = ln(1000×dose_i + 1)] data (see section 3.4)

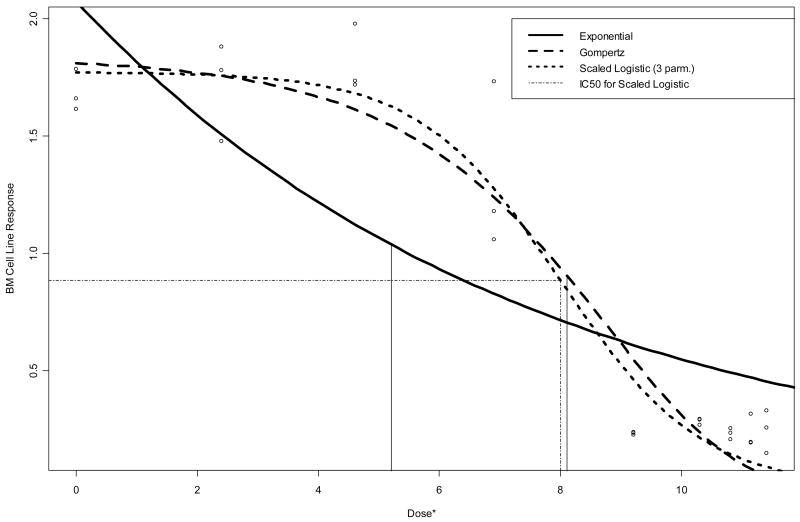
Figure 2 displays the raw data and the fitted curves for the BM data. Vertical lines are drawn from the curves down to the estimated IC₅₀’s on the dose_i* = ln(1000×dose_i + 1) axis scale. A horizontal line is drawn at 50% of the estimated 0-dose response based on the three-parameter logistic model, to illustrate its intersection with the vertical line that marks the corresponding IC₅₀ estimate. Note that Figure 2 agrees with Table 1 visually in the sense that the sigmoidal-shaped curves provide a much better fit to the BM data than does the exponential. The exponential model is woefully inadequate to describe the observed dose-response pattern for BM, resulting in an unrealistically low IC₅₀ estimate.

Figure 2.

Raw data and fitted dose-response curves for BM data. Vertical lines are drawn from the curves down to the estimated IC₅₀’s on the dose* = ln(1000×dose + 1) axis scale.

In what follows, we illustrate the various model extensions described in sections 3.5 and 3.6. Although considerable improvements in fit are possible for both the TR and BM cell line data relative to the three models summarized in Table 1, for simplicity of presentation we use the BM data to illustrate most of these extensions.

Table 2 provides MLEs and standard errors for the BM data under the three-parameter logistic model, after allowing a different residual variance for high as opposed to low doses. Specifically, the residual variance ${\sigma }_1^2$ applies to doses less than or equal to 1 uM (6.91 on the dose_i* scale) for BM, while ${\sigma }_2^2$ applies to doses greater than 1 uM. The estimates and standard errors in Table 2 can be compared to the corresponding ones in Table 1, and the fitted curves are extremely similar. The effect of allowing for heterogeneity is to provide a slightly better fit to the data for higher doses (> 1 uM), which receive greater weight in the analysis. However, the resulting fit is not as good for lower doses, which is verifiable by comparing dose-specific MSEs. In this case, the overall MSE (Table 2) for the scaled logistic heterogeneous variance model is slightly higher than that for the homogeneous variance model (Table 1). There is a modest change in the IC₅₀ estimate after allowing variance heterogeneity (2.43 uM vs. 2.97 uM), and its standard error is somewhat larger (0.89 uM vs. 0.70 uM). We conclude that in this small data set there is no tangible advantage to generalizing the three-parameter logistic model to allow residual variance heterogeneity, although such an investigation remains a worthwhile part of a thorough IC₅₀ estimation process.

Table 2.

Scaled logistic model results for BM, allowing heterogeneous variances ^a,^b

ML estimates (standard errors in parentheses)						MSE
C	α	β	σ1	σ2	IC50 (uM)
1.799 (0.089)	−5.946 (1.354)	0.763 (0.144)	0.219 (0.056)	0.139 (0.031)	2.43 (0.89)	0.032

^aModel fit to scaled [dose_i* = ln(1000×dose_i + 1)] data (see sections 3.4 and 3.5)

^bResidual SD = σ₁ for doses ≤ 1 uM, σ₂ for doses > 1 uM

Table 3 provides the ML estimates based on fitting four-parameter logistic and Gompertz models to the BM cell line data. Several interesting observations are apparent from this table. First, the estimates of D and C, the additive and multiplicative scaling parameters, respectively, are identical based on the two models. The estimated IC₅₀s are almost identical (1.14 vs. 1.11 uM). Second, these IC₅₀ estimates are quite different from those based on the three-parameter models summarized in Table 1, which were both near 3 uM. Third, the MSEs based on the four-parameter models are markedly reduced (0.017 for both models), as compared to 0.031 and 0.042 for the three-parameter logistic and Gompertz models (Table 1). Finally, we note that although the MLEs were numerically stable, standard error estimates accompanying the four-parameter model fits were not. This reflects on the fact that these models are pushing the level of complexity supported by the relatively small data set (only 3 observations at each of the 9 doses).

Table 3.

Four-parameter logistic and Gompertz model results for BM ^a,^b

	ML estimates						MSE
Model	D	C	α	β	σ	IC50 (uM)
Logistic	0.244	1.493	−57.565	8.194	0.131	1.14	0.017
Gompertz	0.244	1.493	−56.685	8.042	0.131	1.11	0.017

^aModels fit to scaled [dose_i* = ln(1000×dose_i + 1)] data (see section 3.4)

^bStandard error estimates were unreliable due to paucity of data

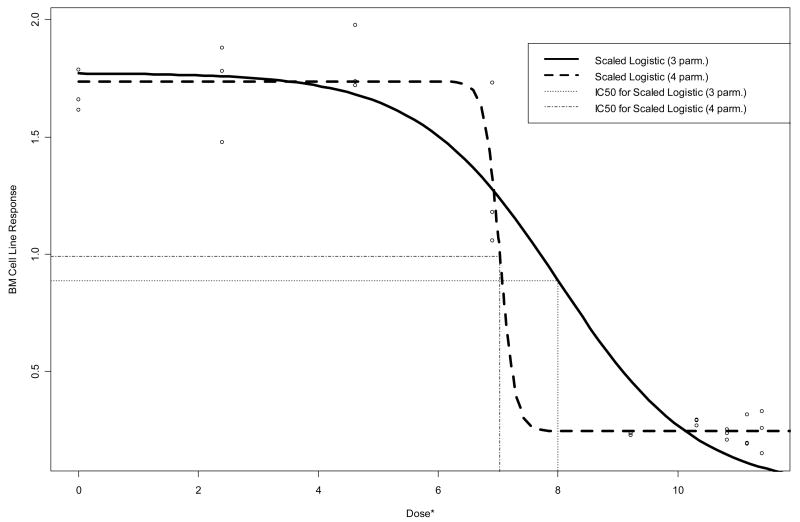
In Figure 3, the fitted four-parameter logistic curve summarized in Table 3 is overlaid with the raw data and the prior three-parameter curve (Table 1). The improved fit is apparent, due to the addition of the lower limit parameter (D) which allows the curve to flatten out at a response value of approximately 0.244 and represents the observed data at higher doses extremely well. The steep descent of the four-parameter curve yields an IC₅₀ estimate of approximately 7 on the dose_i* = ln(1000×dose_i + 1) scale, as opposed to the value of 8 yielded by the three-parameter model (these translate to approximately 1 uM and 3 uM, respectively, as summarized in Tables 1 and 3).

Figure 3.

Raw data and fitted three- and four-parameter logistic dose-response curves for BM data. Vertical lines are drawn from the curves down to the estimated IC₅₀’s on the dose* = ln(1000×dose + 1) axis scale.

Lack of fit tests suggest inadequacy in the two- and three-parameter models summarized in Table 1, which can be alleviated via the four-parameter models. For example, the F statistic (p-value) for lack of fit to the BM cell line data via the three-parameter logistic model was 2.77 (0.044), as compared to 0.26 (0.95) for the four-parameter logistic model. Despite this clear improvement in fit, Figure 3 illustrates an important caution regarding dose-response modeling when doses are relatively sparse and/or few data points are available at each dose. Specifically, the four-parameter model arguably “overfits” the data in the sense that it assumes a great deal about the response pattern between doses of roughly 7 and 9 on the plotted scale, where there are no observed data (see Discussion).

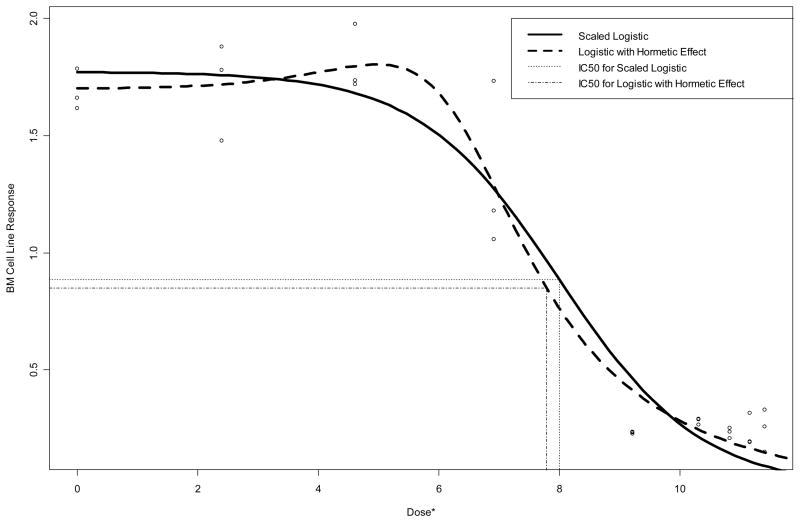
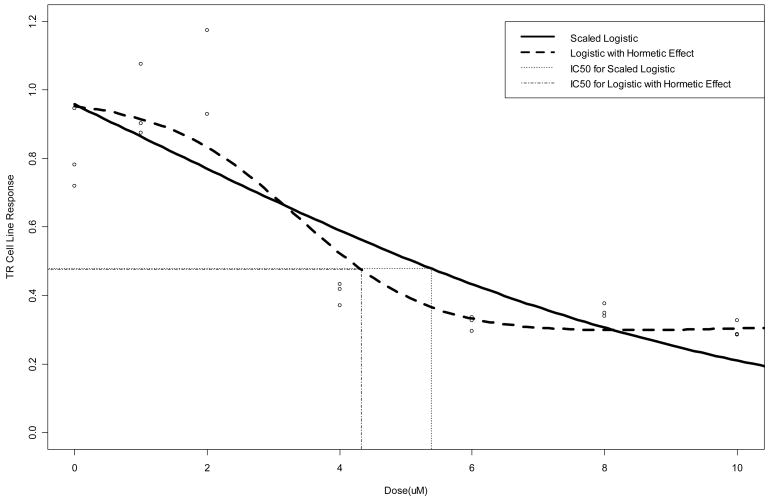
Finally, Table 4 summarizes the fit of the four-parameter logistic model allowing for a hormetic response [equations (3.8) and (3.9)] to the TR and BM cell line data. This model yields a sizable improvement in MSE over the three-parameter logistic model (0.014 vs. 0.025 for TR; 0.022 vs. 0.031 for BM), and provides a more reasonable fit to the data (e.g., lack-of-fit F statistic = 2.66 for BM; p=0.42). Further, standard error estimates are stable, with those corresponding to IC₅₀ markedly lower than those obtained via the three-parameter models in Table 1 (0.40 vs. 0.83 for TR; 0.39 vs. 0.70 for BM). In both cases, the estimated IC₅₀ is lower subsequent to allowing for hormesis in the model. Figures 4 and 5 overlay the fitted curves (Table 4) with the corresponding three-parameter logistic fits (Table 1). Note the improvement in fit for both TR and BM. The improved fit for TR occurs despite the fact that the model does not predict any increase in response at low doses, while there is a slight suggestion of hormesis in the BM data.

Table 4.

Logistic model results for TR and BM cell lines, allowing for hormesis ^a,^b

	ML estimates (standard errors in parentheses)						MSE
Cell line	C	f	α	β	σ	IC50 (uM)
TR	0.977 (0.054)	0.0091 (0.0075)	−3.344 (0.363)	0.982 (0.086)	0.120 (0.018)	4.33 (0.40)	0.014
BM	1.699 (0.074)	0.0014 (0.0015)	−9.249 (0.821)	1.449 (0.071)	0.147 (0.020)	2.41 (0.39)	0.022

^aResults based on model (3.9); model (3.8) was fit to obtain estimate of β

^bModel fit to scaled [dose_i* = ln(1000×dose_i + 1)] data (see section 3.4)

Figure 4.

Raw data and fitted three-parameter and hormetic logistic dose-response curves for BM data. Vertical lines are drawn from the curves down to the estimated IC₅₀’s on the dose* = ln(1000×dose + 1) axis scale.

Figure 5.

Raw data and fitted three-parameter and hormetic logistic dose-response curves for TR data. Vertical lines are drawn from the curves down to the estimated IC₅₀’s on the dose (in uM) axis scale.

5. Discussion

Our goal has been to present a relatively complete overview of statistical considerations involved in IC₅₀ estimation for continuous responses, motivated by data on endothelial cell lines with replicates over a series of doses. While we have chosen to focus upon three primary underlying models (including a Gompertz model that is to our knowledge novel to this purpose), the basic steps characterizing the process are generally not model-specific. We have demonstrated the definition of IC₅₀ based on a specified model for mean response, its estimation with corresponding standard errors via maximum likelihood as implemented in commercial software (with and without reparameterizing directly in terms of IC₅₀), dose axis scaling, the accommodation of heterogeneous variance across doses, flexible model extensions, and assessments of model fit.

Our illustrative motivating examples are indicative of the fact that in real-life studies, dose-response data are not always voluminous or extremely well behaved. For instance, Figure 2 suggests that for the relatively sparse data from the BM cell line experiment, none of the two- or three-parameter models provides a fully adequate fit. To demonstrate potential improvements, we considered the four-parameter curves in section 3.6 [eqn. (3.7)]. These produce a sizeable improvement in fit to the observed data as discussed in section 4, although the concern of overfitting is prominent and reliable standard error estimates are not supported given the modest sample sizes. Without data at intervening doses, it is impossible to know whether the more gradual descent postulated by the three-parameter model (Figure 3) is more realistic in this case. Nevertheless it is clear that, when supported by the available data, substantial improvements in fit are possible via more flexible models for mean response.

Given the instability of standard error estimates for the four-parameter models in Table 3, we prefer in this application to emphasize the extension that allows for a hormetic response in conjunction with the logistic model (Table 4; Figures 4 and 5). This model is arguably the best of those considered for the BM and TR cell line data in light of model fit and stability of standard error estimates. However, the tendency toward an increasing mean response over the first three doses in the case of the BM cell line experiment may be spurious given the sparse data (only three observations per dose); further studies would be required to firmly demonstrate hormesis.

Finally, a heterogeneous variance model allowing for less dispersion in responses at higher doses was not tangibly beneficial for the analysis of the BM cell line data (Table 2). We expect that the accommodation of heterogeneous variance will be more likely to demonstrate efficiency gains for models that fit the data relatively well at each dose. For example, if the four-parameter logistic and Gompertz models [eqn. (3.7)] had been better supported by the small amount of data available, acc ounting for heterogeneity in that context would be more likely to improve precision. Simulation studies conducted for our own benefit (not summarized here) confirm that IC₅₀ and standard error estimation under the four-parameter models with heterogeneous variance is indeed feasible given adequate numbers of doses and replicates at each dose. We close by noting that the logical steps employed here in comparing models and assessing their fit may be useful as a general guide for similar studies involving dose-response data, although our specific results must be interpreted with some restraint in light of the limited available sample size.

APPENDIX 1: First Derivatives for Delta Method Variance Calculations

The analytic expressions (D) for the vectors of first derivatives discussed in section 3.3 with respect to the three-parameter logistic and Gompertz models are as follows:

$$\begin{array}{ll}\text{1)}\text{Exponential}:\hfill & \mathbf{D}=\partial h/\partial \beta =ln(2)/{\beta }^2\hfill \\ \text{2) Scaled}\text{logistic}:\hfill & \mathbf{D}=\left(\begin{array}{c}\partial \text{h}/\partial \alpha \\ \partial \text{h}/\partial \beta \end{array}\right),\partial h/\partial \alpha =\frac{-1}{\beta [2exp(\alpha )+1]},\partial h/\partial \beta =\frac{-\{ln[2exp(\alpha )+1]-\alpha \}}{{\beta }^2}\hfill \\ \text{3)}\text{Gompertz}:\hfill & \mathbf{D}=\left(\begin{array}{c}\partial \text{h}/\partial \alpha \\ \partial \text{h}/\partial \beta \end{array}\right),\partial h/\partial \alpha =\frac{-ln(2)}{\beta [ln(2)+exp(\alpha )]},\partial h/\partial \beta =\frac{\alpha -ln[ln(2)+exp(\alpha )]}{{\beta }^2}\hfill \end{array}$$

APPENDIX 2: Example of SAS NLMIXED Code for Fitting Model (3.9)

data tr;

 input doseuM resp;

 list; cards;

0 0.72

0 0.781

.

.

.

;

PROC NLMIXED data=tr cov;

 parms C = 1 f = 0.01 IC50 = 5 alph = −5 sigma = .3;

 bounds sigma >= 0;

 pi = 2*arsin(1);

mui = C*(1 + f*exp(doseuM))/(1 + exp(alph + doseuM*

 log(2*(1+exp(−alph))*(1+f*exp(IC50))/(1+f) − exp(−alph))/IC50));

 like = (1/(sqrt(2*pi*sigma**2)))*exp(−(1/(2*sigma**2))*(resp − mui)**2);

 loglik=log(like);

model resp ~ general(loglik);

run;