A Systematic Methodology for Defining Coarse-Grained Sites in Large Biomolecules

Abstract

Coarse-grained (CG) models of biomolecules have recently attracted considerable interest because they enable the simulation of complex biological systems on length-scales and timescales that are inaccessible for atomistic molecular dynamics simulation. A CG model is defined by a map that transforms an atomically detailed configuration into a CG configuration. For CG models of relatively small biomolecules or in cases that the CG and all-atom models have similar resolution, the construction of this map is relatively straightforward and can be guided by chemical intuition. However, it is more challenging to construct a CG map when large and complex domains of biomolecules have to be represented by relatively few CG sites. This work introduces a new and systematic methodology called essential dynamics coarse-graining (ED-CG). This approach constructs a CG map of the primary sequence at a chosen resolution for an arbitrarily complex biomolecule. In particular, the resulting ED-CG method variationally determines the CG sites that reflect the essential dynamics characterized by principal component analysis of an atomistic molecular dynamics trajectory. Numerical calculations illustrate this approach for the HIV-1 CA protein dimer and ATP-bound G-actin. Importantly, since the CG sites are constructed from the primary sequence of the biomolecule, the resulting ED-CG model may be better suited to appropriately explore protein conformational space than those from other CG methods at the same degree of resolution.

INTRODUCTION

With ever-increasing computational power, atomistic molecular dynamics (MD) simulations remain an important tool for investigating the structure and dynamics of biomolecules at nanometer length-scales and for nanosecond timescales (1,2). However, there are many biological processes, such as virus capsid assembly and cytoskeletal dynamics, which occur on length and timescales far beyond those feasible for simulations with atomic resolution. To overcome the gap between computational capabilities and real biological processes, it is necessary to study such processes at a coarse-grained (CG) level (3,4).

CG approaches enable one to describe larger systems over longer effective timescales, with a reduced degree of detail. Generally speaking, the aim of CG modeling is to reduce the large number of degrees of freedom in a biomolecule into a significantly smaller set. The choice of CG sites for a given system is therefore an important issue. This problem has two facets, one being the resolution (number) of the CG sites and the other being their location within the biomolecule. The number of CG sites needed to model a system will depend on both the desired level of accuracy and the computational resources available. Once the number of sites has been decided, the logical next question is where to place them reasonably, which is the focus of this article.

A CG model is defined by a map that transforms an atomically detailed configuration into a CG configuration. For a relatively small molecule such as a lipid or a peptide, the construction of the CG map can be guided by chemical intuition. One can, for example, define a CG site for each functional group in the molecule (5,6). Alternatively, CG sites can be defined in a single system with different levels of resolution (7). Curcó et al. (8) and Zanuy et al. (9) have introduced a CG strategy based on chemical intuition, which defines CG sites of different resolution for different amino acids (two, three, or four sites per residue according to the chemical nature of each amino acid). For CG models with somewhat lower resolution, such as elastic network models (ENM) (10,11), an amino acid residue is often reduced to one CG site (located at the position of the C_α atom) and the system is represented by a network of such sites. However, for a CG model of a large biomolecule with an even more reduced resolution it becomes increasingly difficult to define a relatively small number of CG sites by using chemical intuition alone. For example, the type 1 human immunodeficiency virus (HIV-1) capsid is composed of thousands of CA protein dimers (12). Since each CA monomer is composed of >200 residues, the problem of optimally placing just a few CG sites per dimer is critical to faithfully modeling the capsid assembly process. A similar problem arises in the CG analysis of other complex biomolecular systems such as actin filaments (13,14). To solve this problem, a quantitative method to define and assess the quality of different CG maps is needed.

There are several different methods which define the CG map to preserve the underlying structural elements of the biomolecule. For example, Gohlke and Thorpe (15) have suggested that rigid units, identified by a topological algorithm (16), be used as CG sites. Martinez and Schulten (17) and Arkhipov et al. (18) have developed an approach to reproduce the shape and moment of inertia of a protein by a number of CG sites. Both these methods develop a coarse-grained model from a single structure.

However, it is known that protein motions play an important role in their function. Gfeller and De Los Rios, for example, have introduced a spectral coarse-graining technique, which is based on preserving the dynamics of complex networks (19). In this article a different approach is proposed, which defines a CG map that reflects the collective motions computed by a principal component analysis (PCA) of an atomistic trajectory. Several studies have indicated that a small number of PCA modes, which define an essential dynamics (ED) subspace (20), represent most of the biologically relevant collective protein motions (21,22). In fact, the identification of dynamic correlated domains with essential modes was recently employed as the starting point for construction of a CG model (23). In the latter method, groups of atoms are clustered into domains such that the atoms in the same domain adopt similar values of the direction cosines of the essential collective modes. In this method, we pursue a more systematic approach, by using a residual to variationally optimize the CG map, to approximate PCA modes within the essential dynamics subspace. It should be noted that, in principle, this methodology could instead use normal modes or even modes from a higher resolution ENM as the basis for the coarse-graining.

In the subsequent sections of this article, a new essential dynamics coarse-graining (ED-CG) method will be presented, followed by a description of the numerical algorithms and details of the atomistic simulations. We then present the application of the method to two proteins: the HIV-1 CA protein dimer and ATP-bound G-actin. ED-CG is then compared to the topology-representing network method (17,18). Concluding remarks are provided at the end.

THEORY AND METHODS

Principal component analysis and essential dynamics

Principal component analysis of an MD trajectory of a protein distinguishes low frequency, collective motions from high frequency, localized fluctuations. Amadei et al. have demonstrated that the large-amplitude PCA modes obtained by analyzing only the C_α atoms in a protein reproduce the PCA modes obtained from an all-atom analysis quite well (20). Therefore, in discussing the theory and application of the ED-CG method below, only the n C_α atoms will be considered. After eliminating the translational and rotational motion to a reference frame, the internal motion is described by a trajectory r(t), where r(t) ∈ R³ⁿ, is a 3n-dimensional vector of the C_α coordinates: 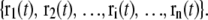The Cartesian coordinates for each atom i at time t are represented by r_i(t) ∈ R³, with components indicated by 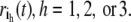Next, a covariance matrix C ∈ R³ⁿ × R³ⁿ of atomistic fluctuations is constructed as

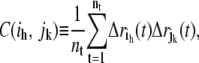(1)

where C(i_h, j_k) is one element in the matrix C, i_h and j_k are the h and k coordinates of atoms i and j, n_t is the number of configurations in the MD trajectory, 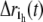is the displacement from equilibrium of the h coordinate for atom i at time t, and 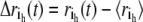with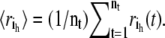

Diagonalization of the covariance matrix (Eq. 1) yields a matrix of eigenvectors Ψ ∈ R³ⁿ × R³ⁿ (PCA modes) and corresponding eigenvalues. The result of this decomposition is

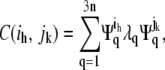(2)

where λ_q is the eigenvalue. Here 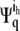and 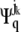are the two components corresponding to the h coordinate of atom i and the k coordinate of atom j, respectively, in the 3n-dimensional eigenvector Ψ_q, which is the q^th column of the matrix Ψ.

Typically, the PCA modes are sorted by their eigenvalues, with the majority of the largest-scale protein motions described by a very limited number (n_ED ≪ 3n) of the lowest frequency (largest eigenvalue) PCA modes. This subset of PCA modes are sometimes called essential modes. Amadei et al. termed a subspace that is spanned by the essential modes an essential subspace, with the motions in this subspace called essential dynamics (20). Thus the essential subspace is defined by 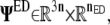which is a matrix having the first n_ED columns of Ψ.

A CG model to reflect essential dynamics

A dynamic domain is a group of atoms that move together in a highly correlated fashion (Fig. 1 a) as identified by essential dynamics (24). With a good decomposition into dynamic domains, intradomain motion is fast and local, while interdomain motion is slow and collective and often functionally relevant (25). In this section, we describe an algorithm to map groups of atoms into CG sites that preserve dynamic domains, so that the CG model may be used to approximate the essential dynamics. In this way, the CG map is systematically defined to represent the functional, interdomain motions of the biomolecule.

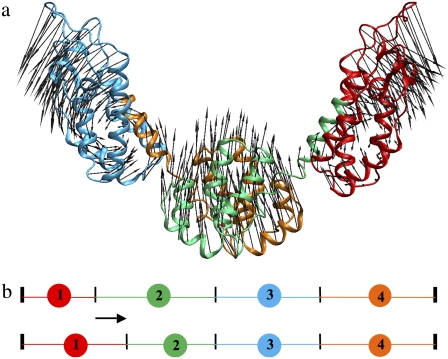
FIGURE 1.

(a) The first PCA mode of the HIV-1 CA protein dimer. A 20-ns atomistic trajectory was used, and only the 440 C_α atoms were considered to perform the PCA. There are dynamic domains in which atoms move highly correlated. (b) Schematic diagram illustrating the ED-CG algorithm. The N- and C-terminus are fixed, and in this case there are three boundary atoms to determine four sequentially contiguous domains. Each CG site is the COM of a domain. The minimal residual (Eq. 5) can be obtained by adjusting the positions of the boundary atoms (as illustrated by the arrow), and the locations of the CG sites are adjusted accordingly.

The displacement of atom i at time t is denoted by Δr_i(t), and its contribution in the essential subspace is 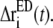If another atom j moves in a correlated fashion with atom i, the displacement difference 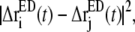should be small. This observation naturally leads to a variational minimization of the residual

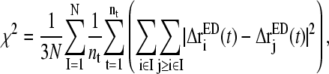(3)

where N is the number of CG sites. Notice that Eq. 3 depends on a particular mapping of the atomistic configuration into a CG configuration through the limits of the summations. The domain motions in a protein can be divided into the intradomain motions and the motions of its center-of-mass (COM), and the latter describe the interdomain motions. If one CG mapping yields a lower residual than other mappings, it means that the intradomain motions are minimized and the motions of COM (interdomain motions) are maximized at the same time. The resulting CG mapping should allow a better representation of the collective interdomain motions, which are probably the slowest in all the protein motions (24,25). The goal is then to minimize χ² (Eq. 3) over a set of potential CG mappings.

For computational convenience, Eq. 3 can be related to the covariance matrix in the essential subspace C^ED ∈ R³ⁿ × R³ⁿ such that

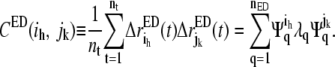(4)

In contrast to the covariance matrix C in the full 3n-dimensional space (Eqs. 1 and 2), C^ED is constructed from the displacements in the n_ED-dimensional essential subspace (Eq. 4). All the high-frequency, nonessential modes are filtered out by constructing C^ED. In Eq. 3, 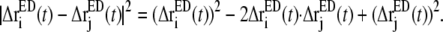Defining the trace of the 3 × 3 submatrix between atoms i and j in C^ED as 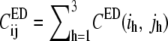such that 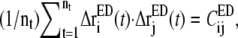Eq. 3 may be recast in a simpler form:

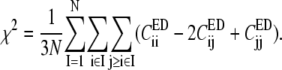(5)

Notice that if a CG mapping simply maps the atomistic model onto itself, χ² is naturally 0 (Eq. 5).

Numerical algorithms

In this section, numerical algorithms are introduced, which search the space of CG mappings for the one with the minimal residual (Eq. 5). In practice, some restrictions on the CG mapping are employed to make the problem more tractable:

1. Each C_α atom i is involved in only one CG site I.

2. Each CG site is located at the center-of-mass (COM) of a group of C_α atoms.

3. The C_α atoms associated with each CG site are assumed contiguous in protein primary sequence (Fig. 1 b).

The group of C_α atoms associated with a CG site will be referred to as a dynamic domain, and the last C_α atom in each domain will be referred to as a boundary atom. An initial CG mapping is first defined by deciding on the number of CG sites, and then locating the domain boundaries randomly along the primary sequence. The residual (Eq. 5) is then minimized by adjusting the positions of the boundaries between domains (Fig. 1 b), using a global simulated annealing followed by a local steepest descent search. After the boundary positions with the minimal residual are determined, the center of each CG site is located at the COM of the C_α atoms in each dynamic domain.

Simulated annealing

Simulated annealing (SA) is a generic algorithm to locate the global minimum of a target function (26), and the target function used here is given by Eq. 5. In this CG algorithm, at each step of SA, the position of a boundary atom is changed randomly in the primary sequence (Fig. 1 b), and the residual of the new CG map is computed (Eq. 5). The new map is accepted or rejected based on the Metropolis criterion (27). If the new map exhibits a lower residual 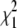than its predecessor 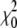(a downhill move), it is accepted as the start for the next SA iteration. If the new map has a higher residual than its predecessor (an uphill move, χ² = 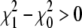), it is accepted with a probability exp (−Δχ²/T), where T is a global parameter (temperature) that controls the likelihood of uphill moves. At the beginning T is large, which allows the boundary atoms to move almost randomly and escape from local minima. The temperature is then gradually decreased during the annealing process, allowing the calculation to settle into the global minimum. The initial temperature of the SA calculation should be approximately the expected residual change χ² to obtain a reasonable acceptance of uphill moves.

Steepest descent

Steepest descent (SD) is a relatively simple iterative optimization algorithm to find a local minimum of a target function. In this CG method, in each iteration each domain boundary (one at a time) is moved forward (+1) or backward (−1) in the primary sequence, and every change that yields a smaller residual (Eq. 5) than its predecessor is accepted. The process continues until a minimum is found as ascertained by examining the gradient of the residual.

It should be noted that both simulated annealing and steepest descent algorithms cannot be guaranteed to find the global minimum (optimal positions of the boundary atoms) (Eq. 5), especially for defining more CG sites in a large biomolecule. Multiple SA and SD minimizations beginning with different initial boundary atoms were therefore performed to assure convergence of the results. The boundary-atom set with the minimal residual was then selected.

MOLECULAR DYNAMICS SIMULATIONS

The HIV-1 CA protein dimer

The initial structure of the HIV-1 CA protein dimer (CA dimer) was obtained from crystal structures of the capsid C-terminal dimer (PDB entry: 1A43 (28)) and the N-terminal dimerization domains (29), and prepared with the CHARMM suite of molecular dynamics programs (30). The system is a homodimer with 440 residues in total. Counterions were added by the SOLVATE software package (31) to compensate for the net negative charge on the protein. To generate a solvated structure, a water box was constructed from a preequilibrated cubic cell of 125 water molecules. A water molecule was removed if its oxygen atom was <2.4 Å away from the heavy atoms of the protein or the counterions. Finally the CA dimer was solvated in TIP3P water (32) giving a composite system consisting of ∼107,000 atoms.

To preequilibrate the system, a 300-timestep conjugate gradient minimization was first performed in CHARMM with long-range electrostatics calculated by particle mesh Ewald summation (33). The system was then equilibrated using the NAMD suite of programs (34,35). In the first stage, a velocity quenching of the system followed by a conjugate minimization was performed for 20 ps while the C_α atoms were constrained with a force constant of 100 kcal mol⁻¹ Å⁻¹. Then the system was heated up to 310 K in an increment of 31 K/ps with the C_α atoms remaining under constraint. After this, the system was equilibrated by rescaling velocities while gradually reducing the constraints on heavy atoms in successive steps of 20 ps each, with each step having a progressively lower constraint force. The production MD run was carried out for 20 ns under constant NPT conditions at 310 K and 1 atm, with Langevin thermostats and barostats used to control the temperature and pressure (36,37).

ATP-bound G-actin

All MD simulations were performed using the NAMD software package (34,35). The crystal structures of ATP-bound G-actin (G-ATP) were used for all actin simulations (PDB entry 1NWK (38)). The missing DNAse I-binding loop (DB loop) (residues 38–50) in the structure for 1NWK was modeled in the same fashion as in previously reported studies (13,38). The CHARMM22 force field (39) was used in all simulations in conjunction with the particle mesh Ewald algorithm (33) for long-range electrostatic interactions. After an initial 20-ps heating period, the system was preequilibrated in the constant NVT ensemble for 50 ps by using velocity rescaling. Simulations were then performed in the constant NPT ensemble (310 K and 1 atm) through use of the Langevin piston Nosé-Hoover method (36,37) as implemented in NAMD. Three independent trajectories of 30 ns each were generated from different initial conditions.

RESULTS AND DISCUSSION

Coarse-grained models of the HIV-1 CA protein dimer

If one wants to build a two-site CG model for the CA dimer, chemical intuition suggests that each monomer should be coarse-grained to a single site (corresponding, respectively, to residues 1–220 and 221–440). However, the real dynamics is not strictly symmetric between the two monomers over the course of the 20-ns MD simulation because of limited sampling. The two-site CG model with the minimal residual (3.462 × 10⁵) when considering only the first essential mode is (1–251, 252–440), which is nonsymmetric (Table 1). However, the residual of the symmetric two-site model (3.476 × 10⁵) is very close to the minimum. The four-, six-, and eight-site models were constructed by the ED-CG method, both with and without enforced symmetry. The residuals obtained for the symmetric and nonsymmetric four-site models are very close in value. The same six-site model is obtained in both cases, and there are only slight differences between the eight-site models (Table 1). The results suggest that it is reasonable to enforce symmetry in the calculations of CG sites for the CA dimer. In the following, only the symmetric results are discussed.

TABLE 1.

CG models of the HIV-1 CA protein dimer obtained by the ED-CG method with and without enforced symmetry

NCG* (nED)†	Symmetric‡	Nonsymmetric§
2 (1)	1–220,¶ 221–440	1–251, 252–440
	χ2 = 3.476 × 105‖	χ2 = 3.462 × 105
4 (6)	1–131, 132–220, 221–351, 352–440	1–136, 137–260, 261–353, 354–440
	χ2 = 7.274 × 104	χ2 = 7.232 × 104
6 (12)	1–72, 73–134, 135–220, 221–292, 293–354, 355–440	1–72, 67–134, 135–220, 221–292, 293–354, 355–440
	χ2 = 1.861 × 104	χ2 = 1.861 × 104
8 (18)	1–23, 24–75, 76–134, 135–220,	1–46, 47–79, 80–134, 135–220,
	221–243, 244–295, 296–354, 355–440	221–242, 243–296, 297–354, 355–440
	χ2 = 1.012 × 104	χ2 = 9.986 × 103

^*Number of CG sites in the CA dimer.

^†Number of PCA modes that characterize the essential dynamics.

^‡CG sites in the two monomers are enforced to be symmetric.

^§CG sites in the two monomers are nonsymmetric.

^¶The first and the last C_α atoms of a dynamic domain, and the CG site is the COM of this domain.

^‖The minimal residual (Eq. 5) of the CG model.

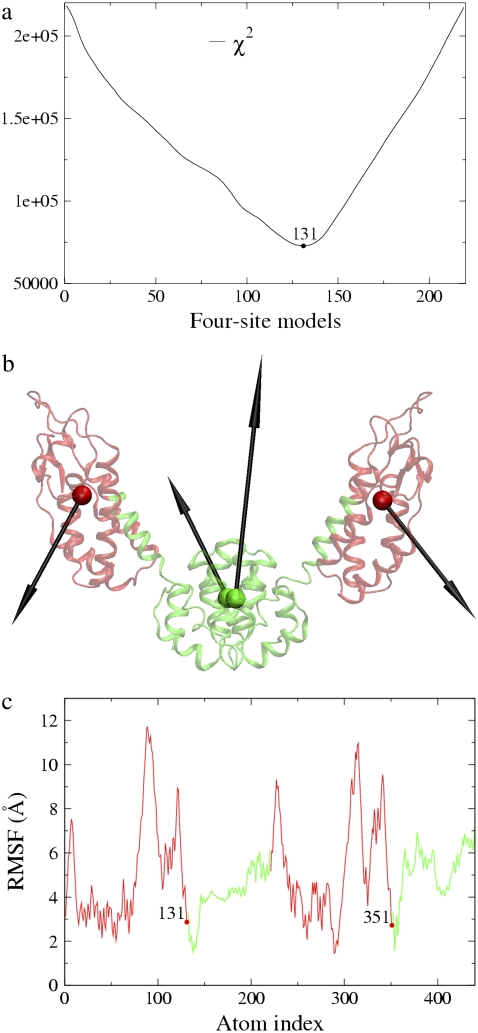
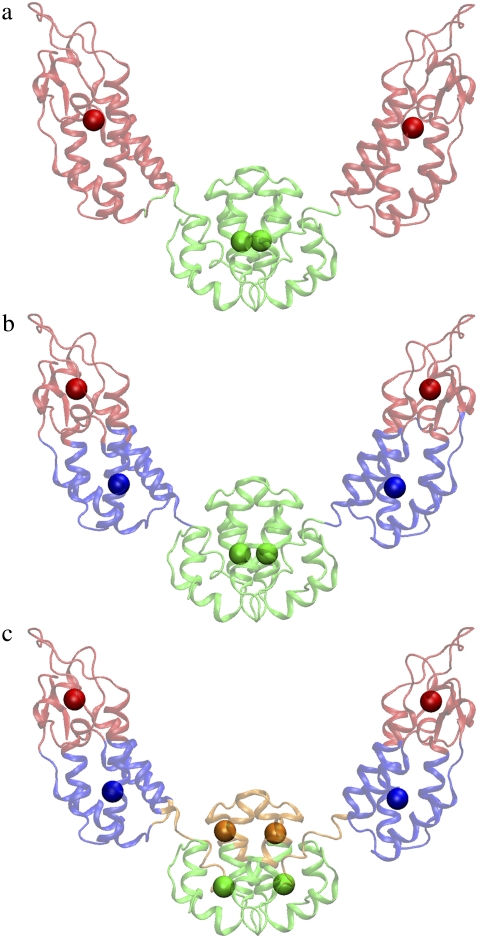
The four-site model was constructed using the essential subspace of the first six PCA modes (n_ED = 6) since four sites have six internal modes after subtracting-off the three translational and the three rotational degrees of freedom (4 × 3 − 6 = 6). The first six modes obtained by PCA of the atomistic MD trajectory contribute ∼94% of the observed fluctuations. The first mode contributed ∼74% of the observed fluctuation, and described a collective motion between the N-terminal and C-terminal domains of the protein (Fig. 1 a). There is only one boundary atom that needs to be determined in the symmetric four-site models of CA dimer, which could be located anywhere from C_α atom 1–219. In Fig. 2 a, the residuals (Eq. 5) of all the four-site models constructed to approximate the first six essential modes are plotted, and the boundary atom with the minimal residual is 131. This symmetric ED-CG four-site model with the minimal residual (7.274 × 10⁴, Table 1) is shown in Fig. 2 b. In each monomer, the boundary atom 131 is located in the linking α-helix hinge region between the N-terminal and the C-terminal domains. The atoms in this hinge region have fewer root mean-square fluctuations (RMSF) in the essential subspace (Fig. 2 c). This model looks very reasonable by chemical intuition because the two dynamic domains in each monomer (Fig. 2 b) exactly correspond to the N- and C-terminal domains in the protein. A CG trajectory was constructed for the ED-CG four-site model from the underlying atomistic MD trajectory, and PCA was then performed on this trajectory to obtain the PCA modes of the CG model. The first CG mode (essential dynamics of the CG model) is indicated by arrows on the CG sites (Fig. 2 b), which represent the collective domain motions quite well (arrows in Fig. 1 a).

FIGURE 2.

Four-site models of the HIV-1 CA protein dimer: (a) The residuals (Eq. 5) of all the symmetric four-site models, and the boundary atom for the model with the minimal residual is 131. (b) The ED-CG four-site model, and the four dynamic domains are (1–131) red; (132–220) green; (221–351) red; and (352–440) green. Each CG site is the COM of its corresponding domain, and the arrows on the sites indicate the first PCA mode of a four-site coarse-grained trajectory that was constructed from the atomistic MD trajectory. (c) The RMSF values of C_α atoms in the essential subspace (n_ED = 6). The four dynamic domains obtained by the ED-CG method are mapped onto the RMSF curve with colors corresponding to panel b, and the boundary atoms are labeled.

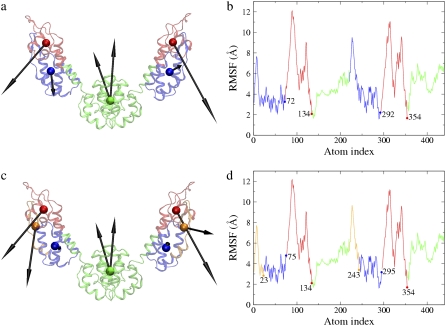
The symmetric six-site model corresponding to the minimal residual (1.861 × 10⁴, Table 1) by including the first 12 essential modes (n_ED = 12) is shown in Fig. 3, a and b. The N-terminal domain in each monomer is divided into two dynamic domains (1–72, 73–134). In the eight-site model with the minimal residual of 1.012 × 10⁴ (Table 1, n_ED = 18), the N-terminal domain is further divided into three dynamic domains (1–23, 24–75, 76–134) (Fig. 3, c and d). The essential dynamics of the six- and the eight-site models (arrows in Fig. 3, a and c) both represent the collective domain motions very well (arrows in Fig. 1 a), and more details are naturally preserved in the CG models with higher resolution and can reach a smaller residual (Table 1).

FIGURE 3.

(a) The symmetric ED-CG six-site model of the HIV-1 CA protein dimer. The six dynamic domains are (1–72) blue; (73–134) red; (135–220) green; (221–292) blue; (293–354) red; and (355–440) green. (b) The RMSF values of C_α atoms in the essential subspace (n_ED = 12). The six dynamic domains obtained by the ED-CG method are mapped onto the RMSF curve with colors corresponding to panel a, and the boundary atoms are labeled. (c) The symmetric ED-CG eight-site model of the HIV-1 CA protein dimer. The eight dynamic domains are (1–23) orange; (24–75) blue; (76–134) red; (135–220) green; (221–243) orange; (244–295) blue; (296–354) red; and (355–440) green. (d) The RMSF values of C_α atoms in the essential subspace (n_ED = 18). The eight dynamic domains obtained by the ED-CG method are mapped onto the RMSF curve with colors corresponding to panel c, and the boundary atoms are labeled. In each model, each CG site is the COM of its corresponding domain, and the arrows on the sites indicate the first PCA mode from the coarse-grained trajectory that was constructed from the atomistic MD trajectory.

In all the ED-CG models (four-, six-, and eight-site), the boundary atoms are all located in the hinge regions of the protein, in which the atoms are more rigid than those in other parts of the protein (Fig. 2 c and Fig. 3, b, and d). These hinge regions are natural boundaries between those independent dynamic domains. In summary, the ED-CG method applied to the HIV-1 CA dimer provides a systematic, quantitative way to design a CG model that reflects the functionally relevant, collective domain motions in the atomistic structure.

Coarse-grained models of ATP-bound G-actin

G-actin has 375 residues, and of particular interest is the DNase I-binding loop (DB loop, residues 40–48), which is believed to undergo a loop-helix transition upon hydrolysis of bound ATP (G-ATP) to ADP (G-ADP) (38). From the three independent trajectories of G-actin, similar ED-CG models were obtained (data not shown). Note that this will be the case for other systems to the extent that the essential PCA subspace (not just the first few modes) is converged. After determining that the ED subspace was converged, the final 15 ns of each trajectory were concatenated into a single 45-ns trajectory to improve statistics. The four-, seven-, and eight-site CG models were therefore built, respectively, by the ED-CG method.

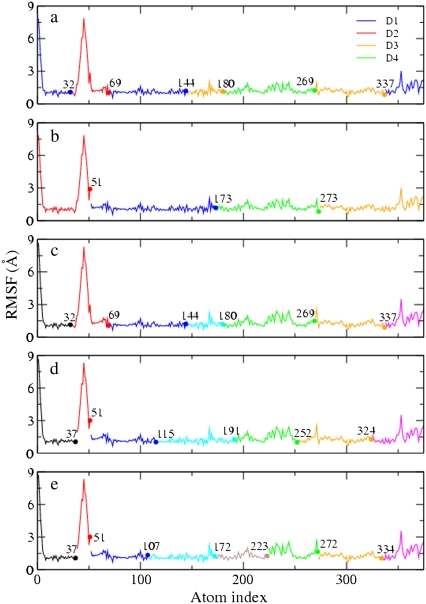
From casual observation, G-actin consists of two domains, each of which can be further subdivided into two subdomains. ADP or ATP binds in the cleft between the domains (40) (Fig. 4 a, G-ATP with no ATP molecule shown). These subdomains are termed D1 (1–32, 70–144, and 338–375; Fig. 5 a, blue), D2 (33–69; Fig. 5 a, red), D3 (145–180, and 270–337; Fig. 5 a, orange), and D4 (181–269; Fig. 5 a, green). Chu and Voth (13,14) developed a four-site CG model of G-actin, based on the work of Kabsch et al. (40), in which each CG site was located at the COM of a subdomain. This model is referred to as the intuitive four-site model in this article. This four-site model is based only on intuition obtained by visual inspection of the protein structure. It is however very useful, because it naturally allows one to study the propeller rotation and the opening/closing of the ATP cleft (38,41). This model was also successful in the CG analysis of the structural and mechanical properties of G-actin as determined by the conformation of the DB loop (13,14). As a result, it is interesting to compare the intuitive CG model to the ED-CG model for G-ATP.

FIGURE 4.

Different CG models of ATP-bound G-actin. (a) The intuitive four-site model: D1 (1–32, 70–144, 338–375), blue; D2 (33–69), red; D3 (145–180, 270–337), orange; and D4 (181–269), green. (b) The ED-CG four-site model: (1–51), red; (52–173), blue; (174–273), green; and (274–375), orange. (c) The intuitive seven-site model: (1–32), black; (33–69), red; (70–144), blue; (145–180), cyan; (181–269), green; (270–337), orange; and (338–375), magenta. (d) The ED-CG seven-site model: (1–37), black; (38–51), red; (52–115), blue; (116–191), cyan; (192–252), green; (253–324), orange; and (325–375), magenta. (e) The ED-CG eight-site model: (1–37), black; (38–51), red; (52–107), blue; (108–172), cyan; (173–223), ocher; (224–272), green; (273–334), orange; and (335–375), magenta. Each CG site is the COM of its corresponding dynamic domain.

FIGURE 5.

The CG models of ATP-bound G-actin mapped onto the RMSF curve of C_α atoms in the essential subspace. (a) The intuitive four-site model. The four subdomains (D1–D4) are labeled, which consist of seven contiguous domains. The colors of the domains correspond to Fig. 4 a. The number of essential PCA modes is n_ED = 6. (b) The ED-CG four-site model. The four dynamic domains are colored corresponding to Fig. 4 b. n_ED = 6. (c) The intuitive seven-site model. The seven domains, which are the same as those in the intuitive four-site model (a), are colored corresponding to Fig. 4 c. n_ED = 15. (d) The ED-CG seven-site model. The seven dynamic domains are colored corresponding to Fig. 4 d. n_ED = 15. (e) The ED-CG eight-site model. The eight dynamic domains are colored corresponding to Fig. 4 e. n_ED = 18. The boundary atoms are labeled in each CG model.

The four dynamic domains defined by the ED-CG method (Figs. 4 b and 5 b) are 1–51 (red), 52–173 (blue), 174–273 (green), and 274–375 (orange). There is one domain that is almost identical to that in the intuitive model (colored by green in Fig. 4, a and b), but the others differ because the domains are constrained to be sequentially contiguous in the ED-CG method. This is an advantage of the ED-CG model compared to other CG models with the same resolution, which will be discussed in the next section. Like the intuitive four-site model, the ED-CG four-site model can also describe the essential motion of the propeller rotation and the opening/closing of the ATP binding cleft based on the locations of the CG sites (Fig. 4 b). The residual of the intuitive model to approximate the motion of the first six essential modes is 7.128 × 10³, while the ED-CG model has a somewhat better minimal residual of 6.211 × 10³.

Seven-site models of G-ATP may also be of interest in the future because there are actually seven contiguous domains in the intuitive four-site model (13,14,40), which are used here to define an intuitive seven-site model (Figs. 4 c and 5 c). The residual of the intuitive seven-site model to approximate the motion of the first 15 essential modes is 2.448 × 10³, while the minimal residual of the ED-CG seven-site model (Figs. 4 d and 5 d) is 2.089 × 10³. In comparing the domain distributions for the two seven-site models, there are some similarities between them (Fig. 5, c and d). However, the DB loop (40–48) is separated into an additional domain in the ED-CG seven-site model (38–51; Figs. 4 d and 5 d, red). The DB loop is of importance in filament polymerization, and in determining the structure of a filament (13,14,41–43), and it has a dominant contribution to the protein dynamics according to the per-residue RMSF (Fig. 5 d). The identification of this region as a separate CG domain in the ED-CG model therefore illustrates the method's ability to identify key functional dynamics in the protein.

In the ED-CG eight-site model (Figs. 4 e and 5 e), the domains look quite similar to those in the ED-CG seven-site model (Figs. 4 d and 5 d), except that the green domain in the seven-site model is subdivided into two domains in the eight-site model (ocher and green).

These ED-CG results suggest that the four-site model may be the lowest resolution model of G-ATP that approximates the most essential dynamics of the protein, namely the propeller rotation and the opening/closing of the ATP cleft. More details can then be resolved by systematically adding more CG sites.

Comparison with the TRN-CG method

To our knowledge, there are relatively few systematic methods for assigning CG sites having a lower resolution than one-site per residue in a biomolecule. Arkhipov et al. (18,44,45) have developed a CG method to approximate the shapes of biomolecules by taking advantage of the topology-representing network (TRN) algorithm (17). This method (called TRN-CG here) was also applied to the CA dimer and G-ATP systems to compare the results with those obtained by the ED-CG method. In the TRN-CG framework, the atomistic mass distribution of the biomolecule is used as a target probability distribution for optimizing the CG map. A neural network algorithm (17) is used to optimize the positions of the CG sites. Once the CG sites are determined, an atomistic domain (i.e., a Voronoi cell) (46) is defined for each site. One domain consists of a set of atoms such that every atom in this set is closer to the corresponding site than to any other sites, and the mass of the CG site is the total mass of the Voronoi cell. In the TRN-CG method, positions of the CG sites are determined first, and then a corresponding domain is assigned for each site. By contrast, in ED-CG dynamic domains are first allocated, and then the COM of each domain is chosen as a CG site.

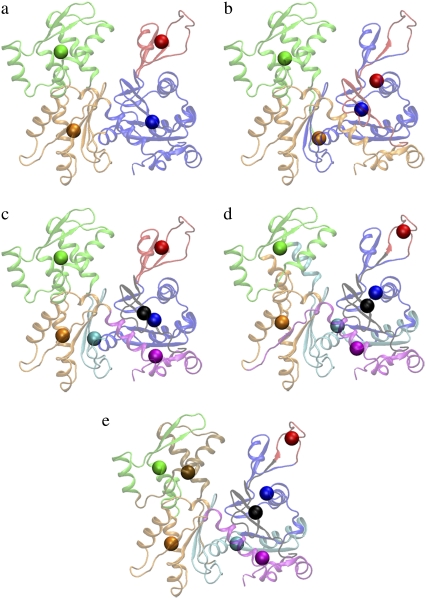
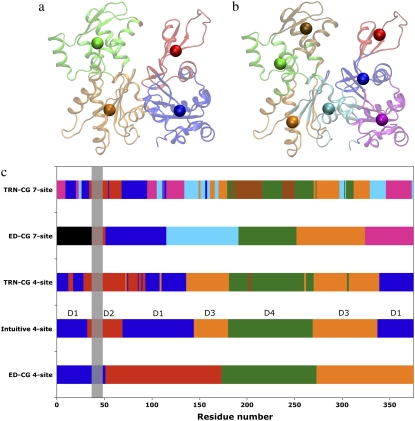
To compare with the symmetric ED-CG models of the CA dimer, the TRN-CG method was applied to each monomer in the CA dimer separately to also enforce symmetry in the TRN-CG models. The TRN-CG four-site model (Fig. 6 a) is similar to the ED-CG four-site model (Fig. 2 b), but the linking α-helix is completely assigned into the N-terminal domain in each monomer. This model also looks reasonable by chemical intuition. If two more sites are added (the TRN-CG six-site model, Fig. 6 b), the N-terminal domain in each monomer is subdivided into two domains as in the ED-CG six-site model (Fig. 3 a). However, the two subdomains are not sequentially contiguous in the TRN-CG model. In the TRN-CG eight-site model (Fig. 6 c), the C-terminal domain is subdivided into two subdomains in each monomer, which is by contrast still kept as a whole domain in the ED-CG eight-site model (Fig. 3 c). The TRN-CG results, which are based on the mass distribution, are therefore significantly different from those obtained by the ED-CG method. If one applies the ED-CG residual calculation (Eq. 5) to the TRN-CG models, the residuals of the four, six, and eight-site models are 7.949 × 10⁴, 1.691 × 10⁴, and 1.120 × 10⁴, respectively, compared to the ED-CG values of 7.274 × 10⁴, 1.861 × 10⁴, and 1.012 × 10⁴ (Table 1), respectively. These results indicate that while the TRN-CG models may approximate the mass distribution of the biomolecule it does not preserve dynamic domains as well as the ED-CG models except for the six-site model. The TRN-CG six-site model gives a smaller residual because the sites are not constrained to be contiguous in sequence.

FIGURE 6.

The TRN-CG models of the HIV-1 CA protein dimer. (a) The four-site model, (b) the six-site model, and (c) the eight-site model. In the TRN-CG method, a CG site is placed first, and then a domain is determined that contains a set of atoms such that every atom in this set is closer to the corresponding site than to any other site.

The TRN-CG four-site model of G-ATP (Fig. 7 a) is very similar to the intuitive four-site model (Fig. 4 a), except that the TRN-CG model is not as contiguous in the primary protein sequence (Fig. 7 c), and in fact begins to mix it. The partition of the four subdomains based on chemical intuition is in reasonable agreement with the mass distribution in the protein. The TRN-CG four-site model has a residual (Eq. 5) of 6.956 × 10³, which is higher than the minimum of the ED-CG model (6.211 × 10³) but smaller than that of the intuitive model (7.128 × 10³). The TRN-CG seven-site model of G-ATP (Fig. 7 b), which significantly scrambles the protein sequence (Fig. 7 c), is very different from both the ED-CG (Fig. 4 d) and the intuitive model (Fig. 4 c), and its residual (2.457 × 10³) is larger than both the ED-CG (2.089 × 10³) and the intuitive model (2.448 × 10³).

FIGURE 7.

The TRN-CG models of ATP-bound G-actin. (a) The four-site model, (b) the seven-site model, and (c) the allocation of domains in the different CG models. The x axis is the residue number of the protein, and the y axis represents the different CG models. The four subdomains (D1–D4) used in the literature (13,14) are indicated in the intuitive four-site model. The dynamic domains in the ED-CG models are colored corresponding to Fig. 4. The DB-loop region (residues 40–48) is marked with a vertical gray box.

As expected, the TRN-CG method captures the mass distribution better than the ED-CG method while the ED-CG method better represents the dynamic domains of the protein. However, the TRN-CG models do have reasonably small residuals, indicating that they approximate collective dynamics fairly well. A possible explanation is that the atoms in a compact domain defined by the TRN-CG method may also move in a well-correlated fashion similar to those in a dynamic domain defined by the ED-CG method. In the latter, the dynamic domains are assumed to be contiguous in protein sequence to simplify the numerical search algorithm, but this is not required in principle. On the other hand, if the protein undergoes large conformational changes, such as protein folding/unfolding, the CG model built from the TRN-CG method cannot likely describe such a process since it has significantly mixed the primary protein sequence in its CG mapping. The ED-CG mapping, by contrast, preserves the underlying primary sequence and can allow large conformational changes without needing to alter the CG representation.

The TRN-CG method does not require any knowledge of a dynamic trajectory, i.e., one can apply it from a single structure without performing any MD simulation. By contrast, ED-CG analysis is performed based on a PCA of MD trajectories.

CONCLUSIONS

A novel and systematic method (ED-CG) for building CG maps of complex biomolecules has been presented. A CG map defines a representation of an atomistic structure with reduced dimension. PCA is one such statistical approach that can be used for dimensionality reduction, which is used to extract essential dynamics from a MD trajectory to describe the motion in terms of a small number of collective degrees of freedom (the essential subspace). In the ED-CG method, a specified number of N dynamic domains are allocated to reflect the motion of the first n_ED PCA modes (in this article, n_ED = 3N – 6 is usually used), and a CG site is placed at the COM of each dynamic domain. Applications of ED-CG to two biologically important systems, the HIV-1 CA protein dimer and ATP-bound G-actin, produce effective CG models that preserve large-scale functional motions in these proteins. The essential dynamics of the four (Fig. 2 b), six (Fig. 3 a), and eight-site models (Fig. 3 c) of the CA dimer all nicely represent the essential collective domain motions of the protein (Fig. 1 a). The atoms in each dynamic domain move in a highly correlated fashion, and the boundary atoms are located in the hinge regions of the protein (Fig. 2 c and Fig. 3, b and d). The ED-CG four-site model of ATP-bound G-actin (the coarsest one, Fig. 4 b) is able to reflect two of the most essential modes of the protein, the propeller rotation and the opening/closing of the ATP binding cleft as does the intuitive four-site model (Fig. 4 a). More detail is obtained by adding more CG sites. In both the seven (Figs. 4 d and 5 d) and eight-site (Figs. 4 e and 5 e) ED-CG models, the DB loop (red domain) that is believed to play a critical role in actin filament polymerization, is identified as its own CG site.

The main focus of this article is how to systematically define a given number of CG sites when the CG resolution is coarser than the scale of individual amino acids. The resolution of the CG system is to be chosen according to the properties of the biological system to be investigated. For example, if one is only interested in the ATP binding of G-actin, the four-site model may be good enough. However, if one wants to investigate the role of the DB-loop in more detail, the seven or eight-site model would be necessary. In the ED-CG method, one can predetermine the number of PCA modes to be preserved in the resulting CG model (for example, the modes that contribute 90% of the total fluctuations), and then build the CG model with the corresponding number of sites.

When using the ED-CG method, it should be considered to what extent the PCA modes have converged (47). The length of simulation needed for convergence naturally depends on the system, and therefore ought to be checked carefully. However, it is worth emphasizing that the essential subspace often converges very well if enough modes are included (48). In this article, the number of PCA modes used to build an ED-CG model with N CG sites is 3N – 6. A stable essential subspace and therefore a robust ED-CG model is obtained when N is large enough. In the case of G-ATP, the ED-CG models with seven and eight CG sites from the three independent simulations are quite similar, which indicates the stability of the ED-CG method. It should be noted that the ED-CG methodology could instead use normal modes or modes from a higher resolution ENM as the basis for the coarse-graining.

The complementary TRN-CG method (17,18) is based on the mass distribution of a single protein configuration, while the ED-CG method presented here is based on the fluctuations of an ensemble of configurations in the MD trajectory. The dynamic domains allocated by the ED-CG algorithm are also defined to be contiguous in primary sequence, which is in contrast with the domains obtained by the TRN-CG method, the latter being spatially contiguous. In particular, two groups of atoms that are close in space but far apart in sequence would not be assigned to a same domain in the ED-CG method, while this is allowed in the TRN-CG approach. Although such a spatially contiguous domain may better reproduce the shape (mass distribution) of the protein, the limitation is that conformational change between the two groups of atoms (e.g., folding/unfolding) is not allowed. The sequentially contiguous domains obtained by the ED-CG method can in principle overcome this limitation because such two groups of atoms are allocated to the different domains while their interactions are still retained in the ED-CG model. Which CG model to choose will depend on the properties to be addressed. The ED-CG method is particularly useful when one wants to build a CG model that preserves the essential large amplitude protein motions in the CG simulations.

The work presented here demonstrates an efficient and systematic methodology to define CG sites in complicated biological systems. Unlike the ENM that usually places sites at C_α atoms, the ED-CG method is most suitable to identify relatively few CG sites in a large biomolecule while still capturing many of the biologically important low-frequency modes. However, the work presented in this article has not addressed the CG dynamics generated by the CG Hamiltonian in a CG simulation. Future research will therefore focus on the construction of proper force fields for the ED-CG models, and then perform CG simulations to investigate the CG dynamics. One possible advantage of the ED-CG method is that the interactions between CG sites can be parameterized ab initio without assuming harmonic motion as in the ENM, which may allow the modeling of large-scale anharmonic conformational motion in CG protein simulations.