Molecular Dynamics Simulation and Coarse-Grained Analysis of the Arp2/3 Complex

Abstract

A molecular dynamics investigation and coarse-grained analysis of inactivated actin-related protein (Arp) 2/3 complex is presented. It was found that the nucleotide binding site within Arp3 remained in a closed position with bound ATP or ADP, but opened when simulation with no nucleotide was performed. In contrast, simulation of the isolated Arp3 subunit with bound ATP, showed a fast opening of the nucleotide binding cleft. A homology model for the missing subdomains 1 and 2 of Arp2 was constructed, and it was also found that the Arp2 binding cleft remained closed with bound nucleotide. Within the nucleotide binding cleft a distinct opening and closing period of 10 ns was observed in many of the simulations of Arp2/3 as well as isolated Arp3. Substitution studies were employed, and several alanine substitutions were found to induce a partial opening of the ATP binding cleft in Arp3 and Arp2, whereas only a single substitution was found to induce opening of the ADP binding cleft. It was also found that the nucleotide type did not cause a substantial change on interfacial contacts between Arp3 and the ArpC2, ArpC3 and ArpC4 subunits. Nucleotide-free Arp3 had generally less stable contacts, but the overall contact architecture was constant. Finally, nucleotide-dependent coarse-grained models for Arp3 are developed that serve to further highlight the structural differences induced in Arp3 by nucleotide hydrolysis.

INTRODUCTION

The actin-related protein (Arp) 2/3 complex is a key component of the dendritic network of actin filaments that drives cell motility. Since its discovery in the mid-1990s the Arp2/3 complex has been the subject of considerable research as researchers have sought to unravel its structure and function (1). Similar to actin, Arp2/3 is highly conserved and found abundantly in nature (2). The major function of the Arp2/3 complex is to serve in the leading edge of motile cells as a nucleation site for new actin filaments as well as an anchor point between existing filaments, i.e., the so-called mother filaments (3). Arp2/3 is therefore an important component of the cytoskeletal machinery.

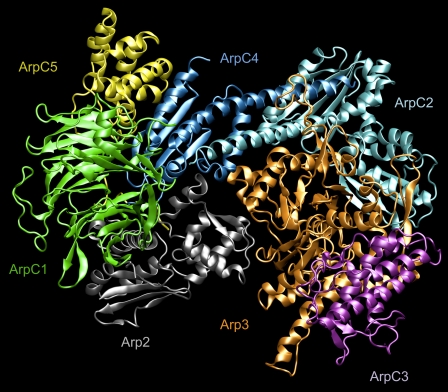
As shown in Fig. 1, Arp2/3 consists of seven different protein subunits. The nomenclature adopted here is the standard nomenclature recommended in the literature (2,4). At the core of the complex are two subunits that are members of the actin family of proteins: Arp2 and Arp3. The remaining five subunits have a standard naming scheme, ArpCx, where x is a number from 1–5 that refers to one of the remaining Arp2/3 subunits. The function of these five units is less understood compared to Arp2 and Arp3, however their primary role is to assist in binding Arp2/3 to mother filaments (2), and possibly to assist in the binding of cofactors that trigger activation or nucleation (5). During filament nucleation and growth the function of the two actin-like subunits, Arp2 and Arp3, is reasonably well understood. Arp2 and Arp3 form the first two monomers in the helical F-actin daughter filament (6). However, the native state of Arp2/3 is an inactivated state in which filament nucleation cannot occur. Large- scale rearrangement of Arp2 via a motion on the order of 30 Å (4) must first occur before Arp2 and Arp3 can fit into the correct pitch and rise of the F-actin helix.

FIGURE 1.

Molecular representation of the entire Arp2/3 complex with bound ATP in the Arp2 and Arp3 subunits. The subunits are labeled in the figure using standard coloring and notation. Figure created using VMD (27).

The exact process of activation of Arp2/3 is still unknown. The process is complex, and there are a host of cofactors involved. Owing to their similarity with G-actin, Arp2 and Arp3 both possess a nucleotide binding cleft. A recent study highlighted the nucleotide hydrolysis cycle within Arp3 (7). Bound ATP is required for Arp2/3 activation as well as for nucleation of filaments (8). However, ATP alone is not sufficient for activation or nucleation. Although a wide range of important cofactors have been identified (8,9), the complete mechanism for activation and branch formation is still unknown. To date there are also no published high-resolution crystal structures of activated Arp2/3, and the majority of published structures of inactivated Arp2/3 feature different bound nucleotides.

Molecular dynamics (MD) has been employed for studying the G-actin monomer as well as the isolated Arp3 subunit. The first reported MD study of G-actin (10) investigated water diffusion mechanisms important for ATP hydrolysis. Later, MD simulations of G-actin, the actin trimer, and the entire F-actin repeat were performed in our group to study the possible biochemical differences between the ATP and ADP bound states of G- and F-actin (11). Recently the effect of nucleotide and nucleotide exchange in G-actin was studied on the 50 ns timescale (12), and a recent MD study investigated nucleotide effects in various Arp3-only and G-actin proteins for simulation times up to 8 ns (13). Despite these contributions there remain a number of key unanswered questions about the influence of the Arp3-bound nucleotide within the entire Arp2/3 complex.

In addition to all-atom MD simulations of actin and actin-related proteins, coarse-grained (CG) models have also been developed. CG models are essential for exploring length and time scales that are beyond the reach of traditional MD simulations (14,15). Moreover, much of biology possesses an inherent multiscale character with large-scale motions or conformational changes often being driven by atomic-level processes (15). Recent examples of CG modeling in the cytoskeleton include a multiscale CG description of the F-actin filament capable of predicting fundamental biophysical properties of actin (16) as well as CG models of spectrin (17,18). As a complex of seven different proteins, Arp2/3 has both local dynamics at the level of each of its individual subunits and a collective dynamics in which the different subunits interact at longer length and timescales. This multiscale character of Arp2/3 inherently suggests that a CG approach will be important to systematically uncover collective motions among the different subunits in the complex.

Herein molecular-level simulations of the entire Arp2/3 complex are presented along with CG analysis of Arp3. The focus of this work is an investigation of the effect of the presence and the type of the Arp3-bound nucleotide on the dynamics of the entire complex. Owing to the size and complexity of Arp2/3 we have also utilized coarse-grained modeling to help understand larger-scale dynamics within the Arp3 subunit as well as to compare with previous CG models of G-actin.

All-atom MD calculations were performed on three different Arp2/3 systems, differing only in the state of the nucleotide bound to Arp2 and Arp3. ATP-bound, ADP-bound, and nucleotide free systems were investigated. For each system, three different trajectories of 16 ns were performed, and one trajectory of each type was continued to a simulation time of 30 ns. Including an additional 15 ns devoted to studying Arp2/3 substitutions and 40 ns for studying a homology model of Arp2 and corresponding substitutions, over 250 ns of trajectories for Arp2/3 were used in this study. Additionally, for comparison purposes the isolated Arp3 complex with bound ATP was simulated for a single 30 ns trajectory.

METHODS

Molecular dynamics simulations

Recently published (7) crystal structures for Arp2/3 with bound ATP/Mg²⁺ and ADP/Ca²⁺ and no nucleotide (Protein Data Bank (PDB) entries 2P9S, 2P9P, and 2P9L) were used for the MD simulations. Within the Arp2/3 complex ATP/ADP is found in a well-defined binding site in both the Arp3 and Arp2 subunits. In all crystal structures of Arp2/3, approximately half of the residues are not resolved in the Arp2 subunit. The available structure of the Arp2 subunit constitutes a contiguous sequence of ∼200 residues. A short trial simulation of the isolated 200-residue sequence of Arp2 was performed to check for stability. The isolated Arp2 fragment was found to be stable, and therefore it was retained in the simulations of Arp2/3 to provide a more realistic environment for Arp3. The Arp2 fragment was found to be quite stable in the simulation of the entire Arp2/3 complex. It is also noted that the Arp2 fragment contains the exposed nucleotide-binding site as well as the positions of the bound ATP/ADP molecules. Since the Arp2-bound nucleotide did not release from the fragment during any simulations, it also was included in the simulation environment. The protein was placed in a box of explicit TIP3P (19) water molecules with a minimum distance of 15 Å between the protein and the border of the periodic boundary conditions. Arp2/3 has a nonuniform charge distribution, therefore counter-ions (KCl) were placed using the SOLVATE program (20). The approximate system size for each of the Arp2/3 simulations was 275,000 atoms. The system size of the isolated Arp3 system was ∼85,000 atoms.

All MD calculations were performed using NAMD (21). The CHARM22 (22) force field was used in conjunction with the particle mesh Ewald sum method (23) for calculating electrostatic interactions. All intramolecular hydrogen bonds were constrained using the SHAKE (24) algorithm allowing for an integration timestep of 2 fs. After heating the system to 310 K, a 50 ps pre-equilibrium was performed in the canonical (NVT) ensemble through use of velocity rescaling. After this procedure, the simulations were continued in the isothermal-isobaric ensemble (310 K, 1.01325 bar) through the use of Langevin dynamics and the Langevin piston method via its implementation in NAMD (25,26). The damping coefficient used for Langevin dynamics was 0.5 ps⁻¹ and the Langevin piston was controlled using a piston period and decay of 2 ps. The simulations were further equilibrated for 2.5 ns after which three independent trajectories were initiated. Each of the three trajectories was then continued for 16 ns with one trajectory of each type continued for an additional 14 ns. Analysis of MD calculations was performed using visual molecular dynamics (VMD) (27). Unless otherwise noted, results reported from MD simulations are based on the last 10 ns of each of the three independent trajectories.

Contact map analysis

The Arp2/3 complex is connected by an extensive series of interprotein contacts. Interprotein contact mapping was used to investigate whether the state of the bound Arp3 nucleotide affected the subunit-subunit contacts within the Arp2/3 complex. After the example of Bonomi et al. (28), C_α–C_α contact maps for two proteins A and B that share a common interface were developed as N_A × N_B matrices, where N_A and N_B represent the number of interfacial C_α atoms in each protein subunit. Each matrix element M_ij is a function of the distance between the bond distance between the C_α atoms of residues A_i and B_j:

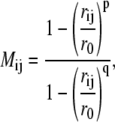(1)

where r_ij is the bond distance in Å, r_o = 8.5 Å, p = 10, and q = 12. Thus, each element in the contact map is a function that varies smoothly between 0, i.e., no contact and 1, i.e., strong contact. The initial set of residues A_i and B_j were chosen as those within 12 Å of the adjacent protein within the crystal structure. To compare among different nucleotide states, a total of nine contact maps were developed for 1), Arp3–ArpC2; 2), Arp3–ArpC3; and 3), Arp3–ArpC4 with Arp3 in the ATP, ADP, and nucleotide-free states. Finally, the average value and fluctuation of each point on each contact map were computed from the 30 ns MD trajectories described above.

Coarse-grained modeling

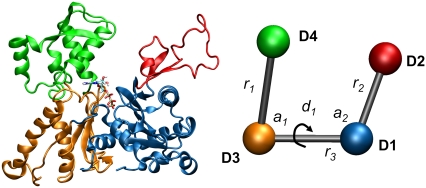
The CG model used in this work is inspired by the four domain model of the G-actin monomer defined by Holmes et al. (29) and subsequently employed by Chu and Voth (11,16) in their CG analysis. Such an approach is quite reasonable given the similarities between Arp3 and G-actin both in structure and amino acid sequence. Additionally, since Arp3 fits into the branched daughter filament, it is logical to model the CG properties of Arp3 in the same fashion as G-actin. The 4-site canonical CG model is important primarily because it gives a direct connection between the equilibrium fluctuations of the protein and larger-scale collective motions of the intrinsic geometric domains of the protein. For the case of Arp3, the domains D1–D4 in the CG model were assigned in terms of amino acid primary sequence as D1: 1–32, 77–160, 370–420, D2: 32–76, D3: 161–195, 291–369, D4: 196–290. We note for clarity that the CG model in actuality consists of seven unique segments of the amino acid sequence that are grouped together into four CG sites based on geometric proximity. As depicted in Fig. 2, the model is a U-shaped propeller that has the capability to reveal global motions in Arp3 as defined by the three effective CG bonds, two angles and single dihedral. The topology of the U-shaped model contains six geometric parameters, which completely specify the 3N-6 required parameters. Although the domain model defined by Holmes et al. is a powerful tool for understanding the G-actin monomer and other proteins in the actin family, its utility does not readily extend to the entire Arp2/3 system. The other subunits in the Arp2/3 complex do not natively suggest a coarse-graining strategy other than an “ultra-coarse” model for Arp2/3 made up of seven sites, one for each protein subunit. Furthermore, the CG-mapping of the G-actin and Arp3 structures is inspired solely via consideration of the static protein structure. Future work from our group will seek to more systematically define the CG sites for the entire Arp2/3 complex.

FIGURE 2.

Molecular and coarse-grained representations of Arp3. The molecular representation is colored to display the CG mapping, and the CG sites are labeled and correspond to the four sites described in the methods section. There are six effective CG geometric parameters labeled in the figure: three bonds, two angles, and one dihedral. Figure created using VMD (27).

RESULTS

MD simulations

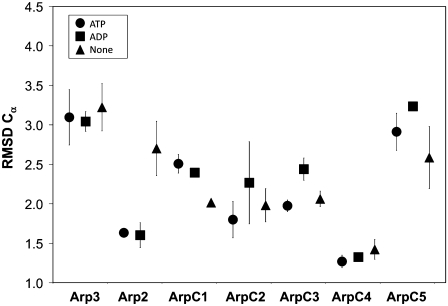
The stability was examined by calculating the root mean-square deviation (RMSD) of C_α atoms. After the convention of Chu and Voth (11), the RMSD was calculated by using the x-ray structure as a reference frame. This is in contrast to Zheng et al. (12) who used the average structure for alignment in their calculation of RMSD. Since Arp2/3 consists of seven subunits that are held together via intermolecular forces, the RMSD of each subunit was calculated using a separate alignment for each subunit, rather than an overall alignment for the entire complex. The individual subunits of Arp2/3 are not chemically bonded to each other, and therefore it was expected that each subunit would exhibit its own equilibrium structure that differed from the x-ray structure. The average RMSD for each subunit is given in Fig. 3 with error bars calculated using the last 10 ns of the three different trajectories described in the Methods section. As seen in Fig. 3 the individual subunits within Arp2/3 are stable. Overall there is no dominant trend observed that links the RMSD and the type or presence of the nucleotide. This does not appear to be the case for the Arp2 fragment in which the nucleotide-free simulation has a noticeably higher RMSD. The increased RMSD in the nucleotide-free Arp2 fragment was attributed to the fact that there are no stabilizing contacts between ATP/ADP and the protein fragment as in the other cases. Recalculating the RMSD for the nucleotide-free Arp2 fragment and omitting the residues that were found to be in contact with ATP or ADP reduced the overall RMSD to 1.8 Å. Finally, the system was checked for equilibration by verifying that the RMSD and total kinetic energy were stabilized.

FIGURE 3.

Effect of bound nucleotide on the overall RMSD of Arp2/3. The error bars are shown as the RMSD for each subunit as a function of nucleotide state. If no error bars are shown, then the variation in RMSD is smaller than the symbol.

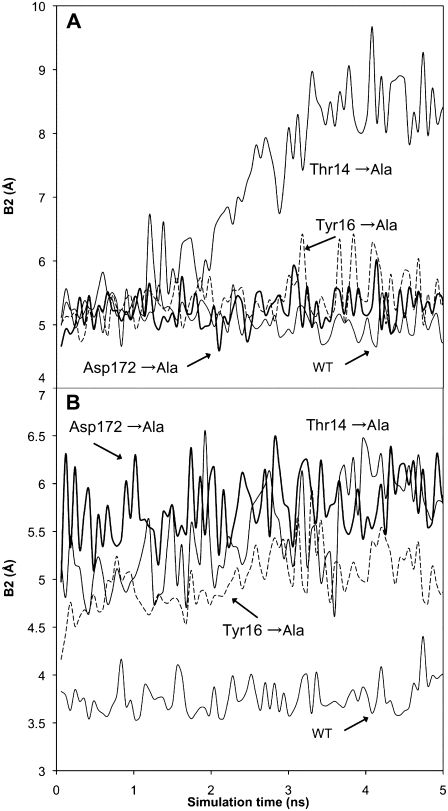
Previously reported MD studies of G-actin (11–13) and the Arp3 subunit (13) have devoted considerable attention to the role of the bound nucleotide on the overall dynamics and biochemical properties of the actin family of proteins. In this study MD simulations of the entire Arp2/3 complex were performed that add further insight into the role of nucleotide. For the purpose of comparison with other studies the opening and closing of the nucleotide binding cleft was characterized using a distance, “B2”, defined as the distance between the C_α atoms of Gly-15 and Asp-172. Additionally, one 30 ns simulation of the isolated Arp3 subunit with bound ATP (taken from the 2P9S PDB entry) was performed so that the relationship between the other Arp2/3 subunits and Arp3 could be directly studied. The nucleotide opening and closing for all four 30 ns trajectories is shown in Fig. 4 A.

FIGURE 4.

Opening of the nucleotide binding cleft of the Arp3 subunit as a function of the bound nucleotide. Each line in A represents the results of a simulation of Arp2/3 with bound ATP (blue), ADP (red), or nucleotide free (green), additionally shown is a simulation of the isolated Arp3 complex with bound ATP (black). B gives a detailed view of the behavior of ADP-bound Arp2/3. The degree of opening and closing is measured by the Gly-15 – Asp-172 C_α distance (B2).

In the case of nucleotide-free Arp2/3 (PDB entry 2P9L) the experimental value of B2 is 7.1 Å and was characterized as being an open structure (7). During simulation the value of B2 had a value of 10.0 ± 0.5 Å further demonstrating the necessity of bound nucleotide for stability of actin-like proteins. For the system with bound ADP, the experimental value of B2 is 6.2 Å, which was characterized as being intermediate between the open and closed states. During simulation of ADP-bound Arp2/3 the value of B2 was 5.3 ± 0.1 Å, which is in reasonable agreement with the experimental value. The value of B2 remained stable for all three trajectories as well. The closed-cleft system with bound ATP had a value of 4.1 ± 0.4 Å, which is also in reasonable agreement with the experimental value of 5.6 Å. It is noted that the experimental measurements of the width of the nucleotide binding cleft are obtained from high-resolution crystal structures, whereas the values from simulation are based on the simulation of the protein in the full solvent environment. It is interesting to see that these simulations with bound nucleotide adopted significantly lower values of B2 compared to those reported by Dalhaimer et al. (13) for Arp3-only. This is likely due to the influence of the four other subunits in this simulation that are in close proximity to Arp3 within the entire complex. To test this hypothesis a 30 ns simulation of just the Arp3 subunit with bound ATP was performed. The average value for B2 during this simulation was 10.2 Å, demonstrating that the surrounding Arp2/3 subunits do exert substantial influence on the average structure and dynamics of Arp3. As stated in the introduction, it has been previously shown that the state of the bound nucleotide in G-actin has been connected to the dynamics of the DNase binding loop region (residues 40–48 in G-actin). It is therefore feasible that the analogous region in Arp3 (residues 38–60) could play a role in the observed stability of the nucleotide binding cleft. This was confirmed when it was found that during simulation of nucleotide-free Arp2/3 this “DNase loop-like” region had an overall RMSD of ∼5 Å, whereas the RMSD of the ATP-bound region was 2.5 Å. This may suggest that Arp3 with bound nucleotide may be stabilized by contacts between the ArpC2 and the “DNase loop-like” region. It is noted that the results provided here are based on the last 10 ns for each of the three separate simulations for each Arp2/3 system (nine simulations total).

During the 30 ns simulation of ATP-bound Arp2/3, nucleotide-free Arp2/3, and the ATP-bound Arp3 subunit several long-timescale opening and closing events were observed as seen in Fig. 4. For the case of ATP-bound Arp2/3, the nucleotide binding cleft changed from ∼4 to 6 Å two times with a period of 10 ns. The nucleotide-free Arp2/3 system also opens and closes with a period of 10 ns, but the average value of B2 continued to increase for the entire 30 ns simulation. This trend was also observed in the Arp3 only system. In contrast, the ADP-bound system was observed to have a much smaller fluctuation. As shown in Fig. 4 B, the distance B2 for the nucleotide binding cleft in ADP-bound Arp3 also was observed to fluctuate periodically but with substantially smaller amplitude. This commonality between all of these systems suggests that the Arp3 subunit possesses an inherent dynamics on the 10 ns timescale that is related to the opening and closing of the nucleotide binding cleft. Finally, we note that the Arp3-bound nucleotide was found to be very stable during the simulations of the Arp2/3 complex. The RMSD of the nucleotide was found to be 1.6 ± 0.02 Å and 1.7 ± 0.05 Å for the ATP and ADP complexes, respectively. In contrast, the RMSD of ATP was 2.4 Å for the simulation of Arp3 only.

Mutation studies

Among the analyses presented in the previous section, it is particularly surprising that the Arp2/3 complex with bound ADP in the Arp3 subunit was found to have the most stable nucleotide binding cleft. It is noted that in this work ADP inside of the Arp3 binding cleft was not found in the unusual bent position as previously described (7) and found in PDB entries 1U2V and 2P9N. The simulations in this work confirmed the experimental finding that ADP-bound Arp2/3 has a wider (compared to ATP-bound) nucleotide binding cleft; however, it was not previously known that the ADP-bound state was more stable. To investigate the origin of this stability the local environment in the Arp3 nucleotide binding cleft was investigated for all three types of Arp2/3 studied. Fig. 5 gives a representative structure of the ADP-bound state at a simulation time of 16 ns is shown. Close inspection of the binding site and comparison with the ATP-bound state reveals that the origin of the observed increased stability originates from two strong nonbonded interactions with residue Thr-14. Strong interactions are formed both with the terminal (β) PO₃ group of bound ADP and across the nucleotide binding cleft to residue Gly-173. In bound ATP the Thr-14 – Gly-173 interaction is substantially weakened because of the interposition of the gamma PO₃ group between the two residues. Additionally, it was observed that the aromatic ring in Tyr-16 (shown in Fig. 5) was very stable for the entire simulation of the ADP-bound Arp2/3 complex. In contrast, for the ATP and nucleotide free states, the dihedral angle for the bond connecting the ring to the peptide backbone (C_β–C_γ bond) fluctuated between two stable states. Finally, because of its close proximity to the nucleotide Asp-172 was also proposed to be important to the opening and closing of the nucleotide binding cleft.

FIGURE 5.

View of the nucleotide binding site of Arp3 with bound ADP taken at a simulation time of 16 ns. The bound ADP molecule and several key residues (labeled in the figure) are shown with licorice representation. Nonbonded interactions discussed in the text are labeled with a black dashed line. Figure created using VMD (27).

With three target residues identified (Thr-14, Tyr-16, and Asp-172), separate alanine point mutations (substitutions) were performed for each residue and three separate ADP-bound Arp2/3 complexes were generated. Each system was simulated for a further 5 ns, and the stability of the nucleotide binding cleft as measured by the distance “B2” was calculated. The results for the substitution studies are given in Fig. 6 A. The D172A substitution had almost no effect on either the average value of the cleft width or the stability. The Y16A substitution increased the variability in the cleft width but overall did not result in a substantially wider nucleotide binding cleft. In contrast, the T14A point substitution had a strong effect on both the fluctuation and average value of the cleft width. These results support the hypothesis stated above regarding the origin of the stability of the ADP-bound Arp2/3 complex and also provide targets for future experimental studies. This view is also consistent with previous work that used substitutions to disrupt ATP binding to Arp2 and Arp3 (30). Since the Arp3 bound nucleotide is not known to hydrolyze during formation of daughter filaments (7), we also performed the same set of point substitutions and simulations with Arp2/3 with bound ATP. As shown in Fig. 6 B, the point substitutions do affect the stability of the nucleotide binding cleft in ATP-Arp3. In contrast to the ADP-bound state, all three of the point substitutions investigated caused a partial opening of the binding cleft.

FIGURE 6.

Opening and closing of the nucleotide binding cleft in Arp3 with bound ADP (A) and bound ATP (B). The behavior of the wild-type and the three point substitutions is shown. Opening and closing is characterized using the bond B2 as described in Fig. 4. All results are taken from simulations of the full Arp2/3 complex.

Incorporation of a homology model for Arp2 subdomains 1 and 2

The analyses described thus far were based on MD simulations of the Arp2/3 complex that was missing subdomains 1 and 2 from the Arp2 subunit. As a means of verification, and additionally to further study the Arp2 subunit, a homology model of the missing residues was developed. The resolved subdomains (3 and 4) of Arp2 bear a strong structural similarity to subdomains 3 and 4 of G-actin. Thus, the model was developed by overlaying G-actin with the resolved residues of Arp2, and grafting subdomains 1 and 2 of G-actin onto subdomains 3 and 4 of Arp2. Using the correct amino acid sequence for Arp2, a constrained MD simulation was performed of only the Arp2 subunit with explicit water to allow the sidechains to relax. The backbone of protein was fixed with harmonic constraints to its starting position with a spring constant of 10 kcal/mol/Ų for 2 ns. After this, an additional 5 ns simulation was performed with no constraints on the protein. The RMSD for the homology model (compared to the starting structure) was ∼3 Å. The final structure from the 5 ns simulation was then used as the starting point for further simulations of the Arp2/3 complex. Using the complete Arp2/3 complex, simulations of 5 ns were performed with bound ATP and ADP. Additionally, point substitutions inspired by the Arp3 substitutions listed above were studied. Six additional 5 ns simulations (three point simulations with both ATP and ADP) were performed.

During the 5 ns simulations of Arp2/3 with the homology model, the nucleotide binding cleft in Arp3 remained in a closed position. Within the Arp3 subunit, the value of B2 was found to be 4.1 Å and 5.3 Å for bound ATP and bound ADP, respectively. These values are in agreement with the values found when simulating only subdomains 3 and 4 of Arp2, indicating that the presence of subdomains 1 and 2 does not appreciably alter the dynamics of the nucleotide binding cleft of Arp3. The nucleotide binding cleft in the Arp2 homology model was characterized by defining the bond B2 between the C_α atoms of Gly-24 and Asp-161. For the ATP and ADP states of Arp2, the value B2 was found to be 5.8 Å and 5.9 Å, respectively. By comparison with Arp3, this constitutes a closed position for Arp2 for both nucleotide states.

Finally, the Arp2 homology model was used to study a similar set of point substitutions used in Arp3 above. Three substitutions in Arp2: S25A, B26A, and D161A were selected as these residues were found in similar proximity to the phosphate groups in bound ATP and ADP when Arp3 and Arp2 were aligned based on their bound nucleotide. For each point substitution a 5 ns simulation was performed. The affect of the point substitution was characterized using the value B2 for both Arp3 and Arp2, and the results are given in Table 1. Overall, the effect of the point substitutions on the nucleotide binding cleft is very similar to that observed in Arp3. The S25A (Arp2) and T14A (Arp3) substitutions were the only substitutions to cause the nucleotide binding cleft to open with bound ADP. For bound ATP, all three point substitutions altered the binding cleft sufficiently to cause it to at least partially open. It is also interesting to see that the Arp2 point substitutions did not affect the nucleotide binding cleft of Arp3. It is possible, however, that 5 ns of simulation time is not sufficient to propagate any affects between adjacent protein subunits.

TABLE 1.

Point substitution studies within the Arp2 subunit

	ADP-bound		ATP-bound
	Arp3	Arp2	Arp3	Arp2
S25A (Å)	5.9	5.3	4.9	8.0
B26A (Å)	5.9	8.4	5.1	8.1
D161A (Å)	5.7	5.6	5.1	7.5

The distance B2 in Arp3 is defined in the text, and B2 within Arp2 is defined as the Gly-24–Asp-161 C_α distance. Each value is the average from a single 5 ns simulation.

Analysis of interfacial contacts

The seven protein subunits in the Arp2/3 complex are held together through an extensive network of interfacial protein-protein contacts. At the center of the complex lies the Arp3 subunit that forms contacts with the Arp2, ArpC2, ArpC3, and ArpC4 subunits. Furthermore, Arp3 plays a key role in the Arp2/3 branch junction. It is the first subunit in the branched actin daughter filament, and it also forms contacts with the actin mother filament. During activation of the Arp2/3 complex, Arp3 also undergoes a minor rotation and movement to fit correctly into the structure of the actin daughter filament (5). Given the centrality of Arp3 within the entire Arp2/3 complex, it is logical to investigate the interfacial bonding topology between Arp3 and its neighbors.

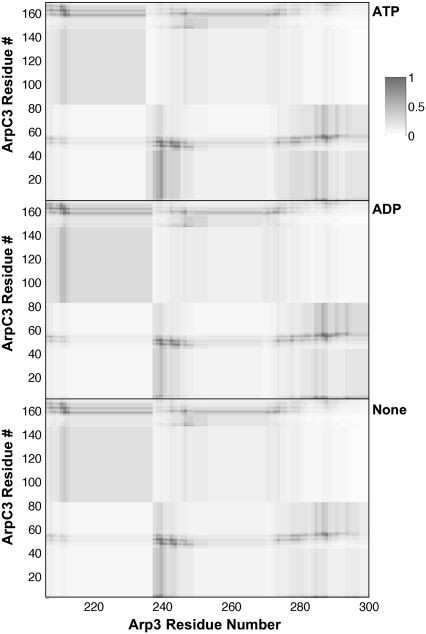
Using the 30 ns trajectories for the three types of Arp2/3 complex, intersubunit contact maps were developed for Arp3-ArpC2, Arp3-ArpC3, and Arp3-ArpC4 subunits. Figs. 7–9 show the interfacial contact maps. Each contact map has three sections corresponding to the state of the Arp3 bound nucleotide. Each contact map shows the strength of interaction, as defined by Eq. 1, for a pair of C_α atoms near the three interfaces under consideration. Darker regions denote strong contacts, whereas lighter regions have little or no contact.

FIGURE 7.

Protein-protein contact maps for the interface between Arp3 and the ArpC2 subunits. The residue number of the primary amino acid sequence is labeled on each axis of the contact map, and one contact map is shown for each nucleotide state. The sidebar shows the correspondence between the degree of shading and the amount of contact, as defined by Eq.1.

FIGURE 8.

Protein-protein contact maps for the interface between Arp3 and the ArpC3 subunits (see Fig. 7 legend for detailed description).

FIGURE 9.

Protein-protein contact maps for the interface between Arp3 and the ArpC4 subunits (see Fig. 7 for detailed description).

A consistent feature among all three interfaces is the similarity of the interfacial contacts regardless of the state of the Arp3 bound nucleotide. However, although the average contact maps are similar for all three interfaces, the fluctuation in the contact map was found to be dependent on the nucleotide state. For regions with many contacts, nucleotide-free Arp3 was found to have a higher overall fluctuation in the contact map. This is consistent with the view that the bound nucleotide stabilizes the entire Arp3 subunit. As seen in the figures, the ArpC2-Arp3 interfaces is the most extended, and overall has the largest number of strong contacts. ArpC3-Arp3 has the next most number of contacts, whereas the ArpC4-Arp3 interface is limited to a small region of both proteins.

Given the importance of Arp3 in the structure and function of the branch junction, these contact maps provide a helpful reference point for future work. The regions of strong contact provide targets for directed study using point substitutions to study the properties and dynamics of the interfaces. Furthermore, during activation of Arp2/3 several structural rearrangements take place. The similarity in the contact maps for all interfaces as a function of nucleotide suggests that neither the presence of bound nucleotide or ATP hydrolysis are sufficient for initiating these changes on the timescale of the simulations in this work. Moreover, it is known that other so-called nucleation promotion factors (NPFs) assist in activation of Arp2/3 (4).

CG analysis of the Arp3 subunit

The three different Arp2/3 complexes investigated in this study differ primarily by the presence and type of bound nucleotide within the Arp3 subunit. As discussed in the Methods section, a structure-based CG model inspired by the 4-domain model of Holmes was developed. Given the long-timescale opening and closing motions that were discussed in the last section, the single 30 ns trajectories were used for all CG modeling. For the three Arp2/3 simulations and also the Arp3-only simulation the equilibrium values of the six geometric properties that define the Arp3 CG model were calculated. Fig. 2 shows an example of the CG model, and the geometric parameters are tabulated in Table 2. It is noted that the parameters are obtained by first calculating the average center-of-mass positions of the four CG sites from the MD results, and subsequently calculating the equilibrium bonds, angles and dihedral. The data in the table are geometric parameters only and not based on any CG dynamics. The main difference in the properties of the three models is in the angle defined in Fig. 2 as a₂. The angle is smallest in the ADP-bound state and is markedly larger in the nucleotide-free and Arp3-only simulations. Additionally the angle a₁ is also significantly larger in the ATP-bound Arp3 only simulation. These results provide a picture of the state of Arp3 as a function of the presence and type of nucleotide. The CG model parameters also support the conclusion that Arp3 alone adopts a much more open conformation when it is simulated.

TABLE 2.

Arp3 CG model parameters

	ATP-bound	ADP-bound	nucleotide free	Arp3 only
r1 (Å)	27.1 ± 0.3	25.9 ± 0.2	27.5 ± 0.3	23.9 ± 0.3
r2 (Å)	27.3 ± 0.3	27.2 ± 0.2	27.8 ± 0.3	27.9 ± 0.3
r3 (Å)	28.3 ± 0.4	29.1 ± 0.3	29.0 ± 0.3	28.5 ± 0.3
a1 (deg.)	82.4 ± 1.2	80.1 ± 0.9	81.1 ± 1.9	86.2 ± 1.1
a2 (deg.)	109.6 ± 1.9	103.9 ± 1.7	116.0 ± 1.9	112.4 ± 2.1
d1 (deg.)	145.3 ± 3.8	136.6 ± 1.8	136.1 ± 3.2	133.0 ± 2.5

The data from MD are calculated using the single 30 ns trajectories described in the text. The error bars are obtained from the fluctuation of the parameter during the long trajectory. The definition of the CG model parameters is depicted in Fig. 2.

Arp3 is often compared to the G-actin monomer because of their commonalities in sequence and structure (13,31). Based on our previous CG studies of G-actin and F-actin (11), it is interesting to compare the CG model of Arp3 with that of G-actin. In both the G-actin (ATP and ADP bound) and F-actin (ADP bound only) systems the angle a2 was found to be greater than the a₁ angle, although to a lesser extent. All of the CG angles (a₁ and a₂) in G-actin and F-actin adopt a value ranging between 91° and 96°. This is significantly different than those observed in Arp3. Moreover, the dihedral angle, d₁, was found to have a greater variance depending on the type of bound nucleotide, ranging from ∼133° to 145°. In contrast, the value in actin ranges from 153° to 157°. These data help to highlight large- scale differences between the Arp3 and actin systems.

The CG analysis of the Arp3 subunit may also help to further our understanding of the role of the nucleotide in the structure and function of Arp2/3. It is known from experiment that Arp2/3 with bound ATP is required for the initiation of branched actin filaments (8) and also that ATP hydrolysis in Arp2/3 promotes dissociation of branched filaments (32,33). Furthermore, ATP-bound Arp2/3 is able to preferentially bind NPFs (34). On the timescale of the MD simulations in this work, the nucleotide state has a pronounced affect on the overall shape and dynamics of Arp3—as evidenced by the coarse-grained analysis. It is therefore conceivable that such changes in shape influence both the ability of Arp2/3 to nucleate new filaments as well as affect the ability of NPFs to dock. Future work based on the point substitutions outlined above would help to further elucidate the nucleotide-dependent properties of Arp2/3.

DISCUSSION

This work has presented the first all-atom MD calculations of the Arp2/3 complex. The effect of type and presence of bound nucleotide to the Arp3 subunit was explored in inactive Arp2/3 via the simulations. Nucleotide effects within the Arp2 subunit were also explored using a homology model for the missing subdomains 1 and 2 of Arp2. Additionally, simulations employing alanine point substitutions were performed to investigate the origin of nucleotide-induced stability within Arp3 and Arp2. The results from the MD calculations and subsequent CG analysis allow us to consider several key questions related to the structure and function of Arp2/3, as stated below.

How does the state of the Arp2 or Arp3-bound nucleotide affect the dynamics of the Arp2/3 complex?

During simulation of ATP or ADP bound Arp3 within the entire Arp2/3 complex, the nucleotide binding cleft remained in a generally closed position for 30 ns and did not open during repeated trials of 16 ns. However, while still remaining in the closed position, the ATP bound system exhibited a persistent fluctuation with a period of ∼10 ns. In addition, the nucleotide-free Arp2/3 simulation as well as the ATP-bound Arp3-only simulation was found to open and adopt a conformation relatively far from their x-ray crystal structures. However, these two structures were also found to exhibit an opening and closing with a period of ∼10 ns. This apparent intrinsic motion could be important for structure and function of the actin branch junction, given that Arp3 forms contacts both with the actin mother filament (via the DNase binding loop region) and also with one or more G-actin monomers in the daughter filament.

It has been previously hypothesized that ATP and ADP-bound Arp2/3 structures would be found to have subtle differences in their conformations, and that these differences would underlie the mode by which ATP hydrolysis regulates Arp2/3 structure and function (34). The studies of the nucleotide binding cleft, in particular demonstrating that ADP-bound Arp3 is markedly more stable and that this stability can be significantly altered via a single point substitution, seem to support this hypothesis and point to a specific origin of these conformational differences.

Finally, the dynamics of the Arp2 subunit were studied using a homology model for subdomains 1 and 2, which are currently unresolved in all x-ray crystal structures. Many similarities between Arp3 and Arp2 were found. First, the nucleotide binding cleft in both subunits remained in a closed position for both the ATP and ADP bound states. Second, for the ADP-bound state, only a single point substitution was found that caused the nucleotide binding site to open. Finally, the three point substitutions tested for the bound ATP states were all found to cause a partial opening of the nucleotide binding cleft.

How are the dynamics of Arp3 affected by the other Arp2/3 subunits?

This question has been addressed in this work by comparing the behavior of ATP-bound Arp3 within the Arp2/3 complex to ATP-bound Arp3 simulated by itself for a time of 30 ns. A key conclusion is that the opening of the nucleotide binding cleft that is observed in simulation of isolated Arp3 in only a few ns was not observed in simulations of the entire Arp2/3 complex. This suggests that the ArpC2, ArpC3, and ArpC4 subunits influence these opening and closing modes. Conversely, there were no major differences observed in Arp3 when Arp2/3 was simulated with only the Arp2 fragment found in the crystal structure or with a homology model for subdomains 1 and 2 of Arp2. The shape of the Arp3 subunit, determined in large part by these opening and closing modes, is important to the formation of actin branch filaments. It was previously determined that Arp3 forms the first subunit of an actin daughter filament (5); however, the results presented here indicate that the neighboring Arp2/3 subunits may play a role in branch formation or stability due to their role in regulating Arp3 shape. We have also shown using coarse-grained analysis that ATP-bound isolated Arp3 and the Arp3 subunit within the entire Arp2/3 complex exhibit distinct features. Namely, ATP-Arp3 within the full Arp2/3 complex adopts a much more compact shape compared to free ATP-Arp3 as evidenced by the CG parameters identified in Table 2.

Does the state of the Arp3 bound nucleotide cause changes in the interfacial contacts with other Arp2/3 subunits?

An intersubunit contact mapping procedure was used to obtain a global view of the network of contacts between Arp3 and its neighbors within the Arp2/3 complex. Contact maps showing the average degree of contact among the interfacial residues were developed for Arp3 and its neighbors ArpC2, ArpC3, and ArpC4. Regions of strong contact with Arp3 were identified, and the contact maps could be used as a basis for targeted studies in the future. Overall it was found that on the 30 ns timescale the contact network is not substantially altered by ATP hydrolysis or release of the bound nucleotide. These results may therefore suggest that the bound nucleotide within Arp3 does not act as a trigger to initiate intersubunit movements during Arp2/3 activation, e.g., rotation of the ArpC3 subunit. The work presented in this article supports the point of view that ATP hydrolysis and release alter Arp3 dynamics without imposing dynamical changes on the adjacent ArpCx subunits, although longer timescale conformational changes beyond the timescale of the MD simulations cannot be ruled out given the link between conformational changes in Arp2/3 and nucleotide presence (34).

This study provides the basis for a more detailed understanding of the nucleotide-dependent structure and dynamics of the important Arp2/3 protein complex. Future work will focus on the development of more advanced CG models for this system, as well as the development of a multiscale model for the Arp2/3-actin branch junction.